注:本文包含 AI 辅助创作
- 参考链接:
Paper Summary
- 整体理解:
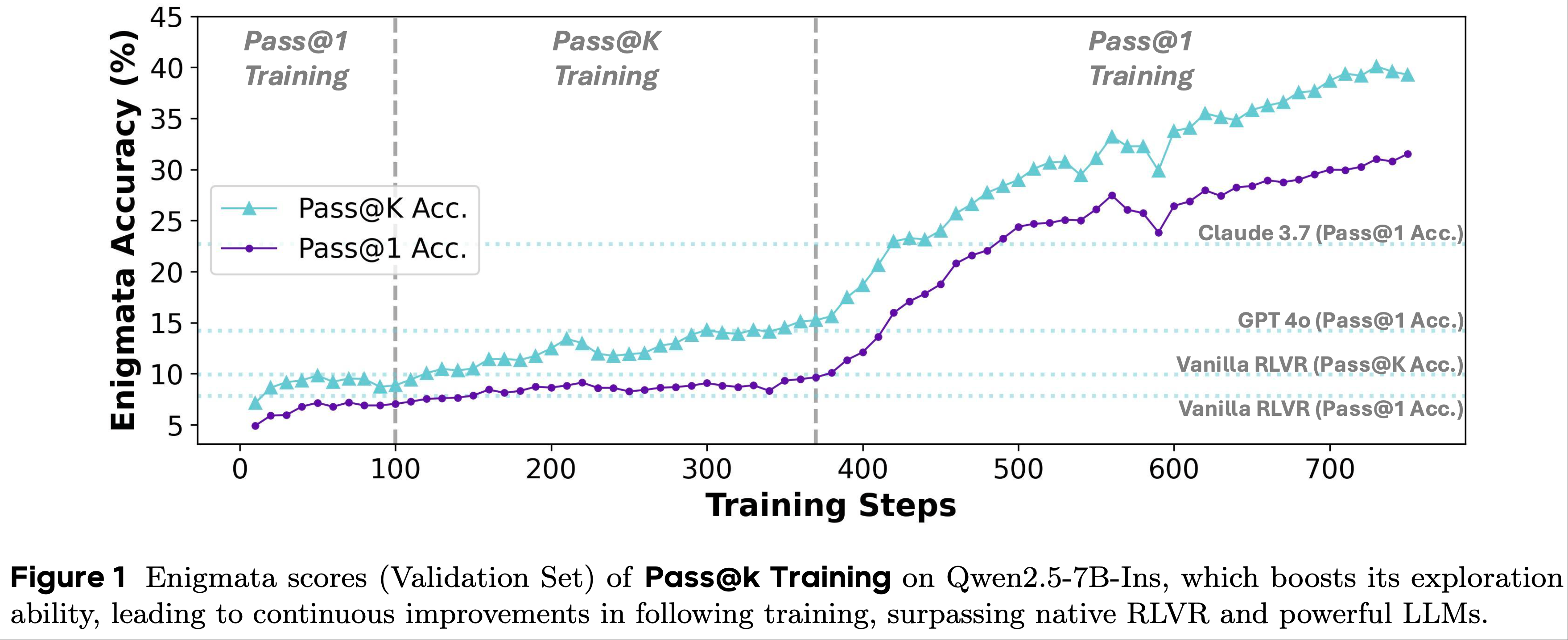
- 论文在 RLVR 框架内提出了 Pass@k Training 方法:实现大语言模型探索和利用能力的相互提升,从而突破其整体性能的极限
- 论文证明了使用 Pass@k 作为奖励可以有效增强模型探索多样化输出的能力,进而提高其利用能力
- 为了提高训练效率和有效性,论文引入了 bootstrap 采样机制和优势函数的解析推导,以优化 Pass@k Training 过程
- 为了更好地理解 Pass@k Training 的内在机制,论文从不同方面提出了五个研究问题,以解答 Pass@k Training 为何有效以及能带来哪些益处
- 检查优势值曲线,论文初步确定了促成 Pass@k Training 成功的两个关键因素 ,即:
- 绝对优势之和 \(\eta\) 的 argmax
- 绝对优势之和 \(\eta\) 的趋势(trend)
- 背景和问题:RLVR 通常采用 Pass@1 作为奖励,在平衡探索(exploration)和利用(exploitation)方面面临挑战,导致策略倾向于保守行为,收敛到局部最优
- Pass@k 在之前的工作中已被用于评估,但它与 RLVR 中 LLM 探索能力的关联在很大程度上被忽视了
- 论文使用 Pass@k 作为奖励来训练策略模型(即 Pass@k Training ),并观察到其探索能力的提升
- 论文还推导了 Pass@k Training 优势的解析解,形成了一个高效且有效的流程
- 作者通过分析得到以下发现:
- 探索和利用并非本质上相互冲突的目标,反而可以相互促进
- 带有解析推导的 Pass@k Training 本质上涉及直接设计优势函数
- 受此启发,论文初步探索了 RLVR 的优势设计,展示了良好的结果,并指出了一个潜在的未来方向
- 思考:论文的重点是公式 14 和 公式 15,这种给与负样本一定的奖励的方式究竟和普通的 RLVR 有何区别,还需要深思
Introduction and Discussion
- RLVR 用于解决复杂推理任务,并显著提升大型语言模型 LLM 的推理能力(2024)
- 在 RLVR 训练过程中,LLM 基于给定的提示生成各种响应,并根据响应获得奖励(2024)
- LLM 从结果级(outcome-level)监督中学习,能够生成更全面的推理过程(2025),从而在下游任务上取得更好的性能
- 大型推理模型(large reasoning models, LRMs,如 OpenAI o1(2024)和 DeepSeek R1(2025))的成功,表明 RLVR 训练突破了 LLM 的能力极限
- 当前 RLVR 训练通常优化 Pass@1 目标,也称为 ** Pass@1 Training**
- LLM 从自身探索中学习,并为给定提示生成最自信的响应(2025),这带来了探索与利用平衡的重大挑战(2025)
- 通常,探索指的是执行新颖且多样的行为(2024),而利用则要求 LLM 调用验证器在已知行为中偏好的可靠行为(2024)
- 在 Pass@1 Training 过程中,LLM 倾向于模仿在先前尝试中能提高奖励分数的行为 ,并避免获得低奖励的行为(2024, 2025)
- 但在结果监督(这是流行的 Pass@1 Training 设置(2025))中,答案正确但推理错误的解会获得正奖励 ,而推理正确但答案错误的解会被赋予负奖励(2024, 2025)
- 在这种情况下,包含正确思路的不成功探索往往不会获得奖励,代价很高,导致利用与探索失衡(2025),可能使策略放弃探索并收敛到局部最优(2021)
- 受强化学习方法(如 PPO 和 GRPO)下奖励的次优性质限制(2013, 2024, 2025),LLM 面临进一步学习的挑战,限制了 RLVR 流程的有效性和提升潜力
- 为了缓解 Pass@1 Training 中 LLM 探索能力受损的问题,论文提出一种以优化为中心的方法,对错误响应有更高的容忍度 ,因为这些响应可能包含有用的思路或推理行为 ,防止模型陷入局部最优 ,从而扩展其能力上限 ,使其逐渐接近全局最优
- Pass@k 已被用于评估策略是否能在 k 次尝试内生成正确响应,这是评估 LLM 能力边界的常用指标(2024)
- 与 Pass@1 指标相比,Pass@k 指标允许策略生成多个错误响应
- 论文考虑是否可以在 RLVR 过程中利用 Pass@k 指标来突破 LLM 的能力边界
- 在 Pass@k 评估中,为了最大化 k 个样本中至少有一个成功的概率,“聪明的(smart)” 的策略会生成 k 个彼此不同且覆盖解空间不同区域的候选解 ,而不是 k 个高度相似的样本
- 更强的探索能力使模型能够获得更全面的知识和更强的鲁棒性
- 理解:为了提升 Pass@k 指标的分数,聪明的策略应该是生成差异较大的多个解,而不是很相似的,这样才能最大化分数(广撒网,总能捞到鱼)
- 论文利用 Pass@k 指标作为奖励,持续训练一个已经过 Pass@1 Training 的模型(称为 Pass@k Training )
- 论文发现,通过这种方法训练的模型在测试集上能获得更高的 Pass@k 分数,同时保持其 Pass@1 分数
- Pass@k Training 的朴素实现存在几个关键问题,论文进一步采用 bootstrap 采样(2004, 2006)和解析推导来优化训练过程,实现了高效且有效的 Pass@k Training(第 2 节)
- 为了进一步理解 Pass@k Training 的特征和内在机制,论文提出了五个研究问题,以探究 Pass@k Training 在 RLVR 训练过程中如何平衡 LLM 的探索和利用能力
- 论文还观察到 Pass@k 阻止了策略分布熵的自然下降,熵也是指示策略探索能力的关键指标(2025)(第 3 节)
- 从隐式奖励设计的角度,论文分析了 Pass@k Training 有效性的关键因素,并探索了其优化的几种可能途径(第 4 节)
- 总体而言,论文工作的主要收获可以总结如下:
- 与 Pass@1 Training 相比,Pass@k Training 显著增强了 LLM 的探索能力,在提高 Pass@k 性能的同时不损害 Pass@1 分数
- 在其三个渐进式变体中,bootstrap 采样比全采样具有更高的训练效率,而解析推导作为其理论渐近形式,减轻了采样引入的方差(第 2 节)
- 与 Pass@1 Training 及其变体相比,Pass@k Training 对 k 的不同取值具有鲁棒性,并且在不同领域和任务中具有可推广性
- LLM 探索能力的增强有助于通过持续训练提高其利用能力,使 7B 规模的 LLM 超越强大的 LLM(如 GPT-4o 和 Claude-3.7),凸显了 Pass@k Training 的实用价值(第 3 节)
- 带有解析推导的 Pass@k Training 直接设计优势函数,可被视为一种隐式奖励设计形式
- 实证实验表明,隐式奖励设计允许更精细的优化控制,例如专注于更难的问题或提高训练效率,而无需复杂的理论推导,这使其成为未来 RLVR 发展的一个有前景的方向(第 4 节)
- 与 Pass@1 Training 相比,Pass@k Training 显著增强了 LLM 的探索能力,在提高 Pass@k 性能的同时不损害 Pass@1 分数
Pass@k as Reward in RLVR Training
- 本节的内容如下,
- 首先阐述推理任务的公式化表达,回顾传统的 Pass@1 Training (第 2.1 节)
- 介绍如何在 RLVR 训练过程中使用 Pass@k 作为奖励(第 2.2 节),然后提出两种渐进式增强方法来提高训练效率和有效性(第 2 节和第 2.4 节)
- 论文在图 2 中展示了概述,并在附录 C 中提供了伪代码,展示 Pass@k Training 的实现细节
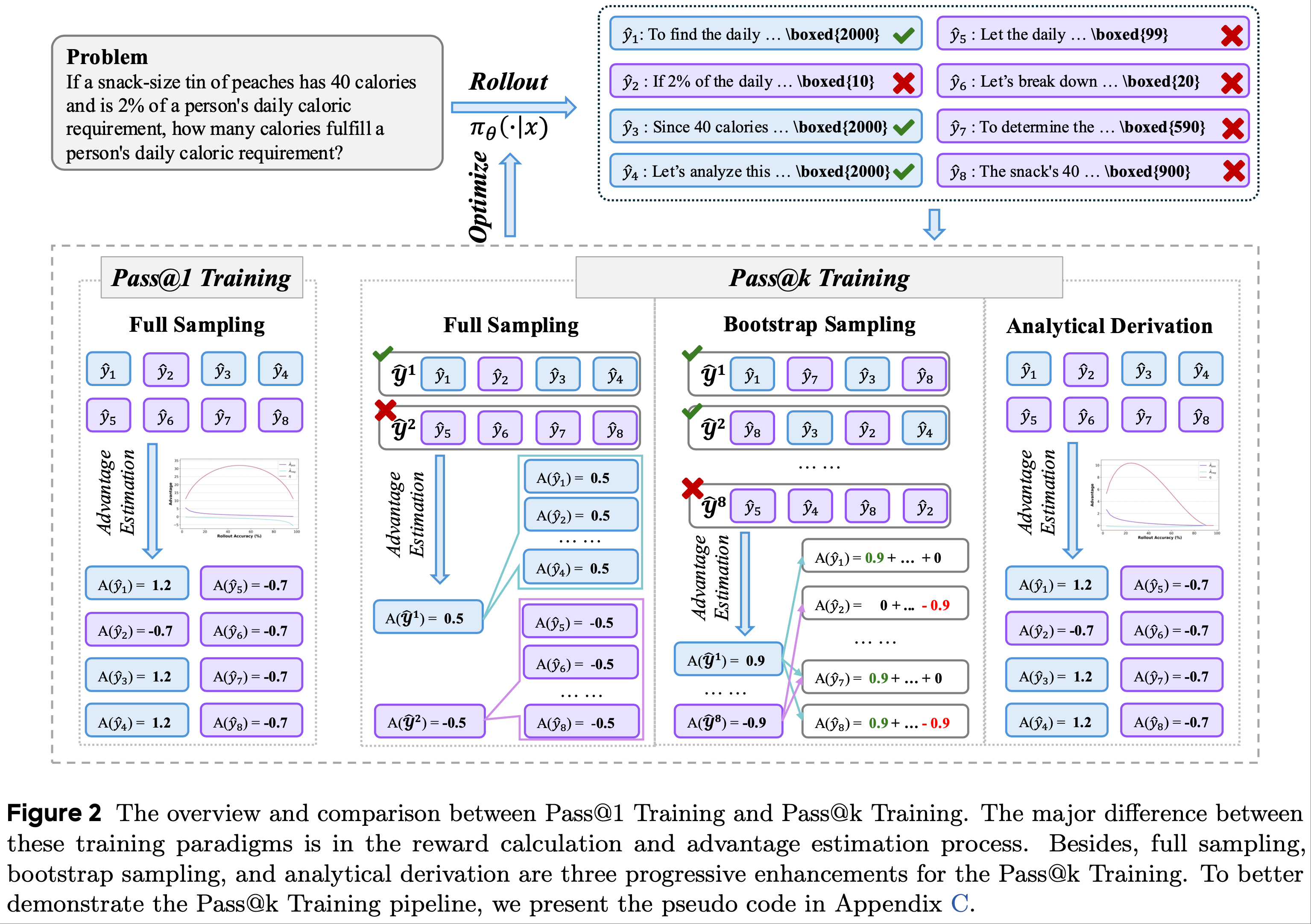
Formulation of Reasoning Tasks and Pass@1 Training
- 复杂推理任务可以评估 LLM 的推理和逻辑能力
- 一般来说:
- 来自数据集 \(D\) 的一个问题包含描述 \(x\) 和真实答案 \(y\)
- 策略 \(\pi_{\theta}\)(即具有参数 \(\theta\) 的 LLM)需要基于 \(x\) 生成响应
$$\hat{y}=\{t_{1}, t_{2}, …, t_{l}\}$$- 其中 \(t_{i}\) 和 \(l\) 分别指第 \(i\) 个 Token 和响应 \(\hat{y}\) 的长度
- 在获得生成的响应 \(\hat{y}\) 后,验证器用于验证 LLM 响应的正确性,并提供奖励
$$ R(y, \hat{y}) \in \{R_\text{neg}, R_\text{pos}\}$$- \(R_\text{neg} < R_\text{pos}\)
- \(R_\text{neg}\) 用于负响应
- \(R_\text{pos}\) 用于正响应
- 为了简化符号,论文用 \(R\) 表示 \(R(y, \hat{y})\)
- 在论文的实验中,论文采用 \(R_\text{neg}=0\) 且 \(R_\text{pos}=1\)
- 基于上述推理任务的公式化表达,在 Pass@1 Training 过程中(例如,GRPO(2024)),优势通过同一组内响应奖励的平均值和标准差来估计,如下所示:
$$\overline{R}=\frac{1}{N_\text{rollout } } \sum_{i=1}^{N_\text{rollout } } R_{i}, \\
\sigma=\frac{1}{N_\text{rollout } } \sqrt{\sum_{i=1}^{N_\text{rollout } }\left(R_{i}-\overline{R}\right)^{2} }, \\
\hat{A}_{i, 1}=\hat{A}_{i, 2}=\cdots=\hat{A}_{i,\left|\hat{y}_{i}\right|}=\frac{R_{i}-\overline{R} }{\sigma},$$- \(N_\text{rollout}\) 表示对应问题的 rollout 响应数量
- \(R_{i}\) 和 \(\hat{y}_{i}\) 分别指第 \(i\) 个响应的奖励和生成的响应
- 获得优势值后,GRPO 利用以下方程计算目标函数 \(T(\theta)\),该函数用于执行梯度下降并优化模型参数:
$$\mathcal{J}(\theta)=\mathbb{E}_{(q, a) \sim D,\left\{o_{i}\right\}_{i=1}^{G} \sim \pi_{\theta}(\cdot | q)}\left[\frac{1}{G} \sum_{i=1}^{G} \frac{1}{\left|\hat{y}_{i}\right|} \sum_{t=1}^{\left|\hat{y}_{i}\right|}\left(min \left(r_{i, t} \hat{A}_{i, t}, clip\left(r_{i, t}, 1-\varepsilon, 1+\varepsilon\right) \hat{A}_{i, t}\right)-\beta D_{kL}\right)\right] .$$ - 由于在 GRPO 中每个 Token 共享相同的优势值,论文在后续讨论中将不再区分 Token 级别,而是用 \(\hat{A}_{i}\) 表示第 \(i\) 个响应的优势值
- 为了提高 RLVR 训练过程的有效性和效率,论文在后续实验中采用了 GRPO 的一个变体(即 DAPO(2025)),仅保留 clip-higher 和 Token 级策略梯度损失
Pass@k Training
- 论文考虑是否可以采用 Pass@k 指标作为奖励来突破 LLM 的能力边界(因为 Pass@k 可以反映 LLM 的探索能力)
- 下面先介绍 Pass@k 指标的定义,在将 Pass@k 指标纳入 RLVR 的奖励函数中
- Pass@k 指标的定义(Definition of Pass@k Metric) :
- 给定问题 \(x\),策略模型通过特定的解码策略或搜索算法(例如,基于采样的解码策略或蒙特卡洛树搜索)rollout \(k\) 个响应
- 第 \(i\) 个采样响应 \(\hat{y}_{i}\) 将获得由验证器提供的奖励 \(R_{i}\)
- Pass@k 指标的值定义为从 \(k\) 个采样响应中获得的预期最大奖励。形式上,Pass@k 指标可以通过以下方程计算:
$$Pass @ k=\mathbb{E}_{(x, y) \sim D,\left\{\hat{y}_{i}\right\}_{i=1}^{k} \sim \pi_{\theta}(\cdot | x)}\left[max \left(R_{1}, …, R_{k}\right)\right] .$$
- Pass@k 实现:全采样(Pass@k Implementation: Full Sampling) :
- 为了将 Pass@k 指标集成到 RLVR 过程中,论文通过全采样机制提出一种基本实现
- 首先利用策略 \(\pi_{\theta}\) 为给定问题 rollout \(N_\text{rollout}\) 个响应
$$ \hat{\mathcal{Y}}=\{\hat{y}_{1}, …, \hat{y}_{N_\text{rollout} }\} $$- 在这种情况下,这些响应被分成 \(N^\text{group}=\left\lfloor\frac{N_\text{rollout} }{k}\right\rfloor\) 个组,多余的响应被丢弃
- 问题:这里有毒吧,生成时刻意生成整数倍的 rollout 就好了,为什么要生成了然后又丢掉?
- 其中第 \(j\) 个组包含 \(k\) 个响应
$$ \hat{\mathcal{Y}}^{j}=\{\hat{y}_{k \times(j-1)+1}, …, \hat{y}_{k \times(j-1)+k}\} $$
- 在这种情况下,这些响应被分成 \(N^\text{group}=\left\lfloor\frac{N_\text{rollout} }{k}\right\rfloor\) 个组,多余的响应被丢弃
- 然后论文根据每个组的 Pass@k 值为其分配奖励分数:
- 验证器将为每个响应提供奖励,组奖励通过该组内响应的奖励的最大值计算
- 遵循 DAPO 算法中的优势估计方法,可以计算第 \(j\) 个组的优势值 \(\hat{A}^{j}\)
- 论文将组优势分配给该组包含的响应 ,即
$$ \hat{A}_{k \times(j-1)+1}=\cdots=\hat{A}_{k \times(j-1)+k}=\hat{A}^{j}$$- 问题:这种分组是随机的,得到的结果真的置信吗?是否仅仅是增加熵损失或者随机对 rollout 结果进行 SFT 也能拿到收益?
- 回答:也不是完全随机,绝对正确的样本始终能拿到正向的奖励
- 问题:这种分组是随机的,得到的结果真的置信吗?是否仅仅是增加熵损失或者随机对 rollout 结果进行 SFT 也能拿到收益?
- 最后,我们可以利用采样的响应及其优势值来优化模型参数
- 实证见解:提高探索能力(Empirical Insight: Improving Exploration) :
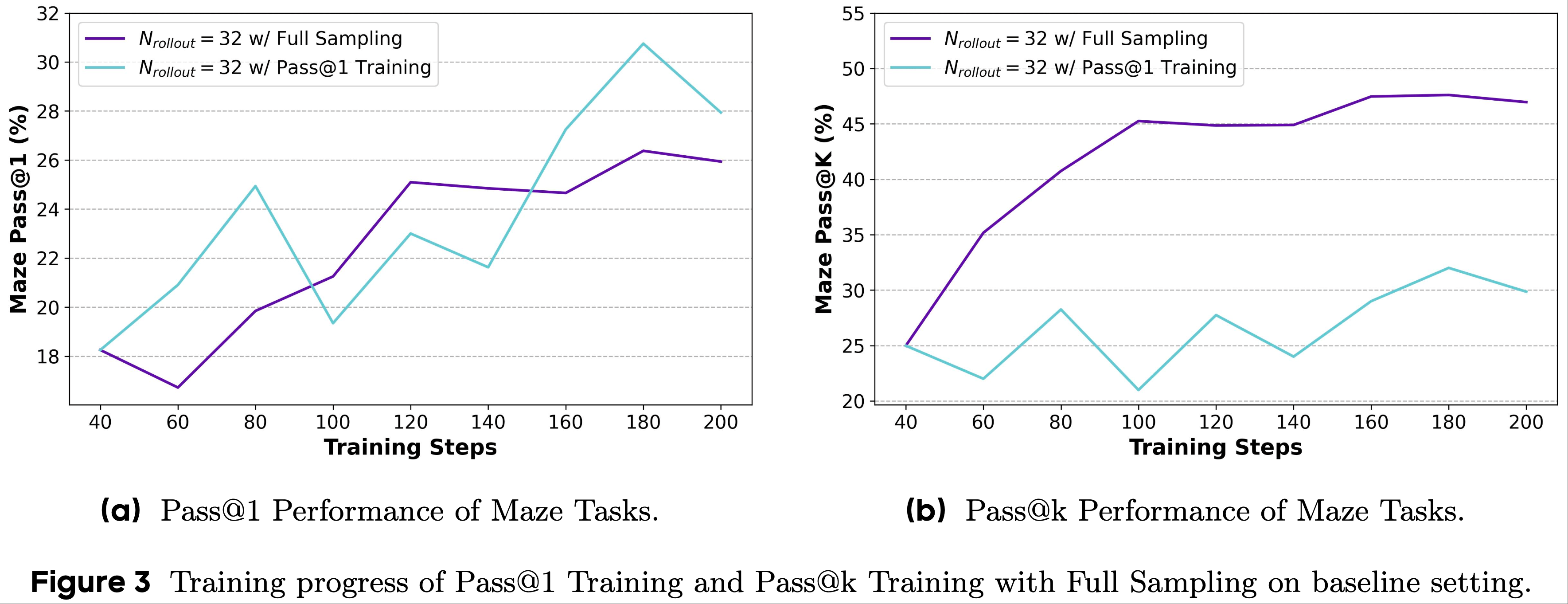
- 为了评估采用 Pass@k 作为奖励的有效性,论文比较了全采样的 Pass@k Training 与常规 Pass@1 Training 的性能,如图 3 所示
- 论文观察到,在 Pass@1 Training 过程中,下游任务的 Pass@k 性能保持稳定且仅有轻微提升
- 虽然 Pass@1 指标在训练初期有所提高,但在后期阶段停滞不前,表明模型已陷入局部最优
- 相比之下,在 RLVR 过程中采用 Pass@k 作为奖励时,LLM 在下游任务上的 Pass@k 性能持续提升 ,更多的训练步骤或更多的 rollout 次数不断带来 LLMs 性能的进一步提升
- 这表明 Pass@k Training 具有可扩展性
- 特别说明:Pass@k Training 不会损害模型的 Pass@1 性能,甚至会带来 Pass@1 性能的提升
- 这表明 Pass@k Training 和 Pass@1 Training 具有相似的优化目标和方向,并且它们可以一起得到改善
- 图 3 基线设置下 Pass@1 Training 和全采样的 Pass@k Training 的训练进度
- Takeaway from Section 2.2
- 与使用 Pass@1 作为奖励函数的传统 RLVR 训练方法相比,使用 Pass@k 作为 RLVR 训练的奖励函数可以有效提高模型在下游任务上的 Pass@k 性能,同时不损害其 Pass@1 性能
Efficient Pass@k Training via Bootstrap Sampling(通过 Bootstrap 采样可实现高效的 Pass@k Training )
- Pass@k Training 可以突破 LLM 的能力极限,但随着 \(N^\text{group}\) 的增加,rollout 次数显著增加,会消耗更多的计算资源
- 论文考虑利用 bootstrap 采样机制来减少 rollout 次数,同时保持组的数量不变
- 在 rollout 过程中,首先使用策略模型 \(\pi_{\theta}\) 为给定问题 \(x\) 生成 \(N_\text{rollout}\) 个响应
$$ \hat{\mathcal{Y}}=\{\hat{y}_{1}, …, \hat{y}_{N_\text{rollout} }\} $$ - 构建用于后续优化过程的 \(N^\text{group}\) 个组的过程
- 从先前生成的响应集 \(\hat{\mathcal{Y}}\) 中随机采样 \(k\) 个响应,这些采样的响应共同构成一个组
- 问题:上面这句话有点多余?
- 为了构建第 \(j\) 个组,论文从 1 到 \(N_\text{rollout}\) 的范围内选择 \(k\) 个不同的值,得到集合
$$ \mathcal{P}=\{p_{j, 1}, …, p_{j, k}\}$$- 然后,索引在集合 \(\mathcal{P}\) 中的响应构成当前组
$$ \hat{\mathcal{Y}}^{j}=\{\hat{y}_{p_{j, 1} }, …, \hat{y}_{p_{j, k} }\}$$
- 然后,索引在集合 \(\mathcal{P}\) 中的响应构成当前组
- 这个过程将重复 \(N^\text{group}\) 次,收集 \(N^\text{group}\) 组响应
- 从先前生成的响应集 \(\hat{\mathcal{Y}}\) 中随机采样 \(k\) 个响应,这些采样的响应共同构成一个组
- 获得这些组后,我们可以估计每个组的优势值并将其分配给响应
- 由于论文使用 bootstrap 采样策略来构建组,一些响应可能出现在多个组中
- 对于每个响应,论文通过对其所属的所有组的优势求和来计算其最终优势,即:
$$\hat{A}_{i}=\sum_{j=1}^{N^\text{group } } \hat{A}^{j} \cdot \mathbb{I}\left[\hat{y}_{i} \in \hat{\mathcal{Y} }^{j}\right],$$- 其中 \(\mathbb{I}[\hat{y}_{i} \in \hat{\mathcal{Y}}^{j}]\) 是一个指示函数,当且仅当第 \(i\) 个响应 \(\hat{y}_{i}\) 属于第 \(j\) 个组 \(\hat{\mathcal{Y}}^{j}\) 时返回 1,否则返回 0
- 在实践中,论文为了高效的 RLVR 过程设置 \(N^\text{group}=N_\text{rollout}\)
- 实证见解:减少训练预算(Empirical Insight: Reduction in Training Budget) :
- 为了评估 bootstrap 采样对 Pass@k Training 的有效性,论文进行了 Pass@1 Training 和具有不同 rollout 次数的全采样 Pass@k Training (如第 2.2 节所述)作为基线方法,并在图 4 中展示了评估结果
- 在相同的 rollout 次数 \(N_\text{rollout}\) 下
- 即“\(N_\text{rollout}=32\) 采用全采样”与“\(N_\text{rollout}=32\) 采用 bootstrap 采样”,bootstrap 采样优于全采样
- 这种改进源于 bootstrap 采样生成了更多的组 ,这反过来减少了采样奖励分布相对于真实分布的方差 ,从而得到更稳定和有效的训练
- 理解:这种 bootstrap 采样的方式更合适,看似能够较为精确的区分相应的优劣(错误的回复是以概率被赋值奖励为 0 的),但本质是一样的,还是所有正确的回复都是正奖励,错误的回复以一定概率获得0奖励 or 正奖励
- 在相同的组数量 \(N^\text{group}\) 下
- 与全采样相比(即“\(N_\text{rollout}=128\) 采用全采样”),bootstrap 采样在 Pass@k 指标上不会导致显著的性能下降,并且它只需要理论计算成本的四分之一,从而实现更高的训练效率
- 此外,它在 Pass@1 指标上达到了与全采样相当的性能
- 总之,带有 bootstrap 采样的 Pass@k Training 优于 Pass@1 Training ,并提高了全采样训练过程的效率
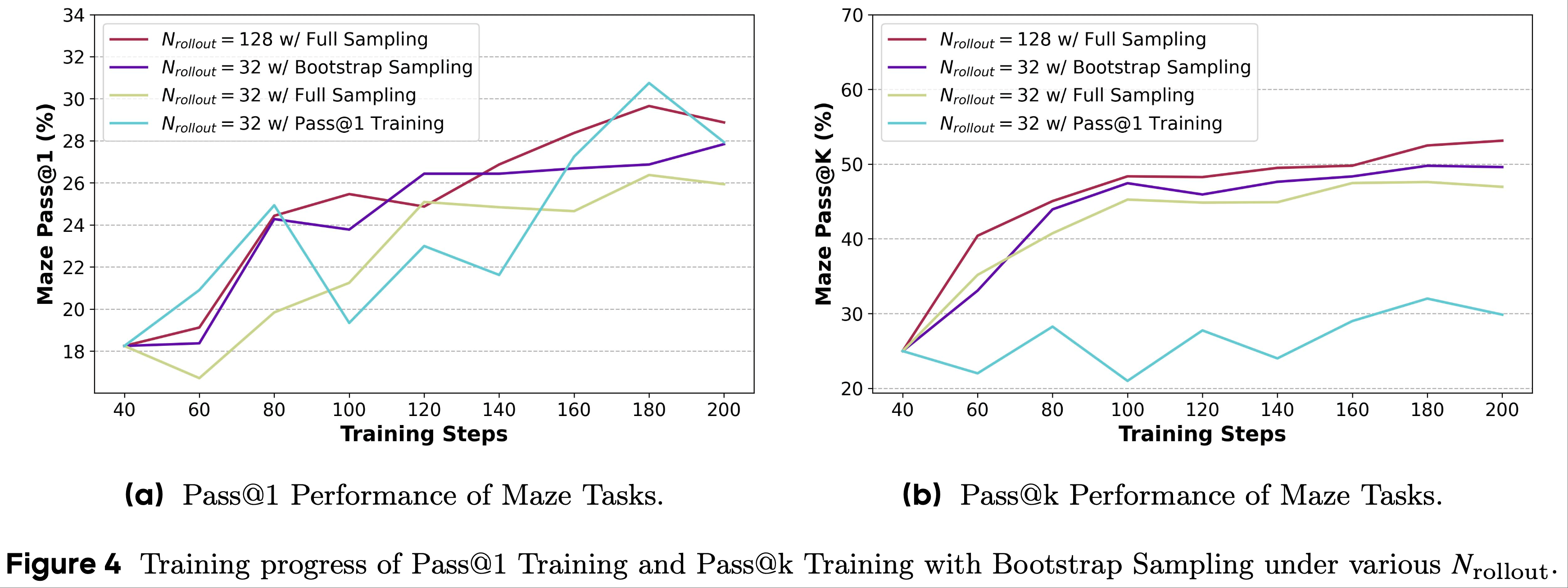
- 图 4 不同 \(N_\text{rollout}\) 下 Pass@1 Training 和带有 Bootstrap 采样的 Pass@k Training 的训练进度
- Takeaway from Section 2.3
- 与基于全采样的 Pass@k Training 方法相比,基于 bootstrap 采样的训练方法在相同的 rollout 次数下可以获得更好的训练结果
- 在相同的组数量下,它可以减少计算开销,同时达到相当的性能
Analytical Derivation(解析推导)of Efficient and Effective Pass@k Training
- 基于第 2.3 节中描述的 bootstrap 采样机制的想法,论文推导了响应优势(即 \(\hat{A}_\text{pos}\) 和 \(\hat{A}_\text{neg}\))的解析解,以消除构建组时的采样操作带来的方差
- 推导的细节在附录 B 中呈现
- 为了推导出优势的解析公式,论文首先分析组的优势奖励和标准差,即 \(\bar{R}^\text{group}\) 和 \(\sigma^\text{group}\)
- 包含至少一个正响应的组(称为正组)将被分配正奖励 \(R_\text{pos}\),而其他组(称为负组)将被赋予负奖励 \(R_\text{neg}\)
- 遵循 DAPO 的优势估计方法,计算组奖励分数的平均值和标准差至关重要
- 首先,组的平均奖励可以表述为以下方程:
$$\overline{R}^\text{group}=\frac{1}{N_\text{total }^\text{group} } × \left( N_\text{pos}^\text{group } × R_\text{pos }+N_\text{neg }^\text{group } × R_\text{neg }\right) ,\tag{7}$$- \(N_\text{total}^\text{group}\) 指组的总数
- \(N_\text{pos}^\text{group}\) 和 \(N_\text{neg}^\text{group}\) 分别表示正组和负组的数量
- 为了计算正组和负组的数量,论文首先定义正响应的数量为 \(N_\text{pos}\),负响应的数量为 \(N_\text{neg}\),通常有:
$$ N_\text{pos}+N_\text{neg}=N_\text{rollout}$$ - 基于上述定义,由于每个组由选择的 \(k\) 个响应构成,我们可以得到组的总数 \(N_\text{total}^\text{group}\) 如下:
$$N_\text{total }^\text{group }=\left(\begin{array}{c}N_\text{rollout } \\ k \end{array}\right) =N_\text{pos}^\text{group }+N_\text{neg }^\text{group } .\tag{8}$$ - 由于负组不包含正响应,当且仅当从所有响应中随机采样 \(k\) 个负响应时,这些采样的响应才能构成负组。因此,负组的数量可以计算如下:
$$N_\text{neg }^\text{group }=\left(\begin{array}{c} N_\text{neg } \\ k \end{array}\right) .\tag{9}$$ - 根据方程 8 和方程 9,我们可以得到正组的数量:
$$N_\text{pos }^\text{group}=N_\text{total}^\text{group}-N_\text{neg}^\text{group}=\left( \begin{array}{c}{N_\text{rollout} } \\ {k}\end{array} \right)-\left( \begin{array}{c}{N_\text{neg} } \\ {k}\end{array} \right) .\tag{10}$$ - 将方程 8、方程 9 和方程 10 代入方程 7,我们可以得到组的平均奖励 \(\bar{R}^\text{group}\):
$$\overline{R}^\text{group }=1-\frac{\left(\begin{array}{c} N_\text{neg } \\ k \end{array}\right)}{\left(\begin{array}{c} N_\text{rollout } \\ k \end{array}\right)} .\tag{11}$$ - 基于组的平均奖励 \(\bar{R}^\text{group}\),标准差可以计算如下:
$$\sigma ^\text{group}=\sqrt {\overline {R}^\text{group}× \left( 1-\overline {R}^\text{group}\right) } .\tag{12}$$ - 基于奖励分数的平均值(方程 11)和标准差(方程 12),论文最终可以推导出正组 \(\hat{A}_\text{pos}^\text{group}\) 和负组 \(\hat{A}_\text{neg}^\text{group}\) 的优势如下:
$$\hat{A}_\text{pos}^\text{group}=\frac{R_\text{pos}-\overline{R}^\text{group} }{\sigma^\text{group} }=\frac{1-\overline{R}^\text{group} }{\sigma^\text{group} }, \hat{A}_\text{neg}^\text{group}=\frac{R_\text{neg}-\overline{R}^\text{group} }{\sigma^\text{group} }=-\frac{\overline {R}^\text{group} }{\sigma ^\text{group} } .\tag{13}$$ - 为了将前一节中获得的组相关优势 \(\hat{A}_\text{pos}^\text{group}\) 和 \(\hat{A}_\text{neg}^\text{group}\) 转换为响应相关优势 \(\hat{A}_\text{pos}\) 和 \(\hat{A}_\text{neg}\),论文需要考虑每个响应所属组的正确性,并按比例计算优势值
- 通常,一个响应将属于 \(\left(\begin{array}{c}N_\text{rollout }-1 \\ k-1\end{array}\right)\) 个组,因为当且仅当从剩余的 \(N_\text{rollout}-1\) 个响应中选择 \(k-1\) 个响应时,才能与当前响应形成一个组
- 此外,对于正响应,它所属的组总能通过 Pass@k 验证(即正组)
- 因此,正响应的优势 \(\hat{A}_\text{pos}\) 可以计算如下:
$$ \color{red}{\hat{A}_\text{pos }=\frac{1-\overline{R}^\text{group } }{\sigma^\text{group } } } .\tag{14}$$
- 然后,考虑负响应,它所属的组是负组当且仅当其他 \(k-1\) 个响应都是负响应。在这种情况下,所需的组数量是 \(\left(\begin{array}{c}N_\text{neg }-1 \\ k-1\end{array}\right)\),即当前响应可以与从剩余的 \(N_\text{neg}-1\) 个负响应中选择的任何 \(k-1\) 个响应形成负组
- 基于负组的数量,我们可以通过从组的总数中减去负组的数量来计算正组的数量,即 \(\left(\begin{array}{c}N_\text{rollout }-1 \\ k-1\end{array}\right)-\left(\begin{array}{c}N_\text{neg }-1 \\ k-1\end{array}\right)\)
- 因此,负响应的优势 \(\hat{A}_\text{neg}\) 可以计算如下:
$$ \color{red}{ \hat{A}_\text{neg}=\left(1-\overline{R}^\text{group }-\frac{\left(\begin{array}{c} N_\text{neg }-1 \\ k-1 \end{array}\right)}{\left(\begin{array}{c} N_\text{rollout }-1 \\ k-1 \end{array}\right)}\right) \times\left(\sigma^\text{group }\right)^{-1} }.\tag{15}$$ - 问题:使用这种相对固定的(因为分母上存在方差,所以不算是严格的固定),比正样本小一些的奖励,是否等价于不给任何奖励啊?
- 在获得响应相关优势 \(\hat{A}_\text{pos}\) 和 \(\hat{A}_\text{neg}\) 的解析解后,论文直接将它们用于优势估计过程,然后优化模型参数
- 通过检查优势值的解析解,论文观察到它仅取决于采样响应的总数 \(N_\text{rollout}\)、正响应的数量 \(N_\text{pos}\)、负响应的数量 \(N_\text{neg}\) 以及 \(k\) 的值
- 因此,在 rollout 过程之后,我们可以直接计算每个响应的优势值用于 RLVR 训练,而无需经过前面描述的繁琐奖励计算过程
- 问题:这是否再次说明了,实际上随机挑选一部分负样本给与一定权重(权重可以是超参数)奖励就可以,不需要那么复杂做什么 Pass@k Training?
- 实证见解:Pass@k 的进一步改进(Empirical Insight: Further Improvement on Pass@k) :
- 为了进行评估和比较,论文将 rollout 次数 \(N_\text{rollout}\) 统一设置为 32,并比较了 Pass@1 Training 以及带有 bootstrap 采样和解析推导的 Pass@k Training 的训练效果
- 实验结果如图 5 所示
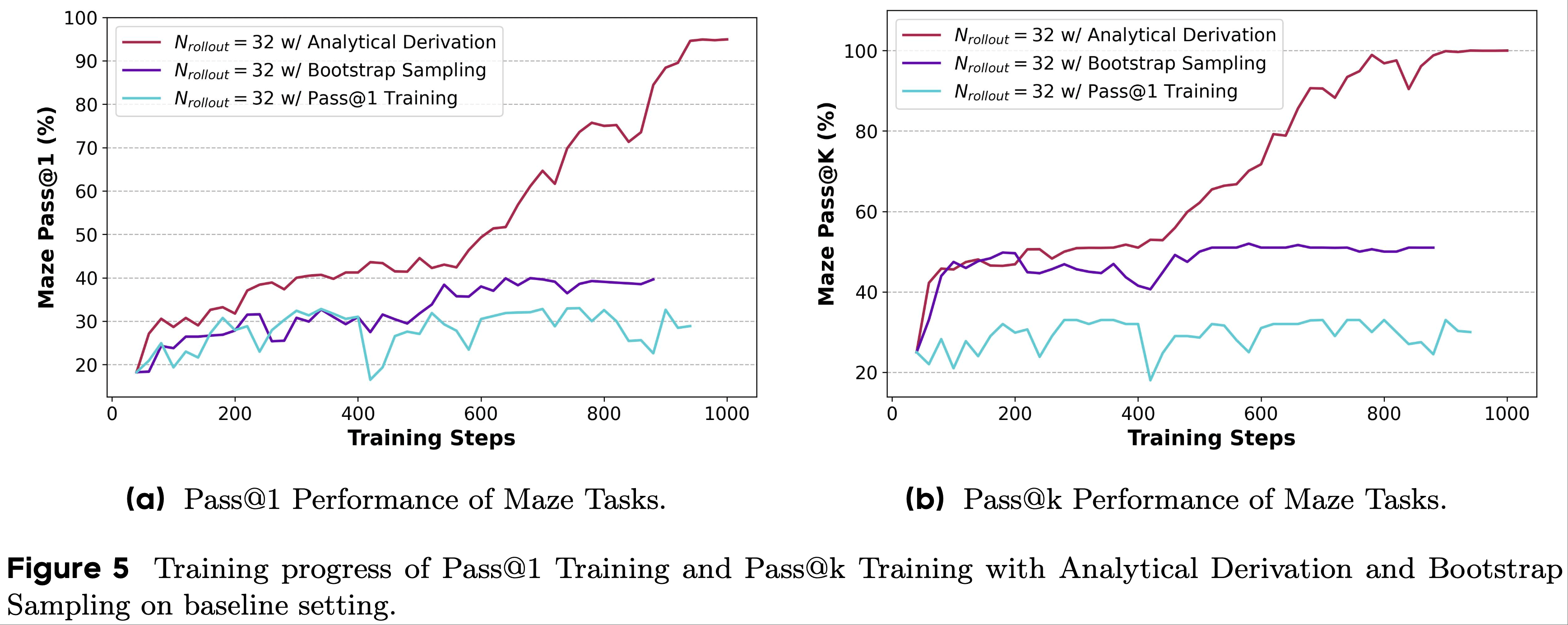
- 为了进行全面评估,论文还进行了不同 LLM 在各种任务上的外部实验,并在附录 E 中展示了结果
- 在实验中,我们可以观察到两种 Pass@k Training 都比 Pass@1 Training 取得了更好的结果,这进一步证实了 Pass@k Training 的有效性
- 当训练步骤增加时,基于 bootstrap 采样的 Pass@k Training 在 400 步时经历了相对剧烈的性能波动,Pass@k 性能下降,这表明该方法存在一定的不稳定性
- 理解:不稳定的原因是因为采样,而使用带有解析推导的 Pass@k Training 则没有采样,会更稳定
- 相比之下,对于基于 bootstrap 采样的方法,带有解析推导的 Pass@k Training 消除了构建组所需的采样过程
- 它通过解析解的计算直接减少了采样过程引起的方差,从而提供了更稳定的训练过程
- 因此,带有解析推导的 Pass@k Training 方法可以减少训练过程中的波动,并随着训练步骤的增加带来持续的性能提升
- Takeaway from Section 2.4
- 带有解析推导的 Pass@k Training 不仅避免了全采样中大量 rollout 带来的计算开销,还消除了 bootstrap 采样中采样引入的方差。这使得 RLVR 训练过程更高效和有效,并且可以引导模型的探索能力随着训练步骤的增加而不断提高
Balancing Exploration and Exploitation with Pass@k Training
- 在本节中,论文进一步研究 Pass@k Training 的特征和有效性
- 第 3.1 节:论文将 Pass@k Training 与常用的增强模型探索能力的方法(2025, 2025)进行比较,以进一步验证其有效性
- 第 3.2 节:为了更深入理解 Pass@k Training 如何影响模型的探索能力,论文考察了模型响应的多样性和策略分布的熵
- 第 3.3 节:论文想知道 Pass@k Training 带来的改进是否可以迁移到其他领域或任务中,进而评估其泛化性能
- 第 3.4 节:由于 RLVR 的稳定性和鲁棒性受到广泛关注(2023, 2025, 2025),论文分析了 k 值对 Pass@k Training 过程的影响
- 第 3.5 节:由于 Pass@1 在实际应用中是一个更重要的指标,论文探索了如何将 Pass@k Training 的收益迁移到模型的 Pass@1 性能上,实验结果证明了 Pass@k Training 的高实用价值
How does Pass@k Training Compare to Noise Rewards or Entropy Regularization?(Pass@k Training 与噪声奖励或熵正则化相比)
- 受 Pass@k Training 流程(第 2.2 节)和先前工作(2025)的启发,论文将 Pass@k Training 与两种基线方法(即噪声奖励(Noise Rewards)和熵正则化(Entropy Regularization))进行了比较
- 噪声奖励(Noise Rewards) :
- 回顾利用 Pass@k 指标作为奖励的 RLVR 流程(如第 2.2 节所述),论文注意到,如果某些负响应属于正组,它们可能会获得正奖励 \(R_\text{pos}\)
- 这引发了一个问题:Pass@k 分数的提升是否部分源于从这些带有反事实正奖励的负响应中学习
- 为了探究这一点,论文进行了一项实验,其中一定比例(即 10%、30% 和 50%)的负响应奖励被翻转
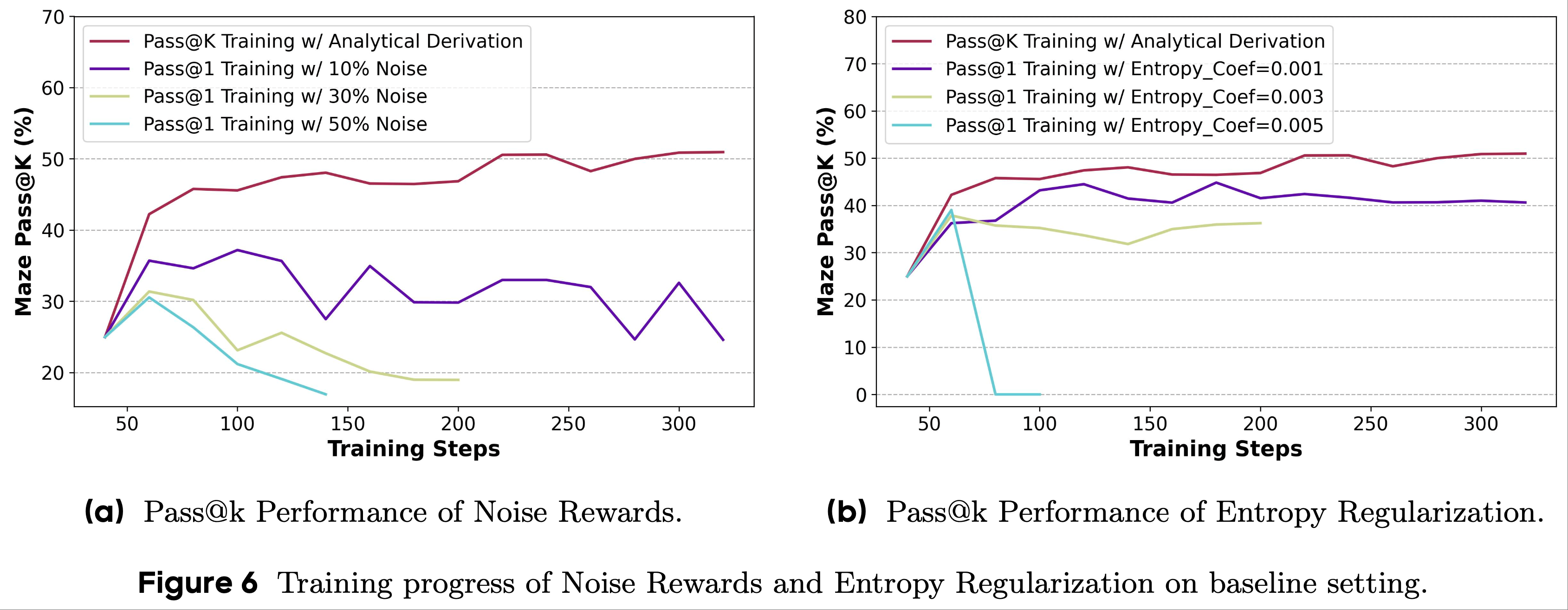
- 结果如图 6a 所示,实证结果表明:
- 鼓励 LLM 从负响应中学习对提高其推理能力没有帮助 ,相反,在奖励中引入更高比例的噪声会显著降低模型性能
- 随着翻转奖励比例的增加,模型在 Pass@1 和 Pass@k 指标上的性能均逐渐下降
- 随着训练步骤的增加,性能继续下降
- 理解:翻转的负样本得到的奖励太高,不行,应该给与较小的奖励才公平?
- 这些发现表明,天真地在奖励中加入噪声并不能增强 LLM 的推理能力
- 相反,必须仔细控制噪声比例,例如通过 Pass@k 指标的结构化设计,这可以引导 LLM 突破其现有推理能力的限制
- 相反,必须仔细控制噪声比例,例如通过 Pass@k 指标的结构化设计,这可以引导 LLM 突破其现有推理能力的限制
- 回顾利用 Pass@k 指标作为奖励的 RLVR 流程(如第 2.2 节所述),论文注意到,如果某些负响应属于正组,它们可能会获得正奖励 \(R_\text{pos}\)
- 熵正则化(Entropy Regularization) :
- 大量研究(2025)指出,熵可以指示 LLM 的探索能力,并且可以纳入目标函数以保持其探索能力
- 遵循先前的工作(2025),论文在 RLVR 训练过程中采用系数为 {0.001, 0.003, 0.005} 的熵正则化,并在图 6b 的右侧部分展示结果
- 结果表名:
- 高熵正则化系数可能导致模型崩溃(例如将系数设置为 0.005 时)
- 尽管小的熵正则化系数不会使 LLM 崩溃,但它仍然无法优于 Pass@k Training,甚至会随着训练步骤的增加导致 LLM 的性能下降
- 上述现象表明,熵正则化可能会影响训练的有效性和稳定性
- 关于其他熵引导方法的讨论(Discussion about Other Entropy-guided Approaches) :
- 论文比较了 Pass@k Training 与熵引导方法的朴素实现(即熵正则化)的有效性
- 此外,还有其他几种方法,例如将熵集成到优势函数中(2025)或关注具有高协方差的 Token(2025)
- 同样,这些方法可能会引入新的权衡:
- 过于严格的约束可能导致欠拟合和模型训练不足,而过于宽松的约束可能导致训练过程中的不稳定性,潜在地影响训练有效性和模型性能(2023, 2025, 2025),因为熵与 Pass@1 指标相冲突
- 因此,在上述方法中,应仔细选择超参数以带来 LLM 的性能提升
- 实际上,这些方法与 Pass@k Training 是正交的 ,这意味着也可以将这些方法与 Pass@k Training 相结合以获得更好的训练结果
- 为了验证这一点,论文在第 4.2.3 节中进行了实验,评估基于策略熵指导的 Pass@k Training 的有效性,结果显示有显著改进
- Takeaway from Section 3.1
- Pass@k Training 优于噪声奖励和熵正则化:随机翻转负响应的奖励可能会降低 LLM 的性能,而引入熵正则化会带来新的权衡问题,难以实现持续改进
Does Pass@k Training Really Improve the Exploration Ability of LLMs?(是否提高 LLM 的探索能力?)
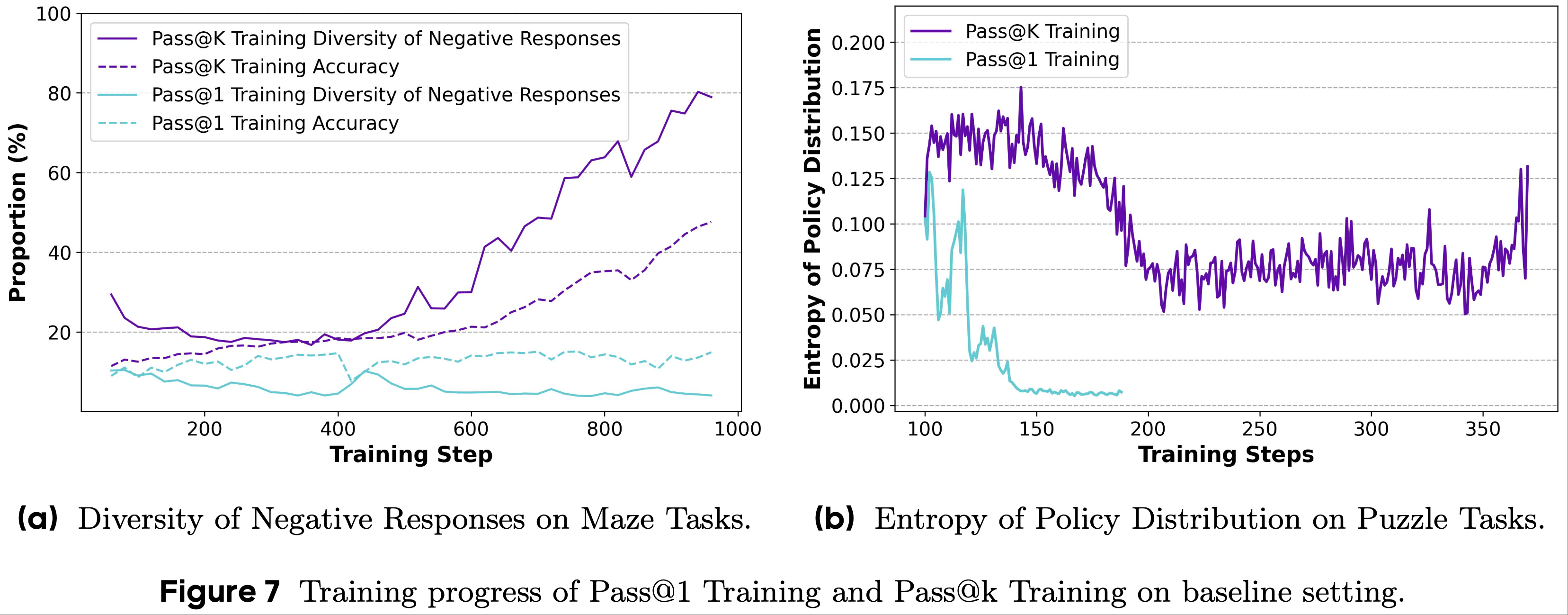
- 为了分析 RLVR 训练过程中 LLM 探索能力的变化,论文从答案多样性和策略分布熵的角度进行了相关实证研究,并在图 7 中展示了相应结果
- 负响应的答案多样性(Answer Diversity of Negative Responses) :
- 论文统计了 Pass@k 和 Pass@1 Training 的负响应中答案的准确性和不同答案的比例,如图 7a 所示,旨在评估 LLM 对不确定答案的探索能力
- 根据结果,论文观察到在 RLVR 训练过程中,负响应的答案多样性保持在同一水平,这表明 LLM 在探索过程中试图选择“安全”的行为,并倾向于生成相似的答案,限制了探索范围并制约了 RLVR 的有效性
- 不同的是,在 Pass@k Training 中,模型被鼓励获得更高的 Pass@k 分数,并在对问题没有足够信心时自然地学习生成多样化答案的策略
- 在这种情况下,LLM 的探索能力得到增强,进而提高了其利用能力(即 Pass@1 分数)
- 策略分布的熵(Entropy of Policy Distribution) :在图 7b 中,结果与论文之前关于答案多样性的讨论得出了相似的结论
- Pass@k Training 将策略分布的熵保持在相对较高的水平,而 Pass@1 Training 导致熵收敛到较低的值
- 这一现象表明,LLM 在 Pass@k Training 过程中能够保持其探索能力,但在 Pass@1 Training 过程中会丧失探索能力
- 另一方面,论文还可以观察到,从 RLVR 过程的 200 步开始,Pass@k Training 导致熵增加。这一现象验证了论文的假设,即使用 Pass@k 作为训练目标可以鼓励模型进行更多探索,从而自然地增加熵
- 总之,探索和利用并不相互冲突,它们可以相互促进,且Pass@k Training 能够实现这一目标
- Takeaway from Section 3.2
- Pass@k Training 可以鼓励模型进行更多探索,在模型没有足够信心生成正确答案时,生成多样化的答案,自然地导致熵的增加
hat is the Generalization Ability of LLMs After Pass@k Training?(泛化能力如何)
- 为了分析 Pass@k Training 的泛化能力,论文进行了相应的实验,并在表 1 中展示了结果
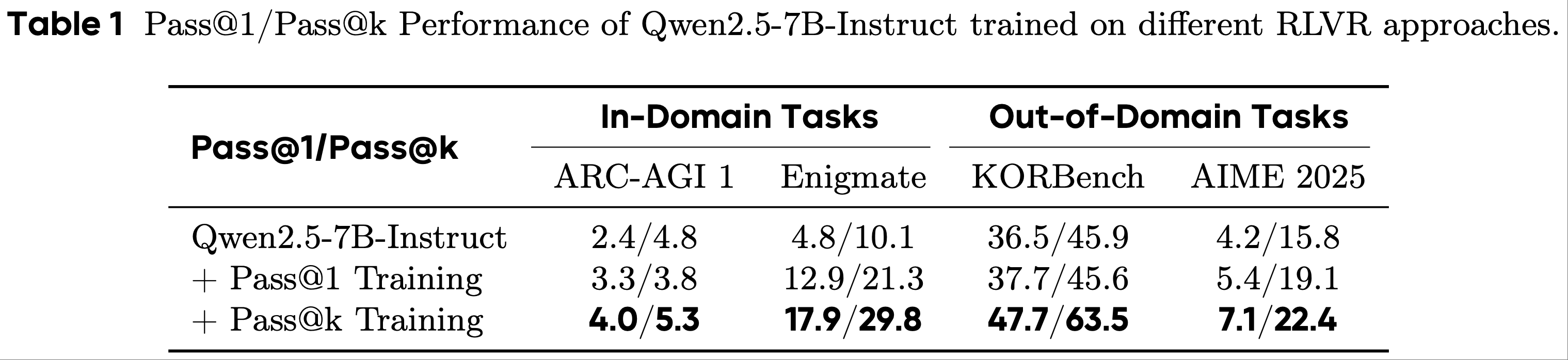
- 我们可以观察到,Pass@1 和 Pass@k Training 都能增强模型在域内和域外任务上的能力 ,这表明 RLVR 训练过程具有很强的泛化能力
- 比较这两种训练方法的性能,通过 Pass@k Training 的模型优于通过 Pass@1 Training 的模型 ,其原因是:
- Pass@k Training 鼓励模型探索更好的解决方案,这些解决方案可以很容易地泛化到其他任务
- Pass@1 Training 使 LLM 行为保守,从而影响 LLM 的域外(OOD)性能
- Takeaway from Section 3.3
- Pass@k Training 比 Pass@1 Training 表现出更强的泛化能力,在域内和域外测试中都比基础模型有更大的改进
How does the Value of k Affect Pass@k Training?(k 值对 Pass@k Training 的影响)
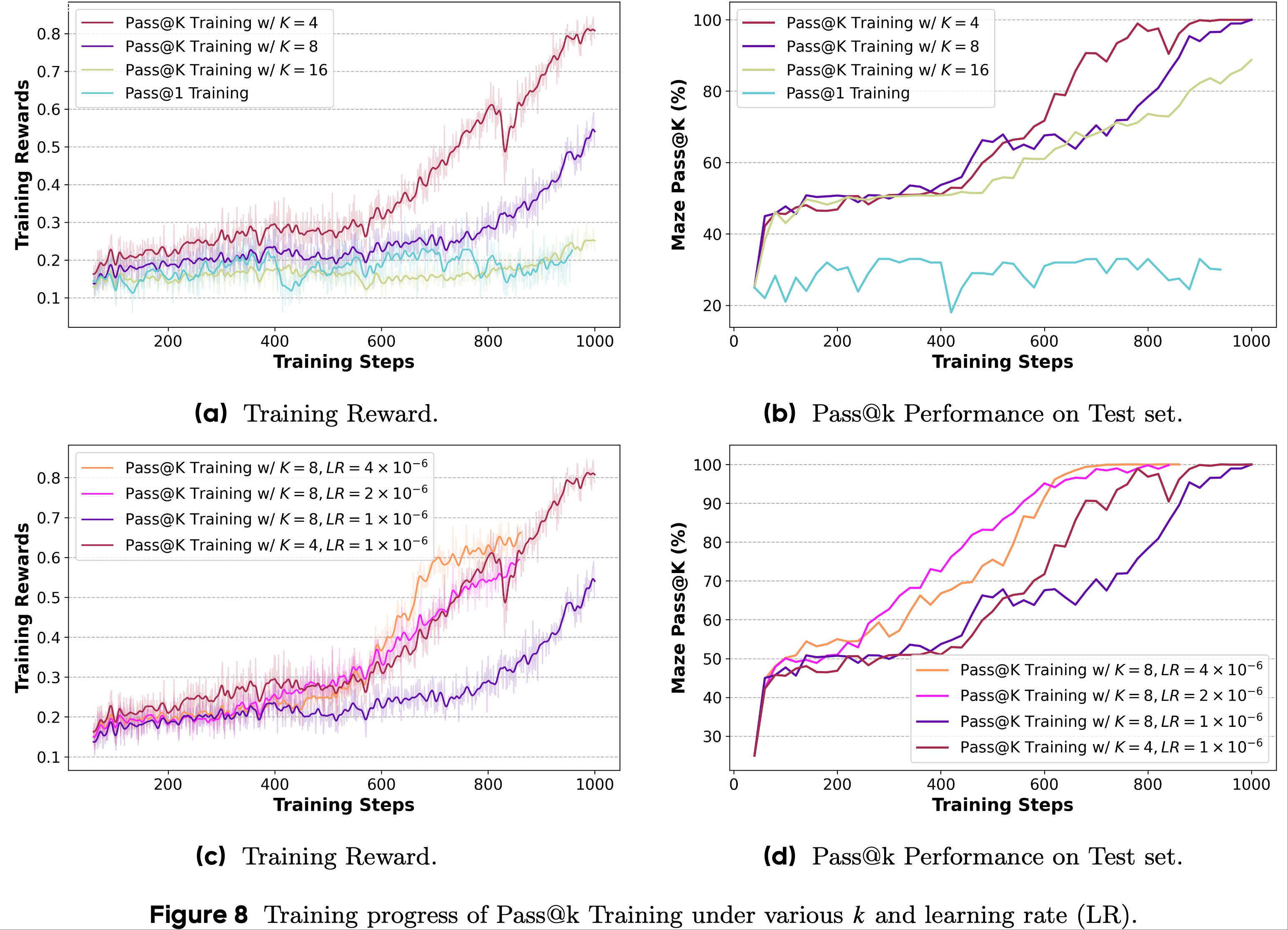
- 为了分析 Pass@k Training 的鲁棒性,论文将 k 值调整为 4、8、16,在迷宫(Maze)任务上进行 RLVR 训练,并分别在图 8a 和图 8b 中展示训练奖励和测试集的 Pass@k 性能
- 无论 k 值如何,随着训练的进行,训练奖励都能提高到相对较高的水平,这表明 k 值并不是帮助 LLM 摆脱 Pass@1 Training 局部最优的关键因素
- 随着 k 值的增加,改进速度减慢,影响训练效率
- 通过分析优势值的解析解(即公式 14 和公式 15),我们可以意识到,更大的 k 值会带来更小的优势值 ,导致更短的优化步骤,从而降低训练效率
- 基于这一现象,论文研究了缩放学习率(LR)以扩大优化步骤是否能提高训练效率
- 基于这一想法,论文在 \(N=32\) 和 \(k=8\) 的设置下采用 \(1×10^{-6}\)、\(2×10^{-6}\)、\(4×10^{-6}\) 的学习率,并在图 8c 和图 8d 中展示结果
- 随着学习率的增加,拐点出现得更早,表明训练效率更高
- 当论文采用 \(4×10^{-6}\) 作为学习率时,Pass@8 训练的训练效率甚至超过了 Pass@4 训练
- 这些结果表明,训练效率问题可以很容易地得到缓解
- Takeaway from Section 3.4
- Pass@k Training 对 k 值的选择具有很强的鲁棒性,能够实现稳定且有效的训练过程
- 尽管随着 k 值的增加,模型的优化效率会有所下降,但这一问题可以通过增大学习率轻松解决
Can the Benefits from Pass@k Training Be Transferred to Pass@1 Performance?(将 Pass@k Training 的收益迁移到 Pass@1 上?)
- 为了将 Pass@k Training 带来的收益迁移到 LLM 的 Pass@1 性能上,一种自然的实现方式是在经过 Pass@k Training 的模型上继续进行 Pass@1 Training
- 论文在 RLVR 训练过程中采用了这种方法,并分别在表 2 和表 3 中展示了 Qwen 模型在谜题(Puzzle)任务上以及 Seed1.5-VL-Small(内部版本)在多模态推理任务上的结果
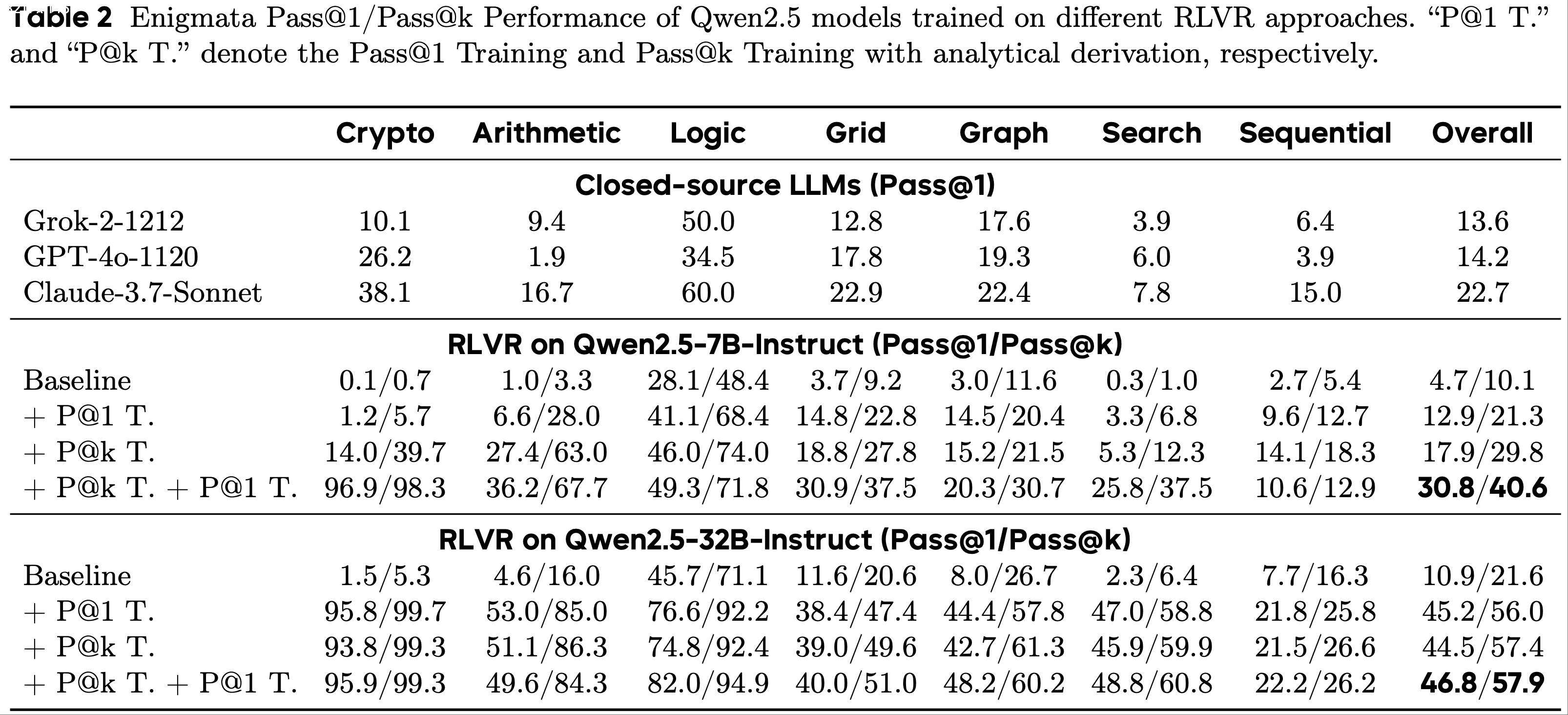
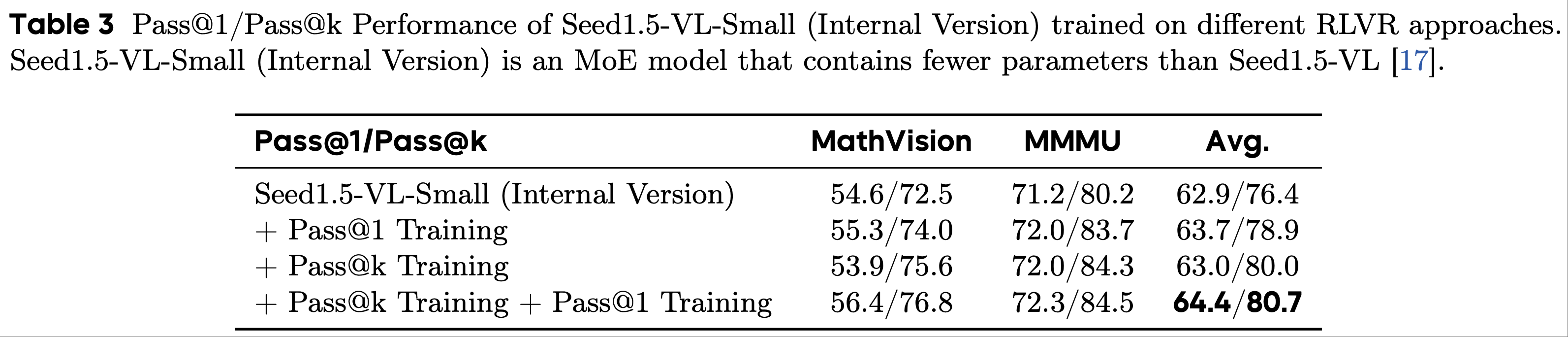
- 为了进行全面评估,论文还在附录 E 中进行了不同 LLM 在 Enigmata 和数学任务(例如,AIME 2024和 AIME 2025)上的外部实验
- 第一,在 Pass@k Training 之后进行 Pass@1 Training 可以显著提高 LLM 的推理能力,实现显著的 Pass@1 性能
- 根据结果,我们可以观察到,即使是 7B 模型也能超越强大的闭源 LLM,包括 Grok-2、GPT-4o 和 Claude-3.7-Sonnet
- 这可能是因为 Pass@k Training 增强了 LLM 的探索能力,引导其摆脱局部最优,并在后续的 RLVR 训练中释放 LLM 的潜力
- 第二,无论是小规模还是大规模的 LLM(例如,具有 7B 或 32B 参数的 Qwen2.5)都能从 Pass@k Training 中受益
- 此外,模型架构和模型系列不会影响持续 Pass@1 Training 的改进。Qwen 模型是密集型模型,而 Seed1.5-VL-Small(内部版本)是 MoE 模型
- 它们的 Pass@1 性能在 Pass@k Training 后都能进一步提高
- 第三,下游任务的领域和形式也不会影响 LLM 的 Pass@k 性能到其 Pass@1 性能的迁移
- 论文的评估包括用自然语言表达的合成谜题任务,以及问题描述中包含图片的多模态推理任务
- 这些任务要求 LLM 具备不同类别的能力,而论文的 Pass@k Training 可以有针对性地增强相应的能力,表现出很强的有效性
- Takeaway from Section 3.5
- Pass@k Training 带来的收益可以迁移到 LLM 的 Pass@1 性能上,这不受模型参数规模(例如,7B 或 32B)、模型架构(例如,密集型模型或 MoE 模型)、模型系列(即 Qwen 模型或 Seed 模型)或下游任务(自然语言任务或多模态任务)的影响
Generalizing Pass@k Training via Implicit Reward Design(隐式奖励设计推广 Pass@k Training)
- 如第2节 所述,论文通过推导优势函数的解析形式,实现了高效且有效的 Pass@k Training
- 在本节中,论文将从优势函数的角度进一步探究 Pass@k Training 成功的关键因素(4.1节)
- 优势函数设计可被视为一种隐式奖励设计,受此启发,论文将探索在难以从奖励函数推导出解析解的场景下,如何基于优化目标直接设计优势函数(4.2节)
Difference Between Pass@1 and Pass@k Training
Analysis Based on Advantage Value Curves
- 为了分析 Pass@k Training 为何能帮助 LLM 摆脱局部最优,论文首先可视化了 Pass@1 Training 和 Pass@k Training 在不同正确性水平响应上的优势曲线
- 在 GRPO 及其变体中,优势值仅取决于模型响应的正确性
- 在优化过程中,优势值直接与梯度相乘,可被解释为梯度的缩放因子
- 在这种情况下,优势值的绝对值越大,意味着梯度的缩放程度越大,相应样本的更新步长也就越大
- 这表明模型会对优势值绝对值较大的样本投入更多的优化精力
- 作者认为优势值的绝对值也是一个值得研究的重要方面
- 基于这一见解,为简化分析,论文计算了所有响应的绝对优势值之和\(\eta\) ,定义如下:
$$
\eta = N_\text{pos} \times \left|\hat{A}_\text{pos}\right| + N_\text{neg} \times \left|\hat{A}_\text{neg}\right|,
$$ - 论文将 \(\eta\) 的曲线(称为绝对优势之和(Sum of Absolute Advantage))添加到可视化中,并展示在图9中
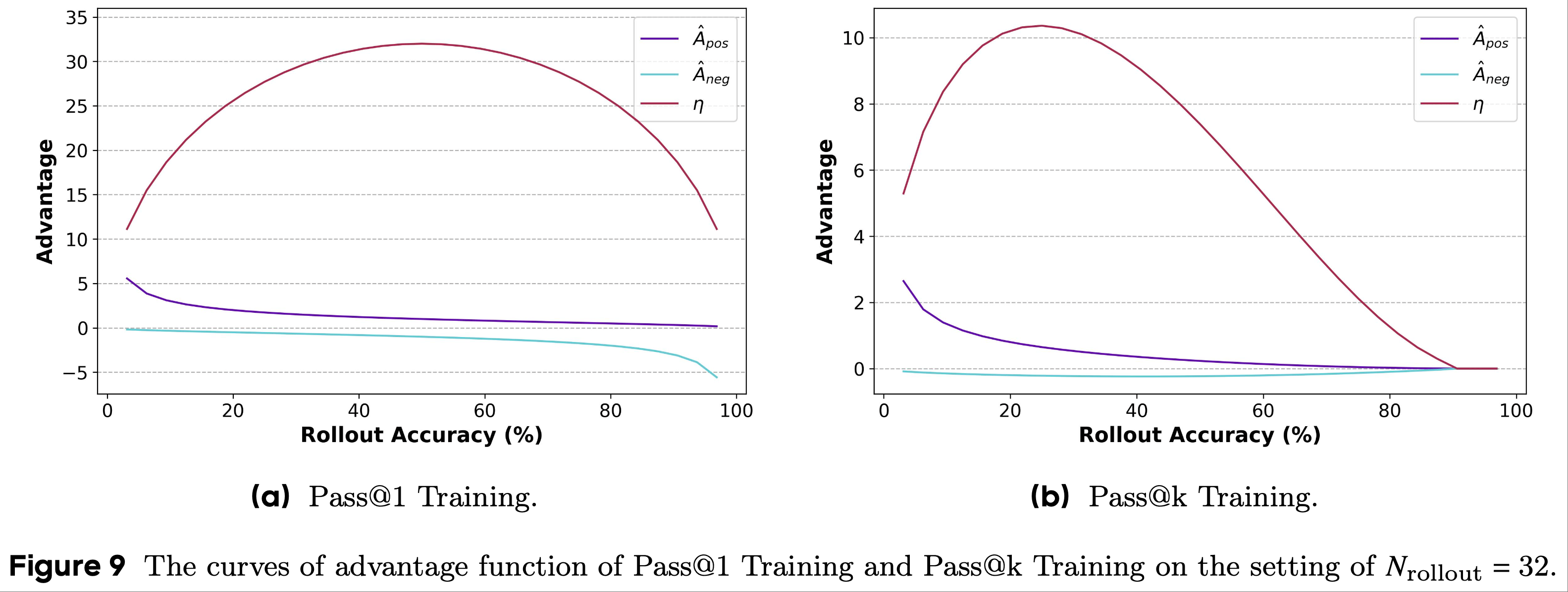
- 对比 Pass@1 Training 和 Pass@k Training 的 \(\eta\) 曲线,论文发现存在三个主要差异
- 绝对优势之和的最大值 :
- Pass@1 Training 方法的 \(\eta\) 最大值远高于 Pass@k Training 方法
- 正如论文在3.4节中讨论的,最大优势值可能会影响训练效率,通过在损失函数上添加系数来调整优势值可以缓解这一问题
- 因此,最大值并非 Pass@k Training 优于 Pass@1 Training 的关键因素
- 绝对优势之和的 argmax :
- 根据图9中的曲线,Pass@1 Training 和 Pass@8 Training 的 \(\eta\) 的 argmax 存在显著差异
- 对于 Pass@1 Training,\(\eta\) 的最大值出现在正确率为 50% 的位置(即 \(N_\text{pos} = 0.5 \times N_\text{rollout}\))
- 对于 Pass@8 Training,最大值的位置为正确率 25%(即 \(N_\text{pos} = 0.25 \times N_\text{rollout}\))
- 这一现象表明,Pass@k Training 侧重于优化更难的问题,而 Pass@1 Training 则侧重于中等难度的问题
- 理解:因为优势函数是权重,权重越高的问题,模型就更侧重他们 \(\eta\) 的 argmax 则表明了模型在关注哪部分问题
- 这进一步证明,Pass@k Training 倾向于引导模型解决先前未解决的或困难的问题,而不是过拟合于已经掌握的问题
- 根据图9中的曲线,Pass@1 Training 和 Pass@8 Training 的 \(\eta\) 的 argmax 存在显著差异
- 绝对优势之和的趋势 :
- Pass@1 Training 和 Pass@k Training 的函数曲线之间的另一个关键差异在于函数本身的趋势
- 在 Pass@k Training 的\(\eta\)曲线中,其值先上升至峰值,然后逐渐下降至零
- 在这种设置下,当问题相对容易时(即正确率高于60%),模型施加的优化强度(由\(\eta\)的值表示)会小于对更难问题的优化强度
- 这进一步表明, Pass@k Training 更注重优化模型尚未掌握的问题
- 相比之下,在 Pass@1 Training 中,\(\eta\)曲线关于最大值点对称,表明训练过程对简单问题和困难问题给予同等关注
- 绝对优势之和的最大值 :
Analysis Based on Model Performance
- 正如论文在前面章节中讨论的,绝对优势之和 \(\eta\) 的 argmax 和趋势对模型性能的影响仍不明确
- 因此,在本节中,论文设计了相应的实验,基于模型性能来分析它们的有效性
- 此外,论文设计了两种介于 Pass@1 和 Pass@k Training 之间的训练方法,即移除简单问题的优势值,以及基于当前提示的正确率结合 Pass@1 和 Pass@k 的优势估计方法
- 这四种训练方法的 \(\hat{A}_\text{pos}\)、\(\hat{A}_\text{neg}\) 和 \(\eta\) 的曲线如图18a和图18b所示
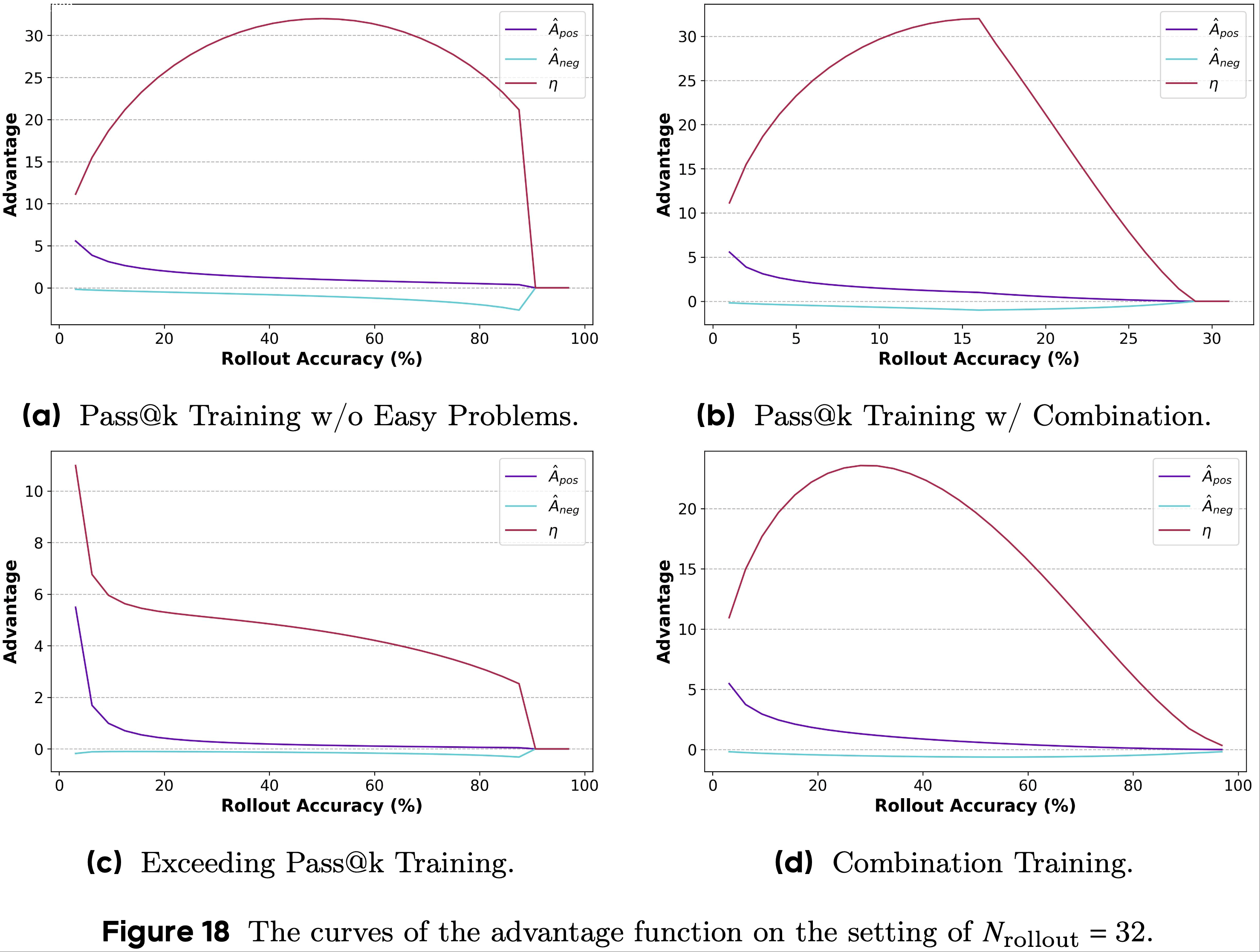
- 第一,当响应的正确率较高时,论文设计优势函数逐渐减小至零
- 这种设置使得优化过程中的训练奖励能够稳步增加,表明模型避免陷入局部最优(即蓝线和紫线)
- 当移除这种优化时,训练集上的奖励无法继续增加,这表明模型已经收敛到局部最优,并且在RLVR过程中不再学习新知识(即红线和绿线)
- 这一现象表明,过度从简单示例中学习是导致模型陷入局部最优的关键因素
- 因此,减少对简单问题的学习程度有助于防止模型陷入此类次优解
- 第二,简单地将简单问题的奖励设置为零并不足以有效防止模型对其过度优化;这只是延迟了模型陷入局部最优的时间点
- 如图10所示,移除对简单问题的优化(以红线表示)比基线(以绿线表示)带来了更高的训练奖励和更好的测试性能
- 然而,两条曲线呈现出相似的趋势:在初始阶段的改进之后,模型性能逐渐趋于平稳,难以取得进一步进展
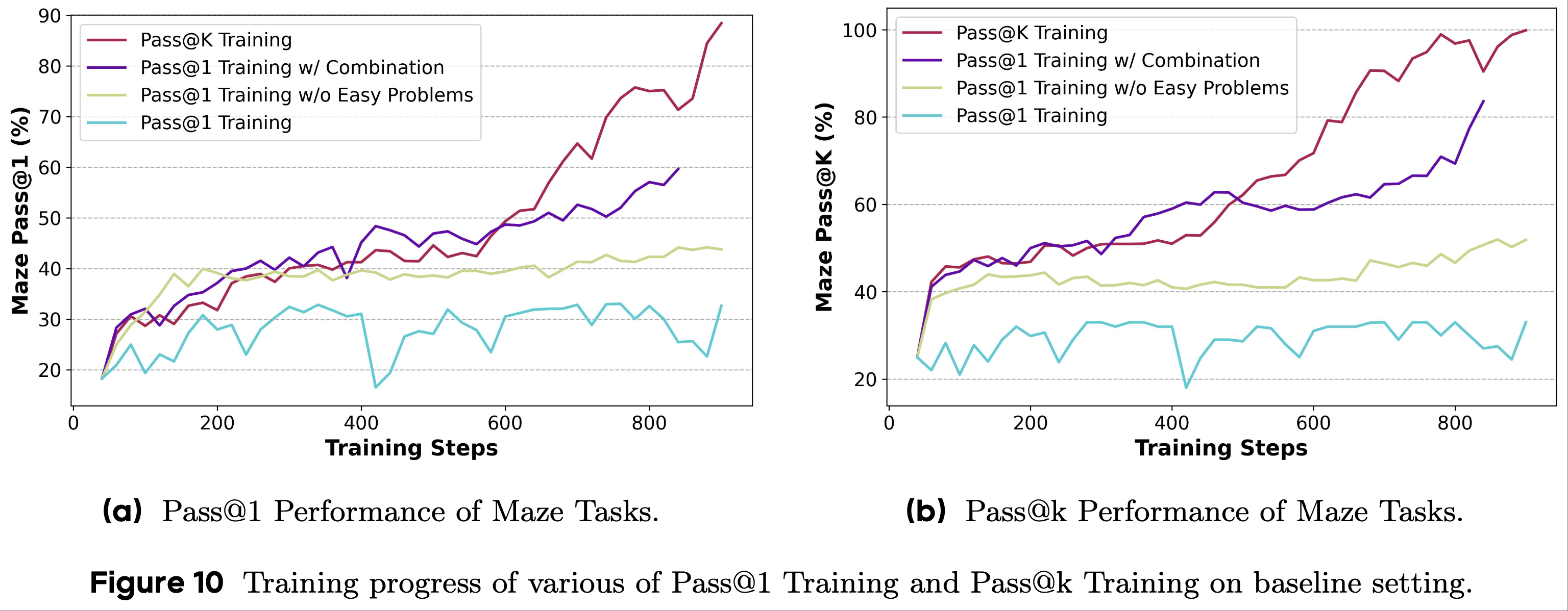
- 第三,关于 \(\eta\) 函数的 argmax 位置的选择 ,对比图10中的曲线可以发现,将 argmax 向前移动会带来更高的优化效率
- 具体而言,模型能够更快地摆脱局部最优,并且训练奖励的转折点出现得更早
- 这一现象表明,困难问题对模型改进的贡献更大,并且能产生更好的优化效果
- 因此,为更难的问题分配更大的优化强度可以有效提高训练效率,使模型用更少的训练步骤达到更好的性能
- 基于上述结果和讨论,可以得出一些初步结论,即 \(\eta\) 的 argmax 会影响训练效率,而 \(\eta\) 的趋势会防止模型陷入局部最优
- 此外,需要注意的是,这只是论文的初步结论。需要针对特定任务和场景进行更全面的实验以进一步验证
- Takeaway from Section 4.1 :
- 在 RLVR 训练过程中,简单问题很容易导致过拟合
- 适当地降低对简单问题的优化强度,有助于防止模型陷入局部最优,从而获得更好的整体性能
RLVR Training Through Implicit Reward Design
- 基于前一节对优势值曲线特性的分析,论文在本节中探索对优势函数的初步修改,即隐式奖励设计
- 论文的目标是探索隐式奖励设计的潜力,并为未来的研究提出几个有前景的方向
Exceeding Pass@k Training
- 在之前的讨论中,论文发现 \(\eta\) 函数的最大值位置会影响训练目标(侧重于 Pass@1 还是 Pass@k)
- 基于这些观察和结论,论文假设\(\eta\)函数的峰值出现得越早, Pass@k Training 的优化性能就越好
- 为了验证这一假设,论文设计了一个转换函数如下:
$$
f\left(N_\text{pos}\right) = \frac{4}{10 \log \left(N_\text{pos} + 0.5\right)}, \hat{A}’ = f\left(N_\text{pos}\right) \times \hat{A}.
$$ - 应用转换函数后的优势值曲线如图18c所示

- 论文观察到,在转换后的曲线中,\(\eta\) 函数的峰值向前移动到正确率为 \(\frac{1}{32}\) 的位置,根据论文的假设,这种优势函数的修改有望为 Pass@k Training 带来更好的优化性能
- 论文将这种转换函数集成到 RLVR 训练过程中(称为超越 Pass@k Training (Exceeding Pass@k Training)),相应的训练结果如图 11 所示
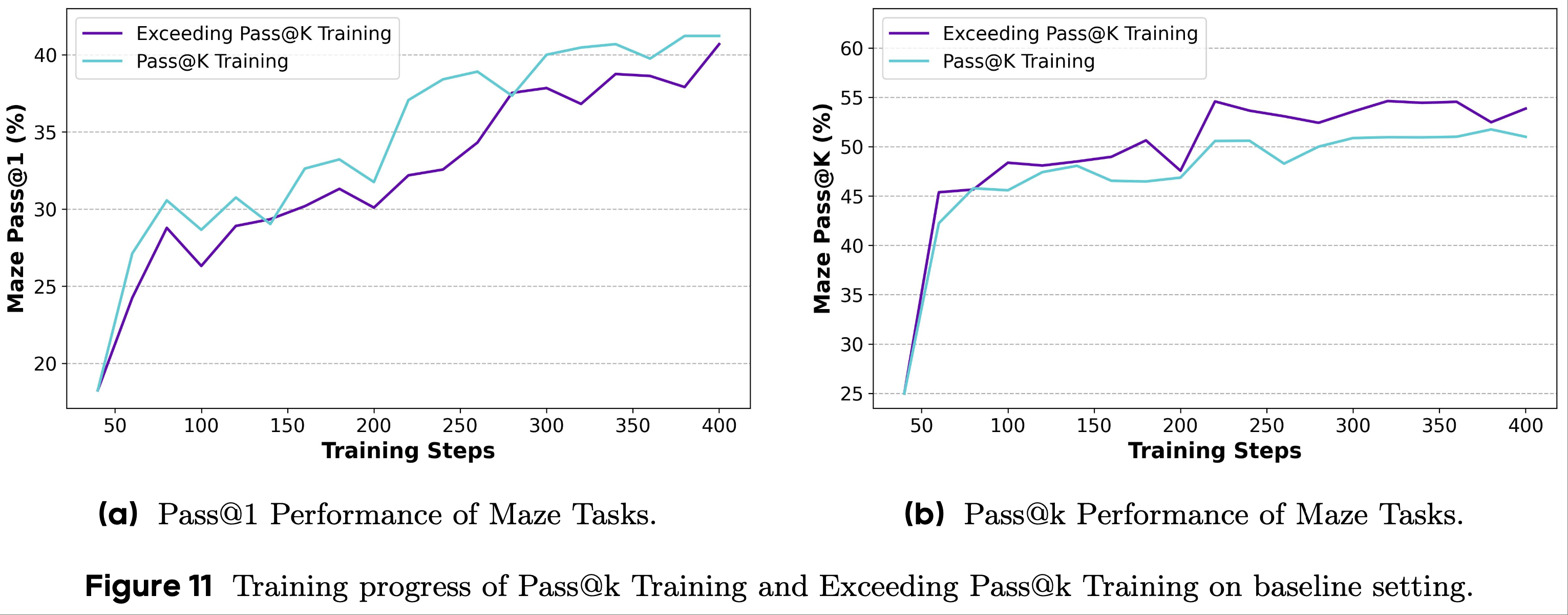
- 从实验结果中,论文观察到超越 Pass@k Training 能够在训练早期有效提高模型的 Pass@k 性能
- 但由于这种方法过分强调困难问题,下游任务的 Pass@1 性能改进进展较为缓慢
- 基于这些观察和分析,论文假设可以根据模型的当前状态自适应地调整优势值的计算(论文将其留作未来的研究方向)
Combination of Pass@1 and Pass@k Training
- 从之前的分析中,论文观察到 Pass@k Training 更注重优化更难的问题,并防止模型过拟合于简单问题
- 受此观察启发,论文考虑将 Pass@1 Training 和 Pass@k Training 结合起来是否有益
- 因此,论文设计了以下公式来估计最终的优势值:
$$
\hat{A} = \frac{N_\text{pos} }{N} \times \hat{A}_{Pass@k} + \left(1 - \frac{N_\text{pos} }{N}\right) \times \hat{A}_{Pass@1}, \tag{18}
$$- 其中,\(\hat{A}_{Pass@k}\) 和 \(\hat{A}_{Pass@1}\) 分别表示通过 Pass@k 和 Pass@1 Training 方法估计的优势值
- 在上述公式(称为组合训练(Combination Training))中
- 当采样响应的正确率较低时,来自 Pass@1 Training 的优势值会被赋予更高的权重并主导训练过程,从而带来较高的训练效率
- 当采样响应的正确率较高时,来自 Pass@k Training 的优势值会被赋予更大的权重,从而避免大语言模型过拟合于已经掌握的问题
- 在图12 中,论文展示了 Qwen 系列模型在 Enigmata 基准上的训练结果
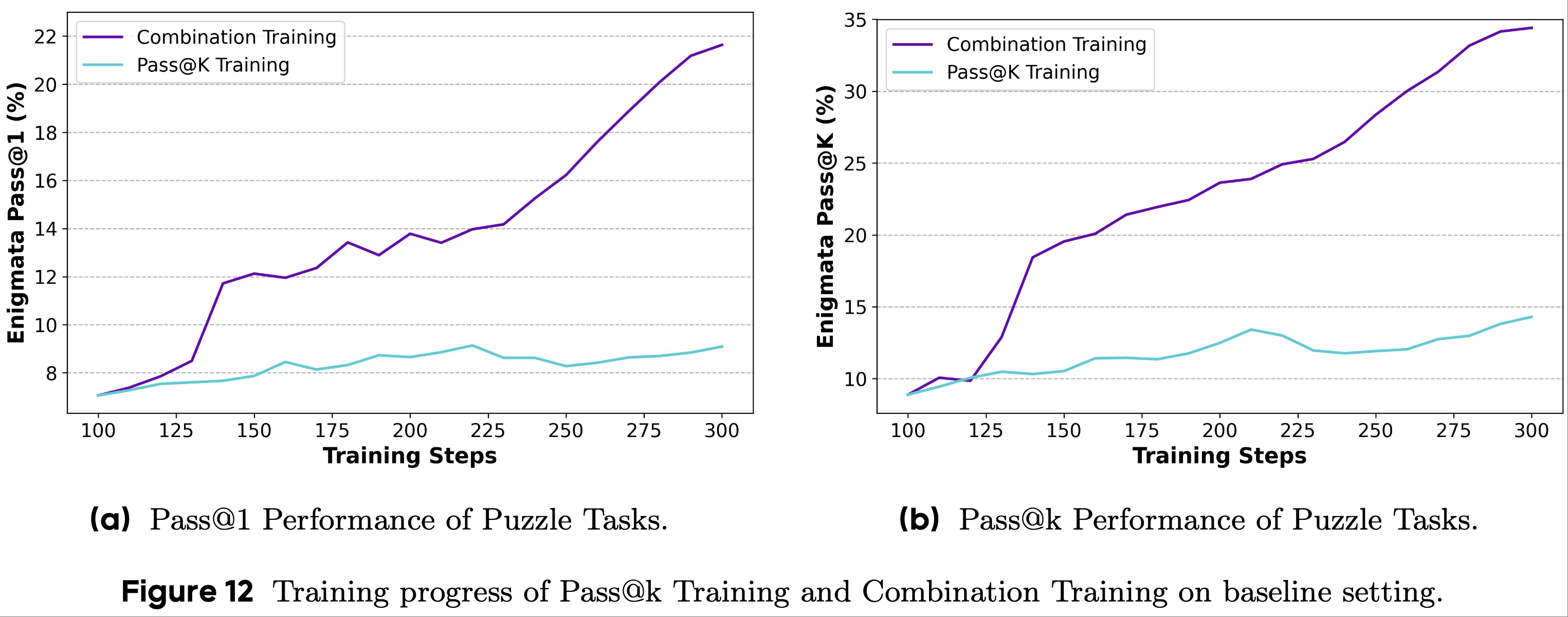
- 论文观察到,对于 Pass@ 和 Pass@8 指标,通过组合训练得到的模型始终优于通过标准 Pass@k Training 得到的模型
- 在组合训练过程中,模型性能提升迅速,并保持较高的增长率,相比之下, Pass@k Training 导致性能提升较慢
- 这是因为:
- 1)困难问题需要模型进行大量探索才能有效学习,因此难以快速改进
- 2)简单问题在训练过程中获得较低但足够的优化强度
- 以上这两个因素共同导致 Pass@k Training 的优化效率低于组合训练
- 这是因为:
- 上述分析进一步支持了基于模型当前状态调整优势函数可以有效提升模型性能的观点
Adaptive Training based on Policy Entropy
- 基于前一节的见解,论文探索是否可以在整个 RLVR 过程中自适应地调整训练目标
- 如先前的工作(2025)所讨论的,策略分布的熵可以指示其探索能力
- 论文进行了基于策略熵指导的 Pass@k Training (称为自适应训练(Adaptive Training))
- 具体而言,论文首先计算每个问题的采样响应的平均熵 \(\bar{E}\),然后根据 \(\bar{E}\) 对每个问题进行排序
- 论文将前 50% 指定为高探索问题,其余为低探索问题
- 对于高探索问题,论文使用 Pass@1 优势函数来帮助模型利用先前的探索成果
- 对于低探索问题,论文应用 Pass@k 优势函数来鼓励进一步探索
- 这种方法利用策略熵来指导优势计算,使论文能够结合不同训练策略的优势
- 论文在图13 中展示了实验结果
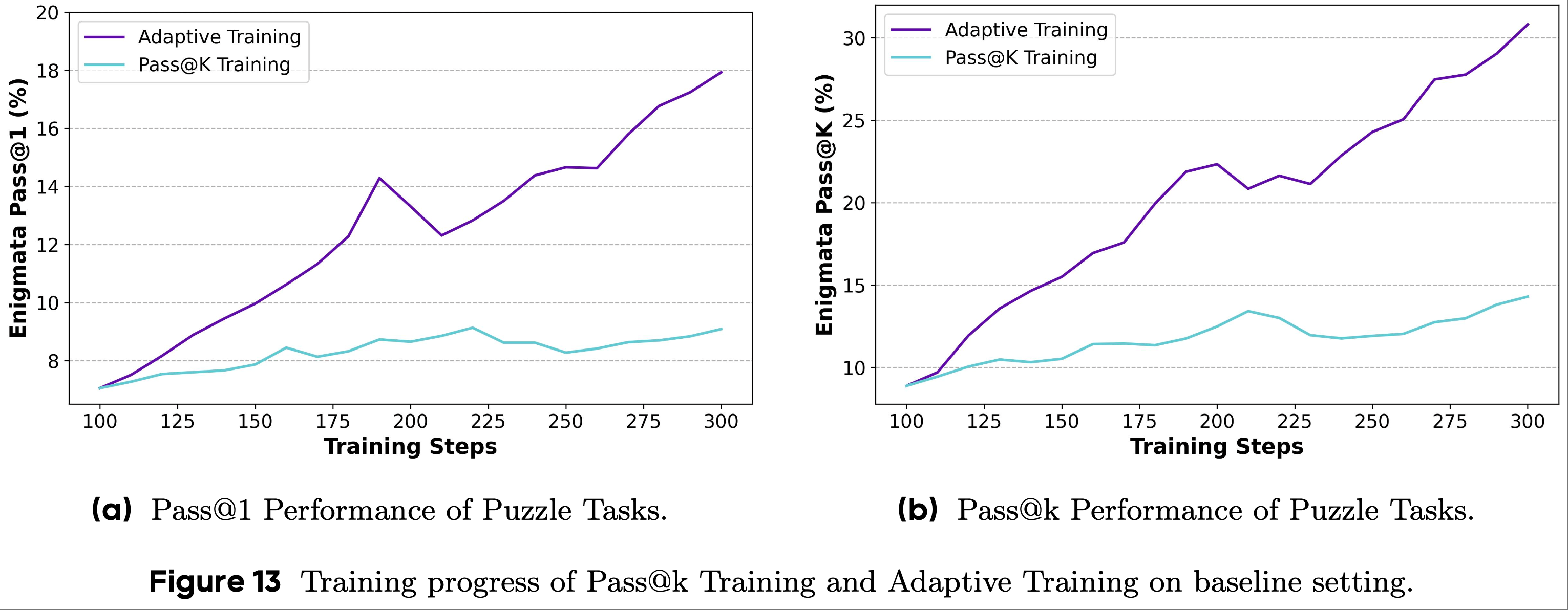
- 图13 的实验结果表明:
- 在自适应训练下,模型在 Pass@1 和 Pass@k 性能上都取得了有效的提升,优于 Pass@1 Training 和 Pass@k Training
- 这表明 Pass@1 Training 和 Pass@k Training 是互补的
- 通过设计适当的适应机制,有可能更好地利用两种训练方法的优势,使模型在下游任务上取得更好的性能
- 这也证实了策略分布的熵可以作为模型探索能力的指标,并且与 Pass@k Training 能够很好地结合
- 使用熵作为监控信号来调整 RLVR 训练比直接将其用作训练目标能产生更好的结果
- 在自适应训练下,模型在 Pass@1 和 Pass@k 性能上都取得了有效的提升,优于 Pass@1 Training 和 Pass@k Training
- Takeaway from Section 4.2 :
- 隐式奖励设计可以更好地控制优化过程,避免复杂的理论推导
- 具体而言,增加对更困难问题的优化强度可以有效提升模型解决这些问题的能力(即 Pass@k 性能),而结合或动态调整不同形式的优势估计可以同时提升探索和利用能力
Related Work
Reinforcement Learning with Verifiable Rewards
- 为了释放 LLM 的推理能力,DeepSeek 直接在 DeepSeek-V3 上采用 RLVR ,得到了大型推理模型 DeepSeek-R1-Zero(2025),该模型能够执行具有复杂推理动作(如反思和验证)的推理过程
- 鉴于 DeepSeek-R1 的成功,大量研究(2025;)探索了 RLVR 在流行的开源大语言模型上的有效性,如 Qwen(2024)、Mistral(2023)和 LLaMA(2024)
- 此外,RLVR 训练范式可以帮助大语言模型控制其推理时间(2025)、切换推理模式(2025;)、增强特定性能指标(2025),以及在无监督的情况下提升自身能力(2025;)
- 然而,最近的研究指出,流行的 RLVR 算法(如 PPO(2017)和 GRPO(2024))仍然面临严峻挑战,如训练不稳定性、模型崩溃和奖励噪声(2025;)
- 为了缓解这些问题,现有研究提出了对采样策略(2025)、目标函数设计(2025;)和数据选择(2025)的优化
- 具体而言,先前的工作(2025)将 Pass@k 用作策略梯度算法(1992)的奖励,以鼓励模型解决更难的问题
- 然而,Pass@k RLVR 训练与大语言模型探索能力之间的内在联系尚未得到充分认识
- 论文通过三种方法(图5)在 GRPO 及其变体中进一步采用 Pass@k 指标,并推导了 RLVR 训练中 Pass@k 奖励的优势值解析解
- 此外,根据实证实验和理论分析,论文讨论了 Pass@k Training 在平衡大语言模型 RLVR 训练过程中的探索和利用能力方面的益处,展示了 Pass@k RLVR 训练的巨大潜力,并指出了未来有前景的研究方向
Effective Exploration in Test-time Scaling
- 最近,测试时扩展被提出,它旨在通过在推理时消耗更多计算资源来提高大语言模型的性能(2025)
- 由于大语言模型不断利用探索获得的经验来优化其性能,因此在测试时扩展过程中,有效的探索是重要且必要的(2025;2025)
- 但现有工作表明,探索能力受到相应基础模型的限制,阻碍了模型性能的持续扩展(2025)
- 为了缓解这一问题,先前的工作提出了几种方法,包括
- 通过调整采样超参数(2025;2025;2025)
- 执行自我验证和自我反思(2025;2025;2025)
- 利用外部模型验证推理过程(2025;2025)
- 除了从模型外部角度出发的这些方法外,通过模型内部机制探索其探索能力也同样重要
- 当前研究从策略分布的熵的角度出发,指出熵可以指示大语言模型的探索能力(2025;2025),并且高熵 token 对模型优化至关重要(2025)
- 基于这些发现,在 RLVR 训练过程中采用了训练关键 token(2025)和添加正则化(2025;2025)的方法,以避免大语言模型探索能力的下降
- 此外,一些研究专注于通过选择有用的采样经验(2025;2025)、将熵集成到优势估计中(2025)来增强大语言模型的探索能力
附录 A:Experiment Setup
A.1 Details of Downstream Tasks
- 本节介绍每个下游评估任务的详细信息
- 迷宫(Maze)
- 论文遵循先前工作提出的框架来合成不同大小的迷宫
- 每个迷宫用文本表示,包含 n 行 n 列,共 n×n 个字符。具体来说,每个字符是以下四种之一:“S”“E”“*”和“.”,分别表示起点、终点、可通行区域和不可通行区域
- 给定迷宫,LLM 可以先生成思路或推理过程,然后生成最终答案,包括“U”“D”“L”“R”四种动作之一,分别表示向上、向下、向左、向右移动
- 对于训练数据,论文构建了 9×9、11×11、13×13 和 15×15 大小的迷宫,以增加训练数据的多样性
- 对于测试数据,为了评估 RLVR 过程的泛化能力,论文不仅使用与训练数据集相同大小的迷宫,还收集了 7×7、17×17、19×19 和 21×21 大小的迷宫
- 为确保实验的有效性,论文在生成训练和测试数据后进行了严格的去重操作
- 数据集的统计信息如表4所示
- 为了更清晰地呈现实证见解,论文在上述正文中只展示了 9×9 迷宫的结果,其余结果在附录E.3中呈现

- Enigmata
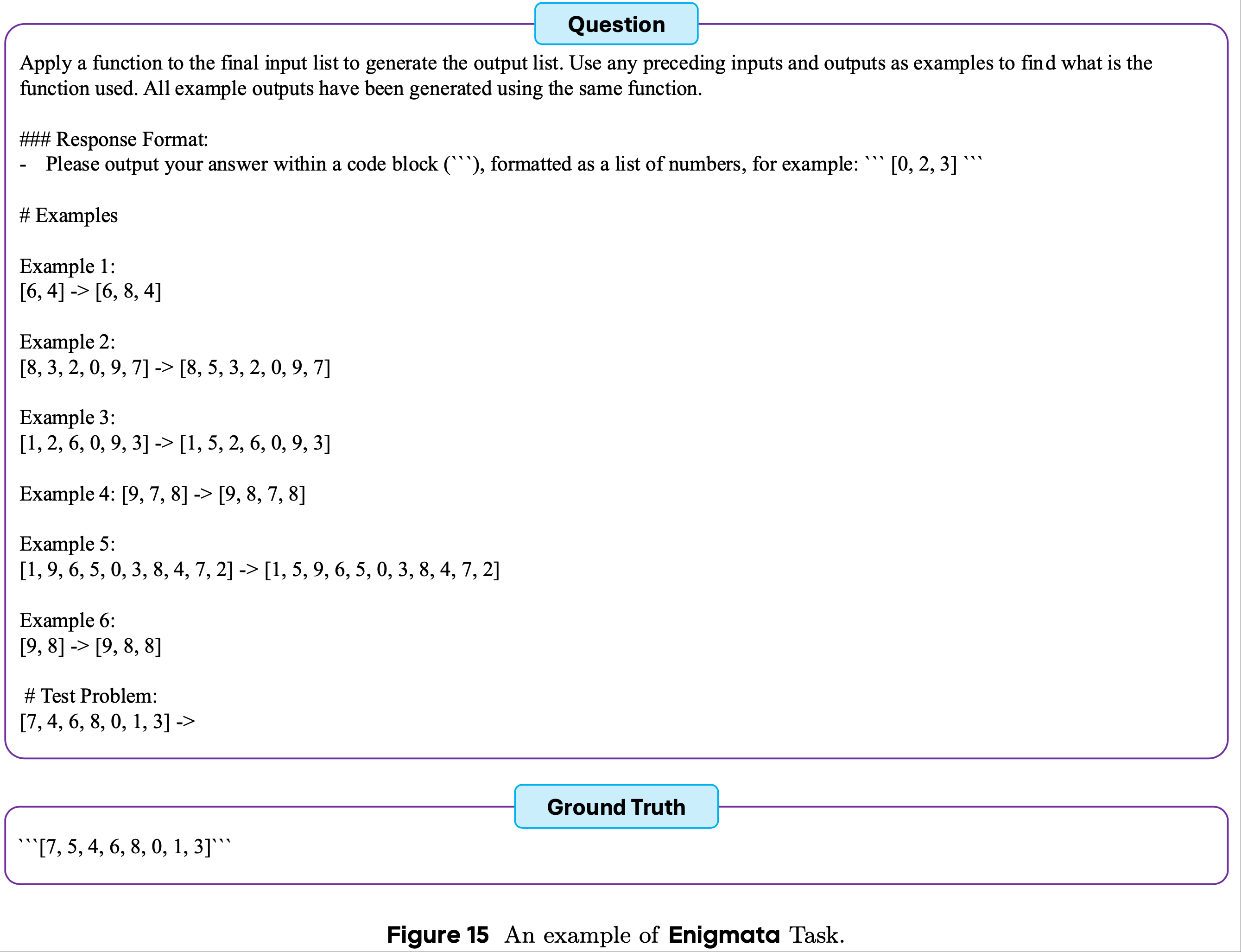
- 为评估大语言模型的推理和逻辑能力,Enigmata 提出了一个综合基准,包括 36 类合成可验证谜题,分属 7 个主要类别,包括密码谜题(Crypto Puzzle)、算术谜题(Arithmetic Puzzle)、逻辑谜题(Logic Puzzle)、网格谜题(Grid Puzzle)、图形谜题(Graph Puzzle)、搜索谜题(Search Puzzle)和序列谜题(Sequential Puzzle)
- 每个类别都能评估大语言模型的不同能力
- 为便于理解,论文在图15 中展示了一个测试实例
- MathVision
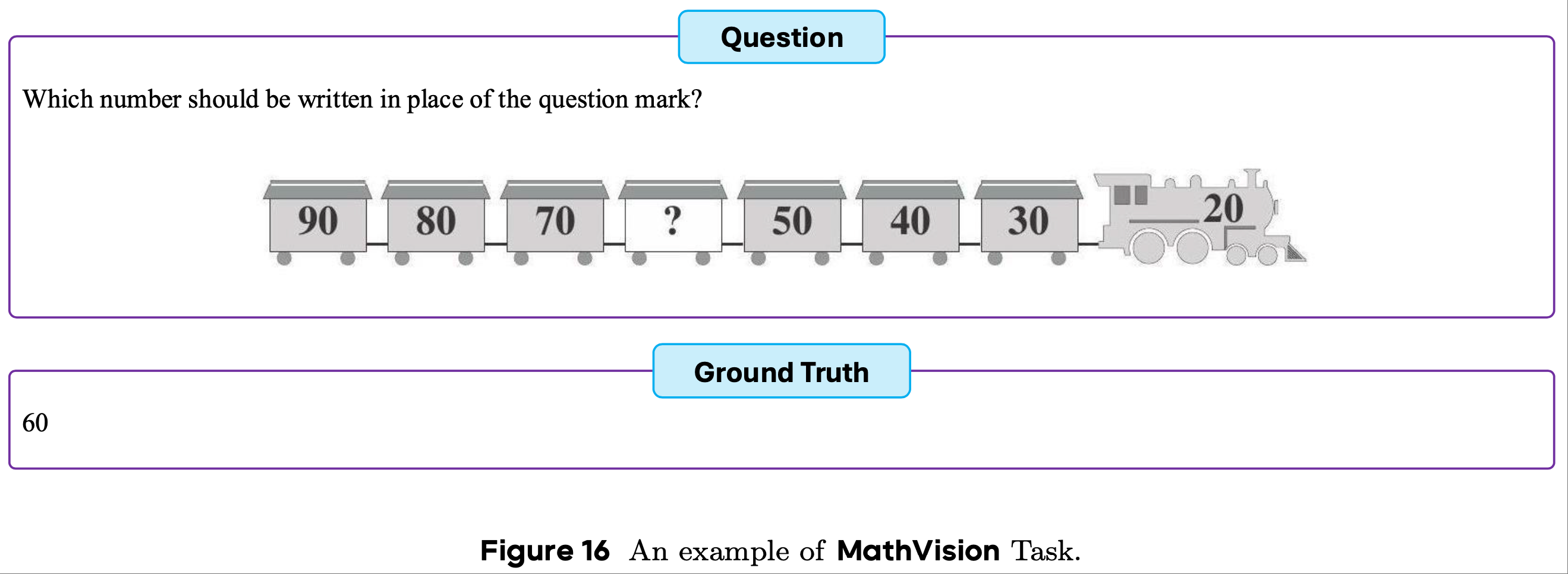
- MathVision 从人类数学竞赛中选取了 3,040 道高质量题目,每道题都附有相关图像
- 解决这些问题需要仔细解读视觉信息和严谨的数学推理
- MathVision 为评估模型的多模态理解能力以及严谨的数学推理能力提供了基准
- 为便于理解,论文在图16 中展示了一个测试实例
- MMMU
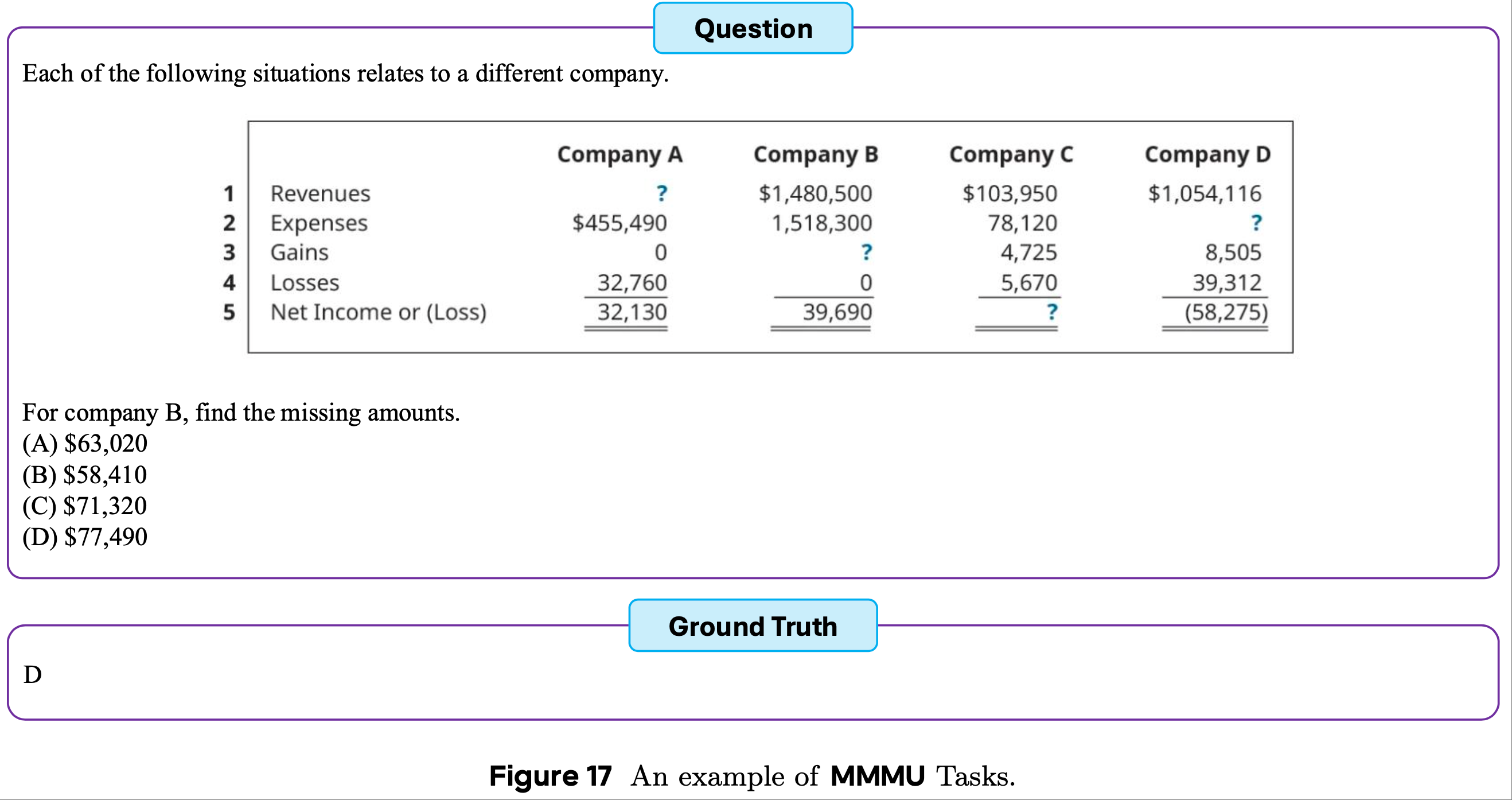
- MMMU 包括六个学科的大学水平推理和理解任务,包括艺术与设计(Art & Design)、商业(Business)、科学(Science)、健康与医学(Health & Medicine)、人文与社会科学(Humanities & Social Science)以及技术与工程(Tech & Engineering)
- 此外,MMMU 包含多种图像类型,能够全面评估模型处理和推理不同形式视觉信息的能力
- 为便于理解,论文在图17中展示了一个测试实例
A.2 Implementation Details
- 训练(Training)
- 在论文的实验中,论文采用 Qwen2.5-7B-Instruct 和 Qwen2.5-32B-Instruct 作为骨干模型,并通过 DAPO 进行训练
- 为提高训练过程的效率,论文只保留 clip-higher(即 \(\varepsilon_{low}=0.2\) 和 \(\varepsilon_{high}=0.28\))和 token-lebel 策略梯度损失,移除其他优化
- 对于训练超参数,论文将策略模型的学习率设置为 \(1×10^{-6}\),预热步骤为10步,并分别采用 128、32 和 32 作为提示批大小 \(BS_{prompt}=128\)、小批大小 \(BS_{mini}=32\) 和 采样次数 \(n_\text{rollout}=32\)
- 对于奖励,通过验证的响应(称为正响应)被赋予正奖励\(R_\text{pos}=1\),其他响应(称为负响应)被赋予负奖励\(R_\text{neg}=0\)
- 论文不采用任何正则化方法,如 KL 或 熵正则化
- Evaluation
- 为评估大语言模型的性能,论文采用
temperature= 1.0和top_p=0.95 - 对于每个问题,论文为迷宫任务从大语言模型中采样 32 个响应,为其他任务采样 8 个响应,然后利用采样的响应计算 Pass@1 和 Pass@k 分数
- 为评估大语言模型的性能,论文采用
附录 B:Details of Analytical Derivation(解析推导)
- 论文在2.4节中提到了解析推导过程的细节,包括组奖励的平均值、组奖励的标准差以及响应相关优势的推导
B.1 Derivation of the Average of Group Reward
$$
\begin{aligned}
\overline{R}^\text{group} &= \frac{1}{N_\text{total}^\text{group} } \times \left(N_\text{pos}^\text{group} \times R_\text{pos} + N_\text{neg}^\text{group} \times R_\text{neg}\right) \\
&= \frac{1}{\binom{N_\text{rollout} }{K} } \times \left( \left( \binom{N_\text{rollout} }{K} - \binom{N_\text{neg} }{K} \right) \times 1 + \binom{N_\text{neg} }{K} \times 0 \right) \\
&= 1 - \frac{\binom{N_\text{neg} }{K} }{\binom{N_\text{rollout} }{K} }.
\end{aligned}
$$
B.2 Derivation of the Standard Deviation of Group Reward
$$
\begin{aligned}
\sigma^\text{group} &= \sqrt{ \frac{1}{N_\text{total}^\text{group} } \left( N_\text{pos}^\text{group} \times \left(1 - \overline{R}^\text{group}\right)^2 + N_\text{neg}^\text{group} \times \left(0 - \overline{R}^\text{group}\right)^2 \right) } \\
&= \sqrt{ \overline{R}^\text{group} \times \left(1 - \overline{R}^\text{group}\right) }.
\end{aligned}
$$
B.3 Derivation of the Response-Relative Advantage
$$
\begin{aligned}
\hat{A}_\text{pos} &= \frac{1}{\binom{N_\text{rollout}-1}{K-1} } \times \left( \binom{N_\text{rollout}-1}{K-1} \times \hat{A}_\text{pos}^\text{group} + 0 \times \hat{A}_\text{neg}^\text{group} \right) \\
&= \frac{1 - \overline{R}^\text{group} }{\sigma^\text{group} }.
\end{aligned}
$$
$$
\begin{aligned}
\hat{A}_\text{neg} &= \frac{1}{\binom{N_\text{rollout}-1}{K-1} } \times \left( \left( \binom{N_\text{rollout}-1}{K-1} - \binom{N_\text{neg}-1}{K-1} \right) \times \hat{A}_\text{pos}^\text{group} + \binom{N_\text{neg}-1}{K-1} \times \hat{A}_\text{neg}^\text{group} \right) \\
&= \left( 1 - \frac{\binom{N_\text{neg}-1}{K-1} }{\binom{N_\text{rollout}-1}{K-1} } \right) \times \frac{1 - \overline{R}^\text{group} }{\sigma^\text{group} } + \frac{\binom{N_\text{neg}-1}{K-1} }{\binom{N_\text{rollout}-1}{K-1} } \times \left( -\frac{\overline{R}^\text{group} }{\sigma^\text{group} } \right) \\
&= \left( 1 - \overline{R}^\text{group} - \frac{\binom{N_\text{neg}-1}{K-1} }{\binom{N_\text{rollout}-1}{K-1} } \right) \times \left( \sigma^\text{group} \right)^{-1}.
\end{aligned}
$$
附录 C: Pass@k Training 的伪代码(Pseudo Code for Pass@k Training)
- 论文给出了全采样(Algorithm 1)、bootstrap采样(Algorithm 2)和解析推导(Algorithm 3)的 Pass@k Training 伪代码
算法1:全采样的 Pass@k Training 伪代码
- 伪代码:

- 具体步骤:
- 输入:问题响应的奖励张量\(R \in \mathbb{R}^{N_\text{rollout} }\)、采样响应数量\(N_\text{rollout}\)以及Pass@k指标中的k
- 输出:该问题响应的估计优势张量\(\hat{A} \in \mathbb{R}^{N_\text{rollout} }\)
- 1 # 构建组并丢弃冗余实例
- 2 将\(R \in \mathbb{R}^{N_\text{rollout} }\)分成\(\left\lfloor \frac{N_\text{rollout} }{K} \right\rfloor\)个组,每个组包含k个实例
- 3 使用公式5计算组的奖励\(R^\text{group} \in \mathbb{R}^{\left\lfloor \frac{N_\text{rollout} }{K} \right\rfloor}\)
- 4 # 遵循GRPO优势估计方法计算组相关优势
- 5 使用公式1计算组的平均奖励\(\bar{R}^\text{group}\)
- 6 使用公式2计算组的标准差\(\sigma^\text{group}\)
- 7 基于\(\bar{R}^\text{group}\)和\(\sigma^\text{group}\),使用公式3计算组相关优势\(\hat{A}^\text{group}\)
- 8 # 计算响应相关优势
- 9 将\(\hat{A}^\text{group}\)分配给组所包含的响应,得到响应相关优势A
算法2:bootstrap采样的 Pass@k Training 伪代码
- 伪代码:

- 具体步骤:
- 输入:问题响应的奖励张量\(R \in \mathbb{R}^{N_\text{rollout} }\)、采样响应数量\(N_\text{rollout}\)以及Pass@k指标中的k
- 输出:该问题响应的估计优势张量\(\hat{A} \in \mathbb{R}^{N_\text{rollout} }\)
- 1 # 通过bootstrap采样构建组
- 2 对于i从1到\(N^\text{group}\):
- 3 从R中随机采样k个实例构建第i个组
- 4 使用公式5计算第i个组的奖励
- 5 得到组的奖励\(R^\text{group} \in \mathbb{R}^{N^\text{group} }\)
- 6 # 遵循GRPO优势估计方法计算组相关优势
- 7 使用公式1计算组的平均奖励\(\bar{R}^\text{group}\)
- 8 使用公式2计算组的标准差\(\sigma^\text{group}\)
- 9 基于\(\bar{R}^\text{group}\)和\(\sigma^\text{group}\),使用公式3计算组相关优势\(\hat{A}^\text{group}\)
- 10 # 计算响应相关优势
- 11 基于\(\hat{A}^\text{group}\),使用公式6计算响应相关优势A
算法3:解析推导的 Pass@k Training 伪代码
- 伪代码:

- 具体步骤:
- 输入:问题响应的奖励张量\(R \in \mathbb{R}^{N_\text{rollout} }\)、采样响应数量\(N_\text{rollout}\)以及Pass@k指标中的k
- 输出:该问题响应的估计优势张量\(\hat{A} \in \mathbb{R}^{N_\text{rollout} }\)
- 1 # 计算组奖励分数的平均值和标准差
- 2 使用公式11计算组的平均奖励\(\bar{R}^\text{group}\)
- 3 使用公式12计算组的标准差\(\sigma^\text{group}\)
- 4 # 计算响应相关优势
- 5 使用公式14计算正响应的优势\(\hat{A}_\text{pos}\)
- 6 使用公式15计算负响应的优势\(\hat{A}_\text{neg}\)
- 7 基于\(\hat{A}_\text{pos}\)、\(\hat{A}_\text{neg}\)和R,为每个实例分配优势,得到响应相关优势A
附录 D:Curves of Advantage Function
- 论文在图18中展示了不同训练方法的优势函数曲线,包括无简单问题的 Pass@k Training (Pass@k Training w/o easy problems)、带组合的 Pass@k Training (Pass@k Training w/ combination)、超越 Pass@k Training (Exceeding Pass@k Training)和组合训练(Combination Training)

附录 E:Experiments on Various LLMs and Tasks
- 在本节中,为进一步验证 Pass@k Training 的有效性,论文提供了通过 Pass@k Training 的各种大语言模型在数学任务(即AIME 2024、AIME 2025和OlymMATH(2025))和合成谜题任务(即Enigmata(2025))上的性能
E.1 数学任务上的 Pass@k Training (Pass@k Training on Mathematical Tasks)
- 论文遵循附录A.2 中描述的实验设置,在 LLaMA 模型(2024)(即 LLaMA3.2-3B-Instruct 和 LLaMA3.1-8B-Instruct)和DeepSeek-R1-Distill-Qwen(2025)(即1.5B和7B版本)上进行 Pass@k Training
- 对于LLaMA模型,论文将最大提示长度和响应长度分别设置为 2048 和 6144
- 对于DeepSeek-R1-Distill-Qwen,论文将响应长度扩展到 10240
- 具体而言,为使大语言模型适应数学任务,论文在 RLVR 训练过程中采用了先前工作(2025)中使用的训练数据
- 此外,论文遵循附录A.2中的设置进行评估,结果如表5 所示
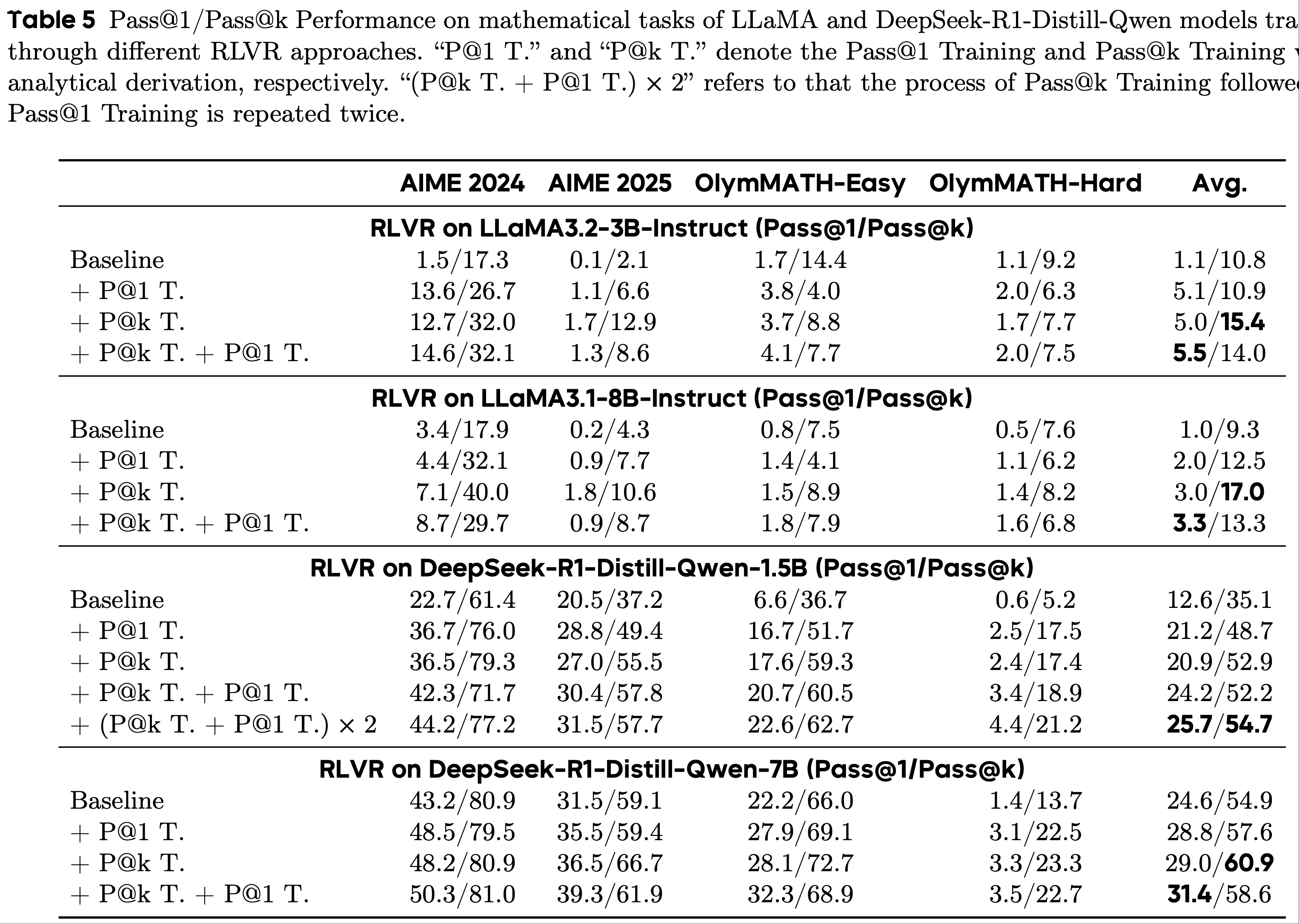
- 由于单轮 Pass@k Training 后再进行 Pass@1 Training 可以显著提高大语言模型的Pass@1性能,论文在表5 中进行了上述训练过程多轮的实验,称为“(P@k T. + P@1 T.) × 2”
E.2 Enigmata任务上的 Pass@k Training (Pass@k Training on Enigmata Task)
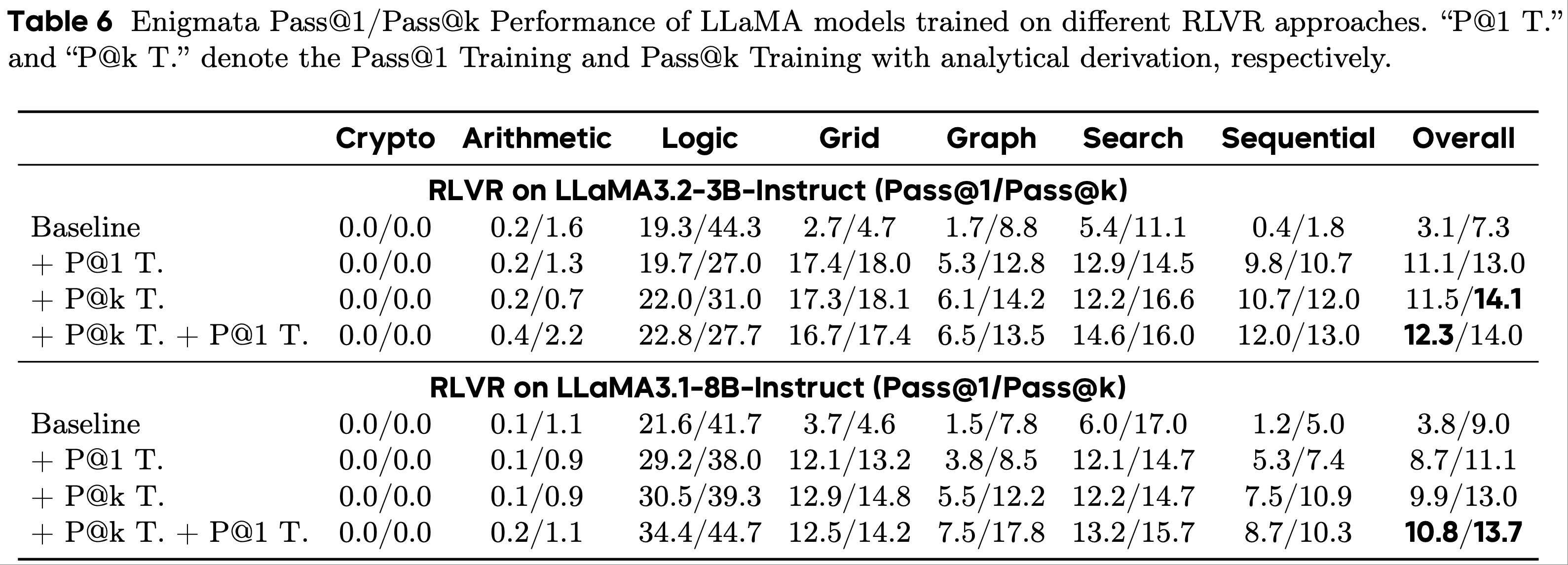
- 论文遵循附录A.2 中描述的实验设置,在各种大语言模型(即 LLaMA3.2-3B-Instruct(2024)和 LLaMA3.1-8B-Instruct(2024))上进行 Pass@k Training ,并将最大提示长度和响应长度都设置为 4096
- 结果如表6所示(对于评估,论文遵循附录A.2中描述的设置)
E.3 迷宫任务上的 Pass@k Training (Pass@k Training on Maze Task)
- 在本部分中,论文在表7中展示了 Pass@k Training 在迷宫任务上的完整结果
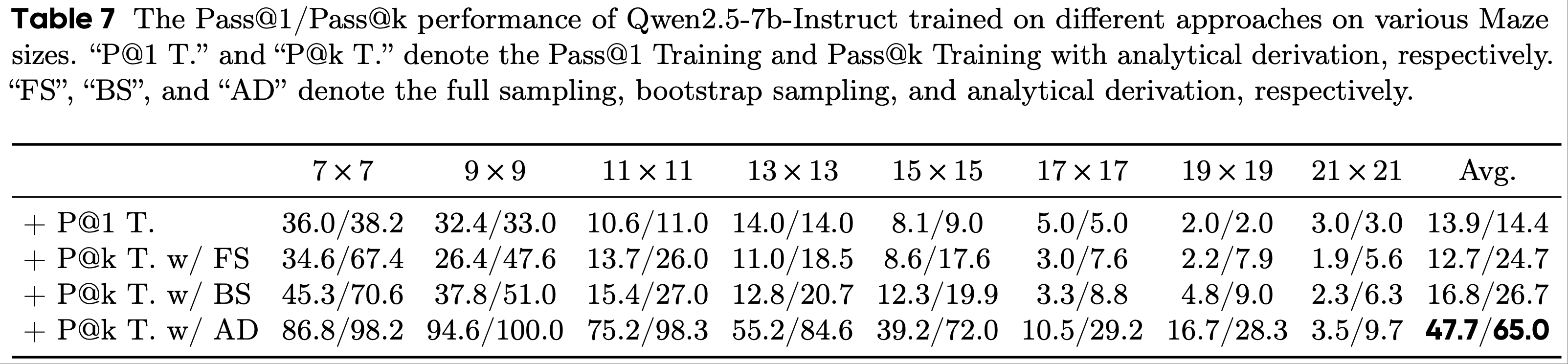
- 没有任何 RLVR 训练时,模型很难解决迷宫任务,因此,论文没有报告骨干模型的性能