注:本文包含 AI 辅助创作
- 参考链接:
- 原始论文:Direct Preference Optimization: Your Language Model is Secretly a Reward Model, NeurIPS 2023, Stanford University
- 论文阅读笔记:DPO——RLHF 的替代之《Direct Preference Optimization: Your Language Model is Secretly a Reward Model》论文阅读
- 一些较为高阶的讨论:RLHF的替代之DPO原理解析:从RLHF、Claude的RAILF到DPO、Zephyr
- DPO 的应用:利用直接偏好优化算法(DPO)微调语言模型, 消除幻觉
Paper Summary
- 核心总结:
- 写在前面:本文的理论推导非常漂亮,值得细看
- DPO 是一个简单的训练范式,用于从偏好中训练语言模型而无需强化学习(24 年底补充:DPO 已经成为了某些领域在 RL 前必不可少的一个基线)
- DPO 识别了语言模型策略和奖励函数之间的映射(区别于传统 RL 的偏好学习方法)
- 使得能够直接训练语言模型以满足人类偏好,使用简单的交叉熵损失,无需强化学习或损失一般性
- 在作者的实验上,在几乎不需要调整超参数的情况下,DPO 的表现与现有的 RLHF 算法(包括基于 PPO 的算法)相当或更好;
- DPO 有降低了从人类偏好训练更多语言模型的门槛
- 实际上比 PPO 好是需要打问号的,PPO 的理论上限是更高的
- 背景:RLHF 是一个复杂且通常不稳定的过程,需要拟合一个反映人类偏好的奖励模型,然后使用 RL 来微调以最大化这个估计的奖励,同时不能偏离原始模型太远
- 论文介绍了 RLHF 中奖励模型的一个新参数化(parameterization)方法(DPO),能够 以闭式(closed form)解提取相应的最优策略
- 这使得我们仅使用一个简单的分类损失来解决标准的 RLHF 问题
Introduction and Discussion
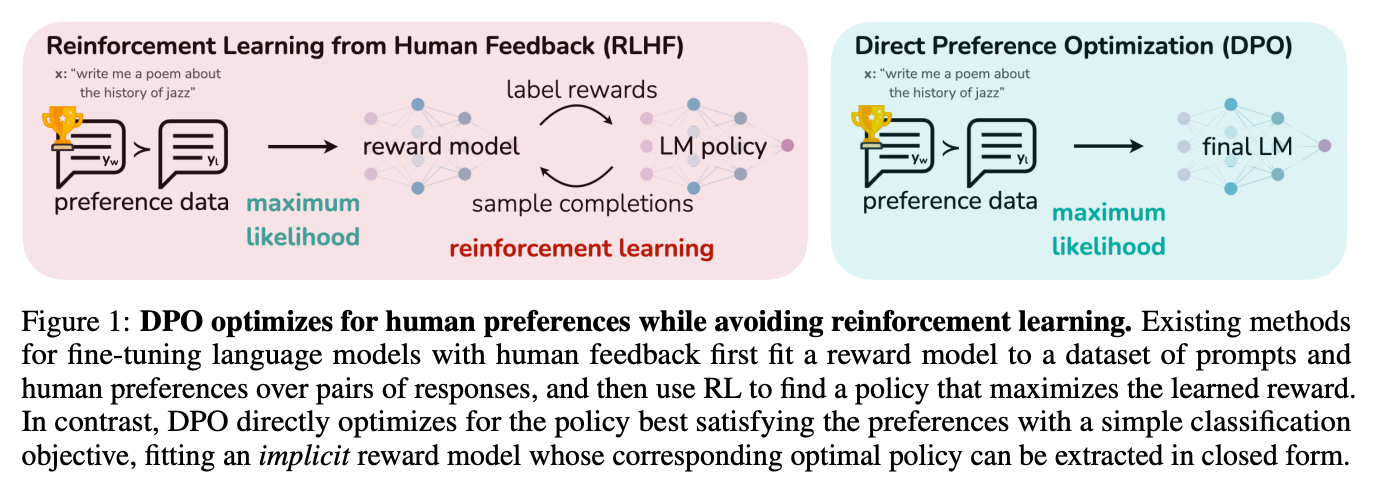
- 论文展示了如何直接优化语言模型以遵循人类偏好,而无需显式的奖励建模或强化学习
- 论文提出了直接偏好优化 (DPO) 算法
- DPO 隐式地优化了与现有 RLHF 算法相同的目标(带有 KL 散度约束的奖励最大化),但实现简单且训练直接
- 直观地说
- DPO 更新增加了优选响应相对于非优选响应的相对对数概率,但它引入了一个动态的、每个样本的重要性权重,防止了论文发现的在朴素概率比目标下发生的模型退化
- 与现有算法类似
- DPO 依赖于一个理论偏好模型(例如 Bradley-Terry 模型 (1952)),该模型衡量给定奖励函数与经验偏好数据的对齐程度
- 现有方法使用偏好模型来定义训练奖励模型的偏好损失,然后训练一个优化所学奖励模型的策略
- DPO 使用变量变换将偏好损失直接定义为策略的函数
- 给定一个关于模型响应的人类偏好的数据集,DPO 可以使用简单的二元交叉熵目标来优化策略,产生拟合到偏好数据的隐式奖励函数的最优策略
- 论文的主要贡献就是 DPO,一种简单的、无 RL 的从偏好中训练语言模型的算法
- 实验表明,在使用多达 6B 参数的语言模型进行情感调节、摘要和对话等任务的偏好学习中,DPO 至少与现有方法(包括基于 PPO 的RLHF)一样有效
Related Work
- 规模不断增长的自监督语言模型学会零样本 (2019) 或少样本提示 (2020; 2021; 2022) 完成某些任务
- 但它们在下游任务上的表现和与用户意图的对齐可以通过在指令和人类编写的补全数据集上进行微调来显著提高 (2022; 2022; 2022; 2022)
- 这种“指令微调”过程使得大型语言模型能够泛化到指令微调集之外的指令,并通常提高其可用性 (2022)
- 但响应质量的相对人类判断通常比专家演示更容易收集,因此后续工作使用人类偏好数据集微调了大型语言模型,提高了在翻译 (2018)、摘要 (2020; 2022)、故事讲述 (2022) 和指令遵循 (2022; 2023) 方面的熟练度
- 这些方法的大致流程是:
- 首先在诸如 Bradley-Terry 模型 (1952) 等偏好模型下,优化一个神经网络奖励函数以与偏好数据集兼容
- 然后通常使用强化学习算法,如 REINFORCE (1992)、PPO 或其变体 (2023),来微调语言模型以最大化给定的奖励
- 这些方法代表了两类工作的融合:
- 一类是关于使用强化学习训练语言模型以实现各种目标的工作 (2015; 2018; 2018)
- 另一类是关于从人类偏好中学习的通用方法的工作 (2017; 2018)
- 尽管使用相对人类偏好具有吸引力,但使用强化学习微调大型语言模型仍然是一个重大的实际挑战;
- DPO 提供了一种理论上有依据的方法来优化相对偏好而无需 RL
在语言领域之外
- 从偏好中学习策略已在赌博机和强化学习设置中都得到了研究,并且已经提出了几种方法
- 使用偏好或行动排序而非奖励的情境赌博机学习被称为情境对决赌博机 (Contextual Dueling Bandit, CDB; (2012; 2015))
- 在没有绝对奖励的情况下,CDB 的理论分析用冯·诺依曼赢家 (von Neumann winner) 的概念替代了最优策略,即一个对任何其他策略的期望获胜率至少为 50% 的策略 (2015)
- 在 CDB 设置中,偏好标签是在线给出的
- 在从人类偏好学习中,通常从固定的离线偏好标注行动对批次中学习 (2022)
- 基于偏好的 RL (Preference-based RL, PbRL) 从由 未知“评分” 函数生成的二元偏好中学习,而不是从奖励中学习 (2014; 2023)
- 存在各种 PbRL 算法,包括可以重用离策略偏好数据的方法,但通常涉及首先显式估计潜在评分函数(即奖励模型),然后对其进行优化 (2013; 2014; 2017; 2018; 2018)
- 论文提出了一种单阶段策略学习方法,直接优化策略以满足偏好
Preliminaries
- 论文回顾一下 Ziegler 等人(以及后来的 (2020; 2022; 2022))中的 RLHF 流程,它通常包括三个阶段:
- 1)监督微调 (Supervised Fine-Tuning, SFT);
- 2)偏好采样和奖励学习;以及
- 3)RL 优化
SF
- RLHF 通常首先在下游感兴趣任务(对话、摘要等)的高质量数据上,使用监督学习对预训练的语言模型进行微调,以获得一个模型 \(\pi^{\text{SFT} }\)
奖励建模阶段
- 使用提示 \(x\) 来提示 SFT 模型,产生成对的答案
$$(y_{1},y_{2})\sim\pi^{\text{SFT} }(y \mid x)$$ - 然将这些答案呈现给人类标注者,他们表达对其中一个答案的偏好,记为
$$ y_{w}\succ y_{l} \mid x$$- 其中 \(y_{w}\) 和 \(y_{l}\) 分别表示 \((y_{1},y_{2})\) 中优选和非优选的补全
- 假设偏好是由某个论文无法访问的潜在奖励模型 \(r^{*}(y,x)\) 生成的
- 有多种方法用于建模偏好,Bradley-Terry (BT) 模型 (1952) 是一个流行的选择(尽管如果论文能访问多个排名的答案,更通用的 Plackett-Luce 排序模型 (1975; 2012) 也与该框架兼容)
- BT 模型规定人类偏好分布 \(p^{*}\) 可以写成:
$$p^{*}(y_{1}\succ y_{2} \mid x)=\frac{\exp\left(r^{*}(x,y_{1})\right)}{\exp\left(r^{*}(x,y_{1})\right)+\exp\left(r^{*}(x,y_{2})\right)} \tag{1}$$ - 假设我们可以访问一个从 \(p^{*}\) 中采样的静态比较数据集
$$ \mathcal{D}=\left\{x^{(i)},y^{(i)}_{w},y^{(i)}_{l}\right\}^{N}_{i=1}$$ - 我们可以参数化一个奖励模型 \(r_{\phi}(x,y)\) 并通过最大似然估计参数
- 将问题构建为二元分类,论文得到负对数似然损失:
$$\mathcal{L}_{R}(r_{\phi},\mathcal{D})=-\mathbb{E}_{(x,y_{w},y_{l})\sim\mathcal{D} }\big{[}\log\sigma(r_{\phi}(x,y_{w})-r_{\phi}(x,y_{l}))\big{]} \tag{2}$$- 其中 \(\sigma\) 是 logistic 函数
- 在语言模型的上下文中,网络 \(r_{\phi}(x,y)\) 通常从 SFT 模型 \(\pi^{\text{SFT} }(y \mid x)\) 初始化,并在最终 transformer 层之上添加一个线性层,该层为奖励值产生单个标量预测 (2022)
- 为了确保奖励函数具有较低的方差,先前的工作对奖励进行了归一化,使得对于所有 \(x\),有
$$\mathbb{E}_{x,y\sim\mathcal{D} }\left[r_{\phi}(x,y)\right]=0$$
RL 微调阶段
- 在 RL 阶段,学习到的奖励函数用于向语言模型提供反馈
- 遵循先前的工作 (2017; 2020),优化问题表述为
$$\max_{\pi_{\theta} }\mathbb{E}_{x\sim\mathcal{D},y\sim\pi_{\theta}(y|x)}\big{[}r_{\phi}(x,y)\big{]}-\beta\mathbb{D}_{\text{KL} }\big{[}\pi_{\theta}(y \mid x) \ | \ |\ \pi_{\text{ref} }(y \mid x)\big{]} \tag{3}$$- 其中 \(\beta\) 是一个控制与基础参考策略 \(\pi_{\text{ref} }\)(即初始 SFT 模型 \(\pi^{\text{SFT} }\))偏离程度的参数
- 在实践中,语言模型策略 \(\pi_{\theta}\) 也被初始化为 \(\pi^{\text{SFT} }\)
- 添加的约束很重要,因为它防止模型偏离奖励模型准确的分布太远,同时保持生成多样性并防止模式崩溃到单一高奖励答案
- 由于语言生成的离散性质,该目标不可微,通常使用强化学习进行优化
- 标准方法 (2022; 2020; 2022; 2022) 是构建奖励函数
$$r(x,y)=r_{\phi}(x,y)-\beta(\log\pi_{\theta}(y \mid x)-\log\pi_{\text{ref} }(y \mid x))$$- 并使用 PPO (2017) 进行最大化
- 标准方法 (2022; 2020; 2022; 2022) 是构建奖励函数
Direct Preference Optimization
- 目标是推导出一种使用偏好直接进行策略优化的简单方法
- 与先前学习奖励然后通过 RL 优化它的 RLHF 方法不同,论文的方法利用了一种特定的奖励模型参数化选择,使得无需 RL 训练循环即可闭式解提取其最优策略
- 论文的关键见解是利用从奖励函数到最优策略的解析映射 ,这使论文能够将关于奖励函数的损失函数转换为关于策略的损失函数
- 这种变量变换方法避免了拟合显式的、独立的奖励模型,同时仍然在现有的人类偏好模型(如 Bradley-Terry 模型)下进行优化
- 本质上,策略网络同时代表了语言模型和(隐式的)奖励
推导 DPO 目标
- 论文从与先前工作相同的 RL 目标开始,即公式 3,在一个通用的奖励函数 \(r\) 下
- 遵循先前的工作 (2007; 2019; 2022; 2023),很容易证明公式 3 中 KL 约束的奖励最大化目标的最优解形式为:
$$\pi_{r}(y \mid x)=\frac{1}{Z(x)}\pi_{\text{ref} }(y \mid x)\exp\left(\frac{1}{\beta}r(x,y)\right) \tag{4}$$- 其中 \(Z(x)=\sum_{y}\pi_{\text{ref} }(y \mid x)\exp\left(\frac{1}{\beta}r(x,y)\right)\) 是配分函数
- 完整的推导见附录 A.1
- 即使论文使用真实奖励函数 \(r^{*}\) 的 MLE 估计 \(r_{\phi}\),估计配分函数 \(Z(x)\) 仍然很昂贵 (2022; 2023),这使得这种表示在实践中难以利用
- 我们可以重新排列公式 4,用其对应的最优策略 \(\pi_{r}\)、参考策略 \(\pi_{\text{ref} }\) 和未知的配分函数 \(Z(\cdot)\) 来表示奖励函数
- 论文首先对公式 4 的两边取对数,然后进行一些代数运算得到:
$$r(x,y)=\beta\log\frac{\pi_{r}(y \mid x)}{\pi_{\text{ref} }(y \mid x)}+\beta\log Z(x). \tag{5}$$
- 论文首先对公式 4 的两边取对数,然后进行一些代数运算得到:
- 我们可以将这个重新参数化应用于真实奖励 \(r^{*}\) 和相应的最优模型 \(\pi^{*}\),注意:Bradley-Terry 模型仅依赖于两个补全之间奖励的差异,即
$$ p^{\*}(y_{1}\succ y_{2} \mid x)=\sigma(r^{\*}(x,y_{1})-r^{\*}(x,y_{2}))$$ - 将公式 5 中 \(r^{*}(x,y)\) 的重新参数化代入偏好模型公式 1,配分函数会抵消掉,我们可以仅用最优策略 \(\pi^{*}\) 和参考策略 \(\pi_{\text{ref} }\) 来表示人类偏好概率
- 因此,在 Bradley-Terry 模型下,最优的 RLHF 策略 \(\pi^{*}\) 满足偏好模型:
$$p^{*}(y_{1}\succ y_{2} \mid x)=\frac{1}{1+\exp\left(\beta\log\frac{\pi^{*}(y_{2} \mid x)}{\pi_{\text{ref} }(y_{2} \mid x)}-\beta\log\frac{\pi^{*}(y_{1} \mid x)}{\pi_{\text{ref} }(y_{1} \mid x)}\right)} \tag{6}$$- 推导过程在附录 A.2 中
- 虽然公式 6 使用了 Bradley-Terry 模型,但我们可以在更一般的 Plackett-Luce 模型 (1975; 2012) 下类似地推导出表达式,如附录 A.3 所示
- 现在论文有了用最优策略而非奖励模型表示的人类偏好数据的概率,我们可以为参数化策略 \(\pi_{\theta}\) 制定一个最大似然目标;类似于奖励建模方法(即公式 2),论文的策略目标变为:
$$\mathcal{L}_{\text{DPO} }(\pi_{\theta};\pi_{\text{ref} })=-\mathbb{E}_{(x,y_{w},y_ {l})\sim\mathcal{D} }\bigg{[}\log\sigma\left(\beta\log\frac{\pi_{\theta}(y_{w} \mid x)}{\pi_{\text{ref} }(y_{w} \mid x)}-\beta\log\frac{\pi_{\theta}(y_{l} \mid x)}{\pi_{\text{ref} }(y_{l} \mid x)}\right)\bigg{]}. \tag{7}$$ - 这样,论文使用一种替代参数化来拟合一个隐式奖励,其最优策略简单地就是 \(\pi_{\theta}\)
- 此外,由于论文的过程等同于拟合一个重新参数化的 Bradley-Terry 模型,它在偏好数据分布的适当假设下享有某些理论性质,例如一致性 (2022)
- 在第 5 节中,论文将进一步讨论 DPO 相对于其他工作的理论性质
DPO 更新做了什么?
- 为了从机制上理解 DPO,分析损失函数 \(\mathcal{L}_{\text{DPO} }\) 的梯度是很有用的
- 关于参数 \(\theta\) 的梯度可以写成:
$$\nabla_{\theta}\mathcal{L}_{\text{DPO} }(\pi_{\theta};\pi_{\text{ref } })=\ -\beta\mathbb{E}_{(x,y_{w},y_{l})\sim\mathcal{D} }\bigg{[}\underbrace{\sigma(\hat{r}_{\theta}(x,y_{l})-\hat{r}_{\theta}(x,y_{w}))}_{\text{higher weight when reward estimate is wrong} }\quad\bigg{[}\underbrace{\nabla_{\theta}\log\pi(y_{w} \mid x)}_{\text{increase likelihood of } y_{w}}-\underbrace{\nabla_{\theta}\log\pi (y_{l} \mid x)}_{\text{decrease likelihood of } y_{l} }\bigg{]}\bigg{]}$$ - 其中 \(\hat{r}_{\theta}(x,y)=\beta\log\frac{\pi_{\theta}(y|x)}{\pi_{\text{ref} }(y|x)}\) 是由语言模型 \(\pi_{\theta}\) 和参考模型 \(\pi_{\text{ref} }\) 隐式定义的奖励(更多内容在第 5 节)
- 直观地说,损失函数 \(\mathcal{L}_{\text{DPO} }\) 的梯度增加了优选补全 \(y_{w}\) 的似然,并降低了非优选补全 \(y_{l}\) 的似然
- 样本的权重由隐式奖励模型 \(\hat{r}_{\theta}\) 对非优选补全评分高出多少来衡量,按 \(\beta\) 缩放,即隐式奖励模型对补全排序的错误程度,同时考虑了 KL 约束的强度
- 论文的实验表明了这种加权的重要性,因为没有加权系数的朴素版本的方法会导致语言模型退化(附录表 3)
DPO outline
- 一般的 DPO 流程如下:
- 1)为每个提示 \(x\) 采样补全 \(y_{1},y_{2}\sim\pi_{\text{ref} }(\cdot \mid x)\),用人类偏好进行标注,以构建离线偏好数据集 \(\mathcal{D}=\{x^{(i)},y^{(i)}_{w},y_{l})^{(i)}\}_{i=1}^{N}\);
- 2)优化语言模型 \(\pi_{\theta}\) 以最小化给定 \(\pi_{\text{ref} }\)、\(\mathcal{D}\) 和期望 \(\beta\) 的 \(\mathcal{L}_{\text{DPO} }\)
- 在实践中,人们可能希望重用公开可用的偏好数据集,而不是生成样本并收集人类偏好
- 由于偏好数据集是使用 \(\pi^{\text{SFT} }\) 采样的,只要可用,论文就初始化 \(\pi_{\text{ref} }=\pi^{\text{SFT} }\)
- 但当 \(\pi^{\text{SFT} }\) 不可用时,论文通过最大化优选补全 \((x,y_{w})\) 的似然来初始化 \(\pi_{\text{ref} }\),即
$$\pi_{\text{ref} }=\arg\max_{\pi}\mathbb{E}_{x,y_{w}\sim\mathcal{D} }\left[\log\pi(y_ {w} \mid x)\right]$$ - 理解:
- 当生成数据的模型不可访问时,可以考虑将损失函数中的 \(\pi_\text{ref}\) 替换为这个?
- 上面的公式本质是找到一个策略 \(\pi\) 使得已知 \(x\) 时 \(y_ {w}\) 出现的对数概率最大化的策略 \(\pi_\text{ref}\)
- 这个过程有助于缓解真实参考分布(不可用)与 DPO 使用的 \(\pi_{\text{ref} }\) 之间的分布偏移
- 与实现和超参数相关的更多细节可以在附录 B 中找到
Theoretical Analysis of DPO
- 本节进一步阐释 DPO 方法,提供理论支持,并将 DPO 的优势与用于 RLHF 的 Actor-Critic 算法(如 PPO (2017))存在的问题联系起来
Your Language Model Is Secretly a Reward Model
- DPO 能够绕过显式拟合奖励函数和执行强化学习这两个步骤,仅使用一个最大似然目标来学习策略
- 优化目标方程 5 等价于一个具有奖励参数化 的 Bradley-Terry 模型:
$$ r^{*}(x,y)=\beta\log\frac{\pi_{\theta}(y|x)}{\pi_{\text{ref} }(y|x)} $$- 并且在变量变换下,论文优化参数化模型 \( \pi_{\theta} \) 等价于方程 2 中的奖励模型优化
- 在本节中,论文将建立这种重新参数化背后的理论,证明它不会约束所学奖励模型的类别,并且允许精确恢复最优策略
- 论文首先定义奖励函数之间的等价关系
- 定义 1.
- 两个奖励函数 \( r(x,y) \) 和 \( r’(x,y) \) 是等价的,当且仅当 \( r(x,y)-r’(x,y)=f(x) \) 对于某个函数 \( f \) 成立
- 很容易看出这确实是一个等价关系,它将奖励函数集合划分为不同的类
- 理解:因为 \(f(x) \) 与 \(y\) 没有关系!
- 我们可以陈述以下两个引理:
- 引理 1.
- 在 Plackett-Luce(特别是 Bradley-Terry)偏好框架下,来自同一等价类的两个奖励函数诱导出相同的偏好分布
- 引理 2.
- 来自同一等价类的两个奖励函数在约束强化学习问题下诱导出相同的最优策略
- 引理 1.
- 定义 1.
- 证明是直接了当的,论文将它们推迟到附录 A.5
- 第一个引理是 Plackett-Luce 模型族 (1975) 中存在的一个众所周知的欠定(under-specification)问题
- 由于这种欠定性,论文通常必须施加额外的可识别性约束,以保证从方程 2 得到的 MLE 估计具有某些性质 (2022)
- 第二个引理指出,来自同一类的所有奖励函数产生相同的最优策略,因此对于论文的最终目标,论文只关心恢复最优类中的任意一个奖励函数
- 第一个引理是 Plackett-Luce 模型族 (1975) 中存在的一个众所周知的欠定(under-specification)问题
- 论文在附录 A.6 中证明了以下定理:
- 定理 1.
- 在温和的假设下,与 Plackett-Luce(特别是 Bradley-Terry)模型一致的所有奖励类都可以用重新参数化 \( r(x,y)=\beta\log\frac{\pi(y|x)}{\pi_{\text{ref} }(y|x)} \) 来表示,对于某个模型 \( \pi(y \mid x) \) 和给定的参考模型 \( \pi_{\text{ref} }(y \mid x) \)
- 证明概要.
- 考虑任何奖励函数 \( r(x,y) \),它诱导出一个相应的最优模型 \( \pi_{r}(y \mid x) \),由方程 4 指定
- 论文将证明,\( r \) 的等价类中的一个奖励函数可以使用上面给出的重新参数化来表示
- 论文定义投影 \( f \) 为:
$$
f(r;\pi_{\text{ref} },\beta)(x,y)=r(x,y)-\beta\log\sum_{y}\pi_{\text{ref} }(y \mid x)\exp\left(\frac{1}{\beta}r(x,y)\right)
$$- 算子 \( f \) 只是用 \( \pi_{r} \) 的配分函数的对数对奖励函数进行归一化
- 由于添加的归一化项仅是前缀 \( x \) 的函数,所以 \( f(r;\pi_{\text{ref} },\beta)(x,y) \) 是 \( r(x,y) \) 等价类中的一个奖励函数
- 最后,将 \( r \) 替换为方程 5 的右边(这对任何奖励函数都成立),论文有 \( f(r;\pi_{\text{ref} },\beta)(x,y)=\beta\log\frac{\pi_{r}(y|x)}{\pi_{\text{ref} }(y|x)} \)
- 也就是说,投影 \( f \) 产生了 \( r \) 等价类中具有所需形式的一个成员,并且论文提出的重新参数化没有损失奖励模型的任何一般性
- 定理 1.
- 也可以将定理 1 视为精确指定了 DPO 重新参数化在每个等价类中选择哪个奖励函数,即满足以下条件的奖励函数:
$$
\sum_{y}\underbrace{\pi_{\text{ref} }(y \mid x)}_{\equiv\pi(y|x), \text{ using Thm. 1 reparam.} }\exp\left(\frac{1}{\beta}r(x,y)\right)=1,
$$- 也就是说,\( \pi(y \mid x) \) 是一个有效的分布(概率为正且和为 1)
- 然而,遵循方程 4,我们可以看到方程 9 是由奖励函数 \( r(x,y) \) 诱导的最优策略的配分函数
- DPO 算法的关键见解是,我们可以对欠定的 Plackett-Luce(特别是 Bradley-Terry)偏好模型族施加某些约束,使得论文能够保留可表示的奖励模型的类别,但同时显式地使得方程 4 中的最优策略对于所有提示 \( x \) 都是解析可解的
Instability of Actor-Critic Algorithms(AC 算法的不稳定性)
- 也可以使用论文的框架来诊断用于 RLHF 的标准 Actor-Critic 算法(如 PPO)的不稳定性
- 论文遵循 RLHF 流程,并专注于第 3 节概述的 RL 微调步骤
- 我们可以与约束强化学习问题的控制即推断框架 (2018) 建立联系
- 论文假设一个参数化模型 \( \pi_{\theta}(y \mid x) \),并最小化
$$ \mathbb{D}_{\text{KL} }[\pi_{\theta}(y|x) \mid \mid \pi^{*}(y \mid x)] $$- 其中 \( \pi^{*} \) 是由奖励函数 \( r_{\phi}(y,x) \) 诱导的方程 7 中的最优策略
- 经过一些代数运算,这可以推出优化目标:
$$
\max_{\pi_{\theta} }\mathbb{E}_{\pi_{\theta}(y|x)}\bigg{[}\underbrace{r_{\phi}(x ,y)-\beta\log\sum_{y}\pi_{\text{ref} }(y \mid x)\exp\left(\frac{1}{\beta}r_{\phi}(x,y)\right)}_{f(r_{\phi},\pi_{\text{ref} },\beta)}-\underbrace{\beta\log\frac{\pi_{\theta}(y \mid x)}{\pi_{\text{ref} }(y \mid x)} }_{\text{KL} }\bigg{]}
$$- 这是先前工作 (2022; 2020; 2022; 2022) 使用与 \( r_{\phi} \) 的奖励类等价的 DPO 奖励所优化的相同目标
- 在这种设置下,我们可以将 \( f(r_{\phi},\pi_{\text{ref} },\beta) \) 中的归一化项解释为参考策略 \( \pi_{\text{ref} } \) 的软价值函数
- 虽然这个项不影响最优解,但没有它,目标的策略梯度可能具有高方差,使得学习不稳定
- 我们可以使用一个学习的价值函数来适应这个归一化项,但这可能也难以优化
- 或者,先前的工作使用人类完成基线来归一化奖励,本质上是归一化项的单样本蒙特卡洛估计
- 相比之下,DPO 重新参数化产生了一个不需要任何基线的奖励函数
Experiments
- 在本节中,论文实证评估 DPO 直接从偏好中训练策略的能力
- 在一个受控良好的文本生成环境中,论文提出:
- 与常见的偏好学习算法(如 PPO)相比,DPO 在最大化奖励和最小化与参考策略的 KL 散度之间进行权衡的效率如何?
- 论文在更大的模型和更困难的 RLHF 任务上评估 DPO 的性能,包括摘要和对话
- 在几乎不需要调整超参数的情况下,DPO 的表现往往与像基于 PPO 的 RLHF 这样的强基线一样好甚至更好,并且在学习的奖励函数下也优于从 \( N \) 个采样轨迹中返回最佳结果的方法
Experiment Setup
- 注:更多细节在附录 C 中
Tasks
- 论文的实验探索了三种不同的开放式文本生成任务
- 对于所有实验,算法从下面的偏好数据集中学习一个策略
$$ \mathcal{D}=\{x^{(i)},y_{w}^{(i)},y_{l}^{(i)} \}_{i=1}^{N} $$ - 在受控情感生成(controlled sentiment generation)中
- \( x \) 是来自 IMDb 数据集 (2011) 的电影评论前缀,策略必须生成具有积极情感的 \( y \)
- 为了进行受控评估,在这个实验中,论文使用预训练的情感分类器生成关于生成的偏好对,其中
$$ p(\text{positive} \mid x,y_{w})>p(\text{positive} \mid x,y_{l}) $$ - 对于 SFT,论文在 IMDB 数据集的训练分割中的评论上微调 GPT-2-large 直到收敛(更多细节见附录 C.1)
- 在摘要(summarization)任务中
- \( x \) 是来自 Reddit 的论坛帖子;策略必须生成一个总结帖子要点的摘要 \( y \)
- 遵循先前的工作,论文使用 Reddit TL;DR 摘要数据集 (2017) 以及 Stiennon 等人收集的人类偏好
- 论文使用在人类撰写的论坛帖子摘要上微调的 SFT 模型,并使用 TRLX (2023) 框架进行 RLHF
- 人类偏好数据集是由 Stiennon 等人在一个不同但训练方式相似的 SFT 模型的样本上收集的
- 在单轮对话(single-turn dialogue)中
- \( x \) 是一个人类查询,可能涉及从天体物理学问题到关系建议的任何内容;策略必须对用户的查询产生一个引人入胜且有用的响应 \( y \);
- 论文使用 Anthropic Helpful and Harmless 对话数据集 (2022),包含 17 万个人类与自动助手之间的对话
- 每个记录都以一个大型(尽管未知)语言模型生成的一对响应结束,并带有一个表示人类偏好响应的人类偏好标签
- 在这种设置下,没有预训练的 SFT 模型可用;因此,论文仅在偏好完成上微调一个现成的语言模型以形成 SFT 模型
Evaluation
- 论文的实验使用两种不同的评估方法
- 为了分析每种算法在优化约束奖励最大化目标方面的有效性,在受控情感生成设置中,论文通过其实现的奖励和与参考策略的 KL 散度的边界来评估每种算法;
- 这个边界是可计算的,因为我们可以访问真实奖励函数(一个情感分类器)
- 但在现实世界中,真实奖励函数是未知的;
- 论文使用算法与基线策略的胜率来评估算法,使用 GPT-4 作为摘要质量和响应帮助度的代理评估,分别用于摘要和单轮对话设置
- 对于摘要,论文使用测试集中的参考摘要作为基线;对于对话,论文使用测试数据集中的偏好响应作为基线。虽然现有研究表明 LM 可以比现有指标更好的自动评估器 (2023),但论文在第 6.4 节进行了一项人类研究来证明论文使用 GPT-4 进行评估的合理性。论文发现 GPT-4 的判断与人类高度相关,人类与 GPT-4 的一致性通常与人类注释者之间的一致性相似或更高
Methods
- 除了 DPO,论文还评估了几种现有的训练语言模型以符合人类偏好的方法
- 论文在摘要任务中探索了使用 GPT-J (2021) 的零样本提示,在对话任务中探索了使用 Pythia-2.8B (2023) 的 2-shot 提示
- 论文还评估了 SFT 模型以及 Preferred-FT
- 这是一个在选自 SFT 模型(在受控情感和摘要中)或通用 LM(在单轮对话中)的所选完成 \( y_{w} \) 上使用监督学习进行微调的模型
- 另一种伪监督方法是 Unlikelihood (2019)
- 它简单地优化策略以最大化分配给 \( y_{w} \) 的概率,并最小化分配给 \( y_{l} \) 的概率;
- 论文在“非似然”项上使用一个可选的系数 \( \alpha\in[0,1] \)
- 论文还考虑了使用从偏好数据学习的奖励函数的 PPO (2017) 和 PPO-GT ,后者是在受控情感设置中可访问真实奖励函数的 Oracle
- 在论文的情感实验中,论文使用了 PPO-GT 的两种实现,一个现成的版本 (2023) 以及一个修改版本,该版本归一化奖励并进一步调整超参数以提高性能(论文在运行使用学习奖励的“普通”PPO 时也使用这些修改)
- 最后,论文考虑了 Best of \( N \) 基线,从 SFT 模型(或对话中的 Preferred-FT)采样 \( N \) 个响应,并返回根据从偏好数据集学习的奖励函数得分最高的响应
- 这种高性能方法将奖励模型的质量与 PPO 优化解耦,但在计算上是不切实际的,即使对于中等的 \( N \),因为它在测试时需要为每个查询采样 \( N \) 个完成
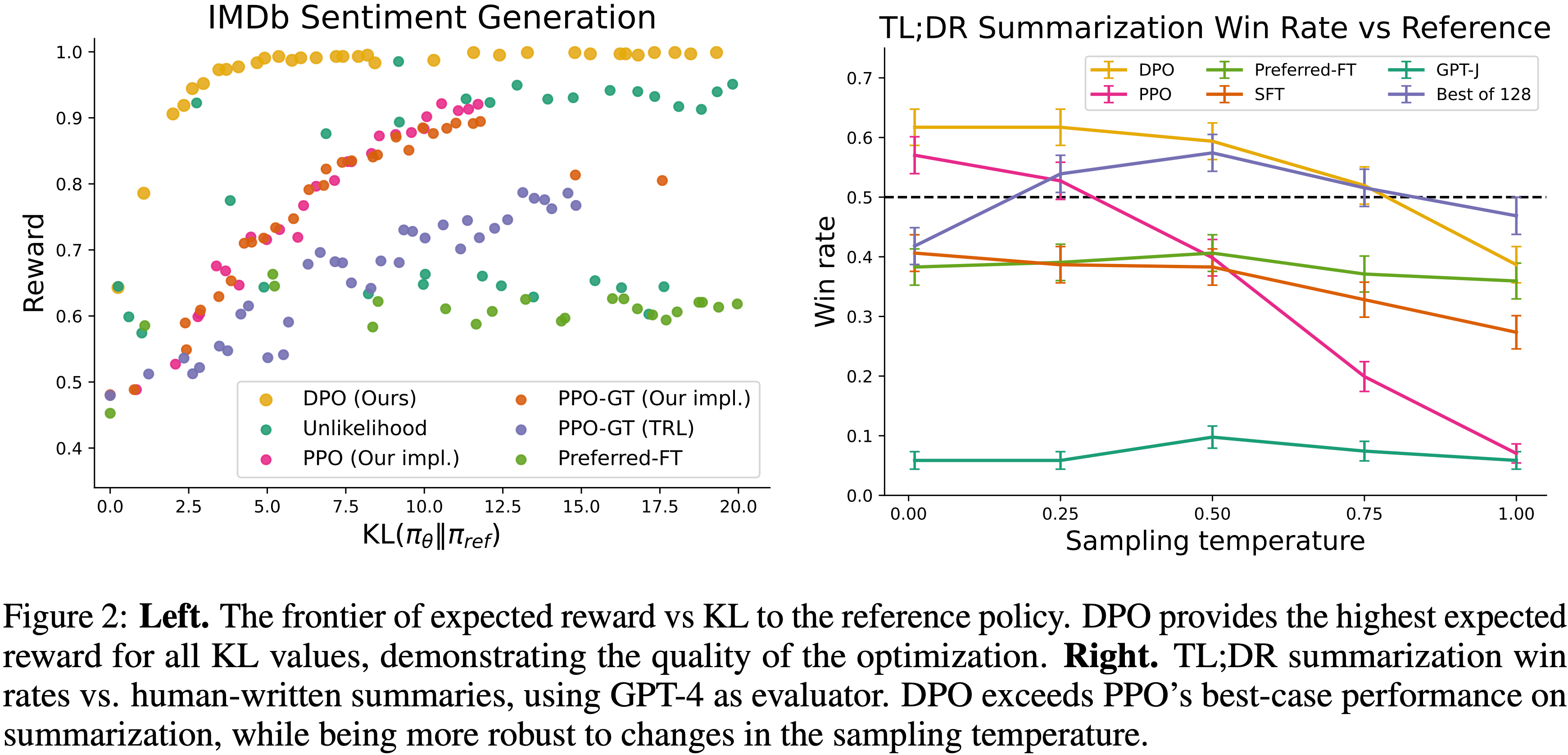
- 图 2:
- 左图:期望奖励与相对于参考策略的 KL 散度的边界。DPO 在所有 KL 值下提供了最高的期望奖励,证明了优化的质量
- 右图:TL;DR 摘要相对于人工撰写摘要的胜率,使用 GPT-4 作为评估器
- DPO 在摘要任务上超过了 PPO 的最佳性能,同时对采样温度的变化更加鲁棒
How well can DPO optimize the RLHF objective?
- 典型 RLHF 算法中使用的 KL 约束奖励最大化目标在利用奖励的同时限制策略偏离参考策略太远之间取得平衡
- 因此,在比较算法时,论文必须同时考虑实现的奖励以及 KL 差异;
- 实现略高的奖励但 KL 高得多并不一定是可取的
- 图 2 显示了在情感设置中各种算法的奖励-KL 边界
- 论文对每种算法执行多次训练运行,每次运行使用不同的策略保守性超参数(PPO 的目标 KL \( \in\{3,6,9,12\} \),DPO 的 \( \beta\in\{0.05,0.1,1,5\} \),Unlikelihood 的 \( \alpha\in\{0.05,0.1,0.5,1\} \),Preferred-FT 的随机种子)
- 扫描总共包括 22 次运行
- 在每 100 个训练步骤直到收敛后,论文在一组测试提示上评估每个策略,计算在真实奖励函数下的平均奖励以及
- 与参考策略的平均序列级 KL3 \( \text{KL} (\pi \mid \mid \pi_{\text{ref} }) \)
- 论文发现 DPO 产生了迄今为止最有效的边界,实现了最高的奖励,同时仍然实现了低 KL
- 这个结果尤其引人注目,原因有几个
- 首先,DPO 和 PPO 优化相同的目标,但 DPO 明显更有效;
- DPO 的奖励/KL 权衡严格优于 PPO
- 其次,DPO 实现了比 PPO 更好的边界,即使 PPO 可以访问真实奖励(PPO-GT)
- 首先,DPO 和 PPO 优化相同的目标,但 DPO 明显更有效;
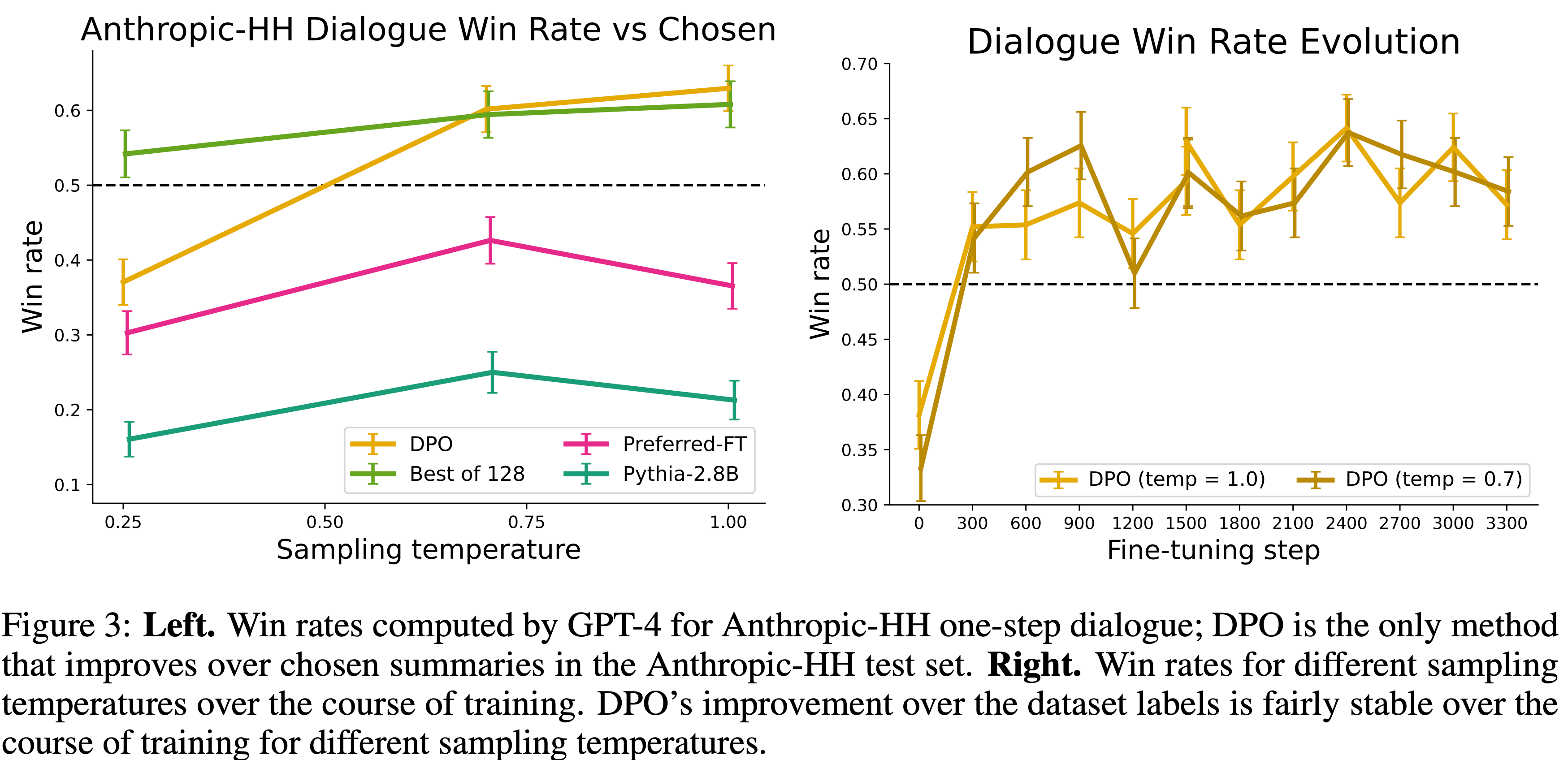
- 图 3:
- 左图:由 GPT-4 计算的 Anthropic-HH 单轮对话胜率;DPO 是唯一一个在 Anthropic-HH 测试集上优于所选摘要的方法
- 右图:在训练过程中不同采样温度的胜率
- 对于不同的采样温度,DPO 相对于数据集标签的改进在训练过程中相当稳定
Can DPO scale to real preference datasets?(将 DPO 扩展到真实的偏好数据集中)
- 接下来,论文评估 DPO 在摘要和单轮对话上的微调性能
- 对于摘要,自动评估指标如 ROUGE 可能与人类偏好相关性很差 (2020),并且先前的工作发现使用 PPO 在人类偏好上微调 LM 可以提供更有效的摘要
- 论文通过在 TL;DR 摘要数据集的测试分割上采样完成来评估不同方法,并计算相对于测试集中参考完成的平均胜率
- 所有方法的完成都是在从 0.0 到 1.0 变化的温度下采样的,胜率如图 2(右)所示
- DPO、PPO 和 Preferred-FT 都微调了相同的 GPT-J SFT 模型4
- 论文发现 DPO 在温度为 0.0 时胜率约为 61%,超过了 PPO 在其最佳采样温度 0.0 时的 57%
- 与 Best of \( N \) 基线相比,DPO 也实现了更高的最大胜率
- 论文没有刻意调整 DPO 的 \( \beta \) 超参数,所以这些结果可能低估了 DPO 的潜力
- 论文还发现 DPO 对采样温度的鲁棒性远高于 PPO,后者的性能在高温度下可能退化到基础 GPT-J 模型的水平
- Preferred-FT 相对于 SFT 模型没有显著改进
- 论文还在第 6.4 节中在人类评估中比较了 DPO 和 PPO,其中温度为 0.25 的 DPO 样本在 58% 的情况下比温度为 0 的 PPO 样本更受偏好
- 在单轮对话上,论文在 Anthropic HH 数据集 (2022) 测试分割的子集上评估不同方法,该子集包含一步人机交互
- GPT-4 评估使用测试集上的偏好完成作为参考,计算不同方法的胜率
- 由于此任务没有标准的 SFT 模型,论文从一个预训练的 Pythia-2.8B 开始,使用 Preferred-FT 在所选完成上训练一个参考模型,使得完成在模型的分布内,然后使用 DPO 进行训练
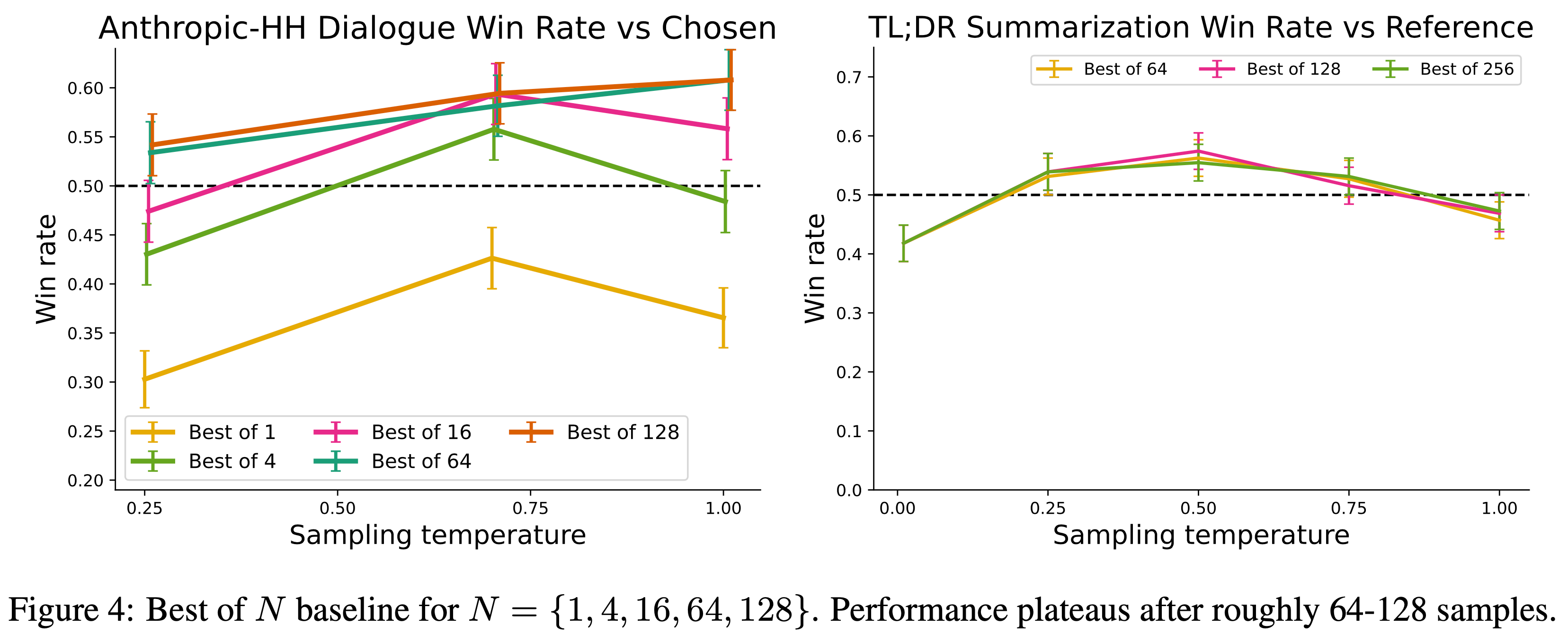
- 论文还与从 Preferred-FT 完成中选出的最佳 128 个完成进行比较(论文发现 Best of \( N \) 基线在此任务上在 128 个完成时达到稳定;见附录图 4)以及一个 2-shot 提示的 Pythia-2.8B 基础模型版本,发现 DPO 在每种方法的最佳性能温度下表现相当或更好
- 论文还评估了一个在 Anthropic HH 数据集5 上使用 PPO 训练的 RLHF 模型,该模型来自一个知名来源6,但未能找到能够提供优于基础 Pythia-2.8B 模型性能的提示或采样温度
- 基于论文从 TL;DR 得到的结果以及两种方法优化相同奖励函数的事实,论文将 Best of 128 视为 PPO 级别性能的粗略代理
- 总体而言,DPO 是唯一一个在计算上高效且改进了 Anthropic HH 数据集中偏好完成的方法,并且提供了与计算量大的 Best of 128 基线相似或更好的性能
- 最后,图 3 显示 DPO 相对较快地收敛到其最佳性能
Generalization to a new input distribution
- 为了进一步比较 PPO 和 DPO 在分布偏移下的性能,论文在不同的分布上评估了来自论文 Reddit TL;DR 摘要实验的 PPO 和 DPO 策略,即 CNN/DailyMail 数据集 (2016) 测试分割中的新闻文章,使用来自 TL;DR 的最佳采样温度(0 和 0.25)
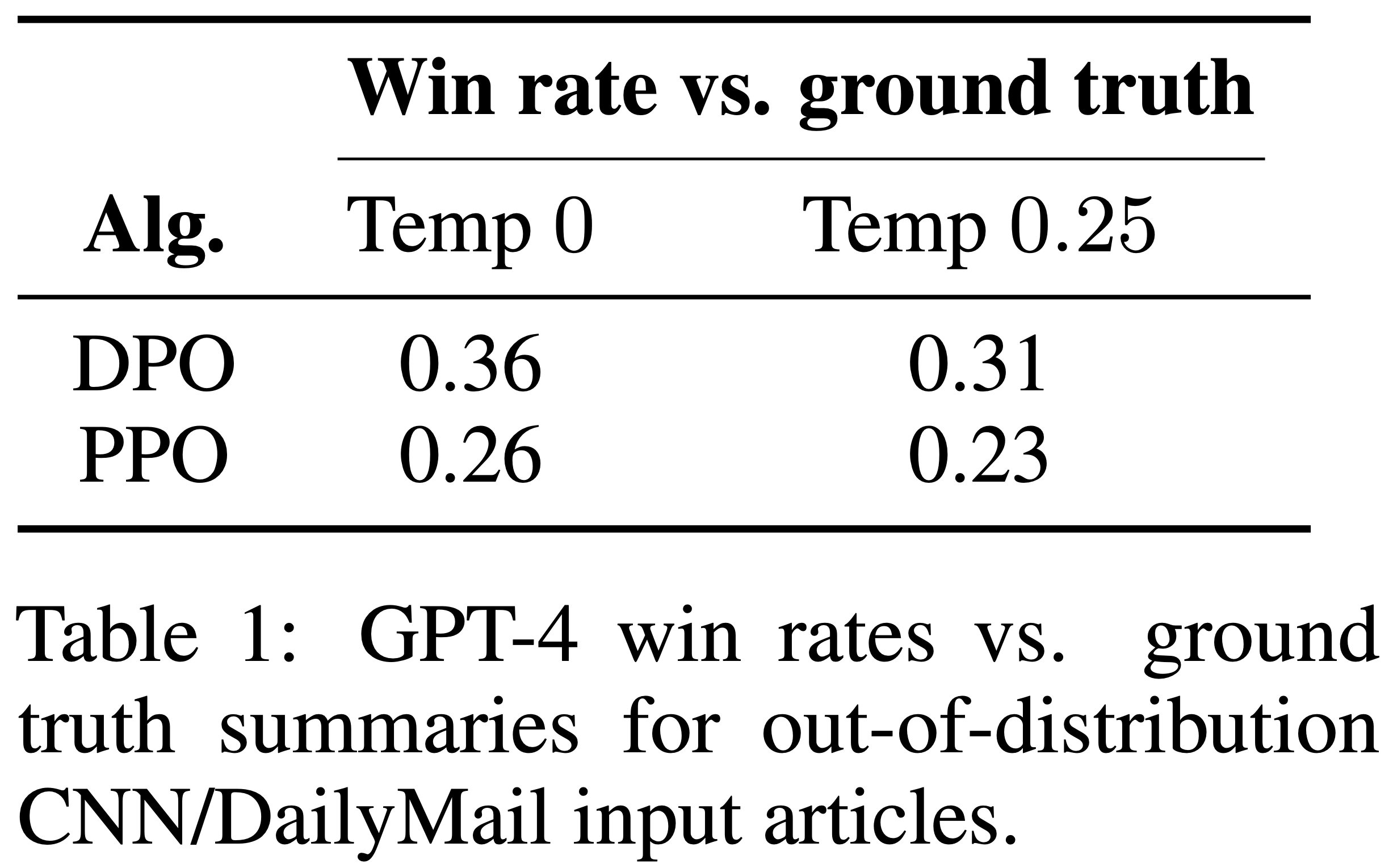
- 结果呈现在表 1 中
- 论文计算了相对于数据集中真实摘要的 GPT-4 胜率,使用了论文用于 Reddit TL;DR 的相同 GPT-4 (C) 提示,但将“论坛帖子”一词替换为“新闻文章”
- 对于这个新的分布,DPO 继续以显著优势优于 PPO 策略。这个实验提供了初步证据,表明 DPO 策略可以像 PPO 策略一样很好地泛化,尽管 DPO 没有使用 PPO 使用的额外的未标记 Reddit TL;DR 提示
- 表 1:对于分布外的 CNN/DailyMail 输入文章,相对于真实摘要的 GPT-4 胜率
- 理解:因为是跟 Ground Truth 的对比,所以他们的省略都不足 50%
- 理解:因为是跟 Ground Truth 的对比,所以他们的省略都不足 50%
Validating GPT-4 judgments with human judgments(用 Human Judgment 验证 GPT-4 judgment 是否准确)
- 论文进行了一项人类研究来验证 GPT-4 判断的可靠性 ,使用了 TL;DR 摘要实验的结果和两种不同的 GPT-4 提示
- GPT-4 (S)(简单)提示简单地询问哪个摘要更好地总结了帖子中的重要信息
- GPT-4 (C)(简洁)提示还询问哪个摘要更简洁;
- 论文评估这个提示是因为论文发现使用 GPT-4 (S) 提示时,GPT-4 比人类更喜欢更长、更重复的摘要
- 完整的提示见附录 C.2
- 论文进行了三次比较,使用了性能最高(DPO,温度 0.25)、最低(PPO,温度 1.0)和中等性能(SFT,温度 0.25)的方法,旨在覆盖多样性的样本质量;
- 所有三种方法都与贪婪采样的 PPO(其最佳性能温度)进行比较
- 论文发现,使用两种提示,GPT-4 与人类一致的程度通常与人类彼此一致的程度相似,这表明 GPT-4 是人类评估的合理代理(由于人类评分者有限,论文只收集了 DPO 和 PPO-1 比较的多人判断)
- 总体而言,GPT-4 (C) 提示通常提供更能代表人类的胜率;因此论文在第 6.2 节的主要结果中使用此提示
- 关于人类研究的更多细节,包括呈现给评分者的网络界面和人类志愿者列表,见附录 D.3
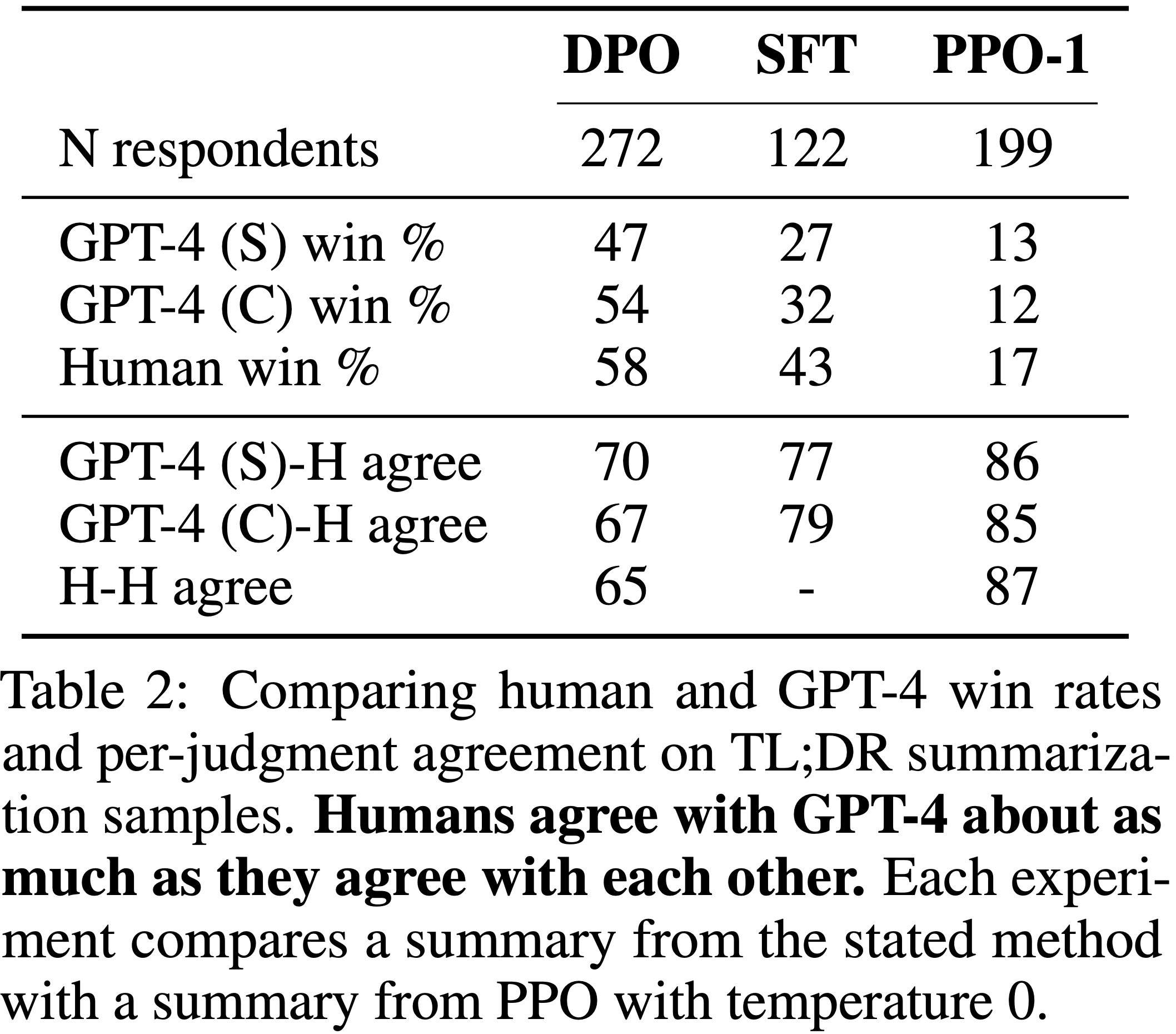
- 表 2:
- 在 TL;DR 摘要样本上比较人类和 GPT-4 的胜率以及每次判断的一致性
- 人类与 GPT-4 的一致程度与人类彼此之间的一致程度大致相同
- 每个实验将所述方法的摘要与温度为 0 的 PPO 摘要进行比较
Limitations & Future Work
- 论文的结果提出了几个未来工作的重要问题
- 第一:与从显式奖励函数学习相比,DPO 策略在分布外的泛化能力如何?
- 论文的初步结果表明 DPO 策略可以类似于基于 PPO 的模型一样泛化,但需要更全面的研究
- 例如,使用来自 DPO 策略的自标注进行训练是否同样能有效利用未标记的提示?
- 第二:在直接偏好优化设置中,奖励过度优化(over-optimization)如何表现
- 图 3 右侧性能的轻微下降是否是它的一个实例?
- 第三:虽然论文评估了最多 6B 参数的模型,但将 DPO 扩展到数量级更大的最先进模型是未来工作的一个令人兴奋的方向
- 关于评估
- 论文发现 GPT-4 计算的胜率受到提示的影响;未来的工作可能会研究从自动化系统中引出高质量判断的最佳方式
- 最后,DPO 的许多可能应用存在于从人类偏好训练语言模型之外,包括在其他模态中训练生成模型
附录 B:DPO Implementation Details and Hyperparameters
DPO 的实现相对简单;下面提供了 DPO 损失的 PyTorch 代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22import torch.nn.functional as F
def dpo_loss(pi_logps, ref_logps, yw_idxs, yl_idxs, beta):
"""
pi_logps: policy logprobs, shape (B,)
ref_logps: reference model logprobs, shape (B,)
yw_idxs: preferred completion indices in [0, B-1], shape (T,)
yl_idxs: dispreferred completion indices in [0, B-1], shape (T,)
beta: temperature controlling strength of KL penalty
Each pair of (yw_idxs[i], yl_idxs[i]) represents the indices of a single preference pair.
"""
pi_yw_logps, pi_yl_logps = pi_logps[yw_idxs], pi_logps[yl_idxs]
ref_yw_logps, ref_yl_logps = ref_logps[yw_idxs], ref_logps[yl_idxs]
pi_logratios = pi_yw_logps - pi_yl_logps
ref_logratios = ref_yw_logps - ref_yl_logps
losses = -F.logsigmoid(beta * (pi_logratios - ref_logratios))
rewards = beta * (pi_logps - ref_logps).detach()
return losses, rewards论文默认使用 \(\beta = 0.1\),批量大小为 64,以及学习率为 1e-6 的 RMSprop 优化器
论文在前 150 步中将学习率从 0 线性预热到 1e-6
对于 TL;DR 摘要任务,论文使用 \(\beta = 0.5\),其余参数保持不变
附录 C:Further Details on the Experimental Set-Up
- 在本节中,论文包含了与实验设计相关的额外细节
C.1 IMDb 情感实验和基线细节 (C.1 IMDb Sentiment Experiment and Baseline Details)
- 提示是来自 IMDB 数据集中长度为 2-8 个词符的前缀
- 论文使用预训练的情感分类器
siebert/sentiment-roberta-large-english作为真实奖励模型,并使用gpt2-large作为基础模型 - 论文发现默认模型生成的文本质量较低且奖励有些不准确,因此使用了这些更大的模型
- 论文首先在 IMDB 数据的一个子集上进行了 1 个周期的监督微调
- 然后,论文使用该模型为 25000 个前缀生成了 4 个补全,并使用 ground-truth 奖励模型为每个前缀创建了 6 个偏好对
- 问题:这里的 ground-truth 奖励模型是什么?
- RLHF 奖励模型从
gpt2-large模型初始化,并在偏好数据集上训练了 3 个周期,论文选择了在验证集上准确率最高的检查点 - “TRL” 运行使用了 TRL 库中的超参数
- 论文的实现在每个 PPO 步骤中使用更大的批量样本,为 1024
C.2 用于计算摘要和对话胜率的 GPT-4 提示 (C.2 GPT-4 prompts for computing summarization and dialogue win rates)
- 论文实验设置的一个关键组成部分是 GPT-4 的胜率判断
- 在本节中,论文包含了用于生成摘要和对话实验胜率的提示
- 论文所有的实验都使用
gpt-4-0314 - 每次评估时,摘要或响应的顺序是随机选择的
摘要 GPT-4 胜率提示 (S) (Summarization GPT-4 win rate prompt (S))
- 提示词:
1
2
3
4
5
6
7
8
9
10
11
12
13Which of the following summaries does a better job of summarizing the most \
important points in the given forum post?
Post:
<post>
Summary A:
<Summary A>
Summary B:
<Summary B>
FIRST provide a one-sentence comparison of the two summaries, explaining which \
you prefer and why. SECOND, on a new line, state only "A" or "B" to indicate your \
choice. Your response should use the format:
Comparison: <one-sentence comparison and explanation>
Preferred: <"A" or "B">
摘要 GPT-4 胜率提示 (C) (Summarization GPT-4 win rate prompt (C))
- 提示词:
1
2
3
4
5
6
7
8
9
10
11
12
13Which of the following summaries does a better job of summarizing the most \
important points in the given forum post, without including unimportant or \
irrelevant details? A good summary is both precise and concise.
Post: <post>
Summary A:
<Summary A>
Summary B:
<Summary B>
FIRST provide a one-sentence comparison of the two summaries, explaining which \
you prefer and why. SECOND, on a new line, state only "A" or "B" to indicate your \
choice. Your response should use the format:
Comparison: <one-sentence comparison and explanation>
Preferred: <"A" or "B">
Dialogue GPT-4 win rate prompt
- 提示词:
1
2
3
4
5
6
7
8
9
10
11
12For the following query to a chatbot, which response is more helpful?
Query: <the user query>
Response A:
<either the test method or baseline>
Response B:
<the other response>
FIRST provide a one-sentence comparison of the two responses and explain \
which you feel is more helpful. SECOND, on a new line, state only "A" or \
"B" to indicate which response is more helpful. Your response should use \
the format:
Comparison: <one-sentence comparison and explanation>
More helpful: <"A" or "B">
C.3 非似然基线 (C.3 Unlikelihood baseline)
- 虽然论文在情感实验中包含了非似然基线 (2019)(简单地最大化偏好响应的对数概率 \(\log p(y_{w}|x)\),同时最小化非偏好响应的对数概率 \(\log p(y_{l}|x)\)),但论文没有在摘要或对话实验中将之作为基线,因为它通常会产生无意义的响应,作者认为这是无约束似然最小化的结果
附录 D:Additional Empirical Results
D.1 不同 N 值的 Best of N 基线性能 (D.1 Performance of Best of N baseline for Various N)
- 论文发现 Best of N 基线在论文的实验中是一个强大(尽管计算成本高,需要多次采样)的基线
- 论文评估了 Best of N 基线在 Anthropic-HH 对话和 TL;DR 摘要任务中不同 N 值的性能;结果如图 4 所示
D.2 样本回复和 GPT-4 判断 (D.2 Sample Responses and GPT-4 Judgments)
- 在本节中,论文展示了 DPO 与基线(摘要任务为 PPO temp 0,对话任务为数据集中选择的真实响应)之间比较的示例
- 摘要示例见表 4-6,对话示例见表 7-10
- 论文未列出,详情见博客

D.3 人类研究细节 (D.3 Human study details)
- 为了验证使用 GPT-4 计算胜率的做法,论文的人类研究在 TL;DR 摘要设置中收集了几组对比的人类偏好数据
- 论文选择了三种不同的算法对比,评估了 DPO (temp. 0.25)、SFT (temp. 0.25) 和 PPO (temp 1.0) 与参考算法 PPO (temp 0.) 的比较
- 通过选择三种独特算法以及相对于参考算法胜率范围广泛的算法,论文捕捉了人类和 GPT-4 胜率在不同响应质量谱上的相似性
- 论文对 DPO vs PPO-0 进行了 150 次随机比较采样,对 PPO-1 vs PPO-0 进行了 100 次随机比较采样,每次比较分配两个人进行标注,为 DPO-PPO’10 产生了 275 个判断,为 PPO-PPO 产生了 200 个判断
- 论文对 SFT 进行了 125 次比较采样,每次分配一个人进行标注
- 论文忽略了人类标记为平局的判断(仅占所有判断的约 1%),并测量了人类 A 和人类 B 之间(对于论文有两个人标注的比较,即不包括 SFT)以及每个人与 GPT-4 之间的原始一致百分比
- 论文总共有 25 名志愿者人类评估者,每人比较了 25 个摘要(一名志愿者较晚完成调查,未纳入最终分析,但在此列出)
- 评估者是斯坦福大学的学生(从本科到博士),或近期的斯坦福毕业生或访问学者,主修 STEM(主要是 CS)领域
- 调查界面截图见图 5

附录:DPO 推导过程
- 根据RLHF中的定义,策略 \(\pi_\theta\) 的训练目标是:在不太偏离 Reference Model 的情况下,最大化 reward,其定义可以写为如下形式
$$
\max_{\pi_\theta} \mathbb{E}_{x\sim D, y\sim \pi_\theta(y|x)} [r_{RM}(x,y)]-\beta \mathbb{D}_{KL}[\pi_\theta(y|x)||\pi_\text{ref}(y|x)]
$$- \(r_{RM}(x,y)\) 是 Reward Model 的返回值
- \(\beta\) 是控制目标策略和 Reference Model 差异的参数
- 在强化学习中,可通过修改使用 reward(Reward Engineering)来实现训练目标:
$$
r(x,y) = r_{RM}(x,y) - \beta(\log\pi_\theta(y|x) - \log\pi_\text{ref}(y|x) )
$$
- DPO推导:
- DPO-最优策略推导 :将原始目标进行转换有

- 理解:(论文中未明确给出说明)上述证明中,转换 KL 散度形式为对形式时,要求 \(y \sim \pi\),即回答 \(y\) 是从当前策略采样的(实际中我们无法严格满足,只能近似做到)
- 公式(12)最后一步推导为:将左边式子中括号内容按照对数法则全部展开,即可发现变化前后的式子相等
- 实际上,推导公式(12)时, \(\log Z(x)\) 可以是任意函数,为了使得 \(\pi^{*}(y|x)\) 是一个分布,所以特意将 \(Z(x)\) 取值为分配函数的形式(物理学中的分配函数是一个统计量)
- 注:可以证明这样构造的 \(\pi^*\) 正是原始 PPO 约束优化问题的最优解(这也是后续推导可以看到后续的目标就是让目标策略和 \(\pi^*\) 的 KL 散度变小),详细证明参考 RL——CQL 的附录部分
- DPO-最优奖励形式推导 :进一步推导得到最优策略对应的奖励形式有

- 这里由于 \(Z(x)\) 并不依赖于策略 \(\pi\),所以最小化公式14 的结果就是最小化其第一项的结果(注:第二项可以单独分出来),且 \(\pi\) 满足下面的形式时取得最小值,即在 KL 约束下,奖励最大化目标的 \(\pi(y|x)\) 的最优解形式为:
$$
\pi^{*}(y|x) = \frac{1}{Z(x)}\pi_\text{ref}(y|x)exp(\frac{1}{\beta}r(x,y))
$$ - 两边同时取对数可得:
$$
\log \pi^{*}(y|x) = -\log Z(x) + \log \pi_\text{ref}(y|x) + \frac{1}{\beta}r(x,y)
$$ - 进一步有:
$$
\frac{1}{\beta}r(x,y) = \log \pi^{*}(y|x) + \log Z(x) - \log \pi_\text{ref}(y|x)
$$ - 即最优策略对应的奖励形式为:
$$
r(x,y) = \beta \log \frac{\pi^{*}(y|x)}{\pi_\text{ref}(y|x)} + \beta\log Z(x)
$$- 对上述奖励形式的理解:如果已知 公式11 问题中的 最优解 ,即 策略 \(\pi\) 的最优策略 \(\pi^{*}\) ,那么 最优的奖励值(最大奖励值)\(r^*(x,y)\) 的形式可以通过上述的形式来表示
- 这里由于 \(Z(x)\) 并不依赖于策略 \(\pi\),所以最小化公式14 的结果就是最小化其第一项的结果(注:第二项可以单独分出来),且 \(\pi\) 满足下面的形式时取得最小值,即在 KL 约束下,奖励最大化目标的 \(\pi(y|x)\) 的最优解形式为:
- DPO-损失函数推导 :在使用 Bradley-Terry (BT)方法建模人类偏好时 ,有 DPO 的训练损失函数如下:

- 推导精髓:上述推导中消除了 \(Z(x)\) ,是通过引入 Bradley-Terry 偏好模型来实现的
- 理解:上述基本推导思路是
- 奖励和策略的关系:由上面已经已知,即指定任意策略为最优策略,则其对应的最优奖励就已知;反过来也一样
- 奖励和概率的关系:借助 BT 偏好建模,可以建模 正样本 优于 负样本的概率 \(p(y_1 \succ y_2|x)\) 和奖励 \(r(x,y_1),r(x,y_2)\) 的关系
- 由此,可以得到概率和策略的关系(注意:这样的好处是,不再需要预估奖励了,直接从优化概率即可优化策略)
- 下面再进一步,最小化负对数概率即可得到目标,当负对数概率最小时,也就是策略最优时
- 目标是让上面的概率 \(p^*(y_1 \succ y_2 )\) 越大越好,最终的损失函数可以定义为负对数概率在数据集上的期望:
$$
Loss_{\text{DPO}}(\pi_\theta;\pi_\text{ref}) = - \mathbb{E}_{(x,y_w,y_l) \sim D}\left [ \log \sigma \left( \beta\log\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)} - \beta\log\frac{\pi_\theta(y_l|x)}{\pi_\text{ref}(y_l|x)} \right)\right ]
$$ - 通过最小化上面的损失函数,即可求得最优参数 \(\theta^*\)
- DPO-最优策略推导 :将原始目标进行转换有
附录:DPO 训练流程
- 一句话总结:用 \(\pi_\text{ref}\) 收集数据 + 人类离线标记偏好 + 按照 DPO 损失函数训练
- 【与 RLHF Reward Model 训练相同】使用SFT模型对同一个Prompt重复生成多个不同Response,记为 \(y_a, y_b, y_c, y_d\)
- 【与 RLHF Reward Model 训练相同】让人类对回答进行排序打分: \(y_a \succ y_b \succ y_c \succ y_d\) ,最终可获得数据集 \(D = \{x^{(i)}, y^{(i)}_w, y^{(i)}_l\}_{i=1}^N\)
- 实际上,对于一个 \(x\) 对应K个 \(y\) 的情况,可以拆开成 \(C_K^2\) 个样本,然后按照Bradley-Terry(BT)Model来建模,在OPENAI原始论文:Training language models to follow instructions with human feedback中训练RM时是这样表述的,论文均按照BT模型来写
- 实际上,DPO原始论文:Direct Preference Optimization: Your Language Model is Secretly a Reward Model中还给出了一种不做样本拆分的等价表达形式:Plackett-Luce Model,在论文最后我们会进行讨论
- 【与 RLHF 不同】对于给定的 \(\pi_\text{ref}\) 和数据集 \(D\) ,优化语言模型 \(\pi_\theta\) 以最小化loss:
$$
Loss_{\text{DPO}}(\pi_\theta;\pi_\text{ref}) = - \mathbb{E}_{(x,y_w,y_l) \sim D}\left [ \log \sigma \left( \beta\log\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)} - \beta\log\frac{\pi_\theta(y_l|x)}{\pi_\text{ref}(y_l|x)} \right)\right ]
$$- 注: \(\sigma(\cdot)\) 表示Sigmod函数 \(\sigma(x) = \frac{1}{1+e^{-x}}\)
- 策略 \(\pi_\text{ref}\) 和数据集 \(D\) 必须是对应的,即数据集 \(D\) 应该是按照策略 \(\pi_\text{ref}\) 中采样得到的;
- 一般来说:数据集 \(D\) 都是策略 \(\pi^{SFT}\) 采样得到的,此时 \(\pi_\text{ref}\) 就是 \(\pi^{SFT}\)
- 当数据集 \(D\) 为公开数据集时,可以使用下面的方法先训练一个 \(\pi_\text{ref}\) (原始论文中描述 \(\pi_\text{ref}\) 的训练过程为initialize \(\pi_\text{ref}\) ,但实际上, \(\pi_\text{ref}\) 在DPO训练 \(\pi_\theta\) 过程中是不会被更新的):
$$
\pi_\text{ref} = \arg\max_{\pi} \mathbb{E}_{(x,y_w) \sim D} log \pi(y_w|x)
$$- 理解:这种情况下 \(\pi_\text{ref}\) 的训练就是在数据集 \((x, y_w) \sim D\) 上的SFT
- 这种设定可以减少未知的真实行为策略与 DPO 使用的 \(\pi_\text{ref}\) 之间的分布偏移(mitigate the distribution shift between the true reference distribution which is unavailable, and \(\pi_\text{ref}\) used by DPO)
- 问题 :如何理解收集数据的行为策略必须和参考策略一致?
- 回答(待补充):在推导过程中并未看到必须要求数据和参考策略一致,但是 DPO-最优策略推导过程中变换 KL 散度形式时,要求 \(y\sim\pi\),即回复 \(y\) 必须从当前策略采样,考虑到参考模型常常作为目标策略的初始值,且更新过程中数据无法变更,则保证数据从参考策略(目前策略初始值)采样是最合适的
- 其他角度的进一步理解:如果能针对当前策略生成的样本进行反馈,则可以最大程度上对当前模型进行高效优化,重点优化模型可能会生成的样本,给与或正或负的高效反馈
- 问题:为什么不能直接用 SFT 的结果作为 \(\pi_\theta\) ?DPO 相对普通 SFT 有什么优点?
- 回答:因为 SFT 没有使用到 \(y_l\) 样本,没有体现出来人类偏好,而 DPO 可以
附录:DPO 更新梯度分析
- DPO-loss 关于参数 \( \theta \) 的梯度可以写成:
$$\begin{aligned}
\nabla_{\theta} \mathcal{L}_{\mathrm{DPO} }\left(\pi_{\theta} ; \pi_{\text {ref } }\right) = -\beta \mathbb{E}_{\left(x, y_{w}, y_{l}\right) \sim \mathcal{D} }[\underbrace{\sigma\left(\hat{r}_{\theta}\left(x, y_{l}\right)-\hat{r}_{\theta}\left(x, y_{w}\right)\right)}_{\text {奖励估计错误时权重更高 } }[\underbrace{\nabla_{\theta} \log \pi\left(y_{w} | x\right)}_{\text {增加 } y_{w} \text { 的概率 } }-\underbrace{\nabla_{\theta} \log \pi\left(y_{l} | x\right)}_{\text {降低 } y_{l} \text { 的概率 } }]]
\end{aligned}$$- 其中 \(\hat{r}_\theta(x,y) = \beta \log\frac{\pi_\theta(y|x)}{\pi_\text{ref}(y|x)}\) 在原始论文中被称为隐式奖励模型,\( \hat{r}_{\theta}(x, y)=\beta \log \frac{\pi_{\theta}(y | x)}{\pi_{\text {ref } }(y | x)} \) 是由语言模型 \( \pi_{\theta} \) 和参考模型 \( \pi_{\text {ref } } \) 隐式定义的奖励
- 从梯度上可以看出:当 \(y_l\) 的奖励大于 \(y_w\) 的奖励时,梯度越大,而损失函数的梯度会增加生成 \(y_w\) 的概率,降低 \(y_l\) 的概率(对应负号 \(-\))
- 直观地说,损失函数 \( \mathcal{L}_{\text {DPO} } \) 的梯度增加了偏好完成项 \( y_{w} \) 的可能性,并降低了非偏好完成项 \( y_{l} \) 的可能性
- 由隐式奖励模型 \( \hat{r}_{\theta} \) 对非偏好完成项的评分高出多少来加权,由 \( \beta \) 缩放(详细讨论见附录),即隐式奖励模型对完成项排序的错误程度,考虑了 KL 约束的强度
- 注:作者在论文中给出了实验来验证隐式奖励模型 \( \hat{r}_{\theta} \) 加权的重要性(注意不是 \(\beta\) 的实验,是整体加权系数的实验),没有加权系数的朴素版本会导致语言模型退化(原文附录表3)
- 补充:梯度的推导过程

附录:DPO 与 RLHF 的关系是什么?
- 对于给定的 \(\pi_\text{ref}\) 和数据集 \(D\)
- DPO是在优化语言模型 \(\pi_\theta\) 以最小化loss:
$$
Loss_{\text{DPO}}(\pi_\theta;\pi_\text{ref}) = - \mathbb{E}_{(x,y_w,y_l) \sim D}\left [ \log \sigma \left( \beta\log\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)} - \beta\log\frac{\pi_\theta(y_l|x)}{\pi_\text{ref}(y_l|x)} \right)\right ]
$$ - RLHF的Reward Model则在优化Reward Model打分模型 \(r_\theta\) 以最小化loss:
$$
Loss_{\text{RM}}(\theta) = -\frac{1}{C_K^2} \mathbb{E}_{(x,y_w,y_l)\sim D}[\log \sigma(r_\theta(x, y_w) - r_\theta(x, y_l))]
$$ - 可以看到 DPO 的损失函数与 RLHF 中 Reward Model 的损失函数很相似,可以理解为 DPO 隐式建模了 Reward Model(在原始论文中 \(\hat{r}(x,y) = \beta \log\frac{\pi_\theta(y|x)}{\pi_\text{ref}(y|x)}\) 被称为隐式奖励模型,与 \(r_\theta(x,y)\) 替换后即和RM中的损失函数形式完全一致)
- DPO 可以看做是一个 off-policy 且 offline 的 RL 方法(实际上不是 RL 方法),而 RLHF 中的 PPO 是 online 且 on-policy 的方法
附录:对于大于2个回答偏好的情况如何处理?
- 处理方法一:Bradley-Terry(BT)Model,如论文所述,对多个偏好进行两两匹配生成多个样本,然后转换为只有两个回答偏好的情况
- 处理方法二:Plackett-Luce Model,使用如下损失函数来训练:


- 可以看到Plackett-Luce Model的损失函数展开以后就是 \(C_K^2\) 个偏好样本对,与先两两匹配生成样本,然后再利用Bradley-Terry Model建模的方法完全一致
- 原论文附录中有关于 Plackett-Luce Model 的详细介绍和推导
附录:DPO 损失函数中 KL 散度和超参数 \(\beta\) 的理解
- 从原始问题定义中理解 :在原始约束优化问题的定义中:
$$
\max_{\pi_\theta} \mathbb{E}_{x\sim D, y\sim \pi_\theta(y|x)} [r_{RM}(x,y)]-\color{red}{\beta} \mathbb{D}_{KL}[\pi_\theta(y|x)||\pi_\text{ref}(y|x)]
$$- \(\beta\) 是作为控制 KL 散度的约束严格程度存在的: \(\beta\) 越大,KL 散度约束越强; \(\beta\) 越小,KL 散度约束越弱
- 在 DPO 最终的损失函数中理解 :从损失函数的数学形式看
$$
Loss_{\text{DPO}}(\pi_\theta;\pi_\text{ref}) = - \mathbb{E}_{(x,y_w,y_l) \sim D}\left [ \log \sigma \left( \color{red}{\beta}\log\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)} - \color{red}{\beta}\log\frac{\pi_\theta(y_l|x)}{\pi_\text{ref}(y_l|x)} \right)\right ]
$$- 从损失函数中不容易理解 \(\beta\) 的作用,需求导以后才好理解,参见下面梯度中的理解
- 在 DPO 更新的梯度中理解 :从梯度更新的式子看:
$$\begin{aligned}
\nabla_{\theta} \mathcal{L}_{\mathrm{DPO} }\left(\pi_{\theta} ; \pi_{\text {ref } }\right) = -\color{red}{\beta} \mathbb{E}_{\left(x, y_{w}, y_{l}\right) \sim \mathcal{D} }[\underbrace{\sigma\left(\hat{r}_{\theta}\left(x, y_{l}\right)-\hat{r}_{\theta}\left(x, y_{w}\right)\right)}_{\text {奖励估计错误时权重更高 } }[\underbrace{\nabla_{\theta} \log \pi\left(y_{w} | x\right)}_{\text {增加 } y_{w} \text { 的概率 } }-\underbrace{\nabla_{\theta} \log \pi\left(y_{l} | x\right)}_{\text {降低 } y_{l} \text { 的概率 } }]]
\end{aligned}$$- 其中 \(\hat{r}_\theta(x,y) = \color{red}{\beta} \log\frac{\pi_\theta(y|x)}{\pi_\text{ref}(y|x)}\)
- 理解:从梯度公式看
- \(\color{red}{\beta \rightarrow 0}\) 时, \(\sigma(\cdot) \rightarrow \sigma(0) = 0.5\),相当于是个固定值,此时模型专注于优化以增大正样本概率,减小负样本概率,几乎没有任何约束
- \(\color{red}{\beta \rightarrow +\infty}\) 时:
- 当 \(\left(\log\frac{\pi_\theta(y_l|x)}{\pi_\text{ref}(y_l|x)} -\log\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)} \right) > 0\),则 \(\sigma(\cdot) \rightarrow \sigma(+\infty) = 1\),梯度对模型的影响正常,模型会优化这种样本,使得 \(y_w\) 出现的概率变大, \(y_l\) 出现的概率变小
- 当 \(\left(\log\frac{\pi_\theta(y_l|x)}{\pi_\text{ref}(y_l|x)} -\log\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)} \right) < 0\),则 \(\sigma(\cdot) \rightarrow \sigma(-\infty) = 0\),梯度对模型影响为 0,模型不再学习这种样本(即使 \(y_w\) 出现的概率比参考策略只大一点点,或\(y_l\) 出现的概率比参考策略仅小一点点)
- 综上,\(\color{red}{\beta \rightarrow +\infty}\) 时,会导致模型学习时,刚刚好学到一个 \(y_w\) 出现的概率比参考策略只大一点点,或\(y_l\) 出现的概率比参考策略仅小一点点的策略即收敛,这会导致策略不再继续偏离参考策略,也就实现了对 KL 散度的极大约束
- \(\beta\) 取值最佳实践 :原始论文中提到 \(\beta\) 默认取值为 \(\beta=0.1\),在 TL;DR summarization 任务(一个摘要生成任务)中取值为 \(\beta=0.5\)
附录:DPO Loss 的代码实现
- 来自原始 DPO 论文的代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17def dpo_loss(pi_logps, ref_logps, yw_idxs, yl_idxs, beta):
"""
pi_logps: policy logprobs, shape (B,)
ref_logps: reference model logprobs, shape (B,)
yw_idxs: preferred completion indices in [0, B-1], shape (T,)
yl_idxs: dispreferred completion indices in [0, B-1], shape (T,)
beta: temperature controlling strength of KL penalty
Each pair of (yw_idxs[i], yl_idxs[i]) represents the
indices of a single preference pair.
"""
pi_yw_logps, pi_yl_logps = pi_logps[yw_idxs], pi_logps[yl_idxs]
ref_yw_logps, ref_yl_logps = ref_logps[yw_idxs], ref_logps[yl_idxs]
pi_logratios = pi_yw_logps - pi_yl_logps
ref_logratios = ref_yw_logps - ref_yl_logps
losses = -F.logsigmoid(beta * (pi_logratios - ref_logratios))
rewards = beta * (pi_logps - ref_logps).detach()
return losses, rewards
附录:针对 DPO 的改进
- DPO 中只保证目标策略生成整个句子 \(y_w\) 或 \(y_l\) 的概率与参考策略一致,并不限制中间每个 Token 生成的过程中概率一致
- DPO 中的损失函数要求的是 \(\left(\log\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)} -\log\frac{\pi_\theta(y_l|x)}{\pi_\text{ref}(y_l|x)} \right) \) 变大;实际上,模型可能学习到的是,让 \(\pi_\theta(y_w|x)\) 和 \(\pi_\theta(y_l|x)\) 同时变小,只要正样本变小的幅度较小即可
附录:DPO 训练时的 \(\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)}\) 应该保证始终大于 1 吗?
- 副标题:DPO 训练时的 \(\frac{\pi_\theta(y_l|x)}{\pi_\text{ref}(y_l|x)}\) 应该保证始终小于 1 吗?
- 现象:在训练时发现 \(\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)} < 1\) 且持续降低(此时 \(\beta=0.1\))
- 设置 \(\beta=0.5\) 后 \(\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)} > 1\) 波动
- 其他指标均正常:
- \(\left(\log\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)} -\log\frac{\pi_\theta(y_l|x)}{\pi_\text{ref}(y_l|x)} \right) \) 逐步变大
- \(\frac{\pi_\theta(y_l|x)}{\pi_\text{ref}(y_l|x)} < 1\) 且持续降低
- 问题:让 \(\pi_\theta(y_w|x)\) 和 \(\pi_\theta(y_l|x)\) 同时变小的结果不是我们想要的吧,我们至少不想要 \(\pi_\theta(y_w|x)\) 降低
- 如何理解 通过调整 \(\beta\) 值可以缓解这个问题呢?
- 个人理解:DPO 的本质是让 \(\left(\log\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)} -\log\frac{\pi_\theta(y_l|x)}{\pi_\text{ref}(y_l|x)} \right) \) 越大越好
- 进一步分析有:
- 当 \(\beta\) 过小时 ,KL 散度约束小,可能导致 \(\pi_\theta(y_w|x)\) 和 \(\pi_\theta(y_l|x)\) 同时变小(持续变小)
- 当 \(\beta\) 过大时 ,KL 散度约束大,可能导致 \(\pi_\theta(y_w|x)\) 和 \(\pi_\theta(y_l|x)\) 都波动很小
- 从梯度上体现就是,当 \(\log\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)}\) 比 \(\log\frac{\pi_\theta(y_l|x)}{\pi_\text{ref}(y_l|x)}\) 大一点点就不学了
- 当 \(\beta\) 适中时 ,KL 散度约束适中,可约束 \(\pi_\theta(y_w|x)\) 和 \(\pi_\theta(y_l|x)\) 不能偏离当前策略太多,让 \(\pi_\theta(y_w|x)\) 变大, \(\pi_\theta(y_l|x)\) 变小,从而实现
附录:对齐人类偏好的其他方法
- RLHF: 基于人类反馈的强化学习方法,基于人类偏好训练 RM 再 RL,ChatGPT 的训练方式
- RLAIF: 基于AI反馈的强化学习方法,基于 AI 偏好模型训练 RM 再 RL,Claude 的训练方式
- 其他参考RLHF的替代之DPO原理解析:从RLHF、Claude的RAILF到DPO、Zephyr:
整个从 SFT 到 RLHF 或 RLAIF 的训练中,ChatGPT 只有最后 1/3 摆脱了人工参与的训练,而 Claude 则希望超过 1/2 摆脱人工参与的训练