NLP——LLM对齐微调-LLDS

注：本文包含 AI 辅助创作

Paper Summary

  • 整体总结：
    • 作者将 LLD 确定为基于 GRPO 的、Search-R1 风格的工具集成 RL 不稳定的核心原因
    • LLD 出现得早，发生频率高，并能可靠地将训练驱动到一个自我强化的 LLD 死亡螺旋中，其特征是单调的似然衰减、熵激增、梯度膨胀和最终崩溃
    • 注意：论文的分析首次提供了系统性证据，表明 GRPO 在工具集成设置下对似然漂移特别脆弱
    • 为了对抗这种故障模式，论文提出了 LLDS，一个简单有效的似然保留正则化器，它仅在似然降低时激活，并且仅针对有问题的 Token
  • 背景 & 问题提出：
    • Tool-Integrated RL(TIRL）让 LLM 能够通过与搜索引擎和检索器等外部工具交互来执行多步推理
    • GRPO，如 Search-R1 (2025) 所示，提供了快速的收敛性和无需价值函数的设定，使其在此场景中具有吸引力，但却持续遭受训练坍缩（training collapse）
  • 作者识别出Lazy Likelihood Displacement（LLD）
    • 即正确与错误响应的似然同时系统性降低或停滞，是驱动 training collapse 的核心机制
    • 理解：这里的 Displacement 是 “移位” 的含义，likelihood displacement 在统计中是一个专有名词，翻译为：“似然位移”，指模型参数的似然估计值因数据分布变化、异常值或模型假设偏差 ，导致与 “真实参数” 产生的系统性偏移（本质是 “似然估计的偏差”）
      • LLD 表面含义是表达 Likelihood 缓慢地发生了错位？但本意是指优化后，策略的质量反而下降了，即 RL 的目标反而下降了
  • LLD 早期出现并触发了自我强化（self-reinforcing）的LLD 死亡螺旋（LLD Death Spiral） ，其中下降的似然导致低置信度响应，从而放大了梯度并最终导致坍缩
  • 作者通过实验在 Search-R1 风格的、搜索集成的问答任务上，跨模型描述了这一过程，揭示了一致的三阶段轨迹：
    • 早期停滞：early stagnation
    • 稳定衰减：steady decay
    • 加速坍缩：accelerated collapse
  • 问题解法：
    • 作者提出了一种轻量级的、保持似然的 LLDS 正则化方法 ，仅当轨迹的似然下降时才激活 ，并且只正则化造成下降的 Token
    • 这种细粒度结构在最小化对优化过程干扰的同时缓解了 LLD
    • 在七个开放域和多跳问答基准测试中，LLDS 稳定了训练，防止了梯度爆炸，并带来了显著的性能提升
      • 包括在 Qwen2.5-3B 上获得 +37.8% 的增益，在 Qwen2.5-7B 上获得 +32.0% 的增益
  • 论文的结果确立了 LLD 是基于 GRPO 的 TIRL 的一个根本瓶颈，并为稳定、可扩展的工具集成 LLM 训练提供了实用路径

Introduction and Discussion

  • LLM 越来越多地利用外部工具，例如搜索引擎 (2025) 和代码执行环境 (2025; 2025)，来增强其推理能力
  • 这个工具集成推理（Tool-Integrated Reasoning, TIR）范式推动了近期在事实性问答 (2025)、基于图像的推理 (2025) 和数学问题求解 (2025; 2025) 方面的进展
  • 通过使模型能够迭代 Query 工具、验证中间步骤并精炼其思考，工具调用显著提升了推理质量 (2023)
  • 这些进展自然促使人们使用 RL 来训练 LLM 进行规划、与工具交互并掌握多步决策，正如最近基于 GRPO 的框架（如 Search-R1 (2025)）所例证的那样
  • 但将 TIR 扩展到 RL 设定引入了严重且持续的训练不稳定性
    • 特别是，在 Search-R1 风格 (2025) 的、搜索集成的问答流程中，GRPO 训练频繁表现出突然的奖励下降和灾难性坍缩 (2025; 2025)
    • 这些失败在多轮设定中尤为明显 (2025)，其中工具反馈成为模型条件上下文的一部分，创造了长且高度纠缠的轨迹
    • 尽管先前工作已观察到这些失败，但其底层机制仍知之甚少
  • 论文首先识别出Lazy Likelihood Displacement（LLD） (2025; 2024; 2024)
    • 即在 GRPO 优化期间，正确和错误响应的似然停滞或减少 (2025)
    • 这是 Search-R1 风格的 Tool-Integrated Reinforcement Learning（TIRL）中先前被忽视的根本坍缩来源
  • 以搜索集成问答为案例研究（见图 2），论文展示了 LLD 早期且持续地出现：
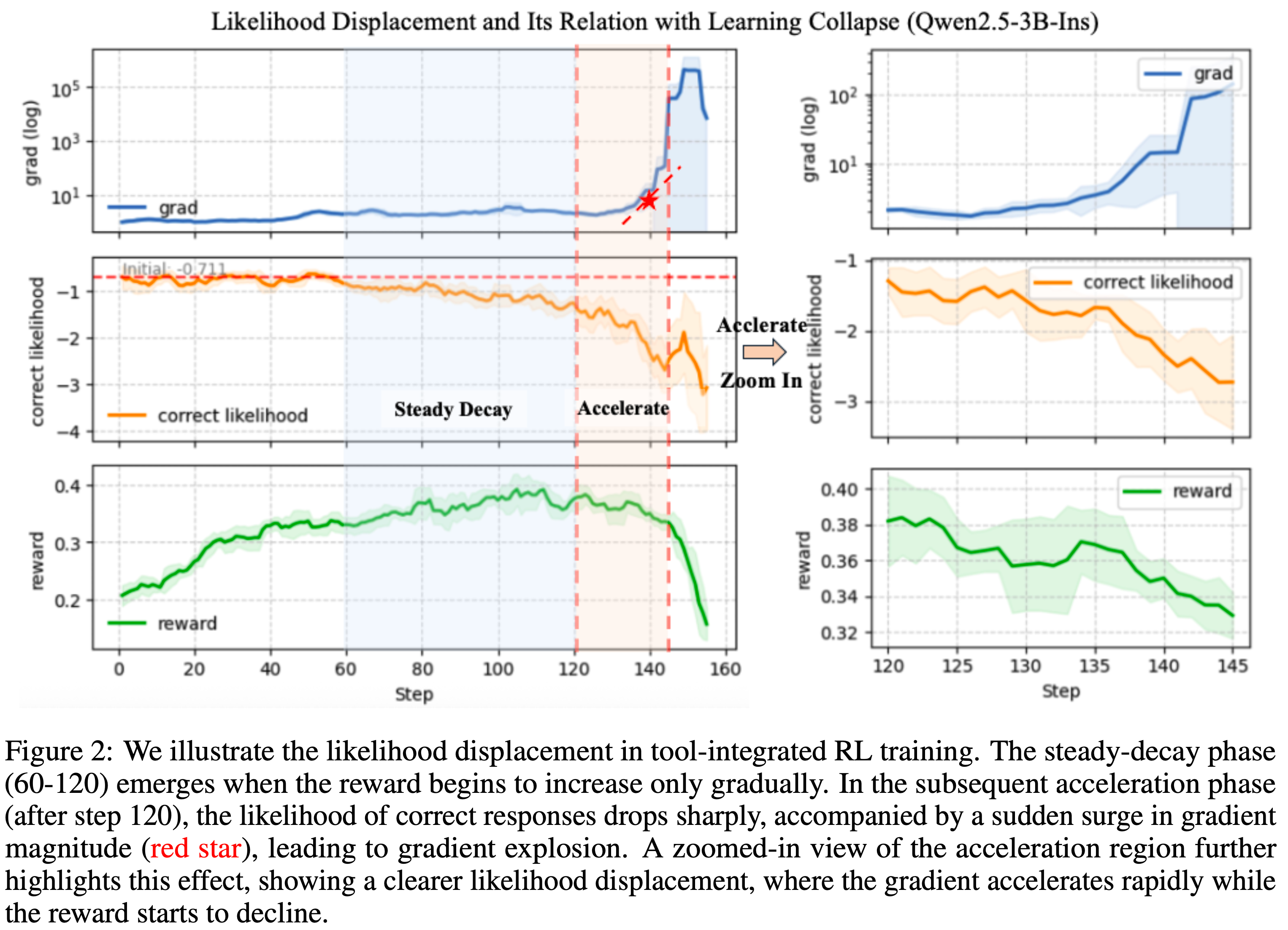
    • 即使在奖励增加时，正确响应的似然也进入单调下降
  • 这种行为在多种模型规模上均出现，表明 LLD 是基于 GRPO 的 TIRL 的一种结构性失败模式，而非特定配置的产物
  • 论文进一步证明 LLD 驱动了一个 self-reinforcing 的LLD 死亡螺旋 ，其中由此产生的低置信度状态放大了来自错误轨迹的负梯度影响，加速了似然衰减，触发了熵（Entropy）尖峰，增大了似然比，并最终导致了引起坍缩的大梯度不稳定性
  • 为对抗此失败模式，论文提出了一种简单而有效的保持似然的正则化方法 LLDS ，用于防止有害的似然减少
    • 论文的方法可与 GRPO 无缝集成，并引入了两层选择性：
      • （i）响应级门控 ，仅当轨迹的总体似然下降时才激活正则化；
      • （ii）Token-level 选择性 ，仅惩罚造成下降的 Token
    • 这种细粒度设计直接缓解了 LLD，同时最小程度地干扰了 GRPO 的优化行为
      • 通过防止无意的向下似然漂移，LLDS 使优化远离不稳定的高梯度状态，并保持了健康的训练动态
    • 实验证明，这转化为稳定的训练、被抑制的梯度爆炸以及在七个开放域和多跳问答基准测试上的一致增益
  • 论文的主要贡献有三方面：
    • 论文首次对 GRPO 驱动的 TIRL 中的 LLD 进行了系统性研究，并表明它高频出现，一致地经历一个特征性的失败轨迹：
      • 稳定的似然衰减，随后是梯度放大和熵爆炸，最终坍缩
    • 论文提出了一种轻量级的保持似然的正则化方法 LLDS，它选择性地正则化似然减少，并解决了 GRPO 训练中的坍缩问题
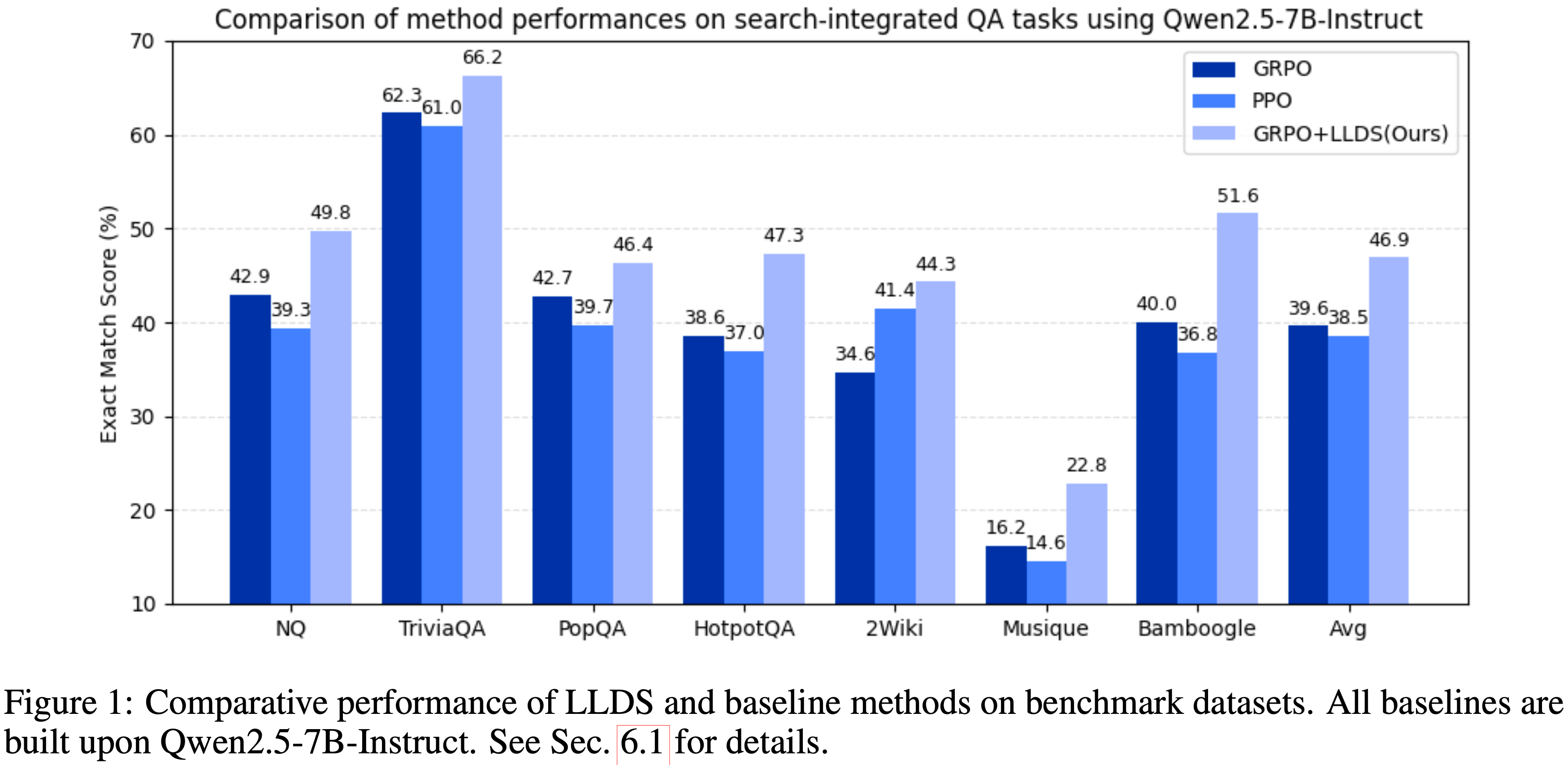
    • 通过稳定训练，论文在七个 QA 基准测试上实现了显著的性能提升（见图 1），展示了一种更鲁棒、更可靠的 RL 驱动 TIR 方法

Preliminary

  • TIRL 使一个 LLM 能够与外部工具交互
  • 论文将 Query 记作 \(\boldsymbol{x}\)，工具反馈记作 \(\boldsymbol{o}\)，模型的动作记作 \(\boldsymbol{y}\)
  • 对于给定的 Query \(\boldsymbol{x}\)，模型在第 \(t\) 轮根据下式自回归地生成一个动作：
    $$
    \pi_{\theta}(\boldsymbol{y}_{t} \mid \boldsymbol{x},\boldsymbol{y}_{0},\boldsymbol{o}_{0},\boldsymbol{y}_{1}, \ldots ,\boldsymbol{o}_{t-1}),
    $$
    • \(\boldsymbol{y}_{t}\) 是基于累积上下文生成的
    • \(\boldsymbol{o}_{t-1} \sim \mathcal{T}\) ：
      • 如果前一个动作 \(\boldsymbol{y}_{t-1}\) 调用了一个工具 \(\mathcal{T}\)（例如，发出搜索 Query ），则在第 \(t-1\) 轮返回的工具反馈
      • 如果未调用任何工具，则 \(\boldsymbol{o}_{t-1}\) 为空字符串
  • 多轮（Multi-turn） 设定对应于涉及多次工具调用，从而涉及多轮工具反馈的轨迹
    • 注意：这里的多轮并不涉及多个用户 Prompt 输入，整个过程中用户仅输入一个 Prompt（或 Query），其他的交互都是工具/环境产生的
  • 工具反馈 \(\boldsymbol{o}_{t}\) 对于预训练语言模型本质上是分布外（Out-of-Distribution, OOD） 的，因为这些反馈来源于外部环境，而非模型自身的生成分布
    • 直接迫使模型拟合这些反馈 Token 会引入巨大的训练-推理不匹配，并可能导致模型记忆环境特定的反馈
    • 因此，先前的工作通常在有监督训练期间将反馈 Token 屏蔽掉，以稳定优化并避免对外部内容过拟合 (2025)

Tool-Integrated GRPO with Feedback Mask

  • 由 DeepSeek-Math (2024) 和 DeepSeek-R1 (2025) 提出的 GRPO 损失函数，通过改进奖励和损失信号的计算方式来增强策略优化
  • 与 PPO (2017) 不同，GRPO 无需价值函数估计，而是使用组内相对奖励归一化进行优化
  • 具体而言，对于一个 Query-Answer 对 \((\boldsymbol{x}, \boldsymbol{a})\)，策略 \(\pi_{\theta}\) 采样 \(G\) 个响应：
    $$\{(y_{i,0}, \boldsymbol{o}_{i,0}, \ldots, y_{i,t}, \boldsymbol{o}_{i,t}, \ldots, \boldsymbol{o}_{i,T_{i}-1}, y_{i,T_{i} })\}_{i=1}^{G},$$
    • \(T_{i}\) 表示 第 \(i\) 次 rollout 中 工具调用的次数（多轮交互的数量）
    • 每个动作 \(\boldsymbol{y}_{i,t}\) 由 \(|y_{i,t}|\) 个 Token 组成，论文用 \(\boldsymbol{y}_{i,t, < k}\) 表示由其前 \(k-1\) 个 Token 组成的前缀，即 \(\mathbf{y}_{i,t,k}\) 表示第 \(i\) 个 rollout 的第 \(t\) 个回合的 第 \(k\) 个 Token，其 在策略 \(\pi_{\theta_\text{old}}\) 下的采样逻辑为：
      $$ \mathbf{y}_{i,t,k}\sim \pi_{\theta_\textrm{old} }(\cdot|\mathbf{x},\cdots,\mathbf{y}_{i,t-1},\mathbf{o}_{i ,t-1},y_{i,t, < k}) $$
    • 令 \(r_{i}\) 表示分配给第 \(i\) 个响应的奖励
    • 第 \(i\) 个响应的第 \(t\) 个动作的优势通过组级归一化定义：
      $$\hat{A}_{i,t,k}:=\frac{r_{i}-\mu}{\sigma}, \qquad k=1,\ldots,|\hat{\boldsymbol{y} }_{i,t}|,$$
      • \(\mu=\widehat{\mathbb{E} }[\{r_{i}\}_{i=1}^{G}]\) 和 \(\sigma=\sqrt{\textrm{Var}[\{r_{i}\}_{i=1}^{G}]}\) 分别是组内奖励的经验均值和标准差
      • 同一轨迹的每个 Token 共享相同的归一化优势
  • 带反馈掩码的工具集成 GRPO 目标函数如下：
    $$\mathcal{J}_{\textrm{GRPO} }(\theta)=\mathbb{E}_{(\boldsymbol{x},\boldsymbol{a})\sim\mathcal{D} \\ \{y_{i,0},…,y_{i,t},\boldsymbol{o}_{i,t},y_{i,T_{i} } \}\sim(\pi_{\theta_\textrm{old} },\mathcal{T}) }\ \left[\frac{1}{\sum_{t=1}^{G}\sum_{t=1}^{T_{i} }|\hat{\boldsymbol{y} }_{i,t}|}\sum_{i=1}^{G}\sum_{t=1}^{T_{i} }\sum_{k=1}^{|\hat{\boldsymbol{y} }_{i,t}|}\min \left(\gamma_{i,t,k}(\theta)\hat{A}_{i,t,k},\hat{A}_{i,t,k}\operatorname{clip}\big(\gamma_{i,t,k}(\theta),1-\varepsilon,1+\varepsilon\big)\right)\right], \tag{1}$$
    • \(\varepsilon\) 是裁剪参数
    • 似然比定义为
      $$ \gamma_{i,k}(\theta)=\frac{\pi_{\theta}(\mathbf{y}_{i,t,k}|\mathbf{x},\cdots,\mathbf{y}_{i,t-1},\mathbf{o}_{i ,t-1},y_{i,t, < k})}{\pi_{\theta_\textrm{old} }(\mathbf{y}_{i,t,k}|\mathbf{x},\cdots,\mathbf{y}_{i,t-1},\mathbf{o}_{i ,t-1},y_{i,t, < k})} $$
    • 注意：尽管在损失计算时反馈 Token \(\mathbf{o}\) 被掩码掉，但它们仍然会影响后续 Token 预测的上下文
    • 注：从上面的公式 1 进一步说明：论文的多轮并不涉及多个用户 Prompt 输入，整个过程中用户仅输入一个 Prompt（或 Query），其他的交互都是工具/环境产生的
    • 问题：上面公式中的采样过程其实应该是表示为下面的式子才对吧？
      $$ \{y_{i,0},…,y_{i,t},\boldsymbol{o}_{i,t},y_{i,T_{i} } \}\sim(\pi_{\theta_\textrm{old} }(\cdot|\boldsymbol{x}), \mathcal{T}) $$

Lazy Likelihood Displacement in Tool-integrated GRPO（工具集成 GRPO 中的 LLD）

  • 近期工作 (2025) 在基于文本的非工具设定中，为 GRPO 引入了Lazy Likelihood Displacement（LLD） ，表明在优化过程中正确响应的似然经常减少或仅微弱改善（improves only marginally）
  • 在本节中，论文将 LLD 扩展到工具集成 RL 领域，并定义：
  • 定义 4.1：Tool-Lazy Likelihood Displacement
    • 令 \(\pi_{\theta_{\textrm{old} } }\) 和 \(\pi_{\theta_{\textrm{fin} } }\) 表示在数据集 \(\mathcal{D}\) 上优化偏好学习目标 \(\mathcal{J}\)（例如，公式 1）之前和之后获得的初始策略和微调策略，且 \(\mathcal{J}(\theta_{\textrm{fin} }) < \mathcal{J}(\theta_{\textrm{old} })\)
      • 理解：
        • 优化前的策略是：\(\pi_{\theta_{\textrm{old} } }\)
        • 优化后的策略是：\(\pi_{\theta_{\textrm{fin} } }\)
        • \(\mathcal{J}(\theta_{\textrm{fin} }) < \mathcal{J}(\theta_{\textrm{old} })\) 表示优化目标下降了
    • 考虑一个由交替动作和反馈组成的工具集成轨迹，\(({\boldsymbol{y} }_{0},{\boldsymbol{o} }_{0},\ {\boldsymbol{y} }_{1},{\boldsymbol{o} }_{1},\ \ldots ,\ {\boldsymbol{y} }_{T})\)，其中仅动作 \(\{ {\boldsymbol{y} }_{t}\}_{t=0}^{T}\) 用于似然计算（反馈被屏蔽）
    • 对于每个响应动作 \({\boldsymbol{y} }_{t}\)，定义其对数似然变化为
      $$
      \Delta_{t}({\bf x},{\boldsymbol{y} }_{t}):=\ln\pi_{\theta_{\textrm{fin} } }({\boldsymbol{y} }_{t} \mid {\bf x},{\boldsymbol{y} }_{ < t},{\boldsymbol{o} }_{ < t})-\ln\pi_{\theta_{\textrm{old} } }({\boldsymbol{y} }_{t} \mid {\bf x},{\boldsymbol{y} }_{ < t},{\boldsymbol{o} }_{ < t}).
      $$
    • 如果
      $$\Delta_{t}({\bf x},{\boldsymbol{y} }_{t}) \ \leq \ \epsilon $$
      • 则称：对于动作 \(t\) 发生了 LLD
      • 其中 \(\epsilon\) 是一个小的或非正的常数
    • 如果
      $$
      \sum_{t=0}^{T}\Delta_{t}({\bf x},{\boldsymbol{y} }_{t}) \ \leq \ \epsilon,
      \tag{2}
      $$
      • 则称：对于整个响应 发生了 LLD
    • 因此，LLD 捕捉了在优化策略下，一个或多个响应动作的似然表现出可忽略甚至负向改进的失败模式
    • 为了更好地理解 LLD 的起源，论文强调负梯度如何抑制正确动作的似然
      • 以下非正式定理（正式版本及证明见附录 A）在工具集成 RL 的设定中重述了 (2025) 中的定理 4.4：
  • 定理 4.2（非正式：工具集成 GRPO 中的 Trajectory-level LLD (Informal: Trajectory-Level LLD in Tool-Integrated GRPO)）： 在工具集成 GRPO 中，当发生下面的情况时，原本正确的响应似然可能会下降
    • （i）低似然的错误响应
    • （ii）其嵌入表示与正确响应相似的错误响应诱导出大的负梯度并主导了正向更新
    • 这些力量共同导致了 Trajectory-level 的 LLD
  • 在工具集成 GRPO 的设定中，论文极其频繁地观察到正确响应的似然未能改善
    • 这表明了一种特别严重的 LLD 形式（\(\epsilon \leq 0\)），导致了模型整体输出似然的渐进衰减
    • 这种复合衰减是 Search-R1 风格工具集成 RL 的一种独特失败模式

Lazy Likelihood Displacement in Tool-Integrated GRPO (工具集成 GRPO 中的 LLD )

  • 本节阐述了 LLD 在工具集成 GRPO 训练中的普遍性，并展示了 LLD (\(\epsilon \leq 0\)) 如何灾难性地将模型驱动至训练崩溃

Likelihood Dynamic

  • 为了说明训练期间 LLD 的普遍性和进展过程，论文可视化了工具集成 RL 中的似然位移轨迹（likelihood-displacement
    trajectory）
  • 如图 2 所示，演化过程呈现出三个特征阶段：
    • 第一阶段（早期停滞, Phase I (early stagnation)）：
      • 即使奖励增加，正确响应的似然也几乎保持不变，显示了 LLD 的初始出现
    • 第二阶段（稳态衰减，步骤 60-120, Phase II (steady-decay, steps 60-120))：
      • 似然表现出缓慢但持续的向下漂移，而奖励仅缓慢增长且梯度范数保持稳定——这表明了持续的 LLD
    • 第三阶段（加速，步骤 120 之后, Phase III (acceleration, after step 120)）：
      • 似然开始急剧崩溃，同时梯度幅度快速激增（由红星 Token ），这触发了梯度爆炸并最终导致训练崩溃
    • 注：后续两个阶段对应于 \(\epsilon \leq 0\) 的机制，即正确响应的似然严格衰减而非改善
  • 图 2 右侧的放大视图突显了这一转变：
    • 似然持续下降，同时梯度加速上升，奖励曲线开始下降
    • 虽然最终的崩溃是由爆炸的梯度引起的，但似然衰减在整个训练过程中都存在，引入了累积的不稳定性，在加速阶段被急剧放大（更多讨论见附录 B.1）

Lazy Likelihood Displacement Death Spiral（LLD 死亡螺旋）

  • 在图 2 中，论文观察到随着训练的进行，响应似然出现加速下降
  • 论文通过将经过 Feedback-masked 轨迹写作 \(\hat{\boldsymbol{y} }=(\boldsymbol{y}_0,\boldsymbol{y}_1,\ldots,\boldsymbol{y}_T)\) 来简化符号
  • 论文正式地将这种加速的似然衰减表征为 LLD 死亡螺旋
  • 定义 5.1（LLD 死亡螺旋, Definition 5.1 (LLD Death Spiral)）：
    • 考虑一个元组 \((\boldsymbol{x},\hat{\boldsymbol{y} }^{+})\) 以及从 \(\pi_{\theta_t}\) 到 \(\pi_{\theta_{t+1} }\) 的策略更新
    • 如果策略演化表现出以下自我强化的进程，论文说系统进入了 LLD 死亡螺旋：
      $$
      \text{LLD}_{t} \implies C^{\mathrm{low} }_{t} \implies \text{LLD}_{t+1}, \quad \epsilon_{t+1}<\epsilon_{t} \leq 0
      $$
    • 其中 \(\text{LLD}_{t}\) 表示时刻 \(t\) 的 LLD ，其似然递减 (\(\epsilon_{t} \leq 0\))，而 \(C^{\mathrm{low} }_{t}\) 表示在 \(\pi_{\theta_t}\) 下似然递减的低置信度轨迹
    • 转换 \(\text{LLD}_{t} \implies C^{\mathrm{low} }_{t}\) 反映了降低的似然导致预测越来越分散，而转换 \(C^{\mathrm{low} }_{t} \implies \text{LLD}_{t+1}\) 的发生是因为低置信度的错误响应通常包含与正确响应中相似的动作，这导致方程 (9) 中产生更大的值，从而产生更强的负梯度影响
    • 当这些效应在多次迭代中复合时，似然衰减加速，创造了一个自我延续的崩溃，论文称之为 LLD 死亡螺旋 (LLD Death Spiral)
  • 论文通过加速的熵爆炸 (accelerated entropy explosion) 和加速的逐样本 LLD (accelerated per-sample LLD) 来演示 LLD 死亡螺旋
Accelerated Per-Sample LLD（加速的逐样本 LLD）
  • 论文在基于搜索的问答数据集 NQ (2019) 上进行了对照实验，以检验 GRPO 的负梯度如何影响正确响应的对数似然
  • 使用 Qwen2.5-3B-Ins (2024)，论文为每个问题生成 8 个回合，并仅保留那些包含正确和错误响应混合的示例，丢弃所有响应完全正确或完全错误的情况
  • 为了分离逐样本的学习动态，论文为每个单独的问题重新初始化模型参数 \(\theta\)，应用一次 GRPO 更新得到 \(\theta’\)，然后测量正确响应的平均对数似然变化：
    $$
    \Delta(\boldsymbol{x}) := \frac{1}{N^{+} } \sum_{i=1}^{N^{+} } \left[ \ln \pi_{\theta’}(\hat{\boldsymbol{y} }^{+}_{i} \mid \boldsymbol{x}) - \ln \pi_{\theta}(\hat{\boldsymbol{y} }^{+}_{i} \mid \boldsymbol{x}) \right],
    $$
  • 其中对于具有 \(N^{+}\) 个正确响应的问题 \(\boldsymbol{x}\)
  • 论文在图 3 中展示了结果
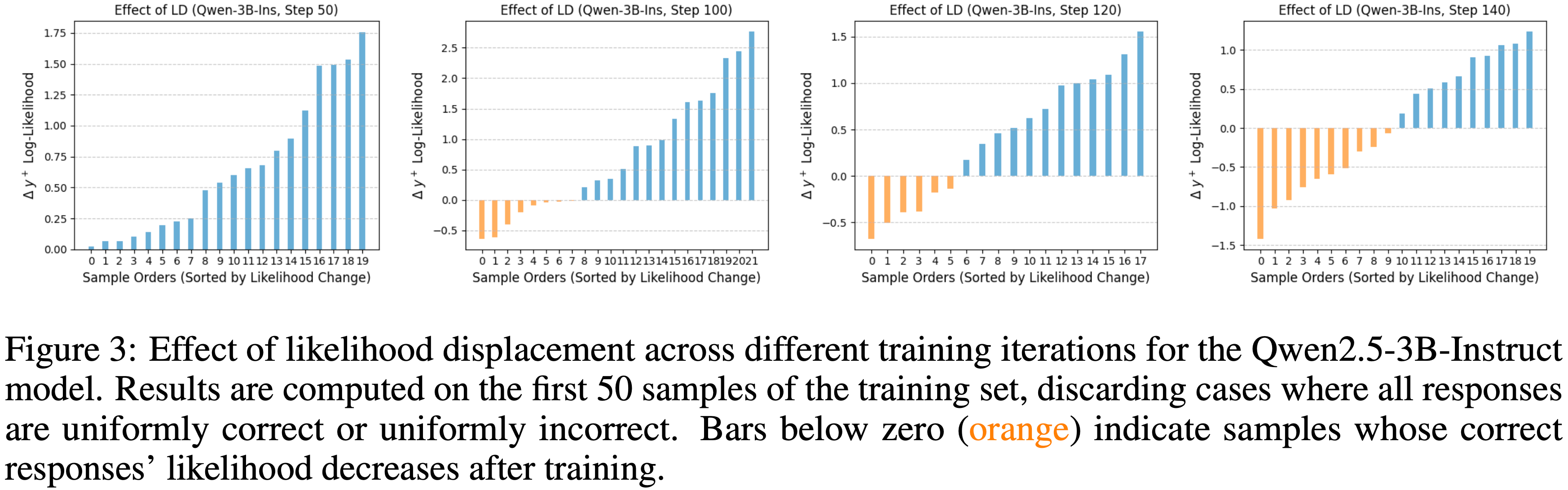
  • 在训练的早期阶段（第 50 次迭代），仅观察到轻微的 LLD：
    • 大多数问题中正确响应的似然减少可以忽略不计，可能是因为正确和错误的轨迹在结构上仍然不相似
  • 随着训练的进行，LLD 变得更加明显
    • 错误响应与正确响应之间结构相似性的增加导致了更广泛的似然下降，如上升的橙色曲线所示
    • 当训练进入加速阶段（第 120-140 次迭代）时，这种趋势加剧为LD 死亡螺旋 (LD death spiral)
    • 在第 140 次迭代时，超过一半的样本显示正确响应的似然大幅下降
      • 这种崩溃是由错误响应极低的似然驱动的，它放大了负梯度的贡献并使学习不稳定
Accelerated Entropy Explosion（加速的熵爆炸）
  • 图 4 可视化了训练期间 Qwen2.5-3B-Ins（图 a）和 Qwen2.5-3B-Base（图 b）的熵、响应长度和有效搜索比率的演变
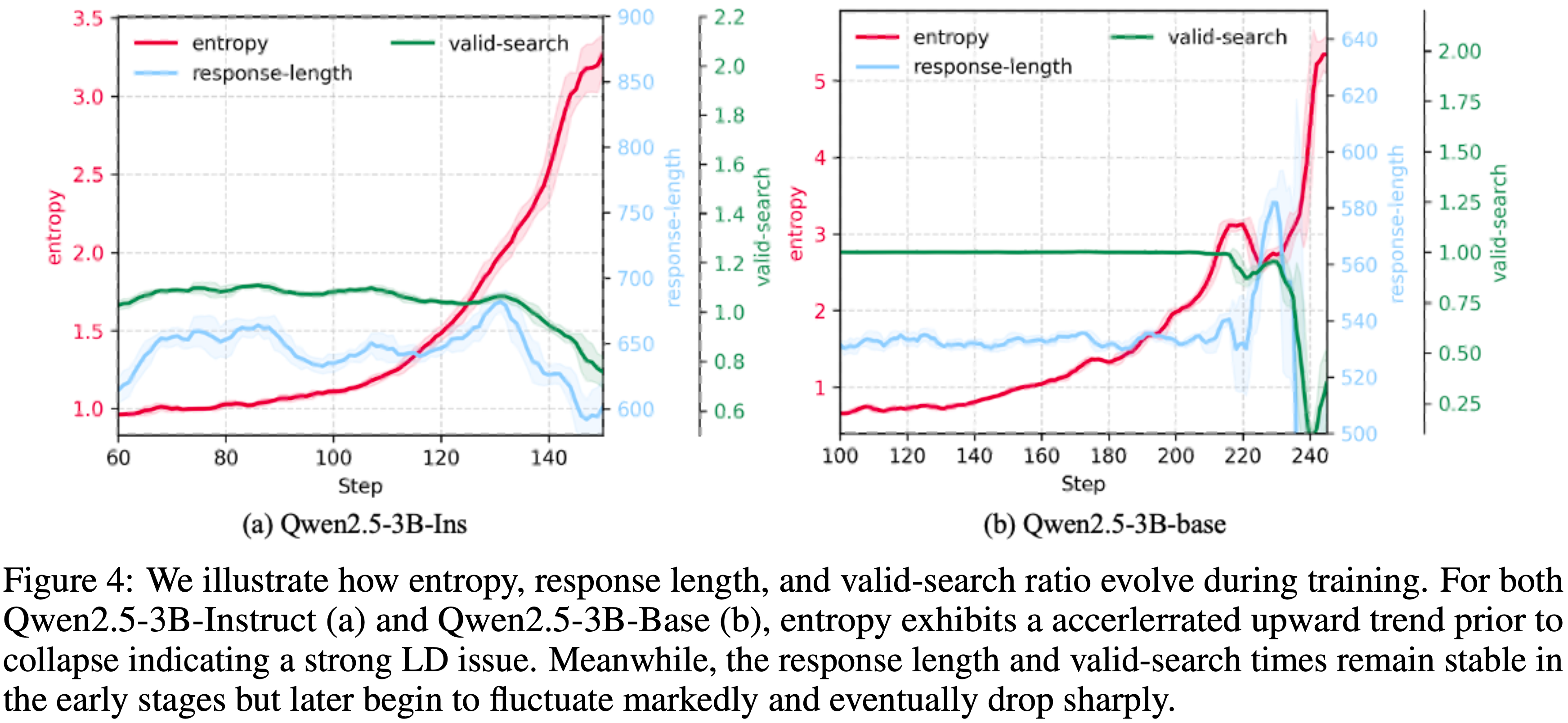
  • 在两个模型中，平均 Token 熵最初缓慢增加，反映了图 2 中早期慢速 LLD 机制，但后来过渡到急剧加速增长的阶段，这与 LLD 轨迹的加速阶段一致
  • 这种陡峭的熵斜率是死亡螺旋的明确证明：
    • 随着低置信度响应的积累，模型为其 Token 分配越来越分散、低概率的分布，这进一步加强了 LD 并将系统推向不稳定
    • 至关重要的是，这种熵加速发生在响应长度和有效搜索次数几乎保持不变的同时，这证实了上升的熵和相应的似然下降不是由轨迹长度或工具 Query 频率引起的，而是 LD 效应本身的直接表现

Watch for correct actions embedded within incorrect responses（在错误响应中嵌入的正确动作）

  • 观察发现工具集成 GRPO 比非工具场景 (2025) 更容易受到 LLD 的影响
  • 本节在响应动作的粒度上检查 LLD，其中每个动作由连续工具调用之间的片段定义
  • 作者对 Qwen2.5-3B-Ins (2024) 的分析揭示了一个工具集成 GRPO 独有的惊人模式：
    • 正确动作经常出现在原本错误的响应中 ，这种混合结构扰乱了似然估计过程，放大了 LLD 并使训练不稳定
  • 错误响应中频繁出现的正确动作 (Frequent correct actions in Incorrect responses)
    • 论文在实验中发现模型通常使用其第一个响应动作来生成搜索 Query ，并且这个初始动作的正确性随着训练的进行稳步提高
    • 具体来说，作者衡量错误响应生成的检索文档是否与正确响应检索到的文档匹配；
      • 如果匹配，论文将第一个动作视为正确
      • 理解：这里是想看看错误的响应中，第一个回答是正确动作的比例
    • 图 5 显示了不同训练阶段下这个初始动作的准确率
      • 如绿色虚线所示，早期阶段准确率较低，反映了模型对搜索能力的初始掌握，但随着时间的推移显著上升
      • 到第 140 步时，大约 60% 的错误响应以一个正确的搜索 Query 开始，突显了正确 & 错误回复中，第一动作共享的高度结构相似性
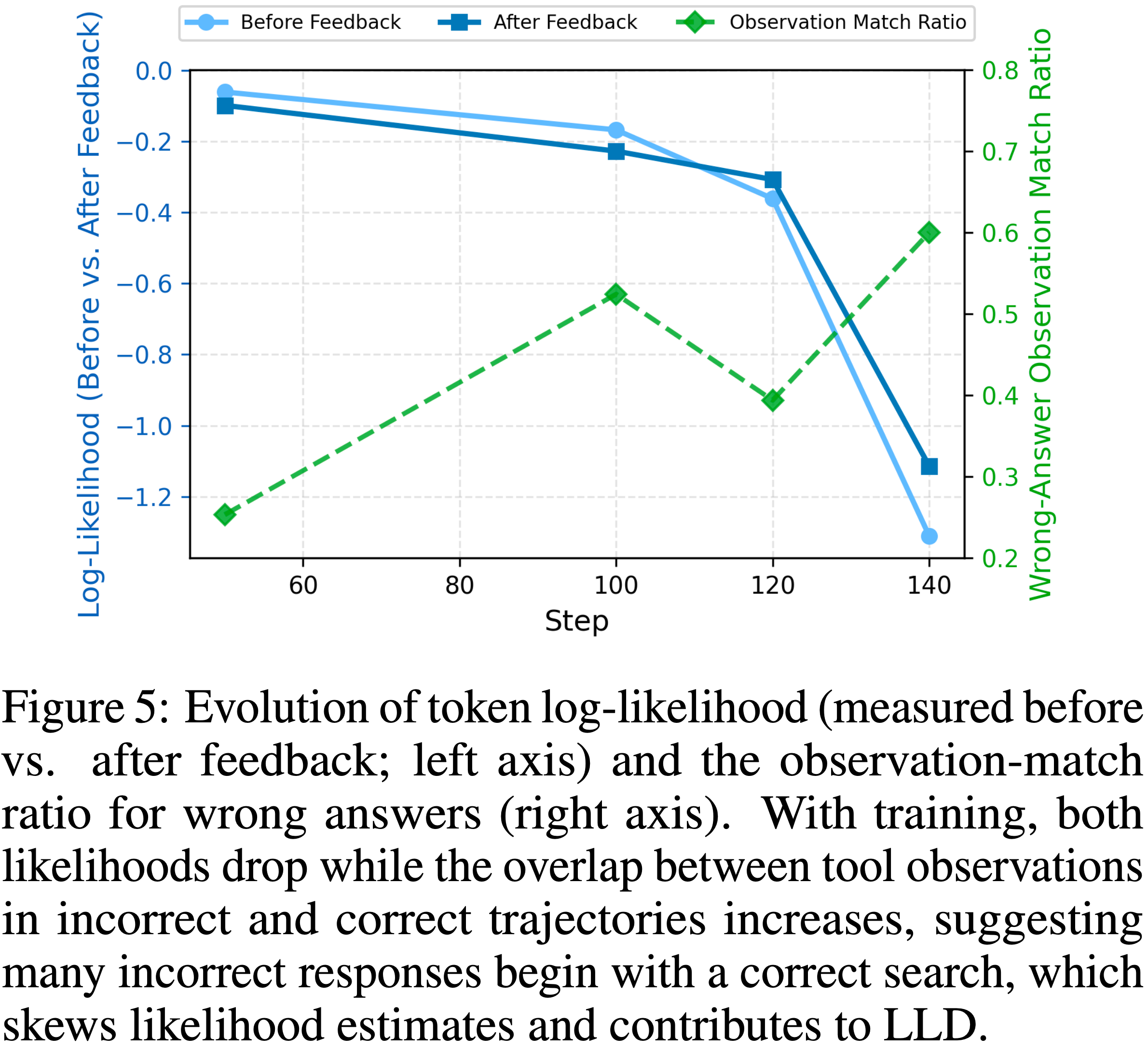
  • 第一动作响应更快的似然衰减 (Faster likelihood decay of the first-action response)
    • 如图 5 所示，论文进一步观察到第一动作（浅蓝色）的似然衰减幅度比第二动作（蓝色）大得多
    • 训练早期，第一动作的似然更高，主要是因为第二动作必须基于分布外（OOD）的反馈进行条件生成
      • 理解：Before Feedback 为第一动作；After Feedback 为第二动作
    • 随着训练的进行，两个动作都表现出似然衰减
      • 第一动作的似然大约在第 110 步附近最终下降到低于第二动作，此时第一动作的正确率大约为 50%，表明正确和错误轨迹之间存在强烈的相似性
      • 在第 120 步之后，这种衰减急剧加速，标志着LLD 死亡螺旋 (LLD death spiral) 的开始，其中低似然的错误部分信号进一步加剧了退化
  • 无意义的第一动作 (Nonsensical first-action)
    • 随着 LLD 加剧和第一动作似然崩溃，模型开始产生无意义的输出
    • 如附录中的图 15 所示，它最终生成随机的、无意义的 Token ，这种效应是由严重降低的响应似然驱动的，这导致采样选择任意单词
    • 虽然在这个阶段可能尚未发生完全崩溃，但模型实际上已经无法使用，因为它无法再产生有意义的响应
  • 因此，必须减少对错误响应中正确动作的无意惩罚
    • 更详细的讨论见第 7 节

LLD regularization

  • 为了解决 LLD 问题，论文引入了一类似然保留正则化器，以防止模型在 GRPO 训练过程中无意地降低响应的似然
  • 对于给定的保留响应 \(\boldsymbol{y}_i \in \mathcal{Y}_{\text{pre} }\)，论文比较其在旧策略（前一步）和微调策略下的 Token-level 似然
    • 理解：这里是提前准备了一个保留集 \(\mathcal{Y}_{\text{pre} }\)，这里面的样本可以认为都是比较好的，也就是正确的，如果在这些样本上，新策略有下降，则给与惩罚
  • 论文的基础正则化器仅惩罚在更新后似然降低的 Token（Likelihood-reducing tokens）
LLD 正则的三种变体
  • LLD： Token-level 似然保留 (LLD: Token-Level Likelihood Preservation)
    • LLD 应用一个 Token-level 惩罚 (token-level penalty) ：
      • 在每个响应 \(\mathbf{y}_i\) 内，只有似然降低的 Token 对损失有贡献：
        $$
        L_{\text{LLD} }=\frac{1}{\sum_{\boldsymbol{y}_i \in \mathcal{Y}_{\text{pre} } } \left| \mathbf{y}_i \right|} \sum_{\boldsymbol{y}_i \in \mathcal{Y}_{\text{pre} } } \sum_{y_i \in \mathbf{y}_i} \underbrace{\max \left(0, \ln \pi_{\theta_{\text{old} } }(y_i|\mathbf{x},\mathbf{y}_{ < i}) - \ln \pi_{\theta}(y_i|\mathbf{y}_{ < i}) \right)}_{\text{Likelihood-reducing tokens} }
        $$
    • 这种 Token-level 选择性确保模型仅因真正有害的似然降低而受到惩罚，而不会干扰整体改善响应的更新
    • 理解：这是一种惩罚机制，也可以称为 正则（Regularization）
      • 在 保留集 \(\mathcal{Y}_{\text{pre} }\) 上
        • 当新策略的似然降低时，给与惩罚
        • 当新策略的似然提升时，不做任何处理
    • 但是：
      • 即使少数个别 Token 似然降低，某些响应可能在全局上仍是改善的；
      • 惩罚这种情况可能会引入过于强烈的约束
  • LLDS：响应级门控 (LLDS: Response-Level Gating)，也是论文默认变体
    • 为了避免对全局改善的响应施加不必要的惩罚，LLDS 引入了响应级门控 (response-level gating) 机制：
      • 仅当响应的总似然降低时，惩罚才激活，LLDS 损失为：
        $$
        L_{\text{LLDS} }=\frac{1}{\sum_{\boldsymbol{y}_i \in \mathcal{Y}_{\text{pre} } }|\mathbf{y}_i|} \sum_{\boldsymbol{y}_i \in \mathcal{Y}_{\text{pre} } } \underbrace{\mathbf{1} \left[ \sum_{\boldsymbol{y}_i \in \mathbf{y}_i} \left( \ln \pi_{\theta_{\text{old} } }(y_i|\mathbf{x},\mathbf{y}_{ < i}) - \ln \pi_{\theta}(y_i|\mathbf{y}_{ < i}) \right) > 0 \right]}_{\text{Activated only when sum} \gt {0} } \cdot \sum_{\boldsymbol{y}_i \in \mathbf{y}_i} \underbrace{\max \left(0, \ln \pi_{\theta_{\text{old} } }(y_i|\mathbf{x},\mathbf{y}_{ < i}) - \ln \pi_{\theta}(y_i|\mathbf{y}_{ < i}) \right)}_{\text{Likelihood Reducing Tokens} }
        $$
    • 这种结构保留了正常的 GRPO 学习，同时直接抑制了遭受 LLD 的响应
  • LLDS-MA：掩码答案 Token (LLDS-MA: Masking Answer Tokens)
    • 为了进一步鼓励多步推理和工具使用，论文将最终答案 Token 从正则项中 Mask 掉
    • LLDS-MA 仅对推理和工具交互 Token 上的似然降低进行惩罚，排除答案部分 \(\boldsymbol{y}_{i,\text{Ans} }\)：
      $$
      \underbrace{\sum_{\boldsymbol{y}_i \in \mathbf{y}_i / \boldsymbol{y}_{i,\text{Ans} } } \max \left(0, \ln \pi_{\theta_{\text{old} } }(y_i|\mathbf{x},\mathbf{y}_{ < i}) - \ln \pi_{\theta}(y_i|\mathbf{y}_{ < i}) \right)}_{\text{Mask Answer Likelihood-reducing tokens}}
      $$
LLD 正则的使用形式
  • 最后，论文将正则化项集成到 GRPO 目标中 ，如下所示：
    $$
    L_{\text{total} } = L_{\text{GRPO} } + \lambda L_{\text{LLDS}(-\text{MA})}
    $$
    • 其中 \(\lambda\) 是正则化权重
  • 论文使用 LLDS 作为默认变体 ，当需要更强地鼓励工具使用时，切换到 LLDS-MA
    • 保留集 \([\mathbf{y}]_{\text{pre} }\) 包括所有具有非负优势 \(\hat{A} \geq 0\) 的响应，确保正确响应 (\(\hat{A} > 0\)) 和未训练的响应 (\(\hat{A} = 0\)) 不会遭受似然降低
    • \(\lambda\) 的影响在图 8 中进行了实证检验

Experiments and Analysis

  • 论文通过全面的实验评估了 \(L_{\text{LLDS}(-\text{MA})}\) 的实证有效性
  • 实验设置 (Experimental settings)
    • 对于训练，论文遵循 Jin 等 (2025) 的设置，并使用两个模型系列进行实验：Qwen-2.5-3B 和 Qwen-2.5-7B ，每个系列都有基础版和指令调优版变体 (2024)
    • 论文考虑两种训练配置
      • (1) 仅 NQ (单跳, NQ-Only (single-hop))： 模型仅在单跳 Natural Questions (NQ) 数据集 (2019) 上训练
      • (2) NQ+Hotpot (单跳+多跳, NQ+Hotpot (single-hop+multi-hop))： 模型在合并了 NQ 和 HotpotQA (2018) 的语料库上训练，提供更广泛的开域和多跳推理覆盖
    • 对于检索数据集，论文使用 2018 年维基百科转储 (2020) 作为知识库，并使用 E5 (2022) 作为密集检索器
    • 为了确保检索增强基线之间的公平比较，论文固定检索到的段落数量为三个，遵循 Jin 等 (2025) 的配置
    • 除非另有说明，论文使用与 Search-R1 (2025) 相同的优化超参数，唯一的修改是减少了最大回合限制：
      • 从 Search-R1 中的 4 回合降至仅 NQ 训练的 2 回合和 NQ+Hotpot 设置的 3 回合，以提高训练效率
      • 除非另有说明，正则化权重固定为 \(\lambda=0.1\)
  • 评估设置 (Evaluation settings)
    • 评估在七个数据集的验证集或测试集上进行，分类如下：
      • (1) 通用问答 (General Question Answering)： NQ (2019), TriviaQA (2017), PopQA (2022)
      • (2) 多跳问答 (Multi-Hop Question Answering)： HotpotQA (2018), 2WikiMultiHopQA (2020), Musique (2022), Bamboogle (2022)
    • 论文采用精确匹配作为主要评估指标，与 Jin 等 (2025) 中的协议一致
    • 这种多样性确保了在多种现实推理场景下对搜索引擎集成 LLM 性能的彻底检验

Experimental Results

  • 论文在七个公开领域域和多跳 QA 基准测试上评估了论文提出的 LLD 缓解策略，使用了两个模型家族：Qwen2.5-3B (基础版/指令版) 和 Qwen2.5-7B (基础版/指令版)
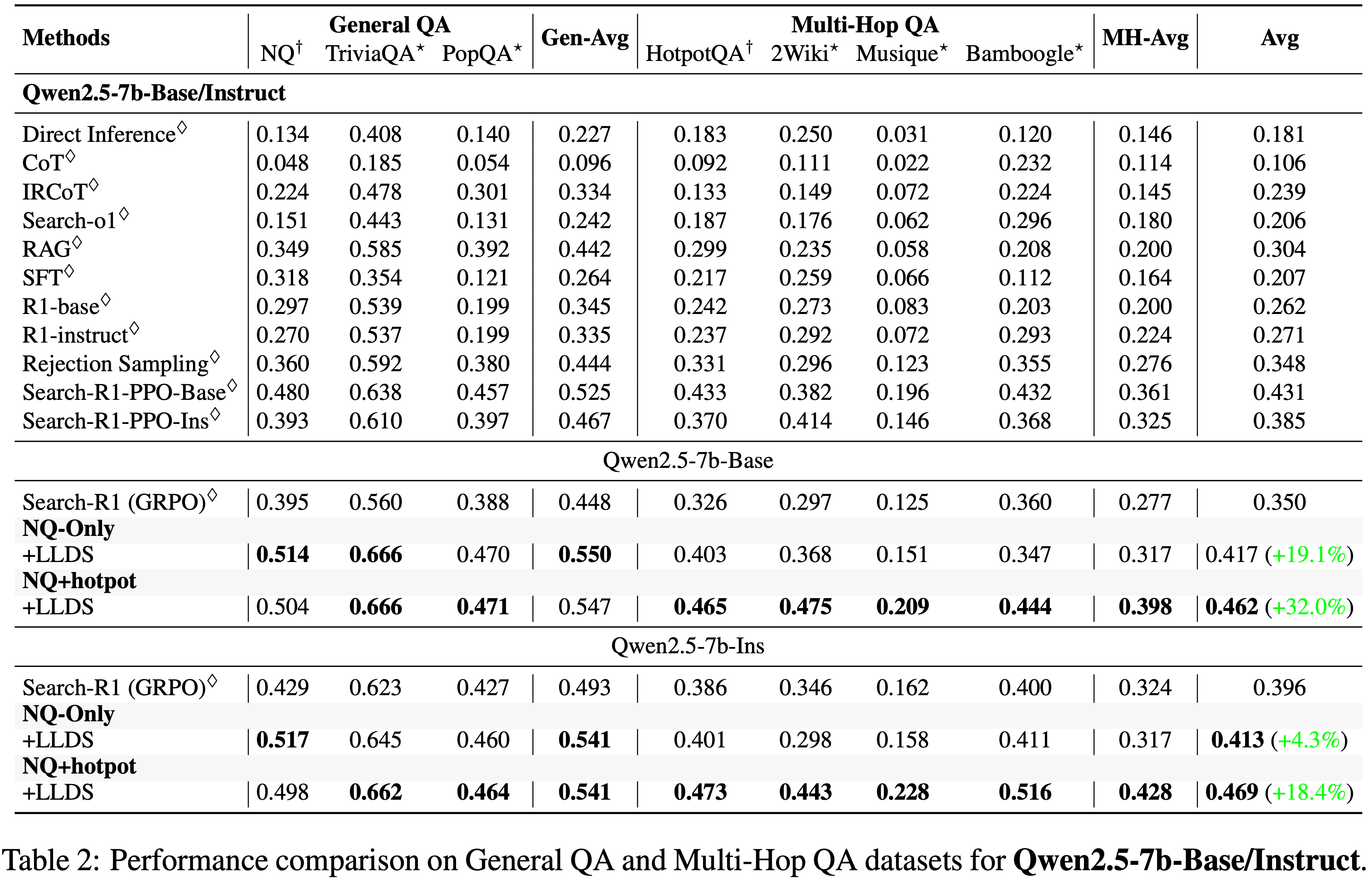
  • 表 1 和表 2 总结了所有设置下的 EM 性能
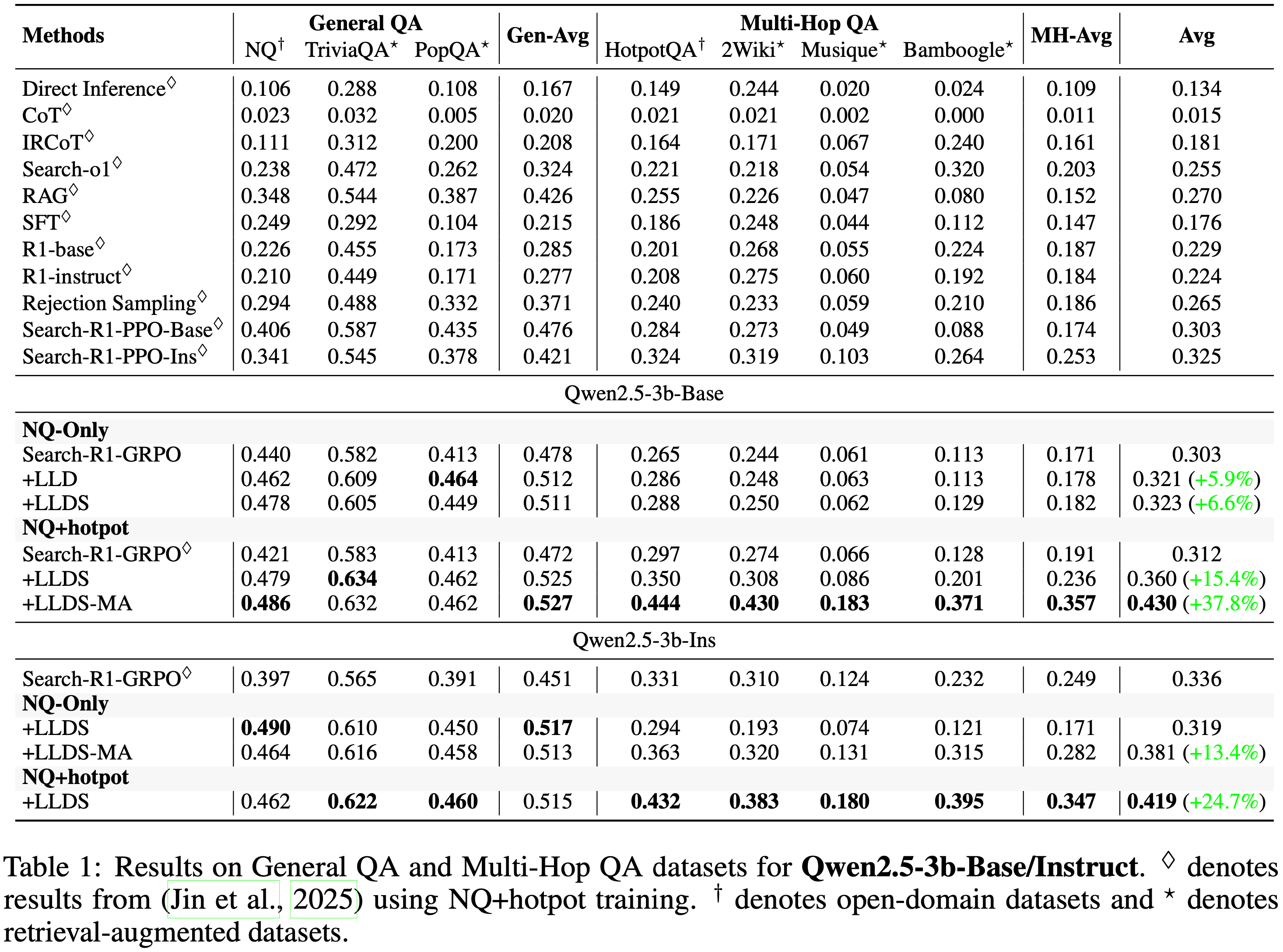
    • 由于普通 GRPO 训练经常崩溃并将奖励降至零，论文使用来自 Search-R1 Jin 等 (2025) 的结果（对应于崩溃前的最佳检查点）作为 GRPO 基线
Results on Qwen2.5-3B
  • 如表 1 所示，在仅 NQ 设置下，GRPO 的平均得分为 0.303
  • 加入 LLD 将性能提升至 0.321 (+5.9%)，LLDS 进一步改进至 0.323 (+6.6%)。在更具挑战性的 NQ+Hotpot 设置下，LLDS 将普通 GRPO 得分从 0.312 提高到 0.360，相对增益 15.4%
  • 由于 LLDS 倾向于将基础模型限制为仅调用一次搜索，论文应用了多视角变体 LLDS-MA，它提供了最强的性能，平均得分为 0.430，相对于普通 GRPO 有 +37.8% 的显著提升率
  • 对于 Qwen2.5-3B-Instruct 也观察到类似的趋势：在仅 NQ 下，LLDS-MA 将性能提升至 0.381；在 NQ+Hotpot 设置下，LLDS 达到 0.419 (+24.7%)
Results on Qwen2.5-7B
  • 如表 2 所示，对于 Qwen2.5-7B-Base，应用 LLDS 带来了显著改进，在仅 NQ 上训练时平均得分达到 0.417，相对于在 NQ+Hotpot 上训练的 GRPO 基线有 19.1% 的相对增益
  • 当在 NQ+Hotpot 训练设置下应用 LLDS 时，性能从 0.350 提高到 0.462，对应更大的 32.0% 的改进
  • LLDS 在几乎所有单个数据集上也取得了最强结果，表明证据检索和多步推理能力得到增强
  • 对于 Qwen2.5-7B-Instruct，论文观察到类似的模式。在 NQ+Hotpot 训练设置下，LLDS 将平均得分从 0.396 提高到 0.469（改善 18.4%）
  • LLDS 在每个多跳 QA 基准测试上都取得了最佳性能，包括 2Wiki 的 0.473、Musique 的 0.443 和 Bamboogle 的 0.516
  • 这些结果突显了 LLDS(-MA) 作为一种稳定 GRPO 训练并显著增强多轮推理的有效方法

Ablation Study and Analysis

  • 响应级门控的影响 (Impact of response-level gating)
    • 应用响应级门控降低了训练期间应用的正则化强度，从而在多跳 QA 任务上带来了可测量的改进
    • 如表 1 所示，尽管平均性能仅小幅提高了 0.2%，但该方法在 Bamboogle 数据集上带来了 1.6% 的显著增益，突显了其在增强多跳推理方面的有效性
  • 仅 NQ 与 NQ+Hotpot 对比 (NQ vs. NQ+Hotpot)
    • 仅在 NQ 上训练的模型在开域单跳 QA 上表现强劲，但在泛化到多跳设置方面能力有限
    • 转向 NQ+Hotpot 能持续改进多步推理：例如，对于 Qwen2.5-3B-Base，GRPO 基线从仅 NQ 的 0.303 提高到 NQ+Hotpot 的 0.312，LLDS 在相同的转变下从 0.323 提高到 0.360。对于 Qwen2.5-7B-Base 也出现了类似的趋势，其中 LLDS 从仅 NQ 的 0.417 上升到 NQ+Hotpot 的 0.462
    • 这些增益表明，添加需要多轮推理才能正确回答并获得奖励的多跳 HotpotQA 问题，比仅在 NQ 上训练更能鼓励模型更有效地检索、整合和推理多个证据片段
  • 掩码答案 (MA) 的影响 (Impact of masking answer (MA))
    • 作者专门对模型变体应用了掩码答案，在这些变体中，普通 GRPO 和 LLDS 退化到仅发出一次搜索调用，限制了它们为多跳推理收集足够证据的能力
    • MA 在最终答案 Token 上禁用 LLDS 正则化，鼓励模型执行额外的搜索步骤或中间推理
    • 如表 1 所示，在 LLDS 之上添加 MA 为这些单搜索限制的模型带来了显著改进
    • 在 NQ+Hotpot 设置下，LLDS-MA 将 Qwen2.5-3B-Base 的平均得分从 LLDS 的 0.360 提高到 0.430，同样将仅 NQ 的指令版变体从 0.319 提高到 0.381
    • 这些增益表明，在底层 GRPO 策略未充分利用搜索动作的场景下，MA 能有效鼓励更深层次的多步推理
    • 更详细的分析见附录 B.3

Effect of LLDS on Training Stability across Models

  • 为了验证 GRPO 中训练崩溃问题的普遍性以及论文提出的解决方案的鲁棒性，论文将实验扩展到不同的模型规模和对齐阶段
  • 图 6 展示了 Qwen-2.5 3B 和 7B 模型（包括基础版和指令版）的训练奖励曲线
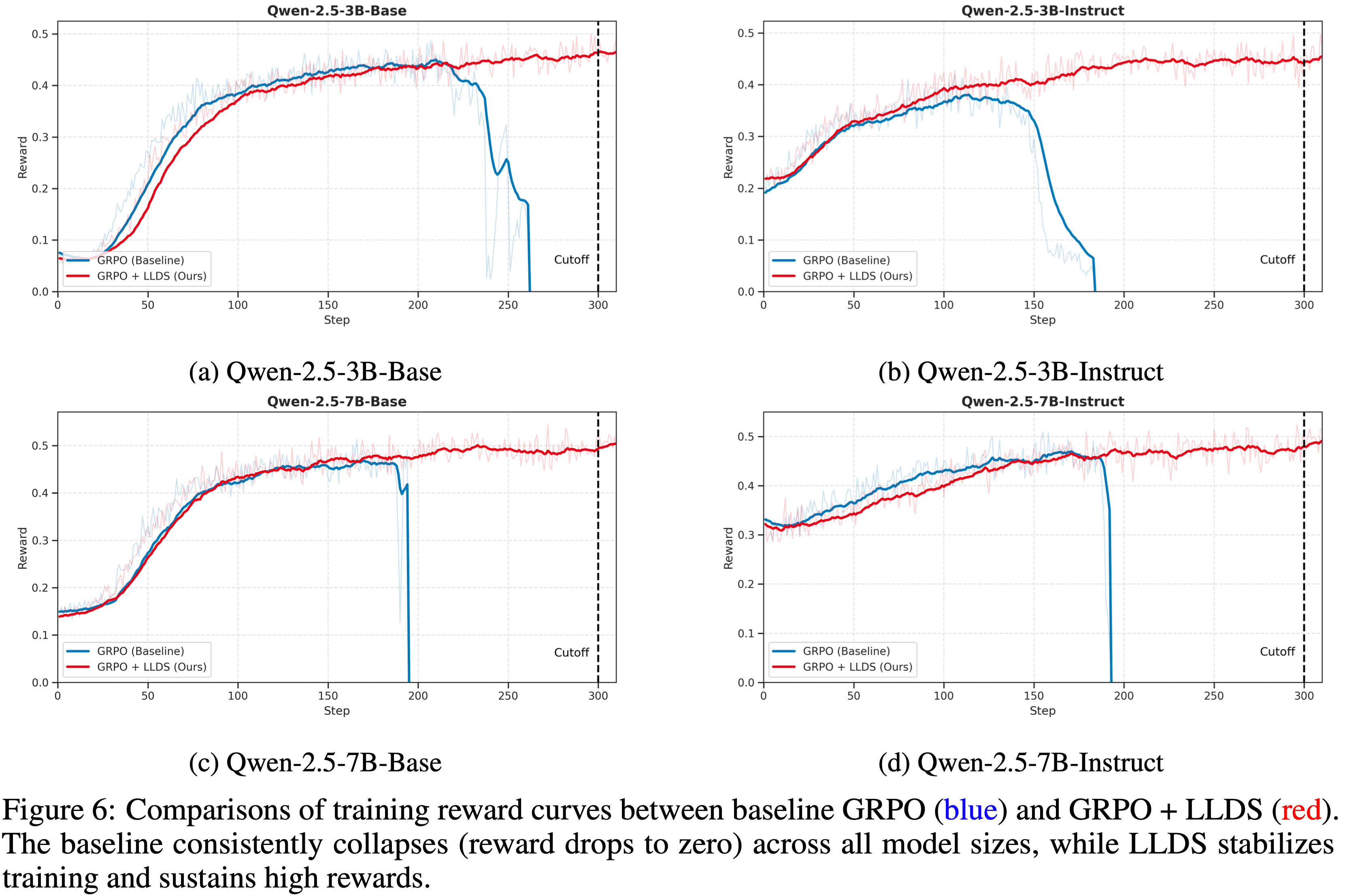
  • 如蓝色曲线所示，基线 GRPO 一致地在前 300 步内遭受灾难性崩溃，无论模型规模（3B 对 7B）或类型（基础版对指令版）如何
    • 这证实了不稳定性是算法的固有特征，而不是特定模型配置的产物
    • 相比之下，LLDS 的集成（红色曲线）有效地缓解了这个问题
  • 在所有四种场景中，使用 LLDS 训练的模型都保持了奖励的稳定上升轨迹，成功地避开了影响基线的崩溃点
    • 这表明 LLDS 是稳定 GRPO 训练的通用且有效的正则化器

More Discussion and Guideline

  • 基于论文对 LLD 的分析以及 LLD 死亡螺旋的出现，作者整合了几个稳定工具集成 GRPO 的实用指导原则
    • 每条建议都直接遵循论文研究中确定的核心故障机制

理解为何工具集成 GRPO 对 LLD 特别脆弱 (Understand why tool-integrated GRPO is uniquely vulnerable to LLD)**

  • 与自由形式的文本 RL 不同，工具增强的智能体引入了放大似然漂移的结构性条件
  • 首先，工具调用注入了固有的 OOD Token（例如搜索结果、API 输出或错误消息）
    • 它们与预训练的语言分布有显著差异
    • 这些 OOD 片段提高了 Token-level 不确定性，并使 GRPO 的相对更新更加不稳定，加速了似然位移的发生
  • 其次，基于工具的推理跨越多个 stages 展开，早期 stages（例如 Query 制定）比后期 stages（例如工具结果解释）更快稳定
    • 由于 GRPO 对所有 Token 应用单一标量奖励，那些在正确和错误轨迹间共享几乎相同前缀的早期 Token 会收到冲突的梯度信号
    • 这种 Reward-Token 错位对稳定前缀的危害不成比例，并放大了 LLD
    • 认识到这些结构性挑战对于诊断和缓解工具集成 RL 系统中的不稳定性至关重要

密切监控似然动态——仅靠奖励是不够的 (Closely monitor likelihood dynamics–reward alone is insufficient)**

  • 论文分析的一个核心见解是，似然退化在奖励出现任何可见下降之前很久就开始了
  • 在所有模型中，奖励在整个早期和稳态衰减 stages 持续上升，即使正确响应的似然已经向下漂移
    • 因为 GRPO 更新由似然比控制，这种早期退化会默默地放大梯度并引发不稳定性
    • 因此，仅监控奖励会掩盖 LLD 的发生
  • 在实践中，可靠的早期预警信号来自于跟踪 Action-level 和 Trajectory-level 对数似然，检查熵轨迹（一旦似然开始崩溃，熵会急剧飙升），以及关注指示梯度放大的似然比突然激增
    • 似然或熵曲线的可视化提供了训练接近不稳定机制的最早和最可靠的指示

补充：Related Work

  • 工具集成推理与智能体 LLMs (Tool-Integrated Reasoning and Agentic LLMs)
    • 工具使用已成为赋能 LLMs 具备自适应推理能力的一个强大范式
    • 早期方法依赖于基于提示的编排 (2023; 2023) 或多智能体委托框架来调用工具，而无需显式训练
    • 经过指令微调的模型 (2023; 2023) 后来通过监督学习引入了结构化的工具调用行为，但这些系统在很大程度上仍是静态的，并受限于单轮交互
    • 更近期的研究表明，强化学习可以通过使模型学习通过环境反馈和任务成功来掌握工具使用策略，从而显著增强工具集成
    • 诸如 RETool (2025)、VERL-Tool (2025) 和智能体 LLM 框架 (2025) 等显著系统通过动态工具使用、自我验证和纠错来支持多步推理
    • 这种从静态指令遵循到反馈驱动优化的转变在一系列领域被证明是有效的，包括结合代码执行的数学问题求解 (2025)、结合检索的开放域问答 (2025)、从自然语言生成 SQL (2025) 以及多模态视觉推理 (2024)

附录 A： 定理与证明

  • 在本节中，论文首先给出定理 4.2 的正式版本：
  • 定理 A.1 （工具集成 GRPO 中的 Trajectory-level LLD）
    • 考虑一个工具集成的轨迹，其中只有响应动作 \(\{\boldsymbol{y}_{t}\}_{t=0}^{T}\) 对似然度有贡献，工具反馈 Token \(\boldsymbol{o}_{t}\) 在似然计算期间被屏蔽，但仍保留在上下文中
    • 令 \(\pi_{\theta(s)}\) 表示训练时间 \(s\) 时的演化策略
    • ** Action-level 似然变化** ：对于第 \(i\) 个正确响应的第 \(t\) 个动作，记作 \(\boldsymbol{y}_{i,t}^{+}\)，其瞬时对数似然变化
      $$
      \frac{d}{ds} \ \ln\pi_{\theta(s)}\big(\boldsymbol{y}_{i,t}^{+} \mid \boldsymbol{x},\boldsymbol{y}_{i,< t}^{+},\boldsymbol{o}_{i,< t}^{+}\big)
      $$
      • 随着以下量的增加而变得越来越懒惰甚至变为负值：
        $$
        \begin{align}
        \mathcal{G}_{i,t}(s)&=p^{-}\underbrace{\sum_{k=0}^{|\boldsymbol{y}_{i,t}^{+}|} \sum_{j=1}^{N^{-} }\sum_{t^{\prime}=0}^{T_{j} }\sum_{k^{\prime}=1}^{|\boldsymbol{y}_{j,t^{\prime} }^{-}|}\alpha_{(i,t,k),(j,t^{\prime},k^{\prime})}^{-} \left\langle \mathbf{h}_{\boldsymbol{x},\boldsymbol{y}_{i,< t}^{+},\boldsymbol{o}_{i,< t}^{+},\boldsymbol{y}_{i,t,<k}^{+} },\mathbf{h}_{\boldsymbol{x},\boldsymbol{y}_{j,< t^{\prime} }^{-},\boldsymbol{o}_{j,< t^{\prime} }^{-},\boldsymbol{y}_{j,t^{\prime},<k^{\prime} }^{-} } \right\rangle}_{\text{impact of negative gradients} } \\
        &-p^{+}\sum_{k=0}^{|\boldsymbol{y}_{i,t}^{+}|}\sum_{t^{\prime}=1}^{N^{+} }\sum_{t^{\prime\prime}=0}^{T_{t^{\prime} } }\sum_{k^{\prime\prime}=1}^{|\boldsymbol{y}_{i^{\prime},t^{\prime\prime} }^{+}|}\alpha_{(i,t,k),(i^{\prime},t^{\prime\prime},k^{\prime\prime})}^{+} \left\langle \mathbf{h}_{\boldsymbol{x},\boldsymbol{y}_{i,< t}^{+},\boldsymbol{o}_{i,< t}^{+},\boldsymbol{y}_{i,t,<k}^{+} },\mathbf{h}_{\boldsymbol{x},\boldsymbol{y}_{i^{\prime},< t^{\prime\prime} }^{+},\boldsymbol{o}_{i^{\prime},< t^{\prime\prime} }^{+},\boldsymbol{y}_{i^{\prime},t^{\prime\prime},<k^{\prime\prime} }^{+} } \right\rangle.
        \end{align}
        \tag{8}
        $$
      • 其中 \(\alpha_{(i,t,k),(j,t^{\prime},k^{\prime})}^{-}\) 和 \(\alpha_{(i,t,k),(i^{\prime},t^{\prime\prime},k^{\prime\prime})}^{+}\) 表示 Token-level 的预测误差相似性权重
    • ** Trajectory-level 似然变化** ：对所有动作求和得到
      $$
      \frac{d}{ds}\ln\pi_{\theta(s)}(\boldsymbol{y}_{0:T} \mid \boldsymbol{x})=\sum_{t=0}^{T}\sum_{k=1}^{|\hat{\boldsymbol{y} }_{t}^{+}|}\frac{d}{ds}\ln\pi_{\theta(s)}(\hat{\boldsymbol{y} }_{t,k}^{+}|\cdot),
      $$
      • 每当发生下面的情况时，该值会变得懒惰或为负
        $$
        \sum_{t=0}^{T}\sum_{k=1}^{|\hat{\boldsymbol{y} }_{t}^{+}|}\mathcal{G}_{t,k}(s) \quad \text{is large.}
        $$
  • 如定理所示，两个核心因素放大了这种负梯度效应：
    • 1）不正确响应的低似然度 ：
      • 模型分配低概率的负响应会产生更大的预测误差权重 \(\alpha_{i,k;t^{\prime},k^{\prime} }^{-}\)，从而放大其影响
      • 在这种情况下，模型将这些低似然度错误解释为严重错误，导致其梯度获得不成比例的大规模缩放
    • 2）嵌入相似性 ：
      • 当不正确响应与正确响应相似时，它们的前缀表示具有较大的内积，从而放大了负贡献
      • 这种高表征重叠意味着模型难以区分正确和错误的延续，导致负例将梯度推向有害方向并使模型缺乏信心

定理 A.1 的证明

  • 设置与屏蔽 ：固定一个 Query \(\boldsymbol{x}\) 和一个正确响应索引 \(i\)，并考虑 Feedback-masked 轨迹
    $$
    \hat{\boldsymbol{y} }_{i}^{+}=(\boldsymbol{y}_{i,0}^{+},\boldsymbol{o}_{i,0}^{+},\boldsymbol{y}_{i,1}^{+},\boldsymbol{o}_{i,1}^{+},\ldots,\boldsymbol{y}_{i,T_{i} }^{+}),
    $$
    • 其中只有动作 Token \(\{\boldsymbol{y}_{i,t}^{+}\}_{t=0}^{T_{i} }\) 对损失有贡献。工具反馈 \(\boldsymbol{o}\) 被排除在 GRPO 目标之外，但保留在条件上下文中。论文研究每个动作 \(\boldsymbol{y}_{i,t}^{+}\) 在演化策略 \(\pi_{\theta(s)}\) 下的对数似然变化：
      $$
      \frac{d}{ds}\ln\pi_{\theta(s)}\big(\boldsymbol{y}_{i,t}^{+} \mid \boldsymbol{x},\boldsymbol{y}_{i,< t}^{+},\boldsymbol{o}_{i,< t}^{+}\big),
      $$
    • 然后对 \(t\) 进行聚合以获得 Trajectory-level 结果
  • 在 Action-level 简化为标准 GRPO ：以前缀 \((\boldsymbol{x},\boldsymbol{y}_{i,< t}^{+},\boldsymbol{o}_{i,< t}^{+})\) 为条件，第 \(t\) 个动作 \(\boldsymbol{y}_{i,t}^{+}\) 以自回归方式生成：
    $$
    \pi_{\theta(s)}\big(\boldsymbol{y}_{i,t}^{+} \mid \boldsymbol{x},\boldsymbol{y}_{i,< t}^{+},\boldsymbol{o}_{i,< t}^{+}\big)=\prod_{k=1}^{|\boldsymbol{y}_{i,t}^{+}|}\pi_{\theta(s)}\Big(\boldsymbol{y}_{i,t,k}^{+} \mid \boldsymbol{x},\boldsymbol{y}_{i,< t}^{+},\boldsymbol{o}_{i,< t}^{+},\boldsymbol{y}_{i,t,<k}^{+}\Big).
    $$
    • 由于反馈 Token 仅在损失中被屏蔽，但仍出现在上下文中，因此工具集成训练（with feedback masking）的 GRPO 目标在函数形式上与应用于动作 Token序列的标准 GRPO 目标完全相同。因此，每一对
      $$
      (\text{question''},\text{response’’})=\big(\boldsymbol{x},\boldsymbol{y}_{i,t}^{+}\big),
      $$
    • 连同上下文 \((\boldsymbol{y}_{i,< t}^{+},\boldsymbol{o}_{i, < t}^{+})\)，都可以被视为非工具 GRPO 分析意义上的单个生成。因此，我们可以直接引用 Deng 等人 (2025) 的 GWHES 定理（定理 4.4），并将其应用于条件分布 \(\pi_{\theta(s)}(\boldsymbol{y}_{i,t}^{+} \mid \boldsymbol{x},\boldsymbol{y}_{i, < t}^{+},\boldsymbol{o}_{i,< t}^{+})\)，从而得到以下 Action-level 结果
  • 定理 A.2 （ Action-level ）
    • 对于任何 \(\boldsymbol{x}\)、任何时间 \(s \geq 0\) 以及任何正确响应 \(\boldsymbol{y}_{i}^{+}\)，其第 \(t\) 个动作的似然变化，
      $$
      \frac{d}{ds}\ln\pi_{\theta(s)}(\boldsymbol{y}_{i,t}^{+} \mid \boldsymbol{x},\boldsymbol{y}_{i,< t}^{+},\boldsymbol{o}_{i,< t}^{+}),
      $$
    • 随着
      $$
      \begin{align}
      \mathcal{G}_{i,t}(s)&=p^{-}\underbrace{\sum_{k=0}^{|\boldsymbol{y}_{i,t}^{+}|} \sum_{j=1}^{N^{-} }\sum_{t^{\prime}=0}^{T_{j} }\sum_{k^{\prime}=1}^{|\boldsymbol{y}_{j,t^{\prime} }^{-}|}\alpha_{(i,t,k),(j,t^{\prime},k^{\prime})}^{-} \left\langle \mathbf{h}_{\boldsymbol{x},\boldsymbol{y}_{i,< t}^{+},\boldsymbol{o}_{i,< t}^{+},\boldsymbol{y}_{i,t,<k}^{+} },\mathbf{h}_{\boldsymbol{x},\boldsymbol{y}_{j,< t^{\prime} }^{-},\boldsymbol{o}_{j,< t^{\prime} }^{-},\boldsymbol{y}_{j,t^{\prime},<k^{\prime} }^{-} } \right\rangle}_{\text{Impact of negative gradients.} } \\
      -p^{+}\sum_{k=0}^{|\boldsymbol{y}_{i,t}^{+}|}\sum_{t^{\prime}=1}^{N^{+} }\sum_{t^{\prime\prime}=0}^{T_{t^{\prime} } }\sum_{k^{\prime\prime}=1}^{|\boldsymbol{y}_{i^{\prime},t^{\prime\prime} }^{+}|}\alpha_{(i,t,k),(i^{\prime},t^{\prime\prime},k^{\prime\prime})}^{+} \left\langle \mathbf{h}_{\boldsymbol{x},\boldsymbol{y}_{i,< t}^{+},\boldsymbol{o}_{i,< t}^{+},\boldsymbol{y}_{i,t,<k}^{+} },\mathbf{h}_{\boldsymbol{x},\boldsymbol{y}_{i^{\prime},< t^{\prime\prime} }^{+},\boldsymbol{o}_{i^{\prime},< t^{\prime\prime} }^{+},\boldsymbol{y}_{i^{\prime},t^{\prime\prime},<k^{\prime\prime} }^{+} } \right\rangle.
      \end{align}
      \tag{9}
      $$
    • 的增加而变得更懒惰（幅度更小，甚至可能为负），其中
      $$
      \alpha_{(i,t,k),(j,t^{\prime},k^{\prime})}^{-} = \left\langle \mathbf{e}_{y_{i,t,k}^{+} }-\pi_{\theta(s)}(\cdot \mid \boldsymbol{x},\boldsymbol{y}_{i,< t}^{+},\boldsymbol{o}_{i,< t}^{+},\boldsymbol{y}_{i,t,<k}^{+}),\mathbf{e}_{y_{j,t^{\prime},k^{\prime} }^{-} }-\pi_{\theta(s)}(\cdot \mid \boldsymbol{x},\boldsymbol{y}_{j,< t^{\prime} }^{-},\boldsymbol{o}_{j,< t^{\prime} }^{-},\boldsymbol{y}_{j,t^{\prime},<k^{\prime} }^{-}) \right\rangle
      $$
    • 且
      $$
      \alpha_{(i,t,k),(i^{\prime},t^{\prime\prime},k^{\prime\prime})}^{+} = \left\langle \mathbf{e}_{y_{i,t,k}^{+} }-\pi_{\theta(s)}(\cdot \mid \boldsymbol{x},\boldsymbol{y}_{i,< t}^{+},\boldsymbol{o}_{i,< t}^{+},\boldsymbol{y}_{i,t,<k}^{+}),\mathbf{e}_{y_{i^{\prime},t^{\prime\prime},k^{\prime\prime} }^{+} }-\pi_{\theta(s)}(\cdot \mid \boldsymbol{x},\boldsymbol{y}_{i^{\prime},< t^{\prime\prime} }^{+},\boldsymbol{o}_{i^{\prime},< t^{\prime\prime} }^{+},\boldsymbol{y}_{i^{\prime},t^{\prime\prime},<k^{\prime\prime} }^{+}) \right\rangle
      $$
    • 是 Token-level 的预测误差相似性权重
  • ** Trajectory-level 作为动作的和** ：工具集成轨迹的似然度在动作上分解：
    $$
    \pi_{\theta(s)}(\boldsymbol{y}_{0:T} \mid \boldsymbol{x})=\prod_{t=0}^{T}\pi_{\theta(s)}(\boldsymbol{y}_{t} \mid \boldsymbol{x},\boldsymbol{y}_{ < t},\boldsymbol{o}_{ < t}).
    $$
    • 取对数并对 \(s\) 求导，得到：
      $$
      \begin{align}
      \frac{d}{ds}\ln\pi_{\theta(s)}(\boldsymbol{y}_{0:T} \mid \boldsymbol{x}) = \sum_{t=0}^{T}\frac{d}{ds}\ln\pi_{\theta(s)}(\boldsymbol{y}_{t} \mid \boldsymbol{x},\boldsymbol{y}_{ < t},\boldsymbol{o}_{ < t}) \\
      = \sum_{t=0}^{T}\sum_{k=1}^{|\boldsymbol{y}_{t}^{+}|}\frac{d}{ds}\ln\pi_{\theta(s)}(\boldsymbol{y}_{t,k}^{+} \mid \cdot),
      \end{align}
      $$
    • 其中“\(\cdot\)”再次表示包含反馈 Token 的屏蔽上下文
    • 根据 Action-level 结果，随着 \(\mathcal{G}_{t,k}(s)\) 增大，求和中的每一项都会变得懒惰或为负，因此只要
      $$
      \sum_{t=0}^{T}\sum_{k=1}^{|\boldsymbol{y}_{t}^{+}|}\mathcal{G}_{t,k}(s)
      $$
    • 很大，整个 Trajectory-level 的导数就会变得懒惰或为负
    • 这确立了定理 A.1 中的 Trajectory-level 陈述

附录 B: 补充分析

Training Instability Prior to Collapse

  • 虽然最终的崩溃确实是由来自负响应的大梯度触发的，但在训练早期就已经出现了显著的不稳定性和明显的性能下降
  • 如图 7 所示，棕色垂直线标志着模型奖励（绿色曲线）的第一次急剧下降，在此期间正确响应的似然度也显著下降，尽管梯度范数仍然相对较小（约 2）
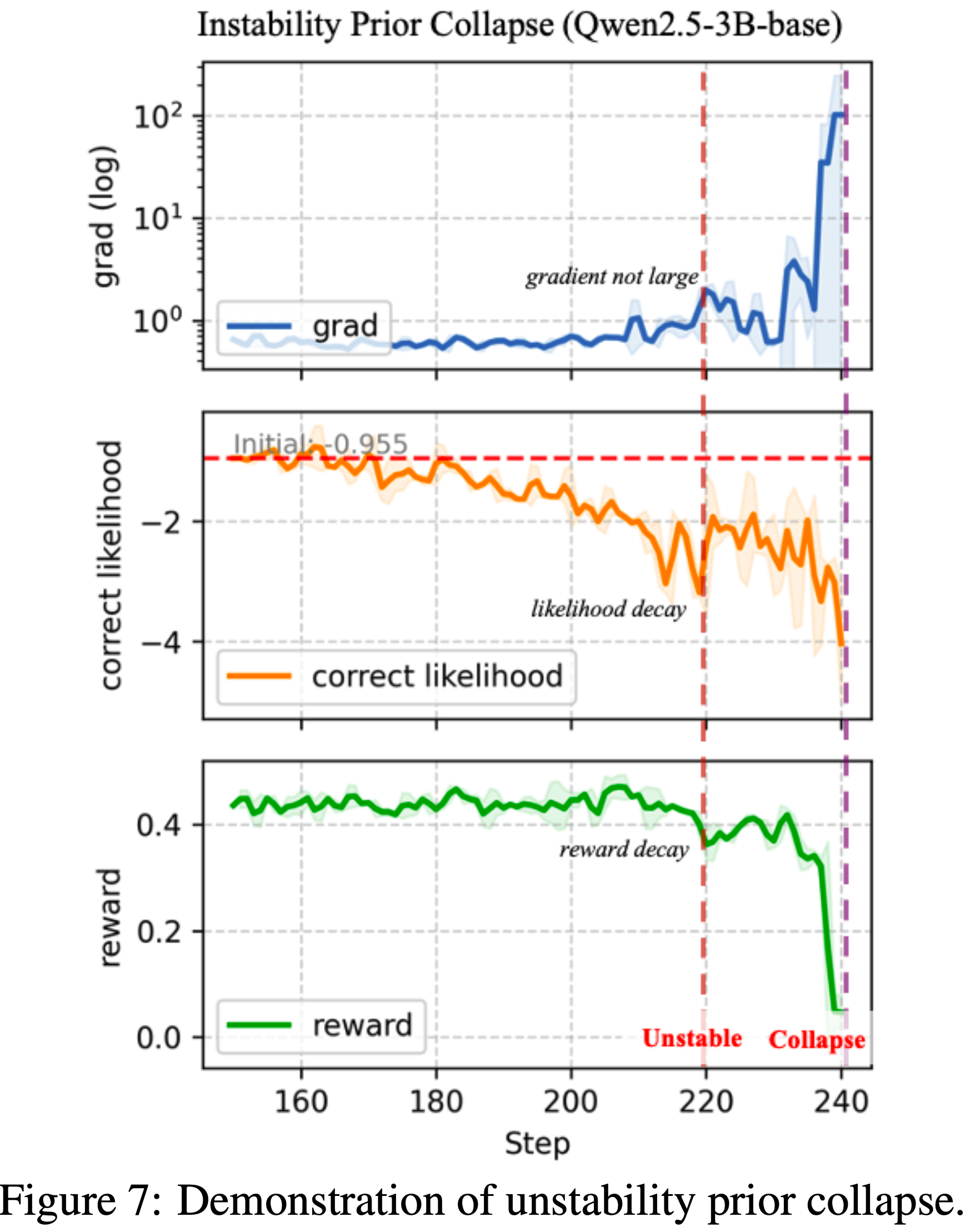
  • 随着训练的进行，LD 问题加剧，低置信度响应导致梯度范数稳步增长，最终导致模型崩溃
  • 这些观察结果表明，早在崩溃点之前就已经存在不稳定性，因此值得密切关注

Impact of Regularization Strength

  • 为了检查正则化强度的影响，论文对 \(\lambda \in \{0, 0.01, 0.1\}\) 进行消融实验，并在图 8 中绘制了相应的训练奖励动态
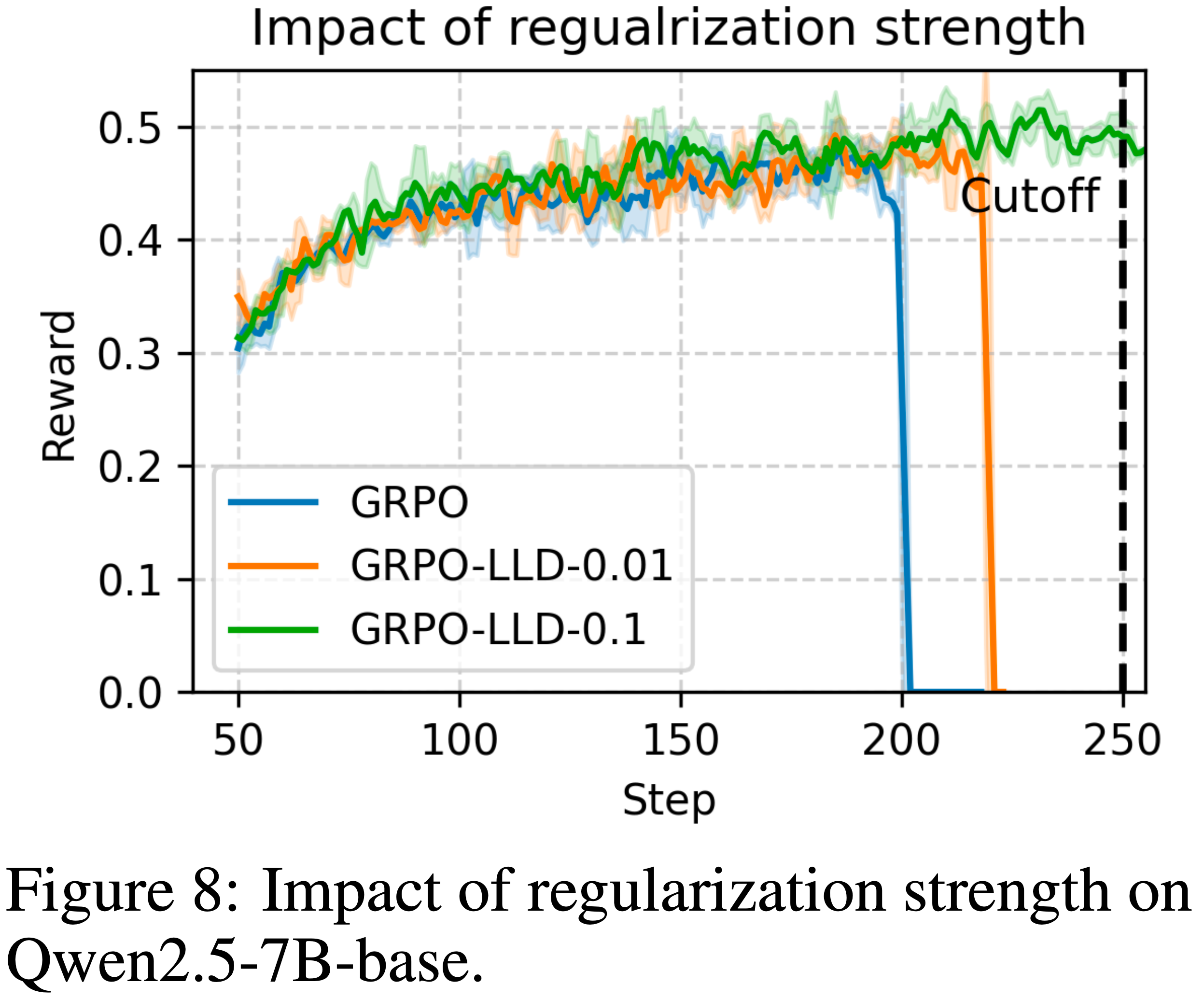
  • 如图所示，在没有正则化的情况下 (\(\lambda=0\))，模型在大约第 200 步崩溃
  • 较小的正则化值 (\(\lambda=0.01\)，橙色曲线) 延迟但未能阻止崩溃，崩溃发生在大约第 220 步
  • 相比之下，更强的正则化 (\(\lambda=0.1\)) 完全稳定了训练，使模型能够平稳地继续而不崩溃
  • 为了清晰起见，论文在第 250 步截断了绘图，尽管训练可以远远超过这一点

Unlocking Multi-Step Reasoning via Answer Masking

  • 为了进一步探索 LLDS 在促进复杂推理行为方面的潜力，论文在 Qwen-2.5-3B-Base 模型上进行了关于正则化范围的消融研究
    • 论文从 \(L_{\text{LLDS} }\) 项的计算中屏蔽掉最终答案 Token （表示为“掩码答案”）
  • Qwen-2.5-3B-Base 本身缺乏多轮工具调用的能力
    • 如图 9 所示，这种限制在标准训练设置中是明显的：基线 GRPO（蓝色曲线）迅速遭受模型崩溃，有效搜索次数降至零
    • 虽然标准的 GRPO + LLDS（红色曲线）成功地稳定了训练并防止了崩溃，但它未能引发任何多步行为，搜索频率停滞在恰好 1.0
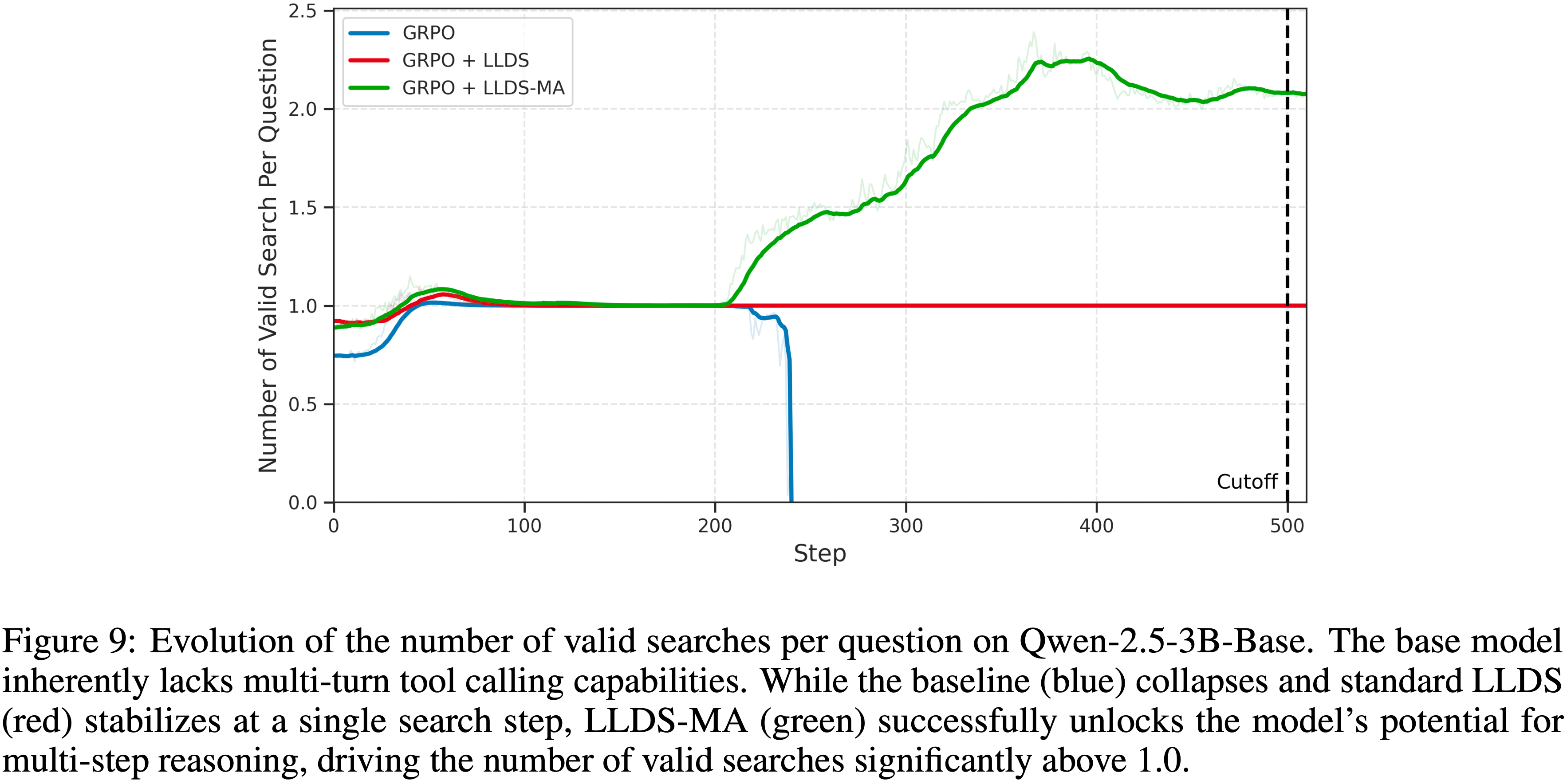
  • “GRPO + LLDS-MA”变体（绿色曲线）展示了一种独特的新兴行为
    • 通过移除对最终答案 Token 的正则化约束，论文观察到每个问题的有效搜索次数显著增加，上升到 2.0 以上
    • 这表明，放松对答案 Token 的惩罚有效地释放了模型参与多步推理和使用外部工具的潜在能力
      • 这是标准方法未能在基础模型中激活的能力

Qualitative Examples of Tool-Integrated Reasoning

  • 为了进一步说明论文训练模型的行为特征，论文展示了由 Qwen2.5-7B 系列生成的定性推理轨迹
  • 这些示例突显了使用论文的 LLD 正则化策略训练的模型如何在轨迹中表现出强大的多步规划、可控的工具使用和稳定的多轮推理
  • 与标准的 GRPO 模型（经常遭受过早崩溃）不同，论文的方法使模型能够在搜索、验证和最终答案生成的整个过程中保持连贯的推理结构
  • 如图 10 和图 11 所示，该模型不仅执行逐步分解和自我验证，还在需要时执行连续的搜索调用，有效整合检索到的证据，并产生正确、简洁的最终答案
  • 这些定性行为与论文的定量发现一致：稳定似然动态可以防止 LLD 死亡螺旋，使 RL 策略能够利用更深的工具集成推理而不会牺牲鲁棒性

附录 C 似然位移的案例研究

  • 为了更好地理解 LLD 如何在实践中体现，论文深入分析了两个有代表性的训练样本（对应于图 3（步骤 140）中受影响最严重的两个样本）
  • 对于每个问题，论文将 SEARCH-R1 策略生成的一个正确轨迹与一个不正确轨迹进行比较。这些配对示例使论文分析中的抽象机制变得具体

案例 1：Embedding similarity under group-relative updates

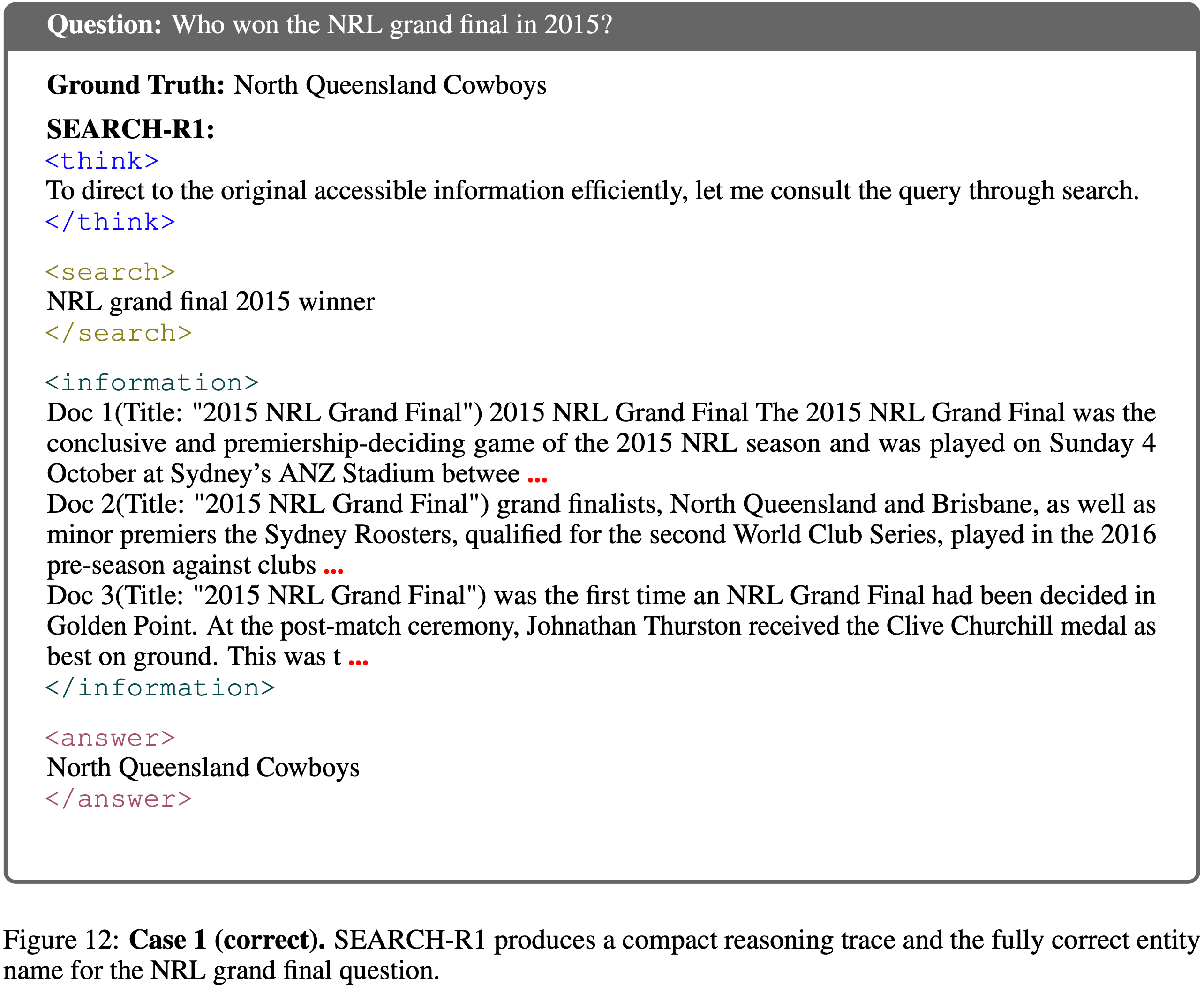
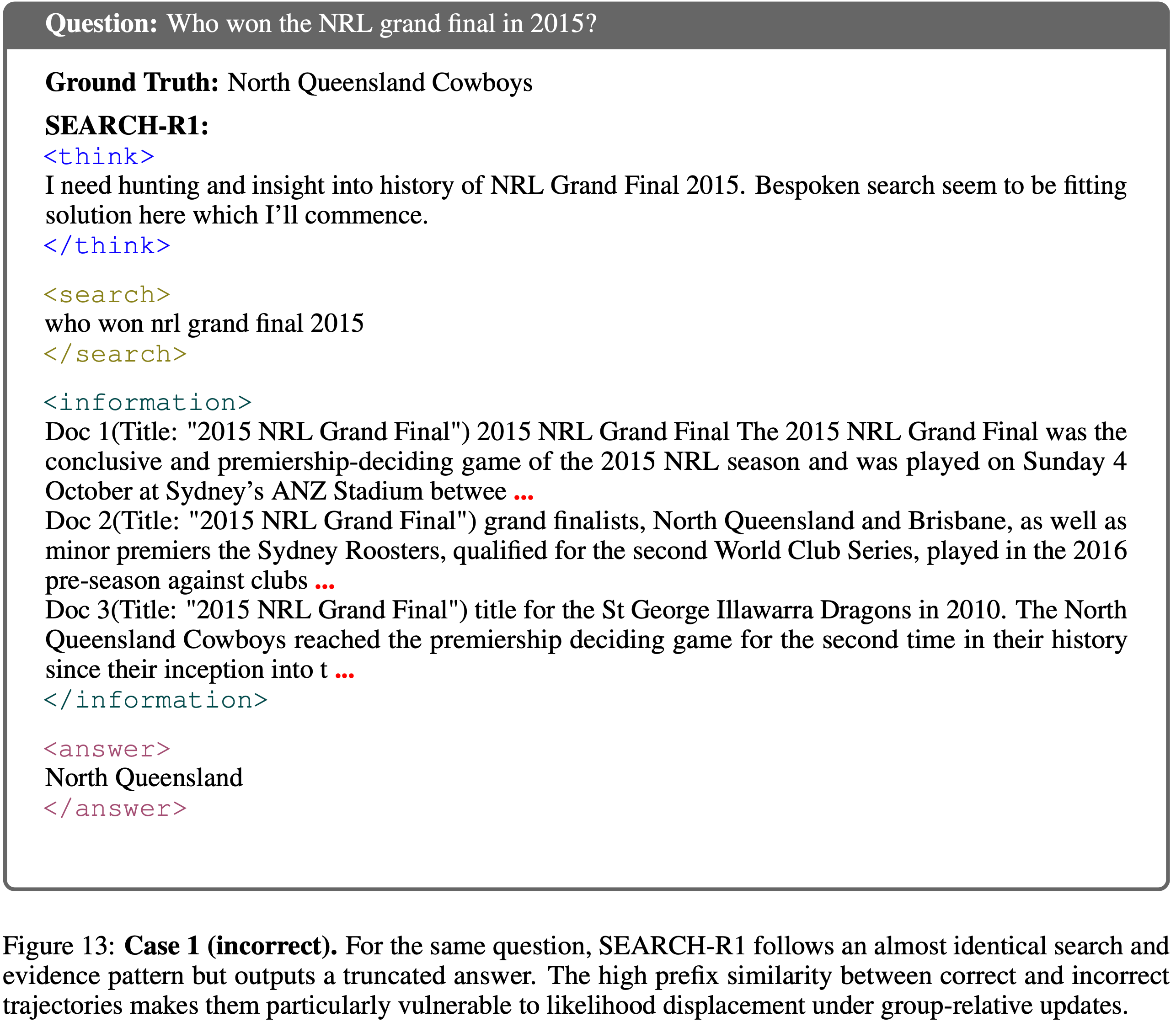
  • 图 12 和图 13 展示了问题“Who won the NRL grand final in 2015?”的两个推演过程
    • 两个轨迹使用了几乎相同的 <think> plans，发出语义等效的搜索 Query ，并检索到相同的 <information> 片段
    • 唯一的区别在于最终答案 Token ：
      • 正确轨迹输出完整的实体“North Queensland Cowboys”
      • 不正确轨迹将名称截断为“North Queensland”
    • 由于 GRPO 为整个轨迹分配一个标量奖励，这两个高度相似的前缀接受了截然不同的更新：
      • 不正确的推演将负梯度推送到与正确推演在嵌入空间中几乎相同的 Token 上
    • 这说明了轨迹末尾的小语义偏差如何通过高前缀相似性，对原本正确的动作产生强烈的似然错位（likelihood displacement）

案例 2：Low-likelihood, longer incorrect trajectories

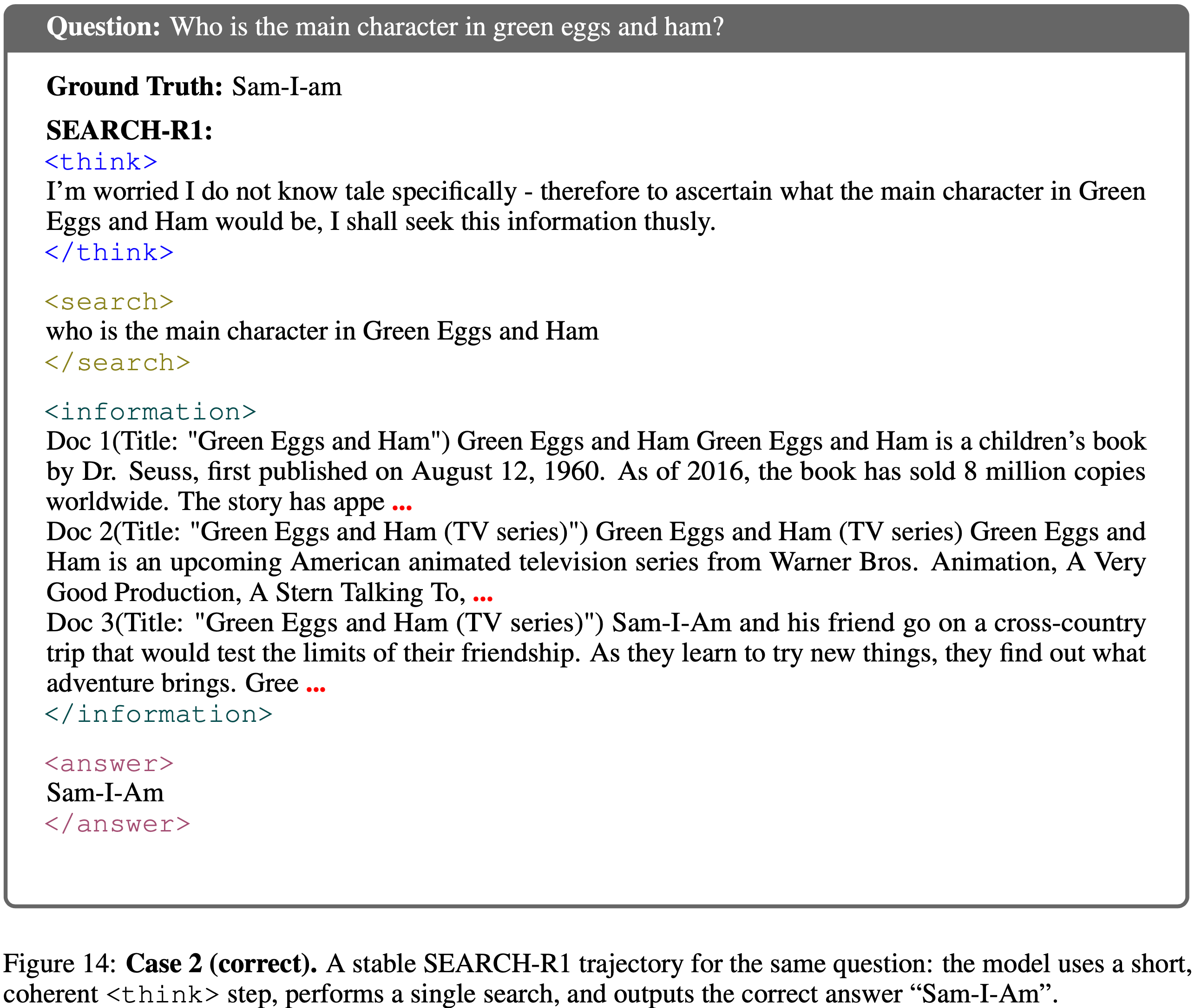
  • 图 14 和图 15 展示了“Who is the main character in green eggs and ham?”的推演过程
    • 在不正确的情况下，模型从一个长的、低似然度的 <think> 片段开始
    • 由于早期 Token 的似然度极小，采样漂移到分布的语义无意义区域，产生了一段冗长的无意义文本
    • 这也导致模型违反了工具协议，随后在 <information> 频道中触发了纠正性反馈
    • 尽管模型最终发出了有效的搜索，但它仍然产生了不正确的答案（“The first-person narrator”）
    • 这个轨迹比其对应的正确轨迹更长且似然度更低 ，导致 GRPO 为其分配了较大的负预测误差权重，并在多个 Token 上累积了许多负梯度的和
    • 相比之下，正确的轨迹保持简短且高置信度，执行单次搜索后给出正确答案“Sam-I-Am”
    • 总之，这些示例具体地展示了低似然度、过长的错误响应如何主导梯度并驱动 LLD 死亡螺旋，即使环境偶尔将模型推回有效的工具使用
      • 问题：将奖励或者梯度按照 Response 粒度做等价归一化是否能解决这种很长的错误回复主导梯度？

附录：提出 LLD 的第一篇文章

LLD（Lazy Likelihood Displacement）定义

  • LLD 是在基于组的策略优化（如 GRPO）训练过程中出现的一种现象：
    • 正确响应（\(y^+\)）的似然（概率）仅轻微增加，甚至出现下降
    • 这一现象源于对错误响应中所有 tokens 的无差别惩罚
      • 由于正确响应与错误响应可能存在共享的结构或语义特征（如部分正确的推理步骤），对错误响应的整体惩罚会无意间降低正确响应的似然，导致模型性能受损
Definition 4.1
  • 设 \(\pi_{\theta_{init} }\) 为训练前的初始语言模型，\(\pi_{\theta_{fin} }\) 为经过偏好学习目标（如 GRPO 损失）优化后的最终模型（满足 \(J(\theta_{fin}) < J(\theta_{init})\)）
    • 对于数据集 \(D\) 中的样本 \((x, y^+)\)，若存在非负小常数 \(\epsilon \geq 0\)，满足以下条件，则称发生 LLD：
      $$
      \ln \pi_{\theta_{fin} }(y^+ | x) < \ln \pi_{\theta_{init} }(y^+ | x) + \epsilon
      $$
    • 核心含义：训练后正确响应的对数似然增长不超过 \(\epsilon\)（或下降），即模型未能有效提升正确响应的生成概率

Theorem 4.4 与 Corollary 4.5

  • LLD 的本质是错误响应的负梯度对正确响应似然的抑制作用，具体源于：
    • 错误响应中部分 tokens 与正确响应的关键推理步骤具有高语义相似度（如“奇数”“质数”等正确术语出现在错误响应中）；
    • GRPO 对错误响应的所有 tokens 施加相同强度的负梯度惩罚，导致这些“部分正确”的 tokens 被过度抑制，进而牵连正确响应的似然
  • 从理论上，正确响应 \(y_i^+\) 的似然变化率 \(\frac{d}{dt}\ln \pi_{\theta(t)}(y_i^+ | x)\) 受以下“组加权隐藏嵌入分数（GWHES）”影响：
    $$
    \underbrace{p^{-} \sum_{k=1}^{|y_i^+|} \sum_{j=1}^{N^-} \sum_{k’=1}^{|y_j^-|} \alpha_{k, k’}^{-} \cdot \left<h_{x, y_{i,<k}^+}, h_{x, y_{j,<k’}^{-} }\right>}_{负梯度的负面影响} - \underbrace{p^{+} \sum_{k=1}^{|y_i^+|} \sum_{i’=1}^{N^+} \sum_{k’’=1}^{|y_{i’}^+|} \alpha_{k, k’’}^{+} \cdot \left<h_{x, y_{i,<k}^+}, h_{x, y_{i’,<k’’}^+}\right>}_{正梯度的正面影响}
    $$
  • 符号说明：
    • \(p^+ = \frac{1-p}{\sqrt{p(1-p)} }\)、\(p^- = \frac{p}{\sqrt{p(1-p)} }\)：正确/错误响应组的权重（\(p\) 为样本正确率）
    • \(N^+\)、\(N^-\)：正确/错误响应的数量
    • \(h_{x, y_{i,< k}^+}\)：正确响应 \(y_i^+\) 前 \(k-1\) 个 tokens 的隐藏嵌入
    • \(\alpha_{k, k’}^{-}\)、\(\alpha_{k, k’’}^{+}\)：token 级预测误差相似度权重（量化不同响应间 tokens 的误差相关性）
  • 关键结论：当“负梯度的负面影响”大于“正梯度的正面影响”时，正确响应的似然增长变慢或下降，即发生 LLD

解决方案：NTHR（Negative Token Hidden Reward，负 Token 隐藏奖励）

NTHR 的定义
  • NTHR 是一种针对 LLD 的解决方案，核心是选择性 token 惩罚 ：
    • 通过识别错误响应中对正确响应似然损害最大的 tokens，降低对这些 tokens 的惩罚强度，从而在不牺牲数据效率的前提下缓解 LLD
  • NTHR 核心思想是：
    • 错误响应中并非所有 tokens 都会导致 LLD，仅那些与正确响应关键步骤高度相关的 tokens（如部分正确的推理术语）才是主要诱因
    • NTHR 通过量化每个错误 token 对正确响应似然的负面影响，对这些“有害 tokens”进行针对性惩罚调整
NTHR 核心公式与步骤
  • NTHR 的实现分为 3 个关键步骤，涉及多个核心公式：
步骤 1：计算错误 token 对正确响应的影响（\(s_{j,< k’}^{-}\)）
  • 对于错误响应 \(y_j^-\) 中的第 \(k’\) 个 token，定义其对所有正确响应似然的负面影响为：
    $$
    s_{j,<k’}^{-} := \sum_{i=1}^{N^+} \sum_{k=1}^{|y_i^+|} \alpha_{k, k’}^{-} \cdot \left<h_{x, y_{i,<k}^+}, h_{x, y_{j,<k’}^{-} }\right>
    $$
  • 符号说明：
    • \(i\) 遍历所有正确响应，\(k\) 遍历正确响应 \(y_i^+\) 的所有 tokens；
    • \(\alpha_{k, k’}^{-}\)：正确响应第 \(k\) 个 token 与错误响应第 \(k’\) 个 token 的预测误差相似度；
    • 该值越大，说明错误 token \(y_{j,k’}^{-}\) 对正确响应似然的抑制作用越强
步骤 2：确定惩罚调整的阈值（\(\tau\)）
  • 阈值 \(\tau\) 基于正确响应间的“平均相互影响”设定，确保仅对损害最大的错误 tokens 进行调整：
    $$
    \tau = \beta \cdot \min_{i’ \in [N^+]} \bar{s}_{i’}^+
    $$
  • 其中，\(\bar{s}_{i’}^+\) 表示第 \(i’\) 个正确响应的 tokens 对其他所有正确响应似然的平均影响（即“正向相互作用强度”）：
    $$
    \bar{s}_{i’}^+ := \frac{1}{|y_{i’}^+|} \sum_{k’’=1}^{|y_{i’}^+|} \sum_{i=1}^{N^+} \sum_{k=1}^{|y_i^+|} \alpha_{k, k’’}^+ \cdot \left<h_{x, y_{i,<k}^+}, h_{x, y_{i’,<k’’}^+}\right>
    $$
  • 符号说明：
    • \(\beta\) 为缩放因子（实验中默认 \(\beta=1\)）；
    • 核心逻辑：仅当错误 token 的影响 \(s_{j,< k’}^{-}\) 超过正确响应间的最小正向相互作用强度（\(\min_{i’} \bar{s}_{i’}^+\)）时，才认为该 token 是 LLD 的主要诱因
步骤 3：选择性调整惩罚强度
  • 对于错误响应中满足 \(s_{j,< k’}^{-} > \tau\) 的 tokens（即“有害 tokens”），通过缩放因子 \(\eta < 1\) 降低其负梯度的惩罚强度：
    $$
    \hat{A}_{j, k’, \eta}^{-} := \eta \cdot \hat{A}_{j, k’}^{-}
    $$
  • 符号说明：
    • \(\hat{A}_{j, k’}^{-}\) 为错误 token 原始的优势函数值（负梯度的核心来源）；
    • \(\eta\) 为惩罚衰减因子（实验中设为 \(\eta=2 \cdot |0.5 - p|\)，\(p\) 为样本正确率）；
    • 效果：降低“有害 tokens”的负梯度强度，避免其过度抑制正确响应的似然
NTHR 的优点
  • 针对性：仅调整错误响应中导致 LLD 的关键 tokens，而非丢弃整个错误样本（避免数据效率损失）
  • 兼容性：适配 GRPO 的在线学习范式，无需修改算法核心结构
  • 有效性：实验证明，在 0.5B~3B 参数模型的数学推理任务中，GRPO+NTHR 能持续缓解 LLD 并提升模型性能
NTHR 的缺点
  • 看起来实现较为复杂，且实操性较低