注:本文包含 AI 辅助创作
- 参考链接:
- 原始论文:(IcePop)Small Leak Can Sink a Great Ship—Boost RL Training on MoE with IcePop!, 20250919, AntGroup
- 有趣的标题:小漏洞可沉巨轮
- 本工作是 TIS(Truncated Importance Sampling)的续作,TIS 的参考链接为 Your Efficient RL Framework Secretly Brings You Off-Policy RL Training
- 原始论文:(IcePop)Small Leak Can Sink a Great Ship—Boost RL Training on MoE with IcePop!, 20250919, AntGroup
TLDR
- 整体内容总结:
- 26年1月回顾补充:本文的方法已经被很多文章用到,比如 GLM 4.7,MiMo-V2 等技术博客
- 论文对 MoE 模型上训练-推理概率不匹配的问题进行了初步分析
- On-policy RL 训练的不稳定性可能源于训练引擎与推理引擎之间不断增大的概率差异
- IcePop 通过在损失函数层面校正这种不匹配来解决该问题(本工作是 TIS 的续作)
- 作者提出:未来的一个重要研究方向是正式刻画 崩溃边界(collapse boundary) 定义为 On-policy 训练变得不稳定时的临界概率差异,并研究该边界如何随模型规模、批次配置和引擎不匹配程度而变化
- 近期工作 (2024) 强调了当前强化学习训练框架中模型训练与生成阶段之间存在不匹配的问题
- 论文观察到,这个问题在 混合专家模型 中会 加剧
- 特别是当模型倾向于生成长回复时,这种差异会 进一步放大
- 尽管先前工作 (2024) 提出通过引入重要性采样校正来缓解此问题,但作者认为这种技术在训练进行时可能会在基准测试上遇到性能瓶颈
- 论文提出了一种简单而有效的方法 IcePop ,即使在强大的经过监督微调的 MoE 模型上,也能通过 RL 实现稳定的训练和卓越的下游性能
The Mismatch Issue on MoE
- 不匹配问题指的是当前 RL 训练框架中训练后端和推理引擎之间的概率差异,这不可避免地使 On-policy 训练变成了 Off-policy (2024)
- 论文观察到,这种实现上的差距在 MoE 模型的 RL 训练期间变得更加显著
- 与稠密模型不同,为了实现更高的参数效率,MoE 架构采用了一种路由机制,该机制在训练和推理期间仅为每个 Token 选择少数排名靠前的“专家”
- 论文发现这种结构设计加剧了 On-policy RL 训练期间的不匹配问题,阻碍了 MoE 模型完全释放强化学习的潜力
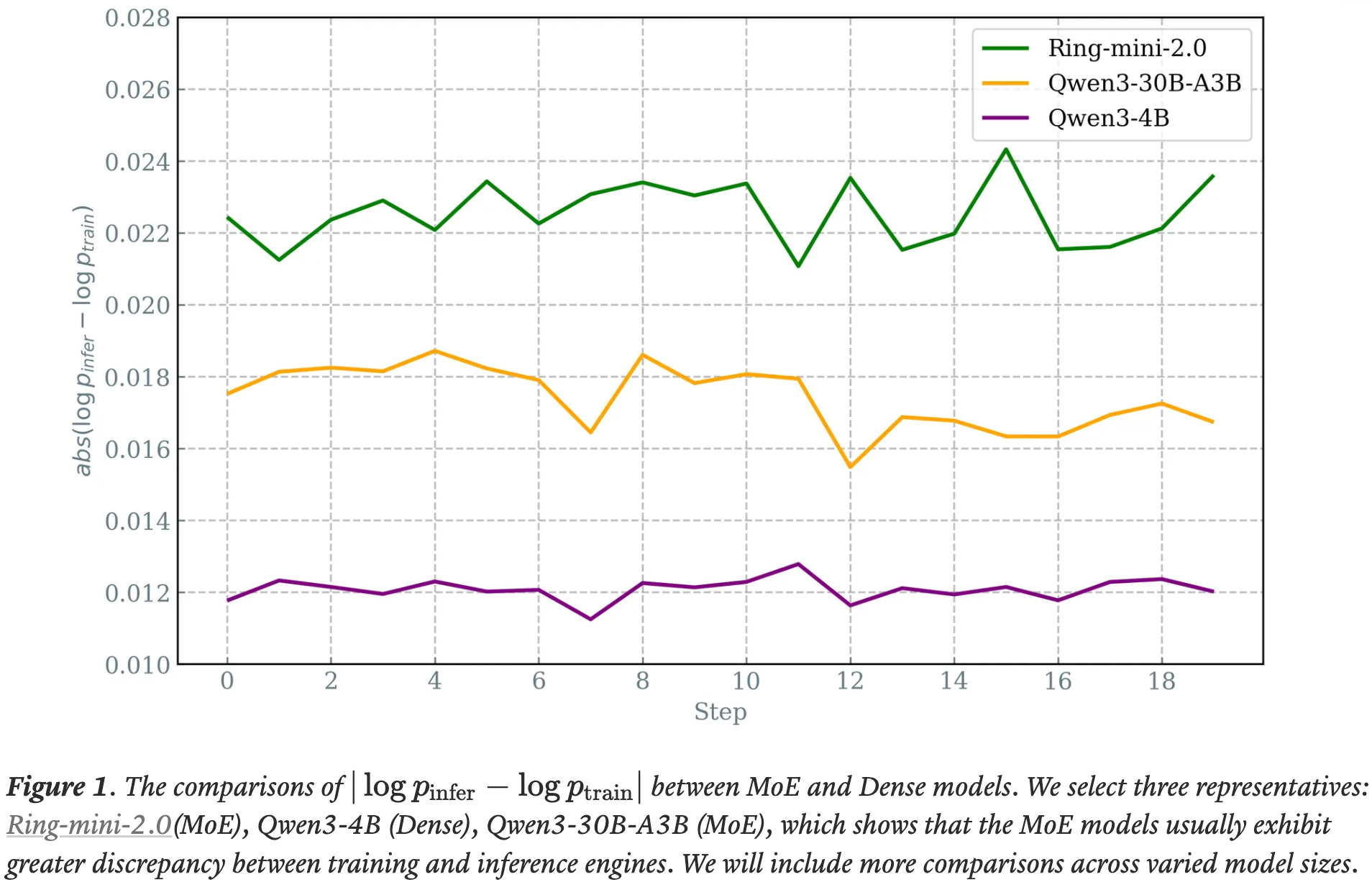
- 图 1. MoE 和稠密模型之间 \( |\log p_{\rm infer} - \log p_{\rm train}| \) 的比较
- 论文选择了三个代表性模型:Ring-mini-2.0 (MoE)、Qwen3-4B (Dense)、Qwen3-30B-A3B (MoE),这表明 MoE 模型通常在训练和推理引擎之间表现出更大的差异
- 论文选择了三个代表性模型:Ring-mini-2.0 (MoE)、Qwen3-4B (Dense)、Qwen3-30B-A3B (MoE),这表明 MoE 模型通常在训练和推理引擎之间表现出更大的差异
- 根据下面的策略梯度方程,我们可以看到另一个不匹配问题出现了,即 \( \color{red}{\theta_{\rm infer} } \) 和 \( \color{blue}{\theta_{\rm train} } \)
- 在 MoE 模型中,路由函数 \( \texttt{TopK}(\cdot) \) 为每个输入 Token 动态激活一个“专家”子集
- 理想情况下,对于固定的输入,\( \texttt{TopK}(\cdot) \) 的输出应该与策略模型部署在哪个引擎上无关
- 然而,当 \( \color{red}{\theta_{\rm infer} } \) 和 \( \color{blue}{\theta_{\rm train} } \) 之间存在显著差距时,将不可避免地导致 \( \color{red}{\pi_{\rm infer} } \) 和 \( \color{blue}{\pi_{\rm train} } \) 之间产生更大的分歧
$$ \small{\begin{equation}\theta \leftarrow \theta + \mu \cdot \mathbb{E}_{a\sim \color{red}{\pi_{ {\rm{infer} } } }(\color{red}{\theta_{\rm infer} } ), \ \color{red}{\theta_{\rm infer} } \sim \mathtt{TopK}_{\rm infer}(a)}\left[ R(a) \cdot \nabla_{\theta}\log \color{blue}{\pi_{\rm{train} } }(a;\color{blue}{\theta_{\rm train} });\color{blue}{\theta_{\rm train} } \sim \texttt{TopK}_{\rm train}(a) \right]\end{equation} } $$ - 对于 MoE 模型,论文确定了训练-推理差异问题的两个主要原因:
- 训练和推理阶段选择的专家可能不同 (The selected experts may vary between training and inference stages.)
- 论文之前的分析表明,即使在第一个 MoE 层,也已经有极少部分的 Token 在训练后端和推理引擎中激活了不同的专家
- 例如,当选择 Top-k 和 Top-(k+1) 专家的概率非常接近时,即使微小的精度差异也可能导致在训练和推理期间选择不同的专家,从而导致计算出的概率出现巨大差异
- 随着堆叠的路由网络增多,不匹配问题变得明显 (The mismatch becomes pronounced as more routing networks are stacked.)
- 论文进一步注意到,随着 MoE 层数的加深,在训练后端和推理引擎中调用相同专家的 Token 比例迅速下降了约 10%
- 在每一层,路由网络决定激活哪些专家。在一个深层的 MoE 模型中,它每层选择多个专家,因此每次调用 \(\texttt{TopK}(\cdot)\) 时即使是很小的差异也会累积起来,并随着深度的增加而被不断放大
- 训练和推理阶段选择的专家可能不同 (The selected experts may vary between training and inference stages.)
What Effects Will It Bring to MoE RL?
概率差异会放大,尤其是对于长序列
- The probability discrepancy becomes magnified, especially for long sequences.
- 在训练刚开始时,论文发现某些 Token 位置已经存在明显的概率差异
- 由于预测的自回归特性,出现在较后位置的 Token 更容易受到差异累积的影响,导致变化范围更广
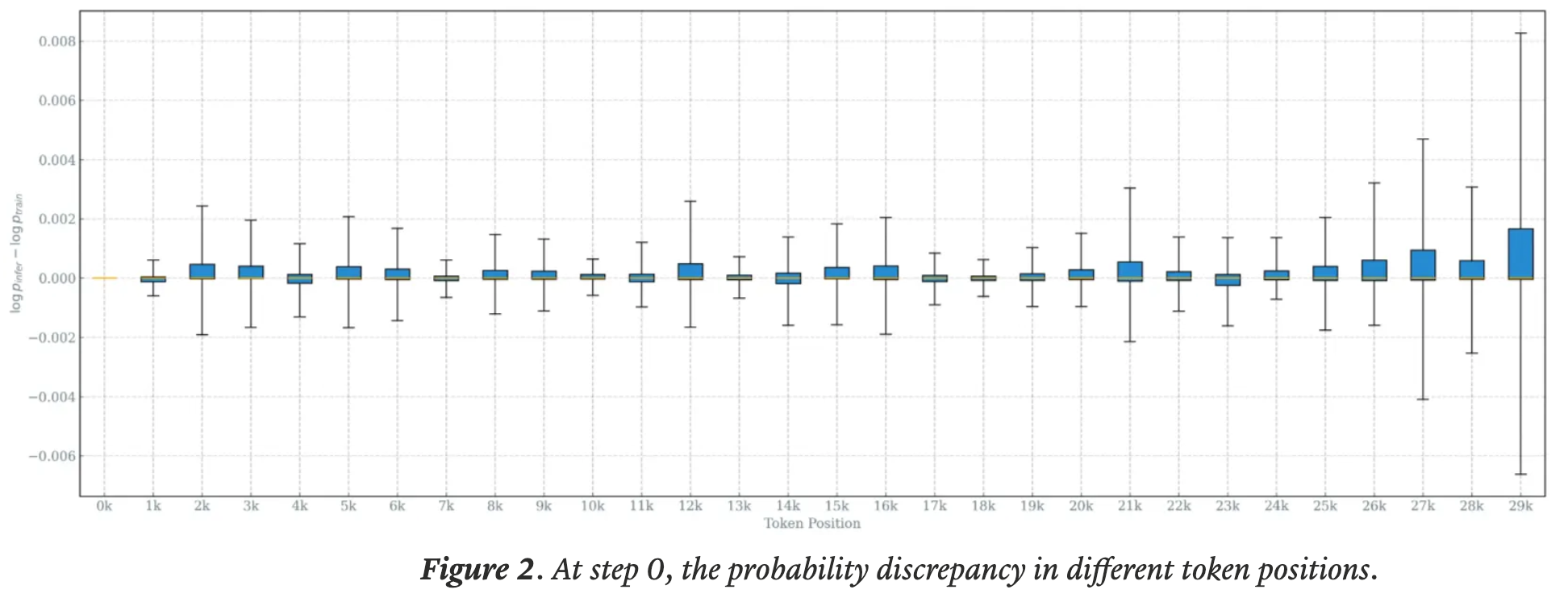
- 随着训练的进行,问题加剧:训练和推理引擎之间同一 Token 的概率差距在多个 Token 位置上持续增加,甚至影响到长序列中前面的 Token ,并使优化过程不稳定
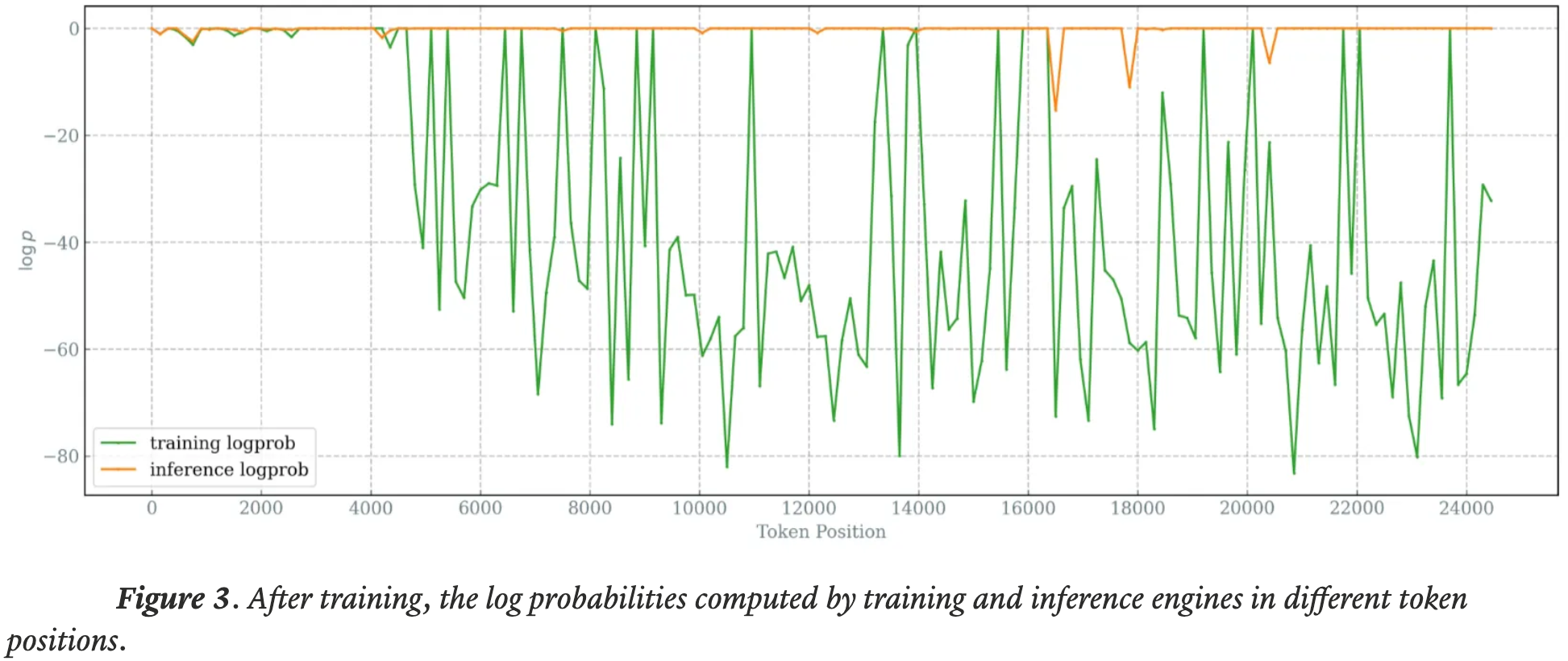
不匹配问题会迅速导致 On-policy MoE RL 训练崩溃
- The mismatch issue quickly causes crashes during on-policy MoE RL training.
- 在 On-policy RL 训练中,与稠密模型相比,论文观察到负责生成长序列的 MoE 模型更容易受到此类不匹配问题的影响,常常导致训练崩溃
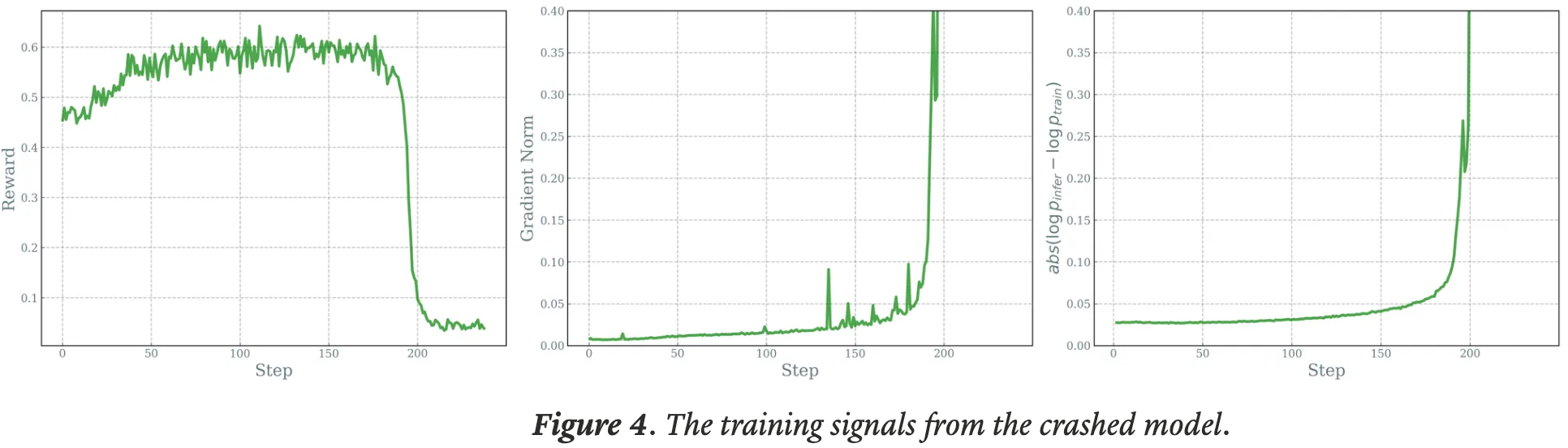
- 例如,上图显示差异在 150 步后逐渐增加,一旦差异超过 0.05,训练基本上就失败了
- 由于实现方式不同,概率差异可能会因复合效应而变得更大
附录:引理 (Compounding Probability Discrepancy,复合概率差异)
- 令 \(\pi_{\text{infer} }(\cdot;\theta)\) 和 \(\pi_{\text{train} }(\cdot;\theta)\) 分别表示推理策略和训练策略
- 定义第 \(t\) 步的概率差异为
$$
\delta_t = D_{\mathrm{KL} }\big(\pi_{\text{infer} }(\cdot;\theta_t)|\pi_{\text{train} }(\cdot;\theta_t)\big).
$$ - 该差异衡量了推理引擎的分布偏离训练引擎分布的程度
- 在使用不匹配引擎进行 RL 训练期间,参数更新为
$$
\theta_{t+1} = \theta_t + \mu g_t,
\qquad
g_t = \mathbb{E}_{a\sim \pi_{\text{infer} }(\theta_t)} \big[R(a)\nabla_\theta \log \pi_{\text{train} }(a;\theta_t)\big].
$$ - On-policy 更新为 \(g_t^* = \mathbb{E}_{a\sim \pi_{\text{train} }(\theta_t)}[R(a)\nabla_\theta \log \pi_{\text{train} }(a;\theta_t)]\),偏差为 \(b_t = g_t - g_t^*\)
- 假设以下局部条件对 \(\theta\) 成立
- 1)平滑差异(Smooth discrepancy)
- \(\delta(\theta)\) 是 \(L\)-平滑(\(L\)-smooth)的,满足 \(\big|\delta(\theta+\Delta)-\delta(\theta)\big| \le L|\Delta| + c_0 |\Delta|^2\),其中 \(c_0\) 是曲率常数
- 这意味着小的参数更新仅导致差异发生小的变化
- 2)偏差与差异成比例(Bias scales with discrepancy)
- \(|b_t| \ge c_1\delta_t, ~~\big\langle \nabla_\theta \delta(\theta_t), b_t \big\rangle \ge c_2\delta_t\),其中 \(c_1\) 是偏差幅度系数,\(c_2\) 是偏差对齐系数
- 不匹配越大,偏差推动其恶化的方向上的作用就越强
- 3)有界的 On-policy 漂移(Bounded on-policy drift)
- 存在 \(M\ge 0\),使得 \(\big|\langle \nabla_\theta \delta(\theta_t), g_t^* \rangle\big| \le M\)
- 仅 On-policy 训练不会导致失控的发散;不稳定性主要源于偏差
- 1)平滑差异(Smooth discrepancy)
Unleash MoE RL with IcePop: Discard All Noisy Gradient Updates(释放 MoE RL 的潜力:丢弃有噪声的梯度更新)
- 为了解决上述问题,论文提出了一种简单而有效的技术,IcePop
- 论文应用双向掩码来减轻概率差异的有害复合效应,仅保留健康的梯度更新
- 双向裁剪(Double-sided clipping) :不仅裁剪那些 训练概率 远大于 推理概率 的 Token ,也裁剪那些 训练概率 远小于 推理概率 的 Token
- 掩码(Masking) :差异过大 的 Token 将从梯度更新中移除
$$ \small{\begin{align}\mathcal{J}_{ {\text{IcePop} } }(\theta) &= \mathbb{E}_{x \sim \mathcal{D}, \{y_i\}_{i=1}^G \sim \pi_{\color{red}{\text{infer} } }(\cdot \mid x; \theta_{\rm old})} \left[ \frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \Big[\mathcal{M}\Bigl(\frac{\pi_{\color{blue}{\text{train} } }(y_{i,t} \mid x, y_{i,<t};\theta_{\text{old} })}{\pi_{\color{red}{\text{infer} } }(y_{i,t} \mid x, y_{i,<t}; \theta_{\mathrm{old} })}; \alpha, \beta\Bigr) \cdot \min \left( r_{i,t}\widehat{A}_{i,t}, \text{clip} \left( r_{i,t}, 1 - \varepsilon, 1 + \varepsilon \right) \widehat{A}_{i,t} \right) \right]\Bigg] &\end{align} } $$- 其中 \( r_{i,t} = \frac{\pi_{\color{blue}{\text{train} } }(y_{i,t} \mid x, y_{i,< t}; \ \theta)}{\pi_{\color{blue}{\text{train} } }(y_{i,t} \mid x, y_{i,< t}; \ \theta_{\text{old} })} \),以及下面的掩码函数,
$$ \begin{equation} \mathcal{M}(k) =\begin{cases} k & \text{if } k \in [\alpha, \beta] \\ 0 & \text{otherwise}\end{cases} \end{equation} $$ - 和两个超参数 \( \alpha \), \( \beta \) 来控制下限和上限
- 其中 \( r_{i,t} = \frac{\pi_{\color{blue}{\text{train} } }(y_{i,t} \mid x, y_{i,< t}; \ \theta)}{\pi_{\color{blue}{\text{train} } }(y_{i,t} \mid x, y_{i,< t}; \ \theta_{\text{old} })} \),以及下面的掩码函数,
- IcePop 的梯度为:
$$ \small{\nabla_\theta \mathcal{J}_{\text{IcePop} }(\theta) \sim \small{\begin{equation}\mathbb{E}_{a \sim \color{red}{\pi_{\text{infer} } }(\theta_{\text{old} })} \Bigg[\mathcal{M}\Bigg(\frac{\color{blue}{\pi_{\text{train} } }(a;\theta_{\text{old} })}{\color{red}{\pi_{\text{infer} } }(a;\theta_{\text{old} })}\Bigg ) \cdot \nabla_\theta \log \color{blue}{\pi_{\text{train} } }(a;\theta) \cdot \hat{A} \cdot r(a)\Bigg)\Bigg].\end{equation} } } $$ - 论文的工作与作者之前的工作 TIS (2024) 的区别:
- 注:TIS(Truncated Importance Sampling)的参考链接为 Your Efficient RL Framework Secretly Brings You Off-Policy RL Training
- 当 \( \dfrac{\color{blue}{\pi_{\text{train} } }(a;\theta_{\text{old} })}{\color{red}{\pi_{\text{infer} } }(a;\theta_{\text{old} })} < \alpha \) 时
- \( \color{blue}{\pi_{\text{train} } } \) 倾向于给该动作分配一个较小的值,相反,\( \color{red}{\pi_{\text{infer} } } \) 输出一个较高的概率,当该比率足够小时,表明训练和推理引擎之间存在巨大差异
- TIS 乘以一个小的系数来减轻有噪声的梯度更新,然而,随着训练的进行,论文发现这种微小的扰动会逐渐被放大,并最终导致基准测试性能陷入瓶颈
- 当 \( \dfrac{\color{blue}{\pi_{\text{train} } }(a;\theta_{\text{old} })}{\color{red}{\pi_{\text{infer} } }(a;\theta_{\text{old} })} > \beta \) 时
- \( \color{blue}{\pi_{\text{train} } } \) 倾向于给该动作分配一个较大的值,而 \( \color{red}{\pi_{\text{infer} } } \) 输出一个较低的概率
- 在这种情况下,TIS 会直接裁剪掉该样本,因为它认为该样本对策略更新没有贡献
- 但作者认为这可能过于激进,因为某些具有高优势估计的动作仍然可能提供有价值的信号
- 论文的方法通过掩码机制,允许在差异可控的范围内保留这些更新
- 个人理解:IcePop 其实和 TIS 是一样的,只是截断多了一个下界而已,原始 TIS 的损失函数为:
$$
\mathbb{E}_{a \sim \color{red}{\pi_{\text{sampler}}}(\theta)} \Bigl[\underbrace{\min\Bigl(\frac{\color{blue}{\pi_{\text{learner}}}(a, \theta)}{\color{red}{\pi_{\text{sampler}}}(a, \theta)}, C\Bigr)}_{\text{truncated importance ratio}} \cdot R(a) \cdot \nabla_\theta \log \color{blue}{\pi_{\text{learner}}}(a, \theta)\Bigr],
$$- 或:
$$
\mathbb{E}_{a \sim \color{red}{\pi_{\text{sampler} }}(\theta_{old})} \left[ \underbrace{\min \left( \frac{\color{blue}{\pi_{\text{learner} }}(a, \theta_{old})}{\color{red}{\pi_{\text{sampler} }}(a, \theta_{old})}, C \right)}_{\text{truncated importance ratio}} \cdot \nabla_{\theta} \min \left( \frac{\color{blue}{\pi_{\text{learner} }}(a, \theta)}{\color{blue}{\pi_{\text{learner} }}(a, \theta_{old})} \hat{A}, \text{ clip} \left( \frac{\color{blue}{\pi_{\text{learner} }}(a, \theta)}{\color{blue}{\pi_{\text{learner} }}(a, \theta_{old})}, 1 - \epsilon, 1 + \epsilon \right) \hat{A} \right) \right]
$$
- 或:
附录:想了解 IcePop 这个名字背后的故事吗?
- 作者是在享用冰棒(ice pops)时想到这个名字的!
- 就像冰棒能缓解过热一样,该算法通过 双向裁剪 极端概率比并 掩码 差异过大的 Token ,来 “冷却” 不稳定的 On-policy 训练
- 这种选择性校正 “剔除” 了不稳定的贡献,同时保留了有效的更新,从而在不拖慢推理速度的情况下稳定了训练
Experiments
- 论文在 Ring-mini-2.0 模型上比较了三种设置,该模型是由 InclusionAI 开发的混合专家模型
- 它拥有 16.8B 总参数和 0.75B 激活参数:
- (1) IcePop
- (2) TIS,
- (3) 基线(不带 KL 项的普通 GRPO,该设置在多次重复运行中均失败并崩溃)
- 论文收集了具有挑战性的推理问题作为训练数据集
- 使用IcePop,论文发现可以有效解决在策略训练的不稳定性,甚至实现了比 TIS 更好的性能
- 在下游任务上,IcePop 的表现优于 TIS 和 基线
模型评估
- 在具有挑战性的基准测试 AIME25 上,IcePop 在整个训练过程中始终以较大优势优于 TIS ,最终将基础分数提高了超过 14% ,并将与 TIS 的性能差距扩大了相对 6%
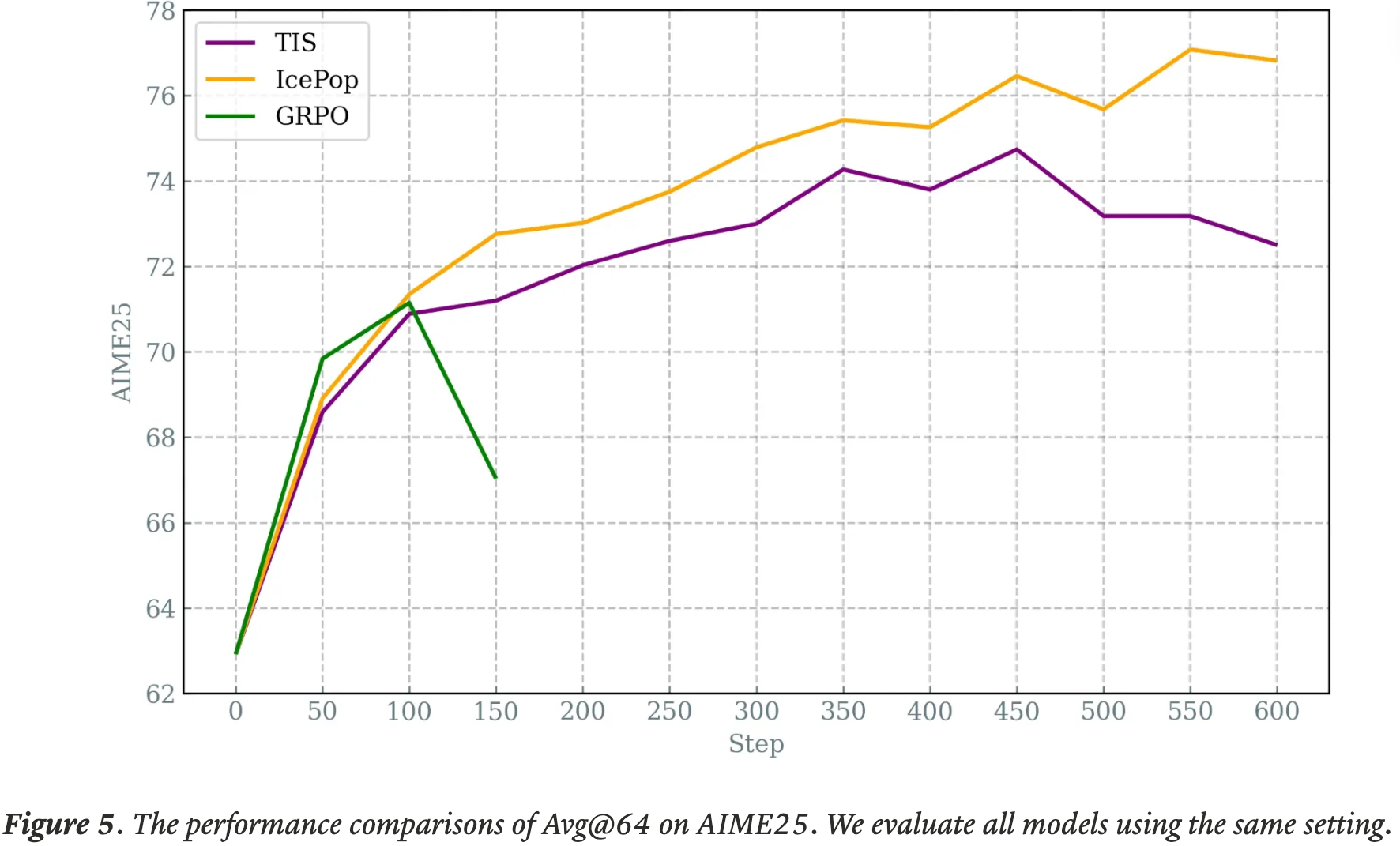
More Analysis
Probability Discrepancy(概率差异)
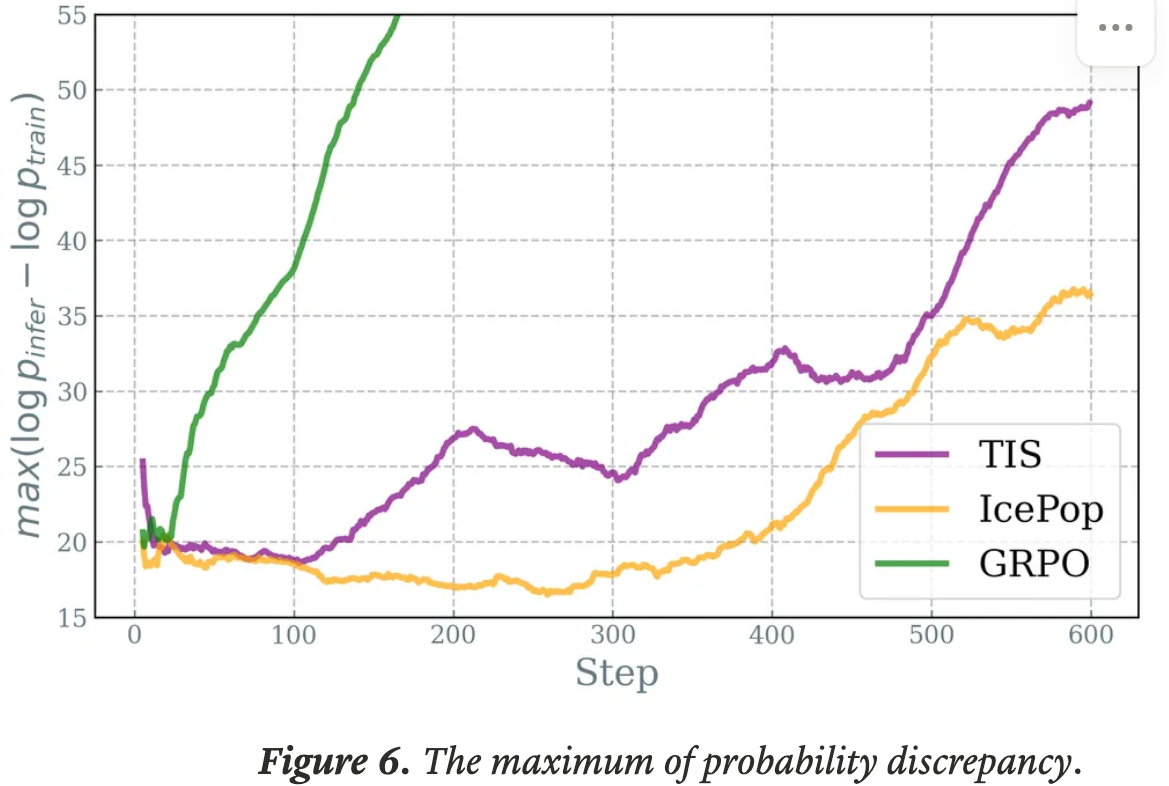
- 若不解决不匹配问题,概率差异会迅速增长,如基线设置所示
- 相比之下,TIS和IcePop都将训练-推断概率的KL散度保持在合理范围内
- 尽管随着训练的进行,三种方法的最大概率差异都在上升,但 IcePop 的差异仍然相对较低,甚至在 400 步内有所下降
- 论文还注意到,TIS 始终表现出比论文的方法更大的极端差异和更快的增长,这可能是由于在训练中包含了噪声策略更新所致
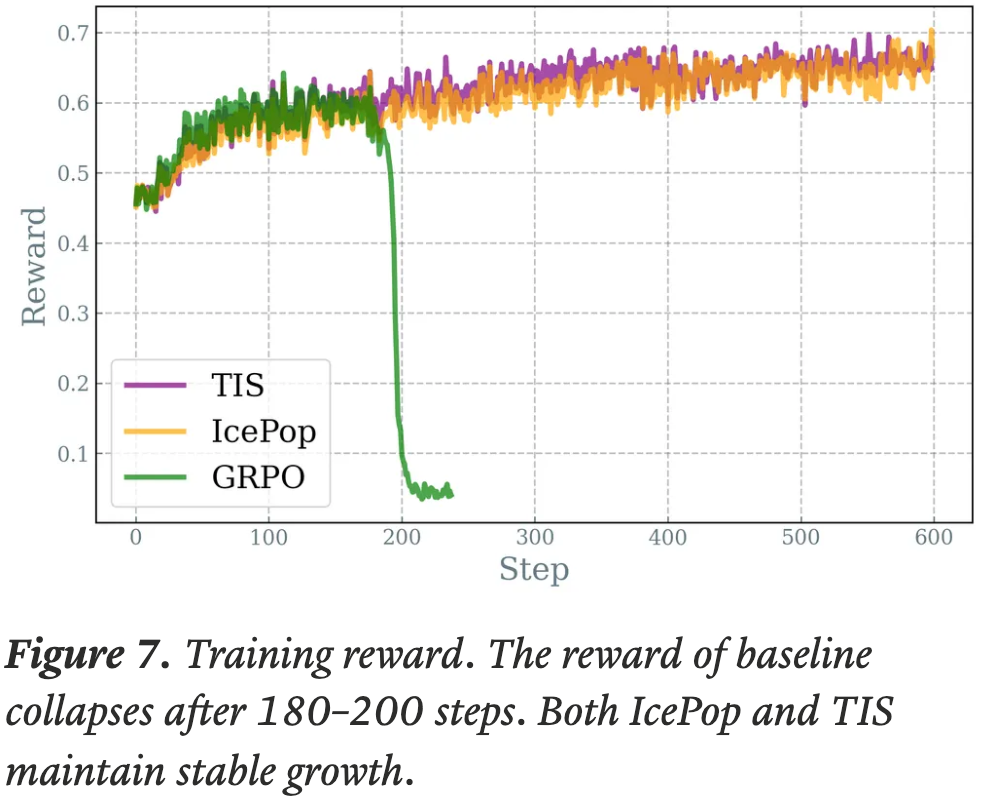
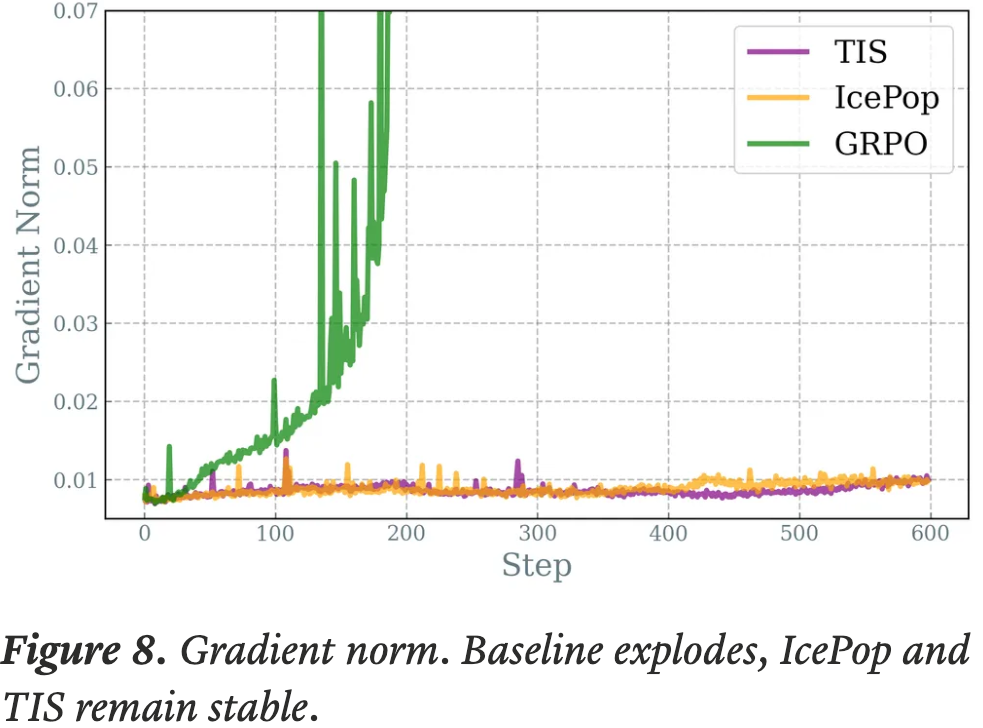
Training Stability, 训练稳定性
- 作者相信,稳定的训练过程是展示强化学习能力的坚实基础和充足空间
- 值得注意的是,IcePop 和 TIS 都在 600 个梯度步内缓解了 RL 训练的不稳定性,避免了基线设置中发生的快速训练崩溃
Exploration Space
- 论文观察到,IcePop 的对数概率始终保持在比 TIS 相对较低的值,这隐式表明论文的方法避免了过度自信的预测,从而确保了更大的探索空间范围,使得低概率 Token 更有可能被选择,最终增加了响应的多样性

Ill-conditioned Tokens(病态 Token)
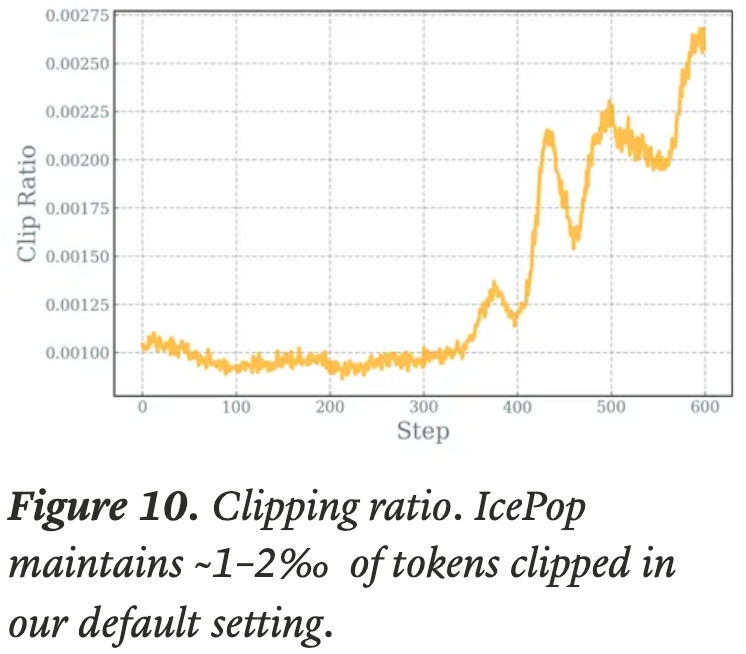
- 在论文的实验中,论文发现来自论文掩码机制的裁剪比率保持在训练 Token 的约 1-2%
- 随着训练的进行,裁剪比率急剧上升,这表明逐渐出现微妙但有害的梯度更新,因此需要更高的裁剪比率
- 论文还对裁剪掉的 Token 进行了详细分析
- 下面的图11 显示,与所有 Token 相比,被裁剪的 Token 表现出更高的熵,这表明被裁剪的 Token 在训练中扮演着重要角色
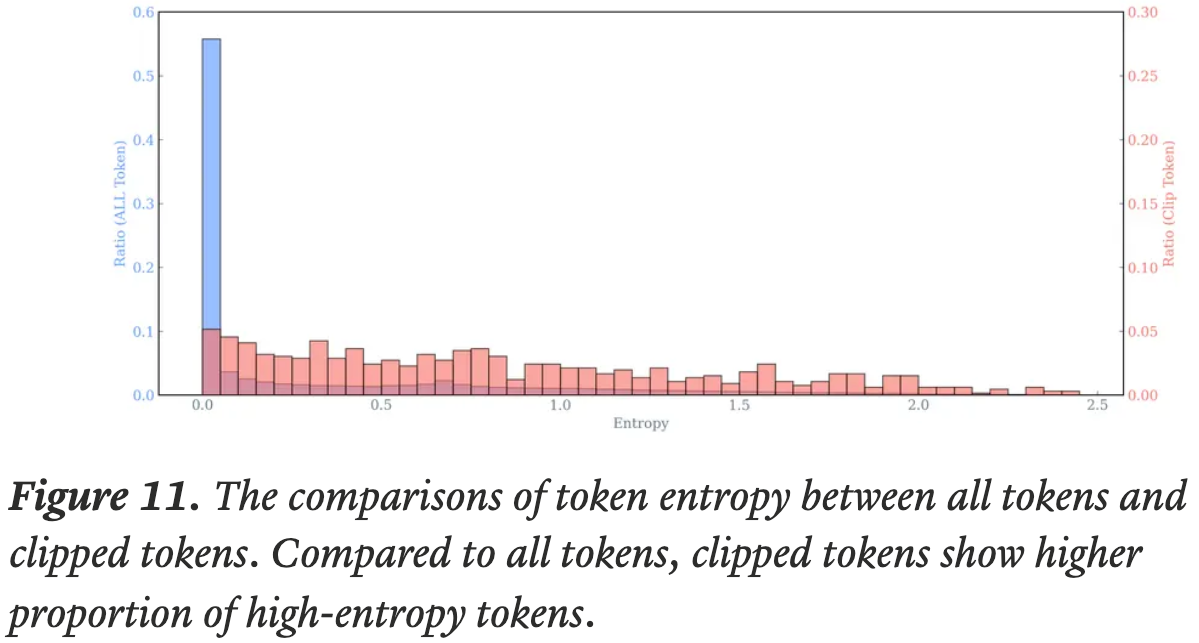
- 理解:
- 熵低的 Token 是确定性比较高的,此时不管用什么引擎估计应该都不会差异太大,所以不容易被裁剪?
- 熵高的 Token 则恰恰相反,不同的引擎差异可能很大,容易被裁剪