注:本文包含 AI 辅助创作
Paper Summary
- 整体总结:
- GSPO 已经成为了 一种非常重要的 LLM RL 方法,是 RL 训练的一个基本选项(尤其在 MoE 模型训练中)
- 群组序列策略优化(Group Sequence Policy Optimization, GSPO) 是一种用于训练 LLM 的新型强化学习算法(稳定、高效、性能优越)
- GSPO 也遵循重要性采样的基本原则,基于序列似然定义重要性权重 ,并在 Sequence-level 进行裁剪、奖励和优化
- 与 GRPO 相比,GSPO 展现出显著更优的训练稳定性、效率和性能,尤其在大规模 MoE 模型的 RL 训练中表现突出,为最新 Qwen3 模型的卓越改进奠定了基础
- 以 GSPO 作为可扩展的算法基石,论文将继续推进 RL 的规模化,并期待由此带来的智能领域的根本性进步
- 个人评价:直观上看,GSPO 更像是 GRPO 的简化版,放弃了对 Token-level 概率比值的使用,理论效果应该是不如 GRPO 的
- 个人理解 GSPO 效果 比 GRPO 好的原因:
- 相对 GRPO Token-level 比例截断的视角,GSPO 是 Sequence-level 的,GSPO 的损失函数设计本质是认为如果一个序列已经飘了(在截断外了),那么这个序列中所有的 Token 都不应该继续更新
- 当整个序列的比例(新旧策略)差异太大时,即使某些 Token 比例差异不大,也不应该继续更新了,反正这个序列整体都已经飘了,所以不应该被用于梯度更新了,GRPO 继续保留的更新可能反而导致模型偏离想要的目标
- GSPO 基于序列似然定义重要性比率(以往算法通常基于 Token-level 重要性比率的算法不同),并在 Sequence-level 进行裁剪、奖励和优化
- 实验表明,GSPO 在训练效率和性能上均优于 GRPO 算法,显著稳定了 MoE 模型的强化学习训练,并具备简化强化学习基础设施设计的潜力
- 注:文中提到,GSPO 的这些优势为最新 Qwen3 模型的显著性能提升做出了重要贡献
Introduction and Discussion
- 强化学习已成为扩展语言模型能力的关键范式(OpenAI;DeepSeek-AI;Qwen)
- 通过大规模强化学习,语言模型能够通过更深层次、更长的推理过程,解决复杂问题,例如竞赛级数学和编程任务
- 为了成功扩展强化学习并投入更多计算资源 ,首要前提是保持训练动态的稳定性和鲁棒性 ,但当前 SOTA 强化学习算法(如 GRPO(2024))在训练超大规模语言模型时表现出严重的稳定性问题
- 常常导致灾难性且不可逆的模型崩溃(Qwen,2025b;MiniMax,2025)
- 这种不稳定性阻碍了通过持续强化学习训练进一步突破语言模型能力边界的努力
- 论文指出,GRPO 的不稳定性源于其算法设计中重要性采样权重的误用和失效
- 这引入了高方差的训练噪声,随着 Response 长度的增加而逐步累积,并进一步被裁剪机制放大,最终导致模型崩溃
- 为了解决这些核心问题,论文提出了 群组序列策略优化(GSPO) ,这是一种用于训练大语言模型的新型强化学习算法
- GSPO 的关键创新在于其基于序列似然(2023)的理论重要性比率定义,与重要性采样的基本原理一致
- GSPO 将归一化奖励计算为对同一 Query 的多个 Response 的优势,确保 Sequence-level 奖励与优化的对齐
- 论文的实验评估表明,GSPO 在训练稳定性、效率和性能上显著优于 GRPO
- 重点:GSPO 从根本上解决了大规模 MoE 强化学习训练的稳定性挑战,无需复杂的稳定策略,并展现出简化强化学习基础设施的潜力
Preliminaries
Notation定义
- 策略 \(\pi_{\theta}\) 表示参数化为 \(\theta\) 的自回归语言模型
- \(x\) 表示 Query ,\(\mathcal{D}\) 表示 Query Set
- 给定 Query \(x\) 的 Response \(y\),其在策略 \(\pi_{\theta}\) 下的似然表示为:
$$
\pi_{\theta}(y|x) = \prod_{t=1}^{|y|} \pi_{\theta}(y_t|x,y_{ < t}),
$$- \(|y|\) 表示 \(y\) 的 Token 数量
- Query-Response 对 \((x,y)\) 可以通过验证器(verifier) \(r\) 评分,得到奖励 \(r(x,y) \in [0,1]\)
Proximal Policy Optimization, PPO
- PPO(2017)使用旧策略 \(\pi_{\theta_{\text{old} } }\) 生成的样本,通过裁剪机制将策略更新限制在旧策略的近端区域内
- PPO 采用以下目标进行策略优化(为简洁起见,省略 KL 正则化项):
$$
\mathcal{J}_{\text{PPO} }(\theta) = \mathbb{E}_{x\sim\mathcal{D},y\sim\pi_{\theta_{\text{old} } }(\cdot|x)} \left[\frac{1}{|y|} \sum_{i=1}^{|y|} \min \left(w_t(\theta)\widehat{A}_t, \text{clip} \left(w_t(\theta),1-\epsilon,1+\epsilon\right) \widehat{A}_t \right) \right], \tag{1}
$$- Token \(y_t\) 的重要性比率定义为 \(w_t(\theta) = \frac{\pi_{\theta}(y_t|x,y_{ < t})}{\pi_{\theta_{\text{old} } }(y_t|x,y_{ < t})}\)
- 优势 \(\widehat{A}_t\) 由另一个价值模型估计
- \(\epsilon\) 是重要性比率的裁剪范围
- PPO 的核心挑战在于其对价值模型的严重依赖:价值模型通常与策略模型规模相当,带来了巨大的内存和计算负担
- 而且 PPO 算法的有效性依赖于其价值估计的可靠性,而获取可靠的价值模型本身具有挑战性,尤其是在处理更长 Response 和更复杂任务时
Group Relative Policy Optimization, GRPO
- GRPO(2024)通过计算同一 Query 的多个 Response 的相对优势,绕过了对价值模型的需求
- GRPO 优化以下目标:
$$
\mathcal{J}_{\text{GRPO} }(\theta) = \mathbb{E}_{x\sim\mathcal{D}, (y_i)_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|x)} \left[\frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \min \left(w_{i,t}(\theta)\widehat{A}_{i,t}, \text{clip} \left(w_{i,t}(\theta),1-\epsilon,1+\epsilon\right) \widehat{A}_{i,t} \right) \right], \tag{2}
$$- \(G\) 是每个 Query \(x\) 生成的 Response 数量(即群组大小)
- Token \(y_{i,t}\) 的重要性比率 \(w_{i,t}(\theta)\) 和优势 \(\widehat{A}_{i,t}\) 定义为:
$$
w_{i,t}(\theta) = \frac{\pi_{\theta}(y_{i,t}|x,y_{i,<t})}{\pi_{\theta_{\text{old} } }(y_{i,t}|x,y_{i,<t})}, \quad \widehat{A}_{i,t} = \widehat{A}_i = \frac{r(x,y_i) - \text{mean}(\{r(x,y_i)\}_{i=1}^G)}{\text{std}(\{r(x,y_i)\}_{i=1}^G)}. \tag{3}
$$- 同一个 \(y_i\) 中所有的 Token \(y_{i,t}\) 共享同一个 \(\widehat{A}_{i}\),即\(\widehat{A}_{i,t} = \widehat{A}_{i}\)
Motivation
- 随着模型规模、稀疏性(例如 MoE)和 Response 长度的增长,为了最大化硬件利用率,需要在强化学习中使用更大的批次大小
- 这里大批次是指样本采样数量
- 为了提高样本效率,通常将大批次数据划分为多个小批次进行梯度更新
- 这一过程不可避免地引入了 off-policy learning 的设置,即 Response \(y\) 是从旧策略 \(\pi_{\theta_{\text{old} } }\) 而非当前优化策略 \(\pi_{\theta}\) 中采样的
- 这也解释了 PPO 和 GRPO 中裁剪机制的必要性,其目的是防止过于 “Off-policy” 的样本参与梯度估计(裁剪等机制旨在管理这种 Off-policy 差异)
- 论文发现 GRPO 存在一个更根本的问题:其目标是不适定的(its objective is ill-posed)
- 注:ill-posed 特指结果对输入数据非常敏感,以至于任何微小的误差都会导致结果有非常大的变化
- 这一问题在训练大模型处理长 Response 任务时尤为突出,会导致灾难性的模型崩溃
- GRPO 目标的不适定性源于重要性采样权重的误用 :重要性采样的基本原理是通过对从行为分布 \(\pi_{\text{beh} }\) 中采样的样本进行重新加权,估计目标分布 \(\pi_{\text{tar} }\) 下函数 \(f\) 的期望:
$$
\mathbb{E}_{z\sim\pi_{\text{tar} } } [f(z)] = \mathbb{E}_{z\sim\pi_{\text{beh} } } \left[\frac{\pi_{\text{tar} }(z)}{\pi_{\text{beh} }(z)} f(z) \right]. \tag{4}
$$ - 关键在于,这依赖于从行为分布 \(\pi_{\text{beh} }\) 中采样多个样本(\(N \gg 1\)),使得重要性权重 \(\frac{\pi_{\text{tar} }(z)}{\pi_{\text{beh} }(z)}\) 能够有效校正分布不匹配
- GRPO 在每个 Token 位置 \(t\) 应用重要性权重 \(\frac{\pi_{\theta}(y_{i,t}|x,y_{i,< t})}{\pi_{\theta_{\text{old} } }(y_{i,t}|x,y_{i, < t})}\)
- 由于该权重基于每个 Next Token 分布 \(\pi_{\theta_{\text{old} } }(\cdot|x,y_{i, < t})\) 的单个样本 \(y_{i,t}\),它无法实现预期的分布校正作用 ,反而向训练梯度中引入了高方差噪声
- 这种噪声会随着长序列累积 ,并被裁剪机制进一步放大,最终导致模型崩溃
- 问题1:为什么单个样本无法校正?
- 问题2:即使真的无法校准,裁剪机制只会缓解这个问题,不会放大这个问题吧?
- 论文通过实验观察到,这种崩溃通常是不可逆的,即使回退到之前的检查点并精心调整超参数(例如裁剪范围)、延长生成长度或切换强化学习 Query,也无法恢复训练
- 上述观察表明 GRPO 的设计存在根本性问题
- Token-level 重要性权重的失效揭示了一个核心原则:优化目标的单位应与奖励的单位一致(the unit of optimization objective should match the unit of reward)
- 由于奖励是针对整个序列分配的,在 Token-level 应用 Off-policy 校正显然存在问题
- 这促使论文放弃 Token-level 目标,探索直接在 Sequence-level 使用重要性权重并进行优化
Algorithm
GSPO: Group Sequence Policy Optimization
- GRPO 中的 Token-level 重要性权重 \(\frac{\pi_{\theta}(y_{i,t}|x,y_{i,< t})} {\pi_{\theta_{\text{old} } }(y_{i,t}|x,y_{i,< t})}\) 存在问题
- 论文观察到,在语言生成的上下文中, Sequence-level 的重要性权重 \(\frac{\pi_{\theta}(y|x)}{\pi_{\theta_{\text{old} } }(y|x)}\) 具有明确的理论意义:
- 它反映了从 \(\pi_{\theta_{\text{old} } }(\cdot|x)\) 采样的 Response \(y\) 与 \(\pi_{\theta}(\cdot|x)\) 的偏离程度,这自然与 Sequence-level 的奖励对齐,同时也可以作为剪裁机制的有意义指标
- 基于这一简单观察,论文提出了序列组策略优化(Group Sequence Policy Optimization, GSPO)算法
- GSPO 采用以下 Sequence-level 的优化目标:
$$
\mathcal{J}_{\text{GSPO} }(\theta) = \mathbb{E}_{x\sim\mathcal{D},\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|x)} \left[\frac{1}{G} \sum_{i=1}^G \min \left(s_i(\theta)\widehat{A}_i, \text{clip}(s_i(\theta), 1-\varepsilon, 1+\varepsilon) \widehat{A}_i\right)\right], \tag{5}
$$- 其中,论文采用基于组的优势估计:
$$
\widehat{A}_i = \frac{r(x,y_i) - \text{mean}(\{r(x,y_i)\}_{i=1}^G)}{\text{std}(\{r(x,y_i)\}_{i=1}^G)}, \tag{6}
$$ - 并基于序列似然(2023)定义重要性比率 \(s_i(\theta)\):
$$
s_i(\theta) = \left(\frac{\pi_{\theta}(y_i|x)}{\pi_{\theta_{\text{old} } }(y_i|x)}\right)^{\frac{1}{|y_i|} } = \exp\left(\frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \log \frac{\pi_{\theta}(y_{i,t}|x,y_{i,<t})}{\pi_{\theta_{\text{old} } }(y_{i,t}|x,y_{i,<t})}\right). \tag{7}
$$- 问题:\(\left(\frac{\pi_{\theta}(y_i|x)}{\pi_{\theta_{\text{old} } }(y_i|x)}\right)^{\color{red}{\frac{1}{|y_i|} }}\) 中为什么要使用 \(\color{red}{\frac{1}{|y_i|} }\) ? 这不符合重要性采样的形式吧!
- 理解:这里是相当于有点对所有的 Token 的比例对数求平均,再求指数的意思,核心是将 Token 粒度的重要性比例替换成经过 “几何平均(Geometric Mean)“ 后的 Sequence 粒度的(同一个 Sequence 所有 Token 共享的)重要性比例
- 补充:几何平均(Geometric Mean,GM)的定义:
$$ \exp\left(\frac{1}{|x|} \sum_{t=1}^{|x|} \log x_t\right) = (\prod_{t=1}^{|x|} x_t)^{\frac{1}{|x|}}$$
- 补充:几何平均(Geometric Mean,GM)的定义:
- 其中,论文采用基于组的优势估计:
- GSPO 对整个 Response 而非单个 token 应用剪裁,以排除过于 “Off-policy” 的样本进行梯度估计 ,这与 Sequence-level 的奖励和优化相匹配
- 问题:过于 “Off-policy” 的样本进行梯度估计 的问题依然存在吧,只是减少了一些,允许一个序列整体进行比较而不是单个Token,波动更小些?
- 特别注意:论文在 \(s_i(\theta)\) 中采用了长度归一化以减少方差 ,并将 \(s_i(\theta)\) 控制在统一的数值范围内
- 否则,少数 token 的似然变化可能导致 Sequence-level 重要性比率的剧烈波动,而不同长度 Response 的重要性比率将需要不同的剪裁范围
- 此外,由于重要性比率的定义不同,GSPO 与先前算法(如 GRPO)的剪裁范围通常在数量级上存在差异
- 补充,对 GSPO 的个人理解 :
- GSPO 更像是将整个序列决策看成是一个 Action,而不是将单个 Token 看成是一个 Action,这在传统强化学习建模的视角看没有问题,但是在 LLM 的场景上看,丢失了很多中间 Token 的生成过程和概率波动,个人感觉不是很合适
Gradient Analysis
- 我们可以推导 GSPO 目标的梯度如下(为简洁起见省略了剪裁部分):
$$
\begin{align}
\nabla_{\theta} \mathcal{J}_{\text{GSPO} }(\theta) &= \nabla_{\theta} \mathbb{E}_{x\sim\mathcal{D},\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|x)} \left[\frac{1}{G} \sum_{i=1}^G s_i(\theta)\widehat{A}_i\right] \\
&= \mathbb{E}_{x\sim\mathcal{D},\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|x)} \left[\frac{1}{G} \sum_{i=1}^G s_i(\theta)\widehat{A}_i \cdot \nabla_{\theta} \log s_i(\theta)\right] \\
&= \mathbb{E}_{x\sim\mathcal{D},\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|x)} \left[\frac{1}{G} \sum_{i=1}^G \left(\frac{\pi_{\theta}(y_i|x)}{\pi_{\theta_{\text{old} } }(y_i|x)}\right)^{\frac{1}{|y_i|} } \widehat{A}_i \cdot \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \nabla_{\theta} \log \pi_{\theta}(y_{i,t}|x,y_{i,<t})\right]. \tag{8-10}
\end{align}
$$ - 作为对比,GRPO 目标的梯度如下(注意 \(\widehat{A}_{i,t} = \widehat{A}_i\)):
$$
\begin{align}
\nabla_{\theta} \mathcal{J}_{\text{GRPO} }(\theta) &= \nabla_{\theta} \mathbb{E}_{x\sim\mathcal{D},\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|x)} \left[\frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} w_{i,t}(\theta)\widehat{A}_{i,t}\right] \\
&= \mathbb{E}_{x\sim\mathcal{D},\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|x)} \left[\frac{1}{G} \sum_{i=1}^G \widehat{A}_i \cdot \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \frac{\pi_{\theta}(y_{i,t}|x,y_{i,<t})}{\pi_{\theta_{\text{old} } }(y_{i,t}|x,y_{i,<t})} \nabla_{\theta} \log \pi_{\theta}(y_{i,t}|x,y_{i,<t})\right]. \tag{11-12}
\end{align}
$$ - 因此,GSPO 与 GRPO 的根本区别在于它们如何对 token 对数似然的梯度进行加权
- 在 GRPO 中,token 根据各自的“重要性权重” \(\frac{\pi_{\theta}(y_{i,t}|x,y_{i,< t})}{\pi_{\theta_{\text{old} } }(y_{i,t}|x,y_{i,< t})}\) 进行加权
- 然而,这些不相等的权重可能在 \((0, 1+\varepsilon]\)(对于 \(\widehat{A}_i > 0\))或 \([1-\varepsilon, +\infty)\)(对于 \(\widehat{A}_i < 0\))之间变化,其影响不可忽视,并且会随着训练的进行累积,导致不可预测的后果
- 问题:这可以通过别的手段来解决吧?有必要直接取消这种 Token-level 方式,转向 Sequence-level 吗?
- GSPO 对 Response 中的所有 token 进行平等加权,消除了 GRPO 的这一不稳定因素
- 在 GRPO 中,token 根据各自的“重要性权重” \(\frac{\pi_{\theta}(y_{i,t}|x,y_{i,< t})}{\pi_{\theta_{\text{old} } }(y_{i,t}|x,y_{i,< t})}\) 进行加权
GSPO-token:A Token-level Objective Variant
- 在多轮强化学习等场景中,论文可能希望比 Sequence-level 更细粒度地调整优势
- 为此,论文引入了 GSPO 的 Token-level 目标变体,即 GSPO-token ,以实现 Token-level 的优势定制:
$$
\mathcal{J}_{\text{GSPO-token} }(\theta) = \mathbb{E}_{x\sim\mathcal{D},\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|x)} \left[\frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \min \left(s_{i,t}(\theta)\widehat{A}_{i,t}, \text{clip}(s_{i,t}(\theta), 1-\varepsilon, 1+\varepsilon) \widehat{A}_{i,t}\right)\right], \tag{13}
$$ - 其中
$$
s_{i,t}(\theta) = \text{sg}[s_i(\theta)] \cdot \frac{\pi_{\theta}(y_{i,t}|x,y_{i,<t})}{\text{sg}[\pi_{\theta}(y_{i,t}|x,y_{i,<t})]},
$$- \(\text{sg}[\cdot]\) 表示仅取值但停止梯度,对应于 PyTorch 中的 detach 操作。GSPO-token 的梯度可以推导为:
$$
\begin{align}
\nabla_{\theta} \mathcal{J}_{\text{GSPO-token} }(\theta) &= \nabla_{\theta} \mathbb{E}_{x\sim\mathcal{D},\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|x)} \left[\frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} s_{i,t}(\theta)\widehat{A}_{i,t}\right] \\
&= \mathbb{E}_{x\sim\mathcal{D},\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|x)} \left[\frac{1}{G} \sum_{i=1}^G s_i(\theta) \cdot \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \widehat{A}_{i,t} \frac{\nabla_{\theta} \pi_{\theta}(y_{i,t}|x,y_{i,<t})}{\pi_{\theta}(y_{i,t}|x,y_{i,<t})}\right] \\
&= \mathbb{E}_{x\sim\mathcal{D},\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|x)} \left[\frac{1}{G} \sum_{i=1}^G \left(\frac{\pi_{\theta}(y_i|x)}{\pi_{\theta_{\text{old} } }(y_i|x)}\right)^{\frac{1}{|y_i|} } \cdot \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \color{red}{\widehat{A}_{i,t}} \nabla_{\theta} \log \pi_{\theta}(y_{i,t}|x,y_{i,<t})\right]. \tag{15-17}
\end{align}
$$- GSPO-token 与原始 GSPO 的主要区别在于:
- GSPO 的目标函数中使用的优势函数是 Sequence-level 的 \(\widehat{A}_{i}\)
- GSPO-token 的目标函数中使用的优势函数是 Token-level 的 \(\color{red}{\widehat{A}_{i,t}}\),这允许同一个序列中,不同的 Token 使用不同的值
- GSPO-token 与原始 GSPO 的主要区别在于:
- \(\text{sg}[\cdot]\) 表示仅取值但停止梯度,对应于 PyTorch 中的 detach 操作。GSPO-token 的梯度可以推导为:
- 论文中特别提到:
- 项 \(\frac{\pi_{\theta}(y_{i,t}|x,y_{i,< t})}{\text{sg}[\pi_{\theta}(y_{i,t}|x,y_{i,< t})]}\) 的数值为 1,因此 \(s_{i,t}(\theta)\) 在数值上等于 \(s_i(\theta)\)
- 比较公式 (5) 和 (13),以及公式 (10) 和 (17),当论文将 Response \(y_i\) 中所有 token 的优势设置为相同值(即 \(\widehat{A}_{i,t} = \widehat{A}_i\))时,GSPO-token 和 GSPO 在优化目标、剪裁条件和理论梯度上是数值相同的,而 GSPO-token 具有更高的灵活性,可以按 token 调整优势
Experiments and Discussion
Empirical Results
- 论文从一个基于 Qwen3-30B-A3B-Base 微调的冷启动模型开始实验,并报告了以下内容:
- 训练奖励曲线
- 在多个基准上的模型性能曲线:
- AIME’24(32 次采样的平均 Pass@1)
- LiveCodeBench(202410-202502,8 次采样的平均 Pass@1)
- CodeForces(Elo 评分)
- 在强化学习训练过程中,每个批次的 rollout 数据被划分为四个小批次用于梯度更新
- 在 GSPO 中,论文做如下设定
- 将公式 (5) 中的左右裁剪范围分别设置为 \(3 \times 10^{-4}\) 和 \(4 \times 10^{-4}\)
- 将 GRPO 作为基线进行比较,并对其公式 (2) 中的左右裁剪范围(the left and right clipping ranges)分别设置为 0.2 和 0.27(这些参数经过精心调整以确保公平比较,原始 GAPO 论文好像用的是0.2 和 0.28?)
- 需要注意的是,GRPO 必须依赖路由回放(Routing Replay)训练策略才能实现 MoE 模型 RL 的正常收敛,论文将在 5.3 节进一步讨论这一点,而 GSPO 则完全不需要这一策略
- 图 1 显示,GSPO 的训练过程始终稳定
- 论文观察到,GSPO 能够通过增加训练计算量、定期更新 Query Set 以及延长生成长度,持续提升模型性能
- 在相同的训练计算量和 Query 消耗下,GSPO 的训练效率和基准测试表现均优于 GRPO
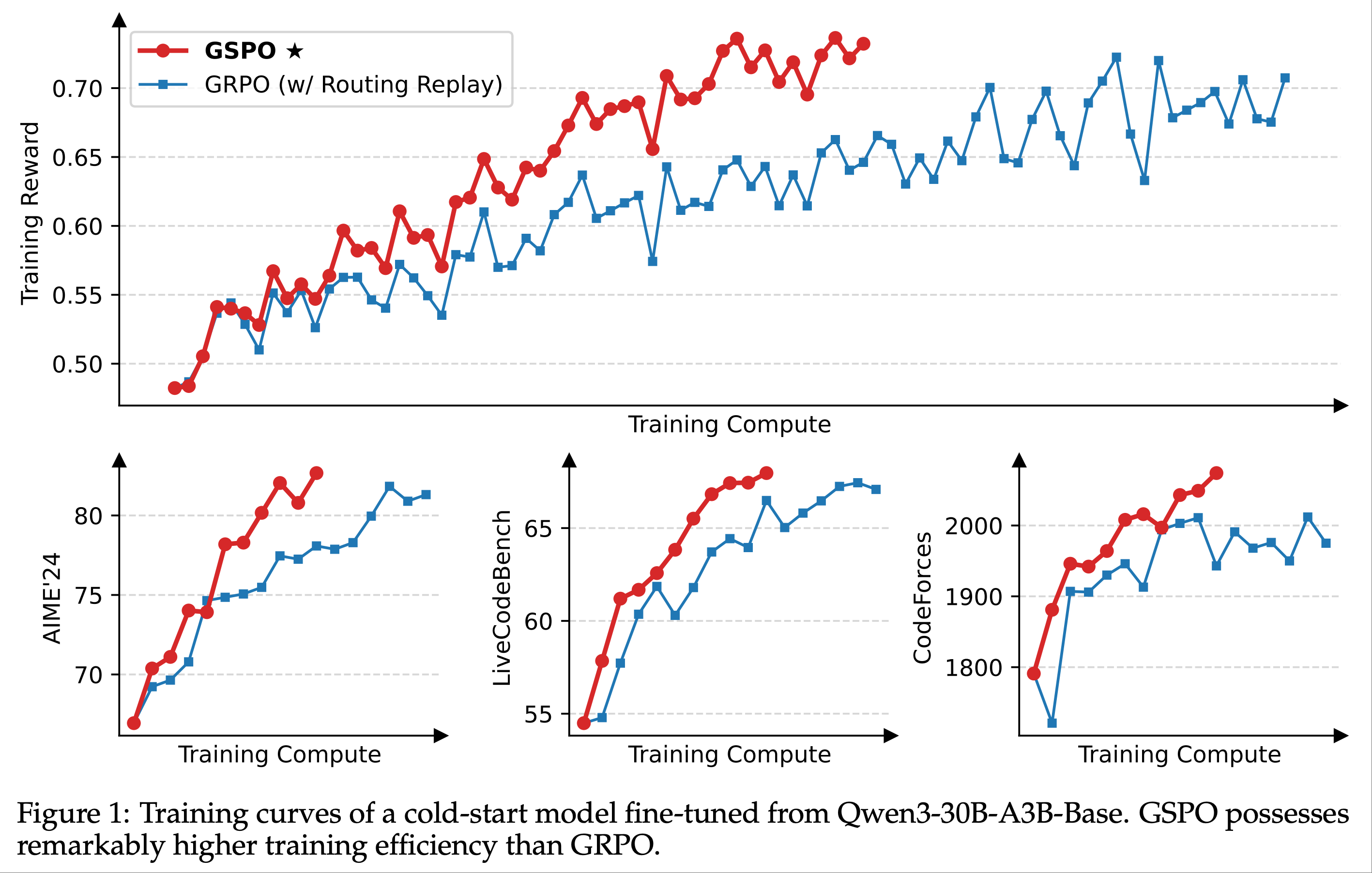
- 最终,论文成功将 GSPO 应用于最新 Qwen3 模型的 RL 训练中 ,充分证明了 GSPO 在释放大规模 RL 训练潜力方面的有效性
Curious Observation on Clipping Fractions
- GSPO 与 GRPO 的一个关键区别在于,GSPO 是对整个 Response 进行裁剪,而非单个 token
- 如图 2 所示,论文观察到 GSPO 和 GRPO 在裁剪 token 比例上存在两个数量级的差异(调整裁剪范围不会改变这种差异)
- 尽管 GSPO 裁剪了更多 token ,从而用于训练的 token 更少(或梯度估计更少),但其训练效率仍高于 GRPO
- 理解(为什么 GSPO 裁剪更多?):因为 GSPO 一旦裁剪就是整个序列一起裁剪,此时整个 Sequence 的所有 Token 都被裁剪了
- 理解(为什么 GSPO 效果更好?):因为当整个序列的比例(新旧策略)差异太大时,即使某些 Token 比例差异不大,也不应该继续更新了?反正这个序列整体都已经飘了,所以不应该被用于梯度更新了,GRPO 继续保留的更新可能反而导致模型偏离想要的目标
- 这一反直觉的发现:裁剪更多 token 反而能带来更高的训练效果 ,进一步表明,GRPO 的 Token-level 梯度估计本质上存在噪声,样本利用效率较低
- 相比之下,GSPO 的 Sequence-level 方法提供了更可靠且高效的学习信号
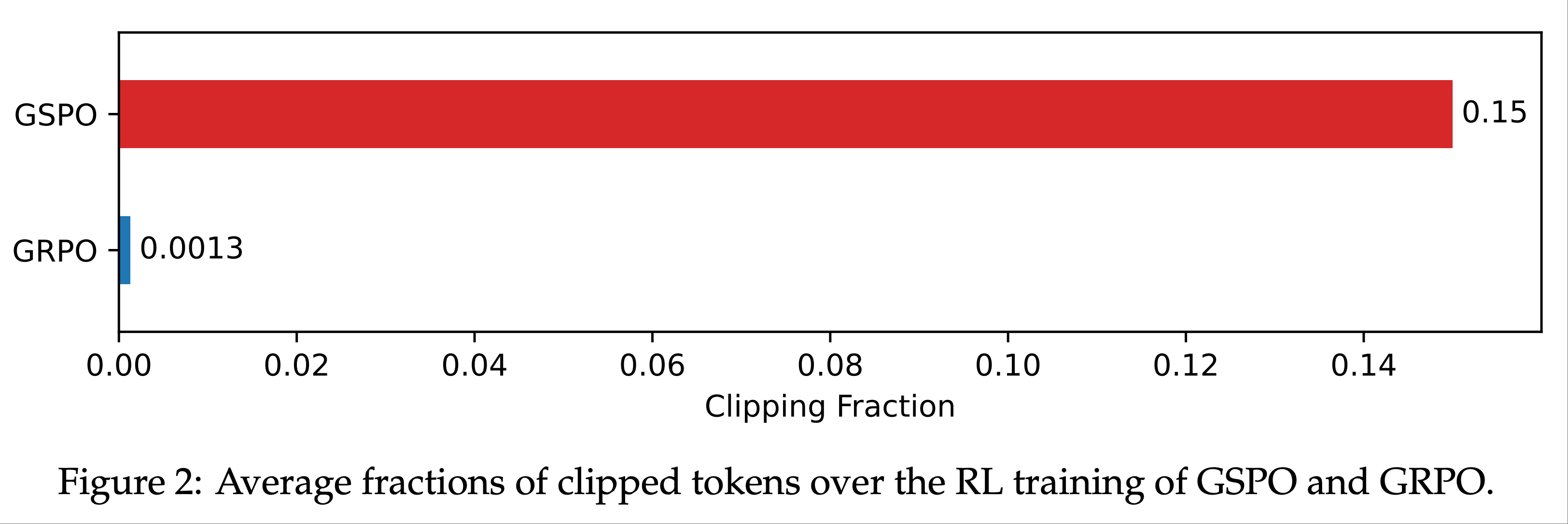
- 尽管 GSPO 裁剪了更多 token ,从而用于训练的 token 更少(或梯度估计更少),但其训练效率仍高于 GRPO
Benefit of GSPO for MoE Training
Background
- 与 Dense 模型的 RL 训练相比,MoE 模型的稀疏激活特性带来了独特的稳定性挑战
- 论文发现,在使用 GRPO 算法时,MoE 模型的 专家激活波动性(expert-activation volatility) 会导致 RL 训练无法正常收敛
- 具体来说:经过一次或多次梯度更新后,同一 Response 激活的专家可能发生显著变化
- 例如,对于 48 层的 Qwen3-30B-A3B-Base 模型,每次 RL 梯度更新后,同一 rollout 样本在新策略 \(\pi_{\theta}\) 下激活的专家中,约有 10% 与旧策略 \(\pi_{\theta_{\text{old} } }\) 不同
- 这一现象在更深的 MoE 模型中更为突出,导致 Token-level 重要性权重 \(w_{i,t}(\theta) = \frac{\pi_{\theta}(y_{i,t}|x,y_{i,< t})}{\pi_{\theta_{\text{old} } }(y_{i,t}|x,y_{i,< t})}\) 剧烈波动,进一步使其失效(如 3 节和 4.2 节所述),从而阻碍 RL 训练的正常收敛
Our Previous Approach
- 为解决这一问题,论文此前采用了 路由回放(Routing Replay) 训练策略
- 具体来说:论文缓存 \(\pi_{\theta_{\text{old} } }\) 中激活的专家,并在计算重要性权重 \(w_{i,t}(\theta)\) 时在 \(\pi_{\theta}\) 中“回放”这些路由模式
- 这样,对于每个 token \(y_{i,t}\),\(\pi_{\theta}(y_{i,t}|x,y_{i,< t})\) 和 \(\pi_{\theta_{\text{old} } }(y_{i,t}|x,y_{i,< t})\) 共享相同的激活网络,从而恢复 Token-level 重要性权重的稳定性,并确保梯度更新中对一致激活网络的优化
- 图 3 表明,路由回放是 GRPO 训练 MoE 模型正常收敛的关键技术
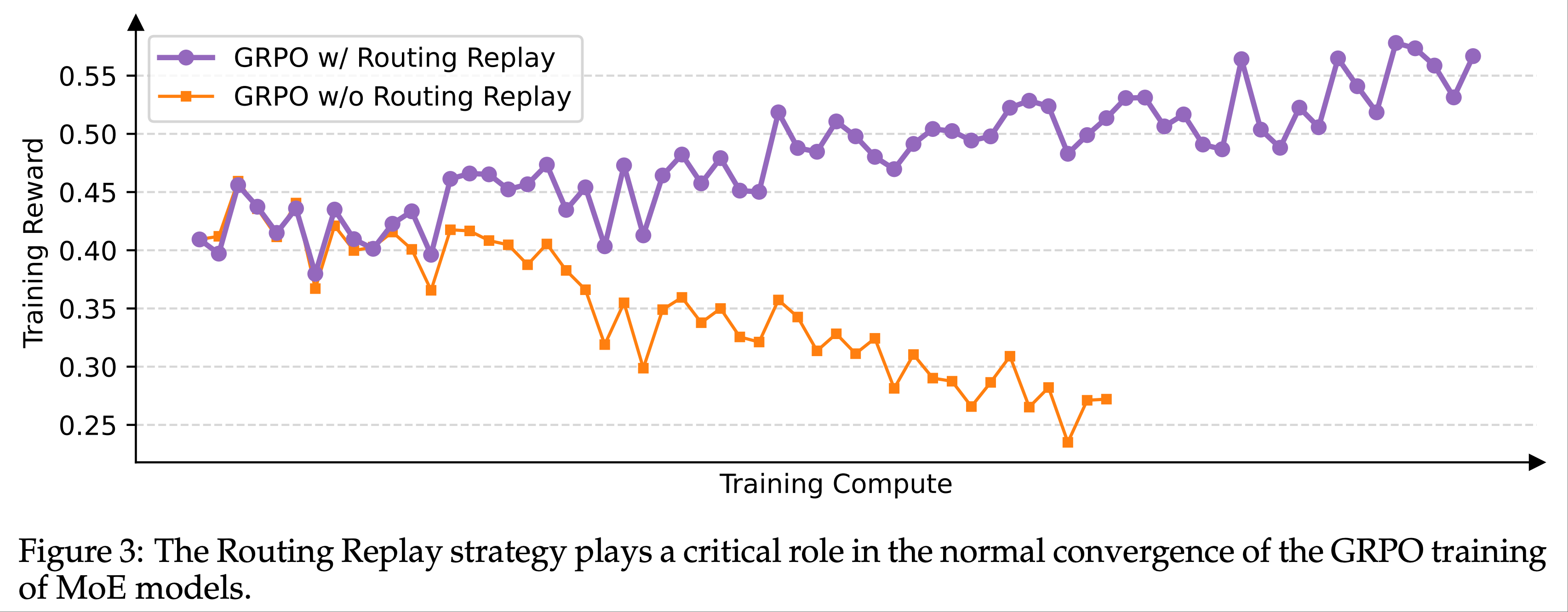
Benefit of GSPO
- 尽管路由回放使 GRPO 训练 MoE 模型能够正常收敛,但其复用路由模式的做法会带来额外的内存和通信开销,并可能限制 MoE 模型的实际容量
- 相比之下,如图 1 所示,GSPO 完全摆脱了对路由回放的依赖,能够常规计算重要性权重 \(s_{i}(\theta)\),正常收敛并稳定优化
- 关键在于,GSPO 仅关注序列似然(即 \(\pi_{\theta}(y_{i}|x)\)),而对单个 token 似然(即 \(\pi_{\theta}(y_{i,t}|x,y_{i,< t})\))不敏感
- 由于 MoE 模型始终保留其语言建模能力,序列似然不会剧烈波动
- 总之,GSPO 从根本上解决了 MoE 模型中的专家激活波动问题,无需复杂的路由回放等变通方法,这不仅简化并稳定了训练过程,还使模型能够充分发挥其全部容量
Benefit of GSPO for RL Infrastructure
- 由于训练引擎(如 Megatron)与推理引擎(如 SGLang 和 vLLM)之间的精度差异,实践中论文通常使用训练引擎重新计算旧策略 \(\pi_{\theta_{\text{old} } }\) 下采样 Response 的似然
- GSPO 仅使用 Sequence-level 而非 Token-level 似然进行优化,而 Sequence-level 对精度差异的容忍度更高
- GSPO 可以直接使用推理引擎返回的似然进行优化 ,从而避免重新计算的开销(注:非常好的做法!!!算是 GSPO 的核心优势了)
- 这在部分 rollout、多轮 RL 以及训练-推理分离框架等场景中尤为有益
附录:Well-posed 问题 和 Ill-posed 问题
- Well-posed 问题 (适定问题) 和 Ill-posed(不适定问题) 通常用于数学和物理领域,用来描述某些问题在解决时存在的困难
- Well-posed 问题 (适定问题) 需要同时满足下面三个条件
- 1)解的存在性 (Existence): 这个问题至少有一个解
- 2)解的唯一性 (Uniqueness): 这个问题只有一个唯一的解
- 3)解的稳定性 (Stability): 问题的解对初始条件或输入数据的微小变化是连续依赖的
- 换句话说,如果输入数据发生一点点变化,解也只会发生一点点变化
- 如果输入数据的一点点变化导致解发生巨大的变化,那么这个问题就是不稳定的
- 一个问题不满足以上三个条件中的至少一个,则称为 Ill-posed 问题 ,是因为它
- 简单来说,ill-posed 问题就是那些在数学上很“棘手”的问题,它们可能没有解,或者解不唯一,或者更常见的是,它们的解对输入数据非常敏感,以至于任何微小的误差都会导致结果完全不可信