注:本文包含 AI 辅助创作
Paper Summary
- 整体总结:
- 作者通过一种新颖的 Token Entropy 视角 分析了 RLVR,为理解 LLM 的推理机制提供了新的见解
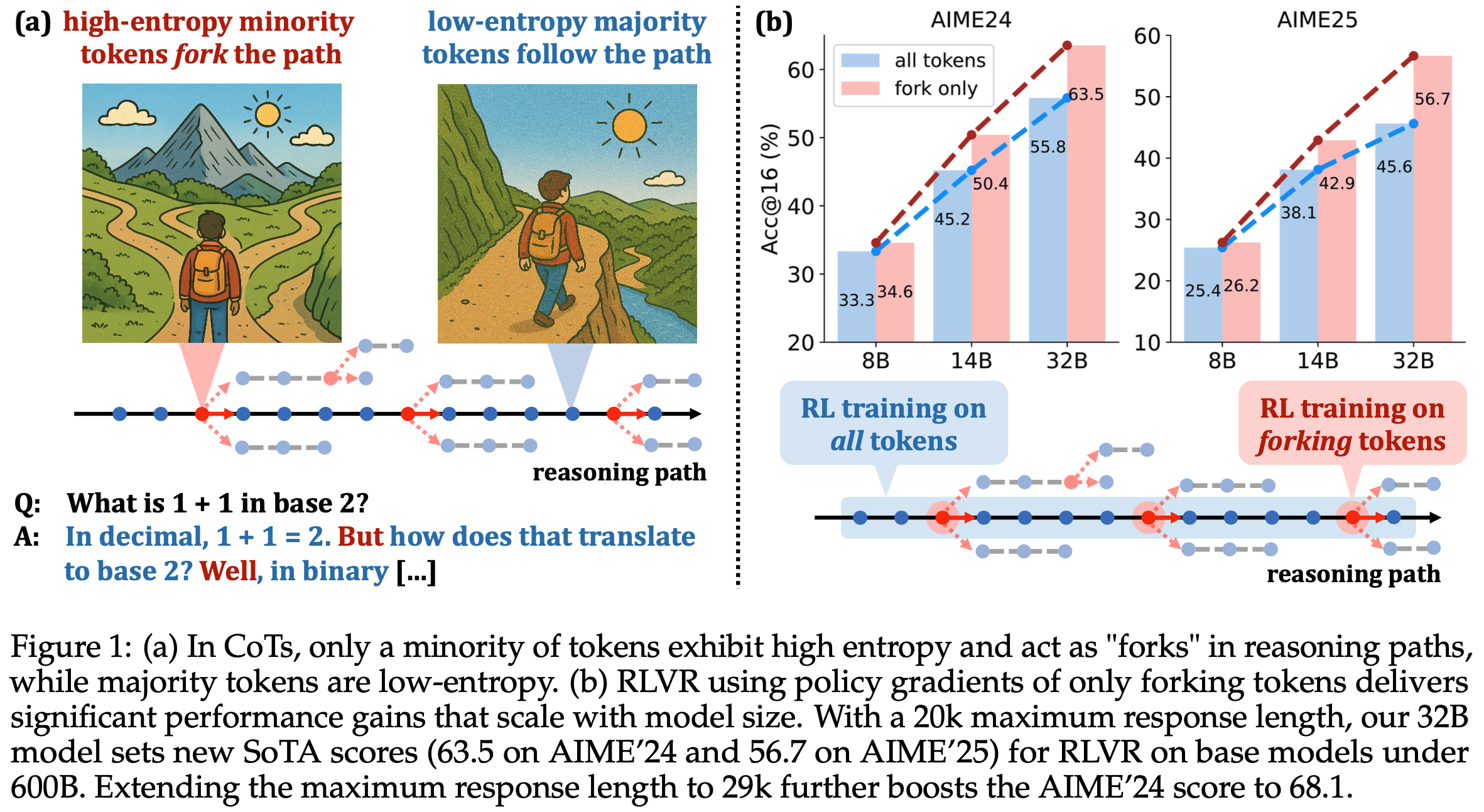
- 论文对 CoT 推理的研究表明,只有一小部分 Token 表现出高熵,并作为推理路径中的“分叉点”(forks)影响推理方向
- 此外,论文对 RLVR 训练过程中熵动态的分析表明,推理模型在很大程度上保留了基础模型的熵模式,而 RLVR 主要调整的是那些本就高熵的 Token 的熵值
- 基于这些发现,论文进一步将 RLVR 的策略梯度更新限制在熵值最高的前 20% 的 Token 上
- 这种方法实现了与全 Token RLVR 训练相当甚至更优的性能,同时表现出随模型规模增长的强扩展趋势
- 相比之下,将优化目标集中在低熵的多数 Token 上会导致性能显著下降
- 这些结果表明,RLVR 的有效性主要源于对高熵 Token 子集的优化,这为提高 LLM 推理能力提供了更聚焦和高效的策略
- RLVR-based RL 已成为提升 LLM Reasoning Capabilities 的强大方法,但其机制尚未得到充分理解
- 论文首次从 Token Entropy 模式(patterns)的新视角探索 RLVR ,全面分析了不同 Token 如何影响推理性能
- 通过研究 CoT 推理中的 Token Entropy 模式,论文发现仅有一小部分 Token 表现出高熵,这些 Token 作为关键 “分叉点(forks)” 引导模型选择多样化的推理路径
- 进一步分析 RLVR 训练中熵模式的演变发现,RLVR 基本遵守(largely adheres)基础模型的熵模式(entropy patterns),仅调整高熵 Token 的熵值
- 以上这些发现凸显了高熵 Token(即分叉 Token,forking Token)对 RLVR 的重要性
- 最终,论文通过限制策略梯度更新仅针对分叉 Token 改进了 RLVR,并发现了一个超越 80/20 法则的现象:
- 在 Qwen3-8B 基础模型上,仅使用 20% 的 Token 即可实现与全 Token 更新相当的性能;
- 而在 Qwen3-32B(AIME’25 +11.04,AIME’24 +7.71)和 Qwen3-14B(AIME’25 +4.79,AIME’24 +5.21)基础模型上,其表现显著优于全 Token 更新,展现出强烈的规模扩展趋势
- 相反,仅针对 80% 最低熵 Token 训练会导致性能显著下降
- 这些结果表明,RLVR 的有效性主要源于对决定推理方向的高熵 Token 的优化
- 论文的研究结果揭示了通过 Token Entropy 视角理解 RLVR 的潜力,并可通过利用高熵少数 Token 进一步优化 LLM 推理
Introduction and Discussion
- LLM 的推理能力在数学和编程等领域取得了显著进展,这得益于 OpenAI o1 (2024)、Claude 3.7 (2025)、DeepSeek R1 (2025)、Kimi K1.5 (2025) 和Qwen3 (2025) 等模型采用的测试时扩展(test-time scaling)方法
- 其中, RLVR (2025; DeepSeek-2025; 2025) 是一项关键技术,它通过基于自动正确性验证的强化学习目标优化模型输出
- 尽管 RLVR 的进步源于算法创新 (2025; 2025b; 2025)、跨领域应用 (2025; 2025; 2025) 以及反直觉的实证发现 (2025; 2025a; 2025),但现有实现通常对所有 Token 进行训练,而对哪些 Token 实际促进推理的理解有限
- 这些方法忽视了 Token 在推理过程中的异质性功能角色,可能因未能优先处理序列推理轨迹中的关键决策点而阻碍性能提升
- 论文通过 Token Entropy 模式的创新视角分析 RLVR 的底层机制,研究不同熵值 Token 如何影响推理性能
- 论文首先指出,在 LLM 的思维链(CoT)过程中,熵分布呈现一种独特模式:大多数 Token 以低熵生成,而少数关键 Token 以高熵出现 ,通过比较这两类 Token 的文本含义,论文发现:
- 最低平均熵(lowest average entropy)的 Token 主要完成既定的语言结构
- 最高平均熵的 Token 则作为关键决策点(pivotal decision points,称为“分叉点(forks)”),决定推理路径的走向(如图1(a)所示)
- 除定性分析(Qualitatively anslysis)外,论文还通过手动调节解码时分叉 Token 的熵进行对照实验
- 定量结果(Quantitative results)表明,适度增加这些高熵分叉 Token 的熵可显著提升推理性能,而人为降低其熵则会导致性能下降,验证了保持高熵及其“分叉”角色对这些 Token 的重要性
- 此外,通过分析 RLVR 训练中 Token Entropy 的演变,论文发现推理模型基本保留了基础模型的熵模式,训练过程中仅出现渐进且微小的变化
- 同时,RLVR 主要改变高熵 Token 的熵,而低熵 Token 的熵仅在较小范围内波动
- 这些观察结果凸显了高熵少数 Token 在 CoT 和 RLVR 训练中的关键作用
- 基于分叉 Token 的发现,论文进一步优化 RLVR ,仅保留熵值最高的 20% Token 的策略梯度更新,并屏蔽其余 80% Token 的梯度
- 实验表明,尽管仅使用 20% 的 Token,该方法在 Qwen3-8B 基础模型上的推理性能仍与全 Token 更新相当(且其有效性随模型规模增大而提升):
- 在 Qwen3-32B 基础模型上,AIME’25 和 AIME’24 的得分分别提升 +11.04 和 +7.71;
- 在 Qwen3-14B 模型上分别提升 +4.79 和 +5.21(如图1(b)所示)
- 仅使用 20% 高熵 Token 训练的 32B 模型在 AIME’24 和 AIME’25 上分别达到 63.5 和 56.7 的分数,为参数规模低于 600B 的基础模型训练的推理模型设立了新的 SoTA
- 将最大响应长度从 20k 扩展至 29k 后,32B 模型的 AIME’24 分数进一步提升至 68.1
- 实验表明,尽管仅使用 20% 的 Token,该方法在 Qwen3-8B 基础模型上的推理性能仍与全 Token 更新相当(且其有效性随模型规模增大而提升):
- 相反,仅针对 80% 最低熵 Token 训练会导致性能严重下降
- 最终结论:
- 20% 的 Token 即可实现与 100% Token 相当甚至更优的性能,甚至超越了 80/20 法则
- 理解:论文的发现远超二八定律的预期:高熵 Token 不仅是“重要的 20%”,而是几乎完全主导了模型性能的提升,低熵 Token 的贡献甚至可以忽略或有害
- RLVR 的性能增益几乎完全源于优化作为推理轨迹关键决策点的高熵少数 Token
- 20% 的 Token 即可实现与 100% Token 相当甚至更优的性能,甚至超越了 80/20 法则
Preliminary
Token entropy calculation
- Token-level 生成熵(简称“token entropy for brevity”)的定义为,对于 Token \( t \),其熵 \( H_t \) 为:
$$
H_t := -\sum_{j=1}^{V} p_{t,j} \log p_{t,j}, \quad \text{where} \quad (p_{t,1}, \cdots, p_{t,V}) = \boldsymbol{p}_t = \pi_{\boldsymbol{\theta} }(\cdot \mid \boldsymbol{q}, \boldsymbol{o}_{ < t}) = \text{Softmax}\left(\frac{z_t}{T}\right). \tag{1}
$$- \( \pi_{\boldsymbol{\theta} } \) 表示参数为 \( \boldsymbol{\theta} \) 的 LLM
- \( \boldsymbol{q} \) 是输入查询
- \( \boldsymbol{o}_{ < t} = (o_1, o_2, \cdots, o_{t-1}) \) 是已生成的 Token 序列
- \( V \) 是词汇表大小(vocabulary size)
- \( z_t \in \mathbb{R}^V \) 是时间步 \( t \) 的 pre-softmax logits
- \( \boldsymbol{p}_t \in \mathbb{R}^V \) 是对词汇表的概率分布(理解:\(p_{t,j}\) 表示生成第 \(t\) 个输出 Token \(o_t\) 时,选择词表中 Token \(j\) 的概率)
- \( T \in \mathbb{R} \) 是解码温度
- 在 off-policy 设定下
- 序列由 rollout 策略 \( \pi_{\boldsymbol{\phi} } \) 生成(理解:行为策略)
- 训练策略为 \( \pi_{\boldsymbol{\theta} } \)(即训练的目标策略,\( \boldsymbol{\phi} \neq \boldsymbol{\theta} \))
- 熵仍按公式 (1) 计算,以衡量训练策略在给定序列中的不确定性(理解:此时相当于序列是行为策略 \( \pi_{\boldsymbol{\phi} } \) 生成的)
- 理解 Token Entropy 的含义:Token Entropy 与 Token 生成分布相关,而非特定 Token
- 论文中,Token Entropy \( H_t \) 指索引 \( t \) 处的熵,由 Token 生成分布 \( \boldsymbol{p}_t \) 决定,而非从 \( \boldsymbol{p}_t \) 采样的特定 Token \( o_t \)
- 为简洁起见,当讨论从 \( \boldsymbol{p}_t \) 采样的 Token \( o_t \) 时,论文将其关联的熵称为 \( H_t \),并称 \( H_t \) 为 \( o_t \) 的 Token Entropy
- 若存在另一索引 \( t’ \neq t \) 满足 \( o_{t’} = o_t \),则 \( o_{t’} \) 的 Token Entropy 未必等于 \( H_t \)
RLVR Algorithms
- 近端策略优化(Proximal Policy Optimization,PPO) :PPO (2017) 是 RLVR 中广泛采用的策略梯度算法
- 为稳定训练,PPO通过以下裁剪替代目标限制策略更新在旧策略 \( \pi_{\boldsymbol{\theta}_{\text{old} } } \) 的邻近区域内:
$$
\begin{align}
J_{\text{PPO} }(\boldsymbol{\theta}) = &\mathbb{E}_{(\boldsymbol{q}, \boldsymbol{a}) \sim \mathcal{D}, \boldsymbol{o} \sim \pi_{\boldsymbol{\theta}_{\text{old} } }(\cdot|\boldsymbol{q})} \left[\min\left(r_t(\boldsymbol{\theta})\hat{A}_t, \text{clip}(r_t(\boldsymbol{\theta}), 1-\epsilon, 1+\epsilon)\hat{A}_t\right)\right], \\
&\text{where} \quad r_t(\boldsymbol{\theta}) = \frac{\pi_{\boldsymbol{\theta} }(o_t|\boldsymbol{q}, \boldsymbol{o}_{ < t})}{\pi_{\boldsymbol{\theta}_{\text{old} } }(o_t|\boldsymbol{q}, \boldsymbol{o}_{ < t})}
\end{align} \tag{2}
$$- \( \mathcal{D} \) 是查询 \( \boldsymbol{q} \) 和对应真实答案 \( \boldsymbol{a} \) 的数据集
- \( \epsilon \in \mathbb{R} \) 是超参数(通常设为 2.0,注:这里是 0.2 吧)
- \( \hat{A}_t \) 是通过价值网络计算的估计优势
- 为稳定训练,PPO通过以下裁剪替代目标限制策略更新在旧策略 \( \pi_{\boldsymbol{\theta}_{\text{old} } } \) 的邻近区域内:
- GRPO :基于公式 (2) 的裁剪目标,GRPO (2024) 通过组内平均奖励估计优势,弃用价值网络
- 具体地,对于每个查询 \( \boldsymbol{q} \) 和真实答案 \( \boldsymbol{a} \),rollout 策略 \( \pi_{\text{Gold} } \) 生成一组响应 \( \{\boldsymbol{o}^i\}_{i=1}^G \),对应结果奖励 \( \{R^i\}_{i=1}^G \),其中 \( G \in \mathbb{R} \) 是组大小。估计优势 \( \hat{A}_t^i \) 计算如下:
$$
\hat{A}_t^i = \frac{R^i - \text{mean}(\{R^i\}_{i=1}^G)}{\text{std}(\{R^i\}_{i=1}^G)}, \quad \text{where} \quad R^i = \begin{cases}
1.0 & \text{if} \quad \text{is_equivalent}(\boldsymbol{a}, \boldsymbol{o}^i), \\
0.0 & \text{otherwise}. \tag{3}
\end{cases}
$$- 除改进的优势估计外,GRPO还在公式 (2) 的裁剪目标中添加了 KL 惩罚项
- 具体地,对于每个查询 \( \boldsymbol{q} \) 和真实答案 \( \boldsymbol{a} \),rollout 策略 \( \pi_{\text{Gold} } \) 生成一组响应 \( \{\boldsymbol{o}^i\}_{i=1}^G \),对应结果奖励 \( \{R^i\}_{i=1}^G \),其中 \( G \in \mathbb{R} \) 是组大小。估计优势 \( \hat{A}_t^i \) 计算如下:
- 动态采样策略优化(DAPO) :基于GRPO,DAPO (2025) 移除 KL 惩罚,引入 clip-higher 机制、动态采样、Token-level 策略梯度损失和超长奖励调整,形成以下最大化目标:
$$
\begin{align}
\mathcal{J}_{\text{DAPO} }(\boldsymbol{\theta}) = \mathbb{E}_{(\boldsymbol{q}, \boldsymbol{a}) \sim \mathcal{D}, \{\boldsymbol{o}^i\}_{i=1}^G \sim \pi_{\text{Gold} } }(\cdot|\boldsymbol{q}) &\left[\frac{1}{\sum_{i=1}^G |\boldsymbol{o}^i|} \sum_{i=1}^G \sum_{t=1}^{|\boldsymbol{o}^i|} \min\left(r_t^i(\boldsymbol{\theta})\hat{A}_t^i, \text{clip}(r_t^i(\boldsymbol{\theta}), 1-\epsilon_{\text{low} }, 1+\epsilon_{\text{high} })\hat{A}_t^i\right)\right], \\
\text{s.t.} &0 < \left|\{\boldsymbol{o}^i \mid \text{is_equivalent}(\boldsymbol{a}, \boldsymbol{o}^i)\}\right| < G
\end{align} \tag{4}
$$ - DAPO是无价值网络的先进 RLVR 算法之一。论文以 DAPO 为基线进行 RLVR 实验
Analyzing Token Entropy in Chain-of-Thought Reasoning
- 尽管先前的工作 (2025) 强调了生成熵(generation entropy)在链式思维推理中的重要性,但它们通常对所有 Token 的熵进行了整体分析
- 在本节中,论文通过 Token-level 的视角更细致地研究了链式思维中的生成熵
- 为此,论文使用 Qwen3-8B (2025)(在同等参数规模下表现优异的推理模型),生成针对 AIME’24 和 AIME’25 问题的回答,解码温度设为 \( T = 1.0 \)
- 论文强制模型对每个问题使用思考模式,并收集了超过 \( 10^6 \) 个响应 Token
- 问题:为什么AIME 题目不多,能搜集 \( 10^6 \) 个响应 Token?
- 对于每个 Token ,其熵值根据公式 (1) 计算
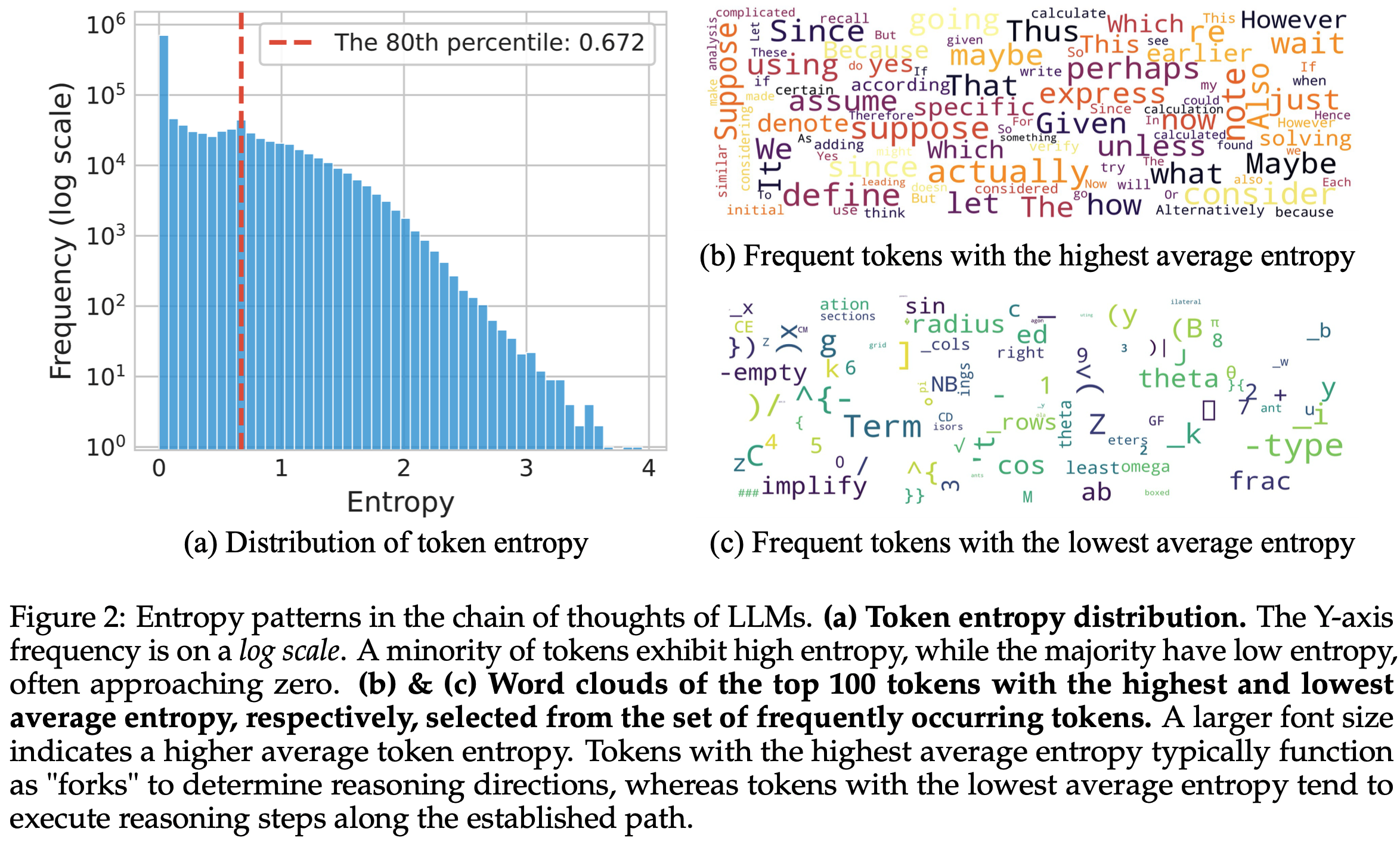
- 这些 Token Entropy 值的统计分析结果如图2 所示
- 此外,附录中的图12 至图17 展示了长链式思维响应中 Token Entropy 的可视化结果
- 通过这些分析,论文发现了以下熵模式:
- 链式思维中的熵模式 1(Entropy Pattern 1 in CoTs) :通常情况下,只有少数 Token 以高熵生成,而大多数 Token 以低熵输出
- 如图2(a) 所示,大量 Token 的熵值非常低,只有少量 Token 的熵值较高。具体而言,超过一半的 Token (约 50.64%)的熵值低于 \( 10^{-2} \),而仅有 20% 的 Token Entropy 值大于 0.672
- 注意:图2 中的频次是经过了 log scale 变换的,看起来差距偏小,实际上是差距很大的长尾分布(吐槽,不如不要做 log scale 更方便看)
- 理解:这里所谓 Token 以高熵生成的意思是,生成(采样)该 Token 前使用的概率分布的熵是高的(即随机性大)
- 如图2(a) 所示,大量 Token 的熵值非常低,只有少量 Token 的熵值较高。具体而言,超过一半的 Token (约 50.64%)的熵值低于 \( 10^{-2} \),而仅有 20% 的 Token Entropy 值大于 0.672
- 链式思维中的熵模式 2(Entropy Pattern 2 in CoTs) :熵值最高的 Token 通常用于连接推理过程中两个连续部分的逻辑关系,而熵值最低的 Token 则倾向于完成当前句子的一部分或构造单词的结尾。其他 Token 则不同程度地兼具这两种功能
- 在图2(b) 和 (c) 中,论文从 \( 10^6 \) 个 Token 中分别选取了平均熵值最高和最低的 100 个 Token
- 为了减少噪声对平均熵的影响,论文仅考虑出现频率超过 100 的 Token
- 高熵 Token 通常是句子内或跨句子的逻辑连接词:
- 例如 “wait” “however” “unless”(表示对比或转折)、“thus”“also”(表示递进或补充)或“since” “because”(表示因果关系)
- 类似地,数学推导中常用的“suppose” “assume” “given” “define” 等 Token 也频繁出现
- 而低熵 Token 通常是单词后缀、源代码片段或数学表达式的组成部分,这些 Token 具有高度的确定性
- 此外,图12 至图17 展示了长链式思维中 Token Entropy 的详细可视化结果,表明大多数 Token 在高熵和低熵组之外,兼具不同程度的连接和延续功能
- 链式思维中的高熵 Token 作为“分叉点”(High-entropy tokens as “forks” in chain-of-thoughts)
- 基于上述两种模式,论文将高熵 Token 称为“分叉 Token ”(forking tokens),因为它们通常在推理过程中以高不确定性引导不同的潜在路径
- 为了定量验证分叉 Token 的作用,论文在 AIME 2024 和 AIME 2025 的评估中为分叉 Token 和其他 Token 分配不同的解码温度
- 具体来说,论文调整每个 Token \( t \) 的概率分布 \( \boldsymbol{p}_t’ \in \mathbb{R}^V \) 如下:
$$
\boldsymbol{p}_t’ = \text{Softmax}\left(\frac{z_t}{T_t’}\right), \quad \text{where} \quad T_t’ = \begin{cases}
T_{\text{high} } & \text{if } H_t > h_{\text{threshold} }, \\
T_{\text{low} } & \text{otherwise}.
\end{cases} \tag{5}
$$- \( z_t \in \mathbb{R}^V \) 表示 Token \( t \) 的 pre-softmax logits
- \( T_t’ \in \mathbb{R} \) 是调整后的温度;
- \( h_{\text{threshold} } = 0.672 \) 是用于区分分叉 Token 和其他 Token 的熵阈值(这个值是通过计算采样的 \( 10^6 \) 个 Token 的 80 分位点得到的)
- \( T_{\text{high} } \in \mathbb{R} \) 和 \( T_{\text{low} } \in \mathbb{R} \) 分别对应分叉 Token 和其他 Token 的温度
- 链式思维中的熵模式 1(Entropy Pattern 1 in CoTs) :通常情况下,只有少数 Token 以高熵生成,而大多数 Token 以低熵输出
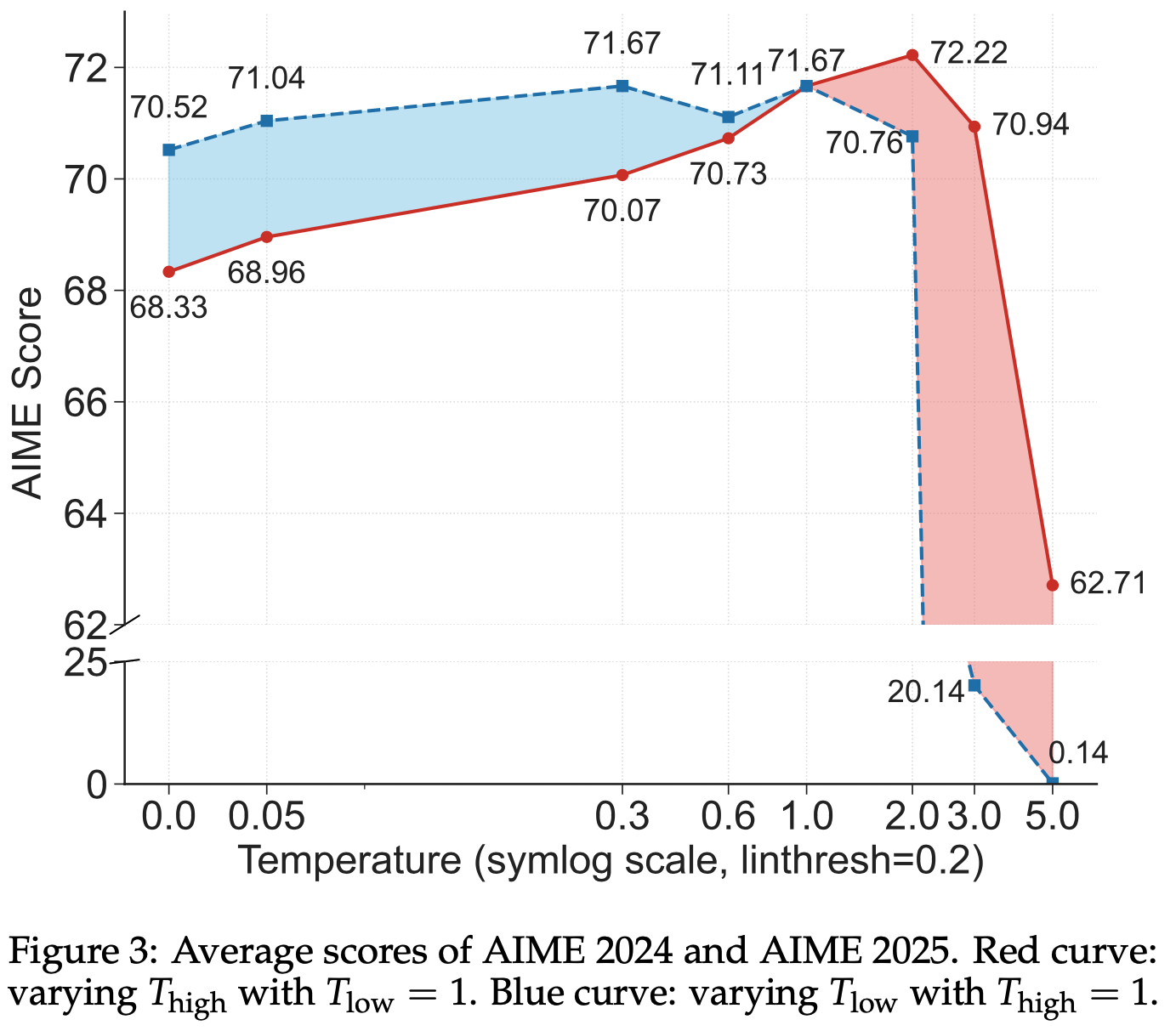
- 图3 展示了不同 \( T_{\text{high} } \) 和 \( T_{\text{low} } \) 值对性能的影响
- \( T_{\text{low} } = 1\) 时:降低 \( T_{\text{high} } \) 会显著降低性能,而提高 \( T_{\text{high} } \) 则能大幅提升性能
- \( T_{\text{high} } = 1\) 时:提高 \( T_{\text{low} } \) 甚至可能导致 LLM 生成无意义的输出
- 这些结果表明,分叉 Token 需要比其他 Token 更高的温度。由于分叉 Token 天然具有更高的熵,这一结果进一步支持了它们需要以更高熵水平运行的假设,这与它们作为“分叉点”的角色一致,高熵使其能够引导多样化的推理路径
RLVR Preserves and Reinforces Base Model Entropy Patterns
在本节中,基于第 3 节对链式思维中熵模式的观察,论文进一步研究了这些模式在 RLVR 训练过程中的演化
RLVR 主要保留基础模型的现有熵模式(RLVR primarily preserves the existing entropy patterns of the base models)
- 为了分析 RLVR 训练过程中熵模式的演化,论文将 DAPO (2025) 应用于 Qwen3-14B 基础模型(详见第 5 节)
- 使用经过 RLVR 训练的推理模型,论文为表2 中的六个基准生成了每个问题 16 个响应
- 包括了六个基准: AIME’24,AIME‘25,AMC’23,MATH500,Minerva,Olympiad
- 问题:Minerva 基准是什么?
- 对于这些响应中的每个 Token,论文计算了不同 RLVR 阶段推理模型的 logits ,并识别出熵值最高的前 20% Token
- 个人理解:一种更简单的方式是不需要计算熵,仅统计每个 Token 被生成时,这个 Token 的对应的采样概率值的均值即可评估 Token 的不确定性
- 然后,论文计算了每个中间模型与基础模型和最终 RLVR 模型之间在熵值最高的前 20% Token 位置上的重叠比例(即共享的高熵位置占比)
- 如表1 所示,尽管与基础模型的重叠比例逐渐下降,与最终 RLVR 模型的重叠比例逐渐上升,但在收敛时(第 1360 步),基础模型的重叠比例仍高于 86%,这表明 RLVR 在很大程度上保留了基础模型关于哪些 Token 具有高熵或低不确定性的熵模式

RLVR 主要调整高熵 Token 的熵值,而低熵 Token 的熵值相对稳定,变化较小(RLVR predominantly alters the entropy of high-entropy tokens, whereas the entropy of low-entropy tokens remains comparatively stable with minimal variations.)
- 使用与表1 相同的设置,论文计算了 RLVR 训练后每个 5% 熵百分位范围内 Token 的平均熵变化
- 观察到,基础模型中初始熵值较高的 Token 在 RLVR 训练后熵值增加较大
- 理解:熵值确实是增加了,见图5,但这好像与之前其他论文所谓的 RL 是再让模型”更自信”并不一致
- 这一观察进一步强化了 RLVR 主要保留基础模型熵模式的观点
- 观察到,基础模型中初始熵值较高的 Token 在 RLVR 训练后熵值增加较大
- 此外,图5 展示了使用 Qwen3-14B 基础模型时熵百分位在 RLVR 训练过程中的演化
- 图中显示,随着从 0 百分位到 100 百分位的推移,整个训练过程中熵值的波动范围逐渐减小(注:是逐渐增大吧)
- 理解:这里是指分位点稳定,但是全局看,熵值上下界其实是 100 分位点最大(只是相邻的几个 Step 之间波动不大)
- 这些观察结果表明,在整个训练过程中,RLVR 主要调整高熵 Token 的熵值,而低熵 Token 的熵值变化较小且相对稳定
- 理解:从图上看,低分位点虽然存在波动,但是波动范围很小,比如 60分位点,40分位点 和 20分位点 训练过程中几乎不动(注意 20分位点和40分位点的纵坐标单位是很小的)
- 特别地(理解):0分位点 对应的是熵最小的一些 Token,这部分 Token 几乎永远不会被选择到,所以他们的熵几乎不会变化(始终很低且固定)
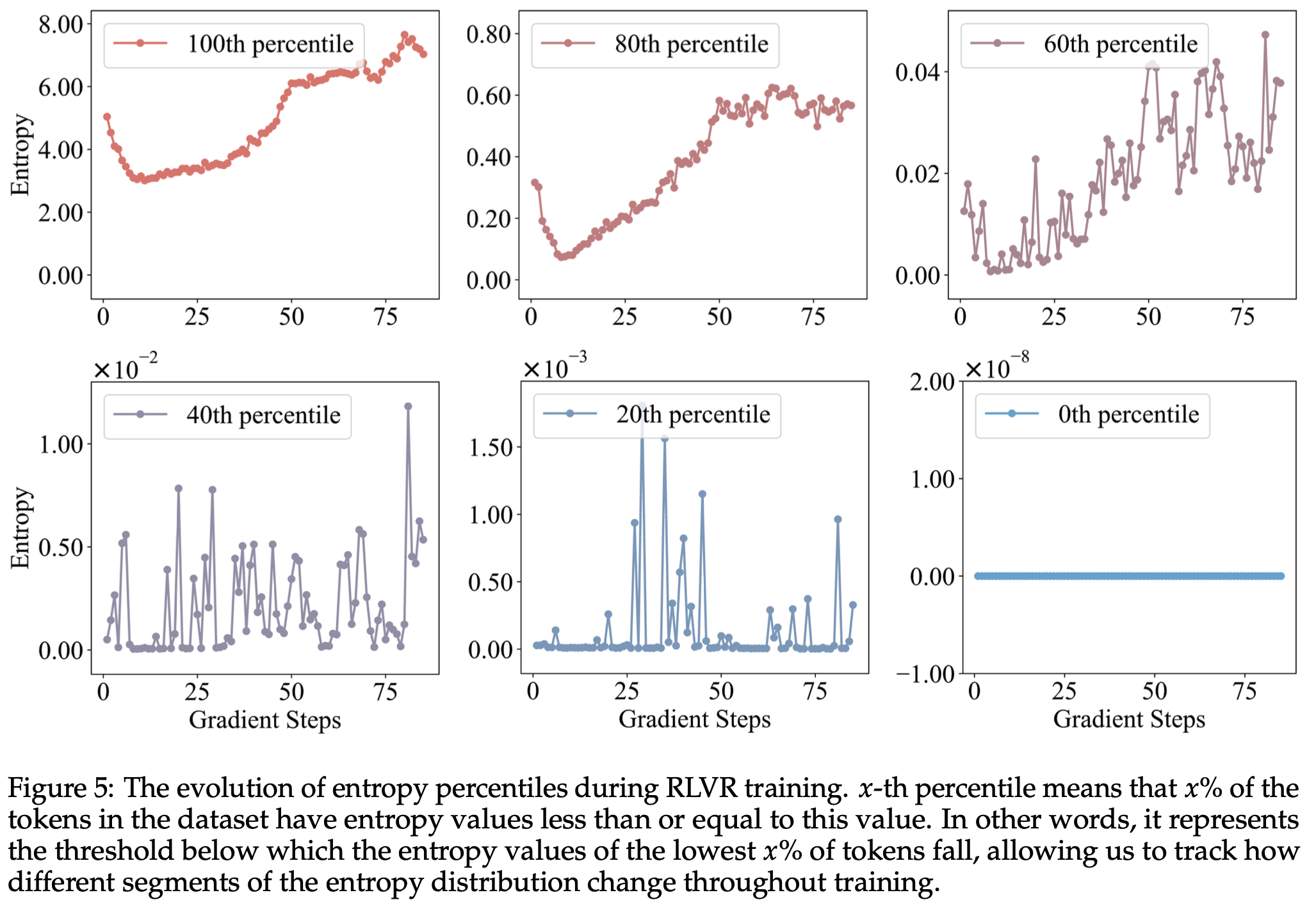
- 图中显示,随着从 0 百分位到 100 百分位的推移,整个训练过程中熵值的波动范围逐渐减小(注:是逐渐增大吧)
- 使用与表1 相同的设置,论文计算了 RLVR 训练后每个 5% 熵百分位范围内 Token 的平均熵变化
High-Entropy Minority Tokens Drive Effective RLVR(少数高熵 Token 就能有效驱动 RLVR)
- RLVR 已成为训练推理模型最广泛使用的方法之一 (2025),但关于哪些类型的 Token 对推理模型学习贡献最大的研究仍然缺乏
- 如第 3 节和第 4 节所述,高熵少数 Token 尤为重要
- 在本节中,论文研究了这些高熵少数 Token (也称为分叉 Token)在 RLVR 过程中对推理能力发展的贡献
Formulation of RLVR Using Only Policy Gradients of the Highest-Entropy Tokens(仅使用最高熵 Token 策略梯度的 RLVR)
- 基于 DAPO 的目标函数(公式 (4)),论文舍弃低熵 Token 的策略梯度,仅使用高熵 Token 的策略梯度训练模型。对于从数据集 \( \mathcal{D} \) 中采样的每个批次 \( \mathcal{B} \),论文计算最大目标函数如下:
$$
\begin{align}
\mathcal{J}_{\text{HighEnt} }^{\mathcal{B} }(\theta) = \mathbb{E}_{\color{red}{\mathcal{B}\sim\mathcal{D},(\boldsymbol{q},\boldsymbol{a})\sim\mathcal{B}},\{\boldsymbol{o}^i\}_{i=1}^G\sim\pi_{\theta_{\text{old} } }(\cdot|\boldsymbol{q})} &\left[\frac{1}{\sum_{i=1}^G|\boldsymbol{o}^i|}\sum_{i=1}^G\sum_{t=1}^{|\boldsymbol{o}^i|} \color{red}{\mathbb{I}\left[H_t^i \geq \tau_\rho^{\mathcal{B} }\right]} \cdot \min\left(r_t^i(\theta)\hat{A}_t^i, \text{clip}\left(r_t^i(\theta),1-\epsilon_{\text{low} },1+\epsilon_{\text{high} }\right)\hat{A}_t^i\right)\right], \\
\text{s.t.} &0 < \left|\{\boldsymbol{o}^i \mid \text{is_equivalent}(\boldsymbol{a}, \boldsymbol{o}^i)\}\right| < G
\end{align} \tag{6}
$$- \( H_t^i \) 表示响应 \( i \) 中 Token \( t \) 的熵
- \( \mathbb{I}[\cdot] \) 是指示函数,当内部条件成立时为 1,否则为 0;
- \( \rho \in (0,1] \) 是一个预定义的比例,指定批次中选择的最高熵 Token 的比例
- \( \tau_\rho^{\mathcal{B} } \) 是批次 \( \mathcal{B} \) 中对应的熵阈值,仅使用满足 \( H_t^i \geq \tau_\rho^{\mathcal{B} } \) 的 Token (即批次中所有 Token 的前 \( \rho \) 部分)计算梯度
- 与公式 (4) 相比,公式 (6) 仅有两处不同(如红色高亮所示):
- 1)优势项乘以 \( \mathbb{I}\left[H_t^i \geq \tau_\rho^{\mathcal{B} }\right] \),确保仅熵值 \( H_t^i \geq \tau_\rho^{\mathcal{B} } \) 的 Token \( o_t^i \) 参与策略梯度损失计算;
- 2)论文从数据集 \( \mathcal{D} \) 采样的每个(微)批次 \( \mathcal{B} \) 中筛选出前 \( \rho \) 的高熵 Token
- 问题1:这里比常规的 DAPO 增加了一次采样 \(\color{red}{\mathcal{B}\sim\mathcal{D}}\),这有什么特殊吗?
- 问题2:从哪里看出来经过了筛选?\(\color{red}{(\boldsymbol{q},\boldsymbol{a})\sim\mathcal{B}}\) 中的 \(\boldsymbol{a}\) 是句子吧,难道是这里面的 Token 经过筛选了?
Experimental Setup
Training details
- 论文从 verl (2024) 的代码库中调整训练配置,并遵循 DAPO (2025) 的训练方法(这是 LLM 中 SOTA 强化学习算法之一)
- 论文进行了实验和对照两个方法,分别对应以下两种配置:
- 使用完整梯度的 RLVR (公式 (4) 描述的原始 DAPO)
- 仅使用分叉 Token 策略梯度的 RLVR (公式 (6) 描述)
- 均采用了 clip-higher、动态采样、Token-level 策略梯度损失和超长奖励塑造等技术 (2025)
- 为了公平比较,论文采用了 DAPO 推荐的相同超参数:
- clip-higher 的 \( \epsilon_{\text{high} } = 0.28 \)
- \( \epsilon_{\text{low} } = 0.2 \);
- 超长奖励塑造的最大响应长度为 20480
- 缓存长度为 4096
- 此外,论文使用 verl 配置中的:
- training batch size 为 512
- mini-batch size 为 32
- 每个训练 Batch 进行 16 次梯度更新
- 学习率为 \( 10^{-6} \),且无学习率预热或调度(问题:为什么不使用预热?是 RLHF 都不需要吗?)
- 重要的是,训练过程中排除了 KL 散度损失和熵损失
- 论文进行了实验和对照两个方法,分别对应以下两种配置:
- 为了评估这些方法的扩展能力,论文在 Qwen3-32B 和 Qwen3-8B 基础模型上进行了 RLVR 实验,使用 DAPO-Math-17K (2025) 作为训练数据集
- 论文在公式 (6) 中设置 \( \rho = 20% \),即仅使用每个批次中前 20% 最高熵 Token 的梯度更新策略
- 作者为 Qwen3 设计的 chat template 是:
“User:\n[question]\nPlease reason step by step, and put your final answer within \boxed{}.\n\nAssistant:\n”
with “<|endoftext|>“ serving as the EOS token, where “[question]” should be replaced by the specific question. - 问题:Qwen3-32B 和 Qwen3-8B 模型是经过后训练的 Chat 模型,Qwen3 模版中,它的 EOS 使用的是
<|im_end|>,这里使用<|endoftext|>真的不会有问题吗?
Evaluation
- 论文在 6 个标准数学推理基准上评估模型,这些基准通常用于评估推理能力:AIME’24、AIME’25、AMC’23、MATH500 (2021)、Minerva 和 OlympiadBench (2024)
- 所有评估均在 Zero-shot setting 下进行
- 对于每个问题,论文在解码温度 \( T = 1.0 \) 下生成 16 个独立响应,并 Report 平均准确率和每个响应的平均 Token 数
Main Results
High-entropy tokens drive reinforcement learning for LLM reasoning(高熵 Token 驱动 LLM Reasoning RL)
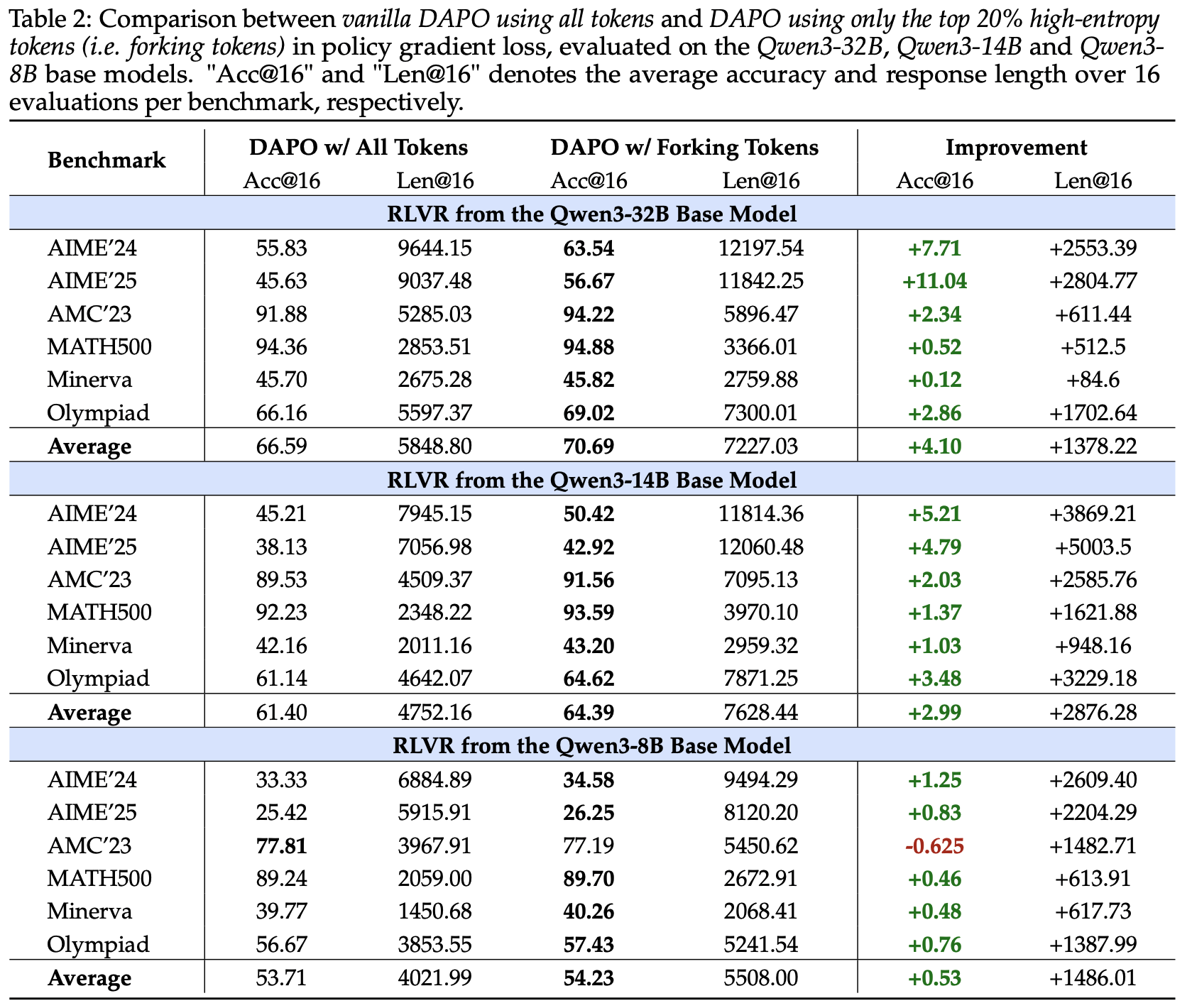
- 图6 和表2 比较了使用所有 Token 的原始 DAPO 和仅在策略梯度损失中保留前 20% 高熵 Token 的方法
- 令人惊讶的是,舍弃底部 80% 的低熵 Token 不仅不会降低推理性能,甚至可以在六个基准上带来性能提升
- Qwen3-32B 基础模型上,这种方法在 AIME’24 上提升了 7.71 分,在 AIME’25 上提升了 11.04 分
- Qwen3-14B 基础模型在 AIME’24 上提升了 5.21 分,在 AIME’25 上提升了 4.79 分
- Qwen3-8B 基础模型,性能未受影响
- 问题1:针对高熵 Token 的优化,为什么模型越大提升越多?小模型熵不能提升?
- 问题2:对所有模型都有,针对高熵 Token 的优化上,响应长度都会长于 Vanilla DAPO,原因是什么?
- 这些结果表明,RLVR 中推理能力的提升主要由高熵 Token 驱动,而低熵 Token 对推理性能的影响较小甚至可能阻碍性能,尤其是在 Qwen3-32B 和 Qwen3-14B 基础模型上
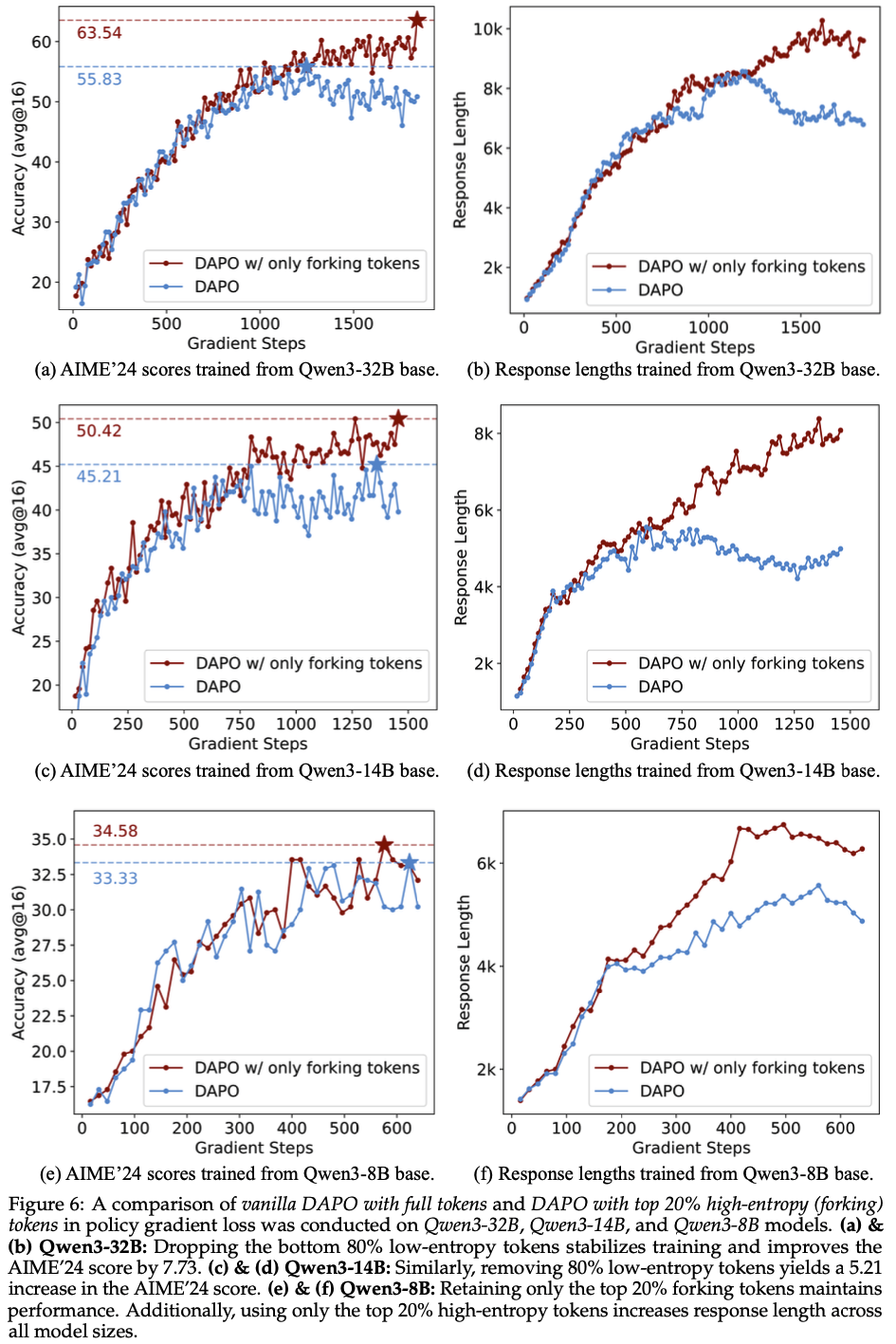
- 为了更深入分析,论文调整公式 (6) 中的比例 \( \rho \) 进行实验,如图7(a) 所示
- 结果显示,Qwen3-8B 基础模型的性能在不同比例(如 10%、20%、50%)下保持相对稳定
- 对于 Qwen3-14B 和 Qwen3-32B 基础模型,图7(c) 和 (e) 表明,将 \( \rho \) 从 20% 降至 10% 会导致性能轻微下降,而将其大幅增至 100% 则会导致性能显著下降(问题:如果是 30% 呢?)
- 这些观察表明,在合理范围内,推理性能对 \( \rho \) 的具体值不敏感。更重要的是,它们表明,专注于高熵 Token 而非所有 Token 通常能保持性能,甚至可能在更大的模型中带来显著提升
Low-entropy tokens contribute minimally to reasoning performance(低熵 Token 对推理性能的贡献微乎其微)
- 如图7(a) 和 (b) 所示,在 RLVR 中仅保留底部 80% 的低熵 Token 会导致性能大幅下降,尽管这些 Token 占训练中总 Token 数的 80%
- 这一发现表明,低熵 Token 对增强推理能力的贡献极小,凸显了高熵 Token 对有效模型训练的重要性
The effectiveness of high-entropy tokens may lie in their ability to enhance exploration(推测:高熵 Token 的有效性可能在于其增强探索的能力)
- 论文的分析表明,专注于约 20% 的高熵 Token 子集(实验中观察到的比例)在 RLVR 中实现了探索和训练稳定性之间的有效平衡 ,如图7(b)、(d) 和 (f) 所示
- 将比例 \( \rho \) 从 20% 调整为 10%、50% 或 100% 会导致整体熵从训练早期开始持续降低 ,直至性能开始收敛
- 问题:实际上,\( \rho=20% \) 时,熵也是先下降再提升的吧
- 使用底部 80% 低熵 Token 训练会导致整体熵显著降低
- 将比例 \( \rho \) 从 20% 调整为 10%、50% 或 100% 会导致整体熵从训练早期开始持续降低 ,直至性能开始收敛
- 这些结果表明,保留一定比例的高熵 Token 可能有助于有效探索,超出这一范围的 Token 可能对探索帮助较小,甚至可能有害,尤其是在性能收敛前的关键阶段
- 这可能解释了高熵 Token 训练下,不同模型表现不同:
- 在 Qwen3-32B 基础模型上,仅使用前 20% 高熵 Token 的 DAPO 优于原始 DAPO(如图6(a) 所示)(理解:关注高熵 Token 有助于探索?)
- 在 Qwen3-8B 基础模型上,由于模型容量较低,增强探索的收益似乎有限
Focusing on forking tokens in the policy gradient loss benefits larger reasoning models(在 PG 损失中,专注于的分叉 Token 有益于更大的推理模型)
- 论文在图8 中展示了仅使用分叉 Token 时的扩展趋势
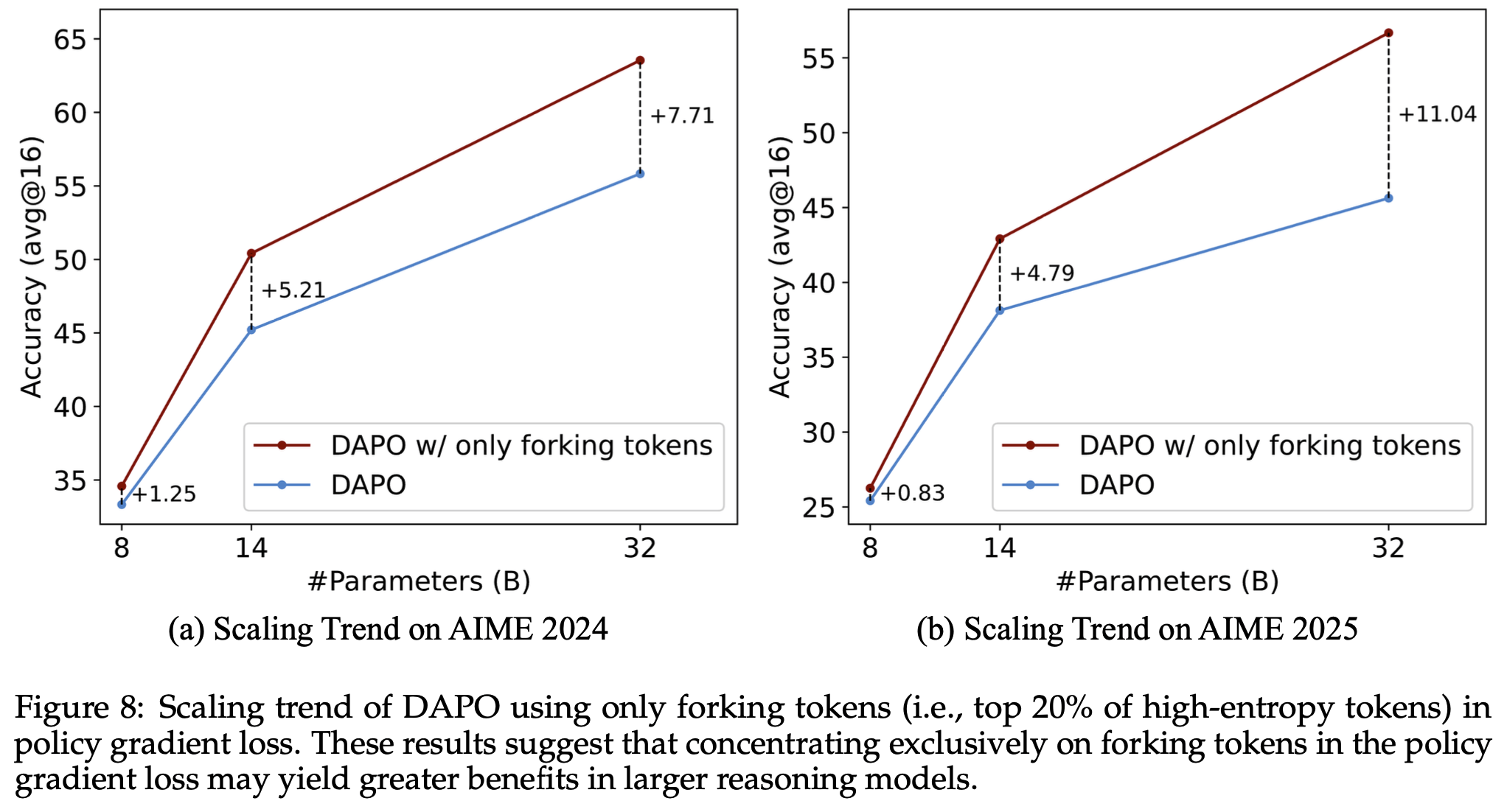
- 在 AIME’24 和 AIME’25 基准上,论文观察到随着模型规模的增大,相对于原始 DAPO 的性能提升越来越显著
- 这表明了一个有希望的结论 :在策略梯度损失中仅专注于分叉 Token **可能在更大的推理模型中带来更大的优势**
Discussion
讨论 1:高熵少数 token(即分叉 token)可能是解释为什么 RL 能泛化而 SFT 只能记忆的关键因素
- Chu 等人 (2025) 通过实验证明,强化学习(尤其是基于结果的奖励)在未见过的规则任务上表现出强大的泛化能力,而 SFT 容易记住训练数据,难以泛化到训练分布之外
- 作者推测,强化学习和监督微调泛化能力差异的一个关键因素可能与分叉 token 的熵有关
- 论文的实验(例如图5 和图7)表明:强化学习倾向于保留甚至增加分叉 token 的熵 ,从而保持推理路径的灵活性
- 相比之下,监督微调将输出 logits 推向 one-hot 分布,导致分叉 token 的熵降低,进而失去推理路径的灵活性
- 这种灵活性可能是推理模型有效泛化到未见任务的关键决定因素
讨论 2:与传统强化学习不同,LLM 的推理结合了先验知识,并且需要生成可读的输出。因此,LLM 的思维链(CoT)包含低熵多数 token 和高熵少数 token 的混合,而传统强化学习可以假设轨迹中所有动作的熵是均匀的
- 如图2(a) 所示,大多数 LLM 思维链 token 的熵较低,只有一小部分 token 表现出高熵
- 相比之下,传统强化学习通常将每个动作分布定义为具有预定义标准差的高斯分布 (2017; 2021; 2022),导致所有动作的熵均匀分布
- 论文将 LLM 思维链中这种独特的熵模式归因于其在大规模先验知识上的预训练以及对语言流畅性的要求
- 这迫使大多数 token 与记忆的语言结构对齐 ,从而表现出低熵
- 只有一小部分在预训练语料库中本身具有不确定性的 token 允许探索 ,因此表现出高熵
- 这一推论与论文在表1 中的结果一致
讨论 3:在 RLVR 中,熵奖励可能是次优的,因为它会增加低熵多数 token 的熵。相比之下,clip-higher 机制能有效提升高熵少数 token 的熵
- 在强化学习中,熵奖励通常被添加到训练损失中以鼓励探索,通过增加动作的熵来实现——这是传统任务中的常见做法 (2017; 1992; 2016),最近也被应用于 LLM 推理 (2024; 2024)
- 然而,如上所述,与传统强化学习轨迹不同,LLM 思维链表现出独特的熵模式
- 对所有 token 均匀增加熵可能会破坏低熵多数 token,从而降低性能,而选择性增加高熵少数 token 的熵则能提升性能(图3)
- 因此,均匀应用的熵奖励对于思维链推理来说是次优的
- 相反,clip-higher (2025) 通过适度提高公式 (4) 中的 \(\epsilon_{\text{high} }\),更好地针对高熵 token
- 从经验上看,论文发现重要性比率 \(r_i(\theta)\) 较高的 token 往往具有更高的熵
- 通过在训练中包含更多这类 token,clip-higher 在不显著影响低熵 token 的情况下增加了整体熵
- 这一结论得到了 Yu 等人 (2025) 的支持,并在图5 中得到了验证
- 问题:高熵 Token 一般伴随着 低概率,所以 clip-higher 有助于提升高熵 Token 的概率(提升概率会降低熵?),这与论文的 整体熵似乎不一致
- 回答:从另一个视角看是一致的,相对于普通 clip,clip-higher 让低概率的 Token 获得了更多提升机会,有助于让概率更平均,从而增大了熵
Related Work
Reinforcement learning for LLM
- 在 OpenAI 的 o1 (2024) 等具备推理能力的模型出现之前, RL 被广泛用于 RLHF ,以改进 LLM 的指令跟随能力和与人类偏好的对齐 (2022)
- RLHF 方法大致分为在线和离线偏好优化
- 在线方法如 PPO (2017)、GRPO (2024) 和 REINFORCE (1992) 在训练过程中生成响应并接收实时反馈
- 离线方法如 DPO (2023)、SimPO (2024) 和 KTO (2024) 使用预先收集的偏好数据(通常来自人类标注者或 LLM )优化策略
- 虽然离线方法训练效率更高,但其性能通常不如在线方法 (2024)
- 最近, RLVR (2025) 成为增强 LLM 推理能力的一种有前景的方法,尤其是在数学和编程领域 (2024; DeepSeek-2025; 2025; 2025)
- OpenAI 的 o1 (2024) 首次证明了强化学习可以有效地大规模激励推理能力
- 在 o1 的基础上,DeepSeek R1 (DeepSeek-2025)、QwQ (Team, 2025)、Kimi k1.5 (2025) 和 Qwen3 (2025) 等模型试图匹配或超越其性能
- DeepSeek R1 通过在线强化学习算法 GRPO (2024) 展示了基于结果的优化可以产生强大的推理能力,同时还引入了“zero RL”范式,即无需传统的强化学习微调即可从基础模型中激发推理能力
- 受这些结果的启发,后续方法如 DAPO (2025)、VAPO (2025b)、SimpleRLZoo (2025) 和 Open-Reasoner-Zero (2025) 进一步探索了基于强化学习的推理
- 在本工作中,论文以 DAPO 为基线,研究强化学习应用于 LLM 的关键方面
Analysis on reinforcement learning with verifiable rewards
- 最近, RLVR 已成为增强 LLM 推理能力的流行方法,多项研究分析了 RLVR 及其相关概念的特征
- Gandhi 等人 (2025) 发现,推理行为的存在(而非答案的正确性)是推动强化学习性能提升的关键因素
- 类似地,Li 等人 (2025) 表明,长思维链(CoT)的结构对学习过程至关重要,而单个推理步骤的内容影响甚微
- 问题:如何理解?
- Vassoyan 等人 (2025) 识别了思维链中的“关键 token”,即模型容易出错的决策点,并提出通过修改 KL 惩罚来鼓励在这些 token 周围进行探索
- Lin 等人 (2024) 同样识别了对错误结果有显著影响的关键 token,并证明识别和替换这些 token 可以改变模型行为
- 论文发现 RLVR 主要关注推理路径中的分叉 token,这一发现可能与 Gandhi 等人 (2025) 和 Li 等人 (2025) 的观察有共通之处,他们认为 RLVR 主要学习格式而非内容。然而,论文的分析更进一步,在 Token-level 上明确了这一发现
- 此外,Vassoyan 等人 (2025) 和 Lin 等人 (2024) 中“关键 token”的概念与论文提出的高熵少数 token 密切相关
- 与之前基于输出正确性判断 token 重要性的工作不同,论文提出 token 熵作为一种可能更准确反映 LLM 底层机制的评判标准
Limitations
- 作者认为本研究仍有改进空间
- 首先,实验可以扩展到 Qwen 系列之外的模型
- 尽管论文尝试在 LLaMA 模型上评估论文的方法,但它们在 AIME 基准测试中难以取得有意义的性能
- 此外,论文的数据集范围可以扩展到数学之外的领域,例如编程或更复杂的任务,如 ARC-AGI(2019;2025)
- 另外,论文的发现基于特定的实验设置,论文的观察和结论可能无法推广到所有 RLVR 场景
- 例如,在不同的 RLVR 设置中,实验中观察到的 20% 有效比例可能需要调整为其他值才能达到最佳效果
Future Directions
- 未来的研究方向包括开发新的 RLVR 算法以更好地利用高熵少数 Token
- 同时探索,除了提升 RLVR外,如何利用这些 insights 改进其他方法
- 例如 SFT 、蒸馏(distillation)、推理(inference)以及多模态训练(multi-modal training)
附录:生成过程中 Token 的熵示例
- 图12 至图17 展示了长链式思维中 Token Entropy 的详细可视化结果,表明大多数 Token 在高熵和低熵组之外,兼具不同程度的连接和延续功能





