注:本文包含 AI 辅助创作
- 参考链接:
Paper Summary
- 整体内容
- 论文提出了一种新颖的难度感知强化学习框架 GHPO(Guided Hybrid Policy Optimization),解决了 LLM 在 RLVR 中面临的训练不稳定和低效问题(这些问题主要源于能力与任务难度之间的不匹配,导致奖励信号稀疏)
- GHPO 通过自适应 Prompt 优化动态校准任务难度,平衡模仿学习(用于当前模型难以解决的问题)和探索式强化学习(用于更易处理的任务),从而形成平滑且优化的学习课程
- GHPO 显著提高了训练稳定性(能智能调整学习过程以适应模型能力的动态变化)
- 背景:
- RLVR 已成为促进 LLM 自我提升的强大范式(尤其在复杂推理任务中)
- 当前主流的 On-policy 强化学习方法常面临严重的训练不稳定(training instability)和低效(inefficiency)问题
- 这主要源于能力与难度的不匹配(capacity-difficulty mismatch) :即训练数据的复杂性往往超出模型当前能力,导致奖励信号极度稀疏和学习停滞
- 这一挑战对于更轻量级的 LLM 尤为突出
- 论文提出一种新颖的难度感知(difficulty-aware)强化学习框架 :GHPO
- GHPO 通过自适应 Prompt 细化动态校准任务难度,提供针对性引导
- GHPO 创新性地平衡了两种学习模式构建平滑优化的学习课程(smooth and optimized learning curriculum):
- 对于超出模型当前能力的问题采用直接模仿学习
- 对较易任务则采用探索式强化学习
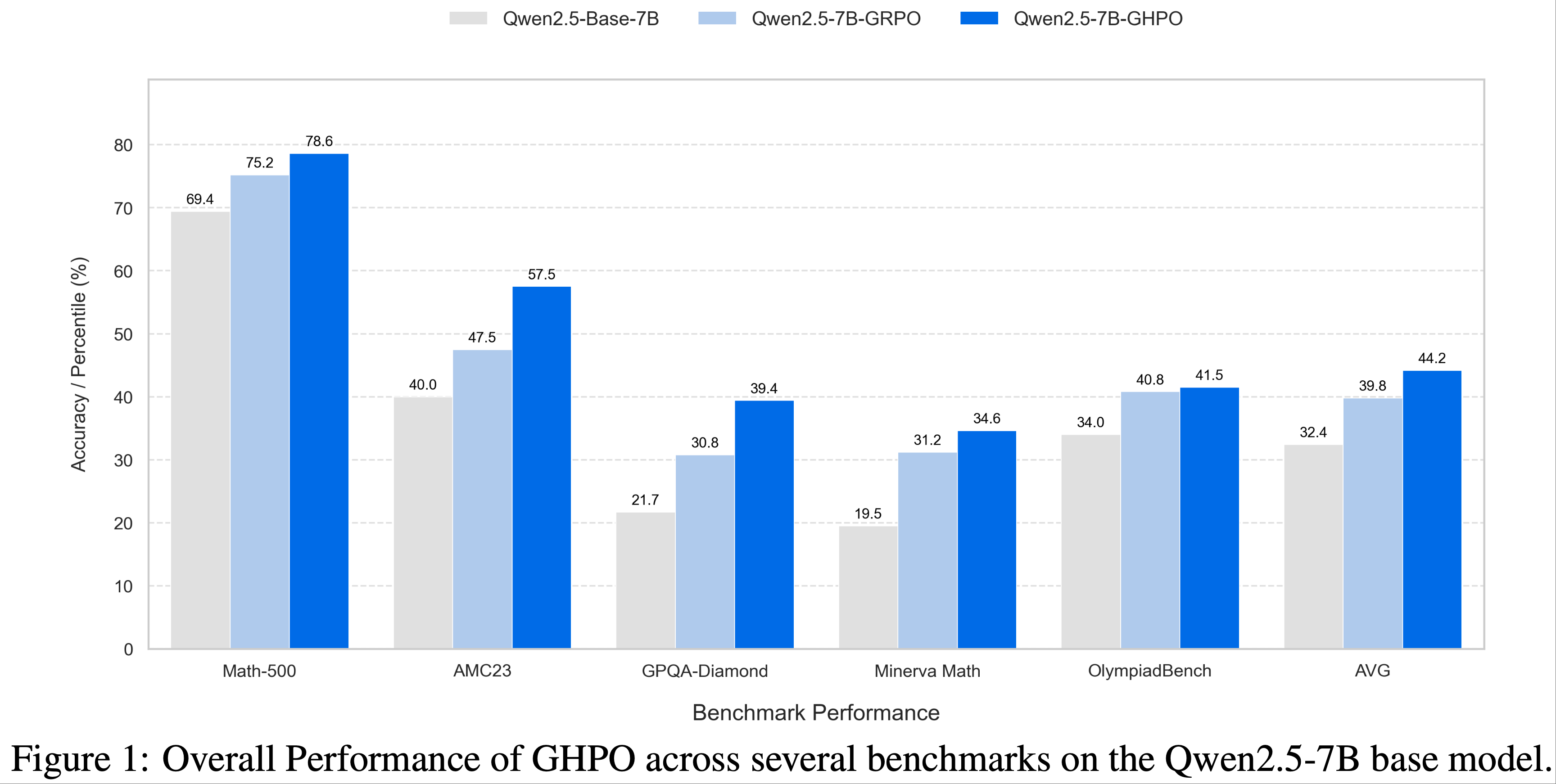
- 实验结果部分:GHPO 在多个高难度数学基准测试中平均性能提升约5%,持续优于强大的在策略强化学习和课程学习基线
- 论文分析证实,GHPO 显著提高了训练稳定性和最终的推理性能 ,为开发强大且稳健的推理模型提供了一种可扩展且高效的解决方案
- 开源情况:实现代码已开源
Introduction and Discussion
- 新一代大推理模型在复杂推理任务中取得了最先进成果
- 这些大模型包括 OpenAI-o3 (2025)、DeepSeek-R1 (2025) 和 Kimi-1.5 (2025) 等
- 这些模型的关键特征是其生成链式思维(2022)和 进行反思式推理的能力
A key characteristic of these models is their proficiency in producing extended Chains-of-Thought (CoT) and engaging in what appears to be reflective reasoning
- 这种被称为”测试时扩展(test-time scaling)”的现象已被证明能有效解决数学和编程难题
- 核心训练方法是 Zero-RL 范式,该范式采用 RLVR
- 基于 RL 的后训练在增强推理能力方面展现出比 SFT 更优的泛化性
- SFT 的本质是模仿学习,SFT 依赖于从人工标注数据或更强模型提炼的 CoT 中进行模仿学习 (2025)
- 当前 RLVR 方法存在显著局限,以 GRPO 为例,作为 On-policy 方法,它们高度依赖当前策略模型的性能,导致两大挑战:
- 1)能力-难度失配导致的奖励稀疏性(Reward Sparsity from Capacity-Difficulty Mismatch) :训练数据固有难度与模型演化能力间的严重不匹配会导致奖励稀疏,即均匀无信息的奖励阻碍学习过程 (2025)
A significant mismatch between the inherent difficulty of the training data and the model’s evolving capabilities often results in reward sparsity, where uniform and uninformative rewards impede the learning process
- 2)次优样本效率(Suboptimal Sample Efficiency) : On-policy 算法常受限于次优样本效率
- 当训练数据集引入更难题以提升基准性能时,策略模型难以有效学习
- 这一局限在容量受限的轻量化模型中更为突出
- 1)能力-难度失配导致的奖励稀疏性(Reward Sparsity from Capacity-Difficulty Mismatch) :训练数据固有难度与模型演化能力间的严重不匹配会导致奖励稀疏,即均匀无信息的奖励阻碍学习过程 (2025)
- 现有解决方案包括
- 课程学习(Curriculum Learning, CL)(2025) 通过逐步引入复杂样本来对齐任务难度与模型能力 ,但需人工启发式划分数据集,缺乏扩展性
- DAPO (2025) 采用动态采样(dynamic sampling)过滤 完全正确 或 完全错误 的 Prompt,但会丢弃大量训练数据
- 另一类研究探索 Off-policy 或混合 RL 方法以缓解 On-policy 学习的不稳定性 (2025),但这些方法需要辅助 LLM,增加了训练成本和复杂度
- 受 SFT 等模仿学习技术启发,论文提出一种简单有效的解决方案:用部分真实解题步骤引导模型
- 具体做法:通过条件化这些解题步骤,将模型的输出分布导向正确答案 ,缓解难题的奖励稀疏问题
- 但直接应用该技术可能使训练数据过于简单,降低模型独立解题的学习效率
- 论文提出 GHPO 框架:
- GHPO 巧妙地将在线RL与模仿学习统一:
- 先动态评估样本难度
- 再通过自适应 Prompt 细化提供差异化引导
- 对于模型可处理的问题,主要采用标准 On-policy RL鼓励探索;
- 对于困难样本,则无缝切换至模仿学习模式,提供显式解题步骤
- 这种混合方法自动平衡探索与直接引导,在提升训练稳定性的同时优化样本效率
- GHPO 巧妙地将在线RL与模仿学习统一:
- 论文主要贡献总结如下:
- 揭示 RLVR 中能力对齐与奖励稀疏问题的关键作用,提出 GHPO 框架以提升训练稳定性与效率
- 提出 GHPO,通过自适应 Prompt 细化动态检测样本难度,并在 On-policy RL与引导模仿学习间切换
- 在六个数学基准测试上开展广泛实验,证明 GHPO 优于最先进 RL 方法,且在不同模型家族中均表现稳健
Preliminaries
- 核心问题:GRPO 训练中的奖励稀疏性挑战
Reinforcement Learning with Verifiable Rewards, RLVR
- RLVR 范式中,LLM 可表示为 \(\pi_{\theta}\),输入 Prompt \(q\),LLM 生成 Token 序列(轨迹)\(\tau = (o_1, o_2, \ldots, o_T)\)
- 上述轨迹生成过程被建模: finite-horizon、 Token-level MDP(注:核心是 Token-level):
- 状态(State) \(s_t\):在生成步骤 \(t\),状态是初始 Prompt \(q\) 与已生成 Token 序列的拼接:\(s_t = (q, o_1, o_2, \ldots, o_{t})\),初始状态 \(s_0 = q\)
- 动作(Action) \(a_t\):从模型词表 \(\mathcal{V}\) 中选择下一个 Token \(o_t\)
- 策略(Policy) \(\pi_{\theta}\):即 LLM 本身,给定当前状态提供下一个动作( Token )的概率分布:\(a_t = o_t \sim \pi_{\theta}(\cdot|s_t)\)
- 奖励(Reward) \(R\):RLVR 采用验证器分配的稀疏终端奖励(仅当完整轨迹结束时分配奖励 ,验证器根据最终答案正确性分配二元奖励):
$$ R = \begin{cases}
1 & \text{if the answer is correct} \\
0 & \text{otherwise}
\end{cases} $$
- 训练目标是学习最优策略参数 \(\theta^*\) 以最大化 Prompt 分布 \(\mathcal{D}\) 上的期望终端奖励。目标函数 \(\mathcal{J}(\theta)\) 定义为:
$$ \mathcal{J}(\theta) = \mathbb{E}_{q\sim\mathcal{D},\tau\sim\pi_{\theta}(\cdot|q)}[R(\tau)] $$- 该目标通常通过策略梯度算法优化(策略更新通过增加高优势轨迹对应 Token 的对数概率实现)
GRPO
- GRPO 在提升 LLM 数学和编程推理能力方面表现卓越,其核心创新是基于组内比较而非绝对奖励值的优势估计方法
- 对于给定 Prompt \(q\),GRPO 首先从策略模型 \(\pi_{\theta_{\text{old} } }\) 采样 \(G\) 个不同响应 \(\{o_i\}_{i=1}^G\),每个轨迹的优势 \(\hat{A}_{i,t}\) 通过其奖励 \(R_i\) 相对于整组统计量归一化计算:
$$ \hat{A}_{i,t} = \frac{R_i - \mu_{\mathcal{R} } }{\sigma_{\mathcal{R} } + \epsilon} $$- \(\mu_{\mathcal{R} } = \frac{1}{G}\sum_{j=1}^G R_j\) 是组内奖励的均值
- \(\sigma_{\mathcal{R} } = \sqrt{\frac{1}{G}\sum_{j=1}^G (R_j - \mu_{\mathcal{R} })^2}\) 是组内奖励的标准差
- \(\epsilon\) 为数值稳定性常数
- GRPO 方法的关键在于同一响应 \(o_i\) 内所有 Token 生成步骤共享此 Response-level 优势
- GRPO 复用了 PPO 框架实现训练稳定性,同时策略梯度目标的简化为:
$$ \mathcal{J}_{\text{GRPO} }(\theta) = \mathbb{E}_{(q,a)\sim D,\{o_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|q)} \left[\frac{1}{G}\sum_{i=1}^G \frac{1}{|o_i|}\sum_{t=1}^{|o_i|} \left(\min\left(\frac{\pi_{\theta}(o_{i,t} \mid q,o_{i,<t})}{\pi_{\theta_{\text{old} } }(o_{i,t} \mid q,o_{i,<t})}\hat{A}_{i,t},\text{clip}\left(\frac{\pi_{\theta}(o_{i,t} \mid q,o_{i,<t})}{\pi_{\theta_{\text{old} } }(o_{i,t} \mid q,o_{i,<t})},1-\epsilon,1+\epsilon\right)\hat{A}_{i,t}\right) -\beta D_{\text{KL} }(\pi_{\theta}|\pi_{\text{ref} })\right)\right] $$- 实际应用中,完整目标可能包含剪切机制和 KL 散度惩罚项以正则化策略更新
- 但近期许多实现发现省略 KL 项(即 \(\beta=0\))仍能成功 (2025; 2025),从而简化优化过程
The Challenge of Reward Sparsity in GRPO
- GRPO 易受训练低效和不稳定性影响(这在实践复现中很常见)
- 论文发现其脆弱性的主因是训练数据难度与策略模型能力间的根本性失配 ,表现为严重的奖励稀疏性 ,这对有效强化学习构成重大障碍
- 当 Query \(q\) 对当前策略 \(\pi_{\theta}\) 来说过于困难时,模型生成的 \(G\) 个响应可能全部错误,导致奖励向量全零(即所有 \(i\in\{1,\ldots,G\}\) 有 \(R_i=0\))
- 此时组内奖励均值与标准差均为零,公式(2)的优势计算对所有轨迹返回 \(\hat{A}_{i,t}=0\)
- 这引发两个关键问题:
- 1)训练低效 :零优势导致该 Query 的梯度消失(模型无法获得学习信号,生成和评估 \(G\) 个响应的计算资源完全浪费)
- 当批次中包含大量此类难题时,多数数据无法贡献策略改进,极大降低整体训练效率
- 2)训练不稳定(Training Instability) :能提供非零学习信号的 “effective” Query 数量在梯度更新间剧烈波动
- 有效批次大小的方差会为梯度估计引入显著噪声,破坏训练稳定性并阻碍可靠收敛
- 问题:这里是指批次大小的方差,而不是梯度本身的方差
- 1)训练低效 :零优势导致该 Query 的梯度消失(模型无法获得学习信号,生成和评估 \(G\) 个响应的计算资源完全浪费)
- 奖励稀疏性挑战在容量受限模型(如设备端部署模型,on-device Model)中尤为严峻
- 为量化能力-难度失配,论文在包含约 900K 竞赛级数学题的 NuminaMath-1.5 (2024) 数据集上评估 Qwen2.5-7B-Instruct (2025) 模型性能。
- 结论是无法解决 52 的问题
- 这一重要发现说明该数据集大部分内容远超对应 Qwen2.5-7B-Base 模型 (2025) 的固有推理能力,更遑论能力更有限的小型 LLM
- 这清晰表明设备端模型面临的奖励稀疏性问题严重性:
- 强化学习中超半数数据集可能产生零奖励轨迹 ,无法提供有效梯度信号,严重阻碍模型学习
The Proposed Framework
From Static Guidance to a Dynamic Framework
- 论文的核心策略是将引导(guidance)直接整合到强化学习循环中 ,通过将策略(policy)与部分真实解轨迹(partial ground-truth traces)结合,以解决第2.3节中详述的奖励稀疏性问题
- 这一方法的动机基于如下的 Assumption 1 ,即对于困难问题,此类引导能够提高成功概率 ,从而在原本无法获得有效学习信号的情况下提供支持
- 对于大多数数学数据,真实解轨迹形式的引导通常是可用的,但在 RLVR 训练过程中,这些宝贵的解轨迹信息通常被忽略,仅使用最终的真实答案
- Assumption 1 :设 \(\mathcal{D}_{in}\) 和 \(\mathcal{D}_{OOD}\) 分别为域内(in-domain)和域外(out-of-distribution)问题分布,\(\pi_{\theta_{0} }\) 为基策略(base policy)
- 策略 \(\pi\) 的域外性能通过其期望奖励 \(\mathcal{R}(\pi):=\mathbb{E}_{b\sim\mathcal{D}_{OOD},\tau\sim\pi(\cdot|b)}[R(\tau)]\) 衡量
- 考虑一个基策略无法解决的问题 \(q \sim \mathcal{D}_{in}\),此时其期望奖励非正(\(\mathbb{E}_{\tau\sim\pi_{\theta_{0} }(\cdot|q)}[R(\tau)] \leq 0\))
- 设 \(h\) 为 \(q\) 的部分真实解轨迹(partial ground-truth solution trace)
- 从 \(\pi_{\theta_{0} }\) 微调两个策略,通过最大化目标 \(\mathcal{J}_{GRPO}\):
- \(\pi_{\theta_{q},h}\),使用轨迹:\(\theta_{q,h}=\arg\max_{\theta}\mathcal{J}_{GRPO}(\theta;\{(q,h)\})\)
- \(\pi_{\theta_{q} }\),不使用轨迹:\(\theta_{q}=\arg\max_{\theta}\mathcal{J}_{GRPO}(\theta;\{q\})\)
- 论文假设 ,对于失败问题使用真实轨迹能提升域外泛化能力:
$$
\mathbb{E}_{b\sim\mathcal{D}_{OOD},\tau\sim\pi_{\theta_{q},h} (\cdot|b)}[R(\tau)] \geq \mathbb{E}_{b\sim\mathcal{D}_{OOD},\tau\sim\pi_{\theta_{q} } (\cdot|b)}[R(\tau)]
$$- 注:这里是只有假设和实验验证吗,是否能给出理论证明?
- 第4节的实验验证了这一假设的有效性。
- 利用这个性质,我们可以获取合法的学习信号,即使在困难样本中(原本会返回 0 奖励并导致梯度消失的样本),但静态应用这一原则(例如预先标记一组固定问题为“困难”并始终对其应用引导)是次优的,存在两个关键限制:
- 人工精选与可扩展性(Manual Curation and Scalability) :静态方法需要繁琐的离线流程来确定何时需要引导
- 静态方法不仅难以扩展,而且具有主观性,可能与模型的实际知识缺口不完全匹配
- 进化中的模型能力(Evolving Model Capability) :训练初期对策略无法解决的问题可能在多次更新后变得简单
- 静态引导策略无法适应模型的动态能力,可能导致对已能通过探索解决的问题“过度引导”,抑制新颖推理路径的学习,降低样本效率
- 人工精选与可扩展性(Manual Curation and Scalability) :静态方法需要繁琐的离线流程来确定何时需要引导
Guided Hybrid Policy Optimization, GHPO
- 论文提出一种自动化框架引导混合策略优化(GHPO) ,旨在提升强化学习效率
- 如图2 所示,GHPO 动态评估样本难度,并自适应地在标准策略强化学习与引导学习之间切换
- 这种创新方法确保仅在真正需要时提供引导,保留对模型当前能力范围内问题的探索,同时对更具挑战性的场景提供自适应优化
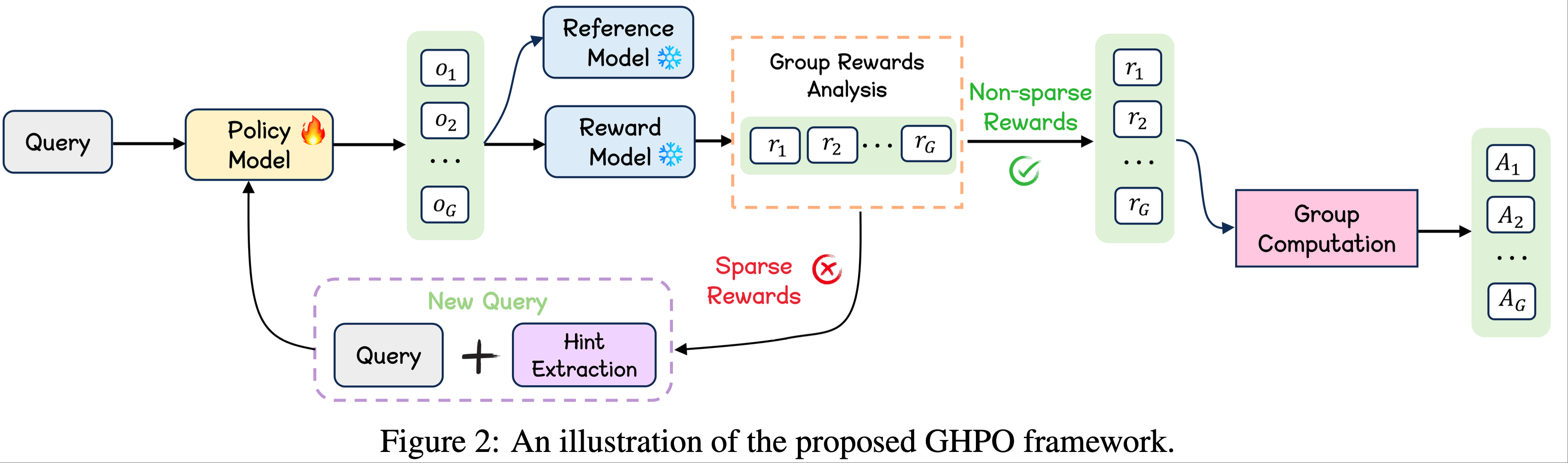
- 这种创新方法确保仅在真正需要时提供引导,保留对模型当前能力范围内问题的探索,同时对更具挑战性的场景提供自适应优化
- GHPO 包含两个核心模块:
- 自动化难度检测(Automated Difficulty Detection) :评估当前问题的固有难度,决定后续学习流程
- 自适应 Prompt 优化(Adaptive Prompt Refinement) :根据检测到的难度,通过融入不同级别的真实引导来优化 Prompt
- 对于给定 Query \(q\) 和真实答案 \(a\),GHPO 首先生成 \(G\) 个独立响应 \(\{o_{i}\}_{i=1}^{G}\),并通过奖励模型获取其二元奖励 \(\{r_{i}\}_{i=1}^{G}\)
- 与 GRPO 不同,这些组级奖励不直接用于优势估计,而是由难度检测模块分析其稀疏性,并根据预设策略优化 Prompt
- 数学上,GHPO通过以下目标优化策略:
$$
\mathcal{J}_{\text{GHPO} }(\theta) =\mathbb{E}_{(q,a)\sim D,\{o_{i}\}_{i=1}^{G}\sim\pi_{\theta_{old} } }(\cdot|q)
\left[\frac{1}{G}\sum_{i=1}^{G}\frac{1}{|o_{i}|}\sum_{t=1}^{|o_{i}|}\Big{(}\min\big{(}r_{i,t}(\theta)\hat{A}_{i,t},\text{clip},(r_{i,t}(\theta),1-\epsilon,1+\epsilon),\hat{A}_{i,t}\big{)} -\beta D_{\text{KL} }(\pi_{\theta}|\pi_{\text{ref} })\Big{)}\right] \\
\text{s.t.} \quad q^{*}=\begin{cases}
q & \sum_{i=1}^{n}f(a,o_{i})>0 \\
q+\omega*h_{f,q} & \text{otherwise}
\end{cases}. \\
r_{i,t}(\theta)=\frac{\pi_{\theta}(o_{i,t}\mid q^{*},o_{i,<t})}{\pi_{\theta_\text{old}}(o_{i,t}\mid q^{*},o_{i,<t})}, \tag{4-6}
$$- 函数 \(f\) 判断预测是否等价于真实答案
- \(h_{f,q}\) 是 Query \(q\) 的完整真实解序列
- \(\omega\) 为分阶段调整的 Hint 比例 (Hint Ratio)
- 通过无缝整合这两个模块,GHPO 能高效切换策略强化学习与引导模仿学习,显著提升训练效率
- 图3 展示了 GHPO 的 Prompt 模板

- 相较于原始 GRPO Prompt ,GHPO 引入增强结构,从真实解中提取 Hints 并附加引导句:“以下文本是答案的开头部分,可供参考以解决问题:”
The following text is the beginning part of the answer, which you can refer to for solving the problem
Automated Difficulty Detection
- 如Assumption 1 所述,通过融入离线真实 Hints,可以为最困难的问题获取有效学习信号
- 然而,静态预定义哪些问题需要引导的方法因第3.2节所述限制而难以扩展
- 论文提出难度检测模块(difficulty detection module) ,在不增加人工成本的情况下评估当前问题的固有难度
- 与其他基于模型的高成本方法不同,论文的方法利用学习过程中固有的准确率奖励
- 对于训练批次中的每个 Query \(q\),论文通过分析其 \(G\) 个响应的组级奖励 \(\{r_{i}\}_{i=1}^{G}\)(公式6定义)来评估其相对于当前策略模型 \(\pi_{\theta}\) 的难度
- 若某 Query 的所有 \(G\) 个奖励均为零,表明即使从其输出分布中采样多次,当前策略模型也未能生成正确推理路径
- 此时,这些稀疏奖励无法为策略改进提供有效梯度信息,因此该 Query \(q\) 被标记为对当前策略模型 \(\pi_{\theta}\) 困难(difficult) ,需自适应引导
Adaptive Prompt Refinement with Multi-Stage Guidance(多阶段指导的自适应 Hint 优化)
- 难度检测模块能够识别出当前策略模型 \(\pi_{\theta}\) 难以处理的 Query 问题
- 此时根据假设 1(Assumption 1),引入真实解答的 Hints (ground-truth solution hints)可以为这些难题提供有效的学习信号
- 这种指导通过 Hint 比例参数 \(\omega\) 来控制(即引入真实解答的特定比例)
- 但确定一个固定的最优 \(\omega\) 值具有挑战性,且对于不同难度分布的逻辑推理任务往往效果不佳,因为更复杂的问题天然需要更大比例的 Hint
- 为了解决这一问题,并确保策略改进过程中的持续学习,论文提出了一种多阶段指导的自适应 Hint 优化策略(Adaptive Prompt Refinement strategy with Multi-stage Guidance)
- 该策略能够动态调整 Hint 比例 \(\omega\)
- 核心设计目标是避免因 Hint 冗余而导致任务过度简化 ,即防止因过度偏离原始 Query 而降低学习效果
- 动态 Hint 注入的核心思想是通过学习阶段的线性调度来控制 Hint 比例
- 论文首先注入一小部分真实解答作为初始 Hint ,若模型仍无法生成正确答案,则在后续阶段逐步增加 Hint 的长度
- 在学习过程的第一阶段 ,论文设置 Hint 比例 \(\omega = 0.25\),旨在平衡数据难度与策略模型当前能力之间的关系
- 如公式 (6) 所定义,对于训练批次中被识别为困难的 Query 问题,论文从真实解答轨迹 \(h_{f,q}\) 中提取 25% 的内容作为辅助 Hint ,并将其与原始 Query 拼接,形成优化后的 Query \(q^{*} = q + \omega \cdot h_{f,q}\),随后用于模型推理
- 在学习过程的第二阶段 :
- 若难度检测模块评估至少有一个生成的响应是正确的 ,则保留原始 Query 用于后续组优势计算;
- 若所有响应均未通过评估(表明问题难度较高),则将 Hint 比例提升至 \(\omega = 0.5\) 以提供更多指导
- 论文采用最多三阶段的线性调度策略,\(\omega\) 的取值序列为 \(\{0.25, 0.5, 0.75\}\)
- 这一策略能够充分利用训练数据提升训练效率,无需直接剔除困难 Query
- 除了自适应优化高难度 Query 外,该策略还可视为一种动态数据增强方法
- 随着策略模型能力在学习过程中逐步提升,最初需要较高 \(\omega\) 的 Query 可能最终仅需较低比例的指导,甚至完全无需指导
- 理解:这种方法也可以看做是一种课程学习的思路
Cold-Start Strategy
- 在初始优化阶段,策略模型常难以遵循特定格式指令(如将答案括在指定框内),导致预测与真实答案不匹配,准确率奖励低下
- 此时,自动化难度检测模块可能错误地将多数 Query 标记为困难,引入偏差并浪费计算资源
- 论文提出可选的冷启动策略(Cold-Start Strategy)
- 在前 \(N\) 步优化(实验中设为 20步)中,暂时禁用难度检测机制,仅使用原始 GRPO 训练流程
- 该方法在初期节省计算资源,同时让模型掌握基础格式能力,避免在引入自适应引导前产生早期偏差
Hint Extraction Example
- 图4展示了 GHPO 如何有效处理检测到的困难问题
- 以原问题“若三角形两边长为5和7单位,第三边可能的整数长度有多少种?”为例,当前模型多次采样均无法生成正确推理响应,导致奖励稀疏问题
- 为此,GHPO 智能干预,提取真实解的 50% 作为 Hint ,与原问题拼接并附加引导句
- 如图4左侧所示,新构建的 GHPO Prompt 包含针对性 Hint ,从而引导模型更有效地推理

Experiment
Training Datasets
- 使用可验证的数学任务评估 GHPO 算法的有效性
- 论文从 MATH (2021) 和 NuminaMath-1.5 (2024) 数据集中构建了两个不同难度的训练数据集:
- Math3to5 :该数据集包含 8,890 道竞赛数学题,难度范围为 3 至 5 级,每道题均附带逐步的真实解答
- 该数据集代表中等难度水平
- NuminaMath-S :这是一个更具挑战性的数据集,包含从 NuminaMath-1.5 中精选的 18,300 道问题,整合了 Math3to5 数据集以及来自 OlympiadBench 和 AMC 的额外问题
- 该数据集中的每道问题也附带 step-by-step 的真实解答
- 该数据集代表困难难度级别
- Math3to5 :该数据集包含 8,890 道竞赛数学题,难度范围为 3 至 5 级,每道题均附带逐步的真实解答
- 这两个数据集旨在模拟现实世界中 RLVR 训练场景中常见的中等和困难问题级别
Baseline Models
- 为了全面评估 GHPO,论文选择了两个基础 LLM ,并实现了多种 RLVR 方法:
- Qwen2.5-Base-7B (2025):Qwen2.5-7B 的基础模型
- Qwen2.5-Math-7B (2024):基于 Qwen2.5-7B 的专用数学大语言模型
- Qwen2.5-7B-GRPO :使用 GRPO 训练流程 (2025) 微调的 Qwen2.5-Base-7B
- Qwen2.5-Math-7B-GRPO :使用 GRPO 训练流程微调的 Qwen2.5-Math-7B
- Qwen2.5-7B-GRPO-CL :该模型采用两阶段训练流程
- 第一阶段:Qwen2.5-Base-7B 在 math3to5 数据集上使用 GRPO 进行训练;
- 第二阶段:使用来自 OlympiadBench 和 AMC 的更困难问题对模型进行微调 ,显著提升第一阶段的难度级别
- Qwen2.5-7B-GRPO-CL-H :该变体在 Qwen2.5-7B-GRPO-CL 的第二训练阶段应用了恒定 Hint 注入策略(constant hint injection strategy) ,旨在通过提供一致的指导来平衡学习过程
- 论文在第二训练阶段应用恒定提示注入,以平衡学习过程
Implementation Details
- 论文使用 openr1 (2025) 代码库和 TRL (2020) 框架进行实验
- GHPO 训练在 8 块高性能 GPU 上完成,每块 GPU 配备 80GB 内存和高带宽
- 奖励设置(Reward Setting) :
- 论文采用 Rule-based 奖励函数,正确答案奖励 +1,错误答案奖励 0
- 论文还引入了Format-based 奖励 ,鼓励模型在给出最终答案前显式执行推理步骤
- 格式奖励的权重与 Rule-based 奖励的比例设置为 2:1
- 超参数与训练配置(Hyperparameters and Training Configuration) :
- 使用 AdamW 优化器 (2017)
- 初始学习率为 \(1 \times 10^{-6}\)
- 采用余弦调度将学习率衰减至零
- 10% 的全局步数预热阶段
- 训练批次大小为 112
- 每个 Query 采样 8 个响应
- 梯度更新的累积步数为 8
- 在训练阶段:
- 采样配置包括温度为 1.0
- 每个响应的最大生成长度为 2048 个 token
- 没有使用 KL 正则化损失或 KL 惩罚
Evaluation Details
- 论文使用 Lighteval 工具包 (2023) 构建评估脚本
- 评估时,温度设置为 0.0 或 1.0(根据基准难度调整),最大生成长度为 4096 个 token
- 为确保一致性,论文使用与训练阶段完全相同的 Prompt 模板,在此阶段不使用任何 Extracted Hint 或 Hint-guided Prompts
- 论文评估了标准数学推理基准上的性能
- 包括:MATH_500 (2021)、OlympiadBench (2024)、Minerva Math (2022)、GPQA-Diamond (2023)
- 论文还评估了竞赛级基准上的性能
- 如 AMC2023 和 AIME2024 上的性能
- 报告指标:
- 对于大多数基准,论文报告 pass@1 结果;
- 对于 AIME2024,论文报告平均准确率(avg@32),即每个问题生成 32 个样本的平均值
Overall Performance
- 论文的实验评估证明了所提出的 GHPO 方法相较于传统方法的显著有效性和优越性
- 论文在不同难度数据集和不同基线模型上展示了实验结果
- 中等难度任务的性能(Performance on Medium-Difficulty Tasks) :
- 首先在 math3to5 训练数据集上进行了初步实验
- 如表 1 所示,标准 GRPO 方法成功将 Qwen-7B 基础模型训练为强大的推理代理,甚至优于经过大量数学数据微调的 Qwen2.5-Math-7B
- 但论文的 GHPO 进一步提升了性能,平均准确率比 GRPO 提高了 4.4%
- 这一提升主要是因为 GHPO 缓解了奖励稀疏性问题
- 在六个评估基准上,GHPO 训练的模型始终表现出更优的推理能力
- 特别是在 AMC2023 和 GPQA-Diamond 上,GHPO 的准确率比 GRPO 提高了超过 8%

- 困难任务的性能(Performance on Challenging Tasks) :
- 为了进一步评估 GHPO 的鲁棒性,论文使用更具挑战性的 NuminaMath-S 数据集训练 Qwen2.5-7B 基础模型
- 除了原始 GRPO,论文还引入了课程学习基线(Qwen2.5-7B-GRPO-CL) ,该基线手动按难度划分训练数据集
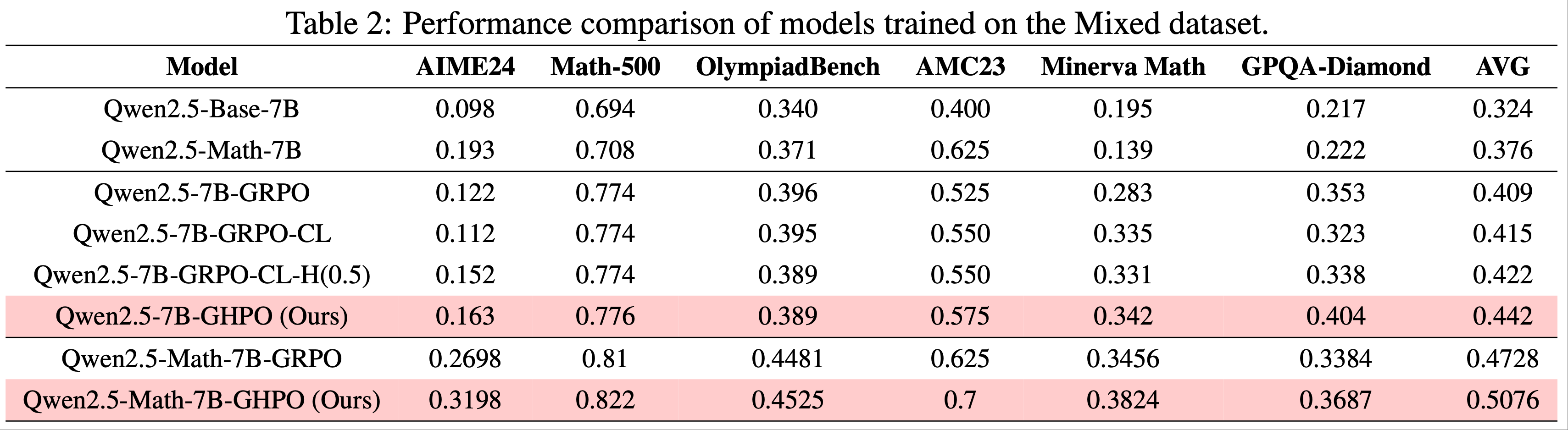
- 如表 2 所示,Qwen2.5-7B-GHPO 模型在五个基准上均优于 Qwen2.5-7B-GRPO 和 Qwen2.5-7B-GRPO-CL
- 这表明奖励稀疏性严重阻碍了有效学习,尤其是对于超出模型当前能力的问题
- 例如,在 AIME2024 问题上,GHPO 的准确率从 0.122 提升至 0.163
- 课程学习和固定 Hints 的影响(Impact curriculum learning and Fixed Hints) :
- 虽然课程学习部分解决了模型能力与问题难度不匹配的问题,但其效果始终不及 GHPO
- 在某些基准(如 AIME2024 和 GPQA-Diamond)上,课程学习的性能甚至可能比原始 GRPO 更差
- 课程学习的一个关键限制是:课程学习依赖于数据集的严格细粒度难度划分(这在实践中往往难以可靠实现)
- 论文还研究了固定 Hints 的场景,结果显示其效果低于 GHPO
- Qwen2.5-7B-GHPO-CL-H0.5 融入了固定 50% 的真实轨迹比例(针对困难问题),实验展示了标准课程学习的提升,从0.415 提升至 0.422(详情见表2),但其效果不如 GHPO
Training Dynamics
- 理解 GHPO 框架在训练期间的行为对于认识其优势至关重要
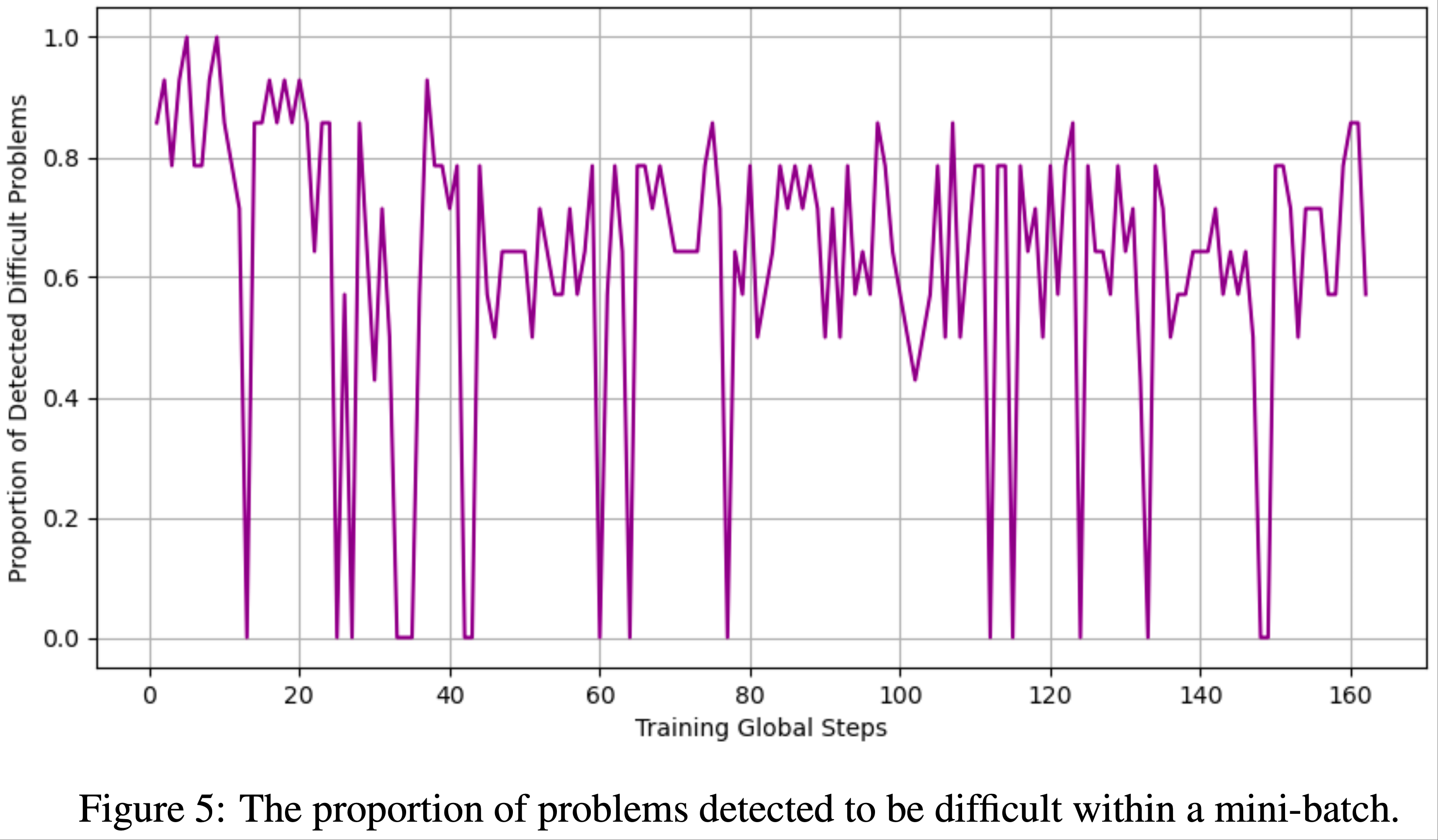
- 图 5 展示了奖励稀疏性的持续挑战:
- 图5 显示了小批次中需要添加 Hints 以缓解此问题的比例
- 在初始训练阶段,大多数问题对当前大语言模型来说过于困难(且这一趋势并未迅速减弱;)
- 即使在后续训练阶段,约 60% 的问题仍超出模型当前能力 ,凸显了奖励稀疏性在强化学习过程中的普遍性
- 为了更深入理解 GRPO 和 GHPO 在训练期间的独特行为,论文仔细检查了四个代表性指标:
- 格式奖励、准确率奖励、平均响应长度和梯度范数
- 这些动态如图 6 所示:
- 格式奖励(Format Reward) :GRPO 和 GHPO 两种算法在训练早期均达到了接近最大值的格式奖励,并始终保持高水平
- 准确率奖励 :GHPO 在所有训练阶段均表现出明显的准确率奖励优势
- 平均响应长度 :GRPO 和 GHPO 两种方法的平均响应长度均随时间稳步增加,但 GHPO 在后期生成的响应显著更长
- 梯度范数 :GHPO 的梯度范数始终显著小于 GRPO,表明其优化过程更平滑稳定
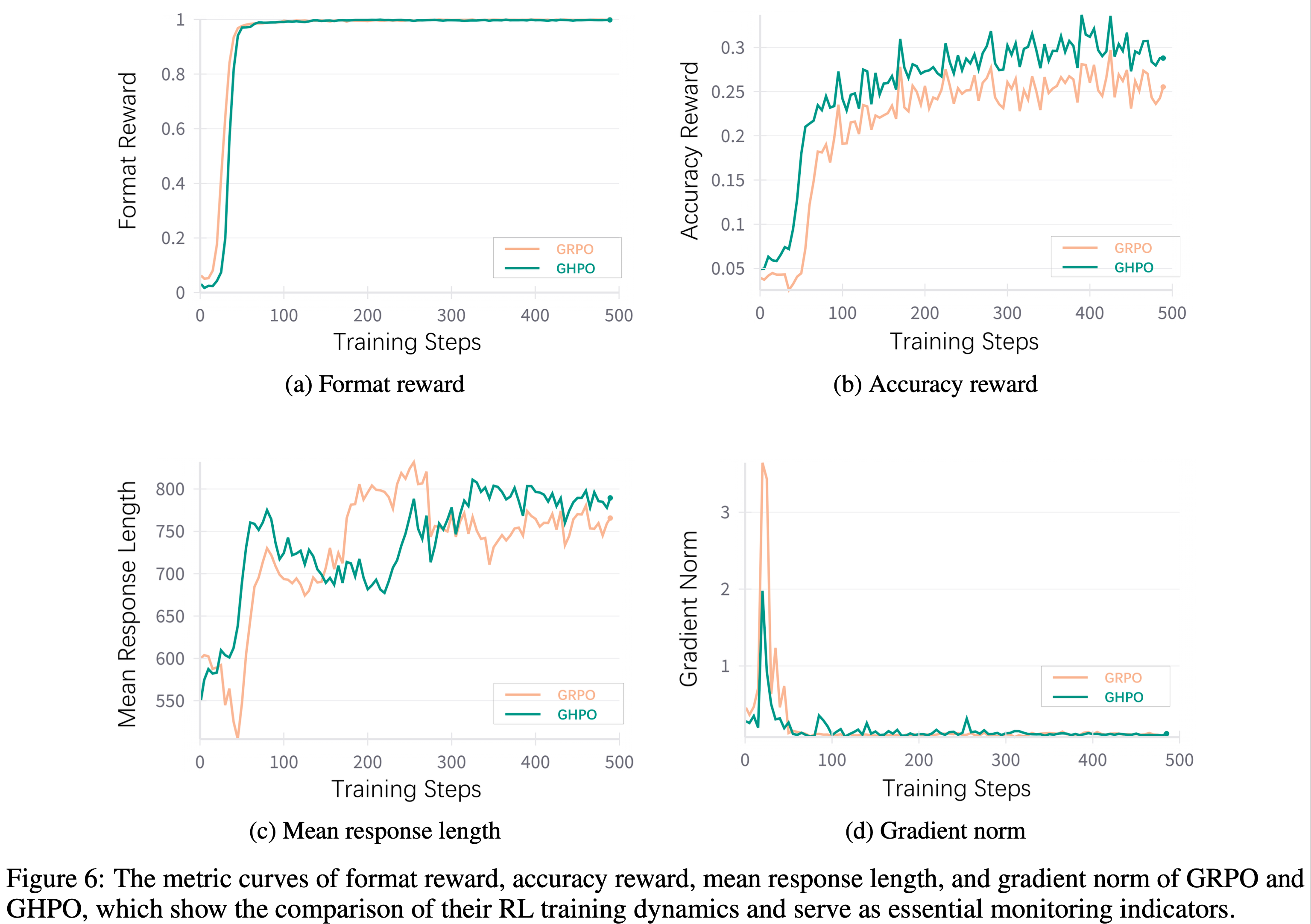
- 以上这些观察结果表明,GHPO 不仅任务性能更优 ,还能促进更详细的推理 ,并在训练过程中实现更稳定的优化轨迹
Generalization to Other Models
- 为了进一步证明论文方法的普适性和鲁棒性,论文使用更强大的基础模型 Qwen2.5-Math-7B 评估了 GHPO 的有效性
- 如表 2 所示,GHPO 始终能生成更强大的推理模型,其性能优于相同基础模型上应用的原始 GRPO 方法
- 这表明 GHPO 的适应性指导机制有效补充了高级预训练,为复杂推理任务提供了更高效的微调
Case Study
- 论文提供了一个详细案例研究,以说明 GRPO 和 GHPO 在解决一个特别困难的数学问题时的比较有效性
- 表 3 展示了该问题及其真实解答
- 在原始 GRPO 框架下,模型通常无法生成正确的推理路径,导致奖励稀疏性问题
- GHPO 通过智能使用 Hint 引导的输入解决了这一挑战
- 如表 4 所示,GHPO 通过将真实解答的前 50% 拼接至原始问题中,成功引导模型生成至少一条正确的推理路径
- 标准 GRPO 训练生成的推理路径往往偏离真实解答,导致错误答案
Related Work
- RL 在提升 LLM 的推理能力方面取得了显著成功
- DeepSeek-R1 (2025) 提出了一种纯强化学习范式,称为 Zero RL training,该方法使用简单但高效的 Rule-based 奖励模型直接从 Base LLM 进行训练
- SimpleRL-Zoo (2025) 通过在不同基础模型和规模上进行全面的实证研究,进一步探索了 Zero RL 训练的行为模式
- 一些变体方法通过优化底层机制或引入新设计元素,进一步推动了 Zero RL 训练的进展
- DAPO (2025) 从策略优化目标的角度分析了 Zero RL 训练的核心机制(DAPO 并不是特别为 Zero RL 做的吧),并提出了四项关键技术,以提高 RL 训练的效率、稳定性和生成长链思维(Chain-of-Thought, CoT)的能力
- Dr. GRPO (2025) 提出了一种无偏优化方法,从原始 GRPO 公式中移除了长度和标准差惩罚项,从而在保持强大推理性能的同时提高了标记效率
- LUFFY (2025) 通过将 Off-policy 推理演示与在策略 Zero RL 训练相结合,平衡模仿与探索,使 LLM 能够超越其固有能力的边界
- VAPO (2025) 提出了首个 value-model-based RL 训练框架(之前的都是 value-model-free),整合了七项创新技术以提升训练稳定性和整体性能
- 以上这些研究推动了 RL 在 LLM 训练中的应用,但奖励稀疏问题在复杂推理任务中仍然是一个持续存在的挑战
- 课程学习(Curriculum Learning, CL)(2025) 通过逐步引入更复杂的样本来对齐任务难度与模型能力
- DAPO (2025) 采用动态采样过滤掉模型认为过于简单或困难的问题
- 这些方法可能会丢弃大量有价值的训练数据
- 论文提出的 GHPO 方法通过自适应难度检测和 Prompt 优化机制,充分利用所有训练数据,提供了一种更高效且稳健的解决方案
附录 A:Supplementary Case
- 详情见原文