注:本文包含 AI 辅助创作
Paper Summary
- 整体总结:
- 本研究重新审视了一个基本但常被忽视的问题:GRPO 是否真的适用于多 Reward 优化
- GDPO 不同于先前主要专注于为多 Reward 强化学习设计新 Reward 函数(这些方法常常将 GRPO 作为默认优化方法)
- 论文的分析表明,将 GRPO 直接应用于求和后的 Reward,会导致不同的 Reward 组合坍缩为相同的 Advantage 值
- 这种坍缩消除了跨 Reward 维度的重要区别,导致不准确的策略更新和较弱的优化性能,并且在许多情况下可能导致早期训练失败
- Group-wise Decoupled Policy Optimization (GDPO) 是为多 Reward 强化学习量身定制的、对 GRPO 的一种简单而有效的修改
- GDPO 对每个 Reward 分别进行归一化,以保留跨 Reward 的差异,并融入 Batch-wise Advantage 归一化,以在纳入更多 Reward 时保持稳定的数值范围
- 这些改变带来了更好的收敛行为,以及能更忠实地反映预期偏好结构的模型
- 论文进一步系统地研究了如何将人类偏好优先级融入训练过程,并解释了当目标之间难度差异较大时如何调整 Reward 函数
- 通过在工具调用、数学推理和代码推理上的大量实验,论文表明 GDPO 始终优于 GRPO
- 其优势适用于不同数量的 Reward、不同的模型和不同的 Reward 函数
- 对于多 Reward 强化学习, GDPO 是比 GRPO 更稳定、更准确、与偏好更对齐的优化方法
- 背景:
- 为实现在不同场景中展现出与多样化人类偏好相一致的行为这一目标
- RL 流程已开始纳入多个奖励,每个奖励对应一种特定偏好,共同引导模型趋向期望的行为
- 问题提出:
- 近期工作默认在多奖励设置下应用 GRPO ,却未检验其适用性
- 论文证明直接将 GRPO 用于归一化不同的 rollout 奖励组合会导致它们坍缩为相同的优势值,从而降低训练信号的分辨率,导致次优收敛甚至训练早期失败
- 论文提出 Group reward-Decoupled Normalization Policy Optimization (GDPO)
- GDPO 是一种新的策略优化方法,通过解耦单个奖励的归一化来解决上述问题,从而更忠实地保留奖励间的相对差异,实现更准确的多奖励优化,并大幅提升训练稳定性
- 论文在三个任务上比较 GDPO 与 GRPO :工具调用、数学推理和代码推理,评估了正确性指标(准确率、bug 率)和约束遵循指标(格式、长度)
- 在所有设置下, GDPO 均稳定优于 GRPO ,证明了其对于多奖励强化学习优化的有效性和泛化能力
Introduction and Discussion
- 语言模型能力的持续进步,对其行为的期望也相应提高
- 要求模型不仅能提供准确的回答,还能在多样化场景中展现出与广泛人类偏好相一致的行为,这种需求在持续增长
- 这些偏好涉及效率(2025, 2025, 2025)、安全性(2024)、回答连贯性与逻辑性(2025, 2025)、性别偏见(2025)等诸多目标
- 在单一模型中满足这些异质性要求是一项具有挑战性的任务
- RL 已成为将大型语言模型与这类多样化人类偏好对齐的事实(de facto)训练流程
- 特别是,近期基于 RL 的方法已开始将多个奖励纳入训练,每个奖励被设计来捕捉不同的人类偏好,共同引导模型朝向人类偏好的行为
- 尽管对多奖励 RL 的兴趣日益增长,但近期工作(2025, 2025, 2025)主要聚焦于奖励设计本身,并且常常直接依赖 GRPO 应用于多奖励 RL 优化,通常并未检验 GRPO 是否真正适用于优化异质性奖励的组合
- 论文重新审视 GRPO 在多奖励设置下的适用性,并表明直接将 GRPO 应用于归一化不同的 rollout 奖励组合可能导致它们坍缩为相同的优势值
- 如图2所示,这实际上限制了训练信号的精度
- 这种坍缩消除了跨奖励维度的重要区分,导致不准确的策略更新、次优的奖励收敛,并且在许多情况下会导致训练早期失败
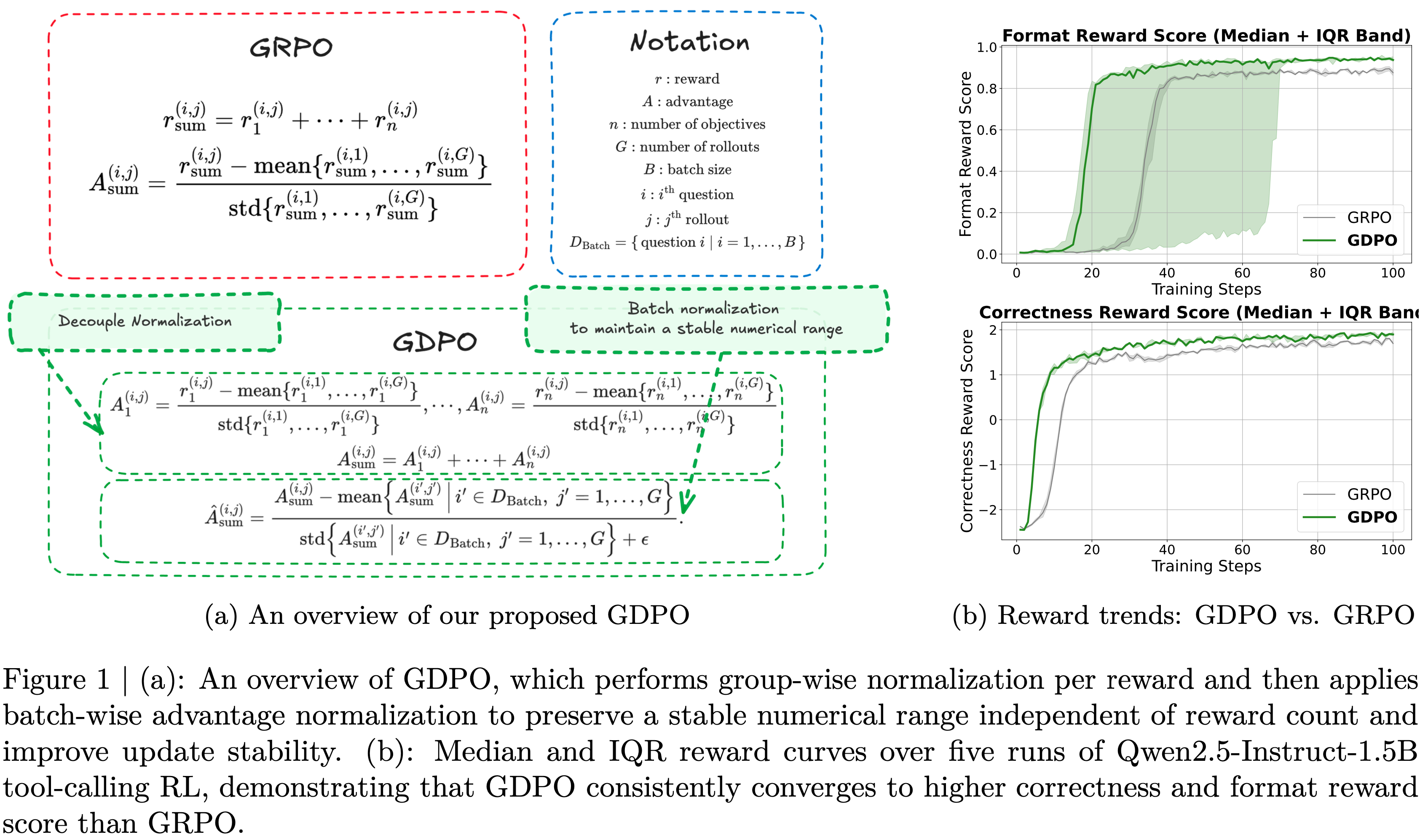
- 为克服这些挑战,论文提出了Group reward-Decoupled Normalization Policy Optimization (GDPO),该方法解耦了对每个个体奖励的组内归一化,如图 1(a) 所示,以确保不同奖励组合之间的区分得以更好保留,并能更准确地反映模型响应间的相对差异
- 这带来了更精确的多奖励优化和显著改善的训练收敛性
- 在解耦组内归一化之后,论文应用批间优势归一化,以确保优势值的大小不会随着个体奖励数量的增加而增大
- 论文在三个任务上比较了 GDPO 和 GRPO :工具调用、数学推理和代码推理
- 这些任务涵盖了广泛的目标,包括工具调用的准确性和格式正确性、数学推理的准确性和对推理长度约束的遵循,以及代码通过率和 bug 率
- 在所有任务中, GDPO 收敛得更好
- 例如,在图 1(b)中,使用 GDPO 训练 Qwen2.5-1.5B-Instruct 在工具调用任务上获得了比 GRPO 更高的正确性和格式遵循度
- 在具有挑战性的数学任务上, GDPO 也持续优于 GRPO
- 例如,使用 GDPO 训练 DeepSeek-R1-1.5B 和 Qwen3-4B-Instruct 相比 GRPO 在 AIME 上分别获得了高达 \(6.3%\) 和 \(2.3%\) 的准确率提升,同时保持更多的简短响应
- 例如,使用 GDPO 训练 DeepSeek-R1-1.5B 和 Qwen3-4B-Instruct 相比 GRPO 在 AIME 上分别获得了高达 \(6.3%\) 和 \(2.3%\) 的准确率提升,同时保持更多的简短响应
- 总而言之,这些结果证明了 GDPO 的有效性和泛化能力,表明其是多奖励 RL 优化中优于 GRPO 的更好替代方案
- 论文的贡献如下:
- GRPO 奖励坍缩分析(Analysis of GRPO reward collapse) :论文证明,天真地应用 GRPO 进行多奖励RL优化可能导致不同的rollout奖励组合坍缩为相同的优势值,从而削弱学习信号的分辨率
- GRPO 奖励坍缩的修正(Remediation of GRPO reward collapse) :论文提出 GDPO ,该方法对每个奖励分别执行组间解耦归一化,以更好地保留跨奖励的区分,实现更准确的多奖励优化
- 除了 GDPO 之外,论文还系统性概述了如何修改奖励函数和调整奖励权重,以更忠实地符合不同优先级的人类偏好
- 论文在三个任务上进行了广泛的实验:工具调用、数学推理和代码推理,并比较了 GDPO 在优化对应准确性、格式正确性、长度约束和代码质量等广泛奖励方面的有效性。在所有设置下, GDPO 均一致地优于 GRPO ,展现出改进的训练收敛性和更强的下游性能,更紧密地符合多样化偏好集
GRPO ‘s propensity for reward signal collapse in multi-reward RL(注:GRPO 在多奖励 RL 中有导致奖励信号坍缩的倾向)
- GRPO (2024)及其变体,包括 DAPO(2025)和 REINFORCE++(或 REINFORCE++ Baseline)(2025),由于效率高且简单,已成为广泛采用的强化学习算法
- 与 PPO(2017)相比, GRPO 通过利用组相对优势估计进行策略更新,消除了对价值模型的需求
- 目前, GRPO 主要用于优化单目标奖励,通常聚焦于准确性
- 然而,随着模型能力持续增长,近期的研究工作越来越多地寻求在准确性之外优化多个奖励,例如响应长度约束和格式质量(2025, 2024, 2025),以更好地与人类偏好对齐
- 现有的多奖励RL方法通常采用一个直接的策略:将所有奖励分量求和,然后直接应用 GRPO
- 形式上,对于给定的问答对 \((q_{i},o_{j})\),其中行为策略 \(\pi_{\theta_{\text{old} } }\) 采样一组 \(G\) 个响应 \(\{o_{j}\}_{j=1}^{G}\),并假设有 \(n\) 个目标,第 \(j\) 个响应的聚合奖励计算为每个目标奖励的总和:
$$r_{\text{sum} }^{(i,j)}=r_{1}^{(i,j)}+\cdots+r_{n}^{(i,j)} \tag{1}$$ - 然后,通过对组级聚合奖励进行归一化来获得第 \(j\) 个响应的组相对优势:
$$A_{\text{sum} }^{(i,j)}=\frac{r_{\text{sum} }^{(i,j)}-\text{mean}\{r_{\text{sum} }^{(i,1)},\ldots,r_{\text{sum} }^{(i,G)}\} }{\text{std}\{r_{\text{sum} }^{(i,1)},\ldots,r_{\text{sum} }^{(i,G)}\} } \tag{2}$$ - 相应的多奖励 GRPO 优化目标可以表达为:
$$\mathcal{J}_{\text{ GRPO } }(\theta)=\mathbb{E}_{(q_{i},o_{j})\sim D, \{o_{j}\}_{j=1}^{G},\sim\pi_{\theta_{\text{old} } }(\cdot|q)}\left[\frac{1}{G}\sum_{j=1}^{G}\frac{1}{|o_{j}|}\sum_{t=1}^{|o_{j}|}\min\left(s_{i,t}(\theta),A_{\text{sum} }^{(i,j)},\text{clip}(s_{i,t}(\theta),1-\epsilon,1+\epsilon),A_{\text{sum} }^{(i,j)}\right)\right] \tag{3}$$- 其中 \(s_{t}(\theta)=\frac{\pi_{\theta}(o_{j}^{\dagger},|,q,o_{j}^{ < t})}{\pi_{\theta_{\text{old} } }(o_{j}^{\dagger},|,q,o_{j}^{>t})}\),\(\epsilon\) 表示裁剪阈值
- 为清晰起见,在此公式中论文省略了 KL 散度损失项
- 论文首先重新审视这种应用 GRPO 进行多奖励 RL 优化的常见做法,并发现一个先前被忽视的问题,即 GRPO 固有地压缩了奖励信号,导致优势估计中的信息丢失
- 为说明这一点,论文从简单的训练设置开始,然后扩展到更一般的情况
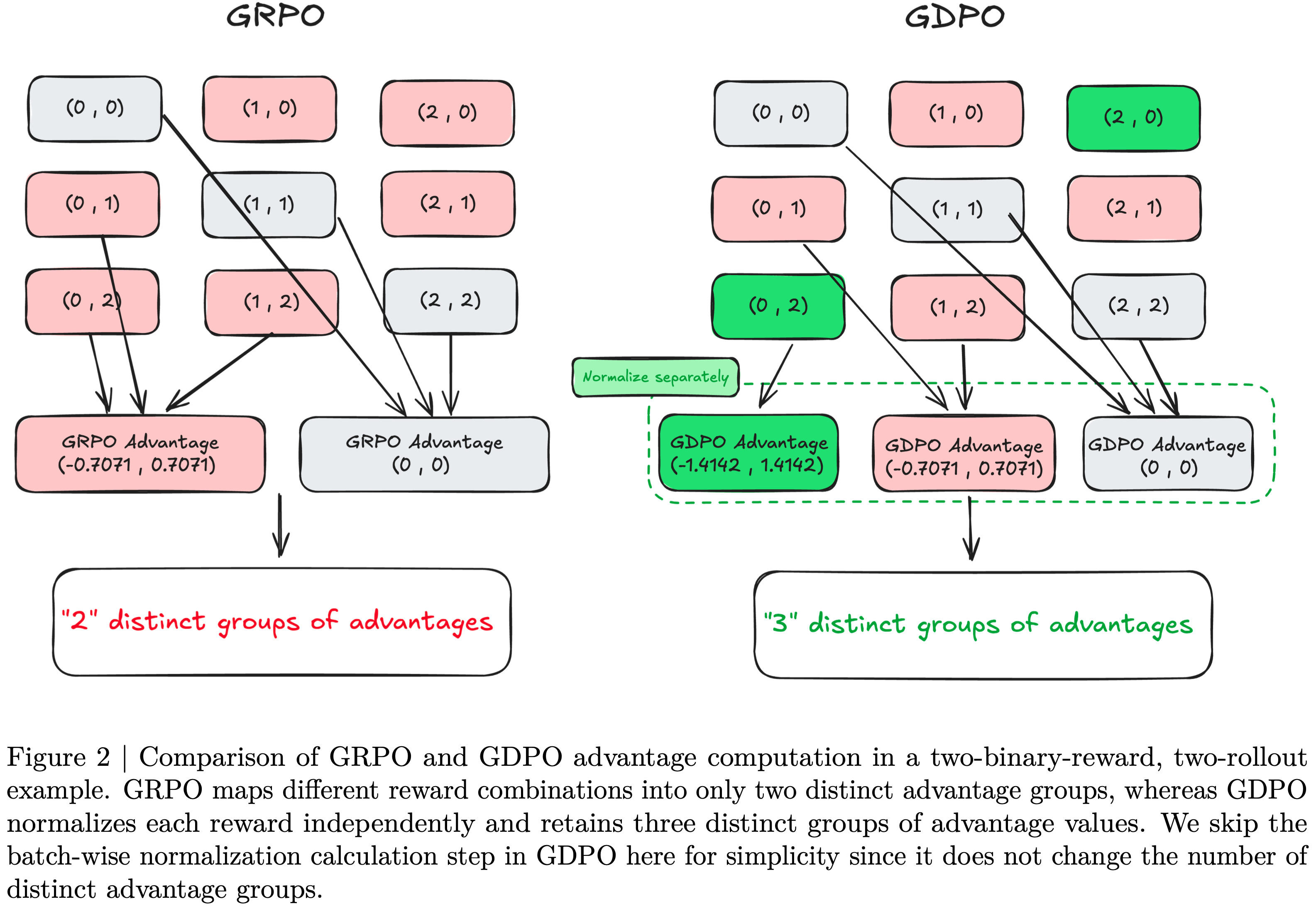
- 考虑一个场景,论文为每个问题生成两个 Rollout 用于计算组相对优势,任务涉及两个二元奖励 \(r_{1},r_{2}\in\{0,1\}\)
- 因此,每个 Rollout 的总奖励可以取值为 \(\{0,1,2\}\)
- 如图 2 所示,论文枚举了组内所有可能的 Rollout 奖励组合,表示为(Rollout 1 的总奖励, rollout 2 的总奖励)以及对应的归一化优势为(rollout 1 的归一化优势, rollout 2 的归一化优势)

- 尽管忽略顺序时有六种不同的组合,但在应用组内奖励归一化后,只出现两个独特优势组
- 具体来说,\((0,1)\)、\((0,2)\) 和 \((1,2)\) 产生相同的归一化优势 \(A_{\text{sum} }\),为 \((-0.7071,\ 0.7071)\),而 \((0,0)\)、\((1,1)\) 和 \((2,2)\) 都导致 \((0,0)\)
- 这揭示了 GRPO 在多奖励优化中优势计算的根本局限性,即过度压缩了丰富的组内奖励信号
- 直观上,\((0,2)\) 应该比 \((0,1)\) 产生更强的学习信号,因为总奖励为2表示同时满足两个奖励,而奖励为 1 仅对应达成一个奖励
- 因此,当另一个rollout只获得零奖励时,\((0,2)\) 应该比 \((0,1)\) 产生更大的相对优势
- 这种局限性还可能因不准确的优势估计而引入训练不稳定的风险
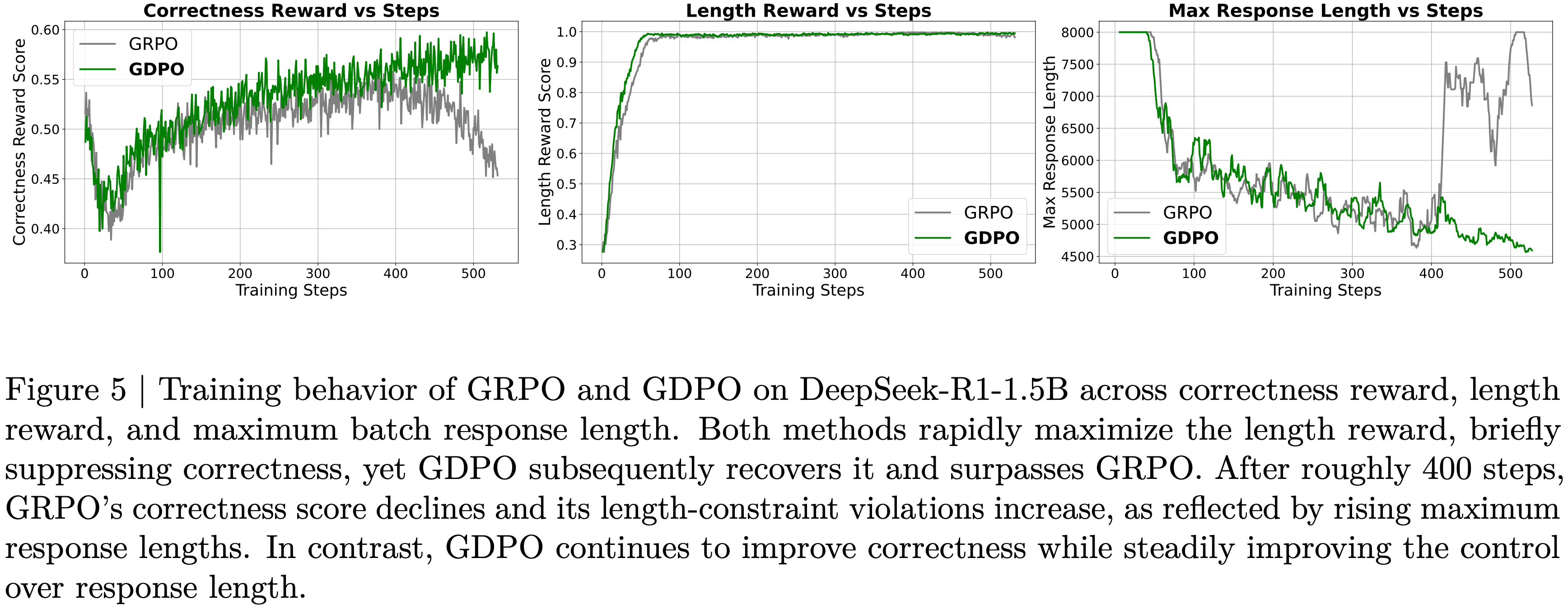
- 如图 5 所示,使用 GRPO 训练时,正确性奖励分数在大约 400 个训练步后开始下降,表明发生了部分训练坍缩
- 最近,Dr.GRPO (2025)和 DeepSeek-v3.2(2025)采用了一种 GRPO 变体,从公式(2)中去除了标准差归一化项,使得
$$ A_{\text{sum} }^{(i,j)}=r_{\text{sum} }^{(i,j)}-\text{mean}\{r_{\text{sum} }^{(i,1)},\ldots,r_{\text{sum} }^{(i,G)}\}$$ - 这些工作引入此修改以缓解问题级难度偏差,但乍看之下,这个改变似乎也能解决论文识别的问题
- 具体来说,去除标准差归一化确实缓解了该问题:\((0,1)\) 和 \((0,2)\) 现在分别产生不同的优势 \((-0.5,0.5)\) 和 \((-1.0,1.0)\)
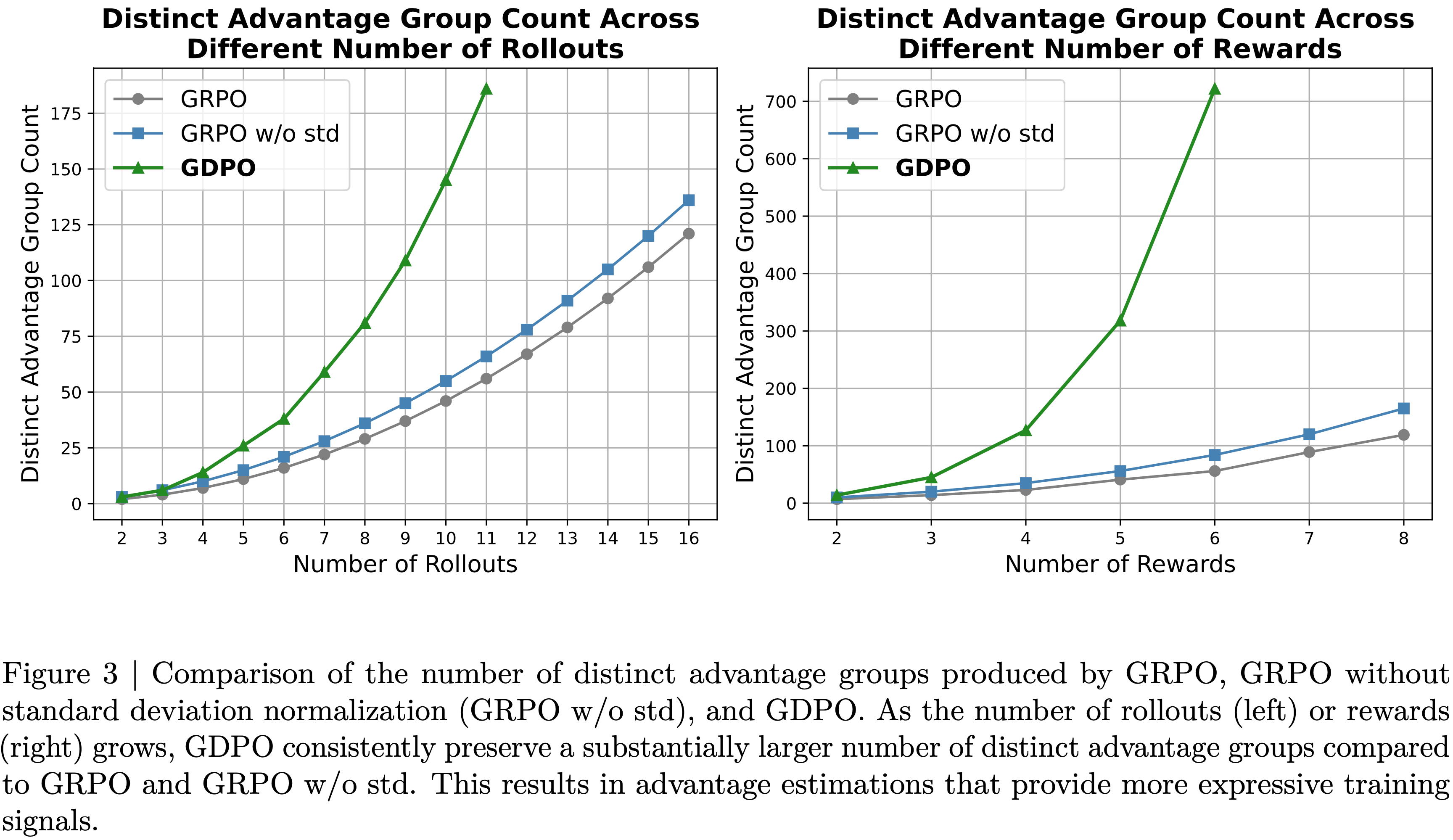
- 然而,当将此设置推广到更多rollout同时保持奖励数量固定时,如图 3 所示,论文观察到与 GRPO 相比,这种修复仅略微增加了独特优势组的数量
- 在 Rollout 数量固定为四个,但奖励数量逐渐增加的情况下,也能观察到类似的趋势
- 在这种情况下,论文也只观察到独特优势组数量有适度的改善
- 论文在第4.1.1节中经验性地检验了去除标准差归一化项的有效性,发现此修改并未带来改进的收敛性或更好的下游评估性能
Method
Group reward-Decoupled normalization Policy Optimization
- 为克服这些挑战,论文提出了Group reward-Decoupled Normalization Policy Optimization (GDPO)
- 这是一种旨在更好地保持不同奖励组合之间的区分,并更准确地捕捉其在最终优势中的相对差异的方法
- 与 GRPO 直接对聚合奖励总和应用组内归一化不同, GDPO 通过先对每个奖励分别执行组内归一化再进行聚合来解耦此过程
- 具体而言, GDPO 不是先对所有 \(n\) 个奖励求和(如公式(1)),然后应用组内归一化获得 \(A_{\text{sum} }\)(公式(2)),而是计算第 \(i\) 个问题第 \(j\) 个rollout的每个奖励的归一化优势:
$$A_{1}^{(i,j)}=\frac{r_{1}^{(i,j)}-\text{mean}\{r_{1}^{(i,1)},\ldots,r_{1}^{(i,G)}\} }{\text{std}\{r_{1}^{(i,1)},\ldots,r_{1}^{(i,G)}\} },\quad\ldots,\quad A_{n}^{(i,j)}=\frac{r_{n}^{(i,j)}-\text{mean}\{r_{n}^{(i,1)},\ldots,r_{n}^{(i,G)}\} }{\text{std}\{r_{n}^{(i,1)},\ldots,r_{n}^{(i,G)}\} } \tag{4}$$ - 用于策略更新的整体优势随后通过首先对所有目标的归一化优势求和获得:
$$A_{\text{sum} }^{(i,j)}=A_{1}^{(i,j)}+\cdots+A_{n}^{(i,j)} \tag{5}$$- 注意:这里优势和是直接相加的,实际中,可能还可以根据不同维度 Rule/RM 的重要性进行加权缩放?
- 然后,对多奖励优势的和应用批间优势归一化,以确保最终优势 \(\hat{A}_{\text{sum} }^{(i,j)}\) 的数值范围保持稳定,且不会随着引入额外奖励而增长:
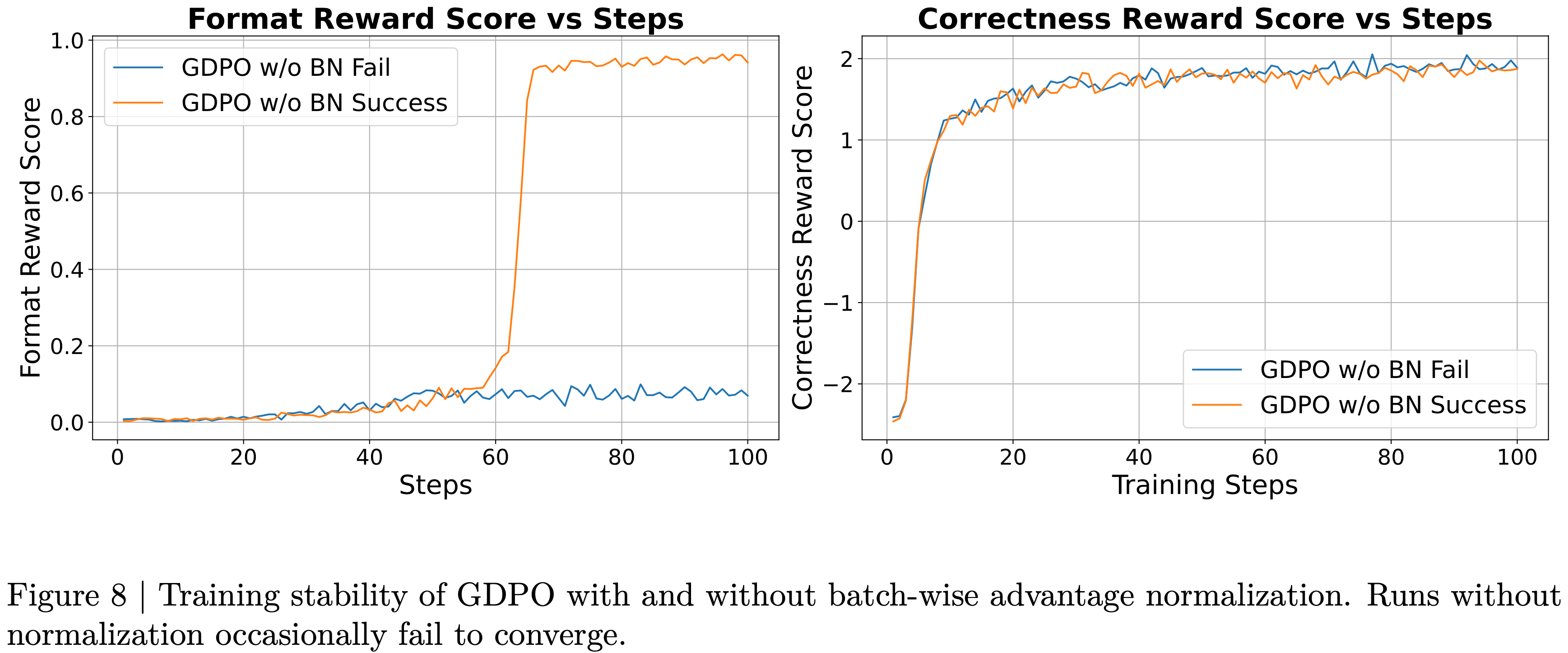
$$\hat{A}_{\text{sum} }^{(i,j)}=\frac{A_{\text{sum} }^{(i,j)}-\text{mean}\left\{A_{\text{sum} }^{(i^{\prime},j^{\prime})}\mid i^{\prime}\in D_{\text{Batch} },j^{\prime}=1,\ldots,G \right\} }{\text{std} \left\{A_{\text{sum} }^{(i^{\prime},j^{\prime})}\mid i^{\prime}\in D_{\text{Batch} },j^{\prime}=1,\ldots,G \right\}+\epsilon} \tag{6}$$ - 经验上,论文还发现这个归一化步骤提高了训练稳定性,如附录 A 所示,其中去除批间归一化偶尔会导致收敛失败
- 通过分离每个奖励的归一化, GDPO 缓解了 GRPO 优势估计中存在的信息丢失问题,如图 2 所示
- 请注意,由于 GDPO 中的批间归一化步骤不会改变不同优势组的数量,为清晰起见,论文在此省略

- 请注意,由于 GDPO 中的批间归一化步骤不会改变不同优势组的数量,为清晰起见,论文在此省略
- 从图中可以看出,当采用 GRPO 时,不同的奖励组合,例如 \((0,2)\) 和 \((0,1)\),会导致相同的归一化优势,掩盖了它们之间的细微差别
- 相比之下, GDPO 通过为每个组合分配不同的优势值来保留这些细粒度差异,例如,\((0,1)\) 的奖励组合在 GDPO 归一化后变为 \((-0.7071,0.7071)\),而 \((0,2)\) 变为 \((-1.4142,1.4142)\),这更恰当地反映了 \((0,2)\) 应比 \((0,1)\) 产生更强的学习信号
- 类似地,当将 rollout 数量扩展到三个时, GRPO 会将优势值 \((0,0,0)\) 分配给 \((1,1,1)\)
- 然而,\((1,1,1)\) 可能由异质的奖励分配产生,例如 \(r_{1}=(1,1,0)\) 或 \(r_{2}=(0,0,1)\),而 GDPO 将产生非零优势,从而保留了跨奖励维度的有意义的差异
- 论文通过比较 GDPO 、 GRPO 和去除标准差的 GRPO 在两种实验设置下的独特优势组数量,进一步量化了 GDPO 的有效性,如图 3 所示
- 在奖励数量为两个且 rollout 数量变化的情况下, GDPO 始终产生显著更多的独特优势组数量,并且随着 rollout 数量增加,差距扩大
- 另一方面,当固定 rollout 数量为四个并增加奖励数量时,也出现了类似的模式, GDPO 随着目标数量增长展现出逐渐增大的优势粒度
- 这证明了解耦归一化方法有效地增加了所有 RL 设置中独特优势组的数量,并实现了更精确的优势估计
- 除了这些理论改进之外,论文观察到使用 GDPO 始终能产生更稳定的训练曲线和改善的收敛性,例如:
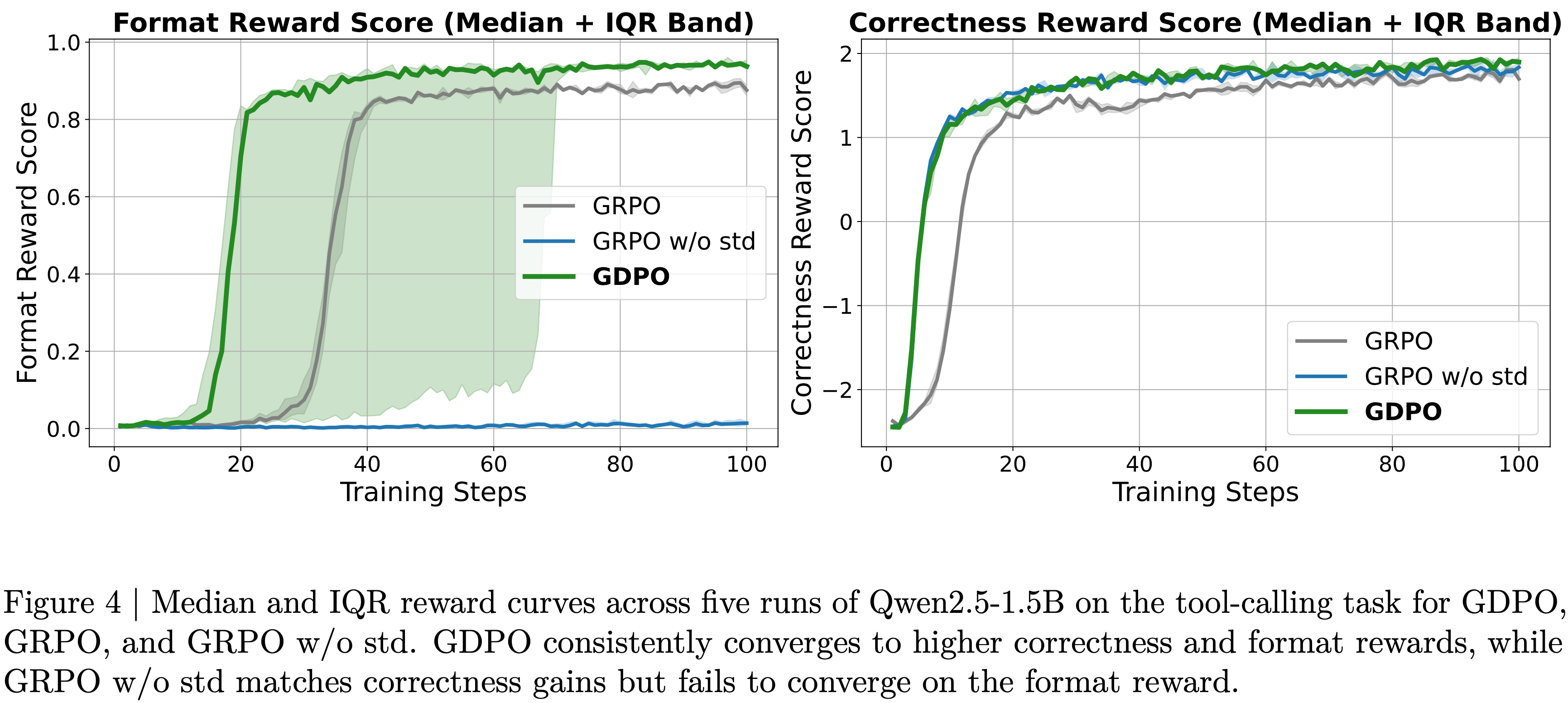
- 如图 4 所示, GDPO 在 工具调用任务 的格式奖励和正确性奖励上都实现了更好的收敛
- 如图 5 所示, GDPO 也消除了在 数学推理任务 中观察到的 GRPO 训练坍缩问题,其中使用 GDPO 训练的模型在整个训练过程中持续改进正确性奖励分数
- 第4节中的额外实证结果进一步证实了 GDPO 在广泛下游任务中实现与目标偏好更强对齐的能力

Effective incorporation of priority variation(考虑优先级差异)
- 到目前为止,论文假设所有目标同等重要
- 实际上,这个假设在现实应用中并不总是成立
- 在本节中,论文系统性地概述了如何调整与不同目标相关的奖励权重或修改奖励函数,以强制优先处理更重要的目标
- 论文还讨论了当基础奖励在难度上差异显著时,这两种设计选择的不同表现
- 常见的做法是为每个奖励分配不同的权重,以编码目标间的不同优先级,使得 \(r_{\text{sum} }=w_{1}r_{1}+\cdots+w_{n}r_{n}\),从而控制每个奖励对用于策略更新的最终优势的贡献
- 对于 GDPO ,此类权重应用于每个奖励的归一化优势,如下:
$$A_{\text{sum} }^{(i,j)}=w_{1}A_{1}^{(i,j)}+\cdots+w_{n}A_{n}^{(i,j)} \tag{7}$$ - 然而,论文发现,当基础目标的难度水平差异显著时,调整奖励权重并不总能产生预期的行为
- 如果一个目标比其他目标容易得多,模型往往会专注于最大化该目标的奖励 ,而不管分配的权重如何
- 因此,为了更有效地迫使模型分配更多注意力到更具挑战性的目标相关的奖励,必须使权重差异足够大以补偿难度差距
- 然而,即使进行此类调整,模型可能仍然倾向于优化更容易的奖励,而不是用户意图优先的目标,这一现象论文将在第4.2.1节进行经验性展示
- 因此,一些近期工作(2025,2024)通过将较容易的奖励条件化于较难的奖励来解决此类 Reward Hacking 问题
- 具体来说,给定两个奖励 \(r_{k}\) 和 \(r_{l}\),将 \(r_{k}\) 条件化于 \(r_{l}\) 可以表述为:
$$r_{k}=\begin{cases}r_{k},&\text{if }r_{l}\geq t\\ 0,&\text{otherwise}.\end{cases} \tag{8}$$ - 通过这样的奖励函数设计,模型只有在奖励 \(r_{l}\) 满足预定义的分数阈值 \(t\) 时才能获得 \(r_{k}\) 的奖励,因此,模型被迫首先最大化人类优先的奖励,从而完全缓解上述问题
- 这种策略的经验有效性展示在第 4.2.1 节,其中使用条件化奖励函数训练的模型,相比仅对优先奖励分配更大权重而未使用条件化的模型,在优先目标上实现了更高的性能
- 论文还观察到,在解决了较易奖励占主导的问题之后,为细粒度优先级调整分配不同的奖励权重也能更忠实地反映在最终模型行为中
- 具体来说,给定两个奖励 \(r_{k}\) 和 \(r_{l}\),将 \(r_{k}\) 条件化于 \(r_{l}\) 可以表述为:
Experiments
- 论文首先在工具调用任务上评估 GDPO 与 GRPO 的有效性(第 4.1 节),该任务涉及优化两个 Reward:
- 工具调用正确性和格式符合性
- Next, 论文进行了一项消融研究,检验了带或不带标准差归一化的 GRPO 的训练收敛性和下游性能
- 然后论文在数学推理任务上比较了 GDPO 和 GRPO ,该任务优化了两个隐含竞争的 Reward:
- 准确性和长度约束(第 4.2 节)
- 论文进一步广泛分析了融入不同 Reward 权重和修改 Reward 函数以更好地反映人类偏好中不同优先级的影响,特别是在 Reward 难度差异显著时
- Finally,论文将优化的 Reward 数量扩展到三个,并在代码推理任务上比较了 GRPO 和 GDPO (第 4.3 节),联合优化了代码生成准确性、对长度约束的遵守程度以及缺陷率,进一步证明了 GDPO 能有效推广到具有三个 Reward 目标的任务场景
Tool calling
- 论文遵循 ToolRL (2025) 的设置,在工具调用任务上比较 GDPO 与 GRPO
- 具体来说,模型被训练学习如何将外部工具整合到推理轨迹中,以按照附录 B 所示的输出格式解决用户任务,其中推理步骤必须包裹在
<think></think>中,工具调用必须出现在<tool_call></tool_call>内,而模型的最终答案必须放置在<response></response>内 - 论文采用与 ToolRL 相同的训练集进行 RL 训练,该数据集包含来自 ToolACE (2024) 的 2k 个样本、来自 Hammar (2024) 的 1k 个样本和来自 xLAM (2025) 的 1k 个样本
- 每个训练实例包含一个问题及其对应的真实工具调用
- 训练涉及两个 Reward:
- 格式 Reward (Format reward) : 格式 Reward \( \mathcal{R}_{\text{format} } \in \{0,1\} \) 检查模型输出是否满足所需的结构,并是否以正确的顺序包含所有必要的字段
- 正确性 Reward (Correctness reward) : 正确性 Reward \( \mathcal{R}_{\text{correct} } \in [-3,, 3] \) 使用三个指标将模型生成的工具调用与真实调用进行比较:工具名称匹配、参数名称匹配和参数内容匹配
- Reward 公式的完整描述见附录 C
- 论文使用 verl (2024) 框架,按照 ToolRL 的 GRPO 配方中的原始超参数设置,使用 GRPO 和 GDPO 训练 Qwen-2.5-Instruct(1.5B 和 3B)(2025) 100 个 step
- 每个训练问题使用 4 个 Rollout,Batch 大小为 512,最大 Response 长度为 1024
- 完整的超参数配置列于附录 D
- 论文在伯克利函数调用排行榜(BFCL-v3)上评估训练好的模型,这是一个涵盖广泛挑战的综合基准测试,包括单步推理、多步工具使用、实时执行、无关工具拒绝、同时多工具选择和多工具执行
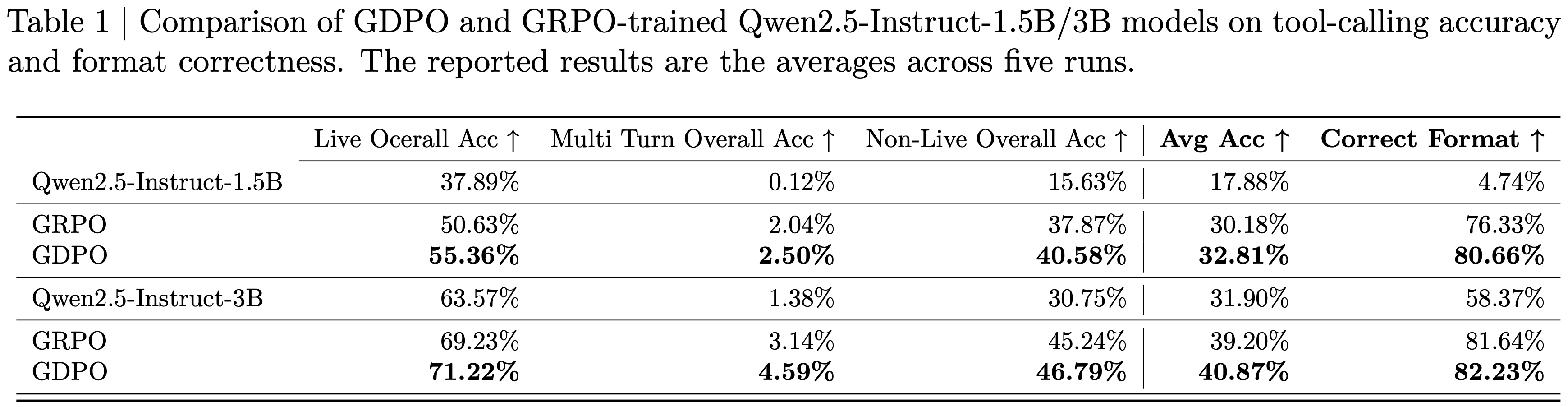
- 论文用 GRPO 和 GDPO 对模型进行了五次微调,并在表 1 中报告了在 BFCL-v3 上的平均准确率和平均格式正确率
- 此外,论文在图 4 中绘制了两种方法在五次运行中的训练曲线中位数和四分位距

- 从训练曲线中,论文观察到在所有运行中, GDPO 在格式和正确性 Reward 得分上都持续收敛到更高的值
- 尽管 GDPO 在格式 Reward 上的收敛所需 step 数方面表现出更大的方差,但最终获得的格式符合性仍优于 GRPO
- 对于正确性 Reward, GDPO 在早期阶段显示出更快的改进,并在后期阶段达到比 GRPO 基线更高的 Reward 分数,这证明了 GDPO 在提供更准确的 Advantage 估计从而实现更好优化方面的有效性
- 在表 1 所示的 BFCL-v3 评估中,与 GRPO 训练的模型相比, GDPO 也持续提高了平均工具调用准确率和格式正确率
- 在训练 Qwen2.5-Instruct-1.5B 时,与 GRPO 相比, GDPO 在实时/非实时任务上的准确率提升了近 5% 和 3%,整体平均准确率提升了约 2.7%,正确格式比率提升了 4% 以上
- 在 3B 模型上也观察到了类似的改进, GDPO 在所有子任务上继续优于 GRPO ,实现了高达 2% 的准确率提升,并提供了更好的格式符合率
Does removing the standard deviation normalization term in GRPO provide any benefit?
- 从图 3 回顾可知,移除 GRPO 中的标准差归一化项(记为 GRPO w/o std)会略微增加不同 Advantage 组的数量

- 在本节中,论文从经验上检验了这种修改的有效性。遵循之前的实验,论文运行 GRPO w/o std 五次,并报告在 BFCL-v3 上的平均准确率和平均格式正确率
- 在图 1(b) (注:需要结合图 4 看)所示的 Reward 训练曲线中,论文观察到,尽管 GRPO w/o std 收敛到的正确性 Reward 与 GDPO 相似且高于标准 GRPO ,但它完全未能改进格式 Reward

- 这种失败导致了在 BFCL-v3 上 0% 的正确格式比率(见表 2),表明模型没有学会所需的输出结构
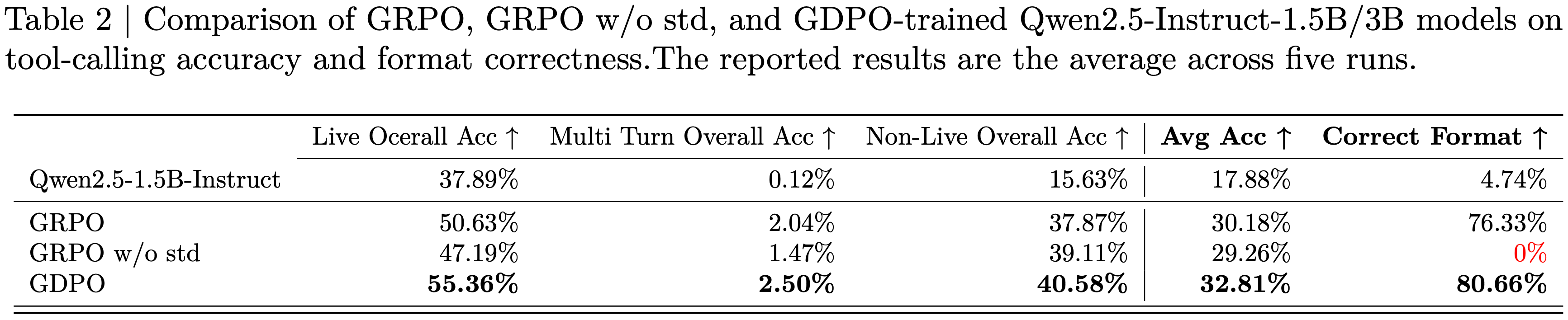
- 这也表明,仅仅为了增加 Advantage 多样性而移除标准差归一化项,可能会给训练带来不稳定性,最终可能阻止多 Reward 强化学习的成功收敛
Mathematical reasoning
- 论文考虑一个数学推理任务,它优化两个隐含竞争的 Reward:
- 准确性和对长度约束的遵守(accuracy and adherence to a length constraint)
- 目标是提高模型在具有挑战性的数学问题上的性能,同时将生成的输出保持在预定义的 Response 长度内 ,以鼓励高效的问题解决
- 论文使用 GRPO 和 GDPO 在 DeepScaleR-Preview 数据集 (2025) 上训练 DeepSeek-R1-1.5B、DeepSeek-R1-7B (2025) 和 Qwen3-4B-Instruct (2025) 500 个 step,该数据集包含 40K 个竞赛级数学问题
- 训练使用 verl (2024) 进行,论文遵循原始的 DeepSeek-R1 提示格式 (2025)
- 遵循 DLER 设置 (2025),论文融入了动态采样、更高的 Clipping 阈值以及来自 DAPO (2025) 的 Token 平均损失,并使用 16 个 Rollout,Batch 大小为 512,最大 Response 长度为 8000 个 Token
- 完整的超参数集在附录 E 中提供
- 训练使用两个 Reward:
- 长度 Reward (Length reward) : 长度 Reward \( \mathcal{R}_{\text{length} } \in \{0,1\} \) 检查模型的输出是否保持在目标长度 \( l \) 内,在所有后续实验中设置为 4000 个 Token:
$$
\mathcal{R}_{\text{length} }=\begin{cases}1, &\text{if response length}\leq l\\ 0, &\text{otherwise.}\end{cases}
$$ - 正确性 Reward (Correctness reward) : 正确性 Reward \( \mathcal{R}_{\text{correct} } \in \{0,1\} \) 表示从模型 Response 中提取的最终答案是否与真实答案匹配
- 长度 Reward (Length reward) : 长度 Reward \( \mathcal{R}_{\text{length} } \in \{0,1\} \) 检查模型的输出是否保持在目标长度 \( l \) 内,在所有后续实验中设置为 4000 个 Token:
- 论文在 AIME-24 (2024)、AMC(AMC 2022 和 AMC 2023)(2024)、MATH (2021)、Minerva (2022) 和 Olympiad Bench (2024) 上比较了 GRPO 和 GDPO 训练的模型
- 所有评估均使用 vLLM 作为推理后端,采样温度为 0.6,\( top_{p}=0.95 \),最大 Response 长度为 32k 个 Token
- 对于每个评估问题,论文生成 16 个样本,并报告平均 pass@1 分数和平均超长比率(记为 Exceed),该比率衡量模型 Response 超过预定义长度限制(4000 个 Token)的百分比
- 从图 5 所示的 GRPO 和 GDPO 在 DeepSeek-R1-1.5B 上的训练曲线中
- 论文首先观察到,无论使用哪种优化方法,模型都倾向于最大化较容易的 Reward。在这种情况下,长度 Reward 更容易优化, GRPO 和 GDPO 在大约前 100 个训练 step 内都达到了满分长度分数
- 论文还看到,长度 Reward 的快速上升与正确性 Reward 的早期下降同时发生,这表明两个 Reward 在竞争
- 在训练的初始阶段,模型优先满足长度约束,通常以牺牲更具挑战性的正确性目标为代价
- 然而,从正确性 Reward 的轨迹来看,论文观察到 GDPO 比 GRPO 更有效地恢复了正确性 Reward,在可比的训练 step 数上取得了更高的正确性分数
- 论文还看到, GRPO 训练在 400 步后开始变得不稳定,正确性 Reward 分数逐渐下降,而 GDPO 则继续提高正确性分数
- 此外,尽管 GDPO 和 GRPO 在整个训练过程中都保持了近乎完美的长度分数,论文还记录了每个训练 Batch 内的最大 Response 长度,以评估模型在更极端情况下对长度约束的遵守程度
- 结果显示,尽管获得了几乎满分的长度 Reward,但 GRPO 的最大 Response 长度在大约 400 个训练 step 后开始急剧增加,而 GDPO 的最大 Response 长度继续下降

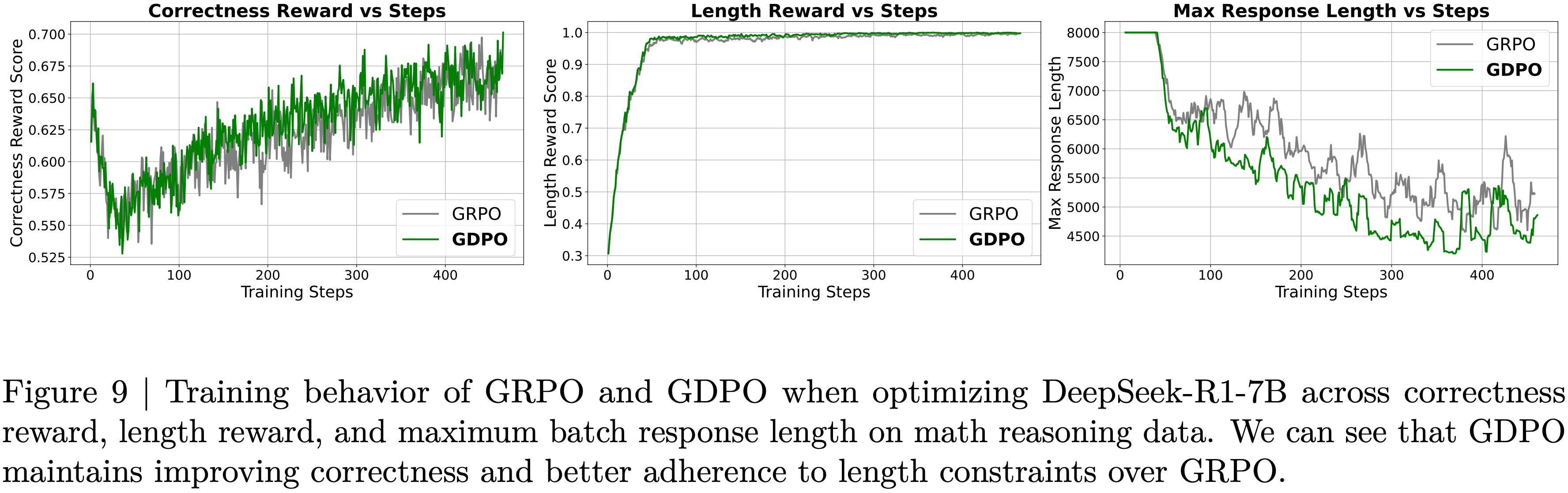
- 在附录中的图 9 和图 10 中,在 DeepSeek-R1-7B 和 Qwen3-4B-Instruct 的训练曲线上也观察到了类似的情况,我们可以看到 GDPO 始终能提供更好的长度约束对齐
- 这种对比进一步说明了 GDPO 在多 Reward 优化方面相较于 GRPO 的有效性
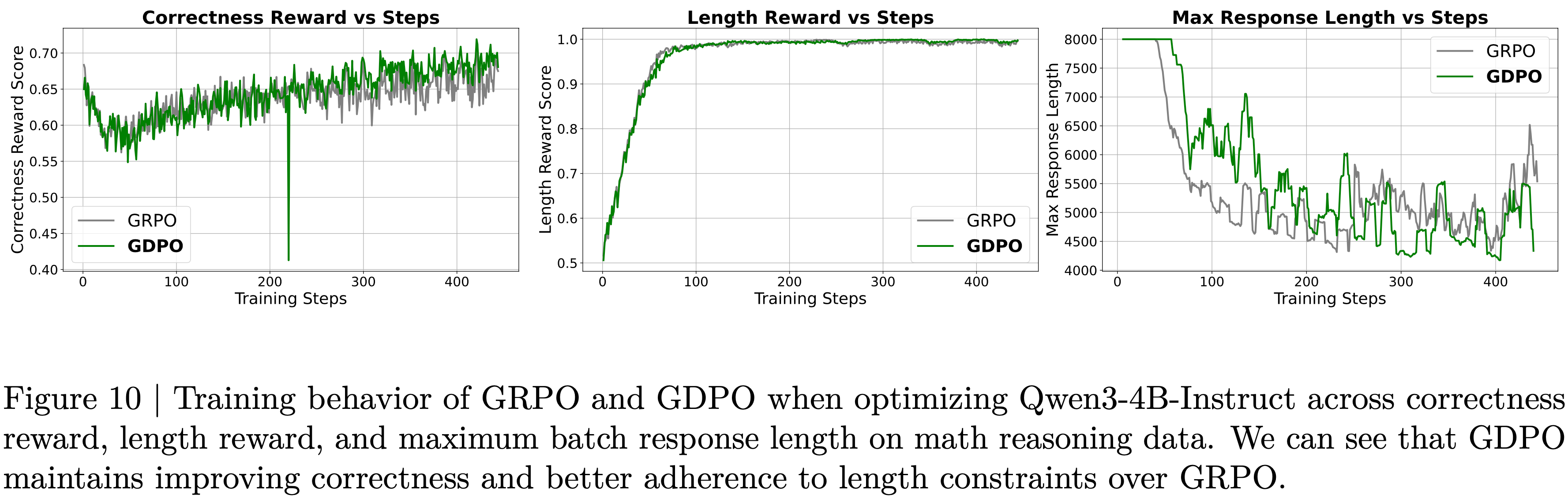
- 这种对比进一步说明了 GDPO 在多 Reward 优化方面相较于 GRPO 的有效性
- 此外,表 3 中的基准测试结果表明, GDPO 训练的模型不仅在推理效率上相比原始模型有显著提高(在 AIME 上超长比率降低了高达 80%),而且在大多数任务上实现了更高的准确性
- 而且, GDPO 在准确性和长度约束目标上通常都优于 GRPO
- 对于 DeepSeek-R1-1.5B, GDPO 在所有基准测试中都优于 GRPO ,在 MATH、AIME 和 Olympiad 上的准确率分别提高了 2.6%/6.7%/2.3%,同时也在所有任务中降低了超长比率
- 问题:数字似乎没有严格对上?
- 类似的趋势也适用于 DeepSeek-R1-7B 和 Qwen3-4B-Instruct, GDPO 实现了更强的准确性-效率权衡
- 在更具挑战性的 AIME 基准测试上,收益尤为显著:与 GRPO 下 DeepSeek-R1-7B 和 Qwen3-4B-Instruct 分别为 2.1% 和 2.5% 的超长率相比, GDPO 将准确率提高了近 3%,同时将超长率降至 0.2% 和 0.1%
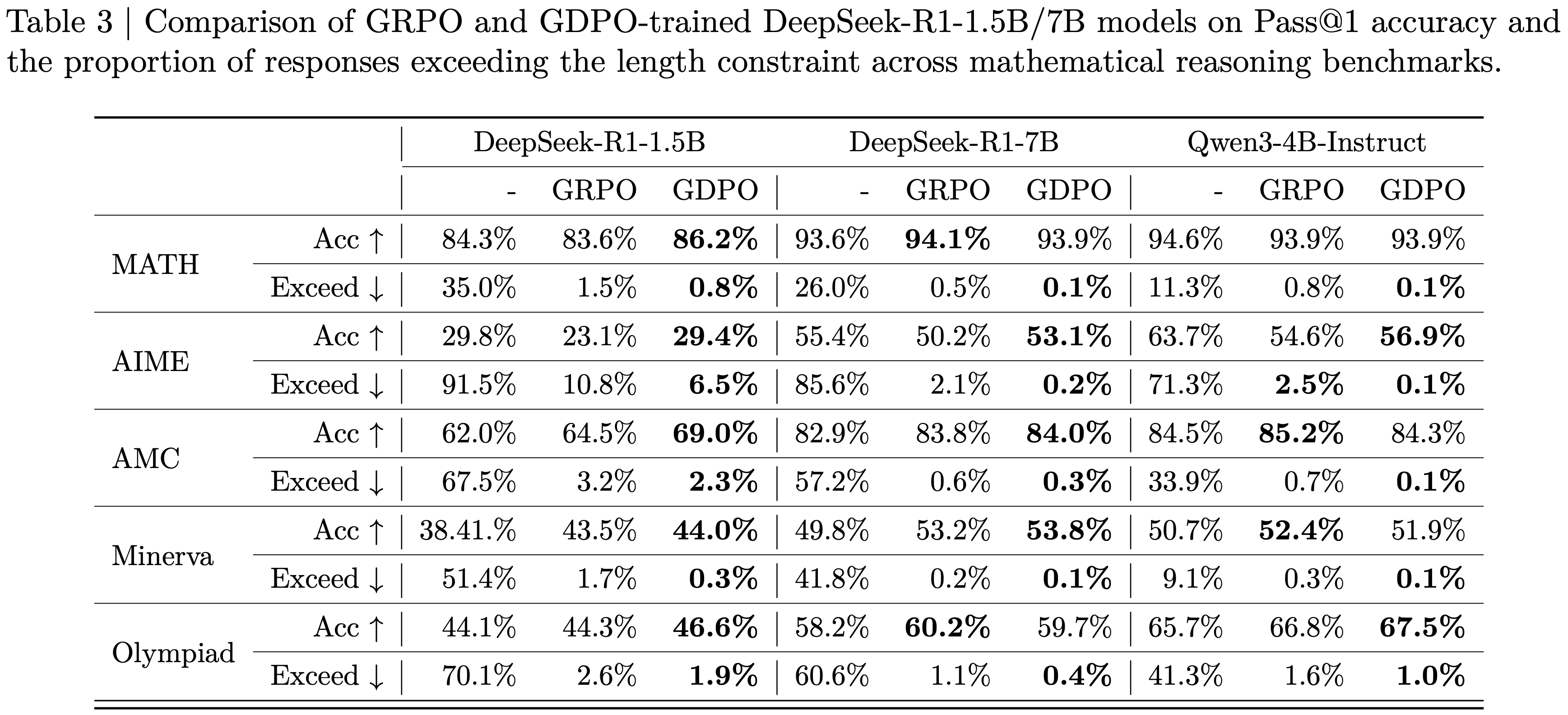
- 总之,这些结果表明, GDPO 不仅在一系列数学任务上提高了推理准确性,而且更有效地遵守了长度约束,突显了其在多 Reward 优化方面的优势
Impact analysis of different reward priority variation configurations(Reward 优先级变化配置的影响)
- 到目前为止,论文假设所有 Reward 都具有同等的优先级
- 然而,如图 5 所示,即使两个目标被分配了相同的 Reward 权重,模型也常常以牺牲更具挑战性的目标为代价来最大化较容易的目标
- 在本节中,论文研究当期望模型优先最大化正确性 Reward 而非长度 Reward 时,并且当两个目标的难度差异明显时,调整 Reward 权重是否能够引导模型实现这种偏好
- 论文首先将 \( \mathcal{R}_{\text{correct} } \) 的 Reward 权重(记为 \( w_{\text{correct} } \) )固定为 1,并将 \( \mathcal{R}_{\text{length} } \) 的 Reward 权重(记为 \( w_{\text{length} } \) )在集合 \( \{0.25,0.5,0.75,1.0\} \) 中变化
- 这个设置允许论文研究降低 \( w_{\text{length} } \) 是否会鼓励模型优先最大化更具挑战性的正确性 Reward
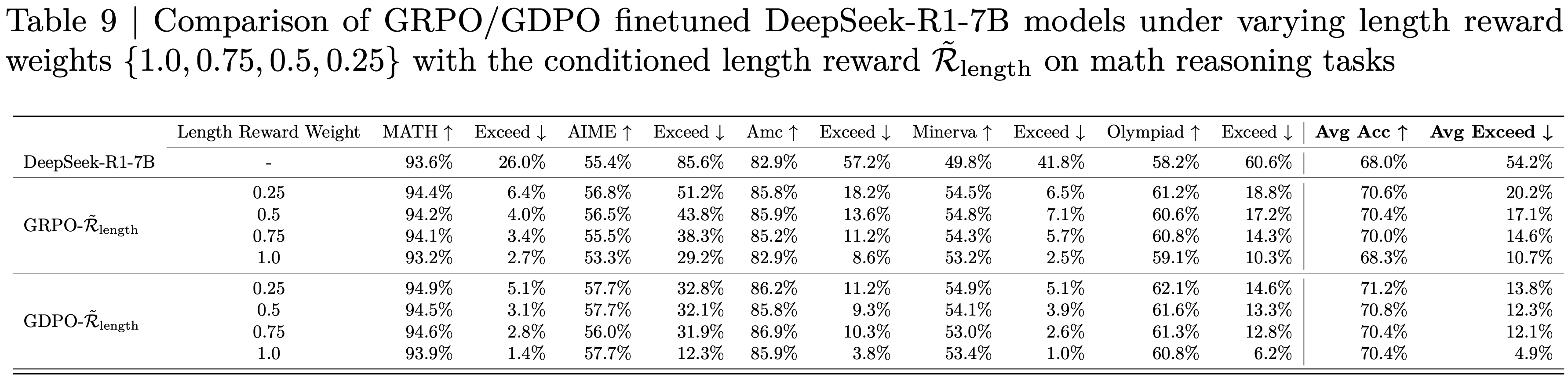
- 论文在 DeepSeek-R1-7B 上进行了这个实验,并将 MATH 和 AIME 的平均准确率和平均超长比率绘制在图 6 中(其中 \(\tilde{\mathcal{R}}_{\text{length}}\) 表示 Conditional Length Reward; \(\mathcal{R}_{\text{length}}\) 表示 normal Length Reward;从图中可以看到,GDPO 准确率不及 GRPO 的地方,一般都是因为长度降低太多导致)
- 其余任务的完整结果在附录 G 中提供(注:表 8 和表 9)
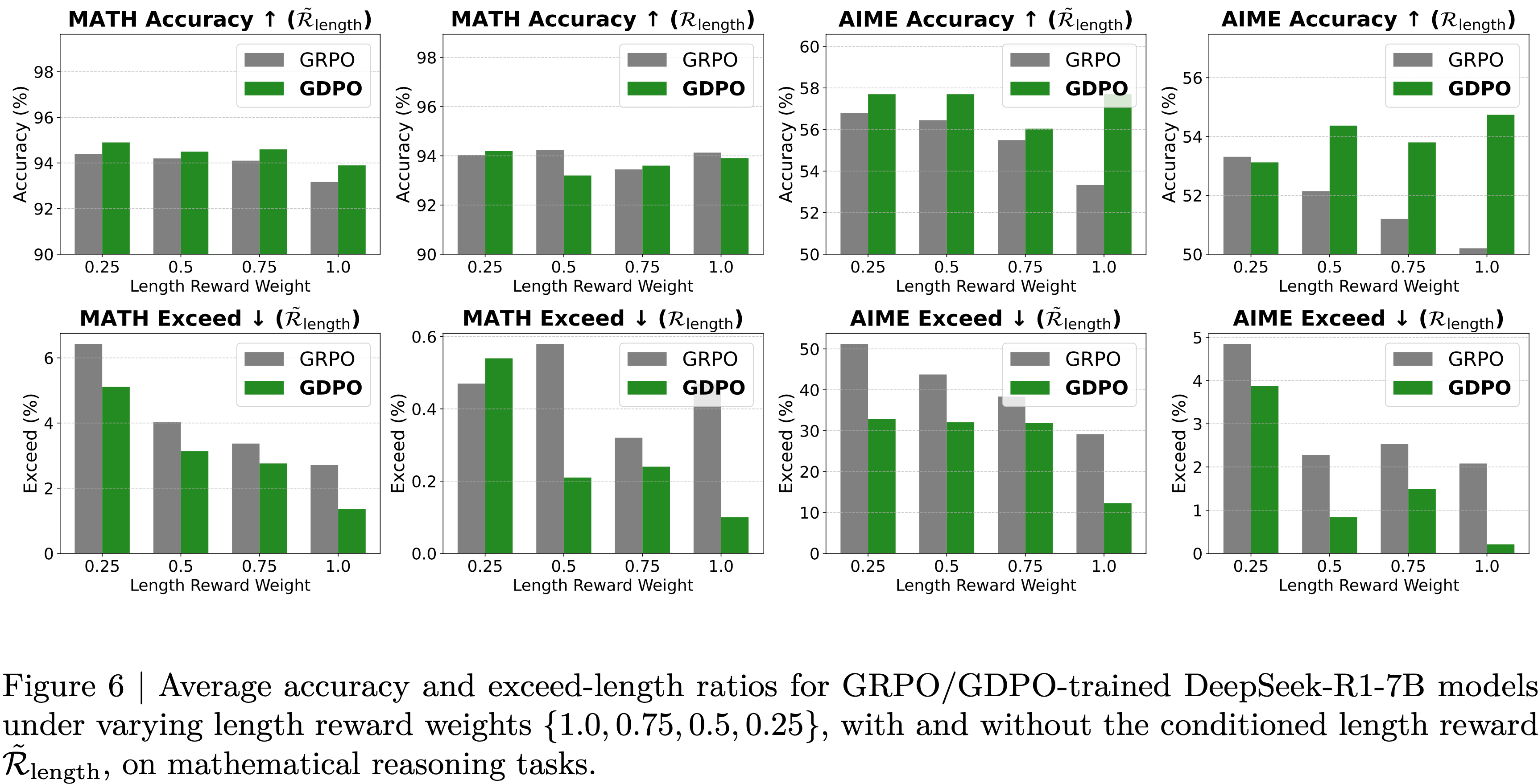
- 其余任务的完整结果在附录 G 中提供(注:表 8 和表 9)
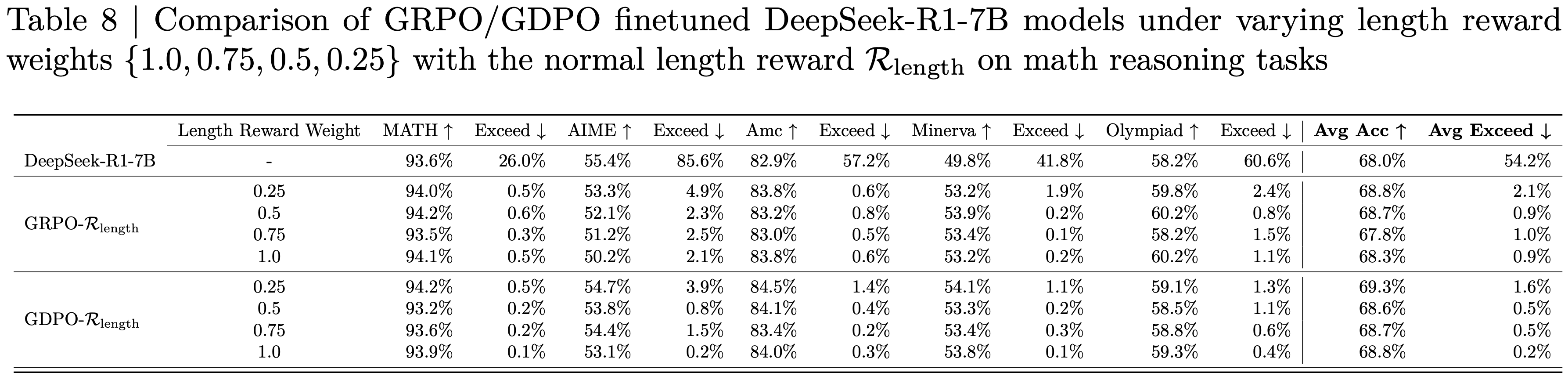
- 从结果中,论文观察到将 \( w_{\text{length} } \) 降低到 0.75 或 0.5 对平均超长比率影响甚微,对于 GRPO 在 AIME 上仅分别变化了 0.4% 和 0.2%,对于 GDPO 分别变化了 1.3% 和 0.6%
- 此外,降低 \( w_{\text{length} } \) 并不一定会放宽长度约束,因为将 \( w_{\text{length} } \) 从 0.75 降低到 0.5 并没有在 GRPO 或 GDPO 的 AIME 或 MATH 上持续增加超长比率
- 这表明,当基础目标在难度上存在显著差异时,仅仅调整 Reward 权重并不能可靠地诱导出预期的优先级排序
- 只有当 \( w_{\text{length} } \) 降低到 0.25,使其足够小以补偿目标之间的难度差距时,论文才观察到 GRPO 和 GDPO 在 AIME 上以及 GDPO 在 MATH 上的超长比率明显增加
- 接下来,论文研究了将较容易的长度 Reward 条件化在更具挑战性的正确性 Reward 上,是否有助于缓解两个目标之间的难度差异,并有助于改进优先级对齐
- 遵循第 3.2 节的公式,论文将原始长度 Reward \( \mathcal{R}_{\text{length} } \) 替换为一个条件化的长度 Reward,其定义如下:
$$
\tilde{\mathcal{R} }_{\text{length} }=\begin{cases}1, &\text{if response length}\leq l\text{ and }\mathcal{R}_{\text{correct} }=1\\0, &\text{otherwise.}\end{cases}
$$ - 在这个公式下,只有当生成的 Response 也是正确的时候,模型才会获得长度 Reward
- 遵循第 3.2 节的公式,论文将原始长度 Reward \( \mathcal{R}_{\text{length} } \) 替换为一个条件化的长度 Reward,其定义如下:
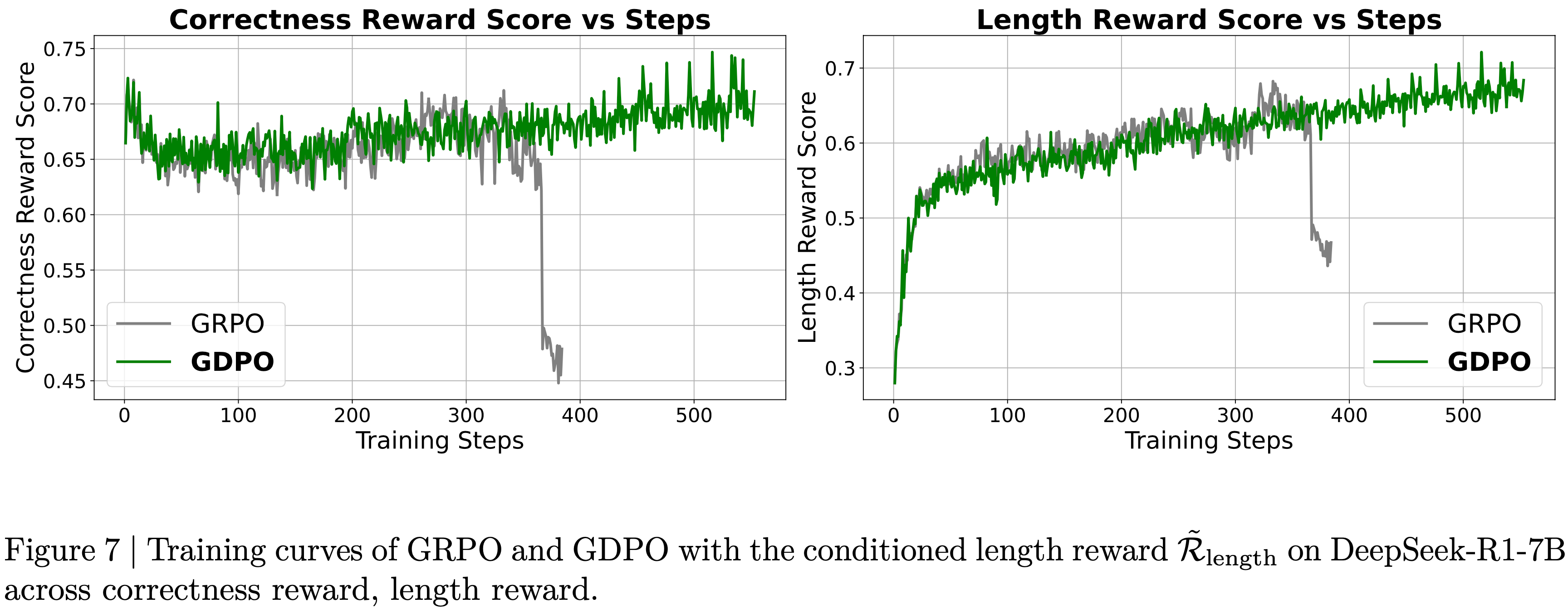
- 首先,论文观察到采用修改后的 Reward 函数 \( \tilde{\mathcal{R} }_{\text{length} } \) 可以防止模型在训练开始时过度最大化长度 Reward
- 这种 Reward 设计也有助于避免当模型试图满足长度约束时正确性 Reward 分数的大幅下降
- 从图 7 中可以看出,平均正确性 Reward 仅在训练初期略微下降,随后逐渐恢复
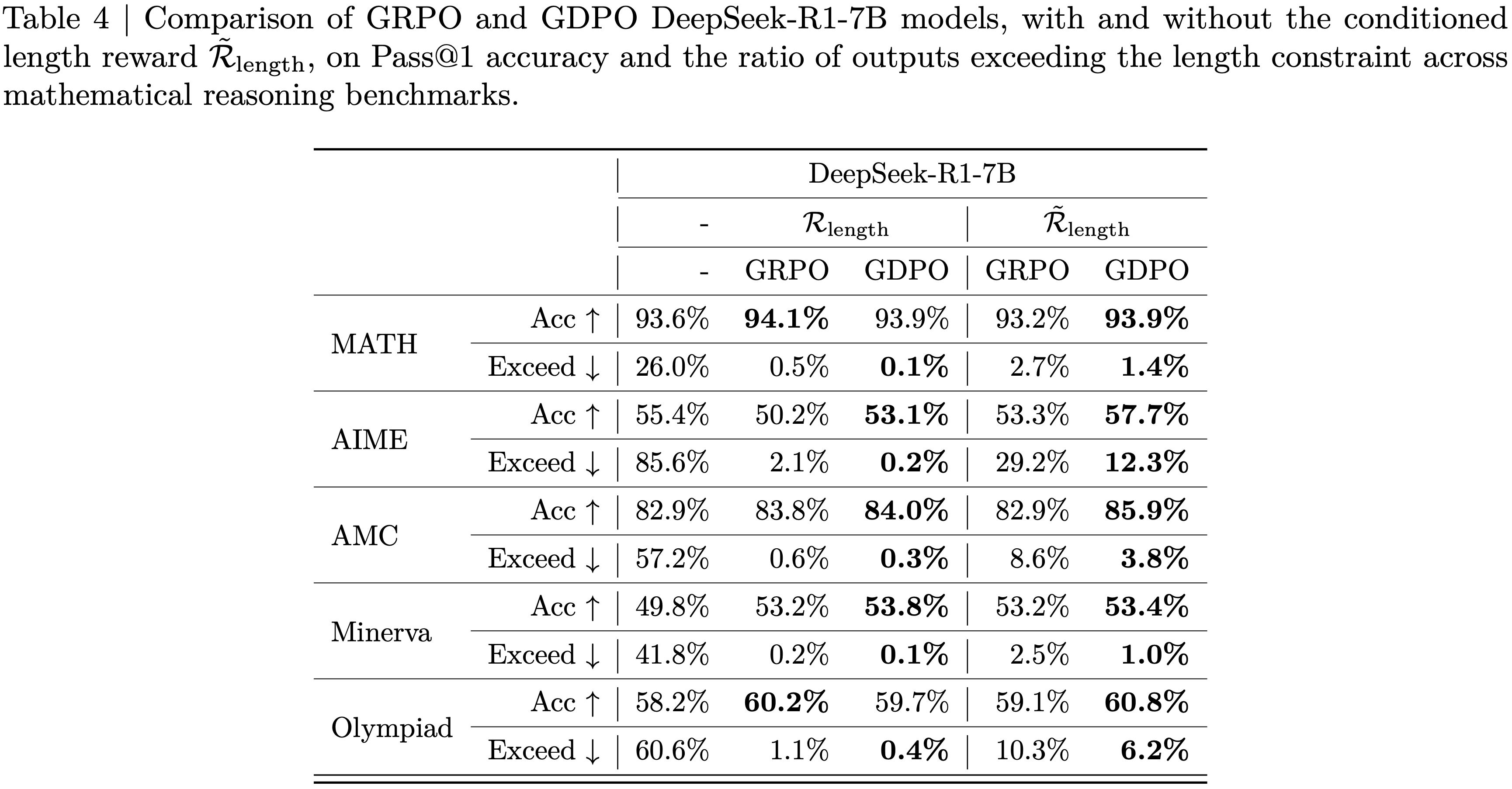
- 从表 4 中,论文还观察到,与仅仅调整 \( \mathcal{R}_{\text{length} } \) 的权重 \( w_{\text{length} } \) 相比,使用 \( \tilde{\mathcal{R} }_{\text{length} } \) 会导致 GRPO 和 GDPO 的平均超长比率有更大的增加,这表明对长度约束的更有效放宽
- 然而, GRPO 未能将这种放宽的约束转化为有意义的准确率提升
- 相比之下, GDPO 更有效地优先考虑正确性 Reward,并在训练中实现了比不使用 \( \tilde{\mathcal{R} }_{\text{length} } \) 时更一致的准确率提升,同时引入的超长违规增加幅度要小得多
- 例如,与使用相同 Reward 函数的 GRPO 相比,在 GDPO 中使用 \( \tilde{\mathcal{R} }_{\text{length} } \) 在 AIME 上带来了 4.4% 的准确率提升,同时超长比率降低了 16.9%;在 AMC 上获得了 3% 的准确率增益,同时超长违规减少了 4.8%
- 接下来,论文研究了在通过条件化长度 Reward 缓解了难度差异之后,改变 \( \tilde{\mathcal{R} }_{\text{length} } \) 的 Reward 权重(记为 \( \hat{w}_{\text{length} } \))是否能更忠实地反映细粒度的偏好调整
- 论文固定正确性 Reward 的权重,并变化 \( \hat{w}_{\text{length} } \in \{0.25,0.5,0.75,1.0\} \)
- 如图 6 所示,使用条件化 Reward 训练的模型表现得更可预测
- 例如,将 \( \hat{w}_{\text{length} } \) 从 1.0 降低到 0.25,稳步增加了 GRPO 和 GDPO 在 MATH 和 AIME 上的超长比率,这与调整原始 \( \mathcal{R}_{\text{length} } \) 权重时观察到的不稳定结果形成对比

- 例如,将 \( \hat{w}_{\text{length} } \) 从 1.0 降低到 0.25,稳步增加了 GRPO 和 GDPO 在 MATH 和 AIME 上的超长比率,这与调整原始 \( \mathcal{R}_{\text{length} } \) 权重时观察到的不稳定结果形成对比
- 最后,在所有设置下,包括不同的 Reward 公式和不同的 Reward 权重, GDPO 始终比 GRPO 提供更好的准确性和效率权衡
Coding reasoning
- 论文考察了在优化多于两个 Reward 的代码推理任务上, GDPO 是否继续优于 GRPO
- 与数学推理设置类似,目标是提高模型的代码性能,同时将其输出限制在预定义的目标长度内
- 论文引入了第三个目标,即鼓励模型生成无缺陷的代码
- 论文通过在 Eurus-2-RL 数据集 (2025) 上训练 DeepSeek-R1-7B 来比较 GDPO 和 GRPO
- 该数据集包含 24K 个编码问题,每个问题有多个测试用例
- 训练使用 verl (2024) 框架进行 400 个 step,并采用与数学推理实验中相同的超参数配置
- 训练优化三个 Reward:
- 通过率 Reward (Passrate reward) : 通过率 Reward \( \mathcal{R}_{\text{pass} } \in [0,1] \) 衡量生成代码通过的测试用例比例:
$$
\mathcal{R}_{\text{pass} }=\frac{\text{number of passed test cases} }{\text{total test cases} }.
$$ - 条件化长度 Reward (Conditioned Length reward) : 长度 Reward \( \tilde{\mathcal{R} }_{\text{length} } \in \{0,1\} \) 检查模型的 Response 是否保持在目标长度 \( l \) 内,以及生成的代码是否满足正确性要求:
$$
\tilde{\mathcal{R} }_{\text{length} }=\begin{cases}1, &\text{if response length }\leq l\text{ and }\mathcal{R}_{\text{pass} }=1,\\0, &\text{otherwise}.\end{cases}
$$ - 缺陷 Reward (Bug reward) : 缺陷 Reward \( \mathcal{R}_{\text{bug} } \in \{0,1\} \) 表示生成的代码是否在运行时或编译时没有错误
- 通过率 Reward (Passrate reward) : 通过率 Reward \( \mathcal{R}_{\text{pass} } \in [0,1] \) 衡量生成代码通过的测试用例比例:
- 对于评估,论文在来自 PRIME (2025) 的验证集上评估训练好的模型,其中包括 Apps (2021)、CodeContests (2022)、Codeforces 和 Taco (2023)
- 遵循与数学推理评估相同的设置,论文使用采样温度 0.6,\( top_{p} \) 值为 0.95,最大 Response 长度为 32k 个 Token。对于每个评估问题,论文生成 16 个 Rollout,并报告平均测试用例通过率、平均超长比率和平均缺陷率,其中缺陷率衡量导致运行时错误或编译错误的生成代码的比例
- 论文在两种配置下比较 GDPO 和 GRPO :
- (1) 使用 \( \mathcal{R}_{\text{pass} } \) 和 \( \tilde{\mathcal{R} }_{\text{length} } \) 的两 Reward 设置
- (2) 使用 \( \mathcal{R}_{\text{pass} } \)、\( \tilde{\mathcal{R} }_{\text{length} } \) 和 \( \mathcal{R}_{\text{bug} } \) 的三 Reward 设置
- 论文将 GRPO 的两 Reward 和三 Reward 版本分别记为 \( GRPO _{2\text{-obj} } \) 和 \( GRPO _{3\text{-obj} } \), GDPO 也使用相同的记法
- 如表 5 所示,与 \( GRPO _{2\text{-obj} } \) 相比,\( GDPO _{2\text{-obj} } \) 在所有任务上都提高了通过率,同时保持了类似的超长比率
- 注:从表 5 中看起来,优势似乎不是很明显
- 例如,\( GDPO _{2\text{-obj} } \) 将 Codecontests 的通过率提高了 2.6%,而超长比率仅增加了 0.1%;与 \( GRPO _{2\text{-obj} } \) 相比,在 Taco 上实现了 3.3% 的通过率提升,同时超长违规减少了 1%
- 在三种 Reward 设置中也可以观察到类似的模式,\( GDPO _{3\text{-obj} } \) 在所有目标上实现了明显更好的平衡,保持了与 \( GRPO _{3\text{-obj} } \) 相似的通过率,同时还显著降低了超长比率和缺陷率
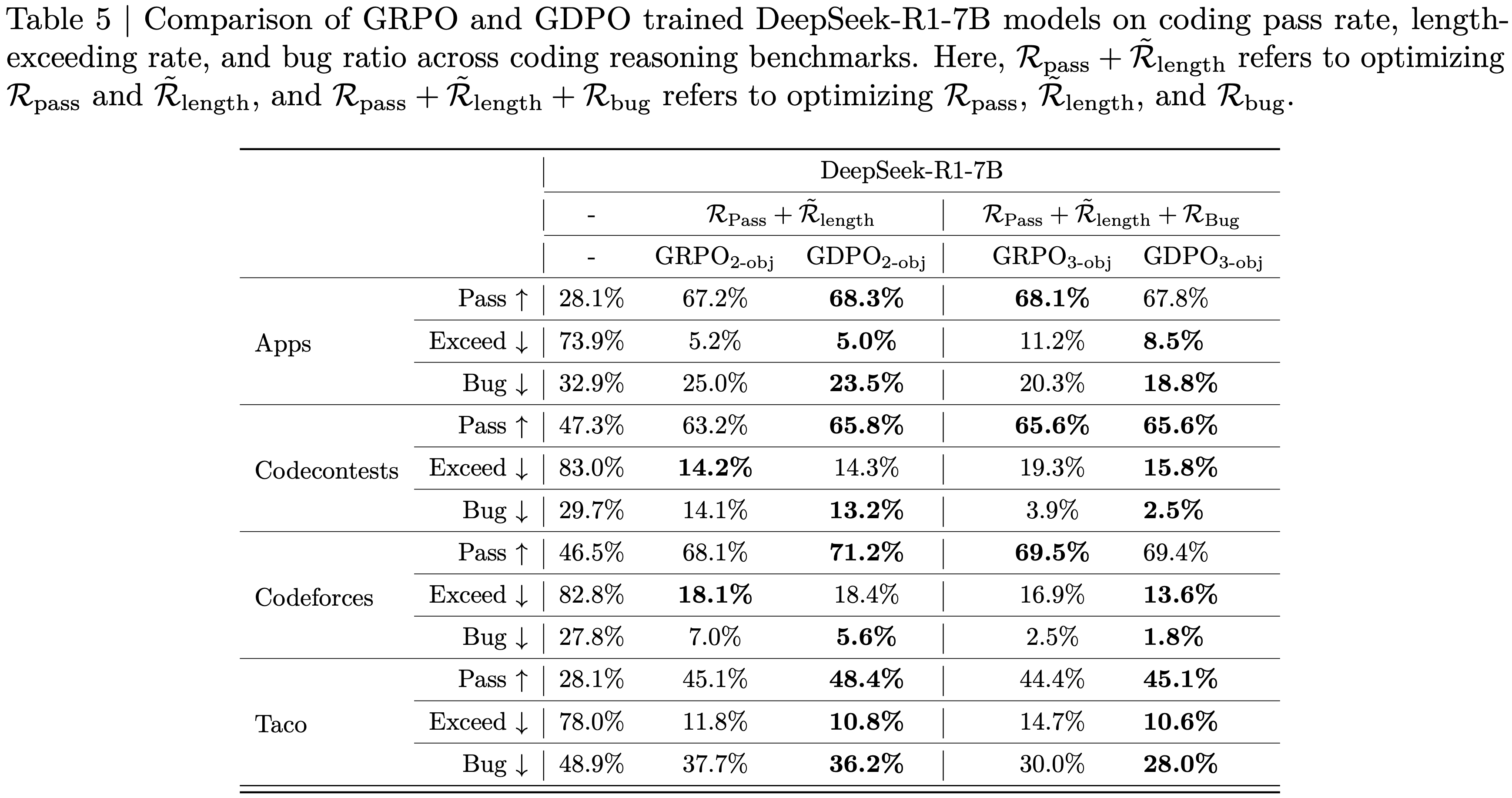
- 如表 5 所示,与 \( GRPO _{2\text{-obj} } \) 相比,\( GDPO _{2\text{-obj} } \) 在所有任务上都提高了通过率,同时保持了类似的超长比率
- 总的来说,这些结果表明,随着 Reward 信号数量的增加, GDPO 仍然有效
- 在两种 Reward 和三 Reward 配置中,它始终比 GRPO 在所有目标上实现更有利的权衡
Related Work
GRPO 变体
- 已经提出了几种 Group Relative Policy Optimization ( GRPO ) (2025) 的扩展,以增强该框架的稳定性、有效性和效率
- 这些方法探索了 Group-wise 归一化或策略更新的替代公式,同时仍基于 GRPO 的核心原理,例如,
- 为了提高稳定性,Group Sequence Policy Optimization (GSPO) (2025) 基于序列可能性而非 Token 级别定义重要性比率,执行序列级别的 Clipping、Rewarding 和优化
- 为了提高 RL 性能,Decoupled Clip and Dynamic sAmpling Policy Optimization (DAPO) (2025) 引入了四项关键技术:Clip-Higher、Dynamic Sampling、Token-Level Policy Gradient Loss 和 Overlong Reward Shaping
- 为了促进高效推理,Group Filtered Policy Optimization (GFPO) (2025) 通过在训练期间为每个问题采样更大的组,并根据其长度和每 Token 奖励率筛选 Response,来解决长度爆炸问题
- 沿着同一方向,Doing Length pEmalty Right (DLER) (2025) 提出了一种结合了 Batch-wise Reward 归一化、Higher Clipping、Dynamic Sampling 和简单截断长度惩罚的训练配方,实现了 SOTA 准确性-效率权衡
Multi-Reward Reinforcement Learning
- 越来越多的工作研究了融入多种 Reward 信号的 RL 方法,一个主要用途是建模多样化的人类偏好,例如
- Safe Reinforcement Learning from Human Feedback (2023) 将人类关于有用性和无害性的偏好解耦,在微调期间动态调整两个目标之间的平衡
- 类似地,Reinforcement Learning from Personalized Human Feedback (RLPHF) (2023) 通过为每种偏好训练不同的策略模型并在推理时合并它们,来优化具有多种(有时是冲突的)偏好的 LLM
- ALARM (Align Language Models via Hierarchical Rewards) (2024) 引入了分层 Reward 结构,共同捕捉 Response 质量、风格、公平性和连贯性等维度
- LLM 的最新进展也整合了多 Reward 优化来处理复杂任务,例如
- DeepSeek V3.2 (2025) 集成了基于规则的结果 Reward、长度惩罚和语言一致性 Reward,以增强推理和代理能力
- 多 Reward RL 的另一个重要近期应用是在保持任务性能的同时提高推理模型的效率,主要是通过引入基于长度的 Reward 函数以及基于结果的 Reward,例如,
- O1-Pruner (2025) 和 (2025) 应用归一化的长度惩罚来确保比例压缩
- 类似地,(2025) 通过惩罚与采样组内最短正确 Response 的偏差来促进简洁性
- L1 (2025) 引入了长度控制策略优化(Length Controlled Policy Optimization,LCPO),以优化准确性同时确保 Response 不超过目标长度
- 最后,(2025) 提出了一种自适应 Reward 塑造方法,根据模型性能动态调整准确性和 Response 长度之间的权衡
附录 A:Training stability issue of GDPO without batch-wise advantage normalization
- 图 8:使用和未使用批量优势归一化的 GDPO 训练稳定性对比,未进行归一化的运行偶尔会无法收敛
附录 B:ToolRL Training Prompt Format
System Prompt for ToolRL Training
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24You are a helpful dialogue assistant capable of leveraging tool calls to solve user tasks and provide structured chat responses.
# Available Tools
In your response, you can use the following tools:
{ { Tool List } }
# Steps for Each Turn
1. Think: Recall relevant context and analyze the current user goal.
2. Decide on Tool Usage: If a tool is needed, specify the tool and its parameters.
3. Respond Appropriately: If a response is needed, generate one while maintaining consistency across user queries.
# Output Format
<think> Your thoughts and reasoning </think>
<tool_call> {“name”: “Tool name”, “parameters”: {“Parameter name”: “Parameter content”, “ ... ...”:
“ ... ...”}}
{“name”: “ ... ...”, “parameters”: {“ ... ...”: “ ... ...”, “ ... ...”: “ ... ...”}}
...
</tool_call>
<response>AI’s final response </response>
# Important Notes
1. You must always include the <think> field to outline your reasoning. Provide at least one of <tool_call> or <response>. Decide whether to use <tool_call> (possibly multiple times), <response>, or both.
2. You can invoke multiple tool calls simultaneously in the <tool_call> fields. Each tool call should be a JSON object with a “name” field and a “parameters” field containing a dictionary of parameters. If no parameters are needed, leave the “parameters” field an empty dictionary.
3. Refer to the previous dialogue records in the history, including the user’s queries, previous <tool_call>, <response>, and any tool feedback noted as <obs> (if exists).- 中文版(ToolRL 训练系统 Prompt):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28你是一个有用的对话助手,能够利用工具调用来解决用户任务并提供结构化的聊天响应
可用工具
在你的回复中,你可以使用以下工具:{ { 工具列表 } }
每个回合的步骤
1. **思考 (Think)**:回忆相关上下文并分析当前的用户目标
2. **决定工具使用 (Decide on Tool Usage)**:如果需要使用工具,请指定工具及其参数
3. **恰当响应 (Respond Appropriately)**:如果需要生成响应,请在响应用户查询时保持一致
输出格式
<think>
你的想法和推理过程
</think>
<tool_call>
{"name": "工具名称", "parameters": {"参数名": "参数内容", "... ...": "... ..."} }
{"name": "... ...", "parameters": {"... ...": "... ...", "... ...": "... ..."} }
...
</tool_call>
<response>
AI 的最终响应
</response>
重要说明
1. 你必须始终包含 `<think>` 字段来概述你的推理。至少提供 `<tool_call>` 或 `<response>` 中的一个。决定是使用 `<tool_call>`(可能多次使用)、`<response>` 还是两者都用
2. 你可以在 `<tool_call>` 字段中同时调用多个工具调用。每个工具调用应是一个包含 "name" 字段和 "parameters" 字段的 JSON 对象,"parameters" 字段包含参数字典。如果不需要参数,请将 "parameters" 字段留空字典
3. 参考历史对话记录,包括用户的查询、之前的 `<tool_call>`、`<response>`,以及任何标记为 `<obs>` 的工具反馈(如果存在)
- 中文版(ToolRL 训练系统 Prompt):
User Prompt for ToolRL Training
1
2
3
4
5
6
7
8## Dialogue History
<user> { { Initial User Input } } </user>
<think> Round 1 Model Thought </think>
{ { Round 1 model output <tool_call> or <response> } }
<obs> Round 1 Observation </obs>
... ...
<user> { { User Input } } </user>
... ...- 中文版(ToolRL 训练用户 Prompt)
1
2
3
4
5
6
7
8
9## 对话历史
<user> { { 初始用户输入 } } </user>
<think> 第 1 轮模型思考 </think>
{ { 第 1 轮模型输出 <tool_call> 或 <response> } }
<obs> 第 1 轮观察 </obs>
... ...
<user> { { 用户输入 } } </user>
... ...
- 中文版(ToolRL 训练用户 Prompt)
附录 C:工具调用奖励函数
Format Reward
- 格式奖励 \(\mathcal{R}_{\text{format} }\in\{0,1\}\) 检查模型输出是否满足所需结构并按正确顺序包含所有必要字段:
$$
\mathcal{R}_{\text{format} }=\begin{cases}1, & \text{if all required fields appear and are in the correct order},\\ 0, & \text{otherwise}.\end{cases}
\tag{9}
$$
Correctness Reward
- 正确性奖励 \(\mathcal{R}_{\text{correct} }\in[-3,,3]\) 将预测的工具调用 \(P=\{P_{1},\ldots,P_{m}\}\) 与真实调用 \(G=\{G_{1},\ldots,G_{n}\}\) 进行比较,正确性奖励由三个部分组成:
- 工具名称匹配 (Tool Name Matching):
$$
r_{\text{name} }=\frac{|N_{G}\cap N_{P}|}{|N_{G}\cup N_{P}|}\in[0,1],
$$- 其中 \(N_{G}\) 和 \(N_{P}\) 分别是真实调用和预测调用的工具名称集合
- 参数名称匹配 (Parameter Name Matching):
$$
r_{\text{param} }=\sum_{G_{j}\in G}\frac{|\text{keys}(G_{j})\cap\text{keys}(P_{j})|}{|\text{keys}(G_{j})\cup\text{keys}(P_{j})|}\in[0,|G|],
$$- 其中 \(\text{keys}(G_{j})\) 和 \(\text{keys}(P_{j})\) 分别是真实调用和预测调用的参数名称
- 参数内容匹配 (Parameter Content Matching):
$$
r_{\text{value} }=\sum_{G_{j}\in G}\sum_{k\in\text{keys}(G_{j})}\mathbf{1}[P_{G}[k]=P_{P}[k]]\in\left[0,\sum_{G_{j}\in G}|\text{keys}(G_{j})|\right],
$$- 其中 \(P_{G}[k]\) 和 \(P_{P}[k]\) 分别是真实调用和预测调用的参数值
- 总匹配分数 (Total Match Score):
$$
r_{\text{match} }=r_{\text{name} }+r_{\text{param} }+r_{\text{value} }\in[0,S_{\text{max} }],
$$- 其中
$$
S_{\text{max} }=1+|G|+\sum_{G_{j}\in G}|\text{keys}(G_{j})|.
$$
- 其中
- 工具名称匹配 (Tool Name Matching):
- 最终的正确性奖励通过寻找 \(P\) 和 \(G\) 之间的最优匹配以最大化总匹配分数来计算:
$$
\mathcal{R}_{\text{correct} }=6\cdot\frac{R_{\text{max} } }{S_{\text{max} } }-3\in[-3,,3].
$$- 其中 \(R_{\text{max} }\) 表示来自最优匹配的总匹配分数
附录 D:ToolRL Hyperparameters Setting
- 表 6: GDPO verl 训练配置
- 所有超参数设置均与 ToolRL (2025) 中使用的保持一致

- 所有超参数设置均与 ToolRL (2025) 中使用的保持一致
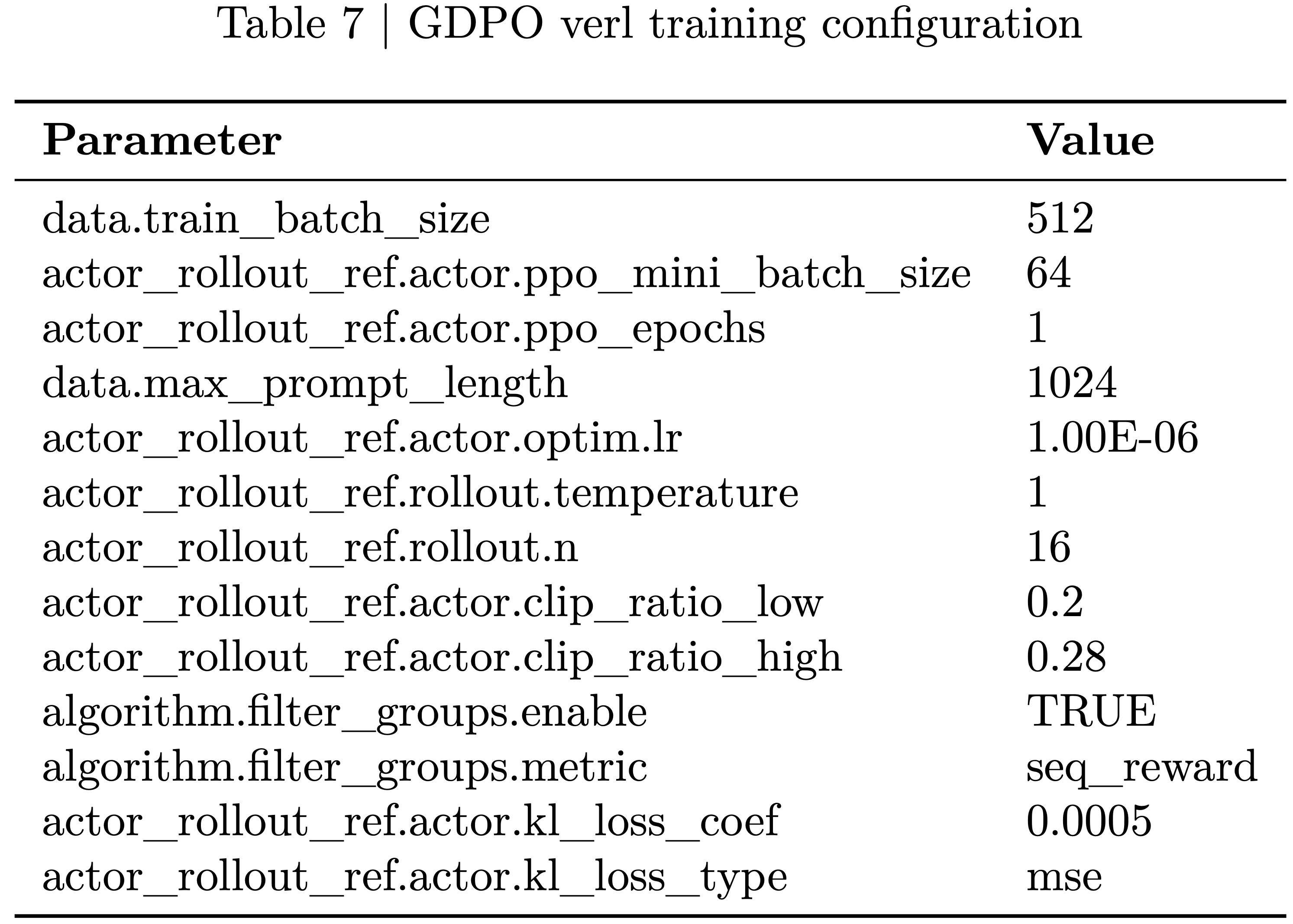
附录 E:数学/代码推理超参数设置(Math/Coding Reasoning Hyperparameters Setting)
- 表 7: GDPO verl 训练配置
附录 F:使用 \(\mathcal{R}_{\text{length} }\) 和 \(\mathcal{R}_{\text{correct} }\) 在数学推理数据上训练 DeepSeek-R1-7B 和 Qwen3-4B-Instruct 时 GRPO 和 GDPO 的训练曲线(Training curves of GRPO and GDPO when training DeepSeek-R1-7B and Qwen3-4B-Instruct with \(\mathcal{R}_{\text{length} }\) and \(\mathcal{R}_{\text{correct} }\) on math reasoning data.)
- 图 9:在数学推理数据上优化 DeepSeek-R1-7B 时, GRPO 和 GDPO 在正确性奖励、长度奖励和批次最大响应长度上的训练行为。我们可以看到 GDPO 在保持正确性提升的同时,对长度约束的遵循也优于 GRPO

- 图 10:在数学推理数据上优化 Qwen3-4B-Instruct 时, GRPO 和 GDPO 在正确性奖励、长度奖励和批次最大响应长度上的训练行为。我们可以看到 GDPO 在保持正确性提升的同时,对长度约束的遵循也优于 GRPO

附录 G:在数学推理任务上,对比 GRPO / GDPO 微调的 DeepSeek-R1-7B 模型在不同长度奖励权重 \(\{1.0,0.75,0.5,0.25\}\) 下,使用和不使用条件化长度奖励 \(\tilde{\mathcal{R} }_{\text{length} }\) 的效果(Comparison of GRPO/GDPO finetuned DeepSeek-R1-7B models under varying length reward weights \(\{1.0,0.75,0.5,0.25\}\) with and without the conditioned length reward \(\tilde{\mathcal{R} }_{\text{length} }\) on math reasoning tasks)
- 表 8:在数学推理任务上,对比 GRPO / GDPO 微调的 DeepSeek-R1-7B 模型在不同长度奖励权重 \(\{1.0,0.75,0.5,0.25\}\) 下,使用普通长度奖励 \(\mathcal{R}_{\text{length} }\) 的效果

- 表 9:在数学推理任务上,对比 GRPO / GDPO 微调的 DeepSeek-R1-7B 模型在不同长度奖励权重 \(\{1.0,0.75,0.5,0.25\}\) 下,使用条件化长度奖励 \(\tilde{\mathcal{R} }_{\text{length} }\) 的效果
