XGBoost,全称: Extreme Gradient Boosting
概述
- CART回归树是XGBoost的基分类器
XGBoost模型推导(假设回归树的结构确定)
模型 \(F\) 的加法定义:
$$
\begin{align}
F(x;w) = \sum_{k=0}^{K} f_{k}(x;w_{k})
\end{align}
$$
- 其中, \(x\) 为输入样本, \(f_{k}\) 为分类回归树,可以是分类回归树空间中的任意一棵树, \(w_{k}\) 是树 \(f_{k}\) 的参数
定义损失函数
$$
\begin{align}
L^{t} &= \sum_{i=1}^{n}l(y_{i},\hat{y}_{i}^{t}) + \Omega(f_{t}) \\
&= \sum_{i=1}^{n}l(y_{i},\hat{y}_{i}^{t-1} + f_{t}(x_{i})) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2
\end{align}
$$
- \(L^{t}\): 第 \(t\) 轮迭代的损失函数
- \(l(y_{i},\hat{y}_{i}^{t})\) 表示单个样本的损失函数定义
- \(\hat{y}_{i}^{t} = \hat{y}_{i}^{t-1} + f_{t}(x_{i})\) 表示第 \(t\) 轮 \(x_{i}\) 样本的预测值
- 加法模型: 第 \(t\) 轮预测值 = 第 \(t-1\) 轮预测值 + 第 \(t\) 棵(轮)决策树的预测值
- \(\Omega(f_{t})\) 表示正则项
- \(n\) 表示样本的个数
- \(T\) 表示叶子结点的个数
- \(w_{j}\) 表示叶节点分数 , 即任意样本落到第 \(t\) 棵(轮)决策树的第 \(j\) 叶子结点时的预测值(可称为第 \(t\) 棵(轮)决策树的第 \(j\) 叶子结点的预测值)
- \(\gamma\) 和 \(\lambda\) 都是正则项参数
第 \(t\) 轮训练的目标
- 找到一个最优的分类器 \(f_t^{\star}(x)\),满足
$$
\begin{align}
f_t^{\star}(x) &= \mathop{\arg\max}_{f_t(x)}L^{t} \\
&= \mathop{\arg\max}_{f_t(x)}\left(\sum_{i=1}^{n}l(y_{i},\hat{y}_{i}^{t}) + \Omega(f_{t})\right) \\
&= \mathop{\arg\max}_{f_t(x)}\left(\sum_{i=1}^{n}l(y_{i},\hat{y}_{i}^{t-1} + f_{t}(x_{i})) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2 \right)
\end{align}
$$
最小化损失函数推导
损失函数二阶泰勒展开
回忆传统泰勒展开:
$$
\begin{aligned}
f(x) &= f(x_0) + f’(x_0)(x-x_0) + \frac{f’’(x_0)}{2!}(x-x_0)^2 + \cdots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n \\
& = \sum\limits_{n=0}^{\infty}\frac{f^{(n)}x_0}{n!}(x - x_0)^n
\end{aligned}
$$二阶泰勒展开公式
$$
\begin{align}
f(x+\Delta x) \approx f(x) + f’(x)\Delta x + \frac{1}{2}f’’(x)\Delta x^2
\end{align}
$$在我们的场景中,令
- \(x = \hat{y}_{i}^{t-1}\)
- \(\Delta x = f_{t}(x_{i})\)
则有对单个样本能得到
$$
\begin{align}
l(y_{i},\hat{y}_{i}^{t-1} + f_{t}(x_{i})) \approx l(y_i,\hat{y}_i^{t-1}) + l’(y_i,\hat{y}_i^{t-1})f_t(x_i) + \frac{1}{2}l’’(y_i,\hat{y}_i^{t-1})f_t^2(x_i)
\end{align}
$$- \(l’(y_i,\hat{y}_i^{t-1})\) 是 \(l(y_i,\hat{y}_i)\) 对 \(\hat{y}_i\) 的一阶导数在 \(\hat{y}_i = \hat{y}_i^{t-1}\) 处的值
- \(l’’(y_i,\hat{y}_i^{t-1})\) 是 \(l(y_i,\hat{y}_i)\) 对 \(\hat{y}_i\) 的二阶导数在 \(\hat{y}_i = \hat{y}_i^{t-1}\) 处的值
我们第 \(t\) 轮的目标是找到一个最优的分类器 \(f_t^{\star}(x)\) 最小化损失函数 \(L^{t}\)
$$
\begin{align}
L^{t} \approx \sum_{i=1}^{n}\left(l(y_i,\hat{y}_i^{t-1}) + l’(y_i,\hat{y}_i^{t-1})f_t(x_i) + \frac{1}{2}l’’(y_i,\hat{y}_i^{t-1})f_t^2(x_i)\right) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2
\end{align}
$$显然上面式子中的 \(l(y_i,\hat{y}_i^{t-1})\) 与 \(f_t(x_i)\) 无关,可以移除,于是有
$$
\begin{align}
L^{t} \approx \sum_{i=1}^{n}\left(l’(y_i,\hat{y}_i^{t-1})f_t(x_i) + \frac{1}{2}l’’(y_i,\hat{y}_i^{t-1})f_t^2(x_i)\right) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2
\end{align}
$$令:
- \(g_i = l’(y_i,\hat{y}_i^{t-1})\) 为 \(l(y_i,\hat{y}_i)\) 对 \(\hat{y}_i\) 的一阶导数在 \(\hat{y}_i = \hat{y}_i^{t-1}\) 处的值
- \(h_i = l’’(y_i,\hat{y}_i^{t-1})\) 是 \(l(y_i,\hat{y}_i)\) 对 \(\hat{y}_i\) 的二阶导数在 \(\hat{y}_i = \hat{y}_i^{t-1}\) 处的值
则有:
$$
\begin{align}
L^{t} \approx \sum_{i=1}^{n}\left(g_if_t(x_i) + \frac{1}{2}h_if_t^2(x_i)\right) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2
\end{align}
$$做一个重要的转换 :
$$f_t(x_i) = w_j, \quad s.t. \ x_i \in I_j$$- 上面的式子前半部分成立的条件是 \(x_i\) 落在叶子结点 \(j\) 上
- 我们将条件 \(x_i\) 落在叶子结点 \(j\) 上表示为 \(\ x_i \in I_j\)
于是: 我们可以将前面对样本的累加变成对叶子结点的累加
$$
\begin{align}
L^{t} &\approx \sum_{j=1}^{T}\left((\sum_{i \in I_j}g_i)w_j + \frac{1}{2}(\sum_{i \in I_j}h_i)w_j^2\right) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2 \\
&\approx \sum_{j=1}^{T}\left((\sum_{i \in I_j}g_i)w_j + \frac{1}{2}(\sum_{i \in I_j}h_i + \lambda)w_j^2\right) + \gamma T
\end{align}
$$令:
- \(G_j = \sum_{i \in I_j}g_i\)
- \(H_j = \sum_{i \in I_j}h_i\)
则有
$$
\begin{align}
L^{t} \approx \sum_{j=1}^{T}\left(G_jw_j + \frac{1}{2}(H_j + \lambda)w_j^2\right) + \gamma T
\end{align}
$$\(L^t\) 对 \(w_j\) 求偏导有
$$
\begin{align}
\frac{\partial L^{t}}{\partial w_j} = G_j + (H_j + \lambda)w_j
\end{align}
$$令导数 \(\frac{\partial L^{t}}{\partial w_j} = 0\) 可得
$$
\begin{align}
w_j^{\star} = -\frac{G_j}{H_j+\lambda}
\end{align}
$$同时
$$
\begin{align}
L^{\star^t} &\approx min(L^t) \\
&\approx \sum_{j=1}^{T}\left(G_j\cdot (-\frac{G_j}{H_j+\lambda}) + \frac{1}{2}(H_j + \lambda)\cdot(-\frac{G_j}{H_j+\lambda})^2\right) + \gamma T \\
&\approx -\frac{1}{2}\sum_{j=1}^{T}\left(\frac{G_j^2}{H_j+\lambda}\right) + \gamma T
\end{align}
$$目标函数的计算示例: 目标分数越小越好
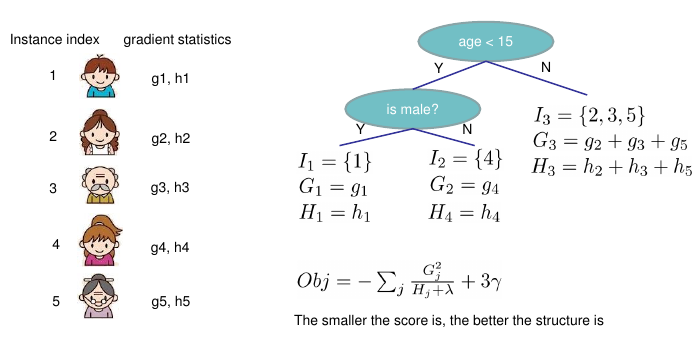
结论
- 在第 \(t\) 轮回归树的结构确定后 ,我们得到的最优叶节点分数与结构无关 \(w_j^{\star} = -\frac{G_j}{H_j+\lambda}\)
- 最小损失与第 \(t\) 轮回归树的结构的复杂度(叶节点数量)相关
- 我们还需要确定第 \(t\) 轮回归树的结构
回归树的结构确定
普通决策树树结构的确定
- 详细情况可参考: ML——DT-决策树
ID3
- 最大化信息增益来选择分裂特征
C4.5
- 最大化信息增益比来选择分裂特征
CART
分类树
- 最小化基尼指数来选择分裂特征
回归树
- 最小化平方误差来选择分裂特征
XGBoost结点分裂前后的信息增益
- 信息增益应该与前面的损失函数相关, 损失越小越好
- 原始损失函数为
$$
\begin{align}
L^{\star^t} \approx -\frac{1}{2}\sum_{j=1}^{T}\left(\frac{G_j^2}{H_j+\lambda}\right) + \gamma T
\end{align}
$$ - 显然,要使得损失函数最小,我们需要使得下面的式子最大:
$$
\begin{align}
\frac{G_j^2}{H_j+\lambda}
\end{align}
$$ - 一个结点分裂后的信息为
$$
\begin{align}
\frac{G_L^2}{H_L+\lambda} + \frac{G_R^2}{H_R+\lambda}
\end{align}
$$- 左子树的信息 + 右子树的信息
- 一个结点分裂前信息为
$$
\begin{align}
\frac{(G_L + G_R)^2}{H_L+ H_R + \lambda}
\end{align}
$$ - 从而我们定义一个结点分列前后的信息增益为:
$$
\begin{align}
Gain = \frac{G_L^2}{H_L+ \lambda} + \frac{G_R^2}{H_R+ \lambda} - \frac{(G_L + G_R)^2}{H_L+ H_R + \lambda} - \gamma
\end{align}
$$- Gain 越大说明当前结点的当前分裂方式越好
- 其中 \(\gamma\) 是一个超参数用于防止过拟合 ,可以理解为有两层含义:
- 用于对叶节点数目进行控制
- 用于增大分裂前后Gain的阈值
- 事实上 \(\gamma\) 不是凭空来的,开始的定义中 \(\gamma\) 就是L1正则化(叶节点数量)的系数, 这里分裂后叶节点数量多了1个, 我们希望树的叶节点越少越好(模型越简单越好),而这个的信息增益越大越好, 所以减去 \(\gamma\) 值,防止结点分裂得太多
- 对于每个特征的每个分裂点, \(\gamma\) 值都相同,所以 \(\gamma\) 值对特征和分裂点的选择没有影响,只是影响了某个结点是否能够被分裂(信息增益太小或者为负时我们可以选择不分裂)
XGBoost树节点分裂
精确分裂算法
- 单个叶节点精确计算信息增益分裂流程(特征和特征分裂取值的选择, 假设一共m个特征)
- 注意: 每次只对叶节点分裂,已经分裂了的就不是叶节点了,不能二次分裂
- 原图来自: https://www.cnblogs.com/massquantity/p/9794480.html

近似分裂算法
- 将每个特征的取值划分为多个分位点
- 每次考察特征时值考察分位点,减少计算复杂度
- 其他的步骤与前面的精确分裂算法相同,包括分数计算和选择最大分数等

分桶策略与GBDT的不同
- 传统的GBDT分桶时每个样本的权重都是相同的
- XGBoost中每个样本的权重为损失函数在该样本点的二阶导数(对不同的样本,计算得到的损失函数的二阶导数是不同的), 这里优点AdaBoost的思想,重点关注某些样本的感觉
- 这里影响的是划分点的位置(我们划分划分点[桶]时都是均匀划分样本到桶里面,当不同样本的权重不同时,每个桶里面的样本数量可能会不同)
- 下图是一个示例
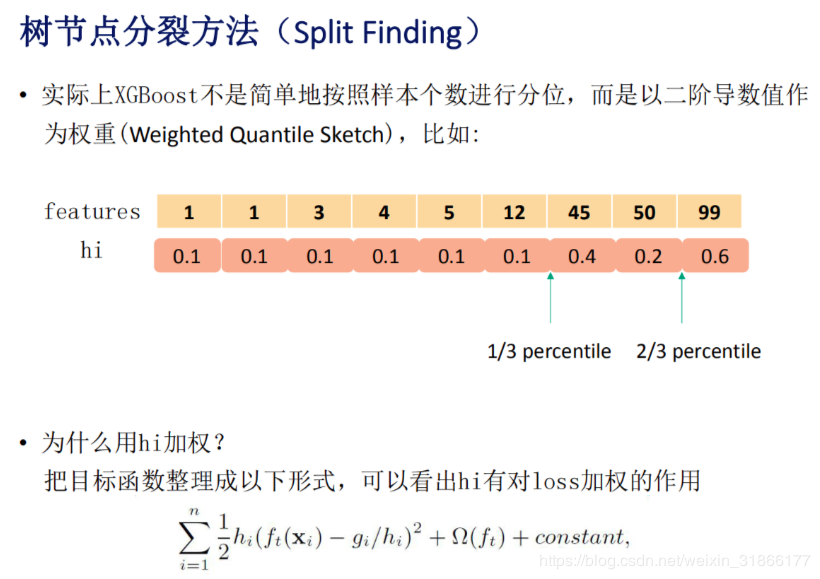
- 详细推导解释,为什么选择损失函数在当前样本的二阶导数作为权重?
$$
\begin{align}
L^{t} &\approx \sum_{i=1}^{n}\left(g_if_t(x_i) + \frac{1}{2}h_if_t^2(x_i)\right) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2 \\
&\approx \sum_{i=1}^{n}\frac{1}{2}h_i\left(2\frac{g_i}{h_i}f_t(x_i) + f_t^2(x_i)\right) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2 \\
&\approx \sum_{i=1}^{n}\frac{1}{2}h_i\left(f_t(x_i) - \frac{g_i}{h_i}\right)^2 + \sum_{i=1}^{n}\left ( \frac{g_i^2}{2h_i} - 2g_if_t(x_i) \right) + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}w_{j}^2 \\
\end{align}
$$- 上面的式子中第二项在原文中用constant来表示,可以被看成某种正则项
- 第一项是一个平方误差表达式,样本 \(x_i\) 对应的输出值为 \(\frac{g_i}{h_i}\),而样本权重就是 \(h_i\)
- 权重代表概率,概率越大说明该点出现的次数或者该点附近的值出现的次数就越多.
- XGBoost分桶流程
- [待更新]
XGBoost整棵树分裂流程
- 初始化 \(f^0(x)\)
- for t=1 to M:
- 计算损失函数对每个训练样本点的一阶导数 \(g_i\),二阶导数 \(h_i\)
- 递归对叶子节点运用树分裂算法生成一颗决策树 \(f^t(x)\),
- (这一步包括叶子节点的分数 \(w_j\) 也都确定下来)
- (这一步可以使用近似分裂算法加快训练速度)
- 把新生成的决策树加入到模型中, \(\hat{y}^t = \hat{y}^{t-1} + f_m(x)\)
传统GDBT与XGBoost的比较
- 参考博客: ML——XGBoost-vs-传统GBDT