ML——共轭梯度法和最速下降法

本文介绍共轭梯度法和最速下降法

  • 最速下降法（Steepest Descent Method）和共轭梯度法（Conjugate Gradient Method, CG）也是求解无约束最优化问题的优化方法，其他无约束优化方法见：ML——求解无约束最优化问题的优化方法
  • 共轭梯度法是以共轭方向为搜索方向的一类算法，最早用于求解线性方程组，后来用于求解无约束最优化问题
  • 最速下降法和共轭梯度法都仅限于求解正定矩阵对应的方程或正定二次型对应的无约束最优化问题

优化问题定义

  • 在满足一定要求的情况下，求解线性方程组的解和求解最优化问题有一定的等价性
  • 当 \(A\) 为对称正定矩阵时，有下面的两个问题等价：
    • 问题一：求解线性方程组
      $$ Ax = b $$
    • 问题二：求解最优化问题的解
      $$ \min_x \frac{1}{2}(x - x^*)^TA(x - x^*) $$
      • 其中 \(x^*\) 为线性方程组的解
    • 等价原因：正定矩阵 \(A\) 使得二次型 \((x - x^*)^TA(x - x^*) \) 一定大于等于0，当二次型 \((x - x^*)^TA(x - x^*) = 0 \) 时，一定有 \(x=x^*\)
  • 对以上最优化问题进一步化简有：
    • 上图中用到了以下性质：
      • 对称正定矩阵的性质： \(A = A^T\)
      • \(x^*\) 为线性方程组的解： \(Ax^* = b\)
    • 上图中 \((Ax,x)\) 表示内积
  • 思考：对于参数数量为2的问题，实际上原始优化问题 \((x - x^*)^TA(x - x^*)\) 的等值线可以理解为是一个椭圆，原始问题的最优解在多个椭圆的圆心
    • 为什么是一个椭圆，因为正定矩阵可以被对角化为一个对角线上元素都是正数的对角矩阵 ，即正定二次型一定可以化简为系数全为正的标准型
    • 假设 \(A\) 已经是一个对角矩阵，对角线上的数字为 \(d_1, d_2\)，那么原始二次型对应的 \(c\) 等值线为： \((x - x^*)^TA(x - x^*) = d_1x_1^2+d_2x_2^2 = c\)

最速下降法

  • 最速下降法推导

    • 上面的式子中，最后一步的推导是直接展开以后得到
      $$
      \begin{align}
      &=\frac{1}{2} (A(x+\alpha r, x+\alpha r)) - (b, (x+\alpha r)) \\
      &= \frac{1}{2} (x^TA^Tx + \alpha r^TA^Tx + \alpha x^TA^Tr + \alpha^2r^TA^Tr) - (b^Tx+\alpha b^T r) \\
      &= \frac{1}{2}( 2\alpha r^TA^Tx) + \frac{1}{2}\alpha^2r^TA^Tr - \alpha b^T r + \frac{1}{2}x^TA^Tx - b^Tx\\
      &= \alpha r^TA^Tx + \frac{1}{2}\alpha^2r^TA^Tr - \alpha (Ax + r)^T r + \frac{1}{2}x^TA^Tx - b^Tx\\
      &= \alpha r^TA^Tx + \frac{1}{2}\alpha^2r^TA^Tr - \alpha x^TA^Tr + \alpha r^Tr + \frac{1}{2}x^TA^Tx - b^Tx\\
      &= \alpha r^TA^Tx - \alpha x^TA^Tr + \frac{1}{2}\alpha^2r^TA^Tr + \alpha r^Tr + \frac{1}{2}x^TA^Tx - b^Tx\\
      &= 0 + \frac{1}{2}\alpha^2r^TA^Tr + \alpha r^Tr + \frac{1}{2}x^TA^Tx - b^Tx\\
      &= \frac{1}{2}\alpha^2r^TA^Tr + \alpha r^Tr + \frac{1}{2}x^TA^Tx - b^Tx\\
      \end{align}
      $$
    • 上面的推导中使用到了 \(b = Ax + r\)，和 \(x^TA^Tr = x^TAr = (x, Ar) = (Ar, x) = r^TA^Tx \)
    • 其中 \( \frac{1}{2}x^TA^Tx - b^Tx\) 与 \(\alpha\) 无关

  • 最速下降法的流程及收敛性分析

    • 收敛速度与特征值有关，当特征值之间的差距过大时，收敛可能会比较慢

  • 最速下降法的收敛性图示分析

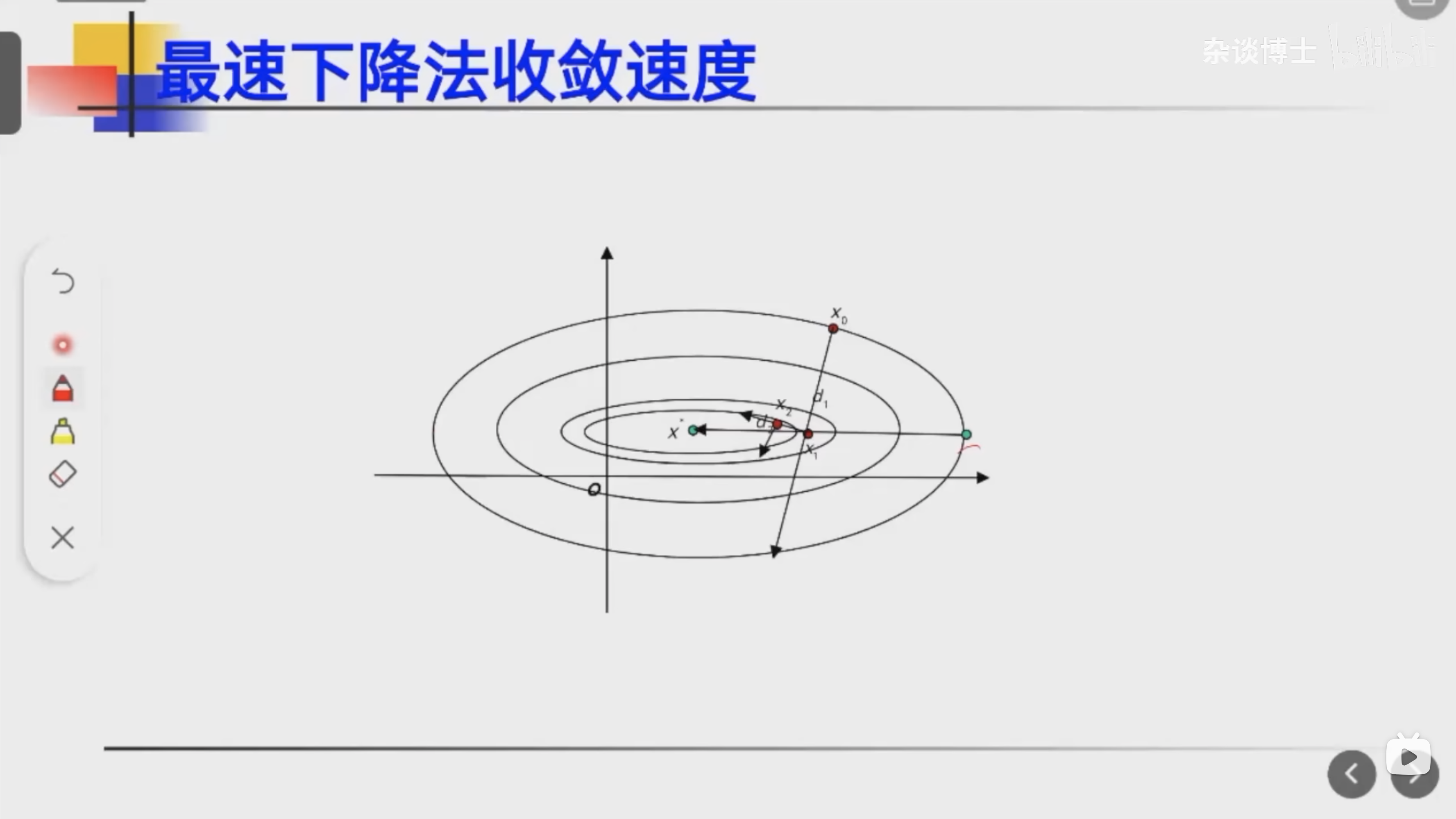
    • 如果运气好，也可能一步到位，如果运气不好则可能要很久才收敛

共轭梯度法

  • 共轭梯度法的引入
    • \(p_{k-1}\) 是上次迭代的方向， \(p_{k}\) 是本次迭代的方向，初始该值设置为 \(p_{-1} = 0\)，或第一步按照 \(p_0 = r_0\) 迭代
    • 步长推导和最速下降法推导一致
  • 共轭梯度法的方向
    • 共轭的含义为：
    • 共轭梯度法名字的由来 ：
      • 共轭来自于： \( \forall i, \quad (Ap_{i},p_{k}) = 0\)，每一步迭代的方向与之前的所有步都是共轭相对于矩阵 \(A\) 共轭的
      • 梯度则来自于下降的方向 \(r\) 是原始目标函数 \(\frac{1}{2}(x - x^*)^TA(x - x^*) = \frac{1}{2}(Ax, x)- (b, x)\) 的梯度，由于 \(r\) 同时也是方程 \(Ax = b\) 的残差 \(r = b-Ax\)，所以也会称 \(r\) 为残差
  • 共轭梯度法的性质
  • 共轭梯度法的流程
    % asset_img Conjugate-Gradient-Method-5.png %}
    • 注意：第0步使用 \(p_0 = r_0\)
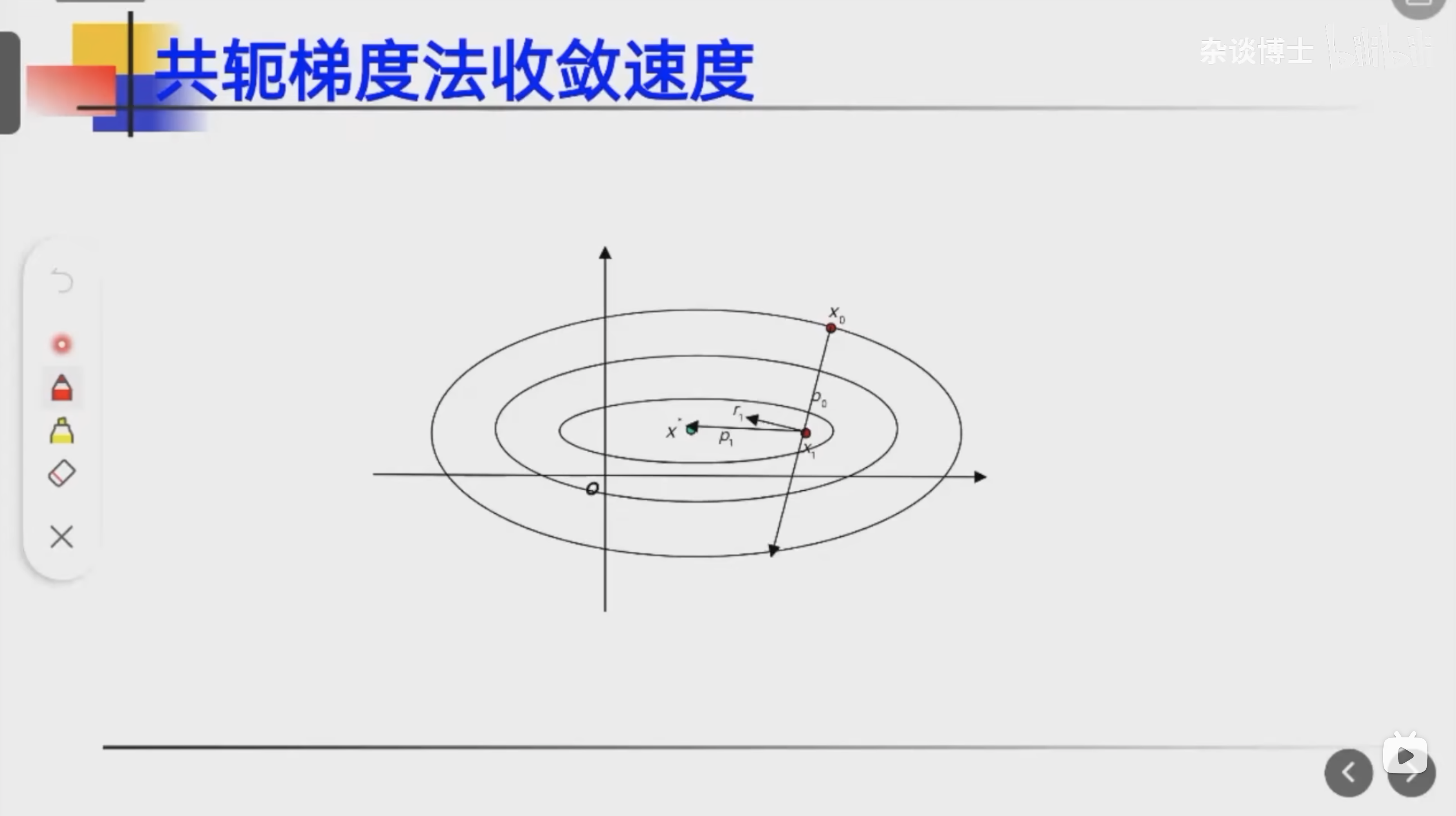
  • 共轭梯度法收敛性