KG——图嵌入综述

Posted on

本文主要介绍图嵌入(Graph Embedding)的发展和方法

图(Graph)

  • 结点和边的集合
  • 经典图论中的图, 知识图谱, 概率图模型中的图等
  • 传统的图算法包括(图论中的):
    • 最小生成树算法: Prim算法, Kruskal算法等
    • 最短路径算法: Dijkstra算法, Floyed算法等
  • 图神经网络算法包括
    • 图嵌入(Graph Embedding): 基于随机游走(Random Walk)生成路径
    • 图卷积神经网络(Graph CNN, GCN): 基于邻居汇聚实现

图嵌入

  • 用低维的向量来表示结点, 同时要求任意在图中相似的节点在向量空间中也接近.
  • 得到的节点的向量表示可以用来解决节点分类等下游任务

DeepWalk

  • 论文链接: DeepWalk KDD 2014
  • 核心思想: 通过将游走路径(walks)当做句子(sentences), 用从截断随机游走(truncated random walks)中得到的局部信息来学习隐式表示
    • 类似于Word2Vec, node对应word, walks对应sentence
  • 核心方法:
    • 随机游走方法进行采样
    • 使用Skip-Gram方法训练采样的样本
  • 实验结果:
    • 论文中展示了DeepWalk在多个多标签网络分类任务中的隐式表示, 比如BlogCatalog, Flickr和YouTube
    • 在某些实验中,仅仅用60%的训练数据即可到达(超过)所有Baseline方法
    • 在稀疏标记数据上F1分数表现良好

随机游走

  • 随机游走方法: 一种可重复访问(有放回采样)的深度优先遍历算法(DFS)
    • 给定起始访问节点A
    • 从A的邻居中随机采样一个节点B作为下一个节点
    • 从B的邻居中随机采样一个节点C作为下一个节点
    • ….
    • 直到序列长度满足truncated条件, 得到一个walk

Skip-Gram 训练

  • 对随机游走采样到的数据进行Skip-Gram训练
  • 最终得到每个节点的表示向量

Node2Vec

  • 论文链接: Node2Vec KDD 2016
  • 核心思想: 综合考虑DFS和BFS的图嵌入方法, 可以视为DeepWalk的一种扩展(DeepWalk的随机游走仅仅是考虑DFS的,不考虑BFS)

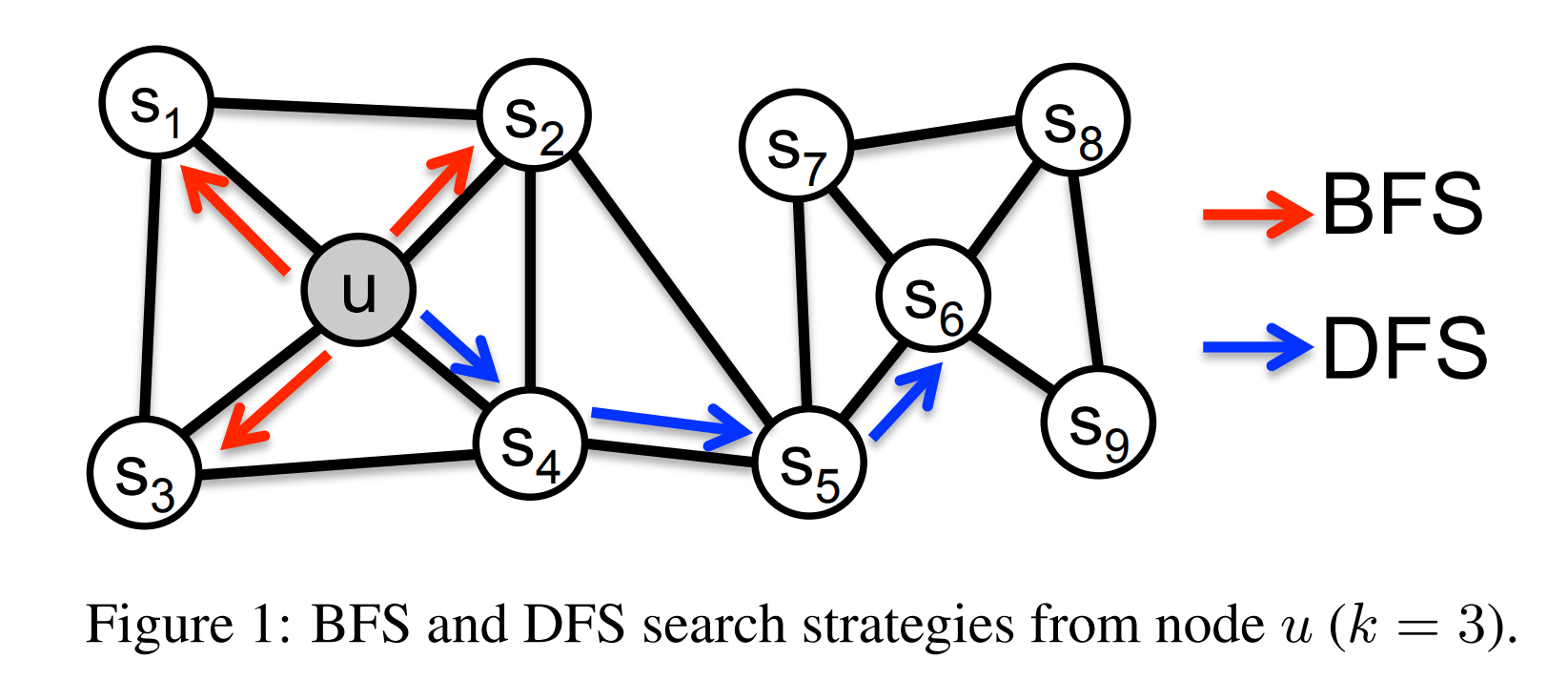
优化目标

  • Node2Vec要解决的问题: 找到一种从节点到embedding向量的映射函数\(f\), 最大化整体后验概率(乘积). 每个节点的后验概率为: 给定某个节点, 相邻节点出现的概率 \(Pr(N_S(u)|f(u))\)
    $$
    \begin{align}
    \max_f\sum_{u \in V} log Pr(N_S(u)|f(u))
    \end{align}
    $$

  • 为了简化上述问题,作者引入两个假设

    • 条件独立性(Conditional independence):
      $$
      \begin{align}
      Pr(N_S(u)|f(u)) = \prod_{n_i \in N_S(u)} Pr(n_i|f(u))
      \end{align}
      $$
    • 特征空间中的对称性(Symmetry in feature space): 假设源节点和邻居节点在特征空间中有对称
      $$
      \begin{align}
      Pr(n_i|f(u)) = \frac{exp(f(n_i)\cdot f(u))}{\prod_{v\in V}exp(f(v)\cdot f(u))}
      \end{align}
      $$
      • 本质上表达的是: 一个节点作为源节点或者邻近节点时都使用同一个特征向量表示
      • 理解: 特征向量的点乘(内积)表示两个点之间的关联程度?