- 参考链接:
名词解释
- VQ-VAE :Vector Quantised - Variational Auto-Encoder,用于将变量编码为离散向量,并可将离线向量恢复为原始向量
- codebook :通常指一种将图像编码为离散向量的机制,实际上指 VQ-VAE 中的 Embedding Space(词表)
- PixelCNN :生成离散像素的自回归模型
PixelCNN的简单介绍
- 原始论文:Conditional Image Generation with PixelCNN Decoders, NIPS 2016, Google DeepMind
- 假设要生成一张 \(32 \times 32 \times 3\) 的三通道图片,矩阵元素是 0-255 的整数,Pixcel将其视为长度为 3072 的句子,词表大小是 256,并用语言模型的方法自回归的生成图片
$$
\begin{align}
p(\mathbf{x})=p(x_1)p(x_2|x_1)p(x_3|x_1,x_2)\dots p(x_{3n^2}|x_1,x_2,\dots,x_{3n^2-1})
\end{align}
$$- 输出类别为 256 维度
- 自回归方法的缺点:
- 序列太长,按照序列依次生成,生成速度慢;长程依赖不容易捕捉(不管是CNN还是RNN)
- 像素值是有连续大小关系的(比如像素值为99时,预估为100也不是不可以,大事预估为10就不可以),但序列化的自回归方法本质是多分类建模,无法捕捉这种含义(但回过头来看,应该还好,毕竟大模型中的相似词也不需要显示建模)
AE、AVE和VQ-VAE
- AE(Auto-Encoder) :包含一个编码器和一个解码器
- 编码器 :将原始输入向量 \(\mathbf{x}\) 编码为一个较小的连续向量 \( \mathbf{z} = encoder(\mathbf{x}) \)
- 解码器 :将连续向量 \(\mathbf{z}\) 解码为和原始输入差不多的向量\( \mathbf{x}’ = decoder(\mathbf{z}) \)
- VAE(Variational Auto-Encoder) :包含一个编码器和一个解码器
- 编码器 :将原始输入向量 \(\mathbf{x}\) 编码为一个服从标准正太分布的连续向量 \( \mathbf{z} = encoder(\mathbf{x}) \),具体实现是先用模型输出 \(\mu,\sigma^2\),再采样得到向量 \( \mathbf{z} \)
- 解码器 :将连续向量 \(\mathbf{z}\) 解码为和原始输入差不多的向量\( \mathbf{x}’ = decoder(\mathbf{z}) \)
- VQ-VAE(Vector Quantised Variational Auto-Encoder) :
- 编码器 :将原始输入向量 \(\mathbf{x}\) 编码为一个较小的离散向量 \( \mathbf{z} = encoder(\mathbf{x}) \)(这里的离散向量是隐式的,是 Embedding Space 中的索引,不会直接表示出来)
- 解码器 :将离散向量 \(\mathbf{z}\) 解码为和原始输入差不多的向量\( \mathbf{x}’ = decoder(\mathbf{z}) \)
- 许多博主认为VQ-VAE更像是一个AE,而不是VAE,因为无法直接从已知分布中采样隐变量来生成图片,而是借助PixelCNN来实现
VQ-VAE讲解
- VQ-VAE整体示意图如下(from Neural Discrete Representation Learning, NIPS 2017, Google DeepMind)
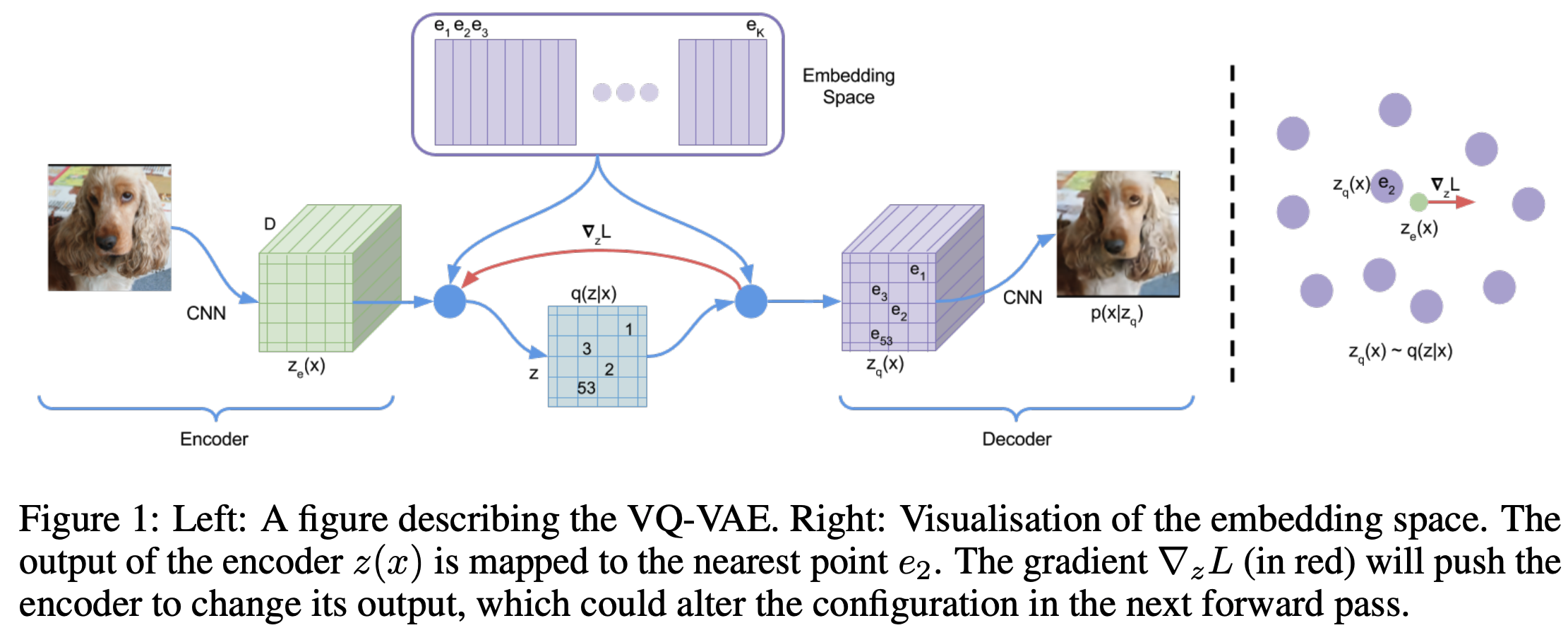
- 其中 Embedding Space 是一个 \(K\times d\) 维的此表,每个向量 \(\mathbf{e}_k\) 都是 \(d\) 维向量
- 如上图所示,从左到右,VQ-VAE的整个过程可以拆解为如下的流程:
- 编码器 :将输入图片 \(\mathbf{x}\) 编码为 \(m\times m\) 个 \(d\) 维的连续向量,得到结果为 \(m\times m \times d\) 维,\(\mathbf{z} = z_e(\mathbf{x})\)
- 最近邻匹配 :用 \(\mathbf{z}\) 在 Embedding Space 词表中通过最近邻匹配 ,将 \(\mathbf{z}\) 中的每个向量都映射为 Embedding Space 中的最近邻点(nearest point \(e_{k^*}\),匹配后得到的结果使用 \(z_q(\mathbf{x})\) 表示
$$ z_q(\mathbf{x})_{i,j} = e_{k^*} = \mathop{\arg\min}_{e_k} \Vert \mathbf{z}_{i,j} - \mathbf{e}_k \Vert_2 $$- 最近邻搜索隐含离散的思想 :实际上,最近邻的匹配过程可以看做是,先将连续向量转化为一个离散值(索引 \(k^*\)),此时得到的是一个 \(m\times m\) 的离散矩阵,称为离散编码或离散隐变量(discrete latents),然后再将离散索引值转换为一个连续向量(索引 \(k^*\) 在 Embedding Space 中抽取向量即可)的过程
- 解码器 :将最近邻搜索的映射结果 \(z_q(\mathbf{x})\) 解码为原始输入大小的向量 \(\hat{\mathbf{x}}\),试图重构原始输入 \(\hat{\mathbf{x}} = decoder(z_q(\mathbf{x}))\)
补充知识:Straight-Through Estimator
- 关于 Straight-Through Estimator 的其他说明:
from VQ-VAE的简明介绍:量子化自编码器
VQ-VAE使用了一个很精巧也很直接的方法,称为Straight-Through Estimator,你也可以称之为“直通估计”,它最早源于Benjio的论文《Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation》,在VQ-VAE原论文中也是直接抛出这篇论文而没有做什么讲解。但事实上直接读这篇原始论文是一个很不友好的选择,还不如直接读源代码
事实上Straight-Through的思想很简单,就是前向传播的时候可以用想要的变量(哪怕不可导),而反向传播的时候,用你自己为它所设计的梯度 - 博客中给了例子来说明,举例来说,设计一个如下的目标函数:
$$ Loss = \Vert x - decoder(z + sg[z_q - z]) \Vert_2^2 $$- 其中 \(sg[\cdot]\) 表示 stop gradient 的含义
- 前向传播时,上面的损失函数等价于 \(\Vert x - decoder(z_q) \Vert_2^2\)
- 后向传播时,上面的损失函数等价于 \(\Vert x - decoder(z) \Vert_2^2\)
- 同理,我们可以任意定义函数的梯度(实现前向和后向不一致)
VQ-VAE的损失函数
重建误差
- 直接优化下面的重建误差是不行的,因为最近邻匹配过程梯度不可导:
$$ L_{reconstruct} = \Vert \mathbf{x} - decoder(z_q(\mathbf{x})) \Vert_2^2 $$ - 作者设计了下面的重建误差:
$$ L_{reconstruct} = \Vert \mathbf{x} - decoder(z_e(\mathbf{x}) + sg[z_q(\mathbf{x}) - z_q(\mathbf{x})]) \Vert_2^2 $$- 前向传播时,上面的损失函数等价于 \(\Vert \mathbf{x} - decoder(z_q(\mathbf{x})) \Vert_2^2\)
- 后向传播时,上面的损失函数等价于 \(\Vert \mathbf{x} - decoder(z_e(\mathbf{x})) \Vert_2^2\)
- 本质上实现了将梯度从 \(z_q(\mathbf{x})\) 全部复制给了 \(z_e(\mathbf{x})\)
- 问题:为什么可以直接这样, \(z_q(\mathbf{x})\) 和 \(z_e(\mathbf{x})\) 不相同,可以直接这样传递梯度吗?如何理解这种传递?
- 回答:VQ-VAE中,同时会增加损失函数,保证 \(z_q(\mathbf{x})\) 和 \(z_e(\mathbf{x})\) 足够接近
Embedding Space 优化
- Embedding Space 优化的目标 :为了保证从 \(z_q(\mathbf{x})\) 向 \(z_e(\mathbf{x})\) 复制梯度传播是OK的,我们需要 \(z_q(\mathbf{x})\) 和 \(z_e(\mathbf{x})\) 足够接近
$$ L_{similar} = \Vert z_e(\mathbf{x}) - z_q(\mathbf{x}) \Vert_2^2$$ - 理论上,至此已经可以了,但是原始论文中,作者将上述的损失拆解成两个了,根据博客 VQ-VAE的简明介绍:量子化自编码器 的说法,考虑到实际上 \(z_q(\mathbf{x})\) 是相对自由的,而 \(z_e(\mathbf{x})\) 则需要保证重构效果,所以希望让 \(z_q(\mathbf{x})\) 去靠近 \(z_e(\mathbf{x})\),而不是 \(z_e(\mathbf{x})\) 去靠近 \(z_q(\mathbf{x})\),所以把上面的损失函数拆解为
$$ L_{similar} = \beta \Vert sg[z_e(\mathbf{x})] - z_q(\mathbf{x}) \Vert_2^2 + \gamma\Vert z_e(\mathbf{x}) - sg[z_q(\mathbf{x})] \Vert_2^2$$- 第一项相当于固定 \(z_e(\mathbf{x})\),让 \(z_q(\mathbf{x})\) 靠近 \(z_e(\mathbf{x})\),第二项同理
- \(\beta,\gamma\) 用于调节学习比重,文章中使用 \(\gamma = 0.25\beta\)
- codebook的其他优化方式-滑动平均方法 :
- 实际上,对于同一个 codebook 向量 \(e_i\),可能会作为多个 \(z_e(\mathbf{x})\) 的最近邻向量而被检索,假设 \(e_i\) 的最近邻向量共 \(n_i\) 个,组合为 \(z_{i,j}\),此时有
$$ e_i = \frac{1}{n_i}\sum_{j=1}^{n_i} z_{i,j}$$ - 由于小批量训练时上面的公式容易出现波动,所以可以使用滑动平均(文章中使用指数移动平均(EMA))来更新 codebook,实现 codebook的在线更新
- 实际上,对于同一个 codebook 向量 \(e_i\),可能会作为多个 \(z_e(\mathbf{x})\) 的最近邻向量而被检索,假设 \(e_i\) 的最近邻向量共 \(n_i\) 个,组合为 \(z_{i,j}\),此时有
VQ-VAE损失函数的最终形式
- VQ-VAE损失函数的最终形式可以表示如下:
$$ L_{vq-vae} = \Vert \mathbf{x} - decoder(z_e(\mathbf{x}) + sg[z_q(\mathbf{x}) - z_q(\mathbf{x})]) \Vert_2^2 + \beta \Vert sg[z_e(\mathbf{x})] - z_q(\mathbf{x}) \Vert_2^2 + \gamma\Vert z_e(\mathbf{x}) - sg[z_q(\mathbf{x})] \Vert_2^2 $$
附录:离散化采样编码
- 有了VQ-VAE以后,我们已经可以将图片编码为 \(m\times m\) 的离散矩阵了,此时使用 PixelCNN 来学习编码分布,然后再利用 PixelCNN 来随机生成新的编码矩阵,再映射回到 \(z_q(\mathbf{x})\),从而可通过解码器生成图片
附录:VQ-VAE与VAE的关系讨论
- 从VAE将图片编码为一个高斯分布,然后再重建的思路看,VQ-VAE将图片编码为一个离散分布,然后再重建,只是VQ-VAE的这个离散分布不容易采样,导致需要使用一个额外的 PixelCNN 来学习
- 相对VAE,VQ-VAE中是没有KL散度项的,但也有人推导,博客 VQ-VAE的简明介绍:量子化自编码器 中的评论

附录:VQ-VAE-2
- 原始论文:Generating Diverse High-Fidelity Images with VQ-VAE-2, NeurIPS 2019, Google
- 整体结构如下:
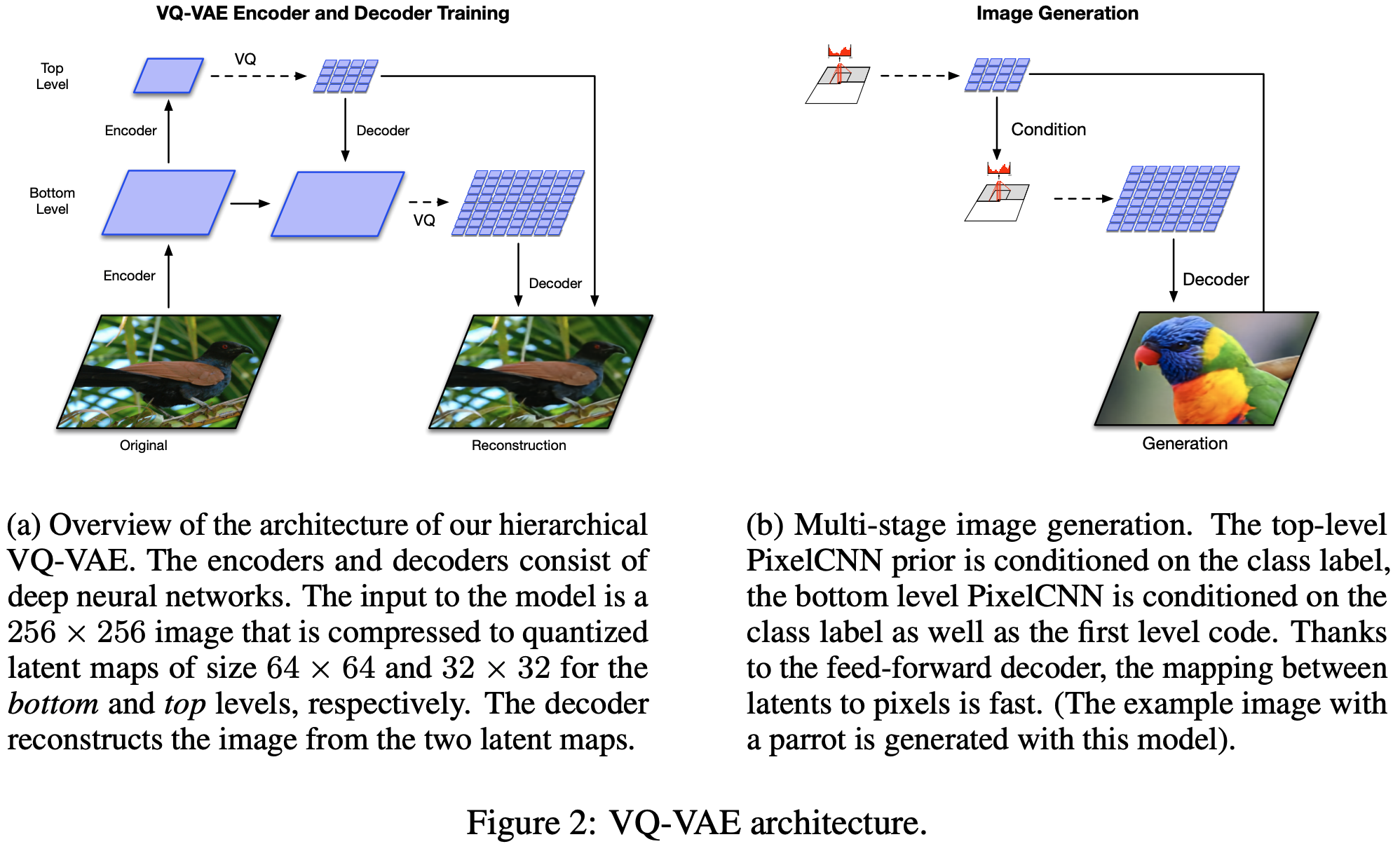
- VQ-VAE-2 相对 VQ-VAE 的核心改进是:
主要变化就是把 VQ-VAE 的 encoder 和 decoder 都进行了分层, bottom层对local feature进行建模,top层采取全局自注意力机制
附录:VQ-VAE中的 Codebook Collapse 问题
- Codebook Collapse(码本坍塌) 是 VQ-VAE(Vector Quantized Variational Autoencoder)及其变体中常见的一个问题,指的是在训练过程中 ,编码本(codebook)中的大量向量从未被使用 ,只有少数几个编码向量被频繁使用的情况
- Codebook Collapse 问题表现 :
- 编码向量利用率低 :大部分codebook向量在训练过程中从未被选择
- 信息损失 :由于实际使用的编码向量远少于设计容量,模型表达能力受限
- 重建质量下降 :有限的活跃编码向量难以充分表示输入的多样性
- Codebook Collapse 问题产生原因 :
- 某些编码向量可能在训练早期更容易被选择,后来跟输出越来越接近,形成”富者愈富”效应;
- VQ的硬分配机制使得未被选择的编码向量无法获得梯度更新,从而导致某些编码向量长期得不到更新
- Codebook Collapse 问题解决方案 :
- 定期重置未被使用的编码向量,让这些向量有机会被更新;
- 引入一定程度的软分配(如Soft-VQ),以一定概率匹配最近邻向量;
- 添加鼓励codebook利用的正则项;
- 注:Codebook 向量越多,Codebook Collapse 问题就越严重
- Codebook collapse问题直接影响VQ-VAE的性能,解决这一问题对于提高模型表现和压缩效率至关重要