- 参考链接:
整体说明
- VQ-VAE的问题 :自回归(autoregressive,AR)模型在高分辨率图像生成中,向量量化(vector quantization,VQ)通过将图像表示为离散编码序列来实现建模。较短的序列长度可降低处理编码间的长程交互的计算成本,作者认为现有VQ方法在率失真权衡下无法同时实现序列缩短和高保真图像生成
- 论文提出了一种两阶段框架 :包括RQ-VAE(Residual-Quantized VAE)和 RQ-Transformer ,以高效生成高分辨率图像
- 在固定码本大小下,RQ-VAE能精确近似图像特征图,并将其表示为多层离散编码的堆叠图
- RQ-Transformer通过学习预测下一位置的量化特征向量(即预测下一组编码)来生成图像。得益于RQ-VAE的精确近似,256×256图像可表示为8×8分辨率的特征图,从而显著降低RQ-Transformer的计算成本
- 实验表明,该框架在无条件与有条件图像生成任务中均优于现有AR模型,且采样速度显著提升
文章引言
- 向量量化(vector quantization,VQ) 已成为自回归(autoregressive,AR)模型生成高分辨率图像的基础技术。具体而言,图像特征图经VQ量化和顺序重排(如光栅扫描)后,被表示为离散编码序列。量化完成后,AR模型通过顺序预测编码序列生成图像,从而避免直接预测所有像素
- 较短的序列能显著降低AR模型的计算成本(因为AR模型需利用历史编码预测后续编码)。然而,现有方法在率失真权衡下难以缩减序列长度。例如,VQ-VAE需指数级增长的码本以降低特征图分辨率并保持重建质量,但大码本会导致参数激增和码本坍缩(Codebook Collapse)问题,使训练不稳定
- 本研究提出RQ-VAE(Residual-Quantized VAE),通过残差量化(residual quantization,RQ)精确近似特征图并降低其空间分辨率:
- RQ在固定码本大小下递归量化特征图,以粗到细的方式生成多层离散编码堆叠图。经D次迭代后,特征图可表示为D层编码的堆叠。由于RQ能组合码本大小的D次方个向量,RQ-VAE无需大码本即可精确近似特征图。例如,RQ-VAE可将256×256图像的特征图分辨率降至8×8
- 此外,论文提出RQ-Transformer来预测RQ-VAE提取的编码。RQ-Transformer将量化特征图转换为特征向量序列,并预测下一位置的D个编码。得益于RQ-VAE降低的分辨率,RQ-Transformer能显著减少计算成本并更易学习长程交互。论文还提出软标签和随机采样技术,缓解训练中的暴露偏差问题
- 主要贡献包括:
- 1)提出RQ-VAE ,以多层编码堆叠图表示图像并实现高保真重建;
- 2)提出RQ-Transformer及其训练技术以解决暴露偏差;
- 3)在图像质量、计算成本和采样速度上显著优于现有AR模型
相关工作
- 图像合成的AR建模 :AR模型在图像生成中表现优异,但直接建模原始像素速度慢且质量低。现有研究结合VQ-VAE将图像表示为离散编码,再由AR模型预测。VQ-GAN通过对抗和感知损失提升重建质量,但特征图分辨率进一步降低时,受限于码本大小难以精确近似
- 其他应用中的VQ :复合量化技术在其他领域用于精确近似向量。乘积量化(product quantization,PQ)通过码本中线性无关向量之和近似向量;加性量化(additive quantizationAQ)使用相关向量,但编码搜索为NP难问题;残差量化(RQ)通过递归量化残差生成多层编码,用于神经网络压缩。RQ-VAE采用RQ离散化图像特征图,并在所有量化步骤中共享单一码本
整体方法(两阶段)
- 论文提出了一个由残差量化变分自编码器(RQ-VAE)和RQ-Transformer组成的两阶段框架,用于图像的自回归建模:
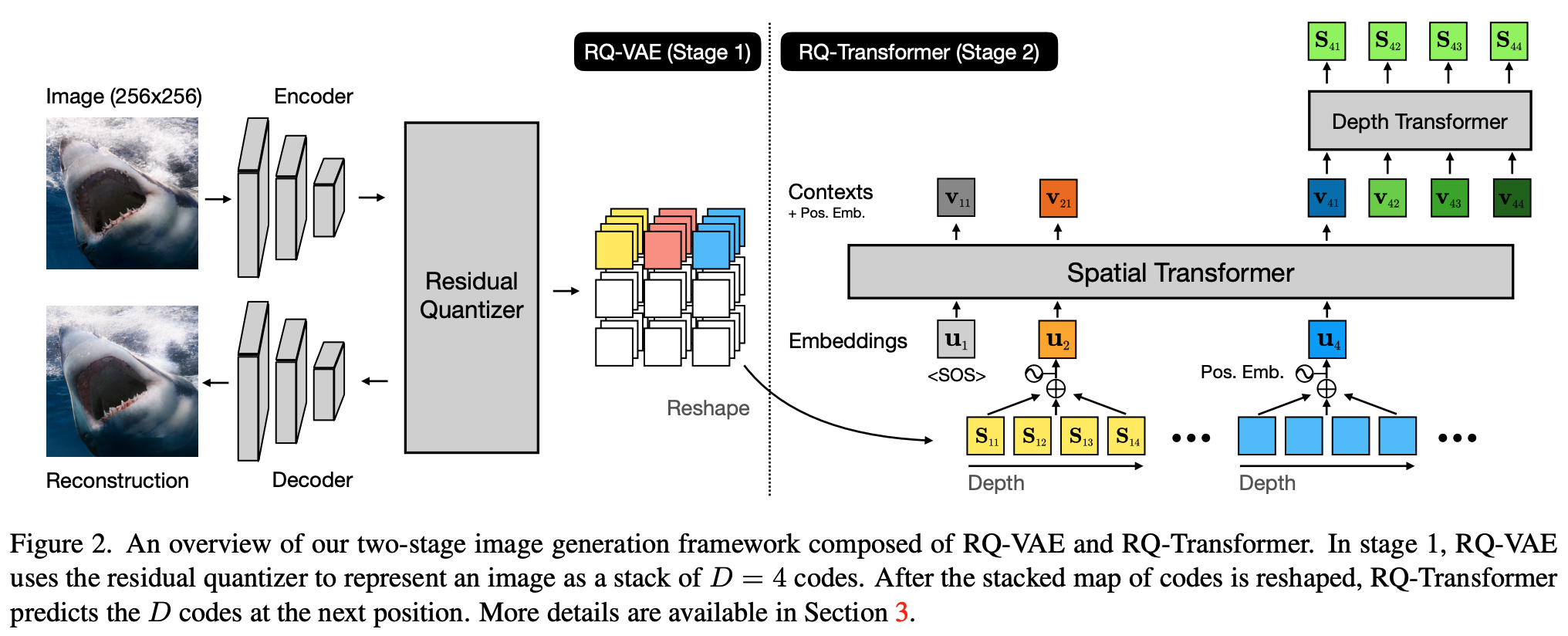
- RQ-VAE利用码本将图像表示为由D个离散编码堆叠而成的映射。随后,论文的RQ-Transformer通过自回归方式预测下一个空间位置的D个编码。论文还介绍了RQ-Transformer如何解决自回归模型训练中的曝光偏差问题
第一阶段:残差量化变分自编码器(RQ-VAE)
- 本节首先介绍向量量化(VQ)和VQ-VAE的公式化表示,随后提出RQ-VAE。RQ-VAE能够在无需增加码本大小的情况下精确逼近特征映射,并解释RQ-VAE如何将图像表示为离散编码的堆叠映射
VQ与VQ-VAE的公式化表示
- 设码本\(\mathcal{C}\)为一个有限集合\(\{(k,\mathbf{e}(k))\}_{k\in[K]}\),其中包含编码\(k\)与其对应的编码嵌入\(\mathbf{e}(k)\in\mathbb{R}^{n_{z} }\)的配对,\(K\)为码本大小,\(n_{z}\)为编码嵌入的维度。给定向量\(\mathbf{z}\in\mathbb{R}^{n_{z} }\),\(\mathcal{Q}(\mathbf{z};\mathcal{C})\)表示对\(\mathbf{z}\)的向量量化,即选择嵌入与\(\mathbf{z}\)最接近的编码:
$$
\mathcal{Q}(\mathbf{z};\mathcal{C})=\operatorname*{arg,min}_{k\in[K]}|\mathbf{z}-\mathbf{e}(k)|^{2}_{2}.
$$ - VQ-VAE将图像编码为离散编码映射后,再从编码映射中重建原始图像。设\(E\)和\(G\)分别为VQ-VAE的编码器和解码器。给定图像\(\mathbf{X}\in\mathbb{R}^{H_{o}\times W_{o}\times 3}\),VQ-VAE提取特征映射\(\mathbf{Z}=E(\mathbf{X})\in\mathbb{R}^{H\times W\times n_{z} }\),其中\((H,W)=(H_{o}/f,W_{o}/f)\)为\(\mathbf{Z}\)的空间分辨率,\(f\)为下采样因子。通过对每个位置的每个特征向量应用VQ,VQ-VAE量化\(\mathbf{Z}\)并返回其编码映射\(\mathbf{M}\in[K]^{H\times W}\)和量化特征映射\(\hat{\mathbf{Z} }\in\mathbb{R}^{H\times W\times n_{z} }\):
$$
\mathbf{M}_{hw}=\mathcal{Q}(\mathbf{Z}_{hw};\mathcal{C}),\\
\hat{\mathbf{Z} }_{hw}=\mathbf{e}(\mathbf{M}_{hw}),
$$- 其中\(\mathbf{Z}_{hw}\in\mathbb{R}^{n_{z} }\)为位置\((h,w)\)处的特征向量,\(\mathbf{M}_{hw}\)为其编码。最终,输入图像被重建为\(\hat{\mathbf{X} }=G(\hat{\mathbf{Z} })\)
- 论文注意到,降低\(\hat{\mathbf{Z} }\)的空间分辨率\((H,W)\)对自回归建模非常重要,因为自回归模型的计算成本随\(HW\)增加。然而,由于VQ-VAE对图像进行了有损压缩,降低\((H,W)\)与保留图像信息之间存在权衡。具体而言,码本大小为\(K\)的VQ-VAE使用\(HW\log_{2}K\)比特表示图像的编码。根据率失真理论[38],最佳重建误差取决于比特数。因此,若要将\((H,W)\)进一步降低至\((H/2,W/2)\)并保持重建质量,VQ-VAE需要大小为\(K^{4}\)的码本。然而,大码本会导致码本崩溃问题[8]和不稳定的训练
残差量化(RQ)
- 论文采用残差量化(Residual-Quantized,RQ)来离散化向量\(\mathbf{z}\),而非增加码本大小。给定量化深度\(D\),RQ将\(\mathbf{z}\)表示为有序的\(D\)个编码:
$$
\mathcal{RQ}(\mathbf{z};\mathcal{C},D)=(k_{1},\cdots,k_{D})\in[K]^{D},
$$- 其中\(\mathcal{C}\)为大小为\(|\mathcal{C}|=K\)的码本;\(k_{d} = 1,\cdots,K\)为深度\(d\)处的编码(离散值);\(d=1,\cdots,D\)
- 从第0个残差\(\mathbf{r}_{0}=\mathbf{z}\)开始,RQ递归计算编码\(k_{d}\)(残差\(\mathbf{r}_{d-1}\)的编码)和下一个残差\(\mathbf{r}_{d}\):
$$
k_{d}=\mathcal{Q}(\mathbf{r}_{d-1};\mathcal{C}),\\
\mathbf{r}_{d}=\mathbf{r}_{d-1}-\mathbf{e}(k_{d}), \tag{4}
$$- \(k_{d}=\mathcal{Q}(\mathbf{r}_{d-1};\mathcal{C})\) 表示从 codebook \(\mathcal{C}\) 中搜索到残差向量 \(\mathbf{r}_{d-1}\) 的最近邻向量的索引(或编码) \(k_{d}\),该索引对应的编码向量为 \(\mathbf{e}(k_{d})\)
- 定义\(\hat{\mathbf{z} }^{(d)}=\sum_{i=1}^{d}\mathbf{e}(k_{i})\)为前\(d\)个编码嵌入的部分和,RQ的递归量化以从粗到细的方式逼近向量。\(\hat{\mathbf{z} }^{(1)}\)是码本中最接近\(\mathbf{z}\)的编码嵌入\(\mathbf{e}(k_{1})\),随后的编码被依次选择以减少量化误差。因此,部分和\(\hat{\mathbf{z} }^{(d)}\)随着\(d\)的增加提供更精细的逼近
- 最终:\(\hat{\mathbf{z} }:=\hat{\mathbf{z} }^{(D)}\)为\(\mathbf{z}\)的量化向量
- 理解:开始的残差比较大,随着不断地用残差最最近邻匹配,随着匹配次数的增加,残差越来越小,越来越精细
- 每层共享codebook :尽管可以为每个深度\(d\)单独构建码本,但论文为所有量化深度使用单一的共享码本\(\mathcal{C}\)。共享码本有两个优势:一是避免了为每个深度确定码本大小的超参数搜索,二是所有编码嵌入在每个深度均可使用,从而最大化其效用
- RQ与VQ的讨论 :值得注意的是,在码本大小相同的情况下,RQ比VQ能更精确地逼近向量。VQ将整个向量空间\(\mathbb{R}^{n_{z} }\)划分为\(K\)个簇,而深度为\(D\)的RQ最多将向量空间划分为\(K^{D}\)个簇。因此,RQ的划分能力与码本大小为\(K^{D}\)的VQ相当
RQ-VAE
- 论文提出RQ-VAE以精确量化图像的特征映射。RQ-VAE同样采用VQ-VAE的编码器-解码器架构,但将VQ模块替换为上述RQ模块。具体而言,深度为\(D\)的RQ-VAE将特征映射\(\mathbf{Z}\)表示为编码的堆叠映射\(\mathbf{M}\in[K]^{H\times W\times D}\),并提取深度\(d\)处的量化特征映射\(\hat{\mathbf{Z} }^{(d)}\in\mathbb{R}^{H\times W\times n_{z} }\):
$$
\mathbf{M}_{hw}=\mathcal{RQ}(E(\mathbf{X})_{hw};\mathcal{C},D),\\
\hat{\mathbf{Z} }_{hw}^{(d)}=\sum_{d^{\prime}=1}^{d}\mathbf{e}(\mathbf{M}_{hwd^{\prime} }). \tag{5}
$$- \(E(\mathbf{X})\) 表示编码器将输入 \(\mathbf{X}\) 编码后输出为 \(H\times W\) 维度的矩阵,\(E(\mathbf{X})_{hw}\) 则表示矩阵中的一个向量(索引为\(h,w\))
- 为简洁起见,深度\(D\)处的量化特征映射\(\hat{\mathbf{Z} }^{(D)}\)也记为\(\hat{\mathbf{Z} }\)。最终,解码器\(G\)从\(\hat{\mathbf{Z} }\)重建输入图像:\(\hat{\mathbf{X} }=G(\hat{\mathbf{Z} })\)
- RQ-VAE能够以较低计算成本高效生成高分辨率图像。对于固定的下采样因子\(f\),RQ-VAE比VQ-VAE能生成更真实的图像重建,因为RQ-VAE可以利用给定的码本大小精确逼近特征映射。此外,RQ-VAE允许进一步增加\(f\)和降低\((H,W)\),同时保持重建质量,从而降低自回归模型的计算成本、提高图像生成速度,并更好地学习编码间的长程交互
- RQ-VAE的训练 :通过梯度下降训练编码器\(E\)和解码器\(G\),损失函数为\(\mathcal{L}=\mathcal{L}_{\textrm{recon} }+\beta\mathcal{L}_{\textrm{commit} }\),其中\(\beta>0\)为乘性因子。重建损失(reconstruction loss)\(\mathcal{L}_{\textrm{recon} }\)和承诺损失(commitment loss)\(\mathcal{L}_{\textrm{commit} }\)定义为:
$$
\mathcal{L}_{\textrm{recon} }=|\mathbf{X}-\hat{\mathbf{X} }|_{2}^{2},\\
\mathcal{L}_{\textrm{commit} }=\sum_{d=1}^{D}\left|\mathbf{Z}-\operatorname{sg}\left[\hat{\mathbf{Z} }^{(d)}\right]\right|_{2}^{2},
$$- 其中\(\operatorname{sg}[\cdot]\)为停止梯度操作,通过RQ模块的反向传播使用直接估计器[40]。承诺损失是所有深度\(d\)的量化误差之和,而非单一项\(|\mathbf{Z}-\operatorname{sg}[\hat{\mathbf{Z} }]|_{2}^{2}\),目的是使\(\hat{\mathbf{Z} }^{(d)}\)随\(d\)增加逐步减少量化误差,从而实现从粗到细的逼近并保持训练稳定。码本\(\mathcal{C}\)通过聚类特征的指数移动平均更新[40]
RQ-VAE的对抗训练
- RQ-VAE还通过对抗学习提升重建图像的感知质量,使用基于块的对抗损失[20]和感知损失[21],具体细节见补充材料
第二阶段:RQ-Transformer
- 本节提出RQ-Transformer ,用于自回归预测RQ-VAE提取的编码堆叠。在形式化RQ-VAE编码的自回归建模后,介绍RQ-Transformer如何高效学习离散编码的堆叠映射,并提出训练技术以解决自回归模型中的曝光偏差问题
深度为D的编码自回归建模
- RQ-VAE提取编码映射\(\mathbf{M}\in[K]^{H\times W\times D}\)后,通过光栅扫描顺序(raster scan order)[30]将其空间索引重排为2D编码数组\(\mathbf{S}\in[K]^{T\times D}\),其中\(T=HW\)。即,\(\mathbf{S}_{t}\)(\(\mathbf{S}\)的第\(t\)行)包含\(D\)个编码:
$$
\mathbf{S}_{t}=(\mathbf{S}_{t1},\cdots,\mathbf{S}_{tD})\in[K]^{D}\quad\textrm{for }t\in[T].
$$ - 将\(\mathbf{S}\)视为图像的离散隐变量,自回归模型学习\(p(\mathbf{S})\),其自回归分解为:
$$
p(\mathbf{S})=\prod_{t=1}^{T}\prod_{d=1}^{D}p(\mathbf{S}_{td},|,\mathbf{S}_{<t,d},\mathbf{S}_{t,<d}).
$$
RQ-Transformer架构
- 一种朴素方法是将\(\mathbf{S}\)展开为长度为\(TD\)的序列并输入传统Transformer[41],但这既未利用RQ-VAE减少的序列长度\(T\),也未降低计算成本。因此,论文提出RQ-Transformer以高效学习RQ-VAE提取的深度为\(D\)的编码。如图2所示,RQ-Transformer由Spatial Transformer和Depth Transformer组成
- Spatial Transformer :Spatial Transformer是一组掩码自注意力块,用于提取汇总先前位置信息的上下文向量。输入\(\mathbf{u}_{t}\)定义为:
$$
\mathbf{u}_{t}=\mathrm{P}\mathrm{E}_{T}(t)+\sum_{d=1}^{D}\mathbf{e}(\mathbf{S}_{t-1,d})\quad\textrm{for }t>1,
$$- 其中\(\mathrm{P}\mathrm{E}_{T}(t)\)为空间位置\(t\)的位置嵌入,第二项为量化特征向量(见式5)。第一位置的输入\(\mathbf{u}_{1}\)为可学习嵌入,表示序列起始。Spatial Transformer处理后,上下文向量\(\mathbf{h}_{t}\)编码\(\mathbf{S}_{ < t}\)的所有信息:
$$
\mathbf{h}_{t}=\text{SpatialTransformer}(\mathbf{u}_{1},\cdots,\mathbf{u}_{t}).
$$
- 其中\(\mathrm{P}\mathrm{E}_{T}(t)\)为空间位置\(t\)的位置嵌入,第二项为量化特征向量(见式5)。第一位置的输入\(\mathbf{u}_{1}\)为可学习嵌入,表示序列起始。Spatial Transformer处理后,上下文向量\(\mathbf{h}_{t}\)编码\(\mathbf{S}_{ < t}\)的所有信息:
- Depth Transformer :基于上下文向量\(\mathbf{h}_{t}\),Depth Transformer自回归预测位置\(t\)的\(D\)个编码\((\mathbf{S}_{t1},\cdots,\mathbf{S}_{tD})\)。输入\(\mathbf{v}_{td}\)定义为:
$$
\mathbf{v}_{td}=\text{PE}_{D}(d)+\sum_{d^{\prime}=1}^{d-1}\mathbf{e}(\mathbf{S}_{td^{\prime} })\quad\textrm{for }d>1,
$$- 其中\(\text{PE}_{D}(d)\)为深度\(d\)的位置嵌入,所有位置\(t\)共享。对于\(d=1\),使用\(\mathbf{v}_{t1}=\text{PE}_{D}(1)+\mathbf{h}_{t}\)。Depth Transformer预测条件分布\(\mathbf{p}_{td}(k)=p(\mathbf{S}_{td}=k|\mathbf{S}_{<t,d},\mathbf{S}_{t,<d})\):
$$
\mathbf{p}_{td}=\text{DepthTransformer}(\mathbf{v}_{t1},\cdots,\mathbf{v}_{td}).
$$
- 其中\(\text{PE}_{D}(d)\)为深度\(d\)的位置嵌入,所有位置\(t\)共享。对于\(d=1\),使用\(\mathbf{v}_{t1}=\text{PE}_{D}(1)+\mathbf{h}_{t}\)。Depth Transformer预测条件分布\(\mathbf{p}_{td}(k)=p(\mathbf{S}_{td}=k|\mathbf{S}_{<t,d},\mathbf{S}_{t,<d})\):
- RQ-Transformer的训练目标是最小化负对数似然损失\(\mathcal{L}_{AR}\):
$$
\mathcal{L}_{AR}=\mathbb{E}_{\mathbf{S} }\mathbb{E}_{t,d}\left[-\log p(\mathbf{S}_{td}|\mathbf{S}_{<t,d},\mathbf{S}_{t,<d})\right].
$$ - 计算复杂度 :RQ-Transformer的计算复杂度远低于朴素方法(展开为1D序列)。Transformer处理长度为\(TD\)的序列时,计算复杂度为\(O(NT^{2}D^{2})\)[41]。而RQ-Transformer的空间和Depth Transformer的计算复杂度分别为\(O(N_{\text{spatial} }T^{2})\)和\(O(N_{\text{depth} }TD^{2})\),总复杂度为\(O(N_{\text{spatial} }T^{2}+N_{\text{depth} }TD^{2})\),显著低于\(O(NT^{2}D^{2})\)。第4.3节显示,RQ-Transformer的图像生成速度更快
软标签与随机采样
- 曝光偏差[34]会因训练与推理间的预测差异导致误差累积,从而降低自回归模型性能。在推理中,预测误差会随深度\(D\)累积,因为更精细的特征向量估计难度增加
- 为此,论文提出软标签和随机采样以缓解曝光偏差。基于RQ-VAE编码嵌入的几何关系,定义分类分布\(\mathcal{Q}_{\tau}(k|\mathbf{z})\):
$$
\mathcal{Q}_{\tau}(k|\mathbf{z})\propto e^{-||\mathbf{z}-\mathbf{e}(k)||_{2}^{2}/\tau}\quad\textrm{for }k\in[K],
$$- 其中\(\tau>0\)为温度参数。当\(\tau\)趋近于0时,\(\mathcal{Q}_{\tau}\)退化为单点分布\(\mathcal{Q}_{0}(k|\mathbf{z})=\mathbf{1}[k=\mathcal{Q}(\mathbf{z};C)]\)
- 目标编码的软标签 :基于编码嵌入的距离,软标签通过显式监督编码间的几何关系改进RQ-Transformer的训练。对于位置\(t\)和深度\(d\),使用软化分布\(\mathcal{Q}_{\tau}(\cdot|\mathbf{r}_{t,d-1})\)替代单点标签\(\mathcal{Q}_{0}(\cdot|\mathbf{r}_{t,d-1})\)
- RQ-VAE编码的随机采样 :通过从\(\mathcal{Q}_{\tau}(\cdot|\mathbf{r}_{t,d-1})\)采样选择编码\(\mathbf{S}_{td}\),替代RQ的确定性编码选择(式4)。随机采样在\(\tau\to 0\)时等价于原始RQ编码选择,为给定特征映射提供不同的编码组合