- 参考链接
IQL 的基本思想
- 常规的方法会直接约束策略或者正则来减少OOD问题,IQL则通过SARSA style的方法仅在见过的state-action上进行学习,不直接面对OOD问题
- 策略学习使用了AWR(Advantage Weighted Regression)方法
多步动态规划和 Single-step 方法
多步动态规划(Multi-step DP)
- 多步动态规划方法(multi-step dynamic programming methods,简写作Multi-step DP)
- 已有Offline RL方法的很大一部分是基于约束或正则化的近似动态规划(例如,Q-learning 或 actor-critic 方法),constraint或Regularization用于限制与行为策略的偏差。 我们将这些方法称为多步动态规划(Multi-step DP)算法,因为它们对多次迭代执行真正的动态规划,因此如果提供高覆盖率数据,原则上可以恢复最优策略。通常情况下Multi-step DP问题也可以分为:
- 显式密度模型(explicit density model):BRAC,BCQ,BEAR等
- 隐式差异约束(implicit divergence constraints):AWAC,CRR,AWR等
- 如何理解显示密度模型和隐式约束模型的定义?
- 显式密度模型:直接建模State-Action的价值分布,从而得到最优策略
- 隐式差异约束:不直接建模State-Action的价值分布,更多是模仿优质策略行为的思想
- 问题:显示密度模型中的“密度”是什么意思?
- 这里的密度是指概率密度,显示密度模型即会直接定义并学习概率密度函数的模型
Single-step 方法
- Single-step 方法(Single-step Methods)是指一类方法,这类方法仅依赖于单步策略迭代的方法,即对行为策略的价值函数或Q函数进行拟合,然后提取相应的贪心策略,或者完全避免价值函数并利用行为克隆目标
- 这类方法避免了访问看不见的状态动作对,因为它们要么根本不使用价值函数,要么学习行为策略的价值函数
- IQL 就是一种 Single-step 方法
- 传统的模仿学习也属于 Single-step 方法
多步动态规划和 Single-step 方法的比较
IQL 之前的方案
一般的 Offline RL 学习方法
- 思路:按照贝尔曼最优方程迭代
- 损失函数:
$$
L_{TD}(\theta) = \mathbb{E}_{(s,a,s’) \sim D} \left[ (r(s, a) + \gamma \max_{a’} Q_{\theta’}(s’, a’) - Q_\theta(s, a))^2 \right]
$$ - 分析:
- 直接使用上述损失函数存在值高估问题
- 大多数最近的离线RL方法修改了上述值函数损失(或直接约束argmax这个策略本身选择动作的方位),以正则化值函数,使其生成的策略接近数据,缓解值高估问题
能避免 OOD 的学习方法
- 思路:按照SARSA-style的方法迭代,即贝尔曼期望方程( \(a’\sim \pi_\beta\) )
- 损失函数:SARSA-style的损失函数如下
$$
L(\theta) = \mathbb{E}_{(s,a,s’,a’) \sim D} \left[ (r(s, a) + \gamma Q_{\theta’}(s’, a’) - Q_\theta(s, a))^2 \right]
$$- 按照上面的损失函数学习,学到的 \(Q_\theta(s,a)\) 本质是行为策略对应的Q值,也就是说,当样本无限时,Q值收敛到
$$
Q_\theta^*(s, a) \approx r(s, a) + \gamma \mathbb{E}_{s’ \sim p(\cdot|s,a), a’ \sim \pi_\beta(\cdot|s’)} \left[ Q_{\theta’}(s’, a’) \right]
$$
- 按照上面的损失函数学习,学到的 \(Q_\theta(s,a)\) 本质是行为策略对应的Q值,也就是说,当样本无限时,Q值收敛到
- 分析:
- 本质上是在估计数据集上的状态和动作分布下,Q值的期望
- 显然上面学到的只是行为策略对应的Q值,不是我们想要的最优Q值(行为策略不一定是最优策略)
- 上面的方法更像是在对行为策略进行模仿
Offline RL 的最优 Q 值目标
- 思路:避免OOD且能学到“最优策略”的迭代形式,限制了argmax动作不访问OOD的状态动作对
- 损失函数:
$$
L(\theta) = \mathbb{E}_{(s,a,s’) \sim D} \left[ (r(s, a) + \gamma \max_{a’ \in A, \pi_\beta(a’|s’) > 0} Q_{\theta’}(s’, a’) - Q_\theta(s, a))^2 \right]
$$ - 分析:
- 既保证使用的最大Q值对饮动作不超过数据集(避免了OOD),又可以在支持集上最大化当前策略
- 上面的定义实际上也可能访问到支持集以外的动作,后续需要使用期望回归来改进为SARSA-style的形式
- 注意:IQL 并不直接学习上述目标( \(\pi_\beta(a’|s’) > 0\) 导致无法学习),只是隐式的学习上述目标 ,具体方法是引入期望回归(Expectile Regression)
- BCQ等方法已经学习过上述目标的改进版本
- 上述目标无法直接学习,因为判断 \(\pi_\beta(a’|s’) > 0\) 需要维护一个表格,统计所有数据,状态动作空间很大时无法实现,除非像BCQ一样,用一个网络去学习概率
IQL 的解决方案
期望回归与分位数回归
期望回归(Expectile Regression) ,是估计随机变量的各种统计量的方法,定义如下:
- 某个随机变量 \(X\) 的 \(\tau \in (0, 1)\) 期望值定义为以下非对称最小二乘问题的解:
$$
\mathop{\arg\min}_{m_\tau} \mathbb{E}_{x \sim X} \left[ L_\tau^2(x - m_\tau) \right], \quad \text{ Where } \quad L_\tau^2(u) = |\tau - 1(u < 0)| u^2.
$$ - \(L_\tau^2(u)\) 也常常写作 \(L_\tau^e(u)\)
- 给定 \(\tau\), \(m_\tau\) 就是在拟合随机变量的某个 \(\tau\) 期望点,不同的 \(\tau\) 下 \(m_\tau\) 也会不同,学到的,比如 \(\tau=0.5\) 时就是对应期望
- 分析:
- 当 \(\tau > 0.5\) 时,这种非对称损失函数会降低小于 \(m_\tau\) 的 \(x\) 值的权重,而增加大于 \(m_\tau\) 的 \(x\) 值的权重
- 当 \(\tau = 0.5\) 时,损失函数退化成对称的,等价于均方误差MSE(这里把 \(u\) 看做是误差项)
$$ L^{\tau=0.5}_{2}(u) = |0.5 - \Bbb{1}(u<0)|u^2 = \frac{1}{2}u^2 $$
- 某个随机变量 \(X\) 的 \(\tau \in (0, 1)\) 期望值定义为以下非对称最小二乘问题的解:
条件随机变量的期望回归
- 对于给定的条件随机变量 \(y = f(x)\),假定 \((x,y)\) 成对出现在数据集 \(\mathcal{D}\) 中,则可以定义:
$$\mathop{\arg\min}_{m_\tau(x)} \mathbb{E}_{(x,y) \sim \mathcal{D}} \left[ L_\tau^2(y - m_\tau(x)) \right]$$ - 给定 \(\tau\), \(m_\tau(x)\) 是一个关于 \(x\) 的函数,不同的 \(\tau\) 得到的拟合函数不同,相同的 \(\tau\),给定不同的 \(x\) 会得到不同的 \(m_\tau(x)\), \(m_\tau(x)\) 本质是在拟合 \(y\),下图中最右侧的图展示了条件随机变量的期望回归
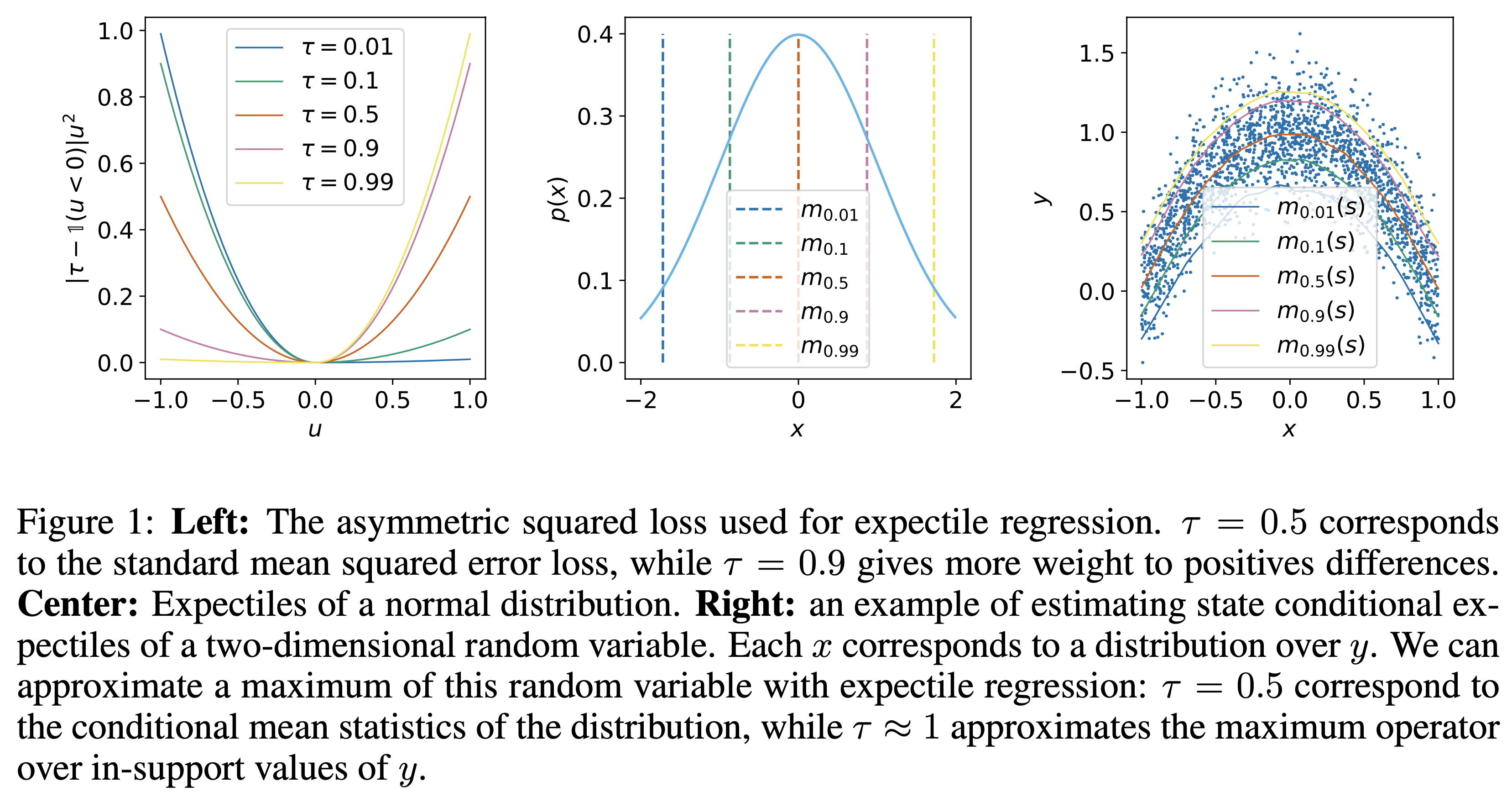
- 对于给定的条件随机变量 \(y = f(x)\),假定 \((x,y)\) 成对出现在数据集 \(\mathcal{D}\) 中,则可以定义:
分位数回归(Quantile Regression)定义如下:
$$
\mathop{\arg\min}_{m_\tau} \mathbb{E}_{x \sim X} \left[ L_\tau^1(x - m_\tau) \right], \quad \text{ Where } \quad L_\tau^1(u) = (\tau - 1(u < 0)) u.
$$- \(L_\tau^1(u)\) 也常常写作 \(L_\tau^q(u)\)
- \((\tau - 1(u < 0)) u\) 不使用绝对值的原因是此时无论 \(u\) 取值正负 \(L_\tau^1(u) \ge 0\) 都成立,相当于已经给整体加了绝对值了,最终目标是类似MAE的形式
分位数回归和期望回归的对比

- 常规的MSE叫做mean,等价于求均值,等价于 \(\tau = 0.5\) 的期望回归(expectile regression)
- 常规的MAE叫做median,等价于求中位数,等价于 \(\tau = 0.5\) 的分位数回归(quantile regression)
更多比较
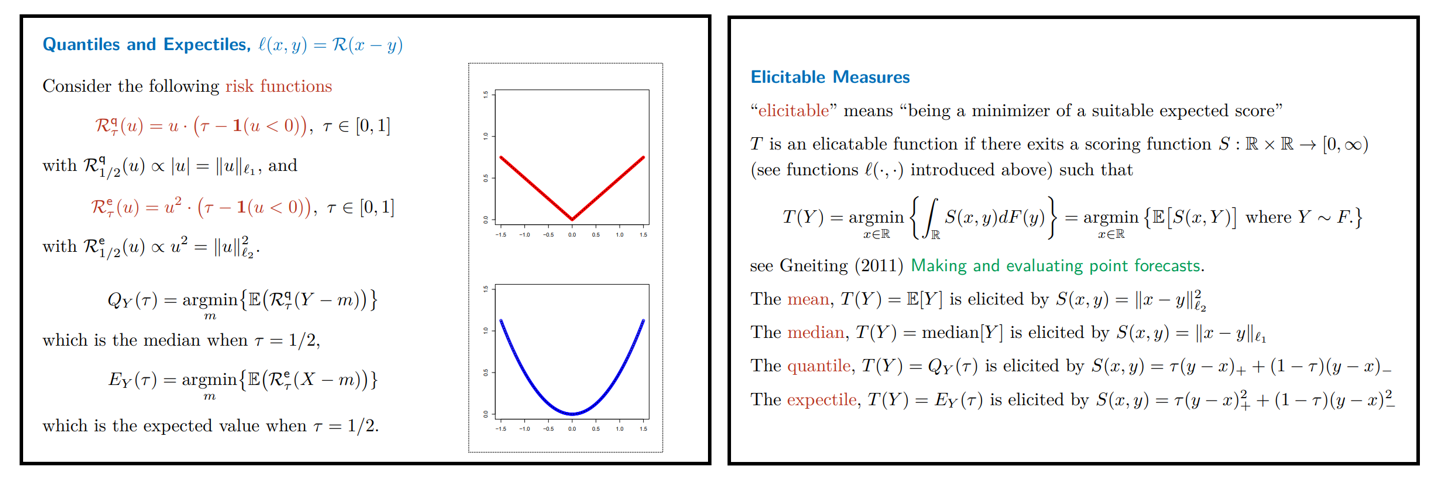
- 修正:左边第二行需要使用绝对值 \(\mathcal{R}_\tau^e(u) = u^2|\tau - \mathbf{1}(u < 0)|\)
问题:为什么使用期望回归而不是分位数回归?
- 审稿人也有这个疑问,作者的回答是实验得到的,没有正面给出回答?, \(\tau=0.9\) 时效果最好
基于期望回归的 Q 值学习
- 借助期望回归来学习Q值:
$$
L(\theta) = \mathbb{E}_{(s,a,s’,a’) \sim D} \left[ L_\tau^2(r(s, a) + \gamma Q_{\theta’}(s’, a’) - Q_\theta(s, a)) \right]
$$ - 其中 \(\mathcal{D} \sim \pi_\beta\),选择合适的 \(\tau\) 后,可以学到一个大于 \(Q^{\pi_\beta}(s,a)\) (行为策略对应的Q值)的 \(Q(s,a)\)
- 理解:给定 \((s,a)\) 的情况下,存在许多不同的 \((s’,a’)\) 样本,当 \(\tau > 0.5\) 时,相当于是通过这种非对称损失函数降低小于 \(Q_\theta(s, a)\) 的动作状态对 \((s’, a’)\) 所对应的目标值 \(r(s, a) + \gamma Q_{\theta’}(s’, a’)\) 的权重,增加大于 \(Q_\theta(s, a)\) 的动作状态对 \((s’, a’)\) 所对应的目标值 \(r(s, a) + \gamma Q_{\theta’}(s’, a’)\) 的权重,从而学到较大的 \((s’,a’)\) 对应的目标值,极端情况下,学到的是最大值 \(r(s, a) + \gamma \max_{(s,a,s’,a’) \sim \mathcal{D}} Q_{\theta’}(s’, a’)\)
- 上面的损失函数还存在一些不足,由于环境可能是动态变化的,状态 \(s’\) 是按照概率 \(p(s’|s,a)\) 出现,所以以上损失函数还使得Q学到了环境转换的信息。具体来说,学到的Q值高不一定是选到了优秀动作的反应,还可能是因为运气好碰上了转移到一个较好的状态 \(s’\) 上
- 补充说明1:即使是随机环境,在状态 \(s\) 下,选择 \(a\) 后有一定概率得到较优秀的 \(s’\),能说明在状态 \(s\) 下,选择 \(a\) 是较为优秀的吗?回答是不一定!因为在这种随机环境的情况下,最优贝尔曼方程里面,我们也需要对 \(s’\) 计算期望 \(\mathbb{E}_{s’\sim p(s’|s,a)}\) 而不是取最大 \(\max_{s’}\),这是我们的目标是找一个策略,使得按照这个策略交互得到的期望收益最大,而线上推断时,我们不能保证一定能走到最大的 \(s’\),除非是确定性环境,即 \((s,a)\) 确定后, \(s’\) 也是确定的
- 补充问题1:如果是确定性的环境,是否可以直接使用上述损失函数?
IQL 的 Q 值学习
- 由于基于期望回归的Q值学习引入了状态转移随机偏差,存在问题,所以需要进行改进:
- 第一步:使用期望回归去从已知的 \(Q_{\hat{\theta}}(s,a)\) 中学习 \(V(s)\)
$$ L_V(\psi) = \mathbb{E}_{(s,a) \sim D} \left[ L_\tau^2(Q_{\theta’}(s, a) - V_\psi(s)) \right] $$- 这里可以看出 \(V(s)\) 学到的是 \(\max_a Q_{\hat{\theta}}(s,a)\) 的思想,即对应V值的贝尔曼最优方程
- 第二步:使用最优的 \(V\) 去学习 \(Q\)
$$L_Q(\theta) = \mathbb{E}_{(s,a,s’) \sim D} \left[ (r(s, a) + \gamma V_\psi(s’) - Q_\theta(s, a))^2 \right] $$- 由于 \(V\) 在上一步已经通过期望回归学到了最优形式,这一步不需要继续使用期望回归了
- 至此,我们已经实现了通过SARSA-style的形式,隐式的学到了近似最优Q值
- 关于参数 \(\tau\) 的一些分析以及以上贝尔曼方程收敛性见附录
IQL 的策略学习
- 虽然我们已经得到了近似最优Q值,但为了避免使用样本外的动作,这里做策略学习时,我们不能直接遍历所有动作
- AWR提供了一种方法从近似最优Q值里面提取策略(因为策略学习并不影响Q值,所以更像是从近似最优Q值中提取策略):
$$
L_\pi(\phi) = \mathbb{E}_{(s,a) \sim D} \left[ \exp(\beta (Q_{\theta’}(s, a) - V_\psi(s))) \log \pi_\phi(a|s) \right]
$$- 其中 \(\beta \ge 0\) 是温度系数。对于较小的超参数值,该目标类似于行为克隆(近似所有样本权重相等的策略梯度,原始策略梯度中,样本权重是温度系数为1的Q值),而对于较大的值,它试图恢复Q函数的最大值(Q值越大,对应的样本权重越大)。正如AWR等先前工作所示,此目标学习一个在分布约束下的最大化Q值的策略
- 注意,策略学习时Q值收敛以后进行的(Q和V是交替更新),Q值学习和策略学习是串行的,且Q值学习彻底完成以后才进行策略学习,并不是交替进行
- 思考:使用期望回归学到的 \(V\) 值是 \(V^{\pi^*} = \max_a Q_{\hat{\theta}}(s,a)\),为什么可以用最优的 \(V\) 值来更新策略 \(Q_{\theta’}(s, a) - V_\psi(s)\) ?
- 这种做法是可以的,Q值和V值符合优势函数的定义,因为传统优势函数的定义也是 \(A^\pi(s,a) = Q^\pi(s,a) - V^\pi(s)\),其中 \(V^\pi(s) = \mathbb{E}_{a \sim \pi(\cdot|s)}[Q^\pi(s,a)]\),看似与 IQL 中学到的 \(V\) 值不同,但此时将当前Q值和V值对应策略 \(\pi(a|s)\) 理解为选择Q值最大的动作或近似动作,实际上 \(Q\) 值和 \(V\) 值都满足传统的优势函数了
- 理解 :(即使不满足原始优势函数)虽然此时的 \(V\) 值是 \(\max_a Q_{\hat{\theta}}(s,a)\),但是 \(Q_{\theta’}(s, a) - V_\psi(s)\) 依然可以对动作的好坏进行区分。实际上,只要可以保证动作越好,优势函数越大即可,即使所有动作都是负的或者都是正的也没问题,因为策略的实现是一个softmax,大家都降低的时候,降的少的动作上对一个的概率自然会提升。实践也告诉我们,\(V\) 值是否是当前状态下动作的期望结果并不重要
- 特别说明 :AWR 中使用的 \(V\) 值是从历史样本的累计奖励上学习的,相当于是历史样本上的期望,也就是行为策略 \(\mu\)(多轮迭代下可能是混合策略)对应的 \(V^\mu\) 值,AWR 的整个推导中奖励 \(\mathcal{R}^\mu_{\mathbf{s},\mathbf{a}}\) 和 \(V^\mu\) 值都是使用行为策略 \(\mu\) 来表示的,奖励使用的是蒙特卡洛估计 \(\mathcal{R}^D_{\mathbf{s},\mathbf{a}} = \sum_{t=0}^T\gamma^t r_t\)
IQL 训练流程
- 伪代码如下(说明:伪代码中最后一行策略更新公式有问题,应该是加号,或者把损失函数添上负号,因为这里是想要最大化目标, 作者开源代码中是正确的github.com/ikostrikov/implicit_q_learning,论文中写错了):

附录:为什么 AWR 和策略梯度法损失函数不同?
- 副标题:不同AC框架算法策略更新公式对比分析,为什么相同的目标推导出来完全不同的更新公式?
- 问题补充:
- 普通AC(策略梯度法)更新公式是:
$$\mathop{\arg\max}_{\theta} \mathbb{E}_{(s,a) \sim \pi_{\theta_k}}\Big[(Q^{\pi_{\theta_k}}(s,a)-V^{\pi_{\theta_k}}(s))\log\pi_\theta(a|s)\Big]$$ - PPO更新公式:
$$\mathop{\arg\max}_{\theta} \mathbb{E}_{(s,a) \sim \pi_{\theta_k}}\Big[\frac{\pi_\theta(a|s)}{\pi_{\theta_k}(a|s)} A^{\pi_{\theta_k}}(s,a) - \beta D_{KL}(\pi_{\theta_{k}}(\cdot|s), \pi_\theta(\cdot|s))\Big]$$ - DDPG更新公式
$$\mathop{\arg\max}_{\theta} \mathbb{E}_{s_t \sim \rho^\beta(s)} [Q_w(s_t,\mu_\theta(s_t))] $$ - SAC更新公式
$$\mathop{\arg\max}_{\theta}\mathbb{E}_{s_t \sim \mathcal{D}, \epsilon_t \sim \mathcal{N}}[\log \pi_\theta(f_\theta(\epsilon_t;s_t)\vert s_t) - Q_\theta(s_t, f_\theta(\epsilon_t; s_t))]$$ - AWR更新公式:
$$\mathop{\arg\max}_{\theta} \mathbb{E}_{(s,a) \sim \pi_\beta}\Big[exp\Big(\frac{1}{\beta}(R_{s,a}^{\mathcal{D}}-V^{\mathcal{D}}(s))\Big)\log\pi_\theta(a|s)\Big]$$- 其中 \(R_{s,a}^{\mathcal{D}} = \sum_{t=0}^\infty \gamma^t r_t\),不是网络,是真实的轨迹收益
- IQL更新公式:
$$\mathop{\arg\max}_{\theta} \mathbb{E}_{(s,a) \sim \pi_\beta}\Big[exp\Big(\beta (Q_{\theta’}(s, a) - V_\psi(s))\Big)\log\pi_\theta(a|s)\Big]$$ - AWAC更新公式:
$$\mathop{\arg\max}_{\theta} \mathbb{E}_{(s,a) \sim \pi_\beta}\Big[exp(\frac{1}{\lambda} A^{\pi_{\theta_k}}(s,a))\log\pi_\theta(a|s)\Big]$$
- 普通AC(策略梯度法)更新公式是:
- 基本推导思路总结:
- 策略梯度法 :推导是直接从最初目标出发,视图求最初目标相对策略的梯度
- PPO :更新公式是从策略提升的视角出发得到梯度提升的目标,通过限制策略变化幅度和重要性采样分别将未知策略的状态和动作采样的问题切换到已知策略
- DDPG :直接以最大化Q值为目标来更新,可直接传导策略梯度
- SAC :的目标中增加了熵,可以看成是DDPG的增加熵的版本
- AWR、IQL和AWAC :更新公式都是相同的形式,是从策略提升的视角出发得到梯度提升的目标,并对该目标进行推导,得到最终的最优策略形式,再带入最优策略形式,从而得到更新公式
- 也就是说,AWR、IQL和AWAC这三个方法的目标是为了策略提升量最大化 ,而策略梯度法的目标是为了原始目标最大化(梯度提升法)
附录:为什么 IQL 效果比 AWR 好?
- IQL和 AWR 的 Q 值是不同策略的优势函数,IQL 的优势函数是在 \(\tau\) 分位点期望动作策略分布上的 Q 和 V,即 \(A^{\pi^*}(s,a) = Q^{\pi^*}(s,a) - V^{\pi^*}(s)\),而AWR的优势函数是真实的轨迹回报和V值 \(A^{\pi_k}(s,a) = R_{s,a}^{\mathcal{D}} - V^{\pi_k}(s)\)
- IQL 不是迭代训练,是先学好 Q 值(不依赖策略),再利用学好的 Q 值一次性提取策略
- 标准的 AWR 是 off-policy 的,是一种迭代训练的流程,V 值学习依赖策略与环境交互的轨迹数据,策略学习也依赖上一步的V值,V值,策略,轨迹三者是不断优化的
- 如果把 AWR 直接用到 Offline R L场景下,则不再与环境交互,AWR 退化到学习一次V值,接着一次性学习策略;
- Offline RL 下学到的 V 值是行为策略对应的 V 值,不是最优的 V 值,但这本身应该没有问题
- 基于统计的 \(R_{s,a}^{\mathcal{D}}\) 方差可能很大
- 使用公式 \(L_\pi(\phi) = \mathbb{E}_{(s,a) \sim D} \left[ \exp(\beta (Q_{\theta’}(s, a) - V_\psi(s))) \log \pi_\phi(a|s) \right]\) 来迭代策略时,Q 值和 V 值应该使用什么样的才是最优的?
- 这个公式是从最大化策略提升项得到的,在推导策略提升时,这里使用的A值(对应到Q值和V值)是上一步策略对应的值 \(A^\mu(s,a)\),即旧策略 \(\mu\) 对应 Q 值和 V 值,而我们的目标是在 \(\mu\) 的基础上有所提升,得到优秀的新策略 \(\pi\),所以 Q 值和 V 值最好是优秀的策略对应的Q值和V值,否则可能我们的策略 \(\pi\) 在不好的策略上提升,结果也可能不是很优秀
- 补充问题:可以随便使用一个策略来评估优势函数吗?
- 回答是不可以,因为不同策略下,A 值选择不同动作以后的值是不同的,显然学到的策略也不同,从推导看,必须使用上一步的才可以
附录:贝尔曼方程收敛性及 \(\tau\) 的分析
关于参数 \(\tau\) 的一些分析,原始论文中关于 \(\tau\) 的分析如下:


当 \(\tau = 0.5\),相当于是SARSA算法;当 \(\tau \rightarrow 1\),相当于是Q-Learning算法
对于任意的 \(\tau\),Q值和V值迭代都会收敛,且Q值和V值会收敛到 \(Q_{\tau}(s,a)\) 和 \(V_{\tau}(s)\),Lamma1中最后两行就是两者的贝尔曼方程,其中 \(\mathbb{E}_{a \sim \mu(\cdot|s)}^\tau\) 表示 \(\mu(\cdot|s)\) 分布下的 \(\tau\) 期望分位值(或 \(\tau\) 阶期望分位数)。注意,我们在说分位数时,还需要说明是那个随机变量或者哪个分布的分位数,否则没有意义
为什么说Q值和V值迭代都会收敛到 \(Q_{\tau}(s,a)\) 和 \(V_{\tau}(s)\) 呢?
- 理解:这里的 \(\tau\) 期望分位动作可以视作是一个策略,每次选择动作时,不选择最优动作,也不选择随机动作,而是选择 \(\tau\) 期望分位点动作,这样,可以得到跟论文中一样的结论:当 \(\tau = 0.5\),相当于是SARSA算法;当 \(\tau \rightarrow 1\),相当于是Q-Learning算法
- 证明:定义一个策略如下:
$$\pi_\tau(s) = \mathop{\text{arg_expectile}^\tau}_a(Q(s,a))$$
该策略表示在状态 \(s\) 下,该策略会选择使得Q值等于 \(Q(s,a)\) 关于动作 \(a\) 的 \(\tau\) 期望分位点的动作,则期望分位动作策略对应的贝尔曼方程跟普通策略下的贝尔曼方程没有区别 - 更详细的来说:
- Q值:假定已经有了 \(V_\tau(s’)\),此时Q值的更新是学习当前状态 \(s\) 下,按照当前状态对应的 \(\tau\) 期望分位动作,以及后续策略也采用 \(\tau\) 期望分位动作得到的价值 \(V_\tau(s’)\) 来进行拟合的目标值(注意,这里跟其他贝尔曼方程一样,一旦动作决定了, \(r(s,a)\) 就确定了,我们所说的期望分位动作就是对动作 \(a\) 的分布而言的, \(Q(s,a)\) 的拟合只考虑 \((s,a)\) 状态动作对即可,不需要考虑期望分位动作);
- V值:假定已经有了 \(Q_{\tau}(s,a)\),V值可以从 \(Q_{\tau}(s,a)\) 中学到 \(V_\tau(s’)\),这里需要使用 \(Q_{\tau}(s,a)\) 而不是 \(Q_{\pi_\beta(s,a)}\) 的原因是,V的本质是 \(Q(s,a)\) 关于动作 \(a\) 期望,但直接求期望只到了当前状态 \(s\) 这一层,如果使用 \(Q_{\pi_\beta(s,a)}\) 来学习那么学到的不是 \(V_\tau(s’)\) ( \(V_\tau(s’)\) 是指后续的动作也是 \(\tau\) 期望分位动作来定义的,正如Q值和V值的常规贝尔曼方程一样)
Implicit 名字的来源
- Implicit 含义是“隐式的”,与隐式约束的隐式不等价,在IQL中表示通过期望回归隐式的学到了最优价值函数 \(V^*(s) = \max Q(s,a)\)
IQL 可能存在的问题
- IQL 没有没有像 CQL 一样对非行为策略的 Q 值进行打压(甚至学习过程中全程未学习未知状态动作对的 Q 值),也没有像 BCQ 一样对动作选择进行限制,理论上可能会因为对 OOD 状态动作 Q 值高估而出现问题
- IQL 源码实现时的解法:采用 Twin Q 来缓解高估问题(理解:对于数据集中存在的,两个 Q 网络都能估准;对于数据集中不存在的,可能都估不准,但是我们取最小的那个,可以缓解对未知状态动作对 Q 值的高估问题)