- 参考链接:
Background
Diffusion Model
- 自 Stable Diffusion 问世以来,Diffusion Model(扩散模型)凭借其强大的生成效果横扫各大图像生成领域
- 在 Diffusion Model 之前,一般的生成模型更多是 VAE 或 GAN,相较于前两者,Diffusion Model 具有更强的建模复杂分布的能力(比如人脸生成,几乎可以做到以假乱真),那么该技术是否可以直接用于生成 MDP 的决策轨迹呢?答案是可以!
- 常规的 Diffusion Model,DDPM 的训练和推断流程如下:

Diffusion Model 如何用于决策
- 模仿生成:一种简单的思路是直接让 Diffusion Model 直接模仿专家策略/行为策略,然后直接在 Serving 是模仿行为策略进行决策,详情见智能体该如何模仿人类行为?通过扩散模型可以这么做
- 引入最大化目标的生成(Diffuser):首先训练一个生成轨迹的 Diffusion 模型,在采样/生成过程中引入目标,本质是 Classifier Guidance Sampling,通过引入最大化收益的目标,引导模型生成使得收益最大的轨迹,并在下一次决策时执行轨迹中的第一步决策,论文的方法就是这种
- 引入最大化目标化和约束的生成(Decision Diffuser):除了引入最大化收益的目标,还引入约束条件,使得生成的轨迹既满足约束,又能最大化指定目标,详细论文见:Is Conditional Generative Modeling all you need for Decision-Making?
Diffuser 整体概述
Diffuser 基本框架
- 论文提出一种trajectory-level Diffusion Probabilistic Model,称为Diffuser,基本结构图如下:
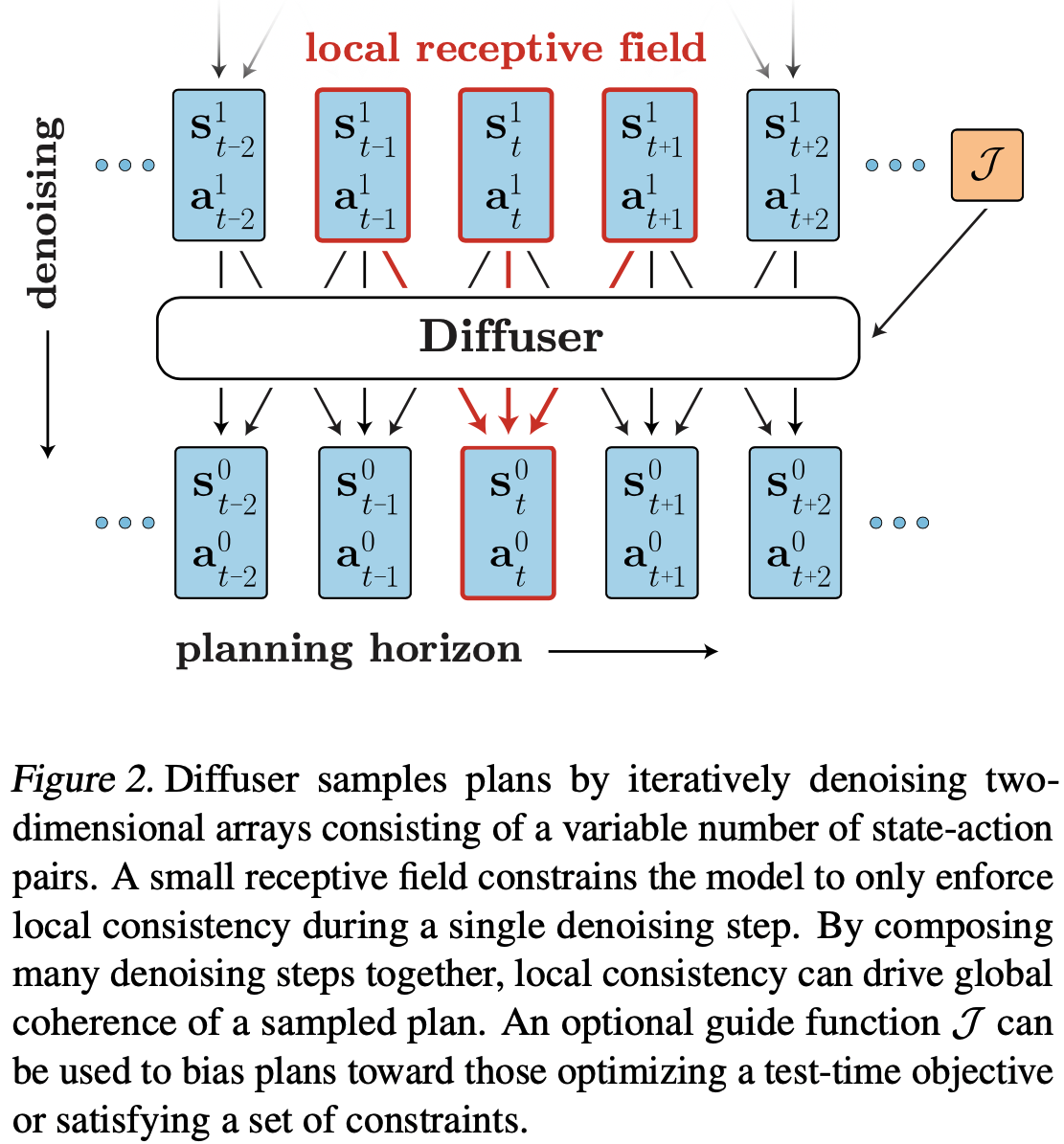
Diffuser 优点分析
- Long-horizon scalability :长周期可扩展性。Diffuser学习目标是生成准确的Trajectory而不是单步的误差,所以不需要面对动态模型中rollout的符合误差问题
- Task compositionality :任务组合性。奖励是以梯度的形式加入生成过程的,引导生成朝指定方向发展,所以可以通过将多个奖励的梯度加起来从而实现奖励组合的Planning,而且任务修改以后不需要重新训练Diffusion模型
- Temporal compositionality :时间组合性。Diffuser通过迭代提升局部一致性来生成全局连贯(Globally Coherent)的轨迹,这使得Diffuser可以通过拼接(Stitching)子序列来生成新的轨迹
- Effective non-greedy planning :高效的规划方法。Diffuser的依赖一个轨迹生成模型来执行Planning,生成模型学的越准确,Planning效果越好,(只要足够生成模型足够好就能保证Planning不会太差),生成过程并不关注奖励是否稀疏,轨迹序列是否长等常规规划方法中比较难的问题。(理解:实际上周期太长也不好做轨迹生成吧?)
论文名称解读
- 论文名称为:Planning with Diffusion for Flexible Behavior Synthesis
- Planning:指出了论文是在解决规划问题
- Flexible:表示灵活性,轨迹生成的目标是在采样阶段引入的,修改目标并不需要重新训练Diffusion模型(即Classifier Guidance 方法)
- Behavior Synthesis:指出了文章的目标是行为合成,即通过生成序列(序列中包含了行为)来完成决策
Diffuser 方案
问题定义
- 对于一个MDP问题,我们的优化目标是:
$$
\begin{align}
a_{0:T}^* = \mathop{\arg\max}_{a_{0:T}} J(s_0, a_{0:T}) = \mathop{\arg\max}_{a_{0:T}} \sum_{t=0}^{T} r(s_t, a_t)
\end{align}
$$ - 目标解读
- \(T\) 表示序列长度,也称为规划范围,planning horizon
- \(a_{0:T}\) 表示动作序列,我们的目标就是找到一个最优的行为序列,使得目标函数最大
- \(\tau = (s_0, a_0, s_1, a_1,\cdots,s_T,a_T)\) 表示轨迹
Diffusion Probabilistic Models
- 扩散概率模型(Diffusion Probabilistic Models)的生成过程是迭代denoising的过程(也称为去噪过程、反向过程或逆过程): \(p_\theta(\tau^{i-1}|\tau^i)\),该过程是扩散过程(Diffusion Process) \(q(\tau^i|\tau^{i-1})\) 的逆过程
- 前向过程,扩散过程: \(q(\tau^i|\tau^{i-1})\),没有参数,是训练模型时提前确定的分布,直接采样即可
- 逆向过程,去噪过程: \(p_\theta(\tau^{i-1}|\tau^i)\),有参数,去噪时需要模型预估误差,从而得到分布再采样
- 数据分布定义:
$$ p_\theta(\tau^0) = \int p(\tau^N)\prod_{i=1}^N p_\theta(\tau^{i-1}|\tau^i) \text{d} \tau^{1:N}$$ - 其中, \(p(\tau^N)\) 是标准高斯先验分布, \(p(\tau^0)\) 表示无去噪后的数据(无噪音数据)
- 参数 \(\theta\) 可以通过最小化去噪过程的负对数似然的变分下界(详情见DDPM)来优化: \(\theta^* = \mathop{\arg\min_\theta} -\mathbb{E}_{\tau^0}[\log p_\theta(\tau^0)]\)
- 去噪过程常常可以参数化为固定的、时间步长相关的协方差高斯分布(在已知 \(\tau^i\) 时 \(\tau^{i-1}\) 的条件概率):
$$ p_\theta(\tau^{i-1}|\tau^i) = \mathcal{N}(\tau^{i-1}|\mu_\theta(\tau^i, i), \Sigma^i)$$- 其中 \(\mathcal{N}(\tau^{i-1}|\mu_\theta(\tau^i, i), \Sigma^i)\) 表示均值为 \(\mu_\theta(\tau^i, i)\),协方差为 \(\Sigma^i\) 的高斯分布,这里加噪时一般假设各个维度变量相互独立,从而协方差矩阵式一个对角阵(详情见:IDDPM, ICML 2021),甚至在原始DDPM下,直接将这个对角阵上的元素设置成相同的值 \(\beta_t\) 效果也不错
- 注:前向过程 \(q(\tau^i|\tau^{i-1})\) 是预先指定的,没有可学习参数,扩散模型 \(\epsilon_\theta(x_t,t)\) 实际上学习的ground truth就是 \(t\) 次前向过程中引入的混合误差 \(\bar{\epsilon}\)
- 符号说明:论文中,使用上标 \(i\) 表示Diffusion时间步,使用下标 \(t\) 表示规划时间步。比如 \(s_t^0\) 表示第 \(t\) 个状态(对应第 \(t\) 个规划时间步)的第0个Diffusion时间步(即无噪音)结果,当不会引起误会时,会省略第0个Diffusion时间步的上标,即 \(\tau = \tau^0\) 。我们也使用 \(\tau_{s_t},\tau_{a_t}\) 表示轨迹 \(\tau\) 的第 \(t\) 个状态和动作
Planning with Diffusion
- 采样过程就是规划过程
$$ \tilde{p}_\theta(\tau) \propto p(\tau)h(\tau) $$- 其中 \(h(\tau)\) 可以包含先验信息(比如观测历史)、期望输出(比如期望达到的目标),或者一般的优化函数目标(比如reward或者costs)等
- 这个采样方式的含义就是,要求找到在分布 \(p_\theta(\tau)\) 下满足物理现实的、在 \(h(\tau)\) 下满足高收益(或满足约束)的轨迹
- 对于相同的环境,只需要建模一个模型 \(p_\theta(\tau)\),即可在多个不同的任务上使用(不同任务使用不同的 \(h(\tau)\) 即可)
轨迹规划的生成模型
Temporal ordering :时间顺序性。Diffuer是同时生成轨迹上的所有状态的,不能再按照顺序自回归地预测状态(因为当前状态生成时之前状态还没生成完成,无法行程时序上的依赖);(个人理解)动力学模型的预测是有因果关系的( \(s_{t+1} = f(s_t, a_t)\) ),但规划和决策可以反因果,比如,强化学习的本质是在建模一个条件状态动作分布 \(p(a_t|s_t, \mathcal{O}_{t:T})\),其中 \(\mathcal{O}_{t:T}\) 是最优性变量, \(\mathcal{O}_{t:T}=1\) 表示从 \(t\) 步开始的未来时间步都是最优的
Temporal locality :时间局部性。Diffuser不遵循自回归或马尔可夫性质,但Diffuser有一种松弛的时间局部性(relaxed temporal locality)。具体来说,每个扩散步骤中,Diffuser模型可以通过时间卷积来建模轨迹局部时间步的关系,从而保证轨迹的局部一致性。虽然单个扩散步骤只能保证局部一致性(卷积),但是将许多去噪步骤组合在一起以后,局部一致性也可以促成全局的连贯性
Trajectory representation :轨迹表示。为了实现规划,我们将动作和状态同时预测出来,其中动作是状态的附加维度。具体来说,Diffuser的输入(和输出是相同的)可以建模为一个如下的二维数组:
$$
\begin{align}
\tau = \begin{bmatrix}
s_{0} & s_{1} & {\ldots} & s_{T} \\
a_{0} & a_{1} & {\ldots} & a_{T}
\end{bmatrix}.
\end{align}
$$- 其中,矩阵中的第 \(t\) 列表示轨迹中状态 \(s_t\) 和动作 \(a_t\) 向量的组合,向量展开按照一列Concat起来
- 理解:整体上,轨迹构造完成后就像一张黑白图片一样,是二维的矩阵
Architecture :模型架构。至此,现在我们可以定义Diffuser了:
- 第一:一个完整的轨迹应该是非自回归地预测的
- 第二:每个去噪步骤在时间上都应该有局部一致性
- 第三:对轨迹的表示在planning horizon维度上应具有等变性(equivariance),而在另外的维度(状态和行为特征维度)上不应具有等变性
- 理解1:这里规划时间上的等变性可以类比于图片的像素平移(将动作在时间步上平移),是指在不同规划时间步,如果遇到相同的状态和动作,输出应该与时间步无关(这里可以作为样本增强的一个方向?)
- 理解2:在其他维度上不具备等变性是指矩阵在其他维度上不能平移(注:直接使用卷积网络会导致其他维度也能平移,这样是不可以的,所以只能使用时间维度上的一维卷积)
- 为了满足以上三个条件,我们使用时间维度上重复的卷积残差块来实现。模型的整体结构类似于在基于图像的扩散模型中成功应用的那种U-Nets(U-Net: Convolutional Networks for Biomedical Image Segmentation),不过但需要把二维空间卷积替换成一维时间卷积
- 由于模型是全卷积的,预测的时域不是由模型结构决定,而是由输入的维度决定;如果需要的话,它可以在规划期间动态地改变。(理解:这里是说不同时间步规划可以使用同一个模型)
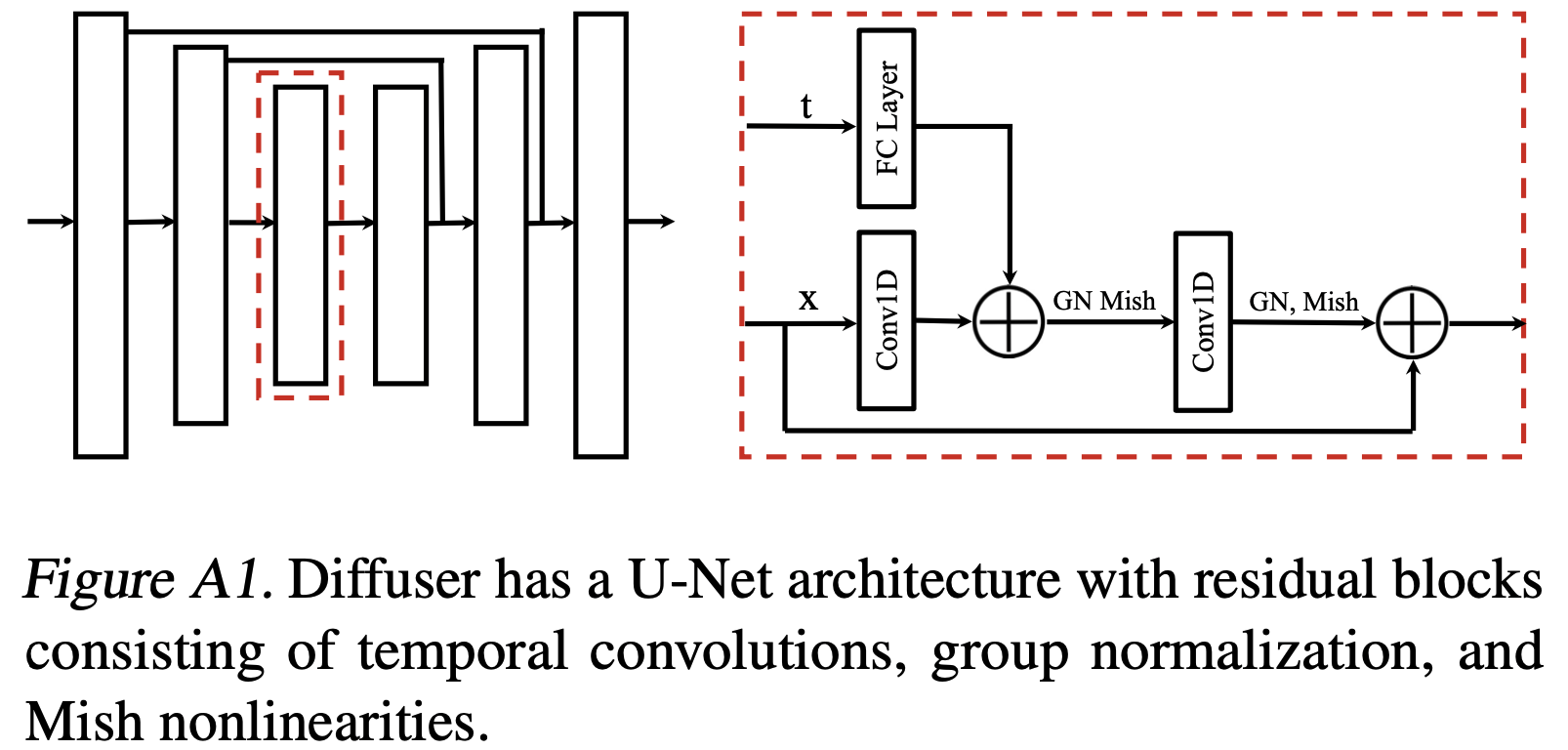
训练过程:
- 我们的最终目标是需要一个均值和方差,在DDPM中,先学习每一步的噪音函数 \(\epsilon_\theta(\tau^i, i)\),然后,可通过推导得到均值和方差的闭式解(Closed-form Solution),推导详情可见Denoising diffusion probabilistic models,其中均值与噪音函数 \(\epsilon_\theta(\tau^i, i)\) 有关,方差是固定值,所以DDPM的训练目标就是学习这个函数 \(\epsilon_\theta(\tau^i, i)\),训练完成以后,可按照下面的定义使用:
- 均值: \(\mu_\theta(x_t,t) = \frac{1}{\sqrt{\alpha_t}}\Big( x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_\theta(x_t, t) \Big)\),其中 \(\bar{\alpha}_t = \prod_{s=1}^t \alpha_s\),且 \(\forall s, \ \text{有} \alpha_s = 1-\beta_s\),而 \(\{\beta_s\}_{s=1}^T\) 是提前确定的序列
- 方差: \(\Sigma_t = \sigma_t^2 \boldsymbol{I}\),在DDPM中可以取 \(\sigma_t^2 = \beta_t\)
- 采样函数为: \(x_{t-1} \sim N(\mu_\theta(x_t, t), \Sigma_t)\)
- Diffuser参数化一个可学习的函数拟合每一步的去噪过程中的梯度 \(\epsilon_\theta(\tau^i, i)\),其中去噪步数用 \(i\) 表示。训练过程与DDPM完全相同:
$$
\mathcal{L}(\theta) = \mathbb{E}_{i,\epsilon,{\tau^{0}}}\left[\lVert \epsilon - \epsilon_\theta({\tau^{i}}, i) \rVert^2\right]
$$- 其中 \(i\sim \mathcal{U}\{1,2,\cdots,N\}\) 表示扩散时间步( \(\mathcal{U}\) 表示从集合中按照均匀分布随机采样,理解:这里是在强调使用的是均匀采样的方式,IDDPM中提出了重要性采样,Diffuser没有使用), \(\epsilon\sim N(0,\boldsymbol{I})\) 表示噪声目标(ground truth), \(\tau^i\) 是 \(\tau^0\) 经过噪声 \(\epsilon\) 干扰的第 \(i\) 扩散时间步的结果
- 反向过程的协方差矩阵 \(\Sigma^i\) 遵循IDDPM(Improved Denoising Diffusion Probabilistic Models)中提出的余弦调度(cosine schedule)(注:IDDPM中对协方差矩阵有两个改进,这里只包含cosine schedule,未明确包含可学习 \(\Sigma_\theta^i\) )
- 我们的最终目标是需要一个均值和方差,在DDPM中,先学习每一步的噪音函数 \(\epsilon_\theta(\tau^i, i)\),然后,可通过推导得到均值和方差的闭式解(Closed-form Solution),推导详情可见Denoising diffusion probabilistic models,其中均值与噪音函数 \(\epsilon_\theta(\tau^i, i)\) 有关,方差是固定值,所以DDPM的训练目标就是学习这个函数 \(\epsilon_\theta(\tau^i, i)\),训练完成以后,可按照下面的定义使用:
强化学习-引导式采样(场景一)
Reinforcement Learning as Guided Sampling
在解决强化学习问题时,我们需要引入奖励,参照Reinforcement Learning and Control as Probabilistic Inference: Tutorial and Review的做法,我们使用概率图模型的方式进行建模(control-as-inference graphical model)
在概率图模型下,假设 \(\mathcal{O}_t\) 是一个二元随机变量,表示轨迹中时间步 \(t\) 的最优性(理解:二元随机变量即取值为0或者为1,即当时间步 \(t\) 最优时 \(\mathcal{O}_t=1\),不是最优时 \(\mathcal{O}_t=0\) ),具体来说,可以用如下分布去表示该变量的概率分布: \( p(\mathcal{O}_t=1) = \exp(r(s_t, a_t)) \)
一个问题: \(\exp(r(s_t, a_t))\) 不能用来表示概率吧,概率不能大于1而reward可能大于1?
- 这里这样定义概率可以表示在某个state下采取某个action能够获得的reward越高,optimality是true的概率也就越大
- 从原始论文中可以看出,这个值 \( p(\mathcal{O}_t=1) = \exp(r(s_t, a_t)) \) 是为了方便推导直接拍出来的,个人理解使用 \( p(\mathcal{O}_t=1) \propto \exp(r(s_t, a_t)) \) 会更准确
- 实际推导中,则可以使用 \(p(\mathcal{O}_t=1|s_t,a_t) \propto \exp(r(s_t, a_t))\) (常常简写为 \(p(\mathcal{O}_t|s_t,a_t) \propto \exp(r(s_t, a_t))\),表示省略 \(\mathcal{O}_t\) 为1的表达)
通过定义采样公式中 \(h(\tau) = p(\mathcal{O}_{1:T}|\tau)\),可得到下面的采样公式:
$$ \tilde{p}_\theta(\tau) = p(\tau|\mathcal{O}_{1:T}=1) \propto p(\tau)p(\mathcal{O}_{1:T}=1|\tau)$$至此,我们已经将一个强化学习问题转变成了一个条件采样(Conditional Sampling)问题。在论文之前有许多基于diffusion模型条件采样相关的研究工作,虽然从一个分布中精确采样是困难的,但是当 \(p(\mathcal{O}_{1:T}=1|\tau^i)\) 足够平滑(平滑值连续性和可导性)时,反向过程的每一步都可以近似为一个高斯分布(详情见Deep unsupervised learning using nonequilibrium thermodynamics):
$$ p_\theta(\tau^{i-1}|\tau^i,\mathcal{O}_{1:T}) \approx N(\tau^{i-1};\mu+\Sigma g, \Sigma) $$- \(\mu,\Sigma\) 分别是反向过程 \(p_\theta(\tau^{i-1}|\tau^i)\) 的参数:
$$
\begin{align}
g &= \nabla_\tau\log p(\mathcal{O}_{1:T}|\tau)\vert_{\tau=\mu} \\
&= \sum_{t=0}^T\nabla_{s_t,a_t} r(s_t,a_t)\vert_{(s_t,a_t) = \mu_t} \\
&= \nabla J(\mu)
\end{align}
$$- 这里推导很关键,完成了从Classifier Guidance Diffusion中对数概率梯度到Diffuser中Reward函数梯度的转变
- 注:文章中使用 \((s_t,a_t)= \mu_t\) 的表达,其中 \(\mu_t\) 是轨迹 \(\mu\) 的第 \(t\) 个规划步骤对应的状态和动作,其中 \(\mu = \mu_\theta(\tau)\)
- \(\mu,\Sigma\) 分别是反向过程 \(p_\theta(\tau^{i-1}|\tau^i)\) 的参数:
按照上面的实现,我们使用了Classifier Guidance Smapling来解决强化学习问题,整个规划过程如下:
- 首先在收集到的轨迹数据上训练一个扩散模型 \(p_\theta(\tau)\)
- 然后再训练一个(独立的,与 \(p_\theta(\tau)\) 无关的)轨迹奖励预测模型 \(J_\phi(\tau)\),用于预估给定轨迹 \(\tau\) 的累计奖励,轨迹奖励预测模型的梯度就是上述采样公式中的梯度 \(g = \nabla J_\phi(\mu)\)
- 在采样得到最优轨迹后,我们可以按照最优轨迹中的动作来执行一步,然后与环境交互
- 收集环境交互数据以后,重新执行规划过程
Guided Diffusion Planning的伪代码

- 输入:已经训练好的Diffuer模型 \(\mu_\theta\),轨迹奖励预测模型 \(J_\phi(\tau)\),scale \(\alpha\),协方差矩阵 \(\Sigma^i\)
- 在每一个决策时间步(直到遇到终止状态)
- 先获取观测状态 \(s\)
- 从高斯分布中采样一个噪音 \(\tau^N \sim N(\mathbf{0}, \boldsymbol{I})\)
- 执行N步反向过程生成 \(\tau^0\),每一步中都将当前步的第一个状态 \(s_0\) 修改为观测状态 \(s\)
- 注意:生成 \(\mathbf{\tau}^{i-1}\) 的过程改一下表达会更好理解: \(\mathbf{\tau}^{i-1} \sim \mathcal{N}(\mu(\mathbf{\tau}^{i}, i)+\alpha \Sigma^i \nabla_{\mathbf{\tau}} J(\mathbf{\tau})\vert_{\mathbf{\tau} = \mu(\mathbf{\tau}^{i}, i)}, \Sigma^i)\) (TODO:关于梯度部分的具体实现还要再确认一下(Diffuser源码-采样函数-实现较为奇怪,与论文中伪代码不同),收益模型输入是 \(x_t\) 还是 \(u_t\) ?求导时是对 \(x_t\) 还是 \(u_t\) ?),详细内容可参考:[Diffusion Models Beat GANs on Image Synthesis, OpenAI, 2021]和[生成扩散模型漫谈(九):条件控制生成结果]
- 理解:轨迹采用滑动窗口实现,对于任意状态,可以都包含固定步长的规划时间步(论文中提到时间步长度可以不固定),即轨迹的长度是固定的;在反向过程的每一步,都将轨迹的初始状态 \(s_0\) 修改为当前观测状态,保证最终的轨迹初始状态一定是当前观测状态 \(s\),从而保证最优轨迹的第一个动作 \(a_0\) 就是当前状态 \(s\) 对应的最优动作
- 可能得优化点讨论:
- 如果每次让Diffusion看到更多历史状态是否更合适?
- 在固定长度(较短)的序列决策中,使用完整的轨迹可能更合适?此时更像是在解决图像修复问题
条件目标强化学习-图像修复(场景二)
- Goal-Conditioned RL as Inpainting
- 对于一些优化问题不需要最大化某个奖励,而是满足特定约束,目标是生成一组满足约束的轨迹(比如想要在某个时间步终止,即设定某个时间状态是终止状态),那么这种问题可以转换为一个图片修补问题(Inpainting Problem),已知状态和动作约束就像是图片中已知的像素,其他未观测位置则由Diffusion模型生成
- 补充知识:Dirac delta 函数,通常记作 \( \delta(x) \),是数学和物理学中非常重要的一个概念。它不是传统意义上的函数,而是一个广义函数(或称为分布),由物理学家保罗·狄拉克(Paul Dirac)引入。这个“函数”用来描述理想化的瞬时事件或者集中于一点的质量、电荷等
$$
\delta(x) = \begin{cases}
+\infty, & x = 0 \\
0, & x \neq 0
\end{cases}
$$ - 在这个场景下,为了满足约束,要求生成的每一步中状态都满足条件约束,所以设定一个条件概率(满足约束的轨迹收益无穷大,否则收益为0)
$$
h(\tau) = \delta_{c_t}(s_0,a_0,\cdots,s_T,a_T) = \begin{cases}
+\infty, & \text{if} \ c_t = s_t \\
0, & \text{otherwise}
\end{cases}
$$ - 注:这个实现跟场景一中设定规划第一个时间步的状态始终保持不变思路一致
Diffusion 规划器的特点
- Diffusion Planner示意图:
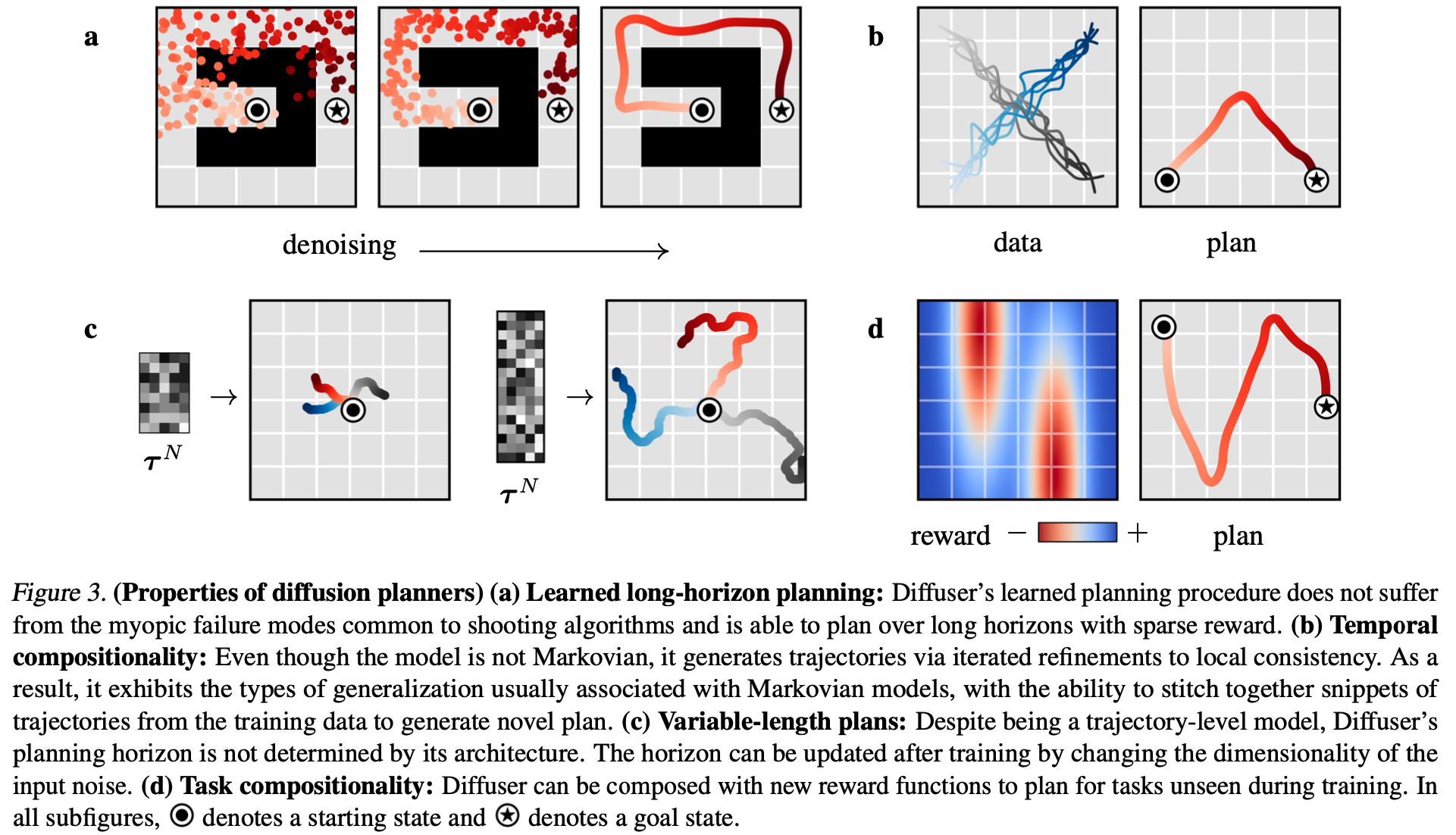
- 图示说明:
- Learned long-horizon planning :长周期可规划性。如图4(a)所示,Diffuser的长程预测可直接用于长程规划
- Temporal compositionality :时间可组合性。将不同轨迹中的子序列组合起来,从而形成新的子序列(理解:对于强化学习来说,随便组合是否是危险的?还是说,满足马尔可夫性的情况下,仅关注上一时间片即可,满足局部一致性就可以)
- Variable-length plans :可变长规划性。规划时间步数由初始化噪声的长度指定,与模型架构无关(类似于一个Diffusion模型可以生成不同大小的图片一样)。可以这样做的原因是模型的预测是在时间维度上进行卷积实现的,时间长度不由模型决定,卷积可以适配任意大小的时间长度。【问题:常规的UNet网络中输入维度不是提前指定的吗?这里为什么可以直接在时间上变长?】
- Task compositionality :任务组合性。奖励函数(或奖励预测模型)与Diffusion模型无关,训练一个Diffusion模型以后,可以在同一场景的很多不同任务(比如最大化收益或最小化路径等)上执行(甚至可以满足多个任务目标组合的情况)
附录:Diffuser 还算是强化学习吗?
- (个人理解)强化学习强调的是从环境中学习,但 Diffuser 训练过程与环境没有直接交互,所以最多算是 Offline RL
- 从是否建模 MDP 的视角看,Diffuser 虽然通过生成轨迹捕捉了 MDP 过程,但 Diffuser 没有建模 MDP 中状态(或状态动作)的价值函数和策略函数,所以基本不是强化学习了
- 注:由于可以用于解决强化学习相关的问题,所以许多博客或者文章依然将 Diffuser 归为离线强化学习的方法
附录:优化思路
- Idea1: 基于 Classifier-free 的 Diffuser
- 思路: 在CV中,已经验证了 Classifier Guidance 方法不如 Classifier-free 方法效果好;在不考虑便携性的情况下,在 Diffuser 里面,是否可以引入 Classifier-free 来优化效果呢?
- Idea2:Classifier 训练中应该看见前向过程中间状态(扰动轨迹)
- 思路:如果训练过程中 Classifier 从没有前向过程中间状态,但是采样的时候需要对这些轨迹求梯度的话,Classifier 的估值会不准确吧?是否应该让 Classifier 在训练过程中看见被扰动后的轨迹?这些轨迹的 Reward 收益又如何评估呢?