RL——1k-Layer-Networks4Self-Supervised-RL

Paper Summary

  • 缩放自监督学习（Scaling up self-supervised learning）推动了语言和视觉领域的突破
    • 但在 RL 中，仍未发现同样的（Comparable）进展
  • 论文研究了能够解锁强化学习可扩展性显著提升的构建模块，其中网络深度是一个关键因素
  • 近年来大多数强化学习论文依赖于浅层架构（大约 \(2-5\) 层）
    • 论文证明将深度增加到 1024 层可以显著提升性能
  • 论文的实验在一个无监督目标条件设置中进行，其中没有提供演示（demonstrations）或奖励，因此智能体必须（from scratch）探索并学习如何最大化达到指定目标的可能性
  • 在模拟运动和控制任务上的评估表明，论文的方法将自监督对比强化学习算法的性能提高了 \(2\times-50\times\)，超越了其他目标条件基线
  • 增加模型深度不仅提高了成功率，而且从质量上改变了习得的行为

Introduction and Discussion

  • 虽然扩大模型规模已成为机器学习许多领域中的有效方法，但其在强化学习中的作用和影响尚不清楚
  • 基于状态的强化学习任务的典型模型规模在 2 到 5 层之间（2021；2022），在其他领域使用非常深的网络并不少见；
    • Llama 3 (2024) 和 Stable Diffusion 3 (2024) 都有数百层
    • 在视觉（2021；2021；2023）和语言（2023）等领域，模型通常只有在规模超过一个临界尺度后才获得解决某些任务的能力
  • 在强化学习场景中，许多研究者一直在寻找类似的新兴现象（2023），但这些论文通常只报告微小的边际收益，并且通常只在小模型已经取得一定成功的任务上（2024a；2024；2024）
    • 当今强化学习的一个关键开放问题是，是否可能通过 Scaling 强化学习网络来实现类似的性能飞跃
  • 乍一看（At first glance），训练非常大的强化学习网络很困难是合理的：
    • 强化学习问题提供的反馈比特非常少（例如，在很长的观察序列后只有稀疏奖励），因此反馈与参数之比非常小
    • 这也反映在许多近期模型中的传统观点（LeCun，2016）（2018；2020；2019）认为，大型人工智能系统必须主要以前馈方式进行训练，而强化学习应仅用于微调这些模型。确实，最近在其他领域的许多突破主要是通过自监督方法实现的，无论是在计算机视觉（2021；2021；2024）、自然语言处理（2023）还是多模态学习（2024）中。因此，如果作者希望扩展强化学习方法，自监督很可能是一个关键要素
  • 论文将研究扩展强化学习的构建模块
  • 第一步：重新思考上述传统观点：
    • “强化学习”和”自监督学习(self-supervised learning)”并非对立的学习规则，而是可以结合成自监督强化学习系统，在不参考奖励函数或演示的情况下进行探索和学习策略（2021，2022；2022）
    • 在这项工作中，论文使用了一个最简单的自监督强化学习算法，对比强化学习（Contrastive RL, CRL）（2022）
  • 第二步：认识到增加可用数据的重要性
    • 论文将通过在最近的 GPU 加速强化学习框架（2021；2023；2022；2024）的基础上进行构建来实现这一点
  • 第三步：增加网络深度，使用深度比先前工作中典型的网络深达 \(100\times\) 的网络
    • 稳定此类网络的训练需要结合先前工作中的架构技术，包括残差连接（2015）、层归一化（2016）和 Swish 激活函数（2018）
  • 论文的实验还将研究批量大小和网络宽度的相对重要性
  • 这项工作的主要贡献在于展示了一种将这些构建模块集成到单一强化学习方法中的方法，该方法展现出强大的可扩展性：
    • 实证可扩展性（Empirical Scalability）： 论文观察到性能显著提升，在一半环境中超过 \(20\times\)，并且超越了其他标准的目标条件基线
      • 这些性能提升对应于随着规模涌现的质量上不同的策略
    • 网络架构中的深度缩放（Scaling Depth in Network Architecture）： 虽然许多先前的强化学习工作主要关注增加网络宽度，但他们通常报告有限甚至负的回报（参见第 4 节）
      • In contrast，论文的方法解锁了沿深度轴进行扩展的能力，超过了仅扩展宽度所能带来的性能提升（见第 4 节）
    • 实证分析（Empirical Analysis）： 论文对扩展方法中的关键组件进行了广泛分析，揭示了关键因素并提供了新的见解
  • 论文预期未来的研究可以在这个基础上进行，发现更多的构建模块
  • 自然语言处理（Natural Language Processing, NLP）和计算机视觉（Computer Vision, CV）最近在采用类似架构（即 Transformer）和共享学习范式（即自监督学习）方面趋于一致，共同实现了大规模模型的变革性能力（2017；2023；2021；2023；2022）
  • In contrast, 在强化学习中实现类似的进展仍然具有挑战性
    • 有几项研究探讨了扩展大型强化学习模型的障碍，包括参数利用不足（parameter underutilization，2024）、可塑性和容量损失（plasticity and capacity loss，2024，2022）、数据稀疏性（data sparsity，2017；LeCun，2016）以及训练不稳定性（training instabilities，2021；2018；Van 2018；2024a）
    • As a result，当前扩展强化学习模型的努力很大程度上局限于特定问题领域，例如模仿学习（2024）、多智能体游戏（2022）、语言引导的强化学习（2023；2022）和离散动作空间（2024；2023）
  • 最近的方法提出了几个有前景的方向，包括
    • 新的架构范式（2024）
    • 分布式训练方法（2021；2018）
    • 分布式强化学习（2023）
    • 蒸馏（2023）
  • 与这些方法相比，论文的方法对现有的自监督强化学习算法（Self-supervised RL algorithm）进行了简单的扩展
    • 这方面最近的工作包括 Lee 等人（2024）和 Nauman 等人（2024a），它们利用残差连接来促进更宽网络的训练
      • 这些努力主要集中在网络宽度上，指出增加深度带来的收益有限，因此两项工作都只使用了具有四层多层感知机（MLP）的架构
    • 在论文的方法中，论文发现扩展宽度确实能提高性能（第 4.4 节）；
      • however，论文的方法也支持沿深度扩展，并且被证明比仅扩展宽度更强大
  • Farebrother 等人（2024）描述了一项训练更深网络的重要努力，他们通过将时序差分（Temporal Difference, TD）目标离散化为分类交叉熵损失，将基于值的强化学习转化为分类问题
    • 这种方法基于一个猜想，即基于分类的方法可能更鲁棒和稳定，因此可能比回归方法展现出更好的扩展特性（1996；2024）
    • 论文使用的对比强化学习算法也有效地使用了交叉熵损失（2022）
      • 其 InfoNCE 目标是交叉熵损失的泛化，通过有效分类当前状态和动作是否属于导致目标状态的同一条轨迹还是不同轨迹来执行强化学习任务
  • 在这方面，论文的工作作为第二个证据表明
    • 分类 （很像交叉熵在自然语言处理成功扩展中的作用）可能是强化学习中一个潜在的构建模块

Preliminaries

  • 本节介绍目标条件强化学习（goal-conditioned RL）和对比强化学习（contrastive RL）的符号和定义
  • 论文的重点是在线强化学习，其中回放缓冲区存储最近的轨迹， Critic 以自监督方式进行训练

目标条件强化学习 (Goal-Conditioned Reinforcement Learning)

  • 论文定义目标条件马尔可夫决策过程（Markov Decision Process, MDP）为一个 7 元组 （其中 \(g\) 为目标）
    $$ \mathcal{M}_{g}=(\mathcal{S},\mathcal{A},p_{0},p,p_{g},r_{g},\gamma)$$
    • 其中智能体与环境交互以达到任意目标（1993；2017；2021）
    • 在每个时间步 \(t\)，智能体观察状态 \(s_{t}\in\mathcal{S}\) 并执行相应的动作 \(a_{t}\in\mathcal{A}\)
    • 智能体从 \(p_{0}(s_{0})\) 采样的状态开始交互，交互动态由转移概率分布 \(p(s_{t+1}\mid s_{t},a_{t})\) 定义
    • 目标 \(g\in\mathcal{G}\) 定义在目标空间 \(\mathcal{G}\) 中，该空间通过映射 \(f:\mathcal{S}\rightarrow\mathcal{G}\) 与 \(\mathcal{S}\) 相关联
      • For Example，\(\mathcal{G}\) 可能对应于状态维度的子集
    • 目标上的先验分布定义为 \(p_{g}(g)\)
    • 奖励函数 \(r_g\) 定义为下一时间步达到目标 \(g\) 的概率密度
      $$ r_{g}(s_{t},a_{t})\triangleq(1-\gamma)p(s_{t+1}=g\mid s_{t},a_{t}) $$
      • 其中 \(\gamma\) 为折扣因子
  • 在此设置中，目标条件策略 \(\pi(a\mid s,g)\) 接收环境的当前观察以及一个目标
  • 论文将折扣状态访问分布定义为
    $$ p^{\pi(\cdot|\cdot,g)}_{\gamma}(s)\triangleq(1-\gamma)\sum_{t=0}^{\infty}\gamma^ {t}p^{\pi(\cdot|\cdot,g)}_{t}(s) $$
    • 其中 \(p^{\pi}_{t}(s)\) 是在给定 \(g\) 的条件下，策略 \(\pi\) 恰好经过 \(t\) 步访问 \(s\) 的概率
  • 策略 \(\pi(\cdot\mid\cdot,g)\) 对于奖励 \(r_{g}\) 的 Q 函数可以用到达目标的额改了来定义：
    $$ Q^{\pi}_{g}(s,a)\triangleq p^{\pi(\cdot|\cdot,g)}_{\gamma}(g\mid s,a)$$
  • Goal-Conditioned RL 的目标是最大化期望奖励：
    $$\max_{\pi}\mathbb{E}_{p_{0}(s_{0}),p_{g}(g),\pi(\cdot|\cdot,g)}\left[\sum_{t=0}^{\infty}\gamma^{t}r_{g}\left(s_{t},a_{t}\right)\right].$$

对比强化学习 (Contrastive Reinforcement Learning)

  • 论文的实验将使用对比强化学习算法（2022）来解决目标条件问题
  • 对比强化学习是一种 Actor-Critic 方法；
    • 论文用 \(f_{\phi,\psi}(s,a,g)\) 表示 Critic ，用 \(\pi_{\theta}(a\mid s,g)\) 表示 Policy（即 Actor）
    • Critic 由两个神经网络参数化，分别返回 State-Action 对嵌入 \(\phi(s,a)\) 和目标嵌入 \(\psi(g)\)
    • Critic 的输出定义为这些嵌入之间的 \(l^{2}\) 范数：
      $$ f_{\phi,\psi}(s,a,g)=|\phi(s,a)-\psi(g)|_{2} $$
      • 理解：衡量的是当前 <s,a> 对 与 目标 \(g\) 之间的距离
  • Critic 使用如先前工作中（2022，2021；2023，2024；2024；2024）的 InfoNCE 目标（Sohn，2016）进行训练
    • 训练在批次 \(\mathcal{B}\) 上进行，其中 \(s_{i},a_{i},g_{i}\) 代表从同一轨迹采样的状态、动作和目标（未来状态），而 \(g_{j}\) 代表从另一个随机轨迹采样的目标
    • 在 批次 \(\mathcal{B}\) 上，Critic 的目标函数定义为：
      $$\min_{\phi,\psi}\mathbb{E}_{\mathcal{B} }\left[-\sum\nolimits_{i=1}^{|\mathcal{B }|}\log\left(\frac{e^{f_{\phi,\psi}(s_{i},a_{i},g_{i})} }{\sum\nolimits_{j=1}^ {K}e^{f_{\phi,\psi}(s_{i},a_{i},g_{j})} }\right)\right].$$
    • 理解：最小化这个目标函数本质上就是最大化 当前 <s,a> 对 与 目标 \(g\) Embedding 之间的距离？
  • 策略（Actor）\(\pi_{\theta}(a\mid s,g)\) 的训练目标则是最大化 Critic ：
    $$\max_{\pi_{\theta} }\mathbb{E}_{p_{0}(s_{0}),p(s_{t+1}|s_{t},a_{t}),\\ p_g(g),\pi_\theta(a|s,g)}\left[f_{\phi,\psi}(s,a,g)\right]$$

残差连接 (Residual Connections)

  • 论文将残差连接（2015）纳入论文的架构，Following 它们在强化学习中的成功应用（2024；2024；2024a）
  • 一个残差块通过将习得的残差函数 \(F_{i}(\mathbf{h}_{i})\) 添加到原始表示来转换给定的表示 \(\mathbf{h}_{i}\)
  • 数学上，这表示为：
    $$\mathbf{h}_{i+1}=\mathbf{h}_{i}+F_{i}\left(\mathbf{h}_{i}\right)$$
    • 其中 \(\mathbf{h}_{i+1}\) 是输出表示，\(\mathbf{h}_{i}\) 是输入表示，\(F_{i}(\mathbf{h}_{i})\) 是通过网络（例如，使用一层或多层）习得的变换
    • 这个加法确保网络学习对输入的修改，而不是全新的变换，有助于保留来自较早层的有用特征
    • 残差连接通过引入捷径路径来改进梯度传播（2016；2016），使得能够更有效地训练深度模型

Experiments

Experimental Setup

Environments
  • 所有的 RL 实验均使用 JaxGCRL 代码库 (2024)，该库基于 Brax (2021) 和 MJX (2012) 环境，便于进行快速的在线 GCRL 实验
  • 使用的具体环境是一系列的运动、导航和机器人操作任务，详情见 B 节
  • 论文使用稀疏奖励设置，仅当智能体在目标附近时 \(r=1\)
  • 对于评估，论文测量智能体接近目标的时间步数 （在总共 1000 步中）
  • 当以单个数字报告算法性能时，论文计算训练最后五个 epoch 的平均得分
Architectural Components
  • 论文采用了来自 ResNet 架构 (2015) 的残差连接，每个残差块由四个重复单元组成：一个 Dense layer、一个层归一化 (Layer Normalization) 层 (2016) 和 Swish 激活函数 (2018)
  • 如图 2 所示，论文在残差块的最终激活之后立即应用残差连接
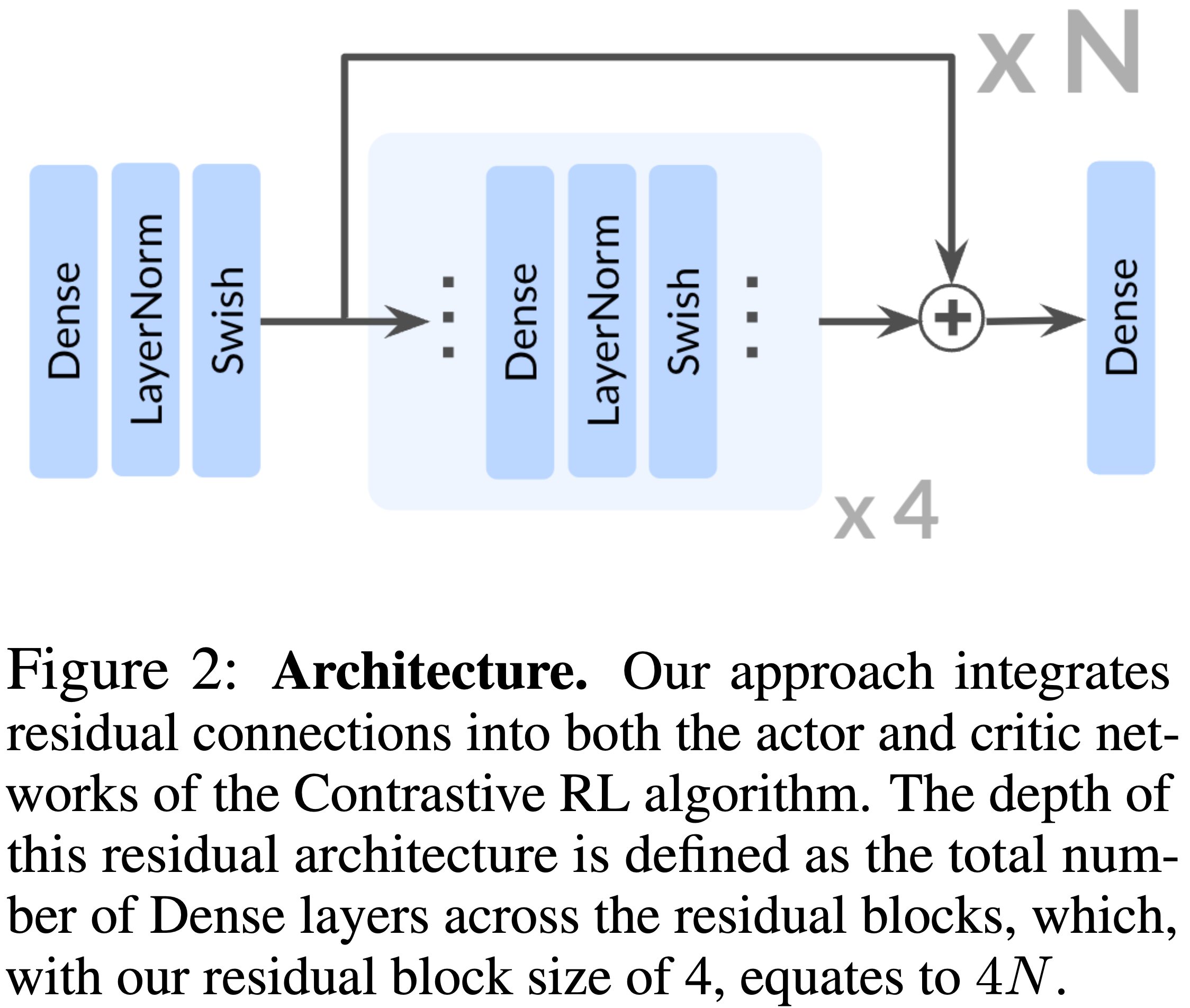
  • 在论文中，论文将网络的深度定义为架构中所有残差块内密集层的总数
  • 在所有实验中，深度指的是 Actor 网络和两个 Critic 编码器网络的配置，它们是联合缩放的，但 4.4 节的消融实验除外

对比强化学习中的深度缩放 (Scaling Depth in Contrastive RL)

  • 论文首先研究增加网络深度如何提高性能
  • JaxGCRL 基准测试和相关先前工作 (2024；2024a；2024) 都使用深度为 4 的 MLP，因此论文将其作为基线
    • 论文将研究深度为 8、16、32 和 64 的网络
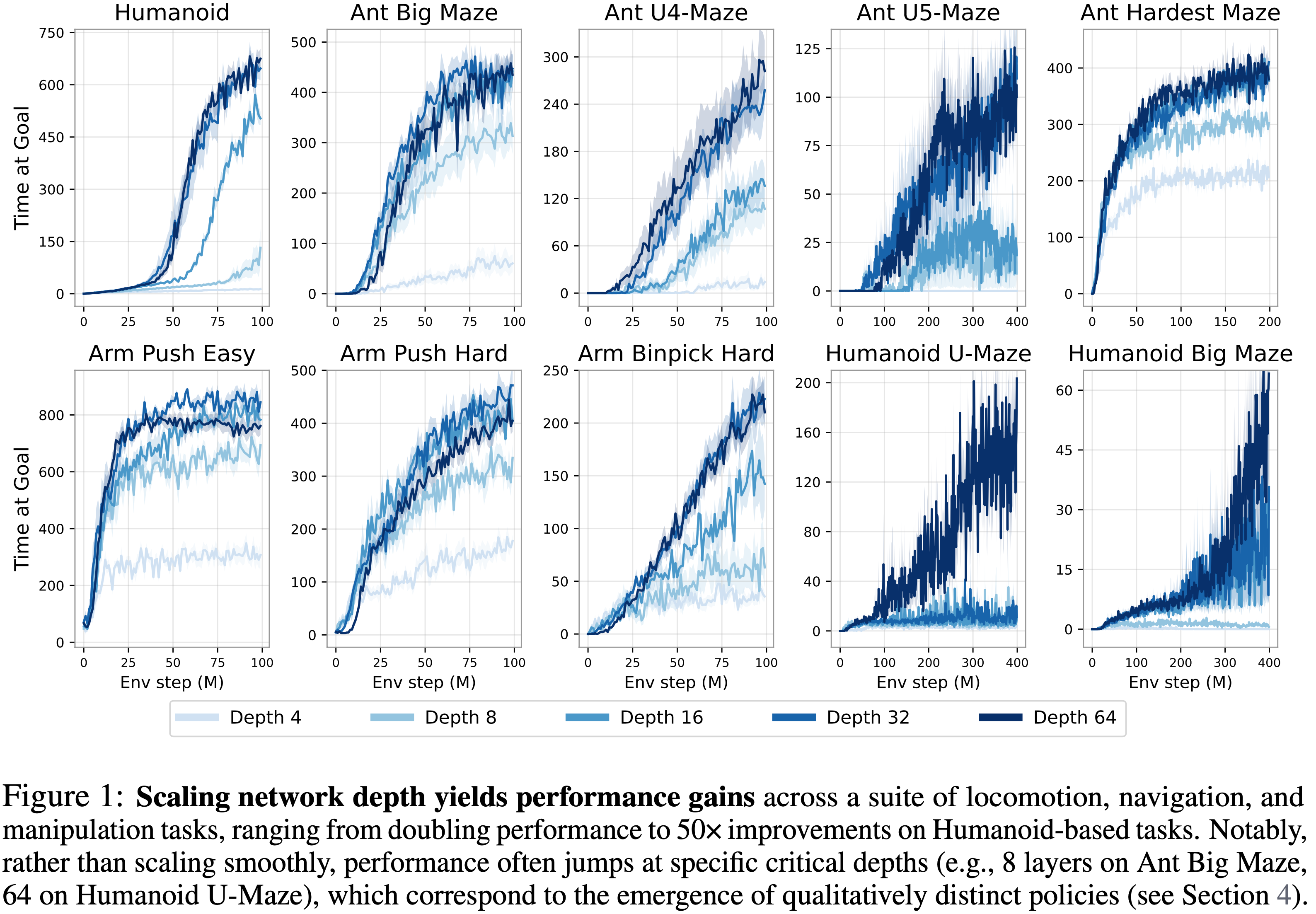
  • 图 1 中的结果表明，在多种运动、导航和操作任务中，更深的网络实现了显著的性能提升
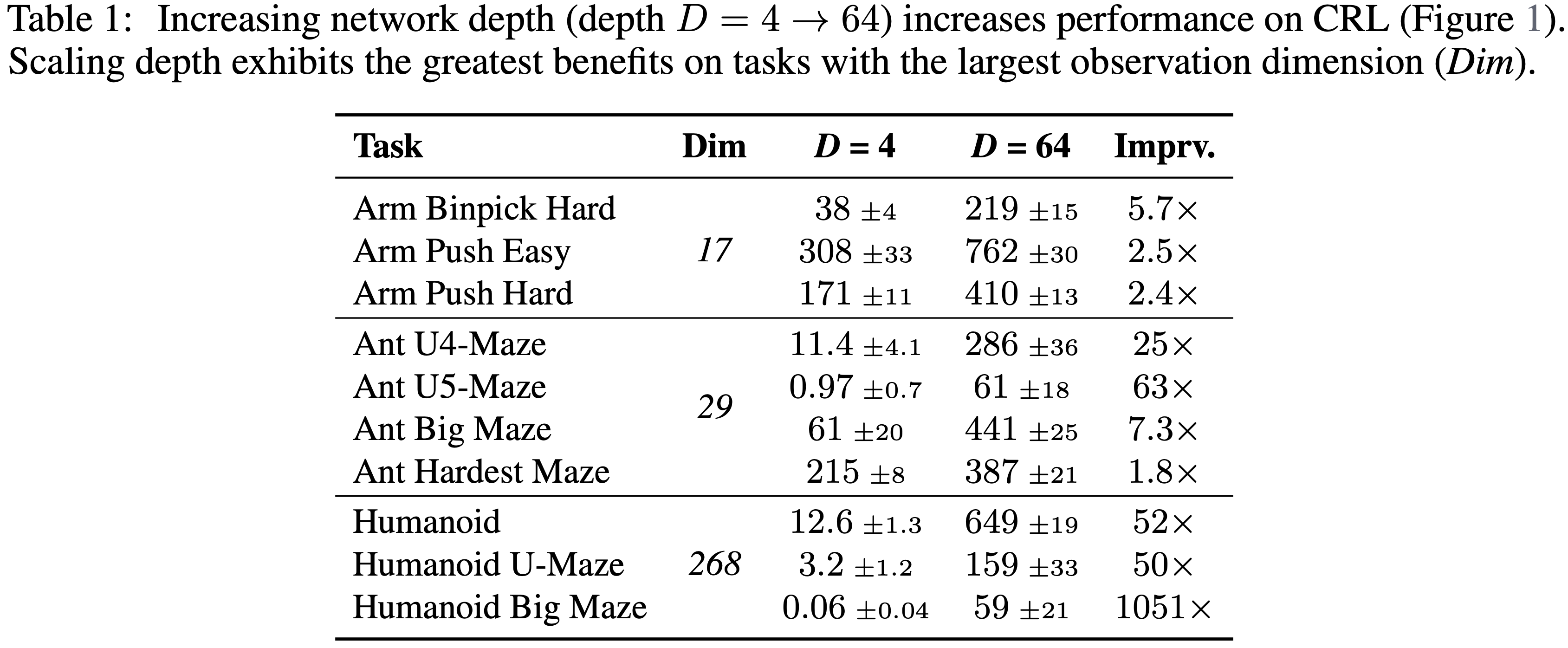
  • 与先前工作中典型的 4 层模型相比，更深的网络在机器人操作任务中实现了 \(2-5\times\) 的提升，在长期视野迷宫任务（如 Ant U4-Maze 和 Ant U5-Maze）中实现了超过 \(20\times\) 的提升，在类人形任务中实现了超过 \(50\times\) 的提升
  • 深度达到 64 的性能提升完整表格见表 1
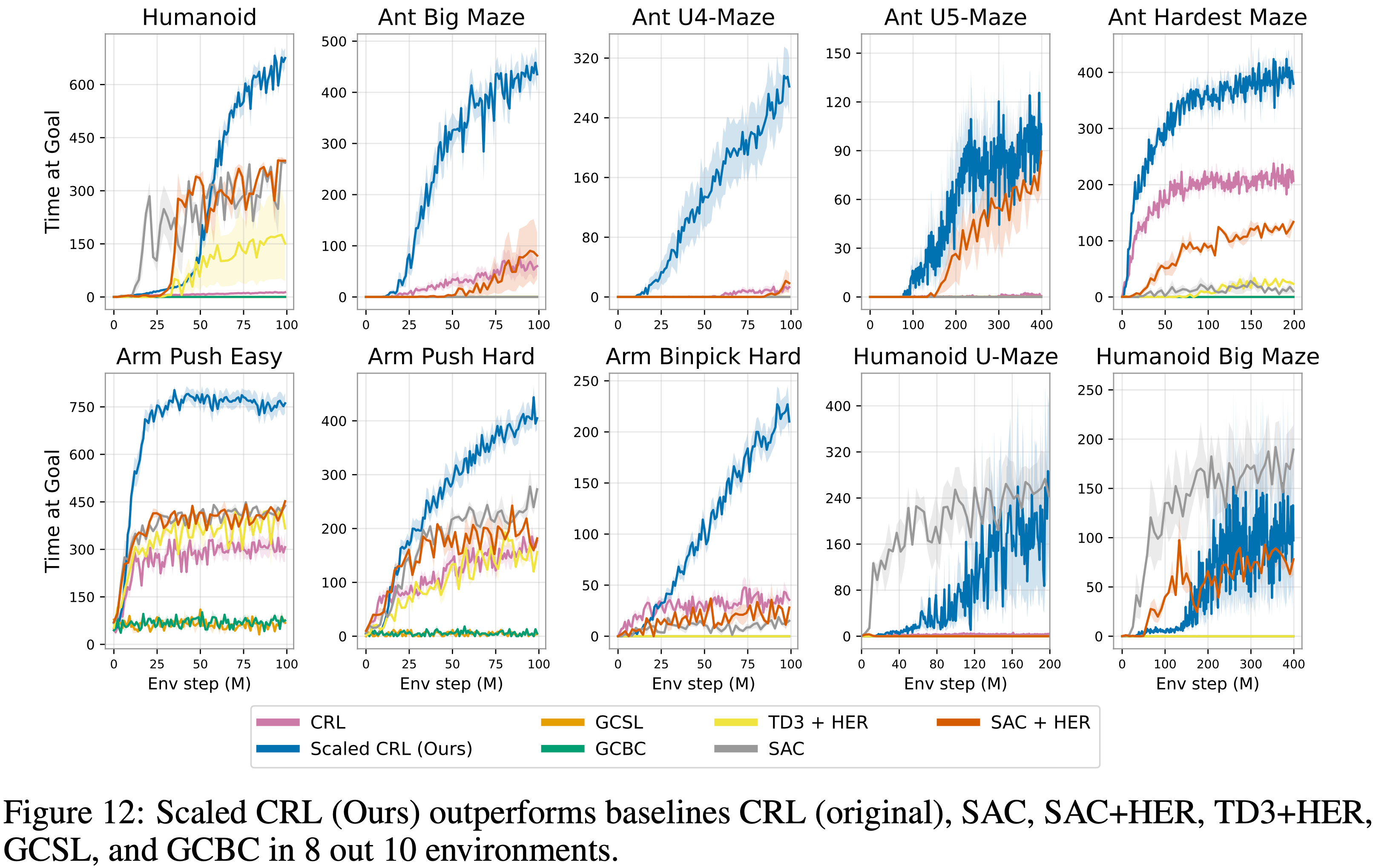
  • 在图 12 中，论文在相同的 10 个环境中展示了与 SAC、SAC+HER、TD3+HER、GCBC 和 GCSL 的对比结果
    • 扩展 CRL 带来了实质性的性能改进，在 10 个任务中的 8 个中优于所有其他基线
    • 唯一的例外是 Humanoid Maze 环境中的 SAC，它在早期表现出更高的样本效率；
      • 但经过扩展的 CRL 最终达到了可比的性能
  • 这些结果突显了，扩展 CRL 算法的深度能够在目标条件强化学习中实现最先进的性能

通过深度涌现的策略 (Emergent Policies Through Depth)

  • 对图 1 中性能曲线的结果进行更仔细的检查揭示了一个值得注意的模式：性能并非随着深度增加而逐渐改善，而是在达到一个 关键深度 (critical depth) 阈值后会出现明显的跳跃（如图 5 所示）
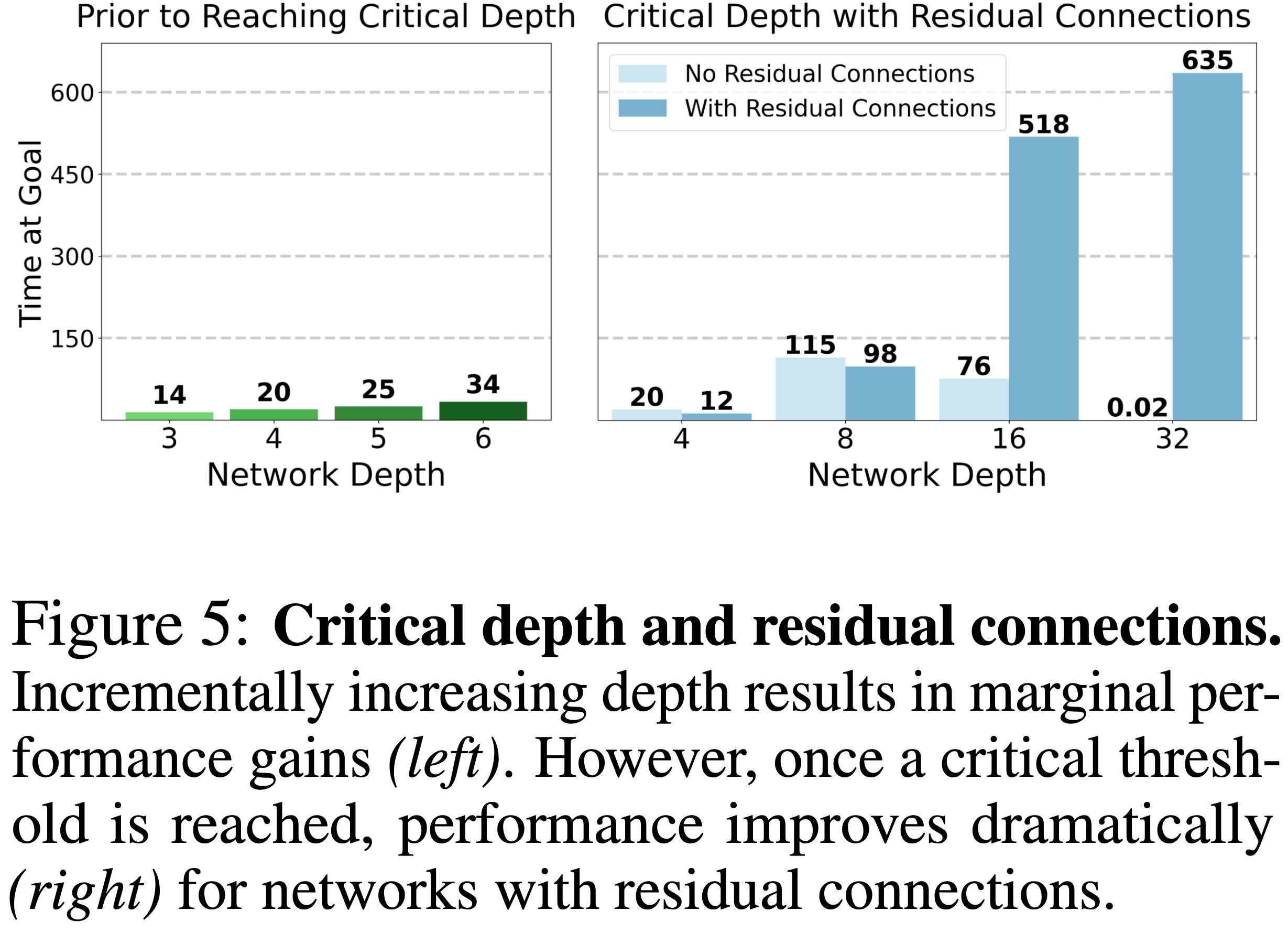
  • 关键深度因环境而异，从 8 层（例如 Ant Big Maze）到 Humanoid U-Maze 任务中的 64 层不等，甚至在深度达到 1024 层时还会出现进一步的跳跃（参见测试极限部分，第 4.4 节）
  • 受此观察启发，论文可视化了不同深度下学到的策略，并发现其表现出性质上不同的技能和行为
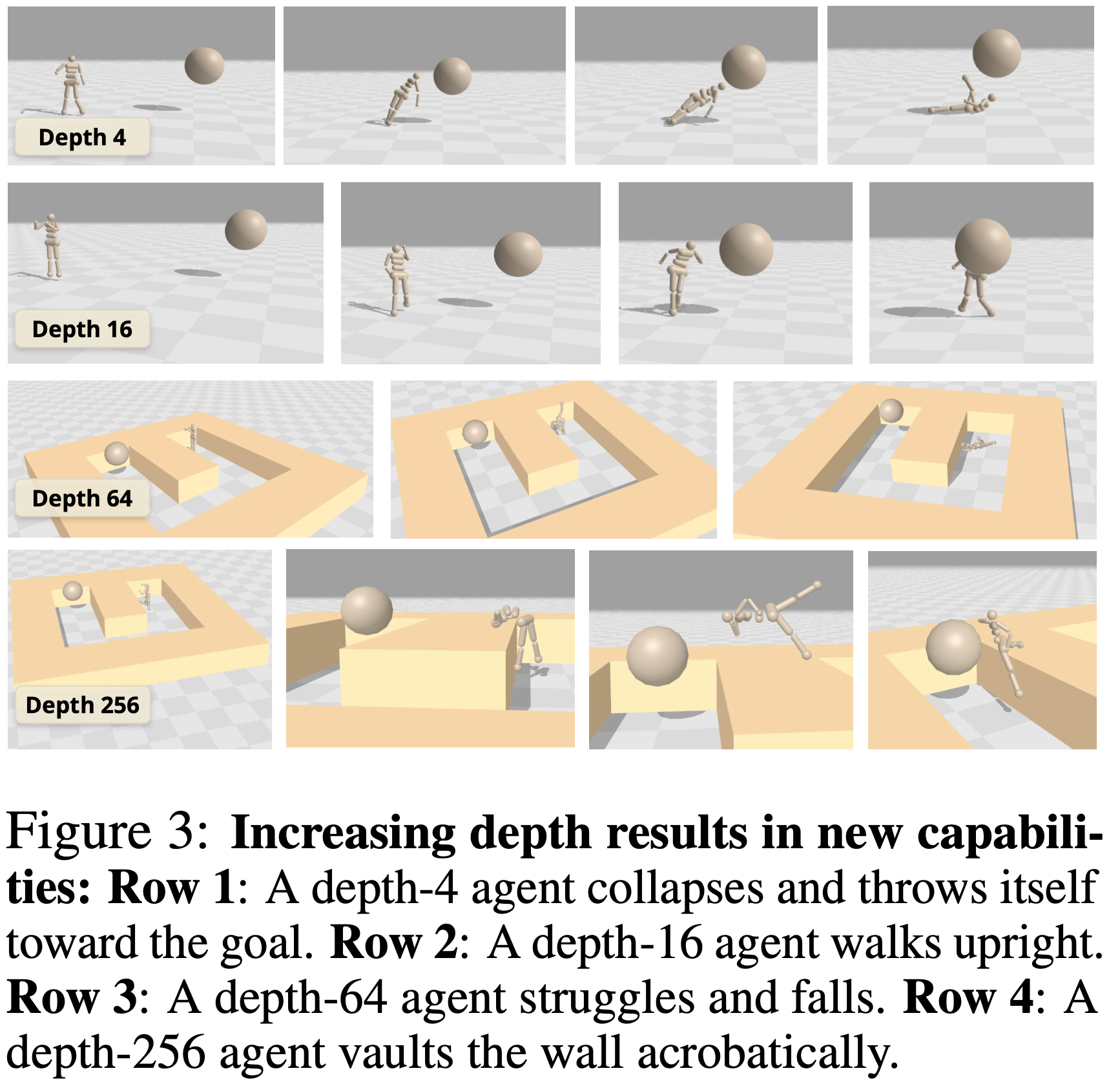
  • 这在类人形任务中尤为明显，如图 3 所示
    • 深度为 4 的网络表现出原始的策略，智能体要么跌倒，要么将自己抛向目标
    • 只有在达到 16 的关键深度时，智能体才发展出直立走向目标的能力
    • 在 Humanoid U-Maze 环境中，深度为 64 的网络难以绕过中间墙壁，会倒在地上
    • 引人注目的是，在深度为 256 时，智能体在 Humanoid U-Maze 上学到了独特的行为
    • 这些行为包括向前折叠成杠杆位置以将自己推过墙壁，以及转变为坐姿以蠕动着越过中间障碍物接近目标（其中一个策略如图 3 第四行所示）
    • 据论文所知，这是首个在类人形环境中记录此类行为的目标条件方法

对 CRL 扩展来说，什么是重要的？ (What Matters for CRL Scaling)

宽度与深度 (Width vs. Depth)
  • 过去的文献表明，扩展网络宽度可能是有效的 (2024；2024a)
  • 在图 4 中，论文发现扩展宽度在论文的实验中也很有帮助：更宽的网络始终优于更窄的网络（深度恒定保持为 4）
  • 然而，深度似乎是更有效的扩展轴：简单地将深度加倍到 8（宽度恒定保持为 256）在所有三个环境中的表现都超过了最宽的网络
  • 深度扩展的优势在 Humanoid 环境（观察维度 268）中最为明显，其次是 Ant Big Maze（维度 29）和 Arm Push Easy（维度 17）
    • 这表明其相对益处可能随着观察维度的增加而增加
  • 另外需要注意的是，参数数量随宽度线性扩展，但随深度呈二次方扩展
    • 作为对比，一个具有 4 个 MLP 层和 2048 个隐藏单元的网络大约有 3500 万个参数，而一个深度为 32、隐藏单元为 256 的网络只有大约 200 万个参数
  • 因此，在固定的 FLOP 计算预算或特定内存约束下运行时，深度扩展可能是一种计算效率更高的方法来提高网络性能
扩展 Actor 与 Critic 网络 (Scaling the Actor vs. Critic Networks)
  • 为了研究 Actor 和 Critic 网络中扩展的作用，图 6 展示了三个环境中不同 Actor 和 Critic 深度组合的最终性能
  • 先前工作 (2024a；2024) 主要关注扩展 Critic 网络，发现扩展 Actor 会降低性能
  • 相比之下，虽然论文确实发现在三个环境中的两个（Humanoid, Arm Push Easy）中扩展 Critic 更有影响，但论文的方法从联合扩展 Actor 网络中获益，其中一个环境（Ant Big Maze）显示扩展 Actor 更有影响
  • 因此，论文的方法表明，同时扩展 Actor 和 Critic 网络可以在提升性能方面发挥互补作用
深度网络解锁批次大小扩展 (Deep Networks Unlock Batch Size Scaling)
  • 扩展批次大小在机器学习的其他领域已得到广泛认可 (2022；2024)
    • 然而，这种方法尚未在强化学习 (RL) 中有效转化，先前工作甚至报告了对基于值的 RL 的负面影响 (2023)
      • 之前有些文章确实提到过 RL 训练不需要较大的 Batch
    • 确实，在论文的实验中，简单地增加原始 CRL 网络的批次大小只会带来微小的性能差异（图 7，左上）
  • 乍一看，这可能违反直觉：
    • 由于强化学习通常每条训练数据包含的信息比特较少 (LeCun, 2016)，人们可能会预期批次损失或梯度的方差更高，这表明需要更大的批次大小来补偿
  • 与此同时，这种可能性取决于所讨论的模型是否真的能利用更大的批次大小，在扩展取得成功的 ML 领域，更大的批次大小通常在与足够大的模型结合时带来最大的好处 (2024；2022)。一个假设是，传统上在 RL 中使用的小型模型可能掩盖了更大批次大小的潜在好处
  • 为了验证这个假设，论文研究了在不同深度网络下增加批次大小的效果
  • 如图 7 所示，随着网络深度的增加，扩展批次大小变得有效
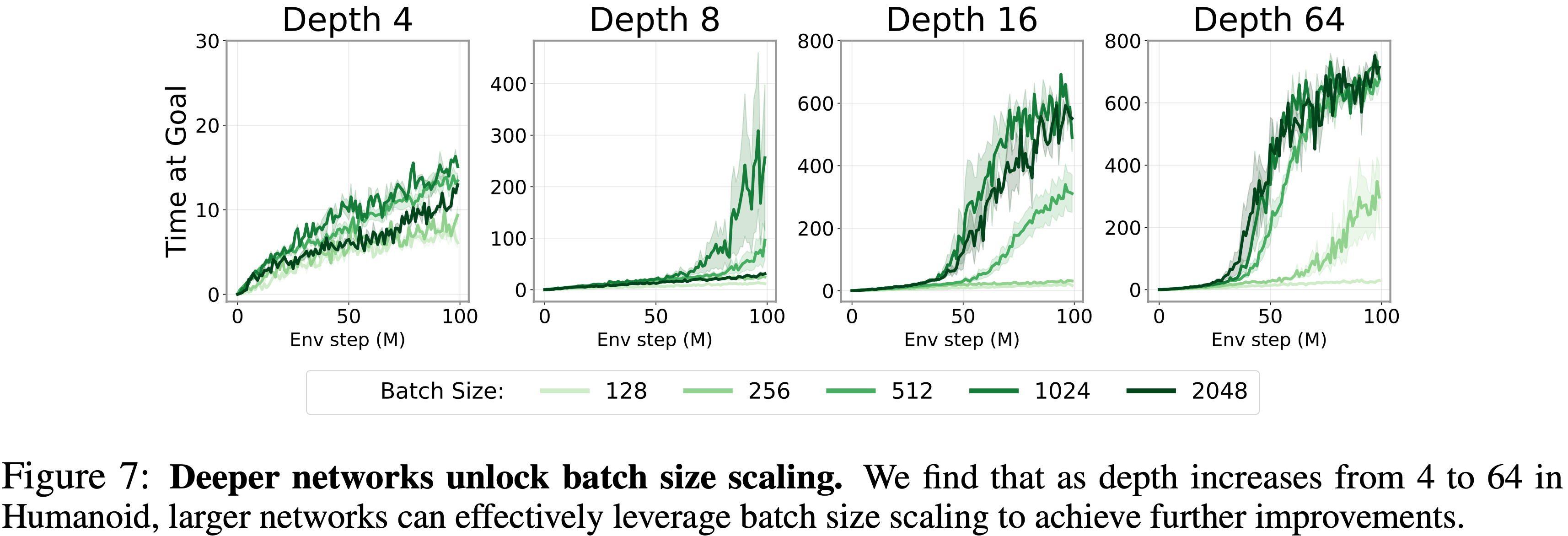
    • 这一发现提供了证据，表明通过扩展网络容量，论文可能同时解锁更大批次大小的好处，使其成为更广泛追求扩展自监督 RL 过程中的一个重要组成部分
使用 1000 层以上训练对比强化学习 (Training Contrastive RL with 1000+ Layers)
  • 接下来论文研究将深度进一步增加到 64 层以上是否还能提升性能
  • 论文使用 Humanoid 迷宫任务，因为这些既是基准测试中最具挑战性的环境，似乎也从最深度的扩展中受益
  • 如图 12 所示的结果表明，当网络深度在 Humanoid U-Maze 环境中达到 256 和 1024 层时，性能持续显著提高
    • 虽然由于计算限制论文无法扩展到 1024 层以上，但论文预计在更具挑战性的任务上，即使深度更大也会看到持续的改进

扩展发生的原因 (Why Scaling Happens)

深度增强对比表征 (Depth Enhances Contrastive Representations)
  • 长期视野设定一直是 RL 中的一个长期挑战，特别是在无监督目标条件设定中，没有辅助的奖励反馈 (2019)
  • U-Maze 系列环境需要全局理解迷宫布局才能有效导航
  • 论文考虑 Ant U-Maze 环境的一个变体，U4-maze，其中智能体必须首先朝着与目标相反的方向移动，绕圈并最终到达目标
  • 如图 9 所示，论文观察到浅层网络（深度 4）与深层网络（深度 64）在行为上存在质的差异
    • 根据 Critic 编码器表示计算的可视化 Q 值表明，深度为 4 的网络似乎依赖于到目标的欧几里得距离作为 Q 值的代理，即使墙壁阻碍了直接路径
    • 相比之下，深度为 64 的 Critic 网络学到了更丰富的表示，使其能够有效地捕获迷宫的拓扑结构，这一点通过沿着内边缘的高 Q 值轨迹可视化得以体现
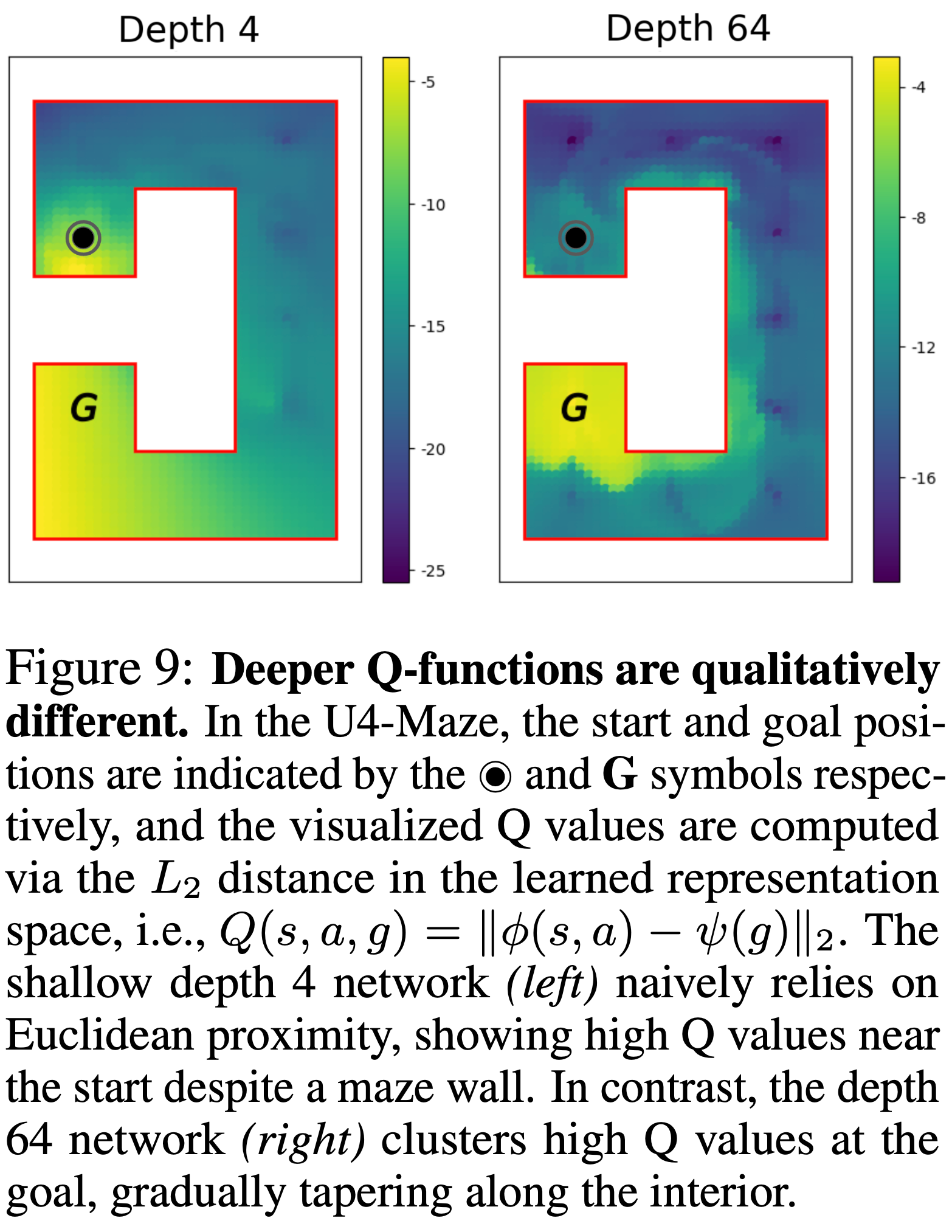
  • 这些发现表明，增加网络深度会导致更丰富的学习表示，使深层网络能够以自监督的方式更好地覆盖环境状态空间
深度以协同方式增强探索和表达能力 (Depth Enhances Exploration and Expressivity in a Synergized Way)
  • 论文之前的结果表明，更深的网络实现了更大的 State-Action 覆盖
  • 为了更好地理解扩展有效的原因，论文试图确定是否仅仅是改进的数据解释了扩展的好处，还是它与其他因素共同作用
  • 因此，论文设计了图 8 中的实验，其中论文并行训练三个网络：
    • 一个网络，即“收集器 (collector)”，与环境交互，并将所有经验写入共享的重放缓冲区
    • 两个额外的“学习器 (learner)”，一个深的和一个浅的，同时进行训练
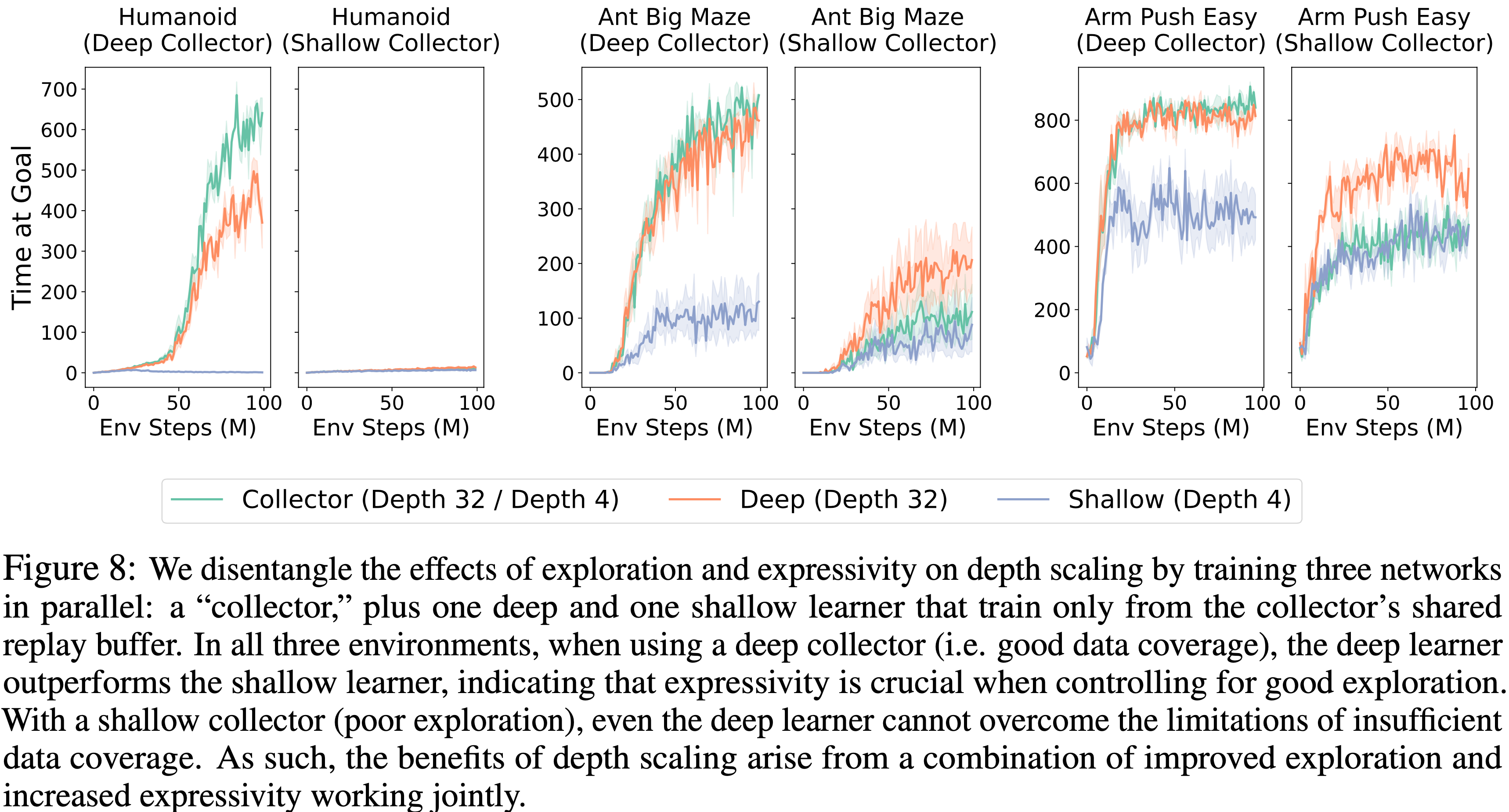
  • 关键在于，这两个学习器从不收集自己的数据；它们仅从收集器的缓冲区进行训练
  • 这个设计在保持数据分布不变的同时，改变了模型的容量，因此深层和浅层学习器之间的任何性能差距必然来自表达能力，而非探索能力
  • 当收集器是深层时（例如，深度 32），在所有三个环境中，深层学习器都大幅优于浅层学习器，这表明深层网络的表达能力至关重要
  • 另一方面，论文重复实验，使用浅层收集器（例如，深度 4），其探索效率较低，因此用低覆盖的经验填充缓冲区
  • 在这里，深层和浅层学习器都表现不佳，并达到相似的较差性能，这表明深层网络额外的容量无法克服数据覆盖不足的限制
  • 因此，扩展深度以一种协同的方式增强了探索和表达能力：
    • 更强的学习能力驱动更广泛的探索，而强大的数据覆盖对于充分发挥更强学习能力的力量至关重要
  • 这两个方面共同促成了性能的提升
深度网络学会为目标附近的状态分配更大的表征容量 (Deep Networks Learn to Allocate Greater Representational Capacity to States Near the Goal)
  • 在图 10 中，论文选取 Humanoid 环境中的一个成功轨迹，并可视化了深层与浅层网络沿着该轨迹的 State-Action 编码器嵌入
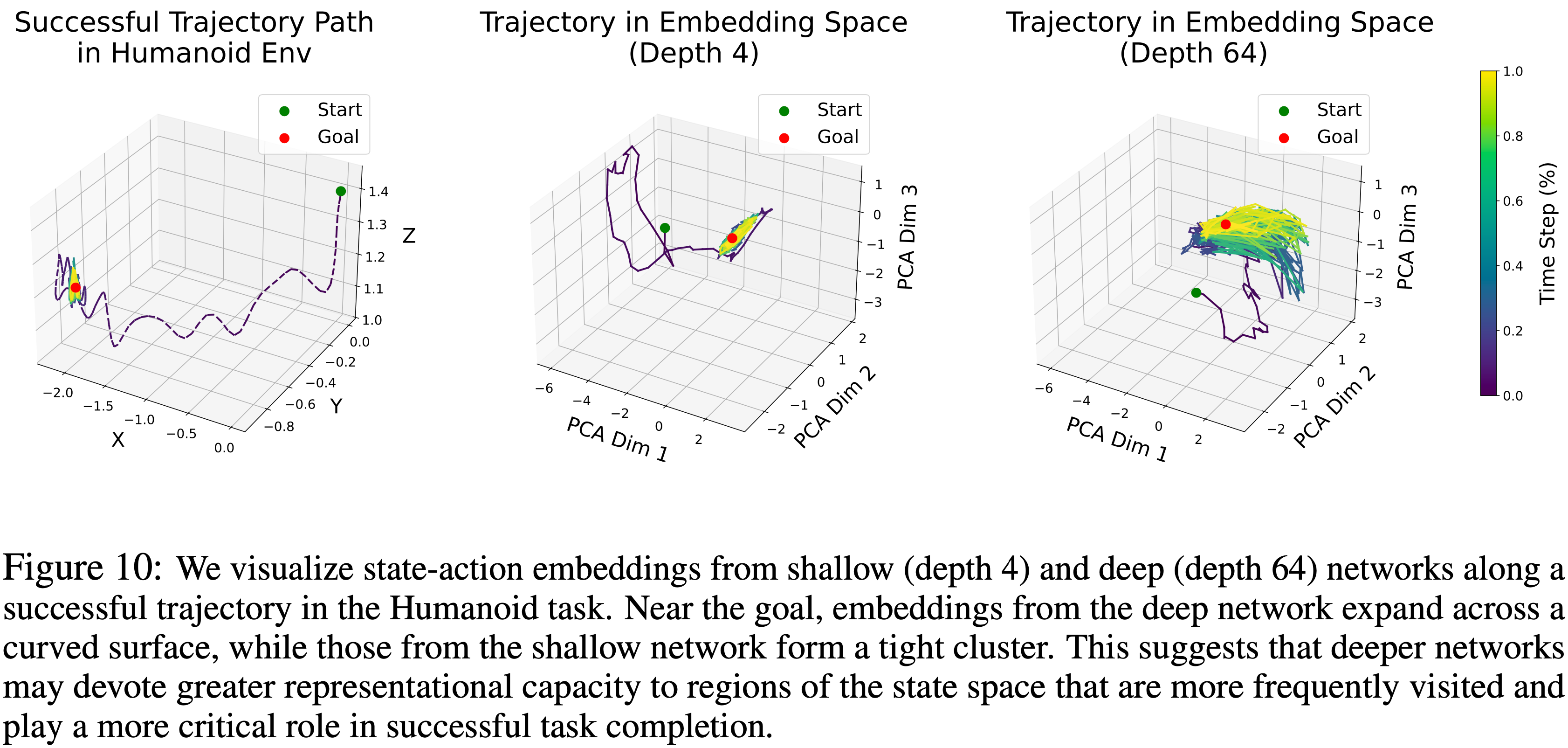
  • 虽然浅层网络（深度 4）倾向于将接近目标的状态紧密地聚集在一起，但深层网络产生更“分散”的表示
  • 这种区别很重要：在自监督设置中，作者希望论文的表示能将重要的状态，特别是未来的或与目标相关的状态，与随机的状态分开
  • 因此，作者希望为此类关键区域分配更多的表征容量
  • 这表明，深层网络可能学会更有效地为对下游任务最重要的状态区域分配表征容量
深度网络实现部分经验拼接 (Deeper Networks Enable Partial Experience Stitching)
  • 强化学习中的另一个关键挑战是学习能够泛化到训练期间未见过的任务的策略
  • 为了评估这种情况，论文设计了一个修改版的 Ant U-Maze 环境
  • 如图 11（右上）所示，原始的 JaxGCRL 基准测试评估智能体在墙壁另一侧三个最远目标位置上的性能
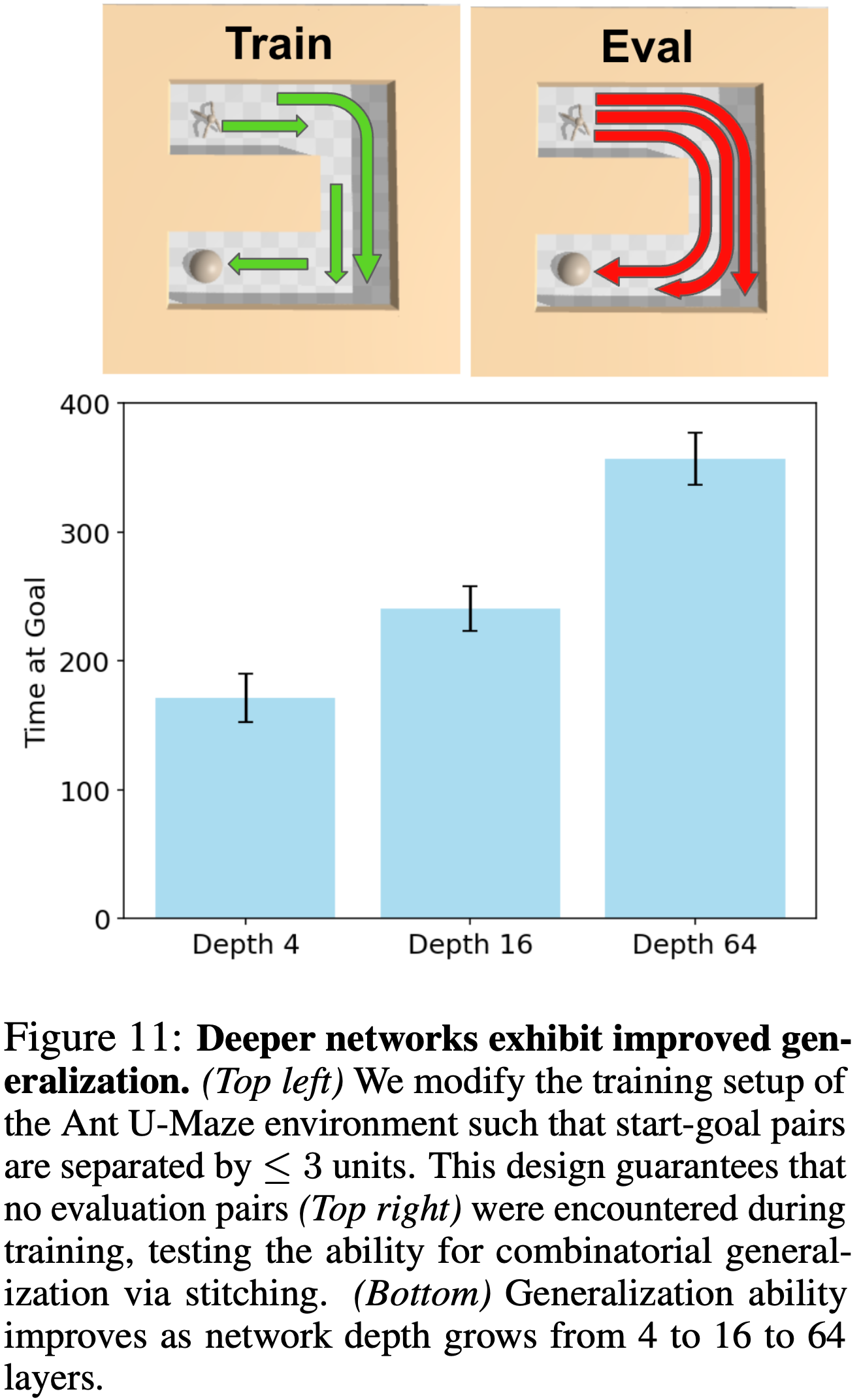
  • 然而，论文没有在所有可能的子目标（评估状态-目标对的超集）上进行训练，而是修改了设置，只训练最多相距 \(3\) 个单位的起点-目标对，确保没有任何评估对出现在训练集中
  • 图 11 表明，深度为 4 的网络显示出有限的泛化能力，仅解决了最简单的目标（距离起点 4 个单位）
  • 深度为 16 的网络取得中等成功，而深度为 64 的网络表现出色，有时能解决最具挑战性的目标位置
  • 这些结果表明，增加网络深度导致了某种程度的拼接，将 \(\leq\)\(3\) 个单位的对组合起来以导航 U-Maze 6 个单位跨度
(CRL) 算法是关键 (The (CRL) Algorithm is Key)
  • 在附录 A 中，论文展示了扩展后的 CRL 优于其他基线目标条件算法，并推进了目标条件 RL 的 SOTA
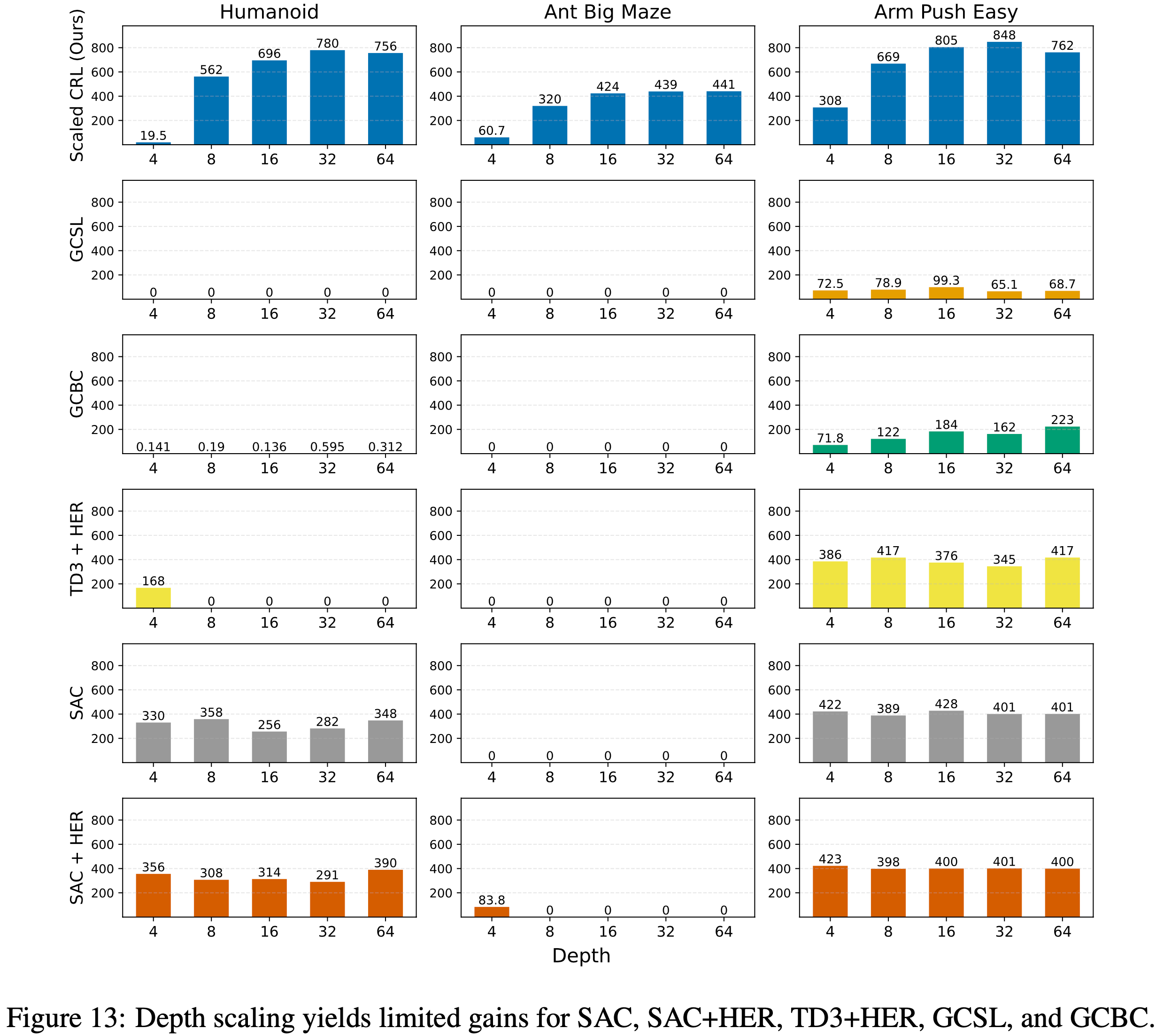
    • 论文观察到，对于时间差分方法 (SAC, SAC+HER, TD3+HER)，性能在深度为 4 的网络时达到饱和，并且更深度的网络带来的性能提升为零或负值
    • 这与先前的研究一致，表明这些方法主要受益于宽度 (2024；2024a)
    • 这些结果表明，自监督的 CRL 算法至关重要
  • 论文还尝试扩展更多的自监督算法，即目标条件行为克隆 (GCBC) 和目标条件监督学习 (GCSL)
    • 虽然这些方法在某些环境中成功率为零，但它们在手臂操作任务中显示了一定的效用
    • 有趣的是，即使是像 GCBC 这样非常简单的自监督算法也能从增加深度中受益
    • 这为未来工作指出了一个有前景的方向，即进一步研究其他自监督方法，以揭示可能不同或互补的扩展自监督 RL 的方法
  • 最后，最近的工作用拟度量架构增强了目标条件 RL，利用了时间距离满足基于三角不等式的不变性这一事实
  • 在附录 A 中，论文也研究了当应用于这些拟度量网络时，深度扩展效应是否仍然存在

深度扩展能改进离线对比强化学习吗？ (4.6 Does Depth Scaling Improve Offline Contrastive RL?)

  • 在初步实验中，论文使用 OGBench (2024) 评估了离线目标条件设定下的深度扩展
  • 论文发现几乎没有证据表明增加 CRL 的网络深度能在此离线设定中提高性能
  • 为了进一步研究这一点，论文进行了消融实验：
    • (1) 扩展 Critic 深度，同时将 Actor 保持在 4 或 8 层；
    • (2) 对 Critic 编码器的最终层应用冷启动 (2024)
  • 在所有情况下，基线深度 4 的网络通常成功率最高
  • 未来工作的一个关键方向是看看论文的方法能否进行调整，以在离线设定中实现扩展

Conclusion

  • 可以说，当今视觉和语言模型的大部分成功归功于它们从规模中表现出的涌现能力 (2023)，导致许多系统将 RL 问题简化为视觉或语言问题
  • 大型 AI 模型的一个关键问题是：
    • 数据从何而来？与监督学习范式不同，RL 方法通过探索联合优化模型和数据收集过程，从而内在性地解决了这个问题
    • 最终，确定构建展现涌现能力的 RL 系统的有效方法，可能对于将该领域转变为训练自己大型模型的领域至关重要
  • 作者相信，论文的工作是朝着这些系统迈出的一步
  • 通过将扩展 RL 的关键组件整合到一个单一方法中，论文展示了在复杂任务中，随着规模的增加，模型性能持续提升
  • 此外，深度模型表现出质地上更好的行为，这可能被解释为隐式获取的、达到目标所必需的技能

Limitations

  • 论文结果的主要局限在于，扩展网络深度是以计算成本为代价的
  • 未来工作的一个重要方向是研究如何使用分布式训练来利用更多的计算资源，以及如何使用剪枝和蒸馏等技术来降低计算成本

附录 A：Additional Experiments

A.1 扩展后的对比RL在10个环境中的8个上优于所有其他基线（Scaled CRL Outperforms All Other Baselines on 8 out of 10 Environments）

  • 在图 1 中，论文展示了增加 CRL 算法的深度可以带来相比原始 CRL 显著的性能提升（另见表 1 ）
  • 这里，论文表明这些提升转化为了在线目标条件强化学习中的最新性能结果，扩展后的 CRL（Scaled CRL）在性能上优于标准的基于时序差分（TD）的方法（如S AC、SAC+HER 和 TD3+HER ），也优于基于自监督模仿的方法（如 GCBC 和 GCSL）

A.2 CRL 算法是关键：深度扩展对其他基线方法效果不佳（The CRL Algorithm is Key: Depth Scaling is Not Effective on Other Baselines）

  • 论文研究了在基线算法中增加网络深度是否能带来与在 CRL 中观察到的类似的性能提升
  • 论文发现 SAC、SAC+HER 和 TD3+HER 法从超过四层的深度中获益，这与之前的研究结果一致（2024；2024）
  • 此外，GCSL 和 GCBC 在 Humanoid 和 Ant Big Maze 任务上未能取得任何有意义的性能
  • 有趣的是，论文确实观察到了一个例外：
    • 在 Arm Push Easy 环境中，GCBC 随着深度增加表现出改进的性能
  • 图 12： 扩展后的 CRL（Ours）在 10 个环境中的 8 个上优于基线 CRL（original）、SAC、SAC+HER、TD3+HER、GCSL 和 GCBC
  • 表 1： 增加网络深度（深度 \(D=4 \to 64\)）可以提高CRL的性能（图1）
    • 深度扩展在具有最大观测维度（Dim）的任务上展现出最大的益处

A.3 额外的扩展实验：离线 GCBC、BC 和 QRL（Additional Scaling Experiments: Offline GCBC, BC, and QRL）

  • 论文进一步研究了几个额外的扩展实验
  • 如图 14 所示，论文的方法在 OGBench 的 antmaze-medium-stitch 任务上的离线 GCBC 设置中成功地实现了深度扩展
  • 论文发现，层归一化（layer normalization）、残差连接（residual connections）和 Swish 激活的组合至关重要，这表明论文的架构选择可能可以应用于解锁其他算法和设置中的深度扩展
  • 论文还尝试扩展行为克隆（behavioral cloning）和 QRL（2023b）算法的深度
    • 然而，在这两种情况下，论文都观察到了负面结果
  • 图 14： 论文的方法在离线GCBC的 antmaze-medium-stitch （OGBench）上成功扩展了深度
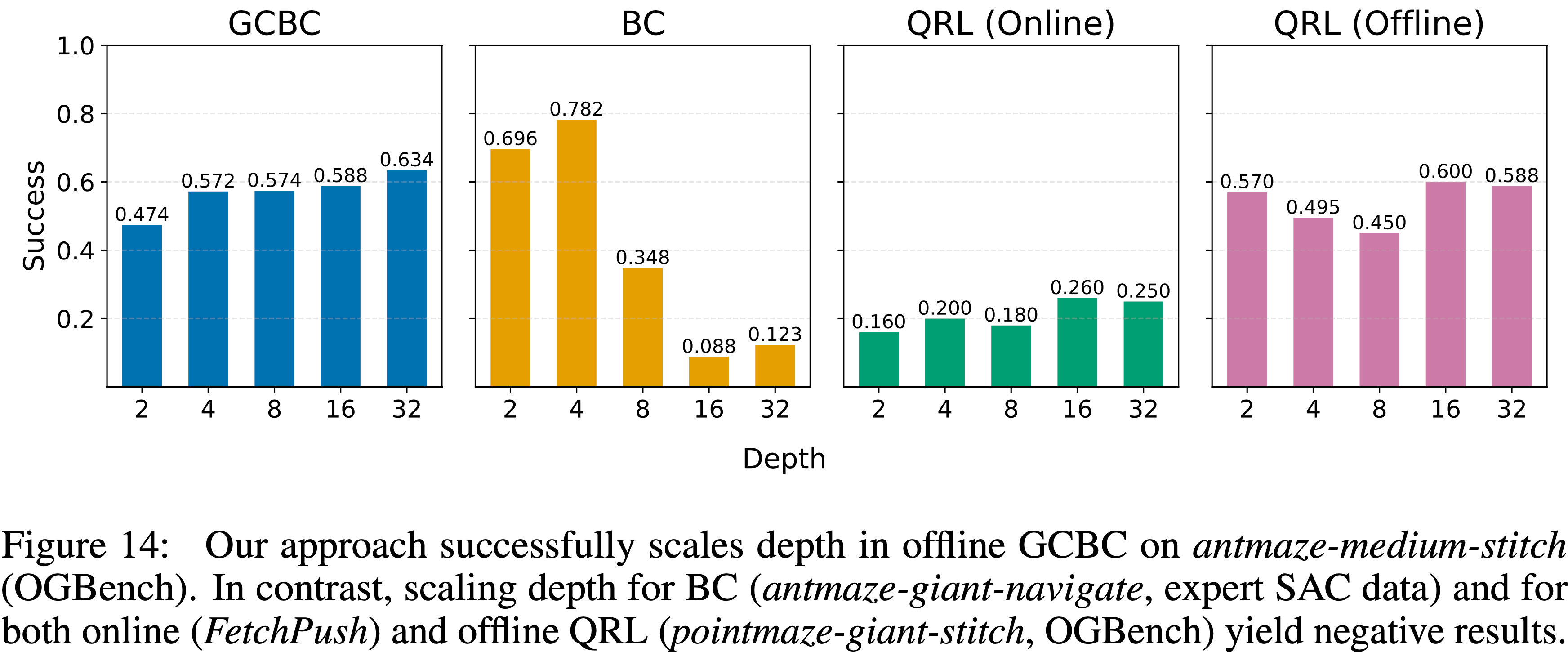
    • 相比之下，为BC（antmaze-giant-navigate ，专家SAC数据）和在线（FetchPush）及离线QRL（pointmaze-giant-stitch ，OGBench）扩展深度则产生了负面结果
  • 图 13： 深度扩展对 SAC、SAC+HER、TD3+HER、GCSL 和 GCBC 带来的增益有限

A.4 深度扩展对拟度量（quasimetric）架构是否也有效？（Can Depth Scaling also be Effective for Quasimetric Architectures?）

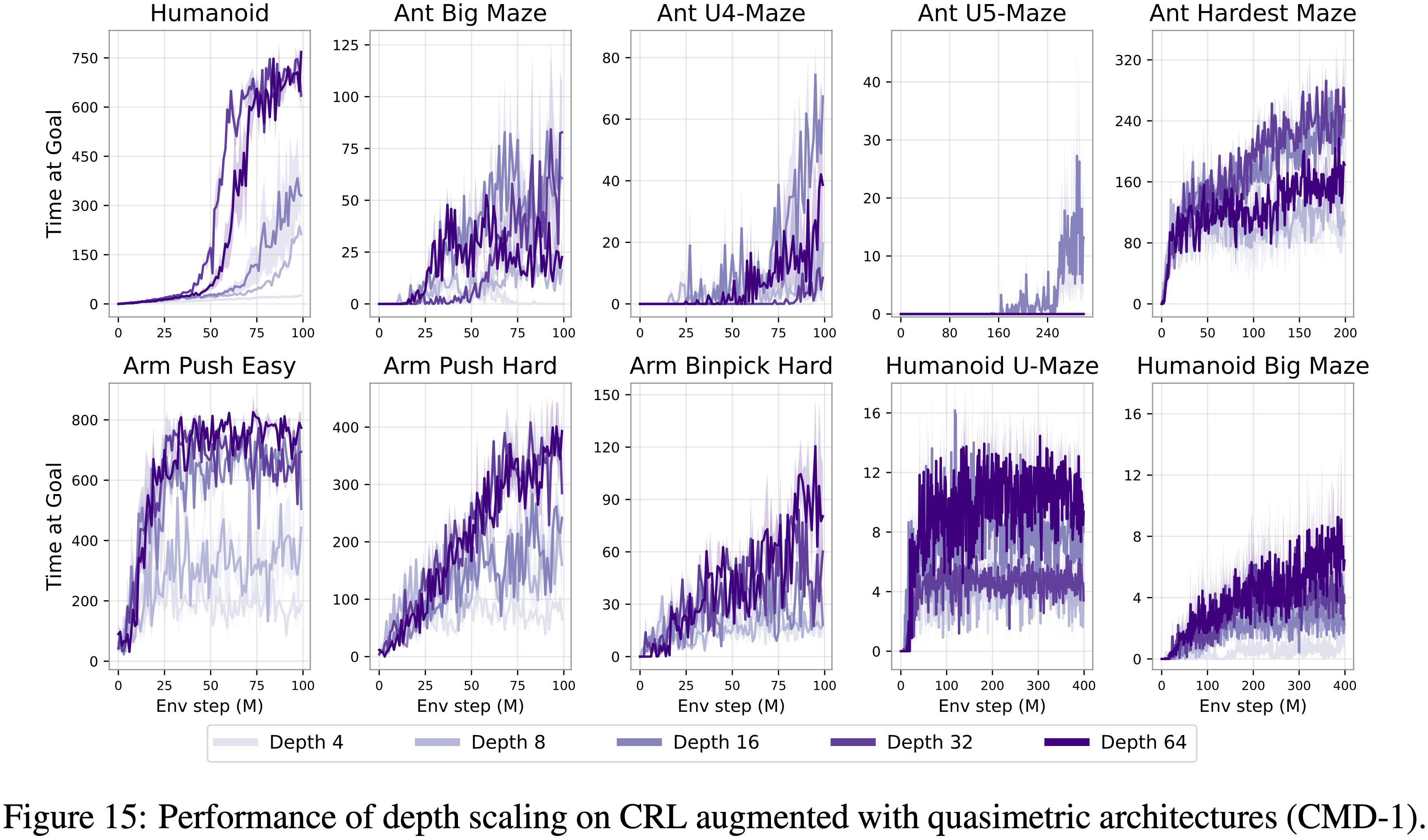
  • 先前的工作（2023b；2023）发现时序距离满足一个重要的不变性属性，这提示在学习时序距离时可以使用拟度量架构
  • 论文的下一个实验测试了改变架构是否会影响自监督 RL 的扩展特性
  • 具体来说，论文使用 CMD-1 算法（2024），该算法采用带有 MRN 表示的反向 NCE 损失
  • 结果表明，扩展的益处并不局限于单一的神经网络参数化。然而，MRN 在 Ant U5-Maze 任务上表现不佳，这表明要实现对拟度量模型的一致扩展还需要进一步创新
  • 图15： 在配备了拟度量架构的CRL上进行深度扩展的性能（CMD-1）

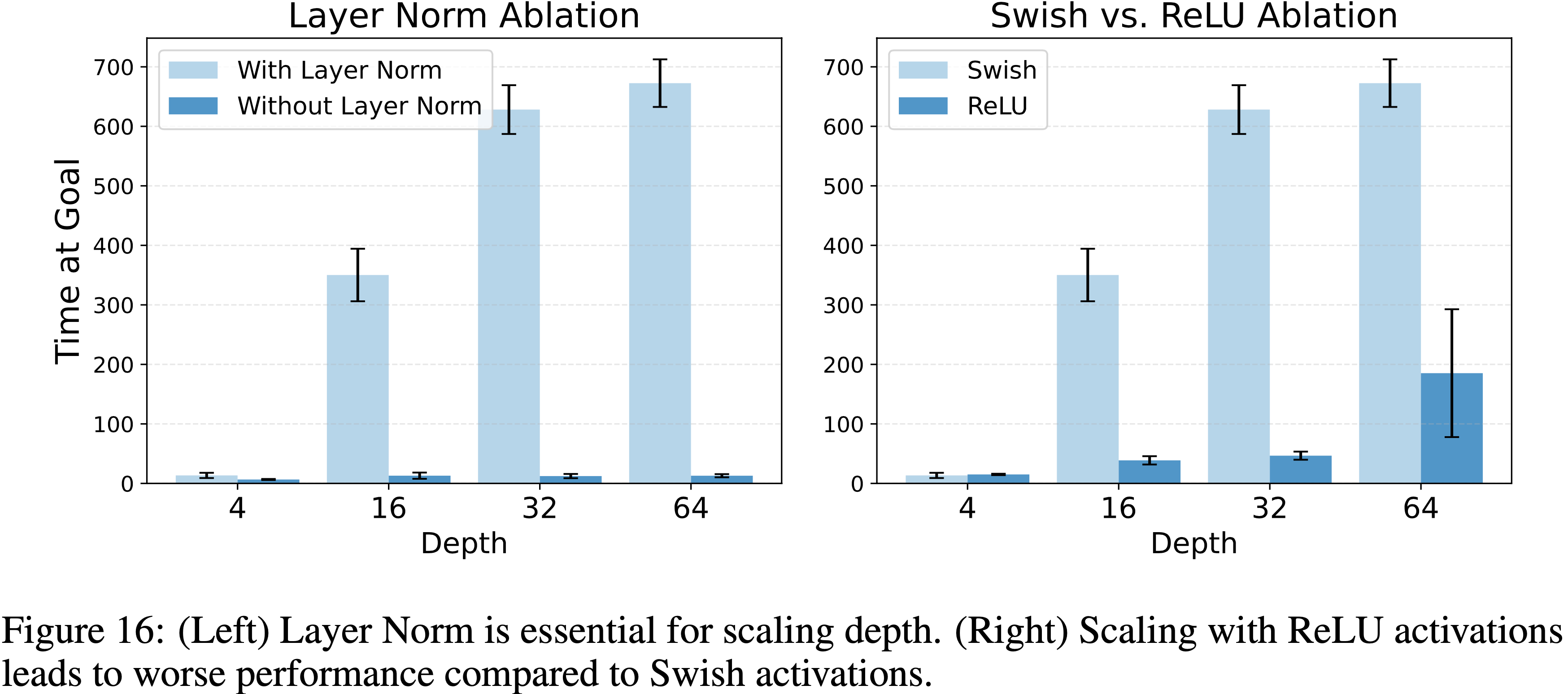
A.5 额外的架构消融实验：层归一化与 Swish 激活（Additional Architectural Ablations: Layer Norm and Swish Activation）

  • 论文进行了消融实验以验证层归一化和 Swish 激活的架构选择
  • 图 16 显示，移除层归一化后性能显著变差
  • 此外，使用ReLU进行扩展会严重阻碍可扩展性
  • 这些结果，连同图5，表明论文所有的架构组件，包括残差连接、层归一化和Swish激活，共同对于释放深度扩展的全部性能至关重要
  • 图16：
    • （左）层归一化对于深度扩展至关重要
    • （右）与 Swish 激活相比，使用 ReLU 激活进行扩展会导致更差的性能

A.6 论文能否整合来自新兴 RL 扩展文献的新架构创新？（Can We Integrate Novel Architectural Innovations from the Emerging RL Scaling Literature?）

  • 最近，Simba-v2 提出了一种用于可扩展 RL 的新架构
    • 其关键创新在于用超球面归一化（hyperspherical normalization）替代了层归一化（超球面归一化在每次梯度更新后将网络权重投影到单位范数超球面上）
    • 如图所示，当将超球面归一化加入到论文的架构中时，同样的深度扩展趋势仍然成立，并且它进一步提高了深度扩展的样本效率
    • 这表明论文的方法可以自然地整合RL扩展文献中出现的新架构创新
      表 2： 将超球面归一化整合到论文的架构中提升了深度扩展的样本效率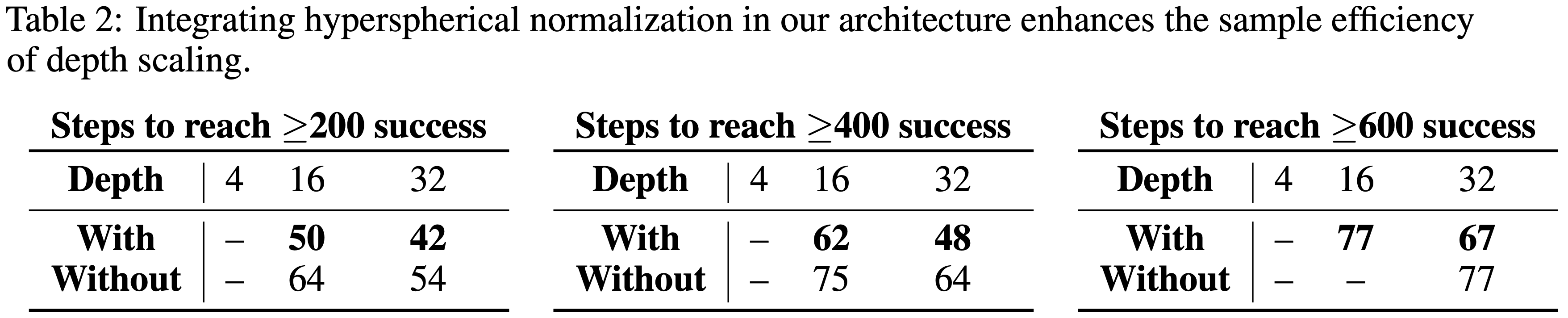

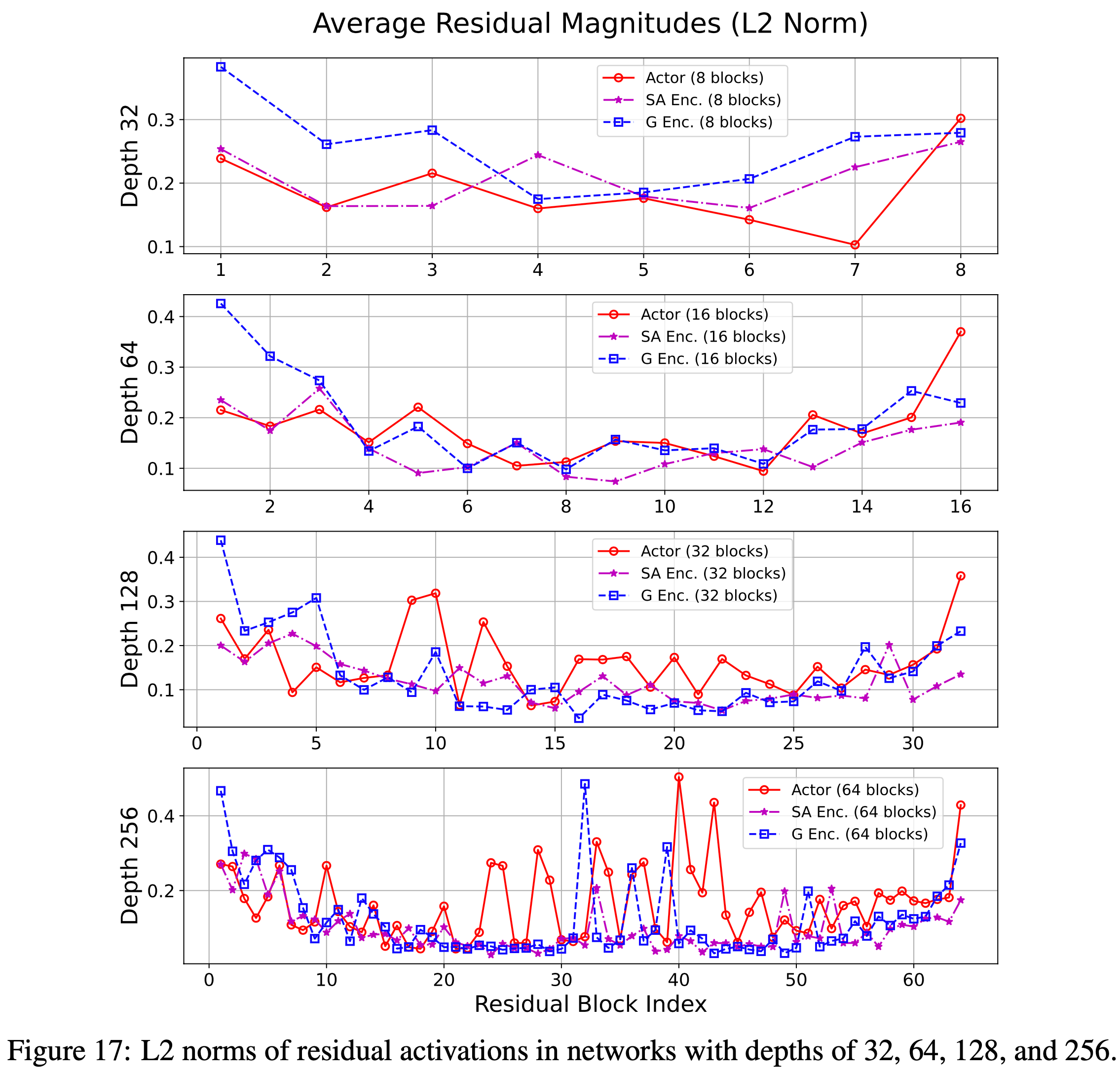
A.7 深度网络中的残差范数（Residuals Norms in Deep Networks）

  • 先前的工作注意到更深层中残差激活范数会减小（2018）
  • 论文研究了这种模式在论文的设置中是否同样存在
    • 对于 Critic 网络，这种趋势通常是明显的，尤其是在非常深的架构中（例如，深度256）
  • 这种效应在行动者（actor）网络中则不那么显著
  • 图 17： 深度为 32、64、128 和 256 的网络中残差激活的 L2 范数

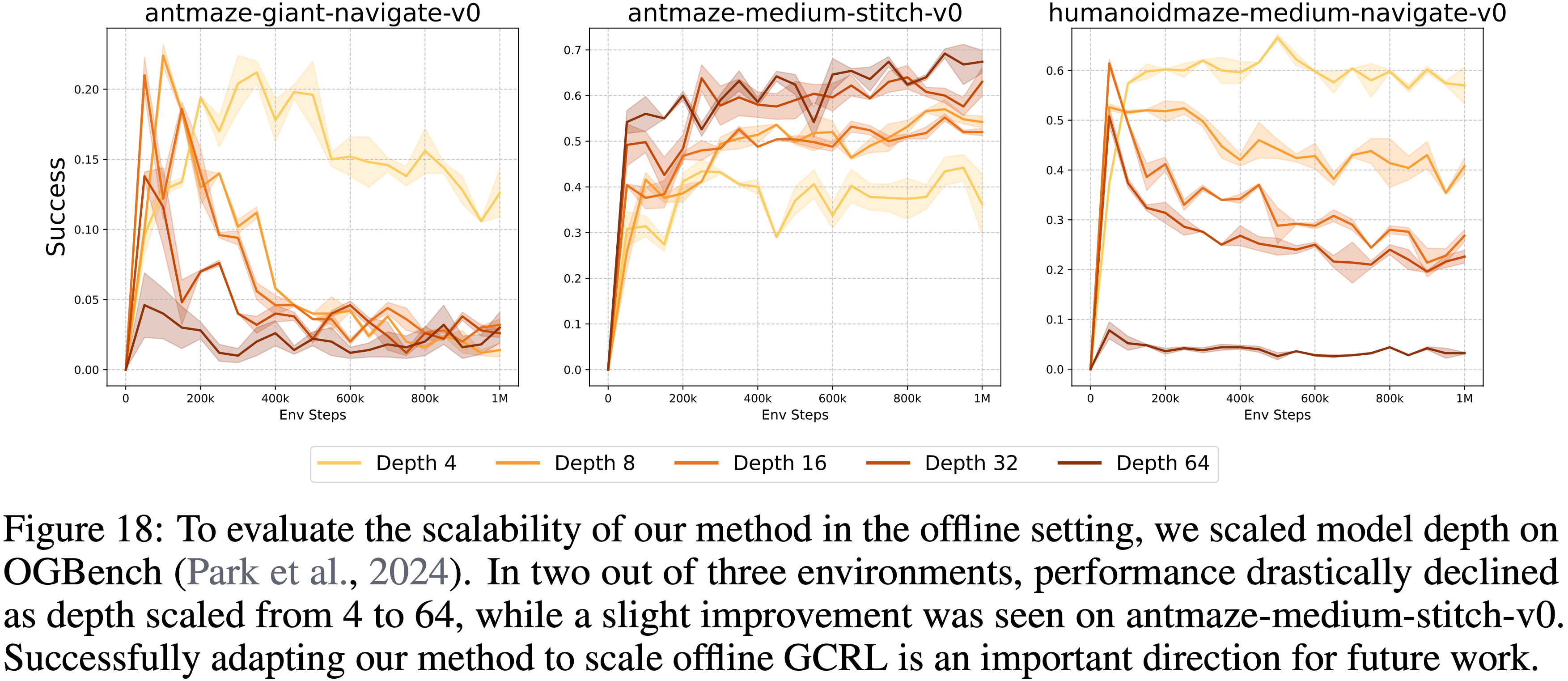
A.8 为离线目标条件RL扩展深度（Scaling Depth for Offline Goal-conditioned RL）

  • 图 18： 为了评估论文的方法在离线设置中的可扩展性，论文在 OGBench（2024）上扩展了模型深度
    • 在三个环境中的两个里，当深度从 4 扩展到 64 时，性能急剧下降
    • 在 antmaze-medium-stitch-v0 上观察到轻微改进
    • 成功调整论文的方法以扩展离线 GCRL 是未来工作的一个重要方向

附录 B：实验细节

B.1 环境设置与超参数（Environment Setup and Hyperparameters）

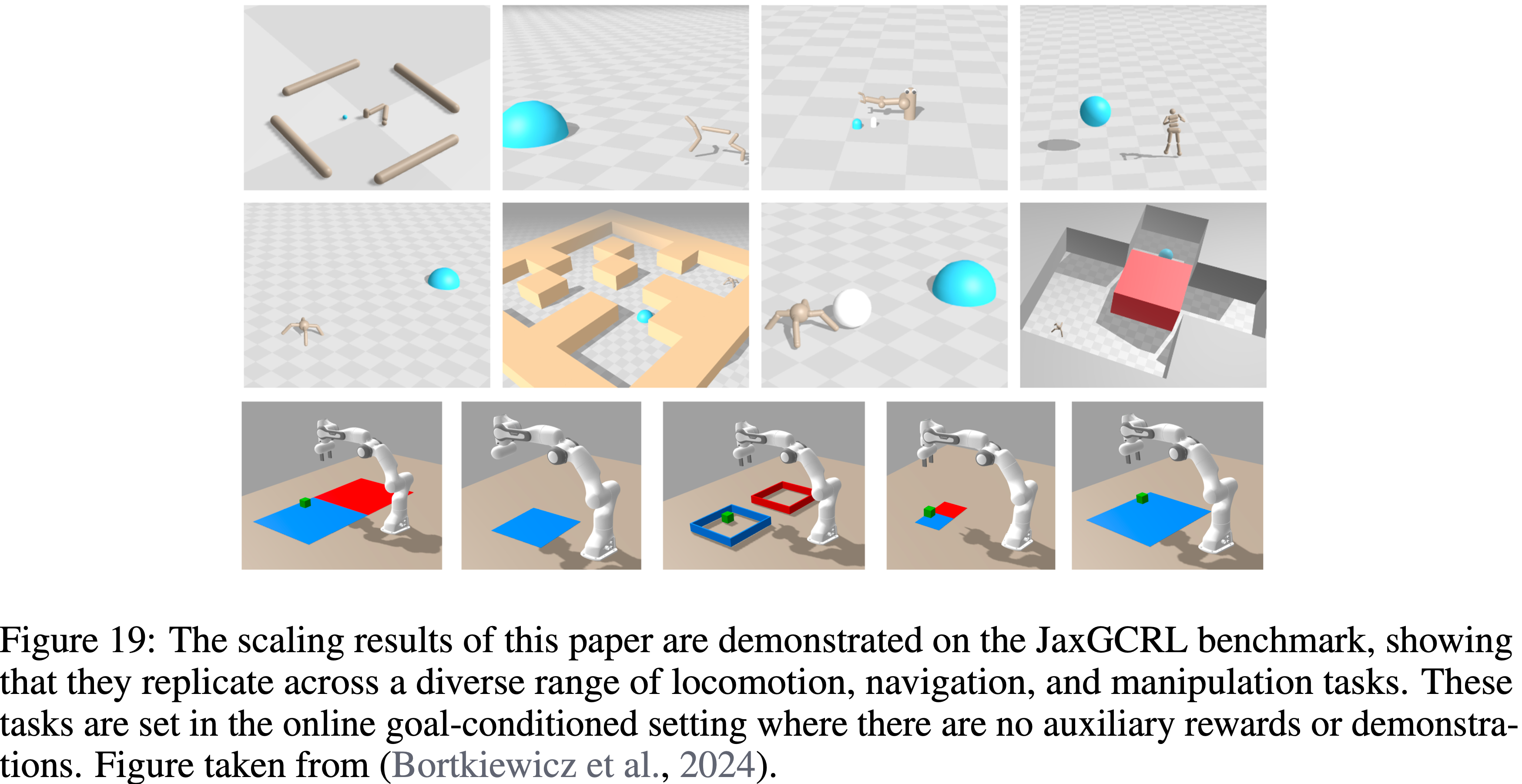
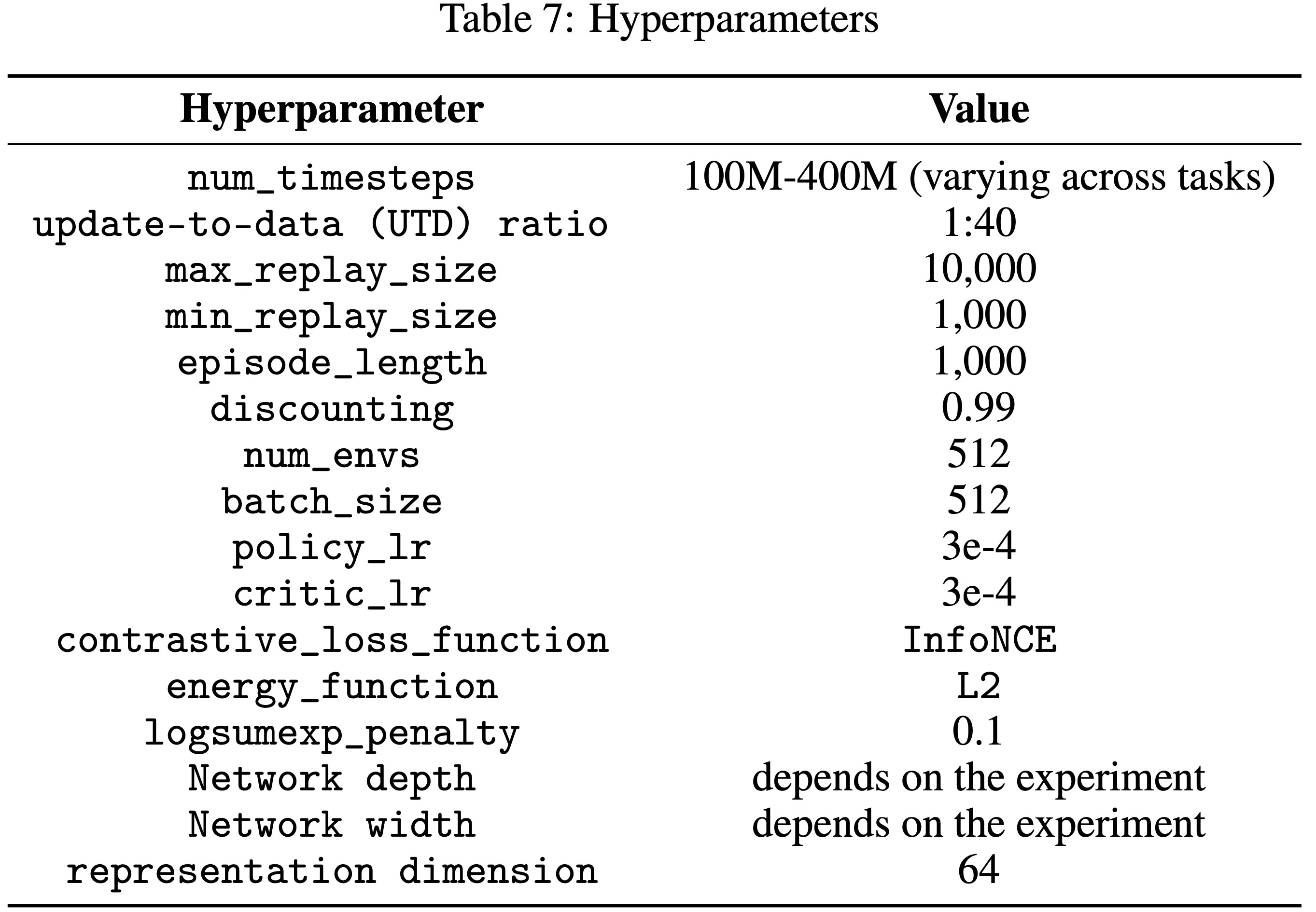
  • 论文的实验使用了 JaxGCRL 套件的 GPU 加速环境（如图 19 所示），以及超参数报告在表 7 中的对比 RL 算法
  • 图 19： 论文的扩展结果在 JaxGCRL 基准测试中得到了展示，表明它们可以复现在多样化的运动、导航和操作任务上
    • 这些任务设置在无辅助奖励或演示的在线目标条件设置中
    • 注：下图取自其他文章（2024）
  • 表7： 超参数
  • 具体来说，论文使用了 10 个环境，分别是：
    • ant_big_maze, ant_hardest_maze, arm_binpick_hard, arm_push_easy, arm_push_hard, humanoid, humanoid_big_maze, humanoid_u_maze, ant_u4_maze, ant_u5_maze

B.2 Python环境差异（Python Environment Differences）

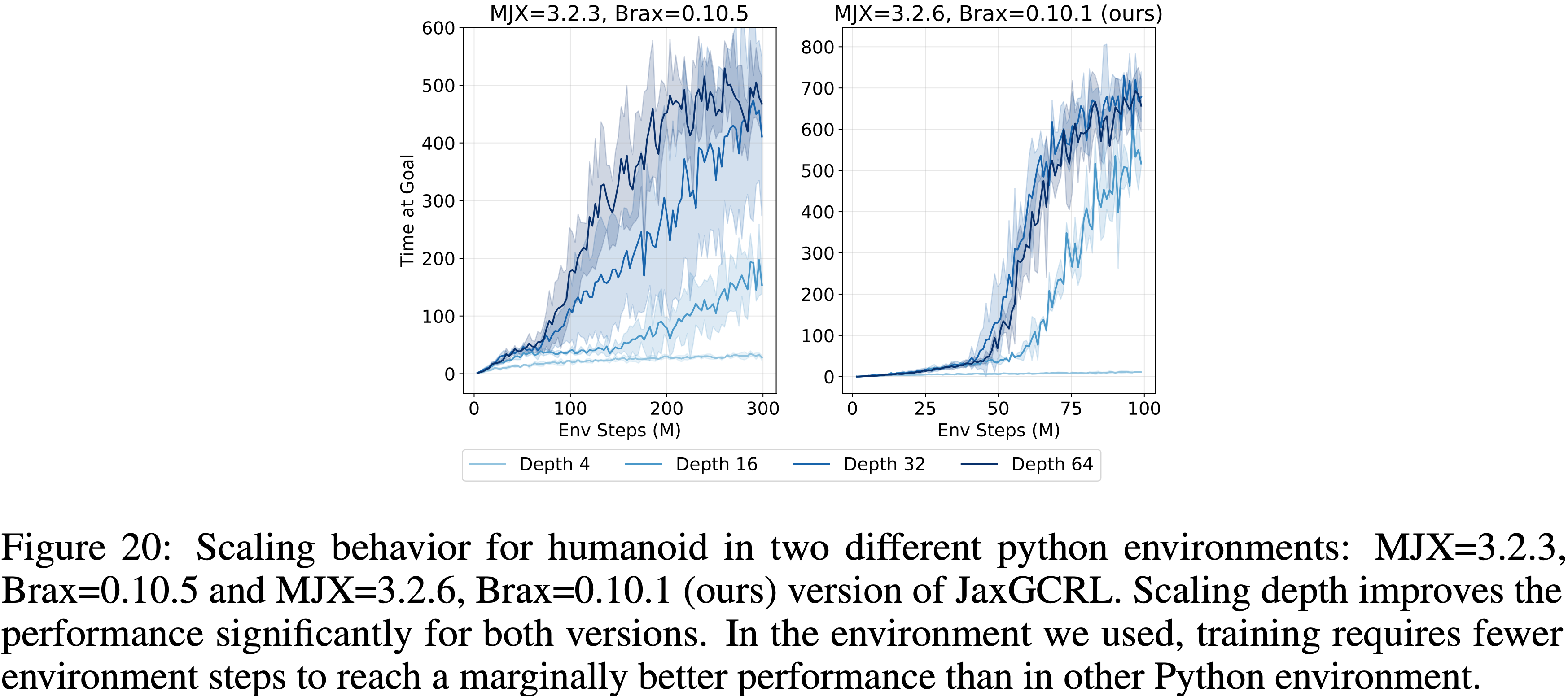
  • 在论文中展示的所有图表中，论文使用了 MJX 3.2.6 和 Brax 0.10.1 以确保公平和一致的比较
  • 在开发过程中，论文注意到论文使用的环境版本（CleanRL 版本的 JaxGCRL）与 JaxGCRL（2024）最近提交版本中推荐的版本之间存在物理行为的差异
  • 经检查，性能差异（如图 20 所示）源于 MJX 和 Brax 包的版本不同
  • 尽管如此，在这两组 MJX 和 Brax 版本中，性能都随着深度单调扩展
  • 图 20： 在两个不同 Python 环境中 humanoid 的扩展行为：
    • MJX=3.2.3, Brax=0.10.5 和 MJX=3.2.6, Brax=0.10.1（论文的）版本的 JaxGCRL
    • 在这两个版本中，扩展深度都显著提高了性能
    • 在论文使用的环境中，训练需要更少的环境步数来达到比另一个 Python 环境中略好的性能

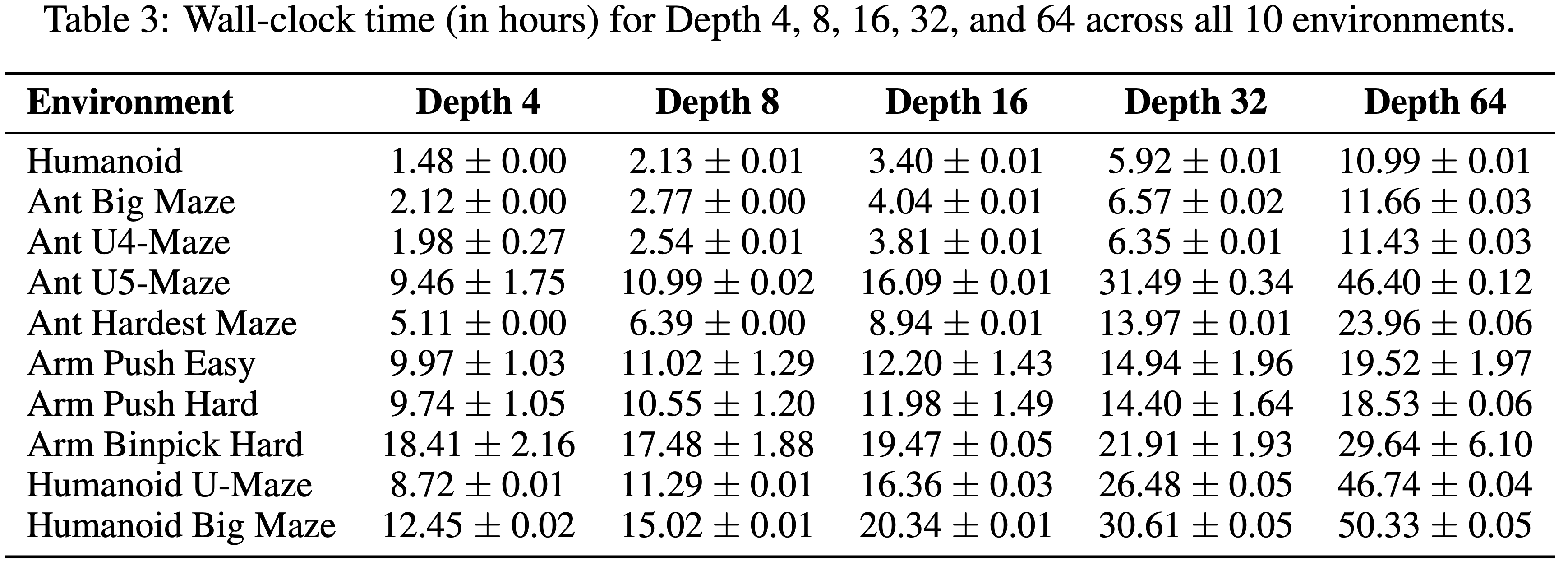
B.3 论文方法的墙上时钟时间（Wall-clock Time of Our Approach）

  • 论文在表 3 中报告了论文方法的墙上时钟时间
  • 该表展示了在所有十个环境中深度为 4、8、16、32 和64 的结果，以及在 Humanoid U-Maze 环境中扩展到 1024 层的结果
  • 总体而言，超过一定点后，墙上时钟时间大约随深度线性增加
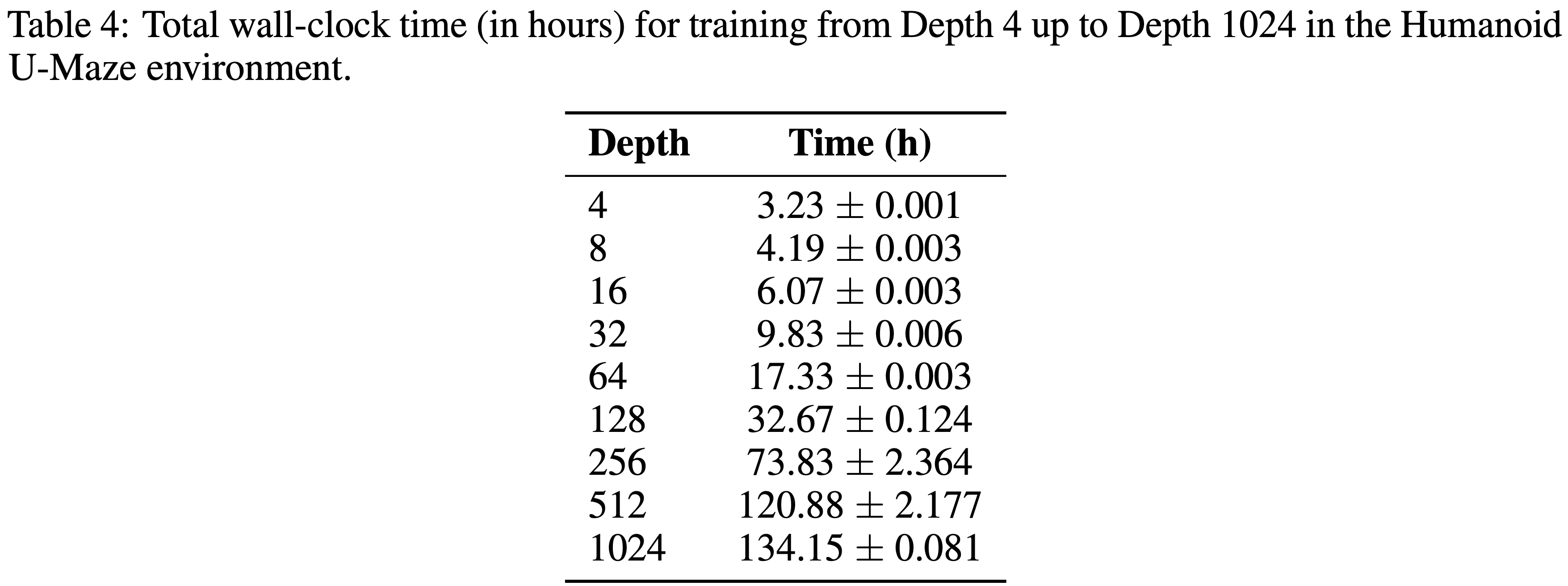
  • 表4： 在 Humanoid U-Maze 环境中，从深度 4 训练到深度 1024 的总墙上时钟时间（小时）

B.4 墙上时钟时间：与基线的比较（Wall-clock Time: Comparison to Baselines）

  • 由于基线使用标准大小的网络，论文的扩展方法自然在每个环境步上产生更高的原始墙上时钟时间（表 5）
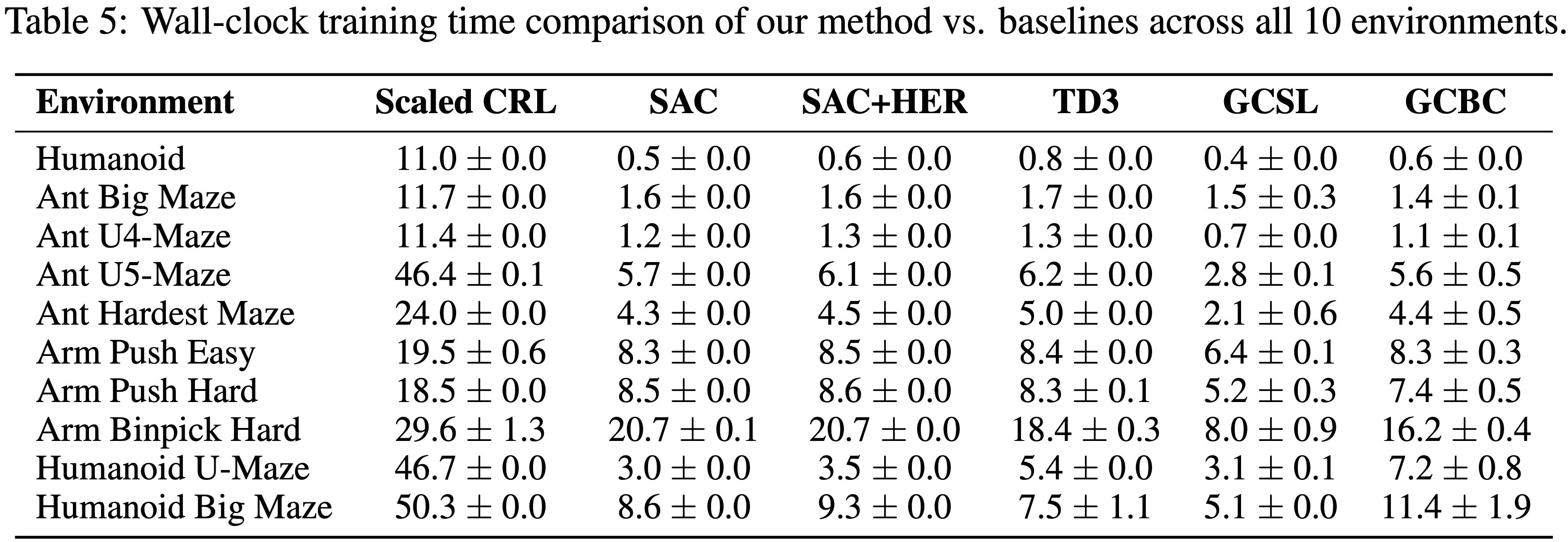
  • 然而，一个更实用的指标是达到给定性能水平所需的时间
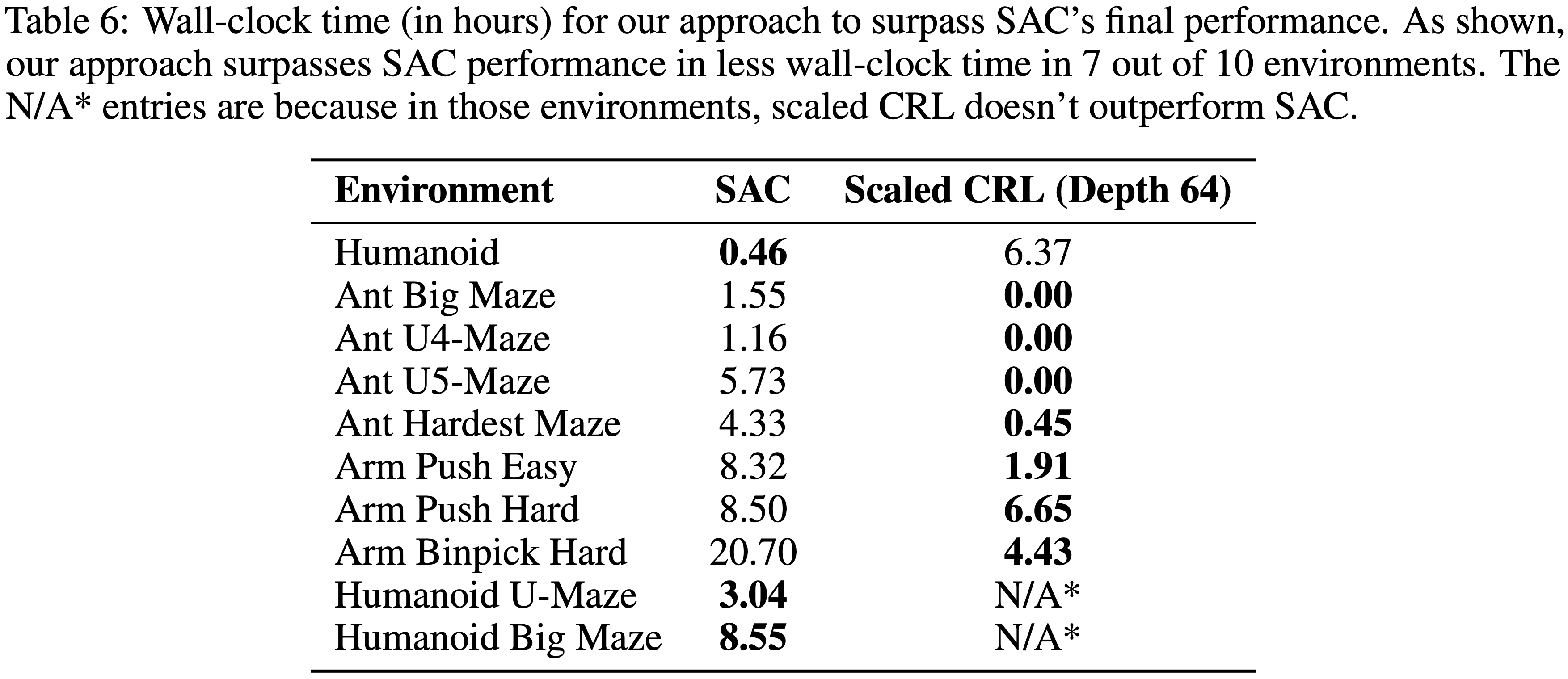
  • 如表 6 所示，论文的方法在 7 个环境中优于最强的基线 SAC，同时所需的墙上时钟时间更少

附录：Contrastive Learning(对比学习)

  • 对比学习是一种无监督/自监督表示学习范式，核心思想是拉近同类样本的表示、推远异类样本的表示
    • 通过构建“正对（positive pair）”和“负对（negative pair）”的对比损失函数，让模型学习到具有判别性的特征表示
  • 对比学习的目标是使模型能够区分相似与不相似的样本，无需人工标注的类别标签
  • 对比学习的核心要素包括：
    • 数据增强：对同一原始样本生成不同视图，构成正对
    • 负样本采样：从样本集中选取其他样本，与当前样本构成负对
    • 对比损失：通过损失函数量化正负样本对的距离差异
  • 经典损失函数公式 ：以最常用的InfoNCE 损失为例（适用于对比学习的核心损失）：
    $$
    \mathcal{L}_{\text{InfoNCE} } = -\log\left(\frac{\exp(\text{sim}(\boldsymbol{h}_i, \boldsymbol{h}_j)/\tau)}{\sum_{k=1}^N \exp(\text{sim}(\boldsymbol{h}_i, \boldsymbol{h}_k)/\tau)}\right)
    $$
    • \(\boldsymbol{h}_i, \boldsymbol{h}_j\)：正对样本的特征表示（如同一图像的两个增强视图的编码输出）
    • \(\boldsymbol{h}_k\)：第 \(k\) 个样本的特征表示，包含 1 个正对和 \(N-1\) 个负对
    • \(\text{sim}(\cdot,\cdot)\)：相似度函数，通常为余弦相似度
      $$\text{sim}(\boldsymbol{a},\boldsymbol{b})=\frac{\boldsymbol{a}^\top \boldsymbol{b} }{|\boldsymbol{a}||\boldsymbol{b}|}$$
    • \(\tau\)：温度系数，用于调节相似度分布的平滑程度，\(\tau>0\)

附录：Contrastive Representation Learning(对比表示学习)

  • 对比表示学习是对比学习的泛化与子集 ，更明确地聚焦于“学习高质量特征表示”这一目标，是对比学习在表示学习任务中的具体应用
  • 对比表示学习的本质与对比学习一致，核心区别在于术语的侧重点不同 ：
    • 对比学习：强调“对比”这一学习策略（方法层面）
    • 对比表示学习：强调“表示学习”这一任务目标（任务层面）
  • 对比表示学习的核心是通过对比机制，让模型学习到的特征表示满足两个关键属性：
    • 不变性 ：对同一样本的不同增强视图，输出的表示尽可能相似
    • 区分性 ：对不同样本的表示，尽可能拉开距离
  • 对比表示学习的数学描述 ：对比表示学习的目标可形式化描述为：
    • 给定样本 \(x\)，其增强视图为 \(x^+\)（正对），负样本集合为 \(\{x^-_1,x^-_2,\dots,x^-_M\}\)，模型编码器为 \(f(\cdot)\)，则目标函数为：
      $$
      \min_{f} \mathcal{L}\left(f(x), f(x^+), \{f(x^-_m)\}_{m=1}^M\right)
      $$
    • 其中 \(\mathcal{L}\) 为对比损失函数（如 InfoNCE、NT-Xent 等），\(f(\cdot)\) 输出的向量即为对比表示
  • 对比表示学习是对比学习的核心应用场景，所有对比表示学习都属于对比学习，但对比学习的应用场景可不限于表示学习（如对比分类、对比检索等）；

附录：Contrastive RL(对比强化学习)

Contrastive RL 方法整体说明

  • Contrastive RL（对比强化学习）是一种将对比表示学习与目标条件强化学习（Goal-Conditioned RL）深度融合的算法框架
    • Contrastive RL 的核心创新在于将对比学习直接转化为强化学习的核心机制，无需额外的辅助损失或数据增强，即可同时学习有效的 State-Action 表示和目标导向的价值函数
  • Contrastive RL vs 传统强化学习
    • 传统强化学习中，表示学习与策略优化常被解耦（如通过辅助损失、数据增强单独优化表示），导致训练不稳定
    • Contrastive RL 提出：对比表示学习本身可作为目标条件 RL 的核心算法 ，即通过对比学习学习 State-Action 对与未来状态的表示，使可达的未来状态（正样本）表示相近，不可达的随机状态（负样本）表示相异
    • 这种表示的内积恰好对应目标条件价值函数（Q-函数），进而直接用于策略优化以实现目标达成

目标条件强化学习（Goal-Conditioned RL）

  • 目标条件 RL 的任务定义为：智能体在状态空间 \( S \) 中执行动作 \( a_t \in A \)，通过动力学模型 \( p(s_{t+1} | s_t, a_t) \) 转移状态，需优化策略 \( \pi(a | s, s_g) \) 以达成目标状态 \( s_g \in S \)（目标服从分布 \( p_g(s_g) \)）
  • 核心奖励函数定义为（无需人工设计距离度量）：
    $$
    r_g(s_t, a_t) \triangleq (1-\gamma) p(s_{t+1}=s_g | s_t, a_t)
    $$
    • 其中 \( \gamma \in [0,1) \) 为折扣因子，奖励本质是“下一步到达目标的概率密度”
    • 理解：下一步到达目标状态 \(s_g\) 的概率越大，则兼顾越大
      • 问题：可能只有最后一步有非 0 奖励，前面的步骤都为 0，其实同样存在奖励稀疏问题
  • 目标条件 Q-函数 定义为未来累积奖励的期望：
    $$
    Q_{s_g}^{\pi}(s, a) \triangleq \mathbb{E}_{\pi(\tau | s_g)} \left[ \sum_{t’=t}^{\infty} \gamma^{t’-t} r_g(s_{t’}, a_{t’}) \bigg|_{s_t=s, a_t=a} \right]
    $$

折扣状态占用度量（Discounted State Occupancy Measure）

  • 定义为策略 \( \pi \) 下，经过折扣后状态被访问的概率密度：
    $$
    p^{\pi(\cdot | \cdot, s_g)}(s_{t+}=s) \triangleq (1-\gamma) \sum_{t=0}^{\infty} \gamma^t p_t^{\pi(\cdot | \cdot, s_g)}(s_t=s)
    $$
    • 其中 \( s_{t+} \) 表示从该测度中采样的状态
    • 时间步 \(t\) 可通过几何分布采样，即 \( t \sim \text{GEOM}(1-\gamma) \) 获得
    • 该测度用于定义对比学习的正样本对

对比表示学习（Contrastive Representation Learning）

  • 对比学习的目标是学习表示函数 \( \phi, \psi \)，使正样本对 \( (u, v^+) \) 的表示变得相似（相近），负样本对 \( (u, v^-) \) 的表示不同（远离）
  • 核心目标函数采用 NCE（Noise-Contrastive Estimation）或 InfoNCE：
    $$
    \max_{f} \mathbb{E}_{\substack{(u, v^+) \sim p(u, v) \\ v^- \sim p(v)} } \left[ \log \sigma(f(u, v^+)) + \log (1-\sigma(f(u, v^-))) \right]
    $$
    • 其中 \( f(u, v) = \phi(u)^T \psi(v) \) 为表示的内积（相似度函数），\( \sigma \) 为 sigmoid 函数

Contrastive RL 的核心理论：对比学习即 Q-函数学习

  • Contrastive RL 的核心贡献是证明：通过特定正负样本设计，对比学习的目标函数等价于学习目标条 Q-函数
命题 1：Q-函数与占用度量的等价性
  • 目标条件 Q-函数可等价表示为目标状态在折扣占用度量下的概率密度：
    $$
    Q_{s_g}^{\pi}(s, a) = p^{\pi(\cdot | \cdot, s_g)}(s_{t+}=s_g | s, a)
    $$
    • 该命题将“累积奖励期望”转化为“目标状态的可达概率”，为对比学习与 RL 的结合提供了理论桥梁
引理 4.1：对比学习的最优判别器即 Q-函数
  • 设对比学习的输入定义为：
    • 锚点 \( u = (s, a) \)（ State-Action 对，从回放缓冲区采样）
    • 正样本 \( v^+ = s_f^+ \)（从折扣占用度量采样的未来状态：\( s_f^+ \sim p^{\pi(\cdot | \cdot)}(s_{t+} | s, a) \)）
    • 负样本 \( v^- = s_f^- \)（从全局状态分布采样的随机状态：\( s_f^- \sim p(s_{t+}) = \int p^{\pi(\cdot | \cdot)}(s_{t+} | s, a) p(s, a) ds da \)）
  • 则对比学习的最优判别器 \( f^* \) 满足：
    $$
    \exp(f^*(s, a, s_f)) = \frac{1}{p(s_f)} \cdot Q_{s_f}^{\pi(\cdot | \cdot)}(s, a)
    $$
    • 其中 \( p(s_f) \) 为目标状态的边际分布（归一化常数）
    • 由于策略选择时该常数对所有动作等价，可忽略
    • 理解：
      • 这里 \(Q_{s_f}^{\pi(\cdot | \cdot)}(s, a)\) 表示在已知状态 \(s\) 下，执行动作 \(a\) 后，经过折扣后状态 \(s_f\) 被访问到的概率（占用度量）
      • \(p(s_f)\) 为归一化常数，即所有可能的状态 \(s_f\)对应的 Q 值 \(Q_{s_f}^{\pi(\cdot | \cdot)}(s, a)\) 总和
  • 因此对比学习的判别器直接编码了 Q-函数的相对大小

Contrastive RL 的核心组件（Actor-Critic 架构）

表示编码器（Representation Encoders）
  • Contrastive RL 包含两个编码器，参数化表示函数：
    • State-Action 编码器 \( \phi: S \times A \to \mathbb{R}^d \)：输入状态 \( s \) 和动作 \( a \)，输出低维表示 \( \phi(s, a) \)
    • 目标编码器 \( \psi: S \to \mathbb{R}^d \)：输入目标状态 \( s_g \)（或未来状态 \( s_f \)），输出表示 \( \psi(s_g) \)
  • 判别器函数定义为表示（Representation）的内积（高效计算且符合对比学习范式）：
    $$
    f(s, a, s_g) = \phi(s, a)^T \psi(s_g)
    $$
判别器损失（也是 Critic Loss）
  • 采用 NCE 目标，通过二元分类区分 “State-Action 对与未来状态是否匹配”
  • 设批次大小为 \( B \)，损失函数为：
    $$
    \text{critic_loss} = \text{sigmoid_binary_cross_entropy}(\text{logits}, \text{labels})
    $$
    • \( \text{logits} = \text{einsum}(ik,jk \to ij, \phi(s,a), \psi(s_f)) \)：
      • 批次内所有 \( (\phi(s_i,a_i), \psi(s_{f,j})) \) 的内积矩阵（维度 \( B \times B \)）
    • \( \text{labels} = \text{eye}(B) \)：
      • 单位矩阵，对角线元素为 1（正样本对：\( s_{f,j} \) 是 \( (s_i,a_i) \) 的未来状态），非对角线为 0（负样本对）
    • 理解：每个批次包含 B 个样本，每个样本为 <State, Action, Target_State> 的三元组，每个样本的 <State, Action> 跟自己的 <Target_State> 对齐（正样本），跟其他样本中的 <Target_State> 无法对齐（负样本）
      • 所以，上面出现 logits 是 \( B \times B \) 矩阵，而 labels 是 \( B \times B \) 的对角矩阵
    • 问题：若在有限状态下，部分样本的目标状态是有重复的，这种训练会出现问题吗？（其实还好，统计意义上看，应该是没问题）
策略损失（Actor Loss）
  • 策略优化的目标是选择使 “State-Action 表示与目标表示内积最大” 的动作（即最大化 Q-函数）
  • 策略 \( \pi(a | s, s_g) \) 为神经网络，输出动作分布，损失函数为：
    $$
    \text{actor_loss} = -\mathbb{E}_{\pi(a | s, s_g), p(s), p(s_g)} \left[ \phi(s, a)^T \psi(s_g) \right]
    $$
    • 通过重参数化梯度（reparametrization gradient）更新策略参数
    • 对于图像观测任务，可添加动作熵项以鼓励探索
    • 理解：这个目标函数的目标是找一个策略 \(\pi(\cdot|s,s_g)\)，使得 \(a \sim \pi(\cdot|s,s_g)\) 时，\(\phi(s, a)^T \psi(s_g)\) 的值最大
      • 其中，\(s_g\) 是目标状态，是包含 \(s,a\) 的轨迹 \( \tau = (s_0,a_0,s_1,a_1,\dots,s_T) \) 中，比 \(s,a\) 靠后的状态，按照折扣占用度量采样

Contrastive RL 完整算法流程（NCE）

  • Contrastive RL 交替进行判别器（Critic）更新、策略（Actor）更新和数据收集，流程如下：
  • 1：初始化 ：初始化 State-Action 编码器 \( \phi \)、目标编码器 \( \psi \)、策略网络 \( \pi \) 的参数；初始化回放缓冲区 \( \mathcal{D} \)
  • 2：数据收集 ：用当前策略 \( \pi \) 与环境交互，收集轨迹 \( \tau = (s_0,a_0,s_1,a_1,\dots,s_T) \)，存入 \( \mathcal{D} \)
  • 3：判别器 Critic 更新 ：
    • 从 \( \mathcal{D} \) 采样批次 \( (s, a, s_f) \)（\( s_f \) 为轨迹中未来状态，按折扣占用度量采样）
    • 计算 \( \phi(s,a) \) 和 \( \psi(s_f) \)
    • 计算 logits 矩阵和单位矩阵标签
    • 最小化二元交叉熵损失更新 \( \phi \) 和 \( \psi \)
  • 4：策略 Actor 更新 ：
    • 从 \( \mathcal{D} \) 采样状态 \( s \) 和目标 \( s_g \)
    • 从 \( \pi(a | s, s_g) \) 采样动作 \( a \)
    • 计算 \( \phi(s,a)^T \psi(s_g) \)
    • 最小化负内积损失更新策略 \( \pi \)
      • 注：这里使用重参数法实现策略的参数更新
  • 重复步骤 2-4 ，直至收敛

Contrastive RL 的关键实现细节

  • 离线适配 ：对于离线 RL 场景（无环境交互），在策略损失中添加目标条件行为克隆项（behavioral cloning）：
    $$
    \text{actor_loss} = -\mathbb{E} \left[ (1-\lambda) \phi(s,a)^T \psi(s_g) + \lambda \log \pi(a_{\text{orig} } | s, s_g) \right]
    $$
    • 其中 \( a_{\text{orig} } \) 为离线数据中的动作，\( \lambda \) 为平衡系数；
  • 计算效率 ：基于 JAX 和 ACME 框架实现，单 TPUv2 上状态任务训练速度达 1100 批次/秒，图像任务达 105 批次/秒（比 DrQ 快 3.9 倍）；
  • 变体扩展 ：可替换对比目标为 InfoNCE（Contrastive RL (CPC)），或融合 C-learning（TD 学习）得到 Contrastive RL (NCE + C-learning)，进一步提升性能

Contrastive RL 方法优势

  • 无需辅助组件：不依赖数据增强（如 DrQ）、辅助重建损失（如 AE）或多 Q 网络（如 TD3），结构简洁
  • 表示与RL统一：表示学习与策略优化共享同一目标（对比损失），避免解耦导致的不稳定
  • 强泛化能力：在图像观测、部分可观测性（移动相机）、离线 RL 等场景中均优于传统方法
  • 理论支撑：严格证明对比学习与 Q-函数的等价性，提供收敛保证（添加轨迹过滤步骤后，满足近似策略改进）

论文中的实验效果

  • Contrastive RL 在多个目标条件 RL 任务中表现突出：
  • 状态型任务（FetchReach、SawyerBin 等）：解决了传统方法（TD3+HER、GCBC）无法完成的高难度任务（如 SawyerBin）；
  • 图像型任务（FetchPush、PointSpiral11x11 等）：无需数据增强，性能超过 TD3+HER+DrQ/CURL 等增强方法；
  • 离线RL任务（D4RL AntMaze）：在 5/6 个任务中优于 IQL、TD3+BC 等方法，尤其在大规模任务上提升 7%-9%