RL——Trajectory-Transformer

Decision-Transformer，简称DT，使用序列预估的思想去实现决策问题

整体思路

  • 传统强化学习：马尔可夫性，建模每个时间步
  • 论文的核心思路：将离线强化学习问题作为一个通用序列建模问题 ，其目标是生成一系列动作，从而产生一系列高奖励
  • 建模和规划：使用Transformer架构建模轨迹分布，并将束搜索（Beam Search）重新用作规划算法
  • RL问题简化：将RL视为序列建模问题简化了一系列设计决策，使论文能够摒弃离线RL算法中常见的许多组件
  • 是按证明：这种方法可以与现有的 Model-free 算法结合，在稀疏奖励、 long-horizon 任务中产生最先进的规划器

整体讨论

  • 传统强化学习：依赖于将一个 long-horizon 问题分解为更小、更局部的子问题
  • 论文：将强化学习问题视为为一个序列生成问题，其目标是生成一系列动作，当在环境中执行时，会产生一系列高奖励
  • 基于序列模型建模强化学习问题可以等价解决诸多问题：
    • Actor-Critic 算法需要建模两个模型
    • Model-based 算法需要预测 Dynamics 模型
    • 离线RL方法通常需要估计行为策略
  • 论文将该模型称为 Trajectory Transformer，并在离线环境中进行评估，以便能够充分利用大量先验交互数据。与传统的动力学模型相比， Trajectory Transformer 在 long-horizon 预测方面表现出显著更高的可靠性（甚至在马尔可夫环境中也一样）
  • 与离线RL算法相比，论文的方法可视为Model-based RL和策略约束 ，但论文的方法无需显式引入此类约束
  • 与论文的工作同时，Decision Transformer 也提出了一种以序列预测为核心的RL方法，侧重于奖励条件化，而非 Trajectory Transformer 采用的束搜索规划。这两篇文章的研究都进一步支持了高容量序列模型可直接应用于强化学习问题而无需传统RL算法组件的可能性

RL和基于序列建模的控制（Control as Sequence Modeling）

  • 这一节描述序列模型 Trajectory Transformer 的训练过程，并讨论如何将其用于控制
  • 论文的模型实现和搜索策略与自然语言处理中的常见方法几乎相同，论文的重点在关注如何表示轨迹数据（可能包含连续状态和动作）以供离散标记架构处理

Trajectory Transformer

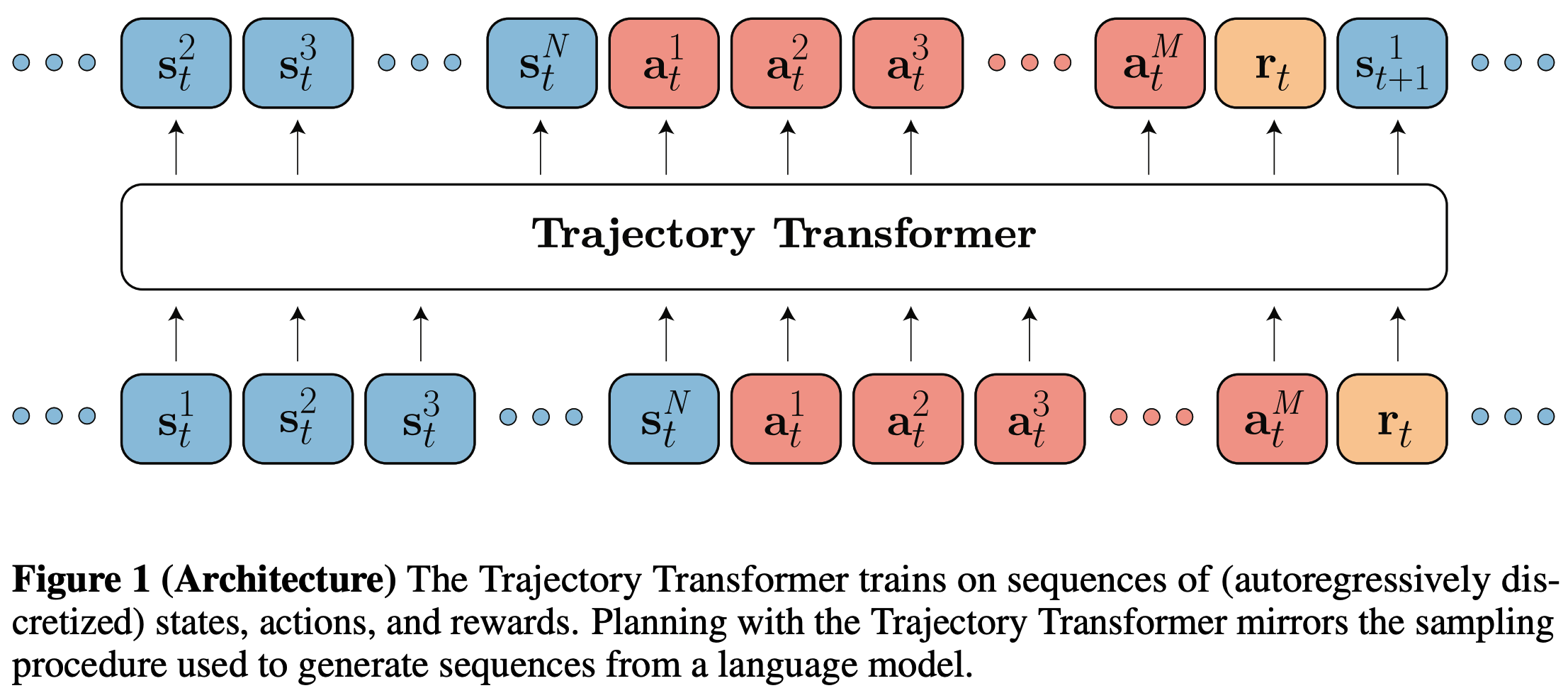
  • 论文方法的核心是将轨迹数据视为非结构化序列 ，由Transformer架构建模，具体来说，轨迹 \(\boldsymbol{\tau}\) 由 \(T\) 个状态、动作和标量奖励组成：
    $$
    \boldsymbol{\tau} = \big(\mathbf{s}_1, \mathbf{a}_1, r_1, \mathbf{s}_2, \mathbf{a}_2, r_2, \ldots, \mathbf{s}_T, \mathbf{a}_T, r_T\big).
    $$
  • 对于连续状态和动作，论文独立离散化每个维度。假设状态为 \(N\) 维，动作为 \(M\) 维，则 \(\boldsymbol{\tau}\) 被转换为长度为 \(T(N+M+1)\) 的序列：
    $$
    \boldsymbol{\tau} = \big(\ldots, s^1_t, s^2_t, \ldots, s^N_t, a^1_t, a^2_t, \ldots, a^M_t, r_t, \ldots\big) \quad t=1,\ldots,T.
    $$
    • 下标 \(t\) 表示时间步，状态和动作的上标表示维度（例如，\(s^i_t\) 是时间步 \(t\) 的状态的第 \(i\) 维）
    • 理解：离散化后并不会做 one-hot 等处理，即每个维度都从连续值变成了离散值，维度没有增加也没有减少
  • 论文中，主要研究了两种简单的离散化方法：
    • 第一种：均匀离散化 ：即固定宽度划分，假设每维词汇量为 \(V\)，状态维度 \(i\) 的标记覆盖宽度为 \(\frac{(\max \mathbf{s}^i - \min \mathbf{s}^i)}{V}\) 的均匀间隔
    • 第二种：分位数离散化 ：按照分位点划分，每个标记覆盖训练数据中每 \(V\) 个数据点中的一个
    • 均匀离散化的优势在于保留了原始连续空间中欧氏距离的信息 ，这可能比分位数离散化更能反映问题的结构，然而，数据中的异常值可能对离散化大小产生过大影响，导致许多标记对应零训练点。分位数离散化则确保所有标记在数据中均有体现。论文将在第4.2节对两者进行实证比较
  • Trajectory Transformer的实现 ：论文的模型是一个与 GPT 架构相似的 Transformer Decoder 部分，包含四层和四个自注意力头，记 Trajectory Transformer 的参数为 \(\theta\)，条件概率为 \(P_\theta\)，训练时最大化的目标函数为：
    $$
    \mathcal{L}(\tau) = \sum_{t=1}^T \left( \sum_{i=1}^N \log P_\theta \big(\mathbf{s}_t^i \mid \mathbf{s}_t^{ < i}, \boldsymbol{\tau}_{ < t}\big) + \sum_{j=1}^M \log P_\theta \big(a_t^j \mid \mathbf{a}_t^{ < j}, \mathbf{s}_t, \boldsymbol{\tau}_{ < t}\big) + \log P_\theta \big(r_t \mid \mathbf{a}_t, \mathbf{s}_t, \boldsymbol{\tau}_{ < t}\big) \right),
    $$
    • 其中，\(\boldsymbol{\tau}_{ < t}\) 表示从时间步 \(0\) 到 \(t-1\) 的轨迹，\(\mathbf{s}_t^{ < i}\) 表示时间步 \(t\) 状态的第 \(0\) 到 \(i-1\) 维，\(\mathbf{a}_t^{ < j}\) 同理。论文使用Adam优化器，学习率为 \(2.5 \times 10^{-4}\) 训练参数 \(\theta\)
    • 训练采用的是自回归（Auto Aggressive）训练目标
    • the standard teacher-forcing procedure 方法
基于束搜索的规划
  • 在训练完成后，如何将 Trajectory Transformer 的序列生成重新用于控制呢？
  • 论文重点关注三种场景：模仿学习、目标条件强化学习和离线强化学习 ，这三种场景所需的修改依次增加，但均基于下面自然语言处理中常用的序列模型解码方法:
    • 其中 \(\log P_\theta(\cdot \mid \mathbf{x})\)，既定义单个序列的似然，也定义一组序列的似然：\(\log P_\theta(Y \mid x) = \sum_{\mathbf{y} \in Y} \log P_\theta(\mathbf{y} \mid \mathbf{x})\)
    • 其中 \(()\) 表示空序列
    • 其中 \(\circ\) 表示拼接
    • 每次保留概率最大的 B 个候选序列
    • 最终返回整个序列 \(\mathbf{y}\)
  • 模仿学习 ：
    • 当目标是复现训练数据中的轨迹分布时，我们可以直接优化轨迹 \(\boldsymbol{\tau}\) 的概率。这种情况与序列建模的目标完全一致，因此我们可以直接使用算法1 ，只需将条件输入 \(\mathbf{x}\) 设为当前状态 \(\mathbf{s}_t\)（以及可选的先前历史 \(\boldsymbol{\tau}_{ < t}\)）
    • 该过程的结果是一个标记化的轨迹 \(\boldsymbol{\tau}\)，从当前状态 \(\mathbf{s}_t\) 开始，且在数据分布下具有高概率。如果执行序列中的第一个动作 \(\mathbf{a}_t\) 并重复束搜索，则得到一个滚动时域控制器。这种方法类似于基于 long-horizon 模型的模仿学习变体，其中优化整个轨迹以匹配参考行为，而不仅仅是即时状态条件下的动作。如果论文将预测序列长度设为动作维度，则论文的方法完全对应于最简单的自回归策略行为克隆
  • 目标条件强化学习 ：
    • Transformer架构采用“因果”注意力掩码，确保预测仅依赖于序列中先前的标记，在轨迹预测中，这一选择体现的是物理因果性，禁止未来事件影响过去。然而，也可以通过未来状态预估现在，论文不仅可以基于已观测到的先前状态、动作和奖励进行条件采样，还可以基于任何作者希望发生的未来上下文进行条件采样。如果未来上下文是轨迹末尾的状态，论文解码的轨迹概率形式为：
      $$
      P_\theta(s_t^i \mid \mathbf{s}_t^{ < i}, \boldsymbol{\tau}_{ < t}, \mathbf{s}_T).
      $$
    • 为了实现该目标，只需对期望的最终状态 \(\mathbf{s}_T\) 进行条件采样。如果论文始终对序列施加最终目标状态的条件，可以保持左下三角注意力掩码不变，只需将输入轨迹置换为 \(\{\mathbf{s}_T, \mathbf{s}_1, \mathbf{s}_2, \ldots, \mathbf{s}_{T-1}\}\)。通过将目标状态置于序列开头，论文确保所有其他预测均可关注它，而无需修改标准注意力实现
    • ？这种条件化过程类似于先前使用监督学习训练目标条件策略的方法（Ghosh et al., 2021），也与 Model-free RL中的重标记技术相关（Andrychowicz et al., 2017）
  • 离线强化学习 ：
    • 实现方式 ：算法1描述的束搜索方法在搜索概率最大化的轨迹，将算法1中的对数概率替换为预测的奖励信号（即概率最大转换成奖励信号最大），可以使用相同的 Trajectory Transformer 和搜索策略来优化奖励最大化的行为
    • reward-to-go的引入 ：使用束搜索作为奖励最大化方法可能导致短视行为。为解决这一问题，论文在训练轨迹的每个转移中增加reward-to-go ：\(R_t = \sum_{t’=t}^T \gamma^{t’-t} r_{t’}\)，将其离散添加到即时奖励 \(r_t\) 之后预测
      • 注：这里的 reward-to-go 在很多论文中也会叫做 return-to-go
    • reward-to-go的估计 ：
      • 难点说明 ：常规离线RL中 reward-to-go 估值 \(R_t\) 是行为策略\(\pi_\theta\)的函数 \(R_t^{\pi_\theta}\)，要估计 Trajectory Transformer 策略的价值函数是困难的，而且直接学习行为策略的价值函数确实比学习最优策略的价值函数简单得多（因为可以直接使用蒙特卡罗估计，而无需依赖贝尔曼更新）
      • 论文实现 ：在论文中，作者先使用了简单的估计方法（不考虑 Trajectory Transformer 策略），在第4.2节中，作者展示了简单的 reward-to-go 估值足以在许多环境中进行 Trajectory Transformer 规划，但在最具挑战性的设置（如稀疏奖励任务）中，改进的 reward-to-go 价值函数更有用（这里的改进价值函数是指学习 Trajectory Transformer 策略的 reward-to-go 价值函数）
    • 采样过程 ：Trajectory Transformer 会做 planning 时会采样多次，比如束搜索的候选序列数为 B，每个样本的序列长度为 n_step 的场景，在每个候选序列的每一步采样时，会采样 \(N+M+1\) 个标记预测一次奖励和 reward-to-go，论文使用似然最大化（跟模仿学习和目标条件强化学习中的步骤一样）束搜索采样完整转移元组 \((\mathbf{s}_t, \mathbf{a}_t, r_t, R_t)\)，然后筛选 截止到当前累积奖励+reward-to-go 最高的 B 个候选序列进行下一轮，直到采样 n_step 轮
      • 注：论文仅将累计奖励的估值作为启发式引导束搜索，因此论文的方法不要求估值像完全依赖估值选择动作的方法那样精确
      • 截止到当前累积奖励的理解 ：假定做第 \(t’\) 步决策，束搜索的候选序列数为 B，每个样本的序列长度为 n_step=T，则从截止到当前累积奖励为： \(\sum_{t=t’}^{t’+T} r_t\)，截止到当前累积奖励+reward-to-go 则为： \((\sum_{t=t’}^{t’+T}r_t) + R_{t’+T}\)。作者开源实现时，还会带上折扣因子（默认0.99），详情见开源项目的./trajectory/search/core.py文件中的 beam_plan 函数，函数详情见论文附录
  • 讨论一：论文中的一个讨论 ：Trajectory Transformer 可以看做 Model-based方法？ ：Trajectory Transformer 通过序列建模的路径实现了一种看似相当简单的 Model-based 规划算法
    • 个人理解：因为序列模型相当于预估了 \(s_t,a_t \rightarrow r_t,s_{t+1}\)，可以算是同时预估了预测状态转移概率 \(T_{\psi_T}(s_{t+1}|s_t,a_t)\) 和奖励函数 \(r_{\psi_r}(s_t,a_t)\)，可以算是 Model-based方法），即采样候选动作序列，并选择预期奖励最大化的轨迹
  • 讨论二：关于 Trajectory Transformer 可以是否可以避免OOD问题的思考 ：文章提到通过联合建模动作与状态并使用相同过程采样，我们可以防止模型访问分布外动作
    • 个人理解：不能做到不会输入未见过的动作吧？因为可能会遇到训练时未见过状态；但是整体来说，可以避免强化学习中的高估问题，因为训练时不会访问未见过的动作

Experiments

  • 论文的实验评估主要关注以下两点：
    • Trajectory Transformer 作为 long-horizon 预测器的准确性 ：这里主要与标准动态模型参数化方法相比；
    • 序列建模工具（尤其是束搜索）作为控制算法的实用性 ：在离线强化学习、模仿学习和目标达成（goal-reaching）任务中的应用

模型分析

  • 论文首先评估 Trajectory Transformer 作为策略条件预测模型的 long-horizon 预测能力
    • 一般来说：常规情况下，需要策略和单步轨迹（状态转移）预测模型 ，使用策略单步决策+单步状态转移模型进行滚动计算来预估给定策略对应的轨迹
    • Trajectory Transformer 不同于标准的马尔可夫方法，它无需访问策略即可进行预测——策略的输出与策略遇到的状态被联合建模
  • 轨迹预测可视化 ：图2展示了论文的模型在训练数据（由已训练的策略收集）上生成的100时间步预测轨迹的可视化结果
    • 常规的 Model-based 方法应用于人形任务 ：这些研究通常有意缩短预测时域以防止模型误差累积（Janner et al., 2019; Amos et al., 2021）
    • 论文选择的对照模型是 ：PETS（Chua et al., 2018，一种MPC方法）的概率集成实现（PETS参考链接）；论文调整了集成内的模型数量、层数和每层大小，但未能生成能准确预测超过几十步的模型
    • 如图所示，Trajectory Transformer 的 long-horizon 预测明显更准确 ，即使在100步预测后，其轨迹在视觉上仍与真实策略在环境中生成的轨迹无法区分。据论文所知，此前尚未有 Model-based RL算法能在类似维度的任务上展示如此精确且 long-horizon 的预测轨迹
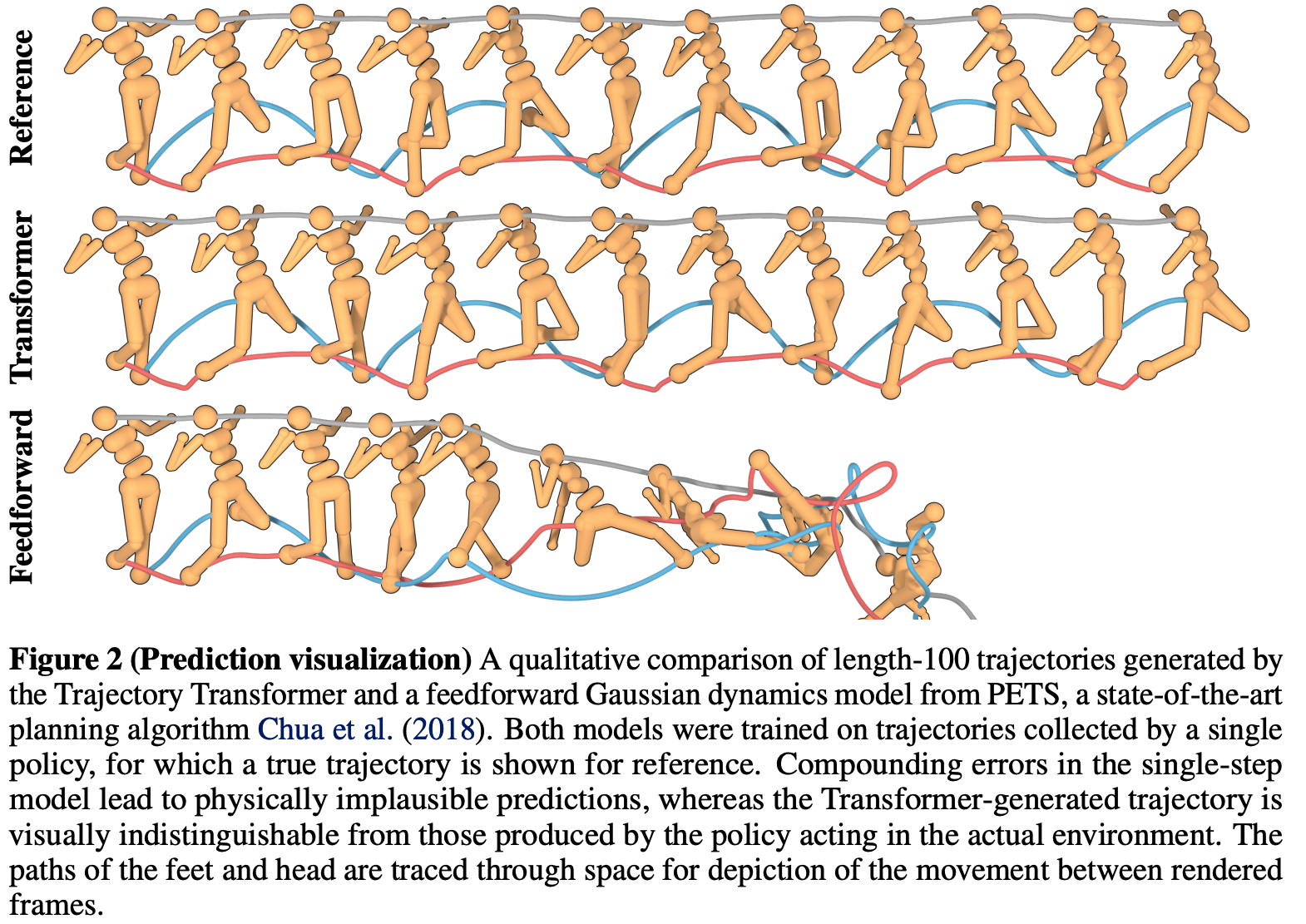
    • 注：第三行效果是Feedforward方法是 feedforward Gaussian dynamics model from PETS，前两行分别为原始行为和 Trajectory Transformer 学到的行为
  • 误差累积 ：图3定量展示了相同发现，论文评估了模型随预测时域增加的累积误差。标准预测模型通常在单步误差上表现优异，但 long-horizon 准确性较差，因此论文未在测试集上评估单步似然，而是从固定起点采样1000条轨迹，以估计每个模型预测的每时间步状态边缘分布。随后，论文报告参考策略在保留轨迹集上访问的状态在这些预测边缘下的似然。为评估离散化模型的似然，论文将每个区间视为其指定范围内的均匀分布；根据设计，模型在此范围外的概率为零
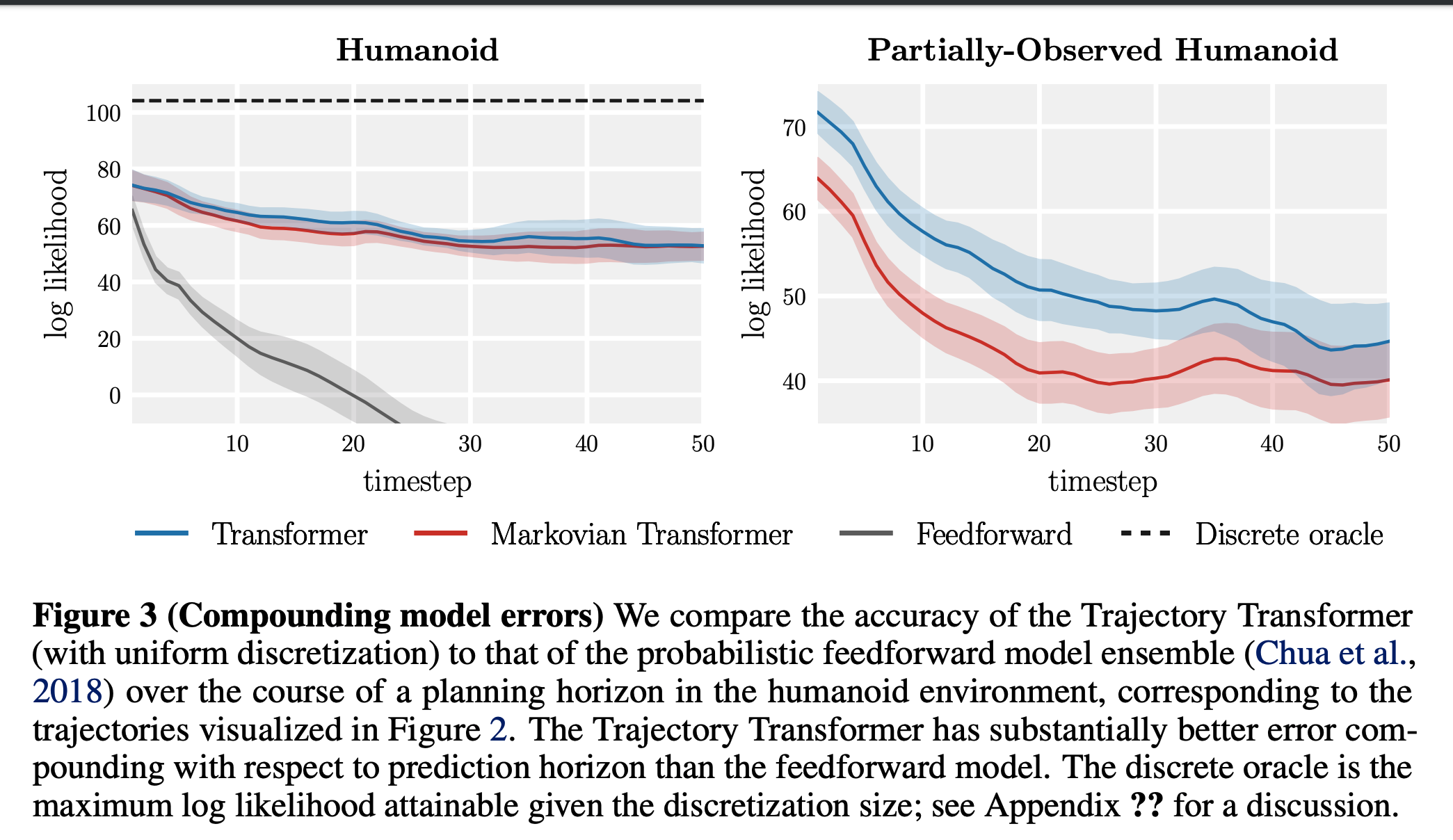
    • Markovian Transformer 是 Trajectory Transformer 的马尔可夫变体，表示对上下文进行截断的模型（其无法关注超过一个过去时间步）：
      • 在完全可观测环境中 ，该模型的表现与 Trajectory Transformer 相似，表明架构差异和自回归状态离散化带来的表达能力提升对 Trajectory Transformer 的 long-horizon 准确性起主要作用（理解：这里说明 TT 的收益来源不是长链路的序列依赖，说明 TT 可以建模MDP环境）
      • 在部分可观测环境（图3右），其中每个状态的每个维度有50%概率被掩码，如预期所示，在这种设置下，long-horizon 条件化对模型准确性影响更大（理解：部分观测时，只看当前状态难以决策，看到更多历史状态会部分补充当前状态的未知维度）
  • 注意力模式 ：图4展示了模型预测时的注意力图可视化。论文观察到两种主要注意力模式（问题：这两种模型分别是怎么设置的？是直接修改了上下文窗口吗？）：
    • 马尔可夫策略(图中第一个) ：状态预测主要关注前一个 Transaction（s,a,r）；
    • 关注过去多步的策略（图中第二个） ：每个状态预测关注多个先前状态的特定维度
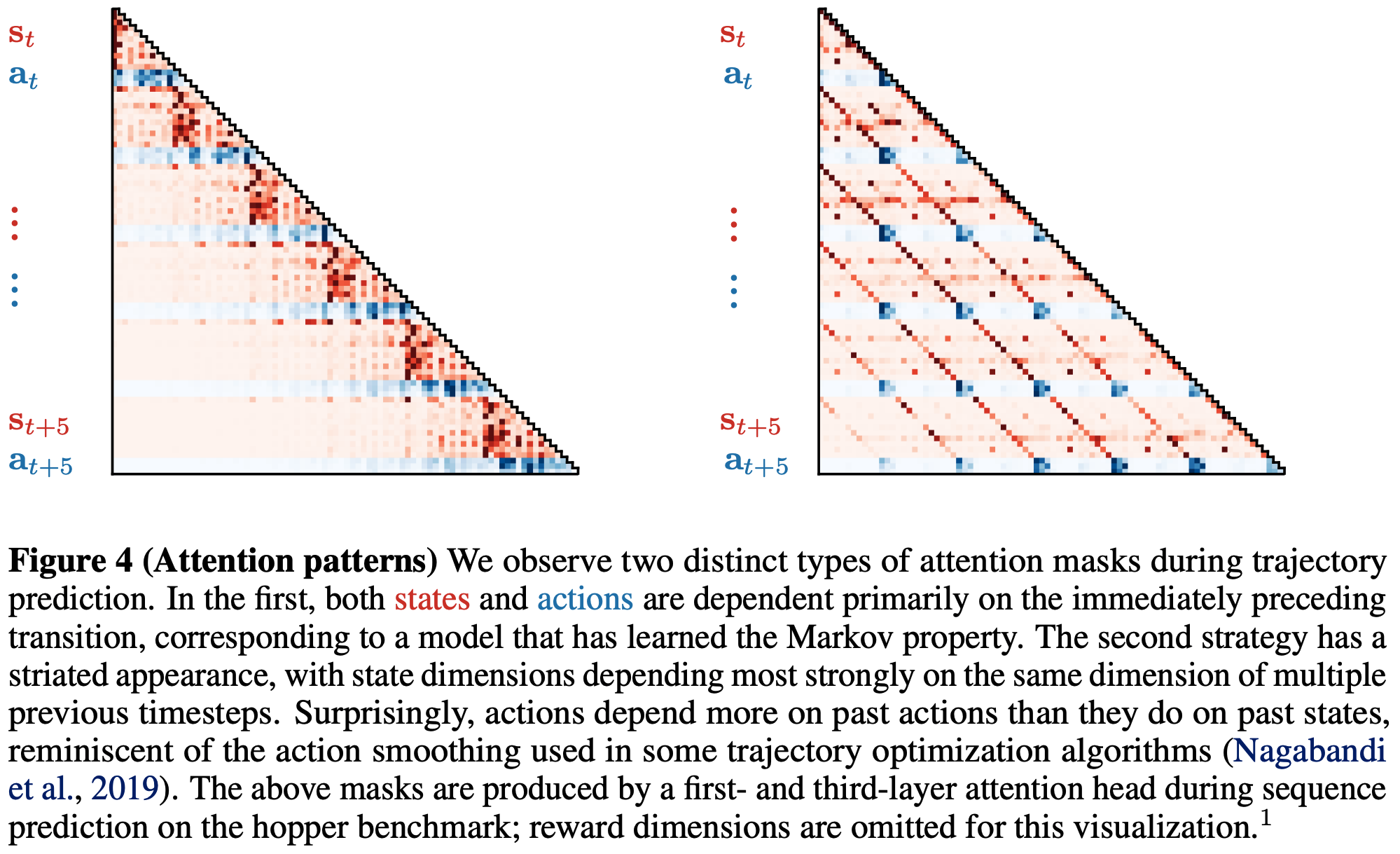
    • 论文提到的一个实验观察：动作预测对先前动作的关注多于对先前状态的关注。这种动作依赖关系与行为克隆的常见表述（动作仅为过去状态的函数）不同，但类似于某些规划算法中用于生成平滑动作序列的动作滤波技术（理解：动作之间有一定的相关性）

强化学习与控制

离线强化学习评估
  • 离线强化学习 ：论文在D4RL离线基准测试套件的多个环境中评估 Trajectory Transformer ，包括运动控制和AntMaze领域。该评估是论文的控制设置中最具挑战性的，因为奖励最大化行为通常与无监督建模相关的行为（即模仿行为）在性质上差异最大
  • 表1展示了运动控制环境的结果。论文与其他五种方法进行了比较，涵盖数据驱动控制的其他方法：
    • 行为正则化 Actor-Critic （BRAC, 2019）和保守Q学习（CQL,2020a）代表当前最先进的离线RL方法；
    • Model-based 离线规划（MBOP, 2021）是先前表现最佳的离线轨迹优化技术；
    • Decision Transformer（DT, 2021）是同期开发的序列建模方法，使用回报条件化而非规划；
    • 行为克隆（BC）提供了纯模仿方法的性能基准
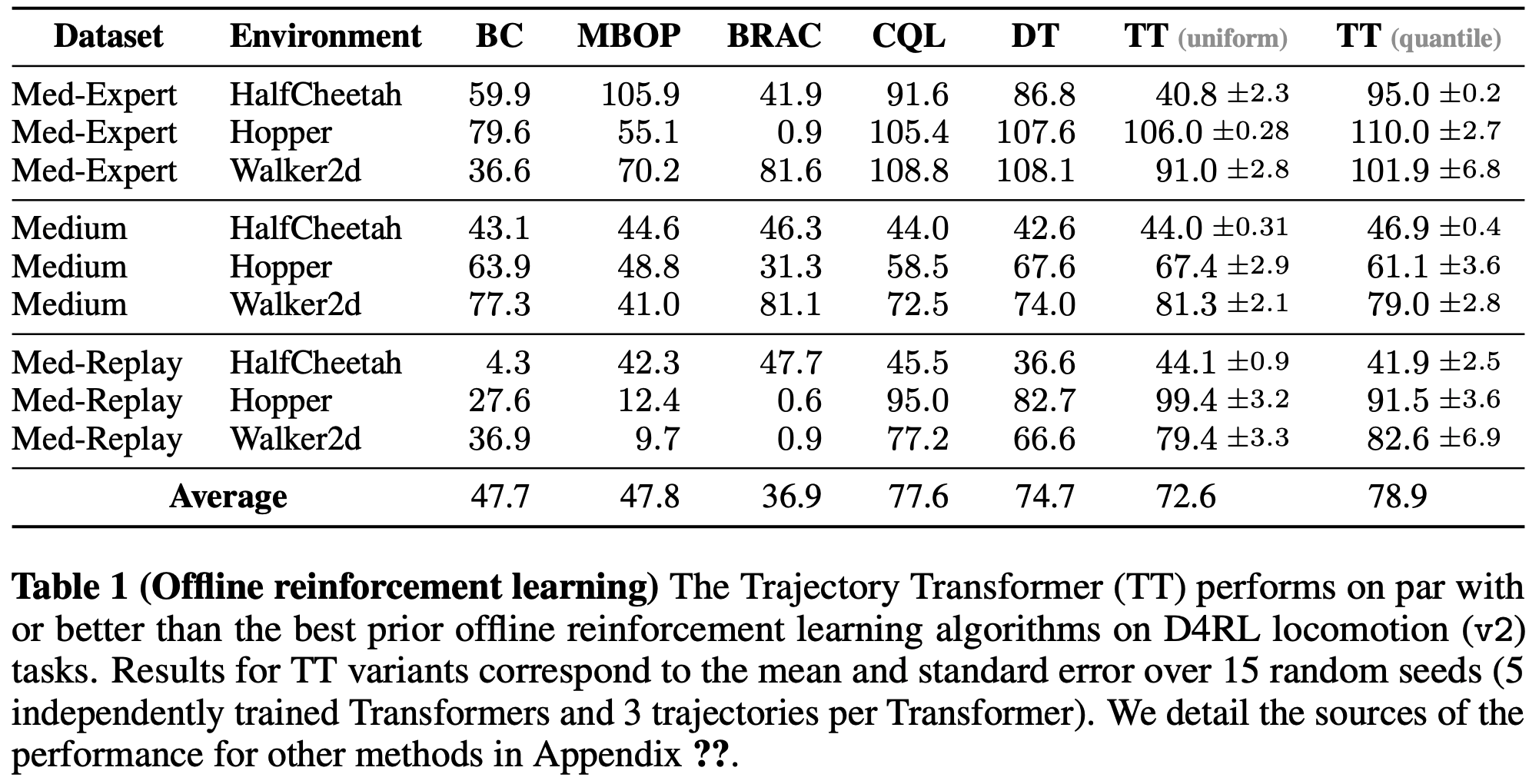
    • 个人观察 ：看起来TT效果和CQL差不多？
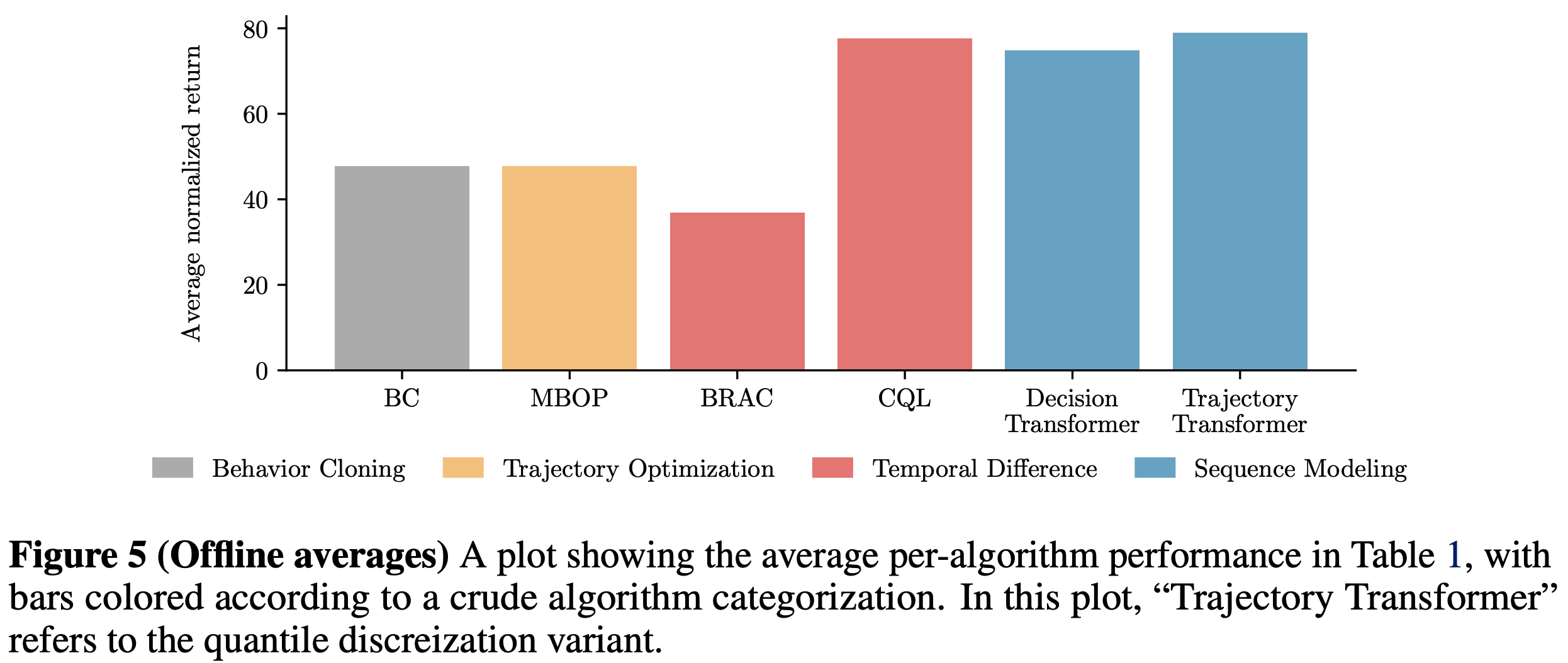
  • Trajectory Transformer 的性能与所有先前方法相当或更优（表1）Trajectory Transformer 的两种离散化变体（均匀和分位数）在除HalfCheetah-Medium-Expert外的所有环境中表现相似。在该环境中，速度的大范围使均匀离散化无法恢复执行专家策略所需的精确动作，因此分位数离散化的回报是均匀离散化的两倍以上
  • 结合Q函数的 Trajectory Transformer ：即IQL的Q+Trajectory Transformer
    • 解决了什么问题 ：蒙特卡罗估值版本的TT，在稀疏奖励和 long-horizon 任务中效果不佳，信息量不足以引导束搜索规划（Reward-to-go与策略无关导致难以最大化Reward）
    • 如何解决的 ：论文提出可以用通过动态规划训练的Q函数替代Transformer的估值（问题这里的估值包括 即时奖励 \(r_t\) 和 reward-to-go \(R_t\)吗？），论文通过在AntMaze导航任务中使用IQL的Q函数来探索这一组合（理解：这里说的动态规划训练就是传统强化学习贝尔曼方程的训练方式，加入动态规划的Q值后，就允许策略从见过的多条路径组合，从而生成未见过的最优路径了）
  • 表2展示了AntMaze的结果：Q引导的 Trajectory Transformer 规划在所有迷宫大小和数据集组合上优于所有先前方法，也包括提供Q函数的IQL方法，这表明将Q函数作为搜索启发式进行规划比策略提取对Q函数误差的敏感性更低
    • 补充结论：由于Q引导规划仍受益于动态规划和规划的时间组合性，它在AntMaze任务中优于回报条件化方法（如Decision Transformer），后者因数据集中缺乏完整示范而表现不佳
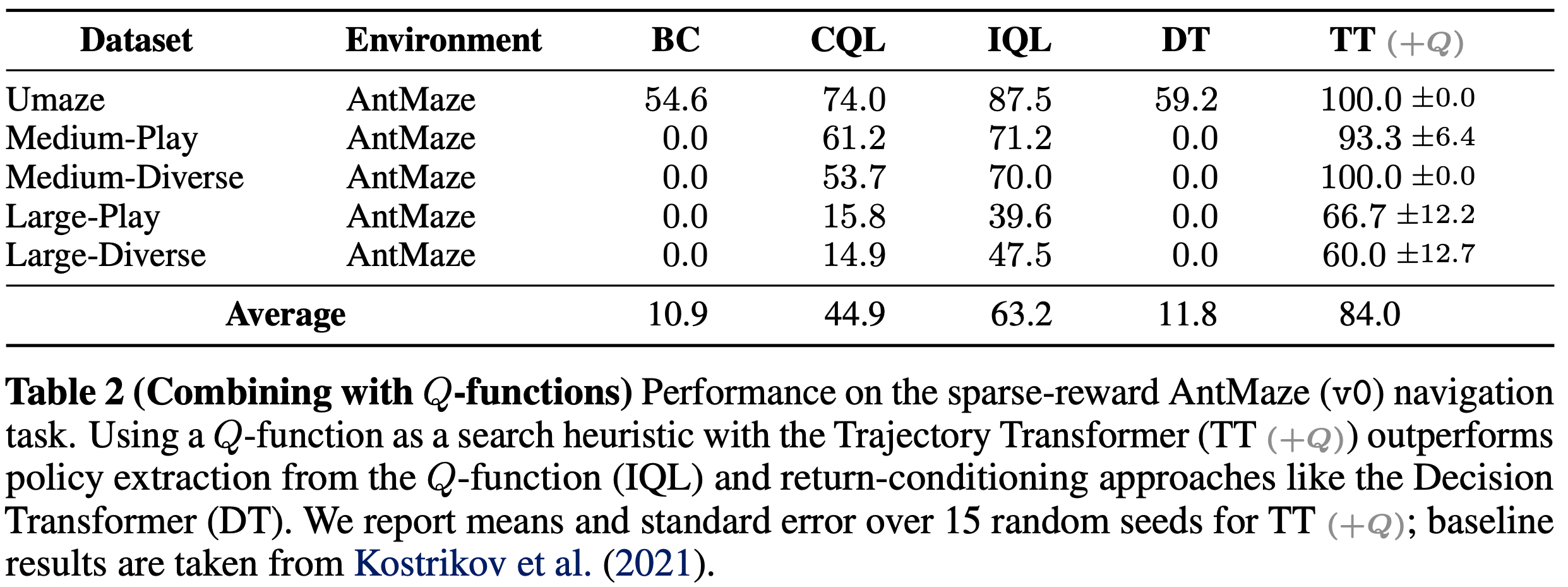
    • 强调一下 ：TT+Q的效果明显由于其他方法，包括IQL方法
模仿学习与目标达成评估
  • 模仿学习与目标达成 ：论文还使用标准的似然最大化束搜索（而非离线RL中使用的回报最大化版本）进行规划。论文发现，在专家策略收集的数据集（即D4RL中的专家数据）上训练模型后，使用束搜索作为滚动时域控制器，在Hopper和Walker2d环境中分别实现了104%和109%的平均归一化回报（与离线RL评估一样，都使用15次运行结果），这说明语言建模中的解码算法可有效重新用于控制（理解：收益来源是专家模仿+束搜索带来的扰动+挑选最大收益轨迹）
基于目标状态条件化的束搜索变体评估
  • 最后，论文评估了基于目标状态条件化的束搜索变体 ，该方法同时对未来期望状态和已观测到的先前状态进行条件化，
    • 论文使用经典四房间环境的连续变体作为测试平台
    • 训练数据由预训练的目标达成（goal-reaching）智能体收集的轨迹组成，起始和目标状态在状态空间中均匀随机采样
    • 图6展示了规划器选择的路径。反因果条件化（基于未来状态）使束搜索可作为目标达成方法，无需任何奖励塑形（或任何形式的奖励），该规划方法完全依赖目标重标记（理解：修改未来目标作为条件从而改变当前动作）
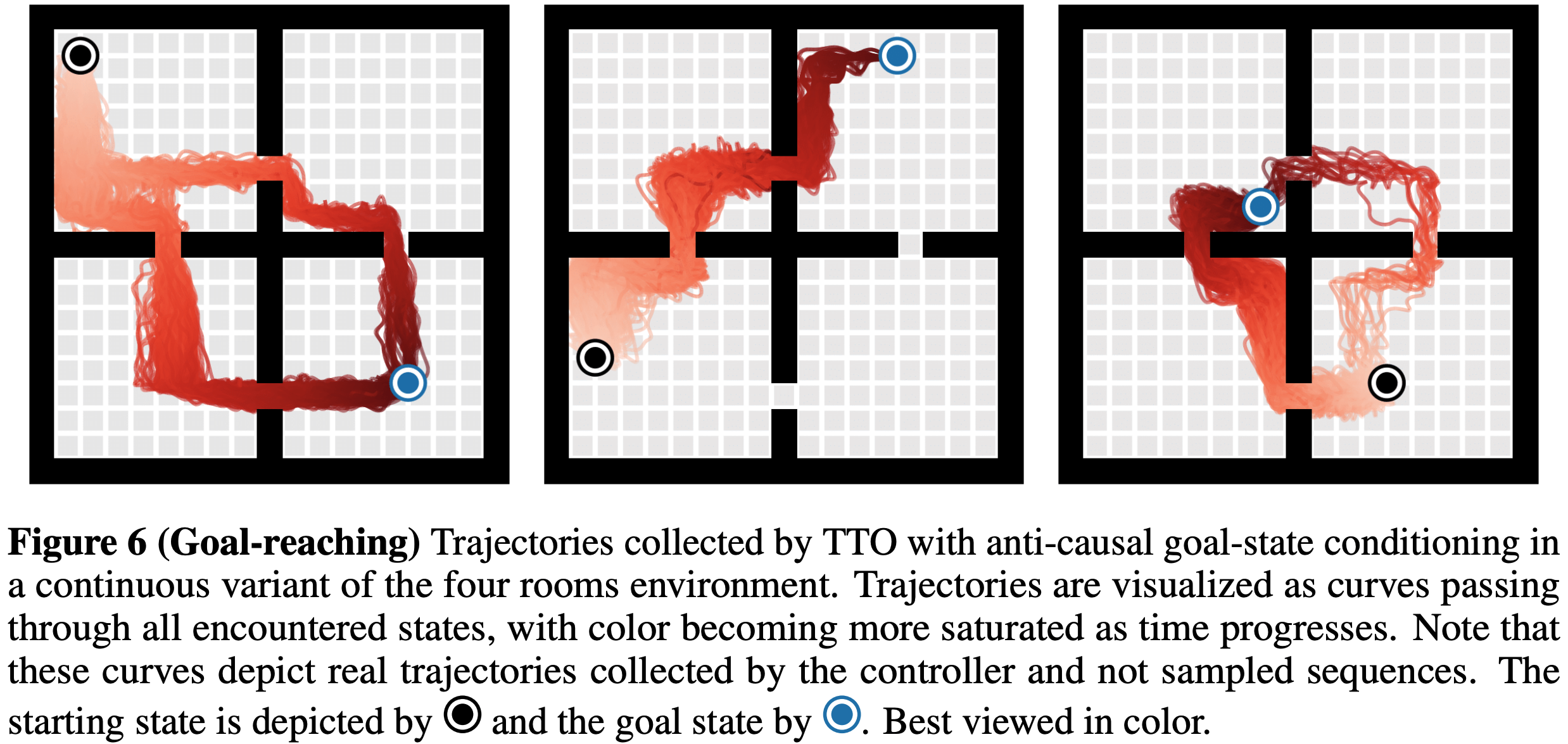
    • 注：附录描述了将该实验扩展到程序化生成地图的延伸工作
  • 注：图5展示了表1中各算法的平均性能，按粗略算法分类着色（图中“ Trajectory Transformer ”指分位数离散化版本TT）

讨论与局限性（原论文内容）

  • 工作总结 ：论文提出了一种将强化学习视为序列建模问题的新视角，使论文能够为多种不同问题场景开发统一的算法，将强化学习算法的标准组件（如策略、模型和价值函数）统一在一个序列模型之下。该算法包括训练一个联合建模状态、动作和奖励的序列模型，并使用经过束搜索进行采样
    • 这种方法借鉴了大规模语言建模工具而非传统控制方法，但论文发现它在模仿学习、目标达成和离线强化学习等任务中均表现出色
  • 缺点 ：目前基于Transformer的预测相比常用于基于模型控制的单步模型预测速度更慢且资源需求更高
    • 窗口越长越慢 ：当上下文窗口过大时，标准Transformer的动作选择可能需要数秒时间，这使其难以用于大多数动态系统的实时控制
    • 束搜索导致速度慢 ：虽然束搜索规划器在概念上属于模型预测控制范畴，理论上可应用于任何基于模型强化学习的场景，但实际应用中缓慢的规划速度也使得在线强化学习实验变得笨拙（注：采用计算高效的Transformer架构可能大幅降低运行时间）
    • 离散化带来的精度损失 ：论文选择对连续数据进行离散化以适应标准架构，而非修改架构来处理连续输入，尽管这一设计比传统连续动态模型有效得多，但原则上它会对预测精度设置上限
  • 写在最后 ：TT+Q可能是最优解（即IQL的Q+Trajectory Transformer）
    • 原文内容 ：论文研究了一种可应用于强化学习问题的最小化算法类型。虽然论文研究结果的一个有趣启示是：通过选择合适的模型，强化学习问题可以被重新表述为监督学习任务，但这一思想最实用的实现可能来自于与动态规划技术的结合——正如Q函数引导的 Trajectory Transformer 规划所展现的优异性能所暗示的那样

附录：Trajectory-Transformer planning 函数

  • 以下代码来自开源项目的./trajectory/search/core.py文件中的 beam_plan 函数： 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    91
    @torch.no_grad()
    def beam_plan(
        model, value_fn, x,
        n_steps, beam_width, n_expand,
        observation_dim, action_dim,
        discount=0.99, max_context_transitions=None,
        k_obs=None, k_act=None, k_rew=1,
        cdf_obs=None, cdf_act=None, cdf_rew=None,
        verbose=True, previous_actions=None,
    ):
        '''
            x : tensor[ 1 x input_sequence_length ]
        '''

        inp = x.clone()

        # convert max number of transitions to max number of tokens
        transition_dim = observation_dim + action_dim + REWARD_DIM + VALUE_DIM
        max_block = max_context_transitions * transition_dim - 1 if max_context_transitions else None

        ## pass in max numer of tokens to sample function
        sample_kwargs = {
            'max_block': max_block,
            'crop_increment': transition_dim,
        }

        ## repeat input for search
        x = x.repeat(beam_width, 1)

        ## construct reward and discount tensors for estimating values
        rewards = torch.zeros(beam_width, n_steps + 1, device=x.device)
        discounts = discount ** torch.arange(n_steps + 1, device=x.device)

        ## logging
        progress = utils.Progress(n_steps) if verbose else utils.Silent()

        for t in range(n_steps):
            ## repeat everything by `n_expand` before we sample actions
            x = x.repeat(n_expand, 1)
            rewards = rewards.repeat(n_expand, 1)

            ## sample actions
            x, _ = sample_n(model, x, action_dim, topk=k_act, cdf=cdf_act, **sample_kwargs)

            ## sample reward and value estimate
            x, r_probs = sample_n(model, x, REWARD_DIM + VALUE_DIM, topk=k_rew, cdf=cdf_rew, **sample_kwargs)

            ## optionally, use a percentile or mean of the reward and
            ## value distributions instead of sampled tokens
            r_t, V_t = value_fn(r_probs)

            ## update rewards tensor
            rewards[:, t] = r_t
            rewards[:, t+1] = V_t

            ## estimate values using rewards up to `t` and terminal value at `t`
            values = (rewards * discounts).sum(dim=-1)

            ## get `beam_width` best actions
            values, inds = torch.topk(values, beam_width)

            ## index into search candidates to retain `beam_width` highest-reward sequences
            x = x[inds]
            rewards = rewards[inds]

            ## sample next observation (unless we have reached the end of the planning horizon)
            if t < n_steps - 1:
                x, _ = sample_n(model, x, observation_dim, topk=k_obs, cdf=cdf_obs, **sample_kwargs)

            ## logging
            progress.update({
                'x': list(x.shape),
                'vmin': values.min(), 'vmax': values.max(),
                'vtmin': V_t.min(), 'vtmax': V_t.max(),
                'discount': discount
            })

        progress.stamp()

        ## [ batch_size x (n_context + n_steps) x transition_dim ]
        x = x.view(beam_width, -1, transition_dim)

        ## crop out context transitions
        ## [ batch_size x n_steps x transition_dim ]
        x = x[:, -n_steps:]

        ## return best sequence
        argmax = values.argmax()
        best_sequence = x[argmax]

        return best_sequence