RL——PPO论文精读

本文是 PPO 的论文精读，经典值的多次回味

• 参考链接：
  • 原始论文：Proximal Policy Optimization Algorithms, OpenAI, 2017
  • 博主的其他解读：RL——PPO

Paper Summary

• 近端策略优化（PPO）是一类新的 Policy Gradient 方法（Actor 与环境中交互采样数据，并使用随机梯度上升优化 surrogate 目标函数，交替进行）
• PPO 兼具 TRPO 的优势，但相对 TRPO，实现更简单、更通用，且样本复杂度更低
• 标准的 Policy Gradient 方法对每个数据样本执行一次梯度更新，而论文提出了一种新的目标函数 ，支持对 minibatch 数据进行多轮更新
  • 注：论文的核心创新点在于这个新的目标函数可以对数据进行多轮更新（使用重要性采样实现类似 off-policy 的更新）
• 在多个基准任务上测试了 PPO，包括模拟机器人运动和 Atari 游戏，结果表明 PPO 优于其他 online Policy Gradient 方法；
  • 在样本复杂度、实现简易性和训练时间之间取得了良好的平衡
• 评价：
  • 在大部分场景下，PPO 都是值得最初尝试的 Online RL 方法，简洁但非常有效的方法，OpenAI 确实有实力
  • 新增补充：LLM 时代来临以后，PPO 已经成为了 RLHF 的默认方法，OpenAI 的含金量还在上升

---

Policy Optimization

• 目前针对神经网络函数逼近的 RL 主要的方法包括：
  • Deep Q-Learning
  • “vanilla” Policy Gradient 方法
  • 信任域/自然策略梯度（trust region / natural policy gradient）方法
    • TRPO与自然策略梯度的关系简单讨论见：RL——自然策略梯度法
• 现有方法在可扩展性（适用于大型模型和并行实现）、数据效率和鲁棒性（即无需调参即可适用于多种问题）方面仍有改进空间
  • Q-Learning（带函数逼近）在许多简单问题上表现不佳且理论理解不足
  • vanilla Policy Gradient 方法的数据效率和鲁棒性较差，而 TRPO 实现复杂，且不兼容包含噪声（如dropout）或参数共享（如策略与值函数共享参数或辅助任务）的架构
• 论文旨在通过提出一种新算法来改进现状，该算法在保持 TRPO 数据效率和可靠性能的同时，仅需一阶优化（注意：TRPO 是包含二阶求导的，所以性能好但很慢）
• 论文提出了一种基于裁剪概率比（clipped probability ratios） 的新目标函数，该函数对策略性能形成悲观估计（即下界）
• 策略优化：交替执行 1）从策略中采样数据；2）在同一批采样数据上进行多轮优化
• 实验内容：
  • 比较不同代理目标函数的性能 ：发现基于 Clip 版本表现最佳
  • 比较 PPO 与文献中的其他算法：在连续控制任务中，PPO 优于其他对比算法；在 Atari 游戏中，其样本复杂度显著优于 A2C，与 ACER 相当，但实现更简单
    • 问题：如何理解这里的样本复杂度？
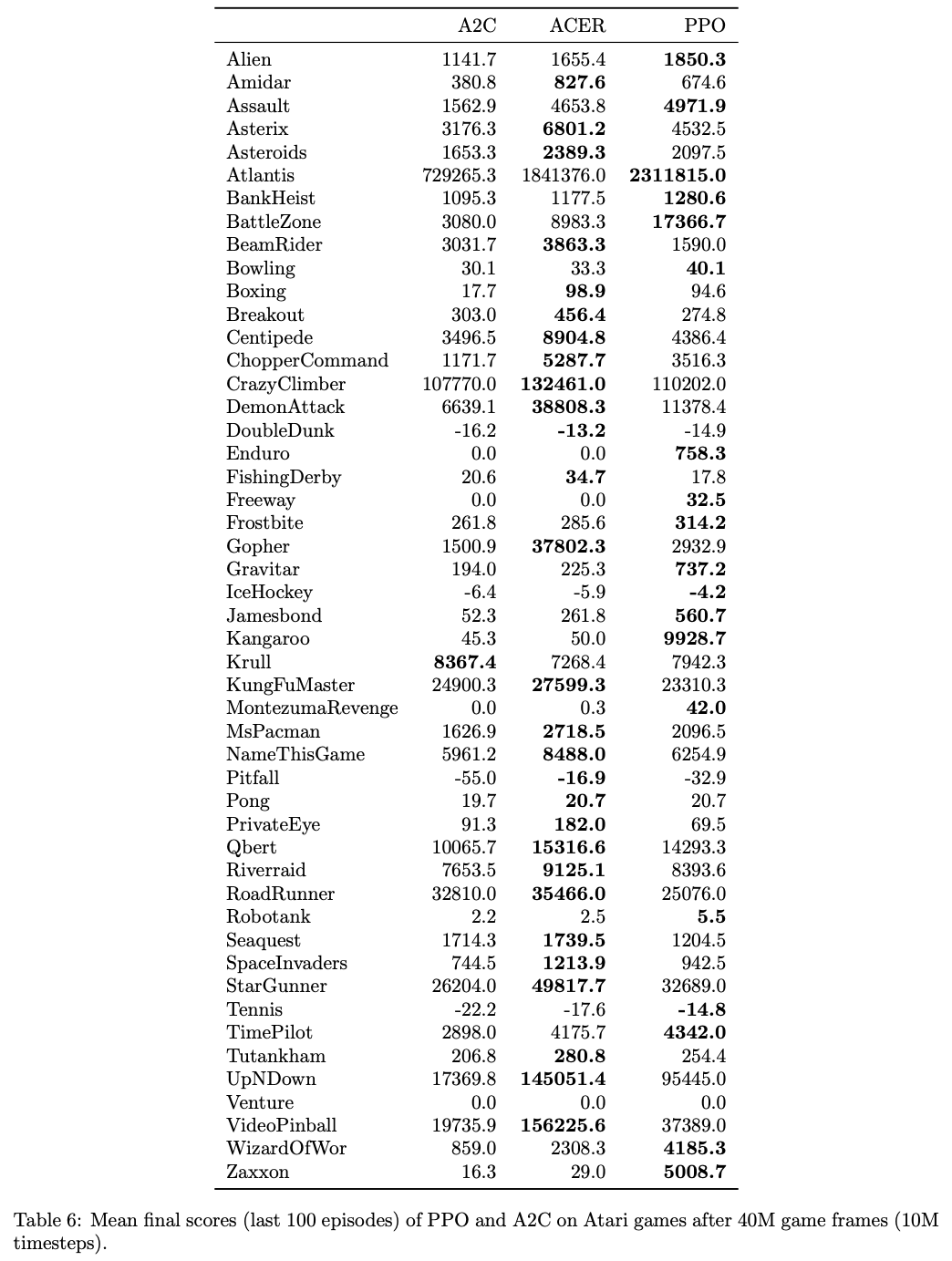
    • 回答：需要采样的样本数，从文章附录图 6 可以看到，收敛速度远远快与 A2C

---

Policy Optimization

Policy Gradient Methods

• Policy Gradient 方法通过计算 Policy Gradient 的估计值，并将其代入随机梯度上升算法中实现优化。最常用的梯度估计器形式为：
  $$
  \hat{g} = \hat{\mathbb{E} }_{t}\left[\nabla_{\theta}\log\pi_{\theta}(a_{t} \mid s_{t})\hat{A}_{t}\right]
  $$
  • \(\pi_{\theta}\) 是随机策略
  • \(\hat{A}_{t}\) 是时间步 \(t\) 的优势函数估计值
  • 这里的期望 \(\hat{\mathbb{E} }_{t}[\dots]\) 表示在有限样本批次上的经验平均，算法交替进行采样和优化
  • 使用自动微分软件的实现通过构造目标函数（其梯度为 Policy Gradient 估计值）实现优化；
  • 梯度估计值 \(\hat{g}\) 通过对以下目标函数求导得到：
    $$
    L^{PG}(\theta) = \hat{\mathbb{E} }_{t}\left[\log\pi_{\theta}(a_{t} \mid s_{t})\hat{A}_{t}\right].
    $$
• 虽然可以基于同一轨迹对损失 \(L^{PG}\) 进行多步优化，但这样做缺乏理论依据，且经验上常导致策略更新过大（见原始论文第6.1节；结果未展示，但与“无裁剪或惩罚”设置相似或更差）
  • 理解：这里第一次更新是 on-policy，第二次更新则是 off-policy，若要继续更新应该是需要重要性采样实现

信任域方法（Trust Region Methods）

• 在 TRPO 中，目标函数（surrogate 目标）在策略更新大小的约束下最大化，具体形式为：
  $$
  \text{maximize} \quad \hat{\mathbb{E} }_{t}\left[\frac{\pi_{\theta}(a_{t} \mid s_{t})}{\pi_{\theta_{\text{old} } }(a_{t} \mid s_{t})}\hat{A}_{t}\right] \\
  \hat{\mathbb{E} }_{t}\left[\text{KL}\left[\pi_{\theta_{\text{old} } }(\cdot \mid s_{t}), \pi_{\theta}(\cdot \mid s_{t})\right]\right] \leq \delta. \tag{3 & 4}
  $$
  • 其中， \(\theta_{\text{old} }\) 是更新前的策略参数向量
  • 通过对目标函数进行线性近似、对约束进行二次近似，可以高效地使用共轭梯度算法近似求解该问题
• TRPO的理论支持使用惩罚项而非约束，即求解以下无约束优化问题：
  $$
  \underset{\theta}{\text{maximize} } \quad \hat{\mathbb{E} }_{t}\left[\frac{\pi_{\theta}(a_{t} \mid s_{t})}{\pi_{\theta_{\text{old} } }(a_{t} \mid s_{t})}\hat{A}_{t} - \beta \text{KL}\left[\pi_{\theta_{\text{old} } }(\cdot \mid s_{t}), \pi_{\theta}(\cdot \mid s_{t})\right]\right] \tag{5}
  $$
  • 其中， \(\beta\) 为系数
  • 这是因为某些代理目标（计算状态上的最大KL而非均值）形成了策略 \(\pi\) 性能的下界（即悲观界）
  • TRPO 使用硬约束而非惩罚项，因为很难选择一个适用于不同问题（甚至同一问题中学习过程中特性变化）的 \(\beta\) 值
  • 因此，为了实现一阶算法模拟 TRPO 的单调改进目标，实验表明仅选择固定惩罚系数 \(\beta\) 并用 SGD 优化惩罚目标（公式5）是不够的，还需额外修改

裁剪代理目标（Clipped Surrogate Objective）

• 设 \(r_{t}(\theta)\) 表示概率比：
  $$r_{t}(\theta) = \frac{\pi_{\theta}(a_{t} \mid s_{t})}{\pi_{\theta_{\text{old} } }(a_{t} \mid s_{t})}$$
  • 特别地：
    $$r(\theta_{\text{old} }) = 1$$
• TRPO 最大化以下 surrogate 目标：
  $$
  L^{CPI}(\theta) = \hat{\mathbb{E} }_{t}\left[\frac{\pi_{\theta}(a_{t} \mid s_{t})}{\pi_{\theta_{\text{old} } }(a_{t} \mid s_{t})}\hat{A}_{t}\right] = \hat{\mathbb{E} }_{t}\left[r_{t}(\theta)\hat{A}_{t}\right].
  $$
  • 上标 \(CPI\) 指代保守策略迭代，该目标函数首次在此提出
    • 理解：其实就是包含重要性采样的 Policy Gradient 损失函数版本
  • 若无约束，最大化 \(L^{CPI}\) 会导致策略更新过大，因此，作者考虑如何修改目标函数，以惩罚使 \(r_{t}(\theta)\) 偏离 1 的策略变化
• 作者提出的主要目标函数如下：
  $$
  L^{CLIP}(\theta) = \hat{\mathbb{E} }_{t}\left[\min\left(r_{t}(\theta)\hat{A}_{t}, \color{red}{\text{clip}(r_{t}(\theta), 1-\epsilon, 1+\epsilon)\hat{A}_{t}}\right)\right]
  $$
  • \(\epsilon\) 为超参数（例如 \(\epsilon = 0.2\) ）
  • 该目标函数的动机如下：
    • min 内的第一项为 \(L^{CPI}\) ；第二项通过裁剪概率比修改代理目标，消除了 \(r_{t}\) 超出区间 \([1-\epsilon, 1+\epsilon]\) 的动机
    • 最后，论文对裁剪和未裁剪目标取最小值，因此最终目标是未裁剪目标的下界（即悲观界）
    • 通过此方案，论文仅在概率比变化使目标改善时忽略该变化，而在其使目标恶化时保留它
    • 注意，在 \(\theta_{\text{old} }\) 附近（即 \(r=1\) 时）， \(L^{CLIP}(\theta)\) 与 \(L^{CPI}(\theta)\) 一阶等价，但随着 \(\theta\) 远离 \(\theta_{\text{old} }\) ，二者差异增大
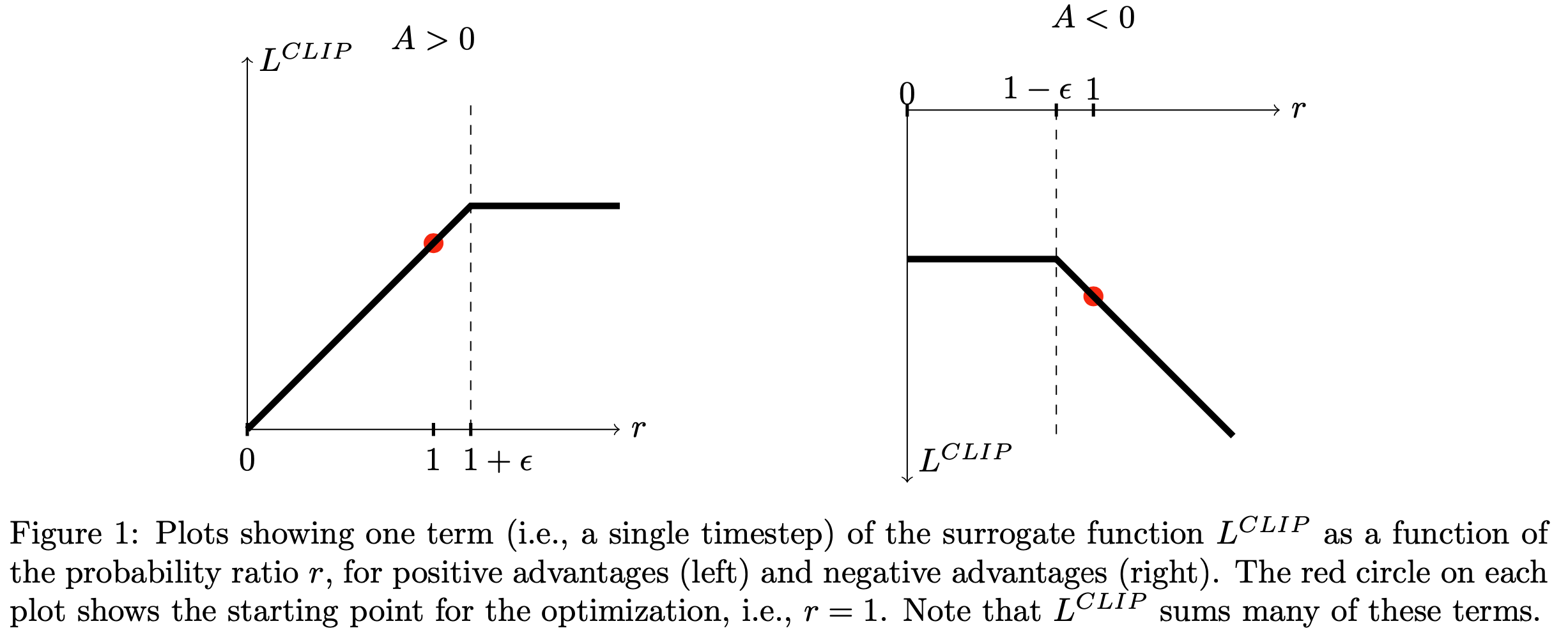
• 图1 绘制了 \(L^{CLIP}\) 中的单一项（即单个时间步 \(t\) ）随概率比 \(r\) 的变化曲线
• 图2 展示了代理目标 \(L^{CLIP}\) 的另一种直观解释，显示了在连续控制问题上沿策略更新方向插值时多个目标的变化情况。可以看出， \(L^{CLIP}\) 是 \(L^{CPI}\) 的下界，并对过大的策略更新施加惩罚
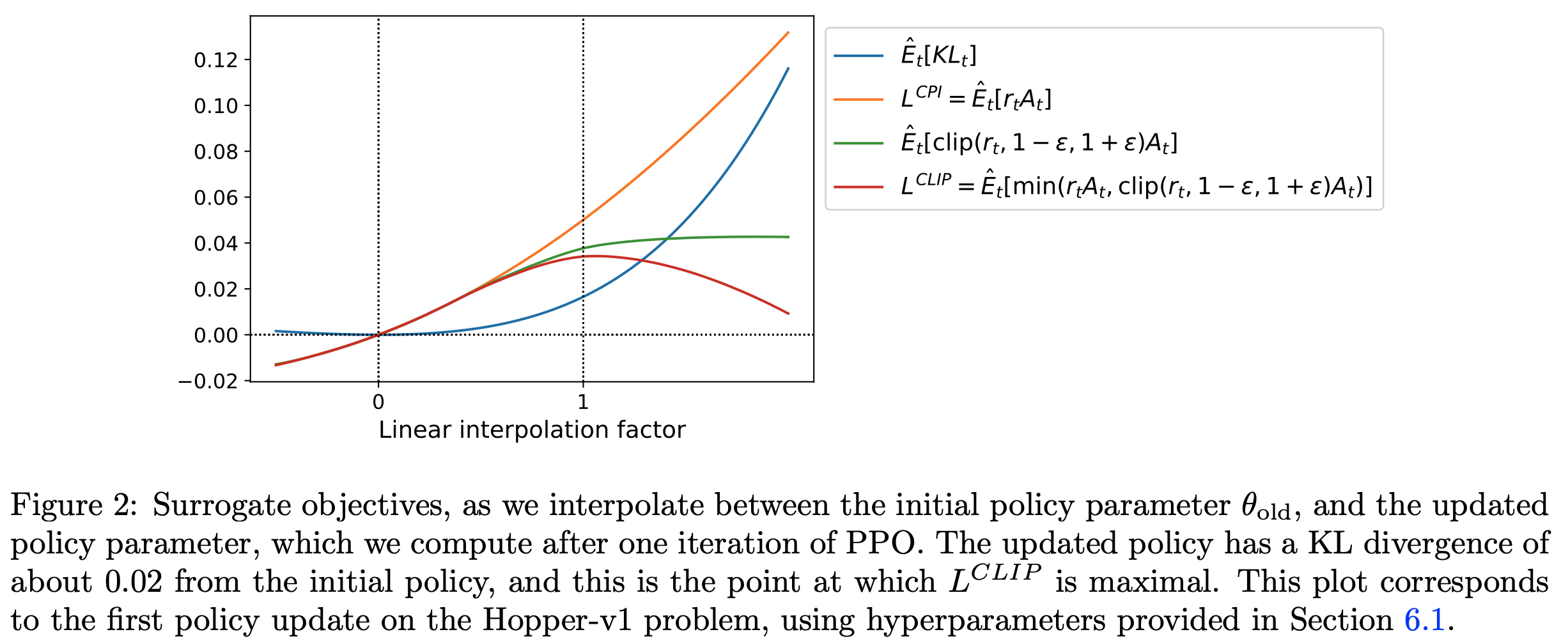
• 吐槽：原始论文对该目标函数的解释不够清楚

---

Adaptive KL Penalty Coefficient

• 另一种方法（可作为裁剪代理目标的替代或补充）是使用KL散度惩罚，并通过调整惩罚系数使得每次策略更新达到目标KL散度值 \(d_{\text{target} }\)
  • 注：实验发现 KL 惩罚的性能不如裁剪代理目标，但因其为重要基线，仍在此介绍
• 该算法最简单的实现步骤如下：
  • 第一步：使用多轮 minibatch SGD 优化以下 KL 惩罚目标：
    $$
    L^{KLPEN}(\theta) = \hat{\mathbb{E} }_{t}\left[\frac{\pi_{\theta}(a_{t} \mid s_{t})}{\pi_{\theta_{\text{old} } }(a_{t} \mid s_{t})}\hat{A}_{t} - \beta \text{KL}\left[\pi_{\theta_{\text{old} } }(\cdot \mid s_{t}), \pi_{\theta}(\cdot \mid s_{t})\right]\right]
    $$
  • 第二步：计算 \(d = \hat{\mathbb{E} }_{t}\left[\text{KL}\left[\pi_{\theta_{\text{old} } }(\cdot \mid s_{t}), \pi_{\theta}(\cdot \mid s_{t})\right]\right]\) ：
    • 若 \(d < d_{\text{target} }/1.5\) ，则 \(\beta \leftarrow \beta/2\)
    • 若 \(d > d_{\text{target} } \times 1.5\) ，则 \(\beta \leftarrow \beta \times 2\)
    • 更新后的 \(\beta\) 用于下一次策略更新
• 实验效果：此方案偶尔会出现KL散度与 \(d_{\text{target} }\) 显著偏离的情况，但这种情况较少，且 \(\beta\) 会快速调整
• 超参数设定和实验结论：
  • 参数 1.5 和 2 为启发式选择，但算法对其不敏感
  • 初始 \(\beta\) 值为另一超参数，但因算法快速调整，实际影响不大

---

Algorithm

• 前几节介绍的代理损失（surrogate losses）可以通过对典型的 Policy Gradient 实现进行微小改动来计算和微分。对于使用自动微分的实现，只需构建损失函数 \( L^{CLIP} \) 或 \( L^{KLPEN} \) 来代替 \( L^{PG} \) ，并对此目标函数执行多步随机梯度上升
• 大多数计算方差缩减的优势函数估计方法会利用学习到的状态价值函数 \( V(s) \) ；例如，广义优势估计（GAE），或有限时域估计器（finite-horizon estimators）
• 如果使用在策略和价值函数之间共享参数的神经网络架构，则必须使用一个结合了策略替代项和价值函数误差项的损失函数。根据以往工作的建议，可以通过添加熵奖励来进一步增强此目标 ，以确保充分的探索。结合这些项，论文得到以下目标函数，每次迭代时（近似）最大化：
  $$
  L_{t}^{CLIP+VF+S}(\theta) = \hat{\mathbb{E} }_{t}\big[L_{t}^{CLIP}(\theta) - c_{1}L_{t}^{VF}(\theta) + c_{2}S[\pi_{\theta}] (s_t)\big],
  $$
  • \( c_{1}, c_{2} \) 是系数
  • \( S \) 表示熵奖励
  • \( L_{t}^{VF} \) 是平方误差损失 \( (V_{\theta}(s_{t}) - V_{t}^{\text{targ} })^{2} \)
• 一种流行的 Policy Gradient 实现风格（特别适合与循环神经网络一起使用）让策略运行 \( T \) 个时间步（其中 \( T \) 远小于回合长度），并使用收集到的样本进行更新。这种风格需要一个不超出时间步 \( T \) 的优势估计器。Asynchronous methods for deep reinforcement learning中使用的估计器为：
  $$
  \hat{A}_{t} = -V(s_{t}) + r_{t} + \gamma r_{t+1} + \cdots + \gamma^{T-t+1}r_{T-1} + \gamma^{T-t}V(s_{T}),
  $$
  • 其中 \( t \) 指定了给定长度为 \( T \) 的轨迹段中的时间索引
  • 推广这一选择，我们可以使用截断的广义优势估计，当 \( \lambda=1 \) 时退化为式(10)：
    $$
    \hat{A}_{t} = \delta_{t} + (\gamma\lambda)\delta_{t+1} + \cdots + (\gamma\lambda)^{T-t+1}\delta_{T-1},\\
    \text{where} \quad \delta_{t} = r_{t} + \gamma V(s_{t+1}) - V(s_{t}).
    $$
• 使用固定长度轨迹段的近端策略优化（PPO）算法如下所示
  • 每次迭代中，\( N \) 个（并行）执行者各收集 \( T \) 个时间步的数据；然后基于这些 \( NT \) 个时间步的数据构建代理损失，并使用 minibatch SGD （或通常为了更好的性能使用Adam）优化它，进行 \( K \) 轮

---

Experiments

代理目标的比较

• 论文在不同超参数下比较了几种代理目标

• 论文将代理目标 \( L^{CLIP} \) 与几种自然变体和消融版本进行比较：

  • 无裁剪或惩罚（No clipping or penalty） ：\( L_{t}(\theta) = r_{t}(\theta)\hat{A}_{t} \)
  • 裁剪（Clipping） ：\( L_{t}(\theta) = \min(r_{t}(\theta)\hat{A}_{t}, \text{clip}(r_{t}(\theta), 1-\epsilon, 1+\epsilon)\hat{A}_{t}) \)
  • KL penalty（fixed or adaptive） ：\( L_{t}(\theta) = r_{t}(\theta)\hat{A}_{t} - \beta \text{KL}[\pi_{\theta_{\text{old} } }, \pi_{\theta}] \)

• 对于KL惩罚，可以使用固定惩罚系数 \( \beta \) 或自适应系数（如第4节所述，目标KL值为 \( d_{\text{target} } \) ），论文还尝试了对数空间裁剪，但发现性能没有提升

  • 问题：这里是指将指数换成对数？

• 由于论文需要为每个算法变体搜索超参数，因此选择了一个计算成本较低的基准测试：

  • 使用了 OpenAI Gym 中实现的 7 个模拟机器人任务，这些任务基于 MuJoCo 物理引擎；
  • 每个任务训练一百万个时间步

• 除了裁剪参数 \( \epsilon \) 和KL惩罚参数 \( \beta, d_{\text{target} } \) 需要搜索外，其他超参数见表3（原文在附录中）

  

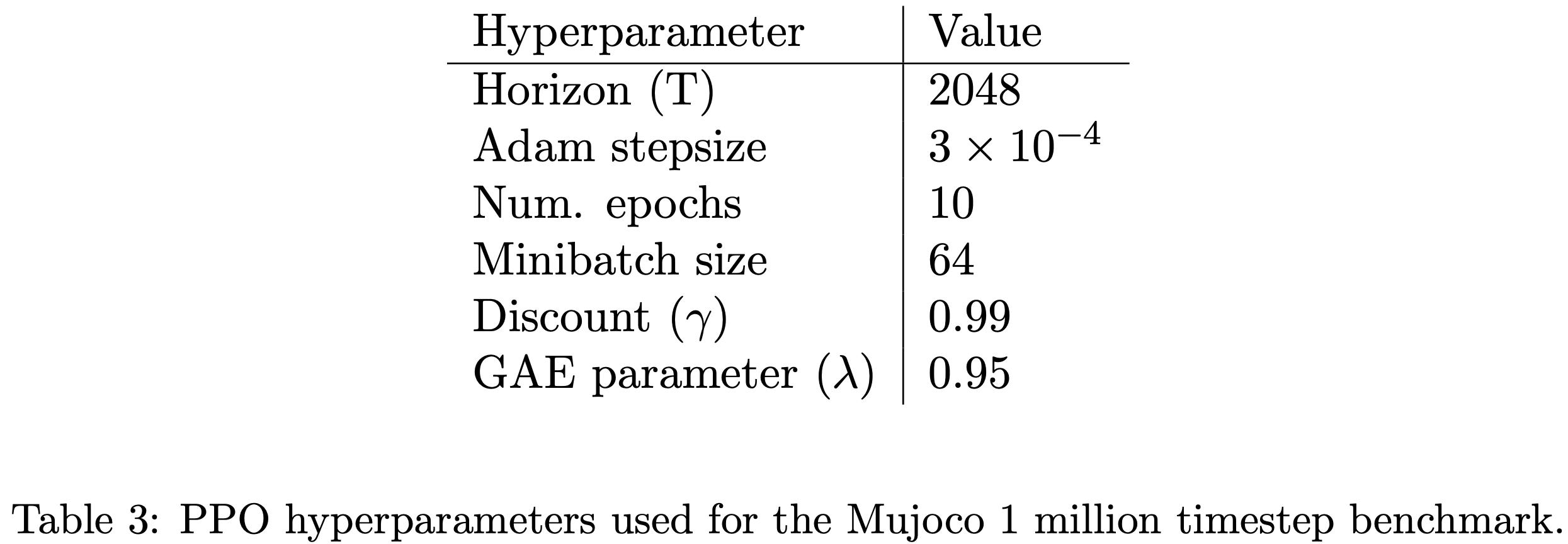
• 论文使用了一个具有两个隐藏层（每层64个单元）的全连接 MLP 来表示策略，输出高斯分布的均值，具有可变标准差

• 论文没有在策略和价值函数之间共享参数（因此系数 \( c_{1} \) 无关），也没有使用熵奖励

• 每个算法在 7 个环境中各运行 3 次随机种子，每次运行的得分通过计算最后 100 回合的平均总奖励来确定

• 论文对每个环境的得分进行了平移和缩放，使得随机策略得分为 0，最佳结果为 1，并在 21 次（\(7 \times 3\)）运行中取平均，为每个算法设置生成一个标量得分

• 结果如表1所示（注意，在没有裁剪或惩罚的设置中，得分为负，因为在某个环境（HalfCheetah）中得分非常低，甚至低于初始随机策略）

  

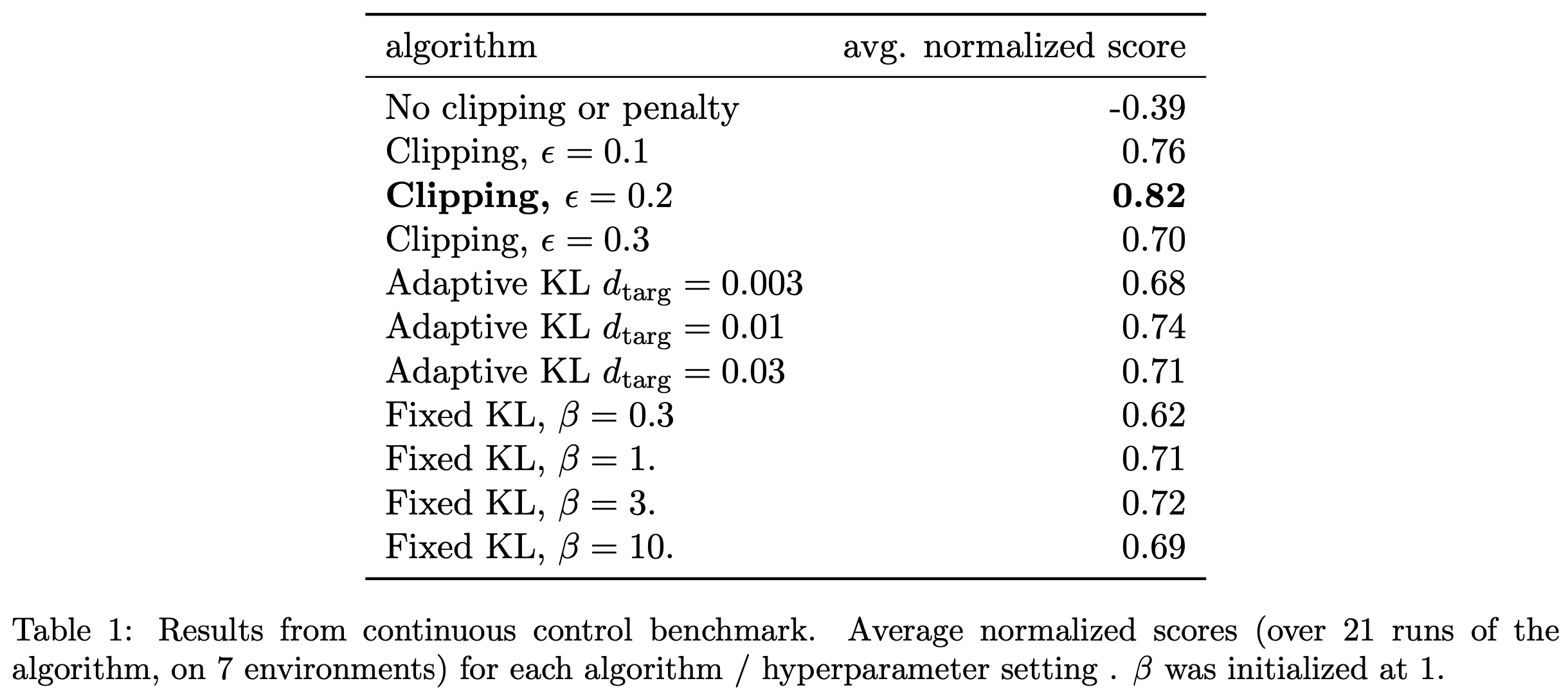
连续控制领域与其他算法的比较

• 论文将PPO（使用 第3节 的“clipped”代理目标）与文献中几种其他方法进行比较（这些方法在连续控制问题上表现良好）
• 论文比较了以下算法的调优实现：
  • 信任域策略优化（TRPO）
  • 交叉熵方法（CEM）
  • 自适应步长的普通 Policy Gradient
  • A2C：A2C代表 Advantage Actor Critic，是 A3C 的同步版本，论文发现其性能与异步版本相同或更好
  • 带信任域的 A2C
• 对于PPO，论文使用上一节的超参数， \( \epsilon=0.2 \)，结果如图3显示，PPO在几乎所有连续控制环境中都优于之前的方法

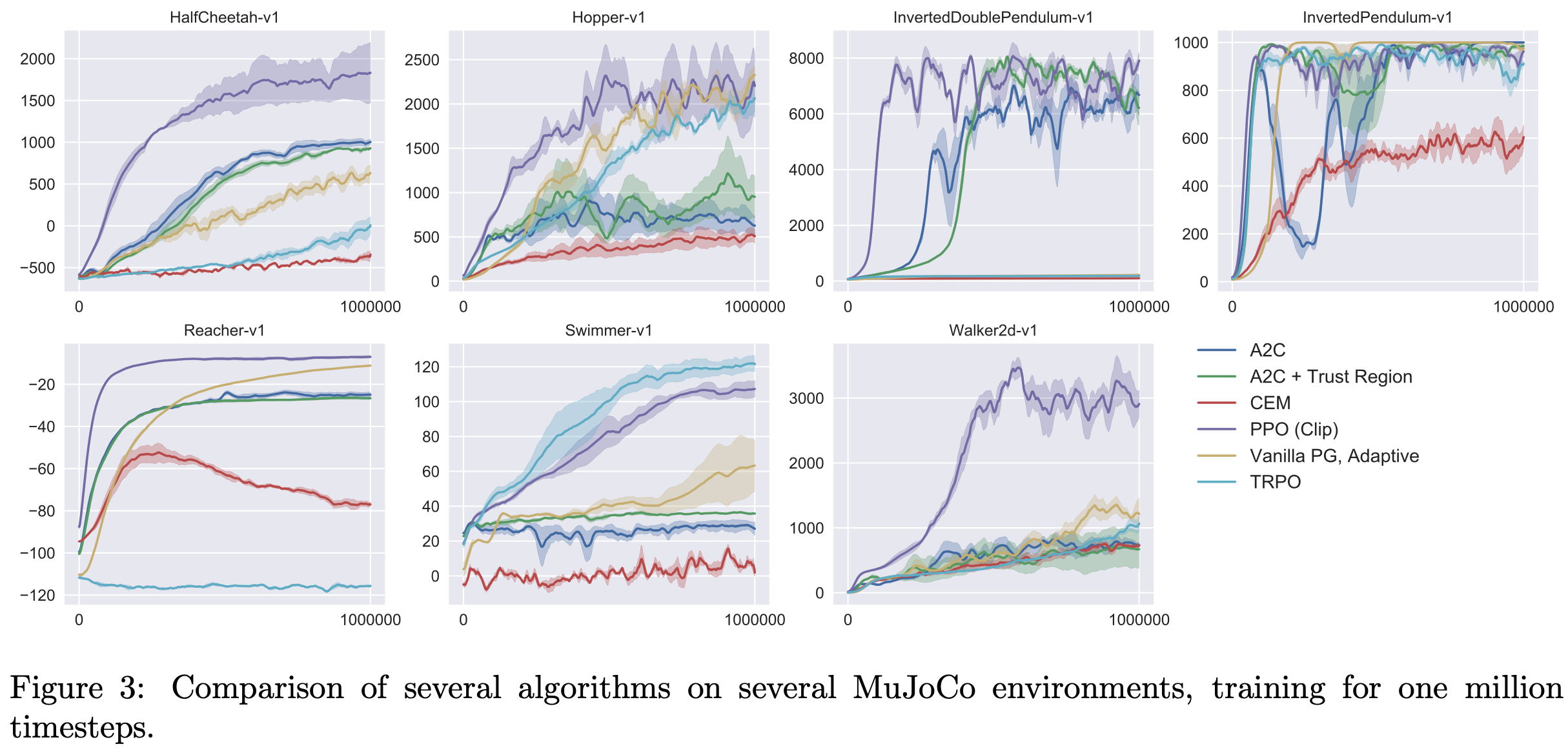
连续控制领域的展示：人形机器人跑步与转向（Humanoid Running and Steering）

• 为了展示 PPO 在高维连续控制问题上的性能，论文在涉及 3D 人形机器人的任务上进行训练，机器人需要跑步、转向，甚至在被方块击中时从地面爬起
• 论文测试的三个任务是：
  • (1) RoboschoolHumanoid：仅向前运动；
  • (2) RoboschoolHumanoidFlagrun：目标位置每200个时间步或达到目标时随机变化；
  • (3) RoboschoolHumanoidFlagrunHarder：机器人被方块击中并需要从地面爬起
• 图5展示了学习策略的静态帧
• 图4展示了三个任务的学习曲线
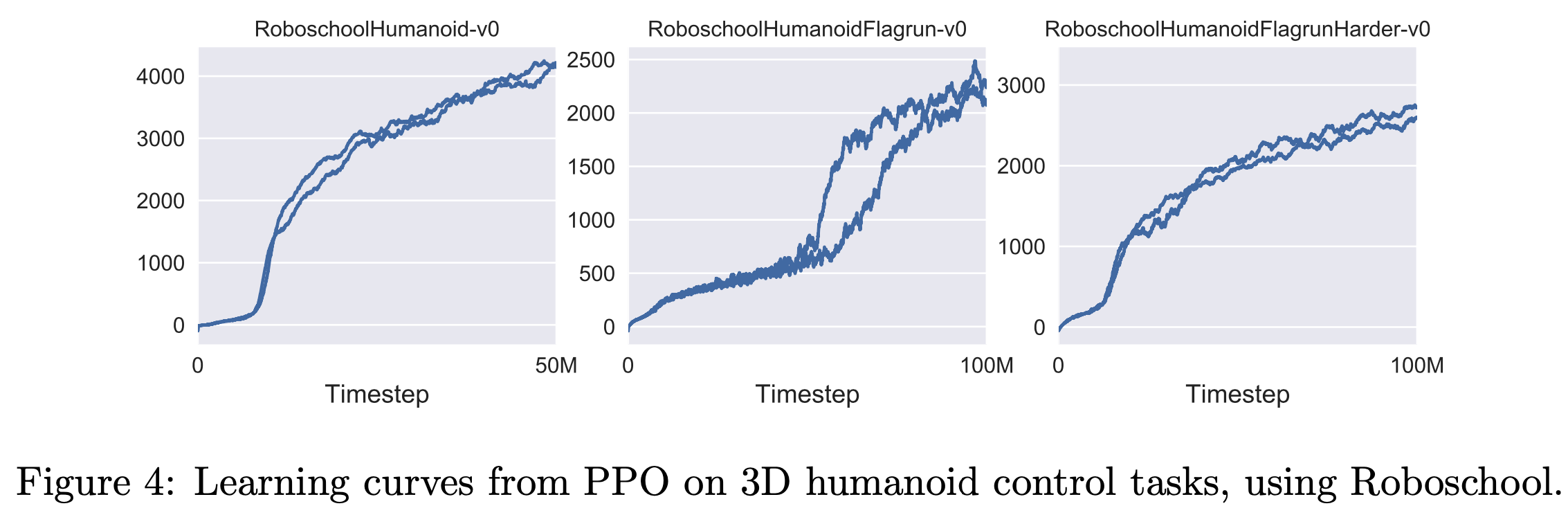
• 超参数见表4，在并行工作中，Heess等人[]使用PPO的自适应KL变体（第4节）学习了3D机器人的运动策略

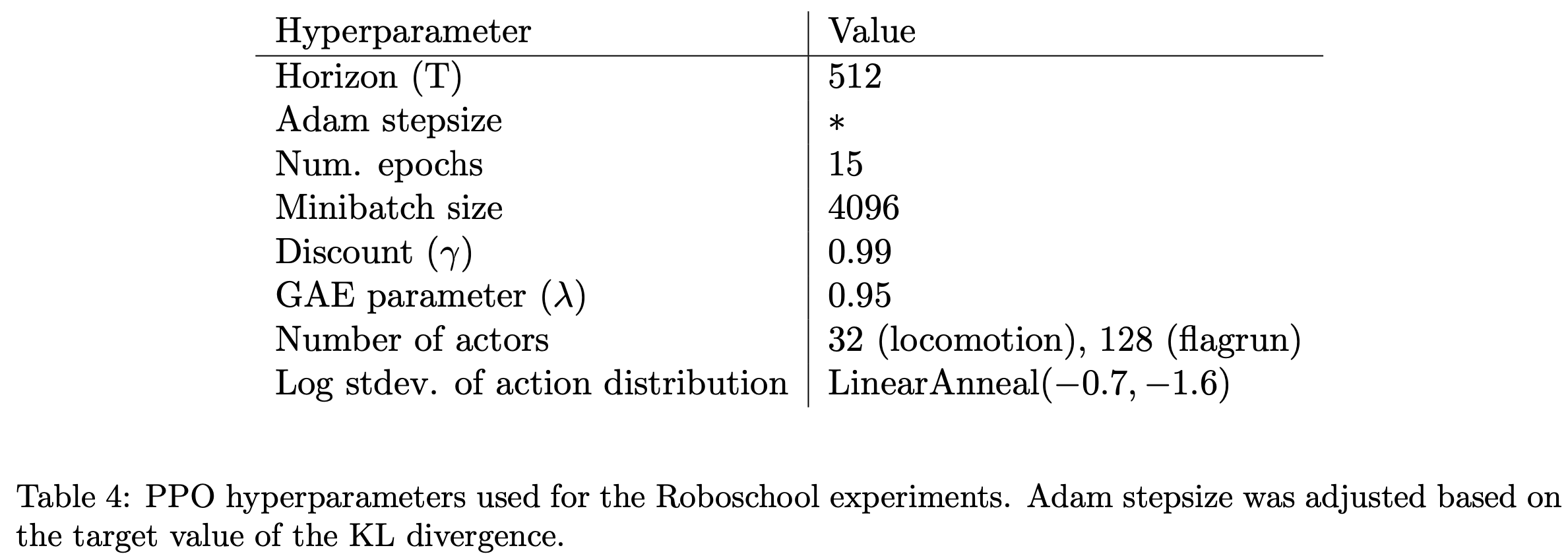
Atari领域与其他算法的比较

• 论文还在 Arcade Learning Environment 基准测试上运行了 PPO，并与调优良好的 A2C 和 ACER 实现进行了比较
• 对于所有三种算法，论文使用了与 Asynchronous methods for deep reinforcement learning 相同的策略网络架构
• PPO的超参数见表5，对于其他两种算法，论文使用了针对此基准测试优化的超参数
• 附录B提供了所有 49 款游戏的结果表和学习曲线
• 论文考虑以下两个评分指标：
  • (1) 整个训练期间每回合的平均奖励（偏向快速学习）；
  • (2) 训练最后100回合的平均奖励（偏向最终性能）
• 表2显示了每种算法“获胜”的游戏数量，其中评分指标是三次试验的平均值

---

附录B：更多Atari游戏上的性能表现

• 此处论文展示了 PPO 与 A2C 在 49 款 Atari 游戏上的对比结果
• 图6：PPO与A2C在OpenAI Gym中所有49款Atari游戏上的对比（截至发表时），图6显示了三种随机种子的学习曲线
• 表6：PPO与A2C在Atari游戏上的平均最终得分（最后100回合，40M游戏帧后），表6列出了平均性能