RL——POMDP

本文是对POMDP这个不常见的概念的一些简单介绍，主要内容参考自POMDP讲解

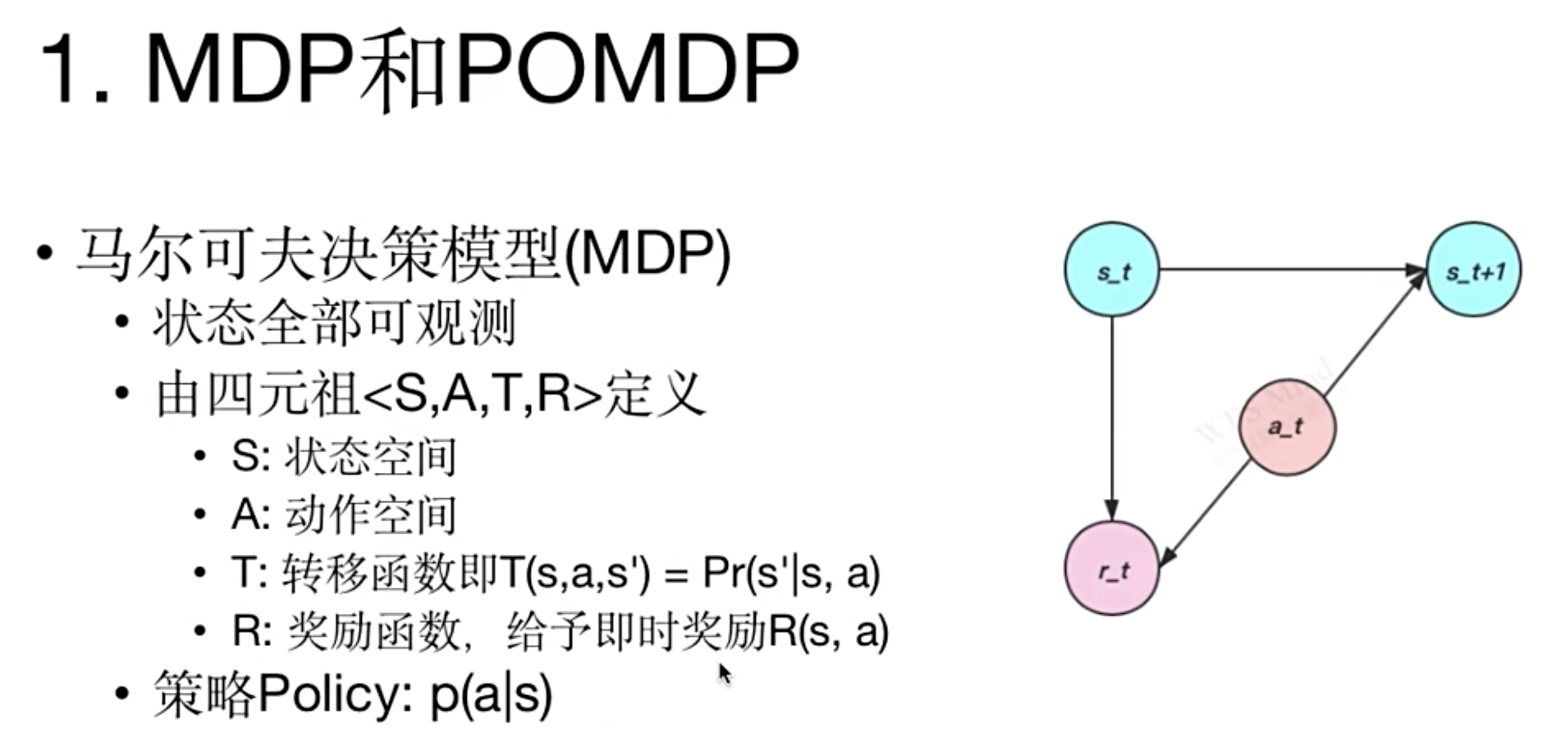
马尔可夫决策模型(MDP)
- 状态全部可观测
- 由四元祖 $\langle S, A, T, R\rangle$ 定义：
  - $S$：状态空间
  - $A$：动作空间
  - $T$：转移函数即 $T(s, a, s’) = Pr(s’|s, a)$
  - $R$：奖励函数，给予即时奖励 $R(s, a)$
- 策略Policy: $p(a|s)$
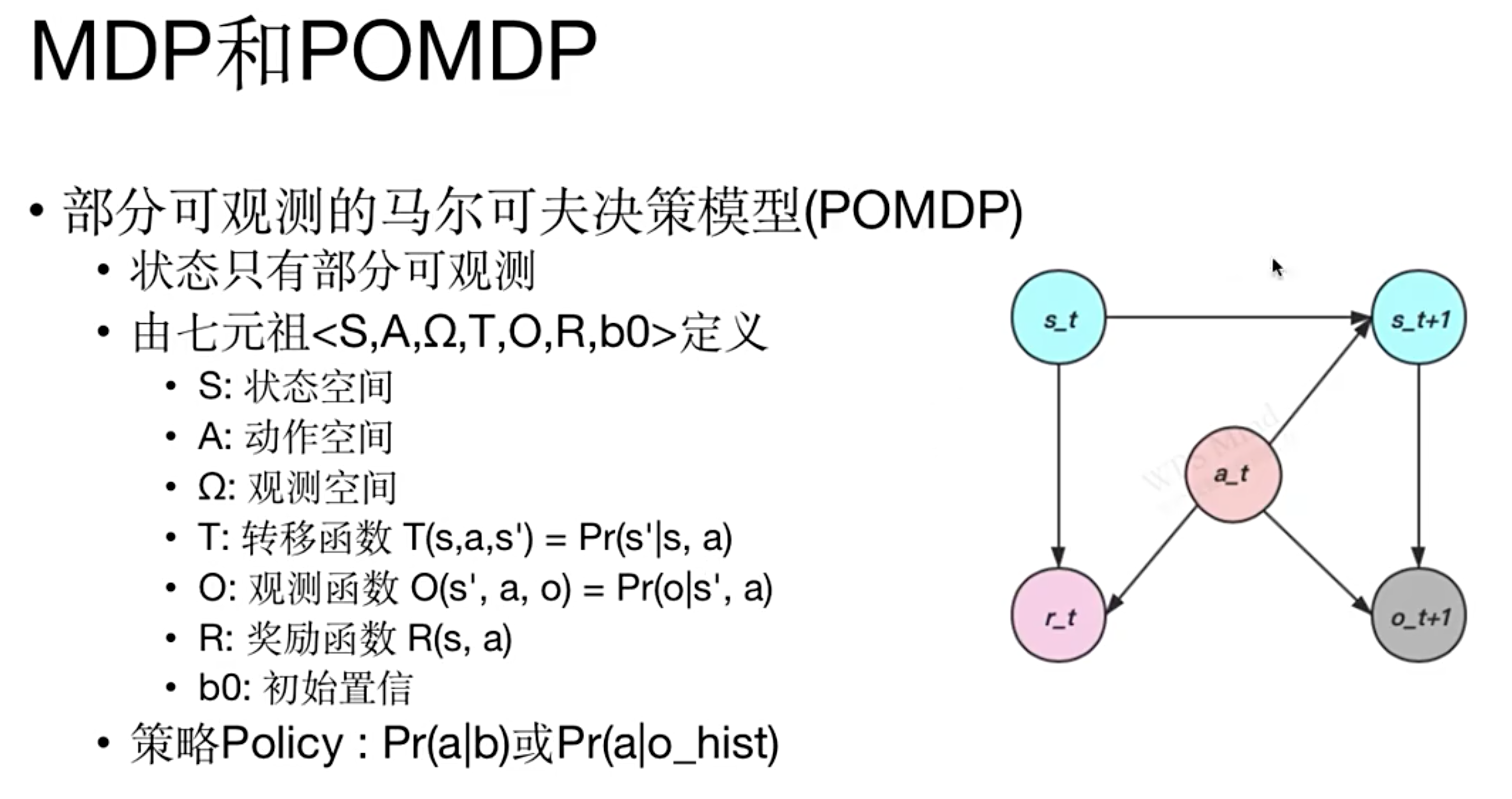
部分可观测的马尔可夫决策模型(POMDP)
- 状态只有部分可观测
- 由七元祖 $\langle S, A, \Omega, T, O, R, b0\rangle$ 定义：
  - $S$：状态空间
  - $A$：动作空间
  - $\Omega$：观测空间
  - $T$：转移函数 $T(s, a, s’) = Pr(s’|s, a)$
  - $O$：观测函数 $O(s’, a, o) = Pr(o|s’, a)$
  - $R$：奖励函数 $R(s, a)$
  - $b0$：初始置信
- 策略Policy: $Pr(a|b)$ 或 $Pr(a|o_{hist})$ ，其中 $o_{hist}$ 表示单帧或多帧的历史观测信息（因为观测 $o$ 是不分更新的，可能已经不满足马尔科夫性了）
POMDP 的观测本身是不完整的系统状态信息，可能已经不满足马尔科夫性了，此时可以通过信念状态（Belief State，写作 $b$）或历史观测序列（写作 $o_{hist}$）来表示当前状态，从而保证智能体看到的观测是尽量完整的

Belief 的定义 ：Belief是智能体对于当前环境的状态分布估计
使用 Belief 的原因 ：因为Belief是充分统计量，也就是说做决策时只需要当前的Belief而不需要其他信息，另外观测历史也是充分统计量。在构建充分统计量后，可以将Belief理解为和MDP里的状态等价的概念，只是Belief是连续的
使用方式 ：当前置信 $b$ 情况下，在执行动作 $a$ 和得到观测 $o$ 后，需要更新置信为 $b’$
Belief 更新公式 ：
$$
\begin{align}
b’(s’) &= P_r(s’|o, a, b) = \frac{P_r(s’, o, a, b)}{P_r(o, a, b)}\\
&= \frac{P_r(o|s’, a, b)P_r(s’|a, b)}{P_r(o|a, b)}\\
&= \frac{P_r(o|s’, a)\sum_s P_r(s’|a, b, s)P_r(s|a, b)}{P_r(o|a, b)}\\
&= \frac{O(s’, a, o)\sum_s T(s, a, s’)b(s)}{P_r(o|a, b)}
\end{align}
$$

在 MDP 里 ：在给定策略 $\pi$ 情况下
- 状态价值函数： $V_{\pi}(s) = \sum_{a\in A}\pi(a|s)Q(s, a)$
- 动作价值函数： $Q_{\pi}(s, a) = R(s, a) + \sum_{a\in A}T(s’, a, s)V_{\pi}(s’)$
- 最优价值函数： $V_{n}^{*}(s) = \max_{a}[R(s, a) + \gamma\sum_{a\in A}T(s’, a, s)V_{n - 1}^{*}(s’)]$
在 POMDP 里 ：在给定策略 $\pi$ 情况下
- 最优价值函数：
  $$
  V_{n}^{*}(b) = \max_{a\in A}[\rho(b, a) + \gamma\sum_{o\in\Omega}Pr(o|b, a)V_{n - 1}^{*}(b’)]
  $$
- 其中 $\rho(b, a)$ 是期望奖励即 $\sum_{s}b(s)R(s, a)$
- $Pr(o|b, a)$ 是在当前置信为 $b$ ，动作为 $a$ 情况下，获得观测 $o$ 的概率，且 $Pr(o|b, a) = \sum_{s’}O(s’, a, o)\sum_{s}T(s, a, s’)b(s)$

RL的设定是对于环境模型未知，常用的RL环境甚至并没有对应模型，并不一定是严格的MDP或POMDP
在假设环境模型是POMDP的强化学习情况下：
- 智能体的观测是 $o$ ，可知观测空间 $\Omega$
- 智能体的动作是 $a$ ，可知动作空间 $A$
- 状态空间 $S$ 对于智能体不可知
- 转移函数 $T$ 对于智能体不可知
- 观测函数 $O$ 对于智能体不可知
- 无法初始置信，因为 $S$ 不可知
- 智能体要学的策略是 $p(a|o)$ 或 $p(a|h)$ ， $p(a|h)$ 是因为智能体可以选择多种方法压缩多帧 $o$ 为一隐含信息 $h$ 。
传统的RL算法本身并不假设知道状态转移矩阵等，所以其实常见的RL算法可以直接用于求解POMDP，只是如果观测到的信息太少，RL不一定能保证收敛（观测不是环境的完整描述，可能不满足马尔可夫性，基于贝尔曼方程迭代的价值函数可能难以收敛）
比如策略梯度法推导过程中始终考虑的是期望收益，并不要求完整观测到环境，所以策略梯度法理论上适用于解决POMDP问题，但是观测不是环境的完整描述，可能不满足马尔可夫性，使用策略梯度法时最好使用REINFORCE方法，不使用Critic网络