RL——MCTS

整体说明

  • 蒙特卡洛树搜索（Monte Carlo Tree Search, MCTS）是一种基于随机模拟的强化学习决策方法 ，尤其在复杂决策问题（如围棋、游戏等）中表现出色。它通过智能地平衡探索（Exploration）和利用（Exploitation） ，逐步构建搜索树并优化策略
  • MCTS决策方法常用于围棋（AlphaGo）、即时战略游戏、扑克等场景中，目前在LLM领域也有所应用
  • 优势 ：适用于高维、稀疏奖励问题；无需预先知识，仅依赖模拟；可并行化，扩展性强
  • 局限 ：初期模拟可能低效（依赖随机探索）；需大量模拟才能收敛

MCTS 的核心思想

  • MCTS通过反复模拟（Simulation）从当前状态出发的可能路径，逐步构建一棵非对称的搜索树
  • MCTS树的节点代表游戏状态 ，边代表动作
  • MCTS的核心优势在于：
    • 无需完整模型 ：仅需模拟环境（如游戏规则）即可
    • 适应大规模状态空间 ：通过选择性扩展树，避免穷举
    • 异步更新 ：模拟结果反向传播，动态优化策略

MCTS 每次迭代的四个阶段

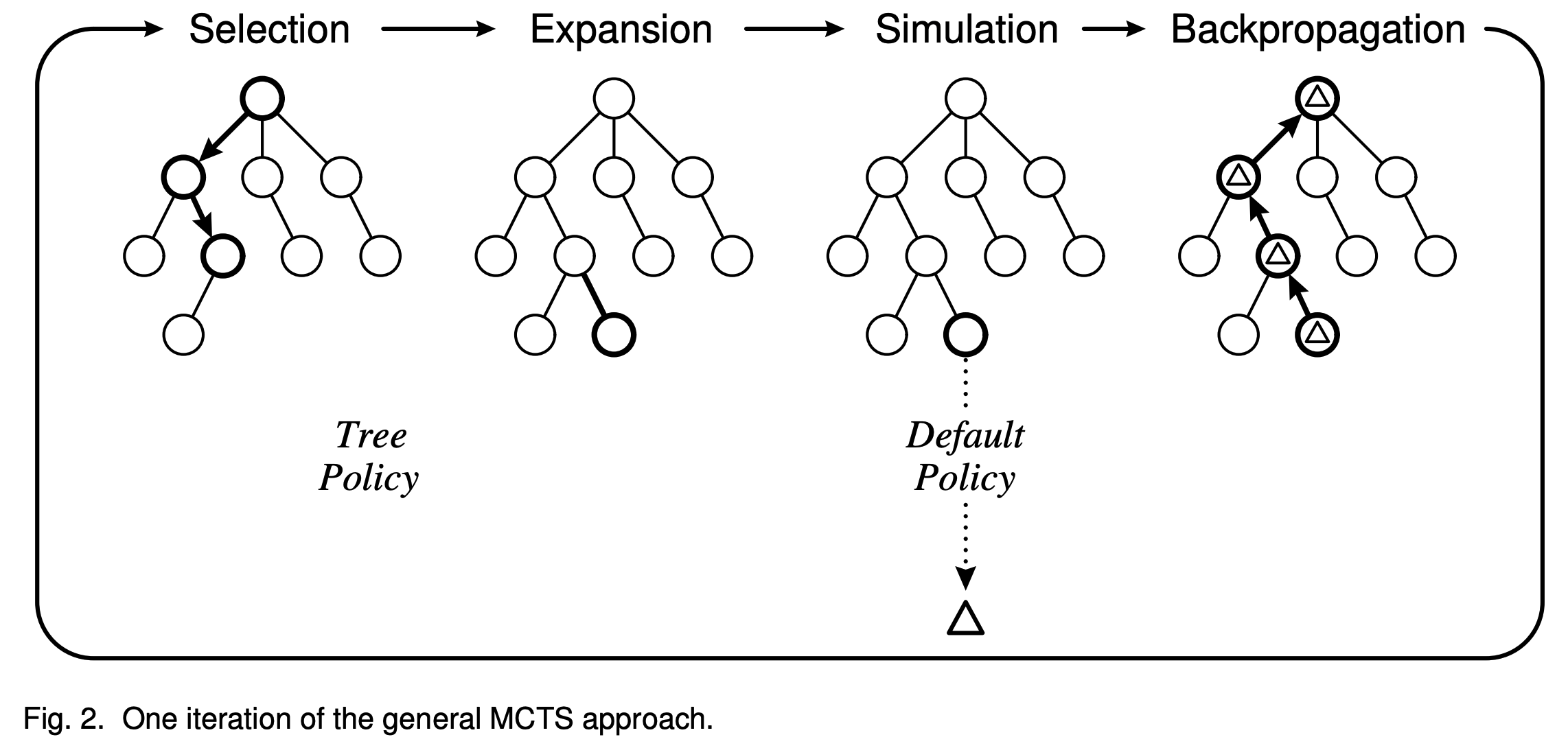
第一步：选择（Selection）

  • 目标 ：从根节点（当前状态）出发，递归选择子节点，直到到达一个可扩展的状态节点（即存在未尝试的动作的状态节点），返回这个被选择的节点
  • 策略 ：使用树策略（如UCT算法或PUCT算法）平衡探索与利用
  • UCT（Upper Confidence Bound applied to Trees）算法 ：
    $$
    \textit{UCT}(s, a) = Q(s, a) + c \sqrt{\frac{\ln N(s)}{N(s, a)} }
    $$
    • \(Q(s, a)\)：动作\(a\)的平均回报
    • \(N(s)\)：状态\(s\)的访问次数，\(N(s, a)\)：动作\(a\)的访问次数（注：如果分母不会为0，此时所有节点都是完整探索过的，不存在为0的情况）
    • \(c\)：探索系数（通常设为\(\sqrt{2}\)），当\(c=\sqrt{2}\)时，UCT的累计遗憾（Regret）有对数上界
    • 探索时选择动作为： \(a^* = \arg\max_a \textit{UCT}(s, a)\)
  • PUCT（Predictor UCT）算法 ：
    $$
    \textit{PUCT}(s, a) = Q(s, a) + c_\textit{puct}\cdot P(s,a)\cdot \frac{\sqrt{N(s)}}{1+N(s, a)}
    $$
    • \(P(s,a)\)：即 \(\pi(a|s)\)，是先验策略网络（Policy Network）给出的先验概率（表示动作 \(a\) 的初始偏好）
    • \(c_\text{puct}\)：探索系数（控制先验权重，AlphaZero中常设为1~2）
    • \(1+N(s,a)\)：（不用为了避免除0操作而增加1吧，毕竟此时所有节点都是完整探索过的，不存在为0的情况）
    • 探索时选择动作为：探索时选择 \(a^* = \arg\max_a \textit{PUCT}(s, a)\)
    • 基本思想：采样次数 \(N(s, a)\) 少时，按照策略 \(\pi(a|s)\) 为主探索；采样次数 \(N(s, a)\) 多时，按照价值 \(Q(s, a)\) 为主探索
    • PUCT被使用到了AlphaZero和MuZero中
      • 注：MuZero是由DeepMind开发的一种通用强化学习模型，它能够在不知道环境规则的情况下，通过自我学习和规划，掌握多种复杂游戏和任务，MuZero采用模型预测控制（Model-Based RL） ，并结合了MCTS

第二步：扩展（Expansion）

  • 前提条件 ：第一步完成后，我们选择到了一个未完全展开的节点（即存在未尝试的动作的节点）时，扩展该节点
  • 节点扩展 ：添加一个新子节点（随机执行一个未尝试的动作，将环境反馈的新状态作为新子节点）

第三步：模拟（Simulation）

  • 在一些资料中，这一步也称为评估，相当与对一个动作的价值评估
  • 模拟 ：从新节点开始，按照随机策略（或其他基于简单策略）Rollout 模拟至终止状态（如游戏结束），最终获得本次模拟的奖励（如胜利/失败）

第四步：回溯（Backpropagation）

  • 回溯 ：将模拟结果（奖励）反向传播到路径上的所有节点
    • 更新访问次数 \(N(s)\) 和 \(N(s, a)\)
    • 更新动作价值 \(Q(s, a)\)（如累加奖励的平均值）

MCTS的终止与决策

  • 终止条件 ：达到预设时间、计算资源或迭代次数
  • 最终决策 ：选择根节点下访问次数最多或价值最高的动作（如AlphaGo选择访问次数最多的动作）
    • 问题：为什么是访问次数最多而不是价值最高的动作作为决策？

一些理解与讨论

  • 棋局中，对手策略如何模拟？
    • AlphaGo中，使用策略网络 \(\pi(a|s)\) 来模拟对手策略
  • 为什么MCTS第三步中使用随机策略模拟采样？
    • 传统的MCTS确实是按照随机采样的，但从直观上看，使用当前策略来模拟采样决策是否才是符合预期的；
    • AlphaGo的做法：
      • 实际上是使用策略网络来模拟决策的
      • 为了加快速度，AlphaGo还训练了一个较小的策略网络专门用来在MCTS的第三步中模拟决策
      • 为了提升稳定性，AlphaGo的价值评估结合了价值网络的输出和MCTS模拟奖励结果 \(V(s_{t+1}) = \frac{1}{2}(reward + V_\theta(s_{t+1}))\)
    • 在LLM等场景中，随机采样是毫无意义的，也需要基于LLM来采样决策
  • 为什么AlphaGo决策时选择访问最多的动作而不是价值最高的动作？
    • 理解：实际上访问最多的动作往往也是价值最高的动作，即使不是价值最高的，也不会太差，且价值最高的动作可能是因为波动带来的，访问最多的动作更置信
    • 节点被访问的次数越多，说明MCTS对其进行了更充分的探索，其Q值的置信度越高。选择高访问次数的动作，相当于选择被反复验证过的最优策略，避免因偶然性导致的风险

附录：MCTS在围棋中的流程

  • 第一步-选择 ：从当前棋盘状态出发，递归选择UCT值最高的落子点
  • 第二步-扩展 ：当遇到一个未尝试的合法落子时，扩展新节点
  • 第三步-模拟 ：随机落子至终局，判断胜负
  • 第四步-回溯 ：若胜利，路径上所有节点的胜利次数+1
  • 决策 ：经过数万次迭代后，选择根节点下胜率最高的落子