RL——Decision-Diffuser

Decision-Diffuser

核心贡献点总结（对比 Diffuser）

  • 序列组织方式 ：
    • Diffuser的序列包含了状态和动作
    • Decision Diffuser的序列仅包含状态，不包含动作 ，这样做的原因是强化学习的状态往往是连续且平滑的，动作则往往是离散或结构化的，此外一些动作可能变化很高，很不平滑，Diffusion模型难以建模
  • Guidance 方法 ：
    • Diffuser使用Classifier Guidance的方法
    • Decision Diffuser采用Classifier-free Guidance的方法
  • 决策过程中的历史轨迹窗口 ：
    • Diffuser使用历史长度为1的滑动窗口 ，在每个Diffusion采样时间步，每次仅保留单个历史状态 \(s_0\)
    • Decision Diffuser使用历史长度为C的滑动窗口 ，在每个Diffusion采样时间步，Decision Diffuser将最近C个历史状态（实验中设置为C=20，planning horizon则根据不同的任务设置不同的值），直接赋值给当前的轨迹的前半部分，类似图片补全功能，保证生成后续的轨迹与当前轨迹一致
  • 决策方式 ：
    • Diffuser直接按照轨迹生成的动作决策
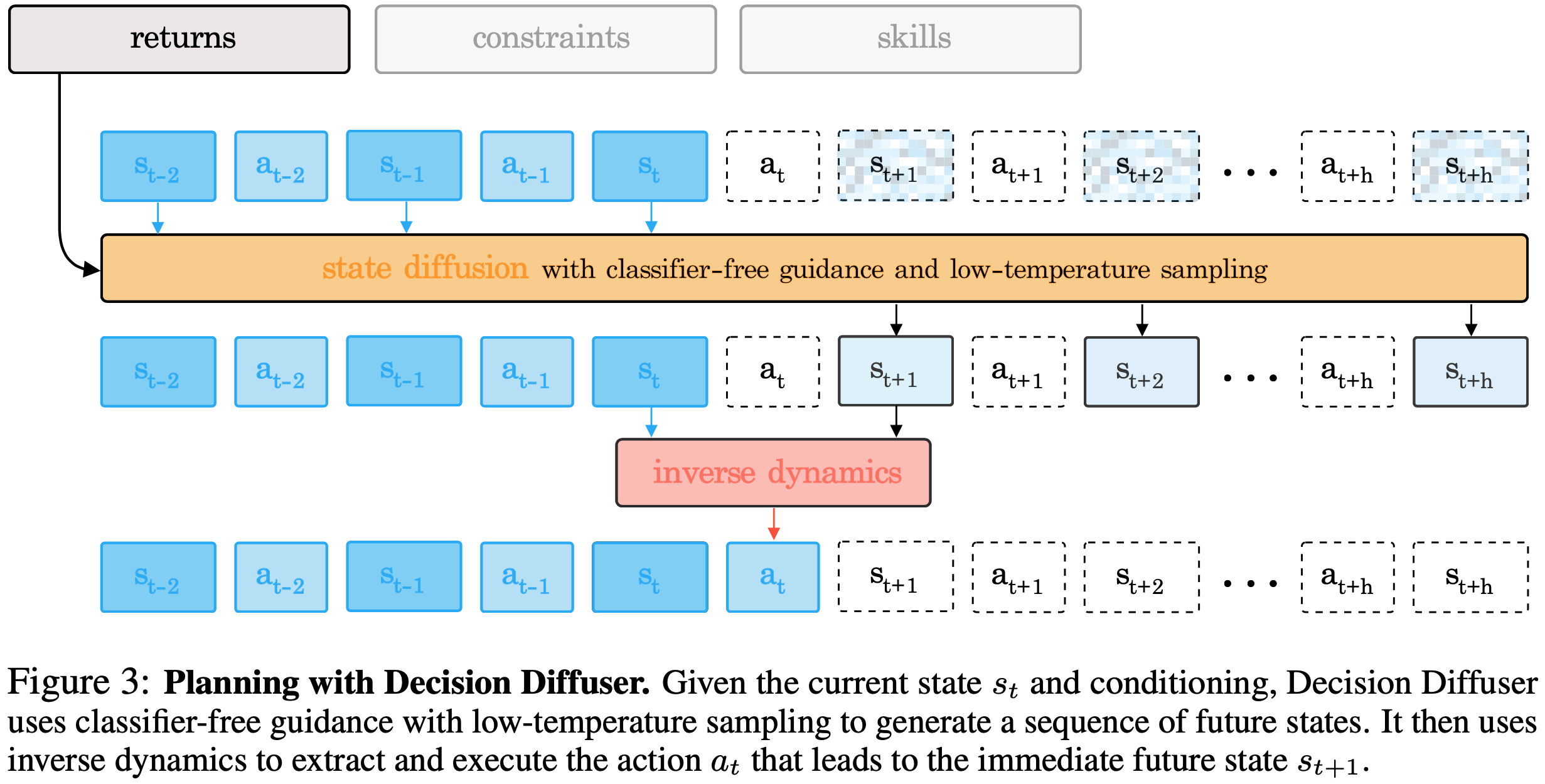
    • Decision Diffuser在轨迹中不直接生成动作，而是在生成轨迹中提取出 \(s_t,s_{t+1}\) 后，使用一个专门训练的策略网络 \(a_t:= f_\phi(s_t,s_{t+1})\) 来决策动作，网络也称为逆向动力学模型（Acting with Inverse-Dynamics），实际上，在其他文章，还可以是使用更多的状态来生成动作，比如AIGB中使用 \(a_t:= f_\phi(s_{t-L:t},s_{t+1})\)
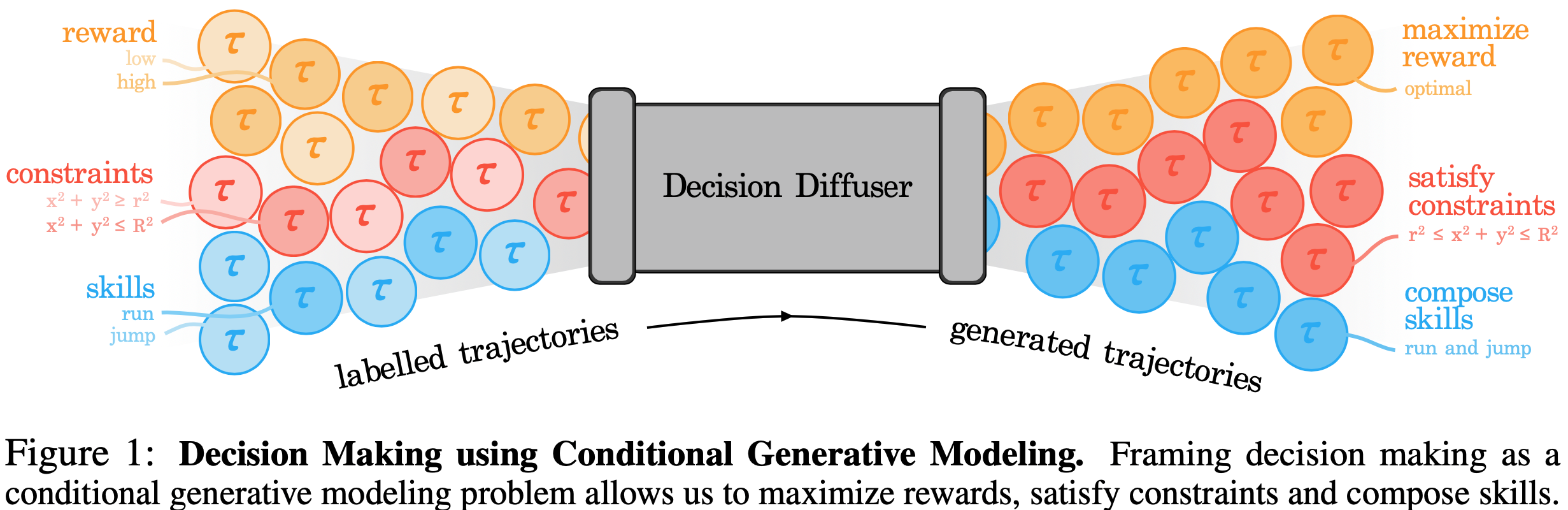
  • 支持不同条件类型：最大化收益、约束满足和组合技能 ：
    • 最大化回报（Maximizing Returns） ：\(\epsilon_\theta(\boldsymbol{x}_k(\tau), \boldsymbol{y}(\tau), k) := \epsilon_\theta(\boldsymbol{x}_k(\tau), R(\tau), k)\)，其中 \(R(\tau) \in [0,1]\) 是经过归一化的奖励函数
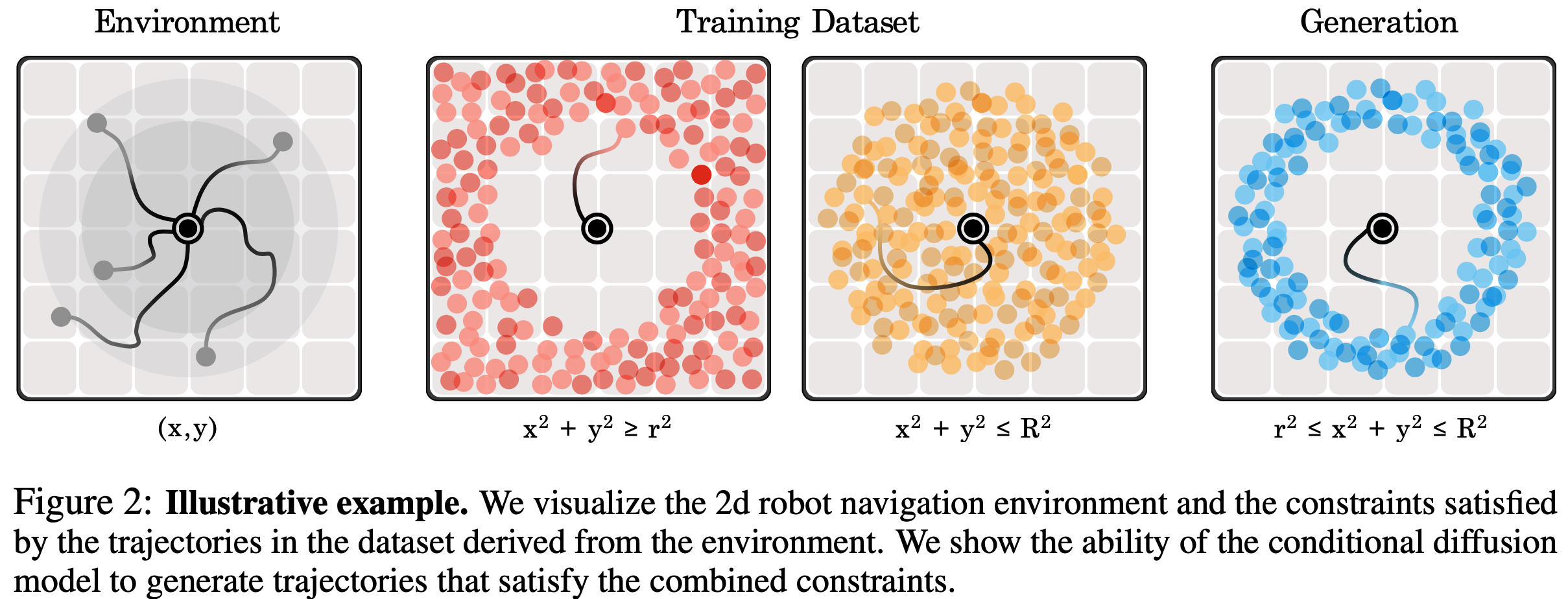
    • 约束满足（Satisfying Constraints） ：Decision Diffuser条件满足的方式引入约束到网络输入端，具体来说，对于约束 \(\mathcal{C}_i\)：\(\epsilon_\theta(\boldsymbol{x}_k(\tau), \boldsymbol{y}(\tau), k) := \epsilon_\theta(\boldsymbol{x}_k(\tau), \mathbb{I}(\tau \in \mathcal{C}_i), k)\)，如果包含多个约束，可以使用one-hot向量来训练，满足约束的维度取1，其他维度取0来训练，虽然训练时只见过单约束，但是在采样时可以体现出多约束（one-hot向量变成多维度为1的向量）
    • 组合技能（Skill Composition） ：在生成轨迹时，Decision Diffuser可以通过不同Diffusion误差函数相加实现组合技能的采样形式，具体地，对于单一技能定义为：\(\epsilon_\theta(\boldsymbol{x}_k(\tau), \boldsymbol{y}(\tau), k) := \epsilon_\theta(\boldsymbol{x}_k(\tau), \mathbb{I}(\tau \in \mathcal{B}_i), k)\)，采样时，多技能组合定义为：
      $$\hat{\epsilon} := \epsilon_\theta(\boldsymbol{x}_k(\tau),\varnothing, k) + \omega \sum_{i=1}^n (\epsilon_\theta(\boldsymbol{x}_k(\tau),\boldsymbol{y}^i(\tau), k) - \epsilon_\theta(\boldsymbol{x}_k(\tau), \varnothing, k))$$
      • 详细推导见附录：多条件组合的证明
    • 其他说明：Decision Diffuser支持约束的“与”运算和“非”运算（做减法），但是不支持或运算（Decision Diffuser 没有为每个条件变量提供显式的密度估计，因此它不能原生支持“或”运算组合）
  • 其他：
    • 低温采样 (Low-temperature Sampling)：在常规的扩散模型采样方式中加入一个低温因子 \(\alpha\)，即 \(\tau^{i-1} \sim \mathcal{N}(\tau^{i-1}|\mu_\theta(\tau^i, i), \color{red}{\alpha}\Sigma^i)\)

Decision Diffuser 具体实现

建模方式

  • 整体思路概览：
  • 序列组织方式如下：
  • 约束同时达成情况示意图：

训练过程

  • 训练过程
    $$ \mathcal{L}(\theta, \phi) := \mathbb{E}_{k, \tau\in\mathcal{D}, \beta\sim\text{Bern}(p)}[||\epsilon - \epsilon_{\theta}(\boldsymbol{x}_{k}(\tau), (1-\beta)\boldsymbol{y}(\tau) + \beta\varnothing, k)||^{2}] + \mathbb{E}_{(s, a, s’) \in \mathcal{D}}[||a-f_{\phi}(s, s’)||^2] $$
  • 两个网络相对独立，实际上写成两个损失函数分别训练也可以的

采样过程

  • Decision Diffuser算法伪代码如下：
  • 其中 \(\hat{\epsilon}\) 的定义与论文Classifier-Free Diffusion Guidance中的方法不同，但事实上通过调整Guidance scale的取值范围，可以得到两者表达式是等价的，详细讨论见附录：关于Guidance scale的讨论

Experiments

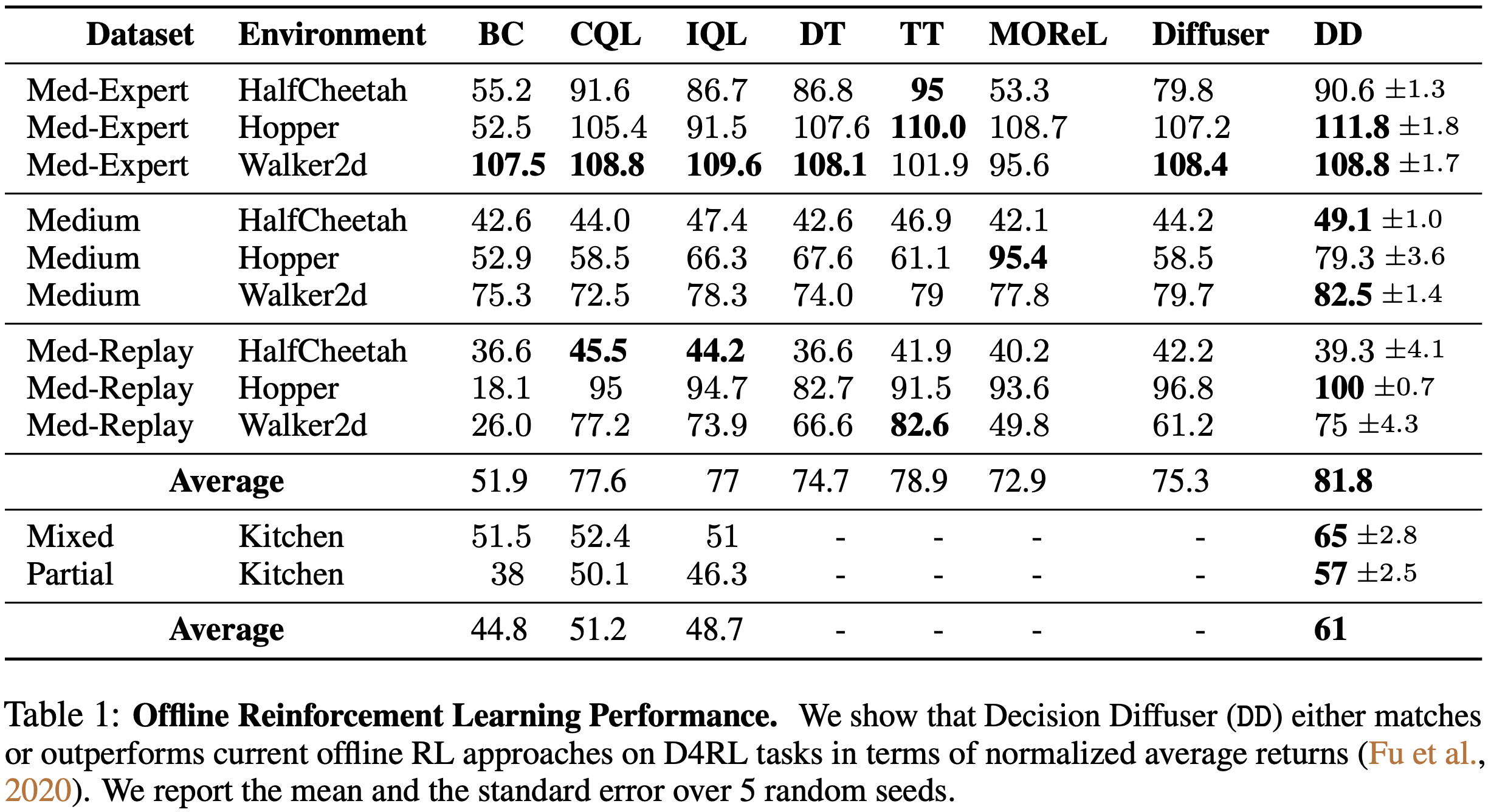
最大化回报(与强化学习方法对照)

  • 实验结论:

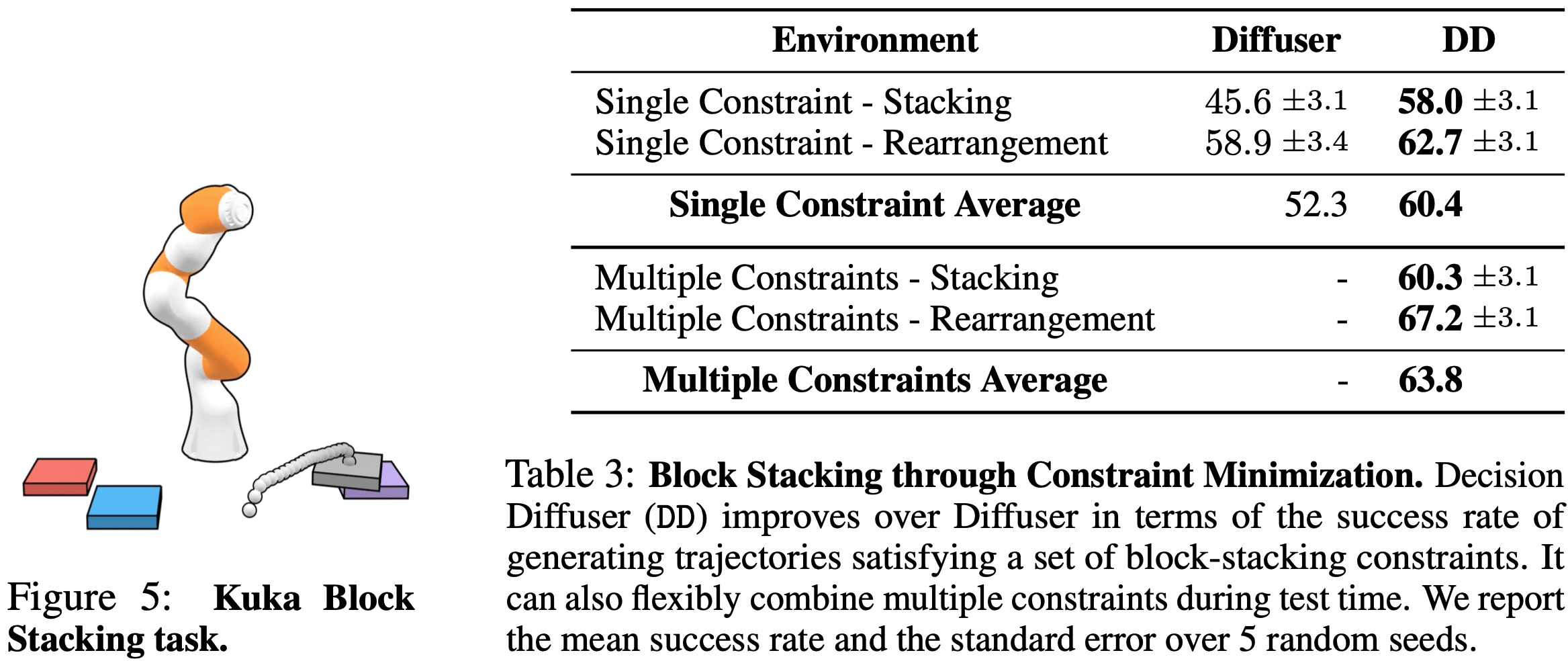
约束达成实验

  • 实验设置
    • 背景：在环境中采样轨迹数据，每个轨迹满足一个约束
    • 测试目标：
      • Single Constraint：满足任意单一约束（数据集中存在的）
      • Multiple Constraints：同时满足一些约束组合（这些组合是训练数据中没有的）
  • 实验结论

组合技能

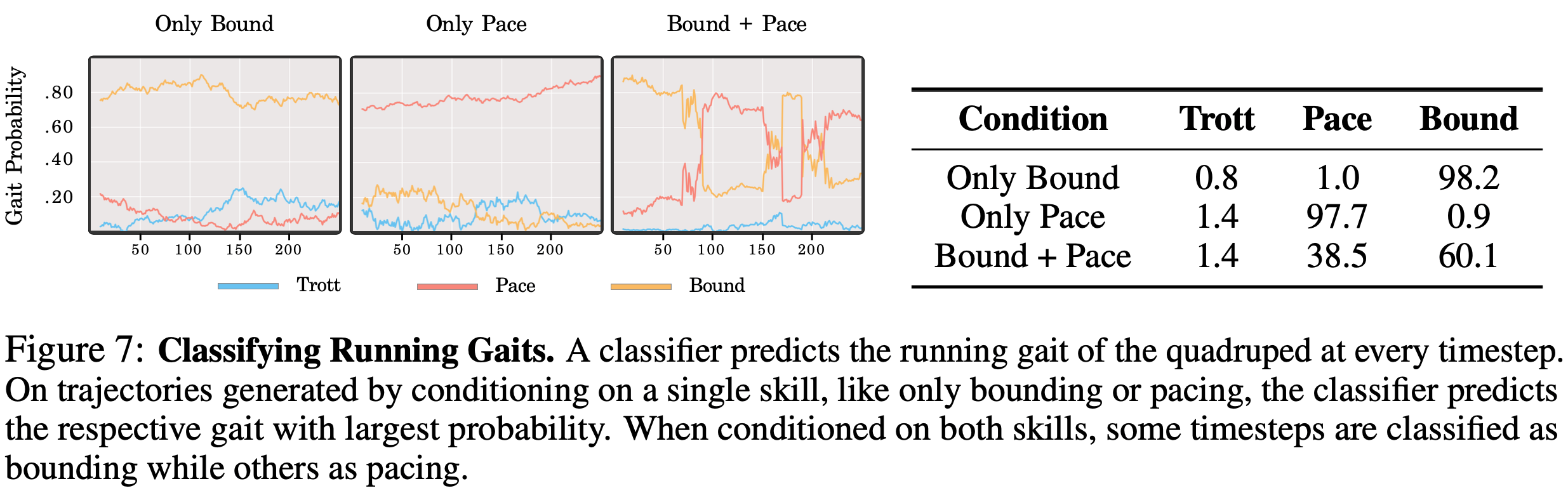
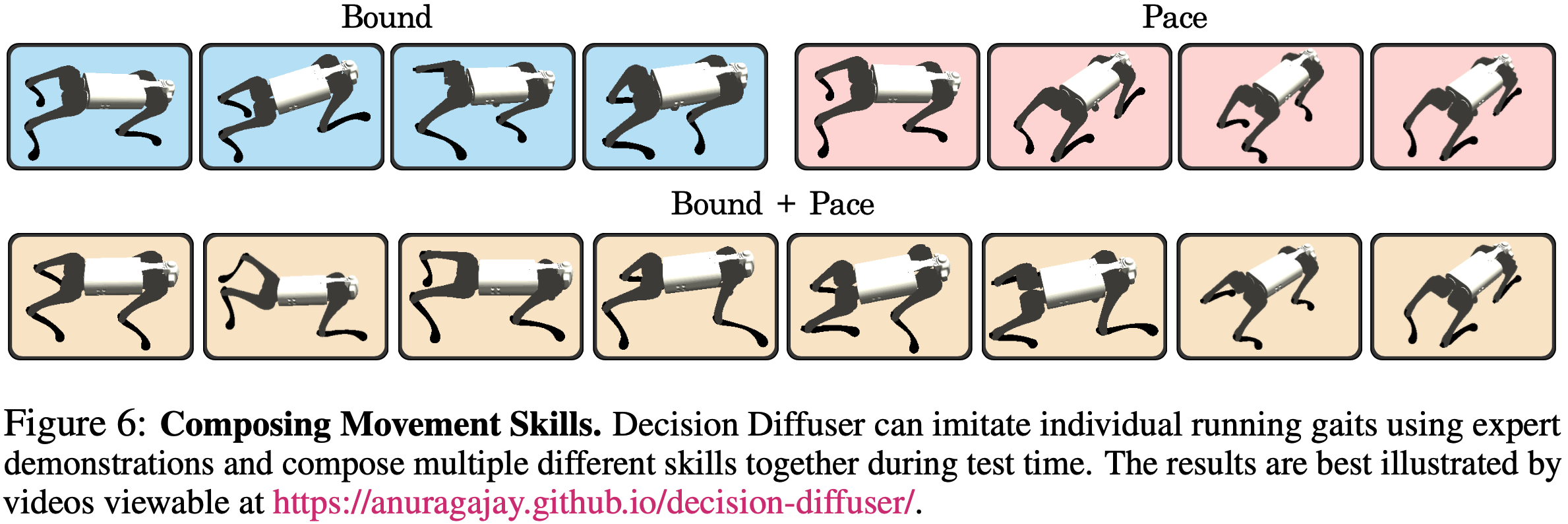
  • 实验设置
    • 在数据集中收集包含单一技能的轨迹，然后让机器人学习各种步态，如跳跃 (bounding) 、踱步 (pacing) 和小跑 (trotting)
    • 采样时，要求机器人能按照组合步态执行运动
  • 实验结果

消融实验

  • 实验设置：

    • CondDiffuser ：与 Diffuser 完全一致（轨迹同时纳入了状态和动作），但是没有使用 classifier guidance 而是 classifier-free guidance，输出动作不通过逆向动力学模型，而是由扩散模型去噪得到

      we also compare with the baseline CondDiffuser, which diffuses over both state and action sequences as in Diffuser without classifier-guidance

    • CondMLPDiffuser ：根据state和target return来去噪生成动作（TODO问题：这个实验设置是想验证什么？target return是如何生成的？）

      We also compare against CondMLPDiffuser, a policy where the current action is denoised according to a diffusion process conditioned on both the state and return

  • 实验结论

  • 补充实验（回答为什么不直接通过Diffusion生成动作，而是在已知状态 \((s,s’)\) 的情况预测动作）

    • 实验结果：
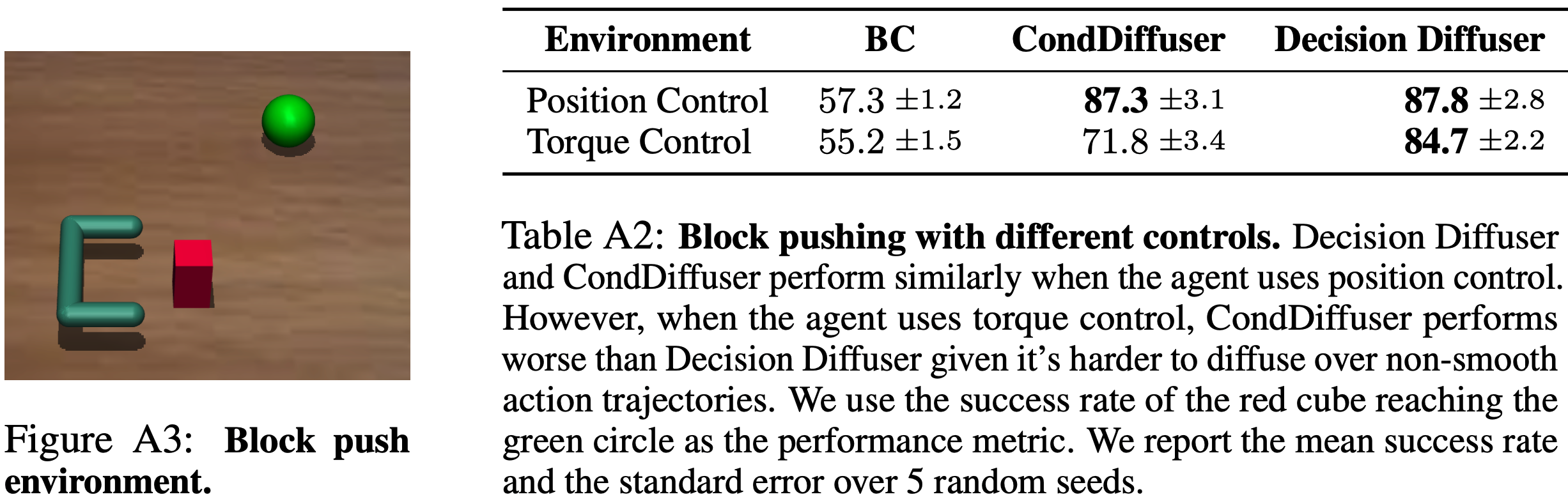
    • 在位姿控制(position control)模式下，CondDiffuser 和 Decision Diffuser 的性能差不多；
    • 在扭矩控制(torque control)模式下，Decision Diffuser 表现明显优于 CondDiffuser
    • 总结来说：较为平滑的动作可以直接使用Diffusion生成，但是对于不平滑的动作，建议使用逆向动力学模型来建模动作

超参数设置

附录：关于Guidance scale的讨论

  • Decision Diffuser使用的是Classifier-free Guidance方法，但是 \(\bar{\epsilon}_\theta(x_t, y, t)\) 的计算与原始论文Classifier-Free Diffusion Guidance, Google Research, Brain team, 2022对不齐
    • 一个说明：AIGB论文写的使用的w=0.2，但代码使用的1.2，Decision-Diffusion论文写的guidance scale s=1.2，代码使用的w=1.2
  • 在论文Classifier-Free Diffusion Guidance中，下面的 \(w\) 我们称为 \(w_\text{cdf}\)：
    $$
    \begin{aligned}
    \bar{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t, y)
    &= \color{red}{\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y)} + \color{red}{w} \big(\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y) - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \big) \\
    &= (w+1) \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y) - w \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)
    \end{aligned}
    $$
  • 在Decision Diffuser中，下面的 \(w\) 我们称为 \(w_\text{dd}\)，实际上，论文GLIDE也使用的这种表达：
    $$\hat{\epsilon} = \color{red}{\epsilon_\theta(\boldsymbol{x}_k(\tau), k)} + \color{red}{w}(\epsilon_\theta(\boldsymbol{x}_k(\tau),\boldsymbol{y}, k) - \epsilon_\theta(\boldsymbol{x}_k(\tau), k))$$
  • 两者的表达式不同，但是本质上，通过调整他们的 guidance scale \(w\) 可以得到相同结论，具体地，可以证明，当 \(w_\text{cfd} = w_\text{dd} - 1\) 时，两者等价
    $$
    \begin{aligned}
    \epsilon(y) + w_\text{cdf}(\epsilon(y)-\epsilon) &= \epsilon(y) + (w_\text{dd} - 1)(\epsilon(y)-\epsilon) \\
    &= \epsilon(y) + w_\text{dd} \epsilon(y) - \epsilon(y) - w_\text{dd} \epsilon + \epsilon \\
    &= \epsilon + w_1(\epsilon(y)-\epsilon)
    \end{aligned}
    $$
  • 实际应用时，Classifier-Free Diffusion Guidance中 \(w_\text{cdf} > 0\) 即可，而Decision Diffuser 和论文GLIDE中要求 \(w_\text{dd} > 1.0\) 即可
    • Decision Diffuser原始论文中未见到 \(w_\text{dd} > 1.0\) 的表达，但是附录B中有超参数 guidance scale \(s \in \{1.2,1.4,1.6,1.8\}\) 这样的表达 （注意，这里的 \(s=w\) 论文中常常混淆使用）
    • 论文GLIDE中则明确有 guidance scale \(s \ge 1.0\) 的表达 （注意，这里的 \(s=w\) 论文中常常混淆使用）
  • Decision Diffuser这种用法有一个好处，可以通过不同Diffusion误差函数相加实现满足多个条件 \(\epsilon_\theta(\boldsymbol{x}_k(\tau),\boldsymbol{y}^i(\tau), k)\) 的采样形式
    $$\hat{\epsilon} := \epsilon_\theta(\boldsymbol{x}_k(\tau),\varnothing, k) + \omega \sum_{i=1}^n (\epsilon_\theta(\boldsymbol{x}_k(\tau),\boldsymbol{y}^i(\tau), k) - \epsilon_\theta(\boldsymbol{x}_k(\tau), \varnothing, k))$$

附录：多条件组合的证明

条件为空和不满足约束都为 0？

  • 在论文中提到条件为空时，去隐向量为0，不满足约束时也是置为0，如果条件为空或者不满足约束都取0值，那么两者会混淆吧，如何理解这种情况？
  • 理解：
    • 使用 one-hot 来编码时，除非所有约束都不满足才会取值为0，不满足约束的情况和条件为空的情况本质上都是无约束的情况，所以两者等价？