本文简单介绍COMBO模型
COMBO 基本思想
- 主要用于解决Offline RL的问题,属于Model-based方法
- COMBO是结合了CQL思想的一种Model-based方法
原始 CQL 的更新公式
- 策略评估更新公式:
$$\hat{Q}^{k+1} = \mathop{\arg\min}_Q \alpha \left(\mathbb{E}_{\color{red}{s\sim \mathcal{D}, a\sim \mu(a\vert s)}}[Q(s, a)] - \mathbb{E}_{\color{blue} {s\sim \mathcal{D}, a\sim\hat{\pi}_\beta(a\vert s)}}[Q(s, a)] \right) + \frac{1}{2} \mathbb{E}_{\color{red} {\mathbf{s}, \mathbf{a}, \mathbf{s’} \sim \mathcal{D}}}\left[\left(Q(\mathbf{s}, \mathbf{a})-\hat{\mathcal{B}}^{\pi} \hat{Q}^{k}(\mathbf{s}, \mathbf{a})\right)^{2}\right]$$ - 注,以上更新公式并不直接用于CQL的训练,是损失函数的中间结果
COMBO 的训练流程
COMBO 训练代码:

模型的训练:
- 模型输入是 \(s,a\),预估目标是 \(s’,r\),上面的训练代码中将输出建模成表达成高斯分布的形式(适用于连续型的场景),如果是离散型的场景,可以使用分类模型
策略评估更新公式:
$$\hat{Q}^{k+1} = \mathop{\arg\min}_Q \color{red}{\beta} \left(\mathbb{E}_{\color{red} {s,a\sim\rho(s,a)}}[Q(s, a)] - \mathbb{E}_{\color{blue} {s,a\sim\mathcal{D}}}[Q(s, a)] \right) + \frac{1}{2} \mathbb{E}_{\color{red} {\mathbf{s}, \mathbf{a}, \mathbf{s’} \sim \mathcal{d_f}}}\left[\left(Q(\mathbf{s}, \mathbf{a})-\hat{\mathcal{B}}^{\pi} \hat{Q}^{k}(\mathbf{s}, \mathbf{a})\right)^{2}\right]$$以上红色部分是COMBO和CQL的核心区别,蓝色部分表达不同,但是本质是相同的,都是从离线的数据集中采样样本
- 第一部分:\(\rho(s,a) = \color{red}{\mathcal{d}^\pi_{\hat{\mathcal{M}}}(s)}\pi(a|s)\),其中 \(\color{red}{\mathcal{d}^\pi_{\hat{\mathcal{M}}}(s)}\) 表示策略 \(\pi\) 与模型 \(\hat{\mathcal{M}}\) 交互时的状态 \(s\) 的访问概率
- 注意这里只有状态的概率 \(\color{red}{\mathcal{d}^\pi_{\hat{\mathcal{M}}}(s)}\) 选取与CQL的 \(\color{red}{\mathcal{D}}\) 不同,后面的策略还是当前策略 \(\pi(a|s)\),策略这个点与CQL是相同的
- 第二部分:\(\mathcal{d}^\mu_f := f\ \mathcal{d}(s,a) + (1-f)\ \mathcal{d}^\mu_{\hat{\mathcal{M}}}(s,a)\),其中 \(f\in [0,1]\) 表示数据混合比例
- CQL中使用的全是真实数据集,在COMBO中则使用到了部分当前策略与模型交互生成的结果
- COMBO论文中关于 \(f\) 的选取一般在0.5或0.8不等,个人理解:在真实数据集较多的场景,这个混合比例不宜过低
- 第一部分:\(\rho(s,a) = \color{red}{\mathcal{d}^\pi_{\hat{\mathcal{M}}}(s)}\pi(a|s)\),其中 \(\color{red}{\mathcal{d}^\pi_{\hat{\mathcal{M}}}(s)}\) 表示策略 \(\pi\) 与模型 \(\hat{\mathcal{M}}\) 交互时的状态 \(s\) 的访问概率
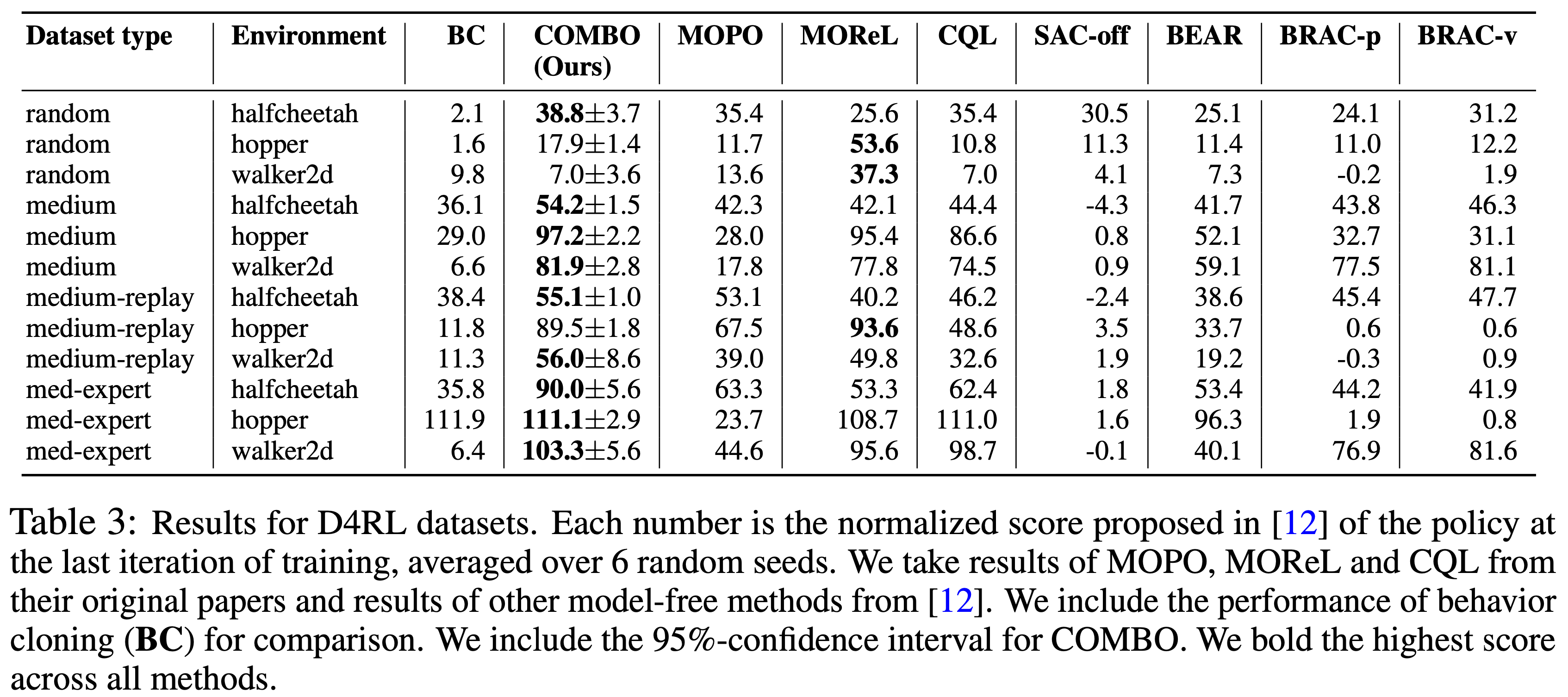
实验结果
- COMBO实验结果