- 参考链接:【笔记】BCQ详解
- 原作者的PPT
- 参考链接:BCQ姊妹篇:Discrete BCQ - Metaqiang的文章 - 知乎
- 参考链接:【代码速读】(RL)1.BCQ - 一条的文章 - 知乎
BCQ 整体介绍
- BCQ(Batch-Constrained deep Q-learning)分为连续版本(Off-Policy Deep Reinforcement Learning without Exploration,2019年8月)和离散版本(Benchmarking Batch Deep Reinforcement Learning Algorithms,2019年10月)两篇文章,一作是同一个作者
- 外推误差(Extrapolation Error)的定义:off-policy值学习中,当前策略真实状态动作访问分布和数据集中的状态动作分布不匹配导致的一种误差
Extrapolation error is an error in off-policy value learning which is introduced by the mismatch between the dataset and true state-action visitation of the current policy
- 背景:off-policy的策略理论上可以从任意行为策略采样的数据中学习最优策略,但是直接将off-policy策略应用到Offline RL(也称为Batch RL)场景中可能面临,Absent Data(状态动作对缺失),Training Mismatch(训练预测分布不一致),Model Bias(随机MDP的状态转移概率有偏差)等问题
- BCQ的基本思想:采取保守策略,让学到的策略对应的状态动作访问空间尽量只在出现过的数据集上,或者相近的数据上
- 基本方法:主要通过限制 \(Q(s’,\pi(s’))\) 中的 \(\pi(s’)\) 不要偏离数据集太多来实现
BCQ 连续版本
关键实验
实验设置:
- 第一个实验(Final Buffer),使用DDPG算法在线训练一个智能体,将智能体训练过程中与环境交互的所有数据保存下来,利用这些数据训练另一个离线DDPG智能体
- 第二个实验(Concurrent),使用DDPG算法在线训练一个智能体,训练时每次从经验回放池中采样,并用相同的数据同步训练离线DDPG智能体,甚至保持训练时使用的数据和数据顺序都完全相同
- 第三个实验(Imitation),使用DDPG算法在线训练一个智能体,将该智能体作为专家,与环境交互采集大量数据,利用这些数据训练另一个离线DDPG智能体
实验结果:
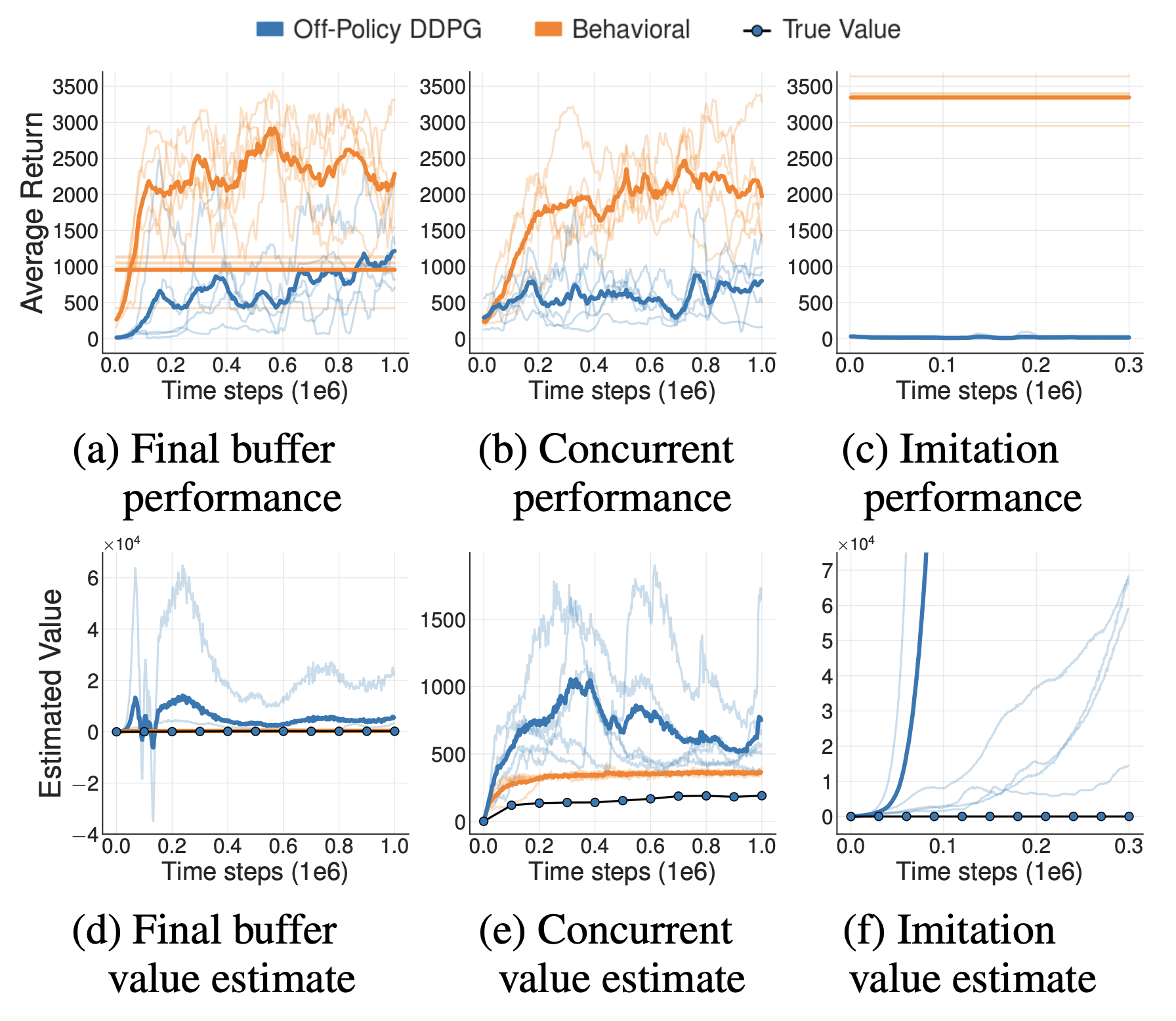
- 第三个实验中使用的样本最好,但是训练得到的离线智能体效果最差,原因分析主要是外推误差导致
- 三个实验的离线DDPG智能体都有不同情况的Q值高估问题,其中第三个实验的Q值高估问题最为严重(注意图2中看起来高估问题大于图1中,其实不是,是因为图二的量纲较小导致的)
理论推导
- 对于给定的真实MDP和数据集 \(\mathcal{B}\),定义外推误差
$$\epsilon_\text{MDP}(s,a) = Q^\pi(s,a) - Q_{\mathcal{B}}^\pi(s,a)$$ - 则有外推误差可推导得到如下结论:
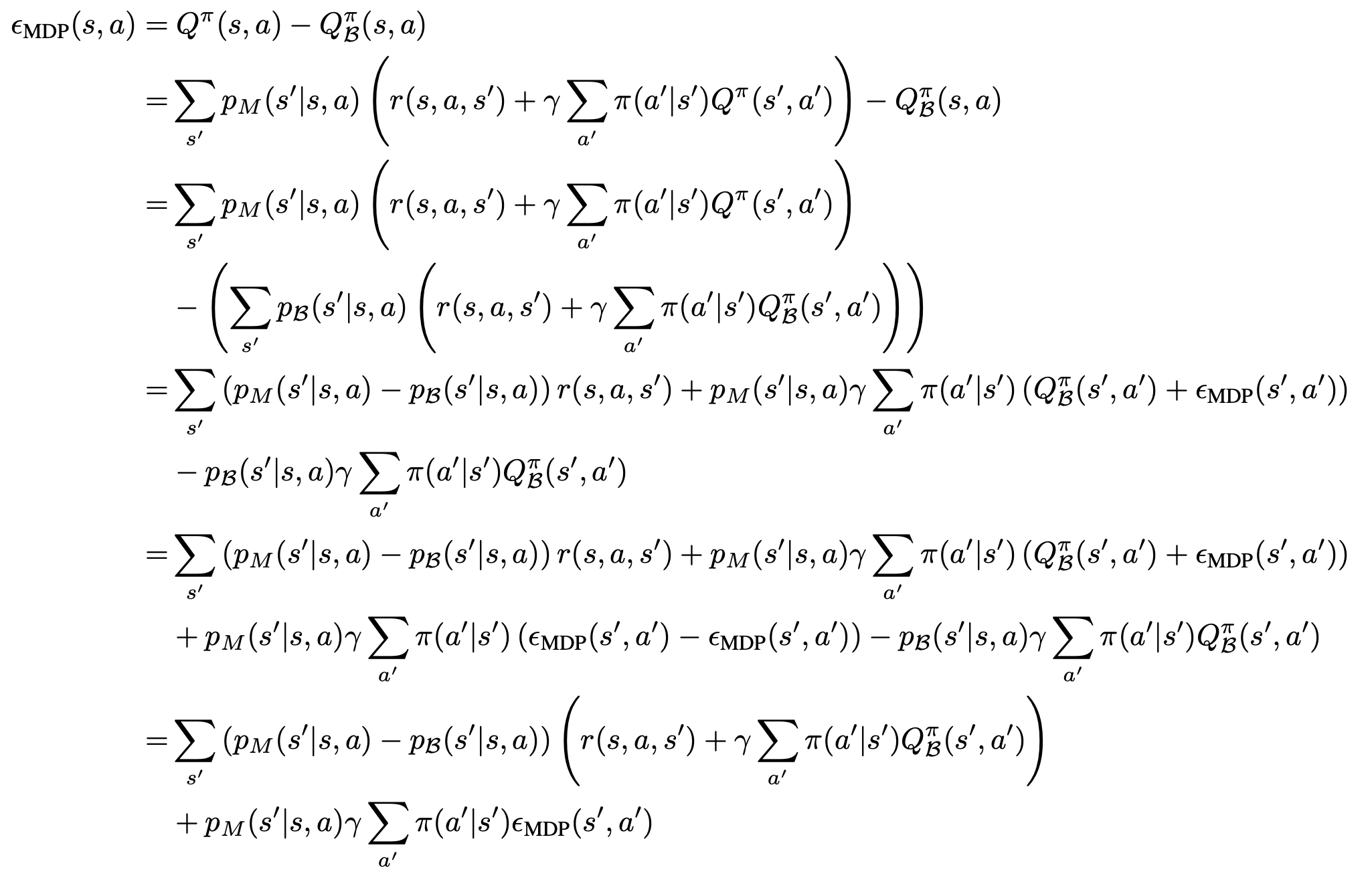
训练流程
整体流程概览:

训练流程解释:
- 训练时,使用4个Q网络(其中两个是Target Q网络),1个策略网络和扰动网络
- 两个Q网络的用途是在计算Q值目标时做他们最大最小值的凸组合(实际上就是最大最小值的加权平均),类似Twin Q中取两个Q的最小值的方法, \(y\) 值计算方法(流程中 \(\color{red}{\text{公式(13)}}\) )
$$ y = r + \gamma \max_{a_i}\Big[ \lambda \min_{j=1,2}Q_{\theta_j}(s’,a_i) + (1-\lambda)\max_{j=1,2}Q_{\theta_j}(s’,a_i) \Big] $$
Serving步骤
- 给定一个状态 \(s\)
- \(\{ a_i \sim G_w(s) \}_{i=1}^n\):通过conditional VAE网络 \(G_w(s)\) 采样 \(n\) 个动作
- \(\xi_{\phi}(s,a_i,\Phi)\):将这些状态和动作经过扰动网络,扰动网络输出是在 \([-\Phi,\Phi]\) 内的,得到的扰动值
- 将扰动添加到原始动作上,再将动作经过Q网络,选取能使Q value最大的动作
- 最终总结如下:
$$ \pi(s) = \mathop{\arg\max}_{a_i + \xi_{\phi}(s,a_i,\Phi)} Q_\theta(s, a_i + \xi_{\phi}(s,a_i,\Phi)), \quad with \quad \{ a_i \sim G_w(s) \}_{i=1}^n $$ - 训练流程解释:
- 相对普通的DQN,主要改进点在于学习Q的目标值选择时动作受到限制,动作与行为策略(离线数据集)的动作差异不能太大
- 学习Q值时,使用的是Huber Loss
$$
l_{\mathcal{k}}(\delta) =
\begin{cases}
\ 0.5\delta^2& \text{if}\ \delta \le \mathcal{k}\\
\mathcal{k}(|\delta| - 0.5\mathcal{k})& \text{otherwise.}
\end{cases}
$$
BCQ 离散版本
训练流程
- 整体流程概览:

Serving 步骤
- 按照如下策略决策:
$$ \pi(s) = \mathop{\arg\max}_{a\vert\frac{G_w(a|s)}{\max_\hat{a} G_w(\hat{a}|s)} \gt \tau} Q_\theta(s,a) $$