RL——策略梯度法

策略梯度法(Policy Gradient)推导，以及REINFORCE算法的介绍

基础概念

• 策略 \(\pi(a|s, \theta)\) (也可以表达为 \(\pi_{ \theta}(a|s)\))是一个从状态 \(s\) 到动作 \(a\) 概率的映射，其中 \(\theta\) 表示策略的参数。
• 整个轨迹的累计回报 \(R_(\tau)\)是轨迹\(\tau\)对应的回报：
  $$
  R(\tau) = \sum_{k=0}^{\infty} r_{k}
  $$
  • 注意：这里没有折扣因子
• 时间t步开始的回报 \(G_t\) 是从时间步 \(t\) 开始到结束的所有奖励的总和，通常定义为折扣累积奖励：
  $$
  G_t = \sum_{k=t}^{\infty} \gamma^k r_{k}
  $$
  其中 \(\gamma\) 是折扣因子，\(r_{k}\) 是在时间步 \(k\) 收到的即时奖励。
• 目标 是找到参数 \(\theta\) 使得长期回报的期望值最大，即 \(\max_\theta J(\theta)\)，其中 \(J(\theta) = E_{\tau \sim p_\theta(\tau)} [R(\tau)]\)。

推导过程

优化目标：

• 目标函数 \(J(\theta)\) 定义为从初始分布开始，遵循策略 \(\pi_\theta\) 时的平均回报：
  $$
  J(\theta) = E_{\tau \sim p_\theta(\tau)} [R(\tau)]
  $$
• 其中 \(\tau = (s_0, a_0, r_1, s_1, a_1, \dots)\) 表示一个轨迹，\(p_\theta(\tau)\) 是在策略 \(\pi_\theta\) 下产生轨迹 \(\tau\) 的概率。

梯度估计：

• 我们的目标是计算目标函数关于参数 \(\theta\) 的梯度 \(\nabla_\theta J(\theta)\)。我们有：
  $$
  \nabla_\theta J(\theta) = \nabla_\theta \int R(\tau) p_\theta(\tau) d\tau = \int R(\tau) \nabla_\theta p_\theta(\tau) d\tau
  $$
• 使用对数概率技巧（log derivative trick，\(\nabla_\theta log y({\theta}) = \frac{\nabla_\theta y({\theta})}{ y({\theta}) }\)）可以将上式转换为：
  $$
  \nabla_\theta J(\theta) = \int R(\tau) p_\theta(\tau) \frac{\nabla_\theta p_\theta(\tau)}{p_\theta(\tau)} d\tau = E_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla_\theta \log p_\theta(\tau)]
  $$
• 如果通过蒙特卡洛采样估计上面的式子，则可以写成：
  $$
  \begin{align}
  \nabla_\theta J(\theta) &= E_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla_\theta \log p_\theta(\tau)] \\
  &\approx \frac{1}{N} \sum_{n=1}^{N} R(\tau^n) \nabla_\theta \log p_\theta(\tau^n)
  \end{align}
  $$
  • 上式是对原始梯度的无偏估计

轨迹展开：

• 轨迹展开后，有 \(p_\theta(\tau) = p(s_0) \prod_t \pi_\theta(a_t|s_t) p(s_{t+1}|s_t, a_t)\)，其中 \(p(s_0)\) 是初始状态的分布，\(p(s_{t+1}|s_t, a_t)\) 是环境的转移概率。
  $$
  \begin{align}
  p_\theta(\tau) &= p_{\pi_\theta}(s_0, a_0, s_1, a_1,\cdots) \\
  &= p(s_0)\pi_\theta(a_0|s_0)p(s_1|s_0,a_0)\cdots \\
  &= p(s_0) \prod_t \pi_\theta(a_t|s_t) p(s_{t+1}|s_t, a_t)
  \end{align}
  $$

• 由于环境的输出与策略无关，即\(\nabla_\theta p(s_1|s_0,a_0) = 0\)，于是有：
  $$
  \begin{align}
  \nabla_\theta \log p_\theta(\tau) &= \nabla_\theta p(s_0) \prod_t \pi_\theta(a_t|s_t) p(s_{t+1}|s_t, a_t) \\
  &= \nabla_\theta \log p(s_0) + \nabla_\theta \sum_t \log \pi_\theta(a_t|s_t) + \nabla_\theta \sum_t \log p(s_{t+1}|s_t, a_t) \\
  &= \nabla_\theta \sum_t \log \pi_\theta(a_t|s_t) \\
  &= \sum_t \nabla_\theta \log \pi_\theta(a_t|s_t)
  \end{align}
  $$

• 所以我们可以进一步简化梯度表达式为：
  $$
  \begin{align}
  \nabla_\theta J(\theta) &= E_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla_\theta \log p_\theta(\tau)] = E_{\tau \sim p_\theta(\tau)} \left[\sum_t \nabla_\theta \log \pi_\theta(a_t|s_t) R(\tau^n) \right] \\
  &\approx \frac{1}{N} \sum_{n=1}^{N} R(\tau^n) \nabla_\theta \log p_\theta(\tau^n) = \frac{1}{N}\sum_{n=1}^N \sum_{t=1}^{T_n} R(\tau^n) \nabla_\theta \log \pi_\theta(a_t|s_t)
  \end{align}
  $$

  • 此时，上式依然是对原始梯度的无偏估计

• 核心理解：

  • \(R(\tau^n)\)表示采样得到的轨迹\(\tau^n\)对应的Reward，上述公式假设一共有N个轨迹
  • 对于任意给定的轨迹\(\tau^n\)，其上面的任意样本对\((s_t,a_t)\)，均使用固定的\(R(\tau^n)\)对 \(\nabla_\theta \log \pi_\theta(a_t|s_t)\)进行加权（实际上在使用中，不会直接使用\(R(\tau^n)\)，因为轨迹中过去的Reward与当前动作无关，所以，我们仅考虑后续的轨迹上的收益即可）

REINFORCE算法：

• 考虑到轨迹中过去的Reward与当前动作无关，且后续轨迹上的收益与当前动作的关系越来越小，所以我们使用\(G_t\)来替换\(R(\tau)\)
  $$
  R(\tau) = \sum_{k=0}^{\infty} r_{k} \quad \rightarrow \quad G_t = \sum_{k=t}^{\infty} \gamma^k r_{k}
  $$
• 此时梯度进一步近似为：
  $$
  \begin{align}
  \nabla_\theta J(\theta) &\approx \frac{1}{N}\sum_{n=1}^N \sum_{t=1}^{T_n} R(\tau^n) \nabla_\theta \log \pi_\theta(a_t|s_t) \\
  &\approx \frac{1}{N}\sum_{n=1}^N \sum_{t=1}^{T_n} G_t^n \nabla_\theta \log \pi_\theta(a_t|s_t)
  \end{align}
  $$
• REINFORCE算法利用上述梯度估计来更新策略参数。具体地，对于轨迹\(R(\tau^n)\)上的状态动作样本对\((s_t,a_t)\)，参数更新规则如下：
  $$
  \theta \leftarrow \theta + \alpha \nabla_\theta \log \pi_\theta(a_t|s_t) G_t^n
  $$
  • 其中 \(\alpha\) 是学习率
  • 因为是累加操作，所以可以展开对每一个状态动作样本对\((s_t,a_t)\)进行累加
  • \(\frac{1}{N}\)可以不需要了，有了学习率了，可以调节到学习率中
• 补充REINFORCE算法伪代码：

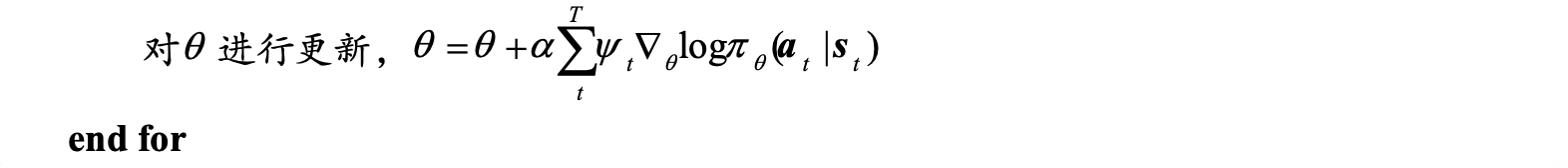
减小方差：

• 为了减少方差，可以在梯度估计中引入一个baseline函数 \(b(s_t)\)，它是一个与动作无关的量。更新规则变为：
  $$
  \theta \leftarrow \theta + \alpha \nabla_\theta \log \pi_\theta(a_t|s_t) (G_t - b(s_t))
  $$

  • 常见的选择是使用价值函数 \(V(s_t)\) 作为基线，这有助于稳定学习过程。
  • 可以证明，增加 \(b(s_t)\) 后，梯度不会发生改变，上式对梯度的估计依然是无偏的

• 性质一：减去一个baseline以后，依然是原始梯度的无偏估计，证明如下：
  $$
  \begin{align}
  \nabla_\theta J(\theta)
  &= E_{\tau \sim p_{\theta}(\tau)} (R(\tau) - b) \nabla_\theta \log p_{\theta}(\tau) \\
  &= E_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla_\theta \log p_\theta(\tau)] - b E_{\tau \sim p_{\theta}(\tau)} \nabla_\theta \log p_{\theta}(\tau) \\
  &= E_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla_\theta \log p_\theta(\tau)] - b \sum_\tau p_{\theta}(\tau) \nabla_\theta \log p_{\theta}(\tau) \\
  &= E_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla_\theta \log p_\theta(\tau)] - b \sum_\tau \nabla_\theta p_{\theta}(\tau) \\
  &= E_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla_\theta \log p_\theta(\tau)] - b \nabla_\theta \sum_\tau p_{\theta}(\tau) \\
  &= E_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla_\theta \log p_\theta(\tau)] - b \nabla_\theta 1 \\
  &= E_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla_\theta \log p_\theta(\tau)] \\
  \end{align}
  $$

  • 第三行到第四行用到了对数概率技巧：\(\nabla_\theta log y({\theta}) = \frac{\nabla_\theta y({\theta})}{ y({\theta}) }\)
  • 第四行到第五行使用了求梯度和加法交换顺序的法则

• 性质二：减去一个合适的baseline函数以后，方差会变小，证明如下：

  • 方差展开
    $$
    \begin{align}
    &\ Var_{\tau \sim p_{\theta}(\tau)} [(R(\tau) - b) \nabla \log p_{\theta}(\tau)] \\
    &= E_{\tau \sim p_{\theta}(\tau)} [(R(\tau) - b)^2 \nabla^2 \log p_{\theta}(\tau)] - [E_{\tau \sim p_{\theta}(\tau)} [(R(\tau) - b) \nabla \log p_{\theta}(\tau)] ]^2 \\
    &= E_{\tau \sim p_{\theta}(\tau)} [R(\tau)^2 \nabla^2 \log p_{\theta}(\tau)] - [E_{\tau \sim p_{\theta}(\tau)} [R(\tau) \nabla \log p_{\theta}(\tau)] ]^2 - 2 b E_{\tau \sim p_{\theta}(\tau)} [R(\tau) \nabla^2 \log p_{\theta}(\tau)] + b^2 E_{\tau \sim p_{\theta}(\tau)} [ \nabla^2 \log p_{\theta}(\tau)] \\
    &= Var_{\tau \sim p_{\theta}(\tau)} [R(\tau) \nabla \log p_{\theta}(\tau) ] - 2 b E_{\tau \sim p_{\theta}(\tau)} [R(\tau) \nabla^2 \log p_{\theta}(\tau)] + b^2 E_{\tau \sim p_{\theta}(\tau)} [ \nabla^2 \log p_{\theta}(\tau)]
    \end{align}
    $$
  • 进一步解的，使得上式取小值的最优\(b\)为：
    $$
    b = \frac{E_{\tau \sim p_{\theta}(\tau)} [R(\tau) \nabla^2 \log p_{\theta}(\tau)] }{E_{\tau \sim p_{\theta}(\tau)} [ \nabla^2 \log p_{\theta}(\tau)]}
    $$
  • 实际应用中，为了方便计算，通常会使用：
    $$
    \hat{b} = E_{\tau \sim p_{\theta}(\tau)} R(\tau)
    $$
  • 那为什么\(\hat{b} = E_{\tau \sim p_{\theta}(\tau)} R(\tau)\)是\(V_{\pi_{\theta}}(s_t)\)呢？因为两者是等价的，证明如下：
    • 对于非确定性策略来说，在状态\(s_t\)下可选的动作服从一个分布\(\pi_{\theta}(s_t)\)，按照\(E_{\tau \sim p_{\theta}(\tau)} R(\tau)\)的逻辑，该值是状态\(s_t\)下按照策略\(\pi_{\theta}(s_t)\)执行得到\(R(\tau)\)期望（注意\(a_t\)服从\(\pi_{\theta}\)分布，后续的执行动作也服从\(\pi_{\theta}\)分布），实际上就是\(V_{\pi_{\theta}}(s_t)\)

实际使用中的\(R(\tau)\)

原始形式

$$ R(\tau) = \sum_{k=0}^{\infty} r_{k} $$

• 上式中实际上是一个固定轨迹的奖励，从第0步开始
• 可基于蒙特卡洛采样得到

REINFORCE方法

• 迭代样本\((s_t,a_t)\)时，使用以下形式：
  $$ G_t = \sum_{k=t}^{\infty} \gamma^k r_{k} $$
  • 丢弃掉动作之前的奖励，这些奖励与当前动作无关
  • 未来越远的动作奖励越小，因为这些奖励受当前动作影响的概率越小
• 使用baseline函数进行改进
  $$\sum_{k=t}^{\infty} \gamma^k r_{k} - b(s_t)$$

用Q值替代

• 用\(Q(s,a)\)值代替\(R(\tau)\)
• 理由，\(Q(s,a)\)值是状态\(s\)执行\(a\)以后的\(G_t\)的期望值：
  $$Q^{\pi_\theta}(s_t,a_t) = E_{\pi_\theta} [G_t|s_t, a_t]$$
• 使用Q值来替代可以降低方差

用优势函数替代

• 用\(A(s,a) = Q(s,a) - V(s)\)来替代
  • 可以减去\(V(s)\)的理由是之前证明过减去一个baseline函数\(V(s)\)可以降低方差，且梯度无偏
• 实际上使用时可以使用单个V网络+TD-Error实现对优势函数的估计
  $$ A(s,a) = r(s,a) + \gamma V(s’) - V(s) $$
• 应用场景：
  • 常规的Actor Critic方法
  • PPO方法的优势函数估计（实际的PPO中常常是GAE方式，是优势函数的一种加权）