- 参考文献
动态规划方法
- 动态规划(Dynamic Programming, DP) 是一种将复杂问题分解为若干子问题,并通过求解这些子问题来获得原问题解的方法。它适用于满足以下两个性质的问题:
- 最优子结构(optimal substructure) :原问题可以分解为多个子问题,通过解决这些子问题并将其解组合起来,可以得到原问题的最优解
- 重叠子问题(overlapping subproblems) :子问题在求解过程中会多次出现,且这些子问题的解可以被存储并重复利用
- 马尔可夫决策过程 (MDP) 恰好满足动态规划的这两个条件:贝尔曼方程将问题分解为递归结构的子问题,而价值函数能够存储并复用其最优解。因此,我们可以使用动态规划来解决马尔可夫决策过程的核心问题:预测和控制
- 预测(prediction) :给定一个马尔可夫决策过程 MDP 和一个策略 \(\pi\),或者给定一个马尔可夫奖励过程 MRP,求解基于该策略的价值函数 \(v_\pi\)。(评估给定策略的效果)
- 控制(control) :给定一个马尔可夫决策过程 MDP,求解最优价值函数 \(v_\∗\) 和最优策略 \(\pi_\∗\)。(即寻找最佳策略)
- 预测问题和控制问题的主要区别在于,预测问题是在策略已知的情况下求解其价值函数,而控制问题则是在没有给定策略的情况下寻找最优价值函数及其对应的策略。两者之间存在递进关系:在强化学习中,我们通常先解决预测问题,再进一步解决控制问题
同步动态规划(Synchronous Dynamic Programming)
- 同步动态规划算法中,每一次迭代都更新所有状态的价值
- 参考链接:策略迭代与值迭代的区别
策略迭代(policy iteration)
- Step1:初始化所有状态的价值 (\(v(s)\)) 和策略 (\(\pi(s)\))
- Step2:策略评估(policy evaluation):按照贝尔曼方程迭代,直到收敛(求解当前策略下的不动点)
- Step3:策略迭代(policy improvement):寻找一个新的策略,在任意状态下都有 \(Q^\pi(s,\pi’(s)) \ge V^\pi(s)\),可以证明此时有 \(V^{\pi’}(s) \ge V^\pi(s)\)
- 循环Step2和Step3直到收敛
值迭代(value iteration)
- Step1:初始化所有状态的价值 (\(v(s)\))
- Step2:迭代找到最优策略(常常隐含直接使用 argmax 作为最优策略决策),直到收敛
- Step3:最优策略提取
- 这种方法仅进行价值函数迭代,不考虑策略,最终迭代到最优价值函数后,即可反向求解得到最优的策略
异步动态规划(Asynchronous Dynamic Programming,非重点)
- 异步动态规划算法中,在每一次迭代时,根据特定规则选择性地更新部分状态的价值(并不更新所有状态的价值)
- 注:这种方法可以显著节省计算资源,并且只要所有状态能够持续被访问和更新,算法最终仍能收敛到最优解
- 目标:解决经典DP需遍历全部状态的问题,通过异步更新提高效率
- 以下是几种常见的异步动态规划方法:
- 就地动态规划(In-place DP) :直接覆盖旧价值函数,而非保留新旧两份
- 优先扫描(Prioritized Sweeping) :根据优先级对状态进行排序,优先更新优先级较高的状态的价值(优先更新贝尔曼误差较大的状态)
- 实时动态规划(Real-time DP) :仅更新当前交互中访问的状态
动态规划的其他说明
- 动态规划算法的缺点 :采用全宽度(full-width)的回溯机制来更新状态价值,算力需求大且容易导致维度灾难
- 无论是同步还是异步动态规划,每次回溯更新某个状态的价值时,都需要追溯到该状态的所有可能后续状态,并结合已知的马尔可夫决策过程的状态转换矩阵和奖励来更新该状态的价值
- 解决方案:可以使用采样回溯方法来近似估计价值,从而减少算力的消耗
- 动态规划算法是model-based算法,因为需要回溯当前状态的所有后续状态(full-width回溯机制)
Model-free方法辨析
- Model-free 不知道环境动力学(Dynamics),无法精确计算精确的目标值,所以通常使用 TD 和 MC 这两种方案来近似估计目标值
- 时序差分(Temporal Difference, TD):Q-learning 和 SARSA 都使用这种方法估计目标值
- 蒙特卡罗方法(Monte-Carlo,MC):REINFORCE方法就使用了MC方法估计目标值
- n-step方法是 TD 和 MC 的结合
- TD 其实同时是结合了 MC 和 DP 的思想,更详细的比较见附录
- 需要模拟交互序列(和MC方法一样);但不需要积累很多交互数据求均值(不同于 MC)
- 使用当前回报和下一时刻的价值预估来更新当前时刻的价值(和DP方法一样);不需要知道状态转移矩阵,也不需要full-width回溯(不同于DP方法)
- Q-learning 和 SARSA 为什么不是DP方法?
- Q-learning 并不基于模型计算期望(不需要依赖状态转移矩阵),是直接使用贪心策略
- SARSA 依赖采样,并不是精确计算期望
附录:Planning、Decision、Prediction和Control的区别
- 在自动化和智能系统中,Planning、Decision、Prediction 和 Control 是四个关键的概念:
- Planning(规划) :制定未来行动步骤,生成一系列行动步骤或策略
- Decision(决策) :在当前时刻选择最佳行动,即在已知状态下决策动作
- Prediction(预测) :推断未来状态或事件,预估环境相关的变化等
- Control(控制) :实时调节系统行为以实现目标,常常涉及到反馈机制,以应对环境变化
- 实际例子举例:自动驾驶中,Prediction用于预测其他车辆行为,Decision用于选择最佳驾驶策略,Planning用于规划路径,Control用于执行驾驶操作
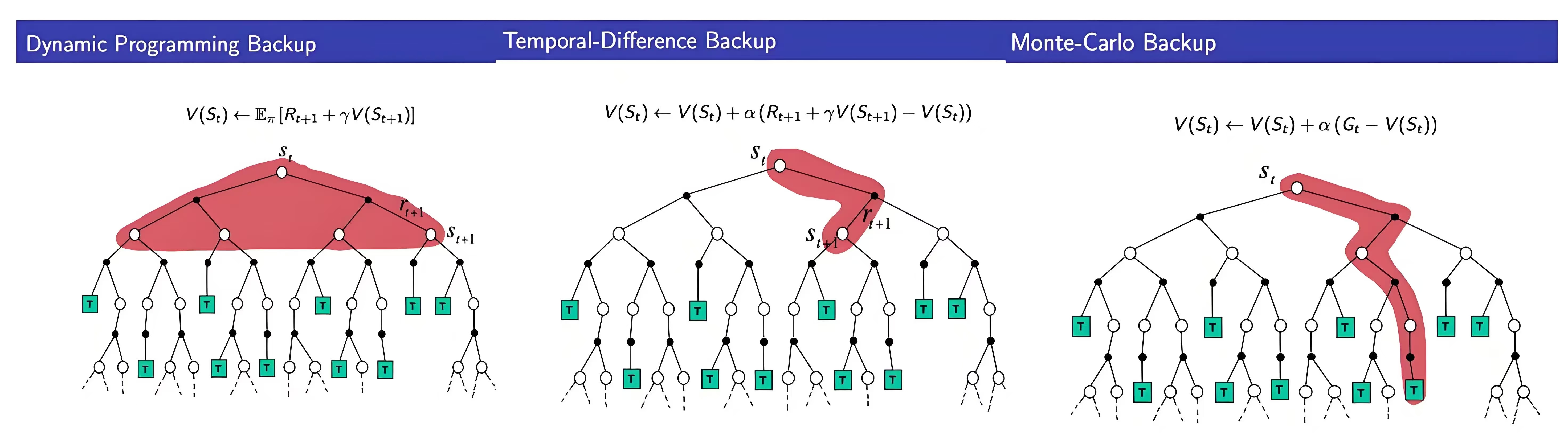
附录:MC、TD和DP 详细比较
- 蒙特卡罗方法(MC) :通过完整回合的采样回报估计值函数,依赖实际经验,无需环境模型
- 时序差分(TD) :结合MC和DP思想,结合当前奖励和后续状态的价值估计来更新当前状态
- 动态规划(DP) :基于模型的全宽度回溯更新,利用贝尔曼方程迭代求解值函数,需已知环境动力学

动态规划(DP)
- 核心思想 :利用贝尔曼方程全宽度回溯更新值函数,需已知状态转移 \( P \) 和奖励函数 \( R \)
- 策略评估(Policy Evaluation) :
$$
V_{k+1}(s) = \sum_a \pi(a|s) \sum_{s’, r} P(s’, r|s, a) \left[ r + \gamma V_k(s’) \right]
$$- 迭代至收敛得到精确值函数
- 策略改进(Policy Improvement) :
$$
\pi’(s) = \arg\max_a \sum_{s’, r} P(s’, r|s, a) \left[ r + \gamma V^\pi(s’) \right]
$$
蒙特卡罗方法(MC)
- 核心思想 :用完整回合的回报均值估计值函数,仅适用于回合制任务
- 值函数更新 :
$$
V(S_t) \leftarrow V(S_t) + \alpha \left[ G_t - V(S_t) \right]
$$- 其中 \( G_t = \sum_{k=t}^T \gamma^{k-t} R_{k+1} \) 是实际回报,\( \alpha \) 为学习率,\( T \) 为回合终止时刻
时序差分(TD)
- 核心思想 :用当前奖励与下一状态估计值(自举)更新值函数,可在线学习
- TD(0) 更新 :
$$
V(S_t) \leftarrow V(S_t) + \alpha \left[ R_{t+1} + \gamma V(S_{t+1}) - V(S_t) \right]
$$- 其中 \( R_{t+1} + \gamma V(S_{t+1}) \) 称为 TD目标 ,\( \delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t) \) 为 TD误差
三者方差偏差比较
- MC :高方差、无偏估计,需完整回合
- TD :低方差、有偏估计,可在线学习
- DP :精确但计算量大,需模型支持。