本文主要介绍值分布强化学习(Distributional RL)的相关内容
- 相关论文(这个系列一共三篇主要文章,均来自Google DeepMind,作者是同一拨人):
- A Distributional Perspective on Reinforcement Learning (C51,2017年6月):C51论文
- Distributional Reinforcement Learning with Quantile Regression (QR-DQN,2017年10月):QR-DQN论文
- Implicit Quantile Networks for Distributional Reinforcement Learning (IQN,2018年1月):IQN论文
- 吐槽:三篇文章用的数据符号比较乱,跟常规强化学习不一样,有些伪代码甚至看不出哪些变量是模型输出的
- 其他参考链接:
值分布强化学习介绍
- 值分布强化学习(Distributional RL)算法是指不仅仅估计Q值的均值,还对Q值的分布进行估计的算法
- 常见算法:包括C51,QR-DQN,IQN等,各种不同值分布强化学习算法的网络结构对比见下图:
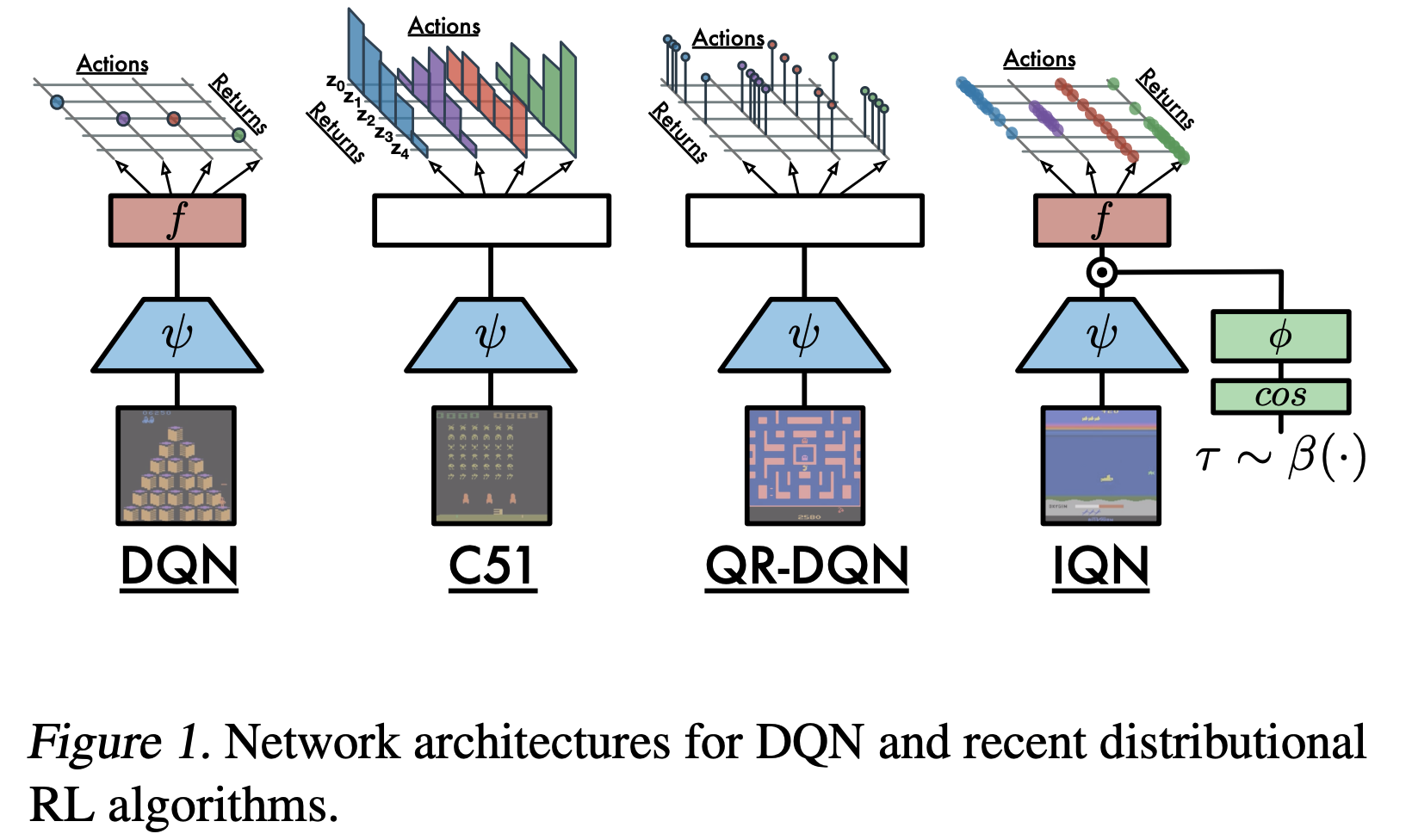
从Distributional RL的视角看DQN
- 从Distributional RL的视角来看,在状态 \(s\) 下执行动作 \(a\) 后,按照策略 \(\pi\) 继续执行的得到的价值为一个随机变量 \(Z^\pi(s,a) = \sum_{t=0}^\infty\gamma^t R(s_t, a_t)\vert_{\forall\ (s_{t},a_t) \ s_{t} \sim P(\cdot|s_{t-1},a_t), a_t \sim \pi(\cdot|s_t),}\),这个随机变量的随机包含以下:
- 整个决策过程中所有动作决策的随机: \(a \sim \pi(\cdot|s)\)
- 整个交互过程中状态转移的随机: \(s’ \sim P(\cdot|s,a)\)
- 注:实际上, \(R(s,a)\) 也可能是随机变量
- 这些随机导致了真实的状态 \(s\) 下执行动作 \(a\) 后得到的价值是一个随机变量,假设该随机变量服从一个特定的分布 \(P(Z^\pi(s,a)|s,a,\pi)\),即:
$$ Z^\pi(s,a) \sim P(\cdot|s,a,\pi) $$
- 而DQN是在拟合随机变量的期望 \(Q^\pi(s,a) = \mathbb{E}_{Z^\pi(s,a) \sim P(\cdot|s,a,\pi)}[Z^\pi(s,a)]\)
C51(Categorical DQN)
这篇文章是值分布强化学习的第一篇,论文中作者不再直接学习Q值期望 \(Q^\pi(s,a)\),而是学习Q价值的分布
论文对分布贝尔曼算子(Distributional Bellman Operator)进行了一些证明:
- 可以证明,在Wasserstein metric下证明了 Distributional Bellman Operator 是一个 \(\gamma\) -压缩( \(\gamma\) -contraction)算子,从而确保该算子存在不动点
- 算子的描述可以简单表述为下图:
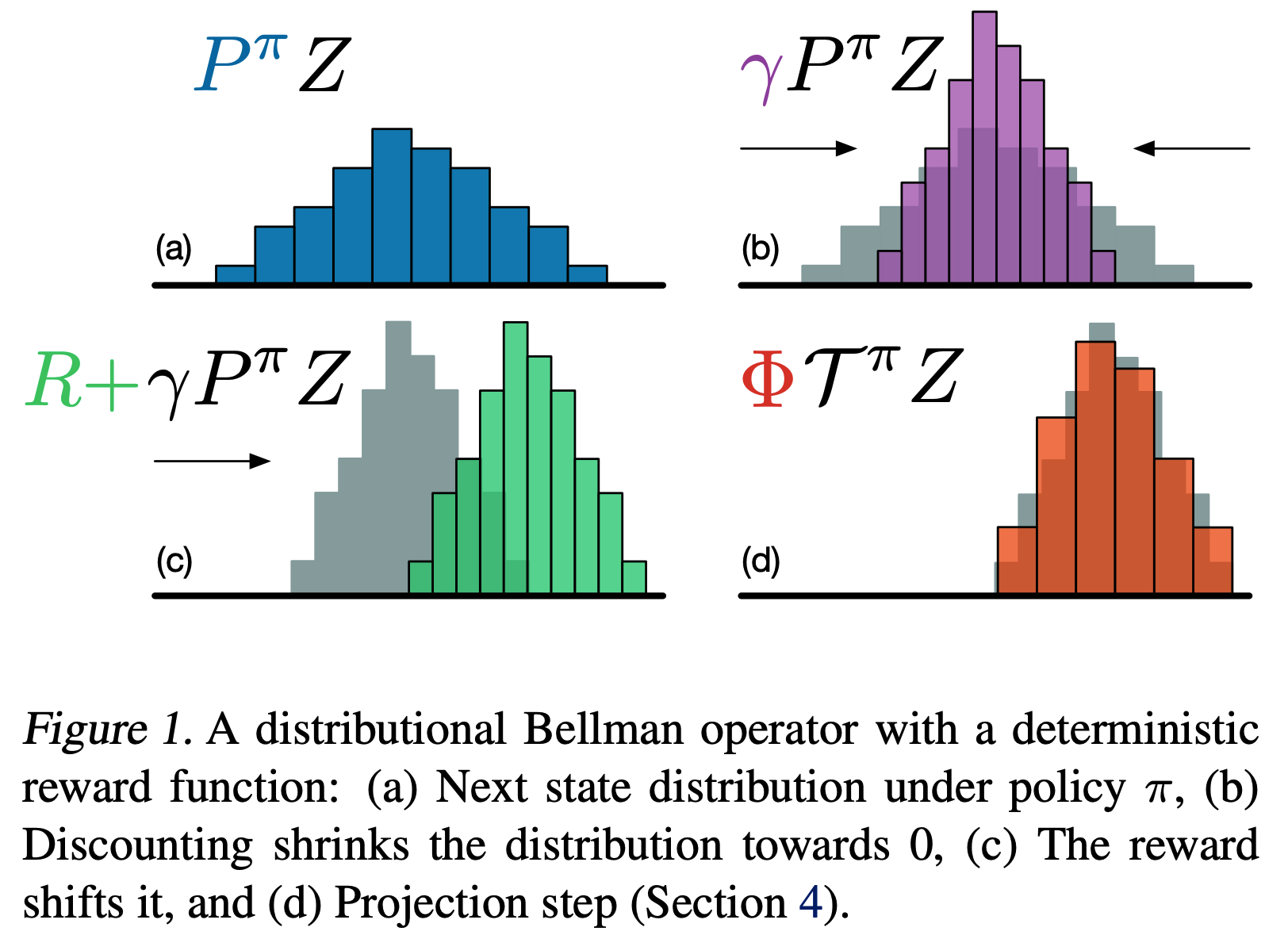
文章中提出了一种名为Categorical DQN的方法,先确定 \(Q(s,a)\) 的最大最小值,然后将其建模为一个等分为 \(N\) 份的价值区间(PS:在后续实验中,由于分了51份,所以也叫做C51),下面是Categorical DQN的伪代码:

算法解读
- 说明: \(x_t\) 表示状态,后续我们也用 \(s_t\) 表示
- 上面的伪代码表示了收集到 \(s_t,a,r,s’\) 后的一次更新过程
- 基本思路是直接将Q值等分为N份,表示在每个区间下Q值出现的概率
- 计算下个状态的目标Q值:使用Q值分布计算期望得到Q值 \(Q(s_{t+1}, a):= \sum_i z_i p_i(x_t, a)\),然后决策下个状态下Q值最大的动作 \(a^* = \arg\max_a Q(s_{t+1}, a)\)
- 更新时,每个区间都需要更新一次:
- 贝尔曼算子计算目标值: \(\hat{\mathcal{T}}z_j \leftarrow [r_t + y_t z_j]_{V_{MIN}}^{V\ _{MAX}}\)
- 计算目标值所在区间的下标序号: \(b_j \leftarrow (\hat{\mathcal{T}}z_j - V_{MIN})/\delta z \)
- 按照序号计算相邻的下标 \(l \leftarrow \lfloor b_j \rfloor, \ u \leftarrow \lceil b_j \rceil\)
- 将概率分配到Q值相邻的下标上(按照接近程度来分配):
$$
\begin{align}
m_l &\leftarrow m_l + p^{\theta_k}_j(s_{t+1}, a^*)(u-b_j)\\
m_u &\leftarrow m_u + p^{\theta_k}_j(s_{t+1}, a^*)(b_j-l)
\end{align}
$$
- 损失函数上,使用交叉熵损失函数 \(-\sum_i m_i \log p^\theta_i(s_t, a_t)\) (注:为了方便看懂,我在概率的表达上增加了参数的标识,说明概率来源于参数表达)
- 补充说明(网络实现中,一个网络输出N个头,然后做softmax得到每个头的概率值):
$$
\begin{align}
Z_\theta(s,a) = z_i \quad \text{w.p.} \ p^\theta_i(x,a) = \frac{e^{\theta_i(s,a)}}{\sum_j e^{\theta_j(s,a)}}
\end{align}
$$- “w.p.” 是 “with probability” 的缩写
- 上面的损失函数是一个多分类的交叉熵损失函数,和普通多分类的唯一区别是Ground Truth不是one-hot的,这里的Ground Truth是 \(\{m_i\}_{i=0}^{N-1}\)
QR-DQN
Quantile Regression DQN(QR-DQN),建模方式是学习Q值的分位数,提前确定要学习哪些分位点,然后通过分位数回归去学习每个分位点的Q值

\(q_j\) 表示:第 \(j\) 个分位点的间隔,可以是固定值,也可以不固定,但是累加和为1
\(\theta_j(s,a)\) 表示:分位点 \(\tau_j\) 对应的Q值,下图是一个分位点和累计分布函数的理解图:

\(Q(s,a) = \sum_jq_j\theta_j(s,a)\) 是Q值:通过分位数的Q值和对应的分位点区域权重,可以近似计算期望值(理解:不一定是精确的期望,因为通过分位点无法准确计算期望,只是一种近似)
其中损失函数是quantile Huber loss:
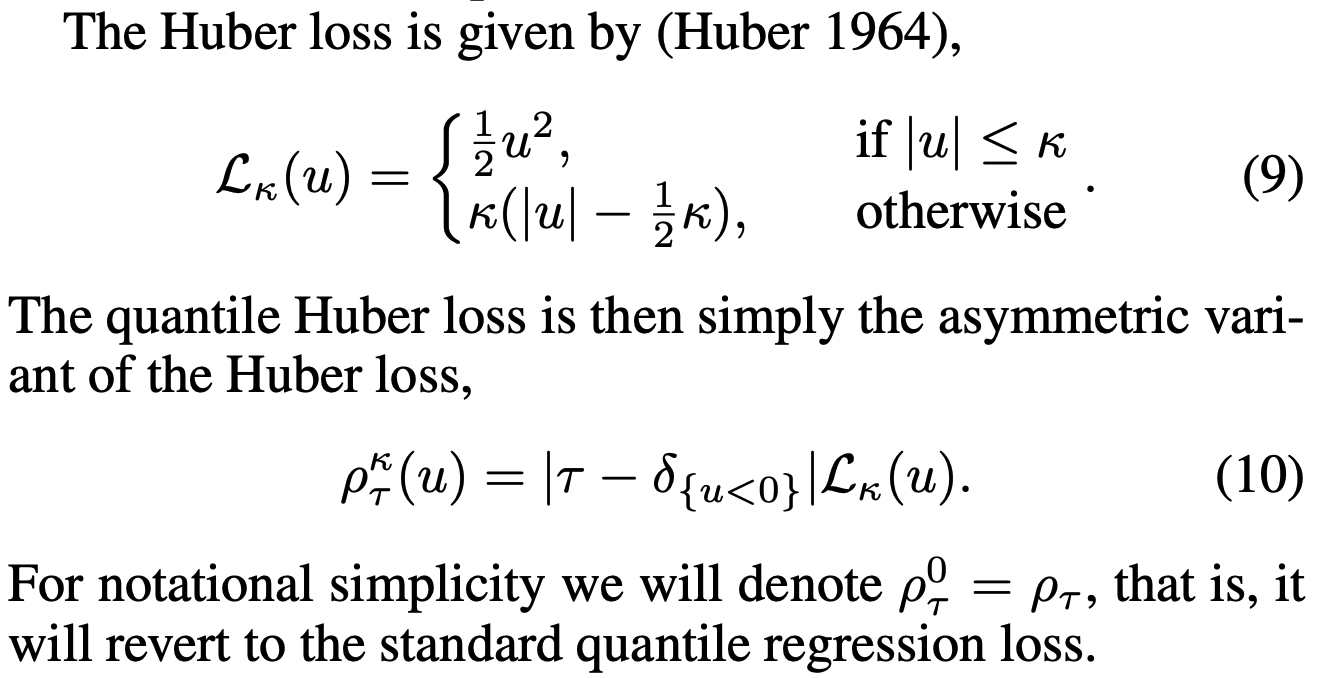
损失函数中 \(\mathcal{T}\theta_j\) 就是目标Q值,即损失函数中Ground Truth
IQN
- 将分位点 \(\tau\) 也作为网络的输入,不再提前假定分位点的值,从而让神经可以拟合整个分布,从而提高对不同分布的表达能力
- 分位数是均匀分布中随机采样的 \(\tau = U[0,1]\)
- 价值函数变为 \(Q_\beta(s,a) = \mathbb{E}_{\tau\sim U[0,1]}[Z_{\beta{\tau}}(s,a)]\)
- 其中 \(\beta(\cdot):[0,1] \rightarrow [0,1]\) 是一个映射函数,可以用于表示不同的风险偏好,借助这个偏好,可以用于实现一些保守策略
- 如果该函数为凸函数(或者在图像上都在单位映射下方),那么就等于往较差情况加了较大的权重,这就产生了风险规避(risk-averse)型的风险偏好;
- 如果该函数为凹函数(或者在图像上都在单位映射上方),那么就等于往较好情况加了较大的权重,这就产生了风险偏好(risk-seeking 或 risk-loving)型的风险偏好;
- 如果该函数就是单位映射,则相当于风险中性(risk-neutral)型的风险偏好
总结
- 相对普通强化学习拟合一个值期望不同,值分布强化学习拟合一个值分布,所以建模难度会更高些
- 值分布有很多用途,比如在风险敏感(Risk-Sensitive)的应用场景中,可以使用分布来帮助决策选择风险低的动作(比如Optimized Cost per Mille in Feeds Advertising中使用借助IQN来选择低风险的出价动作)