PyTorch——einsum函数使用

整体说明：

torch.einsum 是 PyTorch 中一个非常强大且灵活的函数，用于执行基于爱因斯坦求和约定（Einstein summation convention）的张量运算
- 通过这种约定，你可以简洁地表示复杂的多维数组操作，如矩阵乘法、转置、点积等，而不需要显式地编写循环
torch.einsum 提供了极大的灵活性来处理各种复杂的张量运算，但需要注意的是，不恰当的使用可能导致性能下降，因为它可能会隐藏潜在的优化机会（比如矩阵乘法建议直接调用矩阵乘法）
torch.einsum的本质就是爱因斯坦求和约定（一种爱因斯坦发表论文中提到的表达式省略写法），是矩阵乘法的一种表示
- 比如 C = torch.einsum("m,d->nd", A,B)表示矩阵 C[m,d] = A[n]*B[d]，这是个很常用的省略写法

基本用法

torch.einsum 的基本语法如下：
1
torch.einsum(equation, *operands)
- equation：一个字符串，指定了输入张量的下标标签以及输出张量的计算方式
- operands：可变数量的张量参数，它们将根据 equation 进行运算
在 equation 参数中：
- 每个输入张量的维度由字母标记，不同张量之间使用逗号分隔（亲测字符串中间可以随便加空格，不影响最终结果）
  - 相同字母只能表示相同维度Size，但是相同维度Size不要求必须相同字母
  - 下标数量和输入矩阵维度数量一定要对齐
- 输出的维度是在箭头 -> 右侧指定，如果没有指定输出，则自动推断（注意，需要自动推断的场景是没有 -> 的场景，有->的场景不需要推断，->后面为空时表示输出是一个标量）
- 推断思路是：重复下标都去掉，不重复下边按照顺序保留
  - ij,jk == ij,jk->ik
  - j,j == j,j->
  - ijd,jk == ijd,jk->idk
  - idi,jk == idi,jk->djk
举例：给定两个二维张量 A 和 B，要进行矩阵乘法并求和可以写作：
1
torch.einsum('ij,jk->ik', A, B) # 等价于 torch.einsum('ij,jk', A, B)
- 'ij' 表示张量 A 的维度，
- 'jk' 表示张量 B 的维度，
- 'ik' 表示输出张量的维度
- 重复的下标（在这个例子中的 j）意味着沿着这些维度进行乘积和求和（后面会详细讲解）
后面会有详细讲解

爱因斯坦求和约定讲解

以看图学 AI：einsum 爱因斯坦求和约定到底是怎么回事？中的一个例子为例,torch.einsum('ij,jk->ik', A, B) 求解过程相当于下面的图片展示的形式：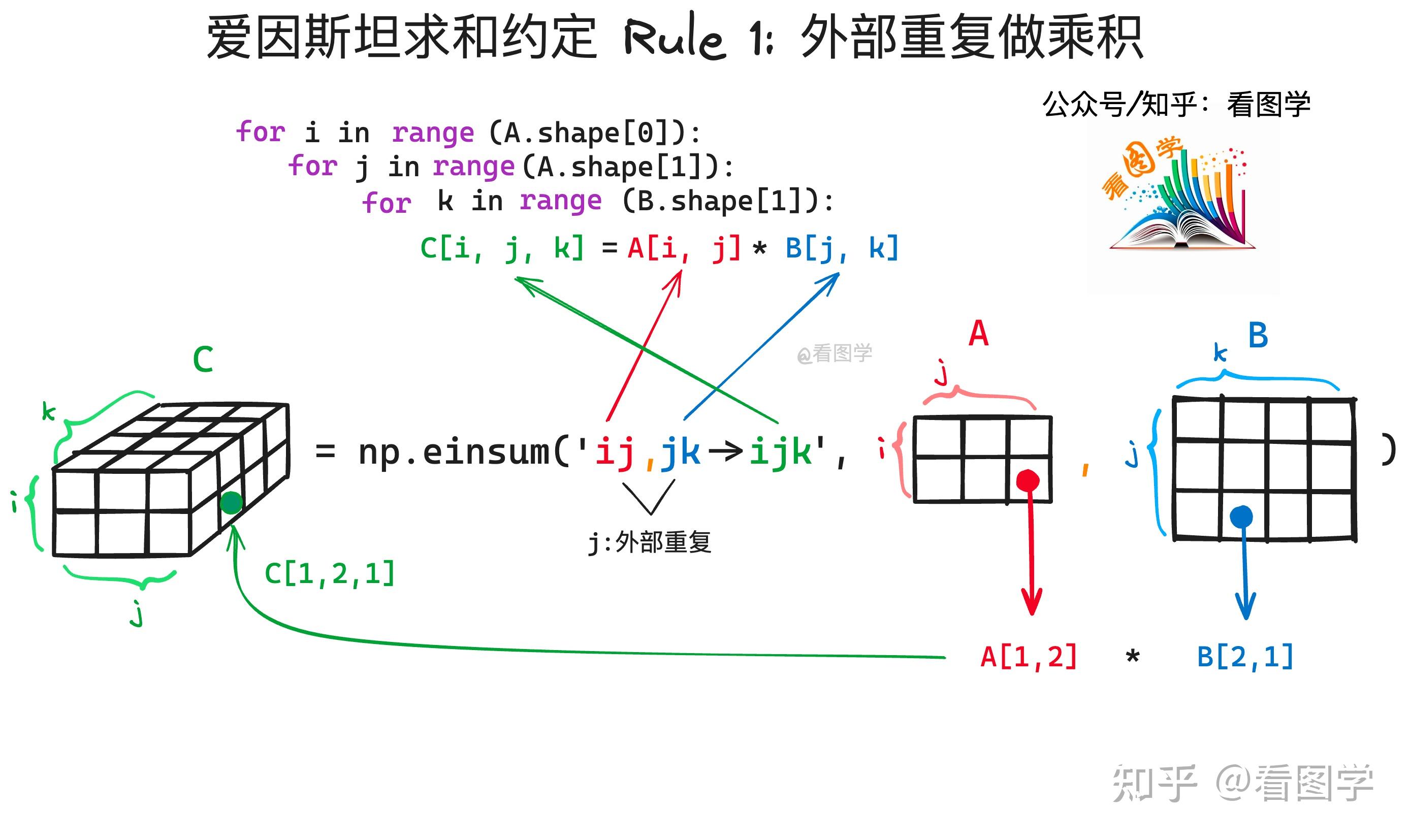
爱因斯坦求和约定的基本理解：
- 对于任意的表达式，结果都等价于一个多重循环乘积（可能包含求和）的过程：
  - 输入：函数参数，字符串 -> 左边表示矩阵的输入下标
  - 输出：返回值，字符串 -> 右边表示矩阵的输出下标
  - 右边的下标有时候可以省略，此时需要自动推断

C = torch.einsum("ij,jk->ijk", A,B) 结果相当于下面的函数（性能上并不想当，因为下面是一种速度较慢的函数）

for i in range(A[0]):
    for j in range(A[1]): # 也可以用 range(B[0])
        for k in range(B[1]):
            C[i][j][k] = A[i][j] * B[j][k]

C = torch.einsum("ij,jk->ik", A,B) 结果相当于下面的函数

for i in range(A[0]):
    for j in range(A[1]): # 也可以用 range(B[0])
        for k in range(B[1]):
            C[i][k] += A[i][j] * B[j][k] # C[i][k]从0开始累加

C = torch.einsum("ii->i", A) 结果相当于下面的函数

1 2	for i in range(A[0]): # 也可用A[1] C[i] = A[i][i]

实际上，所有的表达式都可以表达成同一个形式，只要初始化结果的各个元素为0 ，然后统一使用加法即可

附录：一些简单示例

矩阵乘法 ：

1
2
3

A = torch.randn(3, 4)
B = torch.randn(4, 5)
C = torch.einsum('ij,jk->ik', A, B)  # 等价于 torch.mm(A, B)，C[i][k] += A[i][j] * B[j][k]

向量内积 ：

1
2
3

u = torch.randn(3)
v = torch.randn(3)
C = torch.einsum('i,i->', u, v)  # 等价于 torch.dot(u, v)，C += A[i] * B[i]

张量转置 ：

1 2	A = torch.randn(2, 3, 4) C = torch.einsum('ijk->kji', A) # 转置张量 permute(2,1,0)，C[k][j][i] += A[i][j][k]

批量矩阵乘法 ：

1
2
3

A = torch.randn(3, 2, 5)
B = torch.randn(3, 5, 4)
C = torch.einsum('bij,bjk->bik', A, B)  # 对每一批次做矩阵乘法, C[b][i][k] += A[b][i][k] * B[b][k][k]

乘法+求和 ：

1
2
3

A = torch.randn(3, 4)
B = torch.randn(4, 5)
C = torch.einsum('ij,jk->', A, B)  # 输出为一个标量 C += A[i][j] * B[j][k]

附录：高阶用法之省略号

省略号容易误解，不建议使用！

附录：`einops` 包

除了爱因斯坦求和（包含在 torch 包中）外，还有许多相似的爱因斯坦操作（包含在 einops 包中）
einops 包中的函数支持跨框架的数据格式，不仅仅是 PyTorch，比如 NumPy，TensorFlow 等
最常见的有 rearrange 函数，可用于做下面的工作：
- 对张量做更高阶的 reshape 或 view 操作
- 对张量做 permute 或 transpose 操作
特别地，爱因斯坦操作还有些对应的网络层，如 rearrange 函数对应的 einops.layers.torch.Rearrange 类可以像 nn.Linear 或 nn.ReLU 一样加入到 nn.Sequential() 中作为一个网络模块使用

rearrange 函数的简单示例

import torch
import einops

A = torch.randn(6,2,3,4)
B = einops.rearrange(A, 'b c d e -> b (c d e)') # 等价于 A.reshape(6, -1)
print(B.shape)
# 输出：torch.Size([6, 24])

A = torch.randn(6,2,3,4)
B = A.reshape(6, -1)
print(B.shape)
# 输出：torch.Size([6, 24])

A = torch.randn(6,2,3,4)
B = einops.rearrange(A, 'b c d e -> b e d c') # 等价于 A.permute(0, 3, 2, 1)
print(B.shape)
# 输出：torch.Size([6, 4, 3, 2])

A = torch.randn(6,2,3,4)
B = A.permute(0, 3, 2, 1)
print(B.shape)
# 输出：torch.Size([6, 4, 3, 2])

# 更复杂的用法
A = torch.randn(2, 3, 9, 8)
B = einops.rearrange(A, 'b c (d1 d2) (e1 e2) -> b c (d1 e1) d2 e2', d1=3, e1=2)
print(B.shape)
# 输出：torch.Size([2, 3, 6, 3, 4])

reduce 函数的简单示例（可选的 reduction 参数有 'sum','max','min','mean' 等）：

import torch
import einops

A = torch.randn(6,2,3,4)
B = einops.reduce(A, 'b c d e ->b c d', reduction='sum') # 等价于 A.sum(-1)
print(B.shape)
# 输出：torch.Size([6, 2, 3])

A = torch.randn(6,2,3,4)
B = einops.reduce(A, 'b c d e ->b c', reduction='sum') # 等价于 A.sum(-1).sum(-1)
print(B.shape)
# 输出：torch.Size([6, 2])

A = torch.randn(6,2,3,4)
B = einops.reduce(A, 'b c d e ->b c 1 1', reduction='mean') # 等价于 A.sum(-1).sum(-1)
print(B.shape)
# 输出：torch.Size([6, 2, 1, 1])