注:本文包含 AI 辅助创作
汇总一些暂时没有完整阅读的论文简读结果
Retaining by Doing
- Retaining by Doing: The Role of On-Policy Data in Mitigating Forgetting, 20251021, Princeton University, Danqi Chen Group
- 动机:
- 灾难性遗忘(catastrophic forgetting)发生的原因是什么?
- 如何避免灾难性遗忘
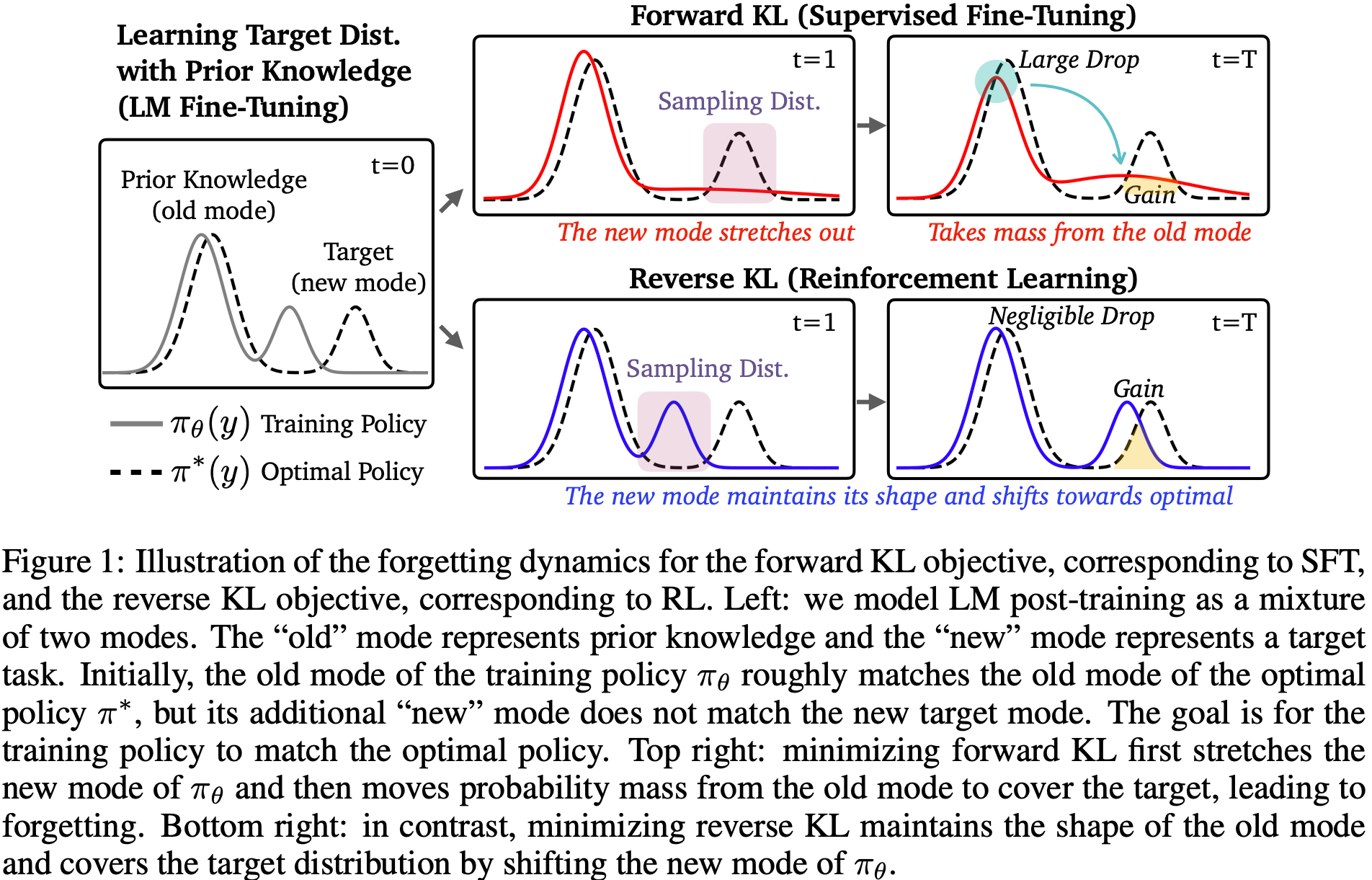
- 一些分析,核心针对 SFT 和 RL 两种对齐手段进行研究,从 forward KL(通过 SFT 最小化交叉熵损失等价于最小化与最优策略 (optimal policy) ) 和 reverse KL 的视角看遗忘问题:
- 贡献、工作:
- 设计了一套评测方式和指标,评估模型在新任务上的 Gain 和在旧任务上的 Drop
- 发现了 RL 更容易记得住的原因是因为 On-policy 数据,而不是损失函数等(GRPO 和 REINFORCE 结论相同)
- 也不是其他算法选择,如优势估计或 KL 正则化的应用
- 提出 Iterative-SFT 来让 SFT 像 RL 一样记住旧任务的数据分布
- 结论:
- 遗忘的本质是分布的错位
- 模型分布错位最主要的原因是因为数据偏移
- 核心 Insights:
- SFT 是 mode-covering,forward KL
- RL 是 mode-seeking,reverse KL
- 如果初始策略是单峰的 (uni-modal)
- 那么 SFT 实际上可能比 RL 对遗忘更鲁棒;
- 如果初始策略是多峰的 (multi-modal):这对于实际的 LM 来说 arguably 是实际情况
- 那么 mode-seeking 的 RL 导致的遗忘比模式覆盖的 SFT 更少
附录:实验中使用到的方法
- SFT 方法:which uses responses generated by Llama-3.3-70B-Instruct as ground truth responses
- Self-SFT 方法:which uses responses generated by the initial model (we keep only the correct responses based on the reward function)
- RL 方法(以 GRPO 为主)
附录:reverse KL 和 forward KL
- 注:reverse KL 的使用还可以参考 On Reinforcement Learning and Distribution Matching for Fine-Tuning Language Models with no Catastrophic Forgetting, NeurIPS 2022
- reverse KL 和 forward KL 是机器学习和概率分布比较中常见的两个概念,都与 KL 散度(Kullback–Leibler Divergence)有关
- KL 散度是用来衡量两个概率分布之间差异的一个非对称度量,对于两个分布 \(P(x)\) 和 \(Q(x)\),KL 散度定义为:
$$
D_{\mathrm{KL} }(P \parallel Q) = \sum_x P(x) \log \frac{P(x)}{Q(x)}
$$ - 或在连续情况下:
$$
D_{\mathrm{KL} }(P \parallel Q) = \int P(x) \log \frac{P(x)}{Q(x)} dx
$$- 非对称性 :\(D_{\mathrm{KL} }(P \parallel Q) \neq D_{\mathrm{KL} }(Q \parallel P)\)
- 意义 :它可以理解为:如果真实分布是 \(P\),而论文用 \(Q\) 来近似,那么 KL 散度表示额外消耗的信息量(即编码代价的增加)
Forward KL
- Forward KL
$$
D_{\mathrm{KL} }(P \parallel Q) = \int P(x) \log \frac{P(x)}{Q(x)} dx
$$ - 优化方向:真实分布 \(P\) 在前,近似分布 \(Q\) 在后
- 特点:
- 优化含义:在模型训练中,最小化 Forward KL 相当于让近似分布 \(Q\) 尽量覆盖真实分布 \(P\) 的所有概率质量
- 对于 \(P\) 中概率较大的区域,若 \(Q\) 赋值过低,会有很大惩罚
- 会倾向于 覆盖所有高概率区域 ,即 mode-covering
- 应用场景:常见于最大似然估计(MLE),比如语言模型训练时用训练数据的分布 \(P\) 拟合模型分布 \(Q\)
Reverse KL
- Reverse KL
$$
D_{\mathrm{KL} }(Q \parallel P) = \int Q(x) \log \frac{Q(x)}{P(x)} dx
$$ - 优化方向:近似分布 \(Q\) 在前,真实分布 \(P\) 在后
- 特点:
优化含义:最小化 Reverse KL 会让 \(Q\) 专注于匹配 \(P\) 中概率较高的区域,而忽略概率很低的部分- 在 \(Q\) 中赋值很高但 \(P\) 非常低的区域会受到强烈惩罚
- 倾向于 集中在一个或几个模式上 ,即 mode-seeking
- 应用场景:常见于变分推断(Variational Inference),因为计算 \(D_{\mathrm{KL} }(Q \parallel P)\) 更容易在某些情况下进行采样和估计
Reverse KL vs Forward KL
- 两者对比表格如下:
对比项 Forward KL (\(P \parallel Q\)) Reverse KL (\(Q \parallel P\)) 惩罚重点 忽略真实分布的高概率区域 包含不真实的低概率区域 行为倾向 Mode-covering(覆盖所有模式) Mode-seeking(集中于少数模式) 常见应用 最大似然估计、监督学习 变分推断、近似推理 计算难度 需要能从 \(P\) 采样 需要能从 \(Q\) 采样
举例理解
- 假设真实分布 \(P\) 有两个峰(双峰分布),而我们用一个单峰分布 \(Q\) 来近似:
- Forward KL 会让 \(Q\) 尽量覆盖两个峰,即可能变得更宽、更平,以覆盖所有高概率区域
- Reverse KL 会让 \(Q\) 只选择其中一个峰(概率最大的那个),从而集中在一个模式上
On-Policy Distillation(Thinking Machines)
On-Policy Distillation,目前常常简称为 OPD
背景:
- 动机:论文主要研究如何高效将大模型的能力蒸馏到小模型上
- Qwen3 技术报告 Qwen3 Technical Report, Qwen, 20250514 中提到了 On-Policy Distillation 方法:
On-policy Distillation: In this phase, the student model generates on-policy sequences for fine-tuning. Specifically, prompts are sampled, and the student model produces responses in either /think or /no think mode. The student model is then fine-tuned by aligning its logits with those of a teacher model (Qwen3-32B or Qwen3-235B-A22B) to minimize the KL divergence
- 方法理解:
- 第一步:使用学生模型采样;
- 第二步:在采样得到的样本上,用学生模型对齐教师模型的输出 logits
On-policy distillation 方法概述:
- 从小模型采样数据(rollout)
- 借助大模型的输出 logits 对小模型进行强化训练(理解:本质是用大模型的输出 logits 作为稠密奖励,此时每个 Token 上都有奖励)
- 注:Qwen3 中主要是直接对齐 logits,这里则是仍然用 RL 的损失形式,KL 散度用作 advantage
三种方法对比:
- SFT 奖励密集,但是是 off-policy 的
- RL 是 On-policy 的,但是奖励稀疏
- On-policy distillation 既是 on-policy 的,奖励也是密集的
- 三种方法对比
Method Sampling Reward signal Supervised finetuning off-policy dense Reinforcement learning on-policy sparse On-policy distillation on-policy dense
On-policy distillation 实现伪代码(具体实现代码地址: github.com/thinking-machines-lab/tinker-cookbook/blob/main/tinker_cookbook/rl/train.py):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17# Initialize teacher client (main):
teacher_client = service_client.create_sampling_client(
base_model=teacher_config.base_model,
model_path=teacher_config.load_checkpoint_path,
)
# Sample trajectories (main):
trajectories = do_group_rollout(student_client, env_group_builder)
sampled_logprobs = trajectories.loss_fn_inputs["logprobs"]
# Compute reward (compute_teacher_reverse_kl):
teacher_logprobs = teacher_client.compute_logprobs(trajectories)
reverse_kl = sampled_logprobs - teacher_logprobs
trajectories["advantages"] = -reverse_kl
# Train with RL (train_step):
training_client.forward_backward(trajectories, loss_fn="importance_sampling")- 注意,这里也用到了 reverse KL:
$$
\begin{align}
\text{Reverse-KL}(\pi_{\theta} \mid\mid \pi_{\text{teacher}}) &= \mathbb{E}_{x \sim \pi_{\theta}} \left[ \log \frac{\pi_{\theta}(x_{t+1} \mid x_{1..t})}{\pi_{\text{teacher}}(x_{t+1} \mid x_{1..t})} \right] \\
&= \mathbb{E}_{x \sim \pi_{\theta}} \left[ \log \pi_{\theta}(x_{t+1} \mid x_{1..t}) - \log \pi_{\text{teacher}}(x_{t+1} \mid x_{1..t}) \right]
\end{align}
$$- 从
student_client采样,则有reverse_kl = sampled_logprobs - teacher_logprobs - 为了最小化
reverse_kl,伪代码中将负的reverse_kl分配给 Advantage:- 赋值代码:
trajectories["advantages"] = -reverse_kl - 代码解读:最大化 Advantage,等于最小化 Reverse-KL 散度
- 赋值代码:
- 从
- 这里的 Advantage 看似和 MiMo-V2-Flash 技术博客的 MOPD 实现是反的,但实际上是一样的,因为 OPD 这里是先是先计算 Reverse-KL 散度的公式,然后再加个 负号的,MiMo-V2-Flash 里相当于没有这个负号了
- 理解:最终含义相同,都是最大化 Advantage,等于最小化 Reverse-KL 散度
- 注意,这里也用到了 reverse KL:
应用场景 1:Distillation for reasoning
- 类似 Qwen3 做的事情,通过蒸馏赋予小模型思考的能力
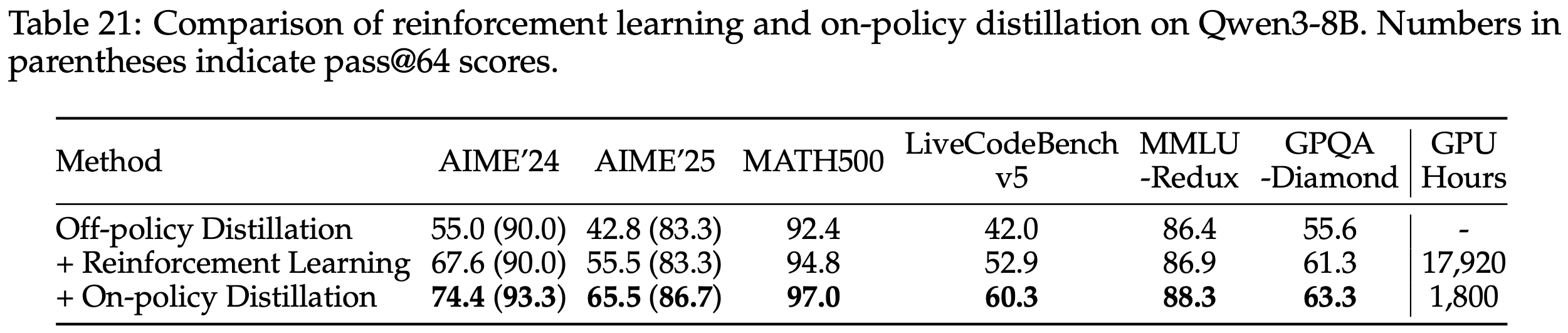
- 论文进行了更详细的实验验证效率(On-policy distillation 和 SFT-2M (extrapolated) 是在性能差不多的情况下对比的)
Method AIME’24 Teacher FLOPs Student FLOPs CE vs SFT-2M Initialization: SFT-400K 60% 8.5 × \(10^{20}\) 3.8 × \(10^{20}\) – SFT-2M (extrapolated) ~70% (extrapolated) 3.4 × \(10^{21}\) 1.5 × \(10^{21}\) 1× Reinforcement learning 68% - - \(\approx\)1× On-policy distillation 70% 8.4 × \(10^{19}\) 8.2 × \(10^{19}\) 9-30× - 9-30 的差异是是否包含 SFT-2M 的分母:
- 9(9 倍加速):表示 CE = (On-policy distillation Student + On-policy distillation Teacher) / (SFT-2M Student)
- 此时表示 SFT 数据已经有了的场景(无需从 大模型重新采样 SFT 数据)
- 30(30 倍加速):表示 CE = (On-policy distillation Student + On-policy distillation Teacher) / (SFT-2M Student + SFT-2M Teacher)
- 此时表示 SFT 数据还没有的一般性场景(需要从大模型重新采样 SFT 数据)
- 注意:On-policy distillation 是不需要使用大模型采样 SFT 的,仅仅需要一次 推理(非生成式推理)得到 logits 即可
- 9(9 倍加速):表示 CE = (On-policy distillation Student + On-policy distillation Teacher) / (SFT-2M Student)
- 关于表格的其他解读
- RL 达到和 SFT 差不多的性能,需要的资源差不多
应用场景 2:Distillation for personalization
- 目标:通过蒸馏赋予小模型一些个性化能力,比如某个领域知识的助手
- 阶段一:首先训练新任务(注:老任务性能会下降)
- 为防止灾难性遗忘(catastrophic forgetting),加入一些预训练数据
- 由于无法获得 Qwen3 的预训练数据,这里使用 Qwen3-8B 在 chat 指令遵循数据集 Tulu3 上生成数据
- 调整了不同混合比例的超参数,但无论如何旧任务 IFEval 性能都有下降
- 使用不同的 LoRA rank,依然无法阻止 IFEval 性能下降
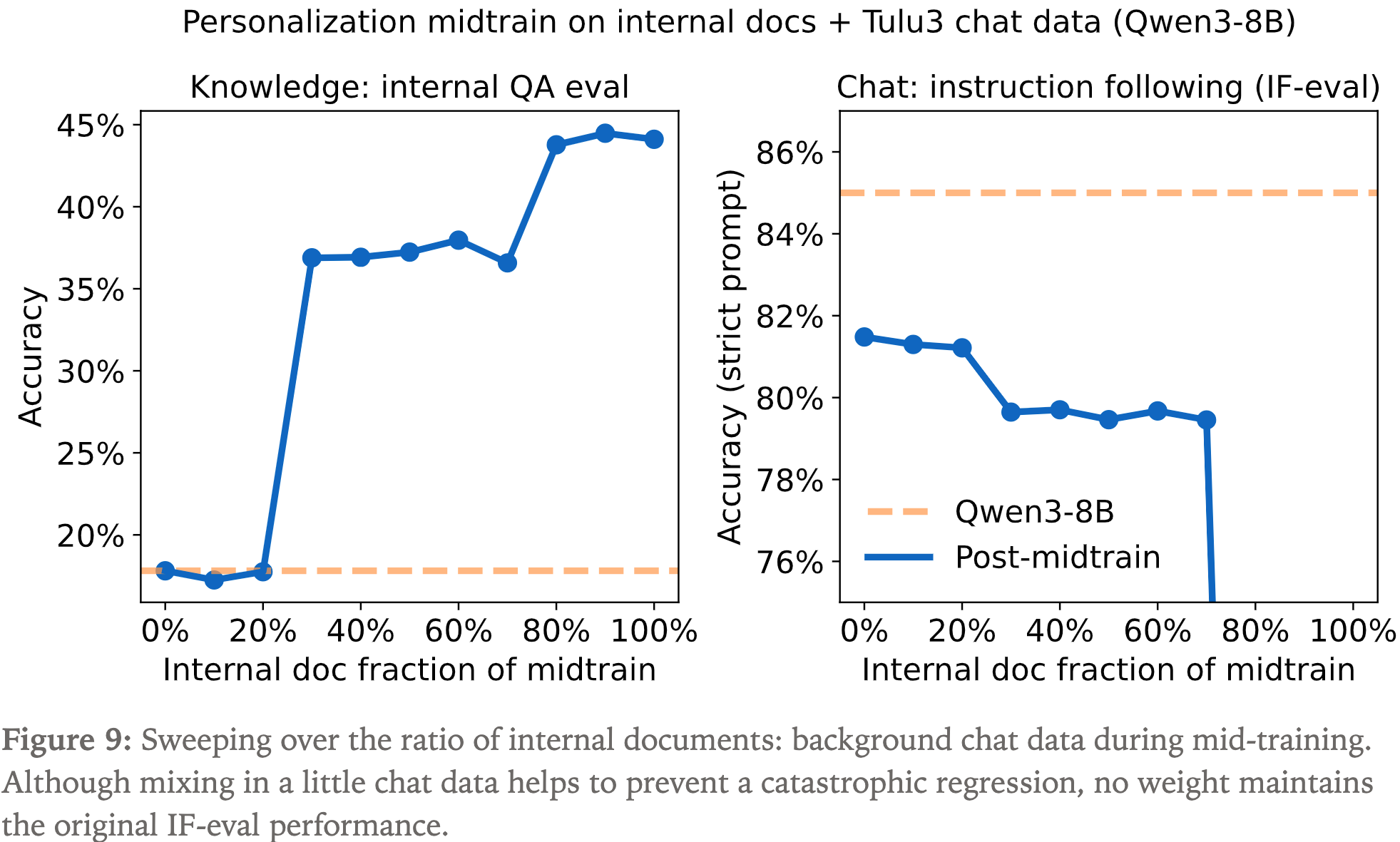
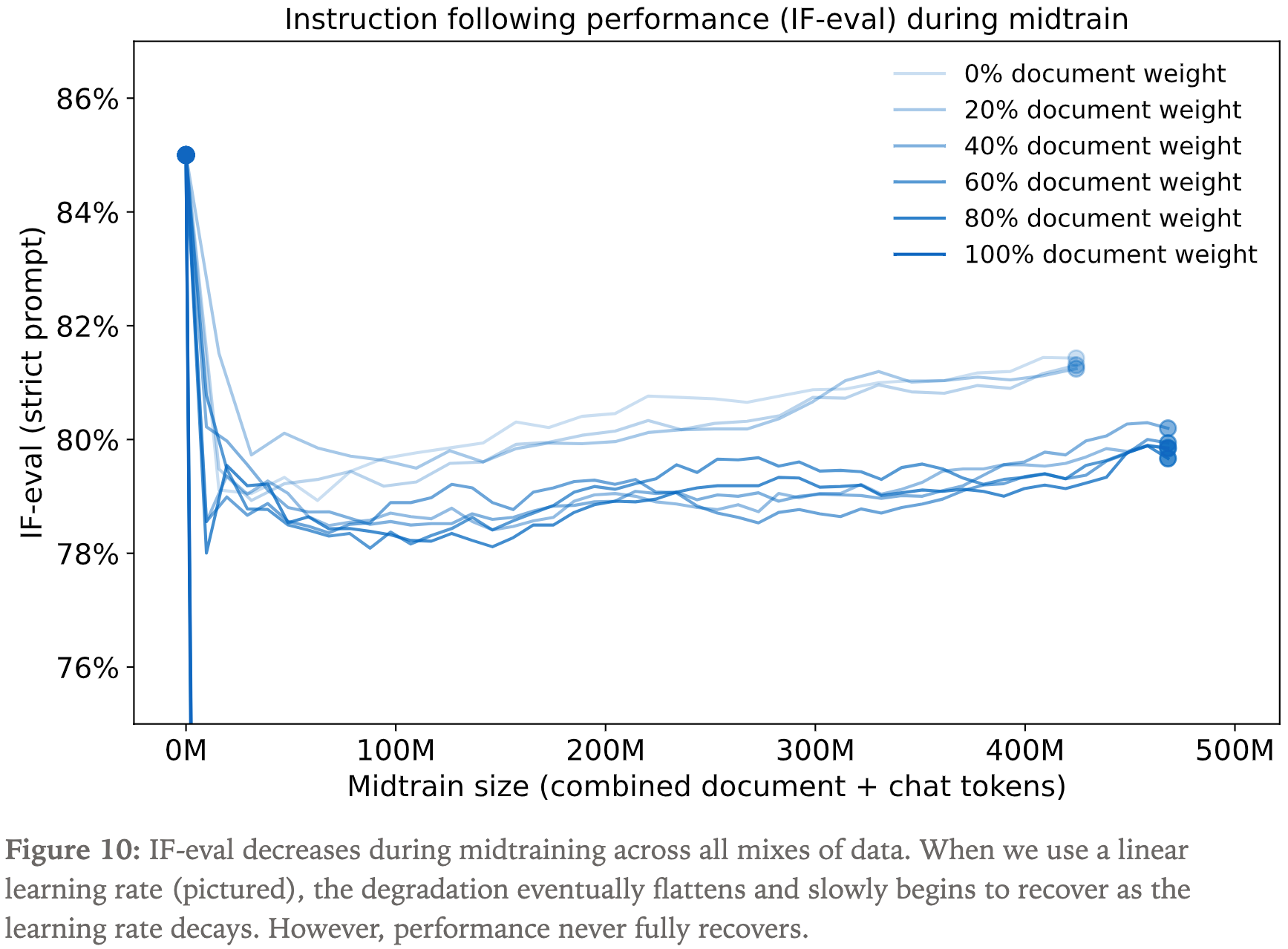
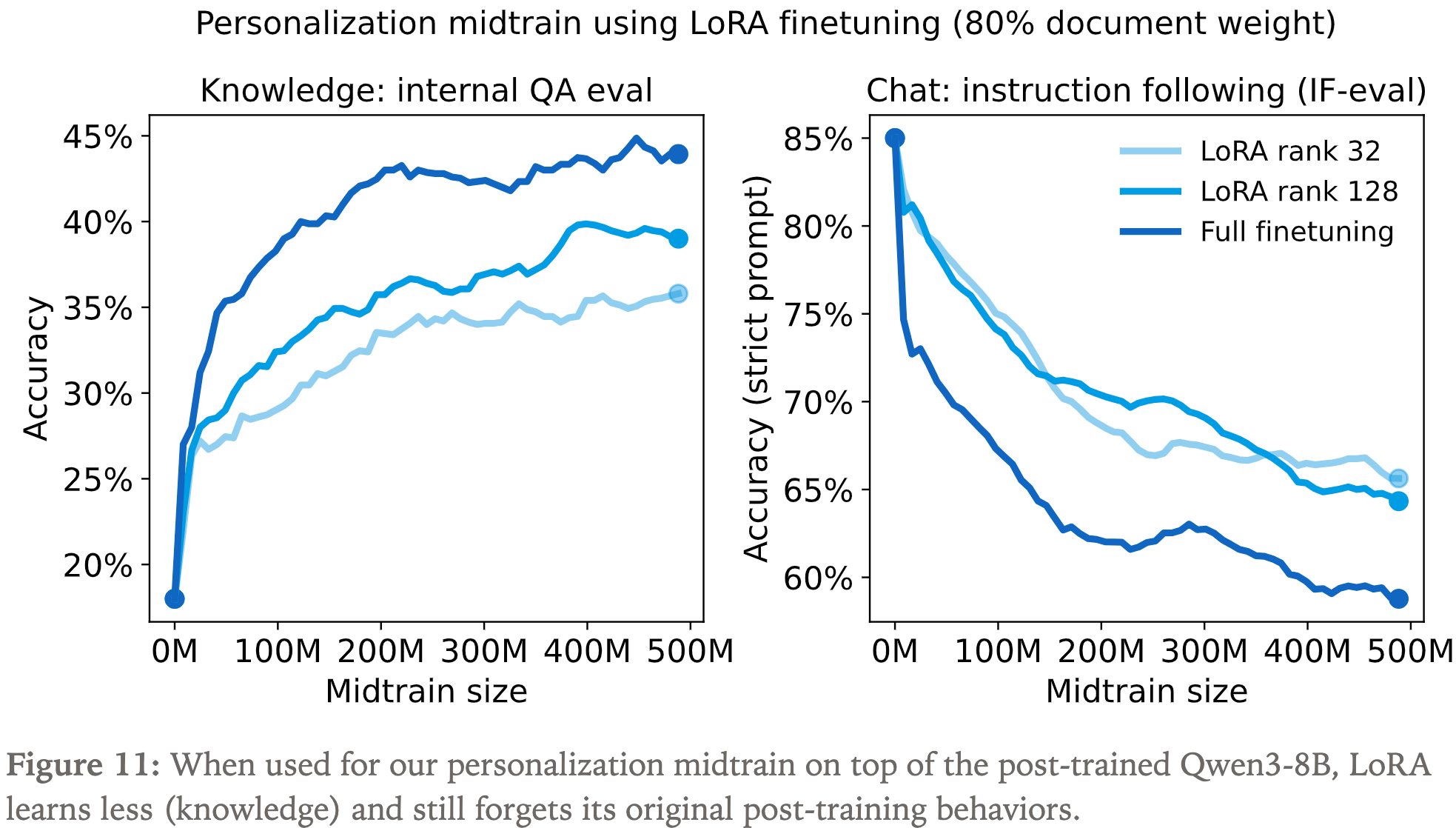
- 为防止灾难性遗忘(catastrophic forgetting),加入一些预训练数据
- 阶段二:接着通过 On-policy Distillation 代替 RL 来激发 IFEval 的能力
- 方法:在 Tulu3 数据集,用 Qwen3-8B 作为教师模型,对上一步得到的目标模型进行蒸馏
- 注:这里是以提升 IFEval 能力为主,这个阶段领域任务旧任务,因为这一阶段的目标是恢复模型 IFEval 的能力
- 提升 IFEval 的同时,为了保留上一阶段学到的 领域知识能力,这里使用数据组合的形式输入
- 最终结论:几乎做到了领域知识和指令遵循能力双高
Model Internal QA Eval (Knowledge) IF-eval (Chat) Qwen3-8B 18% 85% + midtrain (100%) 43% 45% + midtrain (70%) 36% 79% + midtrain (70%) + distill 41% 83%
- 最终结论:几乎做到了领域知识和指令遵循能力双高
- 方法:在 Tulu3 数据集,用 Qwen3-8B 作为教师模型,对上一步得到的目标模型进行蒸馏
- 可以迭代执行第一阶段和第二阶段,循环提升模型效果
讨论和思考
- RL 和 On-policy Distillation 的区别:
- On-policy Distillation 的奖励更稠密,效率更高
- RL 中,每个 rollout 信息只是提供 \(O(1)\) bits 的信息(参见 Thinking Machines 的 LoRA Without Regret 博客)
- On-policy Distillation 中,每个 rollout 信息只是提供 \(O(N)\) bits 的信息
- 作者给出了实验验证这个结论:
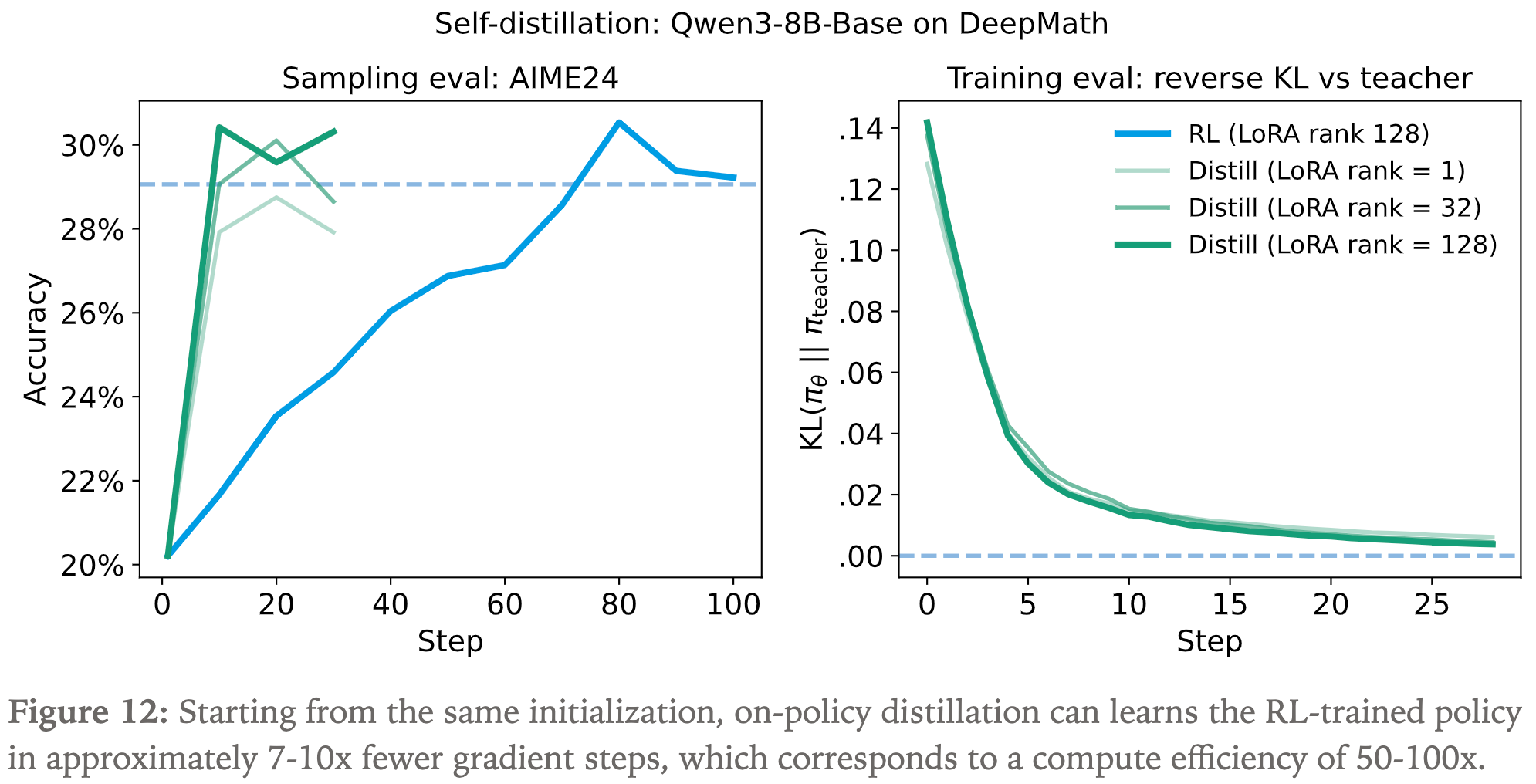
- On-policy Distillation 的奖励更稠密,效率更高
- 重用 Prompt
- Prompt 是稀缺的,可以让一个 Prompt 多次 rollout 来实现多次训练
- On-policy Distillation 是学习教师的完整分布,而不是某个答案
- 实验:仅使用一个 Prompt 来训练,依然在 20 个 Step 后,在 AIME 上得到了较大的效果提升
- 一个新的理解:RL searches in the space of semantic strategies
- 即 RL 是在语义空间中搜索
- 而作为 RL 的良好替代, On-policy Distillation 则直接学习最终的策略,不需要探索过程(这是更简单的)
- 持续学习的应用:On-policy learning as a tool for continual learning
- RL 只能塑造行为,不能学习新知识,不足以用于持续学习
- SFT 训练时,即使使用 On-policy 的方法(使用模型自己 Rollout 得到的样本)进行 SFT,在 Qwen-32B 上看到 IFEval 也是有下降的
- 关于这一点现象的原因,原始博客中的解释有点奇怪
- 更容易理解的解释:模型产生的序列是以一定概率的,直接进行 SFT 相当于要求模型 100% 输出这个序列,所以模型分布会发生改变
- On-policy Distillation 的目标是收敛到教师模型,所以不会像 SFT 一样出现性能的衰退
- 相当于将大模型的知识注入小模型?问题是 Prompt 难以引导小模型生成想要的知识吧
- 个人理解: On-policy Distillation 本质是一个将 教师模型作为 Token-level 稠密奖励模型的 RL 方法
Teacher 和 Student 的分数差多少时,适合使用 OPD ?
- 一般来说,Teacher 比 Student 好的越多,OPD 效果越好,否则 OPD 可能反而会影响 Student 的信号(限制 Student 模型的效果上限)
- 待补充:Teacher 比 Student 好多少时适合用 OPD?
OPD 和其他 RL 方法可以联合使用
- 因为 OPD 和其他 RL 方法,如 GSPO/GRPO/Dr.GRPO 等是正交的,所以可以选择在不同的方法下使用 OPD
TTT(Test-Time Training)
- 原始论文:Learning to (Learn at Test Time): RNNs with Expressive Hidden States, Stanford & Meta AI, 20240705 & 多次更新
- TTT 是一种新型的序列建模层设计框架,是一种将测试时学习机制嵌入序列建模层的新范式
- 其核心思想是将隐藏状态本身定义为一个机器学习模型,并通过自监督学习在测试时动态更新该模型
- TTT 通过将隐藏状态建模为可学习的模型,并在推理过程中持续优化,从而在保持线性复杂度的同时提升对长上下文的建模能力
- 理解:TTT 是一种更高阶的序列建模范式,其覆盖了普通的线性注意力和自注意力机制
TTT 核心方法设计
- 传统序列建模
- 传统的 RNN 层(如 LSTM、Mamba)将历史上下文压缩成一个固定大小的隐藏状态 ,这限制了其在长上下文中的表达能力
- Transformer 虽然表达能力更强,但其注意力机制具有二次复杂度 ,不适合长序列
- TTT 核心思想:
- 隐藏状态 \(s_t\) 是一个模型 \(f\) 的参数 \(W_t\),例如线性模型或 MLP
- 更新规则 是对该模型在输入序列上进行一步自监督学习(如梯度下降)
- 输出规则 是使用当前隐藏状态(即模型参数)对当前输入进行预测:
$$
z_t = f(x_t; W_t)
$$
- TTT 的更新过程
- 更新过程图示:
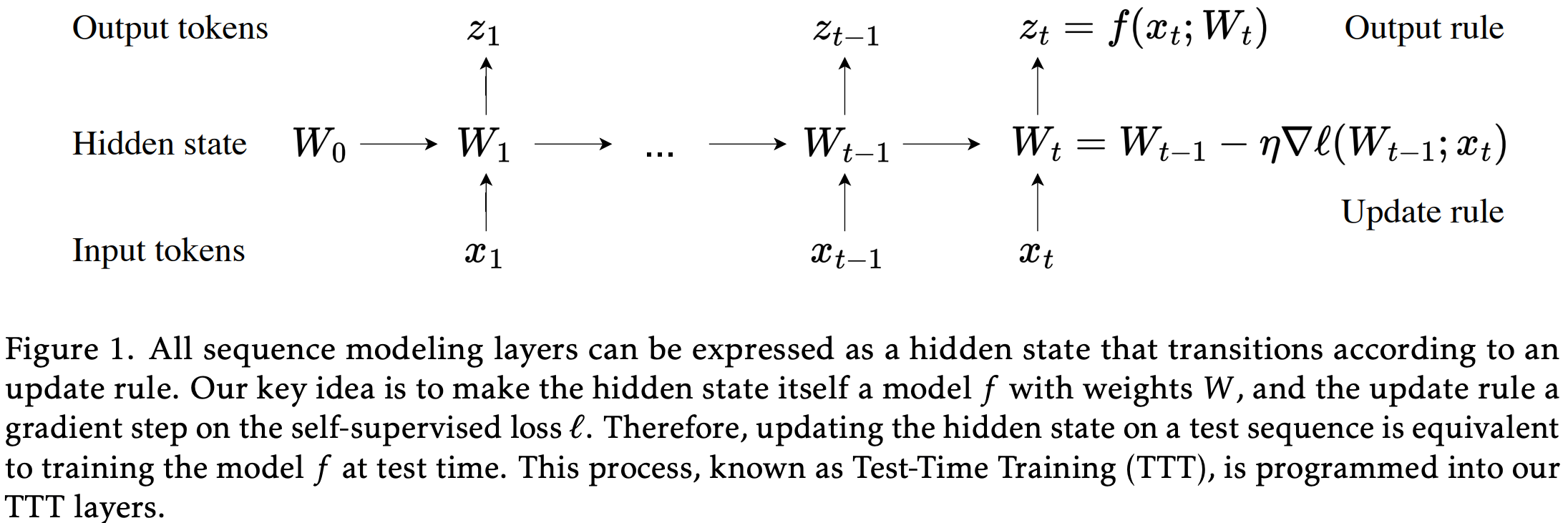
- TTT 层的更新过程可以形式化为:
- 1)初始化隐藏状态 :\(W_0\)(可学习)
- 2)对每个时间步 \(t\) :
- 计算自监督损失(如重建损失):
$$
\ell(W_{t-1}; x_t) = |f(\tilde{x}_t; W_{t-1}) - x_t|^2
$$ - 执行一步梯度下降更新:
$$
W_t = W_{t-1} - \eta \nabla \ell(W_{t-1}; x_t)
$$ - 输出:
$$
z_t = f(x_t; W_t)
$$
- 计算自监督损失(如重建损失):
- 更新过程图示:
- TTT 的两种实例化(论文提出了两种具体的 TTT 层):
- TTT-Linear :隐藏状态是一个线性模型 \(f(x) = Wx\)
- TTT-MLP :隐藏状态是一个两层 MLP,具有更强的表达能力
- 与 Transformer 的对比
对比视角 Transformer TTT层 隐藏状态 KV缓存:一个不断增长的列表,存储所有历史的 \( (K_i, V_i) \) 对 一个机器学习模型的参数 \( W_t \)(如线性模型的权重矩阵);大小固定 更新规则 拼接;将当前词的 \( (K_t, V_t) \) 直接添加到KV缓存列表中 训练/学习;对隐藏状态模型执行一步梯度下降 ,以最小化一个自监督损失(如重建损失);
\( W_t = W_{t-1} - \eta \nabla \ell(W_{t-1}; x_t) \)输出规则 全局注意力;计算当前 Query \( Q_t \) 与缓存中所有历史键 \( K_{1:t} \) 的相似度,然后对值 \( V_{1:t} \) 加权求和;
\( z_t = \text{Attention}(Q_t, K_{1:t}, V_{1:t}) \)前向预测;直接将当前词(或其投影)输入到隐藏状态模型 \( f \) 中,得到输出;
\( z_t = f(x_t; W_t) \)时间复杂度 每生成一个token,都需要扫描整个KV缓存,复杂度为 \( O(t) \);总复杂度为 \( O(n^2) \) 更新和预测的计算量只与隐藏状态模型的大小有关,与序列长度 \( t \) 无关;每token复杂度为 \( O(1) \),总复杂度为 \( O(n) \)
核心实验结论
- TTT 在长上下文(如 16k、32k)中表现优于 Mamba,且能持续利用更多上下文信息降低困惑度
- TTT-Linear 在短上下文中与 Mamba 相当,但在长上下文中优势明显
- TTT-MLP 虽然潜力更大,但由于计算和内存 I/O 的限制,目前效率较低
其他
- 论文还证明了:
- 当 \(f\) 为线性模型且使用批量梯度下降(Batch Gradient Descent)时,TTT 等价于线性注意力
- 当 \(f\) 为 Nadaraya-Watson 核回归估计器时,TTT 等价于自注意力
Titans
- Titans: Learning to Memorize at Test Time, 20241231, Google
- Titans 是一种用于序列建模的架构 ,旨在通过引入长时神经记忆模块 ,解决 Transformer 和现有线性循环模型在处理长序列时的局限性
- Titans 的核心思想是模拟人脑中的短时记忆与长时记忆系统 ,构建一个多模块、可独立运作的记忆体系
- Titans 的优点:
- 长上下文支持 :可扩展到超过 200 万 token 的上下文长度
- 在线记忆学习 :在测试时仍能学习并更新记忆,适应新数据
- 并行化训练 :通过分块和矩阵运算实现高效训练
- 理论表达能力强 :优于 Transformer 和多数线性循环模型,能解决超出 \(\mathrm{TC}^0\) 复杂度的问题
- 总结:Titans 是一个融合短时注意力与长时神经记忆的混合架构 ,通过在线记忆学习、遗忘机制、动量更新和持久记忆 ,实现了对长序列的高效建模和强大推理能力
- 理解:Titans 不仅在多项任务中超越现有模型,还开辟了可测试时学习的记忆增强网络的新方向
Titans 的核心介绍(三个主要模块)
- 模块一:Core(核心模块)
- 负责处理当前上下文,通常使用受限窗口的注意力机制 ,充当短时记忆
- 公式表示:
$$
\mathbf{y}_t = \text{Attn}(\hat{\mathsf{S} }^{(t)})
$$
- 模块二:Long-term Memory(长时记忆模块)
- 是一个神经记忆网络 ,能够在测试时继续学习并存储历史信息
- 使用基于梯度的“惊奇度”机制来决定哪些信息值得记忆:
$$
S_t = \eta_t S_{t-1} - \theta_t \nabla \ell(\mathcal{M}_{t-1}; \boldsymbol{x}_t)
$$ - 包含遗忘机制(权重衰减)来管理记忆容量:
$$
\mathcal{M}_t = (1 - \alpha_t) \mathcal{M}_{t-1} + S_t
$$
- 模块三:Persistent Memory(持久记忆)
- 一组可学习但与输入无关的参数 ,用于存储任务相关的元知识
- 在输入序列前添加:
$$
\boldsymbol{x}_{\text{new} } = [\boldsymbol{p}_1, \dots, \boldsymbol{p}_{N_p}] \parallel \boldsymbol{x}
$$
Titans 的三种变体
- 论文提出了三种将记忆模块整合到架构中的方式:
变体 名称 机制 MAC Memory as a Context 将记忆输出作为当前上下文的补充输入 MAG Memory as a Gate 使用门控机制融合记忆输出与注意力输出 MAL Memory as a Layer 将记忆模块作为网络的一层,与注意力层堆叠
Negative Sample Reinforcement (NSR)
- 原始论文:The Surprising Effectiveness of Negative Reinforcement in LLM Reasoning, Princeton University, Danqi Chen, 20250602 & 20251025
- 参考博客:Negative Sample Reinforcement:负样本强化学习的惊人有效性
- 论文讨论了 RLVR 在 LLM 推理任务中的有效性机制
- 论文聚焦于 RLVR 中正负样本奖励信号的独立作用,核心探究:仅通过惩罚错误样本(负样本强化)是否能提升模型推理性能,以及如何平衡正负样本强化以兼顾推理准确性与输出多样性
Key Decomposition: Positive and Negative Sample Reinforcement
RLVR Objective Function
- RLVR 基于二元奖励(正确 +1、错误 -1)优化模型策略,目标函数为:
$$
\mathcal{L}_{RLVR}(\theta)=-\mathbb{E}_{x \sim \mathcal{D}, y \sim \pi_{\theta}(\cdot | x)}[r(x, y)], \quad r(x, y) \in\{-1,+1\}
$$- 其中 \(\theta\) 为模型参数,\(\mathcal{D}\) 为 Prompt 数据集,\(\pi_{\theta}(y|x)\) 为模型生成响应 \(y\) 的概率分布,\(r(x,y)\) 为可验证奖励函数
Decomposition into PSR and NSR
- 将 RLVR 目标函数拆解为两个独立子目标,分别对应正负样本的学习信号:
- 正样本强化(Positive Sample Reinforcement, PSR):提升正确响应的生成概率,类似有 SFT :
$$
\mathcal{L}_{PSR}(\theta)=-\mathbb{E}_{x \sim \mathcal{D} }\left[\sum_{y: r(x, y)=1} \pi_{\theta}(y | x)\right]
$$ - 负样本强化(Negative Sample Reinforcement, NSR):降低错误响应的生成概率,通过概率重分配优化推理路径:
$$
\mathcal{L}_{NSR}(\theta)=-\mathbb{E}_{x \sim \mathcal{D} }\left[\sum_{y: r(x, y)=-1}-\pi_{\theta}(y | x)\right]
$$ - 完整 RLVR 目标满足
$$ \mathcal{L}_{RLVR}(\theta)=\mathcal{L}_{PSR}(\theta)+\mathcal{L}_{NSR}(\theta)$$- 两者均为在线策略(on-policy)学习,响应样本来自模型自身生成
- 正样本强化(Positive Sample Reinforcement, PSR):提升正确响应的生成概率,类似有 SFT :
Core Method: Negative Sample Reinforcement Mechanism
Gradient Dynamics of NSR
- 通过 Token-level 梯度分析,NSR 的更新规则如下(\(\pi_v=\pi_{\theta}(v|x,y_{ < t})\)为 Token \(v\)的生成概率):
- 对于错误响应中的采样 Token (\(v=y_t\)):抑制其概率
$$
\color{red}{-\frac{\partial \mathcal{L}_{NSR} }{\partial z_{v} } \propto -\pi_{v} \cdot\left(1-\pi_{v}\right)}
$$ - 对于未采样 Token (\(v \neq y_t\)):按当前概率比例提升其权重,保留合理候选
$$
\color{red}{-\frac{\partial \mathcal{L}_{NSR} }{\partial z_{v} } \propto \pi_{y_{t} } \cdot \pi_{v}}
$$ - 其中 \(z_v\) 为 Token \(v\) 的对数几率(logit)
- 对于错误响应中的采样 Token (\(v=y_t\)):抑制其概率
- 该机制具有三大优势:
- 1)保留高置信先验知识:对模型预训练中习得的高概率正确 Token (如语法结构)惩罚较弱;
- 2)先验引导的概率重分配:按模型原有信念优化候选 Token 排序,促进有效探索;
- 3)隐式正则化:错误响应消除后自动停止更新,避免过拟合与多样性坍缩
- 思考:
- 这样可能导致模型长期不收敛,因为未采样到的样本都能分配相同的概率
- 这样还可能导致模型学习很慢,因为正确响应相当于没有被学习,而且不断降低 低概率的 Token,估计得把几乎所有可能的 Token 都访问一遍才能学到?这效率也太低了
Weighted Reinforcement Learning Objective
- 为平衡 PSR 的准确性优势与 NSR 的多样性保留能力,提出加权强化(Weighted-REINFORCE, W-REINFORCE)目标,通过系数 \(\lambda\) 下调 PSR 权重:
$$
\color{red}{\mathcal{L}_{W-REINFORCE }(\theta)=\lambda \cdot \mathcal{L}_{PSR}(\theta) + \mathcal{L}_{NSR}(\theta)}
$$- 其中 \(\lambda=0.1\)(实验最优值),当 \(\lambda=1\) 时退化为标准 REINFORCE,\(\lambda=0\) 时等价于纯NSR
- 思考:
- 相对仅使用 NSR 的方法,这个思路比较合理
Experimental Design
Models and Datasets
- Base Model :Qwen2.5-Math-7B、Qwen3-4B(非思考模式)、Llama-3.1-8B-Instruct;
- 训练数据集:MATH(7500道数学题);
- 评估基准:MATH、AIME 2025、AMC23,核心指标为全谱Pass@k(\(k=1,2,…,256\)),衡量不同采样次数下的正确响应率
Comparative Algorithms
- 包括 PPO(2017)、GRPO(2025)、标准 REINFORCE(1992)、纯 PSR、纯 NSR,其中 PPO 与 GRPO 采用 KL 正则化(系数 1e-3)和裁剪机制(clip ratio=0.2)稳定训练
核心结论
- 纯 NSR 的意外有效性:无需强化正确样本,即可在全 Pass@k 谱上超越 Base Model ,甚至匹配/超越 PPO 与 GRPO,尤其在大 k(如256)时表现更优;
- PSR 的局限性:仅提升 Pass@1(贪心解码准确性),但因多样性坍缩导致大 k 时性能下降;
- W-REINFORCE 的优势:在 MATH、AIME 2025、AMC23 上均实现准确性与多样性的平衡,多数 k 值下超越现有RL算法;
- 模型依赖性:NSR 对 Qwen 系列模型提升显著,但对 Llama-3.1-8B-Instruct 的性能降解最小,说明骨干模型特性影响 RL 效果(2025)
Contrastive Decoding (CD)
- 原始论文:Contrastive Decoding: Open-ended Text Generation as Optimization, Stanford & CMU & FAIR, 2023
- 参考博客:[2]Contrastive Decoding: 一种可提高文本生成质量的解码方法 - 机器爱学习的文章 - 知乎
- 对比解码(Contrastive Decoding, CD) 是一种无额外训练的搜索式解码方法 ,通过利用不同规模语言模型的差异优化生成目标,在保证流畅性的同时提升文本连贯性和多样性,解决了传统解码中重复、不连贯或主题漂移的问题
Core Design Idea
- 核心观察:小型语言模型(Amateur LM)比大型语言模型(Expert LM)更容易出现重复、主题漂移等不良生成行为,而大型模型在合理输出上的概率分配更具优势
- 设计目标:通过对比两个模型的概率差异,强化大型模型的优质生成特征,抑制小型模型的不良生成倾向
- 关键特性:无需对模型进行额外训练,直接使用现成(off-the-shelf)的不同规模模型,推理开销低且泛化性强
Core Components
Contrastive Objective Function
- 目标函数定义为大型模型与小型模型对数概率的差值,用于奖励大型模型偏好的优质文本,惩罚小型模型偏好的不良文本:
$$
\mathcal{L}_{CD}(x_\text{cont}, x_\text{pre}) = \log p_\text{EXP}(x_\text{cont} | x_\text{pre}) - \log p_\text{AMA}(x_\text{cont} | x_\text{pre})
$$- \(x_\text{pre}\) 为输入 Prompt
- \(x_\text{cont}\) 为生成的续文
- \(p_\text{EXP}\) 表示大型专家模型(如 OPT-13B、GPT-2 XL)的概率分布
- \(p_\text{AMA}\) 表示小型 amateur 模型(如 OPT-125M、GPT-2 Small)的概率分布
自适应合理性约束(Adaptive Plausibility Constraint, \(V_{head}\))
- 为解决对比目标可能导致的虚假阳性(奖励不合理 token)和虚假阴性(惩罚合理 token)问题,引入基于大型模型置信度的约束,筛选出概率足够高的候选 token:
$$
\mathcal{V}_{head}(x_{ < i}) = \left\{x_i \in \mathcal{V} : p_\text{EXP}(x_i | x_{ < i}) \geq \alpha \max_w p_\text{EXP}(w | x_{ < i})\right\}
$$- \(\alpha\) 为超参数(论文中固定为 0.1)
- \(\mathcal{V}\) 为词汇表
- \(x_{ < i}\) 表示第 \(i\) 个 token 之前的上下文
- 理解:不用这么麻烦,直接替换 \(\max_w p_\text{EXP}(w | x_{ < i}) \rightarrow 1\) 应该是可以的
Full Decoding Framework
- 结合对比目标和合理性约束,通过束搜索(beam search,束宽设为 5)优化 token-level 得分,流程如下:
- 1)基于 \(V_{head}\) 筛选出大型模型高概率候选 token;
- 2)计算候选 token 的对比得分(CD-score):
$$
\color{red}{\text{CD-score}(x_i; x_{ < i}) =
\begin{cases}
\log \frac{p_\text{EXP}(x_i | x_{ < i})}{p_\text{AMA}(x_i | x_{ < i})}, & \text{if } x_i \in \mathcal{V}_{head}(x_{ < i}), \\
-\inf, & \text{otherwise.}
\end{cases}}
$$ - 3)选择对比得分最高的 token 作为下一个生成 token,迭代完成续文生成
- 理解:核心步骤
Amateur LM Selection Strategy
- 规模差异:优先选择同模型家族中最小的模型作为 amateur(如 OPT-13B 搭配 OPT-125M),规模差距越大,生成质量越优;
- 温度调节:通过调整 amateur 模型的温度参数 \(\tau\)(GPT-2 实验中设为 0.5,OPT 实验中设为 1.0),强化其不良行为特征;
- 上下文限制:可限制 amateur 模型的上下文窗口(如仅使用最后一个 token),进一步突出大型模型的连贯性优势
- 问题:若仅使用最后一个 Token,那还不如用统计了吧?或者说用统计也可以?
- 创新思考:是否可以在学习时基于统计或者学习一个简单模型,然后预训练或者 SFT 直接针对这个比值进行训练?
- 补充:其实最新有论文是这样做的
Key Features and Advantages
- 无额外训练:直接使用预训练模型,无需微调或重新训练,部署成本低;
- 跨模型泛化:适用于 GPT-2、OPT 等不同家族和规模的模型;
- 多维度优化:在自动评估(MAUVE 得分、连贯性得分)和人工评估(流畅性、连贯性)中均显著优于 nucleus sampling、top-k、典型解码等基线方法;
- 鲁棒性强:实验来看,超参数(\(\alpha\)、\(\tau\))在较广范围内(如 \(\tau \in [0.5, 1.0]\))性能稳定
LightReasoner
- 原始论文:LightReasoner: Can Small Language Models Teach Large Language Models Reasoning?, HKU, 20251009
- 参考博客:小模型当老师,大模型反而学得更好了?
- 论文的基本思路来自于 Contrastive Decoding: Open-ended Text Generation as Optimization, Stanford & CMU & FAIR, 2023
- TLDR:针对传统 SFT 资源消耗大、训练效率低的问题,提出一种反直觉框架:
- 利用小语言模型(Small Language Model, SLM)作为“业余模型(Amateur Model)”,通过其与大型语言模型(Large Language Model, LLM)“专家模型(Expert Model)”的行为差异,定位高价值推理时刻,为专家模型提供精准监督信号,实现高效推理能力提升,且无需依赖真实标签(Ground-Truth Labels)
Key Theoretical Foundations
Autoregressive Language Model Generation
- 给定词汇表 \(\mathcal{A}\) 和输入 \(a_0\),语言模型通过前缀 \(s_t = [a_0, …, a_{t-1}]\) 自回归生成响应 \(a_{1:T} = [a_1, …, a_T]\),输出分布为 \(\pi_\text{LM}(\cdot | s_t)\),联合似然分解为:
$$
\pi_\text{LM}(a_{1:T} | a_0) = \prod_{t=1}^T \pi_\text{LM}(a_t | s_t)
$$- 推理能力的提升本质是优化模型的生成策略 \(\pi_\text{LM}\)
Token Informativeness(信息量量化) via Expert-Amateur Divergence
- 通过 KL 散度(Kullback–Leibler Divergence)量化专家模型 \(\pi_\text{E}\) 与业余模型 \(\pi_\text{A}\) 在每个生成步骤的分歧,定位关键推理节点:
$$
D_{KL}\left(\pi_\text{E}(\cdot | s_t) | \pi_\text{A}(\cdot | s_t)\right) = \sum_{a \in \mathcal{A} } \pi_\text{E}(a | s_t) \log \frac{\pi_\text{E}(a | s_t)}{\pi_\text{A}(a | s_t)}
$$- KL 散度值越大,表明该步骤是区分专家与业余推理能力的关键瓶颈,此类 token 仅占总 token 的 20% 左右,但对推理结果起决定性作用(2022; 2025)
Framework Workflow
- LightReasoner 包含两个核心阶段,整体流程如图4所示:
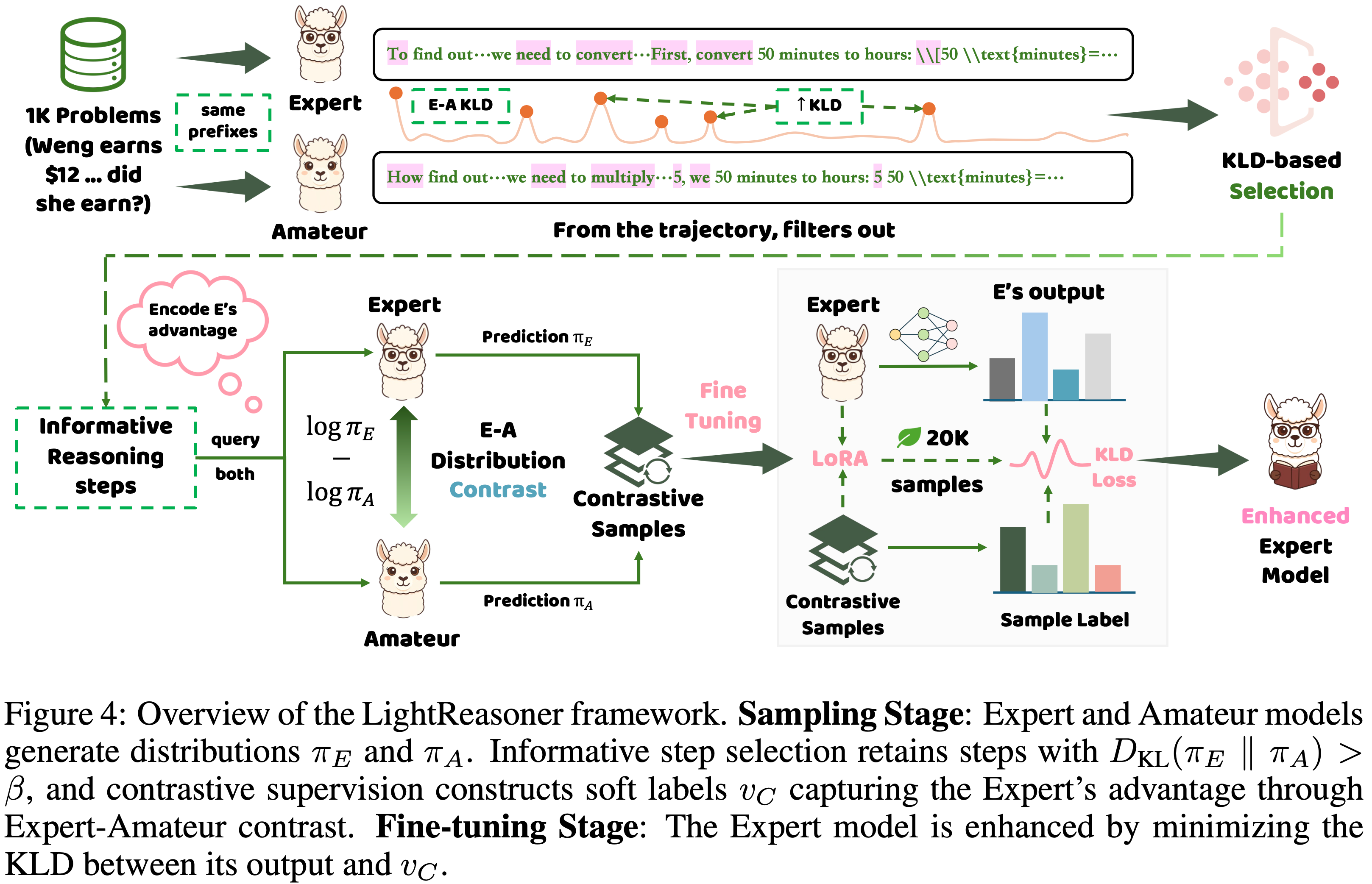

Sampling Stage
第一步:信息性步骤筛选(Informative Step Selection)
- 通过 \(\beta\)-过滤保留KL散度超过阈值的关键步骤,过滤 trivial 步骤以避免学习信号稀释:
$$
D_{KL}\left(\pi_\text{E}(\cdot | s_t) | \pi_\text{A}(\cdot | s_t)\right) > \beta
$$ - 其中 \(\beta = 0.4\)(经实验验证的最优阈值)
- 通过 \(\beta\)-过滤保留KL散度超过阈值的关键步骤,过滤 trivial 步骤以避免学习信号稀释:
第二步:对比分布监督信号构建(Contrastive Distributional Supervision)
- 1)掩码支持集(Masked Support Set):过滤专家模型低置信度 token,避免噪声干扰:
$$
\mathcal{A}_{mask} = \left\{a \in \mathcal{A} : \pi_\text{E}(a | s_t) \geq \alpha \cdot \max_{b \in \mathcal{A} } \pi_\text{E}(b | s_t)\right\}
$$- 其中 \(\alpha = 0.2\),用于平衡监督信号的质量与多样性,跟 Contrastive Decoding: Open-ended Text Generation as Optimization, Stanford & CMU & FAIR, 2023 类似
- 2)对比分数计算:量化专家模型相对业余模型的优势:
$$
v’_C(a | s_t) = \log \frac{\pi_\text{E}(a | s_t)}{\pi_\text{A}(a | s_t)}
$$ - 3)归一化处理:将对比分数转换为有效概率分布,形成最终监督信号 \(v_C(\cdot | s_t)\):
$$
\tilde{v}_C(\cdot | s_t) = \text{softmax}\left(v’_C(\cdot | s_t)\right) \quad (\text{over } \mathcal{A}_{mask}) \\
v_C(a | s_t) = \begin{cases}
\tilde{v}_C(a | s_t) & a \in \mathcal{A}_{mask} \\
0 & \text{otherwise}
\end{cases}
$$
- 1)掩码支持集(Masked Support Set):过滤专家模型低置信度 token,避免噪声干扰:
Fine-Tuning Stage
- 采用自蒸馏训练目标(Self-Distillation Training Objective),使专家模型对齐对比监督信号,强化其推理优势:
$$
\color{red}{\mathcal{L}(s_t) = D_{KL}\left(v_C(\cdot | s_t) | \pi_\text{E}(\cdot | s_t)\right) = \sum_{a \in \mathcal{A} } v_C(a | s_t) \left[\log v_C(a | s_t) - \log \pi_\text{E}(a | s_t)\right]}
$$- 该目标等价于交叉熵最小化,可高效引导专家模型在关键推理步骤上增强与业余模型的分歧
Key Implementation Details
- 1)模型配对(Model Pairing):专家模型选用 Qwen2.5-Math 系列(1.5B/7B)、DeepSeek-R1-Distill-1.5B 等,业余模型固定为 Qwen2.5-0.5B(无专门数学预训练,确保领域 expertise 差异);
- 2)训练配置(Training Configuration):采用 LoRA 进行参数高效微调,
rank=8,scaling factor=16,目标模块为q_proj和v_proj;训练步数 1000 步,有效批次大小 16; - 3)数据处理(Data Processing):基于 GSM8K 数据集生成推理轨迹,采用 CoT Prompt 引导分步推理,轨迹长度限制为 128 token(早期步骤推理信号更可靠)
LightReasoner 核心优势
- 性能卓越(Strong Performance):在7个数学推理基准上,准确率最高提升 28.1%,优于传统 SFT
- 效率极高(Order-of-Magnitude Efficiency):训练时间减少 90%,采样问题减少8 0%,微调 token 减少 99%,无需真实标签验证
- 泛化性强(Cross-Dataset Generalization):仅在 GSM8K 上训练,可迁移至 MATH、SVAMP 等多个基准,捕获通用推理模式
- 灵活适配(Adaptive to Model Architectures):适用于不同规模、不同优化程度的模型( Base Model /指令微调模型)
Idiosyncrasies in Large Language Models
- 原始论文:Idiosyncrasies in Large Language Models, 20250616, ICML 2025, CMU & UC Berkeley
- Idiosyncrasies:特质;特征;癖好
- 核心结论:LLM 存在独特特质,通过微调文本嵌入模型可高准确率区分不同模型的输出,这些特质根植于词汇分布与语义内容,且具有广泛应用与潜在风险
研究目标
- 验证不同 LLMs 是否存在可区分的独特特质
- 构建分类任务量化这些特质,评估分类准确率
- 探究特质的来源与表现形式
- 讨论研究发现的广泛意义与应用场景
核心方法
任务设计:LLM输出分类任务
- 给定 N 个 LLM(记为 \(f_{1}, …, f_{N}\)),每个模型接收 Prompt \(\p) 并输出文本 \(o\),收集每个模型的输出集 \(O_{i}\)
- 构建 N 分类任务,目标是根据输出文本预测其来源模型,以分类准确率衡量模型特质的显著程度
模型与训练设置
- Base Model :采用 Decoder-based Transformer 文本嵌入模型 LLM2vec,添加 \(N\) 分类头
- 训练方法:使用 LoRA 微调,输入序列截断为 512 个 token
- 关键参数:优化器为 AdamW,权重衰减 0.001,动量 \(\beta_{1}=0.9\)、\(\beta_{2}=0.999\),训练轮次 3 轮,批次大小 8,学习率采用余弦衰减,热身比例 10%,梯度裁剪 0.3
实验数据与模型分组
- 数据收集:每个 Prompt 数据集收集11K文本序列,按10K(训练集)和1K(验证集)拆分,跨模型使用相同拆分
- 模型分组:
- 聊天API模型(chat):ChatGPT、Claude、Grok、Gemini、DeepSeek(部分闭源)
- Instruct 模型(instruct):Llama、Gemma、Qwen、Mistral(均为7-9B参数规模)
- Base 模型(base):上述 Instruct 模型的预训练版本(无后训练阶段)
- Prompt 数据集:聊天 API 和 Instruct 模型使用 UltraChat,Base 模型使用 FineWeb
文本变换与分析方法
- 文本变换:包括词汇 Shuffle (词级、字母级)、移除特殊字符、改写(释义、翻译、总结)、格式控制(纯文本、长度限制)等
- 分析工具:使用ROUGE-1、ROUGE-L、BERTScore衡量文本相似度;通过TF-IDF提取特征短语;借助LLM作为评判者进行开放式语言分析
主要实验与结果
跨模型家族分类实验
- 聊天API模型:5 分类任务验证集准确率达 97.1%(随机猜测准确率 20%),两两组合分类准确率均超 90%,部分达 99%
- 注:其中 Gemini 和 DeepSeek 的差异高达 99.9%
- Instruct 模型:多组合分类准确率普遍超 96%,两两组合多数达 99%
- Base 模型:分类准确率达 87.3%,低于聊天 API 和 Instruct 模型,但远高于随机水平
同模型家族分类实验
- 以 Qwen2.5 系列 4 个不同参数规模(7B、14B、32B、72B)的 Instruct 模型为对象,4 分类准确率 59.8%,两两组合最高准确率 85.5%
- 区分同一模型的基础版与指令版:Qwen2.5-7b 的两类模型分类准确率达 96.8%
分布外泛化实验
- 训练集与测试集来自不同 Prompt 数据集(UltraChat、Cosmopedia、LmsysChat、WildChat), Instruct 模型分类准确率维持在 88.3%-99.8%,证明模型学到的特质具有强泛化性
控制变量实验
实验1:Prompt 干预实验
- 长度控制(限制 100 词内单段回复): Instruct 模型分类准确率 93.0%(原始 96.3%)
- 格式控制(纯文本,禁用标记语言): Instruct 模型分类准确率 91.4%,特质不受表面格式约束
实验2:输入序列长度实验
- 仅使用 1 个 token 时,聊天API和 Instruct 模型分类准确率约 50%;输入长度达 256 token 后,准确率趋于饱和
- 结论:初始 token 含独特信号,更多上下文可提升分类效果
实验3:采样方法实验
- 同一模型(Llama3.1-8b instruct)
- 采用不同采样策略(贪心解码、温度 softmax、top-k、top-p),分类准确率最高 59%;
- 5种温度(T=0,0.25,0.5,0.75,1)的 softmax 采样分类准确率 37.9%,仅略高于随机水平
- 采样策略对模型特质影响极小
实验4:文本嵌入模型对比实验
- 不同模型作为基座训练结论
嵌入模型 chat准确率 instruct准确率 base准确率 ELMo 90.8% 91.0% 69.8% BERT 91.1% 91.5% 66.0% T5 90.5% 89.8% 67.9% GPT-2 92.1% 92.3% 80.2% LLM2vec 97.1% 96.3% 87.3% - 先进嵌入模型表现更优,LLM2vec 效果最佳
实验5:训练数据量实验
- 仅 10 个训练样本时,聊天 API 模型分类准确率 40.3%(超随机水平);训练样本达 10K 时,准确率收敛,更多数据可提升分类性能
特质来源分析实验
分析1:词汇与字母层面
- 移除特殊字符:
- chat 准确率 95.1%、instruct 93.8%、base 75.4%,影响极小
- 词级 Shuffle :
- chat 准确率 88.9%、instruct 88.9%、base 68.3%,仍保持高准确率
- 字母级 Shuffle :
- 三类模型准确率均降至 38.6%-39.1%,接近随机水平
- 特征短语:
- 通过 TF-IDF 提取单字/双字特征,逻辑回归分类器在 chat 和 instruct 模型上准确率达 85.5% 和 83.7%
- 注:各模型有独特高频短语(如ChatGPT 常用 “such as”,Claude 常用 “according to”)
- 理解:仅使用 TF-IDF 抽取特征,使用 LR 分类器就已经有很高分类精度了,但远低于 LLM2vec 的 97% 的水平
分析2:标记语言格式层面
- 仅保留 markdown 元素(粗体、斜体、标题等),替换文本为“xxx”:
- chat 准确率 73.1%、instruct 77.7%、base 38.5%
- 各模型格式使用存在差异(如 Claude 极少用粗体和标题,Gemini 常用斜体)
- 理解:仅仅格式方面就有较大差异
分析3:语义层面
- 语义层面的相似度检查
文本处理方式 chat准确率 instruct准确率 base准确率 原始文本 97.8% 96.3% 87.3% 释义改写 91.4% 92.2% 71.7% 翻译(中译) 91.8% 92.7% 74.0% 总结 58.1% 57.5% 44.7% - 语义保留变换(释义、翻译)后仍保持高准确率,总结后准确率下降但超随机水平,证明语义是特质的重要组成
- 开放式语言分析:ChatGPT 倾向详细深入解释,Claude 侧重简洁直接回应,各模型在语气、词汇、结构上有显著差异
研究结论
核心结论
- 不同 LLMs 存在显著且稳定的独特特质,通过微调文本嵌入模型可实现高准确率分类,该现象适用于不同模型家族、规模和 Prompt 数据集
- 特质来源包括三方面:
- 词汇分布(特征短语、高频词使用)
- 标记语言格式习惯
- 语义表达风格(语气、内容详略)
- 特质具有强鲁棒性,不受长度限制、格式约束、采样策略影响,且可通过释义、翻译等语义保留变换传递
意义与应用
- 合成数据训练:使用 LLM 生成的合成数据训练新模型,会继承源模型的特质,需谨慎使用
- 模型相似度推断:可通过分类框架量化不同模型(含闭源与开源)的相似度,如 Grok 输出常被归类为 ChatGPT
- LLM 评估优化:现有投票式排行榜(如 Chatbot Arena)易受特质操纵,需开发更稳健的评估方法
- 理解:很多模型得分高,可能就是特质导致的
未来研究方向
- 验证特质是否适用于非 Transformer 架构的 LLM(如状态空间模型、扩散语言模型)
- 探究训练过程如何导致特质形成
- 扩展至大规模、未知来源模型的分类场景
- 研究特质与模型蒸馏技术的关联
(AEPO) QwenLong-L1.5
- 原始文章:(AEPO)QwenLong-L1.5: Post-Training Recipe for Long-Context Reasoning and Memory Management, Qwen Team, 20251215
- QwenLong-L1.5 是基于 Qwen3-30B-A3B-Thinking 开发的长上下文推理模型,创新点包括:
- 数据合成
- 强化学习优化
- 记忆增强架构
- QwenLong-L1.5 在长上下文推理基准上实现了 9.90 分的平均提升,性能比肩 GPT-5 和 Gemini-2.5-Pro,同时在 1M∼4M Token 的超长任务中展现出显著优势
Background and Contribution
- 背景:长上下文推理是 LLM 的关键能力,但现有研究多集中在预训练或架构创新,缺少成熟的端到端后训练方案,存在三大缺口:
- 高质量长上下文推理数据稀缺
- 缺乏适配长上下文的强化学习方法
- 无针对超上下文窗口任务的智能体架构
- 整体贡献
- 1)提出长上下文数据合成流水线(Long-Context Data Synthesis Pipeline) :解构文档为原子事实及关系,生成多跳推理、数值计算等复杂任务,避免简单检索类任务局限
- 2)设计稳定的长上下文强化学习策略(Stabilized Reinforcement Learning for Long-Context Training) :包括任务平衡采样、任务特定优势估计和 AEPO 方法,解决训练不稳定性
- 3)构建记忆增强架构(Memory-Augmented Architecture for Ultra-Long Contexts) :通过多阶段融合强化学习训练,整合单遍推理与迭代记忆处理,支持超 4M Token 任务
Long-Context Data Synthesis Pipeline
- 数据规模与多样性
- 最终构建 14.1K 高质量训练样本(远超前代 QwenLong-L1 的 1.6K),涵盖代码仓库、学术文献、专业文档等多领域
- 输入长度上限提升至 119,932 Token ,平均输入长度达 34,231 Token ,包含多跳推理、假设场景、时间推理等 9 类复杂问题类型
- 关键合成步骤
- 1)语料收集与预处理:筛选 82,175 份高质量文档(约 92 亿 Token ),覆盖 5 大核心类别
- 2)问答合成:通过知识图谱引导多跳推理、结构化表格引擎生成数值推理、多智能体自演进生成通用任务三类方法,确保信息分散分布以提升推理难度
- 3)数据验证:通过知识接地检查(过滤无需上下文即可回答的样本)和上下文鲁棒性检查(插入无关文档验证答案稳定性)保证数据质量
长上下文后训练范式
- 渐进式训练流程
- 分四阶段逐步扩展输入/输出长度,避免直接切换长上下文任务导致的训练崩溃
- 20K input + 12K output
- 60K input + 20K output
- 120K input + 50K output
- 前三个阶段专注全上下文推理训练,第四阶段融合记忆管理专家模型(通过 SCE 算法合并),最终实现单遍推理与记忆代理能力的统一
- 分四阶段逐步扩展输入/输出长度,避免直接切换长上下文任务导致的训练崩溃
- 多任务强化学习优化
- 任务平衡采样(Task-balanced sampling) :按领域、任务类型分层采样 ,确保每个训练批次中多任务分布均衡,避免数据偏移
- 任务特定优势估计(Task-specific advantage estimation) :针对不同任务的奖励分布差异,基于任务级奖励标准差计算优势值,减少估计偏差,公式如下:
$$A_{i}^{\text{task} }=\frac{r_{i}^{\text{task} }-mean\left(\left\{r_{k}^{\text{task} }\right\}_{k=1}^{G}\right)}{\text{std}\left(r^{\text{task} } | r^{\text{task} } \in \mathcal{B}^{\text{task} }\right)}$$- 其中 \(\mathcal{B}^{\text{task} }\) 为当前批次中同一任务的样本集合,\(r_{i}^{\text{task} }\) 为第 \(i\) 个样本的任务奖励
- 记忆增强架构
- 将超长文档分割为块,通过迭代记忆更新与导航规划实现全局信息整合:
- 记忆更新:每处理一个文档块,基于历史记忆和当前块信息更新记忆状态 \(m_t\)
- 导航规划:生成下一块的信息提取指引 \(p_t\),状态转移公式为:
$$\left(m_{t}, p_{t}\right) \sim \pi_{\theta}\left(\cdot | m_{t-1}, p_{t-1}, x_{t}, q_{core }\right)$$ - 最终答案生成:整合所有块的记忆 \(m_K\) 与格式指令 \(q_{inst }\),生成符合要求的输出
- 将超长文档分割为块,通过迭代记忆更新与导航规划实现全局信息整合:
AEPO(Adaptive Entropy-Controlled Policy Optimization)
Motivation
- 长上下文强化学习中存在两大核心问题:
- 负优势样本与高熵 Token 强相关:高熵 Token (探索性推理步骤)易产生大梯度,增加参数更新方差,导致训练不稳定(Spearman 相关系数 \(\rho=0.96\))
- 奖励分配模糊:长上下文任务中正确与错误推理路径的短语级重叠度高(如 DocMath 任务的 ROUGE-L 达 45.37),负样本包含大量正确步骤,直接惩罚会破坏模型探索能力
- AEPO 通过动态控制负梯度信号,平衡探索与利用,解决训练不稳定性问题
核心定义与公式
Negative Gradient Clipping
- 基于 GRPO 目标函数,加入熵控制的掩码机制 \(\mathbb{I}(i,t)\),筛选参与训练的梯度信号:
$$\mathcal{J}_{GRPO}(\theta)=\mathbb{E}_{c, q \sim \mathcal{D},\left\{y_{i}\right\}_{i=1}^{G} \sim \pi_{\theta_{old } } }\left[\frac{1}{\sum_{j=1}^{G}\left|y_{j}\right|} \sum_{i=1}^{G} A_{i} \sum_{t=1}^{\left|y_{i}\right|} \rho_{i, t}(\theta) \mathbb{I}(i,t)\right]$$- 其中掩码函数 \(\mathbb{I}(i,t)\) 定义为:
$$
\mathbb{I}(i, t)=
\begin{cases}
0 & \text{if}\ A_{i}<0 \text{ and } \left(\left(P_{\text{token_level} } \land H(t | i)>\tau_{token }\right) \lor \left(\neg P_{\text{token_level} } \land \overline{H}(i)>\tau_{\text{sequence} }\right)\right) \\
1 & otherwise
\end{cases}
$$- \(H(t | i)\) 为第 \(i\) 个序列第 \(t\) 个 Token 的 Token-level 熵,\(\overline{H}(i)\) 为 Sequence-level 平均熵
- \(\tau_{token}\) 和 \(\tau_{sequence}\) 分别为 Token-level 和 Sequence-level 熵阈值
- \(P_{\text{token_level}}\) 控制熵筛选粒度(Token-level/Sequence-level)
- 注:\(P_{\text{token_level}}\) 是布尔类型的参数
- 其中掩码函数 \(\mathbb{I}(i,t)\) 定义为:
Batch-level 熵定义
- 用当前训练批次 \(\mathcal{B}\) 的平均熵,量化策略生成 Token 的随机性:
$$H\left(\pi_{\theta}, \mathcal{B}\right)=-\frac{1}{|\mathcal{B}|} \sum_{i=1}^{|\mathcal{B}|} \frac{1}{\left|y_{i}\right|} \sum_{t=1}^{\left|y_{i}\right|} \sum_{v \in V} \pi_{\theta}\left(v | c, q, y_{i,<<t}\right) \log \pi_{\theta}\left(v | c, q, y_{i,<t}\right)$$- 其中 \(V\) 为模型词汇表,\(y_i\) 为第 \(i\) 个样本的生成序列,\(\pi_{\theta}\) 为当前策略模型
熵控制范围
- 设定目标熵区间 \([H_{low}, H_{high}]\),动态调整负梯度参与训练的比例:
- 当批次熵 \(H\left(\pi_{\theta}, \mathcal{B}\right) > H_{high}\):模型探索过度,屏蔽所有负优势样本,仅用正优势样本更新,减少熵值
- 当批次熵 \(H\left(\pi_{\theta}, \mathcal{B}\right) < H_{low}\):模型探索不足,重新引入负梯度,避免熵崩溃
实验效果及分析
- AEPO 核心优势
- 动态平衡探索与利用:通过熵反馈机制自适应调整负梯度参与度,避免过度探索或探索不足
- 稳定训练过程:屏蔽高熵负样本的干扰,减少梯度方差,支持超长序列的持续训练
- 无需额外参数:基于现有策略熵计算,无需引入新的模型组件,易于集成
- 实验结果
- 在 Qwen3-4B-Thinking 上,AEPO 较 GRPO 基线平均提升 3.29 分,在 MRCR(密集奖励任务)和 CorpusQA(长上下文聚合任务)上提升尤为显著
- 在 Qwen3-30B-A3B-Thinking 上,AEPO 保持熵值稳定在目标区间,训练 200 步后无性能下降,支持模型向更长序列扩展
整体实验性能
- 长上下文基准测试
- QwenLong-L1.5-30B-A3B 在 6 大长上下文基准(DocMath、LongBench-V2 等)上平均得分 71.82,较基线提升 9.90 分,其中 MRCR 任务提升 31.72 分,CorpusQA 任务提升 9.69 分,性能接近 Gemini-2.5-Pro(72.40)
- 超长任务性能
- 在 1M∼4M Token 任务中,记忆代理框架较基线提升 9.48 分,在 4M Token 的 CorpusQA 任务中实现 14.29 分,远超传统全上下文模型的处理能力
- 泛化能力
- 长上下文推理能力可迁移至通用领域,在 AIME25(数学推理)提升 3.65 分,LongMemEval(对话记忆)提升 15.60 分,在工具使用、科学推理等场景均有改善
Artificial Hivemind: The Open-Ended Homogeneity of Language Models (and Beyond)
- 原始论文:Artificial Hivemind: The Open-Ended Homogeneity of Language Models (and Beyond), 20251027, UW & CMU & AI2 & Stanford
- Key Contributions
- 1)构建首个大规模真实世界开放式 Query 数据集 INFINITY-CHAT,配套完整分类体系和高密度人类标注,填补开放式生成评估资源空白
- 2)首次系统揭示LM在开放式任务中的“人工蜂群思维”效应,量化模型内重复与模型间同质化,为AI安全风险研究提供实证基础
- 3)发现现有模型在捕捉人类多元偏好上的核心缺陷,为后续多元对齐、多样性优化提供明确方向
- Limitations
- 1)数据集以英文为主,可能低估非英语语境和多元文化场景的多样性,泛化性受限
- 2)依赖文本嵌入相似度衡量多样性,可能未能捕捉创意表达的多维差异
- 3)未完全厘清同质化的根本成因(如训练数据重叠、对齐流程、记忆效应等),需进一步机制分析
- Future Work
- 1)拓展数据集至多语言、多文化场景,完善分类体系的跨语境适应性
- 2)研发多样性感知的训练目标和对齐方案,在保证质量的同时提升输出多样性
- 3)深入探究同质化成因,优化数据筛选、模型训练流程以减轻“人工蜂群思维”效应
核心结论
- LMs 在开放式生成任务中存在显著的 人工蜂群思维(Artificial Hivemind) 效应(或者翻译为 人工乌合之众 更好)
- 具体表现为模型内部输出重复和模型间输出同质化 ,且现有 LM、奖励模型 及 LM Judger 难以匹配人类对开放式 Response 的多元偏好
- 长期可能导致人类思维同质化,需通过针对性数据集和方法优化缓解这一风险
数据集构建:INFINITY-CHAT
- 来源:从 WildChat 数据集筛选、清洗并修订真实用户 Query ,最终得到 26,070 条开放式 Query 和 8,817 条封闭式 Query ,涵盖真实世界多样化使用场景
- 分类体系:构建首个开放式 Query 分类体系,包含 6 个顶层类别(如创意内容生成、头脑风暴与构思、推测性与假设场景等)和 17 个细分类别,通过 GPT-4o 自动标注并经人类验证(89% Query 被判定为真正开放式)
- 人类标注:针对 50 个代表性 Query ,收集 31,250 条人类标注,包括 18,750 条绝对质量评分(1-5分)和 12,500 条 pairwise 偏好评分,每个 Query - Response 对均有25个独立标注,捕捉人类多元偏好
实验设计
- 模型范围:涵盖 70+ 开源与闭源LM(主论文详述 25 个),包括 GPT-4o 系列、Llama-3 系列、Qwen 系列等主流模型
- 生成参数:采用 top-p 采样(
p=0.9,temperature=1.0)和 min-p 采样(p=1.0,min-p=0.1,temperature=2.0),每个模型对每个 Query 生成50条 Response - 评估指标:通过 OpenAI 的 text-embedding-3-small 计算句子嵌入的余弦相似度,衡量输出同质化;采用皮尔逊相关系数和斯皮尔曼相关系数,对比模型评分与人类标注的一致性;使用香农熵量化人类标注分歧
- 子集分析:构建相似质量子集(通过 Tukey’s fences 等 6 种方法筛选)和高分歧子集(通过熵、基尼不纯度等6种方法筛选),验证模型评分与人类偏好的校准程度
关键实验 1:人工蜂群思维效应验证
Intra-model repetition,模型内部重复
- 结果:
- 即使采用高随机性解码参数,同一模型对同一开放式 Query 的输出仍高度重复
- 79% 的 Query Response 平均相似度超过 0.8;
- min-p 采样虽降低极端重复,但 81% 的 Response 对相似度仍超 0.7,61.2% 超 0.8,模式崩塌问题未根本解决
- 例证:
- 单个模型生成的“时间隐喻”类 Response ,核心意象集中于“河流”或“织工”,语义相似度极高
Inter-model homogeneity,模型间同质化
- 结果:
- 不同模型(含不同家族、不同规模)的输出语义重叠显著,平均 pairwise 相似度达 71%-82%;
- 部分模型对(如DeepSeek-V3 与 qwen-max-2025-01-25)相似度高达 0.82,甚至出现完全相同的 Response (如“成功类社交媒体座右铭”生成完全一致的表述)
- 聚类分析:
- 25 个模型对“时间隐喻” Query 的 50 条 Response ,仅形成两大聚类(“时间是河流”主导聚类和“时间是织工”次要聚类),抽象概念收敛明显
关键实验 2:模型与人类偏好的校准分析
相似质量 Response 场景
- 结果:
- 当 Response 质量相近时,LM 困惑度、奖励模型分数、LM Judger 分数与人类评分的相关性显著下降
- 说明现有模型难以区分“同等优质但风格/角度不同”的开放式 Response
- 跨方法验证:
- 6 种相似子集筛选方法均验证了这一结论,模型校准能力不足具有稳健性
高分歧人类偏好场景
- 结果:
- 当人类标注存在高分歧(熵值较高)时,模型评分与人类评分的相关性大幅降低,现有模型倾向于拟合单一“共识质量”,忽略人类多元偏好
- 例证:
- 对“生活意义”“周日海边雾景描述”等 Query ,人类标注熵值高,但模型评分难以反映这种偏好多样性
拓展实验: Prompt 改写对同质化的影响
- 设计:对 30 个原始 Query 生成 4 种改写版本,共 150 个 Prompt,42 个模型各生成 20 条 Response
- 结果:原始 Prompt 与改写 Prompt 的 Response 相似度差异仅为 0.04(分别为 0.821 和 0.781),说明即使调整 Prompt 表述,模型仍倾向于生成同质化内容
From \(f(x)\) and \(g(x)\) to \(f(g(x))\)
- 原始论文:From f(x) and g(x) to f(g(x)): LLMs Learn New Skills in RL by Composing Old Ones, 20250929-20251219, UIUC & THU & Shanghai AI Lab & PKU
- 研究代码开源链接:github.com/PRIME-RL/RL-Compositionality
- 官方博客:From f(x) and g(x) to f(g(x)): LLMs Learn New Skills in RL by Composing Old Ones, 202509
- 论文 证实了 RL 能让 LLMs 通过组合现有原子技能习得真正的新技能,呼应了人类认知技能习得的核心机制(1982),反驳了“RL 仅激活现有技能”的悲观观点
- 论文的亮点是:提出的受控合成框架(明确的原子/组合技能定义、可控难度、无数据污染)为LLM技能习得研究提供了新范式
- 实践启示 :
- Base Model 开发应注重原子技能的构建,为后续组合技能学习奠定基础
- RL 训练需明确设置组合激励,才能有效习得泛化性强的复杂技能
- 组合技能的跨任务迁移特性,可减少不同领域的 RL 训练数据需求
研究背景 & 核心问题
- RL 在提升 LLM 性能方面取得了广泛成功,尤其在推理任务中,特别是近期研究发现,即便无需前置监督微调也能发挥作用
- 但学界对RL的作用存在争议:
- 观点一:认为 RL 能实现显著效果
- 观点二:认为 RL 仅为现有推理策略重新加权,并未让模型习得真正的新技能
- 除此以外,RL 训练中存在熵崩溃、pass@k 评估中性能差距随样本量增大而缩小等现象,进一步引发了对“RL 是否能教会 LLMs 新技能”的质疑
- 本研究聚焦三个核心问题:
- 1)RL 能否教会 LLMs 新技能?
- 2)若问题 1)的答案是能,如何激励这种技能习得?
- 3)习得的技能是否具有泛化性?
)-Figure1.png)
研究框架 & 实验设计
核心假设
- RL 组合性假设 :
- 若模型已通过 Next Token Prediction(NTP)训练掌握任务所需的原子技能(不可分解的基础技能) ,则带有适当激励的 RL 能让模型通过组合原子技能 ,习得解决复杂问题的新技能
任务设计:字符串变换预测任务
- 为避免数据污染和技能边界模糊的问题,研究设计了受控的合成任务,具有以下 3 个特点:
- 1)原子技能定义 :构建 25 个独特的字符串变换函数(如字符去重、元音移除、字符串反转等),每个函数作为原子技能,采用无意义标识符(如
func_16)命名,避免模型通过函数名推断功能 - 2)难度控制 :任务难度按组合深度划分等级,Level-n对应n个函数的嵌套组合。例如:
- Level-1:单一函数应用(如
func_16(x)) - Level-2:双函数组合(如
func_16(func_15(x))) - 更高 Level:更多函数嵌套(如 Level-3 为
func_a(func_b(func_c(x))))
- Level-1:单一函数应用(如
- 3)任务独立性 :RL 训练和评估任务均不包含在 LLM 预训练语料中,确保性能提升源于学习而非记忆
训练方式-两阶段训练
- Stage 1:原子技能获取 :通过拒绝微调(RFT)让模型学习所有 25 个原子技能,训练数据包含函数定义、输入字符串及正确推理轨迹,确保模型内化每个函数的行为
- Stage 2:组合技能训练 :隐藏函数定义,模型仅接收函数名和组合形式(如
func_2(func_16(x))),对比两种训练方式:- RL 训练:基于输出正确性提供二元奖励,采用 GRPO 优化算法
- RFT 基线:使用 NTP 在组合问题的正确推理轨迹上训练
评估方式
- 留存评估(Held-out Evaluation):Stage 2 训练时将函数分为两组,仅在一组上训练,另一组用于评估未见过的函数组合
- 难易泛化评估:在 Level-1 至 Level-6 的任务上评估,测试模型对超出训练难度的泛化能力
- 跨任务迁移评估:以 Countdown 任务(用给定整数通过算术运算构造目标数)为目标任务,测试字符串任务中习得的组合技能能否迁移
实验模型与参数
- 实验采用 Llama-3.1-8B-Instruct 模型,关键参数如下:
- Stage 1:训练 2 个 epoch,学习率 \(2×10^{-5}\), Batch Size 128
- Stage 2:RL 训练采用 DAPO 优化算法,训练 Batch Size 和 Mini-Batch Size 均为 16,学习率 \(1×10^{-6}\),KL 散度和熵损失系数为 0;RFT 基线学习率\(2×10^{-5}\), Batch Size 128,迭代生成训练数据
核心结论
结论 1:RL 能教会 LLMs 新的组合技能
- 仅在 Level-1 原子技能上训练的 RL 模型(RL Level 1),在 Level-2 及以上任务中性能接近 0;
- 在 Level-2 组合任务上训练的 RL 模型(RL Level 2)和混合 Level-1+2 训练的模型(RL Level 1+2),展现出极强的泛化能力:
- Level-3 任务准确率从近 0 提升至 30%
- Level-4 任务准确率从 1% 提升至 15%
- 该泛化能力可延伸至 Level-5 及以上,表明模型习得的是组合推理的通用原则,而非记忆解决方案
)-Figure2.png)
- Takeaway 1:
RL on compositional data teaches new skills that generalize to unseen compositions of known atomic skills.
结论 2:RL 是组合技能习得的关键因素
- 对比 RL Level 2 模型与基于相同 Level-2 数据训练的 RFT 模型:
- RFT 模型在 Level-3 任务上准确率从未超过 2.6%,Level-2 任务准确率仅 15%,无法泛化到未见过的组合或更高难度
- RL 模型在 Level-2 任务上准确率达 64%,Level-3 达 27%,显著优于 RFT
)-Figure3.png)
- 结论:仅靠组合数据的监督训练(RFT)不足以习得组合技能,RL 的激励机制是必要条件
- Takeaway 2:
RFT, even with on compositional data, is suboptimal for learning compositional skills; RL, in addition to compositional training data, is another important factor in learning generalizable compositional skills.
结论 3:RL 习得的组合技能具有跨任务迁移性
- 实验设置:
)-Table1.png)
- 跨任务迁移实验以 Countdown 任务为目标,测试字符串任务中习得的组合技能迁移效果:
- 仅掌握 Countdown 原子技能的模型(Multi-Base):
- 在 Level-3 任务上准确率约 17%,在 Level-4 接近 0 准确率
- 掌握 Countdown 原子技能,叠加原子技能 RL 训练的模型(Multi-Base + RL L1)
- 性能提升微弱(Level-3 约 20%),在 Level-4 接近 0 准确率
- 掌握 Countdown 原子技能,叠加组合技能 RL 训练的模型(Multi-Base + RL L1+2)性能显著提升:
- Level-3 达 35%,Level-4 达 6%
- 无 Countdown 原子技能但有组合 RL 训练的模型(String-Base + RL L1+2)完全失败
- 仅掌握 Countdown 原子技能的模型(Multi-Base):
- 结论:组合技能可跨任务迁移,但目标任务的原子技能是迁移的前提
- Takeaway 3:
Compositional skills learned through RL are transferable to a different task where the model possesses the atomic skills.
结论 4:RL 能突破 Base Model 的性能限制
- 针对“RL 仅重排(Reranking) Base Model 响应,未提升性能上限”的质疑,研究通过细分难度的
pass@k评估验证:- 在 Base Model 已表现较好的简单任务(Level-1、Level-2)中,RL 模型与 Base Model 的
pass@k差距随 k 增大而缩小 ,符合“重排”现象 - 在复杂组合任务(Level-3 至 Level-6)中,RL Level 1+2 模型的
pass@k性能显著优于 Base Model ,且差距随 k 增大而扩大- 如 Level-5 任务中,
pass@1差距 4%,pass@1024差距达 25% - 理解:实际上,如果无限拉大 k,最终一定还会逐步收敛到 1 的,但那种情况下,采样需要的成本就不太可接受了
)-Figure5.png)
- 如 Level-5 任务中,
- 在 Base Model 已表现较好的简单任务(Level-1、Level-2)中,RL 模型与 Base Model 的
- 结论:此前“RL 未提升性能上限”的结论,源于评估任务中 Base Model 已具备较高
pass@k,RL 缺乏学习新技能的激励;- 在 Base Model 表现不佳的复杂任务中,RL 能显著突破性能限制
- Takeaway 4:
The prior conclusion that RLVR only utilizes base models’ reasoning patterns without learning new abilities is likely an artifact of evaluating and RL training on tasks that base models already achieve high pass@k; thus RL has little incentive to learn a new skill.
结论 5:RL 从根本上改变模型的推理行为
- 分析方法:使用 Gemini-2.5-Pro 对模型在 Level 3 任务上的错误进行分类:
- 1)正确
- 2)忽略组合
- 3)不完整追踪
- 4)错误组合
- 5)原子错误(已正确解析组合结构)
- 对 Level-3 任务的失败模式分析显示:
- RFT Base、RFT Level 2 和 RL Level 1 模型的失败主要源于“忽略组合”(>50%)和“误解组合结构”(>35%)
- RL Level 2 模型:
- 完全消除“忽略组合”错误
- 正确率提升至 28.1%
- 主要失败模式变为“原子错误”(55%),表明已掌握组合结构解析,仅在基础技能应用上存在失误
)-Figure6.png)
- 结论:RL 不仅提升准确率,还根本改变了模型的推理行为 ,使其能够正确理解和处理组合结构
- Takeaway 5:
Rather than merely improving accuracy, RL on compositional problems fundamentally transforms the model’s behavior, enabling it to correctly understand and handle compositions.
H-Neurons
- 原始论文:H-Neurons: On the Existence, Impact, and Origin of Hallucination-Associated Neurons in LLMs, THU, 20251202
- H-Neurons:论大型语言模型中幻觉相关神经元的存在、影响与起源:系统性研究了与 LLM 幻觉相关的神经元(称为 H-Neurons)
- 贡献 :
- 揭示了幻觉与过度服从行为在神经元层面的关联
- 证明幻觉机制根植于预训练目标,而非对齐过程
- 为 幻觉检测 提供了鲁棒的神经元级特征
- 为 针对性神经元干预 提供了可能,但需平衡幻觉抑制与模型效用
- 启示:改善 LLM 可靠性需从 预训练目标 和 神经元级机制 入手,而非仅依赖对齐或数据增强
- 个人理解:其实不太严谨,只是说明存在一些神经元对某些幻觉敏感,针对所有场景显然很难成立,一些看似幻觉的东西,在不同上下文、对不同的人可能感觉不同
H-Neurons 的是否存在?
- 副标题:是否存在一组神经元,其激活模式能可靠地区分幻觉输出与忠实输出?
- 确实存在一组 极其稀疏的神经元子集(占总数不到 \(0.1%\)),能有效预测模型是否会产生幻觉
- 使用 TriviaQA 数据集构建训练集,通过 稀疏逻辑回归(L1正则化) 识别出这些神经元
- H-Neurons 在多种场景下具有强泛化能力:
- 领域内知识回忆(TriviaQA、NQ)
- 跨领域鲁棒性(BioASQ)
- 虚构知识检测(NonExist)
- 表1显示,基于 H-Neurons 的分类器在幻觉检测任务上显著优于随机选择神经元的分类器
H-Neurons 对模型行为的影响?
- H-Neurons 与 过度服从(over-compliance) 行为存在因果关联
- 通过 激活缩放(scaling factor \(\alpha \in [0,3]\)) 进行干预实验:
- 放大(\(\alpha>1\)) : 增加过度服从行为
- 抑制(\(\alpha<1\)) : 减少过度服从行为
- 核心方法:缩放神经元激活值 \(z_{j,t} \leftarrow \alpha \cdot z_{j,t}\),观察行为变化
- 过度服现在四个方面:
- 1)无效前提(FalseQA)
- 2)误导性语境(FaithEval)
- 3)怀疑态度(Sycophancy)
- 4)有害指令(Jailbreak)
- 图 3 显示,放大 H-Neurons 导致合规率上升,抑制则提升模型鲁棒性
H-Neurons 的起源?
- 副标题:H-Neurons 是在预训练阶段还是后训练对齐阶段出现的?
- H-Neurons 主要形成于 预训练阶段 ,而非对齐阶段
- 通过 跨模型迁移实验 发现:
- 在指令调优模型中训练的幻觉检测分类器,在对应的基模型中仍保持高预测能力(AUROC 显著高于随机基线)
- 图 4 显示,H-Neurons 在基模型与对齐模型之间的参数变化极小,呈现“参数惯性”
- 结论:幻觉机制根植于预训练目标(如 NTP) ,对齐过程未有效改变这些机制
RLMs(Recursive Language Models)
- (RLMs)Recursive Language Models, 20251231, MIT
- RLM 是一种通用、可扩展的推理框架 ,通过将 Prompt 作为环境变量并支持递归调用,显著提升了 LLM 处理超长上下文的能力
- 实验表明,RLM 在多种长上下文任务上均表现优异,且推理成本可控,为下一代语言模型系统的扩展提供了新方向
- 理解:本质上是一个有规划能力的 Agent 了
- 上下文衰减(Context Rot):LLM 在推理和工具使用方面进步迅速,但其上下文长度仍然有限 ,并且随着上下文变长,模型性能会出现显著下降,这种现象称为 Context rot
核心方法:递归语言模型(即 RLMs)
- RLMs 是一种任务无关的推理范式 ,其核心思想是将长 Prompt 视为外部环境的一部分 ,让 LLM 能够以编程方式交互式地查看、分解和递归调用自身来处理这些内容
- RLM 的工作原理
- 1)环境初始化 :将输入 Prompt \(P\) 作为一个变量加载到 Python REPL(Read-Eval-Print Loop)环境 中
- 2)符号化交互 :LLM 可以在该环境中编写代码来查看、分解 \(P\),并执行递归调用
- 3)递归子调用 :LLM 可以在代码中构建子任务,并递归调用自身(或子模型)来处理这些子任务
- 4)迭代式推理 :通过 REPL 环境的执行反馈,逐步构建最终答案
- 数学表达(概念性)
- 给定一个长 Prompt \(P\),RLM 将其视为一个环境变量,并通过递归调用函数 \(f_{\text{LLM} }\) 来处理:
$$
\text{RLM}(P) = f_{\text{LLM} }^{\text{recursive} }(P, \mathcal{E})
$$- 其中 \(\mathcal{E}\) 是 REPL 环境,支持代码执行、变量存储和递归调用
- 给定一个长 Prompt \(P\),RLM 将其视为一个环境变量,并通过递归调用函数 \(f_{\text{LLM} }\) 来处理:
- 其他公式总结:
- 基础 LLM 调用:\(y = f_{\text{LLM} }(x)\)
- RLM 递归调用:\(y = f_{\text{RLM} }(P, \mathcal{E})\)
- 环境状态更新:\(\mathcal{E}_{t+1} = \text{REPL_Step}(\mathcal{E}_t, \text{code}_t)\)
- 递归子调用:\(\text{sub_answer} = f_{\text{LLM} }(\text{chunk}, \mathcal{E}_{\text{sub} })\)
实验设计与任务
- 论文在多个长上下文任务上评估 RLM,任务复杂度随输入长度呈常数、线性、二次增长 :
任务 描述 复杂度 S-NIAH 单针海任务,在长文本中查找特定信息 常数 BrowseComp+ (1K) 多跳问答,需跨多个文档推理 常数 OOLONG 长推理任务,需对输入进行语义转换与聚合 线性 OOLONG-Pairs 需聚合两两配对信息的长推理任务 二次 LongBench-v2 CodeQA 代码库理解与问答 常数
实验结果与发现
- 1)RLM 可扩展到 1M+ token ,在长上下文任务上显著优于基础模型和现有方法(如摘要代理、检索代理等)
- 2)REPL 环境是关键 ,即使没有递归调用,RLM 仍能处理超长输入
- 3)RLM 性能随任务复杂度增长而缓慢下降 ,优于基础模型的快速衰减
- 4)推理成本与基础模型相当但方差较大 ,因任务复杂度不同导致调用次数差异大
- 5)RLM 是一种模型无关的策略 ,适用于不同架构的 LLM
- 代表性结果(GPT-5 vs RLM(GPT-5))
任务 GPT-5 RLM (GPT-5) OOLONG 44.00 56.50 OOLONG-Pairs 0.04 58.00 BrowseComp+ 0.00 91.33 CodeQA 24.00 62.00
RLM 的典型行为模式分析
- 1)基于先验的代码过滤 :使用正则表达式等工具筛选信息
- 2)分块与递归调用 :将长输入分块后递归处理
- 3)子调用验证答案 :通过递归调用来验证中间结果
- 4)变量式长输出构建 :通过 REPL 变量逐步构建超长输出
相关研究对比
- 长上下文系统 :如 MemWalker、ReSum 等,通常采用有损压缩(摘要、截断)或显式内存层次结构
- 任务分解方法 :如 ViperGPT、THREAD、DisCIPL 等,强调任务分解但 无法处理超长输入
- RLM 的优势 :将 Prompt 作为环境变量,支持符号化操作 和 执行反馈驱动的递归优化
缺点讨论
- 1)同步调用速度慢 :当前使用同步调用,未来可探索异步调用与沙箱环境
- 2)耗时方差大 :平均耗时低,但部分任务或 Prompt 耗时很长
- 3)模型未针对 RLM 训练 :当前使用现有模型,未来可训练专用 RLM 模型
- 4)Prompt 设计敏感 :不同模型需调整 Prompt 以避免过度调用
- 5)对模型能力有要求 :需要能生成代码的强力模型,且依赖模型自身的规划能力好的
AlpacaFarm
- 原始论文:AlpacaFarm: A Simulation Framework for Methods that Learn from Human Feedback, NeurIPS 2023, Stanford
- AlpacaFarm 是一款针对从人类反馈中学习(learning from pairwise feedback, LPF) 的模拟框架,旨在解决该领域数据收集成本高、缺乏可靠评估方法和参考实现的三大核心挑战
- AlpacaFarm 通过 API LLM 模拟人类反馈,成本较人工标注低 45 倍且与人类判断一致性高,提供自动评估方案(与真实人类交互数据相关性强)及 PPO、Best-of-n 等多种参考方法实现
- 经验证,其训练的模型排名与基于真实人类反馈训练的模型排名 Spearman correlation 达 0.98 ,且能复现奖励模型过拟合等人类反馈的定性特征,其中 PPO 方法表现最优,较 Davinci003 胜率提升 10% ,为 LPF 相关研究提供了低成本、高效迭代的解决方案
- LLM 的指令跟随能力依赖于人类反馈训练,但该领域存在三大关键障碍,制约研究推进:
- 1)数据成本高 :人工标注成对反馈价格昂贵,1000条示例成本约300美元,且耗时久(数天);
- 2)评估不可靠 :人类评估成本高、不可复现,缺乏能反映真实人类交互的评估数据;
- 3)方法无参考 :缺乏经过验证的从人类反馈中学习(LPF)方法开源实现,难以对比迭代
- AlpacaFarm 的核心目标是构建一个低成本、高效迭代的模拟框架,支持研究者在模拟环境中开发 LPF 方法,并能迁移至真实人类反馈场景
- 核心一:模拟人类反馈(p_sim)
- 利用 API LLM(如 GPT-4、ChatGPT)设计提示词,模拟人类成对比较偏好;
- 构建 13 个模拟标注者(含不同模型、提示词格式、上下文示例),模拟标注者间变异性;
- 训练阶段注入 25% 标签翻转噪声,模拟标注者内变异性;
- 成本仅为人工标注的 1/45(1000条示例仅需6美元),与人类多数投票一致性达 65%,接近人类标注者间的 66% 一致性
- 利用 API LLM(如 GPT-4、ChatGPT)设计提示词,模拟人类成对比较偏好;
- 核心二:自动评估方案
- 以模型相对于参考模型 Davinci003 的胜率为核心指标,直观反映模型性能;
- 融合 Self-Instruct、OASST、Vicuna 等5个开源数据集,共 805 条指令,覆盖多样化真实人类交互场景;
- 与 Alpaca Demo 真实用户交互数据的胜率相关性达 \(R^2\)=0.97,证明其能有效替代真实场景评估
- 以模型相对于参考模型 Davinci003 的胜率为核心指标,直观反映模型性能;
- 核心三:AlpacaFarm 实现并验证了6种主流 LPF 方法,分为两类:
方法类型 具体方法 核心逻辑 直接学习成对反馈 Binary FeedME 基于成对反馈中偏好的输出继续监督微调 直接学习成对反馈 Binary Reward Conditioning 给偏好/非偏好输出添加正负标记,进行条件微调 优化代理奖励模型 Best-of-n 推理时从SFT模型采样n个输出,选择代理奖励最高的输出(n=1024) 优化代理奖励模型 Expert Iteration 先通过Best-of-n生成优质输出,再用其微调SFT模型 优化代理奖励模型 PPO 强化学习算法,在最大化代理奖励的同时,通过KL惩罚约束与SFT模型差异 优化代理奖励模型 Quark 按奖励分箱,仅用最优分箱数据训练,添加KL和熵正则化 - 通过训练 11 种模型分别在模拟反馈和真实人类反馈上训练,其胜率排名的斯皮尔曼相关系数达 0.98
- 证明在 AlpacaFarm 中迭代的方法能有效迁移至真实人类反馈场景
- 模拟评估标注者(p_sim^eval)与人类多数投票一致性 65%,接近人类标注者间 66% 的一致性;
问题1:AlpacaFarm 如何解决 LPF 研究中的高成本问题?其模拟反馈与真实人类反馈的核心一致性表现如何?
- AlpacaFarm 通过 API LLM(如 GPT-4、ChatGPT)设计提示词模拟人类成对反馈,成本仅为人工标注的 1/45(1000条示例6美元 vs 人工300美元),且标注效率提升(小时级 vs 天级)
- 核心一致性表现:模拟评估标注者与人类多数投票的一致性达 65%,接近人类标注者之间 66% 的一致性;模拟反馈的方差(0.26-0.43)与人类标注方差(0.35)接近,能复现人类反馈的过拟合等定性特征,确保模拟场景的真实性
问题2:在 AlpacaFarm 支持的 6 种 LPF 方法中,哪种性能最优?其核心优势是什么?
- PPO 方法性能最优,其核心表现:在人类反馈训练中对 Davinci003 的胜率达 55.1%,超过 ChatGPT(52.9%),较基础 SFT 10k 提升 10.8 个百分点;在模拟训练中胜率为 46.8%,同样排名第一
- 核心优势:通过强化学习最大化代理奖励,同时引入 KL 惩罚约束模型参数与 SFT 模型的差异,避免过度偏离基础能力,平衡了性能提升与输出稳定性,相比 Expert Iteration 等方法更能充分利用代理奖励信号
问题3:AlpacaFarm 的自动评估方案如何保证与真实场景的相关性?其评估数据和指标有何特点?
- AlpacaFarm 自动评估方案通过“数据融合+指标适配”保证与真实场景的相关性
- 评估数据特点:融合 Self-Instruct、OASST、Vicuna 等5个开源数据集,共 805 条指令,覆盖多样化真实人类交互场景,其根动词、主题分布与真实 Alpaca Demo 交互数据高度匹配;评估指标特点:采用模型相对于 Davinci003 的胜率作为核心指标,直观且可横向对比
- 相关性验证结果:该评估方案与 Alpaca Demo 真实用户交互数据的胜率相关性达 \(R^2\)=0.97,证明能可靠替代真实场景评估,支持研究者快速迭代方法
RL’s Razor
- 原始论文:RL’s Razor: Why Online Reinforcement Learning Forgets Less, 20250904, MIT
- TODO:有一个推导需要补一下
- 相关博客:SFT远不如RL?永不过时的剃刀原则打开「终身学习」大模型训练的大门
- 该论文核心研究 RL 与 SFT 在模型微调中的“灾难性遗忘”问题,主要内容为:
- 核心现象:RL 与 SFT 在新任务上性能相近,但 RL 能显著保留先验知识,SFT 则需以遗忘旧能力为代价换取新任务提升
- 关键发现:提出经验遗忘定律,模型遗忘程度可通过新任务上“微调后与基准策略的 KL 散度” \(\mathbb{E}_{x \sim \tau}[KL(\pi_0 | \pi)]\) 预测
- 核心原理(RL 的剃刀, RL’s Razor):On-policy RL 天然偏向 KL 散度最小的新任务解决方案,而 SFT 可能收敛到与基准模型差异极大的分布
- 实验验证:在 LLM(数学推理、科学问答等)和机器人抓取任务中验证上述结论,Oracle SFT(显式 KL 最小化)甚至比 RL 遗忘更少
- 核心思考启示:未来微调算法应显式最小化与基准模型的 KL 散度,结合 RL 的抗遗忘性与 SFT 的效率,实现模型“终身学习”
核心现象:RL 微调比 SFT 更少遗忘先验知识
- 对比 RL 与 SFT 的微调效果:
- 两者在新任务上可达到相近性能
- RL 能显著更好地保留模型的先验知识和能力,而 SFT 往往通过牺牲先验知识换取新任务性能提升,存在严重的“灾难性遗忘”问题
- 该现象在 LLM 和机器人基础模型的实验中均得到验证,涵盖数学推理、科学问答、工具使用及机器人抓取放置等任务
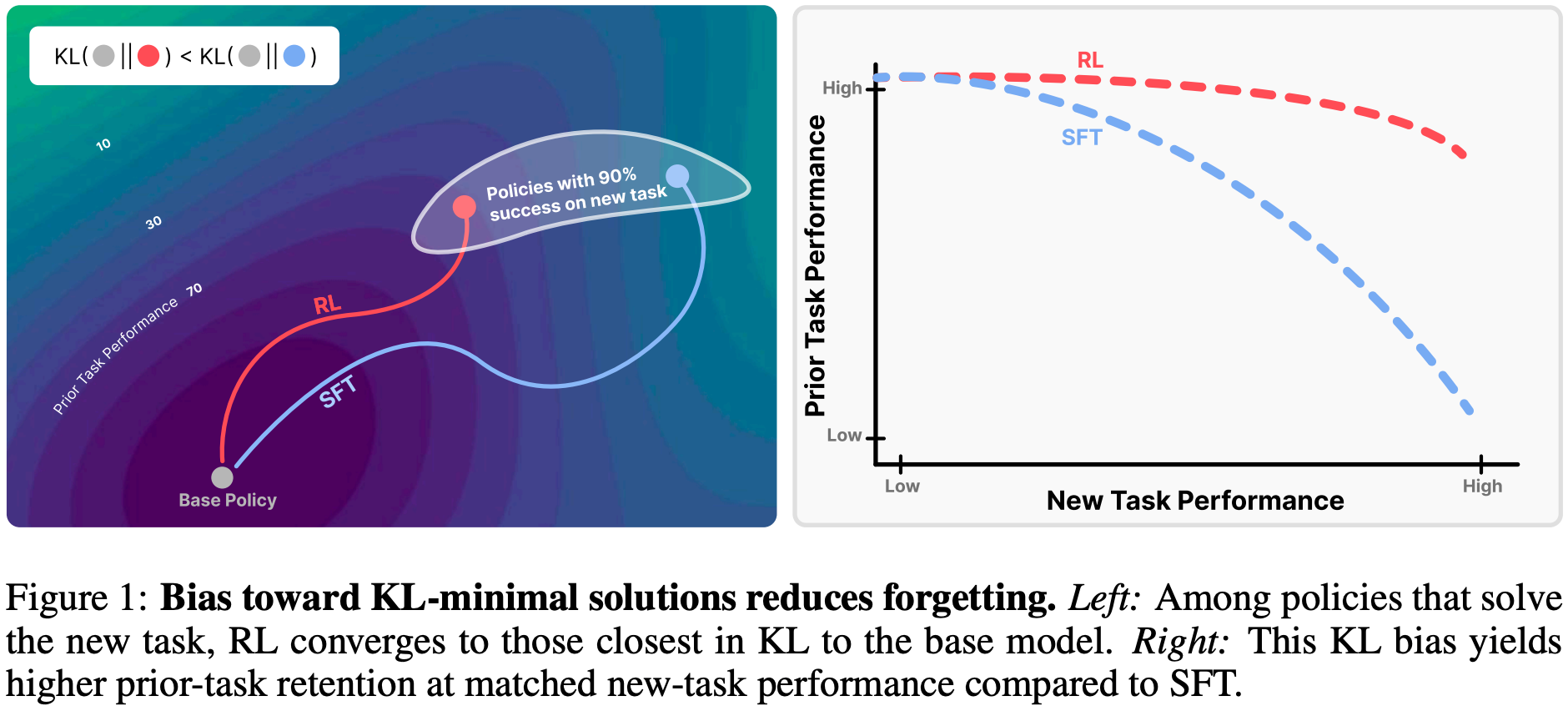
遗忘定律:KL 散度是灾难性遗忘的强预测因子
- 提出经验遗忘定律 :模型在新任务上微调后,其灾难性遗忘程度可通过新任务上微调后策略\(\pi\)与基准策略\(\pi_0\)的 KL 散度准确预测,公式为
$$ \mathbb{E}_{x \sim \tau}[KL(\pi_0 | \pi)] $$- 其中 \(\tau\) 为新任务分布
- 该定律的实用性:无需访问先验任务数据,可在微调过程中直接测量和调控,且在不同模型、不同领域中保持一致性,反映了遗忘的本质属性
- 实验验证:
- 在 ParityMNIST 玩具模型中,遗忘程度与 KL 散度的二次拟合\(R^2=0.96\)
- 在 LLM 实验中,二次拟合 \(R^2=0.71\),残差可归因于噪声
RL 的核心优势:KL 最小化偏好(即 RL’s Razor)
- 定义 RL 的剃刀原理(RL’s Razor) :在所有能解决新任务的高奖励方案中,On-policy RL 天然偏向于与原始策略 KL 散度最小的解决方案,即
$$ \pi^{\dagger}=\arg \min_{\pi \in P^{*} \cap \Pi} D_{KL}(\pi | \pi_0)$$- 其中 \(P^*\) 为最优策略集合,\(\Pi\) 为可行策略集合
- 与 SFT 的差异:SFT 可能收敛到与基准模型 KL 散度任意远的分布(依赖于标注数据),而 RL 的 On-policy 训练机制(从模型自身分布采样)约束学习过程,仅对基准模型已赋予非零概率的输出进行更新,实现“渐进式偏移”而非“任意分布跳转”
On-policy 特性是 KL 散度更小的关键
- 对比 RL 与 SFT 的训练机制差异:
- SFT 目标:最小化与外部监督分布 \(\pi_\beta\) 的交叉熵,训练数据来自固定外部标注;
- RL(策略梯度)目标:最大化 \(\mathbb{E}_{y \sim \pi}[A(x,y) \log \pi(y)]\)(\(A(x,y)\) 为优势函数),训练数据来自模型自身分布,且包含对错误输出的负向惩罚
- 实验验证:
- On-policy 算法(如 GRPO、1-0 Reinforce)无论是否使用负例,均比 Offline 算法(SFT、SimPO)产生更小的 KL 偏移,同时保留更多先验知识;
- SFT 若显式引导至 KL 最小分布(如“Oracle SFT”),可实现比 RL 更优的遗忘-性能权衡,证明 RL 的优势源于隐式 KL 最小化而非算法本身
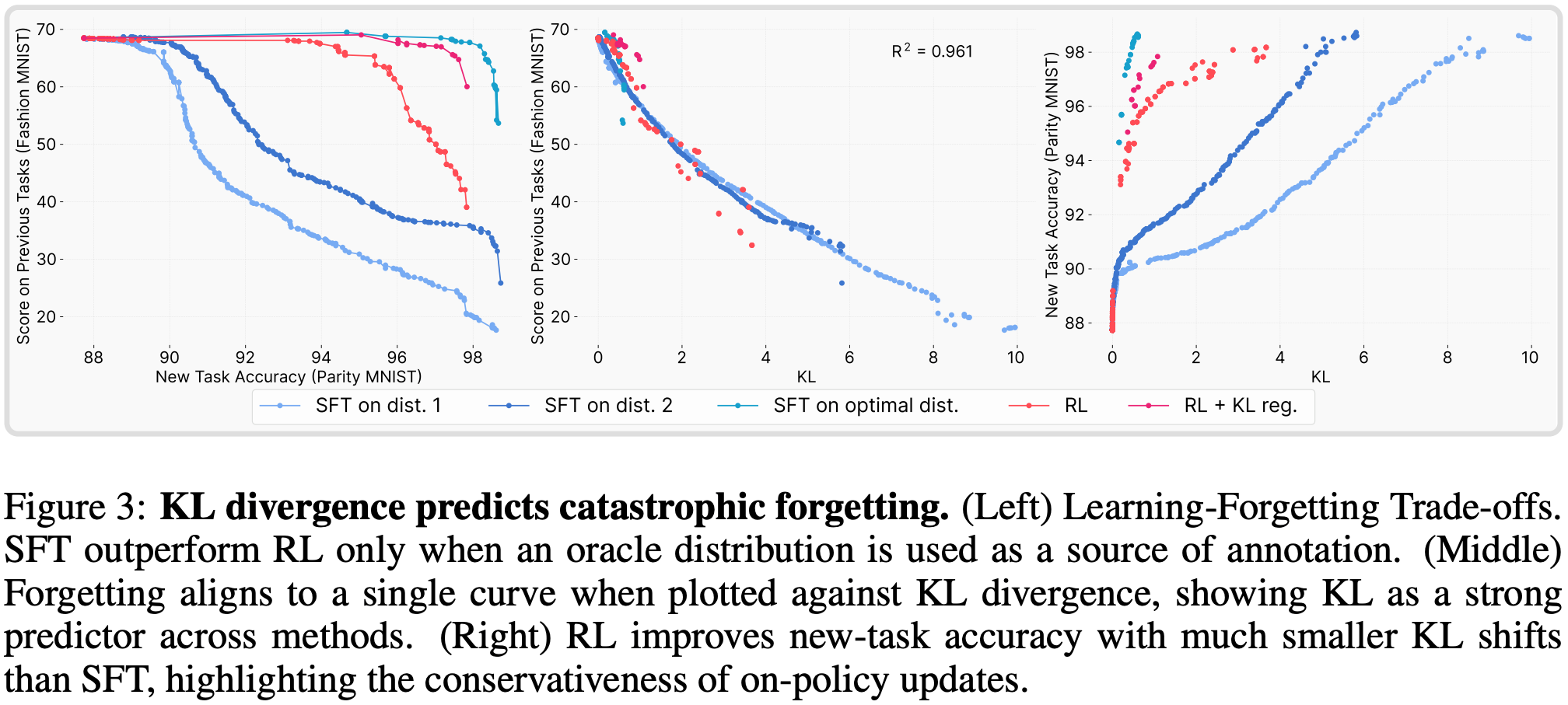
- 关于 Optimal SFT Distribution 的说明
- 为验证 KL 散度是预测变量,作者构建了一个“先知 SFT 分布”(oracle SFT distribution)
- 在 ParityMNIST 任务中,其简洁性使我们能够通过解析方法,在所有达到 100% 准确率的分布中,找到与 Base 模型 KL 散度最小的 labeling(详见附录B.3)
- 补充 附录 B.3 内容:
SFT with oracle distribution: annotations drawn from the minimum-KL distribution consistent with task correctness
- 若 KL 散度完全决定遗忘程度,那么基于该先知分布训练 SFT 应能实现最优的准确率-遗忘权衡
- 补充 附录 B.3 内容:
- 图 3 的实验结果验证了这一预测(基于先知分布训练的 SFT 比 RL 保留了更多先验知识,达成了观测到的最优权衡效果)
- RL 表现出色的原因在于其 On-policy 更新会使解决方案偏向低 KL 散度区域,但当 SFT 被显式引导至 KL 最小分布时,其性能可超越 RL
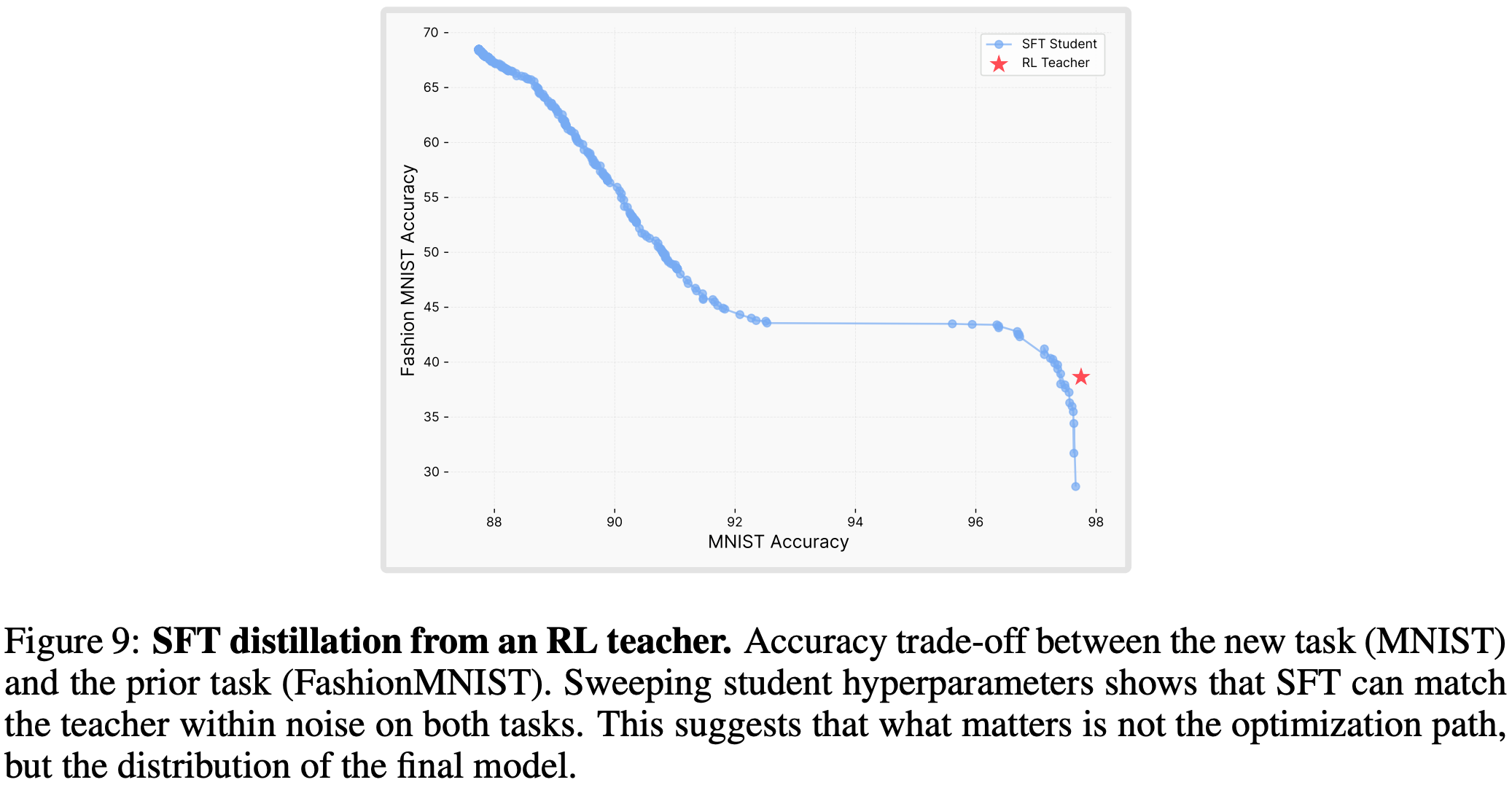
- 作为额外验证,作者使用 RL-trained model 生成的数据训练了一个 SFT 模型(即利用 RL-trained 模型作为教师去蒸馏一个 SFT 模型),该蒸馏后的 SFT 与 RL 的准确率-遗忘权衡效果一致(见图 9),这进一步证明:决定遗忘程度的是所学的分布,而非优化算法本身
理论支撑:RL 与 KL 最小化的等价性
- 定理 A.3:二进制奖励下的单步 RL 目标等价于“带信息投影的 EM 算法”,即通过迭代实现:
- 1)I 步: \(q_t=arg min_{q \in P^{*} } KL(q | \pi_t)\)(找到最优策略集中与当前策略 KL 最小的分布);
- 2)M 步: \(\pi_{t+1}=arg min_{\pi \in \Pi} KL(q_t | \pi)\)(将当前策略投影到该分布),最终收敛到 KL 最小解 \(\pi^\dagger\)
- 命题 A.4:若策略空间 \(\Pi\) 为指数族模型且最优策略集非空,无论M投影是否精确(误差可求和),RL 均收敛到 \(\pi^\dagger\)
延伸发现与启示
- 表征一致性:RL 微调后模型的表征空间与基准模型相似度更高(CKNNA=0.94),而 SFT 出现显著表征漂移(CKNNA=0.56),说明 RL 在不破坏原有表征结构的前提下整合新能力
- 模型规模影响:增大模型规模(3B->7B->14B)无法改变 SFT 的“新任务性能-先验知识遗忘”权衡,仅提升初始通用能力
- 优化动力学:微调步骤中,KL 散度的变化与遗忘梯度方向高度相关,更大的 KL 偏移往往导致更严重的灾难性遗忘
- 实践启示:未来微调算法应显式最小化与基准模型的KL散度,结合RL的遗忘抗性与 SFT 的效率,实现模型“终身学习”
PipelineRL
- 原始论文:PipelineRL: Faster On-policy Reinforcement Learning for Long Sequence Generation, 20250923 & 20250926, ServiceNow AI Research
- 开源地址:github.com/ServiceNow/pipelinerl)
- 提供可扩展、模块化的开源代码,支持灵活配置训练加速器数量与生成批次规模,兼容 vLLM、DeepSpeed 等主流工具
- PipelineRL 是一种针对长序列生成场景 设计的 RL 方法,旨在解决 LLMs 强化学习训练中硬件利用率(Hardware Efficiency)与数据时效性(Data On-policyness)的平衡问题,实现更快的训练速度
- 在数学推理任务(OpenReasoner Zero 数据集,Qwen 2.5 7B 模型)中,PipelineRL 在 MATH500(84.6%)和 AIME2024(19.8%)基准上达到或超过现有方法性能,同时在相同回报下所需时间仅为传统 RL(G=32)的一半
- 注:传统强化学习(Conventional RL)在扩展到多加速器时面临瓶颈:
- 为提升硬件利用率需增大批次规模或增加优化器步数(G),但会导致生成数据与当前训练策略存在滞后(off-policy),损害 REINFORCE、PPO 等算法的性能;
- 但保持完全 on-policy 又会因加速器空闲降低训练吞吐量
- PipelineRL 的核心创新是 并发异步数据生成与模型训练 ,并引入 In-flight 权重更新(in-flight weight updates) 机制:
- 生成引擎在序列生成过程中仅短暂暂停 ,通过高速互联网络接收更新后的模型权重 ,无需等待全部序列生成完成
- 既保证了加速器的高利用率,又最大化了训练数据的新鲜度
- 注:同一个序列可能是多个策略模型 Rollout 的拼接结果得到的
- PipelineRL 的优势:
- 1)训练速度提升:在 128 块 H100 GPU 上,针对长文本推理任务,训练速度较传统 RL 提升约 2 倍;
- 2)高数据时效性:虽最大滞后(max lag)较高,但 ESS 与传统 RL(G=8)相当,保证训练稳定性;
- 3)硬件高效利用:并发执行生成与训练,避免加速器空闲,支持大规模扩展
策略与目标函数
- LLM 的策略表示为
$$ \pi(y | x)=\prod_{i=1}^{n} \pi\left(y_{i} | x, y_{ < i}\right)$$- 其中 \(y_i\) 为生成的第 \(i\) 个 token,\(x\) 为输入 Prompt
- 训练目标是最大化期望回报
$$ J(\pi)=\frac{1}{m} \sum_{j=1}^{m}\left[\mathbb{E}_{y \sim \pi\left(\cdot | x_{j}\right)} R\left(x_{j}, y\right)\right] $$ - 通过策略梯度估计优化:
$$\tilde{\nabla} J(\pi)=\frac{1}{m} \sum_{j=1}^{m} \sum_{t=1}^{T_{j} }\left(R\left(x_{j}, y_{j}\right)-v_{\phi}\left(x_{j}, y_{j, \leq t}\right)\right) \nabla \log \pi\left(y_{j, t} | x_{j}, y_{j,<t}\right)$$- 其中 \(R(x_j,y_j)\) 为回报,\(v_\phi\) 为价值函数
In-flight 权重更新
- 生成过程中动态更新行为策略 \(\mu\),使得序列中近期 token 基于最新权重生成,缓解 off-policy 问题
- 行为策略定义为:
$$\mu :=\mu_{C}(x_{1:t_{1} })… \mu_{C+g}(x_{t_{g}:t_{g+1} } | \hat{x}_{1:t_{1} },… \hat{x}_{t_{g-1}:t_{g} })$$- 其中 \(C\) 为初始检查点,\(g\) 为滞后步数,\(\hat{x}\) 表示保留的KV缓存(平衡效率与时效性)
- 问题:同一个序列中不同的 Token 由不同策略生成,本质就是一个混合策略 Rollout 的结果
性能指标
- 通过有效样本量(Effective Sample Size,ESS)量化数据时效性,定义为
$$ESS=\left( \sum_{i=1}^{N}w_{i}\right) ^{2}\Big/N\sum_{i=1}^{N}w_{i}^{2}$$- 取值接近 1 表示数据接近完全 on-policy
PipelineRL 的架构
- 三阶段流水线:
- 包含 Actor(生成序列)、Preprocessor(计算参考模型对数概率)、Trainer(模型更新)
- 通过 Redis 实现数据流式传输,支持模块化集成各类生成引擎
ArenaRL
- 原始论文:ArenaRL: Scaling RL for Open-Ended Agents via Tournament-based Relative Ranking, 20260110, Alibaba Tongyi & Amap
- ArenaRL 通过组内相对排名替代逐点标量评分 ,有效缓解 Discriminative Collapse;
- ArenaRL 使用 Seeded Single-Elimination 拓扑,在效率与精度之间取得最优平衡;
- ArenaRL 论文构建的两个基准(Open-Travel、Open-DeepResearch)填补了开放式 Agent 全周期评估的空白
ArenaRL 解决的核心问题
- 在开放式任务(Open-Ended Tasks) 中(如旅游规划、深度调研),缺乏客观真实奖励(Ground-Truth Reward) ,传统 RL 方法难以适用
- 现有方法多采用 LLM-as-Judge 进行逐点标量评分(Pointwise Scalar Scoring),但存在 Discriminative Collapse :
- 轨迹组内评分方差(\(\sigma_{\text{group} }\))趋近于零;
- 评分噪声方差(\(\sigma_{\text{noise} }\))较大,导致信噪比(SNR)极低;
- 奖励信号被噪声主导,RL 优化停滞
ArenaRL 核心创新
- 文章提出 ArenaRL ,一种从 Pointwise Scalar Scoring 转向 Intra-Group Relative Ranking 的强化学习范式:
- 引入 Process-Aware Pairwise Evaluation ,基于多维度 Rubrics 进行细粒度比较;
- 设计锦标赛式排名方案(Tournament-Based Ranking Scheme) ,提升优势估计的稳定性与效率
方法框架:ArenaRL 方法框架
任务定义
- 任务建模为条件轨迹生成问题:
$$
\tau = [z_1, a_1, o_1, \dots, z_K, a_K, o_K, y]
$$- 其中 \(z_k\) 为 Chain-of-Thought,\(a_k\) 为工具调用,\(o_k\) 为环境反馈,\(y\) 为最终答案
- RL 目标为:
$$
\mathcal{L}(\theta) = \mathbb{E}_{x \sim \mathcal{D}, \tau \sim \pi_\theta} \left[ r_\theta(x, \tau) - \beta \mathbb{D}_{\text{KL} } \left( \pi_\theta (\cdot|x) | \pi_{\text{ref} } (\cdot|x) \right) \right]
$$
Process-Aware Pairwise Evaluation
- 构建 Arena Judge \(\mathcal{I}\),同时评估两条轨迹 \(\tau_a, \tau_b\),输出各自的评分 \(s_a, s_b\);
- 输入包括:用户 Query \(x\)、两条轨迹的完整过程(含 CoT、工具调用)、细粒度 Rubrics;
- 采用双向评分协议 消除位置偏置:
$$
(s_i, s_j) = \mathcal{I}(x, \tau_i, \tau_j, u) + \mathcal{I}(x, \tau_j, \tau_i, u)
$$- 需要评两次,但是能保证没有位置偏差
Tournament Topologies(锦标赛拓扑结构)
- 研究了五种锦标赛拓扑结构,旨在在计算成本与排名精度之间取得平衡:
拓扑结构 计算复杂度 特点 Round-Robin \(\mathcal{O}(N^2)\) 全配对,精度最高 Anchor-Based Ranking \(\mathcal{O}(N)\) 基于锚点轨迹排名,分辨率低 Seeded Single-Elimination \(\mathcal{O}(N)\) 论文方案 ,基于锚点预排名后构建二叉树 Double-Elimination \(\mathcal{O}(2N)\) 双败淘汰,对随机种子敏感 Swiss-System \(\mathcal{O}(N \log N)\) 非淘汰制,动态配对 - 补充:种子单败淘汰赛(Seeded Single-Elimination)的具体流程
- 种子阶段 :使用 Anchor-Based Ranking 获得初始排名;
- 淘汰阶段 :按种子排名构建二叉树进行配对,胜者晋级;
- 最终排名基于生存深度与累积平均分
Ranking-Based Policy Optimization
- 将排名转换为优势信号:
$$
r_i = 1 - \frac{\mathrm{Rank}(\tau_i)}{N-1} \\
A_i = \frac{r_i - \mu_r}{\sigma_r + \epsilon}
$$- 理解:排名 \(\mathrm{Rank}(\tau_i)\) 越靠后,奖励分数 \(r_i\) 越低
- 目标函数为带 KL 惩罚的 PPO 形式:
$$
\mathcal{L}_{\text{ArenaRL} }(\theta) = \mathbb{E}_{x, \mathcal{G} } \left[ \frac{1}{N} \sum_{i=1}^N \left( \min\left( \frac{\pi_\theta}{\pi_{\text{old} } } A_i, \text{clip}\left( \frac{\pi_\theta}{\pi_{\text{old} } }, 1-\epsilon, 1+\epsilon \right) A_i \right) - \beta \mathbb{D}_{\text{KL} } (\pi_\theta | \pi_{\text{ref} }) \right) \right]
$$
新的基准构建:Open-Travel 与 Open-DeepResearch
- 构建流程
- Stage I :高质量 Query 与参考轨迹构建;
- Stage II :大规模训练数据生成(SFT + RL 数据);
- Stage III :轨迹数据质量控制( LLM-based 质量检查)
- 数据集统计
数据集 SFT 样本数 RL 样本数 测试样本数 语言 领域 Open-Travel 2,600 1,626 250 中文 旅游规划 Open-DeepResearch 2,662 2,216 100 中英混合 Deep Research
实验与结果
- 主要结果
- ArenaRL 在 Open-Travel 上平均胜率 41.8% ,显著高于 GRPO(16.4%)和 GSPO(17.2%)
- 在 Open-DeepResearch 上胜率 64.3% ,有效生成率(Val.%)达 99%
- 在公开写作任务(WritingBench, HelloBench, LongBench-write)上也表现优异,平均得分高于所有基线
- 锦标赛拓扑分析
- Seeded Single-Elimination 在 \(\mathcal{O}(N)\) 复杂度下达到与 Round-Robin 相近的排名精度;
- Anchor-Based 与 Swiss-System 在精度上表现较差
- 其他扩展分析
- 组大小(Group Size) \(N\) 增加可提升性能,尤其在复杂任务中;
- 一致性评估 :LLM 评估与人工评估一致性达 73.9%;
- 无需冷启动的 RL :ArenaRL 可直接从基础模型开始训练,有效缓解冷启动问题;
- 真实业务场景 :在高德地图(Amap)生态中,ArenaRL 在 POI 搜索与开放规划任务中表现优异
实现细节
- 训练:
- 冷启动阶段:基于 Qwen3-8B,SFT 3 个 epoch;
- RL 阶段:使用 Slime 框架,组大小 \(N=16\)(Open-Travel)/ \(N=8\)(Open-DeepResearch),学习率 \(1 \times 10^{-6}\)
- 评估:
- 使用 Qwen3-Max 与 Claude-4-Sonnet 作为双 Judge;
- 采用多维度 Rubrics 进行成对评估
- 工具说明:
- Open-DeepResearch 使用 Google API 搜索 + 摘要模型;
- Open-Travel 集成高德地图 POI 搜索、路线规划等六类工具
附录:论文中提到的 5 个锦标赛对战方法详情
- 在 ArenaRL 中,最终选择 Seeded Single-Elimination 作为主要锦标赛拓扑,因其在 \(\mathcal{O}(N)\) 复杂度下实现了接近 Round-Robin 的排名精度,且通过种子机制有效避免了高质量轨迹的过早淘汰
Round-Robin Tournament(循环赛)
- 对战方法:
- 每一条轨迹 \(\tau_i\) 都会与组内所有其他 \(N-1\) 条轨迹进行成对比较
- 使用 Process-Aware Pairwise Evaluation 机制进行比较
- 每条轨迹的最终得分为其胜率 :
$$
\mathrm{Score}(\tau_i) = \frac{1}{N-1} \sum_{j \neq i} \mathbb{I}(s_i > s_j)
$$- 其中 \(\mathbb{I}(\cdot)\) 为指示函数,若 \(s_i > s_j\) 则为 1,否则为 0
- 最终排名按 \(\mathrm{Score}(\tau_i)\) 降序排列
- 理论最优排名 ,但计算复杂度为 \(\mathcal{O}(N^2)\);
- 适用于小规模组或作为“黄金标准”用于评估其他锦标赛的精度
Anchor-Based Ranking(锚点排名)
- 对战方法:
- 1)生成锚点轨迹 :
- 使用贪心解码(Temperature = 0)生成一个确定性轨迹 \(\tau_{\text{anc} }\),作为质量锚点
- 2)生成探索轨迹 :
- 其余 \(N-1\) 条轨迹通过高熵采样(Temperature = 0.8)生成,保持多样性
- 3)成对比较 :
- 每条探索轨迹 \(\tau_i\) 分别与锚点轨迹 \(\tau_{\text{anc} }\) 进行比较,得到一组评分 \((s_i, s_{\text{anc} }^i)\)
- 4)计算锚点平均分 :
$$
s_{\text{anc} } = \frac{1}{N-1} \sum_{i=1}^{N-1} s_{\text{anc} }^i
$$ - 5)排名 :
- 将所有轨迹的评分集合 \(\{s_1, \dots, s_{N-1}, s_{\text{anc} }\}\) 降序排列
- 1)生成锚点轨迹 :
- 计算复杂度为 \(\mathcal{O}(N)\),效率高;但 无法区分两条探索轨迹之间的细微差异 ,排名分辨率低
Seeded Single-Elimination Tournament(种子单败淘汰赛)
- 对战方法:
- 阶段一:种子阶段(Seeding Phase)
- 1)使用 Anchor-Based Ranking 对组内所有轨迹进行初步排名;
- 2)得到种子排名 \(s_{\text{seed} }^i\),用于构建对战树
- 阶段二:淘汰阶段(Elimination Phase)
- 1)构建二叉树结构 ,根据种子排名进行配对:
- 种子 1 vs 种子 \(N\),种子 2 vs 种子 \(N-1\),以此类推;
- 2)每一场对战中,胜者晋级,败者淘汰:
$$
\tau_{\text{win} } = \mathrm{argmax}_{\tau \in \{\tau_i, \tau_j\} } (s_i, s_j)
$$- 循环多次直到只剩下一个模型没有被淘汰(需要 \(N-1\) 次比较)
- 3)最终排名依据:
- 生存深度 :在锦标赛中走得更远的轨迹排名更高;
- 若在同一轮被淘汰(如四强赛),则根据累积平均分进一步排名
- 1)构建二叉树结构 ,根据种子排名进行配对:
- 阶段一:种子阶段(Seeding Phase)
- 计算复杂度为 \(\mathcal{O}(N)\)(种子阶段 \(N-1\) 次比较 + 淘汰阶段 \(N-1\) 次比较);
- 通过种子机制避免高质量轨迹过早相遇 ,提升排名精度
Double-Elimination Tournament(双败淘汰赛)
- 对战方法:
- 包含胜者组与败者组;
- 轨迹首次失败后进入败者组,再次失败才被淘汰
- 胜者组正常进行单败淘汰;
- 败者组内部也进行淘汰赛,胜者可重新挑战胜者组败者
- 最终排名基于淘汰轮次与累积平均分
- 包含胜者组与败者组;
- 计算复杂度约为 \(\mathcal{O}(2N)\);
- 对偶然失误更鲁棒 ,但若初始种子质量差,排名精度仍有限
Swiss-System Tournament(瑞士制锦标赛)
- 对战方法:
- 1)动态配对 :每轮根据当前胜负记录进行配对(如“1胜0负” vs “1胜0负”);
- 所有轨迹参与固定轮次 \(K \approx \log_2 N\),每轮进行 \(N/2\) 场对战
- 2)最终排名依据 :
- 总胜场数;
- 布赫霍尔兹分(Buchholz Score) :对手的胜场总和,用于衡量对手强度
- 3)排名公式 :
- 综合胜场与对手强度进行排序
- 1)动态配对 :每轮根据当前胜负记录进行配对(如“1胜0负” vs “1胜0负”);
- 计算复杂度为 \(\mathcal{O}(N \log N)\);
- 无淘汰机制,所有轨迹参与全程;
- 适合规模较大、需渐进排名的场景
Prompt-Repetition
- 原始论文:(Prompt-Repetition)Prompt Repetition Improves Non-Reasoning LLMs, Google, 20251217
- 总结:本论文提出并验证了一种简单却有效的 Prompt 增强策略(重复输入 Prompt),能显著提升 LLM 在非推理任务上的性能,且不影响效率
- 基本思路是通过复制 Query 一遍以提升性能,文中提到 Prompt Repetition 是 一种简单有效的非推理任务提升方法 ,适用于多种主流 LLM,不影响延迟与输出长度,建议作为非推理任务的默认策略之一
- 与之前的多种提示技术(如 Chain-of-Thought、Re-reading 等不同),它们常增加输出长度与延迟
- 注:之前有研究显示重复输入可提升文本嵌入质量,其他研究也有重复输入能提升推理表现的发现,但论文重点在非推理任务
Motivation
- 由于 因果语言模型(causal language model)的训练方式,输入 token 的顺序会影响模型预测性能
- 如,“CONTEXT > QUESTION”与“QUESTION > CONTEXT”两种顺序可能导致不同结果
- 核心假设:将输入 Prompt 重复一遍(即
QUERY > QUERY),使每个 prompt token 能关注到所有其他 prompt token,从而缓解顺序依赖问题,提升模型在非推理任务上的性能
具体方法:Prompt Repetition
- 将原始输入
QUERY转换为QUERY > QUERY,即简单复制一次- 在不增加生成 token 数量或延迟的前提下,提升模型在非推理任务上的准确率
- 其他变体:
- Prompt Repetition (Verbose) :加入 “Let me repeat that:” 等引导词
- Prompt Repetition ×3 :重复三次
- Padding :用无关 token(如句点)填充至相同长度,作为对照实验
实验设计:模型与基准测试
- 模型:涵盖 7 个主流 LLM,包括 Gemini 2.0 Flash/ Lite、GPT-4o/4o-mini、Claude 3 Haiku/3.7 Sonnet、Deepseek V3
- Benchmark :
- 标准任务:ARC、OpenBookQA、GSM8K、MMLU-Pro、MATH
- 自定义任务:NameIndex、MiddleMatch(用于验证 Prompt 重复的强效场景)
- 在非推理模式下测试,部分任务测试“选项优先”与“问题优先”两种输入顺序
- 非推理模式 :直接回答
- 推理模式 :使用“Think step by step”引导模型逐步推理
实验结果
- 非推理模式下的表现
- Prompt Repetition 在 47/70 个模型-基准组合中显著优于基线,0 次显著劣于基线
- 在自定义任务 NameIndex 和 MiddleMatch 中效果尤为明显(如 Gemini 2.0 Flash-Lite 准确率从 21.33% 提升至 97.33%)
- Prompt Repetition ×3 在某些任务上表现更优
- 推理模式下的表现
- Prompt Repetition 效果为中性或轻微正面(5 胜 1 负 22 平)
- 因为推理过程本身常会重复部分 Prompt,重复带来的增益有限
- 效率影响
- Prompt Repetition 不增加生成 token 数量 ,不增加延迟(仅影响可并行化的 prefill 阶段)
- 例外:Claude 模型在处理极长输入(如重复三次)时延迟略有增加
- 消融分析
- Padding 对照实验 :仅增加长度而不重复内容,无性能提升,说明增益来自内容重复而非长度增加
- Prompt Repetition ×3 与 Verbose 变体 :在某些任务中表现与标准重复相当或略优
文中提到的未来研究方向(共 13 点)
- 在训练中引入重复 Prompt 进行微调
- 训练推理模型时使用重复 Prompt 以提升效率
- 在生成过程中重复最后生成的 token,探索多轮对话适用性
- 在 KV-cache 中仅保留第二次重复以减少计算负担
- 仅重复部分 Prompt(尤其适用于长 Prompt)
- 重新排序 Prompt(如使用小模型)而非简单重复
- 扩展至非文本模态(如图像)
- 研究多次重复(>2)的效果
- 分析重复对注意力模式的影响
- 结合选择性注意力等技术使用重复
- 探索与 Prefix LM 的交互
- 研究重复有效的情境及 token 表示的变化
- 探索其他有前景的变体
GRADE: Replacing Policy Gradients with Backpropagation for LLM Alignment
- GRADE: Replacing Policy Gradients with Backpropagation for LLM Alignment, 20251230, Lotus Health AI
- Motivation:RLHF 已成为对齐 LLM 与人类偏好的主流范式,但基于 Policy Gradient(策略梯度)的方法(如 PPO)存在以下问题:
- 梯度估计方差高:需要大量样本和精细的超参数调优
- 计算资源需求大:训练不稳定,优化效率低
- 离散采样瓶颈:由于需要采样离散 Token,无法实现从奖励信号到模型参数的端到端梯度流
- 为解决这些问题,论文提出了一种 全新的、完全避免 Policy Gradient 估计的方法
核心方法:GRADE
- GRADE 的全称是 Gumbel-softmax Relaxation for Alignment via Differentiable Estimation(通过可微分估计进行对齐的 Gumbel-Softmax 松弛)
- GRADE 核心思想是:使用可微分的 Token 生成过程替代离散采样,从而允许通过标准的反向传播直接优化奖励目标
- 思考:论文创新主要是直接回传梯度,实际本质与 Offline RL 中的 Batch Loss 类似
相关关键技术
Gumbel-Softmax 重参数化
- 用于生成连续的、可微分的“Soft Token”分布 \(\tilde{y}\),近似离散的类别分布
- 公式:\(\tilde{y}_i = \frac{\exp((\ell_i + g_i) / \tau)}{\sum_{j=1}^{V}\exp((\ell_j + g_j) / \tau)}\),其中 \(g_i \sim \mathrm{Gumbel}(0,1)\),\(\tau\) 为温度参数
- 当 \(\tau \to 0\) 时,输出趋近于 One-Hot 向量(即 Hard Sampling );当 \(\tau \to \infty\) 时,输出趋近于均匀分布。整个过程对 Logits \(\ell\) 是可微的
Straight-Through Estimator, STE
- Straight-Through Estimator,暂时翻译为直通估计器
- 在前向传播中使用 Hard Sampling (离散 Token),在反向传播 中让梯度通过软分布(Gumbel-Softmax 输出)进行流动
$$ y_{\mathrm{STE} } = y_{\mathrm{hard} } - \mathrm{sg}(\tilde{y}) + \tilde{y}$$- 其中 \(\mathrm{sg}(\cdot)\) 是停止梯度算子
- 这确保了生成的文本是离散的(可用于标准奖励函数评估),同时保持了梯度的可传播性
GRADE-STE 变体
- 将 Gumbel-Softmax 与 STE 相结合,形成了论文推荐的方法 GRADE-STE
- 它在前向传递中生成真实的离散文本,在反向传递中通过 Soft Token 分布计算梯度
GRADE 方法流程
- 第一步:可微分 Token 生成
- 在每个生成步骤 \(t\),模型不是采样一个离散 Token,而是生成一个 Soft Token 分布 \(\tilde{y}_t\)
- 通过 Soft Token 的嵌入向量 \(\tilde{e}_t = \tilde{y}_t^{\top}E\) 输入到 Transformer 中,以自回归方式生成后续 Token
- 第二步:可微分奖励计算
- 奖励模型也需要能够处理 Soft Token 输入
- 通过共享词汇表,将 Soft Token 序列 \(\tilde{Y}\) 输入 奖励模型 计算奖励 \(r(x, \tilde{Y})\)
- 第三步:优化训练目标
- 目标函数结合了奖励最大化和KL 散度正则化(防止策略偏离预训练模型太远):
$$
\mathcal{L}(\theta) = -\mathbb{E}_{x\sim \mathcal{D} }\left[r(x,\hat{Y}_{\theta})\right] + \beta \cdot \mathbb{E}_{x\sim \mathcal{D} }\left[\mathrm{KL}(\pi_{\theta}| \pi_{\mathrm{ref} })\right]
$$- 注意:梯度 \(\nabla_{\theta} \mathcal{L}\) 是通过标准的、低方差的反向传播计算得出,而不是通过高方差的 Policy Gradient 估计
- 目标函数结合了奖励最大化和KL 散度正则化(防止策略偏离预训练模型太远):
- 其他:内存优化
- 采用 Top-k Gumbel-Softmax ,仅对 Logits 最高的 k 个 Token(实验中 \(k=256\))进行计算,大幅降低内存开销(从 \(O(T \times V)\) 降至 \(O(T \times k)\))
- 使用梯度检查点(Gradient Checkpointing)和在线 KL 计算等技术
理论分析
- 论文提供了 GRADE 为何能降低梯度方差的理论依据:
- 命题1(方差减少) :
- 在奖励函数平滑的假设下,Gumbel-Softmax 梯度估计器 \(\hat{g}_{GS}\) 的方差小于等于 REINFORCE 策略梯度估计器 \(\hat{g}_{PG}\) 的方差
- 这源于重参数化技巧将随机性隔离在了噪声变量 \(\epsilon\) 中
- 命题2(偏差-方差权衡) :
- Gumbel-Softmax 梯度估计器是有偏的,偏差随温度 \(\tau \to 0\) 而减小(但降低温度后方差会增加)
- 需要采用温度退火 策略:训练初期使用较高的温度以获得低方差梯度,后期降低温度以减少偏差
实验与评估
- 任务:基于 IMDB 电影评论数据集的情感控制文本生成 ,即给定一段评论开头(Prompt),模型需生成表达积极情感的续写
- 基线方法:PPO, REINFORCE, 以及 GRADE(无 STE 的变体)
- 评估设置:严格的数据划分(奖励模型训练集、策略训练集、验证集、测试集),防止数据泄露
- 主要结果(见表1):
- GRADE-STE 取得了最佳性能:测试集奖励达到 \(0.763 \pm 0.344\)
- 显著优于基线:相对 PPO (\(0.510\)) 有 50% 的提升,相对 REINFORCE (\(0.617\)) 有 24% 的提升
- 梯度方差极低:GRADE-STE 的梯度标准差为 \(0.003\),比 REINFORCE (\(0.050\)) 低 14 倍以上
- 泛化能力优秀:GRADE-STE 表现出负的“泛化差距”(测试性能优于验证性能),而 PPO 则显示出过拟合迹象(正泛化差距)
整体评价
- GRADE-STE 成功的原因:
- 1)低梯度方差:通过可微分松弛实现确定性反向传播
- 2)直通估计器(STE)的关键作用:平衡了前向的离散性与反向的连续性
- 3)隐式正则化:在 Soft Token 分布上训练可能起到了防止过拟合的作用
- 适用场景 :
- 当奖励模型能与生成器共享词汇表时
- 当训练稳定性和计算效率是关键考量时
- 局限性 :
- 1)词汇表匹配要求:无法直接使用任意外部奖励函数
- 2)温度敏感性:性能依赖于温度退火策略
- 3)内存需求:尽管有优化, Soft Token 生成仍比 Hard Sampling 需要更多内存
- 4)训练-测试不匹配:模型用 Soft Token 训练,但用 Hard Sampling 测试
SDPO(Self-Distillation Policy Optimization)
- 原始论文:Reinforcement Learning via Self-Distillation, 20260128
- SDPO(Self-Distillation Policy Optimization,自蒸馏策略优化)是一种针对 LLM 在可验证环境(如代码、数学推理)中进行强化学习的方法
- SDPO 通过利用环境提供的丰富反馈(如运行时错误、测试失败信息、评语等),以自蒸馏的方式实现密集信用分配(Dense Credit Assignment) ,从而克服传统 RL 方法中因标量奖励导致的奖励稀疏性 带来的信用分配瓶颈
- 理解:SDPO 的本意实际上就是想使用更丰富的奖励
- 评价:
- 新颖的想法:将符号化反馈转化为密集学习信号;在 Token 级别分配优势,提升学习效率
- 无需外部教师 :完全自监督,适用于在线学习
- 适配性强可作为标准 RLVR 方法的即插即用替代
- 可以用于避免冗余和循环推理,提升模型推理质量
- 可能存在问题:
- 性能依赖于模型的上下文学习能力,对较弱模型可能还不如 GRPO
- 此外,反馈质量直接影响学习效果,要重点关注
SDPO 核心思想
- 背景:
- 传统 RL 方法(如 GRPO)在可验证奖励环境(RLVR)中仅使用标量奖励(如 0/1 表示正确/错误),导致学习信号稀疏
- 许多环境实际上提供结构化、符号化的反馈(如错误信息、失败用例、状态描述等),这些反馈能帮助模型理解为什么失败
- SDPO 将这一设置形式化为 “带丰富反馈的强化学习(Reinforcement Learning with Rich Feedback,RLRF)” ,并利用当前模型作为Self-teacher ,在接收到反馈后重新评估自身生成的序列,生成一个基于上下文的、更优的 Token 分布 ,从而为每个 Token 提供密集的信用信号
SDPO 算法基本流程
- 对于每个问题 \( x \):
- Step 1:学生策略(当前模型 \(\pi_\theta\))生成答案 \( y \sim \pi_\theta(\cdot | x) \)
- Step 2:环境返回丰富反馈 \( f \)(如错误信息、失败用例、成功示例等)
- Step 3:Self-teacher 策略 将反馈 \( f \) 作为上下文,重新评估同一序列 \( y \) 的每个 Token ,得到条件分布:
$$
\pi_\theta(\cdot | x, f, y_{ < t})
$$ - Step 4:通过最小化学生分布与 Self-teacher 分布 之间的 KL 散度,实现自蒸馏:
$$
\mathcal{L}_{\mathrm{SDPO} }(\theta) = \sum_t \mathrm{KL}\big( \pi_\theta(\cdot | x, y_{ < t}) \big| \big| \mathrm{stopgrad}\big( \pi_\theta(\cdot | x, f, y_{ < t}) \big) \big)
$$- 理解:这里 \(\mathrm{stopgrad}\) 防止 Self-teacher 被学生拉回(影响)
- 问题:直观看,这个方式可能打乱模型原本的分布,因为强行拟合一个条件分布可能是比较奇怪的
SDPO 梯度推导
- SDPO 的梯度可表示为:
$$
\nabla_\theta \mathcal{L}_{\mathrm{SDPO} }(\theta) = \mathbb{E}_{y \sim \pi_\theta(\cdot | x)} \left[ \sum_{t=1}^{|y|} \sum_{\hat{y}_t \in \mathcal{V} } \nabla_\theta \log \pi_\theta(\hat{y}_t | x, y_{ < t}) \cdot \log \frac{\pi_\theta(\hat{y}_t | x, y_{ < t})}{\pi_\theta(\hat{y}_t | x, f, y_{ < t})} \right]
$$- 其中 \(\mathcal{V}\) 表示 Token 词表集合,对其进行加和本质就是对输出 Token \(\hat{y}_t\) 进行积分
- 这等价于一个基于对数优势的梯度更新 ,其中优势函数定义为:
$$
A_{t}^{\mathrm{SDPO} }(\hat{y}_t) = \log \frac{\pi_\theta(\hat{y}_t | x, f, y_{ < t})}{\pi_\theta(\hat{y}_t | x, y_{ < t})}
$$- 优势为正表示教师认为该 Token 更优,为负表示更差
- 注意:详细推导见原始论文附录 B.1
- 问题:似乎推导是错误的(具体来讲 \( \nabla_\theta A_{t,k}\) 求导似乎有点问题)
- 回答:已确认,没有问题,将 \(A_{t,k}\) 拆成两个对数的差即可快速得到结果
SDPO vs GRPO 的优势函数比较
- GRPO 的优势函数 :
$$
A_{i,t}^{\mathrm{GRPO} }(\hat{y}_{i,t}) = \color{red}{\mathbb{1}\{y_{i,t} = \hat{y}_{i,t}\}} (r_i - \mathrm{mean}\{r_i\})
$$- 仅为已生成 Token (\(y_t\))分配常数优势,信息稀疏
- 理解:这里是可以将所有可能的 Token 都列出来,再选择命中的(已生成的)Token 作为优势,其他的分配 0 优势,体现稀疏性(相对 SDPO 的优势函数)
- SDPO 优势函数 :
$$
A_{i,t}^{\mathrm{SDPO} }(\hat{y}_{i,t}) = \log \frac{\pi_\theta(\hat{y}_{i,t} | x, f_i, y_{i,<t})}{\pi_\theta(\hat{y}_{i,t} | x, y_{i,<t})}
$$- 为每个可能的 Next Token 分配优势,实现 密集信用分配
其他关键技术细节
- SDPO 可处理(支持)三种反馈类型:
- 环境输出(如错误信息)
- 成功样本(同组内其他成功的尝试)
- 原始尝试(可选,但实验表明可能降低探索性)
- (增加教师正则化)为防止教师过快偏离初始模型,采用以下正则化策略:
- 显式信任域约束(Trust-Region Teacher)
- 指数移动平均参数更新(EMA Teacher)
- (近似计算)为节省内存,使用 Top-K 蒸馏 :
- 仅计算学生 Top-K Token 的分布差异,其余 Token 合并为一个“尾部”概率项
- SDPO 是可扩展的,可以扩展为:
- SDPO+GRPO 混合优势 :结合标量奖励与 Self-teacher 信号
- 离策略训练 :支持PPO风格的重要性采样
SDPO 相关实验效果
无丰富反馈环境(标准 RLVR)
- 在科学推理、工具使用等任务上,SDPO 显著优于 GRPO
- 生成答案更简洁,推理更高效
- 训练速度更快,样本效率更高
有丰富反馈环境(如代码生成等)
- 在 LiveCodeBench v6 上,SDPO 准确率显著高于 GRPO
- 所需生成次数减少约 4 倍
- 特别在中等和难题上表现优异
测试时自蒸馏:Test-Time Self-Distillation
- 对于极难题(pass@64 < 0.03),SDPO 能加速解决方案的发现
- 相比 best-of-\(k\) 采样或多轮对话,发现速度提升约 3 倍
RLPR(Reinforcement Learning with Reference Probability Reward)
- 原始论文:RLPR: Extrapolating RLVR to General Domains without Verifiers, THU & NUS …, 20250623
- 论文提出了一种名为RLPR的新框架,旨在将RLVR(Reinforcement Learning with Verifiable Rewards)方法推广到通用领域,而无需依赖外部验证器(Verifier)
- 论文核心贡献总结
- 1)提出 RLPR 框架 :首次将 RLVR 推广到通用领域,无需外部验证器
- 2)提出概率奖励(Probability Reward,PR) :利用 LLM 内在解码概率作为奖励,优于似然奖励和验证器模型
- 3)提出标准差过滤策略 :动态过滤训练样本,改进 PR 并提升训练稳定性与最终性能
- 4)全面实验验证 :在多个模型和基准上验证了 RLPR 的有效性与通用性
背景 and Insight
- 背景:
- RLVR 已在数学和代码生成任务中表现不错,但其严重依赖于领域特定的验证器(如规则验证器或训练好的验证模型)
- 1)扩展成本高、工程复杂度大;
- 2)难以推广到自然语言回答自由形式多样、难以规则化的通用领域
- RLVR 已在数学和代码生成任务中表现不错,但其严重依赖于领域特定的验证器(如规则验证器或训练好的验证模型)
- 作者的核心 Insight 与动机
- Insight:LLM 生成正确答案的内在概率直接反映了其自身对推理质量的评估
- 动机:能否直接利用这个概率信号作为奖励,从而摆脱对外部验证器的依赖?
RLPR 方法核心思想
- 使用参考答案的解码概率 作为奖励信号,替代传统的外部验证器奖励
- 通过概率去偏和标准差过滤 机制,提升奖励的稳定性和训练效果
Probability Reward(PR)
- 第一步:给定问题 \(Q\)
- 模型生成推理内容 \(z\) 和答案 \(y\) ,参考答案为 \(y^*\)
- 第二步:将生成的答案替换为参考答案,构成新序列 \(o’\)
- 将新序列输入策略模型 \(\pi_\theta\) 得到每个 token 的解码概率 \(p_i\)
- 奖励计算为参考答案对应 token 概率的均值(而非序列似然),以降低方差、提升鲁棒性:
$$
r = \frac{1}{|y^*|} \sum_{o_i’ \in y^*} p_i
$$- 注意这里的 \(p_i\) 是生成参考答案的概率
- 理解:这种 Reward 涉及的一个隐含一个目标 等价于 最大化当前策略 \(\pi_\theta\) 生成参考答案对应的概率
Reward Debiasing
- 概率奖励可能受到问题本身或参考答案的影响,引入偏差
- 定义一个基础分数 \(r’\)
- \(r’\) 为直接解码参考答案 \(y^*\)(无中间推理 \(z\))的概率
- 理解:\(r\) 和 \(r’\) 的区别是 \(r’\) 不包含推理过程 \(z\),\(r\) 包含推理过程,作者认为 不包含推理过程的 \(r’\) 可以用来作为基线
- 问题:但这样会导致最大化目标变成 最大化带推理的概率 - 不带推理的概率 ,且 \(r’\) 对不同的问题是不一样的,这可能是有偏的,更像是再优化推理的准确性,即加上推理以后的效果比原始模型不加推理的效果更好
- 去偏后的奖励为:
$$
\hat{r} = \mathrm{clip}(0, 1, r - r’)
$$- 理解:这里应该只会被下界 0 Clip(概率的均值不会大于 1),此时表示加入推理后生成 reference 的概率更低了(从而分数更低了)
- 目标函数梯度为:
$$
\nabla \mathcal{J}_{\mathrm{RLPR} }(\theta) = \mathbb{E}_{o \sim \pi_\theta(\cdot|x)}[\hat{r} \nabla \log \pi_\theta(o|x)]
$$
Standard Deviation Filtering
- 传统 RLVR 使用准确率过滤(全对或全错的样本),甚至不需要设置阈值,论文提到 PR 是连续值,难以设置阈值
- 理解:其实也不难,毕竟可以设置一个 0.8 这种值(比如当前很多训练时准确率 0.98 的 Query 也可能会被过滤掉的),只是说不是动态的,分数可能无法动态按照难度区分而已
- 作者进一步提出动态标准差过滤 :移除奖励标准差低于阈值 \(\beta\) 的样本(表示样本太简单或太难)
- \(\beta\) 通过指数移动平均 动态更新,适应训练过程中奖励分布的变化
实验结果
实验设置
- Base Model :Gemma2、Llama3.1、Qwen2.5 系列
- 训练数据 :使用 WebInstruct 中非数学类的高质量推理问题,经 GPT-4.1 过滤后保留约 77k 条
- 评估基准 :
- 数学推理:MATH-500、Minerva、AIME24
- 通用推理:MMLU-Pro、GPQA、TheoremQA、WebInstruct
- 基线方法 :包括 Base/Instruct 模型、PRIME、SimpleRL-Zoo、Oat-Zero、TTRL、General Reasoner、VeriFree 等
主要结果
- RLPR 在通用领域和数学推理任务 上均显著优于基线方法
- 在 Qwen2.5-7B 上:
- MMLU-Pro:56.0(优于 General Reasoner 的 55.4)
- TheoremQA:55.4(优于 VeriFree 7.6 分)
- 在 Llama3.1-8B 和 Gemma2-2B 上也取得一致提升
概率奖励质量分析
- PR 在区分正误回答 上优于规则验证器和基于模型的验证器(AUC 更高)
- 即使在小规模模型(如 Qwen2.5-0.5B)上也表现良好
- PR 与生成回答的长度和熵 相关性极低,表明其作为奖励机制的鲁棒性
消融实验
- 去除去偏操作 :性能下降约 2.5-2.7 分
- 去除标准差过滤 :性能下降约 1.4-2.9 分
- 使用序列似然替代 token 平均概率 :性能大幅下降(20+ 分),验证了平均概率的鲁棒性
在可验证领域也可用?
- 在数学数据上,结合规则验证器奖励与 PR 可进一步提升模型性能(Table 4)
- 说明 PR 不仅能用于无验证器场景,也能增强有验证器场景的细粒度判别能力
鲁棒性高
- 在不同提示模板下,RLPR 性能稳定,而 VeriFree 对模板敏感
- 训练过程中响应长度和熵保持稳定,无退化或崩溃现象
ReAct
- 原始论文:ReAct: Synergizing Reasoning and Acting in Language Models, 20221006-20230310, Shunyu Yao, Princeton
Epiplexity
- 原始论文:From Entropy to Epiplexity: Rethinking Information for Computationally Bounded Intelligence, 20260106, CMU & NYU
- 注:epiplexity(/ˌepɪˈpleksəti/) 是作者新造的单词,属于信息论的学术属术语,论文中标注为:epistemic complexity(认知复杂度)