NLP——UNILM论文阅读笔记

本文介绍了MSRA今年的一篇文章: UNILM: Unified Language Model Pre-training for Natural Language Understanding and Generation

---

UNILM基于三个预训练目标

• Unidirectional LM:
• Bidirectional LM:
• Sequence2Sequence LM:

---

贡献

和BERT对比

• BERT是双向模型,所以自然语言的生成(NLG)任务上不适用
• UNILM采用三种(无监督的)LM目标,其中的Sequence2Sequence LM能够解决文本生成问题

其他一些优点

• 仅使用一个LM(由Transformer构成), 在三个不同的预训练任务上共享参数, 泛化能力强
  • 参数共享: 不需要在不同的语言模型(对应不同的预训练任务)上使用不同的模型参数
  • 泛化能力强: 多个训练目标同时优化模型,使得模型能够避开因为训练目标引起的过拟合问题

---

模型结构介绍

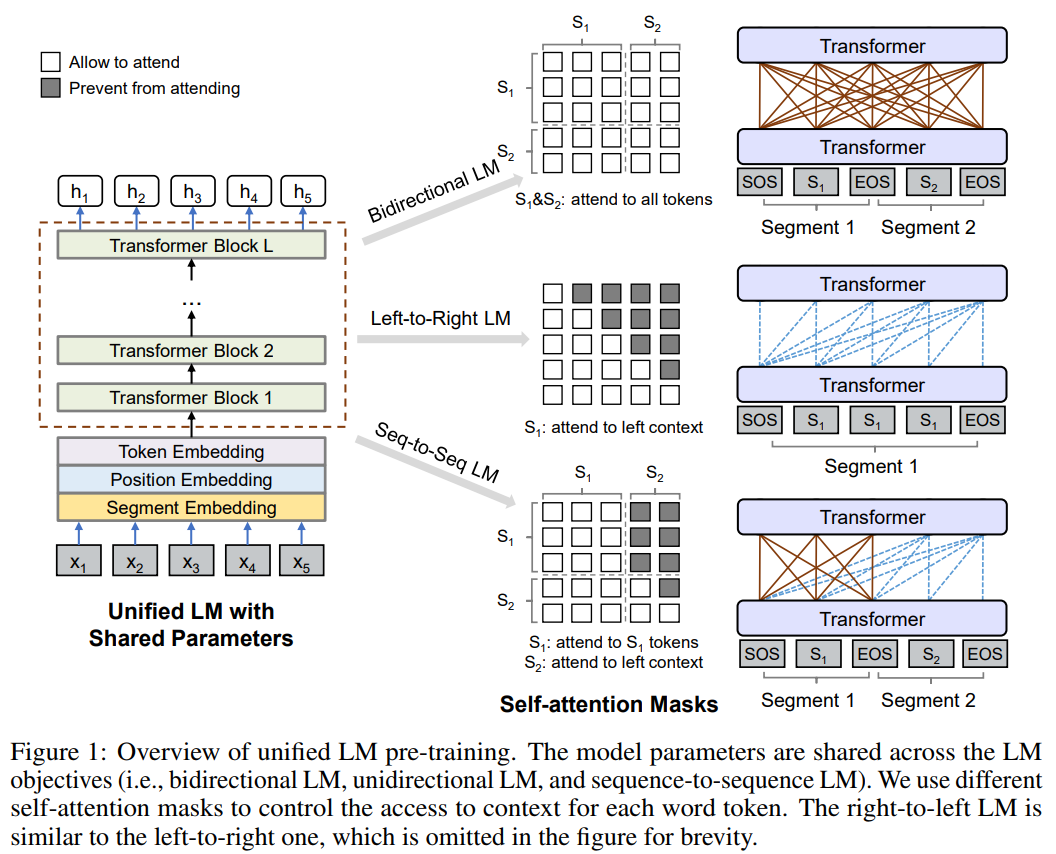
结构图

• 输入向量为 $\vec{x} = (x_1, x_2,,,x_{|x|}$)
• 输入向量表征与BERT相同,由Embedding层(三个Embedding层之和, 和BERT一样):
  • Token Embedding, WordPiece
  • Position Embedding
  • Segment Embedding, 由于UNILM会使用多个LM任务训练,所以Segment Embedding在模型中也扮演着LM标识的作用(对不同的LM目标使用不同的Segment Embeddings)
• 主要网络(Backbone Network)为多层Transformer:
  • 每两个Transformer Blocks之间的Self-Attention Masks: For Each Transformer Block, 使用多头Self-Attention来聚合之前层出现的输入向量.(这里的Self-Attention使用了)
  • Transformer之间的Self-Attention机制决定了模型什么语言模型(任务)
  • 如图所示:
    • Bidirectional LM 对应的 Self-Attention Masks为全0的矩阵, 表示所有的Attention都不屏蔽 (attend to all tokens)
    • Left-to-Right LM 对应的 Self-Attention Masks为拼屏蔽右上三角的矩阵(左下三角全为0)
    • Right-to-Left LM 对应的 Self-Attention Masks为拼屏蔽左下三角的矩阵(右上三角全为0)
    • Seq-to-Seq LM 对应的 Self-Attention为
      • $S_1$-$S_1$ 为全0(0表示开放), 对应为Bidirectional
      • $S_1$-$S_2$ 为负无穷(负无穷表示屏蔽)
      • $S_2$-$S_1$ 为全0
      • $S_2$-$S_2$ 为屏蔽右上三角的矩阵(这里与Left-to-Right的情况相同)

按照结构图分析数据流

• 对于一组输入向量 $\{\vec{x}\}_{i=1}^{|x|}$, 初始编码为 $\mathbf{H}^0 = [\vec{x}_1, \vec{x}_2,,,\vec{x}_{|\vec{x}|}]$
• 第一层后编码为上下文表征$\mathbf{H}^1 = [\vec{h}_1^1, \vec{h}_2^1,,,\vec{h}_{|\vec{x}|}^1]$
• 第 $l$ 层后编码为上下文表征$\mathbf{H}^l = [\vec{h}_1^l, \vec{h}_2^l,,,\vec{h}_{|\vec{x}|}^l]$
• 每一层的 Transformer Block, 使用 multiple self-attention heads去聚合上一层的输出: L-layer的 Transformer对应的数学表达式为 $\mathbf{H}^l = Transformer_l(\mathbf{H}^{l-1}), l \in [1, L]$
• Self-Attention Head $\mathbf{A}_l$的详细计算公式如下:
  $$\begin{align} \mathbf{H} = \mathbf{H}^{l-1}\mathbf{W}_l^Q \\ \mathbf{K} = \mathbf{H}^{l-1}\mathbf{W}_l^K \\ \mathbf{V} = \mathbf{H}^{l-1}\mathbf{W}_l^V \\ \mathbf{A} = softmax(\frac{\mathbf{Q}\mathbf{K}^T}{\sqrt{d_k}} + \mathbf{M})\mathbf{V}_l \\ where, \quad \mathbf{M}_{ij} = 0 \ or \ -\infty \end{align}$$
  • $\mathbf{M}$中的值
    • $-\infty$ 表示屏蔽Attention (prevent from Attention)
    • 0 表示允许 Attention (allow to Attention)