NLP——Reinforcement-Pre-Training

注：本文包含 AI 辅助创作

参考链接：
- 原始论文：(RPT)Reinforcement Pre-Training, arXiv 20250609, Microsoft Research & PKU & THU

Paper Summary

整体内容总结
- 论文提出了一种新颖的，用于预训练大语言模型的新范式，强化预训练（Reinforcement Pre-Training, RPT）
- 通过将下一词预测任务重构为可验证的推理任务，并应用基于正确性的强化学习奖励，RPT 使大语言模型能够在预训练期间利用扩展计算构建更强的基础推理能力
- 实验表明：RPT 提升了下一词预测的准确性 ，在数学和通用推理基准的 Zero-Shot 设置 中表现出色，并为后续强化学习微调 提供了更好的起点
- RPT 通过从根本上重新思考预训练目标本身，为开发更强大、更通用的智能大语言模型提供了新的方向
论文将 Next-Token Prediction（NTP）任务重新定义为一种通过强化学习训练的推理任务，模型在正确预测给定上下文的 Next Token 时会获得可验证的奖励
RPT 提供了一种可扩展的方法，能够利用海量文本数据实现 通用强化学习（general-purpose RL） ，而 无需依赖特定领域的标注答案
- 通过激励 Next Token 推理能力，RPT 显著提升了语言模型在预测 Next Token 时的准确性
RPT 为后续的强化微调提供了强大的预训练基础
实验结果表明，随着训练计算量的增加， Next-Token Prediction 的准确性持续提升
- 作者认为，这些结果证明了 RPT 是一种有效且有前景的规模化范式，能够推动语言模型预训练的进步

Introduction and Discussion

LLM 在各种任务中展现出了卓越的能力，这主要得益于基于海量文本语料的 Next-Token Prediction 目标的可扩展性
- 这种自监督范式已被证明是一种高效的通用预训练方法
RL 已成为一种强大的技术，可用于微调大语言模型，使其与人类偏好对齐或增强特定技能，例如复杂推理 (2022, 2023, 2024)
但当前强化学习在大语言模型训练中的应用面临可扩展性和通用性挑战
- RLHF 在对齐任务中表现有效，但其依赖昂贵的人类偏好数据，且学习到的奖励模型容易受到奖励破解（reward hacking）的影响，从而限制了可扩展性
- RLVR 是一种基于可验证奖励的强化学习（Reinforcement Learning with Verifiable Rewards, RLVR）方法
  - RLVR 利用客观的、基于规则的奖励（通常来自问答对），这种方法能够缓解奖励破解问题
  - 但 RLVR 通常受限于带有可验证答案的标注数据的稀缺性，因此其 应用范围仅限于特定领域的微调 ，而 非通用预训练
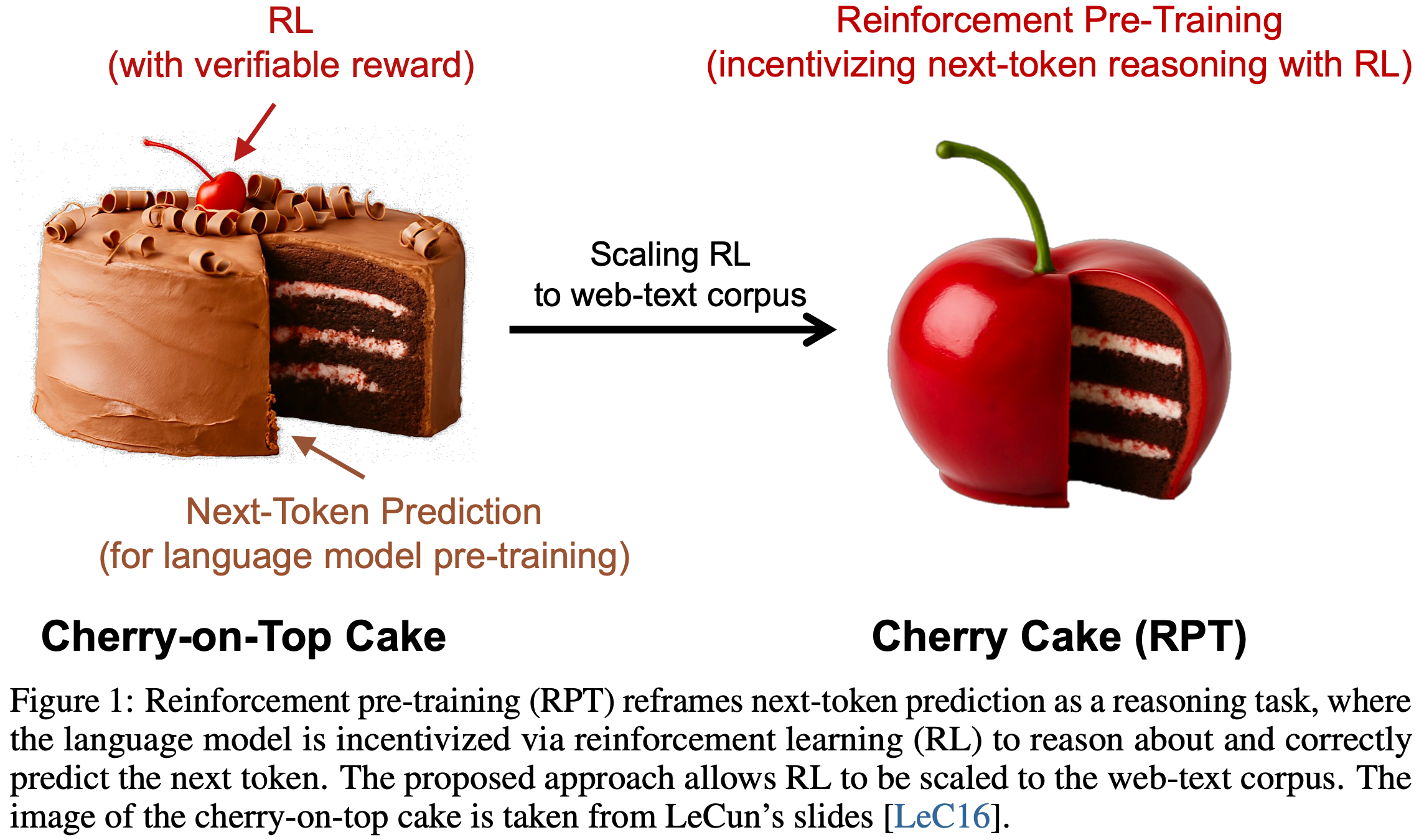
在这项工作中，作者提出了 强化预训练（RPT） ，这是一种新颖的范式，旨在弥合可扩展的自监督预训练与强化学习能力之间的差距
- RPT 将 Next-Token Prediction 任务重新定义为一种 Next Token 推理过程
- 对于预训练语料中的任何给定上下文，模型会被激励在预测 Next Token 之前对其进行推理
- 模型会根据其预测结果与语料中真实 Next Token 的匹配程度，获得一种可验证的内在奖励
- 这种方法将通常用于 Next-Token Prediction 的海量未标注文本数据，转化为一个适用于通用强化学习的庞大数据集，而无需依赖外部标注或特定领域的奖励函数
这种方法具有以下几个关键优势：
- 1）可扩展性与通用性 ：RPT 利用了与标准 Next-Token Prediction 相同的海量未标注文本数据，将其转化为通用强化学习的大规模数据集，无需外部标注
- 2）减少奖励破解风险 ：通过使用直接的、基于规则的奖励信号（即预测 Next Token 的正确性），RPT 从根本上降低了复杂学习奖励模型中常见的奖励破解风险
- 3）促进深度理解与泛化 ：通过显式激励 Next Token 推理模式，RPT 鼓励模型深入理解上下文，而非简单地记忆 Next Token
  - 模型学会探索和验证关于“为何某个 Token 应该出现”的假设，从而构建更鲁棒的表示
- 4）推理过程的计算分配 ：预训练中的内部推理过程使模型能够为每个预测步骤分配更多的“思考”或计算资源，类似于在训练时为每个 Token 应用推理时扩展，从而直接提升 Next-Token Prediction 的准确性
论文的实验表明：
- RPT 显著提升了 Next-Token Prediction 的准确性
- RPT 为后续的强化微调提供了更鲁棒的预训练基础，从而在最终任务中表现更优
- 扩展曲线显示，在 RPT 框架下，增加训练计算量能够持续提升 Next-Token Prediction 的准确性 ，这表明 RPT 是一种可持续的规模化策略
- 这些结果证明了强化预训练是一种有效且有前景的新范式，能够推动大语言模型预训练的进步
论文的主要贡献如下：
- 提出了一种新的规模化范式： 强化预训练（RPT） ，将 Next-Token Prediction 重新定义为通过强化学习训练的推理任务，并利用预训练语料直接生成的内在可验证奖励
- RPT 提供了一种可扩展且通用的强化学习预训练方法，通过基于规则的奖励减少奖励破解风险，并通过激励 Next Token 推理模式（而非机械记忆（rote memorization））促进泛化能力
- RPT 显著提升了 Next-Token Prediction 的准确性，并展现出良好的扩展特性，即性能随着训练计算量的增加而持续提升
- RPT 为后续的强化微调提供了更强的预训练基础，并提升了在多种下游任务中的 Zero-Shot 性能

Preliminary

Next-Token Prediction, NTP

Next-Token Prediction 是现代大语言模型的基本训练目标 (2022)
给定训练语料中的输入序列 $x_{0}\cdots x_{T}$，模型的训练目标是最大化以下目标函数：
$$
\mathcal{J}_{\text{NTP} }(\theta)=\sum_{t=1}^{T}\log P(x_{t}\mid x_{0},x_{1},\ldots,x_{t-1};\theta),
$$
- 其中 $\theta$ 表示语言模型的参数

Reinforcement Learning with Verifiable Rewards, RLVR

RLVR 利用强化学习目标来增强具有可验证答案的特定技能 (2023)
RLVR 需要一个标注的问答对数据集 $\mathcal{D}=\{(q,a)\}$
对于特定的问答对 $(q,a)\in \mathcal{D}$，大语言模型 $\pi_{\theta}$ 会生成一个响应 $o\sim \pi_{\theta}(\cdot \mid q)$
- 然后使用一个确定性的验证器 $\mathcal{V}$ 计算可验证奖励 $r=\mathcal{V}(o,a)$，模型的训练目标是最大化期望奖励：
  $$
  \mathcal{J}_{\text{RLVR} }(\theta)=\mathbb{E}_{(q,a)\sim \mathcal{D},o\sim \pi_{\theta}(\cdot|q)}\left[r(o,a)\right].
  $$

Reinforcement Pre-Training

Pre-Training Task: Next-Token Reasoning

论文提出了 Next Token 推理任务用于语言建模
给定训练语料库中的输入序列 $x_0 \cdots x_T$，对于每个位置 $t \in \{1, \ldots, T\}$，前缀 $x_{ < t}$ 被视为上下文，而真实的 Next Token 是 $x_t$
在 Next Token 推理任务中，模型 $\pi_\theta$ 需要在生成对 Next Token 的预测 $y_t$ 之前生成一个思维链（chain-of-thought）推理序列，记为 $c_t$
模型的整体响应为 $o_t = (c_t, y_t)$，其中 $o_t \sim \pi_\theta(\cdot \mid x_{ < t})$
如图 2 所示， Next Token 推理的长思维链过程可能涉及多种推理模式，例如头脑风暴、自我批判和自我修正
Next Token 推理任务将预训练语料库重构为大量的推理问题集合，使预训练从学习表面的 Token-level 关联转向理解其背后的隐藏知识，并使强化学习的扩展成为可能

Pre-Training with Reinforcement Learning

RPT 通过在线策略强化学习训练 LLM 执行 Next Token 推理，如图 3 所示
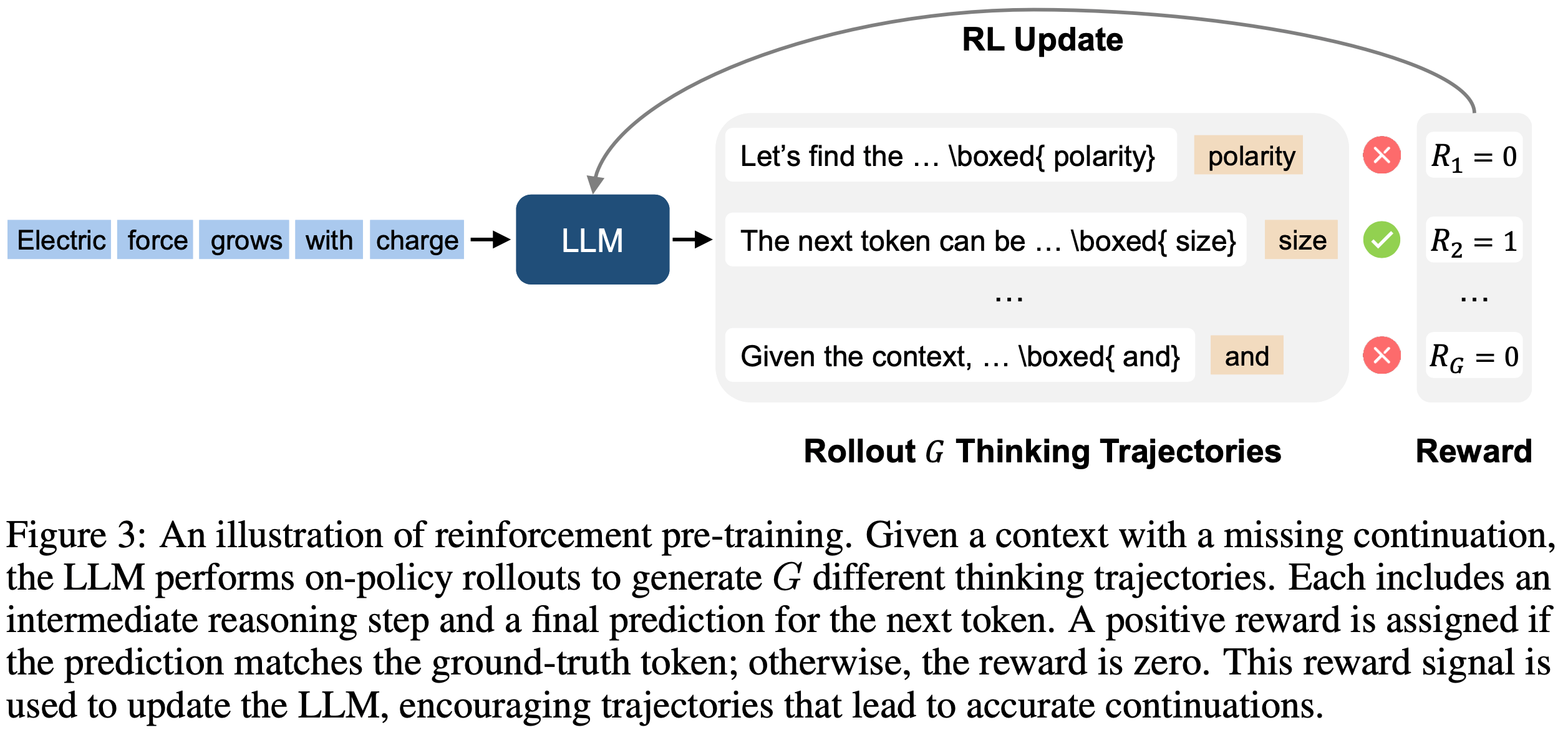
对于上下文 $x_{ < t}$，RPT 提示语言模型 $\pi_\theta$ 生成 $G$ 个响应（思维轨迹），记为 $\{o^i_t\}_{i=1}^G$
每个响应 $o^i_t = (c^i_t, y^i_t)$ 包含一个思维链推理序列 $c^i_t$ 和一个最终的预测序列 $y^i_t$
为了验证 $y^i_t$ 的正确性，论文引入了前缀匹配奖励（prefix matching reward），该奖励支持验证跨越多 Token 或涉及词汇表外 Token 的预测
符号定义如下：
- $x_{\geq t}$ 表示真实补全序列，其字节（byte）序列表示为 $\overline{x}_{\geq t}$
  - 问题：为什么不是单个 token? 论文每次仅预估下一个 token 吧？到底是每次生成单个 token 还是多个 token？
  - 猜测：这里是表示每次推理时，可以只看一个 token，也可以看多个 token
- $y^i_t$ 表示预测的序列，其字节（byte）序列表示为 $\overline{y}^i_t$
- $\overline{y}^i_t$ 的字节长度记为 $l$
- 真实补全序列中 Token 的累积字节长度定义为有效边界，记为 $\mathcal{L}_{gt}$
  - 理解：这里的有效边界是一个整数集合，表示有效的长度值的集合
形式上，对于上下文 $x_{ < t}$ 的第 $i$ 个输出，奖励 $r^i_t$ 定义为：
$$
r^i_t = \begin{cases}
1 & \text{if } \overline{y}^i_t = \overline{x}_{\geq t}[1:l] \text{ and } l \in \mathcal{L}_{gt} \\
0 & \text{otherwise}
\end{cases},
$$
- 如果预测的字节序列是真实补全字节序列的精确前缀且其长度 $l$ 匹配任何有效 Token 边界 ，则奖励为 1
- $\overline{y}^i_t$ 表示预测的字节序列
- $\overline{x}_{\geq t}$ 表示真实补全的字节序列
令 $\mathcal{D}$ 为所有 $\{x_{ < t}\}_{t=1}^T$ 的集合，模型训练的目标是最大化期望奖励：
$$
\mathcal{J}_{\text{RPT} }(\theta) = \mathbb{E}_{(x_{ < t}, x_{\geq t}) \sim \mathcal{D}, \{o^i_t\}_{i=1}^G \sim \pi_\theta(\cdot|x_{ < t})} \left[r^i_t \right].
$$

Pre-Training Setup

论文使用 OmniMATH 数据集（2024）进行强化预训练。OmniMATH 包含 4,428 个竞赛级数学问题及其解答，数据来自 AoPS Wiki 和 AoPS 论坛等官方网站
由于许多 Token 即使无需推理也容易预测，论文在强化预训练前进行了 Token-level 数据过滤
- 论文使用 Deepseek-R1-Distill-Queen-1.5B 作为小型代理模型，计算每个 Token 在前 16 个候选 Token 上的代理模型熵
- 通过应用熵阈值，论文过滤掉低熵位置，优先训练那些需要更多计算努力预测的挑战性 Token（注：高熵的 token 是较难预测的）
在所有实验中，论文以 Deepseek-R1-Distill-Queen-14B（2025）作为基础模型
- R1-Distill-Queen-14B 因其基本的推理能力而成为强化学习的良好起点
论文使用 verl 库（2025）实现训练框架，并使用 vllm 进行推理
论文采用 GRPO 算法（2025），具体超参数详见附录 B
训练时，论文采用 8k 的训练长度，学习率为 $1 \times 10^{-6}$，KL 惩罚为零，批次大小为 256 个问题，每个问题采样 $G=8$ 个响应，在 rollout 过程中使用温度为 0.8
从每个响应中，论文直接提取最后一个 $\backslash$boxed{ } 内的完整序列作为模型对 Next Token 的预测
从第 500 步开始 ，论文使用动态采样以提高训练效率（2025），主实验的总训练步数为 1,000
- 补充：这里的动态采样是 DAPO 中的动态采样技术，把奖励全为 0 或者全为 1 的 Prompt/样本丢弃掉
提示模板及其变体在附录 D 中讨论

Evaluation of Pretrained Models

模型预训练完成后，我们可以直接在下游任务上进行 Next-Token Prediction 和强化微调
论文通过以下设置展示强化预训练如何提升大语言模型的语言建模能力和推理能力
语言建模（Language Modeling）
- 基于 Next Token 推理目标，论文的模型可以自然地用于语言建模
- 论文报告 Next-Token Prediction 准确率，以评估 RPT 的语言建模性能和扩展性
下游任务的强化微调（Reinforcement Fine-Tuning on Downstream Tasks）
- 论文以预训练后微调的方式对 RPT 模型进行持续的强化微调
- 由于 RPT 将预训练过程与强化学习对齐，预训练与后续强化微调之间的目标差距被最小化
- 论文评估强化预训练过程是否进一步提升了最终任务的性能

Experiments

Language Modeling

论文在 OmniMATH 的 200 个验证集样本上评估语言建模性能
根据第 3.3 节描述的基于熵的数据过滤策略，论文根据难度对验证集中的 Token 位置进行分类
- 论文使用 R1-Distill-Queen-14B 计算每个 Token 位置的熵，并根据熵是否超过阈值 0.5、1.0 和 1.5 将位置划分为简单、中等和困难三类
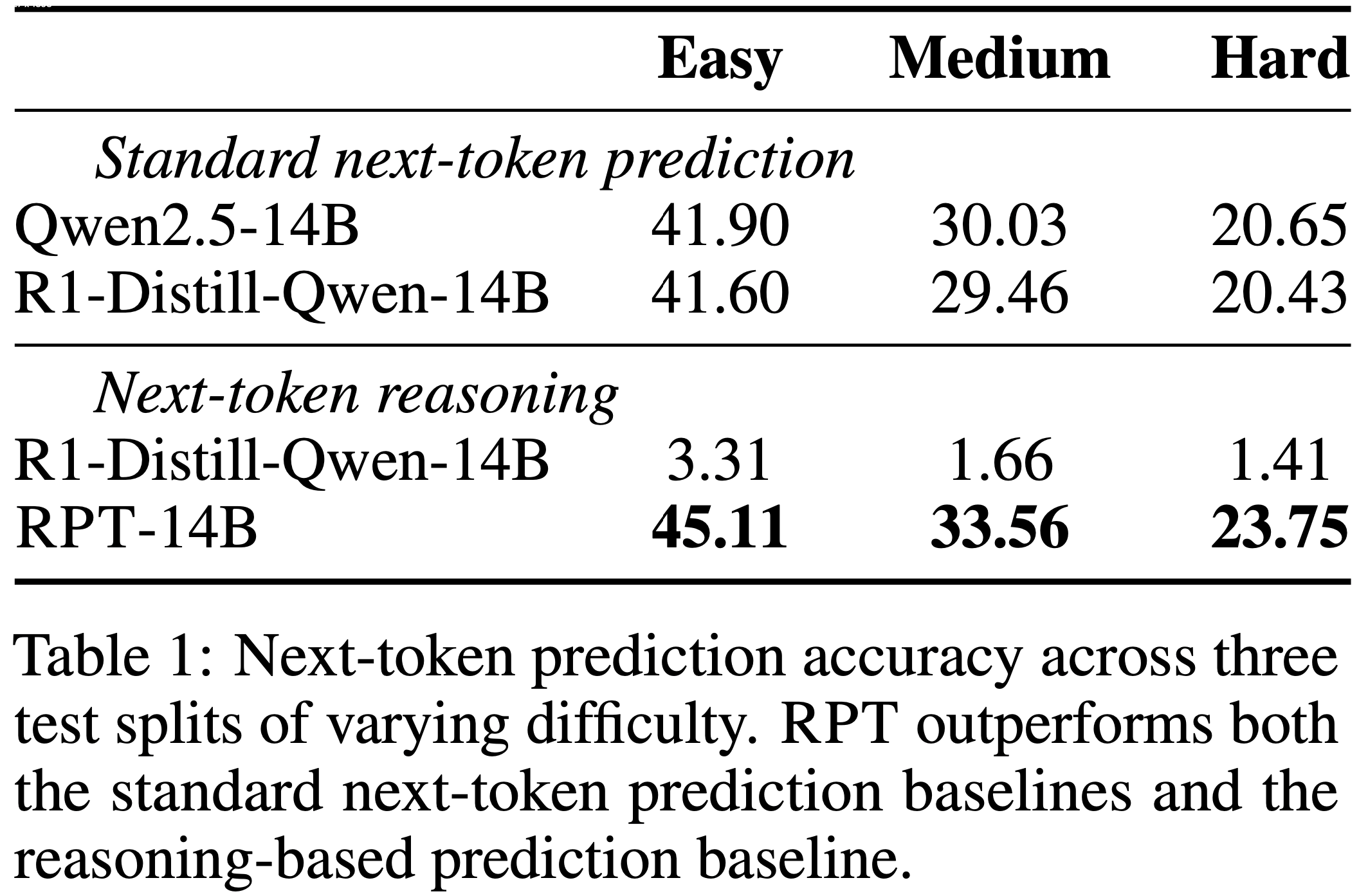
- 为了比较，论文报告了 R1-Distill-Queen-14B 在两种评估方式下的性能：
  - (1) 标准 Next-Token Prediction ，选择概率最高的 Token ；
  - (2) Next Token 推理，生成思维链后再进行最终预测
- 论文还包含了 Qwen2.5-14B 的结果，因为它是 R1-Distill-Queen-14B 的基础模型
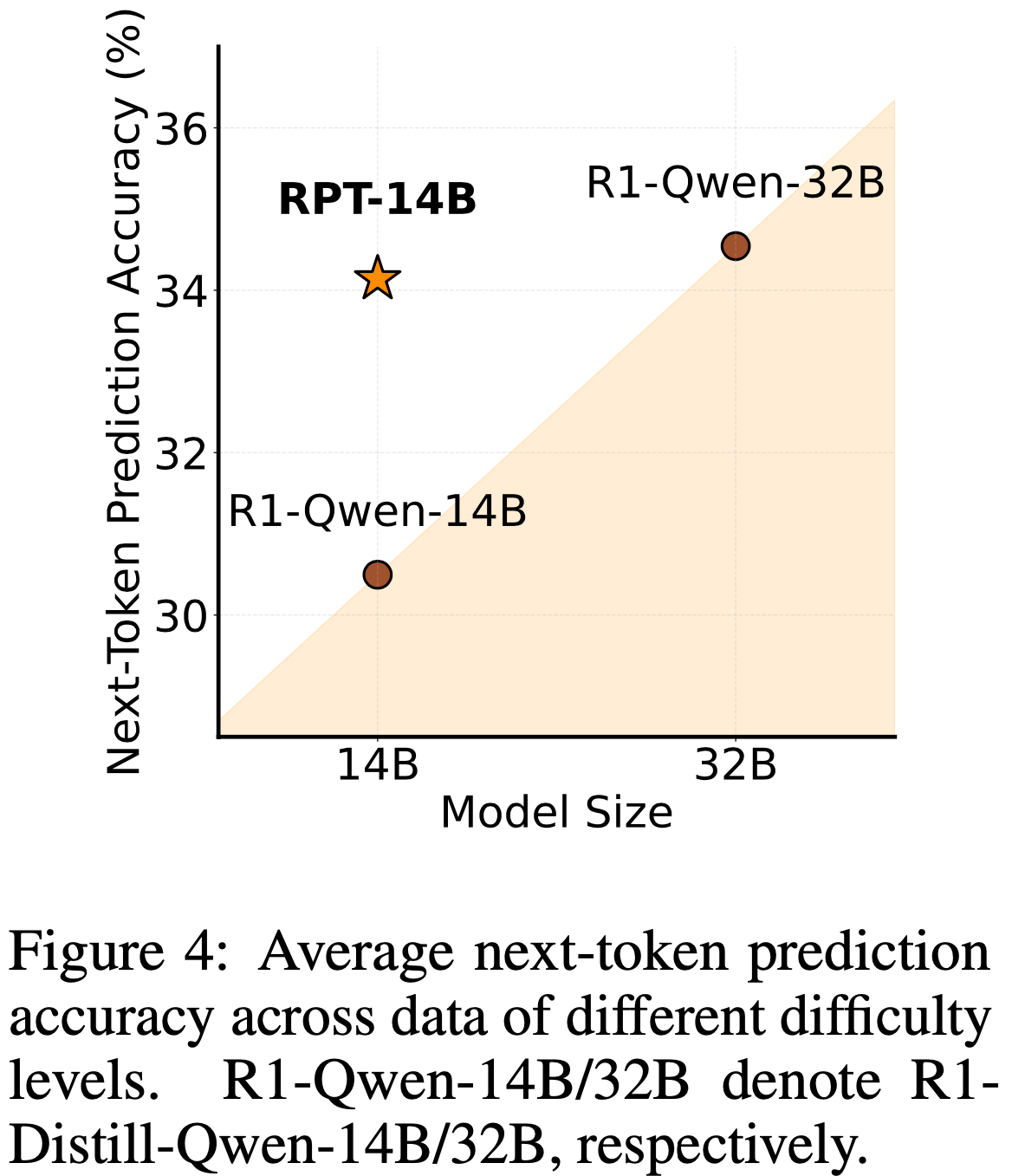
如表 1 所示，RPT-14B 在所有难度级别上的 Next-Token Prediction 准确率均高于 R1-Distill-Queen-14B
- 值得注意的是，它的性能与显著更大的模型 R1-Distill-Queen-32B 相当（图 4）
这些结果表明，强化预训练能有效捕捉 Token 生成背后的复杂推理信号，并具有提升大语言模型语言建模能力的强大潜力

Scaling Properties of Reinforcement Pre-Training

本节论文研究强化预训练的扩展性
自然语言语料库上的 Next Token 预训练损失在模型大小、训练 Token 数量和训练计算量方面通常遵循幂律衰减（2020, 2022）
论文使用以下幂律形式建模训练计算量 $C$ 与性能的关系：
$$
P(C) = \frac{A}{C^\alpha} + P^*, \tag{5}
$$
- 其中 $P(C)$ 表示验证集上的 Next-Token Prediction 准确率，$P^*$、$\alpha$ 和 $A$ 是待估计的参数
论文在不同训练步数（100、200、400、800、1000 和 1200）下评估 RPT 的 Next-Token Prediction 准确率，并将其转换为相应的训练计算量
为了评估数据难度的影响，论文考虑了基于熵阈值 0.5（简单）、1.0（中等）和 1.5（困难）过滤的验证集分割
- 更高的阈值对应更具挑战性的输入
- 对于每个难度级别，论文根据公式 (5) 拟合结果，并使用决定系数 $R^2$ 衡量拟合优度（Goodness of fit）
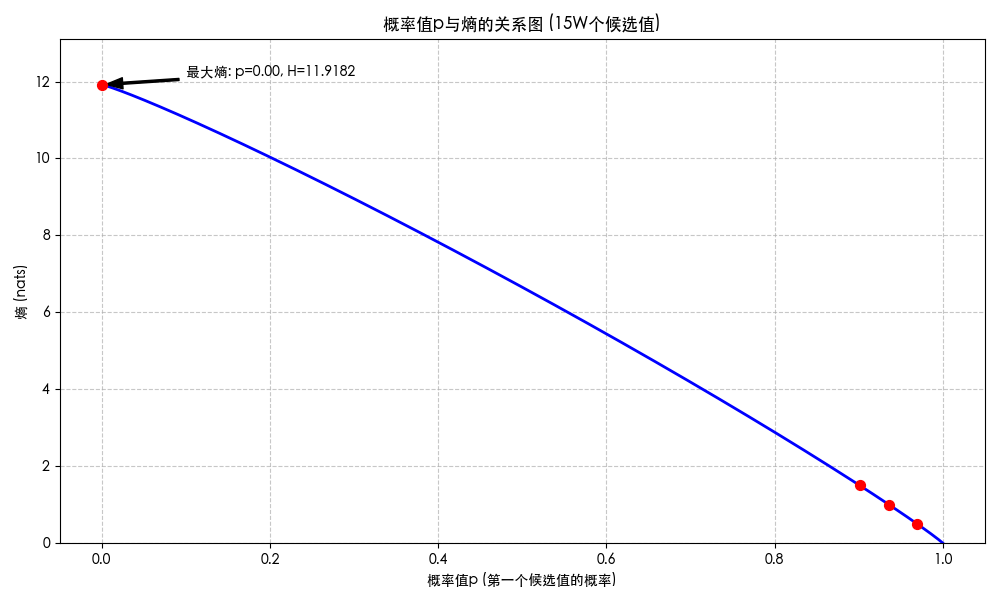
- 理解：按照 15W 词表算：
  - 熵为 0.5 对应这最大的概率差不多是 0.970；
  - 熵为 1.0 对应这最大的概率差不多是 0.936；
  - 熵为 1.5 对应这最大的概率差不多是 0.901；
  - 更多可视化详情见附录
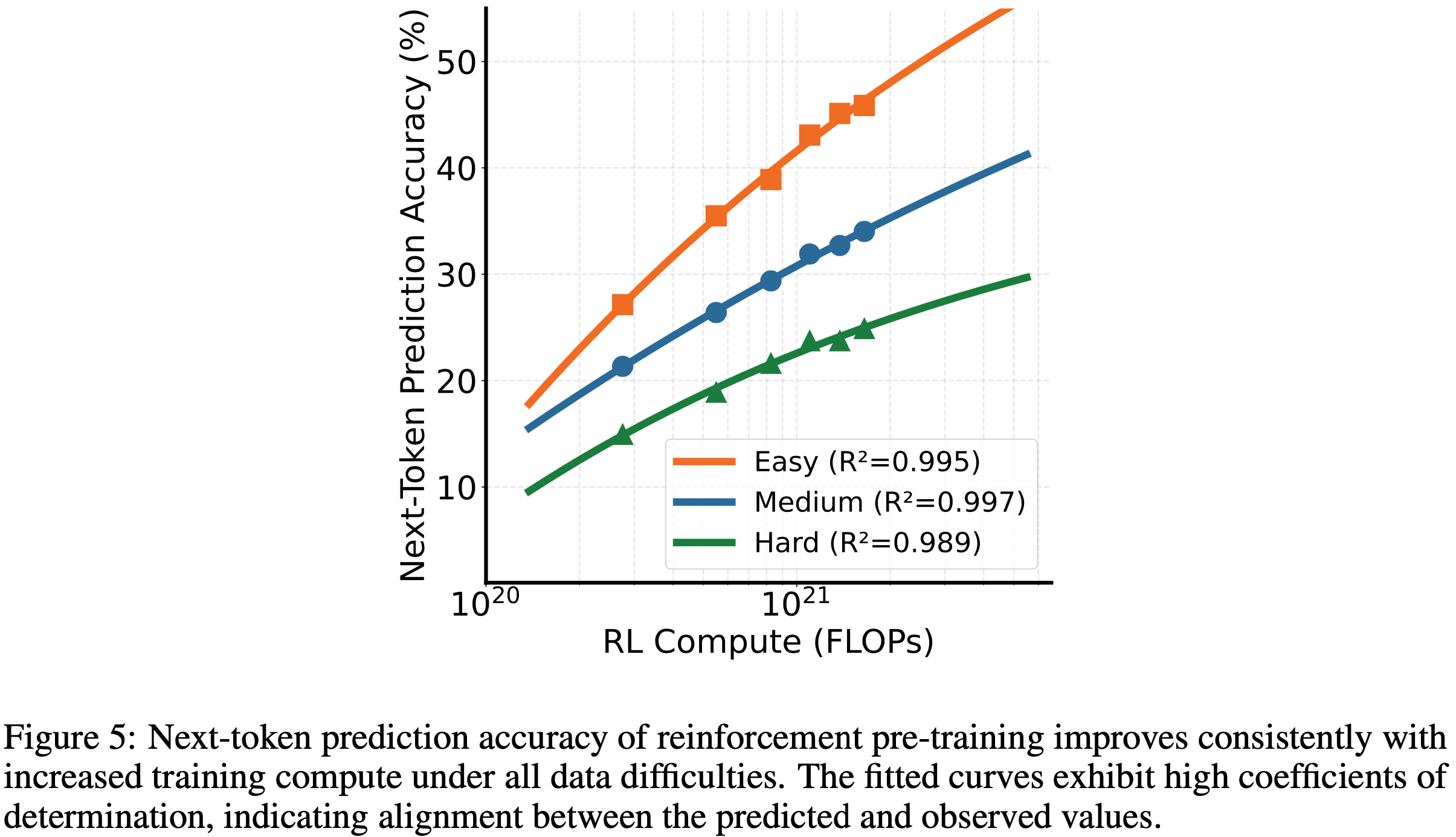
如图 5 所示，随着训练计算量的增加，RPT 的 Next-Token Prediction 准确率持续提升
所有难度级别的高 $R^2$ 值表明拟合曲线能准确捕捉性能趋势（理解：说明在不同难度上，均能很好的拟合到公式 (5) 上）

Reinforcement Fine-Tuning with RPT

为了研究 RPT 模型是否能通过 RLVR 更有效地微调，论文从 Skywork-OR1（2025）随机采样带有可验证答案的问题进行进一步训练
- 论文使用 256 个样本进行训练，200 个样本进行测试
- 遵循 Skywork-OR1 的数据过滤流程（2025），论文使用 R1-Distill-Queen-32B 识别训练中的挑战性实例
- 论文将训练批次大小和 PPO 小批次大小均设为 64，并训练模型 15 个周期
- 评估时，验证的最大 Token 数设为 32,000，温度为 0.6
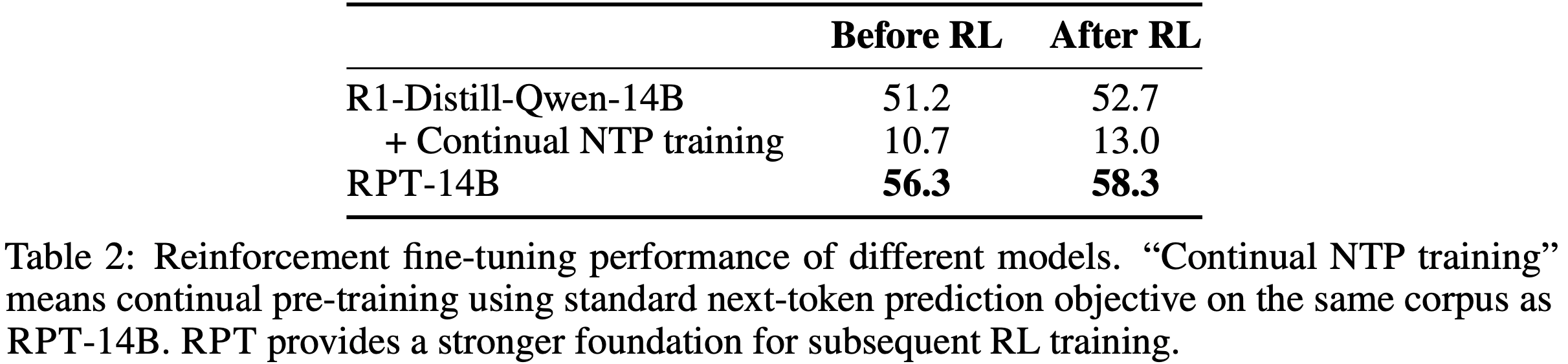
如表 2 所示：
- 强化预训练模型在使用 RLVR 进一步训练时达到了更高的上限
- 当使用相同的 Next-Token Prediction 目标持续训练相同数据时，模型的推理能力显著下降，而后续的 RLVR 仅带来缓慢的性能提升
  - 理解：可以观察到，直接进行普通 NPT 的持续预训练（目标和 RPT 相同）会导致推理能力大幅下降；猜测这里是训练太多次，发生了过拟合了！
    - 引申问题：这里的普通 NPT 和 RPT 训练轮次是相同的吗？
这些结果表明，在数据有限的情况下，强化预训练可以快速将从 Next Token 推理中学到的强化推理模式迁移到最终任务中

Zero-Shot Performance on End Tasks

论文评估了 RPT-14B 在下游任务上的 Zero-Shot 性能
作为比较，论文评估了 R1-Distill-Queen-14B 和 R1-Distill-Queen-32B 的 Next-Token Prediction 性能，以及 RPT-14B 与 R1-Distill-Queen-14B 的推理性能
论文的评估涉及两个广泛认可的基准：
- MMLU-Pro（2020），一个综合性多任务理解基准，评估大语言模型在不同领域的表现；
- SuperGPQA（2025），一个涵盖 285 个学科的研究生级推理问题的大规模基准
在推理设置下，论文将最大 Token 数设为 12,288，温度为 0.8
遵循先前工作（2024, 2025），论文使用多项选择题格式进行评估并报告准确率
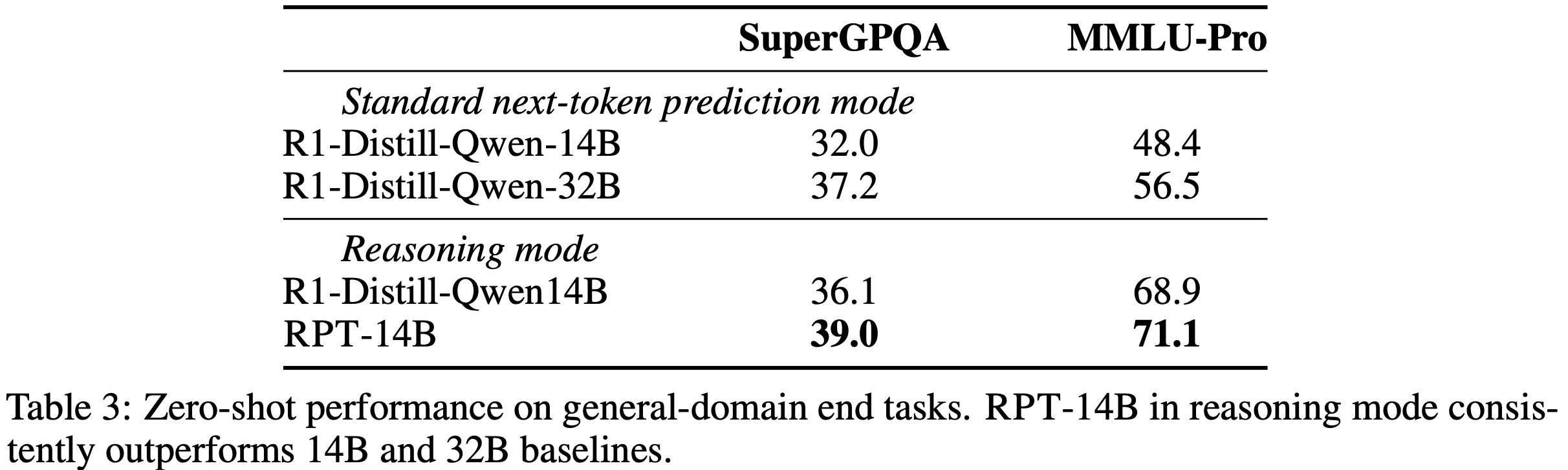
如表 3 所示
- RPT-14B 在所有基准上均优于 R1-Distill-Queen-14B（无论是标准 Next-Token Prediction 还是作为推理模型评估）
- RPT-14B 还超越了显著更大的 R1-Distill-Queen-32B（在 Next-Token Prediction 模式下），在 SuperGPQA 上提升了 7 分，在 MMLU-Pro 上提升了约 22 分
每个基准的详细分科结果见附录 C

Next-Token Reasoning Pattern Analysis

论文分析了 Next Token 推理与显式问题解决（explicit problem solving）在推理模式上的差异
- 根据先前研究（2024, 2025），论文统计了模型响应中包含推理关键词（如“break down”、“alternatively”）的比例
论文的分析比较了两种模型在 OmniMATH 数据集上的思维过程：
- R1-Distill-Queen-14B 用于问题解决
- RPT-14B 用于 Next Token 推理
- 对每个模型，采样 200 个响应
论文将推理模式分为六类：
- 转换（切换策略）、反思（自我检查）、分解（分解问题）、假设（提出并验证假设）、发散思维（探索可能性）和演绎（逻辑推理）
  
  transition (switching strategies), reflection (self-checking), breakdown (decomposing the problem), hypothesis (proposing and verifying assumptions), divergent thinking (exploring possibilities), and deduction (logical inference).
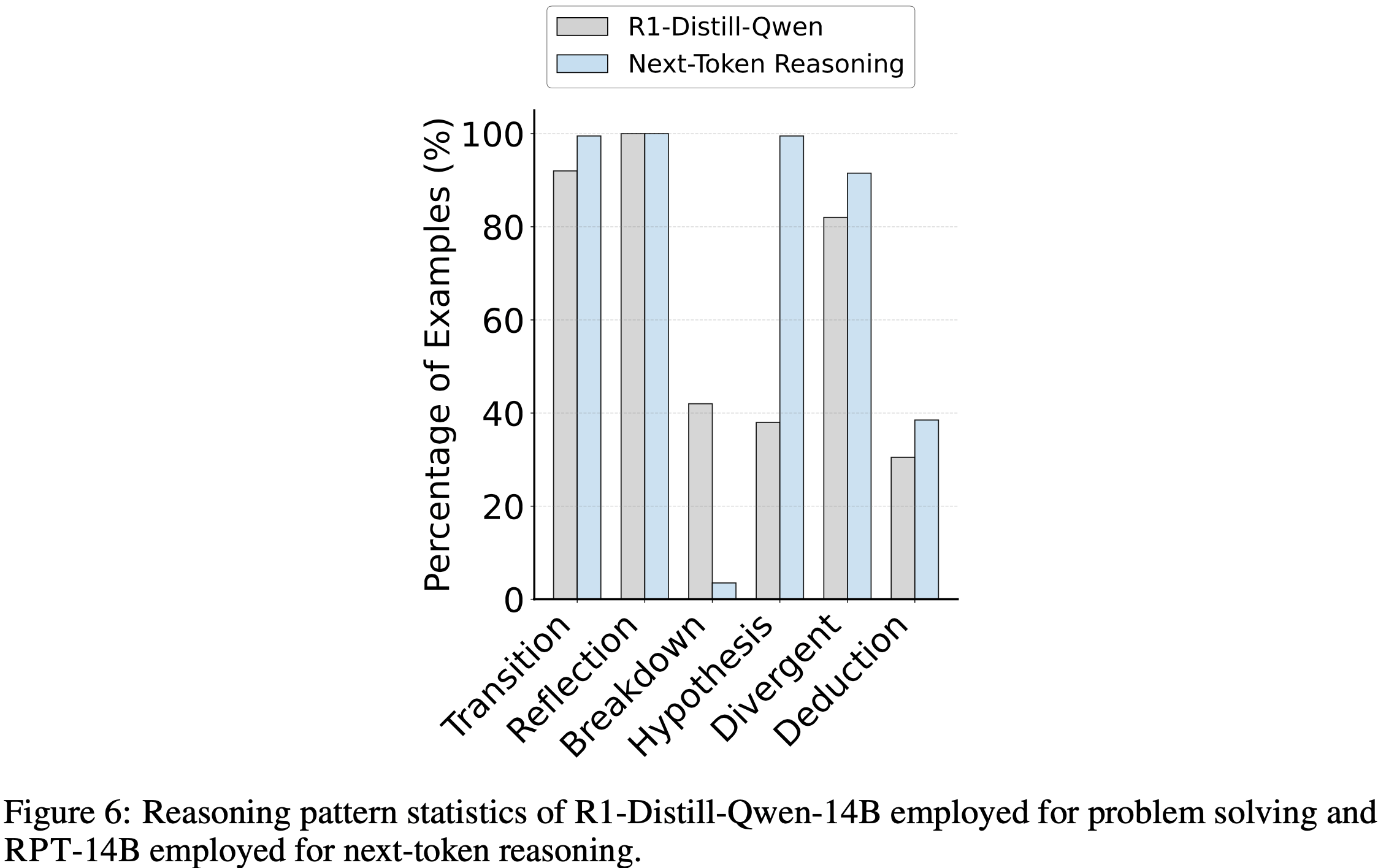
如图 6 所示，RPT-14B 的 Next Token 推理过程与 R1-Distill-Queen-14B 的问题解决过程显著不同
- RPT-14B 相对 R1-Distill-Queen-14B： 假设模式的使用量增加了 161.8%
- RPT-14B 相对 R1-Distill-Queen-14B：演绎模式的使用量增加了 26.2%
- 问题解决过程（R1-Distill-Queen-14B）更依赖分解模式（breakdown） ，这表明 Next Token 推理引发的推理过程在性质上与结构化问题解决不同
表 4 展示了一个推理模式的例子
- 该例子揭示了模型参与的是一个深思熟虑的过程，而非简单的模式匹配
- 它分析了更广泛的语义上下文（“calculating vector magnitude”），识别关键短语（“go over some…”），然后进行头脑风暴并权衡多个可能的延续
- 这涉及假设生成（“the next part is likely going to be…”）、替代方案考虑（“Alternatively, it could be…”）以及对结构线索（“markdown with headers”）甚至细粒度 Token-level 细节（“could have a space”）的反思
- 这种多方面的推理，既包含高级语义理解，又包含低级文本特征，展示了模型通过推理探索推断 Next Token 的努力，与 RPT 培养超越表面关联的更深层次理解的目标一致
更多例子见附录 F

Scaling Paradigms of Large Language Models

LLM 的进步主要由两个扩展维度驱动：
- 训练时计算（training-time compute）（2022a）：通过大幅增加模型参数和训练数据，以下一词预测（next-token prediction）作为预训练任务
- 测试时计算（test-time compute）（2025a）：测试时扩展（2024）通过延长推理计算时间提升大语言模型的推理能力
RPT 独特地整合了上述原则，超越现有扩展范式，将每一词预测任务重构为推理任务

Reinforcement Learning for Large Language Models

强化学习在大语言模型的后训练阶段发挥了关键作用
- RLHF（2022）通过人类偏好数据微调预训练语言模型以提升对齐性
- 除对齐外，大规模强化学习还被用于增强语言模型的推理能力（2025）
最相关的工作（2025）鼓励语言模型为下一词预测生成有帮助的推理过程
- 基于帮助性的奖励容易被生成的推理中重复目标词所“破解” ，这种捷径可能损害模型性能
  - 问题：如何理解这里所谓的奖励破解问题？
    - 参考：Quiet-STaR: Language Models Can Teach Themselves to Think Before Speaking
- 相比之下，论文使用下一词预测的正确性作为基于规则的奖励信号，以最小化奖励破解风险

Future Work

RPT 的初步探索仍存在一些局限性
- 论文的实验主要基于 14B 参数的模型，没有在更大的模型进行测试
- 虽然 RPT 方法设计为通用，但当前预训练语料库 主要由数学文档组成；
  - 未来工作将探索其在更广泛的通用领域文本上的有效性
- RPT 训练是从一个具备基础推理能力的模型初始化（R1-Distill-Qwen-14B）的；
  - 后续可以研究从标准基础语言模型开始的 RPT 训练
  - 这将为 RPT 基础性影响提供进一步分析和结论
未来工作可从以下方向推进：
- 扩展训练语料库的规模和领域覆盖范围，利用大规模通用互联网数据进行强化预训练
- 增加训练计算资源以突破性能边界
- 建立强化预训练的扩展定律（scaling laws），指导大语言模型的扩展
- 探索将混合思维（hybrid thinking）（2025）与 RPT 结合，通过自适应触发下一词推理实现细粒度的适应性思考

附录 A Design Choices of Reward

除了第 3 节描述的基于前缀匹配的奖励机制外，论文还研究了其他几种奖励函数变体以评估其对强化预训练的影响
- 变体一：首词匹配（first-token matching）
  - 在此设置中，奖励仅反映模型预测 $ y_t^i $ 的首词是否与真实下一词 $ x_t $ 匹配，忽略预测中首词之后的所有词
- 变体二：探索了“密集奖励”（dense reward）方案：
  - 正确预测的下一词（即 $ y_t^i[0] = x_t $）获得满分奖励（如 1）；
  - 对于错误预测（$ y_t^i[0] \neq x_t $），奖励为一个较小的正值 ，具体为语言模型生成该错误词的概率 $ P(y_t^i[0] \mid x_{ < t}; \theta) $
    - 问题：为什么是错误词的概率？岂不是错误词的概率越大，奖励越大，应该是正确词的概率吧
  - 这提供了比二元奖励更密集的反馈信号
- 变体三：条件性应用密集奖励结构：
  - 仅当给定前缀 $ x_{ < t} $ 的 $ G $ 次采样中至少有一次正确预测下一词时 ，才使用密集奖励；
  - 若所有 $ G $ 次采样均错误，则应用其他奖励方案（如零奖励或统一的小惩罚）
实验表明，这些替代奖励与前缀匹配奖励相比，性能相当
- 表明强化预训练框架对这些奖励信号的修改具有较强的鲁棒性 ，其核心优势可能对这些特定选择不敏感，至少在测试的变体范围内如此

附录 B Hyperparameters Used for Reinforcement Pre-Training

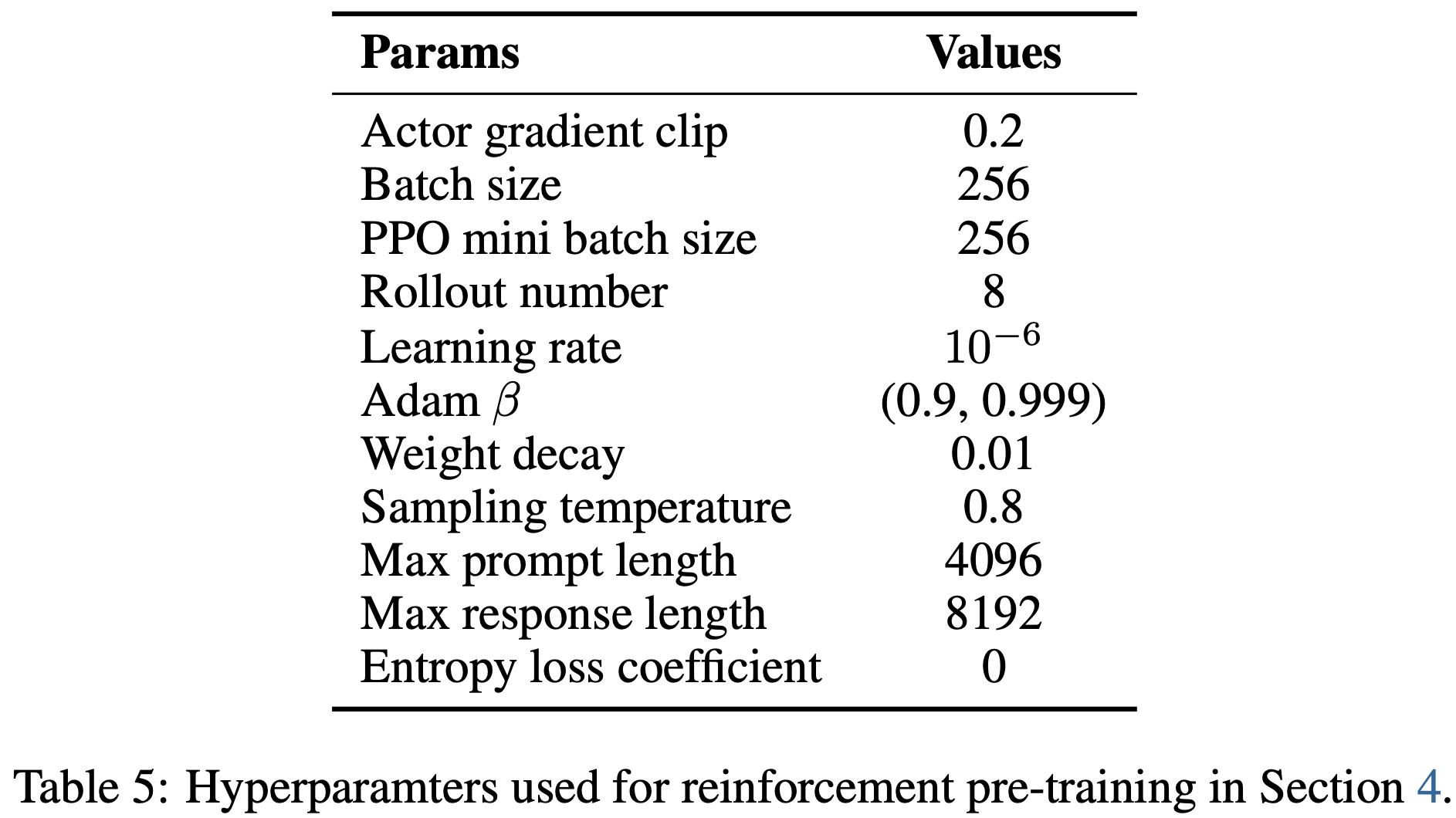
表 5 展示了第 4 节中强化预训练的详细超参数
论文遵循精确策略强化学习（2025）的设置，将熵损失系数设为 0

附录 C Detailed Results on End Tasks

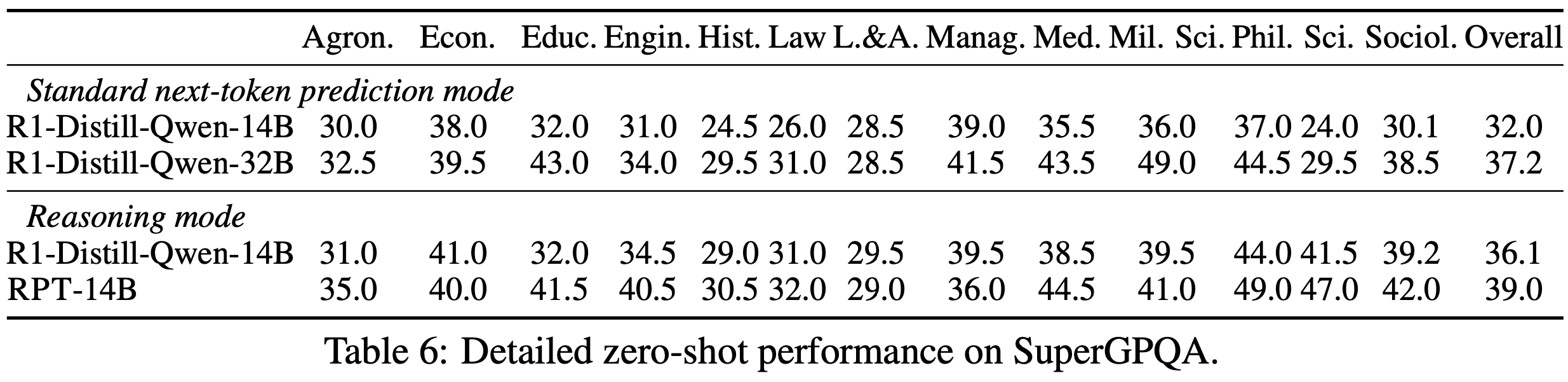
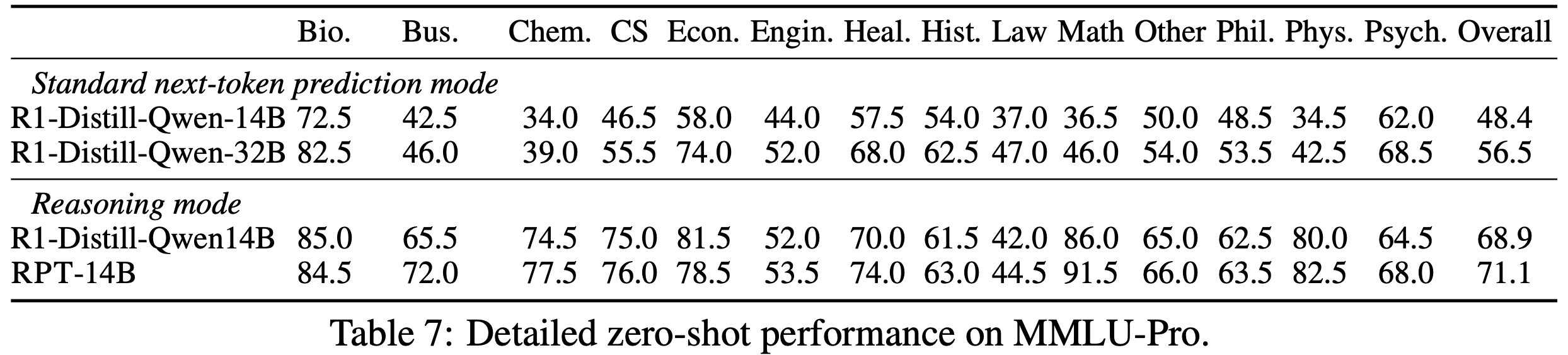
表 6 和表 7 展示了通用终端任务基准的详细分类性能
RPT-14B 模型在大多数类别中表现优于 R1-Distill-Qwen-14B 和 R1-Distill-Qwen-32B

附录 D Impact of Prompt Templates

论文探索了不同提示模板对初始下一词推理性能的影响
表 10 展示了七种模板变体，这些模板使用不同指令片段，并以不同形式包装上下文
如表 8 所示，清晰的 Prompt 能很大程度提升初始表现的准确性
- 第 4 节的强化预训练实验使用了“v0”模板，其他模板变体的优化留待未来工作

附录 E Keywords for Reasoning Pattern Analysis

表 9 列出了第 4.5 节中用于推理模式分析的模式组和关键词

附录 F Case Studies

表 11 展示了 RPT-14B 在下一词推理任务中的三个案例，包括模型对数学问题和文本上下文的推理过程
这些案例揭示了模型如何通过多角度思考生成最终预测

附录：概率和熵的关系图

关键词：entropy curve；熵和概率；概率和熵；曲线图；
假定只有一个 token 的值较大，其他 token 概率相同，此时的熵和最大概率的关系是如何的？

可视化最大概率和熵的关系的代码

import numpy as np
import matplotlib.pyplot as plt

# 设置中文显示
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题

def calculate_entropy(p, n=150000):
    remaining_p = (1 - p) / (n - 1)

    probabilities = np.full(n, remaining_p)
    probabilities[0] = p

    entropy = -np.sum(probabilities * np.log(probabilities))

    return entropy

p_values = np.linspace(0.0001, 0.9999, 9999)

entropy_values = [calculate_entropy(p) for p in p_values]

plt.figure(figsize=(10, 6))
plt.plot(p_values, entropy_values, 'b-', linewidth=2)

max_entropy_idx = np.argmax(entropy_values)
plt.scatter(p_values[max_entropy_idx], entropy_values[max_entropy_idx], color='red', s=50, zorder=5)
plt.annotate(f'最大熵: p={p_values[max_entropy_idx]:.2f}, H={entropy_values[max_entropy_idx]:.4f}',
            xy=(p_values[max_entropy_idx], entropy_values[max_entropy_idx]),
            xytext=(p_values[max_entropy_idx]+0.1, entropy_values[max_entropy_idx]+0.2),
            arrowprops=dict(facecolor='black', shrink=0.05, width=1.5, headwidth=8))

# print(entropy_values)
points = [0.5, 1.0, 1.5]
for point in points:
    for index, entropy in enumerate(entropy_values):
        if entropy <= point:
            print((p_values[index], entropy_values[index]))
            plt.scatter(p_values[index], entropy_values[index], color='red', s=50, zorder=5)
            break

plt.title('概率值p与熵的关系图 (15W个候选值)')
plt.xlabel('概率值p (第一个候选值的概率)')
plt.ylabel('熵 (nats)')
plt.grid(True, linestyle='--', alpha=0.7)
plt.xlim(-0.05, 1.05)
plt.ylim(0, max(entropy_values) * 1.1)

plt.tight_layout()
plt.show()

# (0.9695, 0.4999866540719247)
# (0.9361, 0.9991510505356568)
# (0.9012, 1.4999746052311926)

示意图：

Introduction and Discussion

Preliminary

Next-Token Prediction, NTP

Reinforcement Learning with Verifiable Rewards, RLVR

Reinforcement Pre-Training

Pre-Training Task: Next-Token Reasoning

Pre-Training with Reinforcement Learning

Pre-Training Setup

Evaluation of Pretrained Models

Experiments

Language Modeling

Scaling Properties of Reinforcement Pre-Training

Reinforcement Fine-Tuning with RPT

Zero-Shot Performance on End Tasks

Next-Token Reasoning Pattern Analysis

Related Work

Scaling Paradigms of Large Language Models

Reinforcement Learning for Large Language Models

Future Work

附录 A Design Choices of Reward

附录 B Hyperparameters Used for Reinforcement Pre-Training

附录 C Detailed Results on End Tasks

附录 D Impact of Prompt Templates

附录 E Keywords for Reasoning Pattern Analysis

附录 F Case Studies

附录：概率和熵的关系图