本文主要介绍LoRA和QLoRA
LoRA
参考链接
神经网络模型参数一般都是矩阵形式,比如在Self-Attention中
- 广义上 \(W_q,W_k,W_v,W_o\) 等分别是 \(d_{model}\times d_k, d_{model}\times d_k, d_{model}\times d_v, d_v \times d_{model}\) 维度的(这里的 \(d_v\) 表示所有头的长度的和,与Transformer原论文有所区别,原始论文中 \(d_v\) 是单个头的长度)
- 而实际在Transformer中(包括Transformer原论文和GPT等),如果不考虑多头(或者多头数 \(h=1\) ),常常有 \(d_k = d_v = d_{model}\)
- 在面对多头Attention时,常常有 \(d_v = d_v^{MH} \times N_{head}\),(再次强调,注意这里与原始论文表示不同,原始论文中 \(d_v\) 是单个头的维度,即 \(d_{model} = d_v * h\) )
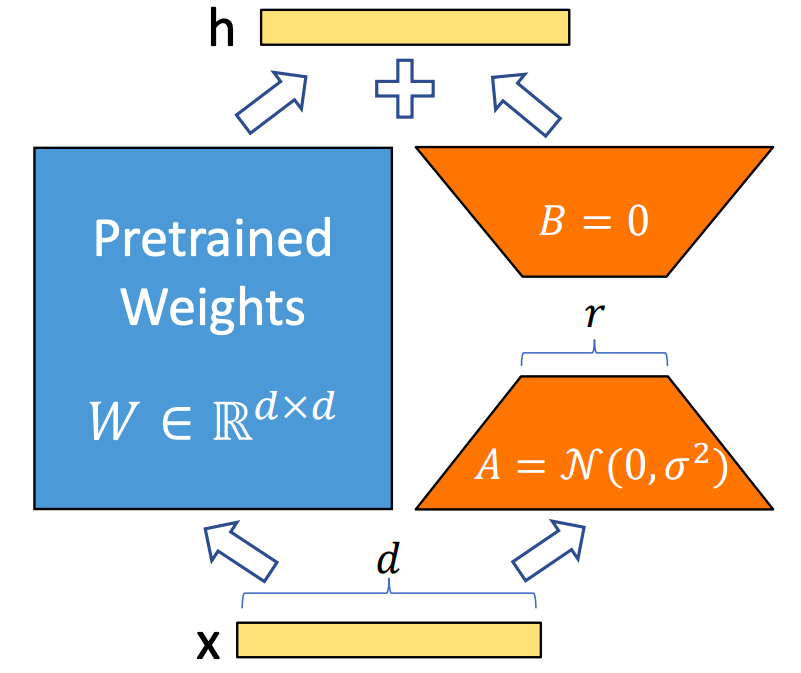
LoRA通常用于预训练模型的微调阶段,训练时在预训练模型上加一个旁路,替代已有的网络模型参数(一般是特别大的参数矩阵,比如Attention参数 \(W_q\) 等
- 对应的模型LoRA代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18input_dim = 768 # 例如,预训练模型的隐藏大小
output_dim = 768 # 例如,层的输出大小
rank = 8 # 低秩适应的等级'r'
W = ... # 来自预训练网络的权重,形状为 input_dim x output_dim
W_A = nn.Parameter(torch.empty(input_dim, rank)) # LoRA权重A
W_B = nn.Parameter(torch.empty(rank, output_dim)) # LoRA权重B
# 初始化LoRA权重
nn.init.kaiming_uniform_(W_A, a=math.sqrt(5))
nn.init.zeros_(W_B)
# 以下写法与论文中公式 h = W @ x不一样的原因是因为这里x是行向量,论文中x是当做列向量来看的
def regular_forward_matmul(x, W):
h = x @ W
return h
def lora_forward_matmul(x, W, W_A, W_B):
h = x @ W # 常规矩阵乘法
h += x @ (W_A @ W_B) * alpha # 使用缩放的LoRA权重
return h
- 对应的模型LoRA代码实现:
假设原始模型中,某个参数矩阵为 \(W^{d \times k}\) (也可以不是方阵),LoRA网络可以用两个小矩阵来表示 \(B^{d\times r}, A^{r\times k}\)
- 在没有LoRA时,参数 \(W_0\) 的前向过程是(下面的 \(h\) 表示参数对应的隐藏层向量, \(x, h\) 均为列向量):
$$h = W_0 x$$ - 加入LoRA时,该参数的前向过程为:
$$h = W_0 x + \frac{\alpha}{r}\Delta W x = W_0 x + \frac{\alpha}{r}BAx$$- 原始论文中提到,一般可以使用 \(\frac{\alpha}{r}\) 来设置LoRA权重
- 理解:权重与 \(r\) 有关的原因是 \(r\) 越大,LoRA矩阵包含的信息越多,对原始模型的影响越大,论文中提到,为了减少超参数数量, \(\alpha\) 的设置一般可以使用 \(\alpha=r\) (
we simply set α to the first r we try and do not tune it),揭秘LoRA与QLoRA:百次实验告诉你如何微调LLM!则给出了更为详细的说明,并得出在LLM中使用 \(\alpha=2r\) 会更好 - 个人观点: \(\alpha\) 理论上可以不调整,因为如果LoRA参数初始化时同时缩放 \(\frac{\alpha}{r}\) 倍,同时调整学习率为 \(lr = \frac{\alpha}{r} \times lr\),则与在 \(\Delta W\) 前使用 \(\frac{\alpha}{r}\) 实现的效果完全一致?
- 理解:权重与 \(r\) 有关的原因是 \(r\) 越大,LoRA矩阵包含的信息越多,对原始模型的影响越大,论文中提到,为了减少超参数数量, \(\alpha\) 的设置一般可以使用 \(\alpha=r\) (
- 原始论文中提到,一般可以使用 \(\frac{\alpha}{r}\) 来设置LoRA权重
- 由于 \(r << min(d,k)\),LoRA可以极大减少参数量,训练时,除了计算量外,优化器需要存储的中间变量与参数量相关,相对全量微调,使用LoRA微调的显存和计算量会极大减少
- 模型存储时,可以将LoRA参数换算成矩阵加到原来的参数权重中,从而保证在推理时不增加额外显存和计算量
$$W_{save} = W_0 + \frac{\alpha}{r}BA$$- 这里用到了矩阵运算的分配律 \((A+B)C = AC + BC\)
- 在没有LoRA时,参数 \(W_0\) 的前向过程是(下面的 \(h\) 表示参数对应的隐藏层向量, \(x, h\) 均为列向量):
其中 \(A\) 矩阵权重参数使用正太分布初始化, \(B\) 矩阵权重参数使用0初始化,保证了如果LoRA部分参数全为0,则无法训练LoRA
- 为什么要这样初始化,换个方式不可以吗?如果B不为0,A为0,或者两个都为0呢?以下回答参考自LoRA与QLoRA快速介绍
这里有一些细节需要注意,LoRA的两个矩阵A和B中,一个是零向量初始化,一个是随机初始化。个人观点是,A和B哪个是0都可以,也可以两个都是0;但至少要有一个是0,这样才能保证未经训练的LoRA作为旁路加到预训练模型中时,LoRA不会对模型的预测产生任何影响,模型能够基于当前性能进一步学习。此外,为什么可以用低秩矩阵来模拟原始矩阵?已有研究发现,大模型往往是过度参数化的,模型实际用到的维度(模型内在维度)可能并没有那么高,所以用低秩矩阵来拟合目标任务也能达到不错的效果
- 为什么要这样初始化,换个方式不可以吗?如果B不为0,A为0,或者两个都为0呢?以下回答参考自LoRA与QLoRA快速介绍
从网络结构上理解,LoRA相对于普通的全连接层,相当于把之前的一层网络拆解成两层,但中间层没有激活函数
QLoRA
- QLoRA(Quantized LoRA)详解
- QLoRA是一个使用量化思想对LoRA进行优化的量化算法
QLoRA的优化有三个核心要点
- 4-bit NormalFloat Quantization : 首先是定义了一种4位标准浮点数(Normal Float 4-bit,NF4)量化,基于分块的分位数量化的量化策略
- Double Quantization :其次是双重量化,包含对普通参数的一次量化和对量化常数的再一次量化,可以进一步减小缓存占用
- 量化常数 :一次量化中,每组被量化的参数都会存储一个绝对值的最大值absmax,这个值通常一般是高精度保存,也会占用大量的显存。【问题:分组这么多吗?能不能通过减少分组来实现】
- Paged Optimizers :最后是分页优化器(Page Optimizer),用来在显存过高时用一部分内存代替显存
LLM中的LoRA
- 每个模型会按照自己的命名习惯为不同的参数模块分配名称
- 一般用
target_modules参数指定LoRA微调目标(目标即模型中的模块名称,每个模块代表一组对应的参数),常用的模型和可作为LoRA目标的,常用配置可参考聊聊LoRA及其target_module配置- 经常被用来作为LoRA微调对象的是 \(W_q, W_v\),对应
target_modules=[q_proj,v_proj]* 为什么 \(W_k\) 不常被用于LoRA微调呢?参考【思考】为什么大模型lora微调经常用在attention的Q和V层而不用在K层呢- 直观上看, \(W_q, W_v\) 分别影响Attention的权重部分和值部分,理论上Attention的表示能力都能被影响到了
- 实践中发现调整 \(W_q, W_v\) 基本够用了
- 也有的模型是 \(W_q, W_k, W_v\) 同时调整的,甚至同时调整其他很多模块
- 经常被用来作为LoRA微调对象的是 \(W_q, W_v\),对应
- 模块在模型中代表的含义可以打印模型结构来看
- 对比使用LoRA前后模型可训练参数数量,参考自LLM微调(一)| 单GPU使用QLoRA微调Llama 2.0实战
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35def print_number_of_trainable_model_parameters(model):
trainable_model_params = 0
all_model_params = 0
for _, param in model.named_parameters():
all_model_params += param.numel()
if param.requires_grad:
trainable_model_params += param.numel()
print(f"trainable model parameters: {trainable_model_params}. All model parameters: {all_model_params} ")
return trainable_model_params
ori_p = print_number_of_trainable_model_parameters(model)
# 输出
# trainable model parameter: 262,410,240
## =================
# LoRA config
model = prepare_model_for_kbit_training(model)
peft_config = LoraConfig(
r=8,
lora_alpha=32,
lora_dropout=0.1,
target_modules=["q_proj", "v_proj"],
bias="none",
task_type="CAUSAL_LM",
)
model = get_peft_model(model, peft_config)
### compare trainable parameters #
peft_p = print_number_of_trainable_model_parameters(model)
print(f"# Trainable Parameter \nBefore: {ori_p} \nAfter: {peft_p} \nPercentage: {round(peft_p / ori_p * 100, 2)}")
# 输出
# trainable model parameter: 4,194,304