本文主要介绍 DeepSeek-R1 相关的解读,笼统而简单的介绍,详情可查看本人的其他博客
- 相关链接:
Background
2025年01月20日,deepseek 正式发布 DeepSeek-R1,并同步开源模型权重
- 开源 DeepSeek-R1 推理大模型,与 o1 性能相近。(冷启动 SFT -> RL -> COT + 通用数据SFT(80W)-> 全场景RL)
- 开源 DeepSeek-R1-Zero,预训练模型直接 RL,不走 SFT。(纯强化学习)
- 开源用 R1 数据蒸馏的 Qwen、Llama 系列小模型,蒸馏模型超过 o1-mini 和 QWQ。(直接使用80W数据进行SFT)
报告核心说明
- 首次验证了纯 RL 也可以训练出大模型的推理能力
- aha moment:顿悟时刻,主要指DeepSeek-R1-Zero模型训练过程中,模型在某个关键时刻突然学会自我反省的情况
DeepSeek-R1-Zero
- 预训练后直接进入RL阶段
DeepSeek-R1-Zero奖励模型
- 直接采用了一种基于规则的奖励系统,包括两种奖励模型作为评估指标,分别是准确率奖励模型和格式奖励模型
- 准确率奖励模型 :评估response是否准确
- 格式奖励模型 :评估格式是否准确,具体来说,格式奖励要求模型将思考过程放在“和”标签之间
DeepSeek-R1-Zero演化过程
DeepSeek-R1
DeepSeek-R1 使用了冷启动 + 多阶段训练的方式:
- 阶段1:使用少量高质量的 CoT 数据进行冷启动,预热模型。(相较于直接RL,冷启动预热能让模型快速进入稳定训练阶段)
- 阶段2:进行面向推理的强化学习,提升模型在推理任务上的性能
- 阶段3:使用拒绝采样和监督微调,进一步提升模型的综合能力
- 阶段4:再次进行强化学习,使模型在所有场景下都表现良好
DeepSeek-R1之MoE
普通的MoE
- Mixture of Experts,混合专家模型。最早1991年的论文《Adaptive Mixtures of Local Experts》中提出了混合专家模型的雏形,架构图如下:
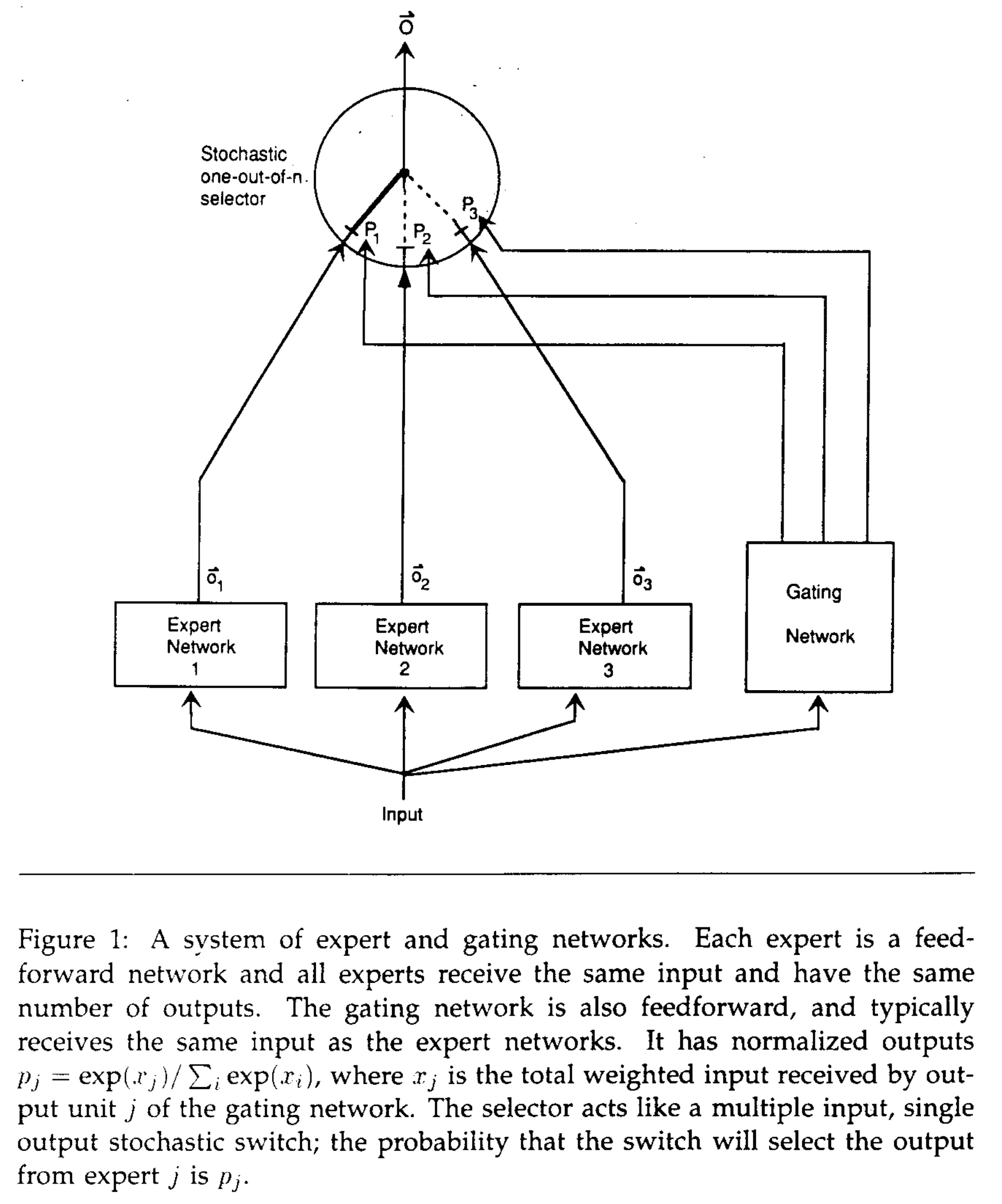
Switch Transformer中的MoE
原始论文:Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity, Google
架构图(后面会在和DeepSeekMoE比较时给出数学表达式)
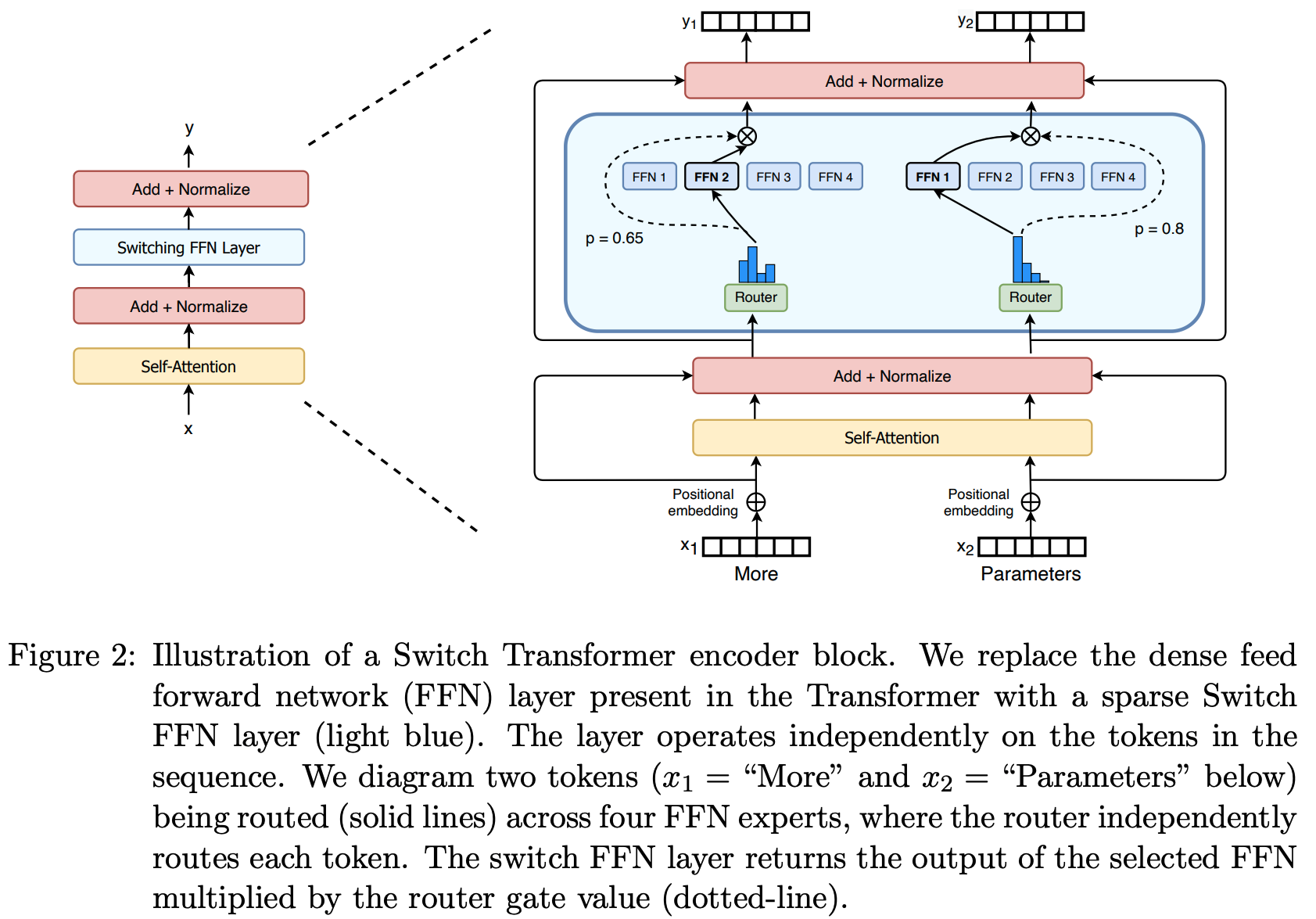
Transformer-MoE的本质是对Transformer层的FNN进行改进,改为带MoE的FNN
DeepSeekMoE(DeepSeek-V1)
原始论文:DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models
传统的Transformer和MoE

问题:上图中说 \(\boldsymbol{e}_i^l\) 是每个专家的质心(Centroid),但是未给出这个质心是怎么来的,是否可训练?
- 回答:在上述原始论文中确实没有说清楚,但是一些文章中有提到,比如 GSHARD: SCALING GIANT MODELS WITH CONDITIONAL COMPUTATION AND AUTOMATIC SHARDING 中 Algorithm1 提到输入门控网络的该值是可训练的权重,上图中的乘法实际上也就是一个线性层,实现可以如下:
1
2
3
4
5
6
7
8
9
10
11
12
13def __init__():
...
# 门控网络
self.gate = nn.Linear(input_dim, num_experts)
def forward(self, x):
# 计算门控权重
gate_logits = self.gate(x)
gate_probs = F.softmax(gate_logits, dim=-1)
# 选择top-k专家
topk_values, topk_indices = torch.topk(gate_probs, self.k)
topk_gates = topk_values / topk_values.sum(dim=-1, keepdim=True)
- 回答:在上述原始论文中确实没有说清楚,但是一些文章中有提到,比如 GSHARD: SCALING GIANT MODELS WITH CONDITIONAL COMPUTATION AND AUTOMATIC SHARDING 中 Algorithm1 提到输入门控网络的该值是可训练的权重,上图中的乘法实际上也就是一个线性层,实现可以如下:
个人思考:以上被选中的FNN系数和不为1(小于1),但因为在每一个Transformer层中,FNN的结果和上一层的隐向量叠加后,都有LayerNorm存在(将每个token的隐向量分别归一化为均值为0,方差为1的向量),所以隐向量的值不会越来越小,在V3版本的公式中,会考虑在选择了 TopK FNN 后,再进行一次归一化
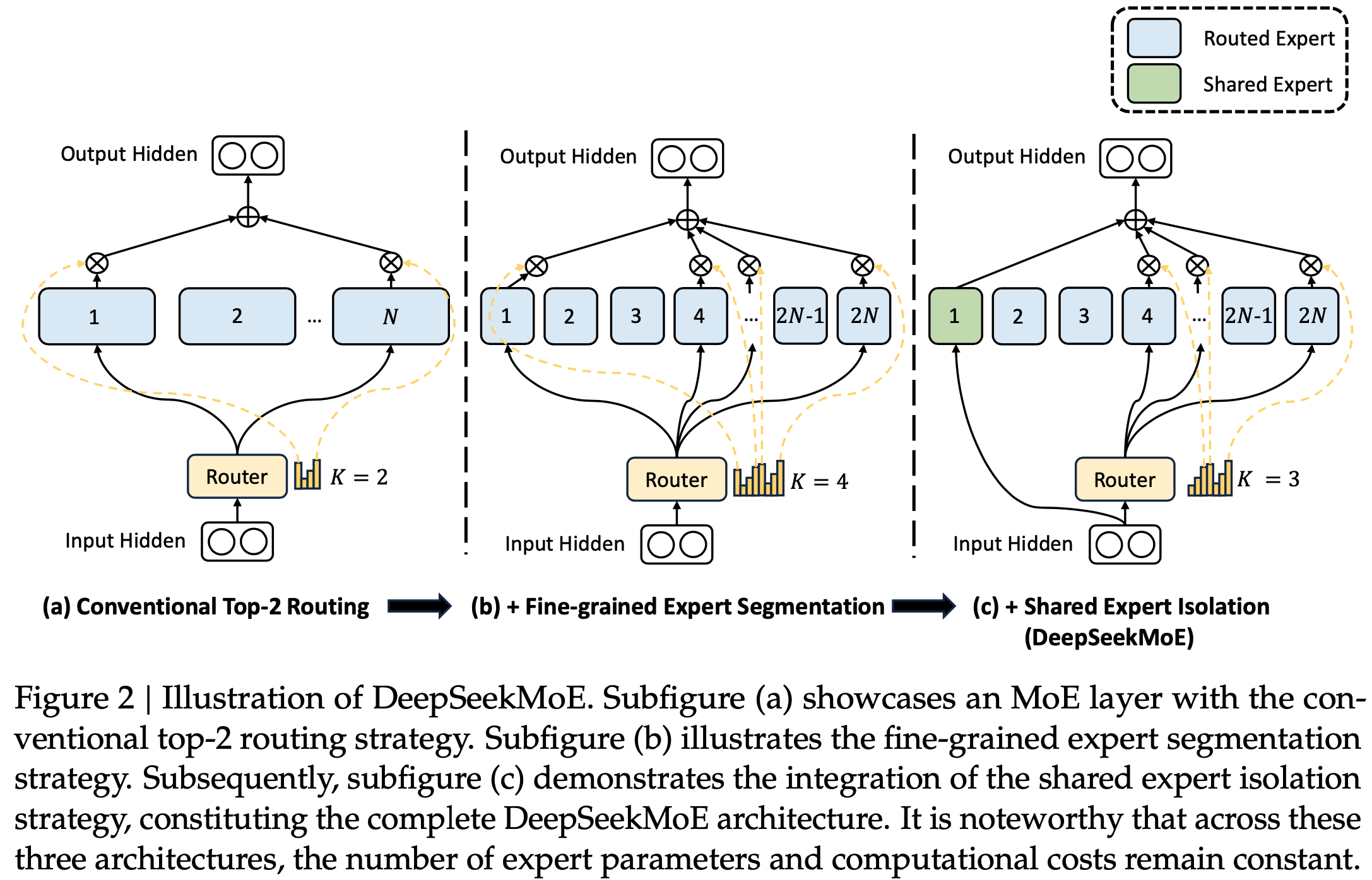
改进一:Fine-Grained Expert Segmentation,更精细化的专家拆分
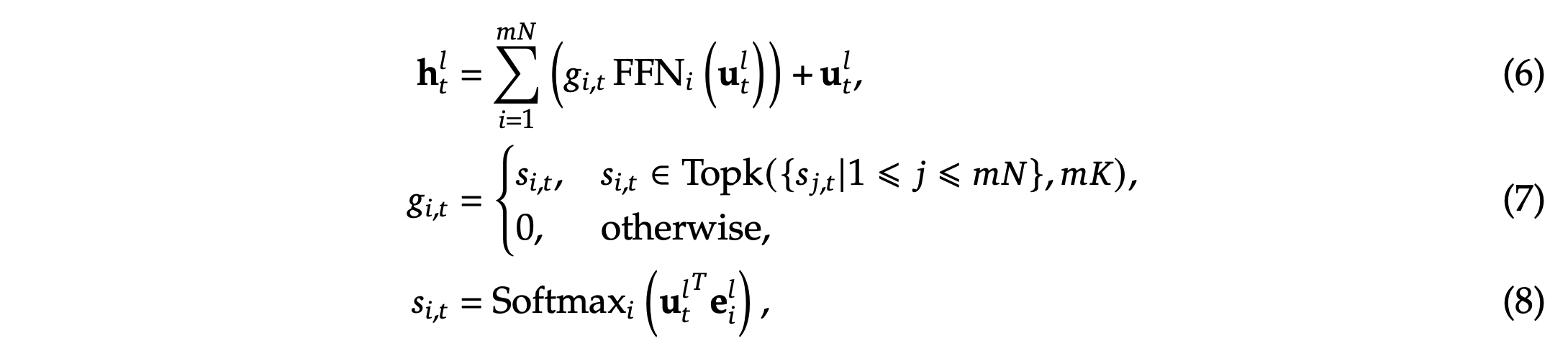
- DeepSeekMoE的精细化MoE:可以看出DeepSeekMoE中将原始的 \(N\) 个FNN扩展为 \(mN\) 个(注意:只是拆分的更细,参数总量是相同的),选择的FNN数量也从 \(K\) 个扩展到 \(mK\) 个
改进二:Shared Expert Isolation,独立的共享专家
- 使用了 \(K_s\) 个固定的共享专家,需要路由的专家数量为 \(mN - K_s\)
- 最终的MOE层输出由3部分组成,共享专家的输出结果 + Top_K个路由专家输出结果 + 残差
改进三:Load Balance Consideration,负载均衡考量
- Expert-Level Balance Loss(专家级别的负载均衡损失函数):
- Device-Level Balance Loss(设备级别的负载均衡损失函数):
DeepSeekMoE结构图:
其他说明:DeepSeek-R1共61个Transformer层,其中前三个层是正常的FNN层,后面的4-61层均用MoE取代FNN层
DeepSeek-V2
- 参考链接:DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model
- 在DeepSeekV1的基础上,沿着负载均衡继续做了3个优化
DeepSeek-V3
参考链接:DeepSeek-V3 Technical Report

门控函数从SoftMax优化为了Sigmoid
- 个人理解:为什么用Sigmoid更好?因为本来选择了topK就还需要再做一次归一化的(这次归一化是直按线性权重分配,不使用Softmax),使用Sigmoid速度更快,不影响选择topK且归一化后效果一致?
DeepSeek-R1之MLA
- 详情参考:NLP——LLM-Attention优化之MLA
- 其他参考链接:
DeepSeek-R1之GRPO
- 原始论文:DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models
- 核心思路:使用多次采样的归一化结果作为reward,放弃Critic Model,减少显存使用
- 一个有趣的对比:DeepSeek GRPO在简单控制系统上和PPO的对比 - 王兴兴的文章 - 知乎
对于整个系统中间过程和信息,比较清晰的问题(中间过程能被价值评价清晰),比如类似上面的控制系统(或者其他机器人系统),PPO还是最简单粗暴出效果很好的;但对于像DeepSeek用来搞数学RL推理,由于中间过程没法很好的描述和计算中间过程的价值,确实还是GRPO更快更方便(只看最终结果);
- 注意,GRPO中使用了KL散度的近似形式,Approximating KL Divergence —— 来自:Deepseek的RL算法GRPO解读 - AIQL的文章 - 知乎
- 估计形式为(注意以下式子中右边是左边的无偏梯度的前提是 \(o_{i,t} \sim \pi_\theta(\cdot \vert q,\mathbf{o}_{i,<t})\) ):
$$
\mathbb{D}_\text{KL}[\pi_\theta\Vert\pi_{\text{ref}}] \approx \frac{\pi_{\text{ref}}(o_{i,t}\vert q,\mathbf{o}_{i,<t})}{\pi_\theta(o_{i,t}\vert q,\mathbf{o}_{i,<t})} - \log \frac{\pi_{\text{ref}}(o_{i,t}\vert q,\mathbf{o}_{i,<t})}{\pi_\theta(o_{i,t}\vert q,\mathbf{o}_{i,<t})} - 1, \quad o_{i,t} \sim \pi_\theta(\cdot \vert q,\mathbf{o}_{i,<t})
$$- 直观理解:上面的式子右边满足KL散度的基本特性
- 当两个分布足够接近时,第一项趋近于1,第二项趋近于0,整体趋近于0;
- 两个分布不相等时,上式右边取值总是大于0,可以通过求导证明:当 \(x>0\) 时,有 \(x - \log x - 1 \ge 0\)
- 直观理解:上面的式子右边满足KL散度的基本特性
- 估计形式为(注意以下式子中右边是左边的无偏梯度的前提是 \(o_{i,t} \sim \pi_\theta(\cdot \vert q,\mathbf{o}_{i,<t})\) ):
- 其他团队对GRPO的改进:阶跃&清华新论文:DeepSeek-R1的GRPO 可以更简洁 - 机器之心的文章 - 知乎
阶跃星辰与清华大学近期的一项研究发现,只需使用带 GAE (λ= 1,γ= 1)的普通 PPO 以及基于规则的简单奖励函数,无需任何 KL 正则化,就足以扩展在推理任务上的响应长度和基准性能,类似于在 DeepSeek-R1-Zero 上观察到的现象
使用这种极简方法,他们打造了 Open-Reasoner-Zero,这是首个面向大规模推理的强化学习训练的开源实现。并且该实现在 GPQA Diamond 基准上的表现优于 DeepSeek-R1-Zero-Qwen-32B,同时仅需使用 1/30 的训练步数。需要强调,该团队不仅开源了代码,还发布了参数设置、训练数据和模型权重
DeepSeek-R1之MTP
- 参考链接:deepseek技术解读(2)-MTP(Multi-Token Prediction)的前世今生 - 姜富春的文章 - 知乎
- 基本思想:
- 预测阶段(Predict) :通过 K 个头一次生成 K 个 token 的预测
- 验证阶段(Verify) :将 K 个 token 组装成 K 个 <input,label> 对,并行地利用输入 Main Model 作为评估验证,如果输出 label 与 Main Model 一致,则接受该 token
- 接受阶段(Accept) :最终接受满足 Main Model 的最大长度 tokens 作为输出
Deepseek MTP实现细节
原始报告:DeepSeek-V3 Technical Report内容如下
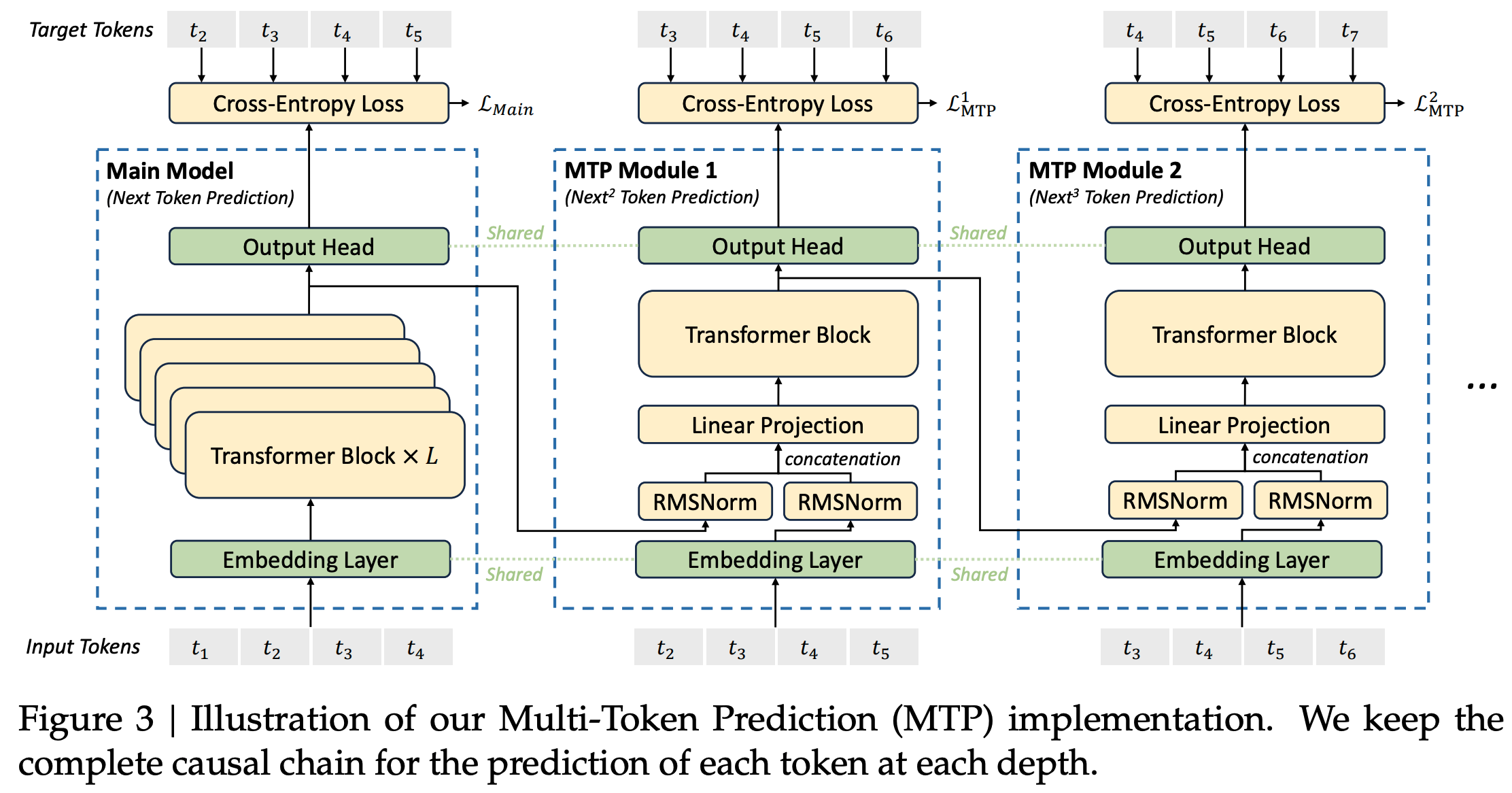
问题:上面图中设计的MTP中,无法做到整整的并行,比如,仅知道 \(t_1\) 时,只能预测得到 \(t_2\) ,无法得到 \(t_3\) ,因为在任意一个Module中, \(t_2\) 都依赖着 \(t_3\) 作为输入(只是输入后不用再过 \(L\) 层Transformer Block了,仅过一层就行)
训练时:使用多个MTP Module,综合大家的损失共同更新梯度
$$\mathcal{L}_\text{MTP} = \frac{\lambda}{D}\sum_{k=1}^D \mathcal{L}_\text{MTP}^k$$推断时:Deepseek直接丢弃了MTP Module,仅使用第一个(相当于跟普通不使用MTP的时候一致,只是吃到了训练的红利),部分文章中提到最多使用2个
Our MTP strategy mainly aims to improve the performance of the main model, so during inference, we can directly discard the MTP modules and the main model can function independently and normally. Additionally, we can also repurpose these MTP modules for speculative decoding to further improve the generation latency.
DeepSeek-R1 API远程调用
附录:Sparse MoE实现Demo
- Sparse MoE 的简单实现示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67import torch
import torch.nn as nn
class Expert(nn.Module):
def __init__(self, input_size, output_size):
super(Expert, self).__init__()
self.fc = nn.Linear(input_size, output_size)
def forward(self, x):
return self.fc(x)
# Dense MoE实现,对每个Token,所有专家都参与计算
class MoE(nn.Module):
def __init__(self, num_experts, input_size, output_size):
super(MoE, self).__init__()
self.experts = nn.ModuleList([Expert(input_size, output_size) for _ in range(num_experts)])
self.gate = nn.Linear(input_size, num_experts)
def forward(self, x):
gate_scores = torch.softmax(self.gate(x), dim=1)
expert_outputs = [expert(x) for expert in self.experts]
expert_outputs = torch.stack(expert_outputs, dim=1)
output = torch.sum(gate_scores.unsqueeze(-1) * expert_outputs, dim=1)
return output
# SparseMoE实现,对每个Token,仅少量专家参与计算
class SparseMoE(nn.Module):
def __init__(self, num_experts, input_size, output_size, k=2):
super(SparseMoE, self).__init__()
self.experts = nn.ModuleList([Expert(input_size, output_size) for _ in range(num_experts)])
self.gate = nn.Linear(input_size, num_experts)
self.k = k
def forward(self, x):
gate_scores = self.gate(x)
topk_scores, topk_indices = torch.topk(gate_scores, k=self.k, dim=1)
batch_size = x.size(0)
expert_outputs = []
for b in range(batch_size):
# 获取当前样本选中的K个专家的输出
selected_outputs = [self.experts[idx](x[b].unsqueeze(0)) for idx in topk_indices[b]]
# 堆叠输出,维度为 (1, k, output_size)
selected_outputs = torch.stack(selected_outputs, dim=1)
expert_outputs.append(selected_outputs)
# 合并所有样本,维度为 (batch_size, k, output_size)
expert_outputs = torch.cat(expert_outputs, dim=0)
# 计算选中专家的权重 (batch_size, k)
weights = torch.softmax(topk_scores, dim=1)
# 加权求和,维度为 (batch_size, output_size)
output = torch.sum(weights.unsqueeze(-1) * expert_outputs, dim=1)
return output
# 使用Demo
num_experts = 4
input_size = 10
output_size = 5
batch_size = 32
moe = SparseMoE(num_experts, input_size, output_size)
input_data = torch.randn(batch_size, input_size)
output = moe(input_data)
print(output.shape)
# torch.Size([32, 5])