NLP——技术报告解读-Skywork-OR1

注：本文包含 AI 辅助创作

• 参考链接：
  • 原始论文：(Skywork-OR1)Skywork Open Reasoner 1 Technical Report, arXiv 20250529, Kunlun Inc Skywork AI
  • GitHub 源码：github.com/SkyworkAI/Skywork-OR1
  • 后训练数据集：huggingface.co/datasets/Skywork/Skywork-OR1-RL-Data
  • 模型权重-7B：huggingface.co/Skywork/Skywork-OR1-7B
  • 模型权重-32B：huggingface.co/Skywork/Skywork-OR1-32B

Paper Summary

• 整体内容总结及评价：
  • 论文提出了一种适用于长 CoT 模型的高效且可扩展的 RL 实现方案 Skywork-OR1
  • 论文通过全面的消融实验，验证了训练流程中核心组件的有效性：
    • 数据混合与筛选
    • 无优势掩码（advantage masking）的多阶段训练
    • 高温采样（high-temperature sampling）
    • 排除 KL 损失
    • 适应熵控制（adaptive entropy control）
  • 论文还探讨了不同的训练资源分配方式对训练效率和最终模型性能的影响
  • 个人评价：
    • 非常详细的报告，非常扎实的工作，有许多新的认知和详尽的消融实验，值得多读几遍
    • 基于开源模型而不是自己的模型进行 RL 后训练微调
    • 仅关注了数学和代码指标涨幅，未关注其他指标降幅
• 基于 DeepSeek-R1-Distill 模型系列 ，论文的 RL 方法实现了显著的性能提升：
  • 对于 32B 模型，在 AIME24、AIME25 和 LiveCodeBench 基准测试中的平均准确率从 57.8% 提升至 72.8%（提升 15.0%）；
  • 对于 7B 模型，平均准确率从 43.6% 提升至 57.5%（提升 13.9%）
• 论文模型性能（注：论文的 7B 模型和 32B 模型分别基于 DeepSeek-R1-Distill-Qwen-7B 和 DeepSeek-R1-Distill-Qwen-32B 进行微调）：
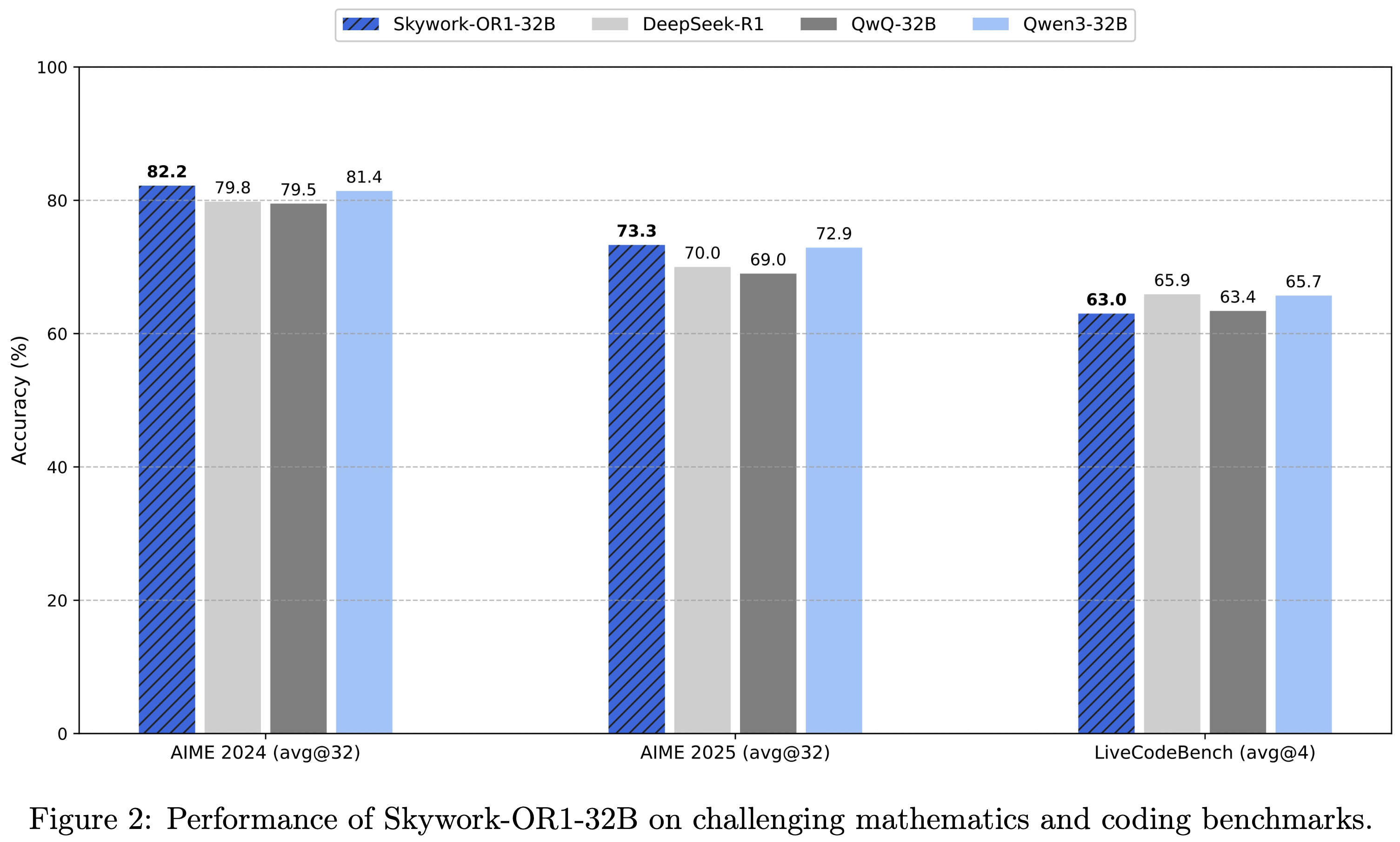
  • Skywork-OR1-32B 模型在 AIME24 和 AIME25 基准测试中表现超过 DeepSeek-R1 和 Qwen3-32B，同时在 LiveCodeBench 上实现了相当的结果
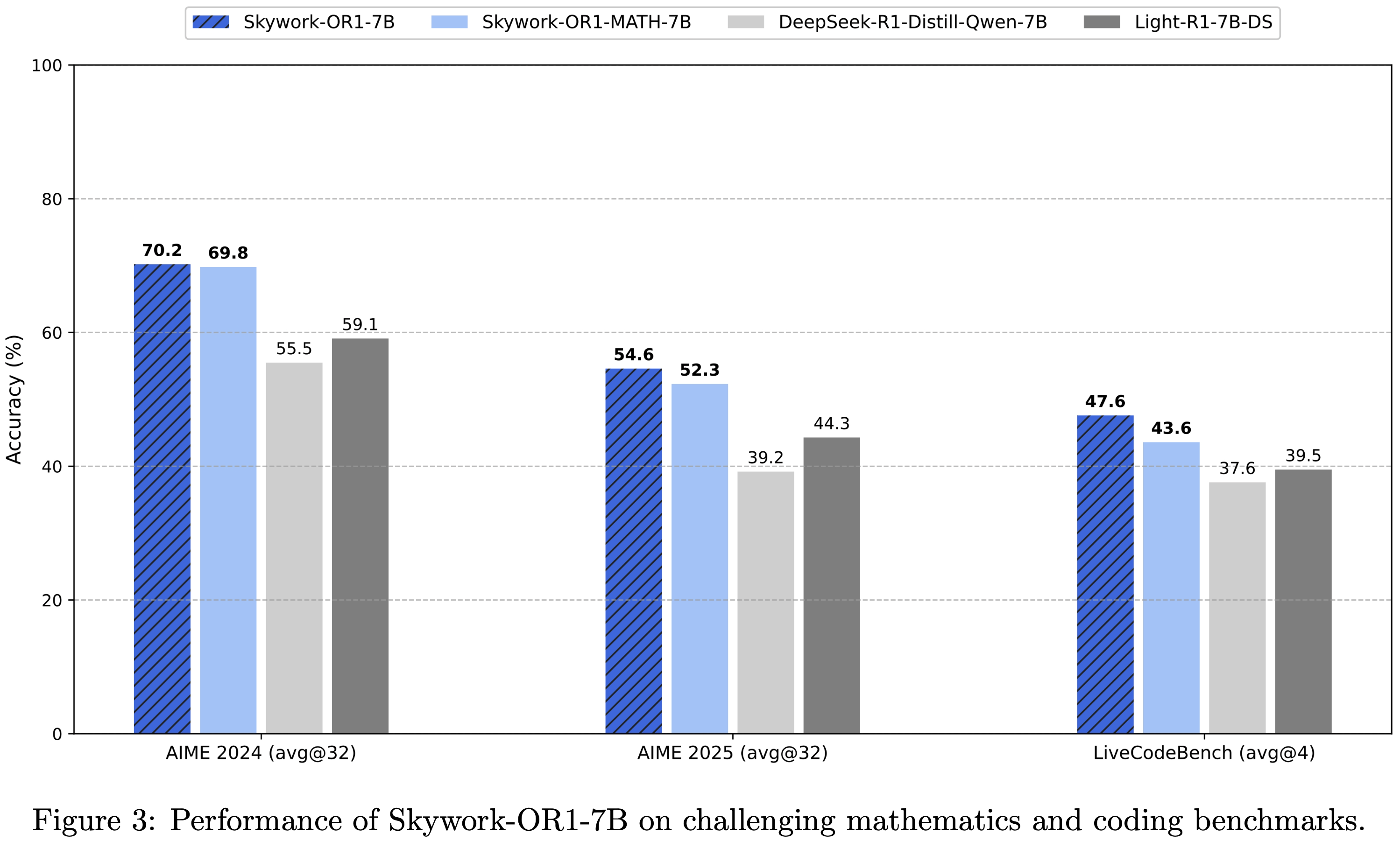
  • Skywork-OR1-7B 和 Skywork-OR1-Math-7B 模型在同等规模的模型中展现出具有竞争力的推理能力
• 论文对训练流程的核心组件进行了全面的消融实验 ，以验证其有效性
• 论文深入研究了熵坍缩（entropy collapse）现象 ，确定了影响熵动态变化的关键因素，并证明缓解过早熵坍缩对于提升测试性能至关重要
• 为支持社区研究，论文将模型权重、训练代码和训练数据集完全开源

---

Introduction and Discussion

• 近几个月来，基于 RL 的训练后技术在提升 LLM 推理能力方面取得了突破性成功，证明了 RL 在显著提升数学和代码任务性能方面的卓越能力
  • 具有代表性的模型，如 OpenAI-o1 (2024)、DeepSeek-R1 (2025) 和 Kimi-K1.5 (2025)
• 尽管以往的 RL 方法主要依赖蒙特卡洛树搜索（Monte Carlo Tree Search, MCTS）或过程奖励模型（Process Reward Models, PRM）来改进 SFT 模型的推理能力，但 DeepSeek-R1 的成功明确表明，采用简单基于规则的奖励机制的在线 RL，足以大幅提升基础模型的推理能力
• 随着模型能力的不断发展， CoT 的长度也在逐步增加
  • 例如，DeepSeek-R1-Distill 模型系列 (2025) 在 AIME24 基准测试中生成的 CoT 序列平均长度超过 10000 个 token
  • 显著超过了早期流行的 SFT 模型，如 Qwen 2.5 模型系列 (2024) 和 Llama 3.1 模型系列 (2024)
• 尽管在 DeepSeek-R1 取得成功后，已有多项复现研究（如 Logic-RL (2025)、Open-Reasoner-Zero (2025)、DAPO (2025)、VAPO (2025)），但这些研究大多聚焦于将 RL 应用于基础模型，而非已完成 SFT 的长 CoT 模型
  • 因此，目前尚不清楚如何以高效且可扩展的方式，利用 RL 提升长 CoT 模型的推理能力
• 尽管近期的研究，如 DeepScaleR (2025)、Light-R1 (2025) 和 DeepCoder (2025)，在长 CoT 模型的高效 RL 优化方面取得了初步进展
  • 但它们的分析并未系统地分离 RL 训练过程中不同算法组件的作用
• 在本研究中，论文提出了 Skywork Open Reasoner 1（简称 Skywork-OR1）
  • 是一种适用于长 CoT 模型的高效且可扩展的 RL 方案
• 论文的实验基于 DeepSeek-R1-Distill 模型系列和经过严格预处理与过滤的开源数据集
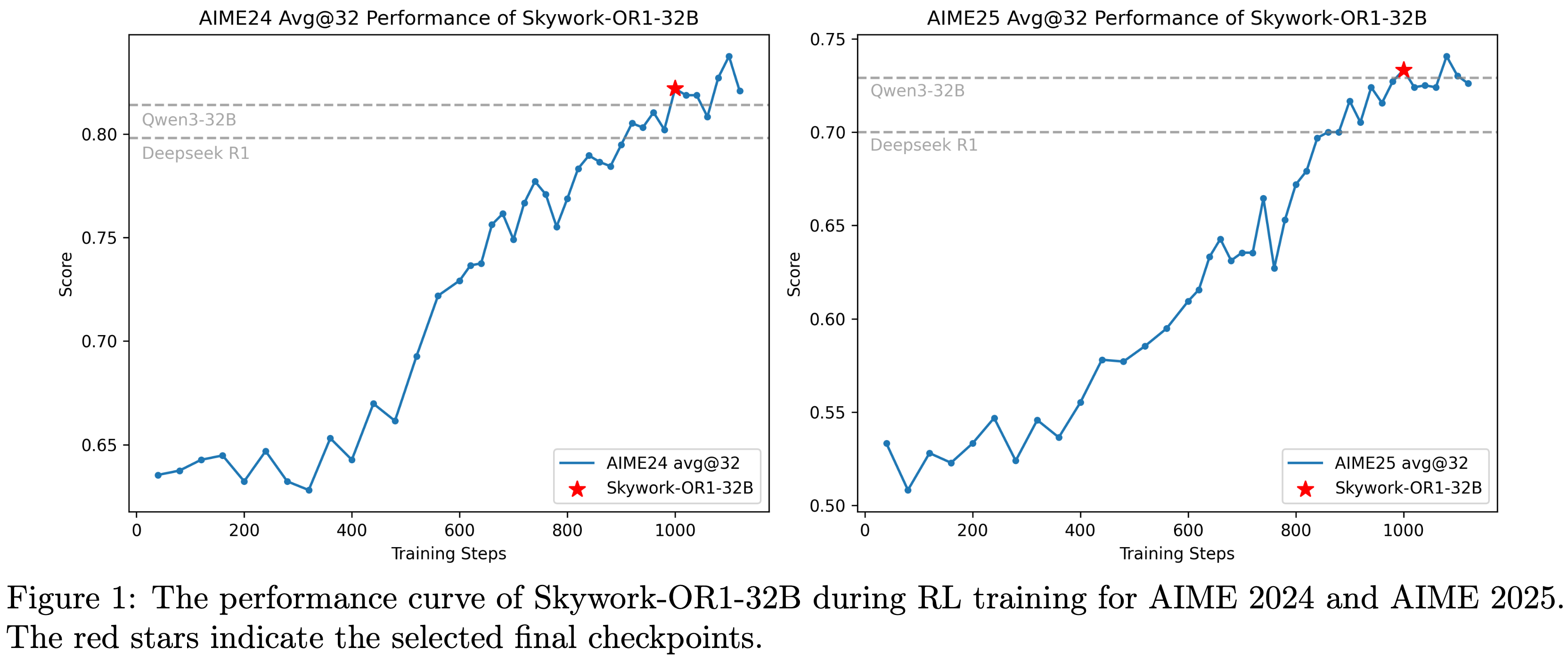
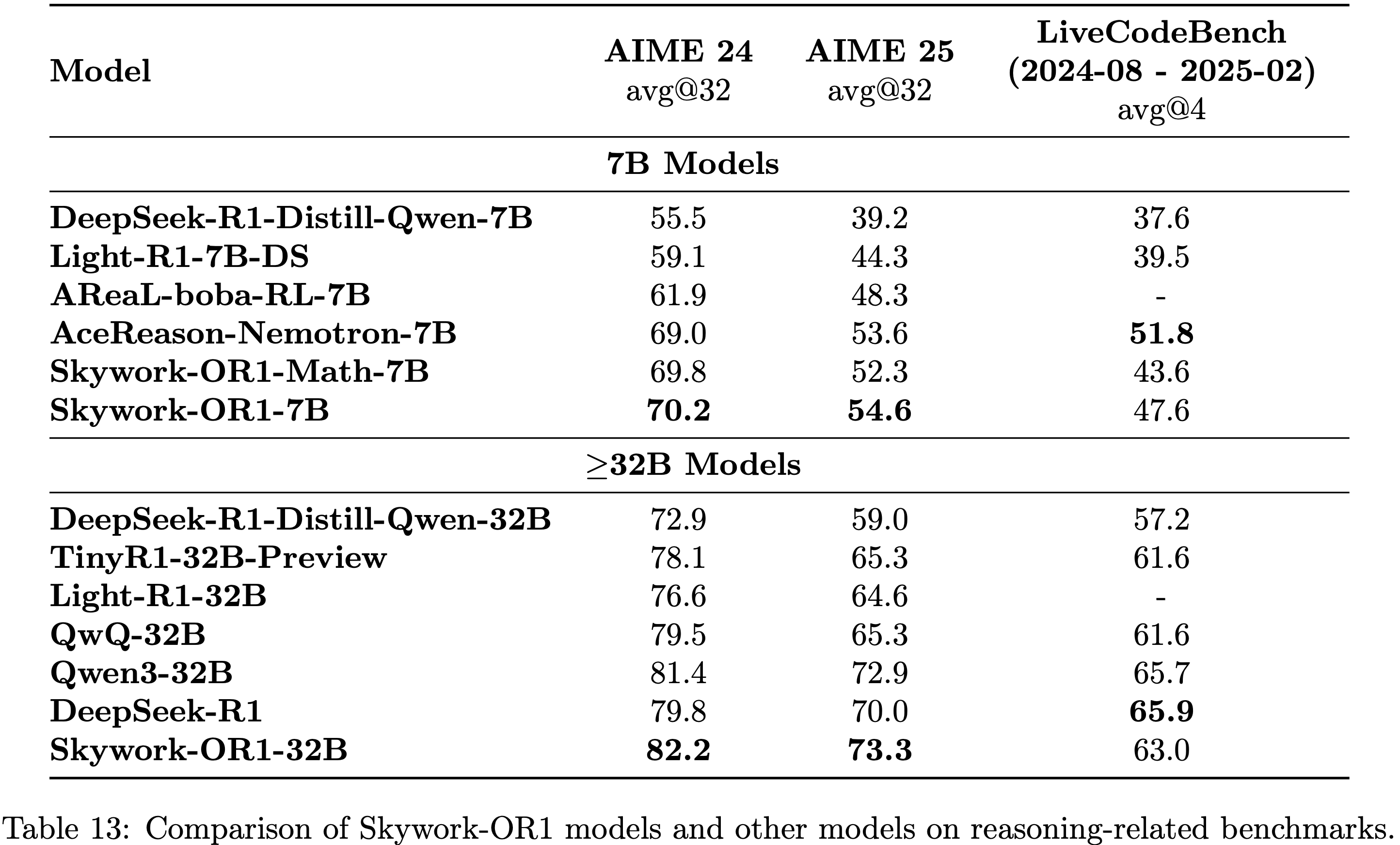
• 如 图1 和 表13 所示，Skywork-OR1 模型系列相对于基础模型实现了显著的性能提升，证明了论文 RL 实现方案的有效性
  • Skywork-OR1-32B 在 AIME24 上得分为 82.2，在 AIME25 上得分为 73.3，在 LiveCodeBench (2024)（2024年8月-2025年2月）上得分为 63.0，在数学领域表现超过 DeepSeek-R1 和 Qwen3-32B
  • Skywork-OR1-7B 在 AIME24 上得分为 70.2，在 AIME25 上得分为 54.6，在 LiveCodeBench 上得分为 47.6，在数学和代码任务中，相对于同等规模的模型展现出具有竞争力的性能
  • 论文之前发布的模型 Skywork-OR1-Math-7B 在同等规模模型中也表现出色，在 AIME24 上得分为 69.8，在 AIME25 上得分为 52.3，在 LiveCodeBench 上得分为 43.6
• 论文通过详尽的消融实验，验证了训练流程中核心组件的有效性
• 在 RL 训练中，平衡探索（exploration）与利用（exploitation）至关重要 (2018)
  • 论文对过早熵坍缩（一种与过度利用相关的现象）进行了全面研究，发现缓解过早熵坍缩对于获得更好的测试性能至关重要
• 通过详尽的消融实验，论文确定了影响熵动态变化的关键因素
• 为确保完全可复现性并支持 LLM 社区的持续研究，论文发布了所有训练资源，包括源代码、后训练数据集、模型权重-7B 和 模型权重-32B
• 此外，论文在数据和算法两个维度进行了广泛的消融实验 ，以阐明适用于长 CoT 模型的有效 RL 实现方案
• 作为论文之前发布的 Notion 博客文章 (2025) 的后续内容，论文在此呈现这份更详细的技术报告，主要研究结果总结如下：

Data Collection

• 1）为确保训练稳定且有效，纳入来自多种不同来源的问题（数据）至关重要
  • 论文发现，如果缺乏一致的质量评估和过滤流程 ，以往成功的数据集在应用于更大规模模型时会出现多种失效模式（见第6节）
• 2）对训练数据进行严格的过滤和质量控制 ，可显著加快学习速度
  • 论文基于严格过滤标准构建的数据混合集 ，其性能优于基于较宽松质量阈值构建的基准混合集（见 3.2.1 节）

Training Strategy

• 1）多阶段训练（Multi-stage Training）在初始阶段显著提升了训练效率，同时在后续阶段保持了可扩展性（见 3.2.2 节）
• 2）解决第一阶段（Stage I）中截断轨迹（truncated trajectories）引入的噪声训练信号，并不会在大上下文长度（如 32K）下带来更好的扩展性（见 3.2.3 节）
  • 问题：如何理解？
• 3）高温采样（High-temperature Sampling）在训练初期会导致较低的测试准确率 ，但最终能带来更大的性能提升（见 3.2.4 节）
• 4）On-policy Training 可缓解熵坍缩 ，并带来更高的测试性能（见第4节）

Loss Function

• 1）自适应熵控制（Adaptive Entropy Control）能在整个训练过程中，有效将模型熵保持在目标熵的下界以上 ，维持模型的探索能力和较高的学习可塑性 ，使测试性能稳步提升（见 3.2.5 节）
• 2）在多阶段训练中，KL 惩罚项（KL penalty）会阻碍测试性能的进一步提升。因此，论文在训练流程中移除了 KL 损失（见 3.2.6 节）

Empirical Results of Our Entropy Collapse Study（熵坍缩研究实证结果）

• 1）熵坍缩速度越快，通常测试性能越差（见 4.2 节）
  • 通过适当的熵控制缓解过早收敛 ，可提升测试结果（见 4.5 节）
• 2）通过增大批次大小（batch size）和组大小（group size）来提高采样多样性 ，对熵动态变化的影响较小（见 4.3 节）；而采用更高的采样温度（sampling temperature），则会对初始熵和学习动态产生显著影响（见 3.2.4 节）
• 3）Off-policy Training（通过增加 mini-batches 数量或数据复用（data reuse）实现），会加速熵坍缩
  • 而且由于引入了 Off-Policy 数据，与 On-Policy 更新（on-policy updates）相比，通常会导致测试性能下降（见 4.4 节）
• 4）熵损失对训练数据和系数均高度敏感
  • 通过自适应调整熵损失系数 ，或采用带有适当裁剪比例的 “上限裁剪”技巧（clip-higher trick），可使熵动态变化更缓慢、更稳定 ，从而提升测试性能
  • 然而，（Off-Policy Training）与 On-Policy Training 相比，熵的收敛速度仍然更快（见 4.5 节）

Organization

• 第2节：介绍了 RL 中几种重要的策略优化方法的基础知识
• 第3节：详细阐述了论文的训练流程，包括验证核心组件有效性的全面消融实验
• 第4节：系统研究了熵坍缩现象，证明在 RL 训练中，缓解策略过早收敛对于增强探索能力和获得更好的测试性能至关重要
• 第5节：讨论了训练资源分配问题
• 第6节和第7节：分别提供了训练数据准备和基于规则的奖励机制的实现细节
• 第8节：全面介绍了论文发布的三个模型（Skywork-OR1-Math-7B、Skywork-OR1-7B 和 Skywork-OR1-32B）的训练和评估细节

---

Preliminaries

• DeepSeek-R1 的成功证明，策略梯度（Policy Gradient, PG）方法 (2018)，尤其是 GRPO (2024)，能够有效提升 LLM 的推理能力
• 一般而言，RL 的目标是找到一个策略 \(\pi\) ，以最大化奖励，即：
  $$\operatorname {max}_{\pi }\left\{\mathcal {J}\left( \pi \right) :=\mathbb {E}_{x\sim \mathcal {D} }\mathbb {E}_{y \sim \pi (\cdot | x)}[r(x, y)]\right\} , \tag{2.1}$$
  • \(x\) 为训练提示（prompt）
  • \(\mathcal{D}\) 为 \(x\) 的采样分布
  • \(y\) 为策略 \(\pi\) 针对输入提示 \(x\) 采样得到的响应
  • \(r\) 表示奖励函数
• 在实际应用中，为了便于优化，论文在批次（batch）层面估计 \(\mathcal{J}(\pi)\) 的代理目标函数（surrogate objective）
  • 在每个训练步骤 \(k\) ，论文从数据分布 \(\mathcal{D}\) 中采样一批包含 \(N\) 个提示的集合 \(x_1, \dots, x_N\) （记为 \(\mathcal{T}_k\) ），并使用当前策略 \(\pi\) ，在上下文长度 \(T\) 和温度参数 \(\tau\) 的设置下，生成对应的响应 \(y_1, \dots, y_N\)
  • 步骤 \(k\) 处的批次层面代理目标函数可表示为：
    $$\operatorname* {max}_{\pi },\left\{\mathcal{J}_{k}\left(\pi\right):=\mathbb{E}_{x_{i} \sim \mathcal{T}_{k} } \mathbb{E}_{y_{i} \sim \pi\left(\cdot | x_{i}\right)}\left[r\left(x_{i}, y_{i}\right)\right]\right\}, \quad \tag{2.2}$$
    • \(\pi_k\) 是参数为 \(\theta_k\) 的策略 \(\pi_{\theta_k}\) 的简写

Vanilla Policy Gradient

• 对于参数化策略 \(\pi_\theta\) ，基础 PG (1999) 采用梯度上升法求解最优参数 \(\theta^*\) ，即：
  $$\theta \leftarrow \theta+\nabla_{\theta} \mathcal{J}\left(\pi_{\theta}\right)$$
• 在每次迭代 \(k\) 中，基础 PG 的一阶有效代理策略损失可表示为：
  $$\mathcal{L}_{k}^{PG}(\theta)=-\mathbb{E}_{x_{i} \sim \mathcal{T}_{k} } \mathbb{E}_{y_{i} \sim \pi_{k}\left(\cdot | x_{i}\right)}\left[\sum_{t=0}^{\left|y_{i}\right|-1} \frac{\pi_{\theta}\left(a_{i}^{t} | s_{i}^{t}\right)}{\pi_{k}\left(a_{i}^{t} | s_{i}^{t}\right)} \cdot A^{\pi_{k} }\left(s_{i}^{t}, a_{i}^{t}\right)\right],$$
  • 响应 \(y_i=(a_i^0, \dots, a_i^{|y|-1})\) 由 \(|y|\) 个 token 组成
  • \(a_i^t\) 是序列 \(y_i\) 中的第 \(t\) 个 token
  • \(s_i^t:=(x_i, a_i^0, \dots, a_i^{t-1})\) 是生成 \(a_i^t\) 时的前缀上下文
• 优势函数 \(A^{\pi_k}\) 定义为：
  $$A^{\pi_{k} }\left( s^{t},a^{t}\right) :=\mathbb {E}_{y\sim \pi_{k}\left( \cdot | x\right) }\left[ r\left( x,y\right) \mid s^{t},a^{t}\right] -\mathbb {E}_{y\sim \pi_{k}\left( \cdot | x\right) }\left[ r\left( x,y\right) \mid s^{t}\right] .$$
• 容易证明 \(\nabla_{\theta} \mathcal{L}_{k}^{PG}(\theta_{k})=-\nabla_{\theta} \mathcal{J}_{k}(\pi_{k})\)

Proximal Policy Optimization, PPO

• 在每个训练步骤 \(k\) ，PPO (2017) 采用裁剪技巧（clip trick），将新策略限制在 \(\pi_k\) 的信任域（trust region）内，并对策略损失 \(\mathcal{L}_k\) 执行多次梯度下降
• PPO 中使用的策略损失表示为：
  $$\mathcal {L}_{k}^{PPO}(\theta )=-\mathbb {E}_{x_{i}\sim \mathcal {T}_{k} }\mathbb {E}_{y_{i}\sim \pi_{k}\left( \cdot | x_{i}\right) }\left[ \sum_{t=0}^{\left| y_{i}\right| -1}\operatorname* {min}\left( \rho_{i}^{t}(\theta )A^{\pi_{k} }\left( s_{i}^{t},a_{i}^{t}\right) , clip\left( \rho_{i}^{t}(\theta ),1-\varepsilon ,1+\varepsilon \right) \cdot A^{\pi_{k} }\left( s_{i}^{t},a_{i}^{t}\right) \right) \right] ,$$
  • \(\rho_i^t(\theta):=\frac{\pi_\theta(a_i^t \mid s_i^t)}{\pi_k(a_i^t \mid s_i^t)}\) ， \(\varepsilon\) 为裁剪超参数
  • 在实际应用中，PPO 通常使用广义优势估计（Generalized Advantage Estimation, GAE）(2015) 来估计 Token-level 优势 \(A^{\pi_k}(s_i^t, a_i^t)\)

Group Relative Policy Optimization, GRPO

• 假设针对每个提示 \(x_i\) ，采样 \(M\) 个独立同分布的响应 \(y_{i1}, \dots, y_{iM}\)
• GRPO (2024) 利用组归一化奖励（group-normalized rewards）估计 Token-level 优势，并为每个响应 \(y_{ij}\) 引入额外的长度归一化项 \(\frac{1}{|y_{ij}|}\) 。GRPO 中使用的策略损失表示为：
  $$\begin{aligned} \mathcal{L}_{k}^{GRPO}(\theta) =-\mathbb{E}_{x_{i} \sim \mathcal{T}_{k} } \mathbb{E}_{\left\{y_{i j}\right\}_{j=1}^{M} \sim \pi_{k}(\cdot | x)} \ & {\left[\frac{1}{M} \sum_{j=1}^{M} \frac{1}{\left|y_{i j}\right|} \sum_{t=0}^{\left|y_{i j}\right|-1} \min \left(\rho_{i j}^{t}(\theta) A_{i j}^{t}, \operatorname{clip}\left(\rho_{i j}^{t}(\theta), 1-\varepsilon, 1+\varepsilon\right) A_{i j}^{t}\right)-\beta D_{i j}^{t}(\theta)\right], } \end{aligned}$$
  • \(y_{ij}=(a_{ij}^0, \dots, a_{ij}^{|y_{ij}|-1})\) ， \(a_{ij}^t\) 是序列 \(y_{ij}\) 中的第 \(t\) 个 token
  • \(s_{ij}^t:=(x_i, a_{ij}^0, \dots, a_{ij}^{t-1})\)
  • \(\rho_{ij}^t(\theta):=\frac{\pi_\theta(a_{ij}^t \mid s_{ij}^t)}{\pi_k(a_{ij}^t \mid s_{ij}^t)}\)
  • \(\varepsilon\) 为裁剪超参数
  • \(D_{ij}^t\) 是应用于 \(a_{ij}^t\) 的 Token-level k3 损失 (2024)，其系数为 \(\beta\) ，用于将策略 \(\pi_\theta\) 限制在参考策略 \(\pi_\text{ref}\) 的信任域内，即：
    $$D_{ij}^{t}\left( \theta \right) :=\frac {\pi_\text{ref}\left( a_{ij}^{t}|s_{ij}^{t}\right) }{\pi_{\theta }\left( a_{ij}^{t}|s_{ij}^{t}\right) }-\log \frac {\pi_\text{ref}\left( a_{ij}^{t}|s_{ij}^{t}\right) }{\pi_{\theta }\left( a_{ij}^{t}|s_{ij}^{t}\right) }-1,$$
• 对于每个提示-响应对 \((x_i, y_{ij})\) ，基于规则的验证器（rule-based verifier）会给出一个二元奖励 \(r(x_i, y_{ij}) \in \{0,1\}\)
  • Token-level 优势 \(A_{ij}^t\) 估计为：
    $$\forall t: A_{i j}^{t}=\frac{r\left(x_{i}, y_{i j}\right)-\operatorname{mean}\left(r\left(x_{i}, y_{i 1}\right), \ldots, r\left(x_{i}, y_{i M}\right)\right)}{\operatorname{std}\left(r\left(x_{i}, y_{i 1}\right), \ldots, r\left(x_{i}, y_{i M}\right)\right)} . \tag{2.5}$$

---

MAGIC in Skywork-OR1

• 论文采用基于改进版 Group Relative Policy Optimization（GRPO）（2024）构建的训练流程，将其命名为 GRPO 多阶段自适应熵调度收敛框架（Multi-stage Adaptive entropy scheduling for GRPO In Convergence, MAGIC）
• 在以下章节中，论文首先介绍 MAGIC 框架的技术方案，然后分析其各组成部分的有效性

Multi-stage Adaptive entropy scheduling for GRPO In Convergence, MAGIC

• 下文将从数据收集（Data Collection）、训练策略（Training Strategy） 和损失函数（Loss Function） 三个维度，通过详细阐述各组成部分来呈现 MAGIC 框架

Data Collection

• 为确保后续训练中查询数据的质量，论文通过 第6节 所述的严格数据准备流程构建初始数据集，并采用 第7节 所述的更精准验证器来提供奖励信号
• 此外，论文还采用以下策略进一步提升样本效率：
  • 1）离线与在线过滤（Offline and Online Filtering） ：
    • 论文在训练前和训练过程中均进行数据过滤
      • 训练前，移除基础模型正确率为1（完全正确）或0（完全错误）的提示词（prompt）；
      • 训练期间，在每个阶段开始时，同样剔除在上一阶段中智能体模型（actor model）正确率达到1的训练提示词
    • 这种动态在线过滤机制可确保智能体模型在每个阶段都能持续在具有挑战性的问题上进行训练
  • 2）拒绝采样（Rejection Sampling） ：
    • 零优势组（定义见公式(2.5)）中的响应不会对策略损失产生贡献，但可能会影响 KL 损失或熵损失，且由于这些损失的隐含相对权重增加，可能导致训练过程更不稳定
    • 为缓解该问题，论文的训练批次仅包含非零优势组；具体而言，若提示词 \(x_i\) 对应的样本满足 \(i \notin \tilde{\mathcal{T} }_k\) ，则将其过滤，其中：
      $$
      \overline{\mathcal{T} }_k := \left\{ i \in [N] : \exists j \in [M] \quad \hat{A}_{ij} \neq 0 \right\}
      $$

Training Strategy

• 论文对基础 GRPO 的训练策略进行了如下优化：
• 1）多阶段训练（Multi-Stage Training） ：受 DeepScaleR（2025）启发，论文逐步增加上下文长度 \(T\) ，并将训练过程划分为多个阶段
  • 实验表明，多阶段训练能在显著降低计算成本的同时保持扩展性，相关证据见3.2.2节
• 2）截断响应的优势掩码（Advantage Mask for Truncated Responses） ：在多阶段训练的早期阶段，许多响应会被截断，而这类截断响应无法推导结果，若对其分配负优势可能引入偏差，从而导致训练信号存在噪声
  • 为缓解该问题，论文初期尝试在训练早期使用优势掩码策略
  • 但如3.2.3节所示，对截断响应进行惩罚并不会阻碍后续阶段的性能提升 ，且能提高 token 效率
    • 基于此结果，论文在最终训练流程中未采用任何优势掩码策略
  • 问题：如何理解这种现象？
• 3）高温采样（High-Temperature Sampling） ：论文将 rollout 温度设置为 \(\tau=1\) ，以增强模型的探索能力并提升学习可塑性
  • 这一决策的依据是：当使用较小的采样温度（如 \(\tau=0.6\) ）时，采样策略在数学数据上会立即进入低熵状态 ，在代码数据上也会快速过渡到低熵状态（详见3.2.4节）
• 4）On-Policy Training ：论文对 Skywork-OR1-7B 和 Skywork-OR1-32B 采用 On-Policy Training
  • 因为实验发现 On-Policy 更新能显著减缓熵坍缩（entropy collapse），并带来更高的测试性能（详见第4节关于熵坍缩的详细研究）
  • 相比之下，Skywork-OR1-Math-7B （注：这个是发布更早一些的版本）的训练中，每个训练步骤执行两次梯度下降（因此并非严格的 On-Policy Training ）
    • 在论文对 Off-Policy 更新与过早熵坍缩之间关系的完整理解前，就已经使用了这种方法，但通过自适应熵控制（3.2.5节）仍有效缓解了熵坍缩问题，使模型实现了优异性能

Loss Function

• 为缓解隐含的长度偏差，论文采用 Token-level 策略损失，移除每个响应的长度归一化项 \(1/|y_{ij}|\) ，策略损失在训练批次的所有 token 上取平均值，公式如下：
  $$
  \mathcal{L}^{\text{MAGIC} }(\theta) = -\frac{1}{T_k} \sum_{i \in \mathcal{T}_k} \sum_{j=1}^M \left\{ \sum_{t=0}^{|y_{ij}|-1} \min\left\{ \rho_{ij}^t(\theta) A_{ij}^t, \text{clip}\left( \rho_{ij}^t(\theta), 1-\varepsilon, 1+\varepsilon \right) A_{ij}^t \right\} + \alpha_k \mathbb{H}_{ij}^t(\theta) \right\}, \quad \tag{3.1}
  $$
  • \(y_{ij} := (a_{ij}^0, \dots, a_{ij}^{|y_{ij}|-1})\)
  • \(a_{ij}^t\) 是序列 \(y_{ij}\) 中的第 \(t\) 个 token
  • \(s_{ij}^t := (x_i, a_{ij}^0, \dots, a_{ij}^{t-1})\) 是生成 \(a_{ij}^t\) 时的前缀上下文
  • \(\rho_{ij}^t(\theta) := \frac{\pi_{\theta}(a_{ij}^t | s_{ij}^t)}{\pi_k(a_{ij}^t | s_{ij}^t)}\)
  • \(\mathbb{H}_{ij}^t(\theta) := H(\pi_{\theta}(\cdot | s_{ij}^t))\) 是token \(a_{ij}^t\) 生成策略的熵
  • \(\alpha_k \geq 0\) 是熵的系数
  • \(T_k := \sum_{i \in \overline{\mathcal{T} }_k} \sum_{j=1}^M |y_{ij}|\) 是训练批次中token的总数
• 同时，论文还在损失函数中引入以下特性：
  • 1）自适应熵控制（Adaptive Entropy Control） ：为保留模型的探索能力并维持较高的学习可塑性，通常会引入额外的熵损失以防止熵坍缩
    • 权重合适的熵损失能提升模型的泛化能力，但实验表明，提前选择合适的系数往往具有挑战性（因为熵损失对系数和训练数据均高度敏感）
    • 为解决这一问题，论文引入额外超参数 target entropy，目标熵 \(\text{tgt-ent}\)
      • 该超参数会根据当前熵与目标熵的差值动态调整系数 \(\alpha_k\) ，确保当前熵始终以 \(\text{tgt-ent}\) 为下界（详见3.2.5节）
  • 2）无 KL 损失（No KL Loss） ：论文发现，包含 KL 损失项会阻碍性能提升，尤其在多阶段训练的后期阶段
    • 因此，论文在训练方案中剔除了 KL 损失（详见3.2.6节）

Effectiveness of MAGIC Components

• 本节将通过大量实验，分析 MAGIC 框架的各组成部分对后续强化学习训练性能提升的影响

Data Mixture

• 在正式训练方案中，论文从 NuminaMath-1.5（2024）中筛选出额外的高难度问题，构建最终的数据混合集
• 为验证这一设计选择的有效性，论文开展了以下消融实验：
  • 主要对比 DeepScaleR（2025）的数据混合集（因为基于该数据集训练的现有模型已展现出优异性能）
• 消融实验1：现有数据混合集 vs 论文的数据混合集（Ablation Experiments 1: Existing Mixture vs. Our Data Mixture）
  • 1）DeepScaleR 混合集（2025）：包含往年 AIME、AMC、Omni-MATH（2024）和 STILL（2025）中的问题
  • 2）Skywork-OR1 混合集：论文在第6节描述的自定义混合集，整合了更多来源（如 NuminaMath-1.5）的问题，并通过难度筛选和质量控制进行选择
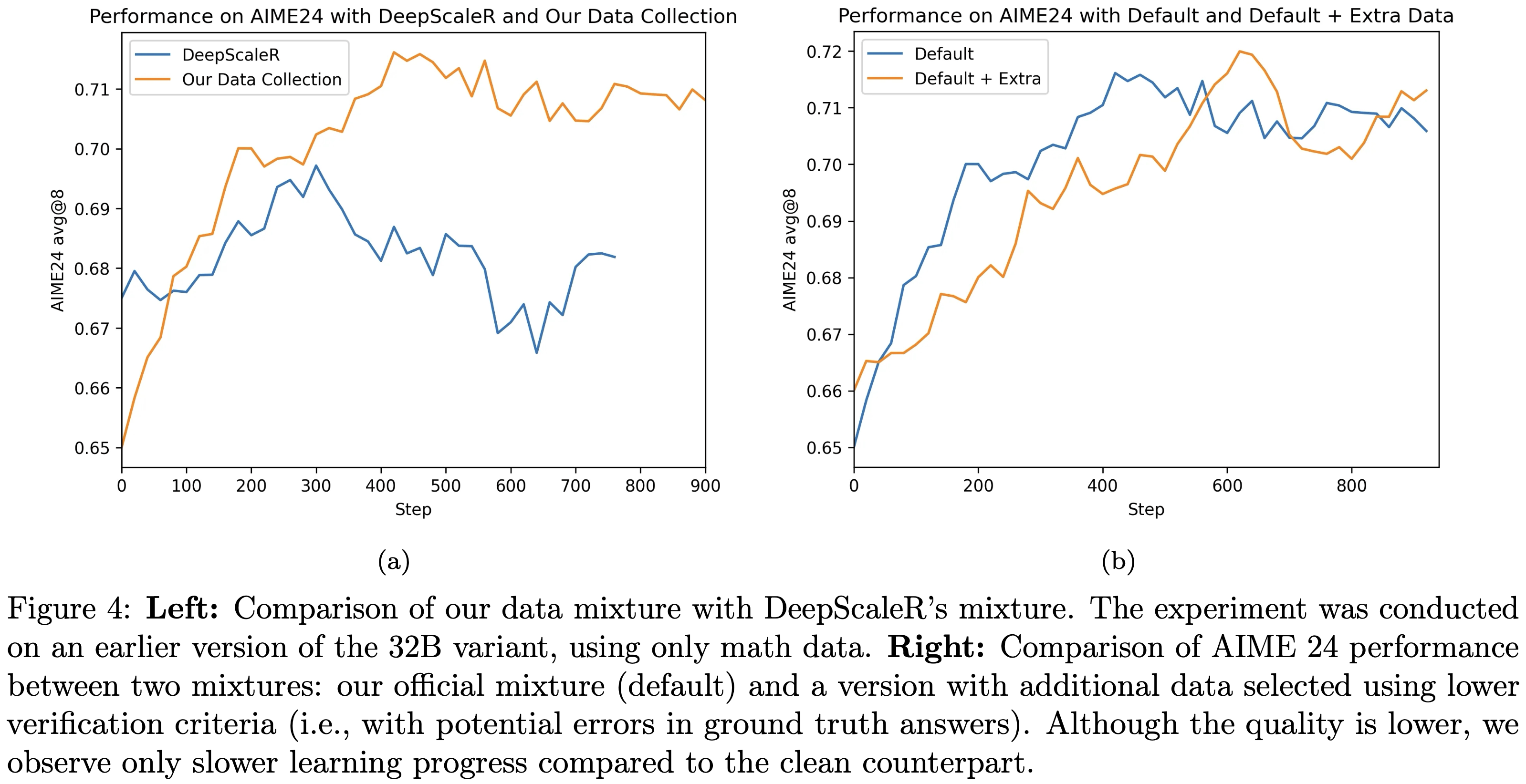
• 为排除数据量的影响，两个实验采用相同的超参数和近似相同的训练步数，结果如图4所示
  • 图4左侧：论文的数据混合集与 DeepScaleR 数据混合集的对比（实验基于32B模型的早期版本，仅使用数学数据）；
  • 图4右侧：官方数据混合集（默认）与“默认+额外数据”混合集在 AIME24 上的性能对比（额外数据通过较低验证标准筛选得到，即其标准答案可能存在误差）
    • 尽管额外数据质量较低 ，但与干净的默认混合集相比 ，仅观察到学习进度变慢（注：最终性能差不多）
• 尽管 DeepScaleR 数据集在较小模型变体上表现良好，且论文观察到其在 AIME24 上初期有轻微性能提升，但在 300 个训练步骤后性能急剧下降，最终回到训练前的准确率水平
• 此外，在图4（b）中，论文测试了将 官方数据混合集 与 通过较宽松验证流程获得的额外子集 相结合的效果（该额外子集包含 NuminaMath-1.5 中的高难度问题）
  • 但由于提取答案与提供的解决方案可能不匹配，这些问题此前已被排除
  • 实验发现，在 900 个训练步骤内，两个混合集的性能差异可忽略不计；
  • 包含额外子集的版本早期学习进度略慢，这可能是由于标准答案存在噪声所致
  • 论文推测 ，强化学习训练对少量标准答案噪声具有鲁棒性 ，这与（2025）的研究结果一致
• 因此，在后续所有探索性实验中，论文均采用第6节描述的默认数据组合

Multi-Stage Training

• 采用强化学习优化长 CoT 模型的主要挑战之一，是处理过长的输出（这会导致收敛缓慢且训练方差大）
• 受 DeepScaleR（2025）启发，论文在所有已发布模型中引入多阶段训练以提升训练效率：
  • 具体而言，在训练初期使用较短的上下文长度 \(T\) ，待模型性能收敛后，在后续阶段增大 \(T\)
  • 该方法不仅显著提升了基准测试的性能，还提高了训练效率

Same Improvement, Higher Efficiency

• 为验证多阶段训练的有效性，论文基于 DeepSeek-R1-Distill-Qwen-7B 开展了两项实验，仅在 \(T\) 的调度方式上存在差异
• 消融实验2：从头训练（From-Scratch） vs 多阶段训练（Multi-Stage）
  1）从头训练：从步骤0开始设置 \(T=16\text{K}\) ，并在训练过程中保持固定
  2）多阶段训练：从步骤0开始设置 \(T=8\text{K}\) ；在后续步骤（如步骤540）切换到第二阶段（Stage II），并将 \(T\) 增大至16K
• 两项实验的其他超参数保持一致，具体见表1，结果如图5（a）和图5（b）所示
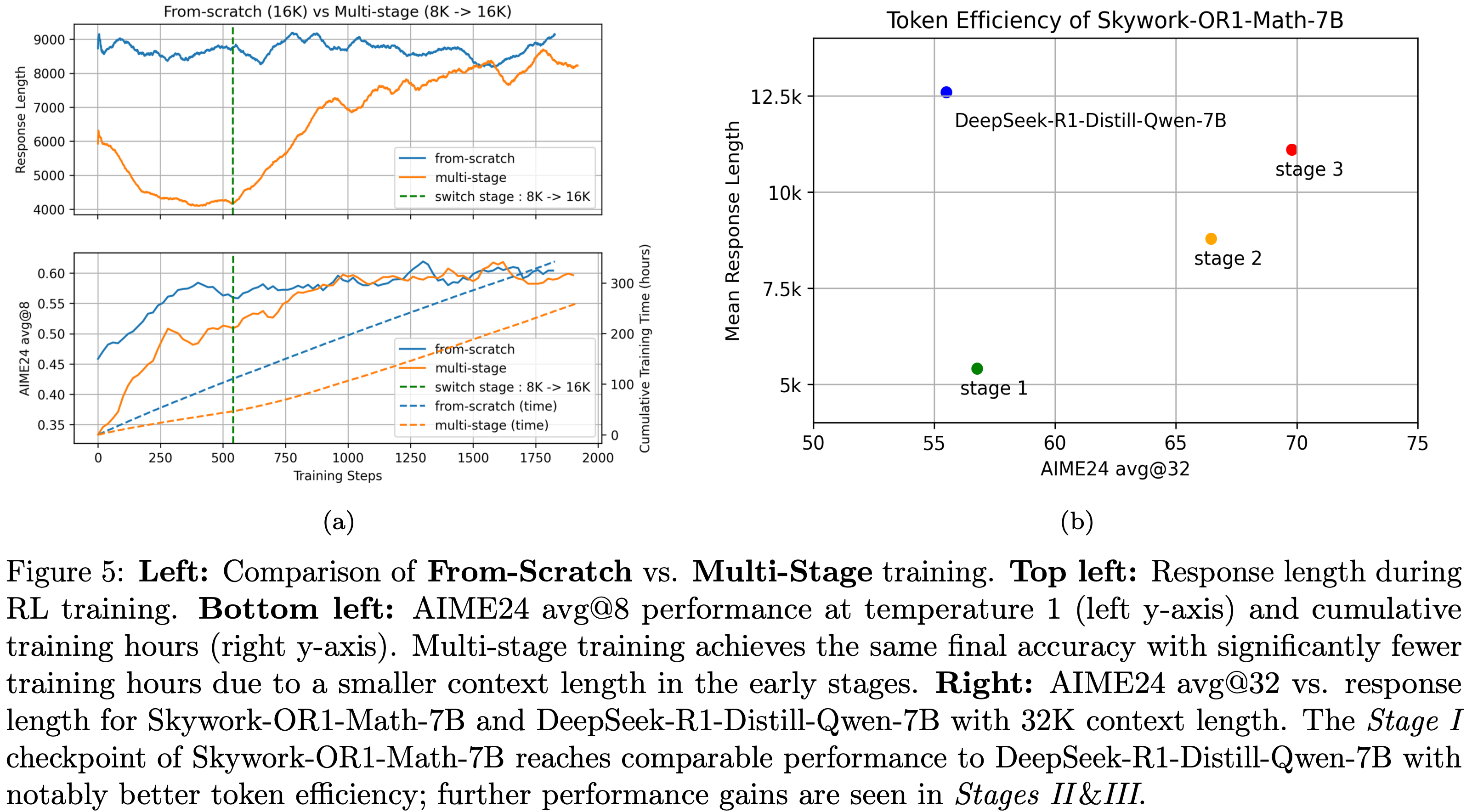
  • 图5（a）：消融实验2中，AIME24 准确率、生成响应长度和累计训练时长随训练步数的变化
    • 如图所示，当训练步数足够大时，两项实验的 AIME24 准确率均收敛至约 60
    • 但在多阶段实验中
      • 第一阶段的上下文长度（8K）仅为从头训练实验（16K）的一半，因此多阶段实验在第一阶段和第二阶段初期的平均响应长度显著更短，推理和计算成本降低，训练效率更高（1000 个训练步骤可节省约 100 小时训练时间）
      • 切换到第二阶段后，响应长度和 AIME24 准确率立即开始上升，在第二阶段约 500 个训练步骤内，多阶段实验的准确率达到与从头训练实验相当的水平
  • 图5（b）的解读见下文：

Improving Token Efficiency While Preserving Scaling Potential

• 在强化学习训练中，截断响应因缺少最终答案而被标记为负样本
• 多阶段训练的一个潜在问题（注：但论文最终证明并不是）是：使用较短的上下文窗口可能会使模型倾向于生成较短的响应，从而限制其探索能力并降低解决复杂问题的能力
• 但论文的研究表明，多阶段训练不仅能在初期提升 token 效率，还能保留模型的扩展能力
• 在图5（b）中可以观察到
  • 第一阶段使用 8K 上下文长度训练时，模型在 32K 上下文长度下的 AIME24 准确率仍与从头训练相当，同时 token 效率显著提升（平均响应长度从约 12.5K token 减少至 5.4K token）
    • 问题：对比的是 DeepSeek-R1-Distill-Qwen-7B（这不算是论文所谓的从头训练的模型吧？数据都对不齐了）
  • 在第二和第三阶段，Skywork-OR1-Math-7B 在响应长度稳步增加的同时，性能也同步提升
• 表1：基于 DeepSeek-R1-Distill-Qwen-7B 的消融实验1中的共享超参数
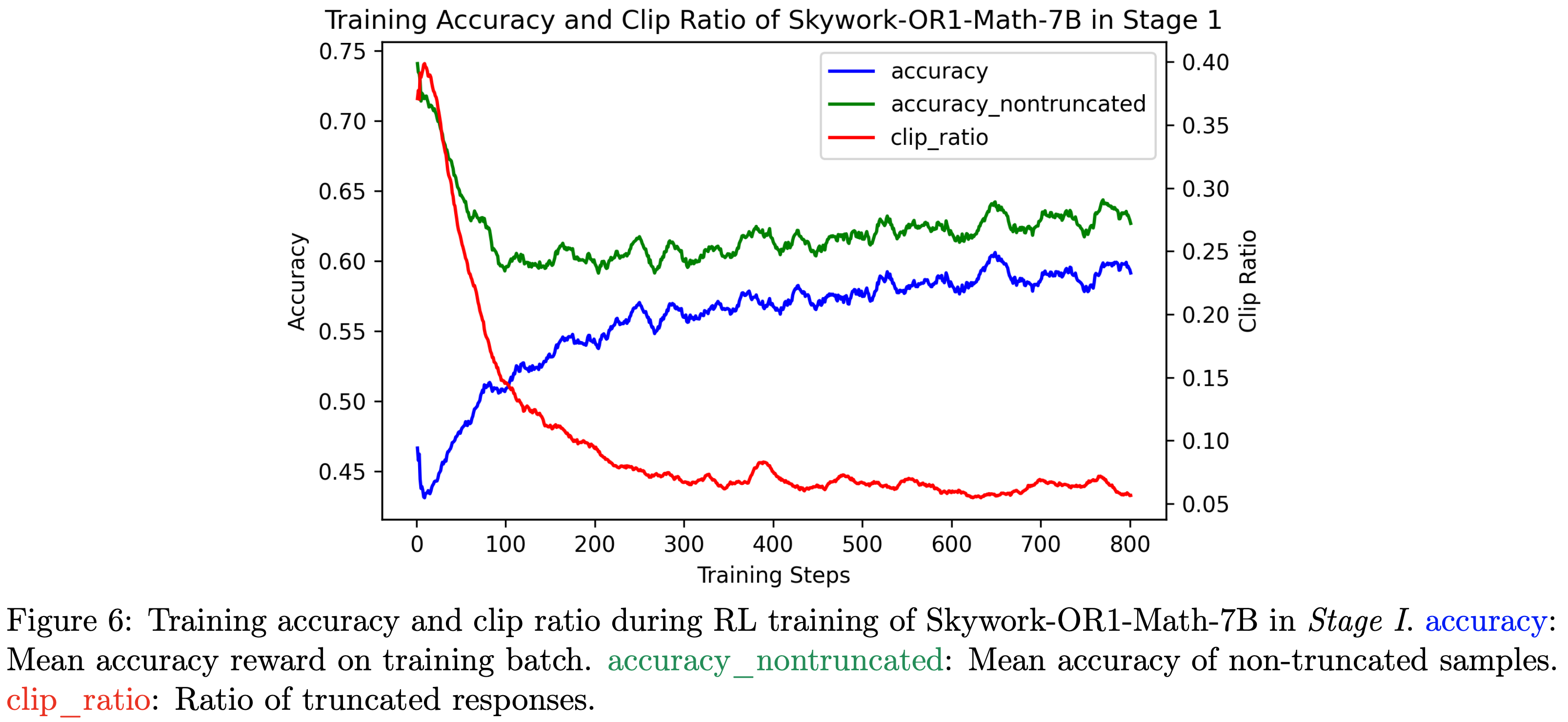
• 图6：Skywork-OR1-Math-7B 在第一阶段强化学习训练中的训练准确率和截断比例（clip ratio）。accuracy：训练批次的平均准确率奖励；accuracy_nontruncated：非截断样本的平均准确率；clip_ratio：截断响应的比例

Advantage Mask for Truncated Responses

• 在实际训练中，响应会在固定上下文长度 \(T\) 内采样生成
• 当响应长度超过 \(T\) 时，无法推导结果，准确率奖励被设为0，导致这些截断响应获得负优势，可能引入偏差
• 为缓解该问题，论文研究了多种优势掩码策略以降低截断响应的影响，但结果表明：
  • 对截断样本分配负优势不仅能提升 token 效率，还能保留模型在后续阶段的扩展能力
    • 注：这有点反直觉，跟之前的一些文章的结论不同，需要自己验一下才能确定
  • 因此，论文在最终训练流程中未应用任何掩码策略

Two Optimization Directions in Short Context Length（两个优化方向）

• 在 Skywork-OR1-Math-7B 的第一阶段训练中，论文设置上下文长度 \(T=8\text{K}\) ，在初始步骤中约 40% 的响应会被截断
• 尽管强化学习训练期间整体训练准确率持续上升，但论文观察到：
  • 非截断样本的准确率在最初 100 个训练步骤内急剧下降，之后才呈现轻微上升趋势（详见图6）
  • 截断响应通常会获得0准确率奖励（即使完整生成后答案可能正确），但由于截断导致缺少最终答案，因此无法获得正奖励
  • 因此，减少截断响应的数量有助于提升可达准确率
  • 图6显示：
    • 训练初期（步骤 0-100）准确率的上升主要源于截断比例（clip ratio）的急剧下降；
    • 步骤 100 后，算法开始提升非截断响应的准确率

A Brief Explanation from a Theoretical Perspective

• 论文用数学语言对上述现象进行形式化阐释。回顾公式(2.1)中强化学习训练的目标：
  $$
  \pi^* \in \arg\max_{\pi} \left\{ \mathcal{J}(\pi) := \mathbb{E}_{x \sim \mathcal{D} } \mathbb{E}_{y \sim \pi(\cdot | x)} [r(x, y)] \right\},
  $$
  • \(x\) 为提示词， \(\mathcal{D}\) 为提示词的分布
  • \(y\) 为从智能体（actor）中采样的响应
  • \(r(x, y) \in \{0, 1\}\) 为二元准确率奖励
• 需注意，响应 \(y\) 是在上下文长度 \(T\) 下采样生成的；对于长度大于 \(T\) 的截断响应（即 \(|y| > T\) ），由于无法从响应中推导结果，其准确率奖励 \(r(x, y)=0\)
• 基于这一观察，可推导出目标函数 \(\mathcal{J}(\pi)\) 满足：
  $$
  \begin{aligned}
  \mathcal{J}(\pi) &= \mathbb{E}_{x \sim \mathcal{D} } \mathbb{E}_{y \sim \pi(\cdot | x)} [r(x, y)] \\
  &= \mathbb{E}_{x \sim \mathcal{D} } \mathbb{E}_{y \sim \pi(\cdot | x)} [r(x, y) \mathbb{I}\{|y| \leq T\}] \\
  &= \mathbb{E}_{x \sim \mathcal{D} } \left[ p_{\text{non-trunc} }^{\pi}(x) \mathbb{E}_{y \sim \pi(\cdot | x)} \left[ \frac{\mathbb{I}\{|y| \leq T\} }{p_{\text{non-trunc} }^{\pi}(x)} r(x, y) \right] \right] \\
  &= \mathbb{E}_{x \sim \mathcal{D} } \left[ p_{\text{non-trunc} }^{\pi}(x) \mathbb{E}_{y \sim \hat{\pi}_T(\cdot | x)} [r(x, y)] \right] \\
  &= \mathbb{E}_{x \sim \mathcal{D} } \left[ p_{\text{non-trunc} }^{\pi}(x) \overline{r}_{\text{non-trunc} }^{\pi}(x) \right],
  \end{aligned}
  $$
  • \(p_{\text{non-trunc} }^{\pi}(x) := \mathbb{P}_{y \sim \pi(\cdot | x)} (|y| \leq T)\) 是响应 \(y\) 未被上下文长度 \(T\) 截断的概率（为简化分析，假设 \(p_{\text{non-trunc} }^{\pi}(x) > 0\) ）
  • \(\overline{r}_{\text{non-trunc} }^{\pi}(x) := \mathbb{E}_{y \sim \hat{\pi}_T(\cdot | x)} [r(x, y)]\) 是策略 \(\pi\) 输出的非截断响应的准确率
    • 问题：这里不完全准确吧，毕竟策略分布 \(\hat{\pi}_T(y | x)\) 是个复合表达式
  • \(\hat{\pi}_T(y | x) := \frac{\pi(y | x)}{p_{\text{non-trunc} }^{\pi}(x)} \mathbb{I}\{|y| \leq T\}\)
• 这表明，训练分布上的准确率（即 \(\mathcal{J}(\pi)\) ）可通过以下两种方式提升：
  • 提高 \(p_{\text{non-trunc} }^{\pi}(x)\) ：减少错误获得0准确率奖励的响应数量
  • 提高 \(\overline{r}_{\text{non-trunc} }^{\pi}(x)\) ：提升上下文长度内的响应质量

Advantage Mask for Truncated Responses

• 为促使算法专注于优化上下文长度内的准确率（即提高 \(\overline{r}_{\text{non-trunc} }^{\pi}(x)\) ）
  • 而非仅通过缩短响应来避免错误获得 0 准确率奖励（即提高 \(p_{\text{non-trunc} }^{\pi}(x)\) ）
• 论文探索了多种优势掩码策略，以减轻截断样本带来的噪声训练信号的影响
• 论文在第一阶段基于 DeepSeek-R1-Distill-Qwen-7B 开展消融实验，评估不同优势掩码策略的效果
• 消融实验3：不同优势掩码策略（Ablation Experiments 3: Different Advantage Mask Strategies）
  • 1）无优势掩码（No-Adv-Mask）：不采用任何优势掩码策略
  • 2）前置优势掩码（Adv-Mask-Before）：截断响应不参与非截断响应的组优势计算，且截断响应的优势设为0（因此不贡献于策略损失）：
    $$
    \forall t: A_{ij}^t =
    \begin{cases}
    \frac{r(x_i, y_{ij}) - \text{mean}(\hat{\mathbb{R} }_i)}{\text{std}(\hat{\mathbb{R} }_i)} & |y| \leq T \\
    0 & |y| > T
    \end{cases}
    $$
    • 其中， \(\hat{\mathbb{R} }_i\) 是提示词 \(x_i\) 的非截断响应的准确率奖励组
  • 3） 后置优势掩码（Adv-Mask-After）：截断响应仍参与非截断响应的组优势计算，但截断响应的优势设为0（因此不贡献于策略损失）：
    $$
    \forall t: A_{ij}^t =
    \begin{cases}
    \frac{r(x_i, y_{ij}) - \text{mean}(\mathbb{R}_i)}{\text{std}(\mathbb{R}_i)} & |y| \leq T \\
    0 & |y| > T
    \end{cases}
    $$
    • 其中， \(\mathbb{R}_i\) 是提示词 \(x_i\) 的所有响应的准确率奖励组
    • 问题：除了优势设置为 0 以外，参与计算其他优势的奖励值使用 0 吗？
      • 回答：猜测是的，先按照 0 参与计算，然后计算完，将自己的优势改成 0，所以叫做 After
• 两项实验的其他超参数保持一致，具体见表2，结果如图7（a）、图7（c）和图8所示（见下文）
• 表2：基于 DeepSeek-R1-Distill-Qwen-7B 的消融实验2中的共享超参数
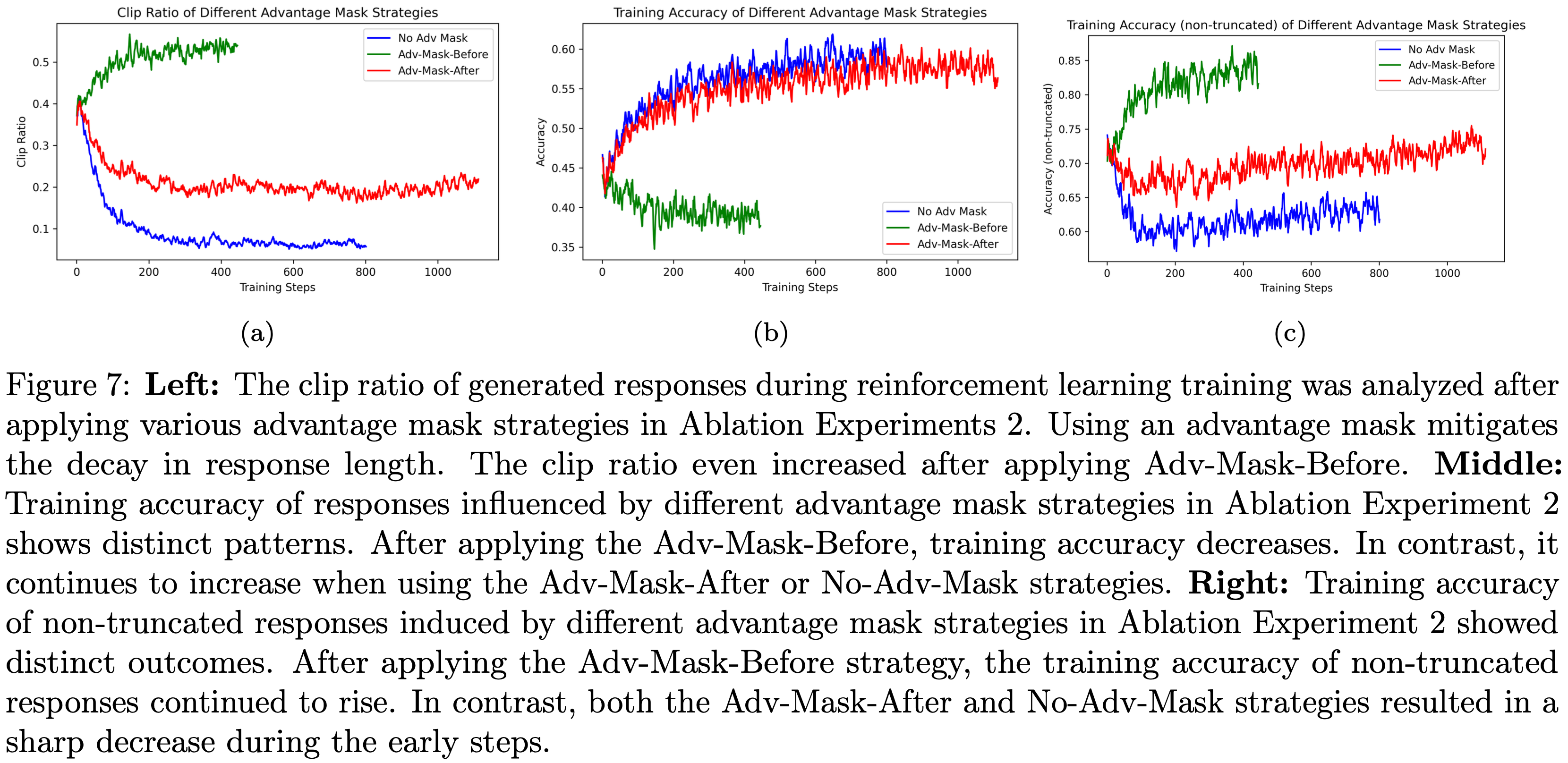
• 图7展示了消融实验2中不同优势掩码策略下的截断比例、整体准确率和非截断响应准确率：
  • 应用优势掩码可缓解响应长度的下降趋势，采用前置优势掩码（Adv-Mask-Before）后，截断比例甚至有所上升
  • 采用前置优势掩码后，训练准确率下降；而采用后置优势掩码（Adv-Mask-After）或无优势掩码时，训练准确率持续上升
  • 采用前置优势掩码后，非截断响应的训练准确率持续上升；而采用后置优势掩码或无优势掩码时，非截断响应的训练准确率在初期步骤急剧下降

Advantage Mask Does Not Exhibit Better Performance Given a Larger Inference Budget（更大推理预算下，优势掩码无性能优势）

• 尽管消融实验3表明，应用优势掩码能在短上下文长度下优化 \(\overline{r}_{\text{untrunc} }^{\pi}(x)\)
• 但论文发现：当上下文长度足够大（如 32K）以避免截断时，准确率并未提升
• 论文对比了不同优势掩码策略训练的模型在 AIME24 上的测试时扩展性能（见图8），结果显示：
  • 第一阶段应用优势掩码 并未改善测试时的扩展性能，32K 上下文长度下的准确率也未发生变化（尽管训练过程中 \(\overline{r}_{\text{non-trunc} }^{\pi}(x)\) 得到了优化）
  • 第一阶段不使用优势掩码 的强化学习训练，不仅能在大上下文长度下保持准确率，还能显著提升 token 效率；
    • 此外，第一阶段学习到的较短响应长度，不会阻碍第二阶段中响应长度和准确率的同步提升
  • 基于这些发现，论文在最终训练方案中未采用任何优势掩码来处理截断样本带来的噪声训练信号
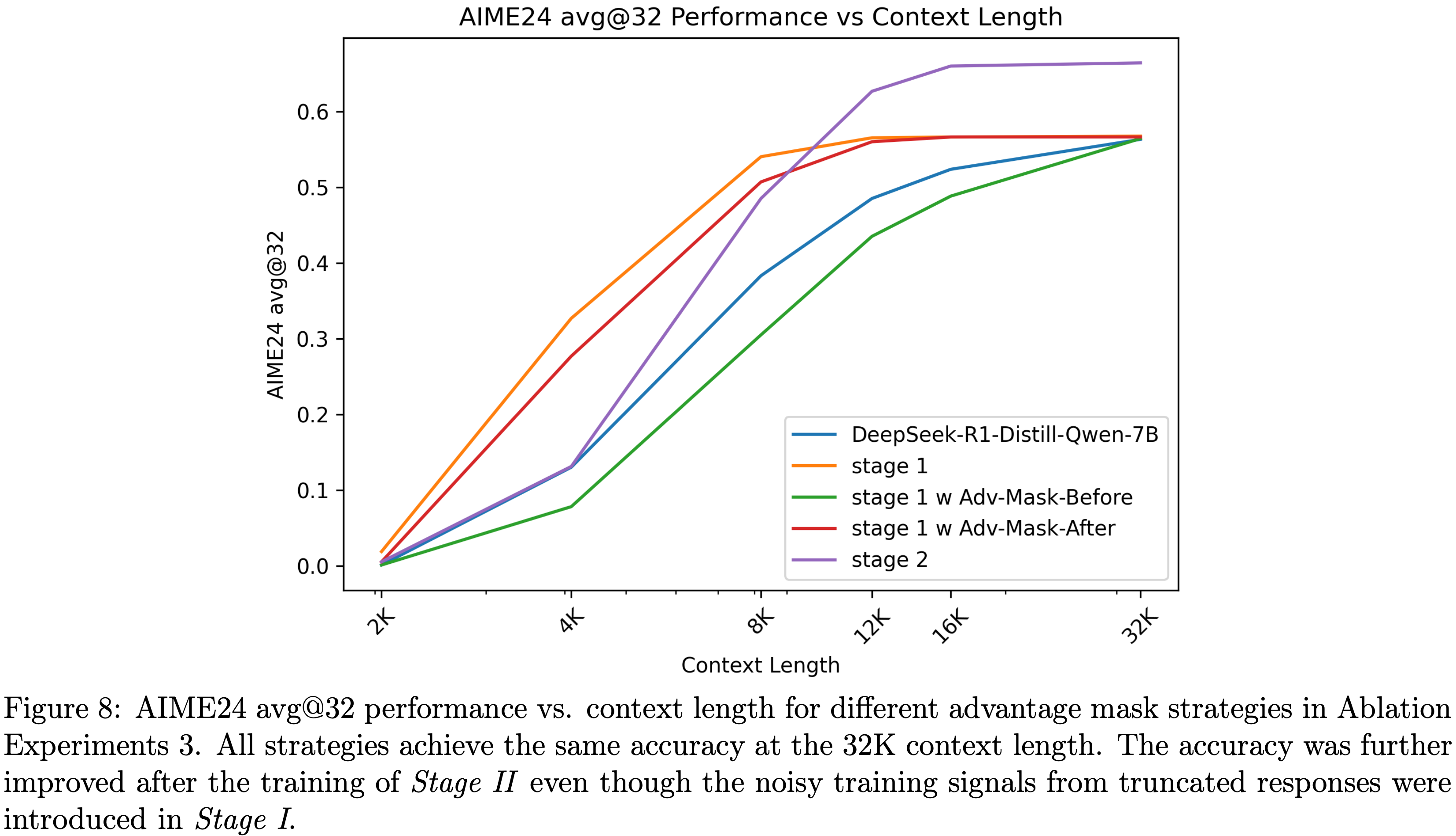
• 图8：消融实验3中不同优势掩码策略下，AIME24 avg@32 性能与上下文长度的关系
  • 所有策略在 32K 上下文长度下均达到相同准确率；
  • 即使第一阶段引入了截断响应的噪声训练信号，第二阶段训练后准确率仍进一步提升
  • 问题：图8中的 DeepSeek-R1-Distill-Qwen-7B 曲线表示什么？Stage I 和 Stage II 是独立的吗？为什么第一和第二阶段都是从同一个点开始？

High-temperature Sampling

• GRPO 的组级特性意味着，响应的采样过程直接影响每组响应的质量和多样性，进而影响学习效果
• 此前研究表明，较高温度通常会因随机性增加导致性能略有下降：
  • 若温度过高，可能会增加采样到仅包含错误响应的组的概率，由于缺少优势信号，训练效率会降低；
  • 较低温度会减少组多样性，导致解决方案高度相似甚至全为正确答案
  • 因此，选择合适的温度对确保组内解决方案具有足够多样性至关重要
• 论文针对采样温度 \(T\) 开展消融实验，结果如图9所示
• 消融实验4：不同在线采样温度 \(\tau\) （Ablation Experiments 4: Different Online Sampling Temperatures \(\tau\)）
  • 论文在在线强化学习训练中对比了两种不同的采样温度：
  • 1）高温（High Temperature）：设置温度超参数 \(\tau=1.0\)
  • 2）低温（Low Temperature）：设置温度超参数 \(\tau=0.6\)
• 两项实验的其他超参数保持一致，具体见表3，结果如图9所示
• 表3：消融实验4中的共享超参数
• 实验中，论文发现了一个与熵相关的额外现象：
  • 当使用较低温度（如0.6）时，模型要么初始熵极低，要么在约 100 个步骤内熵快速坍缩至接近零
  • 这种行为会导致初期学习进度缓慢，最终陷入停滞
  • 论文推测，尽管组内包含正确和错误响应，但解决方案多样性不足会使策略更新过度聚焦于 token 的窄子集 ，导致大量概率质量被分配给采样响应中频繁出现的特定 token
    • 理解：应该是没有区分度，所有正确样本都一样，变成模仿学习了？
  • 当论文将 rollout 温度提高到 1.0 时，模型的初始熵上升到更理想的范围；
    • 尽管熵最终仍会收敛，但较高温度显著增强了初期的学习信号，并为后续训练保留了更大潜力（如图9 所示）
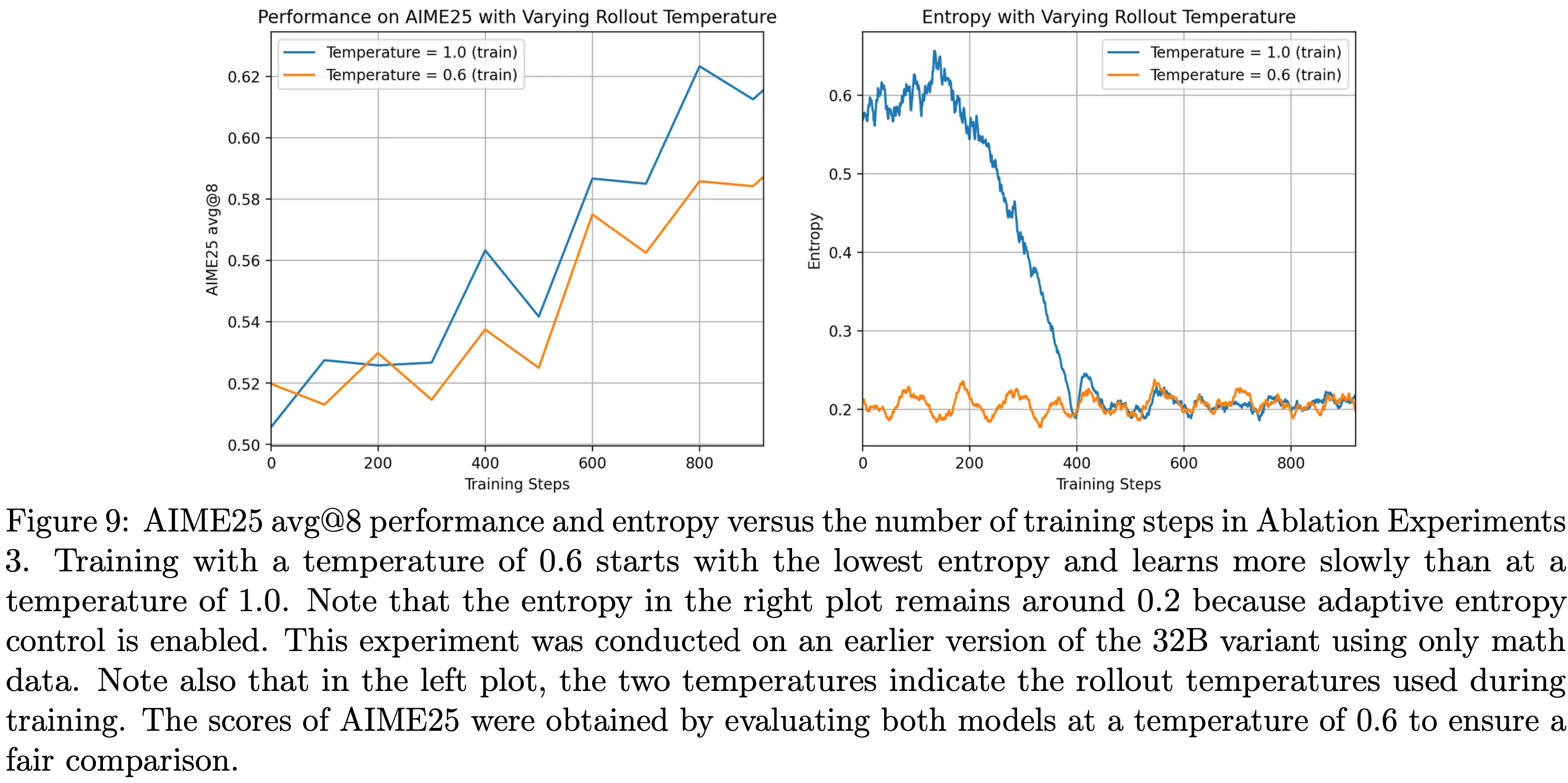
• 图9：消融实验3中，不同 rollout 温度下 AIME25 avg@8 性能和熵随训练步数的变化
  • 使用 0.6 的温度训练时，初始熵最低，学习速度慢于 1.0 的温度
  • 需注意，右图中的熵维持在 0.2 左右，因为已启用自适应熵控制
  • 该实验基于 32B 模型的早期版本，仅使用数学数据；
  • 左图中的两个温度表示训练期间使用的 rollout 温度，为确保公平比较，两个模型的 AIME25 得分均在温度 0.6 下评估

Adaptive Entropy Control

• 第4节的研究表明，通过熵正则化防止过早熵坍缩有益，但选择合适的熵损失系数具有挑战性
• 基于此，论文提出 自适应熵控制（Adaptive Entropy Control） 方法（根据目标熵和当前熵动态调整熵损失系数）
• 具体而言，论文引入两个额外超参数：
  • \(\text{tgt-ent}\) （期望目标熵）
  • \(\Delta\) （熵损失系数的调整步长）
• 将自适应系数初始化为 \(c_0=0\) ；
• 在每个训练步骤 \(k\) ，令 \(e\) 表示智能体的当前熵（从 rollout 缓冲区估计）：
  • 若 \(e\) 小于 \(\text{tgt-ent}\) ，则将 \(c_k\) 增加 \(\Delta\) （即 \(c_{k+1}=c_k+\Delta\) ）；
  • 若 \(e\) 大于 \(\text{tgt-ent}\) ，则将 \(c_k\) 减少 \(\Delta\)
  • 为缓解不必要的熵损失导致的不稳定性，仅当 \(e \leq \text{tgt-ent}\) 时才激活熵损失 ，即 \(\alpha_k = c_k \cdot \mathbb{I}\{e \leq \text{tgt-ent}\}\) ，确保当前熵始终以目标熵为下界
    • 问题：\(e \geq \text{tgt-ent}\) 时熵损失不生效，那此时修改 \(c_k\) 有什么必要呢？
• 通过自适应熵控制，论文能在整个训练过程中将模型的熵维持在合理水平，有效防止过早坍缩
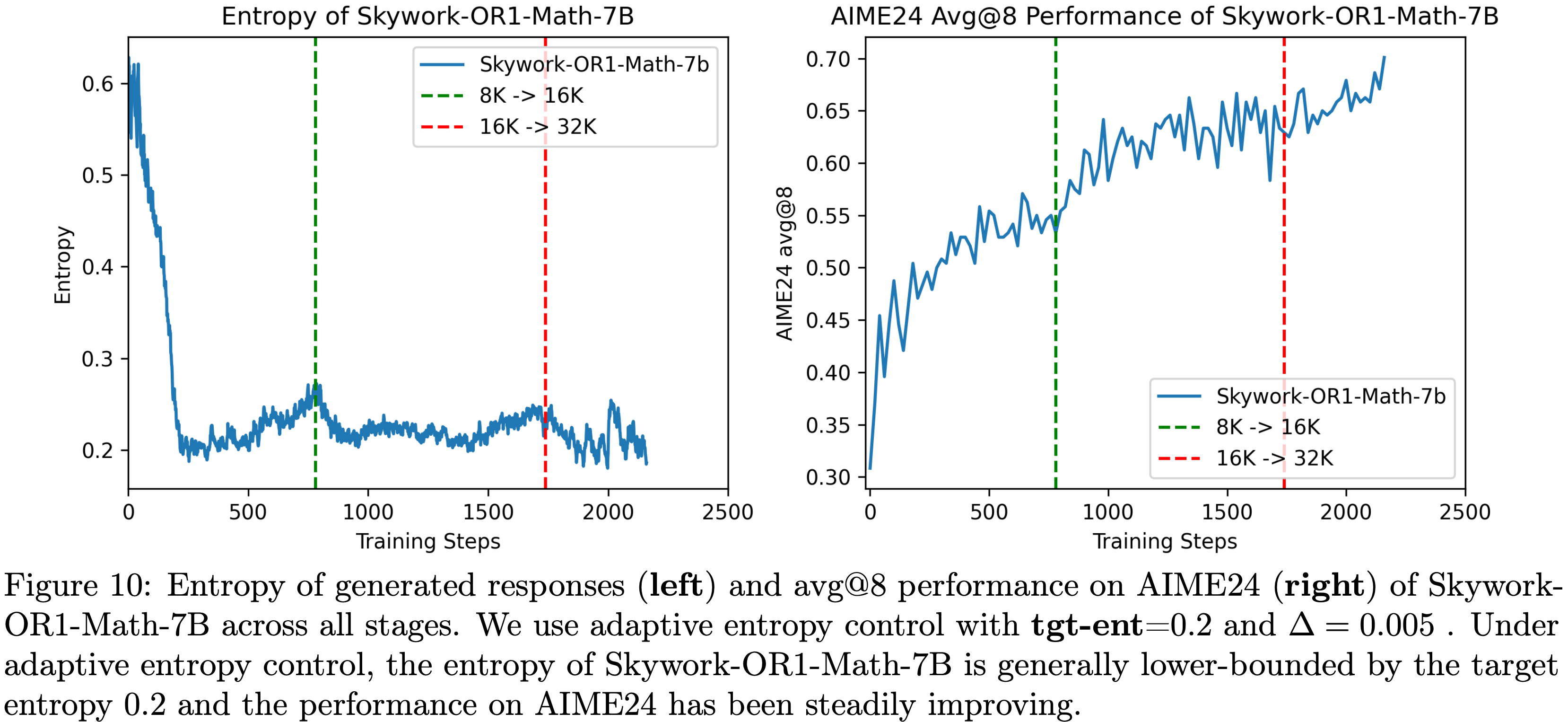
• 图10展示了 Skywork-OR1-Math-7B 在所有训练阶段的熵轨迹
• 实验中，论文设置 \(\text{tgt-ent}=0.2\) ， \(\Delta=0.005\)
• 为进一步验证自适应熵控制的有效性，论文在4.5节开展了详细的消融实验
• 自适应熵控制的系数调整公式如下：
  $$
  \alpha_k = c_k \cdot \mathbb{I}\{e_k \leq \text{tgt-ent}\}, \quad c_{k+1} =
  \begin{cases}
  c_k + \Delta & \text{if } e_k < \text{tgt-ent} \\
  c_k - \Delta & \text{if } e_k > \text{tgt-ent}
  \end{cases}, \quad c_0 = 0
  $$
• 图10：Skywork-OR1-Math-7B 在所有阶段的生成响应熵（左）和 AIME24 avg@8 性能（右）。论文使用自适应熵控制，设置 \(\text{tgt-ent}=0.2\) ， \(\Delta=0.005\) 。在自适应熵控制下，Skywork-OR1-Math-7B 的熵通常以目标熵0.2为下界，且 AIME24 性能稳步提升

No KL Loss

• 为研究KL损失的影响，论文开展了以下消融实验
• 消融实验5：有KL损失（KL Loss） vs 无KL损失（No KL Loss）
  • 论文在消融实验中考虑 Token-level k3损失，采用的 KL 正则化策略损失公式为：
    $$
    \mathcal{L}_{\beta}(\theta) = \mathcal{L}(\theta) + \frac{\beta}{T_k} \sum_{i \in \mathcal{T}_k} \sum_{j=1}^M \sum_{t=0}^{|y_{ij}|-1} \left( \frac{\pi_{\text{ref} }(a_{ij}^t | s_{ij}^t)}{\pi_{\theta}(a_{ij}^t | s_{ij}^t)} - \log \frac{\pi_{\text{ref} }(a_{ij}^t | s_{ij}^t)}{\pi_{\theta}(a_{ij}^t | s_{ij}^t)} - 1 \right),
    $$
  • 其中， \(\mathcal{L}(\theta)\) 是公式(3.1)定义的原始策略损失， \(\beta\) 是KL系数
• 论文首先基于 DeepSeek-R1-Distill-Qwen-7B（参考策略）
  • 在第一阶段以 \(\beta=1e-3\) 开展实验；
  • 然后在第二阶段，基于第一阶段的检查点（checkpoint）开展消融实验，对比 \(\beta=1e-3\) 和 \(\beta=0\) 的效果
• 其他超参数见表4，结果如图11（a）和图11（b）所示
• 表4：基于第一阶段检查点的消融实验5中的共享超参数
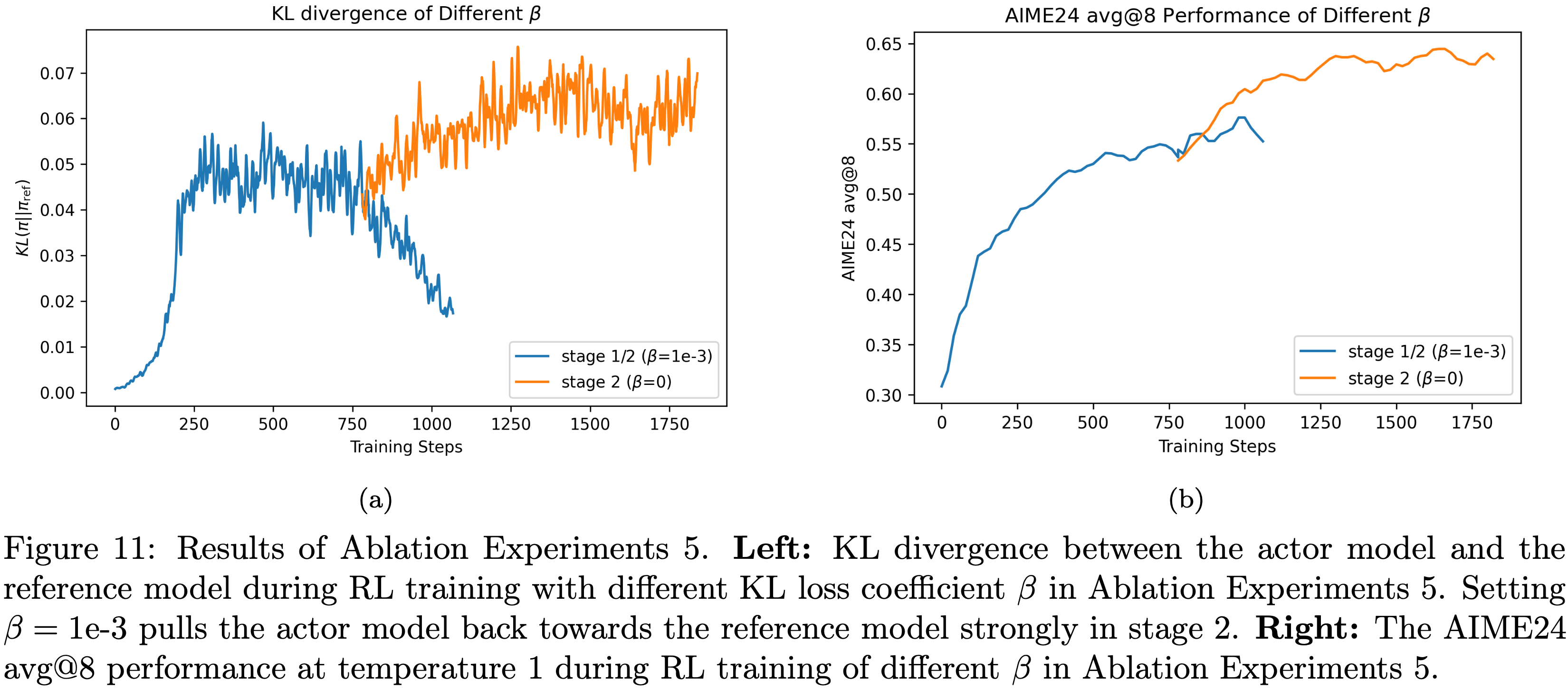
• 实验观察到，在第二阶段，KL 损失会强烈将智能体模型的策略拉回参考模型，导致 KL 散度快速下降至接近零（见图11（a））
  • 因此，当智能体的策略与参考模型过于相似后，AIME24 的性能无法显著提升（见图11（b））
  • 基于这一观察，论文在所有已发布模型的训练阶段均设置 \(\beta=0\)
• 图11：消融实验5的结果；左图：不同 KL 损失系数 \(\beta\) 下，强化学习训练期间智能体模型与参考模型的 KL 散度，在第二阶段设置 \(\beta=1e-3\) 会强烈将智能体模型拉回参考模型；右图：不同 \(\beta\) 下，强化学习训练期间 AIME24 avg@8 性能（温度设为 1）

---

Empirical Studies on Mitigating Policy Entropy Collapse

• 探索与利用是 RL 训练中最核心的矛盾之一（2018），在 On-Policy 算法中尤为突出
  • 简而言之，要实现更优性能，就必须进行充分的探索；
  • 但如果智能体的策略过早收敛到某一特定解，该策略可能并非最优，且这种收敛会阻碍对多样化轨迹的探索
• 策略熵是衡量强化学习算法收敛程度的重要指标：
  • 通常，当模型策略熵收敛到极小值（如接近0）时，策略会趋于稳定，此时模型的生成行为对训练数据的更新不再敏感，导致学习效率下降、输出多样性降低
  • 因此，在实际训练中，为了让模型接触到更有效的训练信号并提升分布外（Out-of-Distribution, OOD）性能，防止过早熵坍缩至关重要
• 本节将研究策略更新过程中的哪些超参数和组件有助于防止熵坍缩，进而提升分布外泛化能力
• 图12展示了论文针对缓解策略熵坍缩的实证研究整体框架
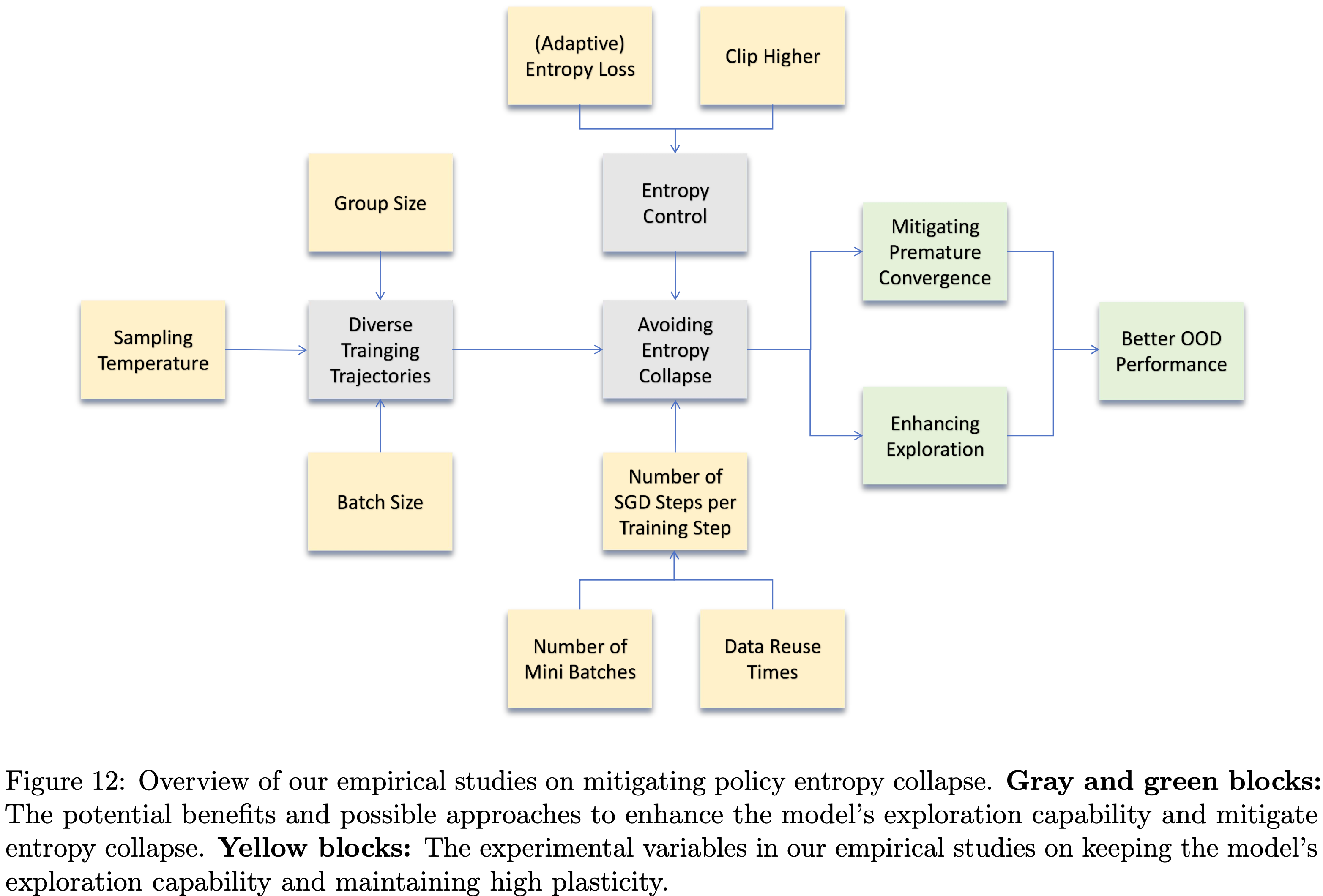
• 最初，论文假设以下两个因素可能会影响模型的熵与收敛行为：
  • 采样多样性（Rollout diversity）：
    • 若采样数据中包含更多样化的正确响应 ，可避免模型过拟合到单一正确轨迹
    • 论文将研究采样温度、采样批次大小、组大小等与采样相关的超参数在强化学习训练过程中对模型策略熵的影响
  • 策略更新（Policy update）：
    • 论文还将研究策略更新的不同组件对熵的影响，本节重点关注每个训练步骤中随机梯度下降（Stochastic Gradient Descent, SGD）的步数，以及额外熵控制方法（如熵损失）的使用
• 通过大量消融实验，论文得出以下主要研究结果：

Ablation Setup

• 第4节中的所有消融实验均基于第3.1节所述的训练流程开展
• 实验以 DeepSeek-R1-Distill-Qwen-7B 为基础模型， baseline 实验的超参数如表5所示，其中关键符号定义如下：
  • \(D_R\) ：采样批次大小（一个训练步骤中用于生成响应的提示词数量）
  • \(D_T\) ：mini-batch 大小（每个策略更新步骤中使用的响应对应的提示词数量）
  • \(N_{reuse}\) ：采样缓冲区的遍历次数
  • \(gs\) ：组大小（为每个提示词生成的响应数量）
  • \(T\) ：上下文长度
  • \(\tau\) ：采样温度
• 除非另有说明，本节所有消融实验的默认训练配置均与上述 baseline 实验保持一致
• 评估数据集采用 AIME24、AIME25 和 LiveCodeBench（2024.08–2025.02）（2024）
• 消融研究中报告的测试性能为 AIME24/25 上的 avg@8 性能与 LiveCodeBench 上的 pass@1 性能的经验平均值
• 值得注意的是，baseline 实验使用 32 块 H800 GPU，经过 2700 个训练步骤后，在 AIME24 上达到 69.2% 的 avg@8 性能，在 AIME25 上达到 53.3% 的 avg@8 性能，在 LiveCodeBench 上达到 50.5% 的 pass@1 性能
  • 这些结果与最终发布的 Skywork-OR1-7B 性能接近，为分析影响测试性能和导致熵坍缩的关键因素奠定了坚实基础
• 表5：第4节消融研究中 baseline 实验的超参数

Premature Entropy Collapse Generally Manifests as Worse Performance：过早熵坍缩通常伴随性能下降

• 如前所述，强化学习训练过程中的熵动态变化反映了策略的收敛程度：
  • 当智能体收敛到特定策略并进入低熵状态时，学习效率和采样多样性通常都会下降
  • 在初步实验中，论文观察到智能体模型的熵在训练过程中往往会快速下降
• 为缓解过早熵坍缩，论文引入了熵损失项，假设这能帮助智能体收敛到更优策略
  • 实验结果验证了这一假设：加入熵损失后，测试性能得到提升
• 图13 展示了两个初步实验中测试基准的准确率曲线和生成响应的熵，这两个实验使用了不同的熵损失系数 \(\alpha_k\) （1e-3和5e-3）
  • 结果表明，使用更大的系数（即5e-3）能更有效地防止熵坍缩，并实现更好的泛化性能
  • 此外，第4.4节的消融实验进一步证实了这一发现：
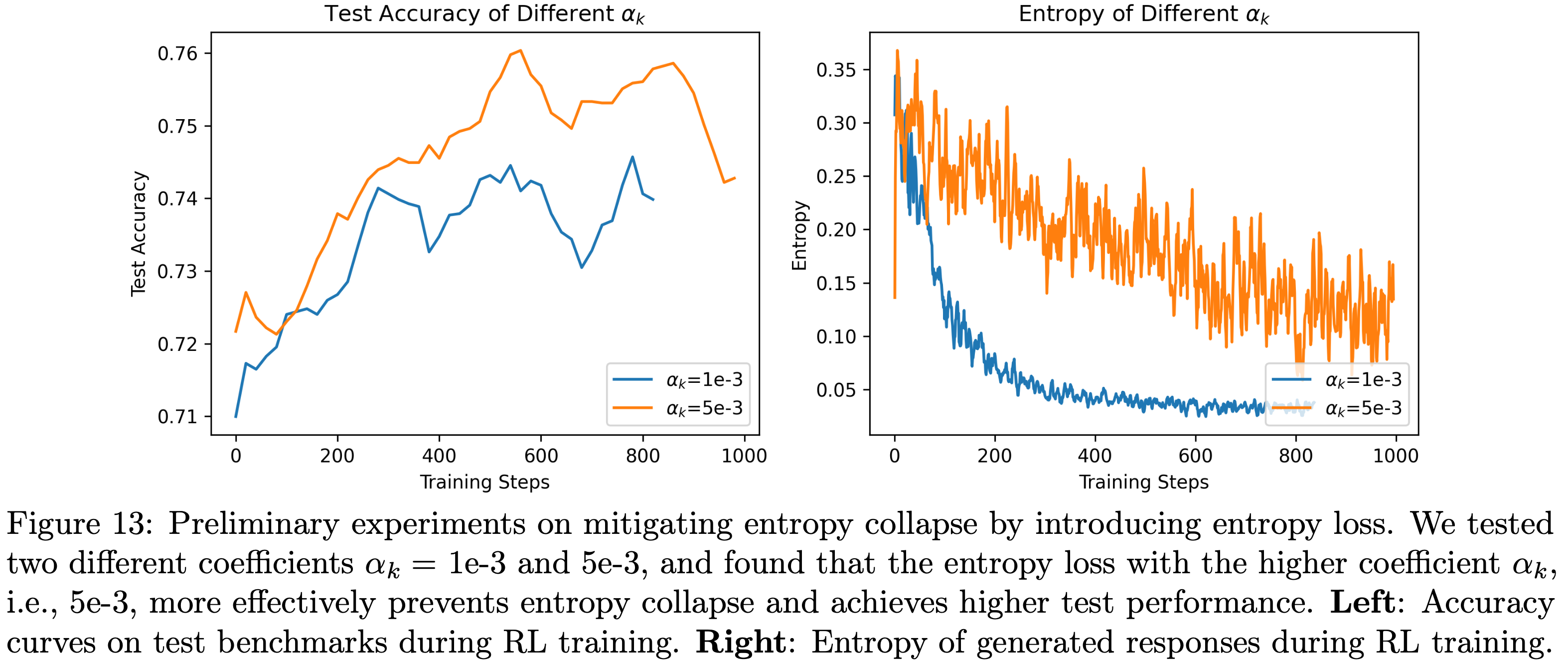
    • 伴随过早熵坍缩的强化学习训练通常会导致更差的测试性能
• 这些观察结果促使论文在训练流程中融入熵控制机制，并系统研究超参数及其他强化学习组件对熵动态变化的影响

The Impact of Rollout-Diversity-Related Hyperparameters（采样多样性相关的超参数）

• 本节研究了采样批次大小 \(D_R\) 、组大小 \(gs\) 和采样温度 \(\tau\) 对熵动态变化的影响
• 需要注意的是，在采样阶段增大采样批次大小 \(D_R\) 和组大小 \(gs\) 会增加采样预算，通常需要更多计算资源来加速训练
• 因此，关于 \(D_R\) 和 \(gs\) 的影响，论文将在第5节（聚焦训练时计算资源分配以提升测试性能）中详细讨论，本节仅呈现与策略熵相关的实验结果
• 具体而言，论文基于第4.1节所述的 baseline 实验，采用不同的采样批次大小（ \(D_R=16,32,64\) ）和组大小（ \(gs=4,8,16\) ）开展消融实验，实验结果如图14所示
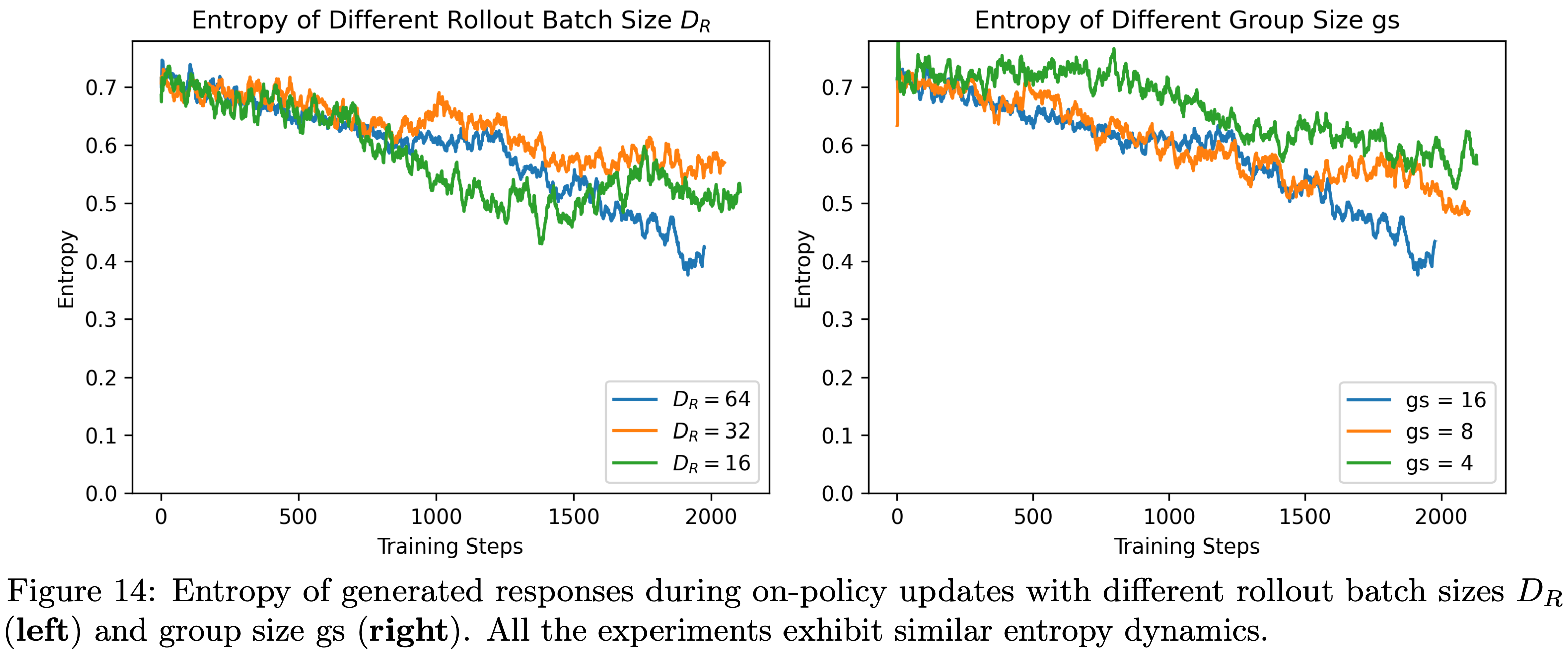
• 结果表明，在这些 On-Policy 配置下，熵的动态变化并无显著差异，且所有实验均未出现熵坍缩现象
• 关于采样温度 \(\tau\)
  • 论文发现选择合适且相对较高的温度时，模型在训练初期的测试准确率较低 ，但最终能实现更显著的性能提升 ，详见第3.2.4节

增加 \(N_\text{SGD}\) 导致的 Off-Policy 更新的影响（The Impact of Off-policy Update by Increasing \(N_\text{SGD}\) ）

• 需要注意的是，MAGIC 中的策略损失（公式3.1）采用 PPO 风格，这使得通过采样批次分解和重用来执行多个 SGD 步骤成为可能（如图15所示）
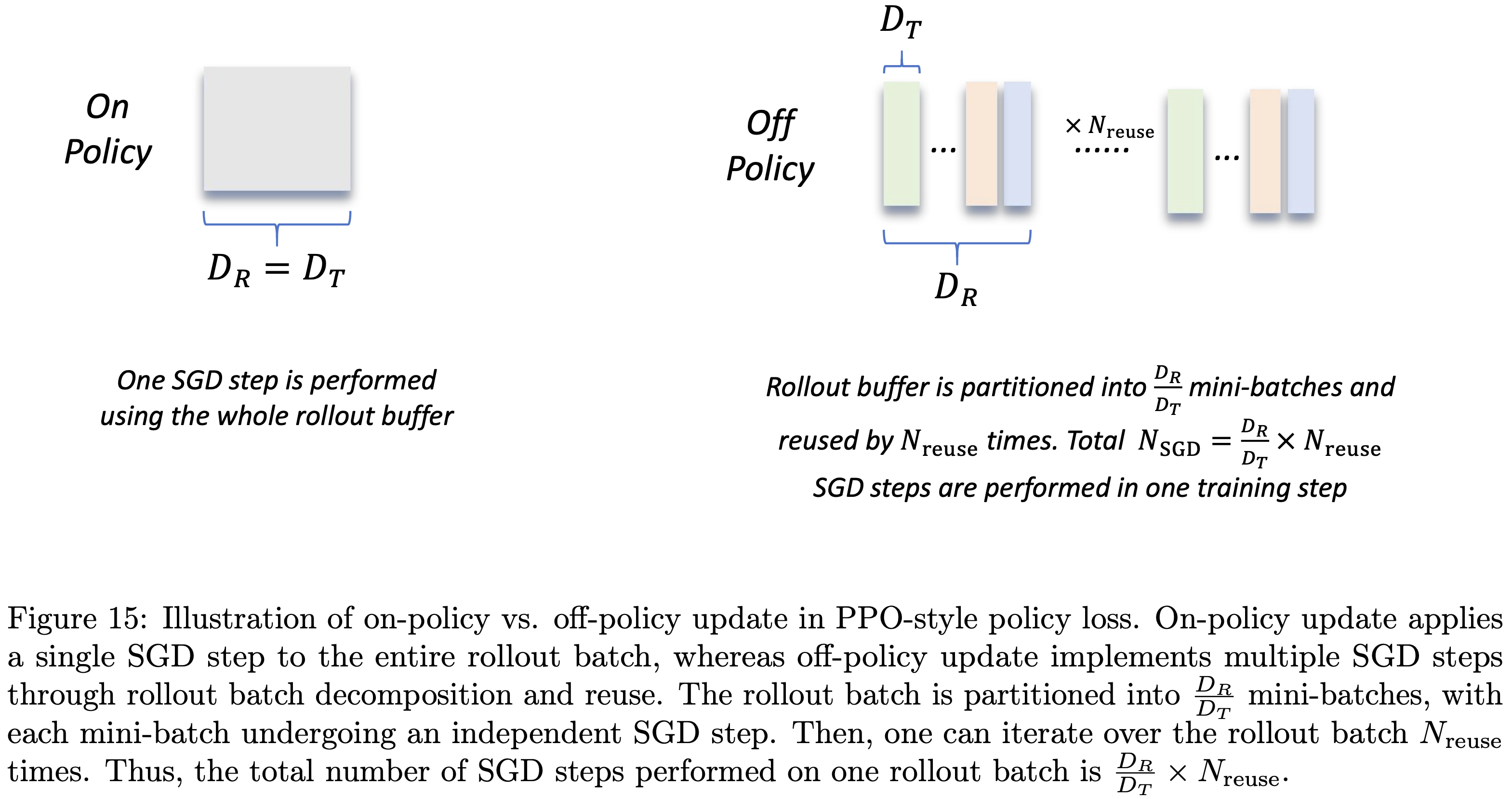
• 回顾第4.1节中 \(D_R\) 、 \(D_T\) 和 \(N_{reuse}\) 的定义，一个训练步骤中执行的 SGD 步数 \(N_\text{SGD}\) 满足：
  $$N_\text{SGD}=\frac{D_{R} }{D_{T} } \cdot N_{reuse } \quad \tag{4.1}$$
  • \(D_R\) ：采样批次大小（一个训练步骤中用于生成响应的提示词数量）
  • \(D_T\) ：mini-batch 大小（每个策略更新步骤中使用的响应对应的提示词数量）
  • \(N_{reuse}\) ：采样缓冲区的遍历次数
  • 当 \(D_R=D_T\) 且 \(N_{reuse}=1\) 时，由于 \(N_\text{SGD}=1\) ，策略更新为纯 On-Policy ；
  • 当 \(D_T< D_R\) 或 \(N_{reuse} \geq2\) 时， \(N_\text{SGD} \geq2\) ，此时 Off-Policy 数据会被引入策略更新
  • 本节将研究 \(N_\text{SGD}\) 如何影响熵的动态变化和测试性能提升

More SGD Steps, Faster Convergence with Worse Test Performance

• SGD 步数越多，收敛越快但测试性能越差
• 在固定 \(D_R\) 的情况下，论文通过减小 \(D_T\) 或增大 \(N_{reuse}\) ，针对不同 \(N_\text{SGD}\) 值开展了以下消融实验：
• 消融实验6：不同SGD步数 \(N_\text{SGD}\) 的影响
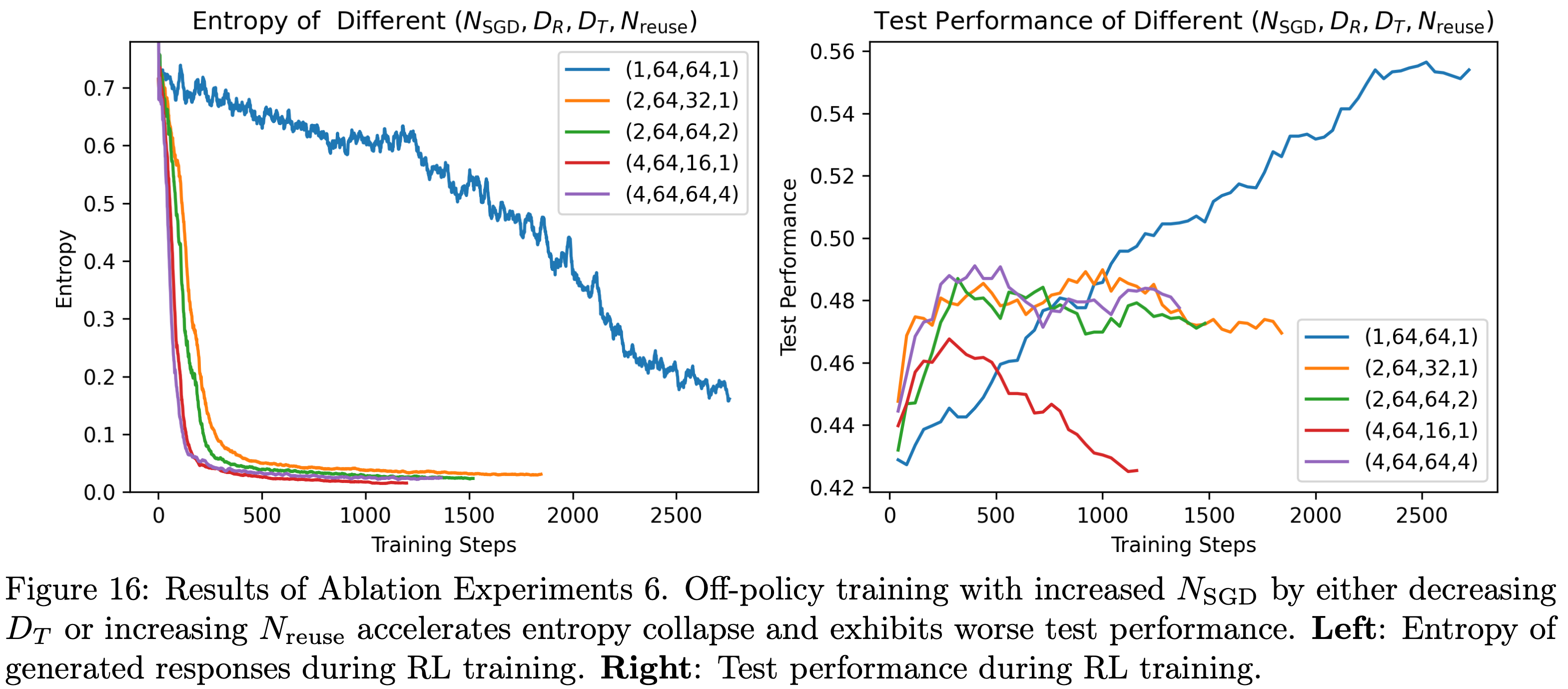
  • 考虑四元组 \((N_\text{SGD}, D_R, D_T, N_{reuse})\) ，论文从第4.1节所述的 baseline 实验（1,64,64,1）出发，通过调整 \(D_T\) 或 \(N_{reuse}\) 来增大 \(N_\text{SGD}\) ，实验设置如下：
    • 1）\(N_\text{SGD}=1\) ：baseline 实验，四元组为（1,64,64,1）
    • 2）\(N_\text{SGD}=2\) ：开展两组实验，四元组分别为（2,64,32,1）和（2,64,64,2）
    • 3）\(N_\text{SGD}=4\) ：开展两组实验，四元组分别为（4,64,16,1）和（4,64,64,4）
• 实验结果如图16所示，由图可知
  • \(N_\text{SGD} \in\{2,4\}\) 的实验中，策略收敛速度更快，熵在几个训练步骤内就衰减到极小值，导致模型进入低熵状态后，测试性能无法持续提升
  • 相反，采用（1,64,64,1）配置的 On-Policy 更新能显著缓解这一问题，熵的下降更为平缓，测试性能虽提升较慢但能持续改善
  • 最终，当训练步骤足够多时，（1,64,64,1）配置的 On-Policy 更新能实现更优的测试性能

Off-Policy Data Harms Test Performance

• Off-Policy 数据损害测试性能
• 论文进一步研究 Off-Policy 更新中哪些因素更可能导致测试性能下降，发现以下两个因素可能影响每个 SGD 步骤中的梯度方向：
  • （1） Mini-batch 大小 \(D_T\) ；
  • （2） Off-Policy 数据的使用
• 在 \(N_{reuse} \in\{2,4\}\) 的数据重用实验中，由于 \(D_T\) 保持不变且与 On-Policy 设置一致，因此测试性能下降可归因于通过采样批次重用来引入的 Off-Policy 数据
• 在涉及更多 Mini-batch 的实验（即 \(D_T \in\{16,32\}\) ）中，与 On-Policy 更新相比，性能下降可能源于两方面：
  • 一是 Mini-batch 规模减小导致梯度方差增大
  • 二是 Off-Policy 数据的存在
• 为进一步明确哪个因素影响更显著，论文开展了以下消融实验：
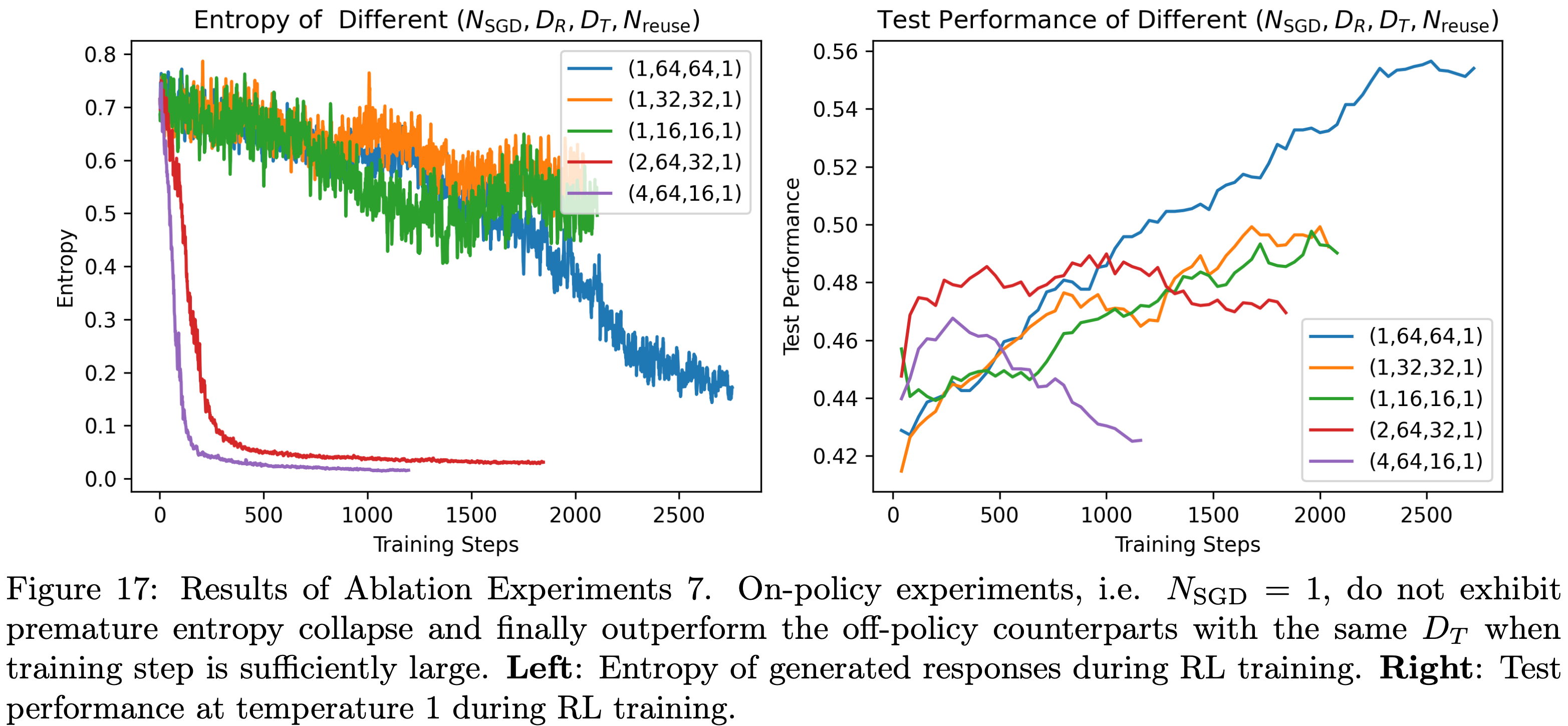
• 消融实验7：相同 SGD 数据量 \(D_T\) 下的 On-Policy 与 Off-Policy 对比
  • 考虑四元组 \((N_\text{SGD}, D_R, D_T, N_{reuse})\) ：
    • 1）Off-Policy 更新：选取消融实验6中的两组 Off-Policy 实验，四元组分别为（2,64,32,1）和（4,64,16,1），其 \(D_T\) 小于baseline实验（1,64,64,1）
    • 2）On-Policy 更新：基于第4.1节的baseline配置，开展两组 On-Policy 实验，四元组分别为（1,32,32,1）和（1,16,16,1），作为上述 Off-Policy 更新的对比组
• 实验结果如图17所示，结果表明：
  • 与 baseline 实验相比， \(D_T\) 更小的 On-Policy 更新仍能实现测试性能的稳步提升，且未出现过早熵坍缩；
  • 当训练步骤足够多时， On-Policy 更新的性能优于相同 \(D_T\) 下的 Off-Policy 更新
    • 问题：哪里有相同的 \(D_T\)? 只有相同的 \(D_R\) 吧
  • 基于这些观察，论文推测 Off-Policy 更新中测试性能下降的主要原因是每个 SGD 步骤中引入了 Off-Policy 数据
  • 注：图17还体现了一个重要的结论：Off-policy 会导致熵过早的坍缩（图17左边）

Off-Policy 更新中增大 \(D_R\) 能否防止过早熵坍缩？（Can a Large \(D_R\) in Off-Policy Updates Prevent Premature Entropy Collapse?）

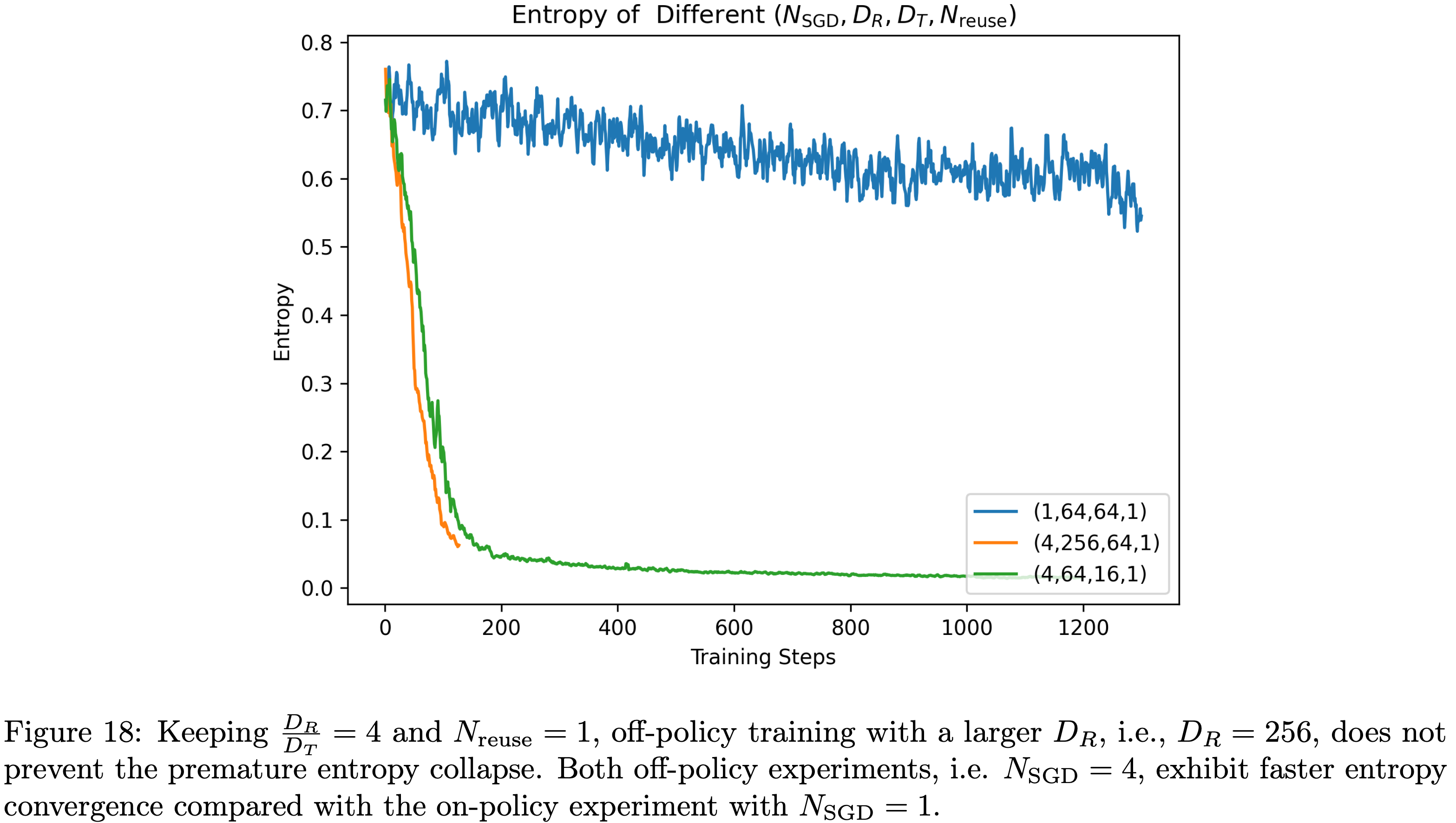
• 以消融实验6中四元组为（4,64,16,1）的 Off-Policy 实验为例，论文尝试将采样批次大小 \(D_R\) 从 64 增大到 256，同时保持 \(N_\text{SGD}=4\) 不变（即配置变为（4,256,64,1）），期望通过引入更多样化的样本避免模型收敛到单一轨迹
• 然而，图18的结果显示，即使增大 \(D_R\) ，过早熵坍缩不仅仍会发生，甚至可能更快

Preventing Premature Entropy Collapse：防止过早熵坍缩

• 如前所述，过早熵坍缩通常与测试性能下降相关，因此合理推测：适当的熵控制可提升测试性能
• 前文已表明，增大每个训练步骤中执行的 SGD 步数 \(N_\text{SGD}\) 和引入 Off-Policy 数据会加速熵收敛，但在实际场景中（如异步训练框架）， Off-Policy 数据的使用往往不可避免
• 因此，研究 Off-Policy 设置下的熵控制机制也具有重要意义
• 论文首先考察熵正则化方法（这是一种直接通过添加熵损失项来防止熵坍缩的简单方法）
• 第4.2节的初步实验表明，选择合适的系数进行熵正则化可缓解熵坍缩并提升测试性能
  • 但后续研究发现，熵正则化的效果对系数选择和训练数据特征高度敏感，难以提前确定最优系数，这促使论文考虑对熵损失系数进行动态调整
  • 此外，论文还将（2025）提出的 clip-higher 技巧作为另一种熵控制方法
• 下文将详细阐述论文的研究发现

熵损失对系数 \(\alpha_k\) 高度敏感（Entropy Loss Is Sensitive to the Coefficient \(\alpha_k\)）

• 为验证熵损失对 \(\alpha_k\) 选择的敏感性，论文开展了以下消融研究：
• 消融实验8：不同系数 \(\alpha_k\) 的熵损失
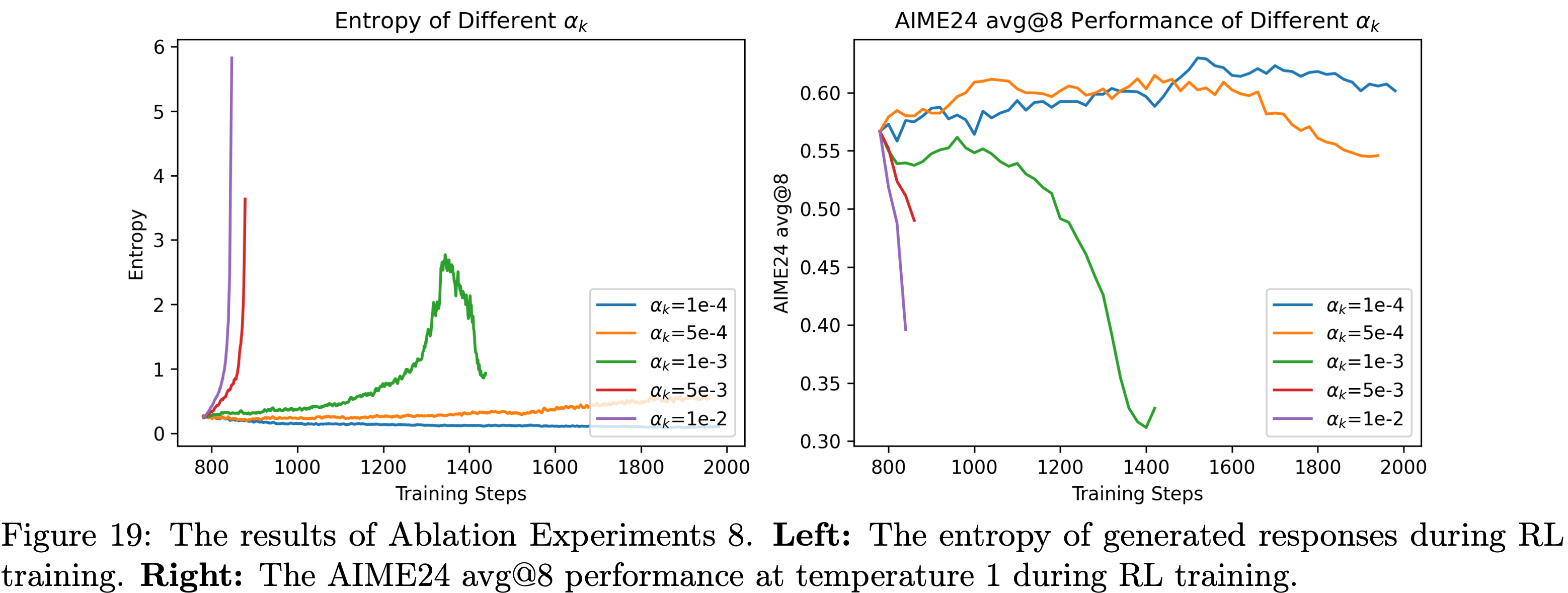
  • 基于 Skywork-OR1-Math-7B-stage1（非第4.1节的 baseline 实验），论文对多种固定系数 \(\alpha_k\) 进行了消融实验，选取的 \(\alpha_k\) 值为 1e-4、5e-4、1e-3、5e-3、1e-2，其他超参数如表6所示，实验结果如图19所示
• 从图19的结果可得出以下结论：
  • 当 \(\alpha_k=5e-4\) 、1e-3、5e-3、1e-2时，熵最终会急剧上升，导致模型崩溃，且 \(\alpha_k\) 越大，熵上升速度越快
  • 当 \(\alpha_k=1e-4\) 时，熵虽未持续上升，但仍会坍缩，持续趋近于0
• 表6：基于 Skywork-OR1-Math-7B-stage1 的消融实验8的共享超参数

Entropy Loss Is Sensitive to Training Data： 熵损失对训练数据高度敏感

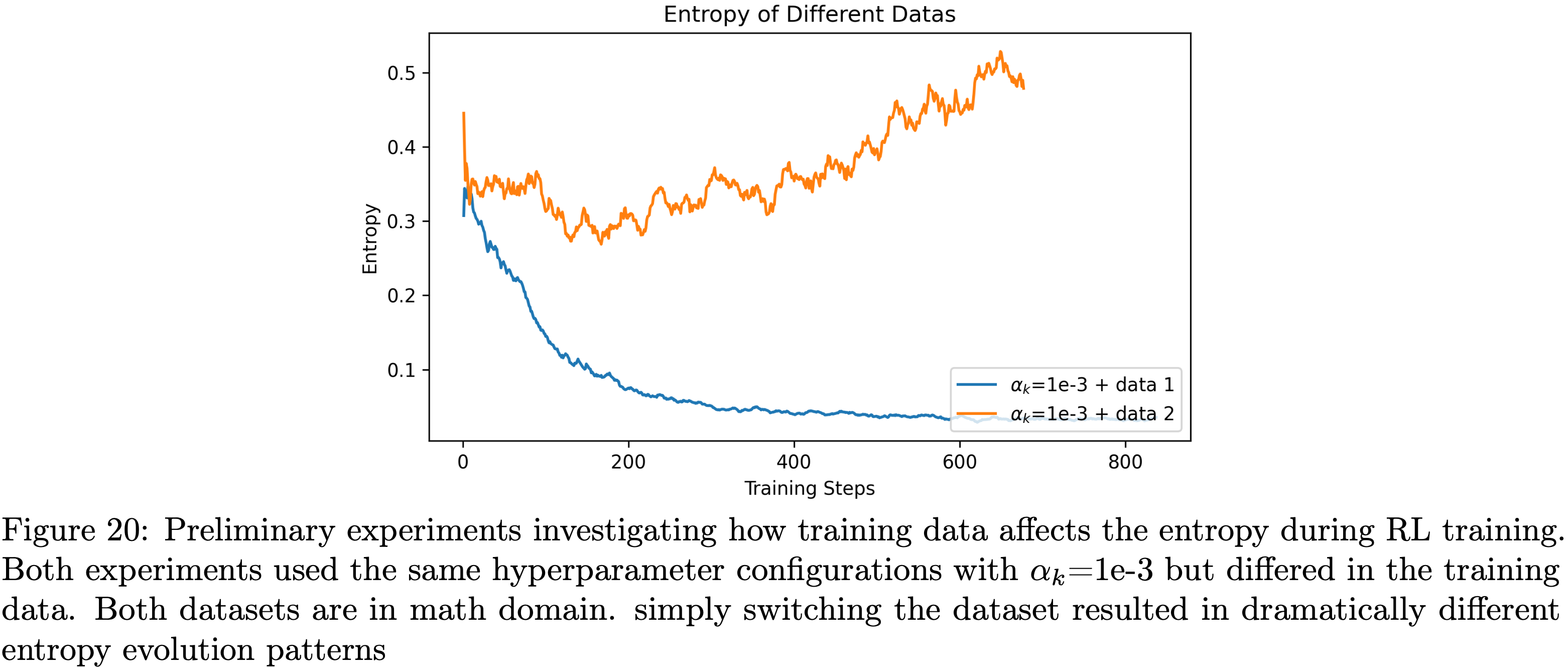
• 通过两组初步实验，论文观察到熵损失对训练数据的变化也高度敏感
• 论文在完全相同的配置下开展了两组实验，均使用 1e-3 的熵损失系数，唯一的区别是所用的训练数据集（两个数据集均属于数学领域）
• 图20的结果显示，两组实验的熵动态变化存在显著差异：
  • 使用原始数据集时，熵在整个训练过程中稳步下降；
  • 使用新数据集时，熵则呈现持续上升趋势
• 这一发现凸显了熵损失系数调优的数据集依赖性

Adjusting the Coefficient of Entropy Loss Adaptively

• 基于熵损失敏感性的研究结果，论文提出了自适应熵控制方法（详见第3.2.5节），该方法可在训练过程中动态调整熵损失系数
• 如图10所示，在整个强化学习训练过程中，Skywork-OR1-Math-7B 的熵始终以目标熵为下界
• 为进一步验证自适应熵控制的有效性，论文开展了以下消融实验：
• 消融实验9：自适应熵控制的有效性（Ablation Experiments 9: Effectiveness of Adaptive Entropy Control）
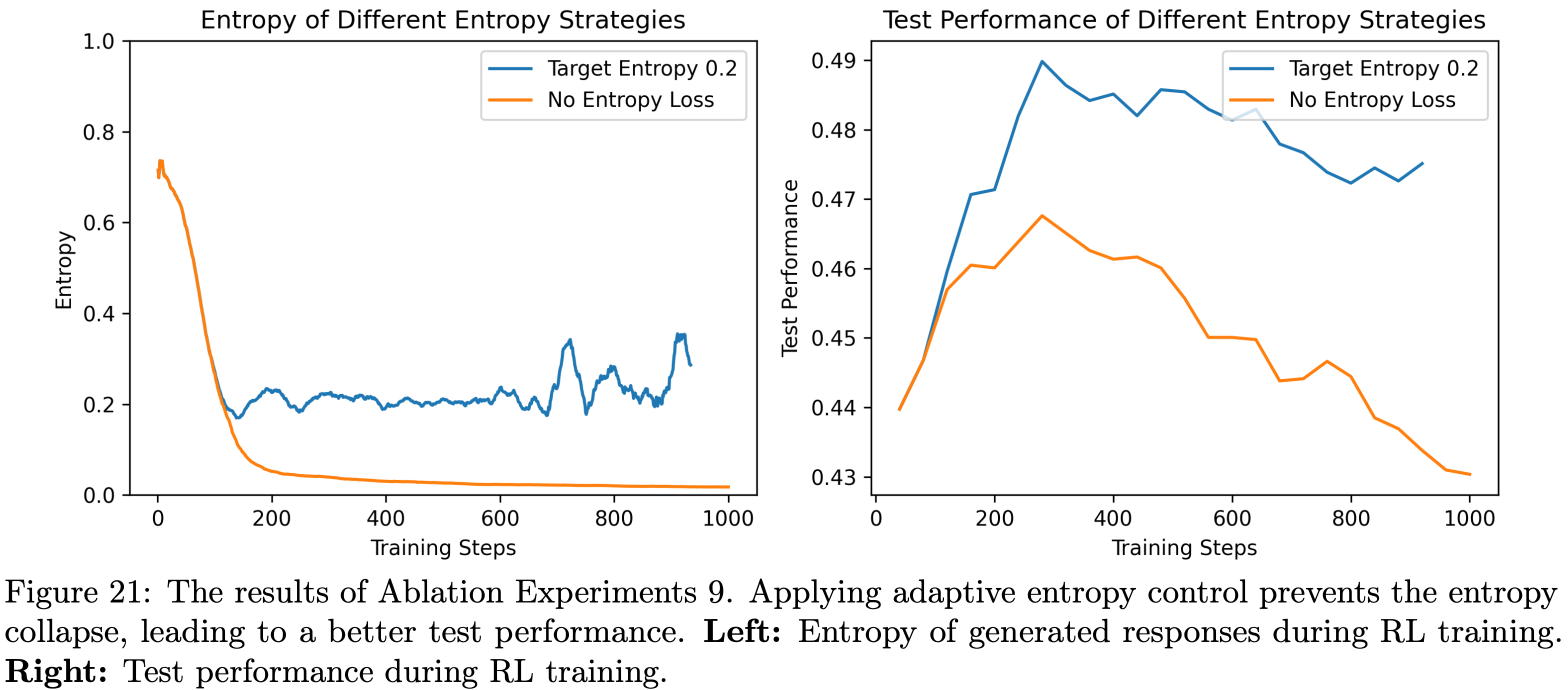
  • 以消融实验6中四元组为（4,64,16,1）的 Off-Policy 实验为基础（该实验存在快速熵坍缩且测试性能较差，且未使用熵损失），论文在其配置基础上启用自适应熵控制（目标熵设为0.2），实验结果如图21所示
• 如前文分析，增大每个训练步骤中执行的 SGD 步数 \(N_\text{SGD}\) 会加速策略收敛并导致测试性能下降
• 从图21可以看出
  • 应用自适应熵控制成功防止了熵坍缩 ，进而实现了更高的测试性能
  • 但需注意的是，尽管系数会自适应调整，但当 \(N_\text{SGD}\) 较大时，熵仍会出现不稳定现象
  • 论文推测，这是因为熵损失是基于整个词汇表计算的，可能会增加许多非预期 tokens 的概率
  • 因此，不建议在 \(N_\text{SGD}\) 较大的场景中使用自适应熵控制
  • 不过，论文发现当 \(N_\text{SGD}=1\) 或 \(N_\text{SGD}=2\) 时，在自适应熵控制下，熵的动态变化仍保持在可接受的稳定范围内
  • 基于这些发现，论文在 Skywork-OR1 系列模型的训练中采用了自适应熵控制方法

The Impact of the Clip-Higher Trick

• 论文测试了PPO风格策略损失中一种常用的 clip-higher 技巧（2025），该技巧用于在 \(N_\text{SGD}>1\) 时防止熵坍缩，并开展了以下消融实验：
• 消融实验10：不同高裁剪比例（Higher-clip Ratios）的影响（Ablation Experiments 10: The Impact of Different Higher-clip Ratios）
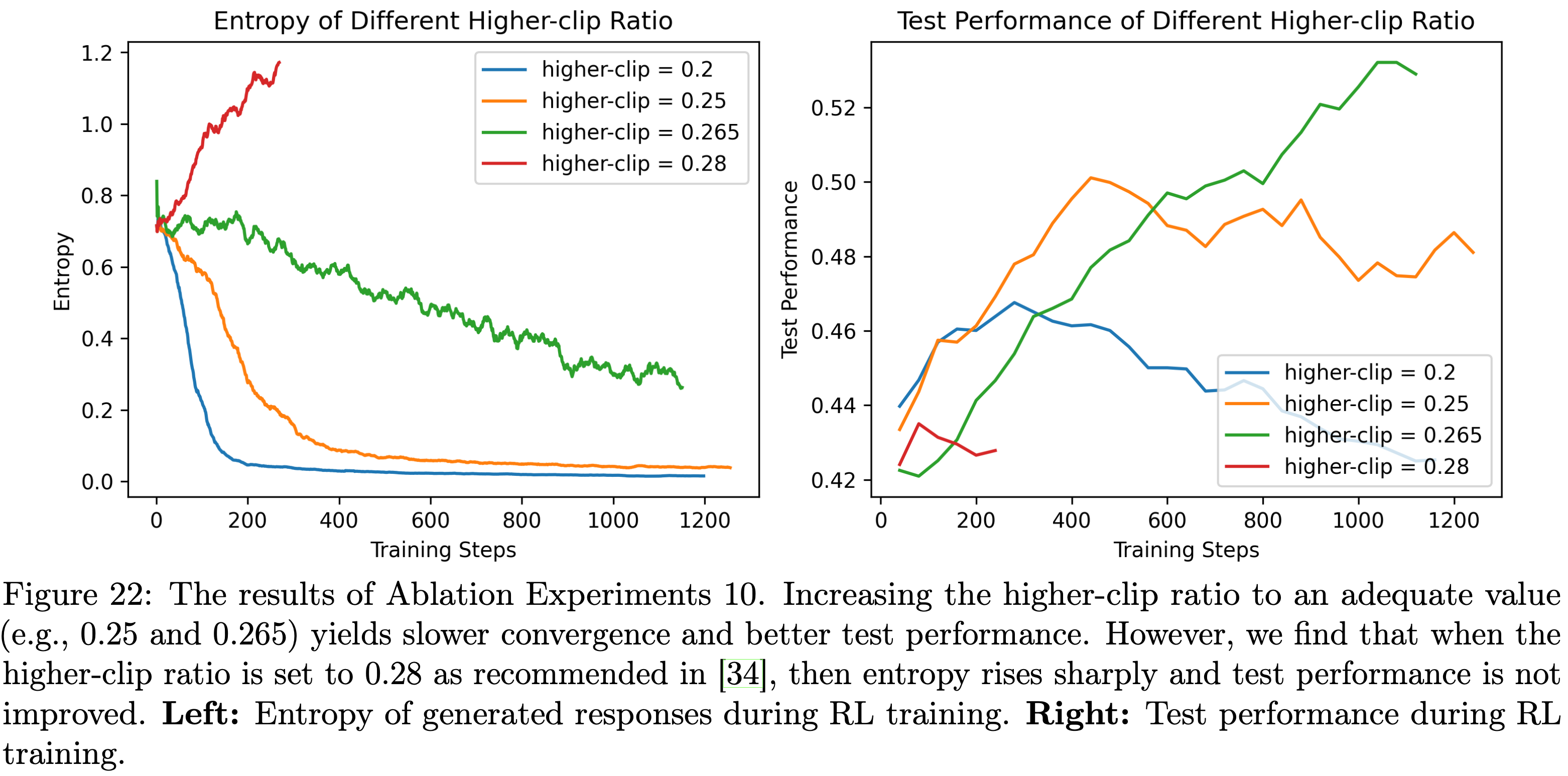
  • 以消融实验6中四元组为（4,64,16,1）的 Off-Policy 实验为基础（该实验存在快速熵坍缩且测试性能较差，裁剪比例 \(\epsilon=0.2\) ），论文将高裁剪比例从 0.20 提高到 0.25、0.265 和 0.28，同时保持低裁剪比例固定为 0.2，实验结果如图22所示
• 图22的结果表明
  • 选择合适的高裁剪比例（如0.25 或 0.265）可防止过早熵坍缩，并实现更优的测试性能
  • 但需注意的是，当高裁剪比例设置为 DAPO（2025）中建议的 0.28 时，熵会急剧上升，导致测试性能变差
  • 这表明最优高裁剪比例具有任务依赖性（task-dependent.）
    • 问题：这跟任务依赖有什么关系？
    • 回答：别人没问题，我们有问题，两边任务不同，所以跟任务相关

---

Empirical Studies on Training Resource Allocation

• 在 RL 训练过程中，论文的目标是选择能让训练兼具效率与效果的超参数。这一目标引出了两个实际问题：
  • 在计算资源固定的情况下，如何提升训练效率？
  • 若有额外计算资源 ，应如何分配以实现更优的测试性能或更高的训练效率？
• 本节将结合大量消融实验结果，在长 CoT 场景下解答上述问题
• 在线强化学习（Online RL）算法的训练过程通常可分为两个不同阶段：
  • 数据生成（rollout）
  • 策略更新（包含前向传播与反向传播）
• 同步训练框架下的总时间消耗为：
  $$t_{total}=t_{R}+t_{T}+t_{O}$$
  • \(t_R\) 表示数据生成 耗费的时间
  • \(t_T\) 表示策略更新 耗费的时间
  • \(t_O\) 表示其他操作（如奖励计算、经验生成）所耗费的时间
• 在上下文长度固定的情况下，数据生成时间 \(t_R\) 主要受数据生成批次大小（rollout batch size） \(D_R\) 和分组大小（group size, \(gs\) ）影响
• 如4.4节所述
  • 策略更新时间 \(t_T\) 取决于随机梯度下降（Stochastic Gradient Descent, SGD）步数 \(N_\text{SGD}\)
  • 其中 \(N_\text{SGD}\) 由 Mini-batch数量 \(\frac{D_R}{D_T}\) 和数据复用系数 \(N_{reuse}\) 决定
• 在以下小节中，论文将探究这些因素对训练效率和最终性能的影响

Improving Training Efficiency with Fixed Computational Resources

• 本节旨在解答第一个问题：在计算资源固定的情况下，如何提升训练效率？

数据生成时间 \(t_R\) 主导总训练时间 \(t_{total}\) （Rollout Time \(t_R\) Dominates the Total Training Time \(t_{total}\)）

• 对于长思维链模型（如 DeepSeek-R1-Distill 模型系列），一个基本发现是：总训练时间主要由数据生成时间决定
• 表7展示了 Skywork-OR1-32B 模型在 1000个 训练步骤中 \(t_{total}\) 、 \(t_R\)（生成） 、 \(t_T\)（训练） 和 \(t_O\)（其他） 的具体数值
  • 显然， \(t_R\) 在 \(t_{total}\) 中占比极高
• 由于长思维链训练中 \(t_{total}\) 的主要瓶颈是 \(t_R\) ，因此合理增加每个训练步骤的随机梯度下降步数（即 \(N_\text{SGD}\) ），对 \(t_{total}\) 的影响极小，同时还能提升训练效率
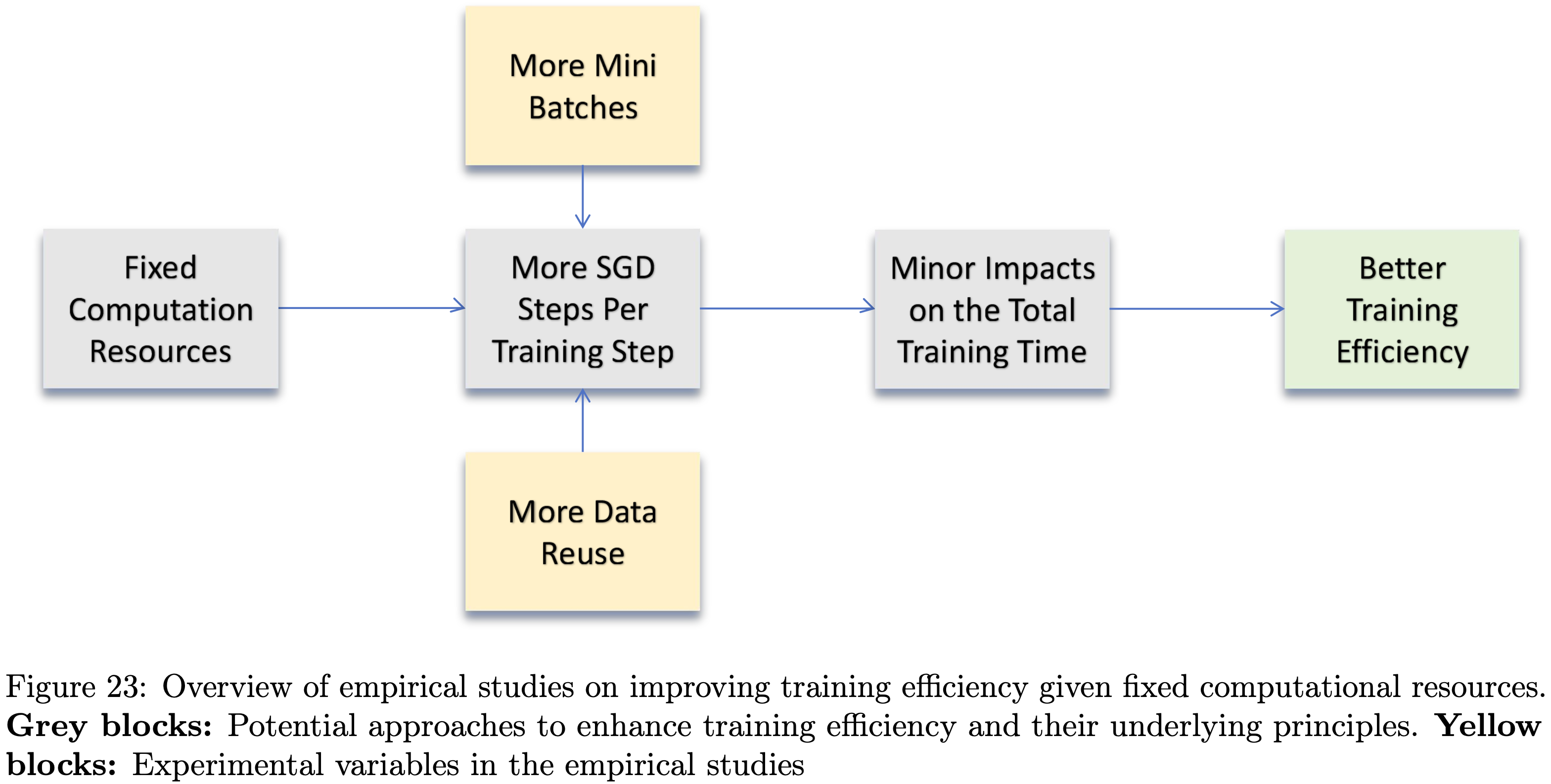
• 基于此，论文接下来将探究 Mini-batch 数量（ \(\frac{D_R}{D_T}\) ）和数据复用次数（ \(N_{reuse}\) ）对总训练时间 \(t_{total}\) 和测试性能的影响。本研究的整体思路如图23所示
• 图23：固定计算资源下提升训练效率的实证研究概述。灰色块：提升训练效率的潜在方法及其原理；黄色块：实证研究中的实验变量

随机梯度下降步数越多，训练效率越高但性能越差

• 在4.4节的消融实验6中，论文已探究过增加 \(N_\text{SGD}\) 对熵动态的影响
• 考虑配置元组 \((N_\text{SGD}, D_R, D_T, N_{reuse})\) ，表8报告了配置为（1, 64, 64, 1）、（2, 64, 32, 1）和（4, 64, 16, 1）的实验的详细时间使用情况
• 显然，增加 \(N_\text{SGD}\) 会导致 \(t_T\) 增加，但在 \(D_R\) 固定的情况下，其对总训练时间 \(t_{total}\) 的影响仍较小
• 因此， \(N_\text{SGD}\in\{2,4\}\) 的配置能在相近训练时间内执行多个随机梯度下降步骤，从而提升训练效率
• 尽管如此，4.4节的实验结果表明：通过数据生成批次分解或数据复用加速训练，会导致熵更快坍缩且测试性能更差
• 因此，除非有合适的机制（尤其是针对离策略更新导致的熵坍缩）来缓解熵坍缩问题，否则不建议仅为提升训练效率而增加 \(N_\text{SGD}\) ，因为这可能导致泛化性能下降
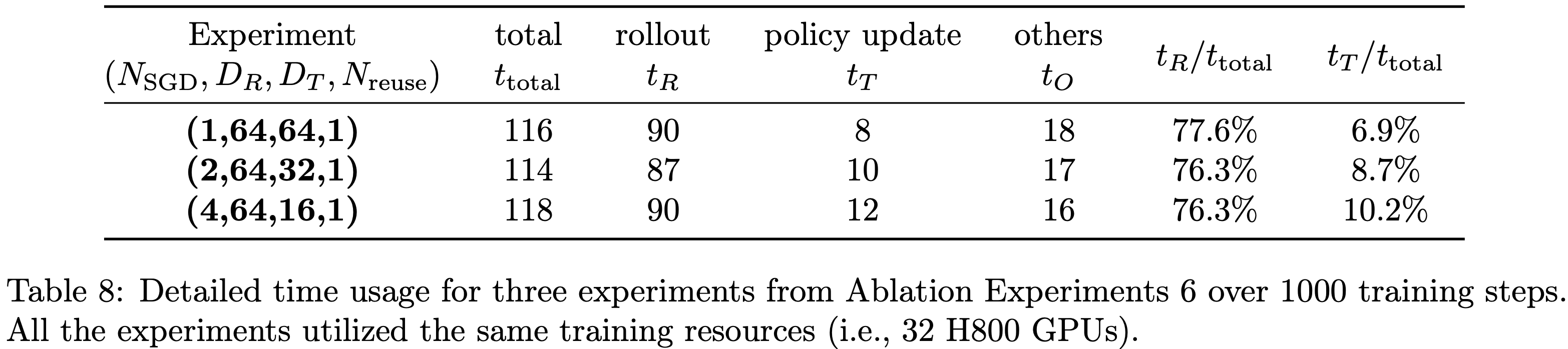
  • 表8：消融实验6中三个实验在 1000 个训练步骤的详细时间使用情况。所有实验均使用相同的训练资源（即 32 块 H800 GPU）

Improving Test Performance with More Computational Resources

• 本节旨在解答第二个问题：若有额外计算资源，应如何分配训练资源以实现更优的测试性能或更高的训练效率？
• 在训练效率方面，可考虑两种方法
  • 一方面，增加随机梯度下降步数（前文已讨论）看似可行，但实验结果并不支持该方法的有效性（见5.1节）
  • 另一方面，在数据生成预算（即需生成的样本数量）固定的情况下，人们可能期望随着训练资源增加，数据生成时间 \(t_R\) 会显著减少
    • 但实际上，这一期望并未完全实现
• 表9展示了不同训练资源下生成 1024 个样本的数据生成时间 \(t_R\) ：随着训练资源增加， \(t_R\) 的减少幅度逐渐减小
  • 这是因为 \(t_R\) 主要由批次大小和生成最长响应所需的时间决定
  • 一旦资源足够，进一步扩展资源对减少由最长样本生成时间主导的处理时间影响不大
  • 理解：边际收益递减
• 因此，当有额外训练资源时，更有效的策略是合理增加数据生成预算（rollout budget） ，使数据生成时间 \(t_R\) 大致保持不变或仅小幅增加
• 通过使用更大的数据生成缓冲区（rollout buffer），可获得更准确的梯度估计，这可能提升训练效率并改善测试性能
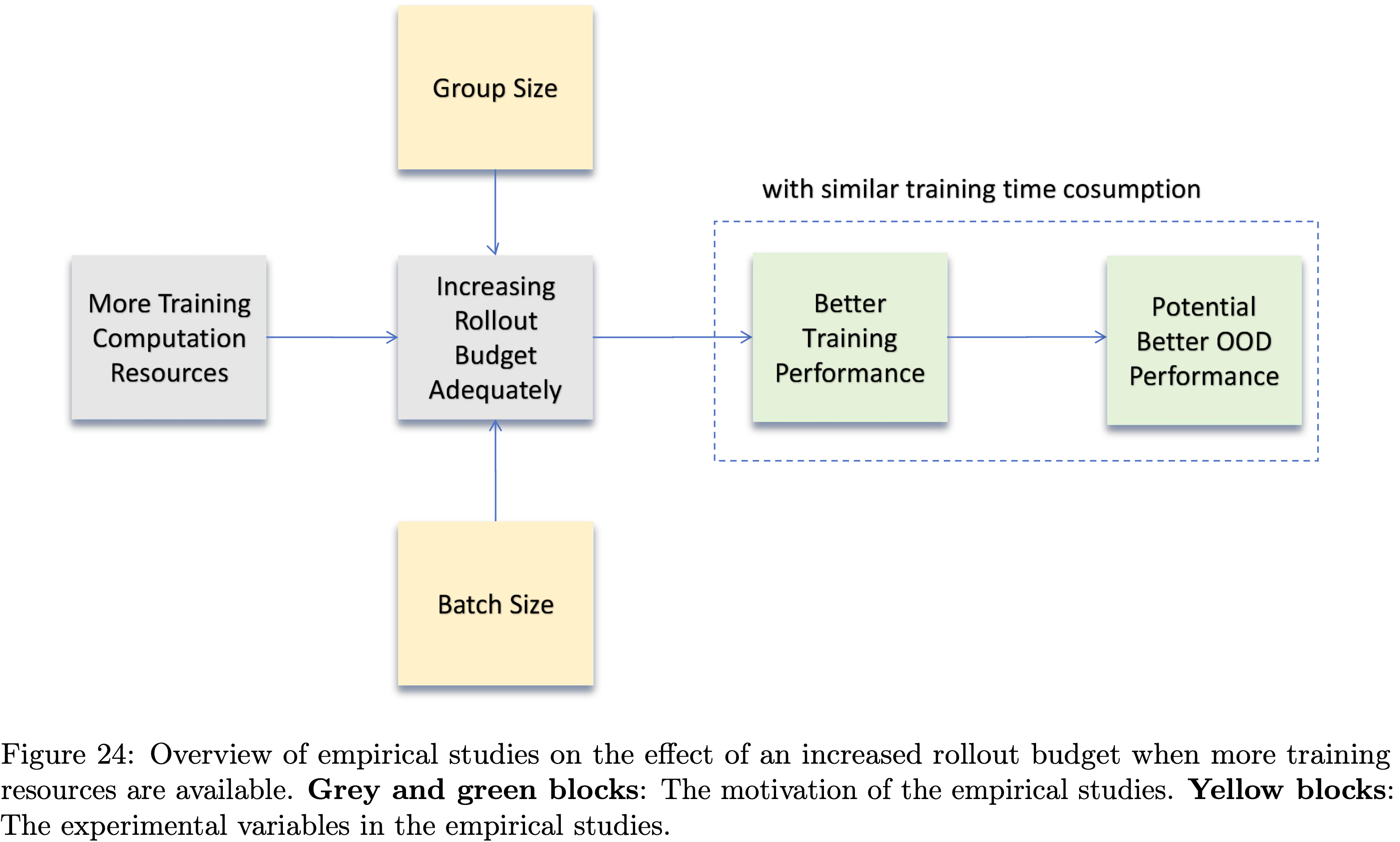
• 在以下内容中，论文将重点探究由数据生成批次大小和分组大小决定的数据生成预算对强化学习性能的影响。这些研究的整体思路如图24所示
• 表9：一个训练步骤中生成1024个响应的数据生成时间 \(t_R\) （单位：秒）。数据显示，随着计算资源增加， \(t_R\) 的增量减少幅度逐渐减小
• 图24：额外训练资源下增加数据生成预算的实证研究概述。灰色和绿色块：实证研究的动机；黄色块：实证研究中的实验变量

Larger Batch Size, Better Test Performance

• 为探究数据生成批次大小 \(D_R\) 对训练动态的影响，论文进行了以下消融实验
  • \(D_R\) ：采样批次大小（一个训练步骤中用于生成响应的提示词数量）
  • \(D_T\) ：mini-batch 大小（每个策略更新步骤中使用的响应对应的提示词数量）
  • \(N_{reuse}\) ：采样缓冲区的遍历次数
  • \(gs\) ：组大小（为每个提示词生成的响应数量）
• 消融实验11：数据生成批次大小 \(D_R\) 的影响（The Impact of Rollout Batch Size \(D_R\) ）
  • 考虑元组 \((N_\text{SGD}, D_R, D_T, N_{reuse})\)
  • 论文选取4.1节中配置为（1, 64, 64, 1）的基准实验，以及消融实验7中两个配置分别为（1, 32, 32, 1）和（1, 16, 16, 1）的在策略实验
  • 这三个实验分别使用 64 块、32 块和 16 块 H800 GPU。实验结果如图25所示
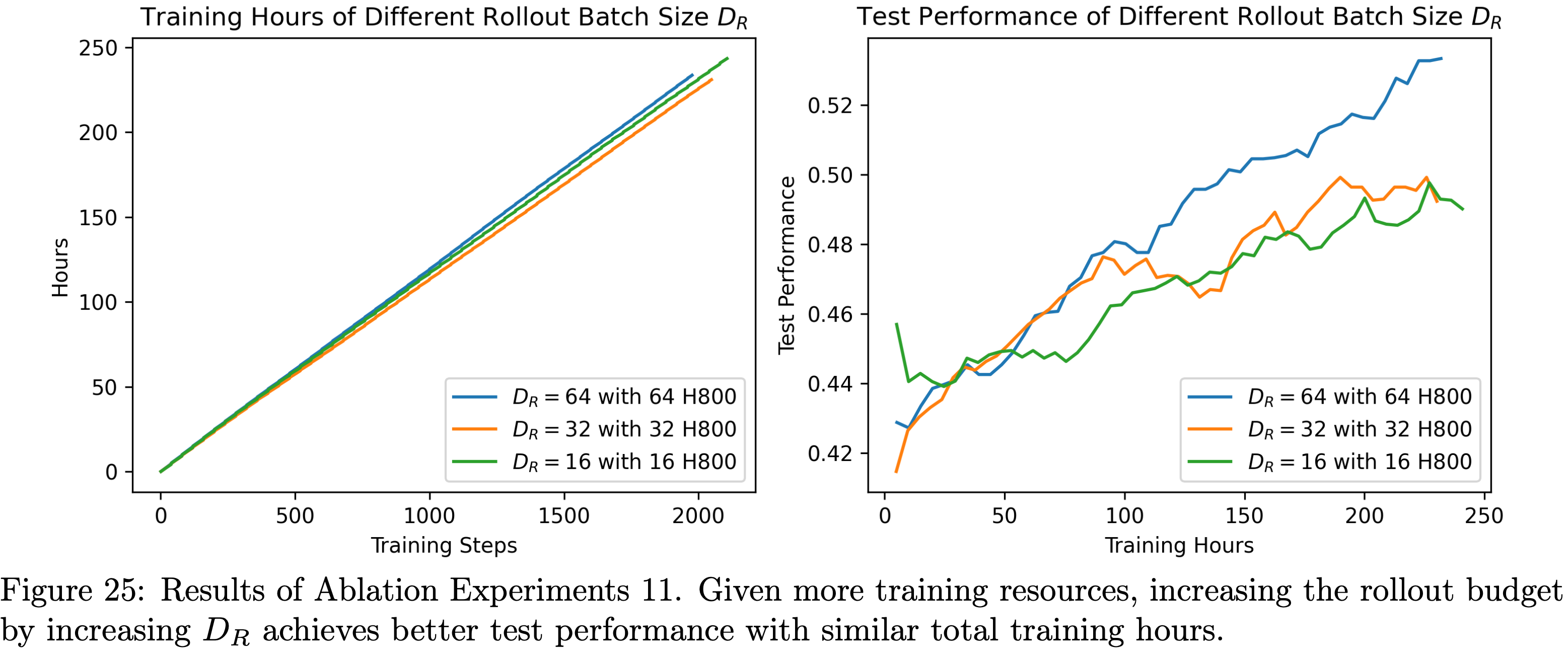
• 图25的结果表明，在训练资源允许的情况下，增加数据生成批次大小 \(D_R\) ，可在训练时间相近的情况下实现更优的测试性能
• 图25：消融实验11的结果。在有更多训练资源的情况下，通过增加 \(D_R\) 来提高数据生成预算，能在总训练时长相近的情况下实现更优的测试性能。左图：不同数据生成批次大小 \(D_R\) 的训练时长；右图：不同数据生成批次大小 \(D_R\) 的测试性能

分组大小越大，测试性能越优

• 为探究分组大小对训练动态的影响，论文进行了以下消融实验
• 消融实验12：分组大小（ \(gs\) ）的影响（The Impact of Group Size (\(gs\))）
  • 选取4.1节中分组大小为 16 的基准实验，另外再进行两个分组大小分别为 8 和 4 的在策略实验
  • 这三个实验分别使用 64 块、32 块和 16 块 H800 GPU。实验结果如图26所示
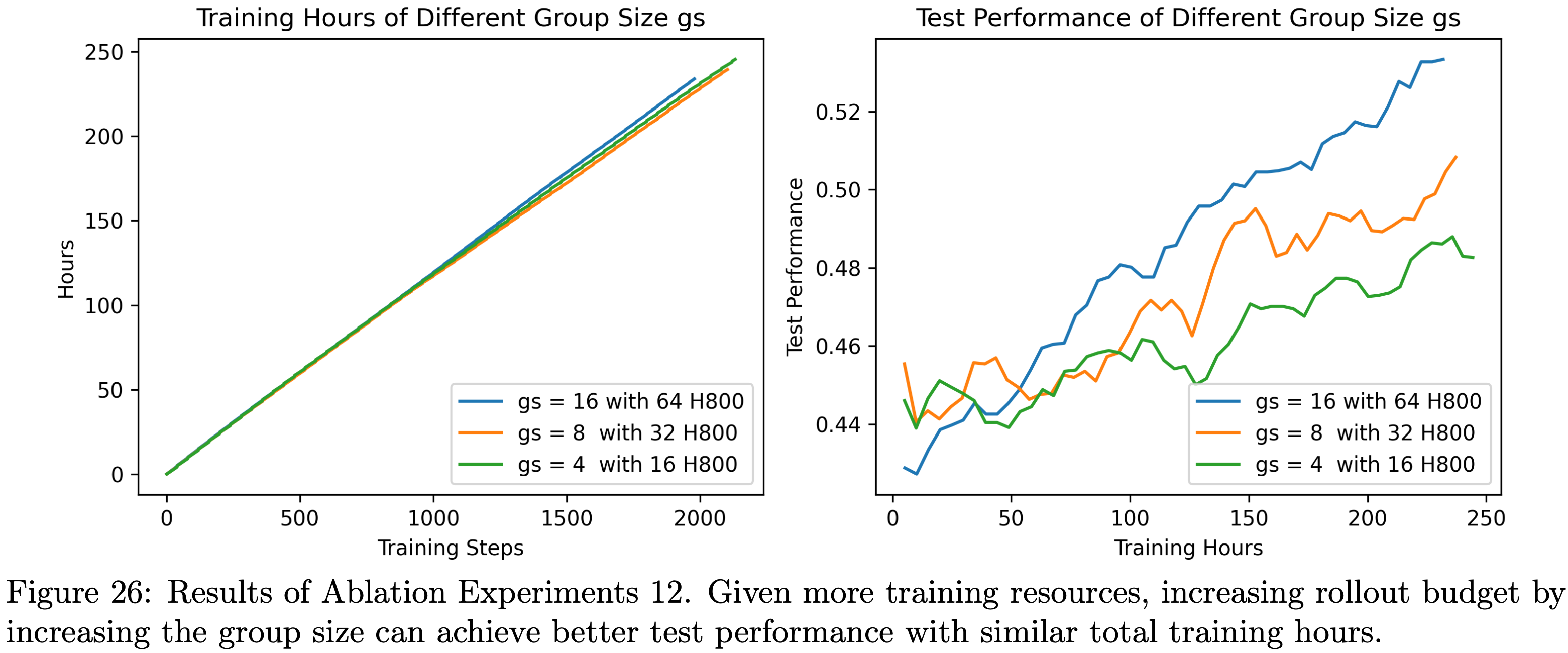
• 从图26中可观察到，在有更多训练资源的情况下，通过增加分组大小来提高数据生成预算，能在总训练时长相近的情况下实现更优的测试性能
• 图26：消融实验12的结果。在有更多训练资源的情况下，通过增加分组大小来提高数据生成预算，能在总训练时长相近的情况下实现更优的测试性能。左图：不同分组大小 \(gs\) 的训练时长；右图：不同分组大小 \(gs\) 的测试性能

---

Dataset Preparation

• 本节将介绍论文强化学习训练数据的处理流程

Data Source Selection and Preprocessing

• 在数学领域，论文主要关注 NuminaMath-1.5 数据集（2024），该数据集包含 89.6 万个数学问题，涵盖常用数据源和高等数学主题
  • 该数据集规模足够大，但在使用前仍需仔细检查其质量
• 在代码领域 ，论文发现可用的数据源选择较为有限 ，且现有数据集的整体难度相对于当前模型的能力而言普遍较低
  • 在试点研究中，论文尝试了多个常用数据集（包括 CODE-RL（2022）、TACO（2023）和 Eurus-RL 数据集集合（2025））的原始混合数据，但未获得理想结果

Selection Criteria

• 为选择和整理高质量的强化学习数据，针对两个数据领域，论文均遵循以下通用标准：
  • 1）可验证性（Verifiable）：排除无法验证的问题，如基于证明的问题和缺少测试用例的代码问题
  • 2）正确性（Correct）：过滤掉答案无效或错误的数学问题，以及缺少完整测试用例的代码问题
  • 3）挑战性（Challenging）：预先过滤掉基础模型的N次生成结果全对或全错的问题
• 根据上述标准，论文从 NuminaMath-1.5 和其他来源中筛选出具有挑战性的问题，以提高数据混合集中问题的难度和多样性：
  • 1）NuminaMath-1.5子集：AMC（美国数学竞赛）、AIME（美国数学邀请赛）、奥林匹克竞赛（olympiads）、奥林匹克竞赛参考题（olympiads ref）、AoPS 论坛（aops forum）、中国竞赛（cn contest）、不等式（inequalities）和数论（number theory）；
  • 2）DeepScaleR 数据集（2025）；
  • 3）STILL3-Preview-RL-Data 数据集（2025）；
  • 4）Omni-MATH 数据集（2024）；
  • 5）2024 年之前的 AIME 题目
• 在代码数据混合集方面，论文主要考虑以下两个来源的问题，它们提供了足够具有挑战性的编程题目：
  • 1）LeetCode 题目（2025）；
  • 2）TACO 数据集（2023）

Preprocessing Pipeline

• 对于数学和代码问题，论文首先进行数据集中的去重处理，以消除冗余。对于所有收集到的数学问题：
  • 论文使用 Math-Verify 工具（2025）从提供的文本解答中重新提取答案，仅保留提取答案与数据集中对应答案一致的问题
  • 移除所有问题描述中包含外部链接或潜在图表的样本
  • 进行跨数据集去重，以消除来自相似来源的潜在重复问题 ，并参照 DeepScaleR 的去重方案，对 AIME24 和 AIME25 的题目进行去污染处理（decontaminate）
  • 经过上述流程，最终得到约 10.5万 个数学问题
• 对于代码问题，论文采用更严格的过滤流程：
  • 丢弃原始单元测试用例为空、不完整或损坏的样本
  • 使用提供的原始解答对所有测试用例进行程序化验证
    • 只有当解答能完美通过所有对应测试用例时，该样本才被标记为有效
  • 基于收集到的代码问题的嵌入（embedding）相似度进行广泛去重 ，因为许多问题本质相同，仅在指令上有细微差异
  • 最终，代码问题数据集共包含 1.37万 个题目（其中 2700 个来自 LeetCode，1.1万 个来自 TACO）

Model-Aware Difficulty Estimation

• 在 GRPO 算法中，若一个分组内所有采样响应全对或全错，会出现零优势（zero-advantage）问题
• 因此，论文需要针对待训练模型，对每个问题进行初始的离线难度估计
  • 对于每个问题：
    • 数学问题采用 1.0 的温度（temperature）和 32K 的最大 token 长度进行 \(N=16\) 次生成（rollout）
    • 代码问题则进行 \(N=8\) 次生成；
  • 将正确解答的百分比作为该问题相对于特定模型的难度指标
  • 在验证采样解答的正确性后，论文排除正确率为 0/N（全错）或 N/N（全对）的问题
  • 表中报告了 7B 和 32B 模型丢弃和保留的数学/代码问题的百分比统计：

Quality Assessment via Human and LLM-as-a-Judge

• 在数据处理阶段，论文发现数学部分的许多问题存在不完整或格式不良的情况
• 因此，论文额外进行了一轮严格的 “human-LLM-combined” 联合检查，以确保数据质量
• 论文从剩余问题池中随机抽取数百个问题，要求人工评估者判断每个问题是否符合以下标准：
  • 1）表述清晰（Clear Wording）：问题描述是否易于理解？
  • 2）信息完整（Complete Information）：问题是否提供了所有必要信息？
  • 3）格式规范（Good Formatting）：数字、符号和公式是否清晰且格式规范？
  • 4）无干扰信息（No Distractions）：问题是否不含无关信息？
• 以下是人工评估者认定为存在问题的原始问题陈述示例：
• 不完整问题（Incomplete Problems）
  • \6. 五个球面可以将空间分成____部分。（NuminaMath-1.5，奥林匹克竞赛（Olympiads））
  • 下列哪个数字等于3300万？（STILL-3-Preview-RL-Data）
  • 哪个数字大于0.7？（STILL-3-Preview-RL-Data）
  • 例27：求 \(\sigma_2(28)=\) ？（NuminaMath-1.5，数论（Number Theory））
• 含无关信息的问题（Irrelevant Information）
  • \250. \(y=\ln(x^3-1)\cdot nn\) 25 0. \(y=\ln(x^3-1)\cdot nn\) 上述文本已翻译为英文，保留了原文的换行和格式。但由于原文是数学表达式，数学表达式通常具有通用性，不随语言变化而改变，因此译文与原文一致。（NuminaMath-1.5，奥林匹克竞赛（Olympiads））
  • \1. （12分）该图形由5个相同的正方形组成。以图形中的12个点为顶点，可以构成个三角形。10.（12分）该图形由5个相同的正方形组成。以图形中的12个点为顶点，可以构成个三角形。（NuminaMath-1.5，奥林匹克竞赛（Olympiads））
• 有趣的是，这些问题都通过了难度估计流程（即模型在面对无效或不完整问题时，仍能生成正确答案）
  • 这表明在 16 次生成过程中，模型至少有一次正确回答了这些问题，可能是因为模型曾训练过类似样本，或是答案易于猜测
  • 理解：甚至有些问题是没有给出选项的都猜对了？
  • 回答：也正常吧？整数或者是选项还是好猜测的，而且模型可能见过数据集
• 为高效整理整个数据集，论文采用 Llama-3.3-70B-Instruct 和 Qwen2.5-72B-Instruct 模型自动过滤低质量问题
  • 论文提示每个模型从清晰度、完整性、格式和相关性四个维度评估给定的数学问题，找出问题可能被判定为低质量的原因，并最终给出二元评分（合格/不合格）
  • 该过程模仿人工评估，同时效率显著提高
  • 对于每个问题和每个大语言模型评判者，论文收集 16 次评估结果 ，每个问题最终共获得 32 票
  • 论文保留至少获得9票有效支持的问题 ，总共移除了约 1000-2000 个数学问题

---

Math & Code Verifiers

Math Verifiers

• 在所有数学推理实验的初始阶段，论文对当时可用的基于规则的数学验证器（verifier）进行了多项初步分析。这些验证器包括：
  • 原始 MATH 验证器（verl 版本）
    • 问题：这里的 verl 版本是什么？
  • PRIME 验证器
  • Qwen2.5 验证器
  • DeepScaleR 的验证器
  • Math-Verify 验证器
  • 问题：这些验证器都如何使用？
• 论文首先抽样了一小部分题目及其相关解答和答案，手动检查了这些验证器的解析器和验证器质量
  • 论文发现，Qwen2.5 验证器在解析过程中往往会丢失信息（例如，在解析 \(\boxed{a^2}\) 时，无法保留 ^2 这一上标部分）
  • 论文还观察到，PRIME 验证器在执行过程中偶尔会出现停滞现象
  • 因此，论文将这两个验证器排除在后续分析之外
• 随后，论文利用难度估计过程中产生的 rollout 数据（注意：这里可以复用），应用剩余的验证器对生成的解答进行评估
  • 论文将各难度级别（0-8 级）对应的题目数量绘制在图 27 中
  • 问题：难度具体等级是如何划分的？
• 图 27：不同验证器的分布对比（基于 NuminaMath-1.5 数据集，经筛选后用于 DeepSeek-R1-Distill-Qwen-7B 模型）。图中 ver1_math、deepscaler、math_verify_0_5_2、math_verify 分别代表不同验证器，纵轴 0-7 代表难度级别，各扇区大小代表对应难度级别的题目数量
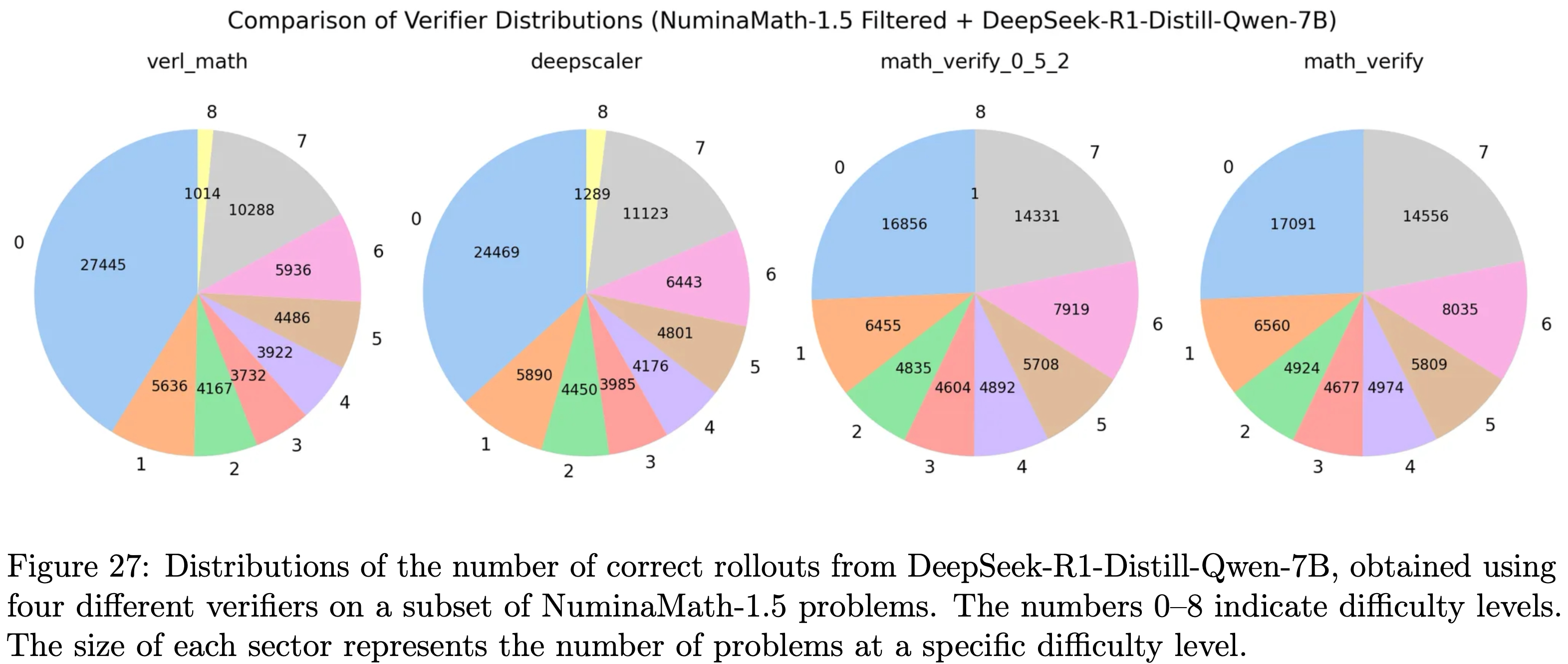
• 结合验证器结果与人工判断，论文得出以下结论：
  • 原始 MATH 验证器（ver1 版本）和 DeepScaleR 的验证器均存在较高的假阳性和假阴性率
  • 对于 Math-Verify 验证器，在论文尝试不同版本的过程中，其部分实现细节有所变化
    • 因此，论文同时纳入了 0.5.2 版本和默认版本（0.6.0 版本，该版本在模型开发过程中被广泛使用），并发现这两个版本之间仅存在微小差异
• 需要注意的是，对于格式不标准或包含 Math-Verify 不支持的数学表达式（例如存在多个答案的题目）的解答，Math-Verify 仍可能给出错误结果
• 在论文最终实现的奖励函数中，论文通过以下步骤验证文本解答中的答案是否正确：
  • 1）从推理过程之后提取答案
  • 2）使用 Math-Verify 的解析器对答案进行解析，得到其字符串表示形式
  • 3）如果该字符串表示形式与标准答案直接匹配，则返回“正确（True）”；否则，调用 Math-Verify 的验证函数（verify function）进行进一步验证
  • 4）将标准答案（gold answer）用 \(\boxed{}\) 包裹后，运行验证程序以获得最终结果
    • 问题：这里是针对 verifier 输入的改进吗？
• 论文发现，用 \(\boxed{}\) 包裹标准答案是至关重要的一步
  • 直接解析标准答案可能会导致数学表达式发生改变

Code Sandboxes

• 在单元测试执行方面，论文基于 LiveCodeBench 的实现，利用子进程（subprocess）处理构建了一个高效且安全的本地代码沙箱
  • 该沙箱支持多种测试方法，包括标准输入输出测试、解答函数单元测试以及基于断言的测试
• 为进一步提升其安全性和稳健性，论文实施了以下措施：
  • 语法验证（Syntax validation）：首先使用抽象语法树（Abstract Syntax Tree, AST）对提交的解答进行语法验证
    • 若检测到语法错误，沙箱会立即终止测试并返回“错误（False）”
  • 内存监控（Memory monitoring）：在训练过程中，论文发现部分生成的解答存在潜在的内存泄漏风险
    • 为缓解这一问题，论文为每个测试进程集成了内存监控机制
    • 若某个进程的内存使用量超过 50GB，沙箱会主动终止该测试并返回“错误（False）”，从而有效避免资源耗尽
  • 并行稳定性优化（Parallel stability optimization）：
    • 起初，论文采用异步测试结合进程池的方式进行并行执行
    • 但后来发现，这种设置下沙箱可能会崩溃，进而导致测试结果不准确
    • 为解决这一问题，论文对方案进行了调整，仅依赖多进程（multiprocessing）实现，确保并行执行的稳定性和高效性
    • 问题：披露的这么细节吗？
• 此外，论文还将论文的沙箱与 PRIME 沙箱进行了性能对比
  • 结果表明，在特定数据集上，论文的实现效果更优
  • 特别地，PRIME 沙箱偶尔会将正确的解答误判为错误 ，而论文的沙箱对解答正确性的评估更为准确
• 在实际使用过程中，论文发现论文的沙箱存在一个局限性：
  • 目前无法处理同一输入可能产生多个有效输出的情况
  • 这类情况在涉及非确定性问题或开放性问题的真实代码测试场景中较为常见

---

Experiments

• 在本节中，论文将呈现三个模型的实验结果，分别是 Skywork-OR1-Math-7B、Skywork-OR1-7B 和 Skywork-OR1-32B
• 首先，论文将详细介绍训练配置，随后分析训练结果，最后讨论评估结果

Training and Evaluation Details

Training Configurations

• 7B 模型和 32B 模型分别基于 DeepSeek-R1-Distill-Qwen-7B 和 DeepSeek-R1-Distill-Qwen-32B 进行微调
• 论文从多个来源收集数学和代码题目，并进行全面的预处理、难度筛选和质量控制，确保最终得到的题目集合具备可验证性、有效性和挑战性（具体细节参见第 6 节）
• 基于这个精心整理的题目集合，论文对三个模型均通过优化策略损失（公式 3.1）进行微调
  • 所采用的学习率为恒定值 \(1e-6\)
  • 裁剪比例（clip ratio）为 0.2
  • 目标熵（target entropy）为 0.2
  • 采样温度（sampling temperature）为 1.0
  • 采用拒绝采样（rejection sampling）方法
  • 论文在训练过程中未使用任何 KL 损失（KL loss）（正如第 3.2.6 节所讨论的）
  • 有关策略更新过程的更多细节，请参见第 3.1 节
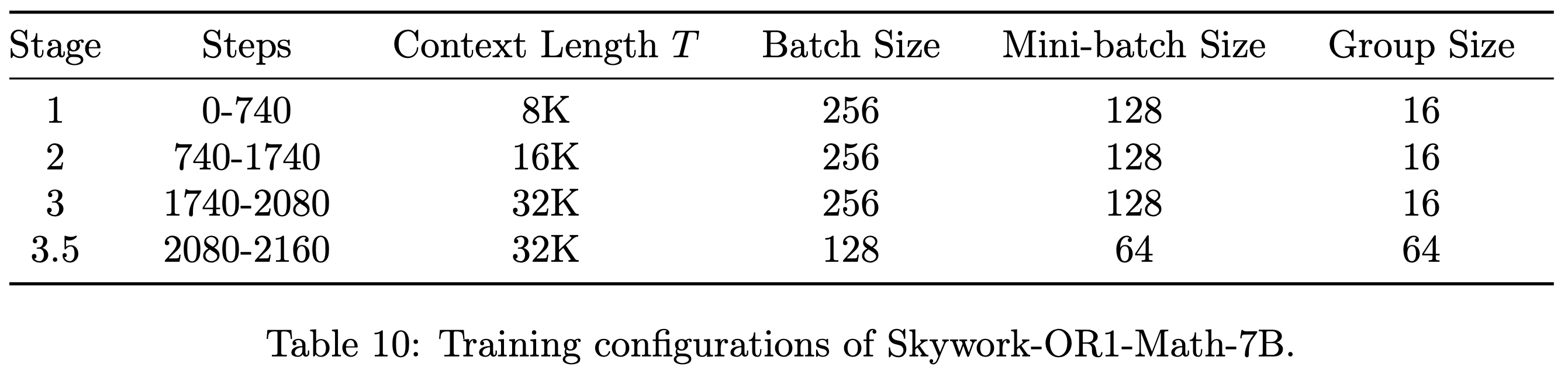
• 所有实验均采用多阶段训练（multi-stage training）方式，表 10、表 11 和表 12 分别报告了每个训练阶段的详细配置
• 发布的检查点（checkpoint）对应的训练步数如下：Skywork-OR1-Math-7B 为 2160 步，Skywork-OR1-7B 为 1320 步，Skywork-OR1-32B 为 1000 步

Benchmarks & Baselines

• 论文在具有挑战性的基准测试集上对模型进行评估
  • 在数学能力方面，论文采用 2024 年和 2025 年美国数学邀请赛（American Invitational Mathematics Examination, AIME）的题目作为评估集；
  • 在代码能力方面，论文使用 LiveCodeBench（2024 年 8 月-2025 年 2 月期间的数据）(2024)
• 论文将模型性能与多个性能强劲的基线模型进行对比
  • 包括 DeepSeek-R1 (2025)、Qwen3-32B (2025)、QwQ-32B (2025)、Light-R1-32B (2025)、TinyR1-32B-Preview (2025)
  • 以及多个基于 DeepSeek-R1-Distill-Qwen-7B 构建的 7B 级强化学习模型
    • 例如 AceReason-Nemotron-7B (2025)、AReaL-boba-RL-7B (2025) 和 Light-R1-7B-DS (2025)

Evaluation Setup

• 论文将所有模型的最大生成长度设置为 32,768 个 tokens
• 在 AIME24/25 测试集上，论文报告 avg@32 性能指标；
• 在 LiveCodeBench（2024 年 8 月-2025 年 2 月）测试集上，论文报告 avg@4 性能指标
• 生成答案时，采用的温度（temperature）为 1，top-P 为 1
• avg@n 指标的定义如下：
  $$avg @ n=\frac{1}{n} \sum_{i=1}^{n} \mathbb{I}\left\{\left(x, y_{i}\right) \text { is correct } \right\}$$
  • 其中， \(x\) 代表评估题目， \(y_i\) 代表第 \(i\) 个生成的答案

Evaluation Results of Skywork-OR1 models

• 如表 13 所示，Skywork-OR1 系列模型相较于其基础的 SFT 模型（例如 DeepSeek-R1-Distill 系列模型）取得了显著的性能提升
  • Skywork-OR1-32B 在 AIME24 测试集上得分为 82.2，在 AIME25 测试集上得分为 73.3，在 LiveCodeBench 测试集上得分为 63.0，在关键的数学基准测试集上性能超过了 DeepSeek-R1 和 Qwen3-32B 等当前性能较强的模型，在发布时创下了新的 SOTA 记录
  • Skywork-OR1-7B 在 AIME24 测试集上得分为 70.2，在 AIME25 测试集上得分为 54.6，在 LiveCodeBench 测试集上得分为 47.6，在数学和代码任务中，相较于同规模模型均展现出具有竞争力的性能
  • 论文早期发布的模型 Skywork-OR1-Math-7B 在同规模模型中也表现出色，在 AIME24 测试集上得分为 69.8，在 AIME25 测试集上得分为 52.3，在 LiveCodeBench 测试集上得分为 43.6
  • 这些最优性能结果尤为值得关注，因为它们是通过对 DeepSeek-R1-Distill 系列模型（初始性能相对一般的 SFT 基础模型）进行微调得到的，这充分体现了论文所提出的训练流程的显著效果
• 表 13：Skywork-OR1 系列模型与其他模型在推理相关基准测试集上的性能对比