注:本文包含 AI 辅助创作
- 参考链接:
- Megatron 系列目前公认的有三篇核心论文如下,它们分别对应了张量并行、3D 并行 与 序列并行/激活重计算优化 三大阶段,本文是第二篇的解读
- 第二篇:(Megatron-LM-2)Efficient Large-Scale Language Model Training on GPU Clusters Using Megatron-LM, SC 2021, NVIDIA
- 核心贡献:提出 3D 并行(数据 + 张量 + 流水线),并给出 interleaved 1F1B 流水线调度,显著降低流水线气泡;在 3072 块 A100 上训练出 530 B 参数的 GPT-3 级模型,GPU 利用率达到 76 %
Paper Summary
- 整体说明:
- 本文是 Megatron-LM原始论文解读-第二篇
- 论文展示了如何将 PTD-P(节点间 PP、节点内 TP 和 DP )组合起来,以在训练具有万亿参数的大模型时实现高聚合吞吐量
- 论文首次实现了端到端训练能够在合理的时间内完成(万亿参数模型的估计时间约为 3 个月)
- 论文通过分析讨论了与每种并行类型相关的各种权衡,以及在组合使用时需要仔细考虑它们之间的相互作用
- 论文中的很多思想是与加速器无关:
- 1)智能地划分模型训练计算图以在保持设备活跃的同时最小化通信量的思想
- 2)通过算子融合和仔细的数据布局来最小化内存受限的内核数量
- 3)其他领域特定的优化(例如,散射-聚集优化)
- 背景 & 问题:
- 高效地训练 LLM 模型具有挑战性,原因在于:
- 1)GPU 内存容量有限,使得即使是在多 GPU 服务器上也无法容纳大型模型;
- 2)所需的计算操作数量可能导致不切实际的长训练时间
- 高效地训练 LLM 模型具有挑战性,原因在于:
- 之前的工作:
- 之前已经提出了 TP (Tensor Parallelism, TP)和 PP (Pipeline Parallelism, PP),但这些方法的简单使用会在数千个 GPU 上导致扩展性问题
- 本文的核心方法贡献:
- 论文展示了如何组合使用 TP 、PP 和 DP (Data Parallelism, DP),以扩展到数千个 GPU
- 论文提出了一种新颖的交错流水线调度方法,在内存占用与现有方法相当的情况下,可以将吞吐量提高 10% 以上
- 特别亮眼的表现:论文的方法使得论文能够在 3072 个 GPU 上以 502 petaFLOP/s 的速度对具有 1 万亿参数的模型执行训练迭代(每 GPU 吞吐量达到理论峰值的 52%)
- 注意:这是在 2021 年实现的,而本文的方法已经是家喻户晓
Introduction and Discussion
- NLP 中基于 Transformer 的语言模型近年来推动了快速进展,因为大规模计算变得更加可用且数据集变得更大
- 最近的工作 (2020) 表明,大语言模型是有效的零样本或少样本学习者,在许多 NLP 任务和数据集上具有高准确率
- 这些大语言模型有许多令人兴奋的下游应用,例如客户反馈摘要、自动对话生成、语义搜索和代码自动补全 (2021;)
- SOTA NLP 模型中的参数数量呈指数级增长(图 1)
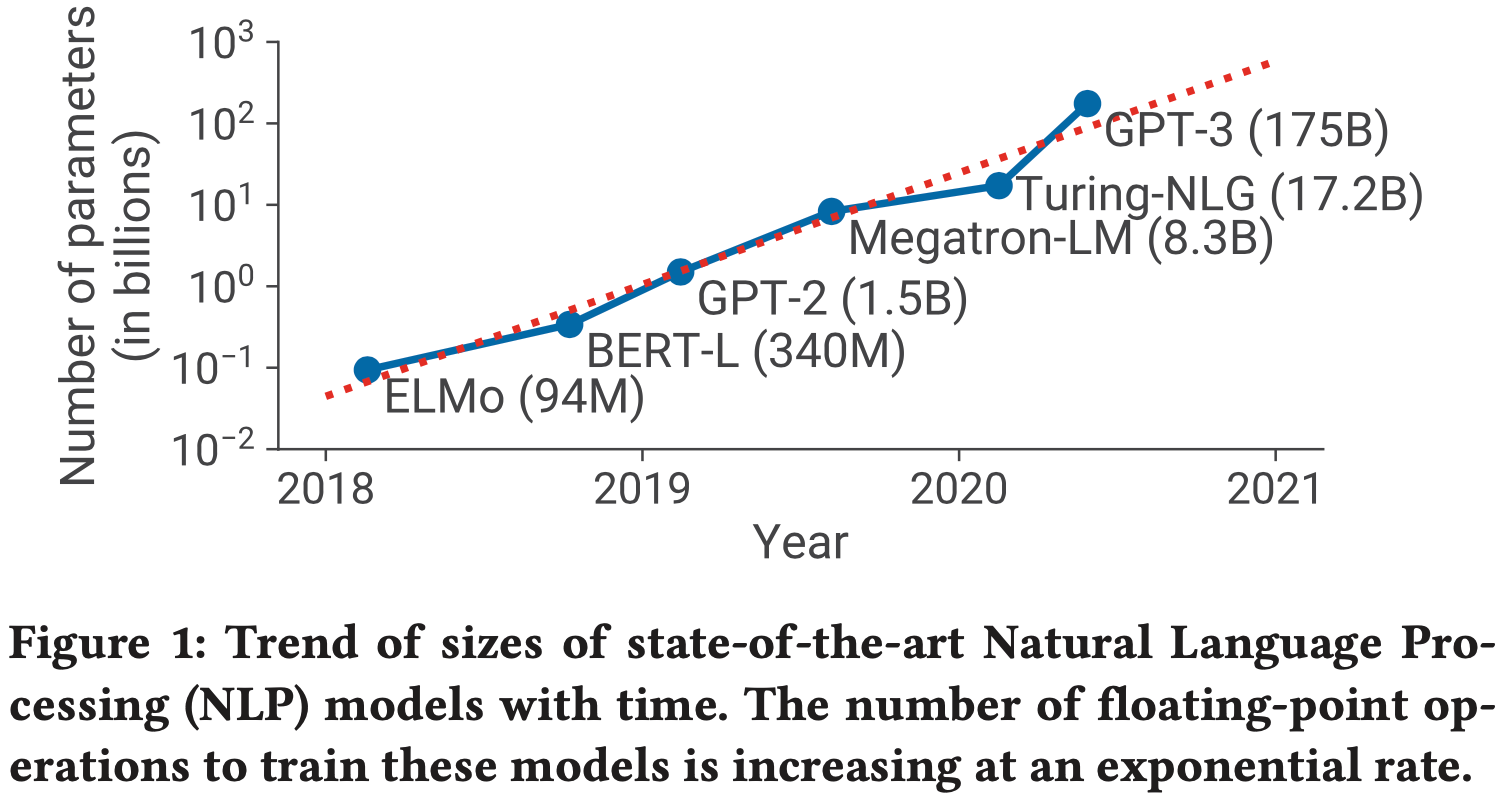
- 训练此类模型具有挑战性,原因有二:
- (a) 即使使用最大的 GPU(NVIDIA 最近发布了 80GB A100 卡),也无法将这些模型的参数容纳在其主内存中;
- (b) 即使论文能够将模型装入单个 GPU(例如,通过在主机和设备内存之间交换参数 (2021)),所需的大量计算操作可能导致不切实际的长训练时间(例如,使用单个 NVIDIA V100 GPU 训练具有 175B 参数的 GPT-3 (2020) 将需要大约 288 年)
- 所以需要并行化, DP 扩展通常效果良好,但受到两个限制:
- a)超过某个点后,每 GPU 批大小变得太小,降低了 GPU 利用率并增加了通信成本;
- b)可使用的最大设备数量等于批大小,限制了可用于训练的加速器数量
- 为了应对这两个挑战,已经提出了各种模型并行技术
- 一些工作 (2019; 2020) 展示了如何使用张量(层内)模型并行(即将每个 Transformer 层内的矩阵乘法拆分到多个 GPU 上)来克服这些限制
- 尽管这种方法对于在 NVIDIA DGX A100 服务器(配备 8 个 80GB A100 GPU)上训练大小达 20B 参数的模型效果良好,但对于更大的模型则会失效
- 更大的模型需要拆分到多个多 GPU 服务器上,这会导致两个问题:
- (a) TP 所需的全局归约(All-Reduce)通信需要通过服务器间链路进行,这些链路比多 GPU 服务器内可用的高带宽 NVLink (2020) 慢;
- (b) 高度的模型并行可能会产生小的矩阵乘法(GEMM),可能降低 GPU 利用率
- PP (2019; 2020; 2021) 是另一种支持训练大模型的技术,它将模型的层分布到多个 GPU 上
- 一个批次被分割成更小的微批次(microbatch),执行过程在这些微批次之间进行流水线化
- 层可以以各种方式分配(assigned)给工作节点,并且可以使用各种输入的前向传播和后向传播调度策略
- 层分配(layer assignment)和调度策略会导致不同的性能权衡
- 无论采用何种调度,为了保持严格的优化器语义,优化器步骤需要在设备间同步,这导致在每个批次结束时进行一次 流水线刷新(pipeline flush) ,此时允许微批次完成执行(并且不注入新的微批次)
- flushing the pipeline 可能会花费多达 50% 的时间(取决于注入流水线的微批次数量)
- 微批次数量与流水线规模(阶段数)的比率越大,花费在流水线刷新上的时间就越少
- 为了实现高效率,通常需要更大的批大小
- 在这项工作中,论文还引入了一种新的流水线调度方案,该方案提高了小批大小下的效率
- 这些技术可以组合使用,但组合这些技术会导致 non-trivial 的相互作用,需要仔细推理才能获得良好的性能
- 在论文中,论文解决了以下问题:
- 在给定批大小并保持严格优化器语义的前提下,应如何组合并行技术以最大化大模型的训练吞吐量?
- 具体来说,论文展示了如何组合 PP 、TP 和 DP,论文称之为 PTD-P(pipeline, tensor, and data parallelism) 的技术,以在数千个 GPU 上以良好的计算性能(达到设备峰值吞吐量的 52%)训练大语言模型
- 论文的方法利用跨多 GPU 服务器的 PP 、多 GPU 服务器内的 TP 以及 DP 的组合,在实际中训练具有万亿参数的模型,并在具有服务器内和服务器间 GPU 高速链路的优化集群环境中实现优雅的扩展
- 给定更多的训练资源,也可以使用类似的思想来训练更大的模型
- 在论文的实验中,论文在一个具有万亿参数的 GPT 模型 (2020) 上,使用混合精度,展示了接近线性的扩展到 3072 个 A100 GPU,实现了每 GPU 163 teraFLOP/s 的端到端训练吞吐量(包括通信、数据处理和优化),以及 502 petaFLOP/s 的总吞吐量
- 这个吞吐量使得实际的训练时间成为可能:论文估计该模型的端到端训练大约需要 3 个月
- 作者相信这是针对该规模模型实现的最快训练吞吐量:过去的系统 (2019; 2020) 无法训练如此大的模型,因为它们没有结合 PP 和 TP
- 论文还将论文的方法与 ZeRO (2019) 进行了比较,发现由于跨节点通信更少,论文的方法对于 175B 和 530B 参数的模型比 ZeRO-3 性能高出 70%
- 这些模型太大,无法容纳在单个多 GPU 服务器上
- 在大规模下实现这种吞吐量需要在多个方面进行创新和精心的工程:
- 高效的内核实现使得大部分计算是计算受限而非内存受限的
- 在设备间智能划分计算图以减少通过网络链路发送的字节数同时限制设备空闲时间
- 领域特定的通信优化以及快速的硬件( SOTA GPU 以及服务器内和服务器间的高速链路)
- 作者希望论文开源的软件(可在 github.com/nvidia/megatron-lm 获取)将使其他团队能够高效地大规模训练大型 NLP 模型
- 论文通过实验和尽可能的分析,研究了影响吞吐量的各个组件之间的相互作用
- 基于这些研究,论文提供以下关于如何配置分布式训练的指导原则 :
- 不同形式的并行化以 non-trivial 的方式相互作用:
- 并行化策略会影响通信量 和 内核执行的计算效率,还会影响工作节点上的气泡时间(因流水线刷新(气泡)所花费的空闲时间)
- 例如,在论文的实验中,论文发现,即使服务器间有高带宽网络链路,次优的 TP 和 PP 组合也可能导致吞吐量降低多达 2 倍;
- TP 在多 GPU 服务器内是有效的 ,但对于更大的模型必须使用 PP
- 并行化策略会影响通信量 和 内核执行的计算效率,还会影响工作节点上的气泡时间(因流水线刷新(气泡)所花费的空闲时间)
- 用于 PP 的调度方案会影响通信量、流水线气泡大小以及用于存储激活值的内存
- 论文提出了一种新颖的交错调度方案,与先前提出的调度方案 (2019; 2020) 相比,在内存占用相当的情况下,可以将吞吐量提高多达 10%
- 微批次大小等超参数的值会影响内存占用、工作节点上执行的内核的算术效率以及流水线气泡大小
- 在论文的实验中,微批次大小的最优值是问题相关的,并且可以将吞吐量提高 15%
- 在大规模下,分布式训练是通信密集型的
- 当在 3072 个 GPU 上训练一个万亿参数模型时,论文的实现用于 PP 通信的有效二分带宽为 892 GB/s,用于 DP 通信的有效二分带宽为 13 TB/s
- 使用较慢的节点间互连或通信更密集的划分会阻碍扩展性能
- 不同形式的并行化以 non-trivial 的方式相互作用:
- 论文不会自动探索并行策略的搜索空间(例如 FlexFlow (2018), PipeDream (2019), Tarnawski 等 (2020), 和 DAPPLE (2021)),而是提出论文在实践中发现效果很好的启发式方法(在 章节3 中)
Models of Parallelism
- 论文关注单个 GPU 无法装下的大型模型进行高效训练的并行技术
- 论文将 PP (pipeline model parallelism) 和 TP (tensor model parallelism)(组合如图 2 所示)与 DP (data parallelism) 结合起来(论文将其简称为 PTD-P)
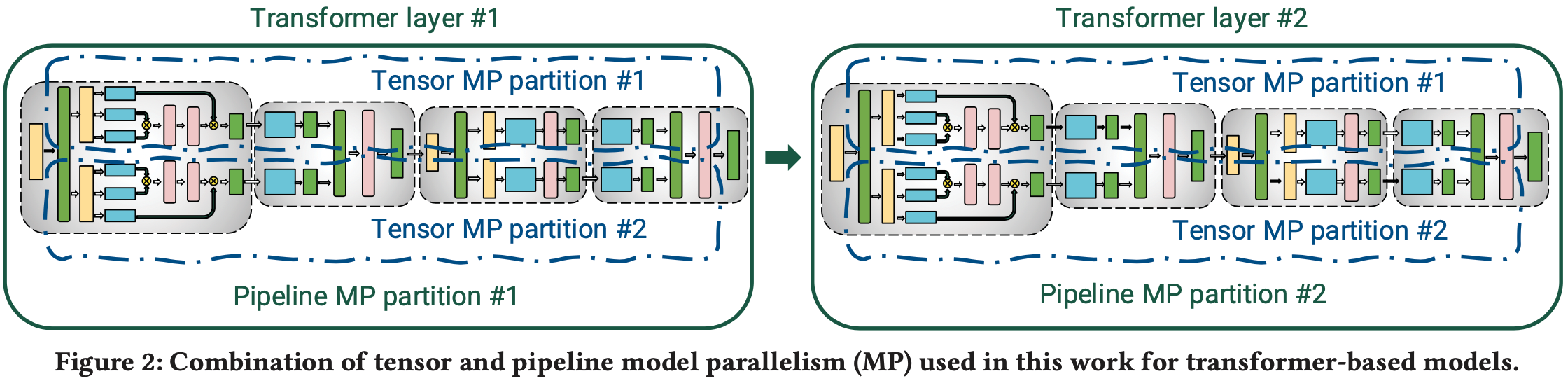
DP (Data Parallelism)
- 使用 DP (2021) 时,每个工作节点 (worker) 都拥有完整模型的一个副本,输入数据集被分片,工作节点定期聚合它们的梯度,以确保所有权重版本一致
- 对于无法放在单个工作节点上的大型模型,可以在较小的模型分片上使用 DP
PP (Pipeline Model Parallelism)
- 使用 PP 时,模型的层被分片到多个设备上
- 当用于具有重复相同 Transformer 块的模型时,可以为每个设备分配相同数量的 Transformer 层
- 论文不考虑更不对称的模型架构 ,因为将层分配给流水线阶段更为困难;论文将这个问题留给相关工作 (2021;) 来解决
- 一个批次 (batch) 被分割成更小的微批次 (microbatch);然后跨微批次进行流水线执行
- 流水线方案需要确保输入在前向传播和后向传播中看到一致的权重版本,以获得明确定义的同步权重更新语义
- 具体来说,简单的流水线可能导致一个输入在后向传播中看到在前向传播中未见的权重更新
- 为了精确保持严格的优化器语义,论文引入了周期性的流水线刷新 (pipeline flush),以便跨设备同步优化器步骤
- 在每个批次的开始和结束时,设备处于空闲状态,论文将此空闲时间称为流水线气泡 (pipeline bubble),并希望使其尽可能小
- 诸如 PipeMare、PipeDream 和 PipeDream-2BW (2019; 2020; 2021) 之类的异步和有界陈旧度 (bounded-staleness) 方法完全取消了刷新,但放宽了权重更新语义
- 论文将对此类方案的考虑留待未来工作
- 有多种可能的方式来跨设备调度前向和后向微批次;每种方法在流水线气泡大小、通信量和内存占用之间提供了不同的权衡
- 论文将在本节讨论两种这样的方法
Default Schedule
- GPipe 提出了一种调度方案,即首先执行一个批次中所有微批次的前向传播(如图 3 所示),然后是所有微批次的后向传播
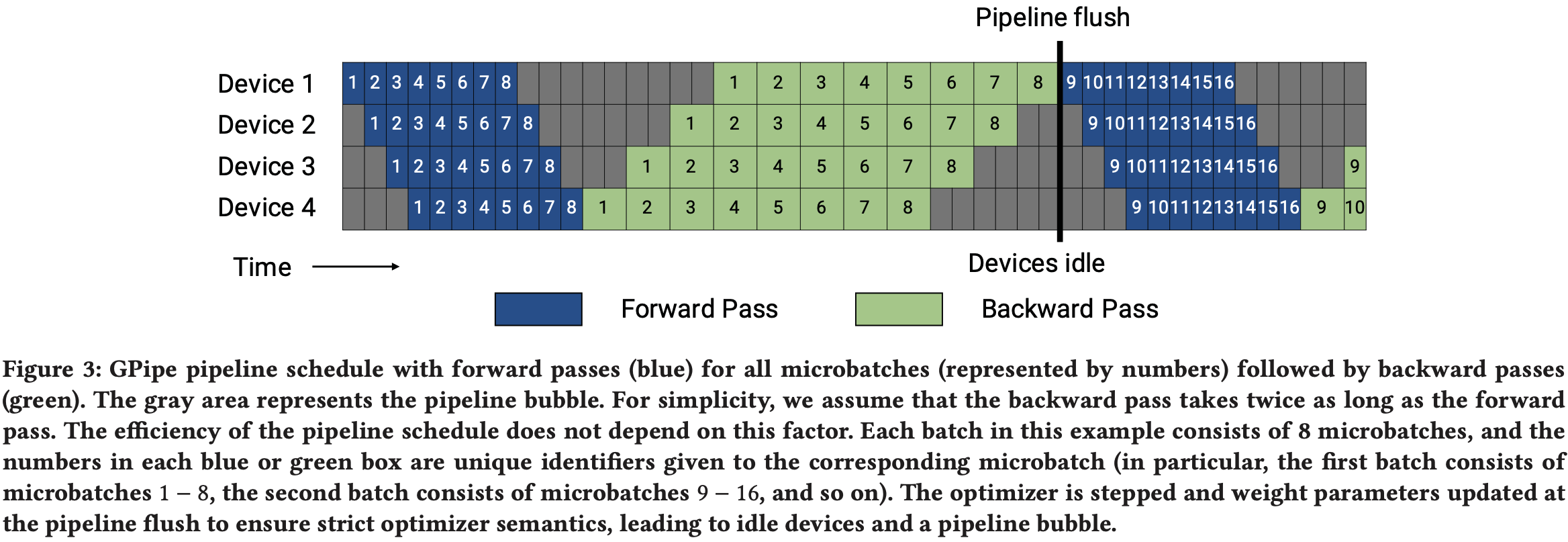
- 我们可以量化 GPipe 的流水线气泡大小 (\(t_{pb}\))
- 用一个批次中的微批次数量记为 \(m\),流水线阶段数(用于 PP 的设备数量)记为 \(p\),每次迭代的理想时间为 \(t_{id}\)(假设完美或理想缩放),执行单个微批次的前向和后向传播的时间记为 \(t_{f}\) 和 \(t_{b}\)
- 在此调度中,流水线气泡包括批次开始时的 \(p-1\) 次前向传播和批次结束时的 \(p-1\) 次后向传播
- 理解:图 3 中,对于 PP=4 的场景,即每个设备 都要有 3 个完整的前向和后向传播气泡
- 花费在流水线气泡中的总时间为:
$$t_{pb}=(p-1)\cdot(t_{f}+t_{b})$$ - 该批次的理想处理时间为:
$$t_{id}=m\cdot(t_{f}+t_{b})$$ - 因此,理想计算时间中花费在流水线气泡中的比例为:
$$\text{Bubble time fraction (pipeline bubble size)} =\frac{t_{pb} }{t_{id} }=\frac{p-1}{m}.$$- 理解:这里分母上算少了,分母上应该再加上分子才对
- 为了使气泡时间比例变小,一般需要 \(m\gg p\),但对于如此大的 \(m\),这种方法具有很高的内存占用,因为它需要在一次训练迭代的整个生命周期内,将所有 \(m\) 个微批次的暂存中间激活值(或者在使用激活重计算时,仅为每个流水线阶段的输入激活值)保存在内存中
- 论文使用 PipeDream-Flush 调度 (2021)
- 论文首先进入一个预热阶段,工作节点执行不同数量的前向传播,如图 4(顶部)所示
- 此调度将进行中的微批次(其后向传播尚未完成且需要维护激活值的微批次)的数量限制为流水线的深度,而不是一个批次中的微批次数量
- 预热阶段之后,每个工作节点进入稳定状态,每个工作节点执行一次前向传播,然后执行一次后向传播(简称 1F1B)
- 最后,在批次结束时,论文完成所有剩余进行中微批次的后向传播
- 这种新调度花费在气泡中的时间是相同的,但对于 PipeDream-Flush 调度,未完成的前向传播数量最多为流水线阶段数
- 因此,此调度需要为 \(p\) 个或更少的微批次暂存激活值(相比之下,GPipe 调度需要为 \(m\) 个微批次暂存)
- 因此,当 \(m\gg p\) 时,PipeDream-Flush 比 GPipe 内存效率高得多
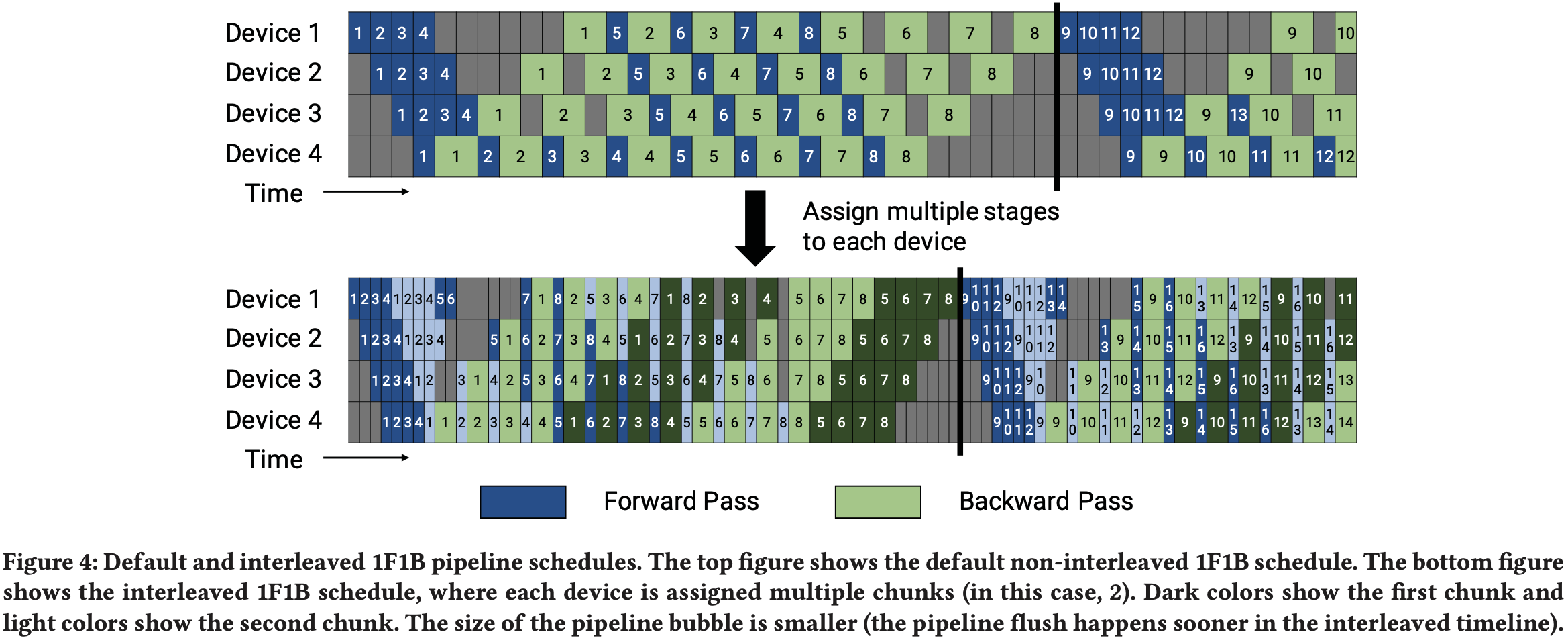
- 论文首先进入一个预热阶段,工作节点执行不同数量的前向传播,如图 4(顶部)所示
Schedule with Interleaved Stages
- 为了减小流水线气泡的大小,每个设备可以执行多个层子集(称为模型块, model chunk)的计算,而不是单个连续的层集
- 例如,如果之前每个设备有 4 层(即设备 1 有第 1-4 层,设备 2 有第 5-8 层,依此类推),我们可以让每个设备执行两个模型块(每个有 2 层)的计算,即设备 1 有第 1, 2, 9, 10 层;设备 2 有第 3, 4, 11, 12 层;依此类推
- 使用这种方案,流水线中的每个设备被分配多个流水线阶段(每个流水线阶段的计算量比之前少)
- 像之前一样,我们可以使用此调度方案的“全部前向,全部后向”版本,但这具有很高的内存占用(与 \(m\) 成正比)
- 论文开发了一种交错调度 (interleaved schedule) ,它适配了之前的内存高效 1F1B 调度
- 这种新调度如图 4 所示,并要求一个批次中的微批次数量是 PP 度(流水线中的设备数量)的整数倍
- 例如,对于 4 个设备,一个批次中的微批次数量必须是 4 的倍数
- 如图 4 所示,相同批次大小的流水线刷新在新调度中发生得更早
- 如果每个设备有 \(v\) 个阶段(或模型块),那么每个阶段或块的微批次的前向和后向时间现在将是 \(t_{f}/v\) 和 \(t_{b}/v\)
- 因此,流水线气泡时间减少到
$$t_{pb}^{\text{int.} }=\frac{(p-1)\cdot(t_{f}+t_{b})}{v}$$- 气泡时间比例则为:
$$\text{Bubble time fraction (pipeline bubble size)} =\frac{t_{pb}^{\text{int.} } }{t_{id} }=\frac{1}{v}\cdot\frac{p-1}{m}.$$
- 气泡时间比例则为:
- 这意味着新调度将气泡时间减少了 \(v\) 倍
- 但这种减小的流水线气泡大小并非没有代价:此调度需要额外的通信
- 定量地说,通信量也增加了 \(v\) 倍
- 在下一节中,论文将讨论如何利用多 GPU 服务器(例如 DGX A100 节点)中的 8 个 InfiniBand 网络卡来减少这种额外通信的影响
TP (Tensor Model Parallelism)
- 使用 TP 时,模型的各个层在多个设备上进行划分
- 在论文中,论文使用 Megatron (2019) 针对语言模型基础 Transformer 层所使用的特定划分策略
- 也可以将类似的思想应用于其他类型的模型,如 CNN
- 论文简要概述此策略,如图 5 所示
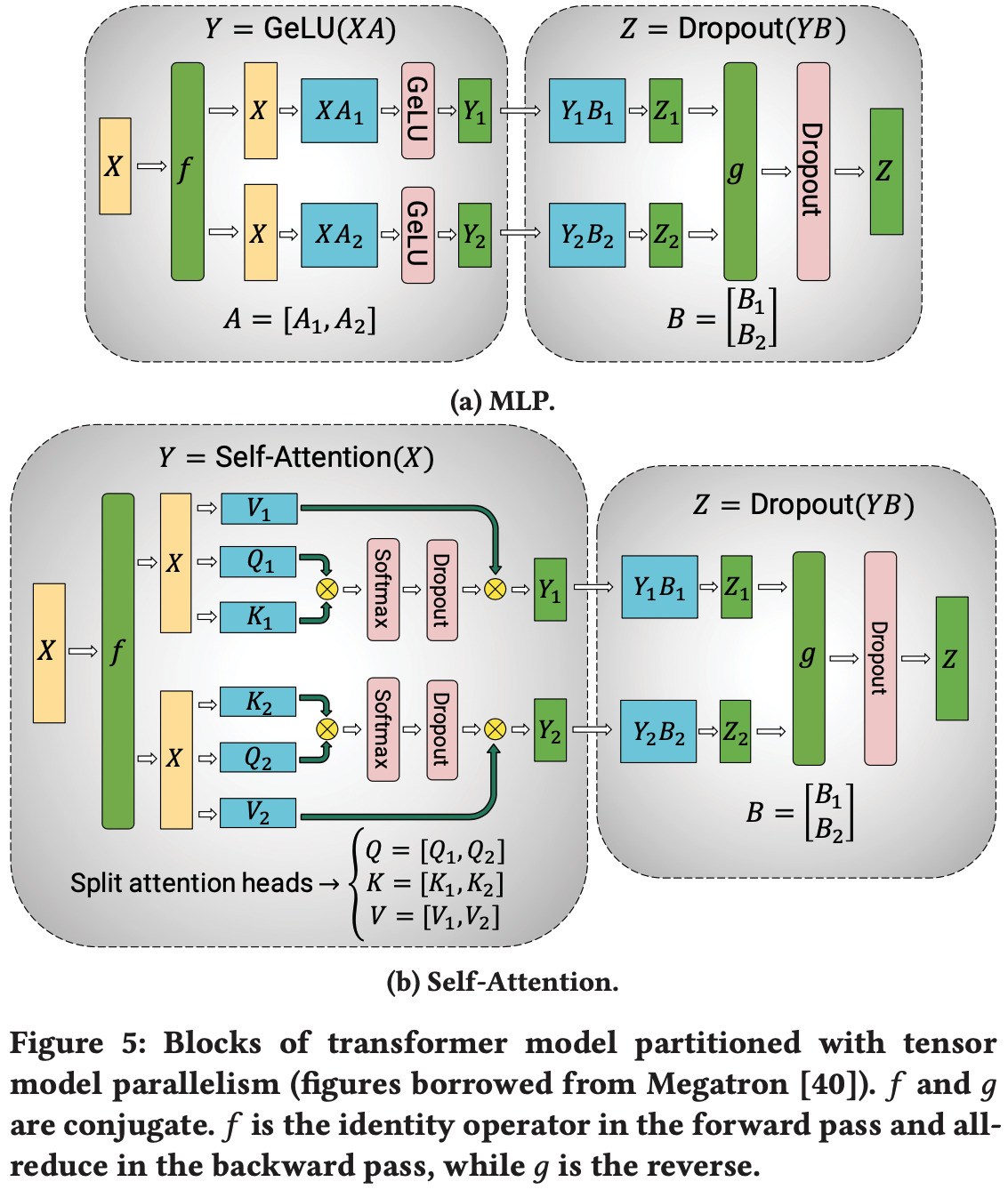
- 一个 Transformer 层由一个自注意力块 (self-attention block) 和一个两层的多层感知机 (MLP) 组成
- MLP 块:MLP 块包含两个 GEMM(通用矩阵乘法,General Matrix Multiply)和一个 GeLU 非线性:
$$Y=\text{GeLU}(XA).\quad Z=\text{Dropout}(YB).$$- 第一个权重矩阵 \(A\) 按列划分,即 \(A=[A_{1}, A_{2}]\)
- 这种划分允许将 GeLU 非线性独立应用于每个划分后 GEMM 的输出:
$$[Y_{1},Y_{2}]=\left[\text{GeLU}(XA_{1}),\text{GeLU}(XA_{2})\right].$$ - 这样做的好处是它消除了同步的需要(如果 \(A\) 沿其行划分则需要同步,因为 GeLU 是非线性的)
- 这种划分允许将 GeLU 非线性独立应用于每个划分后 GEMM 的输出:
- 第二个权重矩阵 \(B\) 的按行划分,以消除 GEMM 之间的任何通信需要(如图 4(a) 所示),如下所示:
$$B=\begin{bmatrix}B_{1}\ B_{2}\end{bmatrix}, Y=[Y_{1},Y_{2}].$$ - 第二个 GEMM 的输出然后在 Dropout 层之前跨 GPU 进行归约 (reduce)
- 第一个权重矩阵 \(A\) 按列划分,即 \(A=[A_{1}, A_{2}]\)
- 自注意力块:利用多头注意力操作中固有的并行来划分自注意力块(如图 4(b) 所示)
- 键 (\(K\))、查询 (\(Q\)) 和值 (\(V\)) 矩阵可以以列并行 (column-parallel) 的方式进行划分(每个设备上负责不同的注意力头,并行计算)
- 输出线性层然后可以直接在注意力操作的划分输出上运行(权重矩阵跨行划分,不需要 GPU 同步通信)
- TP 将 MLP 和自注意力块中的 GEMM 拆分到多个 GPU 上,同时在前向传播中仅需要两次全归约 (All-Reduce) 操作(\(g\) 运算符),在后向传播中需要两次全归约操作(\(f\) 运算符)
- 论文用几行代码实现了 \(f\) 和 \(g\)
Performance Analysis of Parallelization Configurations
- 考虑将 PP (pipeline parallelism) 和 TP (tensor model parallelism) 与 DP (data parallelism) 结合使用的性能影响
- 给定固定的 GPU 预算和批次大小 (batch size),可以使用 PTD-P 中不同维度的并行类型来训练模型;
- 每个维度都在内存占用 (memory footprint)、设备利用率 (device utilization) 和通信量之间进行权衡
- 论文将在本节剩余部分讨论这些权衡,并在 5.4 节展示实证结果
- 论文在分析流水线气泡 (pipeline bubble) 大小时会提供分析模型
- 论文定性地描述通信时间的行为,并提供通信量的成本模型;但是,论文不提供通信时间的直接成本模型,因为对于层次化网络拓扑(同一服务器上 GPU 之间的互连带宽高于服务器之间的互连带宽)来说,通信时间更难建模
- 据论文所知,这是首个分析这些并行化维度性能交互作用的工作
Notation
- 论文在本节中使用以下符号表示:
- \( (p, t, d) \):并行化维度
- \( p \) 表示 PP 大小 (pipeline-model-parallel size),\( t \) 表示 TP 大小 (tensor-model-parallel size),\( d \) 表示 DP 大小 (data-parallel size)
- \( n \):GPU 数量,论文要求 \( p \cdot t \cdot d = n \)
- \( B \):全局批次大小 (global batch size)(作为输入提供)
- \( b \):微批次大小 (microbatch size)
- \( m = \frac{1}{b} \cdot \frac{B}{d} \):每个流水线 (per pipeline) 中一个批次内的微批次数量
- \( (p, t, d) \):并行化维度
TP 和 PP(Tensor and Pipeline Model Parallelism)
- TP 和 PP 均可以用于在多个 GPU 对模型的参数进行分区
- 正如前文所述,使用带有周期性刷新(periodic flushes)的 PP 会产生下面大小的流水线气泡(pipeline bubble):
$$\frac{p-1}{m}$$ - 假设 DP 规模 \(d=1\)( DP 大小,data-parallel size),那么此时总 GPU 数量满足
$$ t \cdot p = n; \quad \text{s.t.} \ d=1 $$ - 基于 TP 规模 \(t\) 的流水线气泡大小可表示为:
$$
\frac{p-1}{m} = \frac{n/t - 1}{m}
$$- 说明:在固定批次大小 \(B\)、微批次大小 \(b\) 以及固定 \(d\)(此时 \(m = \frac{B}{b \cdot d}\) 也保持固定)的前提下,随着 TP 规模 \(t\) 的增大,流水线气泡会逐渐减小
- 不同 GPU 之间的通信量同样会受到 PP 规模 \(p\) 和 TP 规模 \(t\) 的影响
- PP 的特点是点到点通信(point-to-point communication)成本更低;TP 则需要使用 All-Reduce communication
- TP:正向传播(forward pass)需执行两次归约操作;反向传播(backward pass)也需执行两次归约操作(详见第2.3节)
- 在 PP 中,对于每个微批次,每对 PP 相邻设备之间需要执行的PP 通信总量为(一次 点对点通信):
$$ bsh $$- 其中 \(s\) 代表序列长度(sequence length),\(h\) 代表隐藏层大小(hidden size)
- 正向传播和反向传播各需要一次点对点通信,所以总共是 $$ 2bsh $$
- 在 TP 中,对于每个层,总大小为 \(bsh\) 的张量需在 \(t\) 个模型副本(model replicas)间,正向传播和反向传播各两次通信,这使得每个设备、每个微批次、每个层的 TP 通信总量为
$$8bsh \cdot \frac{t-1}{t}$$- 理解:TP 参数通信量估计详情
- MLP 正向和反向各需要一次 TP 通信(All-Reduce),一次 All-Reduce 通信是 \(2\Phi_\text{TP} = 2bsh\)(使用 Ring All-Reduce,一次通信使用 \(2\Phi\frac{t-1}{t}\) 的通信量),单层模型上, MLP TP 累计通讯量是:
$$ 4\Phi\frac{t-1}{t} = 4bsh\frac{t-1}{t} $$ - Attention 部分正向和反向也各需要一次 TP 通信(All-Reduce),单层模型上,Attention TP 累计通讯量是:
$$ 4\Phi\frac{t-1}{t} = 4bsh\frac{t-1}{t} $$ - 注:上述通信量评估详情见:图解大模型训练之:张量模型并行(TP),Megatron-LM - 猛猿的文章 - 知乎
- MLP 正向和反向各需要一次 TP 通信(All-Reduce),一次 All-Reduce 通信是 \(2\Phi_\text{TP} = 2bsh\)(使用 Ring All-Reduce,一次通信使用 \(2\Phi\frac{t-1}{t}\) 的通信量),单层模型上, MLP TP 累计通讯量是:
- 理解:TP 参数通信量估计详情
- 通常每个设备会负责多个层的计算(TP 中,每个层都需要分别与其他设备交互),因此对于每个设备、每个微批次, TP 的总通信量可表示为
$$l^{stage} \cdot (8bsh \cdot \frac{t-1}{t})$$- 其中 \(l^{stage}\) 代表一个流水线阶段(pipeline stage)中包含的层数,即一个设备负责的层数
- PP 的特点是点到点通信(point-to-point communication)成本更低;TP 则需要使用 All-Reduce communication
- 由此可见,TP 会增加设备间的通信量
- 因此,当 TP 规模 \(t\) 大于单个节点(node)中的 GPU 数量时,跨节点链路(inter-node links)的传输速度较慢,此时在这类链路上执行 TP 的开销会变得难以承受
- 这一结果已在第5.4节的实验中得到验证
- Takeaway #1 :TP 不跨 节点
- 对于使用每个节点 \(g\) 个 GPU 的服务器时, TP 的规模通常应不超过 \(g\);若要在多台服务器间扩展以训练更大的模型,则可使用 PP
- 理解:这里指的是 单台机器的 GPU 数为 \(g\),TP 规模 \(t\) 大于 \(g\) 时会导致跨节点的 TP 通信,开销难以接受
DP Data and Model Parallelism
- 注:这里的模型并行(Model Parallelism)包括了 PP(Pipeline Model Parallelism) 和 TP(Tensor Model Parallelism)
- 论文还需要考虑 DP (data parallelism)与两种模型并行( TP 和 PP )之间的相互作用
- 为简化分析,本节将分别对这些相互作用进行讨论
PP (Pipeline Model Parallelism)
- 假设 TP 规模 \(t=1\)(tensor-model-parallel size),则每个流水线的微批次数量为
$$ m = \frac{B}{d \cdot b} = \frac{b’}{d}$$- 其中:
- \( b \) 是微批次大小 (microbatch size)
- \(b’ = \frac{B}{b}\) 表示每个 Global Step 的 微批次数量;
- 注:每个流水线的微批次数量 \(m\) 与 DP 大小 \(d\) 成反比
- 其中:
- 在总 GPU 数量为 \(n\) 的情况下,流水线阶段的数量为
$$ p = \frac{n}{(t \cdot d)} = \frac{n}{d} $$ - 此时流水线气泡大小可表示为:
$$
\frac{p-1}{m} = \frac{n/d - 1}{b’/d} = \frac{n - d}{b’}
$$- 随着 DP 规模 \(d\) 的增大,\(n - d\) 会逐渐减小,因此流水线气泡也会随之变小
- 图6展示了在不同 \(d\)、\(n\) 和 \(b’\)(批次大小与微批次大小的比值,\(b’ = \frac{B}{b}\))下,流水线气泡大小的变化趋势
- 需要注意的是,并非所有模型都能将 \(d\) 增大到 \(n\),因为部分模型的完整训练内存占用(full training memory footprint)可能超过单个加速器(accelerator)的内存容量
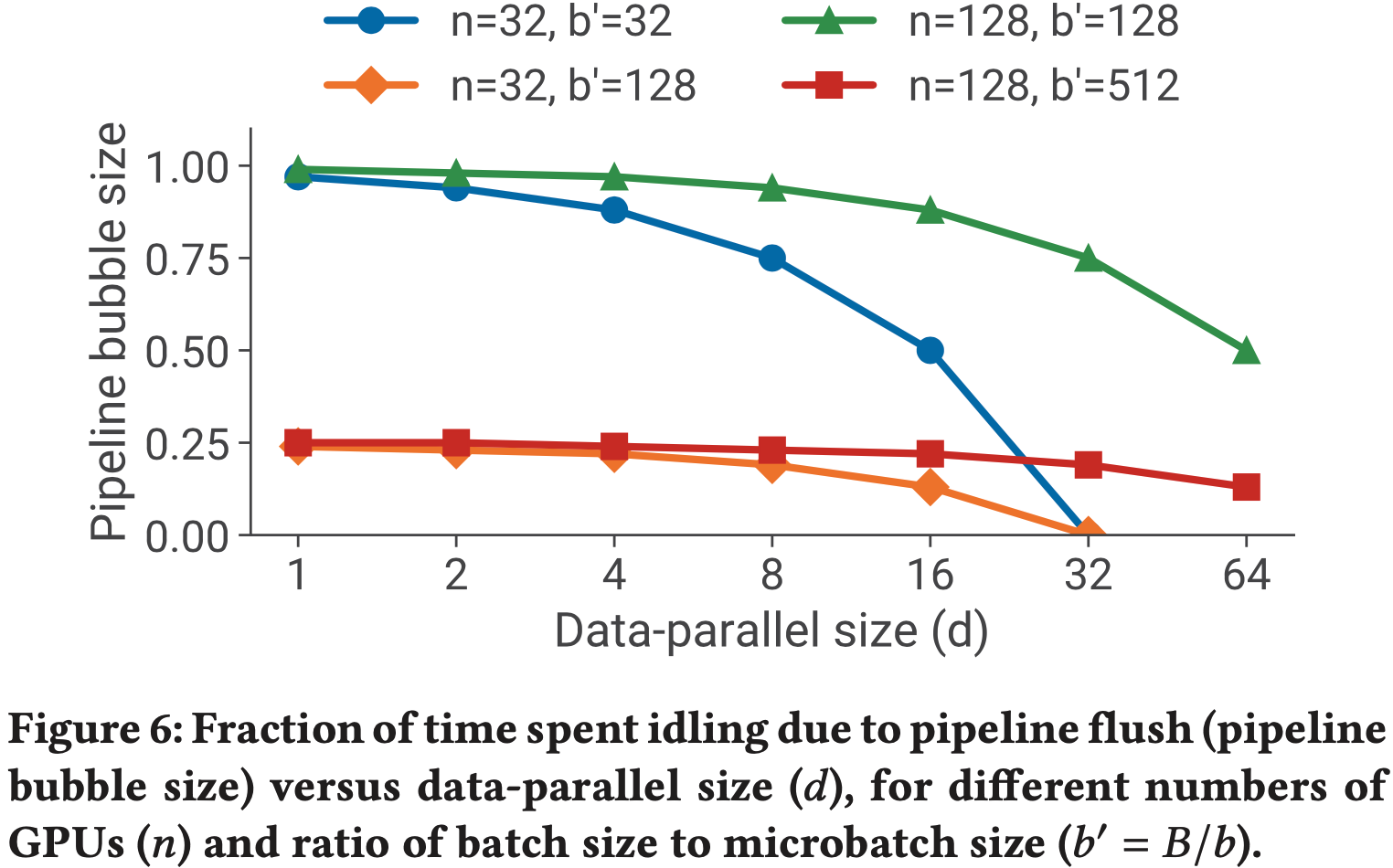
- 需要注意的是,并非所有模型都能将 \(d\) 增大到 \(n\),因为部分模型的完整训练内存占用(full training memory footprint)可能超过单个加速器(accelerator)的内存容量
- 若 DP 所需的归约通信量未随 \(d\) 的增大而大幅增加,那么整体吞吐量(throughput)会随之提升
- 这一假设是成立的,因为基于环形实现(ring-based implementation, 即 Ring All-Reduce)的通信时间与 \(\frac{d-1}{d} = 1 - \frac{1}{d}\) 呈正相关
- 论文还可以分析批次大小 \(B\) 增大带来的影响
- 在特定的并行配置下,随着批次大小 \(B\) 的增加,\(b’ = \frac{B}{b}\) 会增大,进而导致流水线气泡大小 \(\frac{n - d}{b’}\) 减小,最终使吞吐量提升
- 此外,DP 所需的归约通信频率会随 \(B\) 的增大而降低,这也会进一步提升吞吐量
- 理解:这里是指相同的数据量和 epoch 下,\(B\) 越大,需要更新的总步数越少?
DP Data and Tensor Model Parallelism
- TP 中,每个微批次都需要执行归约通信,而跨多 GPU 服务器执行此类通信的成本较高
- DP 仅需在每个批次执行一次高成本的归约通信
- 而且,在 TP 中,每个模型并行进程(model-parallel rank)仅负责模型每层计算中的一部分;
- 若层的规模不够大,现代 GPU 执行这些子矩阵(sub-matrix)计算时可能无法达到峰值效率(peak efficiency)
- Takeaway #2 :
- 在同时使用 DP 和模型并行时,应将模型并行的总规模设为
$$M = t \cdot p$$- 其中 \(t\) 为 TP 规模,\(p\) 为 PP 规模,以确保模型的参数和中间元数据(intermediate metadata)能够放入 GPU 内存;
- 问题:模型并行的总规模本来就是:\(M = t \cdot p\) 吧,还需要什么特殊处理吗?
- 而 DP 则可用于扩展训练规模,以适配更多的 GPU
- 在同时使用 DP 和模型并行时,应将模型并行的总规模设为
Microbatch Size
- 微批次大小 \( b \) 的选择也会影响模型训练吞吐量
- 例如,论文在图 7 中看到,在单个 GPU 上,使用较大的微批次大小,每 GPU 吞吐量最多可提高 1.3 倍
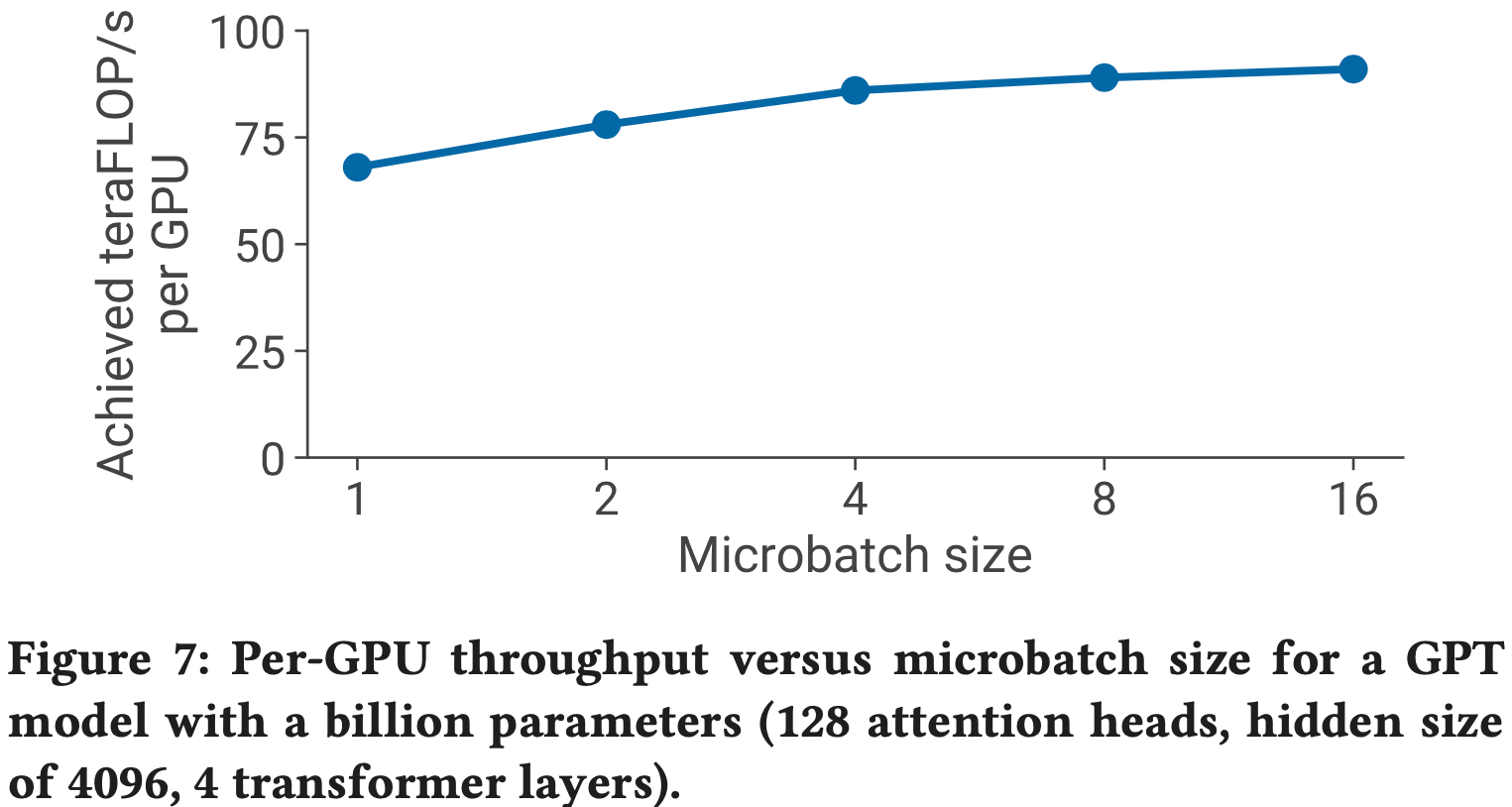
- 本节回答:确定给定并行配置 \( (p, t, d) \) 和批次大小 \( B \) 时,最优微批次大小 \( b \) 是多少呢?
- 无论微批次大小如何, DP 通信量将是相同的
- 给定函数 \( t_{f}(b) \) 和 \( t_{b}(b) \) 它们将微批次大小映射到单个微批次的前向和后向计算时间,则处理一个微批次的总计算时间(忽略通信成本)为(如前所述,定义 \( b’ \) 为 \( \frac{B}{d} \)):
$$ \left(\frac{b’}{b} + p - 1\right) \cdot \left(t_{f}(b) + t_{b}(b)\right). $$- 因此,微批次大小既影响操作的算术强度 (arithmetic intensity),也影响流水线气泡大小(通过影响 \( m \))
- 理解:随着 microbatch size \(b\) 增大,气泡占比变小,处理一个微批次的总时间减少,但总微批次数量增加
- 注:进一步分析总的时间为:
$$ b \cdot \left(\frac{b’}{b} + p - 1\right) \cdot \left(t_{f}(b) + t_{b}(b)\right). $$- 显然,上述式子存在一个处于最大值和最小值中间的最优点(类似二次函数)
- 因此,微批次大小既影响操作的算术强度 (arithmetic intensity),也影响流水线气泡大小(通过影响 \( m \))
- 图 8 显示了一个具有十亿参数且 \( (p, t) = (8, 8) \) 的 GPT 模型的估计吞吐量(使用方程 (1) 估计处理时间)
- 对于两种批次大小,最优的 \( b \) 都是 4
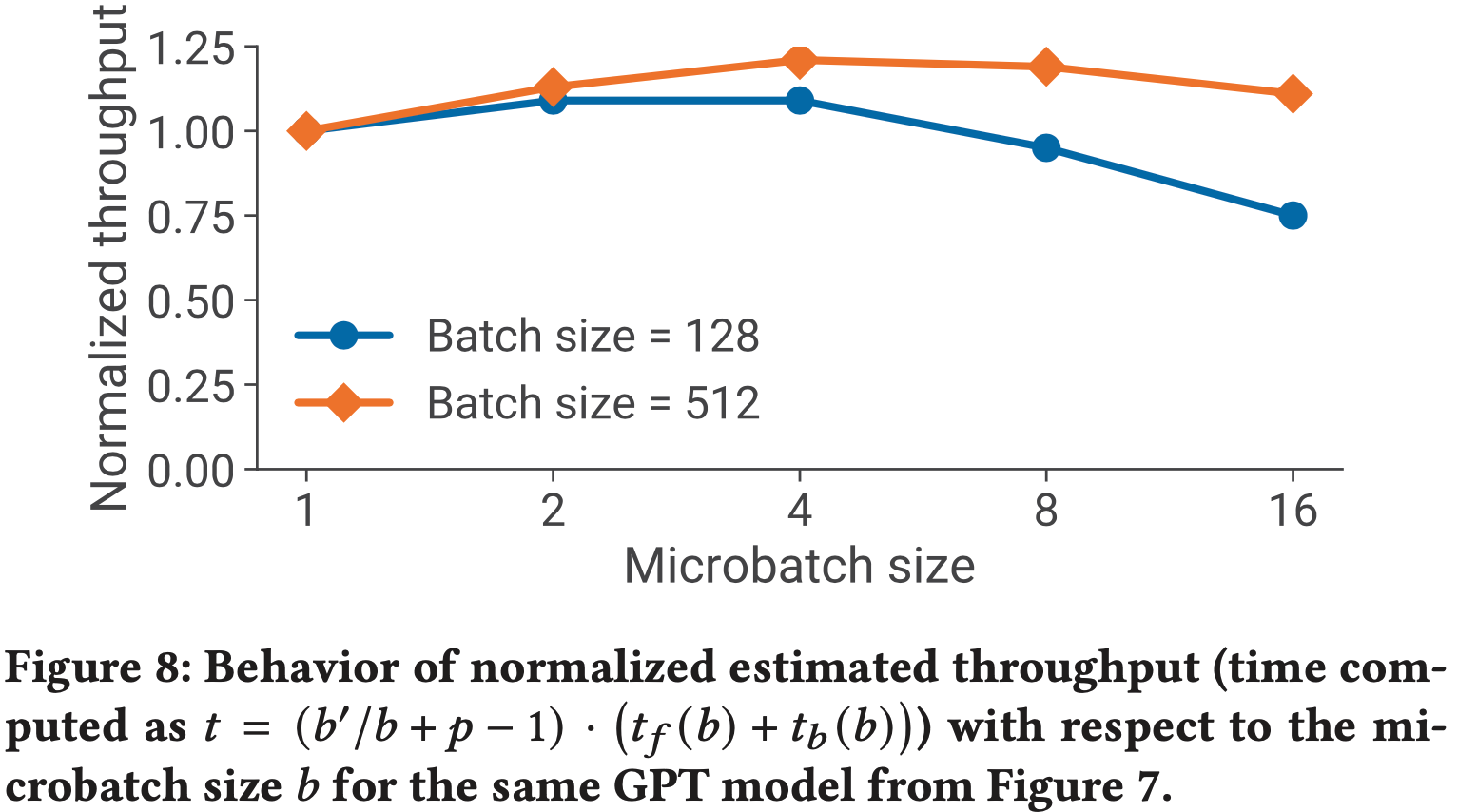
- 对于两种批次大小,最优的 \( b \) 都是 4
- Takeaway #3:
- 最优微批次大小 \( b \) 取决于模型的吞吐量和内存占用特性,以及流水线深度 \( p \)、 DP 大小 \( d \) 和批次大小 \( B \)
激活重计算,Activation Recomputation
- 激活重计算 (activation recomputation) (2016; 2000; 2019; 2020) 是一种可选技术,通过 仅存储给定流水线阶段的输入激活,而不是存储整个中间激活集,后者要大得多,来权衡增加执行的计算操作数量以换取更少的内存占用
- 注:成本是后向传递之前需要按需再次运行前向传递
- 为了在可接受的低内存占用下训练合理的大模型,需要使用激活重计算
- 之前的工作如 PipeDream-2BW (2021) 已经研究了激活重计算的性能影响
- 激活检查点 (activation checkpoint) 的数量不影响吞吐量,但影响内存占用
- 设 \( A^{\text{input} } \) 为一层的输入激活大小,\( A^{\text{intermediate} } \) 为每层的中间激活大小
- 如果一个模型阶段有 \( l \) 层,并且有 \( c \) 个检查点,则总内存占用将为
$$ c \cdot A^{\text{input} } + \frac{l}{c} \cdot A^{\text{intermediate} } $$- \(\frac{l}{c} \cdot A^{\text{intermediate} }\) 为每个时刻在使用的激活大小
- 当 \( c = \sqrt{l \cdot (A^{\text{intermediate} }/A^{\text{input} })} \) 时,该函数取得最小值
- 在实践中,论文通过经验测量 \( A^{\text{intermediate} } \)
- 在大多数情况下,每 1 或 2 个 Transformer 层设置一个检查点是最优的
- 其他技术,如激活分区 (activation partitioning) (2020),也可以与 TP 结合使用,以进一步减少由激活引起的内存占用
Implementation
- 论文将 PTD-P 作为 Megatron-LM 代码库的一个扩展来实现
- 论文的实现基于 PyTorch (2017)
- 论文使用 NCCL (2018) 进行设备间的通信
- 为了获得良好的性能,论文实施了针对通信和计算的优化,下面将概述这些优化
Communication Optimizations
- 当使用 PP 时,作者希望并行地发送和接收前向和后向传播的张量
- 每个 DGX A100 节点配备了 8 个 InfiniBand (IB) 网络卡
- 不幸的是,发送和接收是点对点的,并且只发生在两个服务器上的一对 GPU 之间,这使得很难在流水线内的单个通信调用中利用所有 8 张卡
- 然而,我们可以利用同时使用 TP 和 PP 这一事实来降低跨节点通信的开销
- 特别地,论文注意到每个 Transformer 层的输出在 TP Rank 之间是复制的(在 MLP 块中的 \(g\) 操作之后,见图 5(a))
- 因此,在执行 TP 的两个连续流水线阶段中的 Rank ,会发送和接收完全相同的张量集合(图 5(a))

- 因此,在执行 TP 的两个连续流水线阶段中的 Rank ,会发送和接收完全相同的张量集合(图 5(a))
- 对于足够大的模型,论文使用大小为 8 的 TP
- 这意味着论文在相邻的多 GPU 服务器上的对应 GPU 之间发送相同的张量集合 8 次
- 为了减少这种冗余,我们可以在发送端将张量分割成大小相等的块,然后只将一个块发送到下一个节点上的对应 Rank ,使用该 Rank 自己的 InfiniBand 卡(例如,在图 9 中, Rank 1 发送给 Rank 3, Rank 2 发送给 Rank 4)
- 对于 8 个 TP Rank ,每个块的大小将减小为原来的八分之一
- 然后,在接收端,我们可以通过 NVLink 执行一个 all-gather 操作(这比 InfiniBand 互连快得多)来重新构建完整的张量(如图 5(b) 所示)
- 论文称之为 分散/聚集通信优化 (scatter/gather communication optimization)
- 这种优化有助于更好地利用 DGX A100 服务器上的多个 IB 卡,并使诸如交错调度这样通信密集的调度变得可行
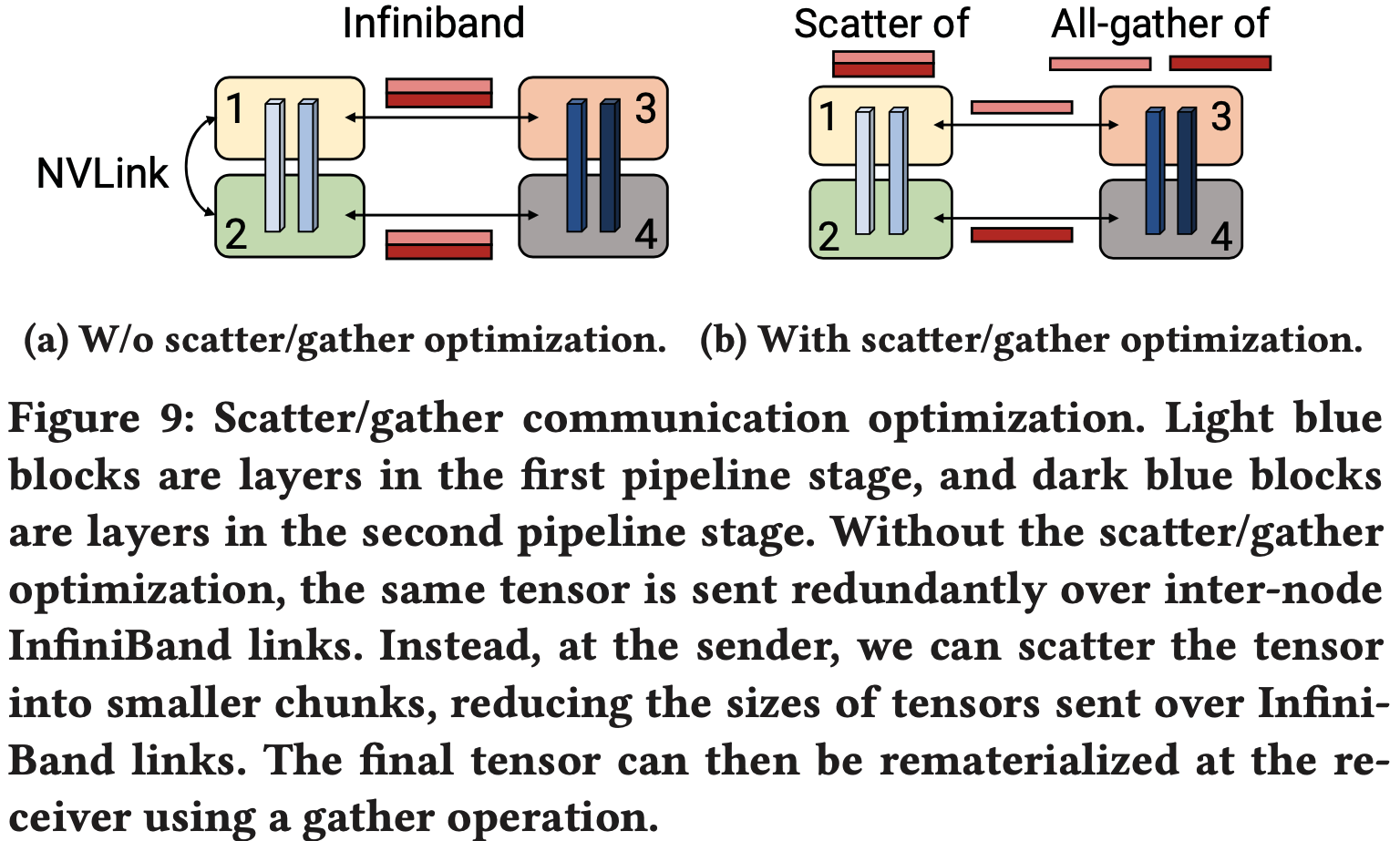
- 这种优化有助于更好地利用 DGX A100 服务器上的多个 IB 卡,并使诸如交错调度这样通信密集的调度变得可行
- 量化来看,通过分散-聚集通信优化,每对连续阶段之间需要执行的总通信量减少到 \(\frac{bsh}{t}\),其中 \(t\) 是 TP 大小,\(s\) 是序列长度,\(h\) 是隐藏层大小(在论文的实验中 \(t=8\))
Computation Optimizations
- 论文对计算图实施了三个模型特定的优化以获得高性能
- 第一,论文改变了 Transformer 层中的数据布局,以避免内存密集的转置操作,并启用跨步批处理 GEMM 内核
- 具体来说,论文将数据布局从 \([b, s, a, h]\) 改为 \([s, b, a, h]\),其中 \(b\)、\(s\)、\(a\) 和 \(h\) 分别是批处理大小、序列长度、注意力头数和隐藏层大小的维度
- 第二,论文使用 PyTorch JIT (2016) 为一序列逐元素操作(偏置 + GeLU 以及偏置 + Dropout + 加法)生成了融合内核
- 第三,论文创建了两个自定义内核来实现缩放、掩码和 Softmax(归约)操作的融合:
- 一个支持通用掩码(用于如 BERT 的模型),另一个支持隐式因果掩码(用于如 GPT 的自回归模型)
- 论文将在下一节量化这些优化的效果
Evaluation
- 在本节中,论文试图回答以下问题:
- PTD-P 的性能如何?它是否能够满足现实的端到端训练时间?
- 对于给定的模型和批处理大小, PP 的扩展性如何?交错调度对性能有多大影响?
- 不同的并行化维度如何相互作用?微批处理大小等超参数的影响是什么?
- 分散-聚集通信优化的影响是什么?在规模上运行训练迭代时,论文对硬件施加了哪些类型的限制?
- 论文所有的结果都是在 Selene 超级计算机 (Selene, 2000) 上使用混合精度运行的
- 每个集群节点有 8 个 NVIDIA 80-GB A100 GPU (2018),通过 NVLink 和 NVSwitch (2018) 相互连接
- 每个节点有八个 NVIDIA Mellanox 200Gbps HDR InfiniBand HCA 用于应用通信,另外每个节点还有两个 HCA 用于专用存储
- 节点通过具有 850 个交换机的三级(叶子、脊柱、核心)胖树拓扑连接
- 这种拓扑支持高效的 All-Reduce 通信(深度学习训练中的主导通信模式)
- 集群使用全 NVME 共享并行文件系统进行高性能数据访问和存储
- 一个具有 16 位精度的 A100 GPU 的峰值设备吞吐量为 312 teraFLOP/s
- 对于论文的大部分结果,论文报告每个 GPU 的吞吐量
- 总吞吐量可以通过乘以使用的 GPU 数量来计算
- 在论文的实验中,论文使用适当大小的 GPT 模型
- 特别地,对于任何给定的微基准测试,模型需要能够适应实验中使用的模型并行 GPU 的数量
- 适当的时候,论文使用标准的模型架构,如 GPT-3 (2016)
End-to-End Performance
- 论文考虑了论文的系统在参数量从十亿到一万亿的 GPT 模型上的端到端性能,使用了张量、流水线和 DP (使用第 3 节中描述的启发式方法选择维度)
- 特别地,论文使用了启用了分散/聚集优化的交错流水线调度
- 所有模型使用词汇表大小(表示为 \(V\))为 51,200(1024 的倍数)和序列长度(表示为 \(s\))为 2048
- 论文改变隐藏层大小(\(h\))、注意力头数和层数(\(l\))
- 模型中的参数量 \(P\) 可以计算为:
$$P=12lh^{2}\left(1+\frac{13}{12h}+\frac{V+s}{12lh}\right). \tag{2}$$
- 随着模型大小的增加,论文也增加批处理大小(\(B\))和 GPU 的数量(\(n\))
- 模型中大部分的浮点运算是在 Transformer 层和 logit 层中的矩阵乘法(GEMMs)中执行的
- 仅考虑这些 GEMMs,每次迭代的 FLOPs 数量为(更多细节见附录):
$$F=96Bslh^{2}\left(1+\frac{s}{6h}+\frac{V}{16lh}\right). \tag{3}$$ - 这是真实 FLOP 计数的下限,但应接近实际值
- 论文将 FLOP 计为浮点运算,无论精度如何
- 方程 (3) 假设了激活重计算,并考虑了与额外前向传播相关的浮点运算
- 仅考虑这些 GEMMs,每次迭代的 FLOPs 数量为(更多细节见附录):
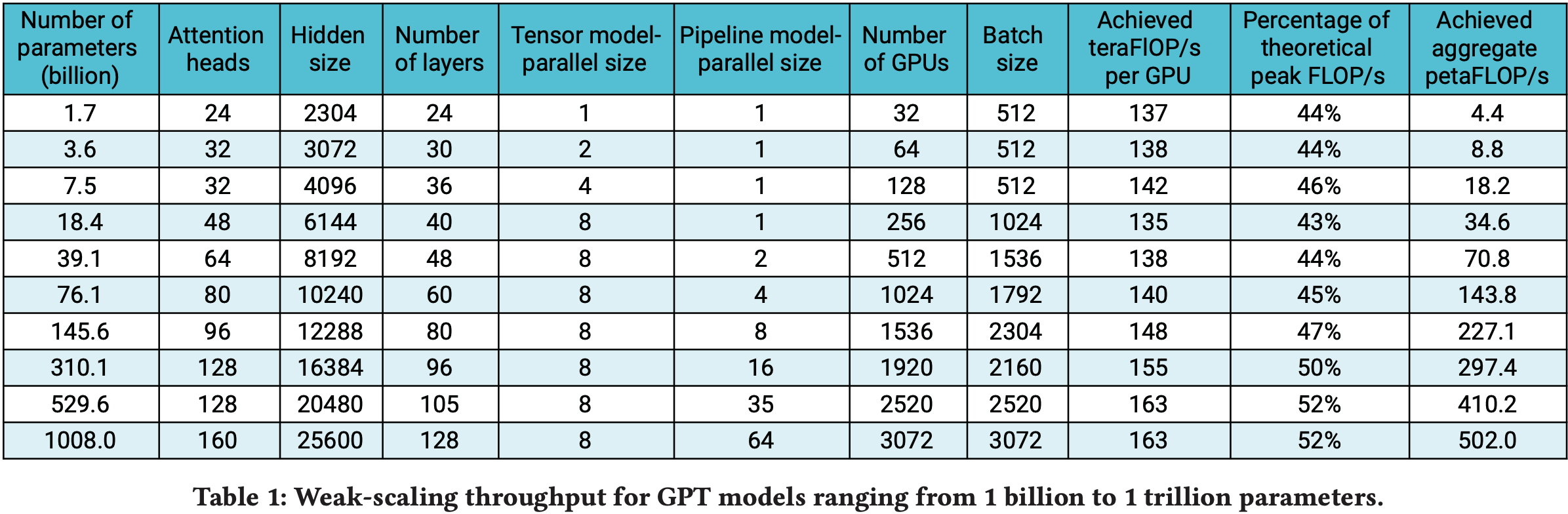
- 表 1 显示了模型配置以及实现的 FLOP/s(包括每个 GPU 的和所有 GPU 的总和)
- 论文看到在 3072 个 A100 GPU(384 个 DGX A100 节点)上实现了超线性扩展,因为随着模型变大(更大的矩阵乘法),GPU 利用率提高,而通信时间相对于计算时间没有显著增加
- 吞吐量是针对端到端训练测量的,即包括所有操作,包括数据加载、优化器步骤、通信和日志记录
- 对于最大的模型,论文达到了峰值设备吞吐量的 52%,对于最小的模型,达到了峰值设备吞吐量的 44%
训练时间估算
- 给定这些吞吐量,论文还可以估算在 \(T\) 个 Token 上进行端到端训练所需的总时间
- 训练需要 \(I=\frac{T}{B\cdot s}\) 次迭代(\(s\) 为序列长度)
- 使用方程 (3) 中的 \(F\) 值和表 1 中的经验端到端吞吐量(表示为 X),我们可以估算总训练时间
- 对于表 1 中的配置,论文有 \(12lh \gg (V+s)\) 和 \(16lh \gg V\)
- 将这些观察结果与方程 (2) 和 (3) 结合,论文得到:
$$\text{End-to-end training time}\approx\frac{8TP}{nX}.$$- 其中:
- \(n\) 为 GPU 数量;
- \(X\) 为每个 GPU 的吞吐量;
- \(T\) 为 Token 数量
- \(P\) 为模型参数量
- 其中:
- 让论文以具有 \(P=\) 175B 参数的 GPT-3 模型为例
- 该模型在 \(T=3000\) 亿个 Token 上进行了训练
- 在 \(n=1024\) 个 A100 GPU 上使用批处理大小 1536,论文实现了每个 GPU \(X=140\) teraFLOP/s 的吞吐量
- 因此,训练该模型所需的时间为 34 天
- 对于 1 万亿参数模型,论文假设端到端训练需要 450B 个 Token
- 使用 3072 个 A100 GPU,我们可以实现每个 GPU 163 teraFLOP/s 的吞吐量,端到端训练时间为 84 天
- 作者认为这些训练时间(使用合理数量的 GPU)是可行的
- 该模型在 \(T=3000\) 亿个 Token 上进行了训练
Comparison to ZeRO-3
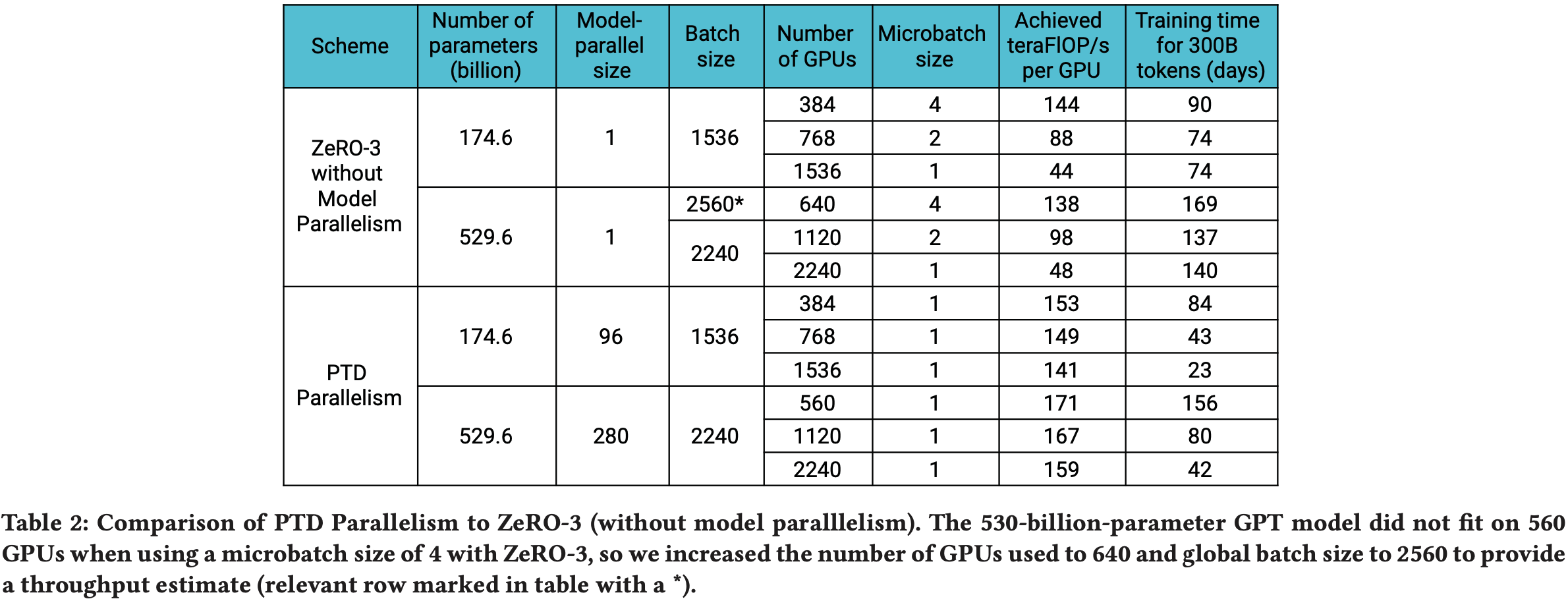
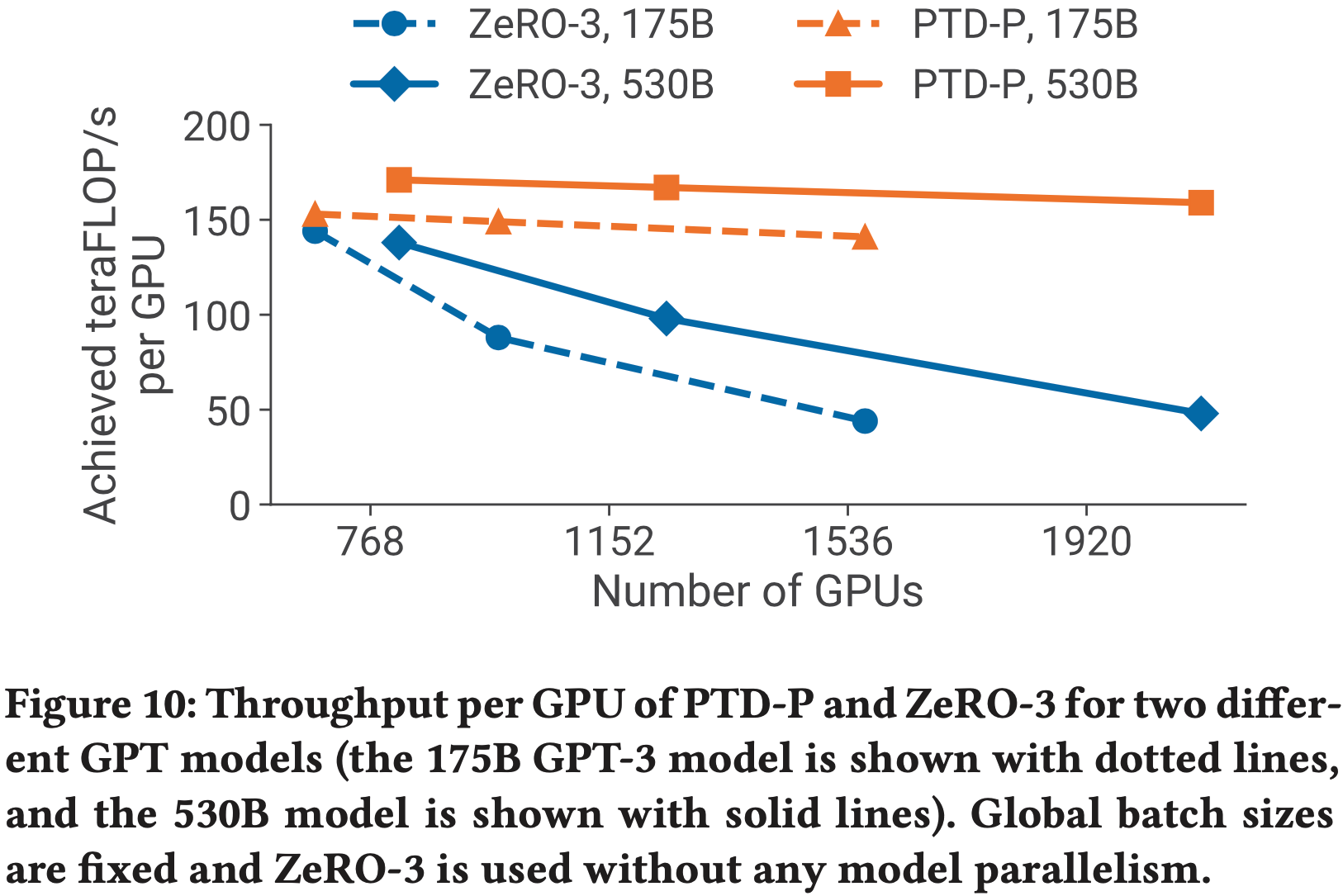
- 论文在表 2 和图 10 中将 PTD-P 与 ZeRO-3 (2020; 2021) 进行了比较(针对标准的 GPT-3 模型架构以及表 1 中的 530B 参数模型)
- 这些结果提供了一个与不使用模型并行的方法的对比点
- 论文使用 DeepSpeed Python 库 (2020) 将 ZeRO 集成到论文的代码库中
- 当论文增加 GPU 数量时,论文保持全局批处理大小不变
- 在 GPU 数量较少且微批处理大小为 4 的情况下,PTD-P 对于 175B 和 530B 参数模型的吞吐量分别高出 6% 和 24%
- 随着论文增加 GPU 数量,PTD-P 比单独使用 ZeRO-3 扩展得更优雅(见图 10)
- 例如,通过将 GPU 数量加倍(保持批处理大小不变),由于跨节点通信更少,PTD-P 对两个模型的性能均优于 ZeRO-3 70%
- 论文只考虑了不使用 TP 的 ZeRO-3
- ZeRO-3 可以与模型并行结合,以潜在地改善其扩展行为
PP (Pipeline Parallelism)
- 论文现在单独评估 PP 的弱扩展性能,并将非交错调度与交错调度的性能进行比较
Weak Scaling
- 论文使用弱扩展设置、一个具有 128 个注意力头和隐藏层大小为 20480 的 GPT 模型以及微批处理大小为 1 来评估默认非交错 PP 调度的扩展性
- 随着论文增加流水线阶段的数量,论文也按比例增加模型中的层数来增加模型的大小
- 例如,当 PP 大小为 1 时,论文使用具有 3 个 Transformer 层和 15B 参数的模型,当 PP 大小为 8 时,论文使用具有 24 个 Transformer 层和 121B 参数的模型
- 论文对所有配置使用 TP 大小为 8,并改变使用的 A100 GPU 总数,从 8 到 64
- 图 11 显示了两种不同批处理大小下每个 GPU 的吞吐量,以说明流水线气泡的影响,其行为符合 \(\frac{p-1}{m}\)(第 2.2.1 节)
- 正如预期的那样,较高的批处理大小扩展性更好,因为流水线气泡被分摊到更多的微批处理上
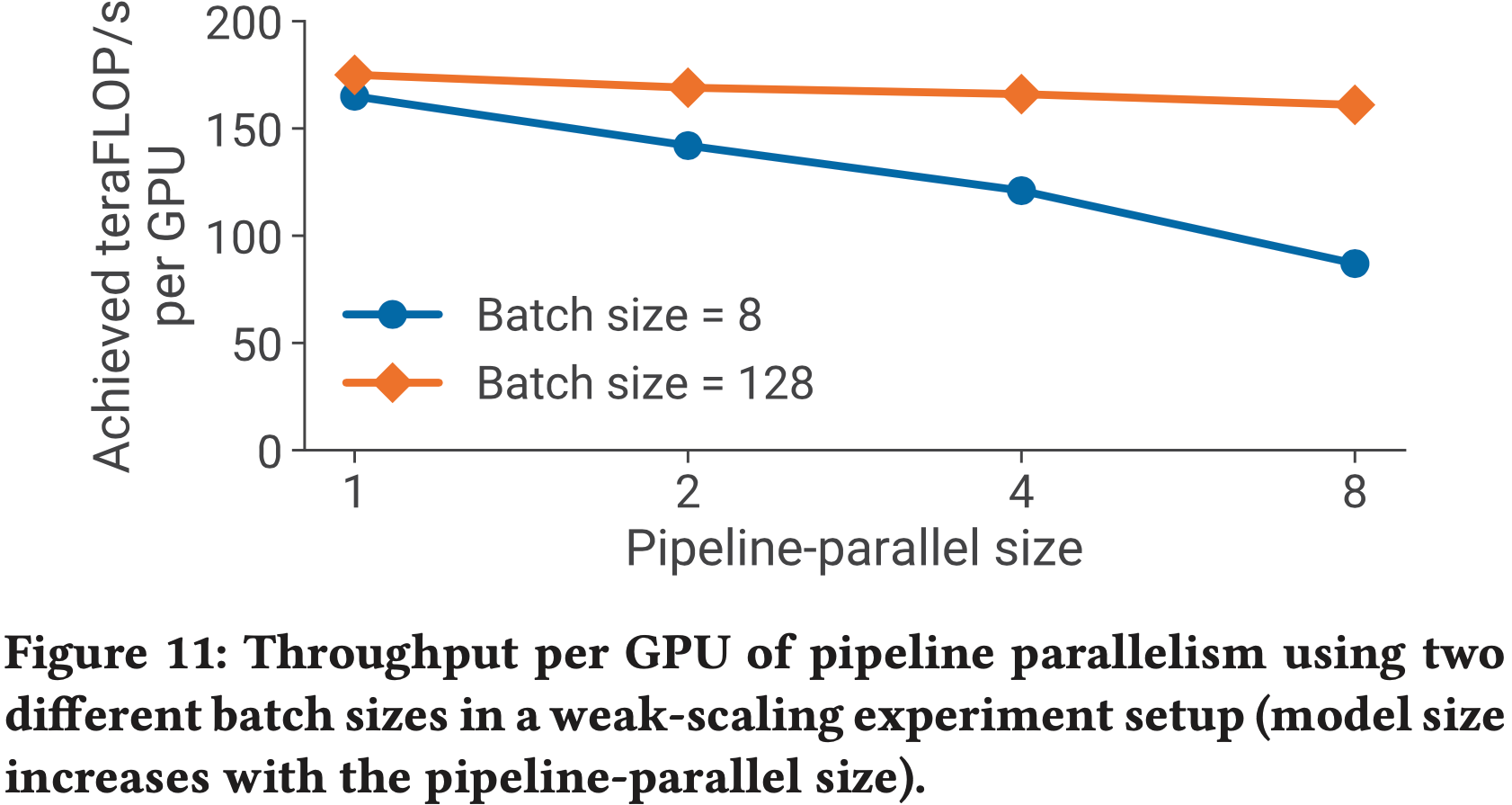
- 正如预期的那样,较高的批处理大小扩展性更好,因为流水线气泡被分摊到更多的微批处理上
Interleaved versus Non-Interleaved Schedule
- 图 12 显示了在具有 175B 参数(96 层,96 个注意力头,隐藏层大小为 12288)的 GPT-3 (2020) 模型上,交错和非交错调度每个 GPU 的吞吐量
- 带有分散/聚集通信优化的交错调度比非交错(默认)调度具有更高的计算性能
- 随着批处理大小的增加,这个差距会缩小,原因有二:
- (a) 随着批处理大小的增加,默认调度中的气泡大小减小
- (b) 流水线内的点对点通信量与批处理大小成正比,因此随着通信量的增加,非交错调度会赶上(交错调度每个样本的通信量更多)
- 在没有分散/聚集优化的情况下,默认调度在较大批处理大小下表现优于交错调度(未显示)
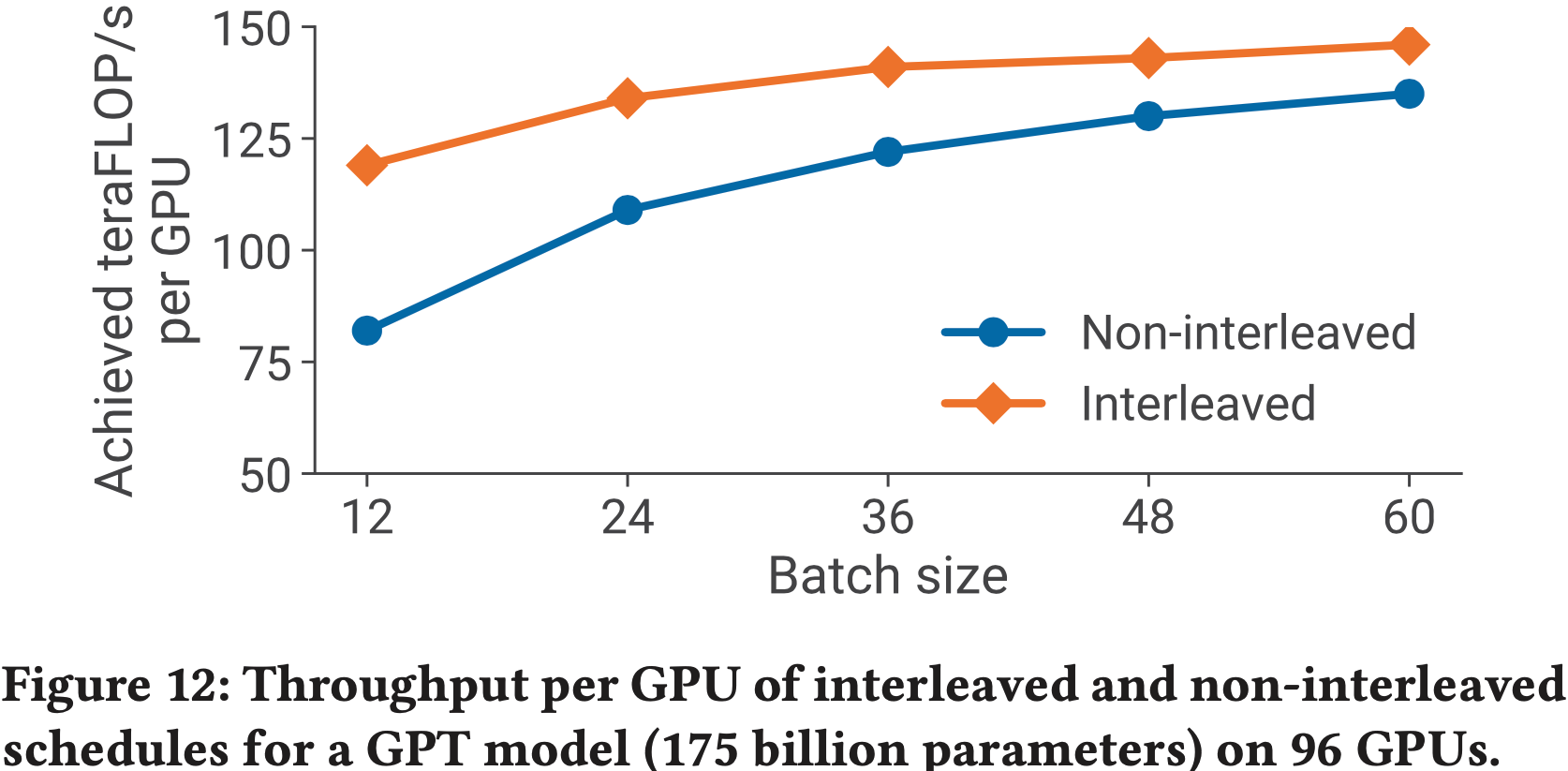
Comparison of Parallel Configurations
- 在本小节中,论文展示了结合不同并行化维度所带来的各种权衡
- 特别地,论文展示了对于给定模型和多个批处理大小,使用相同数量 GPU 的并行配置的性能
TP 与 PP (Tensor versus Pipeline Parallelism)
- 论文评估了对于给定模型和批处理大小,流水线和 TP 对性能的影响
- 图 13 中的实证结果显示了结合使用张量和 PP 来训练一个 161B 参数 GPT 模型(32 个 Transformer 层以支持 PP 大小为 32,128 个注意力头,隐藏层大小为 20480)的重要性,以实现低通信开销和高计算资源利用率
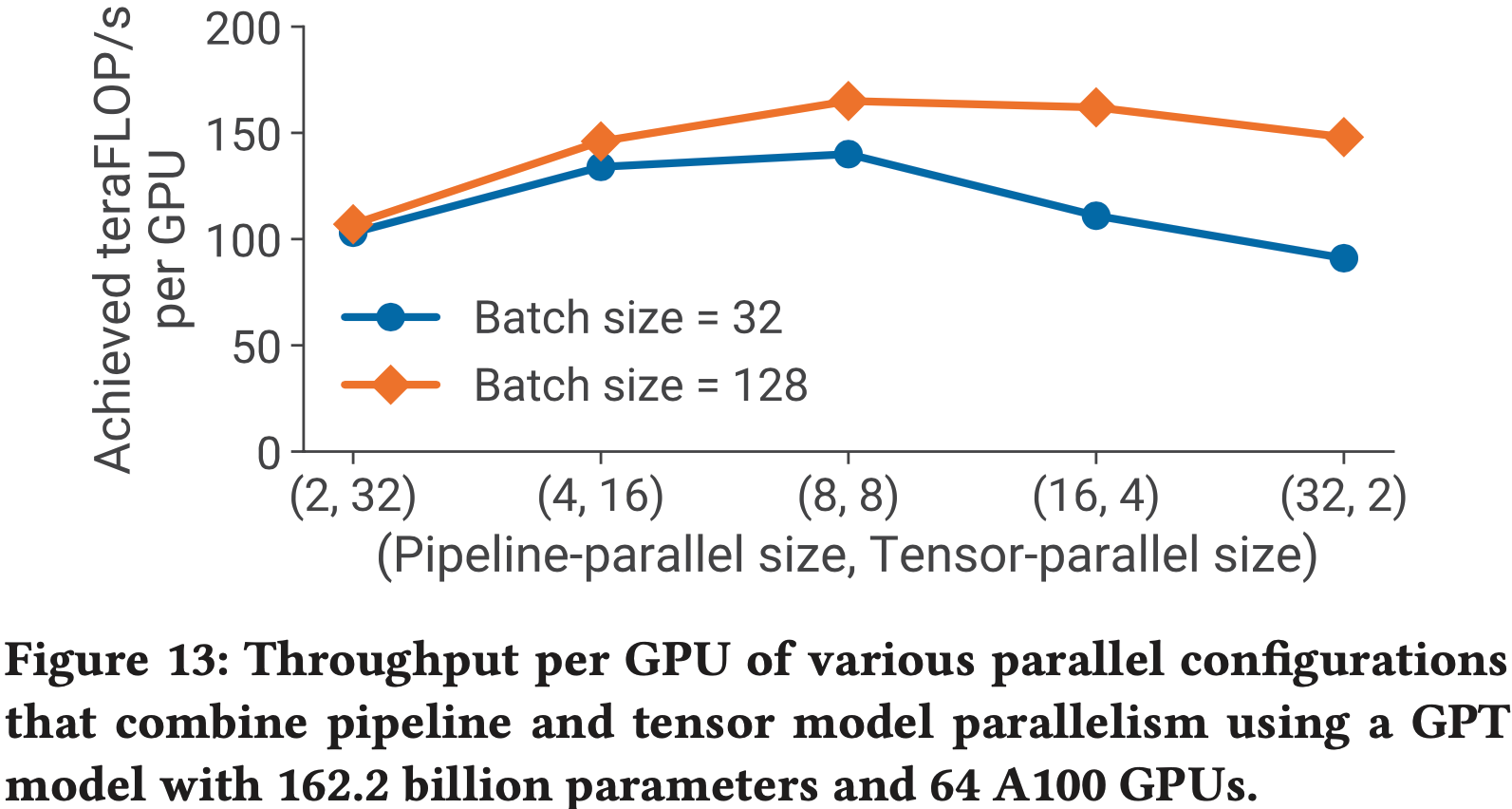
- 论文观察到
- TP 在一个节点(DGX A100 服务器)内效果最好,因为其 All-Reduce 通信开销大
- PP 使用成本低得多的点对点通信,可以在节点之间进行,而不会成为整个计算的瓶颈
- 使用 PP 时,可能会在流水线气泡中花费大量时间:
- 因此,流水线阶段的总数应受到限制,使得流水线中的微批处理数量是流水线阶段数量的合理倍数
- 当 TP 大小等于单个节点中的 GPU 数量(对于 DGX A100 节点为 \(8\))时 ,达到了峰值性能
- 这一结果表明,无论是单独使用 TP (由 Megatron (2019) 使用)还是单独使用 PP (由 PipeDream (2019) 和其他人使用),都无法与结合使用这两种技术的性能相媲美
PP 与 DP (Pipeline versus Data Parallelism)
- 论文在图 14 中评估了数据和 PP 对一个具有 59 亿参数(32 个 Transformer 层,32 个注意力头,隐藏层大小为 3840)的 GPT 模型性能的影响
- 论文使用比之前更小的模型,因为论文想展示当模型并行大小仅为 \(2\) 时模型能够容纳的性能
- 为简单起见,论文在这些实验中保持微批处理大小等于 \(1\)
- 论文看到,对于每个批处理大小,吞吐量随着 PP 大小的增加而降低,这与论文在第 3.3 节中的分析模型相符
- PP 应主要用于支持训练无法容纳在单个工作器上的大模型,而 DP 应用于扩展训练规模
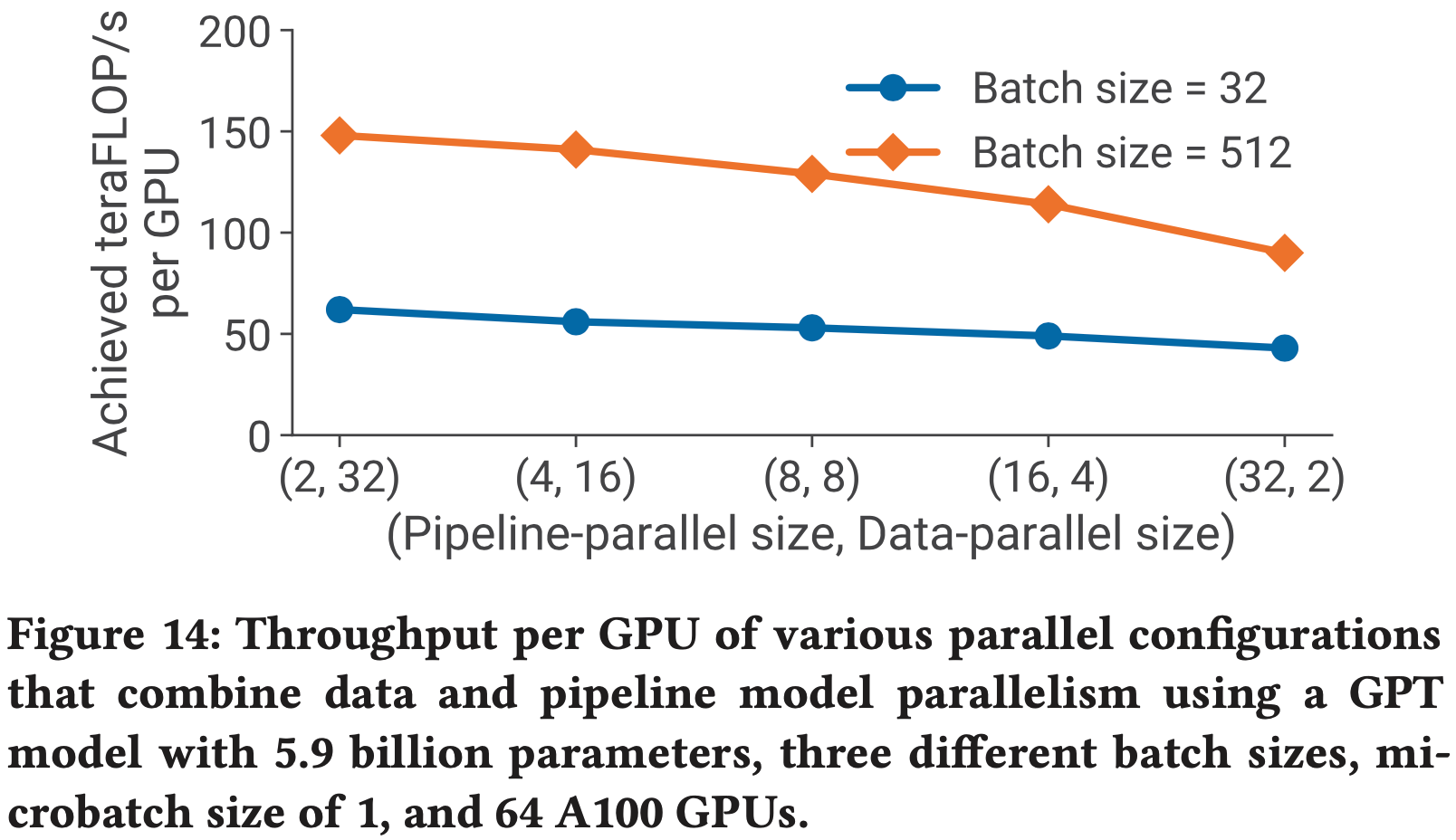
TP 与 DP (Tensor versus Data Parallelism)
- 论文在图 15 中评估了数据和 TP 对同一个 59 亿参数 GPT 模型性能的影响(使用较小模型的原因同上)
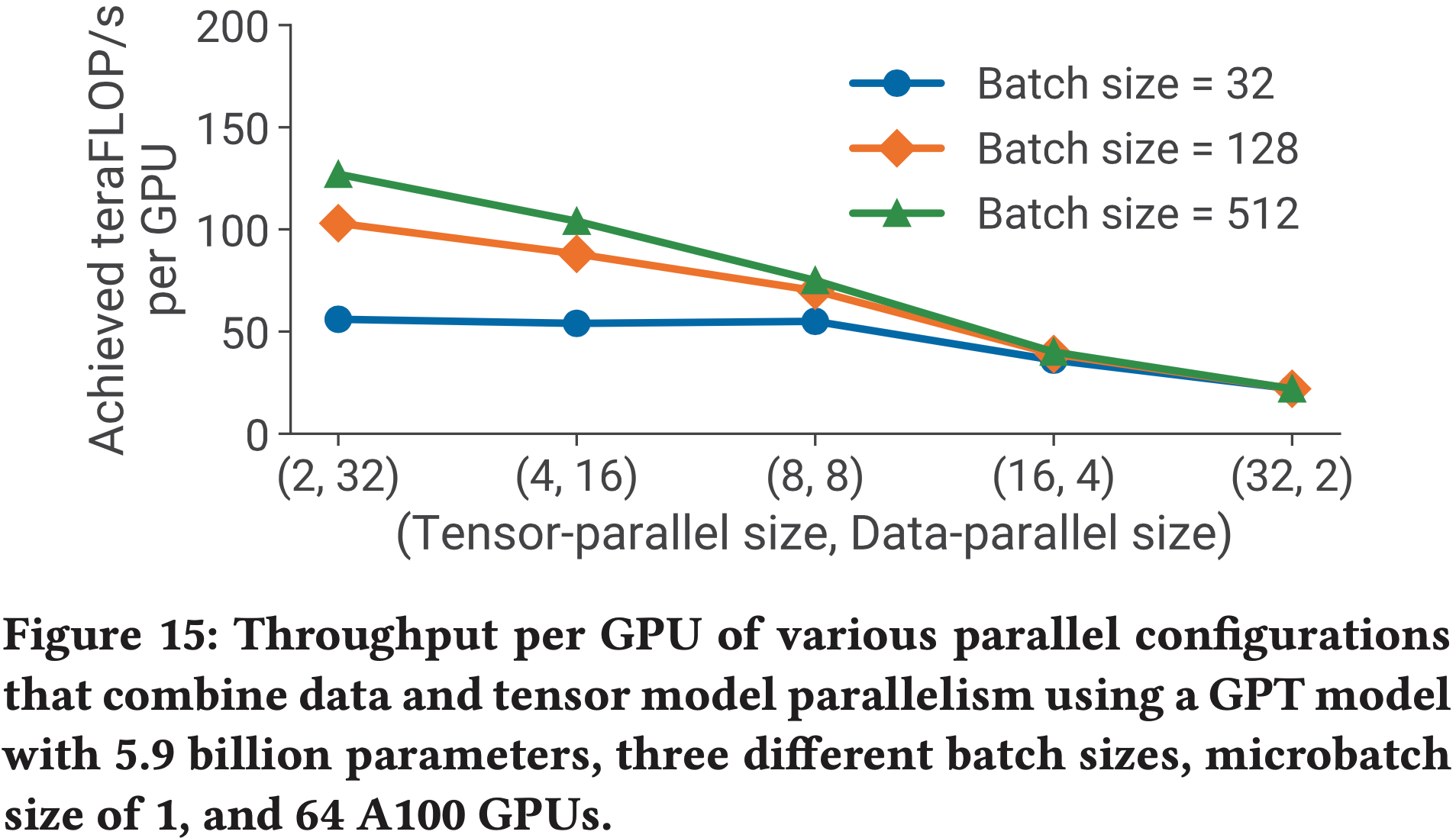
- 如前所述,论文最初保持微批处理大小等于 \(1\)
- 在较大的批处理大小和微批处理大小为 1 的情况下, DP 通信不频繁;
- TP 中所需的 all-to-all 通信需要对批次中的每个微批处理执行
- 这种 TP 的 all-to-all 通信主导了端到端训练时间,特别是当通信需要在多 GPU 节点之间执行时
- 随着 TP 大小的增加,论文在每个 GPU 上执行更小的矩阵乘法,降低了每个 GPU 的利用率
- 尽管 DP 可以导致高效的扩展,但不能单独使用 DP 来处理具有有限训练批处理大小的非常大的模型,原因是
- a) 内存容量不足
- b) DP 的扩展限制
- 例如,GPT-3 是以 1536 的批处理大小训练到收敛的
- 因此, DP 仅支持扩展到 1536 个 GPU;然而,大约使用了 \(10,000\) 个 GPU 来在合理的时间内训练该模型
Microbatch Size
- 论文在图 16 中评估了微批处理大小对结合流水线和 TP 的并行配置性能的影响(针对一个具有 91B 参数(\((t,p)=(8,8)\))的模型)
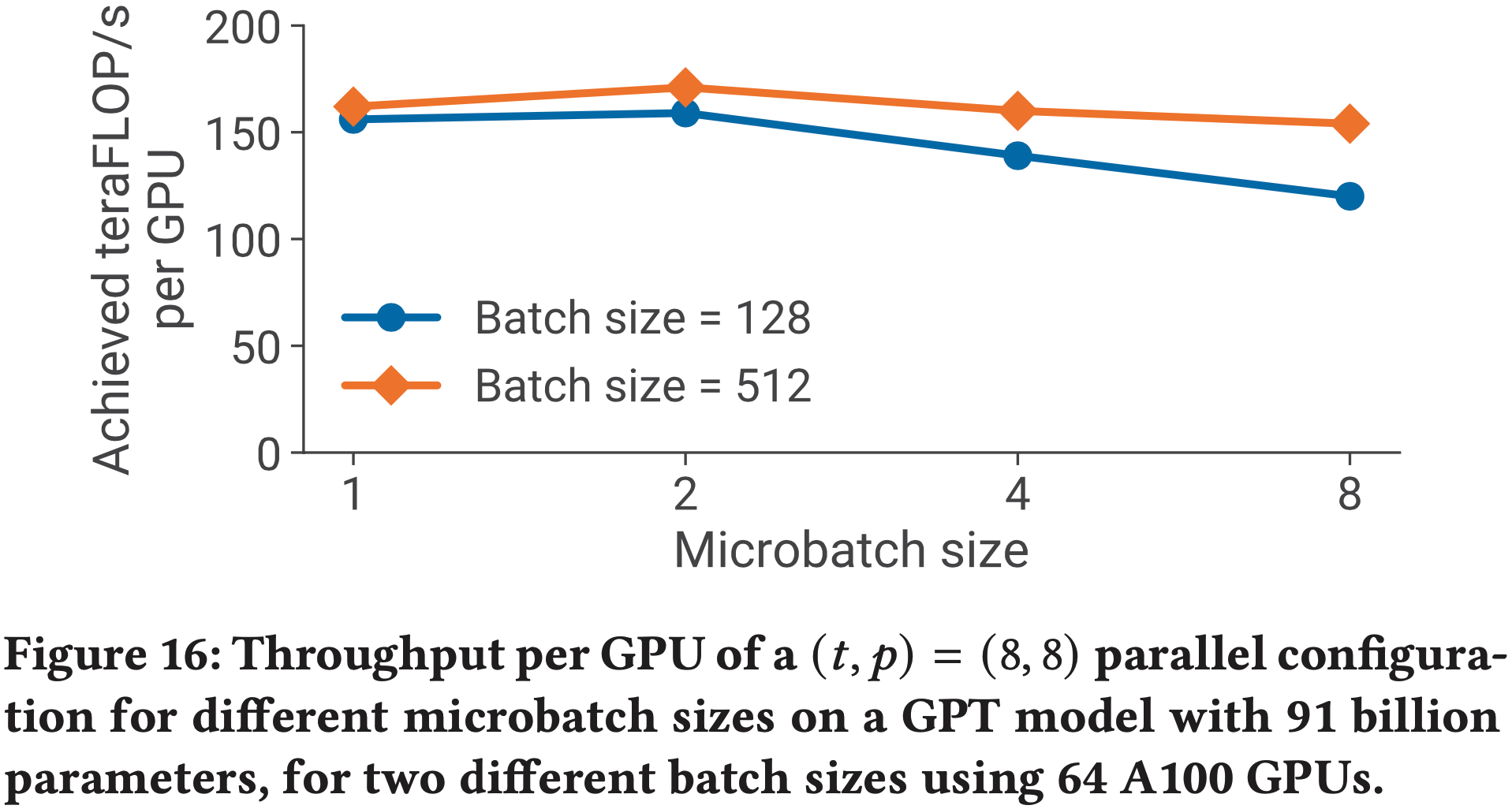
- 论文看到:
- 对于这个模型,最佳微批处理大小是 \(2\);
- 对于其他模型,最佳微批处理大小是不同的(图中未显示)并且是模型依赖的
- 对于给定的批处理大小,
- 增加微批处理大小会减少流水线中的微批处理数量(\(m\)),导致更大的流水线气泡;
- 但增加微批处理大小也可以通过增加执行内核的算术强度来提高 GPU 利用率
- 以上这两个因素是相互矛盾的,这使得选择最佳微批处理大小具有挑战性
- 论文来自第 3.3 节的分析模型合理地近似了真实性能,并且可以作为代理来确定如何为各种训练配置和模型选择此超参数值
Activation Recomputation
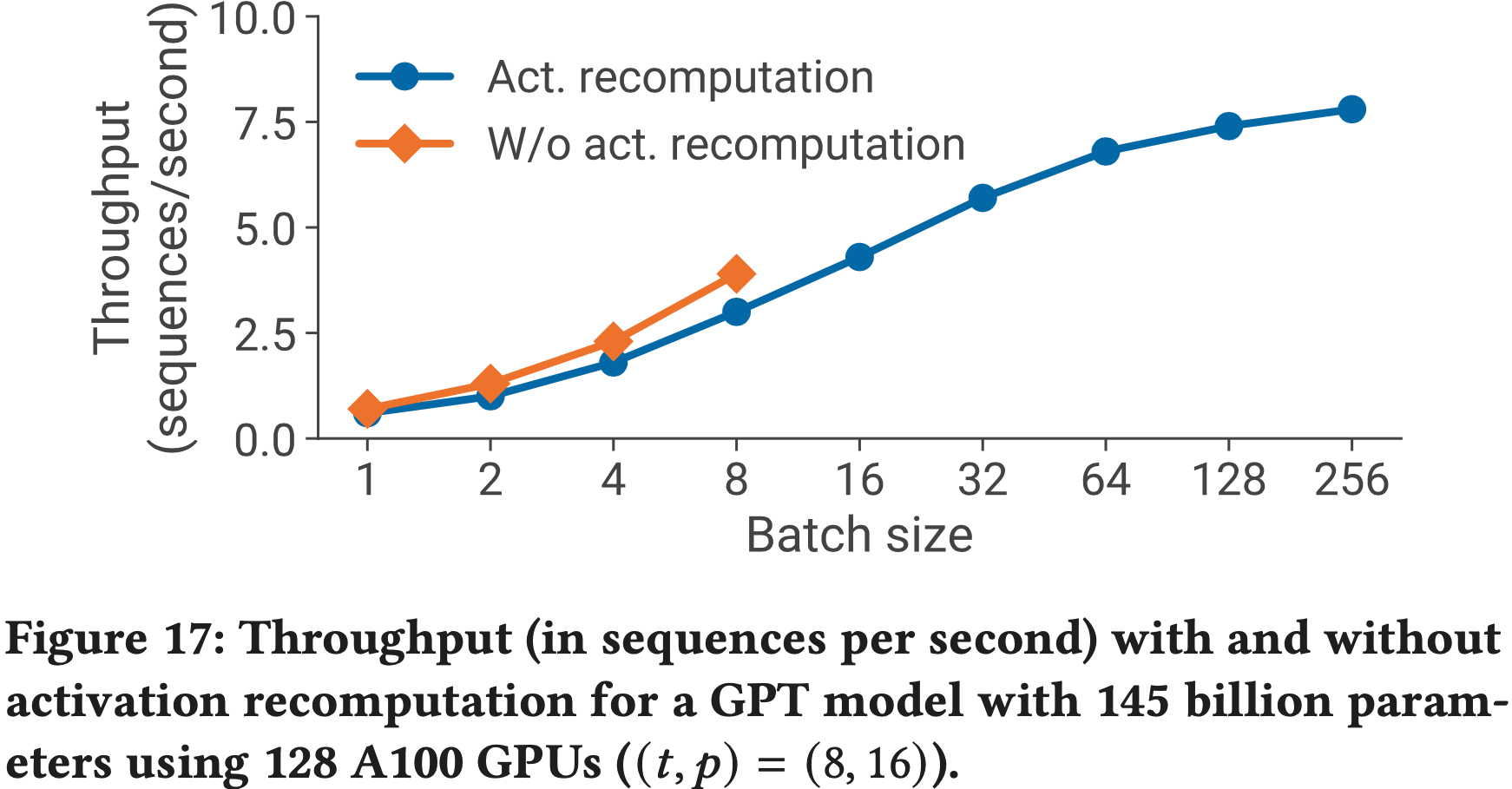
- 图 17 显示了对于具有 145B 参数(80 个 Transformer 层,96 个注意力头,隐藏层大小为 12288)的 GPT 模型,在使用 128 个 A100 GPU、\((t,p)=(8,16)\) 以及一系列批处理大小的情况下,使用和不使用激活重计算的吞吐量
- 对于小批处理大小,由于在反向传播期间需要执行额外的前向传播,激活重计算导致吞吐量(以每秒序列数计)降低高达 33%
- 但激活重计算是支持更大批处理大小所必需的
- 由于流水线气泡更小,使用激活重计算的大批处理大小的吞吐量比不使用激活重计算(对于较小批处理大小)实现的最佳吞吐量高出 up to 2\(\times\)
Scatter-Gather Optimization
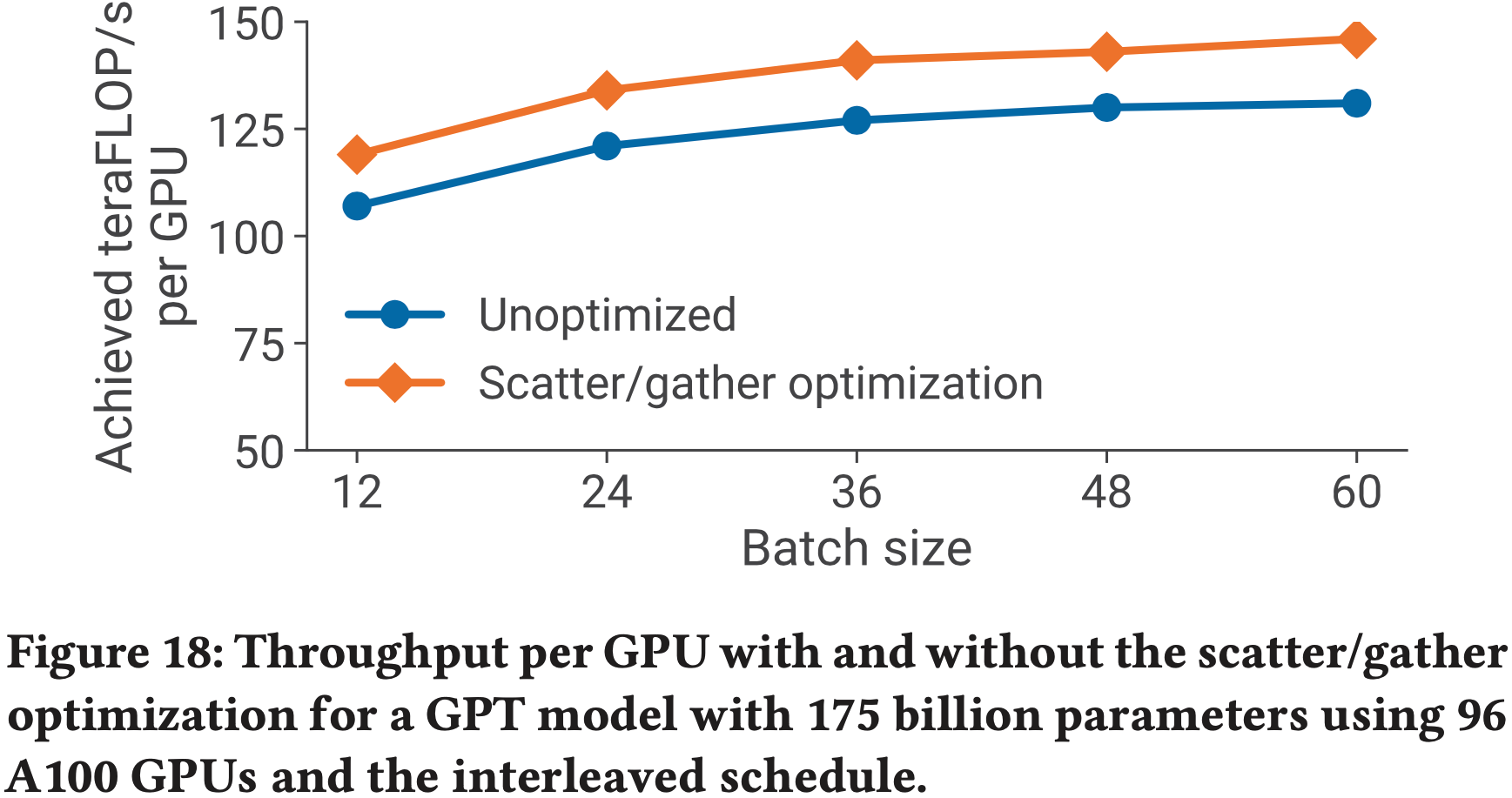
- 图 18 显示了对于具有 175B 参数的 GPT-3 模型,使用和不使用(未优化)分散/聚集通信优化时每个 GPU 的吞吐量
- 论文看到,通过减少跨节点链路上的通信量,对于通信密集的调度(大批处理大小带交错),吞吐量提高了 up to 11%
Fused Operators(融合操作)
- 论文还评估了第 4.2 节中描述的操作符融合对性能的影响
- 对于 GPT-3 模型(175B 参数),通过融合,吞吐量提高了 19%(从每个 GPU 113 teraFLOP/s 到每个 GPU 135 teraFLOP/s)
- 对于更大的 530B 参数 GPT 模型(图 1 中的模型配置),吞吐量提高了 11%(从每个 GPU 133 teraFLOP/s 到每个 GPU 148 teraFLOP/s)
Inter-Node Communication Bandwidth
- 论文强劲的结果是优化软件和硬件栈共同使用的副产品
- 特别地,论文利用了同一服务器内和跨服务器的 GPU 之间的高带宽通信链路
- 在具有 3072 个 GPU 的万亿参数模型上,论文观察到流水线阶段之间点对点通信的有效二分带宽为 892 GB/s,而 DP 副本之间 All-Reduce 操作的有效二分带宽为 12.9 TB/s
- 跨设备的操作符分区若优化不足,会导致更多的节点间通信,从而阻碍扩展性能
Checkpoint Loading and Saving
- 训练大模型的一个重要实际考虑是加载和保存模型检查点,对于论文中考虑的模型,检查点尤其大
- 例如,万亿参数模型的检查点大小为 13.8 TB
- 问题:如果仅考虑参数,换算后不太对,1000000000000*4/1000/1000/1000/1000 = 4 TB,若考虑激活值才会到 12 TB
- 所有 384 个节点(3072 个 GPU)对万亿参数模型的检查点初始加载达到了 1TB/s 的峰值读取带宽,这是并行文件系统可能的最大读取吞吐量
- 检查点保存达到了峰值写入带宽的 40%(273 GB/s)
Related Work
Parallelism for Large Models
- PP(Pipeline model parallelism)是一种用于训练大模型的常用技术
- PP 有几种不同的模式:
- 论文讨论的模式使用流水线刷新(flush)来确保严格(strict)的优化器语义
- TeraPipe (2021) 为像 GPT 这样的自回归模型(auto-regressive models)在单个训练序列的 token 之间暴露了细粒度的 PP
- PipeTransformer (2021) 通过冻结具有“稳定”权重的层,弹性地调整 PP 和 DP 的程度,并将资源专用于训练剩余的“活跃”层
- HetPipe (2020) 在一组异构加速器上结合使用了流水线和 DP
- PP 也可以使用松弛的语义来实现:
- PipeDream-2BW (2021) 维护两个权重版本,并保证权重更新延迟为 1,而无需昂贵的流水线刷新;
- PipeMare (2021) 和 Kosson 等人 (2021) 使用异步 PP
- 与论文考虑的带有流水线刷新的技术相比,这些技术提高了吞吐量,但可能以收敛速度或最终精度为代价
- 此外,单独的 PP 仍然只能扩展到与模型中层数相等数量的设备,这对于某些模型架构来说是有限的
- PipeDream (2019) 以一种原则性的方式结合了 PP 和 DP ,以减少跨设备通信
- DeepSpeed (2021) 将 PP 与 TP 和 DP 结合起来,以训练高达万亿参数规模的模型,但吞吐量低于论文所示的结果(峰值利用率的 52% 对比 36%),原因有几个:
- 通过算子融合使大部分算子图保持计算受限(compute-bound)、使用更高效的 PP 调度以最小化流水线气泡(pipeline bubble)大小、快速的硬件(A100 与 V100 GPU 以及同一服务器内和不同服务器间 GPU 的高带宽链路)以及扩展到更多 GPU 的能力
- 作者希望强调,这种更高的吞吐量使得估计的训练时间更加实用(约 3 个月);37.6 petaFLOP/s 的总吞吐量将需要大约 40 个月来训练一个同等规模的模型
- 也可以扩展到更大的模型,但需要更多的 GPU 来保持训练时间的实用性
- DeepSpeed (2021) 将 PP 与 TP 和 DP 结合起来,以训练高达万亿参数规模的模型,但吞吐量低于论文所示的结果(峰值利用率的 52% 对比 36%),原因有几个:
- Mesh-TensorFlow (2018) 提出了一种语言,用于轻松指定结合数据和模型并行的并行化策略
- Switch Transformers (2021) 使用 Mesh-Tensorflow 训练了一个具有 1.6 万亿参数的稀疏激活(sparsely activated)的基于专家(expert-based)的模型,其预训练速度比 T5-11B 模型 (2019) 有所提高
Sharded Data Parallelism(分片 DP)
- 作为 MLPerf 0.6 (2019) 性能优化的一部分,引入了分片 DP (sharded data parallelism)(2019, 2020),其中优化器状态(optimizer state)在 DP 工作节点(data-parallel workers)上进行分片
- 这种方法有两个优点:
- (a) 它不会在原始 DP (vanilla data parallelism)的基础上引入额外的通信;
- (b) 它将优化器的计算和内存成本分摊到 DP 分区中
- ZeRO (2019, 2021) 扩展了这个思想:
- 权重参数和梯度也在 DP 工作节点上进行分片,工作节点在执行计算前从其“拥有”相应状态的工作节点获取相关状态
- 这增加了额外的通信,但可以通过仔细重叠计算和通信来部分隐藏
- 但如果不使用 TP 或者批大小不够大以隐藏额外的通信开销,这会变得困难(图 10)
- 权重参数和梯度也在 DP 工作节点上进行分片,工作节点在执行计算前从其“拥有”相应状态的工作节点获取相关状态
- ZeRO-Infinity (2021) 使用 NVMe 来高效地交换参数,使得能够在少量 GPU 上训练非常大的模型
- 论文注意到,使用少量 GPU 训练非常大的模型会导致不切实际训练时间(例如,收敛需要数千年)
Automatic Partitioning(自动分区)
- FlexFlow (2018)、PipeDream (2019)、DAPPLE (2021) 和 Tarnawski 等人 (2020) 都借助成本模型(cost models)在多个设备上自动分区模型训练图
- 然而,这些方法都没有考虑论文考虑的所有并行维度:流水线和 TP、DP、微批大小(microbatch size)、以及像激活重计算(activation recomputation)这样的内存节省优化对训练大于加速器内存容量的模型的影响
- 这些增加的维度扩大了需要探索的搜索空间
- Gholami 等人 (2018) 展示了如何对数据和模型并行组合的通信成本进行建模
高性能计算(HPC for Model Training)
- Goyal 等人 (2017) 和 You 等人 (2018) 都展示了使用高性能计算(High Performance Computing, HPC)技术在几分钟内训练高精度 ImageNet 模型
- 但所考虑的图像分类模型可以轻松地放在单个加速器上,使得模型并行变得不必要;
- 它们支持非常大的批大小(\(>32k\)),允许将 DP 扩展到大量工作节点,且通信不频繁;
- 并且它们由紧凑的卷积层组成,这些层本身就很适合 DP 通信