注:本文包含 AI 辅助创作
- 参考链接:
- Megatron 系列目前公认的有三篇核心论文如下,它们分别对应了 张量并行、3D 并行 与 序列并行/激活重计算优化 三大阶段,本文是第三篇的解读
- 第三篇:(Megatron-LM-3)Reducing Activation Recomputation in Large Transformer Models, MLSys 2023, NVIDIA
- 核心贡献:提出 序列并行(Sequence Parallelism) 与 选择性激活重计算 ,将激活显存占用再降 3–5 倍,支持更长序列与更大批训练;与 Flash-Attention 思想互补,现已成为 Megatron-Core 默认配置
- 论文补充材料:Supplementary Material of Megatron-LM-3
Paper Summary
- 整体内容总结:
- 论文提出了 序列并行(Sequence Parallelism) 与 减少激活重计算(Reducing Activation Recomputation)
- 论文证明了将 SP (Sequence Parallelism) 与 TP (Tensor Parallelism) 结合使用可以显著减少所需的激活内存
- 结合选择性激活重计算 (Selective Activation Recomputation),论文证明了可以实现内存占用减少 \(5\times\),并且恢复了使用完全激活重计算 (Full Activation Recomputation) 所引入的计算开销的 90% 以上
- 传统上实现:通过不存储激活值,而是在反向传播时按需要重新计算它们,节省了内存但增加了冗余计算
- 论文表明大部分这种冗余计算是不必要的,因为我们可以有选择的保存部分激活值
- 补充:结合 张量并行 (tensor parallelism, TP),这些技术几乎消除了重计算激活的需要
- 论文在规模 高达一万亿参数 的语言模型上评估了论文的方法,结果表明:
- 论文的方法将激活内存减少了 \(5\times\),同时将激活重计算带来的执行时间开销降低了 90% 以上
- 在 2240 个 NVIDIA A100 GPU 上训练一个 530B 参数的 GPT-3 风格模型 (2022) 时,论文实现了 54.2% 的模型浮点运算利用率 (Model Flops Utilization, MFU),这比使用重计算实现的 42.1% 快了 29%
Introduction and Discussion
- 随着 Transformer 模型规模向万亿参数扩展,需要模型并行 (model parallelism) 来将模型参数、激活值和优化器状态分布到多个设备上,以便它们能够放入设备内存并在现实的时间量内可训练
- 虽然模型并行线性地减少了每个设备的参数数量(例如,当模型并行规模加倍时,每个设备的参数数量减半),但模型并行的扩展是有限度的
- 张量级模型并行 (Tensor-level model parallelism, TP) 增加了通信需求并引入了更小且性能较差的矩阵乘法,使得将模型分割到大量设备上效率低下
- 因此,TP 通常仅限于通过高速带宽连接(例如 DGX 服务器内通过 NVLink 连接的 GPU)的相对较小的 GPU 组
- 流水线并行 (Pipeline parallelism, PP) 需要存储几个微批次 (microbatches) 的激活值以减少流水线气泡 (pipeline bubble) (2021)
- 因此, PP 只能帮助减少存储模型参数和优化器状态所需的内存,无法在保持高设备利用率的同时减少激活值所需的内存
- 因此,激活值的存储迅速成为扩展大型 Transformer 模型的关键问题
- 问题:实际上,对于不适用 Activation Recomputation 的场景,PP 也减少激活存储了;但是对于 Activation Recomputation 的场景,每一层存储的激活基本都还在,所以相当于此时 PP 对激活存储是没有节省的
- 张量级模型并行 (Tensor-level model parallelism, TP) 增加了通信需求并引入了更小且性能较差的矩阵乘法,使得将模型分割到大量设备上效率低下
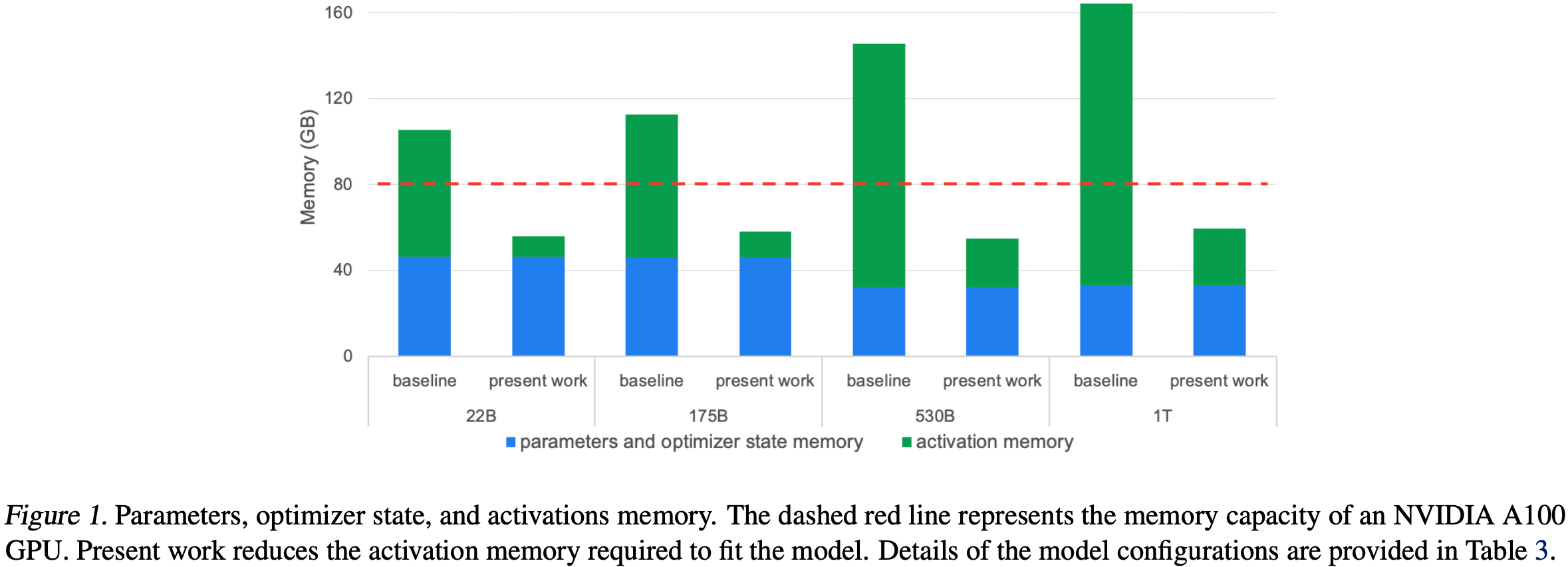
- 为了量化这一点,图 1 显示了从 22B 参数到 1 万亿(1T)参数的四种模型配置所需的内存(模型配置的详细信息在表 3 中提供)
- 可以看出,对于所有这些情况,基线情况所需的内存都超过了 NVIDIA A100 GPU 提供的 80GB 内存
- 缓解这种内存压力的标准方法是简单地不存储大部分激活值,并在反向传播 (backward pass) 期间根据需要重新计算它们以计算梯度 (2016)
- 这种方法通常称为“梯度检查点 (gradient checkpointing)”或“激活重计算 (activation recomputation)”,会带来严重降低训练效率的代价
- 对于 Transformer 架构,大多数先前的工作在 Transformer 层边界处检查点(或存储)激活值,并在反向传播中重新计算其余必要的激活值
- 在论文中,论文将这种方法称为“完全激活重计算 (full activation recomputation)”
- 在论文的训练运行中,论文观察到当使用完全激活重计算时 ,会产生 \(30-40\%\) 的执行时间开销
- 论文提出了新技术,帮助缓解存储激活值的内存压力,从而减少重计算激活值的需求
- 这些技术特定于 Transformer 架构,并且易于实现,对计算效率没有影响或影响非常小
- 正如论文在第 2 节中详细说明的那样,还有其他几种技术可以减少训练大型模型的内存需求,例如:
- 跨数据并行 Rank (data parallel ranks) 分区各种数据
- 将数据卸载到 CPU 内存 (2020; 2021)
- 以上这些技术与论文提出的技术是互补的,可以额外采用以获得更大的内存节省;但通常这些其他技术比论文提出的技术具有更高的实现成本和对计算效率的更大影响
- 将这些技术与论文的技术进行比较的分析超出了论文的范围,留待未来工作
- 论文工作内容包括:
- 首先论文简要回顾 Transformer 架构,然后建立一个近似公式,用于存储 Single Stack Transformer 模型前向传播 (forward pass) 中激活值所需的内存
- 使用这个公式,我们可以研究不同形式的模型并行如何影响激活内存需求
- 然后论文引入序列并行 (sequence parallelism) 与 TP (tensor parallelism) 结合,以防止在不适合标准 TP 的区域中冗余存储激活值
- 论文表明,通过有选择地保存哪些激活值以及重新计算哪些激活值,我们可以消除大部分重计算成本,同时仅使用不进行重计算时所需内存的一小部分
- 最后论文提出了几个实验,测量这些技术对训练各个组成部分以及完整训练吞吐量的改进
- 首先论文简要回顾 Transformer 架构,然后建立一个近似公式,用于存储 Single Stack Transformer 模型前向传播 (forward pass) 中激活值所需的内存
Related Work
- 模型并行 (model parallelism) 使得能够跨多个 GPU 训练非常大的模型
- 模型参数以及这些模型相关的优化器状态需要大量内存,无法容纳在单个 GPU 上
- 即使能够将模型放入单个 GPU(例如,通过在主存和设备内存之间交换参数 (2021)),所需的高计算操作数量可能导致不切实际的长训练时间
- 结论:需要并行化
- 两种常用的模型并行形式用于将模型参数分布到 GPU 上:
- 1) TP (tensor parallelism),其中每层的参数分布在许多设备上 (2018; 2019; 2021);
- 2) PP (pipeline parallelism),其中模型沿网络的层维度分割 (2019; 2021a; 2019)
- 一些最近的方法结合了两种类型的模型并行,以支持训练高达 1T 参数的大型模型 (2021)
- 模型并行的替代方案是结合一些训练技术与数据并行 (data parallelism),以实现大规模模型训练 (2020; 2021;)
- 这种方法基于将优化器状态、梯度和参数跨数据并行 Rank 进行分片 (sharding)
- 最近的一个扩展 (2021) 使用 CPU 卸载技术,使得能够在少量 GPU 上训练数万亿参数的模型
- 与模型并行相比,这些基于数据并行的技术效率较低,并且不能很好地扩展到大量 GPU (2021),因此更适合在资源受限的环境中进行模型微调 (finetuning)
- 论文仅关注模型并行优化,将这些技术与论文的技术进行比较的分析超出了论文的范围
- 模型并行的替代方案是结合一些训练技术与数据并行 (data parallelism),以实现大规模模型训练 (2020; 2021;)
- 此外,Megatron-LM (2019) 中引入的 TP 在一定程度上帮助减少了激活内存
- 在这种方法中,Transformer 的某些部分激活值没有在 TP Rank 之间分割,增加了激活内存开销
- Li 等 (2021a) 提出的序列并行 (sequence parallelism),其中激活值沿序列维度分区贯穿整个网络可以缓解这个问题
- 但他们的方法类似于数据并行,要求在所有设备上复制参数和优化器状态,这使得它不适合大型模型训练
- Sagemaker (2021) 和 GSPMD (2021) 提出了内存高效的 TP 版本,这些版本在整个网络中沿隐藏维度 (hidden dimension) 在设备之间分割激活值
- 这些方法的主要缺点是它们包含多设备层归一化 (multi-device layer normalization),这在计算/通信上非常低效
- LayerNorm 操作需要沿隐藏维度顺序计算均值和方差
- 如果 LayerNorm 沿隐藏维度分割(即使用 TP),它将增加两个额外的全规约 (all-reduce) 操作
- 而且 LayerNorm 反向传播需要两个额外的 sequential reductions(即另外两个 all-reduce)
- 与 LayerNorm 计算时间相比,每个 Transformer 层的这 4 次通信将引入显著的开销
- LayerNorm 操作的这种通信开销可以通过 SP 来避免
- 这些方法的主要缺点是它们包含多设备层归一化 (multi-device layer normalization),这在计算/通信上非常低效
- 在论文中,论文提出了一种新技术,它利用了 TP 和 SP 的优点,而没有先前方法的任何缺点
- 换句话说,论文的技术结合了 TP 和 SP ,显著减少了激活内存,而没有任何额外的计算、通信或内存开销
- 论文的论文特别侧重于研究 Transformer 架构,因为作者相信它是一个重要且广泛使用的架构,足以证明手动检查各个层以了解其内存和计算贡献并推导最佳并行化方案是合理的
- 通过分析建模,论文表明内存(包括激活值和参数)在设备之间均匀分区
- 换句话说,论文的并行化策略在内存需求方面是最优的
- Transformer 网络被广泛使用,足以高度利用这种手动搜索和验证最佳并行化策略的方法
- 自动搜索 (2019; 2019) 有可能找到这种最优策略,但据论文所知,论文尚未看到这些方法应用于 Transformer 网络的任何已发表结果
- 与并行化方案类似,论文提出的选择性激活重计算 (selective activation recomputation) 是基于手动搜索 Transformer 模型在激活内存需求和重计算之间的最佳权衡
- 探索自动方法 (2021) 是否可以补充并可能改进这种权衡是未来工作的一个有趣方向
Transformer Architecture
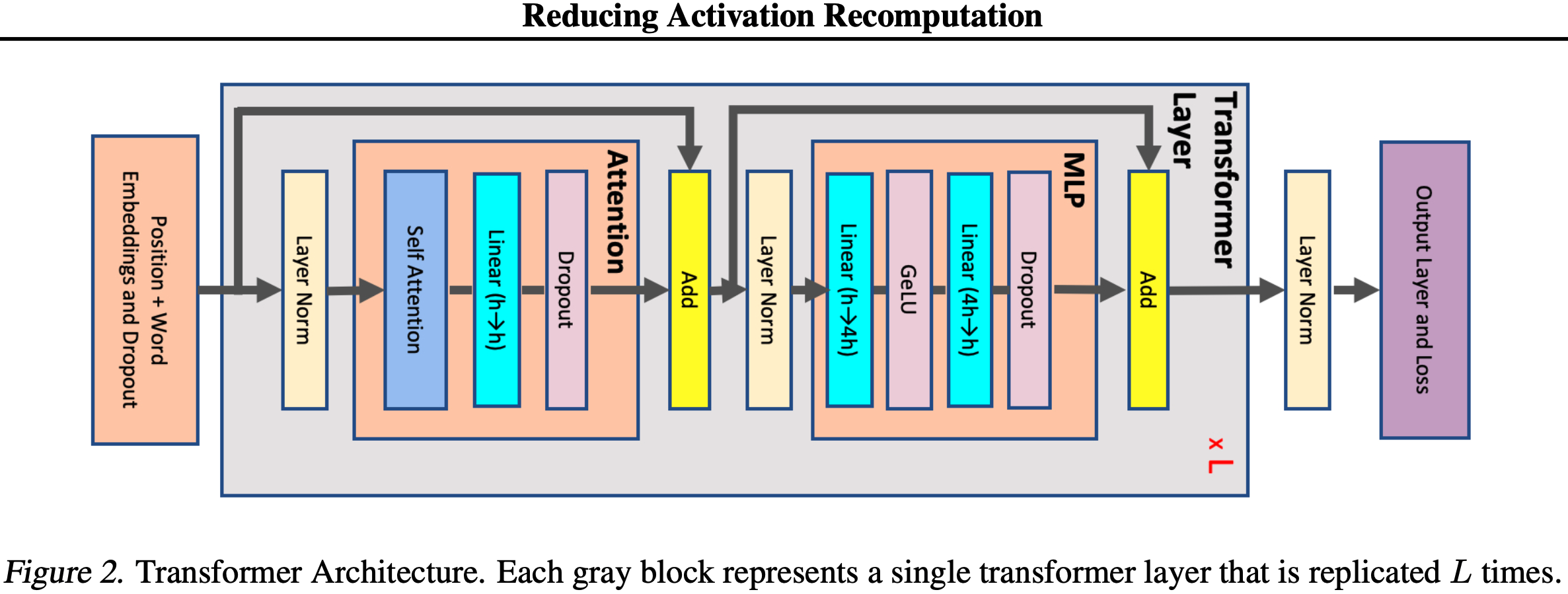
- 论文考虑一个具有 \(L\) 层的 Single Stack Transformer 编码器或解码器,如图 2 所示
- 符号定义:\(s\) 是序列长度 (sequence length),\(h\) 是隐藏维度大小 (hidden dimension size),\(v\) 是词汇表大小 (vocabulary size)
- 在网络的开始,输入 Tokens 被送入一个词嵌入表(word embedding table):
$$v\times h$$ - Token 嵌入与学习到的位置嵌入(positional embeddings) 相结合:
$$s\times h$$ - 嵌入层的输出,即 Transformer 块的输入,是一个 3 维张量:
$$s\times b\times h$$- 其中 \(b\) 是微批次大小 (microbatch size)
- 每个 Transformer 层由一个具有 \(a\) 个注意力头 (attention heads) 的自注意力块 (self-attention block) 和一个具有两层的多层感知器 (MLP) 组成,该 MLP 将隐藏大小增加到 \(4h\),然后将其减小回 \(h\)
- 每个 Transformer 层的输入和输出具有相同的大小
$$ s\times b\times h $$ - 最后一个 Transformer 层的输出被投影回词汇表维度以计算交叉熵损失 (cross-entropy loss)
- 论文假设词嵌入和输出层权重是共享的
- 论文相关变量名称列于表 1 中以供参考:

Activation Memory
- 论文推导出一个近似公式,用于计算如图 2 所示的 Single Stack Transformer 模型在前向传播中存储激活所需的内存
- 请注意,论文中的 “激活(activations)” 指的是 在前向传播中创建并在反向传播期间梯度计算所必需的任何张量
- 注:不包括模型的主要参数和优化器状态,但包括 Dropout 操作使用的掩码
- 论文只考虑内存的主要贡献者,而忽略小的缓冲区
- 小的缓冲区包括 LayerNorm 输入的均值和方差(\(2sb\))以及 GEMM 操作的偏置(\(O(h)\))
- 总的来说,这些缓冲区占激活内存的比例远小于 1%,因为隐藏维度(\(h\))和序列维度(\(s\))的数量级都是数千,因此与 GEMM 和 LayerNorm 激活的 \(O(sbh)\) 大小相比,\(2sb\) 和 \(O(h)\) 都缺少了其中一个因子
- 论文还假设网络和激活以 16-bit 浮点格式存储,因此每个元素需要 2 字节的存储空间
- 唯一的例外是 Dropout 掩码,每个元素只需要 1 个字节
- 请注意,除非明确提及,本节中报告的所有大小均以字节(Bytes)为单位,而不是元素数量
Activations Memory Per Transformer Layer
- 如图 2 所示,每个 Transformer 层包含一个注意力块和一个 MLP 块,通过两个 LayerNorm 连接
- 下面,论文推导存储这些元素激活所需的内存:
- 注意力块 (Attention block):
- 包括自注意力操作,后跟一个线性投影和注意力 Dropout
- 线性投影存储其输入激活,大小为 \(2sbh\),注意力 Dropout 需要一个大小为 \(sbh\) 的掩码
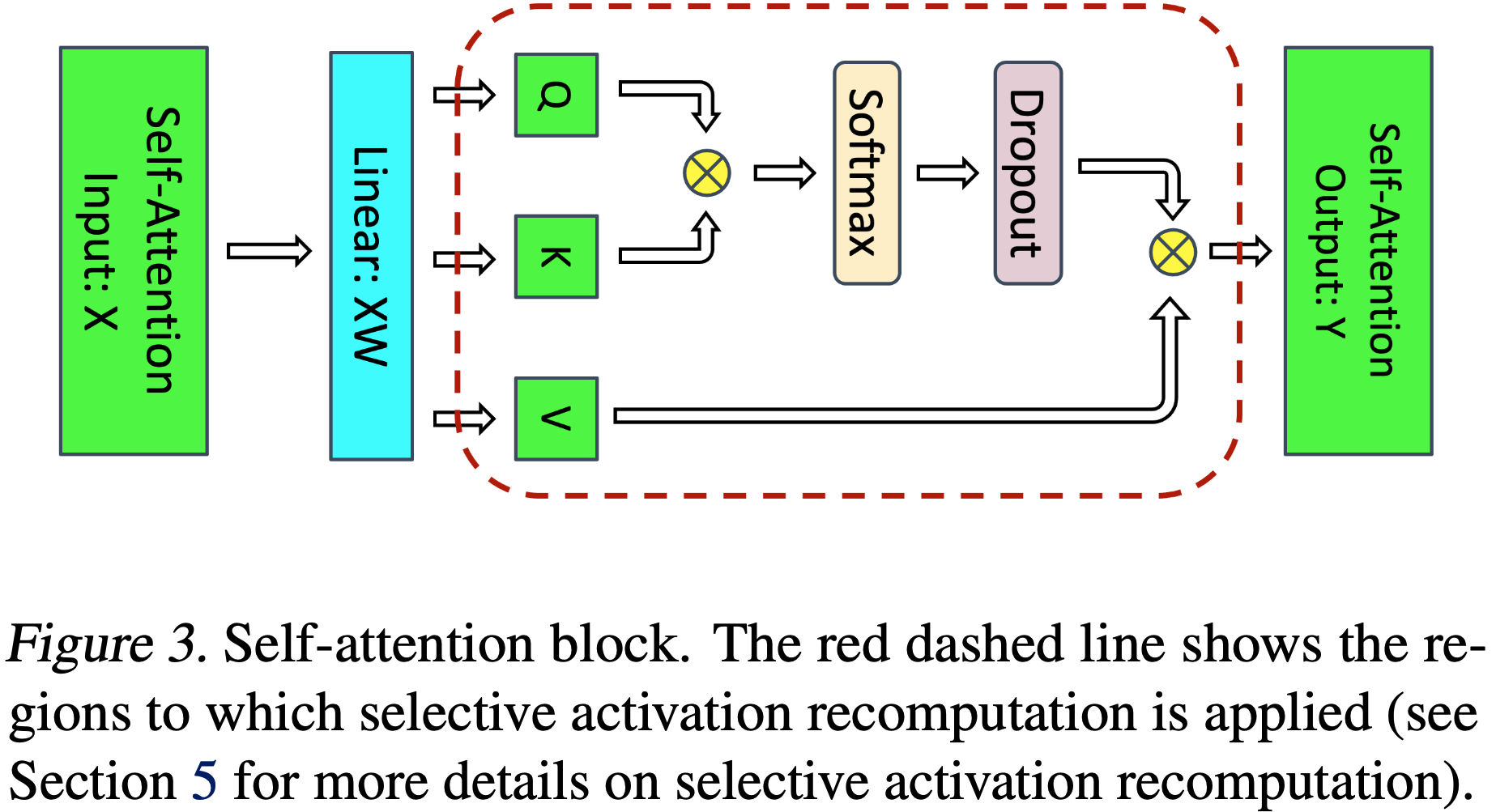
- 图 3 所示的自注意力包含几个元素:
- Query (\(Q\)), Key (\(K\)), and Value (\(V\))矩阵乘法 (matrix multiplies): 论文只需要存储它们共享的输入,大小为 \(2sbh\)
- \(QK^{T}\) 矩阵乘法 (matrix multiply): 需要存储 \(Q\) 和 \(K\),总大小为 \(4sbh\)
- Softmax: 反向传播需要存储 Softmax 输出,大小为 \(2as^{2}b\)
- Softmax Dropout: 只需要一个大小为 \(as^{2}b\) 的掩码
- 问题:Softmax 也有 Dropout 吗?
- 理解:在 Softmax 之后施加 Dropout,随机将部分注意力权重置为 0,目的是防止模型过度依赖某些特定的注意力权重,减少过拟合风险,提高模型的泛化能力,但原始 Transformer 论文中,没看到这部分的 dropout,只有 Residual Dropout(\(P_\text{drop} = 0.1\))
- 注意力作用于值(\(V\))(Attention over Values (\(V\))): 论文需要存储 Dropout 输出(\(2as^{2}b\))和值(\(2sbh\)),因此需要 \(2as^{2}b+2sbh\) 的存储空间
- 将上述值相加,注意力块总共需要 \(11sbh+5as^{2}b\) 字节的存储空间
- MLP:
- 两个线性层存储它们的输入,大小分别为 \(2sbh\) 和 \(8sbh\)
- GeLU 非线性操作也需要其输入(大小为 \(8sbh\))用于反向传播
- 最后,Dropout 存储其掩码,大小为 \(sbh\)
- MLP 块总共需要 \(19sbh\) 字节的存储空间
- LayerNorm:
- 每个 LayerNorm 存储其输入,大小为 \(2sbh\),因此论文总共需要 \(4sbh\) 的存储空间
- 最终,将注意力、MLP 和 LayerNorm 所需的内存相加,存储 Transformer 网络单层激活所需的内存为:
$$\text{Activations memory per layer}=sbh\left(34+5\frac{as}{h}\right) \tag{1}$$ - 上述方程适用于未应用任何形式模型并行的情况
Model Parallelism
- 论文先量化 TP 对每层所需激活内存的影响,然后介绍一种将 SP 与 TP 相结合的新方法,以进一步减少每层激活所需的内存
- 在本小节的最后,论文还讨论了 PP 对激活内存的影响,并推导了激活所需总内存的公式
TP (Tensor Parallelism)
- 论文使用 Shoeybi 等人 (2019) 开发的 TP ,并按照图 4 所示并行化注意力块和 MLP 块
- 这种形式的并行性引入了两个额外的通信操作 \(f\) 和 \(\bar{f}\)
- 更多细节,请参阅该论文 (2019)
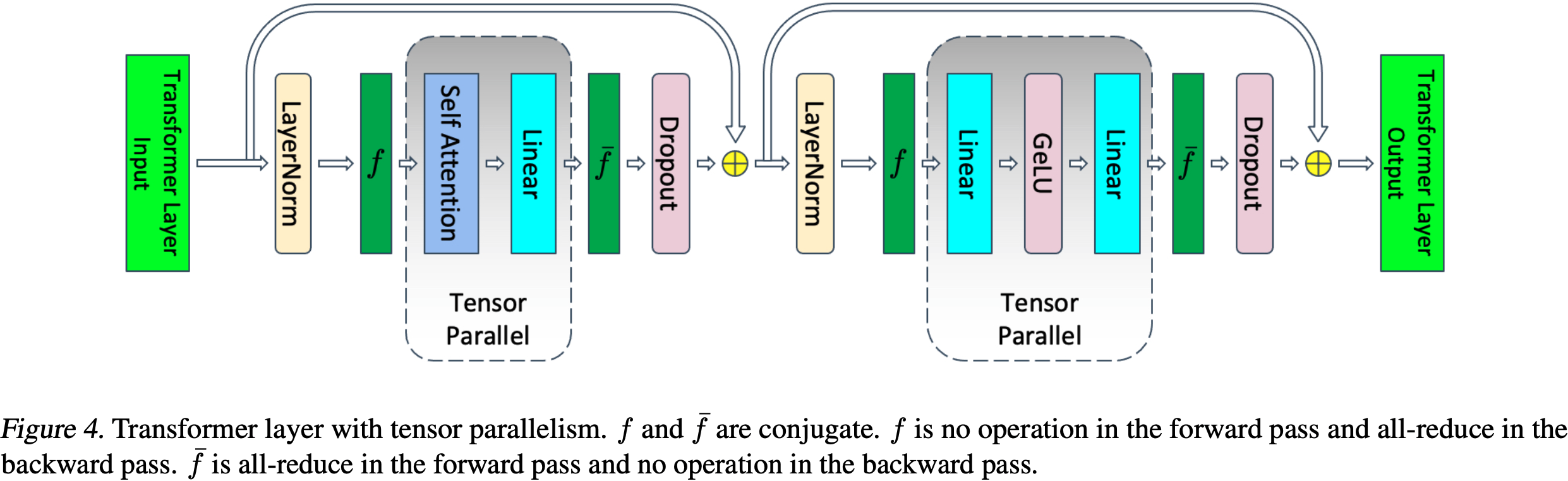
- TP 不仅并行化了注意力块和 MLP 块内的模型参数和优化器状态,还并行化了这些块内部的激活
- 这些块的输入激活(例如,输入到 \(Q\)、\(K\) 和 \(V\) 矩阵乘法的输入,或输入到 \(h \to 4h\) 线性层的输入)没有被并行化,只有每个块内的激活在 TP 组内被划分
- 假设采用 \(t\) 路 TP ,存储激活所需的每层内存从公式 1 减少到:
$$\text{Activations memory per layer}=sbh\left(10+\frac{24}{t}+5\frac{as}{ht}\right) \tag{2}$$
SP (Sequence Parallelism)
- 如图 4 所示, TP 并行化了 Transformer 层中训练过程中最耗时的部分,因此它在计算上是高效的
- 但它保留了 LayerNorm 以及注意力块和 MLP 块之后的 Dropout 操作不变,因此 LayerNorm 和 Dropout 在 TP 组内是复制的(单卡上需要完整保留所有参数和激活)
- 这些元素不需要大量计算,但需要相当数量的激活内存
- 定量地说,公式 2 中的 \(10sbh\) 部分就是由于这些复制操作造成的,因此它们没有除以 TP 大小 \(t\)
- 论文注意到,在 Transformer 层的非 TP 区域中,操作在序列维度上是独立的
- 这一特性允许论文沿序列维度 \(s\) 划分这些区域
- 沿序列维度划分减少了激活所需的内存
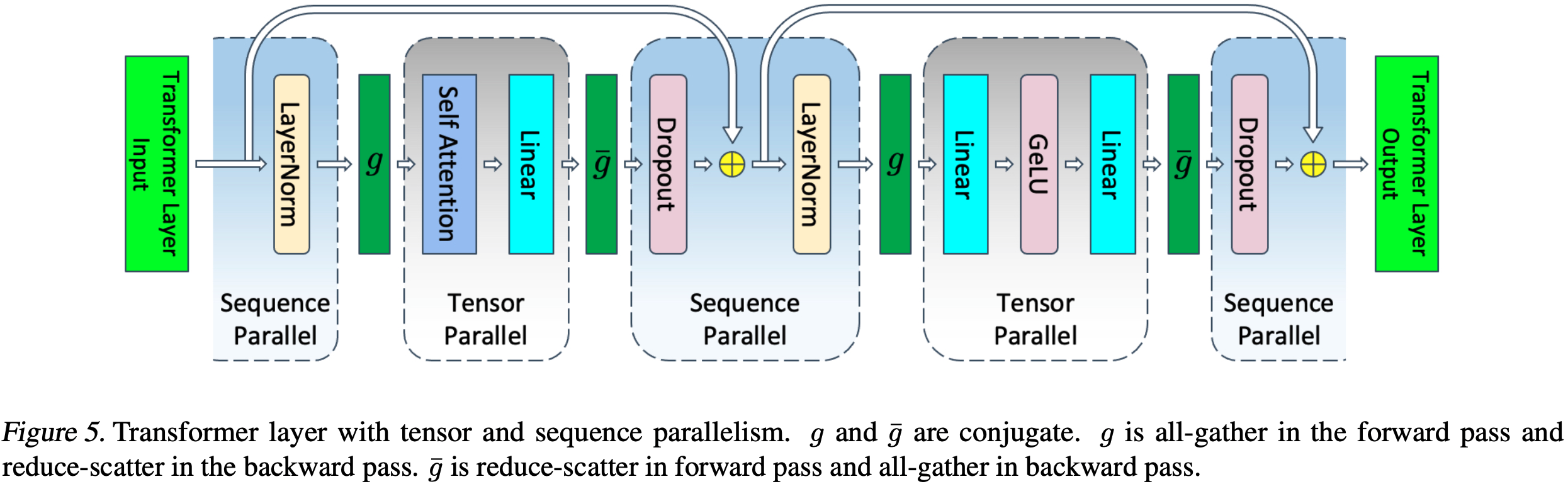
- 这种额外的并行性级别在 \(f\) 之前和 \(\bar{f}\) 之后引入了新的通信集合,这些操作将充当 SP 区域和 TP 区域之间的转换器
- 例如,在前向传播中,论文需要在图 4 中的操作符 \(f\) 之前进行一次额外的 All-Gather
- 这些额外的通信会引入开销并减慢训练速度
- 为了避免这些额外的通信,论文将这些操作与 \(f\) 和 \(\bar{f}\) 操作符结合起来,并引入新的操作 \(g\) 和 \(\bar{g}\),如图 5 所示
- 可以看出,\(g\) 和 \(\bar{g}\) 是 SP 区域和 TP 区域之间的转换器
- 论文在本小节的剩余部分推导这些操作
- 论文使用 MLP 块详细说明 \(g\) 和 \(\bar{g}\) 的推导。在非并行形式中,如图 2 所示,LayerNorm 后接 MLP 块可以表述为:
$$
\begin{align}
Y &=\text{LayerNorm}(X), \\
Z &=\text{GeLU}(YA), \\
W &=ZB, \\
V &=\text{Dropout}(W),
\end{align}
$$- 其中:
- \(X\) 是 LayerNorm 的输入,大小为 \(s\times b\times h\)
- \(A\) 和 \(B\) 是线性层的权重矩阵,大小分别为 \(h\times 4h\) 和 \(4h\times h\)
- 其中:
- 上述操作的张量和 SP 组合形式如图 6 所示
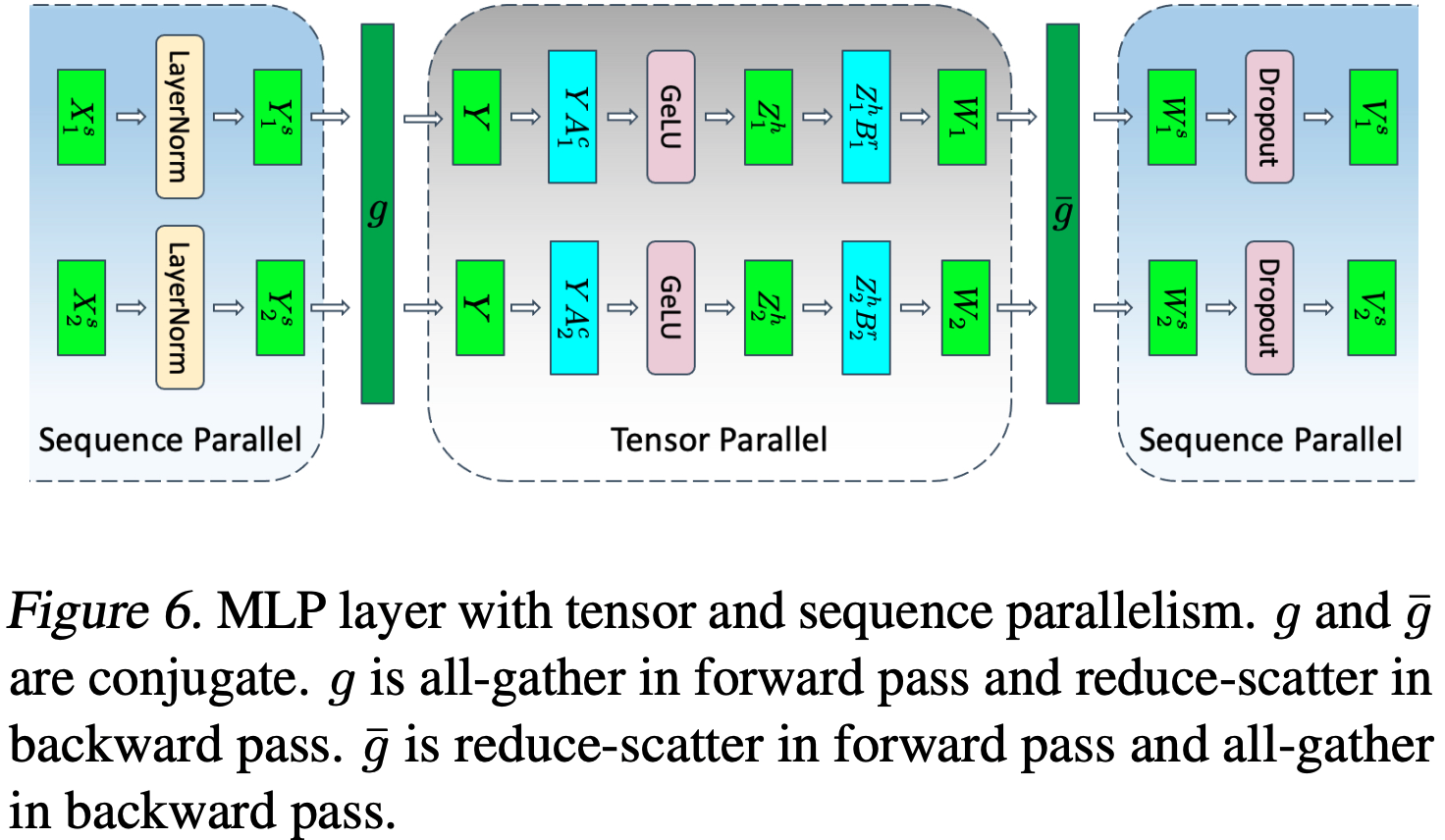
- 下标表示在加速器间的划分(注:理解为 Rank),上标表示划分所沿的维度 ,例如:
- \(X_{1}^{s}\) 是 \(X\) 在第一个加速器上的部分,沿 \(s\) 维度(序列维度)划分
- \(Z_{2}^{h}\) 是 \(Z\) 在第二个加速器上的部分,沿 \(h\) 维度(隐藏维度)划分
- LayerNorm 的输入沿序列维度并行化
$$ X=[X_{1}^{s},X_{2}^{s}]$$ - 因此,LayerNorm 的输出也将沿序列维度并行
$$Y=[Y_{1}^{s},Y_{2}^{s}]$$ - 带有 GeLU 非线性的线性层需要完整的输入 \(Y\),因此论文需要执行一次 All-Gather
- 这意味着 \(g\) 在前向传播中是一个沿序列维度的 All-Gather 操作
- 通过将 \(A\) 沿其列划分(\(A_{1}^{c}\) 和 \(A_{2}^{c}\)),将 \(B\) 沿其行划分(\(B_{1}^{r}\) 和 \(B_{2}^{r}\)),论文避免了通信(更多细节请参见 (2019))并得到 \(W_{1}\) 和 \(W_{2}\)
- 这两个张量不再是并行的,需要在输入到 Dropout 层之前求和为 \(W=W_{1}+W_{2}\) (对应 Reduce 操作)
- 但 Dropout 需要其输入在序列维度 \(s\) 上是并行的 (对应 Scatter 操作)
- 论文不是先求和再在序列维度上并行化,而是将这两个操作合并为一个 Reduce-Scatter 操作
- 因此,\(\bar{g}\) 在前向传播中可以是一个单一的 Reduce-Scatter 操作
- 综上所述,论文得到:
$$
\begin{align}
[Y_{1}^{s},Y_{2}^{s}] &=\text{LayerNorm}([X_{1}^{s},X_{2}^{s}]) \\
Y &=g(Y_{1}^{s},Y_{2}^{s}), \\
[Z_{1}^{h},Z_{2}^{h}] &=[\text{GeLU}(YA_{1}^{c}),\ \text{GeLU}(YA_{2}^{c})],\\
W_{1} &=Z_{1}^{h}B_{1}^{r}\ \text{ and }\ W_{2}=Z_{2}^{h}B_{2}^{r},\\
[W_{1}^{s},W_{2}^{s}] &=\bar{g}(W_{1},W_{2}),\\
[V_{1}^{s},V_{2}^{s}] &=[\text{Dropout}(W_{1}^{s}),\ \text{Dropout}(W_{2}^{s})]
\end{align}
$$ - 如果论文对反向传播进行类似的分解,论文会发现 \(g\) 和 \(\bar{g}\) 是彼此共轭的(Conjugate)
- \(g\) 在前向传播中是 All-Gather,在反向传播中是 Reduce-Scatter;
- \(\bar{g}\) 在前向传播中是 Reduce-Scatter,在反向传播中是 All-Gather
- 对 Transformer 层的 LayerNorm 后接注意力部分进行类似的分解,得到图 5
- TP 在单次前向和反向传播中需要四次 All-Reduce,而 TP 与 SP 结合在单次前向和反向传播中需要四次 All-Gather 和四次 Reduce-Scatter
- 乍一看,似乎张量与 SP 比 TP 需要更多的通信
- 但论文注意到,Ring All-Reduce 由两个步骤组成:
- 一个 Reduce-Scatter 后接一个 All-Gather
- 因此,TP 与张量加 SP 所使用的通信带宽是相同的
- 问题:Reduce-Scatter 和 All-Gather 只有在无缝连着的时候才能说等价于 Ring All-Reduce 吧
- 理解:是的,但是无论是否无缝连着,Reduce-Scatter + All-Gather 的通信都等于 Ring All-Reduce,因为都是 Reduce,然后 Scatter,继而 Gather
- 补充:论文后面的 6.2 章节也提到了:reduce-scatter 和 all-gather 组合的执行速度比单独的 all-reduce 慢
- 所以, SP 不会引入任何通信开销!
- 根据公式 3, SP 与 TP 结合,将反向传播所需的所有激活沿并行维度划分
- 注:第一个线性操作所需的张量 \(Y\))不会被划分
- 为了缓解这个问题,论文不存储完整的张量 \(Y\) 用于反向传播,只在第 \(i\) 个 TP Rank 上存储 \(Y_{i}^{s}\) 部分,并在反向传播中执行一次额外的 All-Gather
- 为了消除这个额外 All-Gather 引入的延迟,论文将此通信与计算 \(Y\) 梯度所需的计算重叠,从而减少了开销
- 使用 SP 与 TP 结合,存储每个 Transformer 层激活所需的内存从公式 2 减少到:
$$
\begin{align}
\text{Activations memory per layer} &= sbh\left(\frac{10}{t}+\frac{24}{t}+5\frac{as}{ht}\right) \\
&=\frac{sbh}{t}\left(34+5\frac{as}{h}\right) \tag{4}
\end{align}
$$ - 上述方程现在是公式 1 除以 TP 大小
- 这意味着使用张量和 SP ,我们可以在 TP 组内分布激活,并将所需内存减少 TP 大小 \(t\) 倍
PP (Pipeline Parallelism)
- PP 简单地将 Transformer 的 \(L\) 层划分为 \(\frac{L}{p}\) 组层,其中 \(p\) 是 PP 大小
- 但 PP 并不会将激活所需的总内存均匀地除以 \(p\)
- 这是由于 PP 调度引入了重叠(overlapping)以减少流水线气泡 (2021)
- 注:overlap 意味着对应的激活需要同时在内存中
- 为了量化这一点,论文考虑 PipeDream (2020) 中开发的 1F1B 流水线调度
- 具有最小化流水线气泡的调度对流水线的第一个阶段施加最大的内存压力
- 流水线的第一阶段指的是第一个 \(\frac{L}{p}\) 层组,也包括输入嵌入
- 激活内存随流水线阶段变化的可视化图见附录 B
- 为了保持流水线加压并避免额外的空闲时间,第一阶段必须存储 \(p\) 个微批次的激活(更多细节参见 (2021) 的图 4-top)
- 每个阶段包含 \(\frac{L}{p}\) 层,因此第一阶段必须存储激活层为:
$$p \times \frac{L}{p} = L$$- 注:(与 PP 大小 \(p\) 无关)
- 因此,第一阶段存储激活所需的总内存为:
$$\text{Total activations memory of 1st stage}=\frac{sbhL}{t}\left(34+5\frac{as}{h}\right) \tag{5}$$
- 具有最小化流水线气泡的调度对流水线的第一个阶段施加最大的内存压力
- 对于其他流水线调度,所需的总内存会略有不同
- 例如,Megatron-LM (2021) 中开发的交错调度需要存储 \(L(1+\frac{p-1}{pm})\) 层的激活,其中 \(m\) 是交错阶段的数量
- 因此,如果使用交错调度,则总激活内存应乘以 \((1+\frac{p-1}{pm})\)
- 例如,Megatron-LM (2021) 中开发的交错调度需要存储 \(L(1+\frac{p-1}{pm})\) 层的激活,其中 \(m\) 是交错阶段的数量
Total Activations Memory
- 总的激活内存的大部分由公式 5 提供,但该公式未包括输入嵌入、最后一个 LayerNorm 和输出层所需的激活内存,如图 2 所示
- 位置和词嵌入不需要存储任何大量的激活用于反向传播,但 Dropout 需要存储
- 嵌入层中的 Dropout 也沿序列维度并行化
- 因此,它将需要 \(\frac{sbhp}{t}\) 的存储空间
- 注意,因子 \(p\) 来自 PP 以及论文需要存储 \(p\) 个微批次的事实(见第 4.2.3 节)
- 输出层之前的 LayerNorm 也使用 SP ,因此需要 \(\frac{2sbh}{t}\) 的存储空间
- 输出层投影到词汇维度需要存储其输入,大小为 \(\frac{2sbh}{t}\)
- 交叉熵损失需要存储以 32 位浮点数计算的 logits,因此需要 \(\frac{4sbv}{t}\) 的存储空间
- 请注意,由于论文只考虑流水线第一阶段的激活,上述激活(即总共 \(\frac{4sbh}{t} \cdot (1+\frac{v}{h})\))仅在没有 PP (\(p=1\))的情况下被计入
- 加上上述内存,由于输入嵌入、最后一个 LayerNorm 和输出层产生的额外内存为:
$$\frac{sbhL}{t}\left(\frac{p}{L}+\delta_{p=1}\frac{4}{L}\left(1+\frac{v}{h}\right)\right)$$- 其中 \(\delta_{p=1}\) 是一个 0-1 函数,在 \(p=1\) 时为 1,否则为 0
- 论文注意到,与公式 5 中的项 \(34+5\frac{as}{h}\) 相比,\(\frac{p}{L}\) 和 \(\frac{4}{L}\cdot (1+\frac{v}{h})\) 都是可以忽略的
- 例如,对于一个具有 22B 参数的模型,这些额外项占总激活内存需求的比例小于 \(0.01\%\)
- 问题:\(\frac{v}{h}\) 对不同配置也不算小吧,也有几十了
- 因此,公式 5 是总所需激活内存的一个良好近似,论文将在论文的其余部分使用它
选择性激活重计算,Selective Activation Recomputation
- 公式 (5) 给出的总激活内存需求对于大型模型而言仍然相当可观
- 激活重计算 (2016) 通过存储(或 checkpoint)一组层的输入激活,并在反向传播期间使用额外的前向传递重新计算其他所需的激活,来克服这一内存限制(论文中称之为完全激活重计算)
- 假设检查组仅包含单个层,并忽略 Transformer 层之外的激活,该方法将激活所需的总内存减少到
$$ 2sbhL $$- 论文也注意到,如果论文只在每个 TP Rank 上存储部分激活,这个所需内存可以进一步减少到
$$ \frac{2sbhL}{t} $$- 但这种方法需要每层额外的 all-gather 操作 ,会增加通信开销,因此论文不考虑这种方法
- 论文也注意到,如果论文只在每个 TP Rank 上存储部分激活,这个所需内存可以进一步减少到
- 与存储所有激活(公式 (5))相比,检查(checkpointing)所有 Transformer 层显著减少了训练模型所需的内存量
- 这种减少确实是以重计算(一次额外的前向传递)为代价的,这可能会带来高达 \( 30-40\% \) 的计算时间开销
- 为了平衡内存节省和计算开销,理想的做法是:仅仅 Checkpointing 足够的激活,使得给定的模型并行配置能够在设备内存的限制下进行训练
- SP 提供的内存节省使得比以往更多的配置可以在不进行重计算的情况下进行训练,但大型模型的最佳模型并行配置通常仍然需要存储和重计算部分激活
- 选择存储与重计算的激活量的一种简单方法是仅 checkpoint 部分 Transformer 层,并存储其他所有层的激活
- 这种方法对于大型模型的扩展性并不好;
- 例如,在训练 MT-NLG 时,每个设备只有三层,限制了平衡内存与计算的粒度
- 此外,论文注意到并非所有激活都需要相同数量的操作来重新计算,因此在选择存储哪些激活和重计算哪些激活时更智能是有益的
- 这种方法对于大型模型的扩展性并不好;
- 论文不是 checkpoint 和重计算完整的 Transformer 层,而是建议仅 checkpoint 和重计算每个 Transformer 层中占用大量内存但重新计算计算成本不高的部分 ,即选择性激活重计算(Selective Activation Recomputation)
- 为此,论文注意到公式 (5) 中的项 \( \frac{5as}{h} \) 是由于在通过计算 Q、K 和 V 值的线性层增加了网络宽度之后的注意力操作(after the width of the network is increased by the linear layer calculating the Q, K, and V values);
- 即如图 3 所示的 \( QK^{T} \) 矩阵乘法、softmax、softmax dropout 和注意力作用于 \( V \)
- 这些操作通常具有大的输入尺寸,因此激活也很大,然而,每个输入元素的浮点操作数非常低
- Transformer 层的其余部分对应公式 (5) 中的常数项 34
- 因此,对于 \( \frac{5as}{h}>34 \) 的大型模型,如果论文 checkpoint 并重计算 Transformer 层的这一部分,论文存储的激活不到一半,并且重计算那些未存储的激活只需付出适度的成本
- 为了量化这一点,让论文考虑 GPT-3 (2020) 和 MT-NLG (2022) 模型,这些是迄今为止训练过的一些最大模型
- 对于 GPT-3,\( a=96 \),\( s=2048 \),\( h=12288 \),因此 \( \frac{5as}{h}=80 \)
- 对于 MT-NLG,\( a=128 \),\( s=2048 \),\( h=20480 \),所以 \( \frac{5as}{h}=64 \)
- 将这些数字与常数项 34(即该层其余部分的因子)进行比较,我们可以看到这些激活占总激活的很大一部分
- 因此,通过使用选择性激活重计算,我们可以分别为 GPT-3 和 MT-NLG 模型节省 \( 70\% \) 和 \( 65\% \) 的激活内存需求
- 这些激活的重计算仅为这两个模型引入了 \( 2.7\% \) 和 \( 1.6\% \) 的 FLOPs 开销
- 有关 FLOPs 计算的更多细节,请参见附录 A
- 随着序列长度的增加,序列长度与隐藏大小的比率 \( (\frac{s}{h}) \) 将增加,执行选择性部分重计算的相对成本也会增加,从而使选择性激活重计算更加昂贵
- 作者认为,对于任何实际的 \( \frac{s}{h} \) 比率,选择性激活重计算仍然是平衡内存节省和计算的最佳重计算策略
- 使用这种形式的选择性激活重计算,存储激活所需的内存从公式 (5) 减少到:
$$
\text{Total required memory}=34\frac{sbhL}{t}.
$$- 上述公式表明,使用选择性激活重计算使得所需的激活内存随序列长度线性缩放,并且与注意力头的数量无关
- 如第 4.2.3 节所述,在使用交错流水线调度的情况下,上述公式需要乘以 \( (1+\frac{p-1}{pm}) \)
- 当使用 PP 时,如第 4.2.3 节所述,尽管给定设备只有 \( \frac{L}{p} \) 层,但第一阶段仍然必须存储相当于 \( L \) 层的激活,因为它必须存储 \( p \) 个微批次的激活以保持流水线压力
- 在这种情况下,可以采用一种额外技术来降低重计算成本,即根据可用设备内存尽可能多地存储所有微批次的激活,并对其余部分进行完全或选择性重计算
- 实际上,论文发现应用 SP 和选择性激活重计算后,重计算开销已经足够小,以至于这种额外技术带来的改进非常有限
- 该技术在附录 C 中有更详细的描述和分析
Evaluations
- 在本节中,论文评估了论文提出的方法对内存使用和训练执行速度的影响
- 表 3 列出了评估中使用的模型配置

- 论文考虑了参数规模高达一万亿的模型,对于所有这些模型,TP 大小设置为 8
- 对于 175B 和 530B 模型,论文使用具有三个交错阶段 (\( m=3 \)) 的交错调度
- 在所有情况下,序列长度设置为 \( s=2048 \),词汇表大小设置为 \( v=51200 \)
- 论文还注意到,在这些评估中没有考虑数据并行,因为论文的方法与数据并行无关
- 因此,论文分析中使用的批大小远低于端到端训练中使用的批大小
- 论文的所有结果都是在 Selene 超级计算机上使用混合精度运行的
- 每个集群节点有 8 个 NVIDIA 80GB A100 GPU,通过 NVLink 和 NVSwitch 相互连接
- 每个节点有八个 NVIDIA Mellanox 200Gbps HDR Infiniband HCA 用于应用程序通信
Memory Usage
- 论文通过借助前向和后向钩子在运行的不同时间点跟踪 GPU 活跃内存和 GPU 总内存(在 PyTorch 中可用)来验证内存消耗模型
- 论文验证了测量的内存使用情况与论文的分析模型密切匹配
- 表 2 的第一列总结了论文讨论的不同技术所需的内存
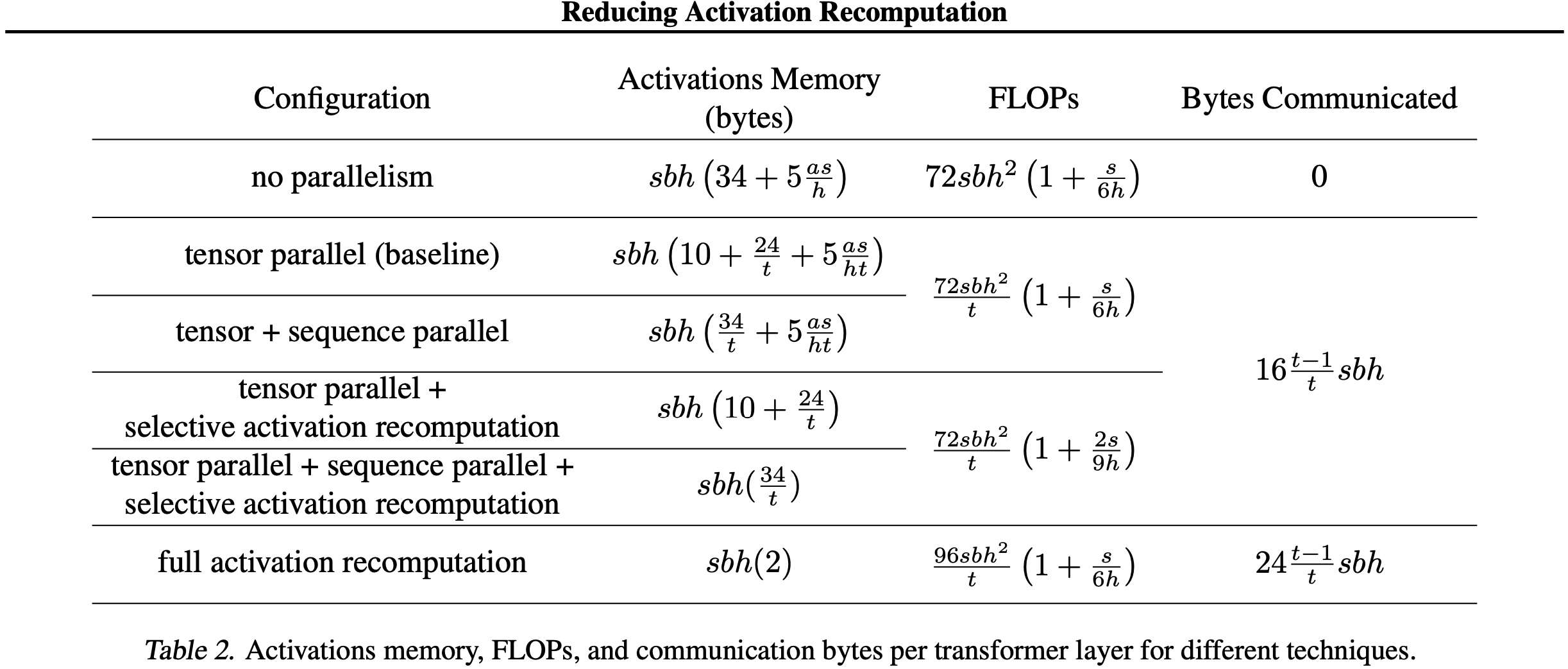
- 为了量化这一点,图 7 显示了不同技术使用的激活内存,表示为在所有 TP Rank 上保持所有激活所需内存的百分比,即公式 (2)
- 单独来看,两种技术都将内存需求减少了近一半,结合使用则提供了 5 倍的减少,将内存需求降至 20% 以下。这仅是完全激活重计算(基线水平的 10%)的约 \( \sim 2\times \)
- 如果没有 SP 和选择性重计算共同提供的内存节省,这些模型都无法装入内存
- 请注意,所有这些结果都包括了附录 B 中描述的内存优化
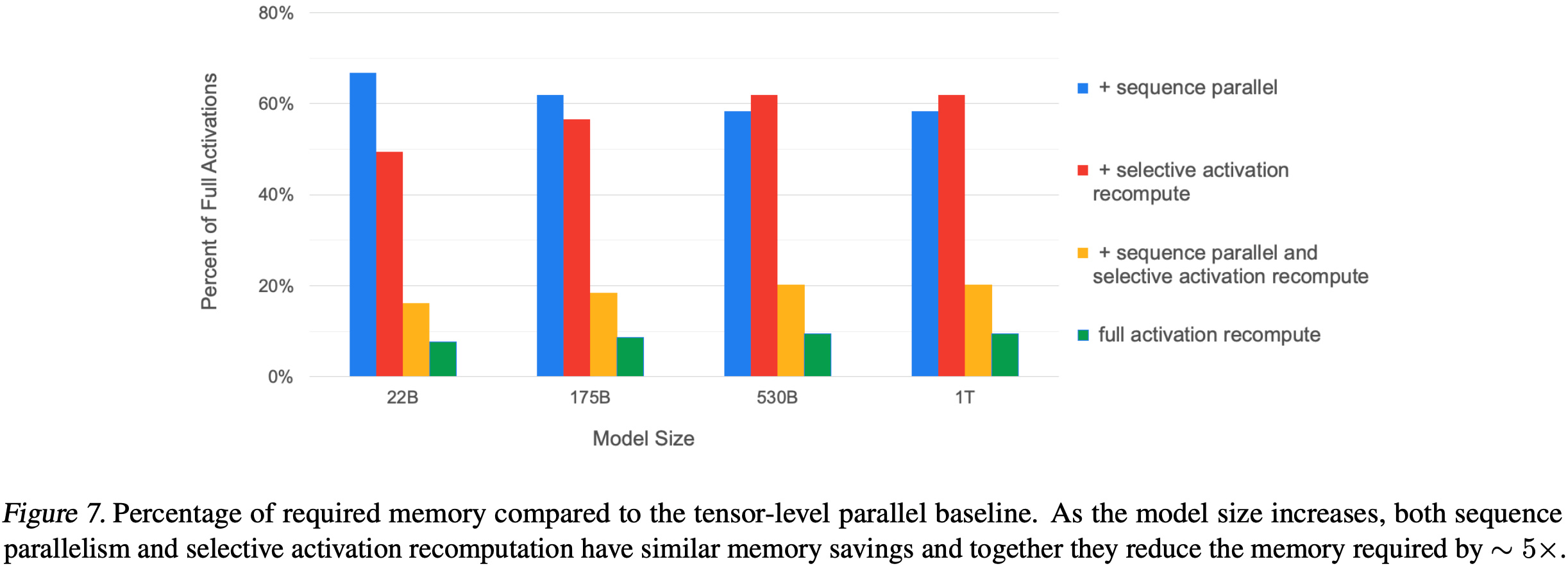
- 请注意,所有这些结果都包括了附录 B 中描述的内存优化
Execution Time per Layer
- 表 2 的第二列和第三列总结了论文讨论的不同技术下每个 Transformer 层的计算量(FLOPs)和通信字节数
- 为了量化这一点,表 4 显示了针对 22B 模型的各种实验下,执行一个 Transformer 层前向和后向传递的时间
- 前两行显示, SP 对完成一个 Transformer 层所需的时间提供了适度的改进,将前向时间从 7.7ms 减少到 7.2ms,加速了 6%
- 这种改进来自于 LayerNorm 和 Dropout 层在 \( \frac{1}{t} \) 的数据上执行
- 论文还发现,尽管移动的数据量是相同的 ,但 reduce-scatter 和 all-gather 组合的执行速度比单独的 all-reduce 慢 ,这降低了 SP 带来的改进
- 请注意,这种加速是使用 SP 主要优势之外的额外好处,其主要优势是节省内存,从而减少激活的重计算
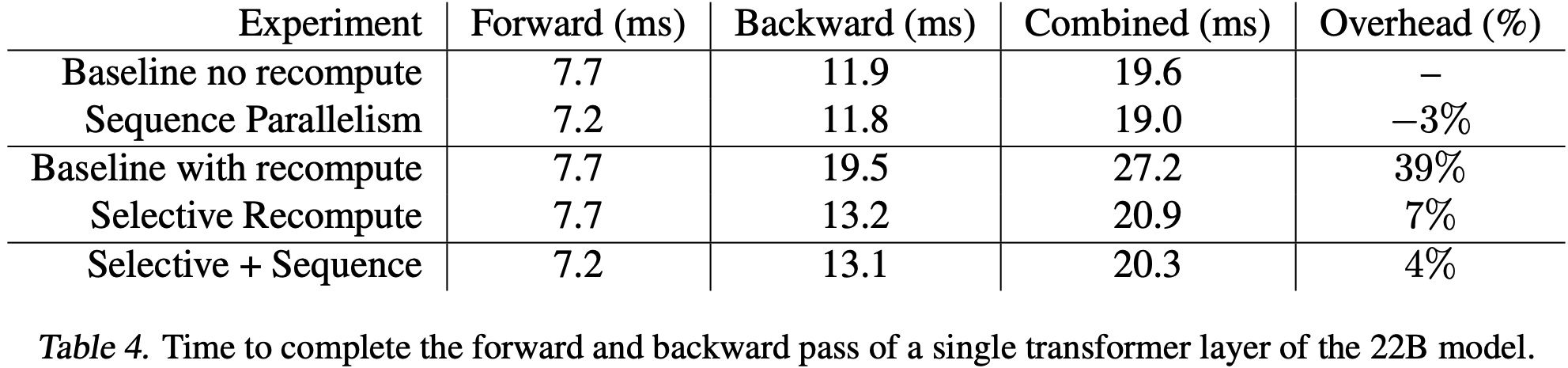
- 请注意,这种加速是使用 SP 主要优势之外的额外好处,其主要优势是节省内存,从而减少激活的重计算
- 前两行显示, SP 对完成一个 Transformer 层所需的时间提供了适度的改进,将前向时间从 7.7ms 减少到 7.2ms,加速了 6%
- 表 4 的后两行显示,如果论文在重计算哪些操作上具有选择性(由于 SP ,我们可以在更多配置中做到这一点),我们可以显著减少后向传递中重计算的开销
- 选择性重计算的开销是 \( 1.3 \)ms,占 11.9ms 基线的 \( 11\% \),而重计算整个层的开销是 \( 7.6 \)ms 或 \( 64\% \)
- 对于前向和后向总时间,开销是 \( 7\% \) 对比 \( 39\% \)
- 请注意,重计算整个层的开销为 \( 39\% \)(而非预期的 \( 33\% \))是由于后向传递中的一项优化,论文将 all-reduce 通信与线性层权重的梯度计算重叠
- 正如论文后面将看到的,这种好处随着模型大小的增加而增加
- 表 4 的最后一行显示了选择性重计算和 SP 结合的好处:当两种技术一起使用时,开销降至仅 \( 4\% \)
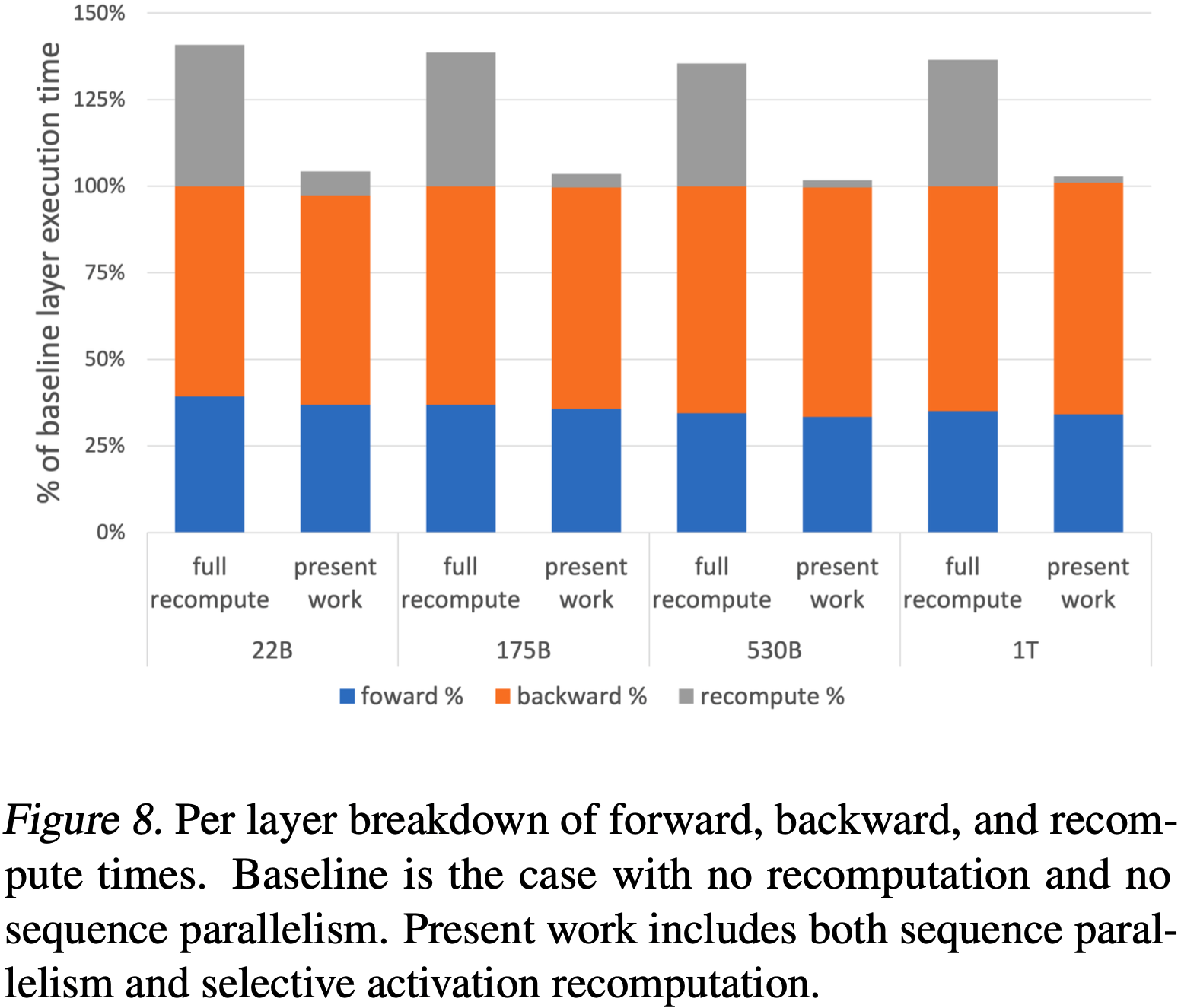
- 图 8 显示了所有测试案例的相同细分
- 论文看到,随着模型规模的增长,开销的减少也在增加
- 对于 \( 530 \)B 和 \( 1 \)T 的情况,开销仅为 \( 2\% \),而完全重计算的开销为 \( 36\% \)
End-to-End Iteration Time
- 表 5 列出了表 3 中列出的四种配置中每一种的完整端到端迭代时间
- 论文发现,对于所有测试的配置,论文提出的技术相比不使用 SP 的完全重计算,在吞吐量上提供了介于 \( 29.0\% \) 和 \( 32.1\% \) 之间的改进。这些节省将直接转化为更短的训练时间
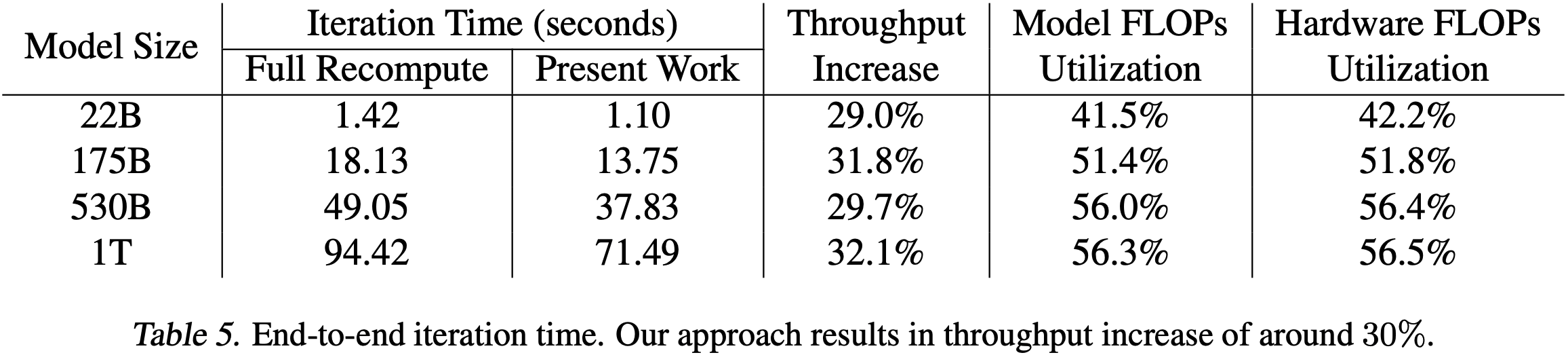
- 论文发现,对于所有测试的配置,论文提出的技术相比不使用 SP 的完全重计算,在吞吐量上提供了介于 \( 29.0\% \) 和 \( 32.1\% \) 之间的改进。这些节省将直接转化为更短的训练时间
- 论文定义了模型 FLOPs 利用率(MFU)和硬件 FLOPs 利用率(HFU) ,定义方式与 Chowdhery 等 (2022) 类似
- 模型 FLOPs 是执行单次前向和后向传递(单次迭代)所需的浮点操作数(不包括激活值),与实现方式和硬件限制无关
- 因此,模型 FLOPs 是硬件和实现无关的,仅取决于底层模型
- 注:但 模型 FLOPs 利用率(MFU)的分母是理论最大峰值 FLOPs,是与硬件有关的
- 硬件 FLOPs 表示硬件上每次迭代实际执行的浮点操作
- 因此,如果实现需要激活重计算(例如论文的实现),那么硬件 FLOPs 将大于模型 FLOPs
- 理解:因为增加了一些激活重计算的操作,这里的硬件主要强调的是实际计算量(包括激活重计算的操作量)
- 注:硬件 FLOPs 利用率(HFU)的分母是也是理论最大峰值 FLOPs
- 论文在附录 A 中提供了模型和硬件 FLOPs 的严格下界公式
- 对于论文的方法,硬件 FLOPs 与模型 FLOPs 的比率约为 \( 1+\frac{s}{18h} \)
- 模型 FLOPs 是执行单次前向和后向传递(单次迭代)所需的浮点操作数(不包括激活值),与实现方式和硬件限制无关
- 随后,论文分别将模型和硬件每秒 FLOPs 定义为模型和硬件 FLOPs 除以迭代时间
- 使用这些定义,MFU 和 HFU 分别定义为模型和硬件每秒 FLOPs 除以加速器的理论峰值每秒 FLOPs
$$
\begin{align}
MFU &= \frac{\text{observed throughput (tokens-per-second) }}{\text{theoretical peak FLOPs of device}} \\
HFU &= \frac{\text{observed FLOPs}}{\text{theoretical peak FLOPs of device}}
\end{align}
$$ - 以上定义参考自:PaLM: Scaling Language Modeling with Pathways, 2022, Google
- 使用这些定义,MFU 和 HFU 分别定义为模型和硬件每秒 FLOPs 除以加速器的理论峰值每秒 FLOPs
- 表 5 提供了所有四种配置的 MFU 和 HFU
- 随着模型规模的增加,论文实现了更好的 GPU 利用率,对于一万亿参数模型,论文分别达到了 \( 56.3\% \) 和 \( 57.0\% \) 的 MFU 和 HFU
- 虽然论文的分析中没有考虑初始化、评估、检查点等时间,但这些时间与迭代时间乘以迭代次数(这主导了端到端训练时间)相比可以忽略不计
- 用于训练大型语言模型的迭代次数根据训练目标而有很大差异
- 因此,作者认为论文报告的迭代时间(即吞吐量),包括了所有必要的操作,如数据加载和优化器步骤,是大型语言模型端到端训练时间的一个良好代理
- 论文还发现迭代时间在整个训练过程中是一致的,因此对吞吐量进行采样可以准确衡量预期结果
- 特别说明:表 5 中的结果没有使用任何数据并行
- 数据并行会由于数据并行组之间所需的梯度 all-reduce 而引入一些开销
- 但对于大型 Transformer 模型,这种开销并不大
- 例如,如果论文将 530B 模型扩展到 8 路数据并行(2240 个 GPU),同时保持每个模型实例的批大小不变(即批大小也乘以数据并行大小)每次迭代的时间从 \( 37.83 \) 秒略微增加到 \( 39.15 \) 秒
- 这导致 MFU 从 \( 56.0\% \) 下降到 \( 54.2\% \),下降幅度不大
- 论文注意到论文没有使用任何梯度 all-reduce 与反向传播的重叠,而高效的重叠几乎可以完全消除迭代时间的增加
Future Work
- 作者未来计划通过解决由大批次 (Large Microbatches) 导致的内存碎片化问题以及由 PP (Pipeline Parallelism) 导致的非均匀内存分配问题,来进一步减少激活内存
- 作者准备研究能够减轻流水线第一级 (First Stage of the Pipeline) 内存压力的方法
附录:论文补充材料
- 详情见论文补充材料:Supplementary Material of Megatron-LM-3