注:本文包含 AI 辅助创作
- 参考链接:
Paper Summary
- 核心总结(本文的核心贡献是 Meta 团队丰富的认知):
- 论文缩放方法论的一个重要见解是:可以系统地使用较小规模的消融来预测更大规模的性能,这使论文能够创建最终的可扩展 Recipe
- 根据论文的消融实验, Off-policy 算法、损失函数和模型精度是最重要的决策
- 其他每个决策单独影响不大,但正如论文从留一法实验中看到的,当它们全部组合时,仍然具有一些累积影响(在效率方面)
- 渐近性能与效率 (Asymptotic performance vs. efficiency)
- 论文发现更好的选项同时提高了效率和渐近性能,但情况并非总是如此(例如,对于 FP32,图 4(b)),当从基线方法开始进行”正向”消融时,论文首先且最主要地选择渐近性能
- 当从 ScaleRL Recipe 进行”反向”留一法消融时,论文发现每个决策对渐近性能的影响非常小,但算法的每个组件似乎都有助于提高效率
- 这表明变化的累积效应是相当鲁棒的
- Generalization:虽然对泛化的全面描述超出了论文工作的范围,但论文确实观察到分布内验证与下游泛化性能之间的相关性
- 有一些算法选择似乎更有助于泛化,作者指出了:
- 更大的批次大小(章节 A.14)
- 减少截断(章节 A.15)
- 更长的生成长度(第 5 节,图 9)
- 更大的模型规模(第 5 节,图 1)
- 有一些算法选择似乎更有助于泛化,作者指出了:
- 多任务强化学习 (Multi-task RL)
- 背景 & 问题:
- RL 已成为训练 LLMs 的核心技术,然而 RL 领域缺乏与预训练阶段相当的预测性 Scaling 方法论
- 计算预算迅速增长,但对于如何评估算法改进以 Scaling RL 计算,目前尚无原则性的理解(principled understanding)
- 论文工作:
- 论文进行了首次大规模系统性研究,总计超过 400,000 GPU hous ,定义了一个原则性框架,用于分析和预测 LLM 中的 RL Scaling
- 论文为 RL 训练拟合了 S 形计算-性能曲线(sigmoidal compute-performance curves),并广泛消融了一系列常见的设计选择,以分析它们对渐近性能和计算效率的影响
- 论文观察到:
- (1) 并非所有 Recipe (recipes)都能产生相似的渐近性能;
- (2) 诸如损失聚合、归一化、课程学习以及 Off-policy 算法等细节主要调节计算效率,而不会显著改变渐近性能;
Details such as loss aggregation, normalization, curriculum, and off-policy algorithm primarily modulate compute efficiency without materially shifting the asymptote
- (3) 稳定、可扩展的 Recipe 遵循可预测的 Scaling 轨迹,使得能够从小规模运行中进行外推
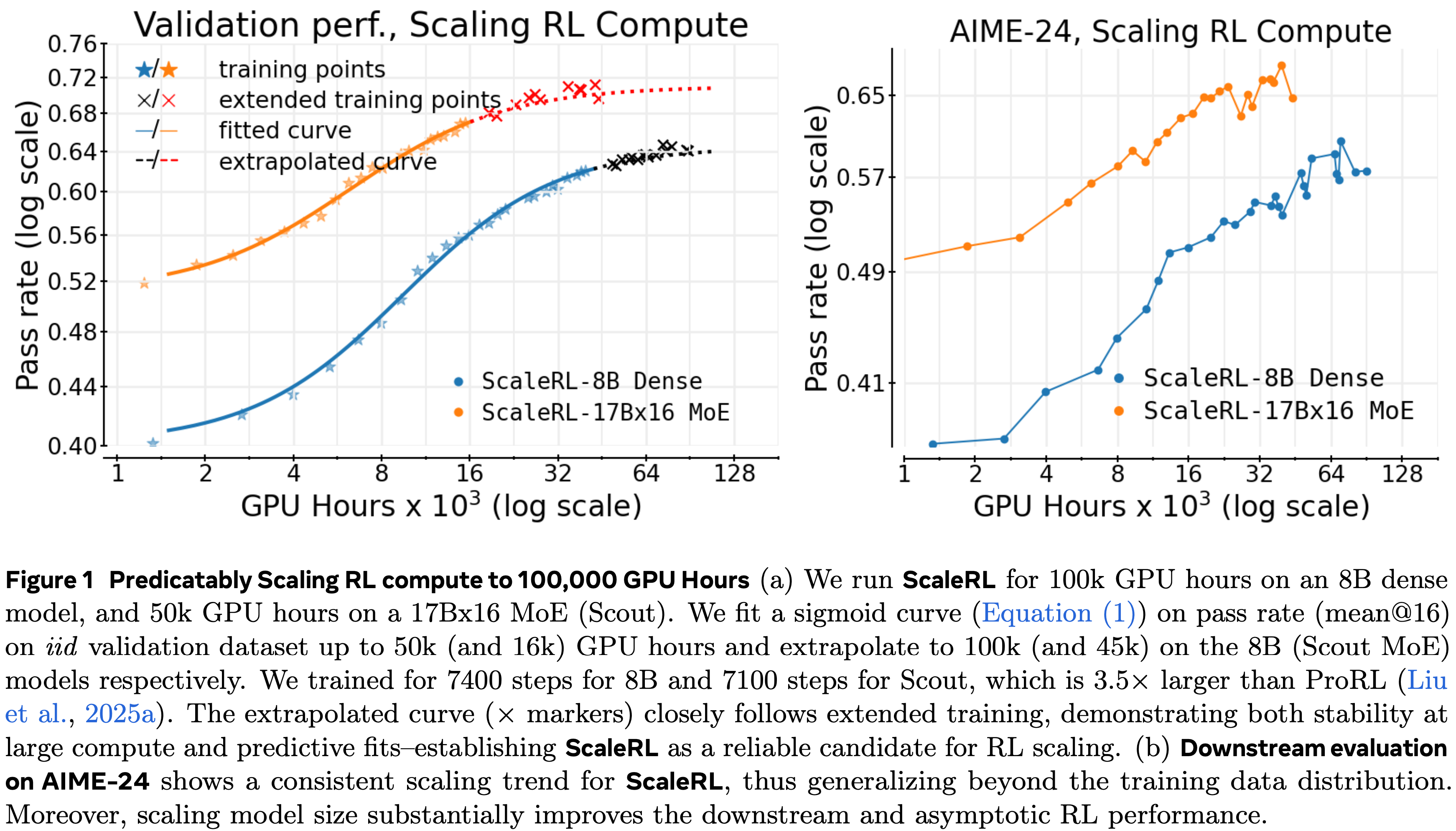
- 结合这些见解,论文提出了一个最佳实践(best-practice) Recipe ScaleRL ,并通过成功地将单个 RL 运行扩展到 100,000 GPU hous 并预测其验证性能,证明了其有效性
- 论文的工作既提供了一个用于分析 RL Scaling 的科学框架,也提供了一个实用的 Recipe ,使 RL 训练更接近预训练中长期实现的预测性
Introduction and Discussion
- Scaling RL 计算正成为推进 LLMs 发展的关键范式
- 预训练奠定了模型的基础;但随后的 RL 训练阶段释放了当今许多最重要的 LLM 能力,从 test-time thinking (OpenAI, 2024; DeepSeek, 2025) 到智能体能力 (Kimi, 2025a)
- 例如 Deepseek-RL-Zero 使用了 100,000 H800 GPU hous 进行 RL 训练,占其预训练计算的 3.75% (DeepSeek, 2025)
- RL 计算的这种急剧增长在前沿 LLM 的各代产品中被放大,从 o1 到 o3 增加了超过 \(10\times\) (OpenAI, 2025),从 Grok-3 到 Grok-4 也有类似的飞跃 (xAI Team, 2025)
- 尽管用于 LLM 的 RL 计算已经大规模扩展,但我们对如何扩展 RL 的理解并未跟上;其方法论仍然更像艺术而非科学
- 最近的 RL 突破主要由针对新颖算法的孤立研究 (例如,DAPO, (2025)) 和特定模型的训练报告所驱动,例如 MiniMax 等 (2025) 和 Magistral (2025)
- 且这些研究提供了针对特定背景的临时解决方案,但并未说明如何开发能够随计算规模扩展的 RL 方法
- 这种 Scaling 方法论的缺乏阻碍了研究进展:
- 由于没有可靠的方法先验地识别有前景的 RL 候选方案,进展与大规模实验绑定,这使得大多数学术界团体被边缘化
- 这项工作通过借鉴预训练中成熟的概念 Scaling Laws ,为 RL Scaling 的科学奠定了基础
- 虽然预训练已经收敛到能够可预测地随计算规模扩展的算法 Recipe (2020; 2022; Owen, 2024),但 RL 领域缺乏明确的标准
- RL 从业者面临着令人眼花缭乱的设计选择,使得如何扩展以及扩展什么这些基本问题悬而未决
- 为了解决这些问题,论文建立了一个使用类 S 形饱和曲线来预测 RL 性能的框架,该曲线描述了在同分布验证集上的期望奖励 (\(R_{C}\)) 与训练计算量 (\(C\)) 之间的关系:
$$\boxed{ \overbrace{R_{C}-R_{0} }^{ \text{Reward Gain} } = \overbrace {(A-R_{0})}^{ \text{Asymptotic Reward Gain} } \times \frac{1}{\underbrace{1+(C_{\rm mid}/C)^{B} }_{ \text{Compute Efficiency} } } } \quad \quad \text{(fixed model and traning data)} \tag{1}$$ - \(0\leq A\leq 1\) 代表渐近通过率
- \(B>0\) 是决定计算效率的缩放指数
- \(C_{\rm mid}\) 设定了 RL 性能曲线的中点
- 注:\((A-R_{0})\) 可以理解为 渐近的奖励增益(Asymptotic Reward Gain), \(A\) 为渐近奖励(Asymptotic Reward)
- 理解:
- \(A-R_0\) 是表示一个系数,越大时,整体收益 \(R_C\) 越大
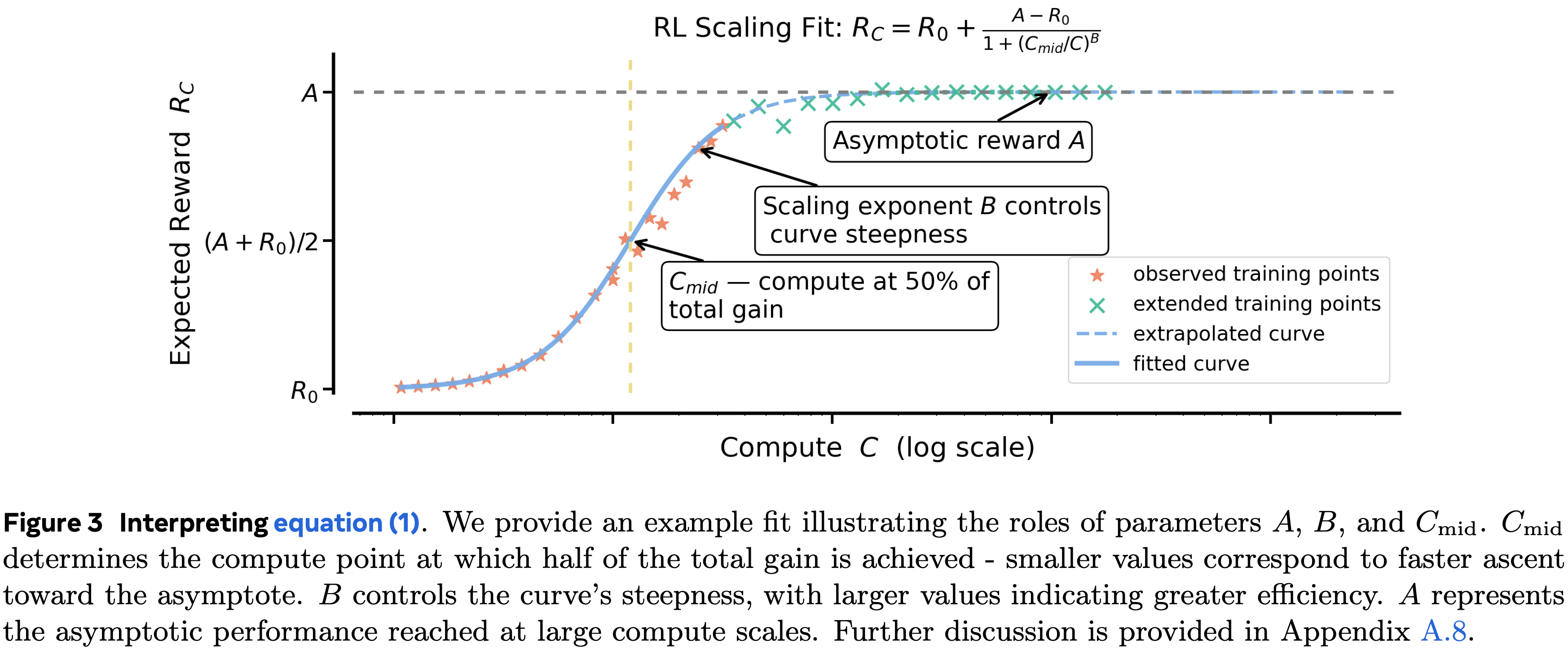
- \(C\) 是一个越大,\(C_{\rm mid}/C\) 变小,\(1+(C_{\rm mid}/C)^B\) 变小,\(\frac{1}{1+(C_{\rm mid}/C)^B}\) 变大,整体曲线如图 3 所示
- 图 3 提供了这些参数的示意图解释
- 公式 (1) 中的框架使研究人员能够从低计算量运行外推性能到高计算预算,从而能够在无需承担将每个实验都运行到其计算极限的成本的情况下,评估 RL 方法的可扩展性
- 在这个框架的指导下,论文开发了 ScaleRL ,这是一个能够可预测地随计算规模扩展的 RL Recipe
- 在一个大规模的100,000 GPU hous 训练运行中,论文展示了 ScaleRL 的性能与论文的框架预测的扩展曲线紧密匹配(图 1)
- 仅从训练的初始阶段外推的扩展曲线与最终观察到的性能紧密匹配,证实了论文的框架在极端计算规模下的预测能力
- ScaleRL 的设计基于一项全面的 RL Scaling 实证研究,该研究跨越了超过 400,000 GPU hous(在 Nvidia GB200 GPU 上)
- 这项研究在 8B 模型参数规模上探索了众多设计选择,其中单个运行使用高达 16,000 GPU hous,使其比在论文最大训练运行规模上进行实验便宜 6 倍
- 这项调查得出了三个关键原则:
- RL 性能上限并非普适(RL Performance Ceilings are Not Universal) :当我们为不同方法扩展训练计算量时,它们会遇到不同的可达到性能上限 (\(A\))
- 这个限制可以通过诸如损失类型和批次大小等选择来改变
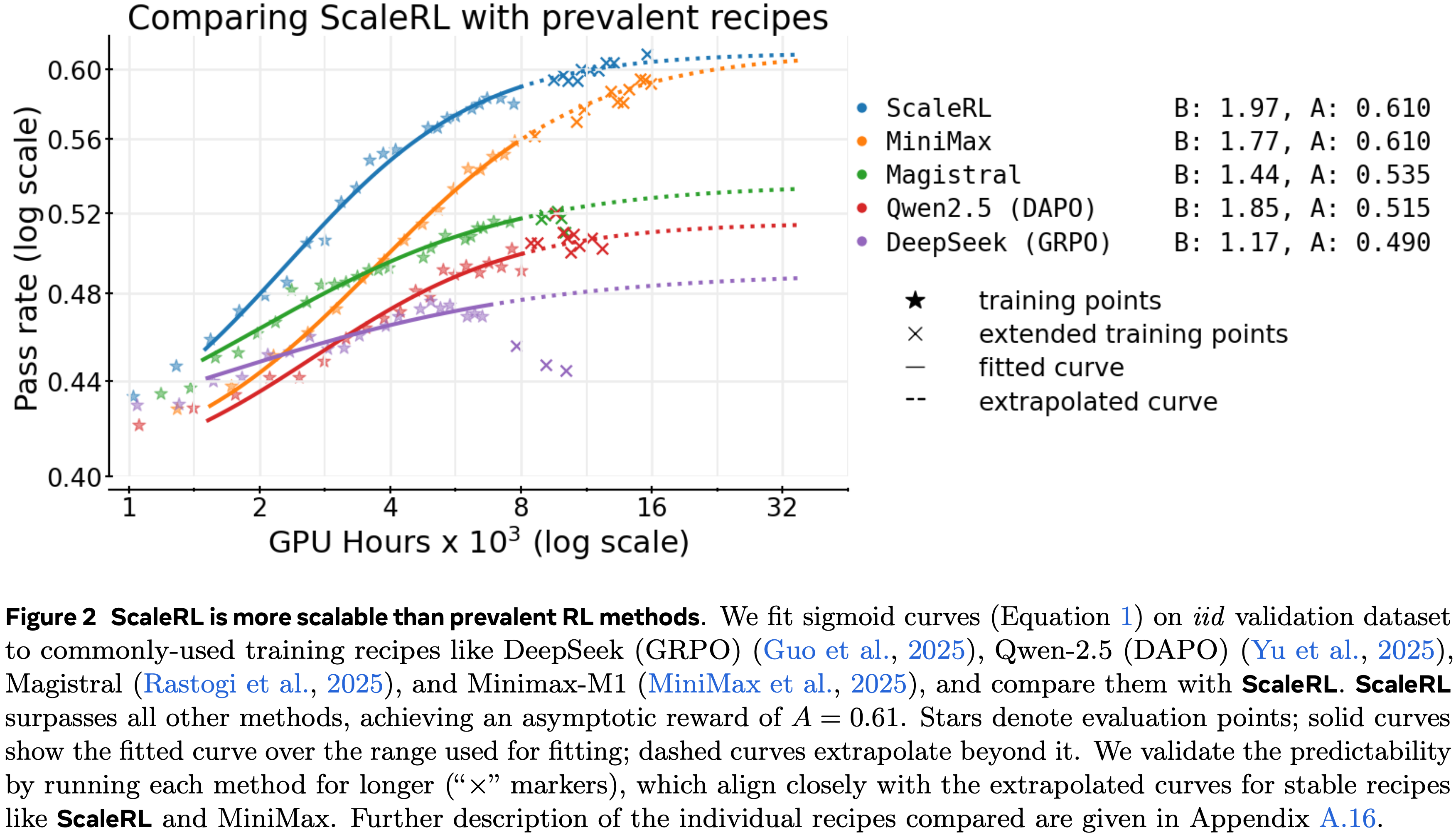
- 拥抱苦涩教训(Embracing the Bitter Lesson) :在小计算预算下表现优越的方法,在外推到大规模计算区域时可能更差(图 2)
- 仍然可以通过使用论文的框架(公式 (1))从早期训练动态中估计缩放参数 (\(A\), \(B\)) 来识别可扩展的方法
- 仍然可以通过使用论文的框架(公式 (1))从早期训练动态中估计缩放参数 (\(A\), \(B\)) 来识别可扩展的方法
- 重新评估常见智慧 :通常被认为能提高峰值性能的干预措施(例如,损失聚合、数据课程、长度惩罚、优势归一化)主要调整计算效率 (\(B\)),而不会显著改变性能上限
- RL 性能上限并非普适(RL Performance Ceilings are Not Universal) :当我们为不同方法扩展训练计算量时,它们会遇到不同的可达到性能上限 (\(A\))
- 基于这些见解,ScaleRL 通过整合现有方法而非发明新方法来实现可预测的扩展
- 具体来说,ScaleRL 结合了异步 Pipeline-RL 设置(第 3.1 节)、强制长度中断、截断重要性采样 RL 损失 (CISPO from MiniMax-M1)、提示级损失平均、批次级优势归一化、logits 处的 FP32 精度、零方差过滤和 No-Positive-Resampling
- 以上每个组件的贡献都在消耗 16,000 GPU hous 每次运行的留一法消融实验中得到了验证
- ScaleRL 实现可预测地扩展,且建立了新的SOTA(图 2)
- 与已建立的 RL Recipe 相比,它实现了更高的渐近性能和计算效率
- ScaleRL 在跨多个训练轴增加计算量时保持了可预测的扩展性(第 5 节)
- 包括 \(2.5\times\) 更大的批次大小、长达 32,768 个 Token 的生成长度、使用数学和代码的多任务 RL 以及更大的混合专家模型 (Llama-4 17B\(\times\)16);
- 其益处持续迁移到下游任务
- 总的来说,这项工作建立了一种严谨的方法论,用于成本效益地预测新 RL 算法的可扩展性
Preliminaries & Setup
- 论文使用 LLM 进行强化学习,其中提示 \(x\) 从数据分布 \(D\) 中采样
- 论文的设置遵循在 GPU 上的 Generator-Trainer 分离:
- Generator GPU 使用优化的推理内核进行高通量 rollout 生成
- Trainer GPU(其余的 GPU)运行训练后端 (FSDP) 并更新参数
- 论文分别用 \(\pi^{\theta}_{\text{gen} }\) 和 \(\pi^{\theta}_{\text{train} }\) 表示 Generator 和训练后端上具有参数 \(\theta\) 的模型
- 对于每个提示, Generator GPU 上的旧策略 \(\pi^{\theta_\text{old} }_\text{gen}\) 产生候选补全,然后被分配标量奖励
- 策略优化通过最大化一个裁剪的 Surrogate Objective 进行,对 \(x\sim D\) 和来自 \(\pi^{\theta_\text{old} }_\text{gen}\) 的 rollout 取期望
Training Regimen(安排,规划)
- 所有实验均在用于推理的 RL 领域进行,其中模型产生一个用特殊 Token(<think> … </think>)包围的思考轨迹和一个最终解决方案
- 除非另有说明,训练使用 16,384 个 Token 的序列长度:
- 12,288 用于思考,2,048 用于解决方案,另外 2,048 用于输入提示
- 论文采用 12,288 的思考预算以加快迭代速度,并在第 5 节展示 ScaleRL 外推在使用更大思考预算 (32,768) 进行训练时仍保持预测性
- 对于数学 RL 实验,论文使用 Polaris-53K 数据集 (2025),批次大小为 768(48 个提示,每个提示 16 次生成)
- 在论文的设置中,扩展 RL 计算对应于在训练提示上运行多个周期
- 关于训练的更多细节,包括 SFT 和超参数,见附录 A.3
Base RL Algorithm
- 作为论文在第 3 节的起点,论文从一个“基础”算法开始
- 该算法类似于没有 KL 正则化项的 GRPO (2024),与大规模训练报告一致 (Magistral, 2025; MiniMax, 2025)
- 论文包含了非对称 DAPO 裁剪 (2025),它作为避免熵崩溃和保持输出多样性的默认方法被广泛采用
- 对于给定的提示 \(x\),旧策略 \(\pi_{\text{gen} }(\theta_{\text{old} })\) 生成 \(G\) 个候选补全 \(\{y_{i}\}_{i=1}^{G}\),每个被分配一个标量奖励 \(r_{i}\)。论文计算优势 \(\hat{A}_{i}\) 并使用组归一化优势:
$$\hat{A}_{i}=r_{i}-\text{mean}(\{r_{j}\}_{j=1}^{G}),\quad\hat{A}_{i}^{G}=\hat{A}_ {i}/(\text{std}(\{r_{j}\}_{j=1}^{G})+\epsilon).$$- 每个长度为 \(|y_{i}|\) 的补全 \(y_{i}\) 在 Token-level 的重要性采样 (IS) 比率 \(\rho_{i,t}(\theta)\) 上做出贡献,具有非对称的上限和下限裁剪阈值,类似于 DAPO (2025):
$$\rho_{i,t}(\theta):=\frac{\pi^{\theta}_\text{train}(y_{i,t}\mid x,y_{i,<t})}{\pi^{ \theta_{\text{old} } }_\text{gen }(y_{i,t}\mid x,y_{i,<t})}=\frac{\pi^ {\theta}_\text{train}(y_{i,t})}{\pi^{\theta_{\text{old} } }_\text{gen }(y_{ i,t})};\quad\text{clip}_{\text{asym} }(\rho,\epsilon^{-},\epsilon^{+}):=\text{ clip}(\rho,1-\epsilon^{-},1+\epsilon^{+}). \tag{2}$$ - 论文在 Sample-level 聚合损失,即在跨样本平均之前,先平均每个样本的 Token 损失
- Surrogate Objective 为:
$$\mathcal{J}(\theta)=\mathbb{E}_{x\sim D,\atop\{y_{i}\}_{i=1}^{G}\sim\pi^{ \theta_{\text{old} } }_\text{gen }(\cdot|x)}\left[\frac{1}{G}\sum_{i=1}^{G}\frac{1 }{|y_{i}|}\sum_{t=1}^{|y_{i}|}\min\Bigl{(}\rho_{i,t}(\theta)\hat{A}_{i}^{G}, \text{clip}_{\text{asym} }(\rho_{i,t}(\theta),\epsilon^{-},\epsilon^{+})\hat{A}_ {i}^{G}\Bigr{)}\right]. \tag{3}$$
- 每个长度为 \(|y_{i}|\) 的补全 \(y_{i}\) 在 Token-level 的重要性采样 (IS) 比率 \(\rho_{i,t}(\theta)\) 上做出贡献,具有非对称的上限和下限裁剪阈值,类似于 DAPO (2025):
- 控制生成长度 (Controlling Generation Lengths)
- 为了防止训练过程中推理输出长度爆炸性增长,这有害于训练稳定性和效率,论文使用中断 (GLM-V Team, 2025; 2025),通过附加一个思考结束短语(例如,“</think>”)来强制停止过长的生成,示意 LLM 终止其推理并产生最终答案
- 论文将在后面的第 4 节重新讨论这个选择,并将其与惩罚长生成的长度惩罚进行比较 (2025; Kimi Team, 2025b)
Predictive compute-scaling and fitting curves
- 与通常使用幂律拟合预测曲线的预训练不同,论文使用 S 形函数(公式 (1))来模拟通过率与 \(\log(compute)\) 的关系
- 论文这样做是因为论文经验发现 S 形拟合比幂律拟合更鲁棒和稳定,论文将在附录 A.4 中进一步讨论
- 论文的选择与先前使用类 S 形幂律来捕捉有界指标(如准确率)的工作一致 (2024; 2022)
- 与预训练研究类似 (2025b; 2025),论文发现排除非常早期的低计算区域(low-compute regime)会产生更稳定的拟合,之后训练遵循可预测的轨迹
- 除非另有说明,论文所有的缩放拟合都在约 1.5k GPU hous 之后开始
- 拟合过程的进一步细节在附录 A.5 中提供,论文曲线拟合的鲁棒性在附录 A.7 中讨论
- 问题:这里是指拟合 S 形曲线时,排除早期的训练结果,理解是因为此时模型没有得到良好的训练,不排除会受波动影响较大
- 解释缩放曲线 (Interpreting scaling curves)
- 直观地说,S 形曲线捕捉了饱和回报:
- 在低计算区域增长缓慢,在高效缩放的中段急剧加速,然后在计算量高时饱和
- 论文还在图 3 中提供了 S 形曲线参数 \(A,B,\text{ 和 }C_{mid}\) 的示意图解释
- 可以看到,\(B,C_{\text{mid} }\) 主要影响运行的效率,\(A\) 表示在大型计算规模下的渐近性能
- 关于这些参数的进一步讨论在附录 A.8 中提供
- 直观地说,S 形曲线捕捉了饱和回报:
- 在留出验证集上的缩放曲线 (Scaling curve on held-out validation)
- 与预训练实践一致 (2022; 2025),论文在同分布验证数据上测量预测性能
- 由于训练运行跨越多个 Epochs,论文从 Polaris-53k 数据集中随机留出 \(1,000\) 个提示用于验证,并使用其余部分进行训练
- 缩放曲线拟合在验证点上,这些点每 100 个训练步骤测量一次平均通过率,在 \(1,000\) 个留出提示上每个提示有 16 次生成
An Empirical Study of RL Scaling
- 论文使用一个 8B 参数的稠密模型在可验证的数学问题上进行 RL 实验
- 使用第 2 节中描述的设置,论文研究了几个设计轴在其可预测的计算缩放行为方面,即渐近性能 (asymptotic performance, \(A\)) 和计算效率 (compute efficiency, \(B\)),如图 3 所示

- 论文将实验结构分为三个阶段
- 首先,在 3.5k 到 4k GPU hous 的基线之上消融设计选择,因为一些实验选择在此规模之外会变得不稳定(附录 A.15)
- 每当一个设计改变被证明是稳定的,论文就将其训练更长时间
- 然后,将最佳选择组合成 ScaleRL ,并在第 4 节进行 16k GPU hous 的留一法 (LOO) 实验
- 在这里,论文通过在前 8k GPU hous 上拟合并外推运行的剩余部分来评估可预测性
- 最后,为了证明使用 ScaleRL 的可预测缩放,论文在第 5 节还考虑了具有更大批次大小、混合专家模型、多任务(数学和代码)和更长序列长度的训练设置
- 首先,在 3.5k 到 4k GPU hous 的基线之上消融设计选择,因为一些实验选择在此规模之外会变得不稳定(附录 A.15)
Asynchronous RL Setup
- 论文首先研究异步 Off-policy RL 设置 (2024) 的选择,因为它控制着训练稳定性和效率,通常独立于所有其他设计选择
- 论文考虑两种 Off-policy 学习方法:PPO-off-policy-\(k\) 和 PipelineRL-\(k\)
- PPO-off-policy-\(k\) 是异步 RL 的默认方法,先前已被 Qwen3 (2025) 和 ProRL (2025a) 使用
- 在这种设置中,旧策略 \(\pi_{\theta^{\text{old} }_{\text{gen} } }^{op}\) 为一批 \(B\) 个提示生成推理轨迹
- 每次梯度更新处理一个包含 \(\hat{B}\) 个提示的小批次,导致每个批次有 \(k=B/\hat{B}\) 次梯度更新
- 在论文的实验中,论文固定 \(\hat{B}=48\) 个提示(每个提示 16 次生成),并通过设置 \(B=k\times 48\) 来改变 \(k\in \{1,8\}\)
- PipelineRL-\(k\) 是来自 Piche 等 (2025) 的一种新方法,并被 Magistral (2025) 使用
- 在 PipelineRL-\(k\) 中, Generator 以流式方式持续产生推理轨迹
- 每当 Trainer 完成一次策略更新时,新参数立即推送到 Generator , Generator 继续使用更新后的权重但使用来自旧策略的陈旧 KV 缓存进行生成
- 一旦生成完整的轨迹批次,它就被传递给 Trainer 进行下一次更新
- 在论文的设置中,论文引入了一个参数 \(k\):如果 Trainer 比 Generator 提前 \(k\) 步,它们就会等待
- 论文在图 4(a) 中比较了这些方法
- PipelineRL 和 PPO-off-policy 实现了相似的渐近性能 \(A\),但 PipelineRL 显著提高了计算效率 \(B\);从而更快地达到上限 \(A\)
- 因为 PipelineRL 减少了训练过程中的空闲时间
- 这种选择以更少的 Token 产生可靠的收益,使得在较低计算预算下进行更大范围的扫描成为可能
- 论文还改变了 PipelineRL 的最大 Off-policy 程度,并发现 \(k=8\) 是最优的,如图 4(b) 所示,论文将在附录 A.11 中进一步讨论
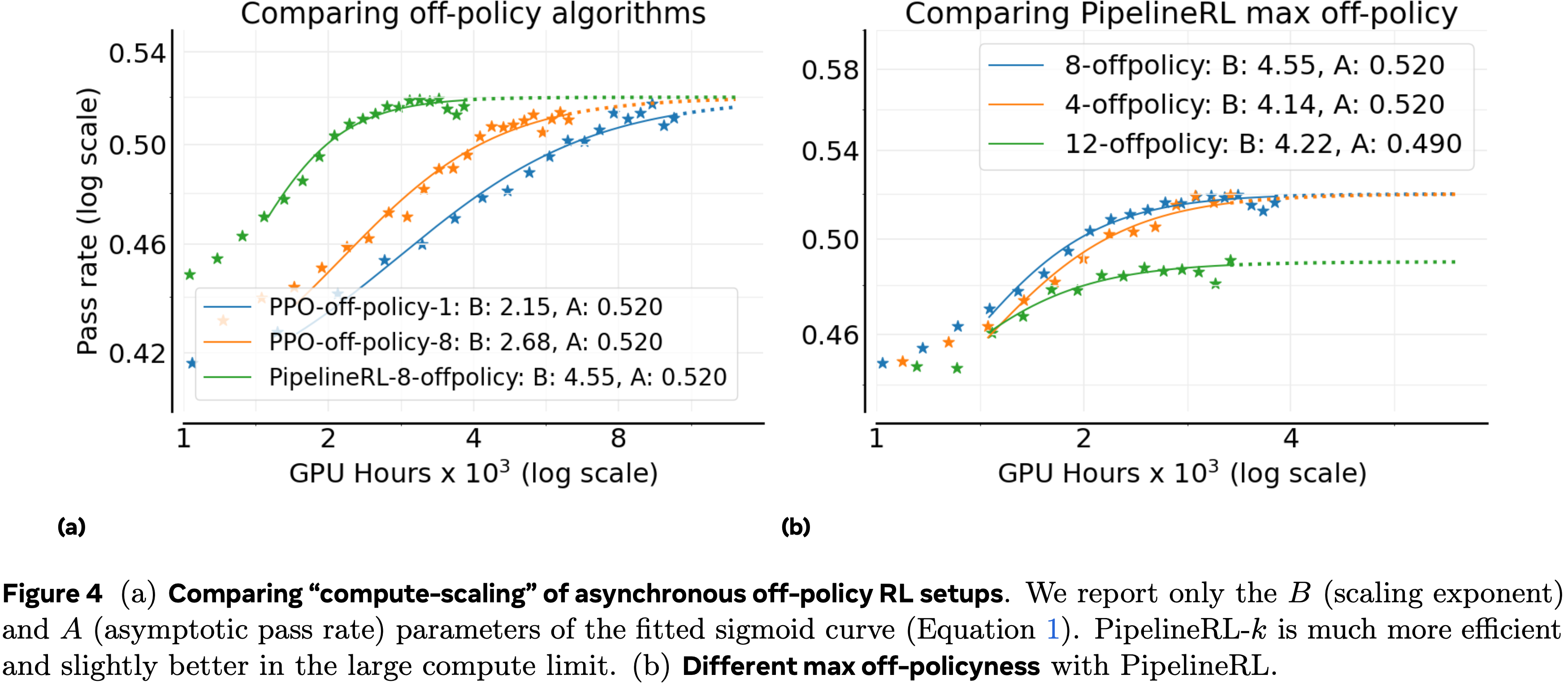
- PipelineRL 和 PPO-off-policy 实现了相似的渐近性能 \(A\),但 PipelineRL 显著提高了计算效率 \(B\);从而更快地达到上限 \(A\)
Algorithmic Choices
- 基于以上结果,论文采用 PipelineRL-8 作为论文更新后的基线。然后论文研究了六个额外的算法轴:
- (a) 损失聚合, loss aggregation
- (b) 优势归一化,advantage normalization
- (c) 精度修正,precision fixes
- (d) 数据课程,data curriculum
- (e) 批次定义,batch definition
- (f) 损失类型,loss type
- 在第 4 节,论文将最佳选项组合成一个统一的 Recipe ,称为 ScaleRL (Scale-able RL),并在 16,000 GPU hous 的更大规模上进行留一法实验
Loss type
- 论文将非对称 DAPO 损失(公式 8)与两个最近提出的替代方案进行比较:GSPO (Qwen, 2025a) 和 CISPO (MiniMax, 2025; 2025)
- GSPO 在序列级别应用重要性采样,而不是 GRPO 的 Token-level 公式。具体来说,GSPO 将 Token-level 的 IS 比率(公式 2)改变为序列级别的比率:
$$ \rho_{i}(\theta)=\frac{ {\pi_\text{train}(y_{i}|x,\theta)} }{ {\pi_{gen}(y_{i}|x,\theta_{\text{old} })} }$$ - CISPO 简单地将截断 IS 与普通策略梯度 (Ionides, 2008) 结合起来,其中 \(\mathbf{sg}\) 是停止梯度函数:
$$\mathcal{J}_{\text{CISPO} }(\theta)=\underset{\begin{subarray}{c}x\sim D,\ (y_{t})_{t=1}^{G}\sim\pi_{gen}(\cdot|x,\theta_{\text{old} })\end{subarray} }{\mathbb {E} }\left[\frac{1}{T}\sum_{t=1}^{G}\sum_{t=1}^{\lvert y_{t}\rvert}\mathbf{sg}(\min(\rho_{i,t},\epsilon_{\max}))\hat{A}_{i}\log \left(\pi_\text{train}(y_{i,t}|x,y_{i<t},\theta)\right)\right] \tag{4}$$ - 图 5(a) 显示 GSPO 和 CISPO 都显著优于 DAPO,大幅提高了渐近通过率 \(A\)
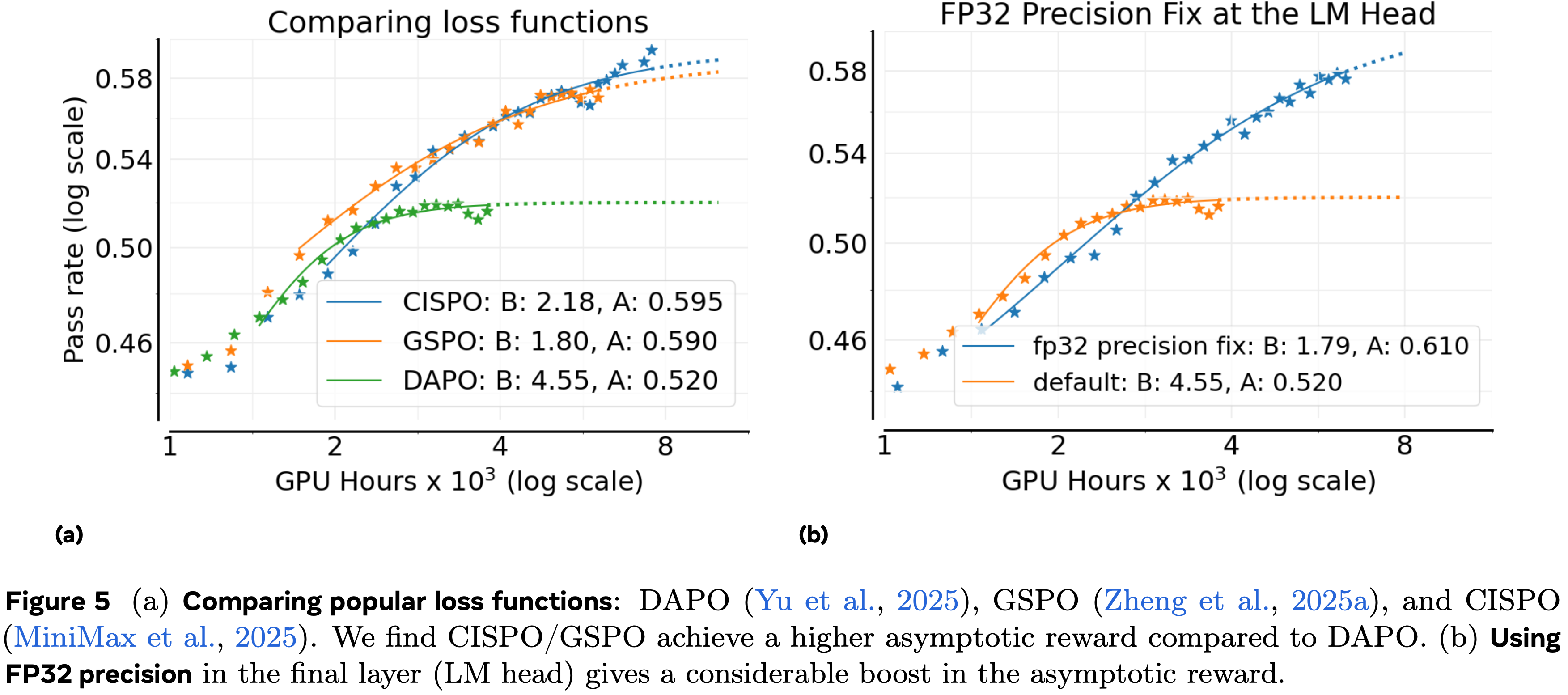
- CISPO 表现出延长的近线性奖励增长,并且在训练后期略优于 GSPO,因此论文选择 CISPO 作为论文的最佳损失类型
- 关于 Off-policy 损失类型及其超参数鲁棒性的进一步讨论在第 4 节和附录 A.17 中详述
FP32 Precision for LLM logits
- Generator 和 Trainer 依赖不同的内核进行推理和训练,导致它们的 Token 概率存在小的数值不匹配 (ThinkingMachine Defeating nondeterminism in LLM inference, 2025)
- RL 训练对此类差异高度敏感,因为它们直接影响 Surrogate Objective 中的 IS 比率
- MiniMax (2025) 发现这些不匹配在语言模型头(language model head)尤其明显,并通过在 Generator 和 Trainer 的 Head 使用 FP32 计算来缓解这个问题
- 如图 5(b) 所示,精度修正将渐近性能 \(A\) 从 \(0.52\) 显著提高到 \(0.61\)
- 鉴于这个明显的好处,论文将 FP32 精度修正包含在论文的 ScaleRL Recipe 中
Loss Aggregation
- 论文评估了三种聚合 RL 损失的策略:
- (a) 样本平均(Sample average) ,每个 rollout 贡献相等(如 GRPO,附录 A.2)
- (b) 提示平均(Prompt average) ,每个提示贡献相等(如 DAPO,附录 A.2)
- (c) Token 平均(Token average) ,批次中的所有 Token 损失直接平均,没有中间分组
- 比较结果见附录 A.9(图 14(a))
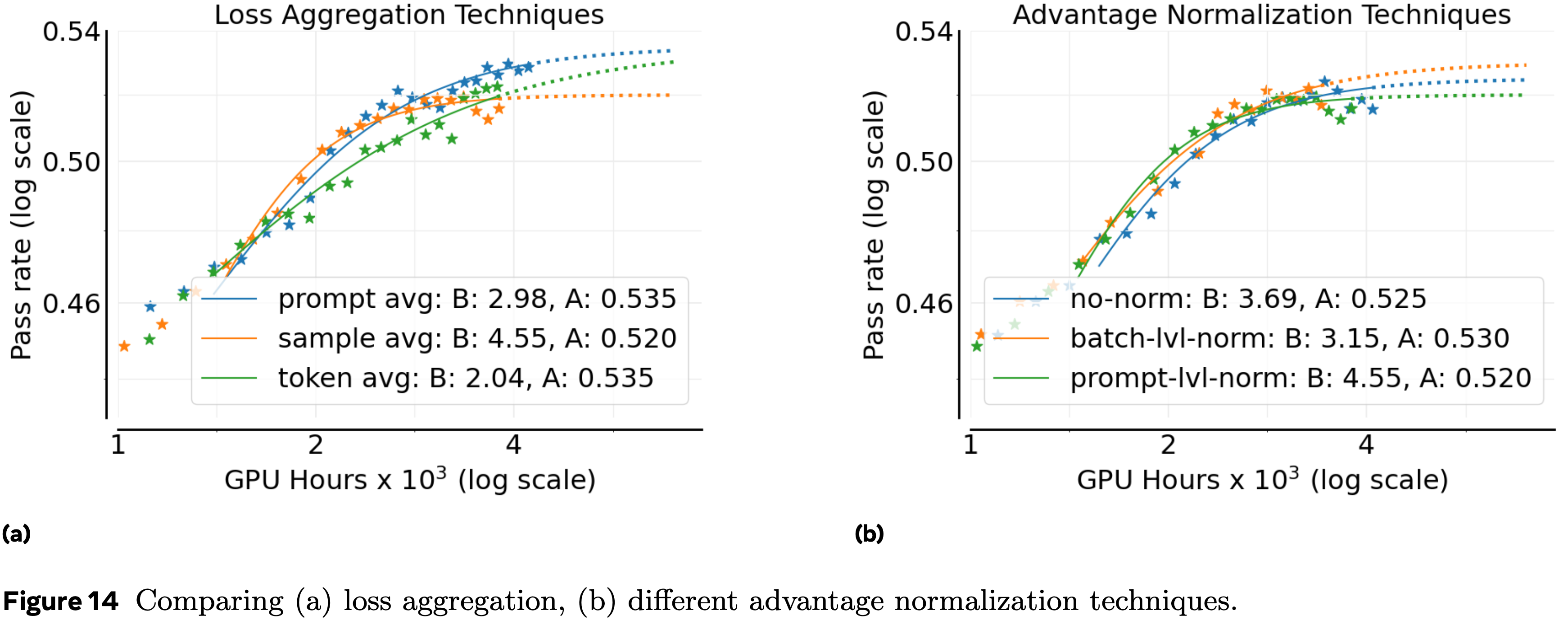
- 论文发现 Prompt average 实现了最高的渐近性能,因此在 ScaleRL 中使用此选择
Advantage Normalization
- 论文比较了三种优势归一化的变体:
- (a) 提示级别(Prompt level) ,优势通过同一提示的 rollout 奖励的标准差进行归一化(如 GRPO,附录 A.2)
- (b) 批次级别(Batch level) ,优势通过批次中所有生成的标准差进行归一化,如 Reinforce++ (2025a); Magistral (2025) 所用
- (c) 无归一化(No normalization) ,优势计算为原始奖励减去提示生成的平均奖励,没有方差缩放(如 Dr. GRPO (2025c) 所提出)
- 比较图见附录 A.9(图 14(b)),观察到所有三种方法产生相似的性能
- 因此论文采用 Batch level 归一化,因为它在理论上合理且略好
- 这个选择在第 4 节的更大规模留一法实验中也得到了进一步证实
Zero-Variance Filtering
- 在每个批次中,一些提示在其所有生成中产生相同的奖励
- 这些“零方差”提示具有零优势,因此贡献零策略梯度
- 默认基线在损失计算中包含这些提示,但尚不清楚是否应将它们包含在有效批次中
- 为了测试这一点,论文将默认设置与有效批次(effective batch)方法进行比较
- 在 effective batch approach 中,只有具有非零方差的提示被包含在损失计算中(如 Seed (2025) 所做)
- 请注意:零方差过滤不同于 DAPO (2025) 中的动态采样
- 零方差过滤仅仅是丢弃 Prompt ,而 DAPO 是重新采样更多提示直到批次满员(until the batch is full)
- 论文在图 6(a) 中显示使用有效批次在渐近性能上表现更好;论文将其纳入论文的 ScaleRL Recipe
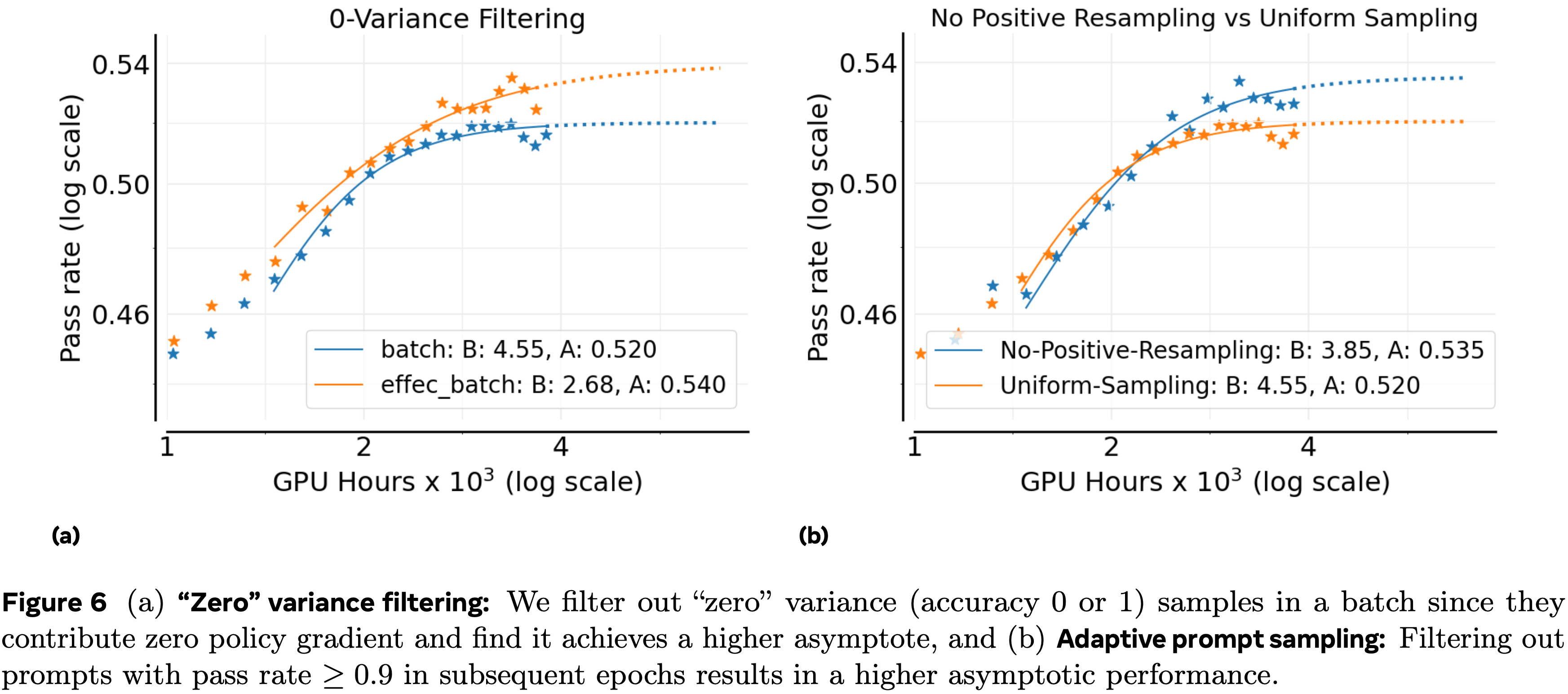
Adaptive Prompt Filtering
- 已经提出了许多用于 RL 训练的数据课程策略以提高样本效率 (2025; 2025b; 2025b)
- 这里论文评估一个简单的变体,由 (2025) 引入,其关键观察是
- 一旦一个提示对策略变得过于简单,它通常会持续保持简单
- 由于这样的提示消耗一些计算但不再贡献有用的梯度信号(第 3.2 节),最好将它们从未来的训练中排除
- 论文通过维护一个通过率历史记录并永久移除任何通过率 \(\geq 0.9\) 的提示在后续周期中来实现这一点(论文称之为 No-Positive-Resampling)
- 在图 6(b) 中,论文将此课程与默认设置(所有提示在整个训练过程中均匀重新采样)进行比较
- 论文看到课程提高了可扩展性和渐近奖励 \(A\)
ScaleRL: 有效且可预测地扩展强化学习计算 (ScaleRL: Scaling RL Compute Effectively & Predictably)
- 根据上述研究的设计维度,论文将性能最佳的设置整合到一个单一的 Recipe 中,论文称之为 ScaleRL (Scale-able RL)
- ScaleRL 是一种异步强化学习 Recipe ,它使用下面的配置:
- 具有 8 步 Off-policy 性的 PipelineRL
- 基于中断的长度控制进行截断(interruption-based length control for truncation)
- 注:后文有提到,对于强制中断,论文使用思考结束短语:”Okay, time is up. Let me stop thinking and formulate a final answer now. </think>“
- FP32 计算用于逻辑单元
- 优化 \(\mathcal{J}_{\texttt{ScaleRL} }(\theta)\) 损失
- \(\mathcal{J}_{\texttt{ScaleRL} }(\theta)\) 损失结合了:
- Prompt-level 损失聚合
- Batch-level 优势归一化
- 注意:是按照批次做 Advantage 归一化的,不是 GRPO 方法,而是类似 REINFORCE++ 方法
- 补充:REINFORCE++ 的方法:
- 记录历史平均奖励作为基线,判断模型是否在进步
- 使用历史奖励的均值和方差做归一化,类似 Batch Normalization)
- 截断重要性采样(truncated importance-sampling)REINFORCE 损失 (CISPO)
- 零方差过滤(zero-variance filtering)
- 无正例重采样(no-positive resampling)
$$\begin{split}\mathcal{J}_{\texttt{ScaleRL} }(\theta)=& \underset{x\sim D,\atop\{y_{i}\}_{i=1}^{G},\sim\pi^{data}_{g\in h}( \cdot|x)}{\mathbb{E} }\left[\frac{1}{\sum_{g=1}^{G}|y_{g}|}\sum_{i=1}^{G}\sum_{t=1 }^{|y_{i}|}\mathsf{sg}(\min(\rho_{i,t},\epsilon))\hat{A}^{\text{norm} }_{i}\log \pi^{ {\theta} }_\text{train}(y_{i,t})\right],\\ \rho_{i,t}=&\frac{\pi^{ {\theta} }_\text{train}(y_{i,t})}{\pi^{ {\theta}_{add} }_{g\in h}(y_{i,t})},\hat{A}^{\text{norm} }_{i}=\hat{A}_{i}/\hat{A}_{\text{std} },0<\text{mean}(\{r_{j}\}_{j=1}^{G})<1,\text{pass_rate} (x)<0.9,\end{split}$$ - 其中 \(\mathsf{sg}\) 是停止梯度函数
- \(\hat{A}_{\text{std} }\) 是一个批次中所有优势 \(\hat{A}_{i}\) 的标准差
- pass_rate\((x)\) 表示提示 \(x\) 的历史通过率
留一法消融实验 (Leave-One-Out (LOO) Ablations)
- 为了验证这些选择在组合后仍然是最优的,论文进行了留一法 (LOO) 实验:
- 从 ScaleRL 开始,论文每次将一个维度恢复到其在第 2 节中的基线对应项
- 这确保了每个设计决策即使在其他所有决策都存在的情况下也能做出积极贡献
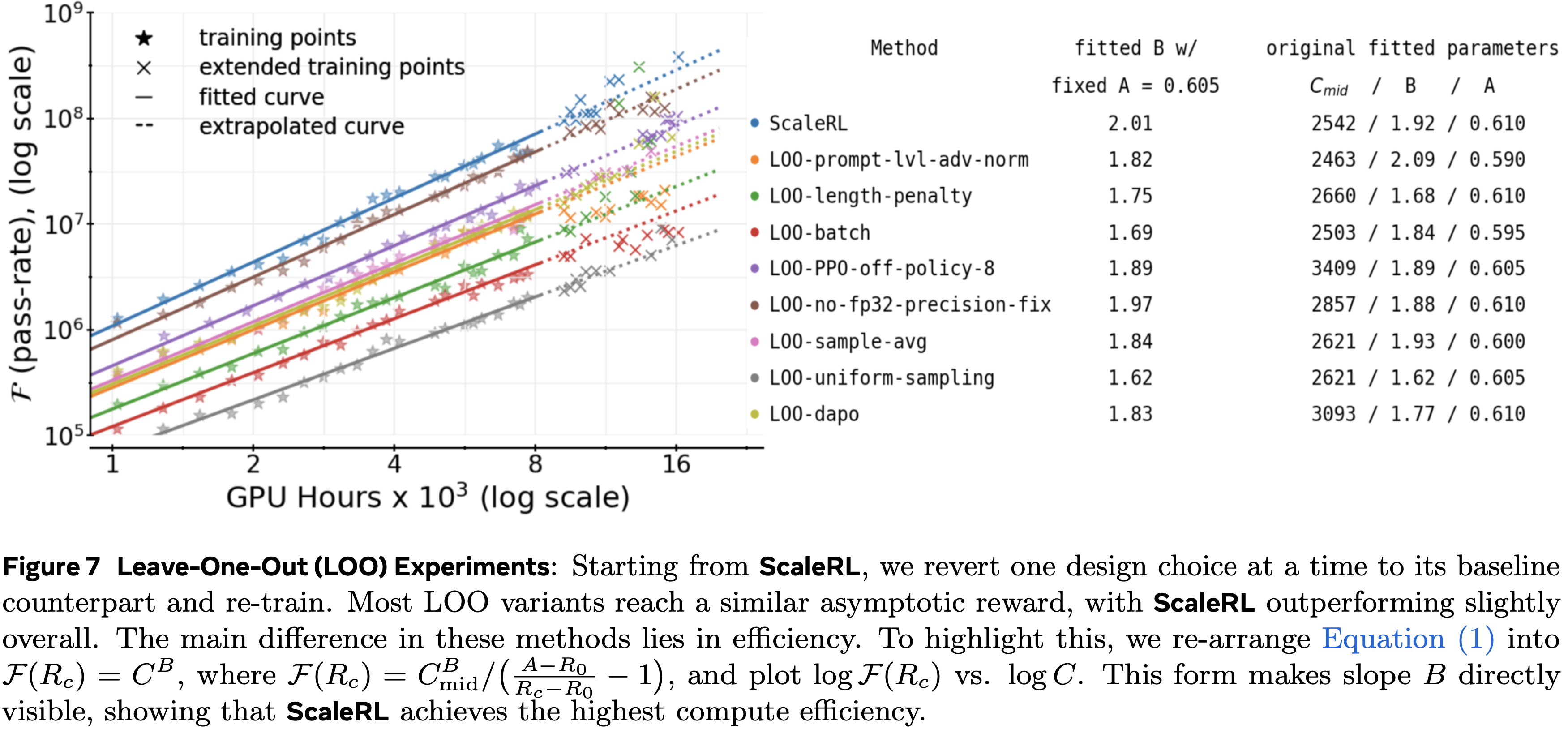
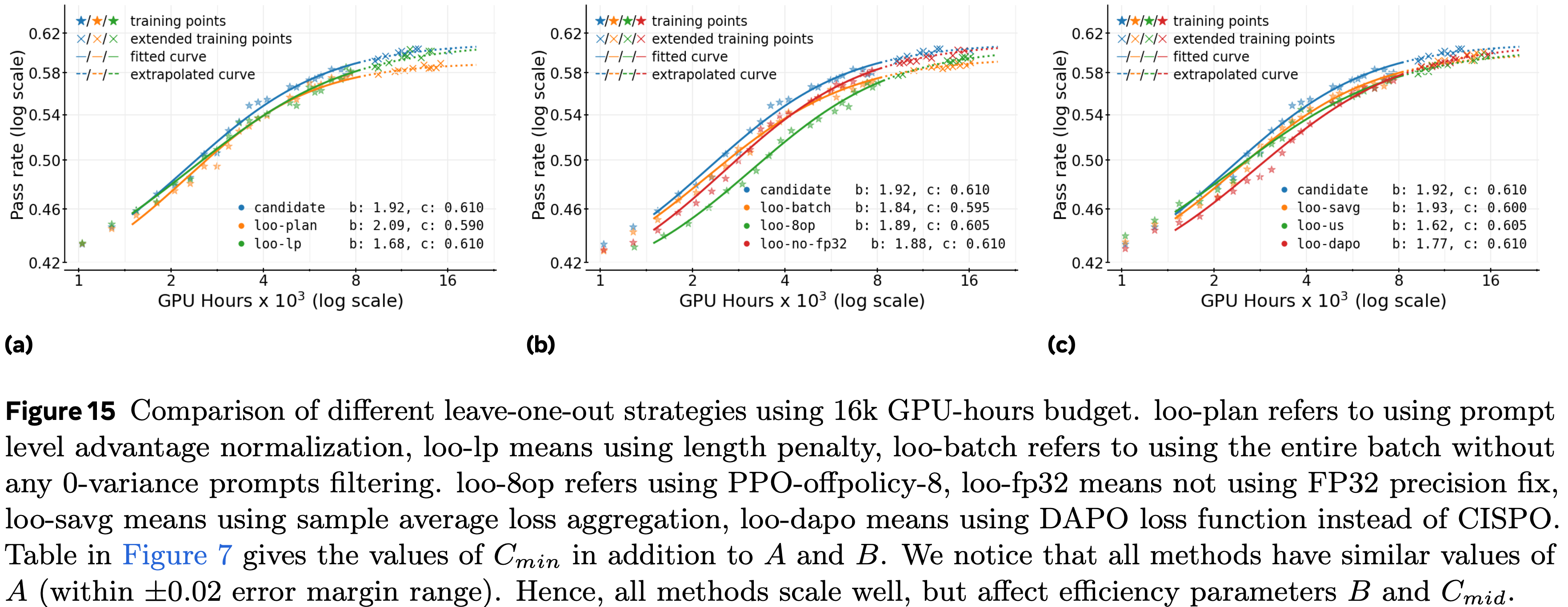
- 图 7 报告了这些实验,每个实验扩展到 16k GPU hous
- 在所有维度上,ScaleRL 始终是最有效的配置,在渐近奖励或计算效率上略微优于 LOO 变体(参见图 7 表格的最后一列)
- 由于大多数 LOO 变体达到相似的渐近通过率,论文将 sigmoid 拟合转换为幂律拟合,以通过斜率 \(B\) 突出效率差异(细节见图 7)
- 具体来说,论文平均所有运行的渐近奖励 \(A\),用这个固定的 \(A\) 重新拟合曲线,然后在图 7 中比较斜率(衡量效率)
- 相应的未转换的通过率与计算曲线在附录 A.2 中提供
Error margin(误差范围)in fitting scaling curves
- 由于强化学习训练已知具有高方差 (2021),论文使用三个独立的 ScaleRL 运行(图 8a)来估计拟合缩放系数的变异性
- 观察到的渐近奖励和效率参数的方差作为论文的经验误差范围,用于确定两个不同运行的计算效率或渐近性能的变化是否具有统计意义 (2024)
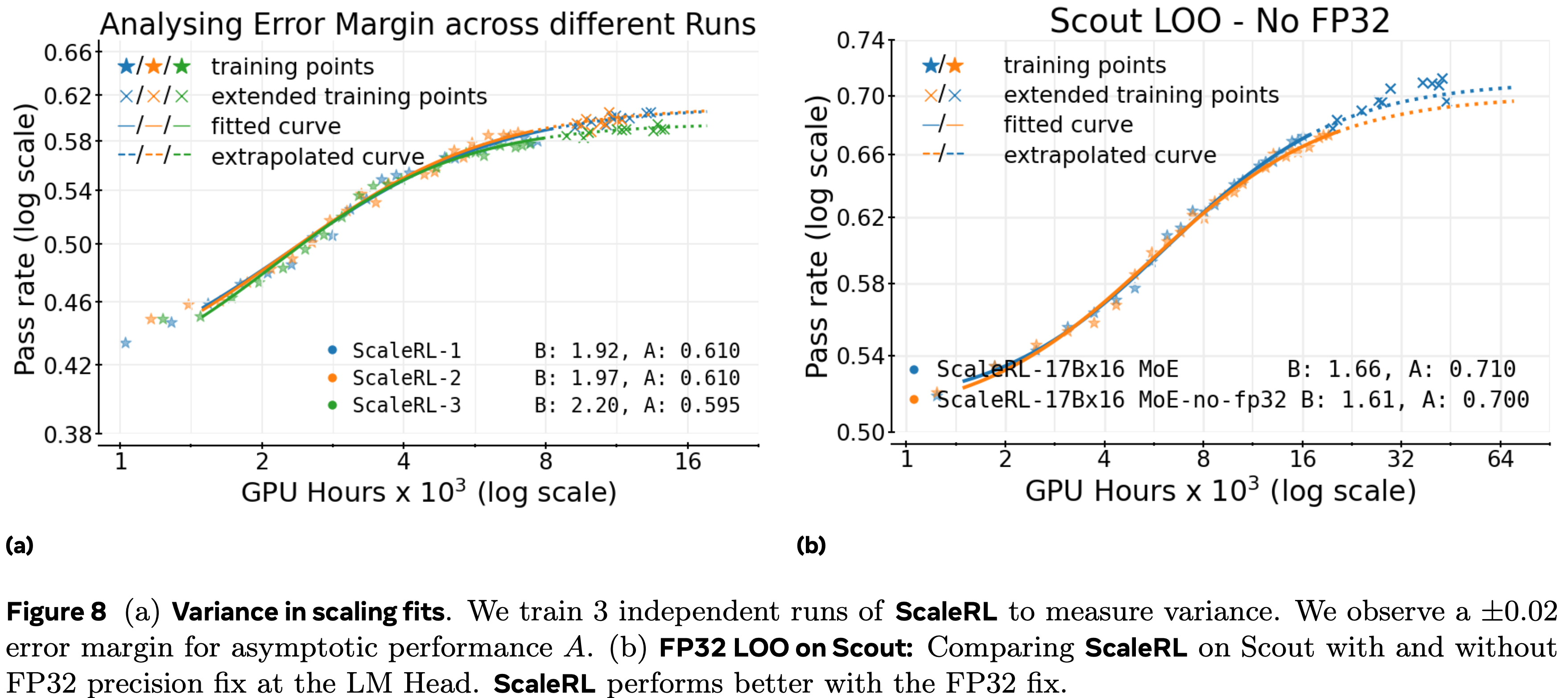
- 观察到的渐近奖励和效率参数的方差作为论文的经验误差范围,用于确定两个不同运行的计算效率或渐近性能的变化是否具有统计意义 (2024)
Extrapolating Scaling Curves
- 在论文所有的 LOO 实验以及独立的 ScaleRL 运行中,论文拟合了高达 8000 GPU hous 的 sigmoid 曲线,并外推到 16000 GPU hous ,观察到预测曲线与训练点和扩展点都紧密对齐
- 这证明了 ScaleRL 和其他稳定、可扩展的 Recipe 在大规模强化学习训练下的稳定性和可预测性
Are the design choices worth it?
- 在第 3.2 节中,某些设计选择改变了渐近性能,例如损失类型(图 5a)和 FP32 精度(图 5b)

- 但在论文使用 ScaleRL 的 LOO 实验中(图 7),这些组件单独来看似乎不那么关键(图中最后一列)
- 这就提出了一个问题:某些设计选择是否可以安全地保留其”默认”值
- 作者认为上述问题的答案是否定的
- 即使一个选择在组合 Recipe 中显得多余,它仍然可以提供稳定性或鲁棒性,这在其他情况下可能变得至关重要
- 问题:如何理解显得多余又能提供稳定性或鲁棒性,是指不使用这些指标时,不同随机种子下表现差异大吗?还是说在不同的 模型规模或者数据集上表现差异大?
- 例如,虽然 FP32 精度修复在使用 ScaleRL 训练的密集 8B 模型上差异不大(图 7),但它在 GRPO/DAPO 风格的损失中通过减轻数值不稳定性带来了巨大收益
- 这表明它的好处超出了论文研究的特定 ScaleRL 配置
- 为了进一步测试这一点,论文在 Scout 17Bx16 MoE 上进行了留一法实验,观察到 FP32 精度提高了整体可扩展性(图 8b)
- 损失类型也出现了类似的情况
- 在图 7 中,恢复到 DAPO 在 ScaleRL 内产生了与 CISPO 相似的渐近性能
- 但如论文在附录 A.17 中讨论的那样,CISPO 对 IS 裁剪参数 \(\epsilon_{\text{max} }\) 的选择明显更鲁棒,降低了训练对超参数调整的敏感性
- 而且它在 LOO 实验中比 DAPO 更高效(\(B=2.01\) 对比 \(B=1.77\))
- 这证明了即使一个经过仔细调整的 DAPO 变体在渐近性能上可能相似,也倾向于选择 CISPO 是合理的
- 总之,即使个别设计选择在组合 Recipe 中显得多余,它们通常也能以跨模型和设置泛化的方式增强训练稳定性、鲁棒性或效率
- ScaleRL 保留这些组件不仅仅是为了在特定配置中获得边际收益,而是因为它们解决了在强化学习体系中反复出现的不稳定性和方差来源
- 注:本节的主要目标是说明,很多改进点看似在论文特定场景下没有收益,但在更通用的其他场景(随机种子,数据集,模型等)下,可能会有收益,为了保证方法的稳定性,建议加上一些确定性的改进点
Predictable Scaling Returns Across RL Compute Axes(跨强化学习计算轴的可预测缩放回报)
- 给定固定或增长的计算预算,哪个缩放旋钮(上下文长度、批次大小、每个提示的生成次数和模型大小)能带来最可靠的性能增益,并且论文多早可以预测到这种回报?
- 论文通过以下方式回答这个问题:
- (i) 在每种设置的训练早期(精确地说,是目标预算的一半)拟合方程 (1) 中的饱和幂律;
- (ii) 外推到目标预算;
- (iii) 扩展训练以验证预测
- 在下面所有的轴线上,论文观察到清晰、可预测的拟合,其外推曲线与扩展轨迹对齐,反映了论文在 100,000 GPU hous 运行(图 1)和图 2 中的跨 Recipe 比较中看到的行为


模型规模(Model scale (MoE))
- ScaleRL 在更大模型上是否仍然保持可预测性和稳定性?(注:即论文的 Scaling Law 是否能泛化到其他模型上)
- 使用 ScaleRL 训练 17B\(\times\)16 Llama-4 Scout MoE 表现出与 8B 模型相同的可预测缩放行为 ,具有低截断率且没有不稳定性问题(附录 A.15, A.17)
- 图 1 显示了训练曲线
- 扩展点与拟合曲线对齐,支持了论文 Recipe 对模型规模的不变性
- 更大的 17B\(\times\)16 MoE 表现出比 8B 密集模型高得多的渐近强化学习性能,仅使用其 1/6 的强化学习训练计算量就超越了 8B 的性能
Generation length(context budget,即上下文预算)
- 将生成长度从 14k 增加到 32k 个 Token 会减缓早期进展(更低的 \(B\) 和更高的 \(C_{mid}\)),但会持续提升了拟合的渐近线 (A)
- 提供足够的计算量后,可以产生更高的最终性能(图 9)
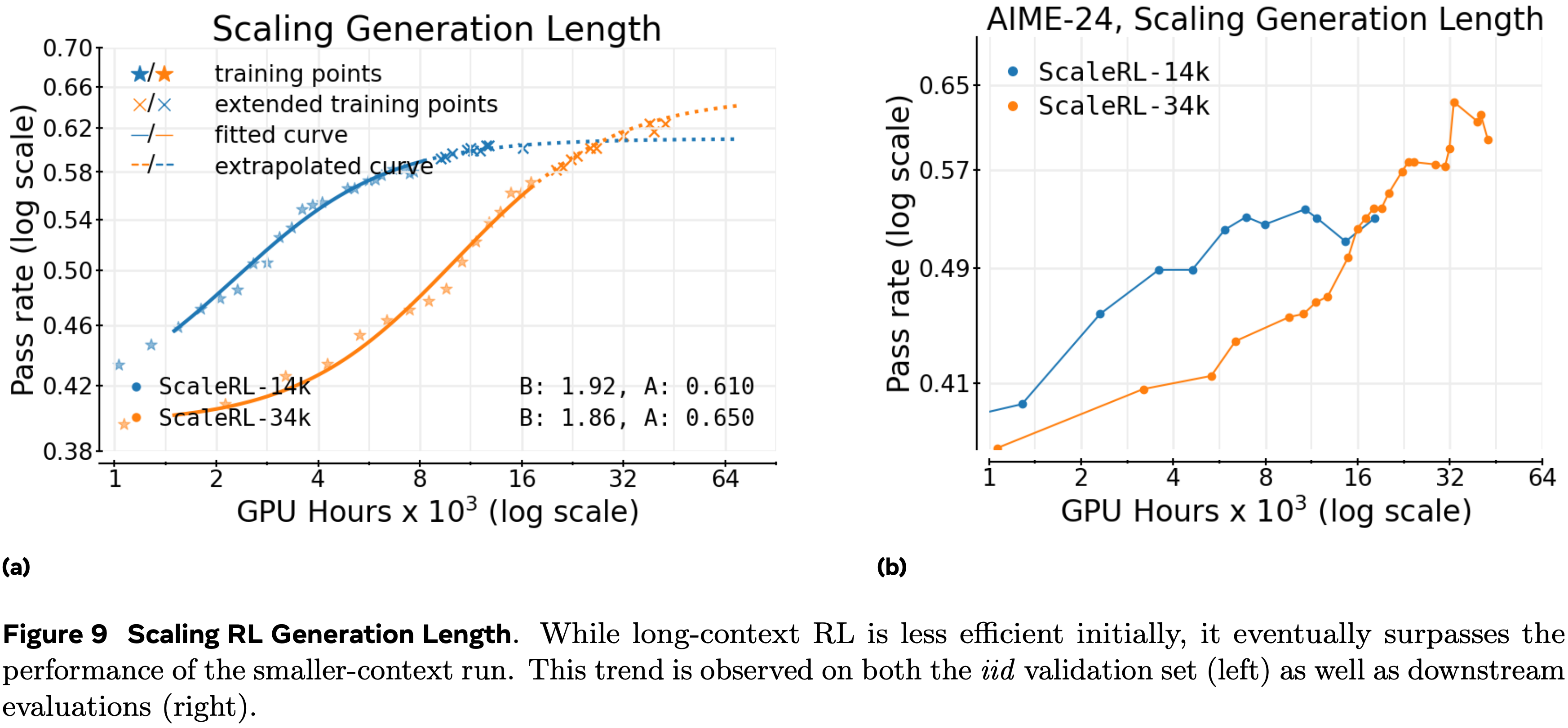
- 提供足够的计算量后,可以产生更高的最终性能(图 9)
- 这验证了长上下文强化学习是一个提升性能上限的旋钮,而不仅仅是效率权衡
- 从拟合中做出的外推正确地预测了当训练扩展时更高的 32k Token 轨迹
Global batch size(prompts,即提示数)
- 较小的批次运行在下游基准测试中显示出早期停滞(即使分布内验证性能持续提高)
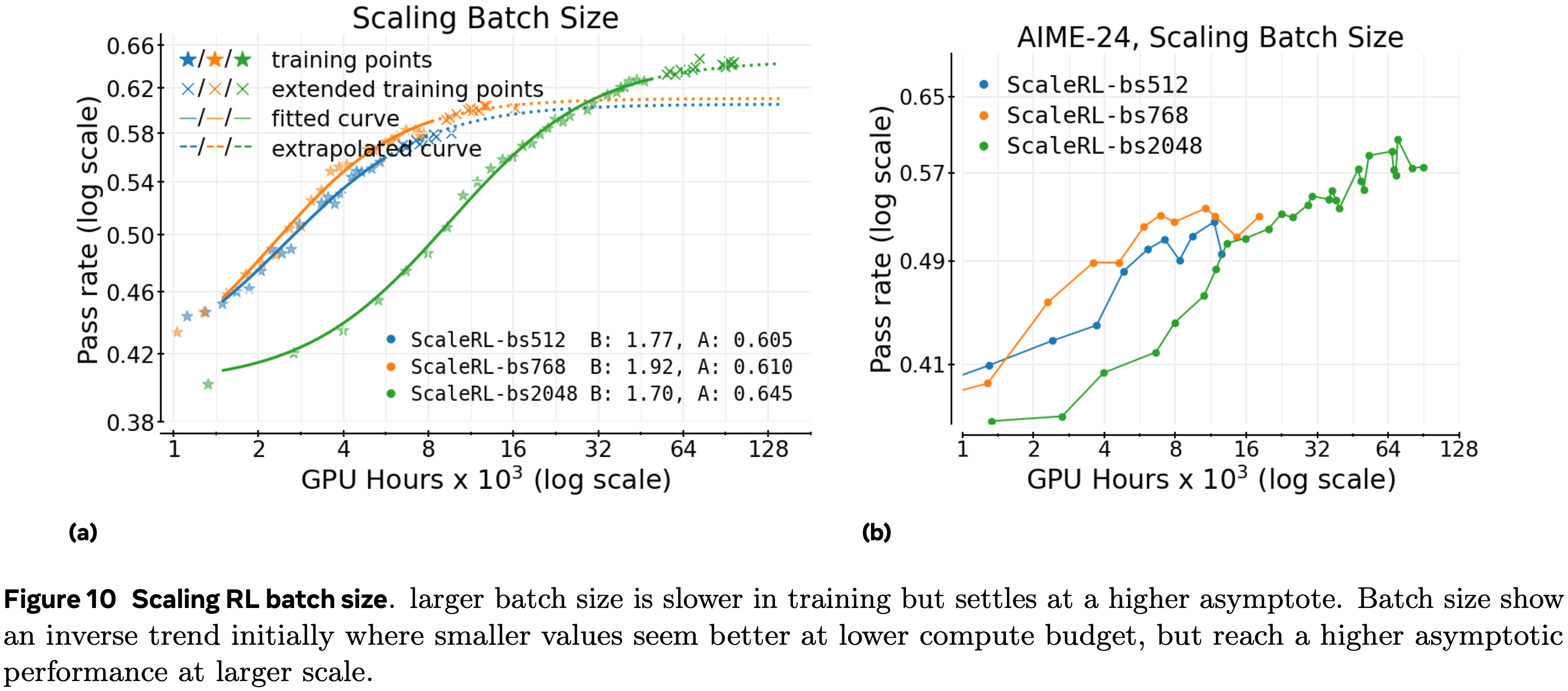
- 较大的批次可靠地改善了渐近线,并避免了论文在较小批次运行中观察到的下游停滞
- 图 10a 在中尺度上显示了相同的定性模式:
- 小批次可能在早期表现更好,但随着计算量的增长会被超越
- 在论文图 1 中最大的数学运行中,将批次大小增加到 2048 个提示既稳定了训练,又产生了一个可以从高达 50k GPU hous 外推到最终 100k 点的拟合
每个提示的生成次数(固定总批次)(Generations per prompt (fixed total batch))
- 对于固定的总批次,是分配更多提示还是每个提示分配更多生成次数更好?
- 扫描每个提示的生成次数 8,16,24,32 并调整提示数以保持总批次固定,得到的拟合缩放曲线基本不变(附录 A.13)
- 这表明在中等批次下,这种分配对于 A 和 B 都是次要选择
- 在更大批次(例如,2k+)下可能会出现更明显的差异,论文将其留待未来工作
Related Work
- 论文在本节中详细介绍了与论文研究最相关的两项工作
- ProRL (2025a) 证明,在大型语言模型上进行长时间的强化学习微调(约 2000 个优化步骤,批次大小 64),使用混合推理任务进行 16K GPU hous ,可以发现超越模型基础能力的新解决方案策略
- 这种更长的训练方案在 1.5B 模型上带来了显著收益,在某些基准测试中媲美更大模型的性能
- ProRL 的贡献在于特定的稳定性启发式方法(KL 正则化、策略重置、熵控制等),以实现 1.5B 模型的高性能
- Alibaba Group 等 (2025c), Part I: Tricks or Traps? A Deep Dive into RL for LLM Reasoning 提供了一个互补的视角
- 在 Qwen-3 4B/8B (2025) 上的一致条件下消融了各种设计选择,并提出了一种极简组合 LitePPO
- LitePPO 在较小规模的模型和计算量上优于更复杂的方法,如 GRPO (2024) 和 DAPO (2025)
- 这产生了有价值的算法见解,但重点是比较实证发现,而不是缩放行为
- 在 Qwen-3 4B/8B (2025) 上的一致条件下消融了各种设计选择,并提出了一种极简组合 LitePPO
- 这些工作都没有研究这些方法的”缩放(scaling)”特性
- 事实上,主要的比较是在下游评估上进行的,这可能不是研究可预测缩放的正确指标
- 正如在预训练和论文这里的工作中所做的那样,论文研究分布内留出验证集上的性能
- 与上述提到的相关工作相比,论文的工作开发并验证了一个具有预测拟合的计算-性能框架,同时在更大的计算预算(例如,比 ProRL 大 6 倍)和模型规模上运行
- 论文的研究结果产生了一个近乎 SOTA 强化学习 Recipe ,可以可预测地扩展到超过 100,000 GPU hous 而没有任何稳定性问题
- 其余相关工作推迟到附录 A.1
Discussion & Conclusion
- 在这项工作中,论文研究了用于大型语言模型强化学习的各种技术的缩放特性,以寻求一个可预测、可扩展的 Recipe
- 基于此使命,论文推导出一种为验证集准确率拟合预测性缩放曲线的方法,使论文能够量化强化学习方法的渐近性能和计算效率
- 使用这种方法论,论文的主要贡献是仔细进行了一系列消融实验,涉及构成强化学习 Recipe 的若干算法选项
- 对于每次消融,论文尽可能选择具有更高渐近性能的选项,否则选择效率更高的选项
- 结合这些选择产生了 ScaleRL Recipe ,它在论文的实验中比所有现有 Recipe 缩放得更好
- 以下几点观察值得注意:
- 计算缩放外推 (Compute scaling extrapolation)
- 论文缩放方法论的一个重要见解是,我们可以系统地使用较小规模的消融来预测更大规模的性能
- 这使论文能够创建最终的可扩展 Recipe
- 最重要的决策 (Most important decisions)
- 根据论文的消融实验, Off-policy 算法、损失函数和模型精度是最重要的决策
- 其他每个决策单独影响不大,但正如论文从留一法实验中看到的,当它们全部组合时,仍然具有一些累积影响(在效率方面)
- 渐近性能与效率 (Asymptotic performance vs. efficiency)
- 对于论文许多消融实验,论文发现更好的选项同时提高了效率和渐近性能,但情况并非总是如此(例如,对于 FP32,图 4(b))
- 当从基线方法开始进行”正向”消融时,论文首先且最主要地选择渐近性能
- 有趣的是,当从 ScaleRL Recipe 进行”反向”留一法消融时,论文发现每个决策对渐近性能的影响非常小,但算法的每个组件似乎都有助于提高效率
- 这表明变化的累积效应是相当鲁棒的
- 对于论文许多消融实验,论文发现更好的选项同时提高了效率和渐近性能,但情况并非总是如此(例如,对于 FP32,图 4(b))
- 泛化 (Generalization)
- 虽然论文报告了下游评估的迁移情况,但论文的主要重点是研究预测性缩放,这是通过在训练提示的留出数据集上的分布内性能曲线来表征的 (2022;2025)
- 这仍然留下了大型语言模型从训练分布到留出测试集的泛化能力如何的问题
- 虽然对泛化的全面描述超出了论文工作的范围,但论文确实观察到分布内验证与下游泛化性能之间的相关性
- 但有一些算法选择似乎更有助于泛化,论文在此想指出,包括:
- 更大的批次大小(章节 A.14)
- 减少截断(章节 A.15)
- 更长的生成长度(第 5 节,图 9)
- 更大的模型规模(第 5 节,图 1)
- 虽然论文报告了下游评估的迁移情况,但论文的主要重点是研究预测性缩放,这是通过在训练提示的留出数据集上的分布内性能曲线来表征的 (2022;2025)
- 多任务强化学习 (Multi-task RL)
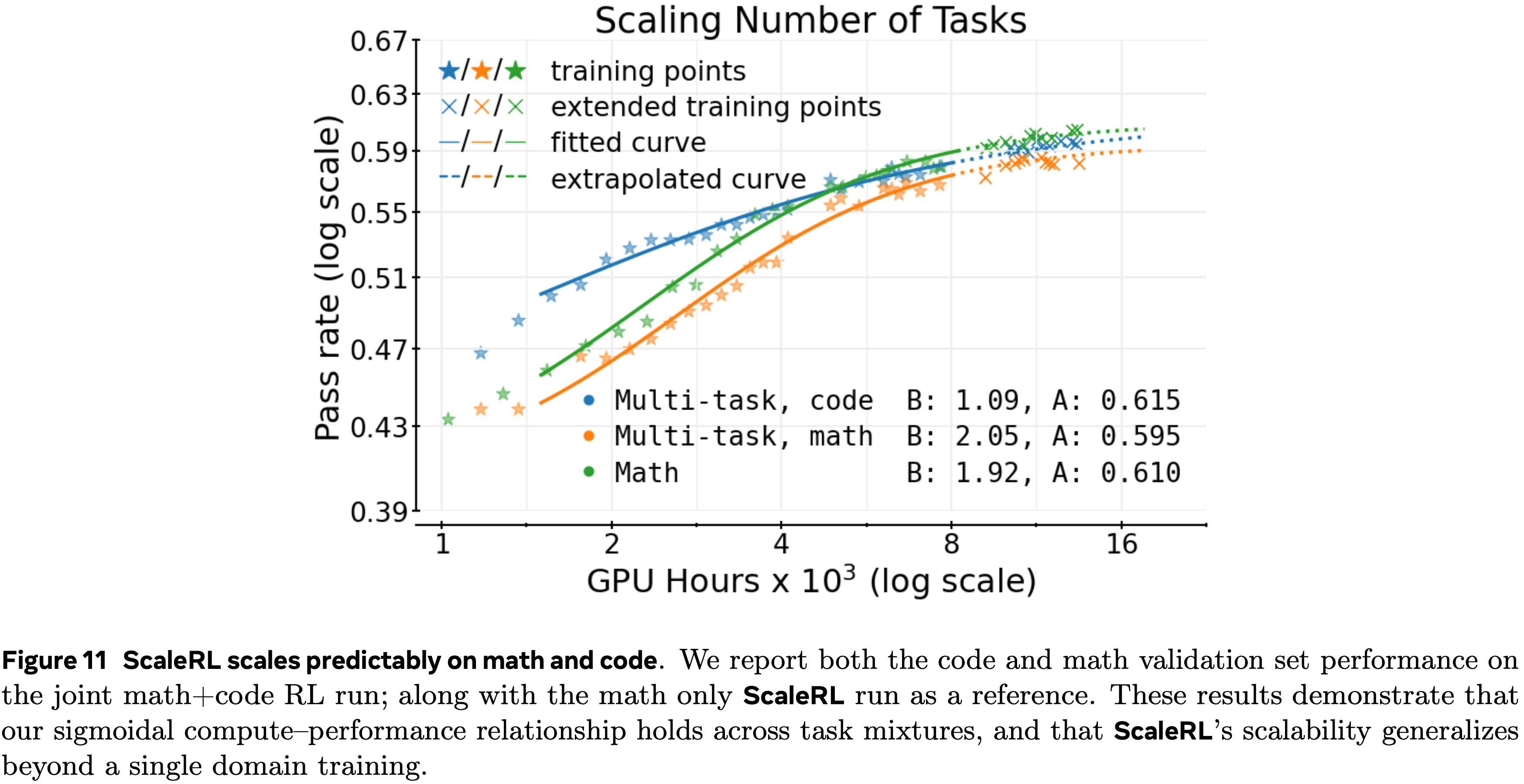
- 虽然论文的实验主要集中在数学领域,但论文也在多任务强化学习训练下评估了 ScaleRL
- 如图 11 所示,在数学和代码上联合训练为每个领域产生了清晰、平行的幂律趋势,扩展的运行保持与外推曲线对齐
- 虽然论文的初步结果是有希望的,但彻底研究具有不同训练数据混合的多任务强化学习的计算缩放可预测性将是很有趣的
- 计算缩放外推 (Compute scaling extrapolation)
Future work
- 一个自然的下一步是为强化学习在预训练计算、模型大小和强化学习训练数据方面推导预测性的”Scaling Laws”
- 未来的研究还可以包括其他强化学习计算缩放的轴(Axes),例如结合结构化或密集奖励 (2025b;2024) 和更计算密集的生成验证器 (2025a),以找到强化学习训练的最佳计算分配
- 最后,这里介绍的方法论框架可以应用于研究其他后训练机制的缩放行为,包括多轮强化学习、智能体交互和长形式推理
- 强化学习中有许多设计选择,因此作者认为论文的 ScaleRL Recipe 并非故事的终点
- 作者希望论文对可扩展强化学习的关注以及预测可扩展性的方法能够激励未来的工作,进一步推动大型语言模型强化学习的前沿
- 为了使未来的研究能够拟合计算-性能强化学习缩放曲线,论文在 www.devvrit.com/scalerl_curve_fitting 发布了一个最小代码库
附录 A:Appendix
A.1 Extended Related Work
- 近期涌现的一波工作将强化学习应用于提升大语言模型的推理能力;这些工作通常能在具有挑战性的任务上取得 SOTA 结果 (2024; 2025; 2025; 2025)
- OpenAI 的 o1 系列模型证实了大规模强化学习能显著增强长程推理能力,但并未发布这些模型训练方式的任何细节
- Deepseek R1(以及 R1-Zero)(2025) 提供了首个关于主要通过强化学习训练高性能长思维链模型的全面研究,记录了在扩展强化学习下不依赖奖励模型 (2023) 或蒙特卡洛树搜索 (2024) 而出现的涌现行为
- 这波推理发展浪潮中最早被广泛引用的 RLVR(可验证奖励)算法是 GRPO
- GRPO 是一种无评论员、分组相对的策略梯度方法,采用 PPO 风格的裁剪,用分组基线替代学习的价值基线,以降低计算成本并稳定长思维链的信用分配
- 虽然 GRPO 催化了快速进展,但后续工作记录了其局限性( Token-Level 裁剪、模型崩溃风险)并推动了不同分组或序列级别的变体 (2025; 2025; 2025; 2025)
- DAPO 提出了解耦裁剪和动态采样策略优化
- DAPO 在 GRPO 目标中解耦了 \(\epsilon_{\text{low} }\) 和 \(\epsilon_{\text{high} }\) 裁剪,并对 \(\epsilon_{\text{high} }\) 进行 Clip-Higher操作以避免熵崩溃
- DAPO 在给定批次中对提示进行动态采样,以避免方差(或优势)为零的样本,这些样本对策略梯度没有贡献
- DAPO 采用 Token-Level 损失聚合(注:GRPO 使用样本级损失平均)
- 通过以上这些修改,DAPO 能够在避免强化学习训练中熵崩溃的同时超越原始 GRPO 基线
- 与此同时提出的 VAPO 是一种专为长思维链设计的价值增强型 PPO,具有强大的稳定性,并优于像 GRPO 和 DAPO 这样的无价值基线
- VAPO 结合了价值预训练和来自 VC-PPO (2025) 的解耦广义优势估计、来自 DAPO 的损失目标修改,并提出了长度自适应的 GAE,从而形成了一个开放的 Recipe VAPO,该 Recipe 已被用于训练 Seed1.5-thinking (2025) 中的大型混合专家模型
- 类似地,其他技术报告如 Magistral (2025)、Kimi-k1.5 (2025)、Minimax-01 (2025) 详细介绍了他们强化学习训练 Recipe 的各种细节,但并未分享关于其设计选择为何优于基线的广泛实验
A.2 面向大语言模型的强化学习:GRPO 和 DAPO (RL for LLMs: GRPO and DAPO)
GRPO (2024)
- GRPO 将 PPO (2017) 应用于具有可验证奖励的大语言模型微调
- 对于给定的提示 \(x\),旧策略 \(\pi_{\text{gen} }(\theta_{\text{old} })\) 生成 \(G\) 个候选补全 \(\{y_i\}_{i=1}^G\),每个补全被分配一个标量奖励 \(r_i\)
- 为了强调组内的相对质量,奖励被归一化为
$$
\hat{A}_i=\frac{r_i-\text{mean}(\{r_j\}_{j=1}^G)}{\text{std}(\{r_j\}_{j=1}^G)+\epsilon}.
$$ - 每个长度为 \(|y_i|\) 的补全 \(y_i\) 通过比率在 Token-level 上做出贡献
$$
\rho_{i,t}(\theta)=\frac{\pi_\text{train}(y_{i,t} \mid x,y_{i,<t},\theta)}{\pi_{gen}(y_{i,t} \mid x,y_{i,<t},\theta_{\text{old} })}.
$$ - GRPO 目标在补全和 Token 之间进行平均:
$$
\mathcal{J}_{\text{GRPO} }(\theta)=\mathbb{E}_{x\sim D,\atop\{y_i\}_{i=1}^G,\sim\pi_{\text{gen}(\cdot \mid x,\theta_{\text{old} })} }\left[\frac{1}{G}\sum_{i=1}^G\frac{1}{|y_i|}\sum_{t=1}^{|y_i|}\min\Big(\rho_{i,t}(\theta)\hat{A}_i,\ \operatorname{clip}(\rho_{i,t}(\theta),1\pm\epsilon)\hat{A}_i\Big)\right].
$$ - GRPO 像 PPO 一样保留了 Token-level 的策略比率,同时使用序列级别、分组归一化的优势来在稀疏奖励下稳定学习
DAPO
- DAPO (2025) 通过两个关键修改扩展了 GRPO
- 第一个改进点:用 非对称裁剪 替代了对称裁剪,对向上和向下的偏差使用不同的阈值:
$$ \text{clip}_{\text{asym} }(\rho,a)=\text{clip}(\rho,,1-\epsilon^{-},1+\epsilon^{+})$$- 其中 \(\epsilon^{-}\) 和 \(\epsilon^{+}\) 是超参数
- 第二个改进点:DAPO 将聚合方案更改为在 提示级别 操作
- 对于给定的提示 \(x\sim D\),旧策略产生 \(G\) 个补全 \(\{y_i\}_{i=1}^G\),其优势为 \(\{\hat{A}_i\}\)(公式 (5))
- 令 \(T=\sum_{i=1}^G|y_i|\) 表示所有补全的总 Token 数
- Token-level 比率如公式 (2) 所示
- DAPO 代理目标为
$$
\mathcal{J}_{\text{DAPO} }(\theta)=\mathbb{E}_{x\sim D,\atop\{y_i\}_{i=1}^G\sim\pi_{\text{gen}(-|x,\theta_{\text{old} })} }\left[\frac{1}{T}\sum_{i=1}^G\sum_{t=1}^{|y_i|}\min\Bigl(\rho_{i,t}(\theta)\hat{A}_i,\ \text{clip}_{\text{asym} }(\rho_{i,t}(\theta))\hat{A}_i\Bigr)\right].
$$ - 这种提示级别的归一化确保每个 Token 对提示的损失贡献相等,无论其采样补全的数量或长度如何
- DAPO 还引入了在训练期间动态丢弃批次中方差为零的提示,并用更多提示填充批次直到批次满员(论文在此跳过该更改,因为其效果类似于拥有更大的批次大小)
A.3 Training Setup
- 数据集
- 对于小规模监督微调,论文使用精心策划的推理轨迹数据混合
- 论文通过移除琐碎的提示、丢弃超过 12\(k\) 个 Token 的解决方案轨迹,并使用 AIME 2024/2025 和 MATH-500 (2021) 基准进行去污染来过滤此数据集
- 对于强化学习阶段,论文在大多数运行中使用 Polaris-53K 数据集 (2025);
- 对于同时包含数学和代码的运行,使用 Deepcoder 数据集 (2025)
- 监督微调
- 论文使用 2M Token 的批次大小、最大序列长度 12288 和学习率 \(3\times 10^{-5}\),在 32 个 H100 GPU 节点上使用 AdamW 优化器 (2019) 运行监督微调,总共大约 4 个轮次和 32B Token
- 强化学习
- 论文在强化学习训练期间分配 14k 的生成预算,其中 12k Token 分配给中间推理(“思考”),随后 2k Token 用于最终解决方案和答案
- 论文在每个批次中采样 48 个提示,每个提示有 16 个生成(即每个梯度更新步骤的总批次大小为 768 个回复)
- 奖励分别给予正确和错误的轨迹 \(\pm 1\)
- 使用恒定学习率 \(5\times 10^{-7}\)
- AdamW 优化器 (2019),其中 \(\epsilon=10^{-15}\),权重衰减为 0.01(AdamW 中的默认值)
- 注:较低的 \(\epsilon\) 是为了避免梯度裁剪(epsilon 下溢)(2023)
- 100 步的线性预热
- 数学问题评估:
- 论文使用自动化检查器,如 Sympy (2017) 或 Math-Verify 来评估数学问题在剥离思考轨迹(\(<\)think\(>\)\(\cdots\)\(<\)/think\(>\))后最终答案的正确性
- 代码问题:
- 对于涉及单元测试和期望输出的代码问题,论文使用自定义代码执行环境
- 硬件:
- 论文使用 80 个 Nvidia GB200 GPU 进行单次运行
- 3.5-4K GPU hous(用于在第 3.2 节中建立不同的设计选择)
- 16K GPU hous 用于留一法实验(第 4 节)
- 30k-100K GPU hous 用于论文更大规模的运行(第 5 节)
- 论文在 GPU 之间采用 Generator-Trainer 分离
- 对于 80 个 GPU 的实验,论文将其中的 64 个设置为 Generator ,负责使用优化的推理代码库生成推理轨迹
- 其余的 16 个 GPU 作为 Trainer ,接收生成的轨迹,执行策略更新,并定期将更新后的参数广播回 Generator
- 论文使用 80 个 Nvidia GB200 GPU 进行单次运行
A.4 拟合什么曲线? (What curve to fit?)
- 预训练曲线通常使用幂律方程进行拟合 (2025; 2020; 2025)
- 在论文的情况下,这将性能建模为 \(R_C=A-D/C^B, C\geq C_0\),其中 \(D\) 是常数,\(C_0\) 标志着超出该阈值后定律成立的计算量阈值
- 直观地说,这意味着计算的每次倍增都会带来性能的恒定比例增益
- 但对于强化学习后训练,论文发现 S 形曲线(公式 (1))更合适,原因如下
- 首先,对于有界指标,如准确率或奖励,S 形曲线提供了更好的预测拟合 (2024; 2022);论文观察到同样的情况,能够准确外推到更高的计算量(图 1)
- 其次,幂律在低计算量时是无界的,并且通常只在超过阈值 \(C_0\) 后才进行拟合
- 在强化学习中,总训练步数要少得多(例如,图 1 中只有约 75 个评估点可供拟合),丢弃早期点会进一步减少本已有限的拟合数据
- 第三,根据经验,S 形拟合比幂律拟合更加稳健和稳定
- 具体来说,考虑图 1 中所示的在 8B 稠密模型上进行的 100k GPU hous 运行
- 当论文在 1.5k-50k GPU hous 之间拟合幂律曲线时,它预测的渐近性能为 \(A=1.0\),这显然是错误的(实际曲线在 0.65 附近饱和)
- 相比之下,S 形拟合给出了 \(A=0.645\) 的准确预测
- 此外,幂律拟合对所选拟合区间高度敏感:
- 在 (5\(\text{k}\),50\(\text{k}\)) GPU hous 上拟合则得到 \(A=0.74\),而 S 形拟合仍然稳健,并且仍然预测 \(A=0.645\)
- 幂律模型只有在专门在高计算量区间(例如,30k-60k GPU hous )拟合时才能恢复正确的渐近线
- 但论文的目标是从低计算量区间预测大规模性能,而在这些区间无法获得如此长的运行
- 具体来说,考虑图 1 中所示的在 8B 稠密模型上进行的 100k GPU hous 运行
- 考虑到这些因素,论文在整个分析中使用 S 形形式
- S 形曲线捕捉了收益递减规律,即在低计算量区间增长缓慢,在高效缩放的中等区间急剧加速,然后在计算量高时饱和,接近有限的性能上限
- 需要注意的一点是,在高计算量区间,S 形曲线的行为与幂律相同
- 具体来说,我们可以对 S 形曲线进行以下近似:
$$
\begin{align}
R_C &=R_0+\frac{A-R_0}{1+(C_{mid}/C)^B} \quad \text{(来自公式 (1) 的 S 形曲线)} \\
\implies R_C &\approx R_0+(A-R_0)\left(1-\frac{C^{B}_{mid} }{C^{B} }\right) \quad \text{(对于 \(C>>C_{mid}\), 高计算量区间(high compute regime))} \\
&=A-\frac{(A-R_0)C^{B}_{mid} }{C^{B} } \\
&=A-\frac{D}{C^{B} }
\end{align}
$$ - 其中 \(D=(A-R_0)C^{B}_{mid}\)
- 这与本节开头提到的幂律形式相同
- 具体来说,我们可以对 S 形曲线进行以下近似:
A.5 Fitting scaling curves
- 论文将公式 (1) 中的 S 形定律方程拟合到论文留出验证集上的平均奖励
- 包含从 Polaris-53k (2025) 数学数据集中留出的 1,000 个提示,每 100 个训练步骤进行一次评估,每次在留出的 1,000 个提示上采样 16 个生成
- 直接拟合所有三个参数 \(\{A,B,C_{mid}\}\) 具有挑战性
- 所以论文执行网格搜索,遍历 \(A\in\{0.450,0.455,0.460,\ldots,0.800\}\) 和 \(C_{mid}\in[100,40000]\)(搜索 100 个线性分隔的值),并对每个候选的 \(A,C_{mid}\) 拟合 \(B\)
- 在此网格上最佳拟合(通过残差平方和衡量)作为最终曲线
- 论文使用 SciPy 的 curve_fit 和默认初始化;改变初始化策略产生了相同的结果
- 为了使未来的研究能够拟合计算性能强化学习缩放曲线,论文在 www.dewrit.com/scalerl_curve_fitting 发布了一个最小的代码库
- 所以论文执行网格搜索,遍历 \(A\in\{0.450,0.455,0.460,\ldots,0.800\}\) 和 \(C_{mid}\in[100,40000]\)(搜索 100 个线性分隔的值),并对每个候选的 \(A,C_{mid}\) 拟合 \(B\)
- 为了估计论文拟合的误差范围,论文训练了三个独立的 ScaleRL 运行,批次大小为 768,生成长度为 14k(如第 4 节所用),如图 8a 所示
- \(A\) 的拟合值最多变化 \(\pm 0.015\),表明在渐近性能估计上 0.02 是一个合理的误差范围
- 估计拟合值 \(B\) 的误差范围很困难,因为具有不同 \(A\) 值的不同算法可能对 \(B\) 有不同的误差范围
- 为了比较算法的目的,我们可以安全地推断,如果两种方法达到相似的 \(A\) 值(在 0.02 范围内),那么当使用 \(A\) 值的平均值重新拟合时,具有较高 \(B\) 值的方法在可扩展效率方面至少同样好
A.6 Comparing algorithms
- 与大规模预训练中的观察一致,损失在初始急剧下降后进入可预测的幂律衰减阶段 (2025),论文在强化学习中也观察到类似的两阶段行为
- 平均奖励在约第一个 epoch(约 1k 步,或对于大多数运行约 1.5k GPU hous )期间快速、几乎线性地增加,之后曲线遵循 S 形定律行为(见图 15 查看“S 形”曲线)
- 论文的 S 形定律拟合应用于训练曲线的后一部分
- 与预训练不同,论文的主要目标不是预测固定 Recipe 的性能,而是识别哪些算法和设计选择能够可靠地扩展,并设计出具有可预测性的算法
- 实现高度稳健的拟合通常需要具有数百或数千个评估点的非常大的运行,这在论文的设置中是不切实际的,原因有两个
- 第一个原因:在此规模上运行所有消融实验在计算上是不可行的
- 第二个原因:论文比较的许多强化学习算法本身无法扩展到如此极端的预算:它们通常更早饱和,甚至由于不稳定性而在计算量增加时性能下降
- 例如,论文的基线方法(第 3.2 节)在超过约 3500 GPU hous 后变得不稳定,因为过长的生成截断超过了生成的 10%,降低了有效批次大小
- 关于此点的更多讨论见第 A.15 节
- 当论文在第 3.2 节中跨不同轴进行消融时,论文发现了能在更高计算量下提高稳定性的设计选择
- 一些消融变体可以进一步扩展,例如,DAPO 中 \(\epsilon=0.26\) 的情况下约 5k GPU hous ,使用 FP32 精度修复(第 3.2 节)的情况下约 6k GPU hous ,以及 CISPO 的情况下约 7k GPU hous
- 结合论文最佳的设计选择是一个稳定且可扩展的 Recipe ,这使论文能够以每次运行约 1600 GPU hous 的预算进行留一法实验
问题:怎么还变少了?
A.7 Robustness of fits
- 对于稳定且可扩展的实验,包括从第 4 节开始的所有运行,改变拟合区间(例如,包含或排除初始 1.5k GPU hous 范围)会产生类似的可预测结果
- 例如,在 8B 稠密模型上的 100k GPU hous 运行中,在 (1.5\(\text{k}\),50\(\text{k}\)) 上拟合得到 \(B=1.70\),\(A=0.645\),而 (0,100\(\text{k}\)) 得到 \(B=1.56\),\(A=0.655\),(0,50\(\text{k}\)) 得到 \(B=1.7,A=0.645\),以及 (5\(\text{k}\),50\(\text{k}\)) 得到 \(B=1.67\),\(A=0.645\)。在这些区间内,参数值保持在预期误差范围内(第 7 节)
- 此外,论文跳过低计算量区间,因为早期训练阶段,尤其是在第 3.2 节中不太稳定的设置中,常常由于短暂的不稳定性而过早达到平台期或偏离 S 形趋势(见附录 A.6, A.15)
- 排除此区域可以使拟合专注于中高计算量范围,在该范围内饱和行为更清晰、更一致
- 1.5k GPU hous 阈值是根据经验选择的启发式方法:
- 它大约对应于第 3.2 节中大多数实验的一个 epoch
- 较大的截止值减少了拟合点的数量,而较小的截止值常常引入噪声
- 论文发现 1.5k GPU hous 能在拟合稳定性和样本覆盖率之间提供最佳平衡,这与在预训练缩放分析和拟合中跳过低 FLOPs 区间的做法一致 (2025)
A.8 Interpreting Sigmoidal Curves
- 图 3 展示了一个示例拟合,说明了参数 \(A\)、\(B\) 和 \(C_{\text{mid} }\) 的影响

- 通过额外的图示扩展了这一点:图 12a、图 12b 和图 13a 分别改变了 \(B\)、\(C_{\text{mid} }\) 和 \(A\),同时保持其他参数不变
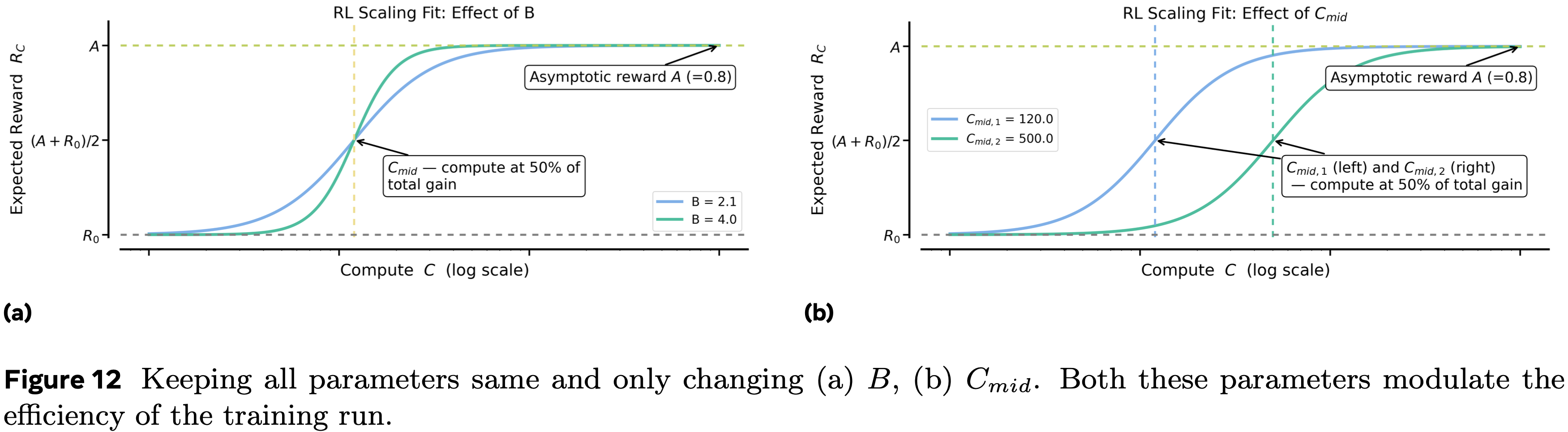
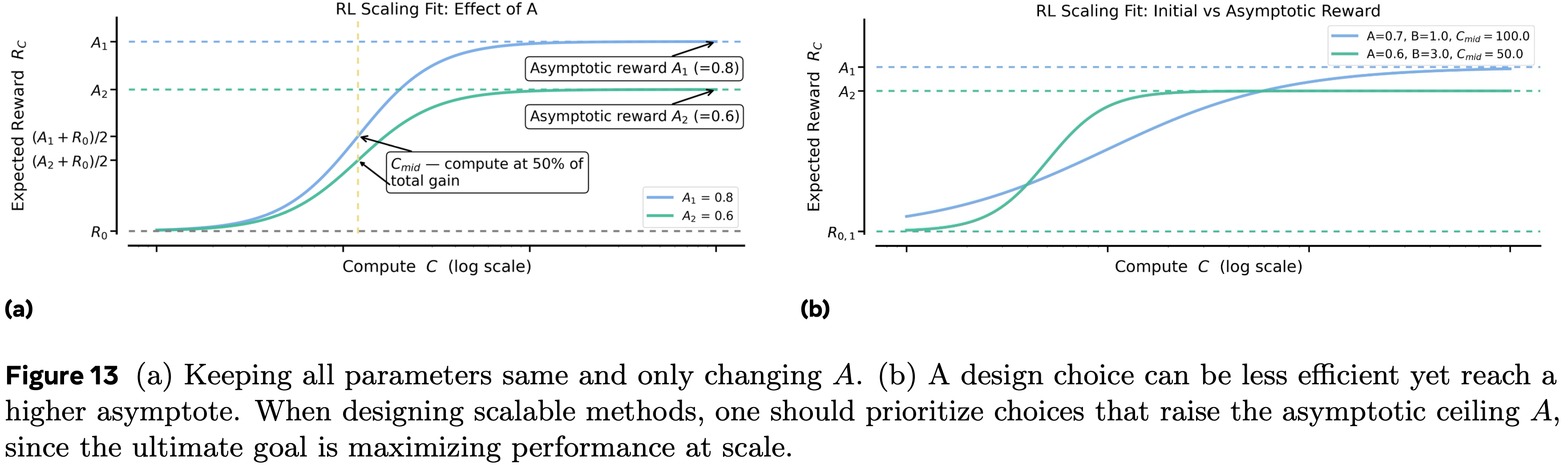
- \(B\) 和 \(C_{\text{mid} }\) 主要影响缩放的效率 ,而 \(A\) 决定了在大计算量下可实现的渐近性能
- 在图 13b 中,论文看到一个两个运行的案例,其中一个效率高得多,因此显示出初期有希望的收益,但收敛到较低的渐近线,而另一个进展较慢,但由于更高的 \(A\) 最终超过了前者
- 在实践中,缩放策略应优先考虑提高渐近上限 \(A\) 的设计选择,然后才优化效率参数,如 \(B\) 或 \(C_{\text{mid} }\)
A.9 Forward and LOO Ablations
- 论文在图 14a-14b 中展示了第 3.2 节的额外结果

- 图 15 中绘制了第 4 节中关于通过率与计算量的留一法实验

A.10 Controlling generation length
- 推理强化学习中一个常见的担忧是控制爆炸性增长的生成长度,这会损害训练效率和稳定性(附录 A.15)
- 论文考虑两种方法:
- (a) 中断(Interruptions),用于像 GLM-4.1V (2025) 和 Qwen3 (2025) 这样的工作;
- (b) 长度惩罚(Length penalties),用于像 DAPO (2025)、Kimi (2025)、Magistral (2025) 和 Minimax-M1 (2025) 这样的工作
中断,Interruptions
- 通过附加一个标记性短语(例如“Okay, time is up. Let me stop thinking and formulate a final answer \(<\)/think\(>\)”)来强制停止生成,指示模型终止其推理并产生最终答案
- 在论文的设置中,中断 Token 被随机放置在 \([10k,12k]\) Token 长度之间,以诱导对不同生成长度的泛化
Length penalties
- 用于重塑奖励
- 遵循 DAPO (2025),论文使用容忍区间 \(L_{\text{cache} }\) 来惩罚过长的补全:
$$
R_{\text{length} }(y)=clip\left(\frac{L_{\max}-|y|}{L_{\text{cache} } }-1,-1,0\right)
$$ - 此惩罚仅添加到正确的轨迹上,以阻止过长的生成
- 在长度惩罚实验中,论文设置 \(L_{\max}=14\text{k}\) 个 Token 和 \(L_{\text{cache} }=2\text{k}\) 个 Token
- 在第 4 节中,论文在 16\(\text{k}\) GPU hous 的规模上比较了长度惩罚和中断
- 在论文的最终 ScaleRL Recipe 中用长度惩罚替换中断不能提高性能
A.11 PipelineRL
- 使用基线设置,论文在 PipelineRL 中消融了 Off-policy 参数(图 4(b))

- Off-policy 度为 4 和 8 的表现同样好,论文在第 3.1 节更新基线时采用 8 作为默认设置
- 为什么 8 比 1 效果好?是因为横坐标不是 step,而是 GPU 时间吗?
- 为什么 PipelineRL 始终优于经典的 PPO-off-policy 方法(第 3.1 节和 第 4 节)?
- 论文将其归因于其与 On-policy 训练更紧密的对齐
- 在 PPO-off-policy 中,生成和训练交替进行:
- Trainer 严格处理与所选参数 \(k\) 一样 Off-policy 的批次,基于过时的 Rollout 更新进行更新
- PipelineRL 以流式方式运行:
- 一旦批次可用,它就传递给 Trainer ;
- 同样,一旦模型更新就绪,它就立即共享回 Generator ,Generator 立即使用它(包括在部分生成的轨迹的延续中)
- 这种紧密的反馈循环使训练更接近 On-policy 状态,减少了 Generator 和 Trainer 分布之间的不匹配
- 重要的是,这种区别影响了缩放曲线的渐近性能 \(c\),而不仅仅是效率指数 \(b\)
- 很少有轴能以这种方式移动渐近线,使得 Off-policy 算法的选择成为强化学习后训练中最关键的设计决策之一
A.12 熵曲线:缩放批次大小 (Entropy Curves: Scaling Batch Size)
- 论文在整个训练过程中跟踪了留出验证集上的熵
- 在所有实验中(包括批次大小、任务数量、生成长度和模型规模的变体)论文观察到熵总体一致下降

- 在所有实验中(包括批次大小、任务数量、生成长度和模型规模的变体)论文观察到熵总体一致下降
- 一个有趣的发现是,熵可能并不总是能提供对性能的预测性洞察,正如最近一些工作如 (2025) 所提出的那样
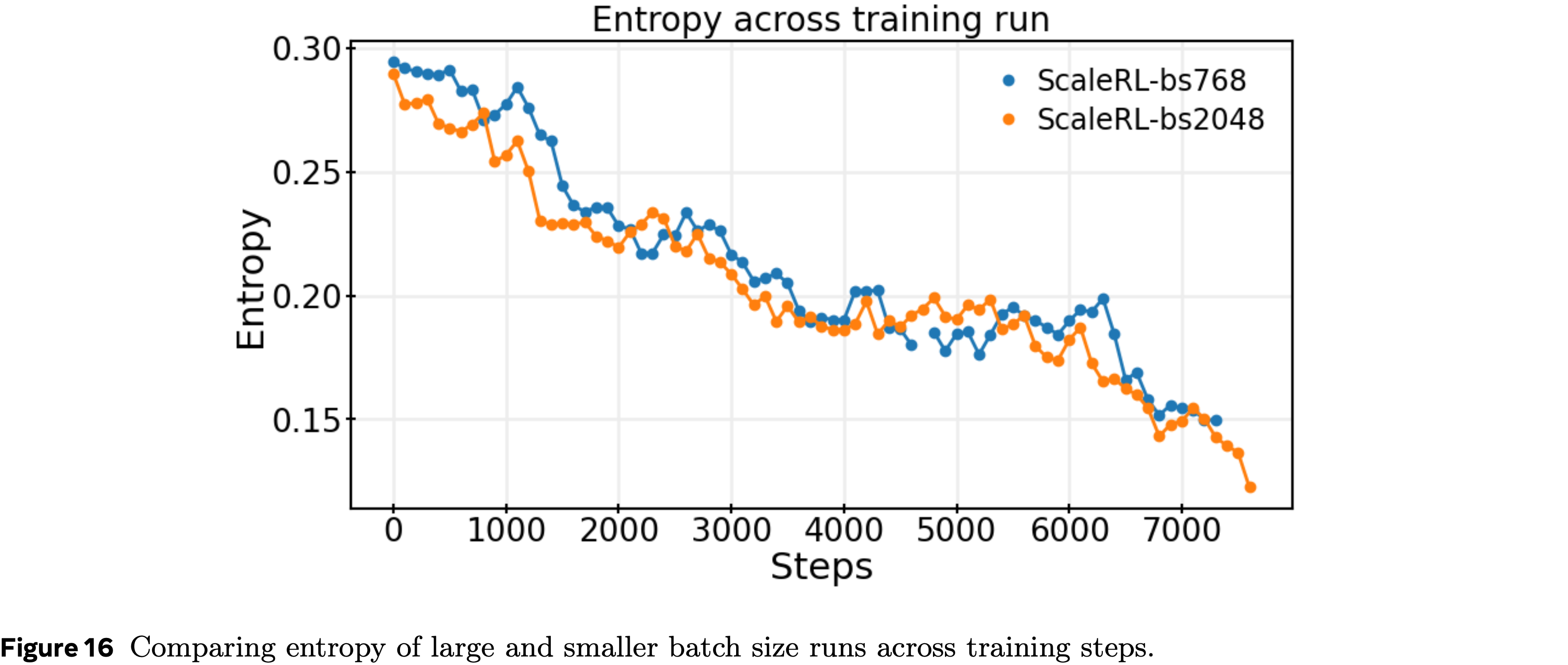
- 在第本节中,论文绘制了批次大小为 768 和 2048 的 ScaleRL 运行的熵
- 2048 批次大小的运行在每个阶段都实现了更强的下游性能(图 10b),但两个运行在每一步都遵循几乎相同的熵轨迹(第 A.12 节)
- 这突出了一个重要点,尽管熵有时被用作探索的代理指标,但仅仅保持较高的熵并不能转化为更好的泛化
- 相反,较大的批次每一步减少了有效探索,类似于较小的批次,但仍然产生了显著更好的性能——强调了批次大小是一个重要的决定性因素
- 2048 批次大小的运行在每个阶段都实现了更强的下游性能(图 10b),但两个运行在每一步都遵循几乎相同的熵轨迹(第 A.12 节)
- 在第本节中,论文绘制了批次大小为 768 和 2048 的 ScaleRL 运行的熵
- 总的来说,论文的发现表明,虽然熵在训练期间持续下降,但它不一定是下游性能的可靠预测指标
- 这一观察结果强化了在旨在提高训练分布以及下游任务分布性能时,除了熵动态之外,还需要关注算法和缩放选择(例如,批次大小、 Off-policy 方法)的必要性
A.13 Scaling on multiple axes
- 在图 17 中提供了剩余的不同轴缩放的图表(问题:如何理解这里的轴?是指不同的维度的超参)
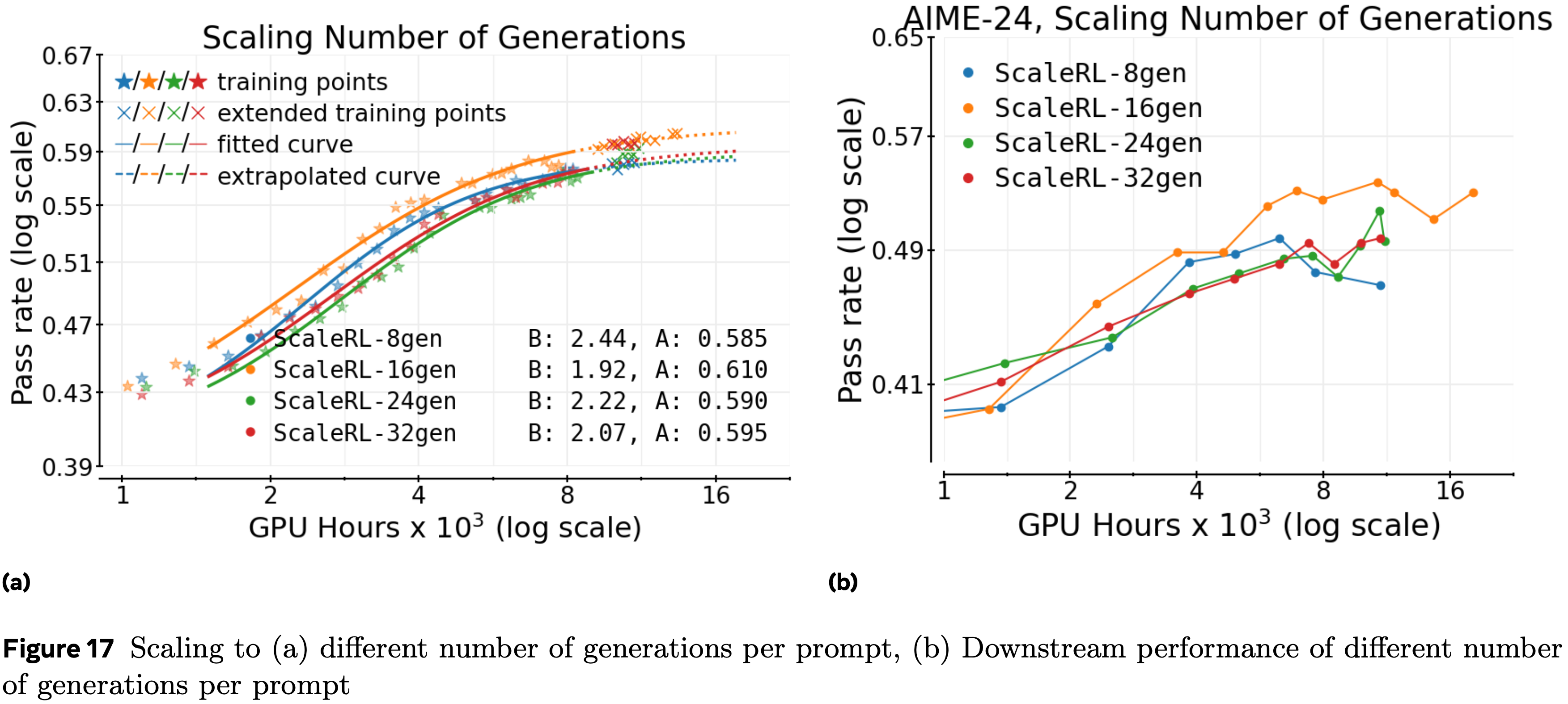
- 在图 18 中提供了相应的下游评估
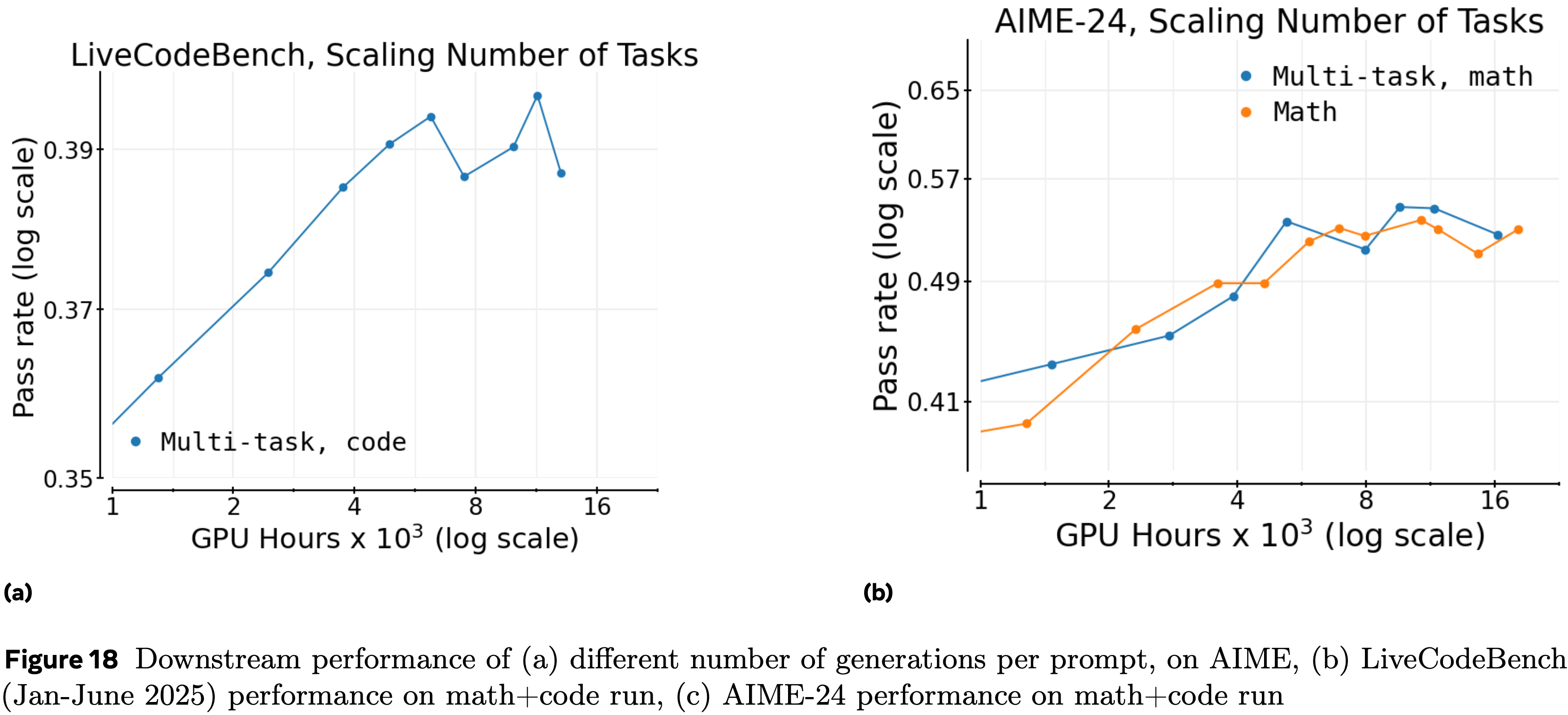
- 论文还在表 1 中提供了 \(A,B,C_{mid}\) 的值
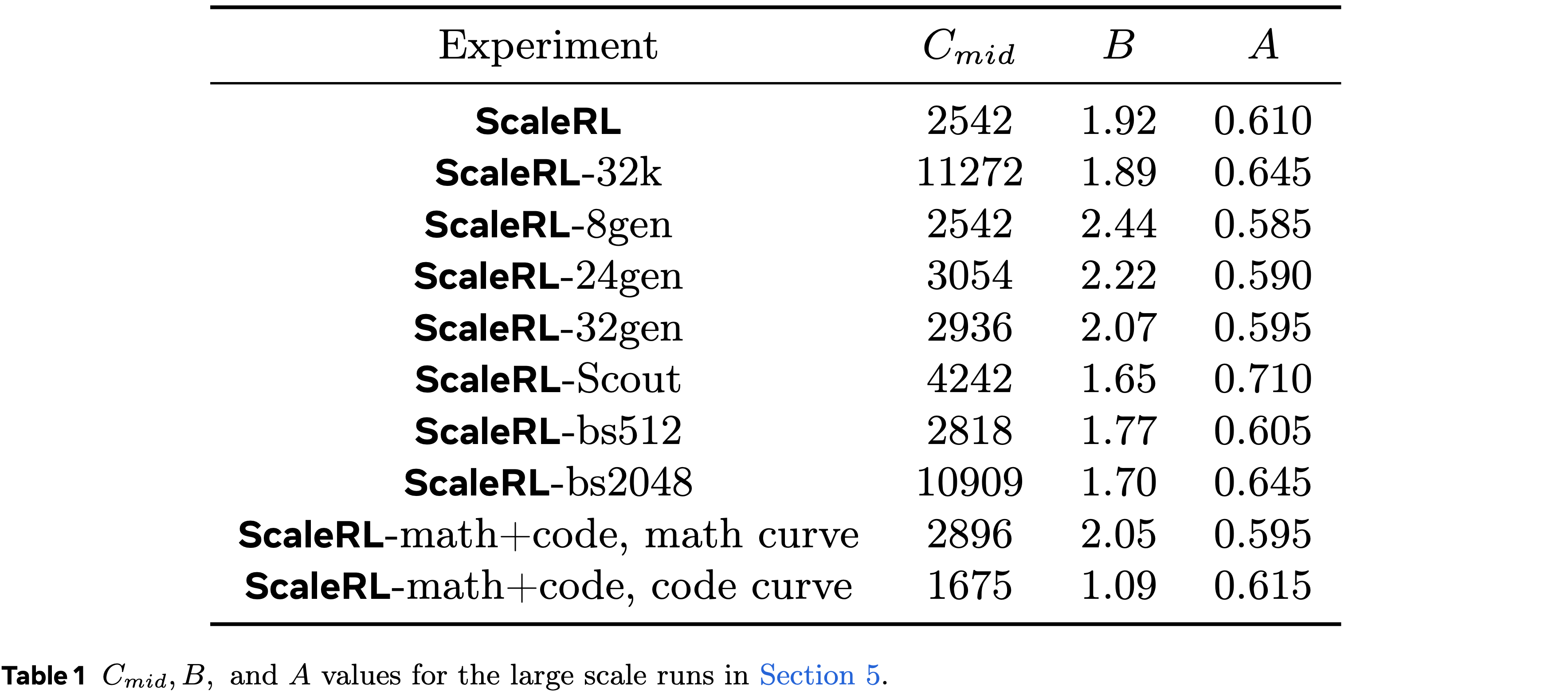
A.14 Downstream performance
- 在图 1、9、10b 和 18 中报告了一组具有代表性的下游评估曲线
- 这些包括具有批次大小 \(\{512,768,2048\}\) 的 ScaleRL 运行、具有 32k 生成长度的长上下文训练运行、大模型(Scout)训练运行、多任务运行(数学 + 代码)以及不同每个提示生成数量(固定批次大小)的运行
- 对于每种设置,论文绘制了性能与计算量的关系
- 结论:对于像更大批次大小、更长生成长度和更大模型大小这样的实验,下游性能更好(与验证集曲线的顺序相似)
A.15 Truncations and training instabilities
- 在论文的所有实验中,论文发现训练不稳定性通常与截断有关
- 随着生成长度的增加,许多强化学习运行表现出波动的截断率,有时在训练过程中增加
- 在批次大小 768 的情况下,论文观察到 10-15% 范围内的截断通常会破坏训练稳定性 ,性能下降且无干预就无法恢复
- 例子包括图 2 中扩展的 GRPO 运行,其中不稳定性与上升的截断率相关,以及第 3.2 节中使用的更新基线
- 相比之下,ScaleRL 运行更加稳定
- 在 8B 模型上,超过 90% 的训练时间内截断率保持在 5% 以下
- 在批次大小 2048 时,截断率略高,偶尔接近约 7%
- 这种增加主要归因于训练期间观察到的更长的平均生成长度,这自然增加了超过预算的机会
- 但,即使排除截断样本后,有效批次仍然很大,训练稳定性得以保持
- 直观地说,更大的生成长度预算应有助于减少截断
- 使用 34k 生成长度(批次 768)进行训练保持稳定(截断率短暂飙升至约 4%,但迅速降至 2% 以下)
- 更大的模型更稳健
- 在 Scout 运行中,截断率始终低于 2%,并且在 > 90% 的训练步数中低于 1%
- 这可能反映了更大模型调节生成长度的固有能力以及它们更强的指令遵循能力,这使得中断信号更有效
- 总结:论文建议实践者密切监控截断率
- 论文的发现表明,高截断率是不稳定性的可靠警告信号 ,而更大的模型、更高的生成预算和谨慎的设计选择(如在 ScaleRL 中)可以显著降低这种风险
A.16 Comparing Prevalent Methods
- 在图 2 中,论文将一些流行的训练 Recipe 与 ScaleRL 进行了比较,论文在此简要描述这些现有 Recipe

DeepSeek (GRPO)
- 这个 Recipe 主要遵循 DeepSeek (2025) 的工作
- 论文使用 GRPO 作为损失函数(第 A.2 节),其中 \(\epsilon_{min}=\epsilon_{max}=0.2\),样本平均损失聚合,以及 PPO-offpolicy-8 算法
- 训练在 6k GPU hous 后由于截断(第 A.15 节)变得不稳定
Qwen2.5 (DAPO)
- 这个 Recipe 遵循 DAPO (2025),包括 DAPO 损失函数(附录 A.2),其中 \(\epsilon_{min}=0.2,\epsilon_{max}=0.26\)(附录 A.17.1)
- 这个 Recipe 使用 PPO-offpolicy-8 和提示平均损失聚合
- 与原始 DAPO 论文 (2025) 的唯一区别是关于动态填充批次
- DAPO 丢弃方差为零的提示,并采样更多提示直到批次满员
- 在论文的代码库中,这效率不高
- 因为对于 PPO-offpolicy 算法,Generator 会预先决定每个 Generator 将为 #prompts/#generators 生成 Rollout
- 如果某个特定的 Generator 有更多方差为零的提示 ,它会采样更多的提示来完成其 #prompts/#generators 的份额
- 这可能导致其他 Generator 停滞和整体速度减慢
- 为了解决这个问题,论文保持一个更大的批次大小 1280(80 个提示,每个 16 个生成),并从批次中丢弃方差为零的提示
- 论文注意到,丢弃后,有效批次仍然大于 768,即论文用于 ScaleRL 的大小
Magistral
- 这指的是 (2025) 中使用的 Recipe
- 这个 Recipe 包括与 DAPO 类似的 Recipe ,主要区别在于使用 PipelineRL 作为 Off-policy 算法
MiniMax
- 这指的是 (2025) 中使用的 Recipe
- 这个 Recipe 使用 CISPO 损失、LM 头部的 FP32 精度修复、PPO-offpolicy 算法和提示平均
- 与 DAPO 类似,它也丢弃方差为零的提示,因此论文也给它一个更大的批次大小 1280
A.17 Loss Type - Stability and Robustness
- GRPO/DAPO 风格的损失对裁剪比率超参数 \(\epsilon_{\text{max} }\) 的选择高度敏感;CISPO 和 GSPO 显示出远更强的稳健性
- 例如,在附录 A.17.2 中,将 CISPO 的 \(\epsilon_{\text{max} }\) 在 \(\{4,5,8\}\) 之间变化,性能没有显著差异
- 对于 GSPO ,原始论文 (2025) 中使用的 \(10^{-4}\) 裁剪尺度在论文的设置中效果不佳
- 论文在更广泛的尺度上进行了消融,发现确定了正确的数量级(例如,\(4\times 10^{-3}\) 及更高)以后,性能就稳定了,并且对细粒度的变化(例如,\(\{4\times 10^{-3},5\times 10^{-3}\}\))基本不敏感
A.17.1 DAPO clipping ratios
- 在本节中,论文分析了 DAPO 损失函数(公式 (8))中裁剪阈值 \(\epsilon_{\text{max} }\) 的作用
- \(\epsilon_{max}\) 的超参数敏感性已在先前工作中观察到
- 例如,GRPO 通常设置 \(\epsilon_{\text{max} }=0.2\),而 DAPO 使用 \(0.28\)
- 除了调整敏感性之外,论文发现 \(\epsilon_{\text{max} }\) 直接改变了算法的缩放行为
- 随着 \(\epsilon_{\text{max} }\) 增加,终端奖励 \(A\) 增加,直到达到一个最佳范围,之后 \(A\) 再次下降
- 这是一个显著的效果:与许多仅改变收敛速度的超参数不同,\(\epsilon_{\text{max} }\) 控制着渐近误差本身
A.17.2 CISPO Clipping Ratios
- 论文消融了 CISPO 的较高裁剪比率,将较低裁剪比率固定为 \(0\)(图 19b)
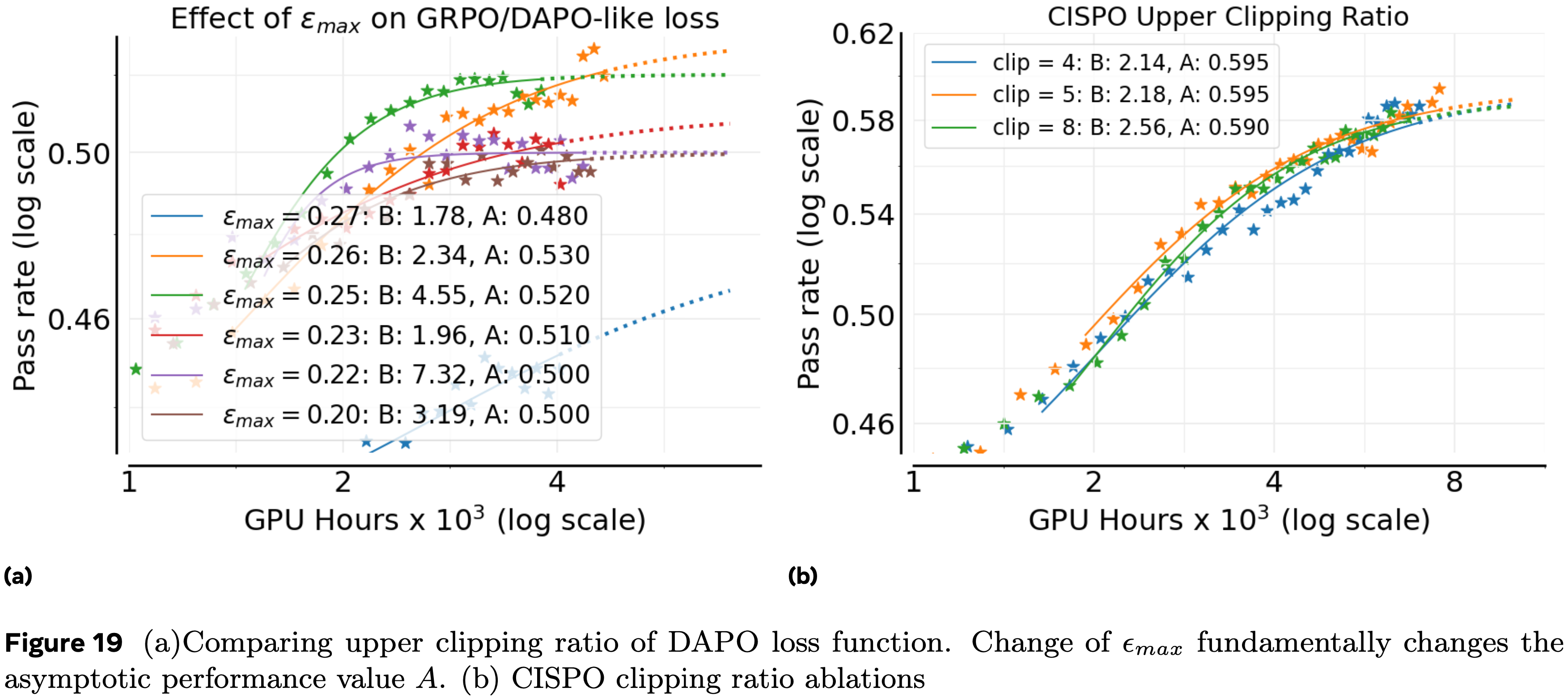
- 在很宽的值范围内,论文发现性能差异很小,表明 CISPO 对这个超参数基本不敏感
- 这种稳健性反映了论文对 GSPO 的发现(第 A.17.3 节),并且与 DAPO/GRPO 风格的目标形成对比,后者对裁剪阈值的精确选择高度敏感
- 这种在超参数变化下的稳定性使 CISPO 成为大规模训练中默认使用的有力候选者
A.17.3 GSPO ablations
- 论文消融了 GSPO 中使用的裁剪比率尺度,如图 20a 所示
- GSPO 论文 (2025) 中给出的默认 \(10^{-4}\) 尺度对论文的 8B 模型缩放效果不是最好
- \(10^{-3}\) 尺度的表现与其他替代方案一样好,或者更好(图 20a)
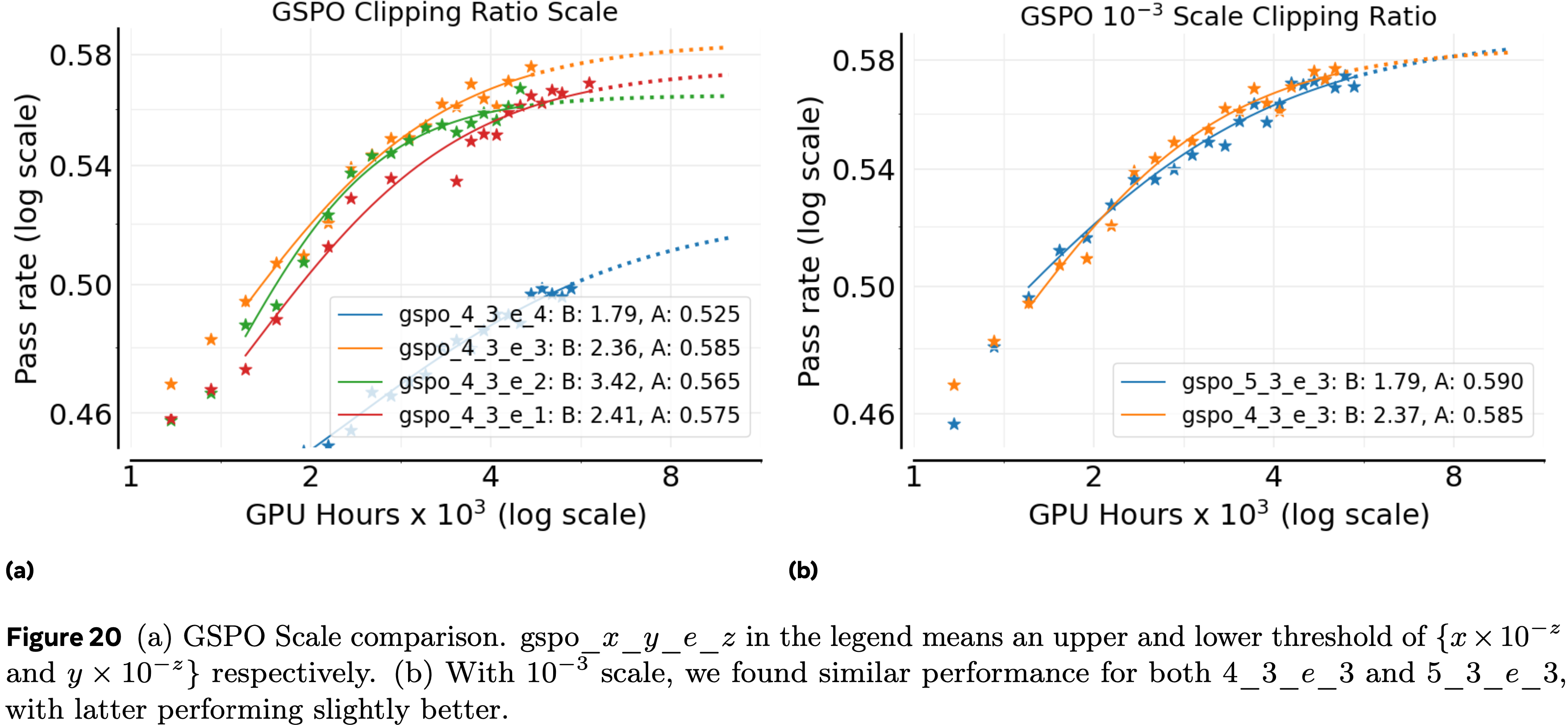
- 给定这个尺度,论文进一步将上裁剪比率在 \(\{4\times 10^{-3},5\times 10^{-3}\}\) 之间变化,并发现 \(\{5\times 10^{-3}\}\) 产生了稍好的拟合(图 20b)
- GSPO 对裁剪比率的选择相当稳健
- 确定了正确的尺度以后,大多数附近的值甚至更大的尺度表现相似
- 这种稳健性与 DAPO 风格的损失形成鲜明对比,后者对上裁剪比率的精确值高度敏感,如第 3.2 节所述
A.17.4 GSPO vs CISPO
- 尽管具有超参数稳健性,但论文遇到了 GSPO 的稳定性问题
- 在多次情况下,GSPO 运行在训练中期发散,导致性能突然下降
- 对于 8B 模型,从稳定检查点重新启动可以恢复,但此策略在更大的模型(如 Scout)上失败,尽管重复重置到稳定检查点,不稳定性仍然存在
- 虽然论文尽最大努力检查了任何实现错误,但论文没有发现
- 总的来说,虽然所有三种损失系列在调整好的设置下都可以具有竞争力,但 CISPO 在稳定性和对超参数的稳健性方面提供了最佳平衡 ,使其成为论文推荐的选择