NLP——LLM对齐微调相关总结

本文简单录对齐微调的一些方法，部分方法的详细内容可以在本人其他博客搜索到

熵的定义

熵的一般定义：
$$ H = -\sum_a \pi(a) \log \pi(a) = - \mathbb{E}_{a\sim \pi(a)} \log \pi(a)$$

SFT 的 Loss

SFT 的目标为最大化 Next Token 的对数概率和（本质是最大化所有 Token 的联合概率分布）：
$$ \mathcal{J}_\text{SFT}(\theta) = \max_\theta \mathbb{E}_{q,o\sim P_\text{SFT}(Q,o)}\left[\frac{1}{|o|} \sum_t \log \pi_\theta(o_t| x,o_{< t})\right]$$
SFT 下的 Loss 为：
$$ L_\text{SFT} = -\frac{1}{|o|} \sum_t \log \pi_\theta(o_t| x,o_{< t}) $$

RM 的 Loss

遵循 Bradley-Terry 模型，论文使用如下所述的奖励函数 $r_{\psi}(x, y)$ 来制定偏好分布：
$$
\begin{aligned}
p_{\psi}(y_{c} \succ y_{r}|x) & = \frac{\exp(r_{\psi}(x, y_{c}))}{\exp(r_{\psi}(x, y_{c})) + \exp(r_{\psi}(x, y_{r}))}, \\
& = \sigma(r_{\psi}(x, y_{c}) - r_{\psi}(x, y_{r})),
\end{aligned}
$$
- 其中 $\sigma$ 是逻辑函数
- 理解：这相当于是将正样本大于负样本的概率定义为一个 sigmoid 函数
将该问题视为二分类任务，得到负对数似然损失函数（negative log-likelihood loss function）：
$$
\mathcal{L}(r_{\psi}) = -\mathbb{E}_{(x, y) \sim \mathcal{D}_\text{rm} }[\log\sigma(r_{\psi}(x, y_{c}) - r_{\psi}(x, y_{r}))],
$$
- 理解：这里的损失函数本质上是相当于是二元交叉熵损失（Binary Cross-Entropy, BCE）函数，但因为已知有正负样本了，所以不需要分 label=1 和 label=0 来分别计算了
  $$
  L_\text{BCE} = -\frac{1}{N}\sum_{i=1}^N \big[y_i\log(\hat{y}_i) + (1-y_i)\log(1-\hat{y}_i)\big]
  $$
  - $y_i$：真实标签（0 或 1），在 RM 中固定为 1（因为我们已知 Chosen 比 Rejected 更好）
  - $\hat{y}_i$：模型预测概率 $\sigma(r_{\psi}(x, y_{c}) - r_{\psi}(x, y_{r}))$
  - 将 $y_i=1$ 带入上面的 BCE 即可化简得到
    $$
    \begin{align}
    L_\text{BCE}
    &= -\frac{1}{N}\sum_{i=1}^N 1 \cdot \log(\hat{y}_i) \\
    &= -\frac{1}{N}\sum_{i=1}^N \log \sigma(r_{\psi}(x, y_{c}) - r_{\psi}(x, y_{r})) \\
    \end{align}
    $$
- 其中数据集由表示为 $D_\text{rm} = \{x^{(i)}, y_{c}^{(i)}, y_{r}^{(i)}\}_{i=1}^{N}$ 的 comparisons 组成
- 在语言模型（LMs）领域，网络 $r_{\psi}(x, y)$ 通常使用 SFT 模型 $\pi^\text{SFT}(y|x)$ 进行初始化，并在它在最终的 Transformer 层上加入一个额外的线性层，以生成单个标量预测（singular scalar prediction）来表示奖励值

PPO

PPO 是最原始的 RLHF 方法
PPO 的替代目标函数定义为：
$$
\mathcal{L}^{CLIP}(\theta) = \hat{\mathbb{E} }_t \left[ \min \left( r_t(\theta) \hat{A}_t, \text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon) \hat{A}_t \right) \right]
$$
- $ \pi_\theta(a|s) $ 为当前策略，$ \pi_{\theta_{\text{old} } }(a|s) $ 为上一轮迭代的旧策略
- $ r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{\text{old} } }(a_t|s_t)} $ 是概率比
- $ \hat{A}_t $ 是时间步 $ t $ 的优势估计
- $ \epsilon $ 是控制裁剪范围的超参数
广义优势估计 (GAE) 是一种用于在 PPO 中更准确估计优势函数的技术
- 对于长度为 $ T $ 的轨迹，时间步 $ t $ 的优势估计 $ \hat{A}_t $ 计算如下：
  $$
  \hat{A}_t = \sum_{l=0}^{T-t-1} (\gamma \lambda)^l \delta_{t+l}
  $$
  - $ \gamma $ 是折扣因子
  - $ \lambda \in [0,1] $ 是 GAE 参数
  - $ \delta_t = R(s_t, a_t) + \gamma V(s_{t+1}) - V(s_t) $ 是时序差分（Temporal-Difference, TD）误差
  - 这里 $ R(s_t, a_t) $ 是时间步 $ t $ 的奖励，$ V(s) $ 是价值函数
注：在 RLHF 中通常设置折扣因子 $ \gamma = 1.0 $，为简化表示，论文后续章节将省略 $ \gamma $
LLM 中，更具体的写法可以是：
$$
\mathcal{J}_{\textit{PPO}}(\theta)=\mathbb{E}_{q\sim P(Q),o\sim\pi_{\theta_{old}}(O|q)}\frac{1}{|o|}\sum_{t=1}^{|o|}\min\left[\frac{\pi_{\theta}(o_ {t}|q,o_{<t})}{\pi_{\theta_{old}}(o_{t}|q,o_{<t})}A_{t},\textrm{clip}\left( \frac{\pi_{\theta}(o_{t}|q,o_{<t})}{\pi_{\theta_{old}}(o_{t}|q,o_{<t})},1-\epsilon ,1+\epsilon\right)A_{t}\right],
$$

CPPO（Continual Proximal Policy Optimization）

原始论文：CPPO: Continual Learning for Reinforcement Learning with Human Feedback, ICLR 2024, Harbin Institute of Technology (Shenzhen)：截止到 20250612，cited by 25
其他容易误解论文：CPPO: Accelerating the Training of Group Relative Policy Optimization-Based Reasoning Models, arXiv 202503, Xiamen University：截止到 20250612，cited by 12
- 不厚道，命名与别人相同，容易造成读者误解

REINFORCE

不需要 Value Model，蒙特卡罗法评估奖励
对 PPO 的简化

REINFORCE++

原始论文：REINFORCE++: An Efficient RLHF Algorithm with Robustness to Both Prompt and Reward Models, 20250104-20251110, Jian Hu & Jason Klein Liu & Wei Shen
REINFORCE++ 方法介绍
本质可以理解为 REINFORCE 方法（不是基于 Prompt 组的，有一个基于历史全局的基线）
在 REINFORCE 的基础上，记录历史平均奖励作为基线，判断模型是否在进步（相比 GRPO，基线不是 Prompt 粒度的，而是历史）
使用历史奖励的均值和方差做归一化，类似 Batch Normalization（论文认为 GRPO 的方法会出现 Prompt 粒度的有偏问题）
REINFORCE++ 方法出现在 ReMax, GRPO 和 RLOO 之后，对比如下：
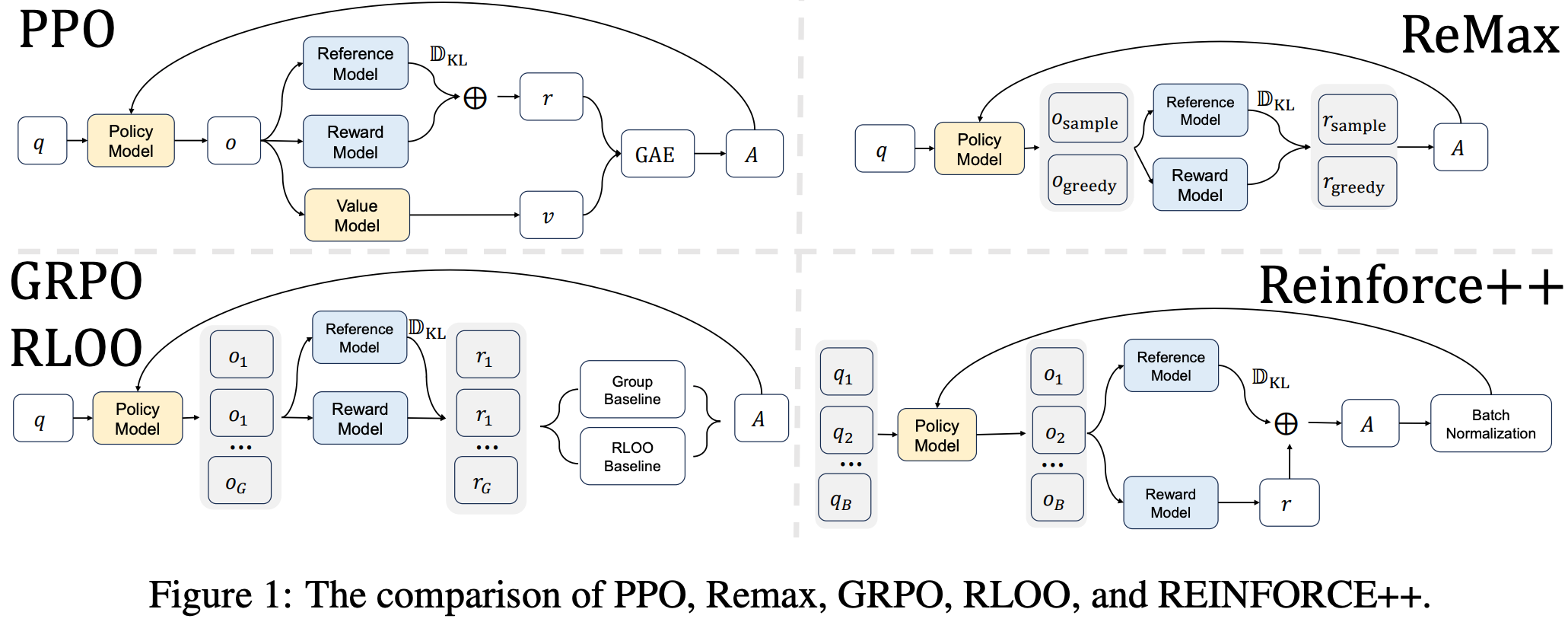
其他讨论：
- REINFORCE++ 使用的是 k2 KL 散度估计而不是 k3，论文参考了博客 Rethinking KL Regularization in RLHF: From Value Estimation to Gradient Optimization 中的内容

ReMax

参考链接：ReMax: A Simple, Effective, and Efficient Reinforcement Learning Method for Aligning Large Language Models, 2023, ICML 2024, 香港中文大学，南京大学
本质是 REINFORCE 方法
使用当前策略下每个状态下概率最高的动作对应的样本的奖励作为基线（每一步都贪心决策）
注意：概率最高的动作会持续走到最后直到拿到一个完整的 rollout，再来计算奖励
注意：与 GRPO 和 RLOO 不同，每次仅采样两个样本（其中一个是目标样本，另一个是贪心决策的样本）

ReMax 在 RLOO 之前一点点提出，算是并行的工作

# Algorithm 1: ReMax for Aligning LLMs
1 Input: reward_model(rm), language_model(lm)
2 for prompt in datasets:
3     seq=lm.sample(prompt, greedy=False)
4     seq_max=lm.sample(prompt, greedy=True)
5     rew=rm(prompt, seq)−rm(prompt, seq_max)
6     logp=lm.inference(prompt, seq)
7     loss=−(logp.sum(dim=−1)*rew).mean()
8     lm.minimize(loss)
9 Output: language_model

GRPO（Group Relative Policy Optimization）

每次生成一组样本，并对这组样本进行归一化
具体公式：
$$
\begin{split}
\mathcal{J}_{GRPO}(\theta)&=\mathbb{E}_{q\sim p(Q),\{\mathbf{o}_i\}_{i=1}^{G}\sim\pi_{\theta_{old}}(O|q)}\\
&\frac{1}{G}\sum_{i=1}^{G}\frac{1}{|\mathbf{o}_i|}\sum_{t=1}^{|o_{t}|}\left\{\min\left[\frac{\pi_{\theta}(o_{i,t}|q,\mathbf{o}_{i,<t})}{\pi_{\theta_{old}}(o_{i,t}|q,\mathbf{o}_{i,<t})}\hat{A}_{i,t},\text{clip}\left(\frac{\pi_{\theta}(o_{i,t}|q,\mathbf{o}_{i,<t})}{\pi_{\theta_{old}}(o_{i,t}|q,\mathbf{o}_{i,<t})},1-\epsilon,1+\epsilon\right)\hat{A}_{i,t}\right]-\beta\text{D}_{\text{KL}}\left[\pi_{\theta}||\pi_{ref}|\right) \right\},
\end{split}
$$
- 其中 $\hat{A}_{i,t}$ 的计算方式为在同一个 Query 采样的多个 Response 内部做归一化：
  $$\hat{A}_{i,t}=\overline{r}_{i}=\frac{r_{i}-\text{mean}(\mathbf{r})}{\text{std}(\mathbf{r})}$$

RLOO（REINFORCE Leave-One-Out）

参考链接：LLM RLHF 2024论文（四）RLOO - sanmuyang的文章 - 知乎
类似于 GRPO（发表时间也类似），每次生成一组样本
与 GRPO 的主要区别是：减去的是其他样本（不包含当前样本）的均值，且没有除以方差
RLOO 没有使用限制 KL 散度约束?

DPO（Direct Preference Optimization）

DPO 及其相关改进参见 NLP——LLM对齐微调-DPO 和 NLP——LLM对齐微调-DPO相关改进
DPO 目标：
$$\mathcal{L}_{\text{DPO} }(\pi_{\theta};\pi_{\text{ref} })=-\mathbb{E}_{(x,y_{w},y_ {l})\sim\mathcal{D} }\bigg{[}\log\sigma\left(\beta\log\frac{\pi_{\theta}(y_{w} \mid x)}{\pi_{\text{ref} }(y_{w} \mid x)}-\beta\log\frac{\pi_{\theta}(y_{l} \mid x)}{\pi_{\text{ref} }(y_{l} \mid x)}\right)\bigg{]}. \tag{7}$$
DPO 梯度：关于参数 $\theta$ 的梯度可以写成：
$$\nabla_{\theta}\mathcal{L}_{\text{DPO} }(\pi_{\theta};\pi_{\text{ref } })=\ -\beta\mathbb{E}_{(x,y_{w},y_{l})\sim\mathcal{D} }\bigg{[}\underbrace{\sigma(\hat{r}_{\theta}(x,y_{l})-\hat{r}_{\theta}(x,y_{w}))}_{\text{higher weight when reward estimate is wrong} }\quad\bigg{[}\underbrace{\nabla_{\theta}\log\pi(y_{w} \mid x)}_{\text{increase likelihood of } y_{w}}-\underbrace{\nabla_{\theta}\log\pi (y_{l} \mid x)}_{\text{decrease likelihood of } y_{l} }\bigg{]}\bigg{]}$$
- 其中 $\hat{r}_{\theta}(x,y)=\beta\log\frac{\pi_{\theta}(y|x)}{\pi_{\text{ref} }(y|x)}$ 是由语言模型 $\pi_{\theta}$ 和参考模型 $\pi_{\text{ref} }$ 隐式定义的奖励（更多内容在第 5 节）
- 直观地说：损失函数 $\mathcal{L}_{\text{DPO} }$ 的梯度增加了优选补全 $y_{w}$ 的似然，并降低了非优选补全 $y_{l}$ 的似然
- 样本的权重由隐式奖励模型 $\hat{r}_{\theta}$ 对非优选补全评分高出多少来衡量，按 $\beta$ 缩放，即隐式奖励模型对补全排序的错误程度，同时考虑了 KL 约束的强度
- 论文的实验表明了这种加权的重要性，因为没有加权系数的朴素版本的方法会导致语言模型退化（附录表 3）

RAFT（Reward rAnked FineTuning）

RAFT，即 Reward rAnked FineTuning，出自 Raft: Reward ranked finetuning for generative foundation model alignment, 2023.
RAFT 是 RL-free 方法，其核心步骤包括：
- 数据收集：可以利用正在训练的生成模型、预训练模型或它们的混合模型作为生成器，提升数据生成的多样性和质量
- 数据排序：利用与目标需求对齐的分类器或者回归器，筛选出最符合人类需求的样本
- 模型微调：利用筛选出的样本对模型进行微调，使训练后的模型与人类需求相匹配

RAHF（Representation Alignment from Human Feedback）

(RAHF)Aligning Large Language Models with Human Preferences through Representation Engineering, 2024, Fudan
RAHF（Representation Alignment from Human Feedback）的训练流程聚焦于通过表示工程实现大语言模型与人类偏好的对齐，整体方法描述如下

步骤一：指导LLM理解人类偏好

单模型对比指令微调（RAHF-SCIT） (Single Large Language Model through Contrastive Instruction Tuning (SCIT))
- 使用对比指令（如“生成受人类偏好的响应”和“生成不受人类偏好的响应”）对单个LLM进行微调
- 训练目标：通过最小化损失函数，使模型在给定正偏好指令时提高生成偏好响应的概率，给定负偏好指令时降低该概率
- 优势：通过同一模型学习偏好与非偏好的差异，避免特征空间不一致问题
双模型监督训练（RAHF-Dual）
- 分别微调两个LLM：
  - 偏好模型 ：使用偏好响应数据进行监督训练，学习生成符合人类偏好的输出
  - 非偏好模型 ：使用非偏好响应数据训练，学习生成不符合偏好的输出
- 特点：通过不同模型分别捕捉偏好与非偏好的表征，但需注意双模型特征空间可能存在的偏差

步骤二：收集模型 Activity Pattern

输入处理 ：将查询-响应对与偏好/非偏好指令拼接，输入模型以获取中间层隐藏状态（即内部表征）。为确保长度一致，对指令和响应进行 padding 处理
差异向量计算 ：提取偏好刺激（$A_{p^{+}, \pi, l}$）和非偏好刺激（$A_{p^{-}, \pi, l}$）下的隐藏状态，计算差值 $v_l = A_{p^{+}, \pi, l} - A_{p^{-}, \pi, l}$，该向量表征人类偏好相关的 Activity Pattern 差异

步骤三：构建最终对齐模型

LoRA适配器微调 ：利用低秩适配器（LoRA）拟合差异向量 $v_l$，通过均方误差（MSE）损失函数将差异向量融入模型表征：
$$
\mathcal{L}_{Align} = \left| A_{p, \pi_{LoRA}, l} - (A_{p, \pi_{base}, l} + \alpha v_l) \right|_2
$$
其中 $\alpha$ 控制差异向量的干预强度，通过调整该超参数平衡模型原始能力与偏好对齐效果
目标层选择 ：优先选择模型中间层（如LLaMA2-7B的第10、20层）进行操作，因中间层更易捕捉与偏好相关的全局表征，避免顶层任务特异性或底层表征不完整的问题

SimpleRL

原始论文：SimpleRL-Zoo: Investigating and Taming Zero Reinforcement Learning for Open Base Models in the Wild, HKUST & TikTok Meituan, 20250524 & 202508076
没有提出新的方法，就是原始的 GRPO 方法，但是对 GRPO 方法进行了微调
与 DAPO 类似，SimpleRL 将 GRPO 公式中的长度归一化挪到更外层的循环中去
SimpleRL 这篇论文提出了适用于多种开源基础模型的 Zero RL 训练方法
- 注：Zero RL：指直接基于基础模型训练的方法，这种方法不依赖 SFT
- SimpleRL 的贡献在于通过优化奖励设计、数据难度匹配等关键策略，实现 Zero RL 训练方法下推理能力提升
具体设计：
- 训练方法：直接从基础模型出发进行强化学习，不进行任何前置的 SFT，采用GRPO算法作为训练核心，仅依赖基于正确性的规则奖励和简单训练设置
- 关键训练组件
  - 算法：采用移除目标函数中长度归一化的 GRPO 算法，优化计算效率，无需单独价值模型，直接通过组归一化奖励估计优势函数
  - 奖励函数：仅基于答案正确性设计，正确答案奖励+1，错误奖励0，摒弃严格格式奖励（如强制答案入盒），避免限制模型探索
  - 数据处理：将 GSM8K 和 MATH 数据集按难度分为 Easy（GSM8K+MATH lv.1）、Medium（MATH lv.1-4）、Hard（MATH lv.3-5）三类，每类含约 8000 个样本，根据模型能力匹配对应难度数据
  - 模型与 Prompt：覆盖 10 种不同家族和规模的模型（Llama3-8B、Mistral 系列、Qwen2.5 系列等），对指令跟随能力弱的模型采用简单提示（仅要求分步推理），能力强的模型采用复杂提示
对 GRPO 目标函数作为微小修改（实际上这种改法与 DAPO 一致）
$$
\mathcal{J}_{\text{GRPO}}(\theta)=\underbrace{\frac{1}{\color{red}{\sum_{i=1}^{G}\left|o_{i}\right|}} \color{red}{\sum_{i=1}^{G} \sum_{t=1}^{\left|o_{i}\right|}} min \left[r_{i, t}(\theta) \hat{A}_{i}, clip\left(r_{i, t}(\theta) ; 1-\epsilon, 1+\epsilon\right) \hat{A}_{i}\right]}_{\text{Clipped policy update } }-\underbrace{\beta \mathbb{D}_{KL}\left[\pi_{\theta} | \pi_{ref }\right]}_{\text{KL penalty } }
$$
- 理解：这样可以消除长度归一化对模型响应长度的不当约束，更贴合 Zero RL 训练中“鼓励模型自由探索合理推理长度”的需求
总结思考： SimpleRL 关键优化策略
- 1）摒弃刚性格式奖励，优先保证响应可验证性，避免抑制模型探索
- 2）严格匹配训练数据难度与模型固有能力，难度不匹配会导致训练崩溃或效果不佳
- 3）调整探索相关超参数：采用较大采样量（N≥8）和合适温度（训练温度 1.0-1.2），稳定训练过程
- 4）避免传统 SFT 冷启动：传统 SFT 会限制模型探索能力，降低RL阶段的推理行为涌现潜力

SEED-GRPO（Semantic Entropy EnhanceD GRPO）

SEED-GRPO: Semantic Entropy Enhanced GRPO for Uncertainty-Aware Policy Optimization, 20250518, Zhejiang University
传统的 GRPO 算法在策略更新时对所有 Prompt 一视同仁，SEED-GRPO 引入语义熵（Semantic Entropy） 来量化模型对每个 Prompt 的不确定性，并利用该信息动态地调整策略更新的幅度，从而实现更稳定、更高效的训练
- 标准的 GRPO 对每个问题（Prompt）生成的多个 Response 计算相对优势（Advantage），并以此为依据进行等幅度的策略更新。然而，模型对于不同问题的掌握程度不同
- 直觉：
  - 当一个模型面对一个它熟悉的问题时，多次采样生成的 Response 虽然在措辞上有所不同，但核心语义（Meaning）是趋同的（例如，都得出 x=3 的结论）
    - 此时，模型表现出低不确定性
  - 反之，当问题超出模型能力时，生成的 Response 可能千差万别，语义上无法形成共识，即高不确定性
- 受 Curriculum Learning 启发，SEED-GRPO 提出了一种不确定性感知的训练机制
  - 对于高不确定性的问题，采取更保守的更新策略（减小更新步长），避免模型在“不懂”的问题上学习到噪声
  - 对于低不确定性的问题，则进行正常更新，充分利用模型“懂”的知识
SEED-GRPO 的完整流程如图 2 所示，具体步骤如下：
- 1）采样 Rollout ：对于给定的数学问题 $ q $（Prompt），使用当前策略模型 $ \pi_{\theta_{\text{old} } } $ 采样 $ G $ 个独立的 Response，记作 $ \{o_1, o_2, \ldots, o_G\} $
- 2）计算 Reward ：对每个 Response $ o_i $，根据其最终答案的正确性赋予奖励 $ r_i $。在数学任务中，通常 $ r_i = 1 $ 表示答案正确，$ r_i = 0 $ 表示错误
- 3）计算原始 Advantage ：以组内平均奖励 $ \bar{r} = \frac{1}{G}\sum_{i=1}^{G} r_i $ 作为 Baseline，计算每个 Response 的优势值：
  $$
  A_i = r_i - \bar{r}
  $$
  - $ A_i \in \mathbb{R} $，正值表示该 Response 优于组内平均，负值则表示劣于平均
- 4）计算语义熵（Semantic Entropy）以量化不确定性 ：这是 SEED-GRPO 的核心步骤
  - 聚类（Clustering） ：将 $ G $ 个 Response 根据其语义进行聚类，形成 $ K $ 个语义簇
    $$ \mathcal{C} = \{C_1, C_2, \ldots, C_K\} $$
  - 每个簇 $ C_k $ 内的 Response 尽管措辞不同，但表达的核心意思一致
    - 论文中为了简化，采用比较最终答案是否相同作为聚类依据
  - 熵估计 ：基于观察到的 $ K $ 个簇，使用蒙特卡洛方法估计该 Prompt 的语义熵 $ \text{SE}(q) $：
    $$
    \text{SE}(q) \approx -\frac{1}{K} \sum_{k=1}^{K} \log p(C_k \mid q)
    $$
    - $ p(C_k \mid q) = \sum_{o_i \in C_k} \pi_{\theta_{\text{old} } }(o_i \mid q) $ 表示在旧策略下，生成属于第 $ k $ 个语义簇的所有 Response 的总概率质量
    - 语义熵的意义 ：$ \text{SE}(q) $ 值越高，表示模型生成的 Response 语义越分散，模型对该问题的不确定性越高
      - $ \text{SE}_{\text{max} } = \log G $ 是熵的最大值（当所有 Response 各成一类时）
- 5）不确定性感知的优势调制（Uncertainty-Aware Advantage Modulation） ：
  - 利用计算出的语义熵来调制原始的 Advantage $ A_i $，得到新的调制后优势 $ \hat{A}_i $：
    $$
    \hat{A}_i = A_i \cdot f(\alpha \cdot \text{SE}(q) / \text{SE}_{\text{max} }(q))
    $$
    - $ \alpha $ 是一个超参数，用于控制对不确定性的敏感度
    - $ f(\cdot) $ 是一个调制函数（论文默认使用线性函数）
      - 当不确定性高时，$ f(\cdot) $ 值变小，从而整体上缩小了 Advantage 的幅度
      - 论文比较了 Linear, Exponential, Focal 等函数。结果表明，线性函数在不同任务上表现最稳健，因此被选为默认配置
- 6）策略更新 ：使用 PPO 风格的 Clipped Surrogate Objective 进行优化。对于第 $ i $ 个 Response，其损失函数为：
  $$
  \mathcal{L}_i(\theta) = \min \left(\text{ratio}_i(\theta)\hat{A}_i, \text{clip}(\text{ratio}_i(\theta), 1 - \epsilon, 1 + \epsilon)\hat{A}_i\right)
  $$
  - $ \epsilon = 0.2 $，$ \text{ratio}_i(\theta) = \frac{\pi_\theta(o_i|q)}{\pi_{\theta_{\text{old} } }(o_i|q)} $ 是新旧策略的采样概率比率。最终，目标函数为 $ \mathcal{L}(\theta) = \frac{1}{G}\sum_{i=1}^{G}\mathcal{L}_i(\theta) $

SEED-GRPO 梯度分析

从梯度角度分析了不确定性感知优势的作用，为简化，忽略 Clipping 项，梯度为：
$$
\nabla_{\theta}\mathcal{L}_i(\theta) = \nabla_{\theta}\log \pi_{\theta}(o_i\mid q)\cdot \text{ratio}_i(\theta)\cdot \hat{A}_i
$$
对应的参数更新为：
$$
\theta \gets \theta +\eta \cdot \nabla_{\theta}\log \pi_{\theta}(o_i\mid q)\cdot \text{ratio}_i(\theta)\cdot \hat{A}_i
$$
- $ \eta $ 是全局学习率
由于 $ \hat{A}_i $ 中包含了 $ f(\alpha \cdot \text{SE}(q) / \text{SE}_{\text{max} }(q)) $ 因子，该机制等效于为每个问题动态调整学习率
- 对于高熵（高不确定性）问题，有效学习率被降低，模型更新更保守
- 反之，对于低熵（高确定性）问题，则保持较大的更新步长

附录：语义熵（Semantic Entropy）的定义

语义熵（Semantic Entropy） 本质上是在语义等价类（而非 Token 序列） 上定义的香农熵（Shannon Entropy）
其一般化数学定义如下：
$$
\text{SE}(q) = -\sum_{c} \left( \sum_{o_i \in c} p(o_i \mid q) \right) \log \left[ \sum_{o_i \in c} p(o_i \mid q) \right]
$$
- $ q $ ：输入的 Prompt（问题）
- $ o_i $ ：模型针对 $ q $ 生成的第 $ i $ 个完整 Response（回复序列）
- $ p(o_i \mid q) $ ：在当前策略模型 $ \pi $ 下，给定 Prompt $ q $ 生成特定 Response $ o_i $ 的精确概率
- $ c $ ：代表一个语义等价类（Semantic Equivalence Class）。它指的是所有在意义上相同（即使措辞、句法不同）的 Response 所构成的集合
- $ \sum_{o_i \in c} p(o_i \mid q) $ ：属于同一个语义类 $ c $ 的所有 Response 的概率质量之和，可以简写为 $ p(c \mid q) $
直观理解：这个定义将传统香农熵中的“事件”从“Token 序列”换成了“语义含义”
- 1）如果模型生成的 8 个 Response 虽然用词不同，但全部归属于同一个语义类（即 $ K=1 $），那么该类总概率质量 $ p(c \mid q) = 1 $，代入公式计算得 $ \text{SE}(q) = -1 \cdot \log(1) = 0 $，表示完全确定
- 2）如果 8 个 Response 分属 8 个不同的语义类，每个类的概率质量约为 $ 1/8 $，则 $ \text{SE}(q) = -8 \cdot (1/8) \log(1/8) = \log 8 $，达到最大值，表示极度不确定
语义熵 vs 香农熵
- 香农熵（Shannon Entropy） ：基于 Token 的分布计算，对表面的措辞、句法变化非常敏感
  - 如果模型生成“答案是 3”、“x 等于 3”或“The answer is three”等语义相同但表述不同的 Response，香农熵会错误地显示为“高不确定性”
- 语义熵（Semantic Entropy） ：基于语义而非形式进行聚类，能有效区分“措辞多样性”和“语义多样性”
  - 只有当模型真正产出不同含义的答案时，语义熵才会升高，因此是衡量模型认知不确定性的更准确、更鲁棒的指标

DAPO

在 GRPO 的基础上提出四个改进：
- 提升上界
- 动态过滤（全对或全错的）
- 损失平均方式：Sequence 内部的 Token Loss 平均 -> 批次粒度的 Token Loss 平均
- 长度惩罚（[0;L_max - L_cache;L_max;+inf]，在 [L_max - L_cache;L_max] 长度区间内，使用逐步增大惩罚，超过 L_max 部分，固定惩罚）

VAPO（Value-model-based Augmented Proximal Policy Optimization）

VAPO: Efficient and Reliable Reinforcement Learning for Advanced Reasoning Tasks, arXiv 202504, ByteDance Seed
字节 Seed 团队的作品，是对 DAPO 的进一步改进
在 DAPO 的基础上，增加了：
- Value Pretraining
- Decoupled-GAE，即 $\lambda_\text{critic} = 1.0$，$\lambda_\text{actor} = 0.95$
- 长度自适应的 GAE

VC-PPO（Value-Calibrated PPO）

(VC-PPO)What’s Behind PPO’s Collapse in Long-CoT? Value Optimization Holds the Secret, arXiv 20250303, ByteDance Seed
核心贡献：
- Pretrained value：开始 RL 前先预训练价值网络
- Decoupled-GAE：计算 Advantage （for Actor 损失）时和计算 Target Reward（for Critic 损失）时使用不同的 $\lambda$

ORZ（Open-Reasoner-Zero）

原始论文：Open-Reasoner-Zero: An Open Source Approach to Scaling Up Reinforcement Learning on the Base Model, arXiv 20250401, StepFun & THU
第一个开源的 LLM 上面向推理的 zero RL 实现（即从 Base Model 直接进入 RL）
相关链接
- GitHub: https://github.com/Open-Reasoner-Zero/Open-Reasoner-Zero
- HuggingFace: https://huggingface.co/Open-Reasoner-Zero
效果：
- ORZ-32B 在 GPQA Diamond 基准上优于 DeepSeek-R1-Zero-Qwen-32B，训练步骤仅为其 1/30
- ORZ-32B 在 AIME 2024 上获得 48.1分（同 Size 模型上，后来字节的 VAPO 做到了 60分）
- ORZ-7B 做到了 17.9 分
注：包含很多训练经验，值得一看

GVPO（Group Variance Policy Optimization）

原始论文：GVPO: Group Variance Policy Optimization for Large Language Model Post-Training, arXiv 20250319, HKUST
核心贡献：
- GVPO 推到了一个 RL 约束优化问题的唯一最优解
- 提出一种灵活的采样分布避免了 on-policy 和重要性采样
结果：用 Qwen-7B 模型为基线，在 AIME 2024 上，做到了 20.72分（注：比 ORZ 和 GRPO 等都高）
GVPO 的梯度定义为：
梯度定义：
$$
\nabla_{\theta}\mathcal{L}_{\text{GVPO} }(\theta) = -\beta \sum_{(x,\{y_i\})}\sum_{i=1}^{k} \Big[ \big(R(x,y_i) - \overline{R}(x)\big) - \beta\Big(\log \frac{\pi_{\theta}(y_i|x)}{\pi_{\theta’}(y_i|x)} - \overline{\log \frac{\pi_{\theta} }{\pi_{\theta’} } }(x)\Big) \Big] \nabla_{\theta}\log \pi_{\theta}(y_i|x)
$$
- $R(x,y_i)$：Actual Reward，由 Reward Model 给出
- $\overline{R}(x) = \frac{1}{k}\sum_{i=1}^{k} R(x,y_i)$：组内 Reward 均值
- $\log \frac{\pi_{\theta}(y_i|x)}{\pi_{\theta’}(y_i|x)}$：当前策略与参考策略的 Log-Likelihood 比值，构成 Implicit Reward
- $\overline{\log \frac{\pi_{\theta} }{\pi_{\theta’} } }(x)$：组内 Implicit Reward 均值
- $\beta > 0$：KL 散度惩罚系数
- $\pi_{\theta’}$：Reference Policy，在 Online 训练中通常设为 $\pi_{\theta_{\text{old} } }$
该梯度满足 $\sum_i w_i = 0$，因此 Partition Function 自动抵消

GVPO 的三种等价解释

GVPO 的 Loss 函数具有三种物理意义明确的等价形式：

Mean Squared Error（MSE）解释

VPO 的梯度等价于以下 MSE Loss 的梯度：
$$
\mathcal{L}_{\text{GVPO} }(\theta) = \frac{1}{2} \sum_{(x,\{y_i\})} \sum_{i=1}^{k} \Big[ \big(R_{\theta}(x,y_i) - \overline{R}_{\theta}(x)\big) - \big(R(x,y_i) - \overline{R}(x)\big) \Big]^2
$$
其中 $R_{\theta}(x,y)$ 为 Implicit Reward
$$
R_{\theta}(x,y) = \beta \log \frac{\pi_{\theta}(y|x)}{\pi_{\theta’}(y|x)} + \beta \log Z(x)
$$
该解释表明：GVPO 通过最小化 Implicit Reward 与 Actual Reward 的中心距离差异来更新策略，使得高 Actual Reward 的 Response 获得更高的 Implicit Reward

Variance 解释（名称由来）

展开 MSE Loss 可得 Variance 形式的损失函数：
$$
\mathcal{L}_{\text{GVPO} }(\theta) \propto -2\mathbb{E}_{x,y}\Big[ (R - \overline{R})\log \pi_{\theta} + \text{Cov}(\log \pi_{\theta}, \log \pi_{\theta’}) - \frac{1}{2}\text{Var}(\log \pi_{\theta}) \Big]
$$
- $\text{Var}(\log \pi_{\theta}) = \mathbb{E}_y[(\log \pi_{\theta} - \mathbb{E}_y\log \pi_{\theta})^2]$：当前策略 Log-Probability 的方差
- $\text{Cov}(\log \pi_{\theta}, \log \pi_{\theta’}) = \mathbb{E}_y[(\log \pi_{\theta} - \mathbb{E}_y\log \pi_{\theta})(\log \pi_{\theta’} - \mathbb{E}_y\log \pi_{\theta’})]$：当前策略与参考策略的协方差
三项分别对应：
- 1）优势最大化（Advantage Maximization）：$(R - \overline{R})\log \pi_{\theta}$
- 2）信任域约束（Trust-Region）：$\text{Cov}(\log \pi_{\theta}, \log \pi_{\theta’})$，防止策略偏离过远
- 3）内在探索-利用平衡（Exploration-Exploitation）：$\text{Var}(\log \pi_{\theta})$，鼓励适度熵

RL 解释

GVPO 的梯度可重写为：
$$
\nabla_{\theta}\mathcal{L}_{\text{GVPO} }(\theta) = \mathbb{E}_{x,y\sim \pi_s}\Big[ \underbrace{R - \overline{R} }_{\text{Advantage} } - \beta\Big(\log \frac{\pi_{\theta} }{\pi_{\theta’} } - \overline{\log \frac{\pi_{\theta} }{\pi_{\theta’} } }\Big) \Big] \nabla_{\theta}\log \pi_{\theta}
$$
与经典 Policy Gradient 在 Trust-Region 约束下的梯度形式一致，但 GVPO 的采样分布 $\pi_s$ 与策略 $\pi_{\theta}$ 可以解耦

GPG（Group Policy Gradient）

原始论文：GPG: A Simple and Strong Reinforcement Learning Baseline for Model Reasoning, arXiv 20250501, AMAP Alibaba：AMAP是高德地图的简称
效果明显优于 GRPO
GPG 方法的特点：移除所有花里胡哨的组件（问题：效果真的好吗？）
GPG 方法的训练算法：
各种方法的损失函数比较：
补充趣事：GPG 对 Dr.GRPO 的批判：

In addition to these methods to improve efficiency and stability, a very recent and concurrent work Dr.GRPO [31] studies the details of reward and loss normalization and states GRPO tends to generate more tokens. However, although it reveals the reward bias in the advantage function, we observe that its performance did not significantly outperform GRPO.

ORPO（Odds Ratio Preference Optimization）

原始论文：ORPO: Monolithic Preference Optimization without Reference Model, arXiv 20240314, KAIST AI：截止到 20250616 日，cited by 244
- 注：KAIST AI 是韩国科学技术院（KAIST）的一个机构
核心思路：
- 偏好对齐的同时考虑 SFT 损失

ECPO（Early Clipped GRPO）

来源于快手的 OneREc OneRec Technical Report，用于 LLM4Rec 领域的偏好对齐
具体来说，对于用户 $ u $，论文使用旧策略模型生成 $ G $ 个物品。每个物品与用户一起输入偏好奖励模型，得到 P-Score 作为奖励 $ r_i $。优化目标如下：
$$
\mathcal{J}_{\text{ECPO}}(\theta) = \mathbb{E}_{u \sim P(U), \{o_i\}_{i=1}^G \sim \pi_{\theta_{old} } } \left[ \frac{1}{G} \sum_{i=1}^G \min \left( \frac{\pi_\theta(o_i|u)}{\color{red}{\pi’_{\theta_{old} }}(o_i|u)} A_i, \text{clip} \left( \frac{\pi_\theta(o_i|u)}{\color{red}{\pi’_{\theta_{old}} }(o_i|u)}, 1 - \epsilon, 1 + \epsilon \right) A_i \right) \right], \\
A_i = \frac{r_i - \text{mean}(\{r_1, r_2, \ldots, r_G\})}{\text{std}(\{r_1, r_2, \ldots, r_G\})},\\
\color{red}{\pi’_{\theta_{old} }(o_i|u) = \max \left( \frac{\text{sg}(\pi_\theta(o_i|u))}{1 + \epsilon + \delta}, \pi_{\theta_{old} }(o_i|u) \right), \quad \delta > 0,}
$$
- $\text{sg}$ 表示停止梯度操作（stop gradient operation）
- $\delta$ 是一个大于 0 的超参数
ECPO 对 GRPO（Group Policy Relative Optimization）(2024) 进行了修改，使其训练过程更加稳定
- 如图 6 所示，在原始 GRPO 中，允许负优势（negative advantages）的策略比率（$\pi_\theta / \pi_{\theta_{old} }$）较大，这容易导致梯度爆炸
- 因此，论文预先对具有较大比率的策略进行截断，以确保训练稳定性，同时仍允许相应的负优势生效
- $\delta$ 越大，可容忍的策略比率越大，意味着可容忍的梯度越大，这可以根据实际需求确定
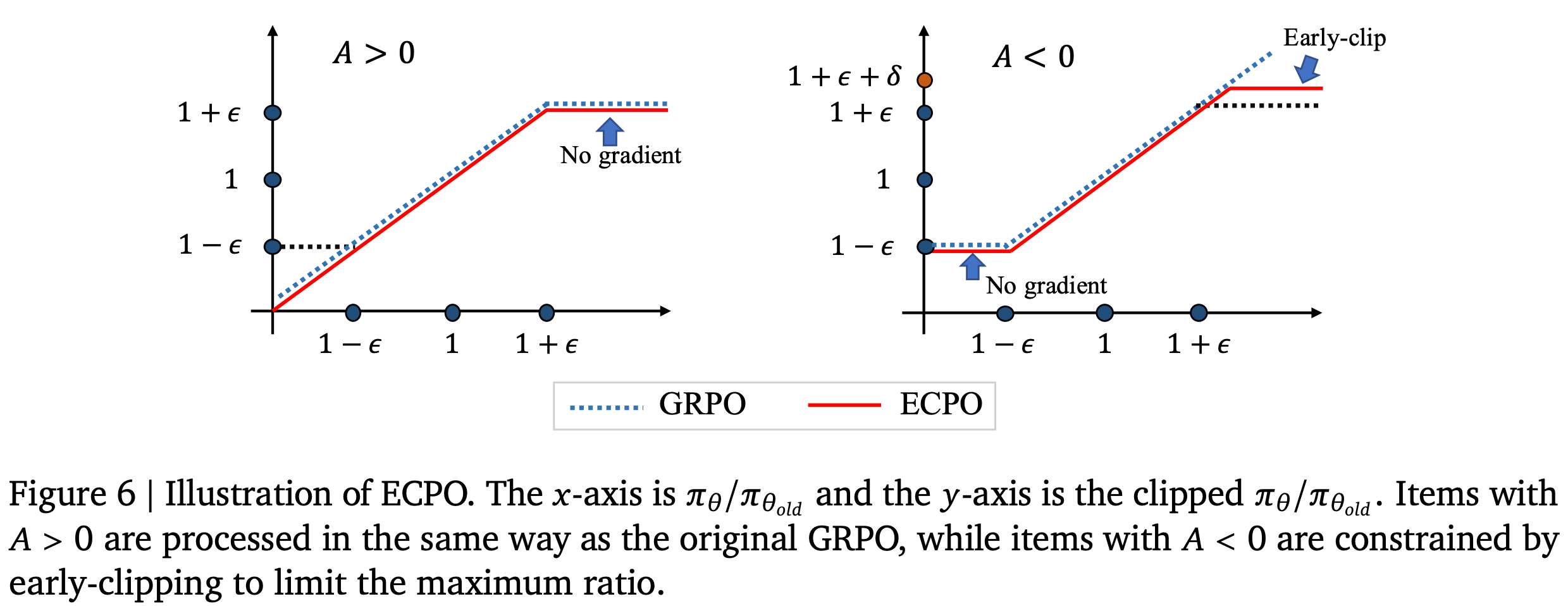
在 OneRec 中，论文将 $\delta$ 设为 0.1，表示允许负优势的策略比率略微超过 $1 + \epsilon$

CISPO（Clipped IS-weight Policy Optimization）

原始论文：MiniMax-M1: Scaling Test-Time Compute Efficiently with Lightning Attention, arXiv 20250616, MiniMax
名字说明：Clipped IS-weight Policy Optimization 中 IS 表示 Importance Sampling
效果：相对 DAPO，实现两倍加速
核心思路：不再裁剪 token 更新（影响是否反传梯度），而是裁剪重要性采样权重
- 注：思路和最近的 ECPO 有点相近
- 理解：这种做法是不对的，相当于忽略了 PPO 本身的优势
CISPO 目标函数：
$$
\mathcal{J}_{\text{CISPO} }(\theta) = \mathbb{E}_{(q,a)\sim\mathcal{D},\{o_i\}_{i=1}^G\sim\pi_{\theta_{\text{old} } }(\cdot|q)} \left[\frac{1}{\sum_{i=1}^G |o_i|} \sum_{i=1}^G \sum_{t=1}^{|o_i|} \mathbf{sg}(\hat{r}_{i,t}(\theta))\hat{A}_{i,t}\log\pi_\theta(o_{i,t} \mid q,o_{i,<t})\right], \tag{4}
$$
- 其中 $\hat{r}_{i,t}(\theta)$ 是裁剪后的重要性采样权重：
  $$
  \hat{r}_{i,t}(\theta) = \text{clip}\left(r_{i,t}(\theta),1-\epsilon_{low}^{IS},1+\epsilon_{high}^{IS}\right).
  $$
- 优势计算与 GRPO 一致：
  $$
  \hat{A}_{i,t} = \frac{R_i - \text{mean}(\{R_j\}_{j=1}^G)}{\text{std}(\{R_j\}_{j=1}^G)},
  $$
  - $R_i$ 是响应的奖励，每个问题采样 $G$ 个响应 $\{o_i\}_{i=1}^G$

Efficient RL Scaling with CISPO

Background

对于数据集 $\mathcal{D}$ 中的问题 $q$，论文将策略模型表示为参数化的 $\pi_\theta$，生成的响应为 $o$。PPO（2017）采用以下目标函数来优化策略以最大化预期回报，并通过裁剪操作稳定训练：
$$
\mathcal{J}_{\text{PPO} }(\theta) = \mathbb{E}_{q\sim\mathcal{D},o_i\sim\pi_{\theta_{\text{old} } }(\cdot|q)} \left[\frac{1}{|o_i|}\sum_{t=1}^{|o_i|}\min\left(r_{i,t}(\theta)\hat{A}_{i,t}, \text{clip}(r_{i,t}(\theta),1-\epsilon,1+\epsilon)\hat{A}_{i,t}\right) - \beta D_{KL}(\pi_\theta||\pi_{\text{ref} })\right],
$$
- 其中 $r_{i,t}(\theta) = \frac{\pi_\theta(o_{i,t}|q,o_{i,< t})} {\pi_{\theta_{\text{old} } } (o_{i,t}|q,o_{i, < t})}$ 是重要性采样权重（Importance Sampling, IS），用于在 Off-policy 更新时校正分布
PPO 需要一个单独的价值模型来计算优势 $\hat{A}_{i,t}$，GRPO（2024）则通过将优势定义为响应组内相对奖励来消除价值模型：
$$
\hat{A}_{i,t} = \frac{R_i - \text{mean}(\{R_j\}_{j=1}^G)}{\text{std}(\{R_j\}_{j=1}^G)},
$$
- 其中 $R_i$ 是响应的奖励，每个问题采样 $G$ 个响应 $\{o_i\}_{i=1}^G$
- 奖励可以来自基于规则的验证器（如数学问题求解）或奖励模型
对比，回顾带有校正分布（重要性采样）的原始 REINFORCE 目标函数 ：
$$
\mathcal{J}_{\text{REINFORCE} }(\theta) = \mathbb{E}_{(q,a)\sim\mathcal{D},o_t\sim\pi_{\theta_{\text{old} } }(\cdot|q)} \left[\frac{1}{|o_i|}\sum_{t=1}^{|o_i|} \mathbf{sg}(r_{i,t}(\theta))\hat{A}_{i,t}\log\pi_\theta(o_{i,t} \mid q,o_{i,<t})\right], \tag{3}
$$
GISPO 的本质是：基于组计算 Advantage 的（类似GRPO），带重要性采样的（可 Off-policy 更新的）REINFORCE 方法

GPPO（Gradient-Preserving Clipping Policy Optimization）

Klear-Reasoner: Advancing Reasoning Capability via Gradient-Preserving Clipping Policy Optimization, Klear, arXiv 20250812
Hugging Face地址：https://huggingface.co/Suu/Klear-Reasoner-8B
GitHub 地址：https://github.com/suu990901/KlearReasoner/tree/main
GPPO 方法用于解决传统强化学习（如PPO、GRPO）中的剪辑机制（Clipping）存在两个关键问题：
- 高熵token梯度被抑制 ：超出上阈值（$1+\epsilon$）的高熵 token（对应关键探索行为）的梯度被直接丢弃，限制模型探索能力
- 负样本收敛延迟 ：低于下阈值（$1-\epsilon$）的次优轨迹梯度被截断，导致模型难以从负样本中学习，收敛速度减慢
GPPO 不丢弃任何token的梯度，即使是超出剪辑范围的 token，其梯度也会被纳入反向传播计算图。通过有界且温和的梯度传播 ，平衡训练稳定性与有价值梯度信息的保留：
- 对高熵token（超出上阈值），保留其梯度以增强探索；
- 对次优轨迹（低于下阈值），保留其梯度以加速负样本学习
GPPO 的优势：
- 增强探索能力 ：保留高熵token的梯度，避免过早终止探索；
- 加速负样本学习 ：利用次优轨迹的梯度，减少重复采样，加快收敛；
- 稳定训练 ：通过有界梯度控制，避免梯度爆炸，维持训练稳定性
实验表明，GPPO 在数学（AIME）和编程（LiveCodeBench）任务上的性能优于传统剪辑方法（如 GRPO w/ Clip-Higher）和并发方法（如 CISPO）
GPPO 损失函数（基于 GRPO 的 token-level 损失修改而来），公式如下：
$$\mathcal{L}^{GPPO}(\theta)=\mathbb{E}_{x \sim \mathcal{D}}\left[\frac{1}{\sum_{j=1}^{M} T_{j}} \sum_{j=1}^{M} \sum_{t=1}^{T_{j}} min \left(\delta \tilde{A}^{(j)}, clip\left(\delta, \frac{1-\epsilon_{l}}{sg(\delta)} \delta, \frac{1+\epsilon_{h}}{sg(\delta)} \delta\right) \overline{A}^{(j)}\right)\right]$$
- $\delta = r_{t}^{(j)}(\theta)$ ：token 级重要性采样比（当前策略与旧策略的概率比）；
- $sg(\cdot)$ ：停止梯度（stop-gradient）操作，确保 $\frac{\delta}{sg(\delta)}$ 数值上恒为1，前向计算不变；
- $\epsilon_l, \epsilon_h$ ：剪辑的下、上阈值（如 $\epsilon_l=0.2, \epsilon_h=0.28$）；
- $\tilde{A}^{(j)}$ ：组相对优势（group-relative advantage），通过组内奖励标准化计算；
- $\sum_{j=1}^{M} T_j$ ：所有token的总长度，用于归一化
GPPO 梯度表达式，（梯度计算保留所有 token 的贡献），公式如下：
$$\nabla_{\theta} \mathcal{L}^{GPPO}(\theta) = \mathbb{E}_{x \sim \mathcal{D}}\left[\frac{1}{\sum_{j=1}^{M} T_{j}} \sum_{j=1}^{M} \sum_{t=1}^{T_{j}} \mathcal{F}_{j, t}(\theta) \cdot \phi_{\theta}\left(a_{j, t}, s_{j, t}\right) \cdot \tilde{A}^{(j)}\right]$$
- 其中，$\mathcal{F}_{j, t}(\theta)$（梯度权重函数）定义为：
  $$\mathcal{F}_{j, t}(\theta) = \begin{cases}
  1-\epsilon_{l} & \text{if } \delta<1-\epsilon_{l} \text{ and } \tilde{A}^{(j)}<0, \\
  1+\epsilon_{h} & \text{if } \delta>1+\epsilon_{h} \text{ and } \tilde{A}^{(j)}>0, \\
  \delta & \text{otherwise}
  \end{cases}$$
- $\phi_{\theta}(a_{j,t}, s_{j,t})$ ：策略网络输出的 logits 关于参数 $\theta$ 的导数（减去基线项）；
  - 当 $\delta$ 超出剪辑范围时，$\mathcal{F}_{j,t}(\theta)$ 被约束为 $1-\epsilon_l$ 或 $1+\epsilon_h$，确保梯度有界
- 当 $\delta$ 在范围内时，直接使用 $\delta$，保留原始梯度

Reflect-Retry-Reward

原始论文：Reflect, Retry, Reward: Self-Improving LLMs via Reinforcement Learning, 20250530, Writer，Writer 是一家美国 AI 公司
Reflect-Retry-Reward 机制的基本框架：
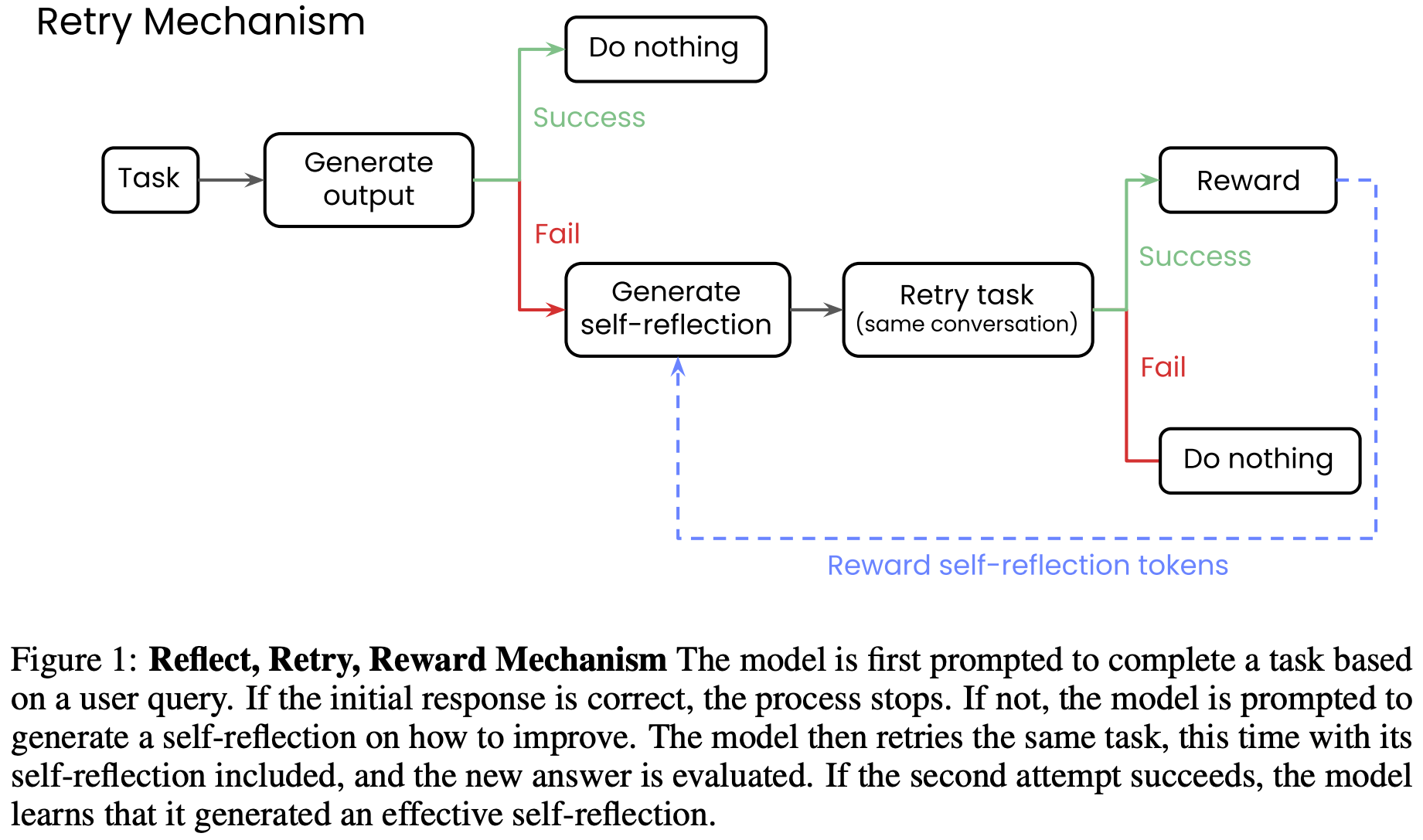
基本流程：
- 第一次生成结果
  - 如果成功则不进行任何训练
  - 如果失败则生成 Self-reflection token，重新将带着 Self-reflection token 的任务继续输入模型
- 第二次生成结果
  - 如果成功则进行训练，并对刚刚 Self-reflection token 增加赋予奖励？
  - 如果失败则不进行训练？

DFT（Dynamic Fine-Tuning）

今天在损失函数上添加一个权重，将 SFT 的损失函数对齐 RLHF
- 不能做到像 RL 一样探索，但是能尽量让 SFT 的损失函数贴近 RL
注意：
- SFT 的原始目标是最大化专家数据集的似然函数，故而其极大似然法推导出来的损失交（即叉熵损失）
- 经过修改以后，SFT 的损失函数已经不太能说得上其含义了，目标是最大化专家数据对应的奖励？

iw-SFT（Importance Weighted Supervised Fine-tuning）

iw-SFT 是 Importance weighted supervised fine-tuning，详情见论文：Supervised Fine Tuning on Curated Data is Reinforcement Learning (and can be improved), 20250717
待补充

CHORD（Controllable Harmonization of On-and Off-Policy Reinforcement Learning via Dynamic Weighting）

原始论文：(CHORD)On-Policy RL Meets Off-Policy Experts: Harmonizing Supervised Fine-Tuning and Reinforcement Learning via Dynamic Weighting, arXiv 20250815, Alibaba Group
解读博客：【千问大模型官方】先SFT后RL但是效果不佳？你可能没用好“离线专家数据”！
CHORD（Controllable Harmonization of On-and Off-Policy Reinforcement Learning via Dynamic Weighting）是一种结合了 RL 和 SFT 的方法，可以在 Token 粒度上识别重要性，从而调整学习损失函数或权重
CHORD 提出了思路相似的两种变体 CHORD-$\mu$ 和 CHORD-$\phi$，实验结果如下：

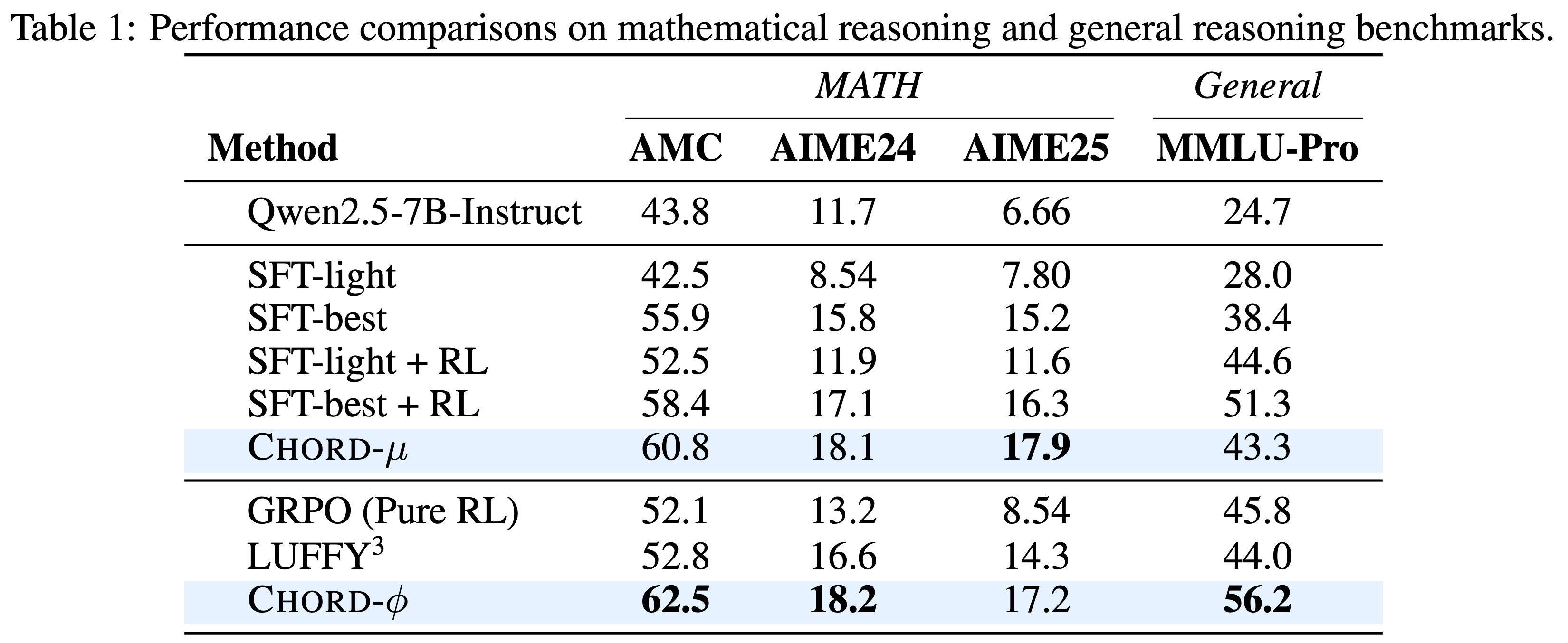
CHORD-$\mu$

CHORD-$\mu$ 通过动态调整全局系数 $\mu$ 来平衡 off-policy 专家数据（SFT 损失）和 on-policy 探索（GRPO 损失）的影响，其混合损失函数表达式为：
$$
\mathcal{L}_{\text{Hybrid}}(\theta) = (1-\mu) \mathcal{L}_{\text{GRPO}}(\theta) + \mu \mathcal{L}_{\text{SFT}}(\theta)
$$
$\mathcal{L}_{\text{GRPO}}(\theta)$ 是基于 GRPO 的 RL 损失函数，定义为：
$$
\mathcal{L}_{\text{GRPO}}(\theta) = -\frac{1}{\sum_{i=1}^{\hat{B}} \sum_{k=1}^{K} |\tau_{i,k}|} \sum_{i=1}^{\hat{B}} \sum_{k=1}^{K} \sum_{t=1}^{|\tau_{i,k}|} \min\left(r_{i,k,t}(\theta) A_{i,k}, \text{clip}(r_{i,k,t}(\theta), 1-\epsilon, 1+\epsilon) A_{i,k}\right)
$$
- 式中 $r_{i,k,t}(\theta)$ 为 token-level 重要性采样比率，$A_{i,k}$ 为优势值，$\hat{B}$ 为批量提示数，$K$ 为每个提示的候选响应数
$\mathcal{L}_{\text{SFT}}(\theta)$ 是监督微调损失函数，定义为：
$$
\mathcal{L}_{\text{SFT}}(\theta) = -\frac{1}{\sum_{i=1}^{B} |y_i^*|} \sum_{i=1}^{B} \sum_{t=1}^{|y_i^*|} \log \pi_{\theta}(y_{i,t}^* | x_i, y_{i,< t}^*)
$$
- 式中 $B$ 为批量大小，$y_i^*$ 为专家响应序列，$\pi_{\theta}$ 为模型策略
$\mu \in [0,1]$ 是动态衰减的全局系数 ，初始值较高（侧重 SFT），随训练逐步降低（侧重 RL）

CHORD-$\phi$

CHORD-$\phi$ 在 CHORD-$\mu$ 的基础上引入 token-level 加权函数 $\phi(\cdot)$，进一步细化对 off-policy 数据的控制，其损失函数表达式为：
$$
\mathcal{L}_{\text{Hybrid-}\phi}(\theta) = (1-\mu) \mathcal{L}_{\text{GRPO}}(\theta) + \mu \mathcal{L}_{\text{SFT-}\phi}(\theta)
$$
$\mathcal{L}_{\text{SFT-}\phi}(\theta)$ 是带 token 加权的 SFT 损失函数，定义为：
$$
\mathcal{L}_{\text{SFT-}\phi}(\theta) = -\mathbb{E}_{(x,y^*) \sim \mathcal{D}_{\text{SFT}}} \left[ \sum_{t=1}^{|y^*|} \phi(y_t^*; \pi_{\theta}) \cdot \log \pi_{\theta}(y_t^* | x, y_{<t}^*) \right]
$$
加权函数 $\phi(y_t^*; \pi_{\theta})$ 基于模型对专家 token 的生成概率 $p_t = \pi_{\theta}(y_t^* | x, y_{< t}^*)$ 定义为：
$$
\phi(y_t^*; \pi_{\theta}) = p_t (1 - p_t)
$$
- 该函数呈抛物线形，在 $p_t=0.5$ 时权重最大，对高概率（$p_t \to 1$）和低概率（$p_t \to 0$）的 token 均降权，平衡探索与稳定性

BAPO（Balanced Policy Optimization with Adaptive Clipping）

原始论文：BAPO: Stabilizing Off-Policy Reinforcement Learning for LLMsvia Balanced Policy Optimization with Adaptive Clipping, 20251021, Fudan
GitHub 链接：github.com/WooooDyy/BAPO
BAPO 用于解决 Off-policy RL 训练中 “优化失衡（imbalance in optimization）” 和 “熵坍缩” 两大问题，通过动态调整裁剪边界实现正 / 负样本贡献平衡与熵保留，最终提升训练稳定性、数据效率与模型性能
- 优化失衡 ：负优势样本（Advantage < 0）在策略梯度中占主导，抑制有效行为且易引发梯度爆炸
- 熵坍缩 ：PPO 类方法的固定对称裁剪机制会系统性阻断“熵增更新”（排除低概率正样本、过度惩罚低概率负样本），导致策略过度利用（Exploitation）而丧失探索能力（Exploration）
- 注：BAPO 是针对 PPO 进行改进的
BAPO 上述问题，提出动态非对称裁剪机制 ，核心目标是：
- 平衡正/负样本对损失的贡献
- 保留低概率正样本以维持熵，过滤过度负样本以避免梯度爆炸
- 无需复杂手动调参，适配不同离线场景（样本重放、部分轨迹生成、不同数据陈旧度）
BAPO 核心优势
- 稳定性：在不同数据陈旧度（2×、4×）、部分轨迹生成场景下，训练奖励持续上升，熵保持稳定（无坍缩），梯度范数可控
- 通用性：适配 DeepSeek-R1、Llama3.2 等不同底座模型，无需针对模型规模重新调参
- 注：论文中看起来得分似乎没有比 GRPO 高太多

BAPO 目标函数（动态裁剪改进）

BAPO 保留 PPO 的“最小化裁剪项”结构，但将固定对称边界替换为动态非对称边界（$c_{low}$ 为下边界，$c_{high}$ 为上边界），目标函数为：
$$
J^{BAPO}(\theta) = \mathbb{E}_{y \sim \pi_{\theta_{rollout} }(\cdot | x)} \sum_{t=1}^{T} min\left(r_t \cdot A_t, clip\left(r_t, c_{low}, c_{high}\right) \cdot A_t\right)
$$
- 其中，$c_{low}$ 和 $c_{high}$ 不再是固定值，而是通过每批次数据动态调整 ，核心约束是“正样本对策略梯度损失的贡献达到目标阈值 $\rho_0$”
- 注意：再次强调 BAPO 是针对 PPO 的改进

动态裁剪边界调整规则

BAPO 每轮训练（Step）中，通过迭代调整 $c_{low}$ 和 $c_{high}$，满足“正样本贡献目标 $\rho_0$”，具体规则如下：
（1）调整目标约束
- 设 $\rho$ 为当前批次中正样本对策略梯度损失的实际贡献占比，需满足：
  $$
  \rho \geq \rho_0
  $$
  - 其中 $\rho_0$ 为预设目标（实验中设为 0.4），确保正样本不被负样本压制
- 理解：在 BAPO 论文中，当前批次中正样本对策略梯度损失的实际贡献占比 $\rho$ 的评估方式，论文并未给出显式的计算公式 ，下面从其描述和算法目标中推导出清晰的评估逻辑
  - 原论文（第6页，Equation 8）中，BAPO 的目标是找到一个 clipping 上下界 $(c_{\text{low} }, c_{\text{high} })$，使得：
    $$
    \frac{|\sum_{A_t > 0} \pi_{\theta_{\text{rollout} } }(y_t) \cdot [\min(r_t \cdot A_t, \text{clip}(r_t, 0, c_{\text{high} }) \cdot A_t)]|}
    {|\sum_{A_t} \pi_{\theta_{\text{rollout} } }(y_t) \cdot [\min(r_t \cdot A_t, \text{clip}(r_t, c_{\text{low} }, c_{\text{high} }) \cdot A_t)]|} \geq \rho_0
    $$
    - 其中 $\rho_0$ 是目标正样本贡献比例（target contribution of positive signals），论文中设置为 $0.4$
    - 注意：上面的分子分母都有绝对值
  - 从上述不等式可以反推：
    - 正样本贡献（分子）：
      $$
      \text{PosContribution} = \left| \sum_{A_t > 0} \pi_{\theta_{\text{rollout} } }(y_t) \cdot \left[ \min\left(r_t \cdot A_t,; \text{clip}(r_t, 0, c_{\text{high} }) \cdot A_t\right) \right] \right|
      $$
      - 注意：是基于 PPO 的损失函数，所以 Advantage 有正有负
    - 总贡献（分母）：
      $$
      \text{TotalContribution} = \left| \sum_{A_t} \pi_{\theta_{\text{rollout} } }(y_t) \cdot \left[ \min\left(r_t \cdot A_t,; \text{clip}(r_t, c_{\text{low} }, c_{\text{high} }) \cdot A_t\right) \right] \right|
      $$
      - 注意：是基于 PPO 的损失函数，所以 Advantage 有正有负（即使样本为负样本时）
    - 实际正样本贡献占比 为：
      $$
      \rho = \frac{\text{PosContribution} }{\text{TotalContribution} }
      $$
（2）边界调整范围与步长
- 下边界 $c_{low}$：取值范围 $[a^-, b^-]$（实验中设为 [0.6, 0.9]），调整步长 $\delta_2$（实验中设为 0.02）
- 上边界 $c_{high}$：取值范围 $[a^+, b^+]$（实验中设为 [1.2, 3.0]），调整步长 $\delta_1$（实验中设为 0.05）
（3）迭代调整逻辑
- 1）初始化：$c_{low} = a^-$，$c_{high} = a^+$
- 2）若 $\rho < \rho_0$ 且 $c_{low} + \delta_2 \leq b^-$：
  - 优先提升 $c_{high}$（若 $c_{high} + \delta_1 \leq b^+$），纳入更多低概率正样本（$r_t$ 较大的正样本）
  - 若 $c_{high}$ 已达上限，则提升 $c_{low}$，过滤更多过度负样本（$r_t$ 过小的负样本）
- 3）重复步骤 2，直至 $\rho \geq \rho_0$ 或边界达上限

一些关于熵的理论基础讨论

BAPO 通过纳入低概率正样本维持熵，其理论基础是“熵-裁剪规则”（Entropy-Clip Rule）：策略熵的变化由未裁剪样本的“对数概率与优势值的协方差”决定，公式推导如下（详细证明见附录 B）：
$$
\Delta \mathcal{H}(\pi_{\theta} | x, y_{ < t}) \approx -\eta \cdot Cov_{y_t \sim \pi_{\theta} } \left( log \pi_{\theta}(y_t), A_t \cdot \mathcal{X}(y_t) \right) + C
$$
其中：
- $\Delta \mathcal{H}$：策略熵的变化量
- $\eta$：学习率
- $\mathcal{X}(y_t)$：指示函数，$\mathcal{X}(y_t)=1$ 表示样本未被裁剪，$\mathcal{X}(y_t)=0$ 表示被裁剪
- $C$：与 $y_t$ 无关的常数
关键结论：
- 低概率正样本（$\pi_{\theta}(y_t) \to 0$，$A_t > 0$）未被裁剪时，会增大协方差，进而提升熵
- BAPO 动态提升 $c_{high}$ 可纳入更多此类样本，避免熵坍缩

BAPO 训练流程：Algorithm 1

BAPO 每轮训练包含“样本生成-动态裁剪-策略更新”三步，具体流程如下：
1）初始化输入：
- 初始 LLM 策略 $\pi_{\theta}$、训练数据集 $\mathcal{D}$、奖励函数 $R$、数据陈旧度上限 $E$
- 裁剪边界范围 $[a^-, b^-]$（$c_{low}$）和 $[a^+, b^+]$（$c_{high}$）、步长 $\delta_1/\delta_2$、正样本贡献阈值 $\rho_0$
2）样本生成与过滤（每轮 Step s）：
- 更新行为策略：$\pi_{\theta_{rollout} } \leftarrow \pi_{\theta}$
- 从 $\mathcal{D}$ 采样批次数据 $\mathcal{D}_s$，基于 $\pi_{\theta_{rollout} }$ 生成 G 条响应 $y_i$
- 计算每条响应的奖励（基于 $R$）和优势值 $A_t$
3）动态调整裁剪边界（适配不同陈旧度）：
- 初始化 $c_{low} = a^-$，$c_{high} = a^+$
- 循环：若 $\rho < \rho_0$ 且 $c_{low} + \delta_2 \leq b^-$：
  - 若 $c_{high} + \delta_1 \leq b^+$，则 $c_{high} \leftarrow c_{high} + \delta_1$
  - 否则，$c_{low} \leftarrow c_{low} + \delta_2$
4）策略更新：
- 通过最大化 $J^{BAPO}(\theta)$ 更新 $\pi_{\theta}$，完成一轮训练

Trianing-free GRPO

原始论文：Training-Free Group Relative Policy Optimization, 20251009, Tencent Youtu-Agent Team
亮点：不修改模型参数，仅通过改进上下文来提升模型推理能力
Training-free GRPO 保留了传统 GRPO 的“多轮学习”框架，但将“参数更新”替换为“经验知识迭代优化”，核心流程可分为 4 步：
1）初始化：经验库与基础配置
- 初始化外部经验库 ：存储领域相关的“语义优势知识”，初始为空或包含少量基础经验
- 固定LLM参数：使用冻结的大模型（如 DeepSeek-V3.1-Terminus ）作为基础策略，避免参数更新
- 配置训练参数：仅需少量训练样本（如 100 个）、3-5轮迭代（epoch）、每组生成 5 个输出（group size=5）
2）Rollout 与奖励计算（复刻传统 GRPO）：对每个查询（query）执行并行输出生成 ：
- 基于当前经验库 $\varepsilon$，让 LLM 生成一组输出（rollout，如 5 个不同推理轨迹），即策略 $\pi_\theta(o_i | q, \varepsilon)$
- 使用奖励模型（R）对每个输出 $o_i$ 打分，得到 scalar reward $r_i = R(q, o_i)$（如数学推理的“答案正确性”、网页搜索的“任务完成率”）
3）群体语义优势计算（核心创新）：传统 GRPO 通过数值优势（ $\hat{A}_i = \frac{r_i - mean(r)}{std(r)}$）指导参数更新，而Training-free GRPO 替换为语义优势（自然语言形式的经验知识），具体步骤：
- 轨迹总结 ：用同一LLM对每个输出 $o_i$ 生成结构化总结 $s_i$，包含“推理步骤、工具使用、错误点（若有）”
- 语义优势提炼 ：基于总结 $\{s_1,…,s_G\}$ 和当前经验库，让 LLM 分析“成功/失败原因”，提炼通用经验（如“几何题需验证解是否在边界内”），形成语义优势 $A_{text}$
- 筛选有效群体 ：仅对“存在明显优劣差异”的群体（即 $std(r) \neq 0$）提炼语义优势，避免无意义经验
4）经验库优化（无参数更新的“策略优化”）：通过语义优势 $A_{text}$ 迭代更新经验库，LLM 生成 4 类操作指令：
- Add（添加） ：将新提炼的有效经验直接加入经验库
- Delete（删除） ：移除经验库中过时或低质量的经验
- Modify（修改） ：基于新经验优化现有经验的通用性（如扩展“几何题验证”到“代数题验证”）
- Keep（保留） ：经验库无需调整时维持现状
更新后的经验库会作为“token 先验”注入下一轮 LLM 调用，引导模型输出向高奖励方向偏移，实现“参数冻结下的策略优化”

SRL（Supervised Reinforcement Learning）

原始论文：Supervised Reinforcement Learning: From Expert Trajectories to Step-wise Reasoning, 20251029, Google Cloud AI Research, UCLA
SRL 是一种针对复杂多步推理任务的 LLM 训练框架，核心是将问题拆解为序列决策过程，通过分步专家动作引导和密集奖励信号实现高效学习
- 用于弥补SFT（刚性逐 token 模仿易过拟合）和 RLVR（依赖最终结果奖励、稀疏信号难学难问题）的缺陷
- 核心思路是把专家解决方案分解为一系列“逻辑动作”，模型先生成内部推理独白，再输出每步动作，基于与专家动作的相似度获得分步奖励

整体流程概述

整体流程图
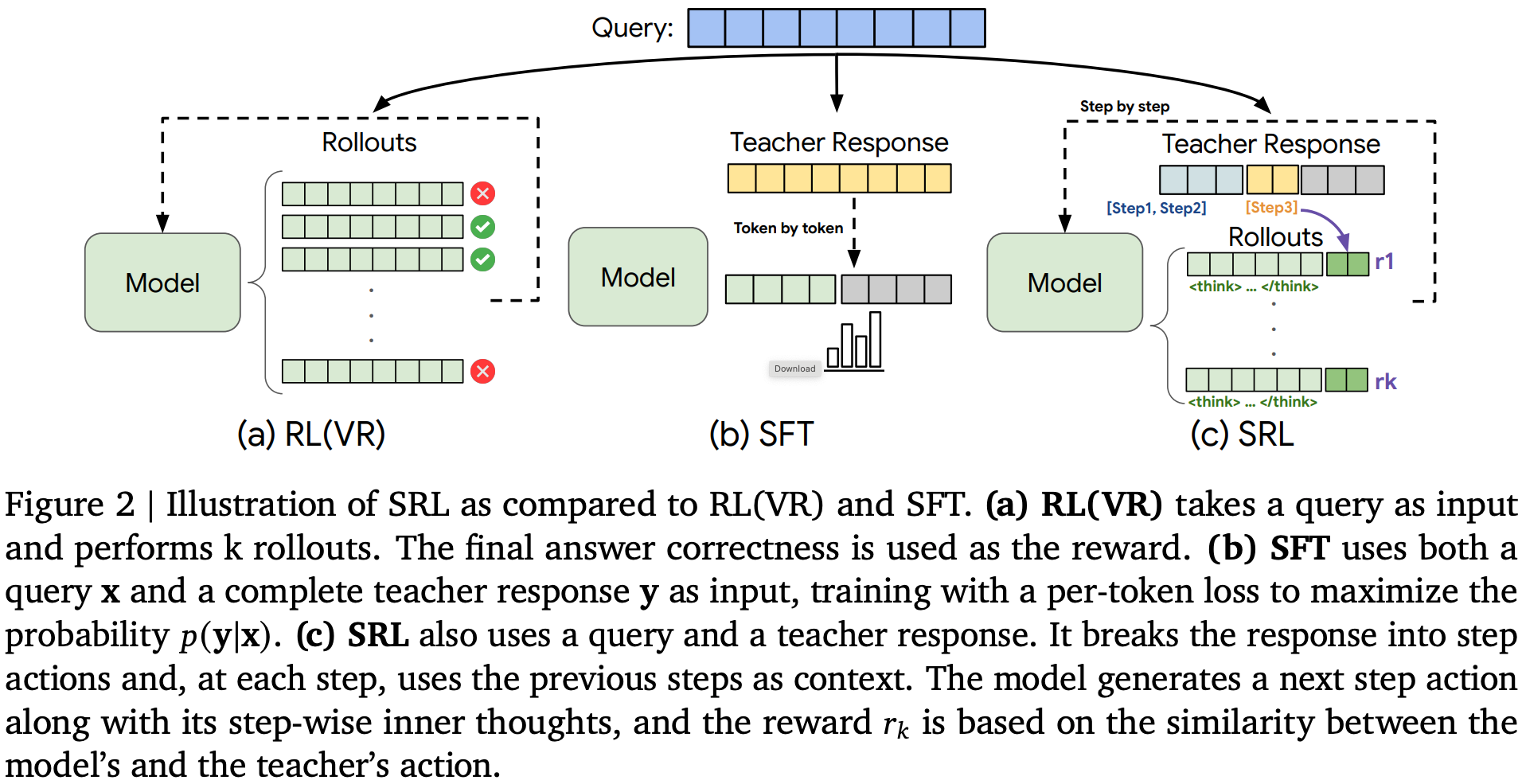
动作化问题构建
- 将专家（优秀的大模型）轨迹 $ \mathbf{y} $ 拆解为步骤动作序列 $ \mathbf{y} = \{\mathbf{y}_{\text{step}_n}\}_{n=1}^N $，每个动作代表一个有意义的决策步骤（如数学中的代数运算、软件任务中的命令执行）
- 构建分步训练数据：从单个专家解决方案生成 $ N-1 $ 个部分轨迹，输入提示 $ x_{\text{step}_k} = [x, \mathbf{y}_{\text{step}_1}, …, \mathbf{y}_{\text{step}_{k-1} }] $，目标是预测下一步动作 $ \mathbf{y}_{\text{step}_k} $
分步推理与奖励计算
- 模型生成格式：
  $$ \mathbf{y}’ \sim p_{\theta}(\cdot | x_{\text{step}_k}) = [\mathbf{y}_{think}’, \mathbf{y}_{\text{step}_k}’] $$
  - 其中 $ \mathbf{y}_{think}’ $ 是内部推理独白（用特定标签封装），$ \mathbf{y}_{\text{step}_k}’ $ 是预测动作
- 序列相似度奖励公式：
  $$ R(\mathbf{y}_{\text{step}_k}’, \mathbf{y}_{\text{step}_k}) = \frac{2 \sum_{(i,j,n) \in \text{MatchingBlocks}} n}{|S_1| + |S_2|} $$
  - $ S_1 $ 为模型预测动作序列，$ S_2 $ 为专家动作序列
  - $ \text{MatchingBlocks} $ 是两序列中非重叠匹配块的集合，$ n $ 为每个匹配块的长度
  - 若输出格式错误，奖励为 -1，最终奖励范围 $ r \in [0,1] \cup \{-1\} $
动态采样策略
- 过滤奖励方差接近零的样本，保留标准偏差超过阈值 $ \epsilon $ 的样本：
  $$ \sqrt{\frac{\sum_{i=1}^G (r(o_i, \mathbf{y}) - \bar{r})^2}{G} } > \epsilon $$
  - $ G $ 为生成的轨迹数量，$ r(o_i, \mathbf{y}) $ 是第 $ i $ 条轨迹的奖励，$ \bar{r} $ 为样本平均奖励
采用 GRPO 目标函数优化策略，仅基于逻辑动作计算奖励，不约束内部推理独白，兼顾动作一致性与推理灵活性

核心优势

密集奖励：即使所有轨迹均错误，仍能通过分步动作相似度提供有效学习信号
灵活推理：避免SFT的刚性模仿，允许模型发展自身推理风格
跨域通用：在数学推理和软件工程代理任务中均表现优异

性能表现

数学推理任务：在 AMC23、AIME24 等竞赛级基准上，SRL 平均性能超 SFT 和 RLVR，SRL+RLVR pipeline 实现最优（平均28.3%）
软件工程任务：在 SWE-Bench 上，Oracle 设置下 resolve rate 达 14.8%，较 SFT 基线提升 74%；端到端设置下性能翻倍

AWPO

原始论文：AWPO: Enhancing Tool-Use of Large Language Models through Explicit Integration of Reasoning Rewards
AWPO（Advantage-Weighted Policy Optimization）是用于工具集成方向的 LLM，其核心思想是 通过显式地集成推理奖励（reasoning rewards）来提升模型在复杂任务中的推理和工具调用能力 ，同时避免与基于结果的奖励（outcome rewards）发生冲突
背景：
- 现有的基于 RL 的工具使用 LLM 训练方法通常仅依赖 可验证的结果奖励（如工具调用的格式正确性、执行结果匹配度），而 忽视了推理过程的质量（如逻辑连贯性、步骤合理性、工具选择恰当性）
- 若直接简单混合推理奖励与结果奖励可能导致：优化目标冲突、训练不稳定、性能提升有限等问题
AWPO 建立在 策略改进上界理论 之上，

核心：奖励设计与优势计算

结果奖励 $R^{\text{out} }$ ：基于规则计算，包括格式正确性（精确匹配）和执行正确性（工具名、参数名、参数值的相似度）
推理奖励 $R^{\text{reasoning} }$ ：由 LLM-as-a-Judge 模型评估生成推理链的逻辑连贯性、工具选择合理性、参数设置准确性等，得分范围 $[0, 1]$
混合奖励 ：
$$
R^{\text{mix} } = R^{\text{out} } + R^{\text{reasoning} }
$$
优势计算 ：分别计算基于结果奖励和混合奖励的归一化优势：
$$
A^{\text{out} }_{g,j} = \frac{R^{\text{out} }_{g,j} - \bar{R}^{\text{out} }_{g} }{\widehat{\sigma}^{\text{out} }_{g} + \epsilon}, \quad
A^{\text{mix} }_{g,j} = \frac{R^{\text{mix} }_{g,j} - \bar{R}^{\text{mix} }_{g} }{\widehat{\sigma}^{\text{mix} }_{g} + \epsilon}
$$
最终加权优势 ：结合门控权重与难度权重：
$$
A^{\text{hyper} }_{g,j} := d_{g}\left[ (1 - w_{g}^{\text{mix} }) A^{\text{out} }_{g,j} + w_{g}^{\text{mix} } A^{\text{mix} }_{g,j} \right]
$$

创新1：方差感知门控，Variance-Aware Gating

用于自适应调节推理奖励的权重，避免在结果奖励方差不足时引入噪声
对于每组样本，计算混合奖励与结果奖励的标准差比值：
$$
r_{g} := \frac{\widehat{\sigma}_{g}^{\text{mix} } }{\widehat{\sigma}_{g}^{\text{out} }+\widehat{\sigma}_{g}^{\text{mix} }+\varepsilon_{\text{std} } }
$$
最终得到 门控权重 ：
$$
w_{g}^{\text{mix} } := \mathbf{1}(\bar{R}_{g}^{\text{out} } < R_{\text{out} }^{\text{max} }) \cdot \mathbf{1}(r_{g} < \varepsilon_{\text{mix} }) \cdot r_{g}
$$
- 仅当结果奖励未饱和且混合奖励方差相对可控时，才引入推理奖励信号

创新2：Difficulty-Aware Weighting（难度感知加权）

优先从中等难度样本组中学习，避免过于简单或过于困难的样本主导优化过程
根据结果奖励的组内均值设定权重：
$$
d_{g} := \alpha_{\text{base} } + (\alpha_{\text{prio} } - \alpha_{\text{base} }) \cdot \mathbf{1}(\tau_{\text{low} } < \bar{R}_{g}^{\text{out} } < \tau_{\text{high} })
$$
- 中等难度区间 $(\tau_{\text{low} }, \tau_{\text{high} })$ 内的样本获得更高权重 $\alpha_{\text{prio} }$

创新3：Dynamic Clipping

根据混合信号依赖程度动态调整 PPO 裁剪范围，在高方差信号下收紧信任域以控制噪声风险
裁剪半径随批次平均混合权重自适应调整：
$$
\varepsilon := \varepsilon_{\min} + (1 - \bar{w}_{\mathcal{B} })(\varepsilon_{\max} - \varepsilon_{\min})
$$
- 当模型更多依赖高方差的推理奖励时（$\bar{w}_{\mathcal{B} }$ 大），裁剪范围收紧，防止梯度更新过大

Self-Rewarding

原始论文：Self-Rewarding Language Models, ICML 2024, Meta
Self-rewarding 是用模型自身替代独立外部奖励模型（RM），以自评估生成响应并提供奖励信号、驱动迭代对齐的范式，核心是单模型兼具生成（Actor）与评估（Judge）能力，降低对人类偏好标注的依赖
论文贡献：
- 提出了一体化框架，让模型同时具备指令生成、响应生成与自我评估能力，无需分离的奖励模型
- 验证了迭代式自奖励训练的可行性，实现模型在两大核心能力上的协同提升
- 为突破人类反馈瓶颈、实现模型持续自我改进提供了新路径
方法流程：
- 初始化：SFT
- 自指令生成（Self-Instruction Creation）：
  - 为每个指令生成多个候选响应（注：论文中似乎 Instruction 也是模型自己生成的）
  - 模型通过 “LLM-as-a-Judge” 提示自我评估候选响应，给出 0-5 分评分（基于相关性、完整性、实用性等5个维度）
- 模型训练：从生成的候选响应中筛选出最高分（获胜者）和最低分（失败者）组成偏好对，通过直接偏好优化（DPO）训练下一轮模型
- 迭代优化：重复上述步骤

DLER

原始论文：DLER: Doing Length pEnalty Right - Incentivizing More Intelligence per Token via Reinforcement Learning, 20251016, NVIDIA
DLER（Doing Length pEnalty Right）是一种通过 RL 优化推理语言模型效率的训练方案，核心目标是在不损失准确率的前提下最大化“每 token 智能度”（准确率与响应长度的比值），解决现有长链推理模型输出冗长、延迟高的问题
DLER 的核心创新在于：无需复杂的长度惩罚设计，通过优化 RL 训练过程即可实现最优的准确率-效率权衡
- 长度缩减：相较于原始模型（如 DeepSeek-R1-7B），DLER 将响应长度削减 69%-77%，DA-DLER 进一步降至 80%
- 准确率提升：在 MATH、AIME-24 等 5 个推理基准上，DLER 不仅恢复原始模型准确率，还实现 1%-3% 的提升
- 推理效率：并行推理时，DLER-7B 生成多轮响应的 latency 降低6 2%，且准确率提升 28%
- 泛化性：兼容多种长度惩罚函数（如 Cosine、Laser），且简单截断惩罚的效果优于复杂惩罚，同时训练成本更低
现有基于RL的长度优化方法常采用复杂长度惩罚函数，但存在三大关键问题：
- 1）优势估计偏差：GRPO 的分组奖励归一化在截断惩罚下产生显著奖励噪声，导致优势估计偏差
- 2）熵崩溃：重要性采样比率裁剪会过滤掉低概率、高熵的推理过渡 token，限制推理路径探索
- 3）奖励信号稀疏：大量训练样本因响应超截断长度被分配零奖励，导致训练信号失衡
DLER 整合四大关键技术，针对性解决上述挑战：
- 1）批次级奖励归一化（Batch-wise Reward Normalization） ：将GRPO的分组级优势归一化改为批次级归一化，缓解奖励噪声导致的偏差，优势计算方式为：
  $$A_{i, t}^{norm }=\frac{A_{i, t}-mean_{batch}\left(A_{i, t}\right)}{std_{batch}\left(A_{i, t}\right)}$$
  - 其中 $A_{i, t}=R_{i}’-mean(\{R_{i}’\}_{i=1}^{G})$，$R_i’$ 为包含正确性奖励与长度惩罚的总奖励
- 2）更高裁剪阈值（Higher Clipping Threshold） ：解耦GRPO中上下裁剪阈值，提高上阈值（$\epsilon_{high}$），保留高熵探索性token的梯度更新，避免熵崩溃
- 3）动态采样（Dynamic Sampling） ：过滤所有rollout均为零奖励（过难样本）或全为正奖励（过易样本）的训练样本，重新采样至目标批次大小，构建均衡的训练信号
- 4）简单截断惩罚（Simple Truncation Penalty） ：采用最简洁的长度惩罚机制——对超过固定长度限制的响应分配零奖励，避免复杂惩罚函数带来的训练不稳定

DLER 扩展变体

难度感知DLER（DA-DLER） ：根据问题难度动态调整截断长度，模型已可靠解答的简单问题进一步缩短截断长度，复杂问题保留更长token预算，额外降低11%-15%的响应长度
更新选择性权重融合（Update-selective Weight Merging） ：针对公开训练数据质量不足导致的准确率下降，融合原始基线模型与DLER训练模型的权重（保留Top25%最大参数更新量并缩放），在恢复基线准确率的同时保持47%的长度缩减

GSPO（包含 GSPO 和 GSPO-Token 两个版本）

GSPO: Group Sequence Policy Optimization

原版的的 序列组策略优化（Group Sequence Policy Optimization, GSPO）算法采用以下 Sequence-level 的优化目标：
$$
\mathcal{J}_{\text{GSPO} }(\theta) = \mathbb{E}_{x\sim\mathcal{D},\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|x)} \left[\frac{1}{G} \sum_{i=1}^G \min \left(s_i(\theta)\widehat{A}_i, \text{clip}(s_i(\theta), 1-\varepsilon, 1+\varepsilon) \widehat{A}_i\right)\right], \tag{5}
$$
- 其中，论文采用基于组的优势估计：
  $$
  \widehat{A}_i = \frac{r(x,y_i) - \text{mean}(\{r(x,y_i)\}_{i=1}^G)}{\text{std}(\{r(x,y_i)\}_{i=1}^G)}, \tag{6}
  $$
- 并基于序列似然（2023）定义重要性比率 $s_i(\theta)$：
  $$
  s_i(\theta) = \left(\frac{\pi_{\theta}(y_i|x)}{\pi_{\theta_{\text{old} } }(y_i|x)}\right)^{\frac{1}{|y_i|} } = \exp\left(\frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \log \frac{\pi_{\theta}(y_{i,t}|x,y_{i,<t})}{\pi_{\theta_{\text{old} } }(y_{i,t}|x,y_{i,<t})}\right). \tag{7}
  $$
  - 理解：这里是相当于有点对所有的 Token 的比例对数求平均，再求指数的意思，核心是将 Token 粒度的重要性比例替换成经过 “几何平均（Geometric Mean）“ 后的 Sequence 粒度的（同一个 Sequence 所有 Token 共享的）重要性比例
    - 补充：几何平均（Geometric Mean，GM）的定义：
      $$ \exp\left(\frac{1}{|x|} \sum_{t=1}^{|x|} \log x_t\right) = (\prod_{t=1}^{|x|} x_t)^{\frac{1}{|x|}}$$

GSPO-token：A Token-level Objective Variant

在多轮强化学习等场景中，论文可能希望比 Sequence-level 更细粒度地调整优势
为此，论文引入了 GSPO 的 Token-level 目标变体，即 GSPO-token ，以实现 Token-level 的优势定制：
$$
\mathcal{J}_{\text{GSPO-token} }(\theta) = \mathbb{E}_{x\sim\mathcal{D},\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|x)} \left[\frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \min \left(s_{i,t}(\theta)\widehat{A}_{i,t}, \text{clip}(s_{i,t}(\theta), 1-\varepsilon, 1+\varepsilon) \widehat{A}_{i,t}\right)\right], \tag{13}
$$
- 其中
  $$
  s_{i,t}(\theta) = \text{sg}[s_i(\theta)] \cdot \frac{\pi_{\theta}(y_{i,t}|x,y_{i,<t})}{\text{sg}[\pi_{\theta}(y_{i,t}|x,y_{i,<t})]},
  $$
- $\text{sg}[\cdot]$ 表示仅取值但停止梯度，对应于 PyTorch 中的 detach 操作。GSPO-token 的梯度可以推导为：
  $$
  \begin{align}
  \nabla_{\theta} \mathcal{J}_{\text{GSPO-token} }(\theta) &= \nabla_{\theta} \mathbb{E}_{x\sim\mathcal{D},\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|x)} \left[\frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} s_{i,t}(\theta)\widehat{A}_{i,t}\right] \\
  &= \mathbb{E}_{x\sim\mathcal{D},\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|x)} \left[\frac{1}{G} \sum_{i=1}^G s_i(\theta) \cdot \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \widehat{A}_{i,t} \frac{\nabla_{\theta} \pi_{\theta}(y_{i,t}|x,y_{i,<t})}{\pi_{\theta}(y_{i,t}|x,y_{i,<t})}\right] \\
  &= \mathbb{E}_{x\sim\mathcal{D},\{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old} } }(\cdot|x)} \left[\frac{1}{G} \sum_{i=1}^G \left(\frac{\pi_{\theta}(y_i|x)}{\pi_{\theta_{\text{old} } }(y_i|x)}\right)^{\frac{1}{|y_i|} } \cdot \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \color{red}{\widehat{A}_{i,t}} \nabla_{\theta} \log \pi_{\theta}(y_{i,t}|x,y_{i,<t})\right]. \tag{15-17}
  \end{align}
  $$
  - GSPO-token 与原始 GSPO 的主要区别在于：
    - GSPO 的目标函数中使用的优势函数是 Sequence-level 的 $\widehat{A}_{i}$
    - GSPO-token 的目标函数中使用的优势函数是 Token-level 的 $\color{red}{\widehat{A}_{i,t}}$，这允许同一个序列中，不同的 Token 使用不同的值
当 Response $y_i$ 中所有 token 的优势设置为相同值（即 $\widehat{A}_{i,t} = \widehat{A}_i$）时，GSPO-token 和 GSPO 在优化目标、剪裁条件和理论梯度上是数值相同的

OPSD（On-Policy Self-Distillation）

原始论文：(OPSD)Self-Distilled Reasoner: On-Policy Self-Distillation for Large Language Models, 20260126 - 20260305, UCLA & Meta
OPSD 损失函数定义如下：
$$
\mathcal{L}_{\mathrm{OPSD} }(\theta) = \mathbb{E}_{(x,y^*)\sim \mathcal{S} } \mathbb{E}_{\hat{y} \sim p_S(\cdot | x)} \left[ \frac{1}{|\hat{y}|} \sum_{n=1}^{|\hat{y}|} D\big(p_T | p_S\big) \right]
$$
- 用 hint 增强的 Prompt 得到教师模型

TOPR

原始论文：(TOPR)Tapered Off-Policy REINFORCE: Stable and efficient reinforcement learning for LLMs, 20250319, Mila & Reliant AI
TOPR (Tapered Off-Policy REINFORCE) 本质更像是对 SFT 的改进（在奖励为固定二值（+1 或 -1）的情况下，本质更像是是一个带负向惩罚的 SFT）
TOPR 的核心思想是对正负样本采用非对称的梯度更新策略
TOPR 关键梯度更新公式如下：
$$
\nabla J_{\text{TOPR} }(\pi) = \sum_{\tau :R(\tau)\geq 0}\mu (\tau)R(\tau)\nabla \log \pi (\tau) + \sum_{\tau :R(\tau)< 0}\mu (\tau)\left[\frac{\pi(\tau)}{\mu(\tau)}\right]_0^1 R(\tau)\nabla \log \pi (\tau)
\tag{1}
$$
- $\pi$：当前正在训练的目标策略（Policy，即 LLM）
- $\mu$：生成训练数据的参考策略或行为策略（Reference Policy）
- $\tau$：一个轨迹（Trajectory），即 LLM 针对一个 Prompt 生成的完整 Response
- $R(\tau)$：轨迹 $\tau$ 获得的奖励（Reward），文中为二元奖励（正确为 +1，错误为 -1）
- $\left[\frac{\pi(\tau)}{\mu(\tau)}\right]_0^1$：是 clipping function ，将重要性权重 $\frac{\pi(\tau)}{\mu(\tau)}$ 截断在 0 到 1 之间
- $\nabla \log \pi (\tau)$：策略 $\pi$ 的 Score Function 梯度

TOPR 算法流程详细解析

TOPR 的算法流程（如论文 Algorithm 1 所示）非常简洁，易于实现：
输入：
- 当前语言模型策略 $\pi$
- 参考策略 $\mu$（通常是采样数据集时使用的模型）
- 一组 Prompts $x_1, \dots, x_m$
步骤：
- 1）数据采样 (Rollout) ：
  - 对于每个 Prompt $x_i$，从参考策略 $\mu$ 中采样 $n$ 个 Responses：$y_i^1, \dots, y_i^n \sim \mu(\cdot | x_i)$
  - 构建离线数据集 $\mathcal{D} = \{x_i, y_i^j\}$
- 2）计算损失并进行梯度更新 ：
  - 遍历数据集 $\mathcal{D}$ 中的每一个数据点 $(x, y)$
  - 计算重要性权重比值 $\frac{\pi(y|x)}{\mu(y|x)}$
  - 关键步骤：非对称梯度计算
    - 如果轨迹是正样本（$R(x,y) \ge 0$） ：
      - 设定系数 $\alpha = 1$
      - 这意味着梯度更新不依赖于重要性权重，直接使用原始的奖励 $R(x,y)$ 乘以 $\nabla \log \pi(y|x)$
      - 这等同于监督微调（SFT）的梯度 ，目的是快速提升正样本的概率，即使当前策略 $\pi$ 生成该正样本的概率很低
    - 如果轨迹是负样本（$R(x,y) < 0$） ：
      - 设定系数 $\alpha = \left[\frac{\pi(y|x)}{\mu(y|x)}\right]_0^1$，即截断后的重要性权重
      - 计算损失项 $\ell = \text{STOP_GRAD}(\alpha) \times R(x,y) \times \log \pi(y|x)$
      - STOP_GRAD 操作意味着在反向传播时，$\alpha$ 被视为常数，不计算其梯度。这确保了该损失项只影响 $\log \pi(y|x)$ 的梯度，而不会通过重要性权重影响 $\mu$
  - 对所有数据点的损失 $\ell$ 求和，执行一次梯度下降步骤，更新策略 $\pi$ 的参数
理解：
- 正样本 ：采用 SFT 式的更新，保证模型能快速学习到好的行为
- 负样本 ：采用截断重要性采样的更新
  - 当 $\pi$ 生成该负样本的概率 $\pi(\tau)$ 小于等于 $\mu(\tau)$ 时，重要性权重 $\in [0, 1]$，梯度会按比例降低该负样本的概率
  - 当 $\pi(\tau) > \mu(\tau)$ 时，重要性权重被截断为 1，此时负样本的梯度与 Naive REINFORCE 相同，防止模型过度惩罚那些已经比参考模型更可能生成的负样本，从而避免梯度爆炸

SRPO

原始论文；SRPO: A Cross-Domain Implementation of Large-Scale Reinforcement Learning on LLM, 20250422, Kuaishou Kwaipilot Team
核心创新1：两阶段训练范式：
- 阶段 1：推理能力激发（Eliciting Reasoning Abilities）
  - 数据：仅使用高难度数学数据
  - 目标：促使模型发展长 CoT 能力，包括：
    - 反思性停顿（Reflective Pauses）
    - 回溯行为（Backtracking）
    - 逐步分解（Step-by-Step Decomposition）
- 阶段 2：技能集成（Skill Integration）
  - 数据：引入代码数据，与数学数据混合
  - 目标：在已建立的推理基础上
    - 提升代码生成能力
    - 激发程序化思维（Procedural Thinking）
    - 激发递归和工具调用能力
核心创新2：History Resampling（HR），历史重采样
- 每个 Epoch 结束后，记录该 Epoch 内所有样本的 Rollout Reward 结果，按以下规则重建下一 Epoch 的数据集：
  - 过滤 “太简单” 样本：若某样本的所有 Rollout 都正确，则从数据集中移除
    - 因为这类样本无法提供对比信号（Contrastive Signal），Advantage 为零
- 保留 “信息性” 样本：
  - 混合结果样本：既有正确也有错误的 Rollout → 产生正方差，Advantage 非零
  - 全错误样本：所有 Rollout 都错误 → 保留，因为随着策略更新，这些困难样本可能变得可解，从而在后续 Epoch 中产生有效梯度
- 理解：本质是一种课程学习

OPO

原始论文：(OPO)On-Policy RL with Optimal Reward Baseline, 20250604, Microsoft Research
本质是 Sequence-level Reward + Advantage 的建模方式，依然是 Critic-free 的
核心方法
- 第一：使用 Pure On-policy 更新
- 第二：使用最优 Reward Baseline 来作为价值估计 V 的角色计算 Advantage
  - 为了在保持梯度期望不变的同时最小化方差，理论上存在一个最优基线 $ b^* $，其原始形式为：
    $$
    b^* = \frac{\mathbb{E}_{y \sim \pi_{\theta}(\cdot | x)} \left[ \left( \nabla_{\theta} \log \pi_{\theta}(y|x) \right)^2 \cdot r(x, y) \right]}{\mathbb{E}_{y \sim \pi_{\theta}(\cdot | x)} \left[ \left( \nabla_{\theta} \log \pi_{\theta}(y|x) \right)^2 \right]}
    $$
  - 但该公式在 LLM 中不实用，因为每个 Response 的梯度范数计算代价极高
    - 简化假设与推导 ：对于自回归序列生成任务，假设各 Token 的梯度近似正交且分布相同，则整个 Response 的梯度平方范数与序列长度 $ l_y $ 成正比：$|\nabla_{\theta} \log \pi_{\theta}(y|x)|^2 \propto l_y$
    - 简化后的最优基线 ：代入上式，化简为 长度加权平均奖励 ：
      $$
      b^*(x) = \frac{\mathbb{E}_{y \sim \pi_{\theta}(\cdot | x)} \left[ l_y \cdot r(x, y) \right]}{\mathbb{E}_{y \sim \pi_{\theta}(\cdot | x)} \left[ l_y \right]}
      $$
    - 实际实现 ：对于每个 Prompt $ x $，采样 $ K $ 个 Responses $ \{y_i\}_{i=1}^K $，优势计算为：
      $$
      A_i = r(x, y_i) - b^*(x), \quad \text{其中} \quad b^*(x) = \frac{\sum_{i=1}^K l_{y_i} \cdot r(x, y_i)}{\sum_{i=1}^K l_{y_i} }
      $$
- OPO 的最终目标函数退化为一个简洁的梯度形式（无 Clip、无 KL、无 Entropy）：
  $$
  \mathcal{J}_{\text{OPO} }(\theta) = \mathbb{E}_{x \sim \mathcal{D}, \{y_i\}_{i=1}^K \sim \pi_{\theta}(\cdot|x)} \left[ \frac{1}{K} \sum_{i=1}^K \log \pi_{\theta}(y_i | x) \cdot A_i \right]
  $$
- 该基线使得长 Response 的奖励贡献被适当放大（因为长序列梯度方差更大），从而在理论上达到最小梯度方差，且计算极其轻量

EMPO

(EMPO)Right Question is Already Half the Answer: Fully Unsupervised LLM Reasoning Incentivization, NeurIPS 2025, TJU & SJTU & Tencent AI Lab
Entropy-Minimized Policy Optimization (EMPO) 是一种完全无监督 的 LLM RL 方法
- 不依赖任何外部监督(不要奖励系统)，仅通过最小化模型在无标注问题上的 语义熵（Semantic Entropy） 来提升模型的推理能力
- 在数学推理和自由形式的问答任务上均取得了与监督方法相当的性能
设计思路
- 1）语义熵作为内在奖励信号 ：
  - 发现：LLM 输出的语义熵与模型准确率存在强烈的负相关关系
    - 语义熵衡量的是模型输出在语义空间中的不确定性（即输出是否指向同一含义）
    - 低语义熵意味着模型的多次生成结果在语义上高度一致，这通常预示着更高的正确率
- 2）完全无监督的 RL 优化 ：EMPO 利用上述发现，将最小化语义熵作为优化目标，通过RL算法直接优化模型参数，使其在生成时更倾向于产生语义上连贯、一致的输出，而无需任何外部验证
- 3）缓解 Reward Hacking ：为防止模型通过输出高置信度但错误的单一语义簇来“作弊”，EMPO 引入了熵阈值过滤（Entropy Thresholding） 策略
  - 只对具有中等水平语义熵的问题进行优化，过滤掉模型极度不确定（熵过高）或已经非常确定（熵过低）的样本，从而稳定训练过程

EMPO 详细方法流程

1）采样：对于给定的无标注问题 $ q $，策略模型 $ \pi_\theta $ 生成一组 $ G $ 个 Response：
$$ \{o_1, \dots, o_G\} \sim \pi_\theta(O|q) $$
2）语义聚类（Semantic Clustering） ：将生成的 $ G $ 个 Response 按其含义进行聚类，得到 $ M $ 个语义簇 $ \{c_1, \dots, c_M\} $。若两个 Response 在语义上等价（如数学上答案相同，或自然语言中表述同一意思），则归入同一簇
3）计算语义熵与簇概率 ：
- 每个语义簇 $ c_j $ 的概率近似为其包含的样本数占总样本数的比例：
  $$ p(c_j|q) \approx |c_j| / G $$
- 整个生成的语义熵为：
  $$ H = -\sum_{c_j \in \{c\} } p(c_j|q) \log p(c_j|q) $$
4）计算Reward与Advantage ：
- 对于生成的每个 Response $ o_i $，其Reward $ r_i $ 被定义为它所属语义簇的概率（而非外部正确性标签）：
  $$ r_i = p(c_j|q), \text{ where } l(o_i) = c_j $$
- 使用组内归一化计算每个Response的Advantage $ A_i $，鼓励属于高概率语义簇的Response，抑制属于低概率簇的Response：
  $$ A_i = \frac{r_i - \text{mean}(\{r_1, \dots, r_G\})}{\text{std}(\{r_1, \dots, r_G\})} $$
5）策略优化 ：最大化裁剪过的Advantage期望，并使用熵阈值 $ \delta_{low}, \delta_{high} $ 过滤掉不合适的训练样本，避免Reward Hacking和过度自信
$$ \mathcal{J}_{\text{EMPO} } = \mathbb{E}_{[q \sim P(Q), \{o_i\}_{i=1}^G \sim \pi_\theta(O|q)]} \left[ \frac{1}{G} \sum_{i=1}^G \left( \min(A_i, \text{clip}(1, 1-\epsilon, 1+\epsilon) A_i) \right) \right], \text{ s.t. } \delta_{low} < H < \delta_{high} $$

GRPO-LEAD

GRPO-LEAD: A Difficulty-Aware Reinforcement Learning Approach for Concise Mathematical Reasoning in Language Models, Johns Hopkins University, 2025
背景：GRPO 被广泛用于 R1 类推理模型，但其存在三个主要缺陷：
- 1）奖励稀疏 ：基于正确/错误的二元奖励信号缺乏区分度，导致学习信号弱
- 2）冗余输出 ：模型倾向于生成过长的 CoT 以提高正确率，导致推理效率低
- 3）忽视问题难度 ：奖励统一应用于所有问题，模型过度优化简单任务，忽视难题

GRPO-LEAD 核心方法

GRPO-LEAD 在 GRPO 基础上引入三项关键改进：

长度正则化奖励（Length-Dependent Accuracy Reward）

思路：对正确回答按其相对简洁度进行奖励，而不是统一奖励，目标是鼓励模型生成更紧凑的推理过程
对每个问题 $q$，采样一组 Response $\{o_i\}$
选出其中正确的 Response，计算其 Token 长度的均值 $\mu$ 和标准差 $\sigma$
对每个正确 Response $o$，计算标准化长度偏差：
$$
z = \frac{|o| - \mu}{\sigma + \epsilon}
$$
奖励函数为：
$$
R_{\text{accuracy} }(o|q) =
\begin{cases}
\exp(-\alpha z), & \text{if } o \text{ is correct} \\
0, & \text{if } o \text{ is incorrect}
\end{cases}
$$
```
* \$\alpha > 0\$ 控制长度惩罚强度
```

显式错误惩罚（Explicit Penalty for Incorrect Answers）

思路：原有方法中错误回答得 0 分，模型可能“猜测”答案以求获得非零奖励，损害精度，引入负奖励以建立更严格的决策边界
奖励函数 改为：
$$
R_{\text{accuracy} }(o|q) =
\begin{cases}
\exp(-\alpha z), & \text{if } o \text{ is correct} \\
-1, & \text{if } o \text{ is incorrect}
\end{cases}
$$
若正确回答的长度惩罚忽略不计，则期望奖励近似为：
$$
\mathbb{E}[R] \approx 2P(\text{correct}) - 1
$$
只有当正确概率 $P(\text{correct}) > 0.5$ 时，期望奖励才为正。这有效抑制了盲目猜测

难度感知优势重加权（Difficulty-Aware Advantage Reweighting）

思路：不同难度的问题应获得不同的更新幅度，难题的正确回答应获得更大更新，简单问题的错误回答应受到更强惩罚
- 效果：对难题的正确回答放大更新，对简单问题的错误回答加重惩罚，使模型更关注困难样本
对每个问题 $q$，计算其正确率：
$$
\rho_q = \frac{\text{number of correct responses for } q}{\text{total number of responses for } q}
$$
该值越低，表示问题越难
定义 Logistic 重加权因子：
$$
w(\rho_q) = A + \frac{B - A}{1 + \exp(k(\rho_q - \rho_0))}
$$
其中 $A, B, \rho_0, k$ 为超参数，控制权重对难度的敏感度
计算每个 Response 的标准优势估计：
$$
\tilde{A}_i = \frac{R(o_i|q) - \mu_q}{\sigma_q + \epsilon}
$$
最终难度感知优势为：
$$
A’_i = \tilde{A}_i \cdot
\begin{cases}
w(\rho_q), & \text{if } \tilde{A}_i > 0 \\
w(1 - \rho_q), & \text{if } \tilde{A}_i \leq 0
\end{cases}
$$

CPPO

CPPO: Accelerating the Training of Group Relative Policy Optimization-Based Reasoning Models, NeurIPS 2025, XMU
Completion Pruning Policy Optimization（CPPO）的核心方法是 Completion Pruning
- 设定剪枝率 $P \in (0, 1]$，计算保留数量：
  $$
  k = \lfloor G \times (1 - P) \rfloor
  $$
- 对每个 question 的 $G$ 个 completions 按 $|A_i|$ 从大到小排序
- 仅保留 top-$k$ 个高绝对 advantage 的 completions，其余全部丢弃
CPPO 目标函数
$$
\mathcal{J}_{CPPO}(\theta) = \mathbb{E}_{q \sim P(Q), \{o_i\}_{i=1}^G \sim \pi_{\theta_{old} } } \left\{ \frac{1}{k} \sum_{i \in \mathcal{I} } \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \left[ \min\left( \frac{\pi_{\theta} }{\pi_{\theta_{old} } } A_i,; \text{clip}\left(\frac{\pi_{\theta} }{\pi_{\theta_{old} } }, 1-\epsilon, 1+\epsilon\right) A_i \right) - \beta \mathbb{D}_{KL}[\pi_{\theta} | \pi_{ref}] \right] \right\}
$$
- $\mathcal{I}$：top-$k$ 高绝对 advantage 的 completion 索引集合
- $\epsilon$：PPO 裁剪超参数（设为 0.2）
- $\beta$：KL 散度系数（设为 0.04）
- $\pi_{ref}$：Reference 模型（通常为 RL 初始模型）
- $\mathbb{D}_{KL}$：KL 散度约束，用于稳定训练

S-GRPO

S-GRPO: Early Exit via Reinforcement Learning in Reasoning Models, 2025, Huawei
目标：解决 “过度思考”（Overthinking） 的问题
S-GRPO 的核心设计思路：
- 将传统 GRPO 的并行采样思路，转变为在一条完整推理路径上的串行采样 ，并通过奖励衰减策略来引导模型学习何时可以提前终止思考

S-GRPO 方法

阶段一：串行组生成（Serial-Group Generation）

通过一个两步 Rollout 过程，为每个问题构建一个包含不同“思考深度”的串行组（Serial Group）
- 1）完整思维 Rollout（Full Thought Rollout） ：
  - 模型对一个 $q$，生成一条完整的推理路径
    $$ O^0 = \{T_1, T_2, \ldots, T_n, \text{}, C_0\} $$
    - $T_i$ 是思考过程中的一个 Token，$C_0$ 是基于完整思考生成的最终答案
- 2）提前退出思维 Rollout（Early-exit Thought Rollout） ：
  - 从第一步生成的完整路径中，随机挑选 $m$ 个不同的位置 $P_i$（$P_i = T_i, i \sim \text{Uniform}(1, n)$）
    - 随机采样的目的是让模型适应各种长度，防止过拟合
  - 构建 $m$ 个提前退出的推理路径 $\{CoT^1, CoT^2, \dots, CoT^m\}$
    - 其中，每个 $CoT^i$ 都是从原始路径开头截断到 $P_i$ 位置的子串 $O^0[:P_i]$，并在截断处拼接一个特殊 Prompt：
      
      “Time is limited, stop thinking and start answering.\n\n\n”
  - 最后让模型基于每个截断的思维路径 $CoT^i$，分别生成对应的答案 $C_i$
最终得到一个“串行组”（Serial Group），它包含一个完整推理路径和多个截断推理路径，以及它们各自产生的答案
$$\{C_1, C_2, \ldots, C_m, C_0\}$$

阶段二：衰减奖励策略（Decaying Reward Strategy）

目标:在保证答案正确的前提下，奖励那些“更早”做出正确决策的路径。奖励值 $r^i$ 的计算方式如下：
$$
r^i = \begin{cases}
\frac{1}{2^{N_{\text{right} } - 1} }, & \text{if } C^i \text{ is correct},\
0, & \text{if } C^i \text{ is incorrect}.
\end{cases}
$$
- 正确性优先 ：如果答案 $C^i$ 是错误的，直接给 0 分，确保模型不会为了缩短长度而牺牲正确率
- 指数衰减 ：$N_{\text{right} }$ 表示从第一个截断位置开始，到当前为止，累计正确回答的数量
  - 如果一个路径是第一个正确的，$N_{\text{right} }=1$，它的奖励就是 $1/2^{0}=1$（最高）
  - 第二个正确的路径，$N_{\text{right} }=2$，奖励变为 $1/2^{1}=0.5$
  - 第三个正确的奖励为 0.25，以此类推
  - 这个指数衰减机制会强烈地驱使模型在序列中尽可能地早地给出正确答案

阶段三：优势计算与参数更新（Advantage Computation and Parameter Update）

优势函数 ：计算每个 Response 的奖励与组内平均奖励的差值
$$
\hat{A}_i = r_i - \text{mean}(r_i)
$$
- 这里去掉了 GRPO 中除以标准差的步骤，以保证训练稳定性
- 每个 Token 的 Advantage $\hat{A}_{i,t}$ 都等于其所在序列的 $\hat{A}_i$
优化目标 ：S-GRPO 使用类似 PPO 的 Clipped Surrogate Objective 来进行参数更新，确保训练稳定
$$
\mathcal{J}_{\text{S-GRPO} }(\theta) = \mathbb{E}_{[q\sim P(Q),\{o_i\}_{i=1}^G\sim \pi_{\theta_{\text{old} } }(O|q)]} \left[ \frac{1}{G} \sum_{i=1}^{G} \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \min \left( \frac{\pi_{\theta}^{i,t} }{\pi_{\theta_{\text{old} } }^{i,t} } \hat{A}_{i,t}, \text{clip}\left(\frac{\pi_{\theta}^{i,t} }{\pi_{\theta_{\text{old} } }^{i,t} }, 1-\epsilon, 1+\epsilon\right) \hat{A}_{i,t} \right) \right]
$$
- $\frac{\pi_{\theta}^{i,t} }{\pi_{\theta_{\text{old} } }^{i,t} }$ 是新旧策略在 Token $t$ 上的概率比，$\epsilon$ 是裁剪超参数

Ada-GRPO

(Ada-GRPO)ARM: Adaptive Reasoning Model, NeurIPS 2025, Shanghai AI Lab
Ada-GRPO 的目标是通过 Reward Reshaping 来解决格式问题
核心思路：
- 设计一个前期关注格式+正确性，后期只关注正确性的奖励

GRPO-lambda，GRPO-$\lambda$，GRPO-λ

作者观点：Reasoning 模型在不同能力阶段需要不同的优化目标：
- 当推理能力尚不足时，应优先保证 准确率 ，即 Accuracy Priority
- 当模型已具备足够的正确推理能力时，才应引入长度惩罚以优化 推理效率 ，即 Efficiency Priority

GRPO-λ 方法细节

Query-Sampled Group 生成

对 Batch 中的每一个训练 Query $ Q_k $，模型生成 $ m $ 个候选 Response：
$$
\{O_k^1, O_k^2, \ldots, O_k^m\}
$$
- 每个 Response $ O_k^i $ 关联两个属性：
  - 长度 $ L_k^i $：Response 的 Token 数量
  - 结果奖励 $ r_k^i \in \{0, 1\} $：该 Response 是否正确

Batch-Wise Top-λ 选择

对 Batch 内每个 Query 对应的 Group，计算其 正确率 ：
$$
\text{CR}_k = \frac{\text{正确 Response 数量} }{m}
$$
- 将所有 Group 按照正确率从高到低排序
  - 选择 Top-λ 比例（如 $ \lambda = 20% $）的 Group 作为 效率优先优化组
    - 因为这些 Group 已表现出足够的推理能力，可以安全地施加长度惩罚
  - 其余 Group 则保留为 准确率优先优化组 ，继续使用 0/1 结果奖励，以巩固推理能力

动态 Reward 策略调整

(1) 效率优先优化（施加 Length Penalty）

对于 Top-λ 的 Group，Reward 定义为：
$$
r_k^i =
\begin{cases}
1 - \alpha \cdot \sigma \left( \dfrac{L_k^i - \text{mean}(L_k)_{\text{correct} } }{\text{std}(L_k)_{\text{correct} } } \right) & \text{若 } O_k^i \text{ 正确} \\
0 & \text{若 } O_k^i \text{ 错误}
\end{cases}
$$
- $ \alpha $：长度惩罚系数（论文中设为 0.2），控制惩罚强度
- $ \text{mean}(L_k)_{\text{correct} } $：该 Group 内所有正确 Response 的 Token 长度均值
- $ \text{std}(L_k)_{\text{correct} } $：该 Group 内所有正确 Response 的 Token 长度标准差
- $ \sigma(\cdot) $：Sigmoid 函数，用于将归一化后的长度映射到 (0, 1) 区间
该设计使得：
- 正确且更短 的 Response 获得更高 Reward，正确但更长的 Response 获得较低 Reward
- 错误 Response 统一为 0

(2) 准确率优先优化（0/1 结果奖励）

对于剩余 Group，Reward 采用标准 GRPO 的 0/1 结果奖励：
$$
r_k^i =
\begin{cases}
1 & \text{若 } O_k^i \text{ 正确} \\
0 & \text{若 } O_k^i \text{ 错误}
\end{cases}
$$
该策略确保推理能力尚未成熟的 Group 不受长度惩罚干扰，继续专注于提升正确率

Advantage 计算与参数更新

获得每个 Response 的 Reward $ r_i $ 后，GRPO-λ 沿用 GRPO 的方式，在 Group 内计算 Advantage：
$$
\hat{A}_i = \frac{r_i - \text{mean}(r)}{\text{std}(r)}
$$
- mean($ r $) 和 std($ r $) 分别是该 Group 内所有 Reward 的均值和标准差
将 Advantage 广播到对应 Response 的每个 Token，并用于 Policy 的参数更新（如采用 PPO 风格的 Loss）

PODS

(PODS)Not All Rollouts are Useful: Down-Sampling Rollouts in LLM Reinforcement Learning, 20260422, CMU
PODS 基于一个关键观察：并非所有 Rollout 都对模型改进有同等贡献
- 当 Rollout 数量超过一定规模后，额外的 Rollout 提供的信息增益递减，甚至可能因冗余信息而稀释有效的学习信号
PODS 的策略是：
- 在推理阶段生成大量 Rollout（充分利用推理的并行能力）
- 在策略更新阶段，仅选择其中 $ m $ 个最具信息量的 Rollout 进行训练（$ m < n $，其中 $ n $ 为生成的 Rollout 总数）
这样既最大化了推理硬件的利用率，又避免了策略更新阶段因批量过大而引入的内存和通信开销，同时还可能通过去除冗余信息提供更清晰的学习信号

RePO

RePO: Replay-Enhanced Policy Optimization, CUHK, 20250611
GRPO 存在两个主要缺陷：
- 计算开销大 ：每个训练步需要为每个 Prompt 生成多个 On‑Policy 样本，且每次更新后这些样本即被丢弃，无法复用
- 优化信号可能消失 ：当同一 Prompt 下的所有样本获得的 Reward 相同时（例如全对或全错），Advantage 均为零，梯度信号消失，导致该步无效更新
RePO 的核心思想是：
- 将先前采样过的 Off‑Policy 输出存入 Replay Buffer，并在后续更新中重新利用这些样本，与当前的 On‑Policy 样本共同参与优化，从而扩大每个 Prompt 可用的样本集，提高有效优化步数，并缓解过拟合

RePO 目标函数

RePO 的目标函数由两项相加组成：
$$
\mathcal{J}_{\text{RePO} }(\theta; S) =
\underbrace{\mathcal{J}_{\text{on-policy} }(\theta)}_{\text{当前样本} } +
\underbrace{\mathcal{J}_{\text{off-policy} }(\theta; S)}_{\text{回放样本} }
$$
- 其中 $S$ 表示从 Replay Buffer 中检索 Off‑Policy 样本的策略（Replay Strategy）
On‑Policy 更新项：On‑Policy 部分与 GRPO 基本一致，但不使用 KL 惩罚项（遵循近期工作）：
$$
\mathcal{J}_{\text{on-policy} }(\theta) =
\mathbb{E}_{q \sim P(Q), \{o_i^{\text{on} }\}_{i=1}^{G^{\text{on} } } \sim \pi_{\theta_{\text{old} } }(O|q)}
\frac{1}{G^{\text{on} } } \sum_{i=1}^{G^{\text{on} } } \frac{1}{|o_i^{\text{on} }|} \sum_{t=1}^{|o_i^{\text{on} }|}
\min\left[
r_{i,t}^{\text{on} } A_{i,t}^{\text{on} },;
\operatorname{clip}(r_{i,t}^{\text{on} }, 1-\epsilon, 1+\epsilon) A_{i,t}^{\text{on} }
\right]
$$
- $q$ 为 Prompt，$o_i^{\text{on} }$ 为当前策略 $\pi_{\theta_{\text{old} } }$ 采样得到的第 $i$ 个输出序列
- $G^{\text{on} }$ 为 On‑Policy 样本数
- $|o_i^{\text{on} }|$ 为输出序列长度
- $r_{i,t}^{\text{on} } = \dfrac{\pi_{\theta}(o_{i,t}^{\text{on} } \mid q, o_{i,< t}^{\text{on} })}{\pi_{\theta_{\text{old} } }(o_{i,t}^{\text{on} } \mid q, o_{i, < t}^{\text{on} })}$ 为当前策略与旧策略的概率比值（Importance Sampling Ratio）
- $\epsilon$ 为裁剪超参数，限制策略更新幅度
- $A_{i,t}^{\text{on} }$ 为第 $i$ 个输出第 $t$ 个 Token 的 Advantage 估计
Off‑Policy 更新项：Off‑Policy 部分使用从 Replay Buffer $\mathcal{B}$ 中检索到的历史样本：
$$
\mathcal{J}_{\text{off-policy} }(\theta; S) =
\mathbb{E}_{q \sim P(Q),
\{o_i^{\text{off} }, \pi_{\theta_{\text{off} } }(o_i^{\text{off} }|q)\}_{i=1}^{G^{\text{off} } } \sim \mathcal{B}(q,S)}
\frac{1}{G^{\text{off} } } \sum_{i=1}^{G^{\text{off} } } \frac{1}{|o_i^{\text{off} }|} \sum_{t=1}^{|o_i^{\text{off} }|}
\min\left[
r_{i,t}^{\text{off} } A_{i,t}^{\text{off} },;
\operatorname{clip}(r_{i,t}^{\text{off} }, 1-\epsilon, 1+\epsilon) A_{i,t}^{\text{off} }
\right]
$$
- $o_i^{\text{off} }$ 为之前某次迭代中生成的输出，$\pi_{\theta_{\text{off} } }(o_i^{\text{off} }|q)$ 为生成该输出时的策略（Behavior Policy）赋予的生成概率
- $\mathcal{B}(q,S)$ 表示根据策略 $S$ 从 Buffer 中为 Prompt $q$ 检索一组历史样本
- $r_{i,t}^{\text{off} } = \dfrac{\pi_{\theta}(o_{i,t}^{\text{off} } \mid q, o_{i,< t}^{\text{off} })}{\pi_{\theta_{\text{off} } }(o_{i,t}^{\text{off} } \mid q, o_{i,< t}^{\text{off} })}$，注意分母是生成该样本时的旧策略概率，而非当前旧策略
- $G^{\text{off} }$ 为 Off‑Policy 样本数
- $A_{i,t}^{\text{off} }$ 为 Off‑Policy 样本的 Advantage
RePO 采用 Split 策略，即 On‑Policy 和 Off‑Policy 样本各自独立计算 Advantage：
$$
A_{i}^{\text{on} } = \frac{R(o_i^{\text{on} }) - \text{mean}(\mathcal{G}^{\text{on} })}{\text{std}(\mathcal{G}^{\text{on} })}, \qquad
A_{i}^{\text{off} } = \frac{R(o_i^{\text{off} }) - \text{mean}(\mathcal{G}^{\text{off} })}{\text{std}(\mathcal{G}^{\text{off} })}
$$
Replay Strategy（回放策略）
提出了四种可选的检索策略 $S$，用于从 Replay Buffer 中挑选 Off‑Policy 样本：
- Full‑scope ：检索该 Prompt 下所有历史样本，数据量最大但可能引入过时干扰
- Recency‑based ：检索最近的 $K$ 个样本，与当前策略分布更接近
- Reward‑oriented ：优先选择历史中 Reward 最高的样本，强化良好行为
- Variance‑driven ：选择 Reward 方差最大的样本，以应对当前 Reward 区分度低导致梯度微弱的问题
实验结论：
- 对 Base 模型（如 Qwen2.5‑Math‑1.5B/7B）采用 Recency‑based，对 Instruct 模型（如 Qwen2.5‑Math‑1.5B‑Instruct/7B‑Instruct 和 Qwen3‑1.7B）采用 Reward‑oriented，效果最佳

INTUITER

(INTUITER)Learning to Reason without External Rewards, ICLR 2026, UC Berkeley
INTUITOR 是 Reinforcement Learning from Internal Feedback (RLIF) 范式
RLIF 是指 LLM 仅依赖自身生成的内在信号（intrinsic signals）来提升推理能力，完全不依赖外部监督或标注数据 的 RL 方法
INTUITOR 的核心思想是：使用模型自身的“自我确定性”（Self-Certainty）作为唯一的奖励信号 ，取代传统 RLVR 方法中需要的外部可验证奖励（如数学问题的标准答案或代码的测试用例）
INTUITOR 的优化目标为：
$$
\max_{\pi_{\theta} } \mathbb{E}_{o \sim \pi_{\theta}(q)} \left[ u(q, o) - \beta \cdot \text{KL}[\pi_{\theta}(o|q) | \pi_{\text{ref} }(o|q)] \right]
$$
- $\pi_{\theta}$：当前策略（Policy），即正在训练的 LLM
- $q$：输入查询（Query/Prompt）
- $o$：模型生成的输出（Response）
- $u(q, o)$：内在奖励信号（Intrinsic Reward），在 INTUITOR 中为 Self-Certainty
- $\pi_{\text{ref} }$：参考策略（Reference Policy），通常是初始模型或 SFT 后的模型
- $\beta$：KL 散度惩罚系数，控制当前策略偏离参考策略的程度

Self-Certainty 奖励信号

INTUITOR 采用 Self-Certainty 作为奖励信号 $u(q, o)$，其定义为模型输出分布与均匀分布之间的平均 KL 散度：
$$
\text{Self-Certainty}(o|q) := \frac{1}{|o|} \sum_{i=1}^{|o|} \text{KL}(U \parallel p_{\pi_{\theta} }(\cdot|q, o_{ < i}))
$$
展开为：
$$
\text{Self-Certainty}(o|q) = -\frac{1}{|o| \cdot |\mathcal{V}|} \sum_{i=1}^{|o|} \sum_{j=1}^{|\mathcal{V}|} \log \left( |\mathcal{V}| \cdot p_{\pi_{\theta} }(j|q, o_{ < i}) \right)
$$
- $|o|$：输出序列的长度
- $\mathcal{V}$：词表（Vocabulary）
- $|\mathcal{V}|$：词表大小
- $o_{< i}$：第 $i$ 个 Token 之前已生成的所有 Token
- $p_{\pi_{\theta} }(j|q, o_{< i})$：模型在给定上下文下预测第 $j$ 个 Token 的概率
- $U$：词表上的均匀分布
Self-Certainty 的物理含义 ：
- 数值越高，表示模型的输出分布越“尖锐”（即更集中在少数 Token 上），代表模型对自己的输出越有信心
Self-Certainty 与熵的关键区别 ：
- 熵是 $\text{KL}(p | U)$，即模型分布到均匀分布的 KL 散度
- Self-Certainty 是 $\text{KL}(U | p)$，即均匀分布到模型分布的 KL 散度
- Self-Certainty 对序列长度不敏感，更不容易受到“生成长度偏置”（length bias）的影响

熵的定义

SFT 的 Loss

RM 的 Loss

PPO

CPPO（Continual Proximal Policy Optimization）

REINFORCE

REINFORCE++

ReMax

GRPO（Group Relative Policy Optimization）

RLOO（REINFORCE Leave-One-Out）

DPO（Direct Preference Optimization）

RAFT（Reward rAnked FineTuning）

RAHF（Representation Alignment from Human Feedback）

步骤一：指导LLM理解人类偏好

步骤二：收集模型 Activity Pattern

步骤三：构建最终对齐模型

SimpleRL

SEED-GRPO（Semantic Entropy EnhanceD GRPO）

SEED-GRPO 梯度分析

附录：语义熵（Semantic Entropy）的定义

DAPO

VAPO（Value-model-based Augmented Proximal Policy Optimization）

VC-PPO（Value-Calibrated PPO）

ORZ（Open-Reasoner-Zero）

GVPO（Group Variance Policy Optimization）

GVPO 的梯度定义为：

GVPO 的三种等价解释

Mean Squared Error（MSE）解释

Variance 解释（名称由来）

RL 解释

GPG（Group Policy Gradient）

ORPO（Odds Ratio Preference Optimization）

ECPO（Early Clipped GRPO）

CISPO（Clipped IS-weight Policy Optimization）

Efficient RL Scaling with CISPO

Background

GPPO（Gradient-Preserving Clipping Policy Optimization）

Reflect-Retry-Reward

DFT（Dynamic Fine-Tuning）

iw-SFT（Importance Weighted Supervised Fine-tuning）

CHORD（Controllable Harmonization of On-and Off-Policy Reinforcement Learning via Dynamic Weighting）

CHORD-\(\mu\)

CHORD-\(\phi\)

BAPO（Balanced Policy Optimization with Adaptive Clipping）

BAPO 目标函数（动态裁剪改进）

动态裁剪边界调整规则

一些关于熵的理论基础讨论

BAPO 训练流程：Algorithm 1

Trianing-free GRPO

SRL（Supervised Reinforcement Learning）

整体流程概述

核心优势

性能表现

AWPO

核心：奖励设计与优势计算

创新1：方差感知门控，Variance-Aware Gating

创新2：Difficulty-Aware Weighting（难度感知加权）

创新3：Dynamic Clipping

Self-Rewarding

DLER

DLER 扩展变体

GSPO（包含 GSPO 和 GSPO-Token 两个版本）

GSPO: Group Sequence Policy Optimization

GSPO-token：A Token-level Objective Variant

OPSD（On-Policy Self-Distillation）

TOPR

TOPR 算法流程详细解析

SRPO

OPO

EMPO

EMPO 详细方法流程

GRPO-LEAD

GRPO-LEAD 核心方法

长度正则化奖励（Length-Dependent Accuracy Reward）

显式错误惩罚（Explicit Penalty for Incorrect Answers）

难度感知优势重加权（Difficulty-Aware Advantage Reweighting）

CPPO

S-GRPO

S-GRPO 方法

阶段一：串行组生成（Serial-Group Generation）