注:本文包含 AI 辅助创作
- 参考链接:
- 原始博客:(TIS)Your Efficient RL Framework Secretly Brings You Off-Policy RL Training, 20250805-20251013
- 博客最早发表于 20250805,目前还在持续更新,最近一次更新为 20251013
- TIS,即 Truncated Importance Sampling
- 原始博客:(TIS)Your Efficient RL Framework Secretly Brings You Off-Policy RL Training, 20250805-20251013
Blog Summary
- 在现代强化学习训练框架(例如 VeRL)中, rollout 生成(例如使用 vLLM)和模型训练(例如使用 FSDP)采用了不同的实现方式
- 博客揭示了这种 实现差距(implementation gap) 如何隐式地将 On-policy 强化学习转变为 Off-policy,并讨论了一种简单而有效的重要性采样技术来处理这种差异
The Mismatch Problem
- 为简单起见,博客以 REINFORCE 算法为例,该算法本应通过以下方式更新策略,即一个由 \(\theta\) 参数化的大语言模型:
$$
\theta \leftarrow \theta + \mu \cdot \mathbb{E}_{\underbrace{a \sim{\pi}(\theta)}_{\color{red}{\text{rollout}}}} [R(a)\cdot \underbrace{\nabla_\theta \log {\pi}(a, \theta)}_{\color{blue}{\text{training}}}].
$$ - 在实践中,rollout 生成成本高昂,现代强化学习框架(例如 VeRL)通常采用高度优化的推理引擎(例如 vLLM, SGLang)来提高吞吐量,同时使用单独的后端(例如 FSDP, Megatron)进行模型训练。这种混合设计使得更新变为:
$$
\theta \leftarrow \theta + \mu \cdot \mathbb{E}_{a \sim \color{red}{\pi_{\text{sampler}}}(\theta)} [R(a)\cdot \nabla_\theta \log \color{blue}{\pi_{\text{learner}}}(a, \theta)].
$$- \(\color{red}{\pi_{\text{sampler} }}\) 代表加载了推理引擎(例如 vLLM, SGLang)的模型
- \(\color{blue}{\pi_{\text{learner} }}\) 代表用训练后端(例如 FSDP, Megatron)实例化的同一模型
- 除非特别说明,博客的实验使用 vLLM 和 FSDP 作为 Sampler 和 Learner 后端
- 可以观察到意外的 rollout-training 不匹配
- 如图 1 所示,尽管 \(\color{blue}{\pi_{\text{fsdp}} }\) 和 \(\color{red}{\pi_{\text{vllm} }}\) 共享相同的模型参数 \(\theta\),它们可以产生 显著不同的 Token 概率
- 对于某些 Token \(a\),它们甚至产生矛盾的预测,例如 \(\color{red}{\pi_{\text{vllm} }}(a, \theta) = 1\) 和 \(\color{blue}{\pi_{\text{fsdp}} }(a, \theta) = 0\)
- 理解:图 1 左图中的最大差异为 1 的地方就是这样
- 这种意外行为隐式地破坏了 On-policy 假设,秘密地使强化学习训练变成了 Off-policy
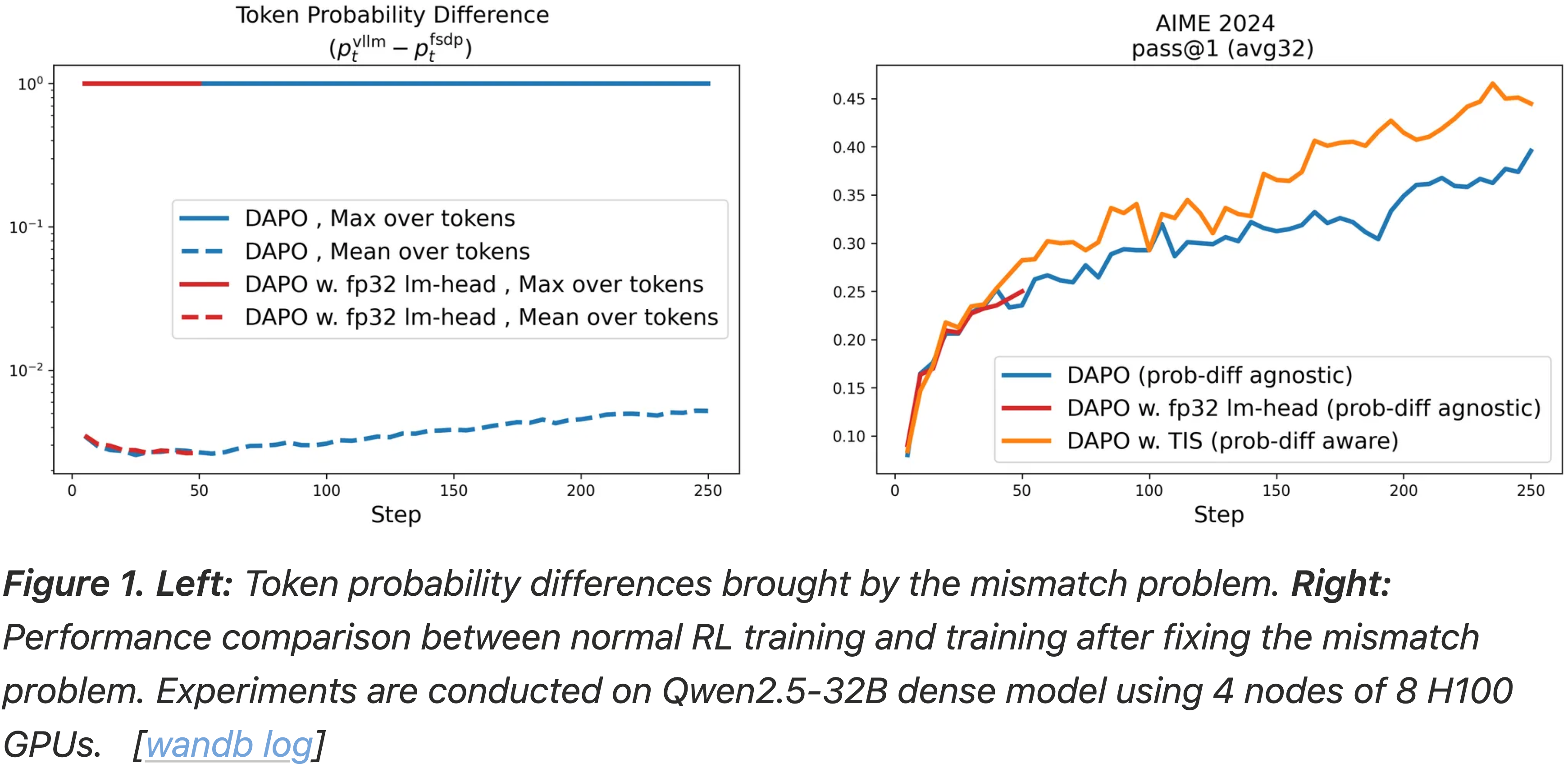
- 图 1:
- 左图:由不匹配问题带来的 Token 概率差异(图中横轴是训练步骤,纵轴是差异的 最大值或平均值等)
- 右图:正常 RL 训练与修复不匹配问题后训练的性能比较
- 实验在 Qwen2.5-32B Dense 模型上进行,使用了 4 个节点,每个节点 8 张 H100 GPU
How to Fix It?
Mitigate the system-level mismatch(缓解系统级不匹配 )
- 更高精度的 vLLM 有帮助吗?博客首先假设 vLLM 是根本原因,因此博客修补了 vLLM 以解决两个常被怀疑导致不匹配问题的因素
- 无法访问的真实采样概率(Inaccessible true sampling probabilities) :vLLM v1 引擎不支持直接返回用于采样的调整后概率,这引入了额外的差距
- 博客的补丁强制 vLLM 返回用于采样的实际概率 [非流式]
- 后端数值差异(Backend numerical differences) :vLLM 的 im_head 精度与 HuggingFace transformers 不匹配,这在 MinMax-M1 技术报告中也有提及
- 博客的补丁提供了强制 vLLM 将 im_head 转换为 fp32 的选项
- 无法访问的真实采样概率(Inaccessible true sampling probabilities) :vLLM v1 引擎不支持直接返回用于采样的调整后概率,这引入了额外的差距
- 如图 1 左图所示,在应用了两个补丁之后,不匹配问题仍然存在
Embrace the mismatch — Apply algorithm-level fix(接受不匹配 and 应用算法级修复 )
- 与其在系统层面缓解分布不匹配,博客建议调整模型更新,使其意识到这种不匹配
- 一个简单的方法是通过重要性采样校正
- 具体来说,博客通过添加重要性权重比来处理 \(\color{blue}{\pi_{\text{learner} }}\) 和 \(\color{red}{\pi_{\text{sampler} }}\) 之间的不匹配,即将当前的梯度计算从:
$$
\mathbb{E}_{a \sim \color{red}{\pi_{\text{sampler}}}(\theta)} [R(a)\cdot \nabla_\theta \log \color{blue}{\pi_{\text{learner}}}(a, \theta)],
$$ - 改为:
$$
\mathbb{E}_{a \sim \color{red}{\pi_{\text{sampler}}}(\theta)} \Bigl[\frac{\color{blue}{\pi_{\text{learner}}}(a, \theta)}{\color{red}{\pi_{\text{sampler}}}(a, \theta)} \cdot R(a)\cdot \nabla_\theta \log \color{blue}{\pi_{\text{learner}}}(a, \theta)\Bigr].
$$
- 具体来说,博客通过添加重要性权重比来处理 \(\color{blue}{\pi_{\text{learner} }}\) 和 \(\color{red}{\pi_{\text{sampler} }}\) 之间的不匹配,即将当前的梯度计算从:
- 尽管已有大量研究关于如何设计稳定有效的重要性采样,但在实践中博客发现通常使用一种经典技术就足够了,即截断重要性采样(Truncated Importance Sampling, TIS):
$$
\mathbb{E}_{a \sim \color{red}{\pi_{\text{sampler}}}(\theta)} \Bigl[\underbrace{\min\Bigl(\frac{\color{blue}{\pi_{\text{learner}}}(a, \theta)}{\color{red}{\pi_{\text{sampler}}}(a, \theta)}, C\Bigr)}_{\text{truncated importance ratio}} \cdot R(a) \cdot \nabla_\theta \log \color{blue}{\pi_{\text{learner}}}(a, \theta)\Bigr],
$$- 其中 C 是一个超参数
- 注意:这里仅针对单向进行截断(对上界进行截断),详细讨论见下文
Extension to Other Algorithms
- 将上述分析扩展到其他算法是直接的,因为可以将梯度计算的确切形式从 REINFORCE \( R(a) \cdot \nabla \log \pi (a, \theta) \) 切换到任何形式
- 这里,博客以常用的 PPO 算法为例进行类似的分析
- PPO 的策略梯度 \(\nabla_{\theta} L^\text{CLIP}(\theta)\) 定义为:
$$
\small{ \mathbb{E}_{a\sim\pi_{\theta_{\mathrm{old}}}}
\Bigl[
\nabla_\theta \min\Bigl(
\frac{\pi_\theta(a)}{\pi_{\theta_{\mathrm{old}}}(a)}\hat A,
\mathrm{clip}\bigl(\frac{\pi_\theta(a)}{\pi_{\theta_{\mathrm{old}}}(a)},1-\epsilon,1+\epsilon\bigr)\hat A
\Bigr)
\Bigr]}.
$$ - 为了提高吞吐量,混合强化学习系统采用 vLLM 引擎进行 rollout 生成(从 \(\pi_{\theta_{old} }\) 采样 Token a),同时使用 FSDP 后端既从 \(\pi_{\theta}\) 采样(注:这里应该是表达错误,这里仅仅是在计算概率值,不会真的进行采样了),又为 \(\pi_{\theta_{old} }\) 重新计算 Token 概率以进行梯度计算:
$$
\small{
\mathbb{E}_{a\sim\color{red}{\pi_{\text{sampler}}}(\theta_{\mathrm{old}})}
\Bigl[
\nabla_\theta \min\Bigl(
\frac{\color{blue}{\pi_{\text{learner}}}(a, \theta)}{\color{blue}{\pi_{\text{learner}}}(a, \theta_{\mathrm{old}})}\hat A,
\mathrm{clip}\bigl(\frac{\color{blue}{\pi_{\text{learner}}}(a, \theta)}{\color{blue}{\pi_{\text{learner}}}(a, \theta_{\mathrm{old}})},1-\epsilon,1+\epsilon\bigr)\hat A
\Bigr)
\Bigr]
}.
$$- 注意,对 vLLM 引擎通过 \(\pi_{\theta_{old} }\) rollout 到的样本,还要经过 以 FSDP 为引擎的 \(\color{blue}{\pi_{\text{learner}}}\) 来对 \(\pi_{\theta_{old} }\) 重新计算概率,从而得到 \(\color{blue}{\pi_{\text{learner}}}(a, \theta_{\mathrm{old}})\)
- 与上述分析类似,\(\color{blue}{\pi_{\text{learner} }}\) 和 \(\color{red}{\pi_{\text{sampler} }}\) 之间的差距再次出现,博客使用截断重要性采样来修复它:
$$
\mathbb{E}_{a \sim \color{red}{\pi_{\text{sampler} }}(\theta_{old})} \left[ \underbrace{\min \left( \frac{\color{blue}{\pi_{\text{learner} }}(a, \theta_{old})}{\color{red}{\pi_{\text{sampler} }}(a, \theta_{old})}, C \right)}_{\text{truncated importance ratio}} \cdot \nabla_{\theta} \min \left( \frac{\color{blue}{\pi_{\text{learner} }}(a, \theta)}{\color{blue}{\pi_{\text{learner} }}(a, \theta_{old})} \hat{A}, \text{ clip} \left( \frac{\color{blue}{\pi_{\text{learner} }}(a, \theta)}{\color{blue}{\pi_{\text{learner} }}(a, \theta_{old})}, 1 - \epsilon, 1 + \epsilon \right) \hat{A} \right) \right]
$$- 其中 \(C\) 是一个超参数
Additional Discussion on PG, Sequence, and Token
- 上面的讨论没有涉及状态和行动的具体形式化
- 博客作者之前还讨论了 Token-level 和 Sequence-level 的策略梯度,它们如何相互关联,以及 learner-sampler 不匹配的影响,下面是参考链接:
Connection to Classical Wisdom(智慧)
Importance Sampling
- 当直接蒙特卡洛估计目标分布下的期望值很困难时,重要性采样允许博客从另一个分布中采样
- 在博客的案例中,目标分布是 \(\color{blue}{\pi_{\text{learner} }}\),但从中采样非常慢
- 使用单独的后端(例如 vLLM)进行 rollout 生成意味着博客是从 \(\color{red}{\pi_{\text{sampler} }}\) 中采样
- 然后通过用重要性权重比对每个样本进行加权来校正差异:
$$
\mathbb{E}_{a \sim \color{blue}{\pi_{\text{learner}}}(\theta)} [R(a)]
= \mathbb{E}_{a \sim \color{red}{\pi_{\text{sampler}}}(\theta)} \left[
\underbrace{\frac{\color{blue}{\pi_{\text{learner}}}(a, \theta)}{\color{red}{\pi_{\text{sampler}}}(a, \theta)}}_{\tiny\text{importance ratio}} \cdot R(a)
\right].
$$
Decoupled PPO
- 解耦 PPO 是使用重要性采样来弥合 rollout 生成和梯度计算之间差距的一个特例,它已被诸如 AReaL 之类的异步强化学习框架采用
- AReaL 没有像博客这里讨论的那样实现截断重要性权重比
- 如果重要性权重比超过预定义的阈值,AReaL 会完全丢弃训练样本
Experiments
- 博客进一步进行了实证分析,以阐述分布差距的影响以及所提出的截断重要性采样(TIS)修复的有效性
Does the gap matter a lot?
- 博客使用 Qwen2.5-32B Dense 模型和流行的 DAPO 配方进行实验;数据按照社区指南进行处理,得到的结果如图 1 所示

- 由于资源限制,博客只完成了训练的前 250 步,但意识到差距的修复方法 TIS 已经显著提升了性能
- 由于这两个运行之间唯一的区别是引入的项,即 \(\min \left( \frac{\color{blue}{\pi_{\text{learner} }}(a, \theta_{old})}{\color{red}{\pi_{\text{sampler} }}(a, \theta_{old})}, C \right)\),这一改进展示了分布差距的潜在影响
How well can TIS fix it?(TIS 能修复多少?)
- 博客设计了一个受控实验来衡量 TIS 修复问题的效果
- 按照 verl 教程中的 GSM8K 示例进行 RL 训练,并使用两种不同的设置:
- 1)正常 RL 训练:最大 Token 概率差相当小(约 0.4),比之前的设置(在 Qwen-2.5-32B Dense 模型上的 DAPO 为 1.0)要小
- 2)使用 INT8 量化 rollouts 而非 bf16 rollouts 的 RL 训练:最大 Token 概率差相当大(1.0),比正常 RL 训练大
- 博客在设置 1 中进行常规 PPO 训练,这“几乎”是 On-policy 的;
- 在设置 2 中同时进行常规 PPO 训练和带有截断重要性采样的 PPO 训练,其生成 rollout 和梯度计算有更大的差距
- 按照 verl 教程中的 GSM8K 示例进行 RL 训练,并使用两种不同的设置:
- 如图 2 所示
- 与设置 1 中的 PPO 相比,在设置 2 中执行 PPO 会导致显著的性能下降
- 同时,应用截断重要性采样成功地大大缓解了差距,有效地使设置 2 的运行达到了与设置 1 相似的性能
- 更多分析在下面的 TIS 分析 部分提供
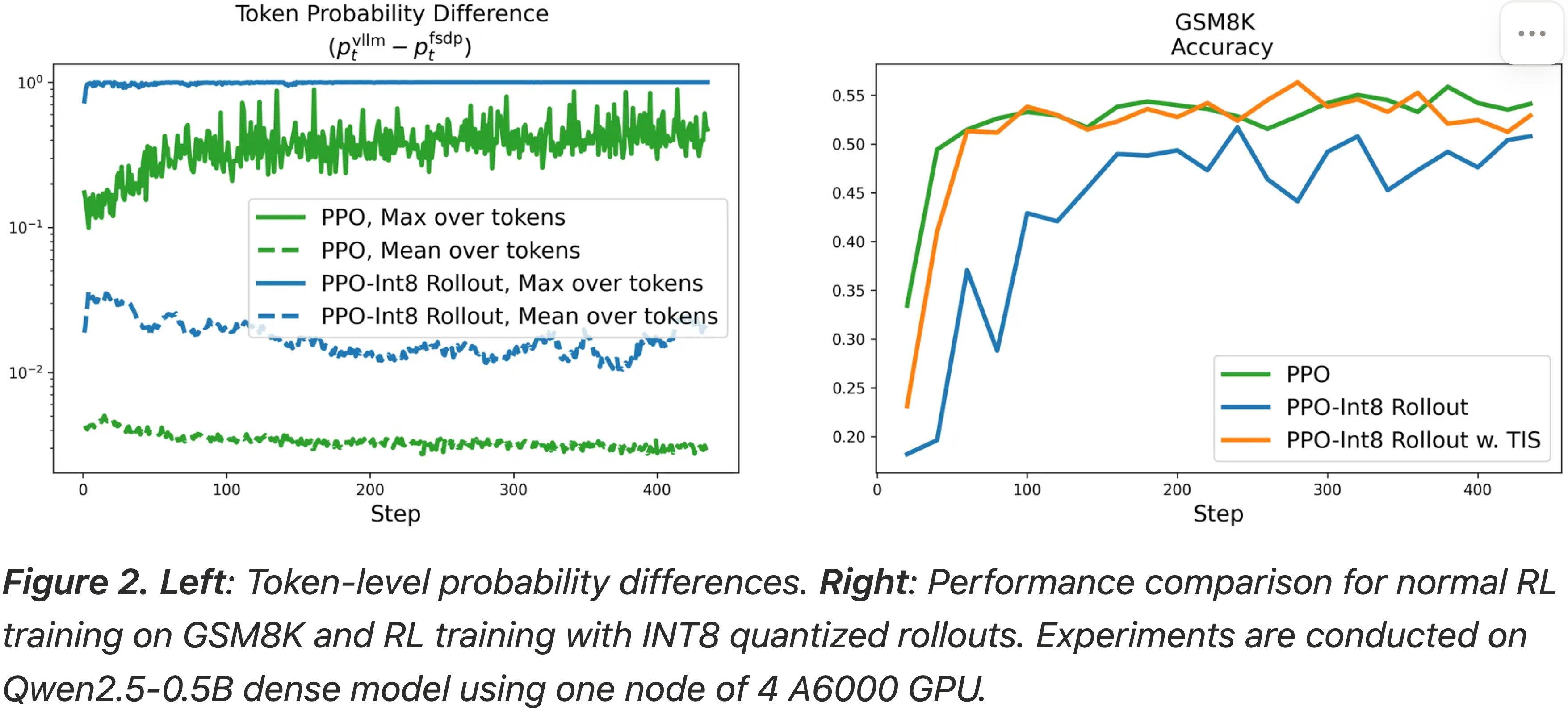
- 图 2:
- 左图:Token-level 概率差异
- 右图:在 GSM8K 上正常 RL 训练和使用 INT8 量化 rollouts 的 RL 训练的性能比较
- 实验在 Qwen2.5-0.5B Dense 模型上进行,使用一个节点(4 张 A6000 GPU)
Does TIS always help?
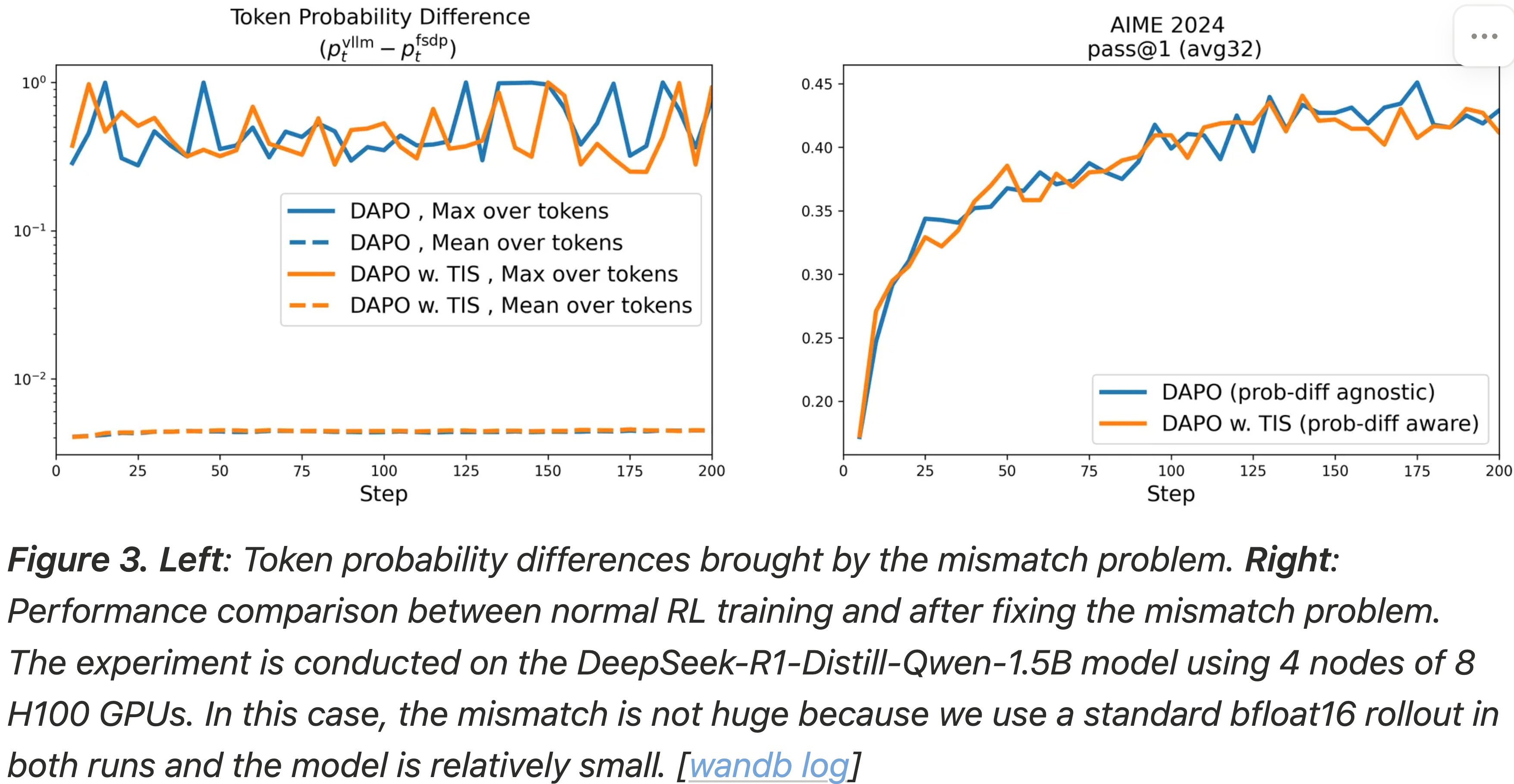
- 图 3:
- 左图:由不匹配问题带来的 Token 概率差异
- 右图:正常 RL 训练与修复不匹配问题后的性能比较
- 实验在 DeepSeek-R1-Distill-Qwen-1.5B 模型上进行,使用 4 个节点,每个节点 8 张 H100 GPU
- 在这种情况下,不匹配并不大,因为博客在两次运行中都使用了标准的 bfloat16 rollout 并且模型相对较小
- 博客还观察到,在概率差异相对较小的情况下,引入额外的截断重要性采样项不能带来性能提升
- 同时,值得一提的是,在严格的 On-policy 强化学习设置中,重要性采样权重比项的值将为 1.0
TIS Analysis
Analysis about different TIS-Variants
- 博客总结了两种缓解分布差距的替代方案
- PPO 重要性采样 (PPO Importance Sampling, PPO-IS)
$$
\small{ \mathbb{E}_{a\sim\color{red}{\pi_{\mathrm{sampler}}}(\theta_{\mathrm{old}})}\Bigl[\nabla_{\theta}\min\Bigl( \frac{\color{blue}{\pi_{\mathrm{learner}}}(a, \theta)}{\color{red}{\pi_{\mathrm{sampler}}}(a, \theta_{\mathrm{old}})}\hat{A}, \mathrm{clip}\Bigl( \frac{\color{blue}{\pi_{\mathrm{learner}}}(a, \theta)}{\color{red}{\pi_{\mathrm{sampler}}}(a, \theta_{\mathrm{old}})}, 1-\epsilon, 1+\epsilon \Bigr)\hat{A}\Bigr)\Bigr]}
$$- 注意:Colossal 框架使用此实现
- 理解:这个方法中不再重新使用 FSDP 引擎(用 \(\pi_\text{old}\))对 之前 rollout 的结果进行重新计算概率
- 注:之前 rollout 的结果是 vLLM 引擎用 \(\pi_\text{old}\) 采样得到的
- 原始重要性采样 (Vanilla Importance Sampling, vanilla-IS)
$$
\mathbb{E}_{a \sim \color{red}{\pi_{\text{sampler} }}(\theta_{old})} \left[ \underbrace{\frac{\color{blue}{\pi_{\text{learner} }}(a, \theta_{old})}{\color{red}{\pi_{\text{sampler} }}(a, \theta_{old})}}_{\text{importance ratio}} \cdot \nabla_{\theta} \min \left( \frac{\color{blue}{\pi_{\text{learner} }}(a, \theta)}{\color{blue}{\pi_{\text{learner} }}(a, \theta_{old})} \hat{A}, \text{ clip} \left( \frac{\color{blue}{\pi_{\text{learner} }}(a, \theta)}{\color{blue}{\pi_{\text{learner} }}(a, \theta_{old})}, 1 - \epsilon, 1 + \epsilon \right) \hat{A} \right) \right]
$$- 注意:Memo-RL 使用此实现
- 理解:这个方法和 TIS 的最大区别是缺少 TIS 中的 Clip 操作
- 为了评估 TIS 的有效性并理解其设计选择的影响,博客进行了实验,将 TIS 与上述两种变体进行比较
- TIS 始终优于这两种变体,尤其是在差距较大的情况下(例如 FP8/INT8)
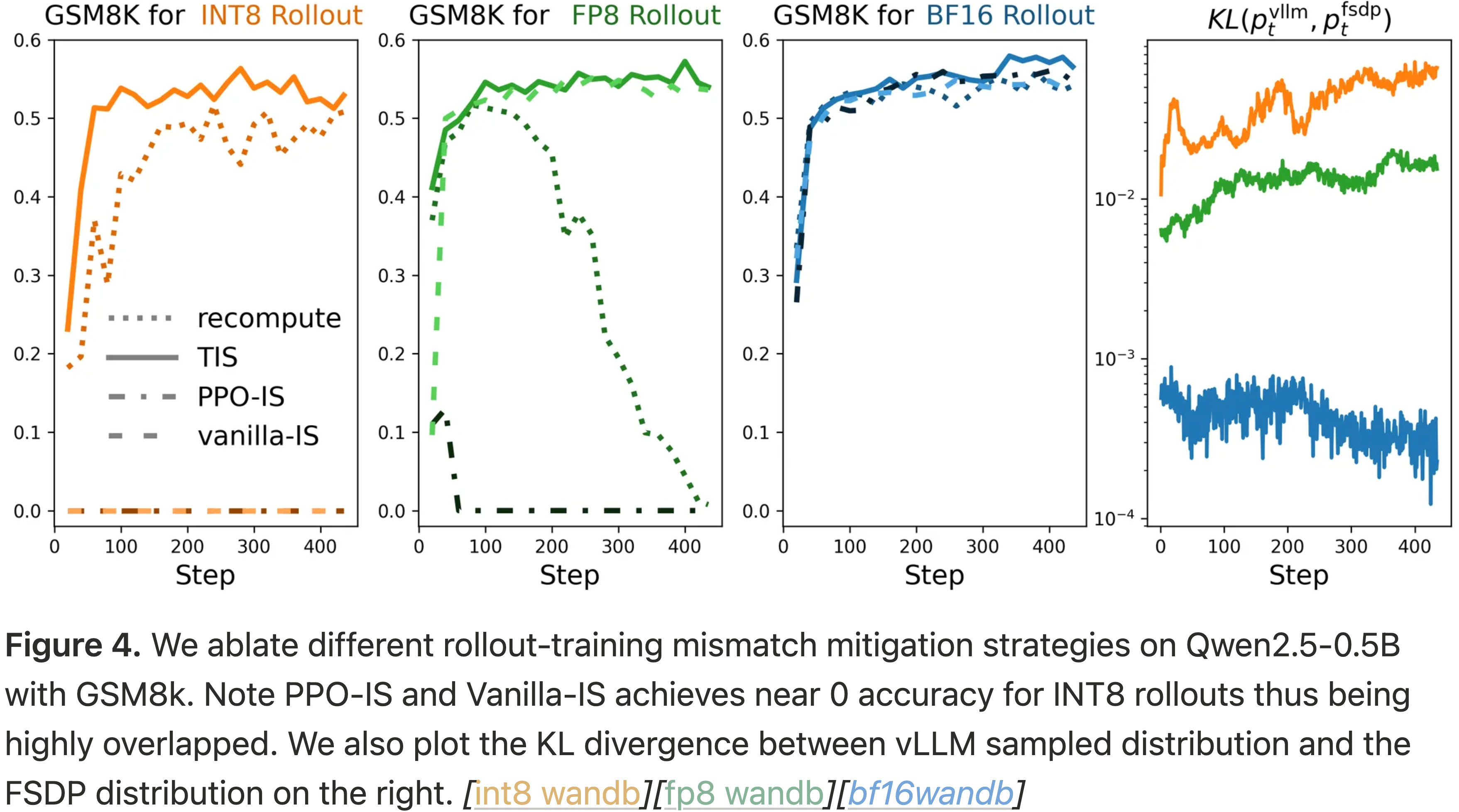
- 图 4:
- 博客在 Qwen2.5-0.5B 和 GSM8K 上消融了不同的 rollout-training 不匹配缓解策略
- 注意 PPO-IS 和 Vanilla-IS 在 INT8 rollouts 下准确率接近 0,因此高度重叠
- 博客还在右侧绘制了 vLLM 采样分布与 FSDP 分布之间的 KL 散度
附录:为什么这里的两种变体(PPO-IS 和 vanilla-IS)会导致训练不稳定?(Why the two variants (PPO-IS and vanilla-IS) here gives unstable training?)
Vanilla-IS v.s. TIS
- 关于 vanilla-IS,不稳定性主要来自于 rollout \(a \sim \color{red}{\pi_{\text{sampler} }}(a, \theta_{old})\) 以低概率采样的情况,因此重要性权重比很大,通过 \(\left( \frac{\color{blue}{\pi_{\text{learner} }}(a, \theta_{old})}{\color{red}{\pi_{\text{sampler} }}(a, \theta_{old})} \right)^2\) 放大了梯度方差
- 问题:\(\left( \frac{\color{blue}{\pi_{\text{learner} }}(a, \theta_{old})}{\color{red}{\pi_{\text{sampler} }}(a, \theta_{old})} \right)^2\) 是怎么来的?
- 回答:应该是想表达 当 rollout \(a \sim \color{red}{\pi_{\text{sampler} }}(a, \theta_{old})\) 以低概率采样时,\(\left( \frac{1}{\color{red}{\pi_{\text{sampler} }}(a, \theta_{old})} \right)^2\) 放大了方差吧;
- 这里的表达应该是假设了 \(\color{blue}{\pi_{\text{learner} }}(a, \theta_{old})\) 和 \(\color{blue}{\pi_{\text{learner} }}(a, \theta)\) 近似相等
- 因此,博客在截断重要性采样中使用 clamp 操作来稳定训练
- 例如,当权重比 \(\frac{\color{blue}{\pi_{\text{learner} }}(a, \theta_{old})}{\color{red}{\pi_{\text{sampler} }}(a, \theta_{old})}\) 对于某个 Token 达到 16 时,通过 Vanilla-IS 该 Token 的梯度噪声将被放大 256 倍,通过 TIS-2 放大 4 倍,或通过 TIS-8 放大 64 倍
PPO-IS v.s. TIS
- 自从作者的博客发布以来,很多人问博客为什么不直接将重要性采样纳入 PPO(即上面的 PPO-IS 变体)
- 作者表示“坦率地说,博客一开始就像 PPO-IS 那样直接更改 PPO 的 clip,但在博客的实验设置中效果不佳”
- 至于根本原因,通过执行 PPO-IS,梯度实际上仍然与 On-policy 版本的 PPO 存在偏差
- 换句话说,尽管它可能仍然朝着无偏的目标进行优化,但与 PPO 相比可能效果较差
- 此外,作者指出 PPO 信任区域技术的提出是为了限制 rollout \(\theta_{old}\) 和当前模型 \(\theta\) 之间的概率比接近 1 ,以近似 On-policy REINFORCE 梯度
- 然而在 PPO-IS 中,即使当 \(\theta = \theta_{old}\) 时,由于不匹配,概率比 \(\frac{\color{blue}{\pi_{\text{learner} }}(a, \theta)}{\color{red}{\pi_{\text{sampler} }}(a, \theta_{old})}\) 已经不等于 1
- 这使得裁剪很有可能发生,并且训练的信息量大大减少
- 此外,在博客的 TIS 方法中,博客分别裁剪 \(\frac{\color{blue}{\pi_{\text{learner} }}(a, \theta_{old})}{\color{red}{\pi_{\text{sampler} }}(a, \theta_{old})}\) 和 \(\frac{\color{blue}{\pi_{\text{learner} }}(a, \theta)}{\color{blue}{\pi_{\text{learner} }}(a, \theta_{old})}\),因此要温和得多;
- 注意当 \(\theta = \theta_{old}\) 时, \(\frac{\color{blue}{\pi_{\text{learner} }}(a, \theta)}{\color{blue}{\pi_{\text{learner} }}(a, \theta_{old})}\) 等于 1,这适合于信任区域约束
- 然而在 PPO-IS 中,即使当 \(\theta = \theta_{old}\) 时,由于不匹配,概率比 \(\frac{\color{blue}{\pi_{\text{learner} }}(a, \theta)}{\color{red}{\pi_{\text{sampler} }}(a, \theta_{old})}\) 已经不等于 1
From Ill-conditioned to Benign(恶性到良性)
- 除了 rollout 加速之外,rollout 量化也是检验 rollout 生成和梯度计算之间分布差距影响的有效测试平台
- 博客证明了
- 1)当不解决这种差距时,使用量化 rollouts 的 RL 训练表现出在其他场景中常见的典型不稳定性
- 2)引入 TIS 项使 RL 训练变得稳定和良性
Entropy Collapse and Abnormal Response Length(熵崩溃和异常响应长度)
- 许多先前的工作表明,在大语言模型中进行 RL 训练会导致熵崩溃
- Token-level 分类分布接近 one-hot 分布,从而有效地限制了 RL 训练的探索
- 博客的 INT8 rollout 实验揭示了严重的熵崩溃
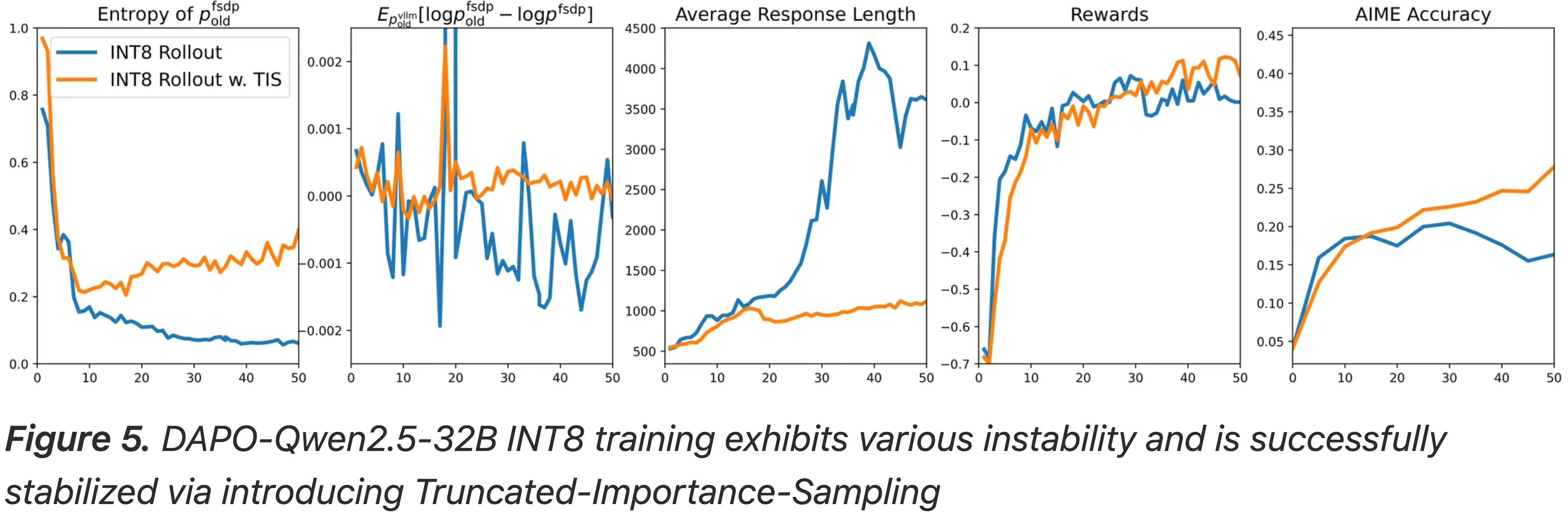
- 图 5 显示熵降至 0.2 以下并在整个训练过程中持续下降
- 博客还观察到了异常长的响应生成
- 这是 RL 训练中的另一种失败模式
- 引入 TIS 项逆转了这一趋势,使模型能够以稳定和良性的方式进行训练
- 图 5:DAPO-Qwen2.5-32B INT8 训练表现出各种不稳定性,并通过引入截断重要性采样成功稳定
- 相比之下,BF16 rollout 实验没有显示出严重的熵崩溃
- 尽管如此,TIS 项仍然增加了熵值
- 与 INT8 rollouts 相比,分布差距较小,响应长度保持在合理范围内
- 图 6:DAPO-Qwen2.5-32B BF16 训练表现出各种不稳定性,并可以通过引入的截断重要性采样成功稳定
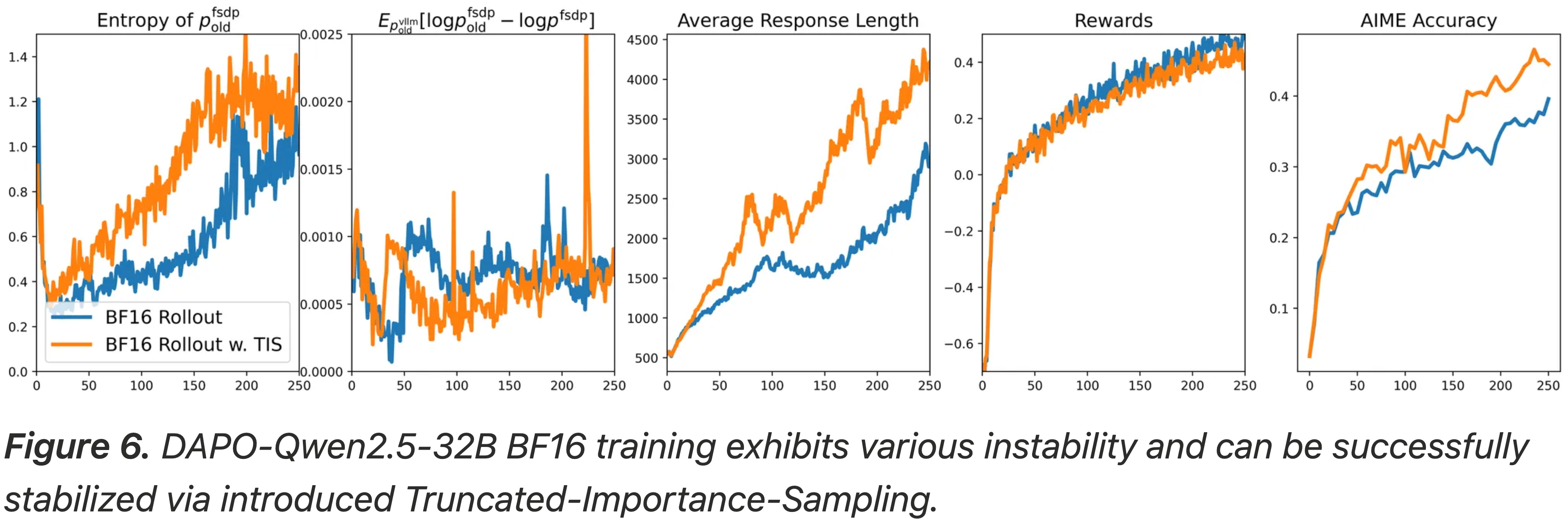
- 个人观察 & 理解:从图 6 中第一个图可以看到,熵是先降低后增加的
On the Impact of Distribution Gap: A Case Study on KL Estimation
- \(\text{KL}(\color{blue}{\pi_{\text{old} }^{\text{fsdp}} } | \color{blue}{\pi^{\text{fsdp} }})\) 的一个无偏 KL 估计器是 \(k_1\) 估计器
$$\log \color{blue}{\pi_{\text{old} }^{\text{fsdp}} }(a) - \log \color{blue}{\color{blue}{\pi^{\text{fsdp} }}}(a) $$- 其中 \(a \sim \color{blue}{\pi_{\text{old} }^{\text{fsdp}} }(a)\)
- 然而,现代 RL 训练框架从 \(\color{red}{\pi_{\text{old} }^{\text{vllm} }}\) 生成 rollouts,而不是从 \(\color{blue}{\pi_{\text{old} }^{\text{fsdp}} }\),这给 KL 估计引入了偏差,类似于前面讨论的梯度估计偏差
- 因此,博客可以使用 KL 估计作为案例研究来探索 \(\color{blue}{\pi_{\text{old} }^{\text{fsdp}} }\) 和 \(\color{red}{\pi_{\text{old} }^{\text{vllm} }}\) 之间不匹配的影响
- 在无任何偏差的情况下,根据定义 KL 散度是非负的
- 然而,INT8 rollouts 中显著的分布不匹配导致有偏的 \(k_1\) 估计器频繁产生负值,如图 5 所示
- 理解:图 5 第 2 个图所示
- 这些负的 KL 估计值标志着训练动态处于病态
- 当 TIS 被纳入 RL 训练时,相同的 \(k_1\) 估计器(虽然仍然受到底层分布不匹配的影响)在大部分训练过程中保持正值
- 这种预期符号的保持表明 TIS 成功恢复了良性的训练行为
Biased Reward in Training Log
- 集成 TIS 的一个有趣现象是,它可能导致更差的奖励日志记录,同时带来更好的下游性能
- 这是因为 \(\color{red}{\pi_{\text{sampler} }}\) 和 \(\color{blue}{\pi_{\text{learner} }}\) 之间的差距不仅给梯度估计引入了偏差,也给日志记录中的奖励估计引入了偏差
- 记录的奖励来自 rollout 策略,即 \(\mathbb{E}_{a \sim \color{red}{\pi_{\text{sampler} }} } [R]\) 而不是 \(\mathbb{E}_{a \sim \color{blue}{\pi_{\text{learner} }} } [R]\)
- 如图 6(右侧两个子图)所示,记录的奖励指标显示 BF16-Rollout 优于 BF16-Rollout w. TIS
- 然而,如果查看下游的 AIME 准确率性能,BF16-Rollout w. TIS 显著优于原始的 BF16-Rollout
- 问题:rollout 策略来自 \(\mathbb{E}_{a \sim \color{red}{\pi_{\text{sampler} }} } [R]\) 而不是 \(\mathbb{E}_{a \sim \color{blue}{\pi_{\text{learner} }} } [R]\) 影响这么大吗?
Intuitions of TIS’s Working Mechanism
- 虽然 TIS 的确切机制仍然是一个 Open Question,但博客提供了关于 TIS 如何缓解分布差距的高层直觉
- 忽略具有 \(\frac{\color{blue}{\pi_{\text{learner} }}(a_{t}, \theta_{old})}{\color{red}{\pi_{\text{sampler} }}(a_{t}, \theta_{old})} < 1\) 的 rollouts 的偏差(注:这里是指忽略偏差不行)可能通过以下机制导致熵崩溃:
- 对于具有负优势的 rollouts,策略梯度倾向于减少 \(\color{blue}{\pi_{\text{learner} }}\)
- 当参数更新后存在大的分布差距时,\(\color{blue}{\pi_{\text{learner} }}\) 的减少可能不会反映在 \(\color{red}{\pi_{\text{sampler} }}\) 中
- 理解:这里是因为两层 diff 导致,第一层是策略本身是 Off-policy 的,第二层是使用的引擎是 vLLM
- 因此,策略梯度继续指向进一步减少 \(\color{blue}{\pi_{\text{learner} }}\) 的方向
- 问题:此时确实会导致 \(\frac{\color{blue}{\pi_{\text{learner} }}(a_{t}, \theta_{old})}{\color{red}{\pi_{\text{sampler} }}(a_{t}, \theta_{old})} < 1\),这里是想强调什么呢?
- 理解:这里是想强调这种偏差的存在,使用 TIS 修正以后,可以抵消这种偏差
- 直观地说,这种惩罚可能迫使模型过度 commit 于一个具有小熵的输出分布
- 问题:如何理解这里会过度提交于一个小熵的输出分布?
- 进一步减少 \(\color{blue}{\pi_{\text{learner} }}\) 不一定指向更小的熵吧?
- 理解:过度更新可能导致模型向不确定的方向更新,不一定是熵减少或增加
- 其他理解1:持续减少一些动作的概率确实可能加速这些动作概率的降低,从而促进某些其他动作概率的增加,也就意味着熵会减少
- 其他理解2:一个动作因为过度打压导致动作概率降低以后,后续被采样到的概率也降低了,很难被修正了
- 问题:如何理解这里会过度提交于一个小熵的输出分布?
- TIS 坚持对 \(\frac{\color{blue}{\pi_{\text{learner} }}(a_{t}, \theta_{old})}{\color{red}{\pi_{\text{sampler} }}(a_{t}, \theta_{old})} < 1\) 使用非截断的重要性权重比
- 从而消除了这部分 rollouts 的偏差,并打破了这一机制
- 注意:这里 TIS 的截断是单向的,使用的是 \(\min\) 来作为截断,只有当 \(\frac{\color{blue}{\pi_{\text{learner} }}(a_{t}, \theta_{old})}{\color{red}{\pi_{\text{sampler} }}(a_{t}, \theta_{old})} > 1\) 时才会截断
- 问题:为什么 \(\frac{\color{blue}{\pi_{\text{learner} }}(a_{t}, \theta_{old})}{\color{red}{\pi_{\text{sampler} }}(a_{t}, \theta_{old})} > 1\) 时需要截断?
- 如上所述,\(\frac{\color{blue}{\pi_{\text{learner} }}(a_{t}, \theta_{old})}{\color{red}{\pi_{\text{sampler} }}(a_{t}, \theta_{old})} < 1\) 时应该不要截断以修正偏差
- 当 \(\frac{\color{blue}{\pi_{\text{learner} }}(a_{t}, \theta_{old})}{\color{red}{\pi_{\text{sampler} }}(a_{t}, \theta_{old})} > 1\) 时,很如果不截断,方差太大了(因为分母太小就容易出现数倍差异的情况),导致梯度波动太大
- \(\frac{\color{blue}{\pi_{\text{learner} }}(a_{t}, \theta_{old})}{\color{red}{\pi_{\text{sampler} }}(a_{t}, \theta_{old})} < 1\) 时这个值最多在 \([0, 1)\) 之间
- 实际上,这也是可以截断的,作者在新的博客中已经给出一些结论了,下界也可以加以限制 (IcePop)Small Leak Can Sink a Great Ship—Boost RL Training on MoE with IcePop!, 20250919, AntGroup
Rollout-Training Mismatch Analysis
- 博客进行了一系列受控实验,以识别引入或放大 rollout 生成和梯度计算之间差异的因素
- 博客发现并行策略的差异和长响应长度导致了不匹配,而仅 Sampler 后端的选择影响有限
Analysis Setup
Model & Data
- 博客使用两个代表性模型进行实验(使用 DAPO 配方训练的 DAPO-32B 和 使用 Polaris RL 配方训练的 Polaris-7B)
- 对于评估,博客使用 DAPO-Math-T2k 数据集的前 512 个提示来评估 Sampler 和 Learner 输出之间的差异指标
- 博客使用两个指标测量响应级别的 Mismatch :
- 每个响应的 Max Mismatch :
$$ \max_{a \in \text{response}} |p_\text{sampler}(a) - p_\text{learner}(a)|$$ - 每个响应的平均 Mismatch :
$$
\frac{1}{|\text{response}|} \sum_{a \in \text{response} } |p_{\text{sample} }(a) - p_{\text{learner} }(a)|
$$ - 这些指标使博客能够捕捉到最坏情况的 Token 差异以及响应内的平均差异水平
- 博客在不同设置下为相同提示的响应计算它们,以隔离特定因素的影响
- 每个响应的 Max Mismatch :
Visualization(可视化)
- 博客使用右侧显示的可视化格式呈现这两个指标
- 这是一个用于解释图的说明性示例
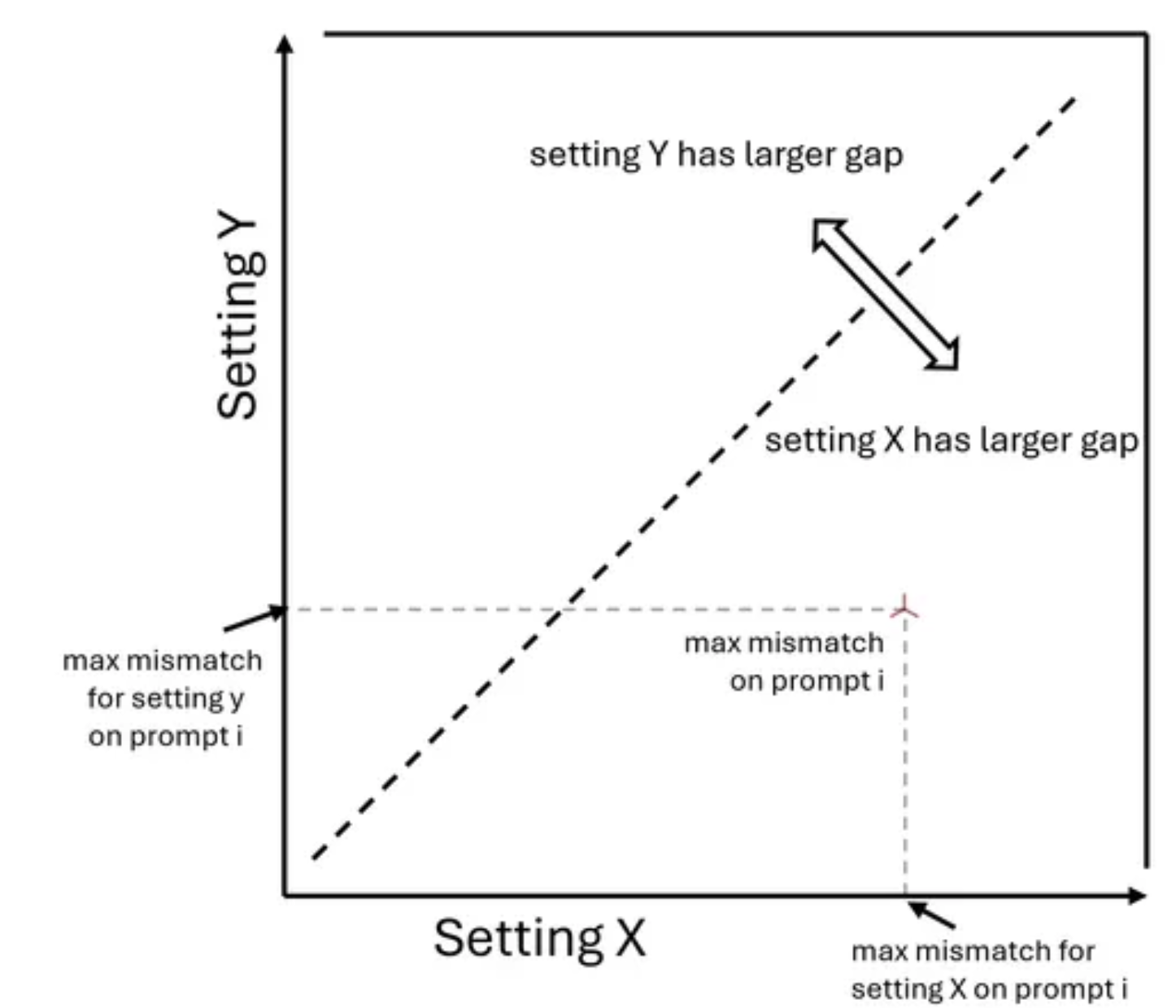
- 这是一个用于解释图的说明性示例
Larger Parallelism Difference, Larger Max Gap(并行性差异越大,Max Gap 越大 )
- 博客观察到 Sampler 和 Learner 之间的并行性差异对 Max Mismatch 指标有显著贡献
- 理解:这里是说因为 Sampler 和 Learner 是部署在不同的引擎上的,所以各种并行方式也可能不同
Simplest Setting
- 使用 DAPO-32B 模型,博客从最简单的配置开始:
- Sampler 在 vLLM 上以 TP1 运行, Learner 使用 FSDP 以 SP1 运行
- 由于 Sampler 和 Learner 具有相同的并行设置,博客称之为相同并行性(Same Parallelism),其分布差距归因于并行性差异之外的因素
- 问题 :为什么说这里「Sampler 在 vLLM 上以 TP1 运行, Learner 使用 FSDP 以 SP1 运行」是相同的并行设置?
- 回答 :先澄清几个缩写:
- TP1 = Tensor Parallelism degree 1
- SP1 =(在 FSDP 语境里)Shard/Shard-Parallelism degree 1,也就是把模型参数完整地放到一张卡上,不做任何分片
- 在两种框架里,“degree=1” 都意味着:
- 1)整个模型权重 不拆、不复制到多张卡;
- 2)一张 GPU 就能装下全部参数;
- 3)不需要任何跨卡通信来维护参数一致性。
- 因此,虽然一个叫 TP、一个叫 SP,但它们的“并行粒度”相同(都是“单卡单副本”)
- 既然两边都只做 degree=1,就称它们为 Same Parallelism
Adding Tensor Parallelism
- 为了研究 TP 差异的影响,博客将 Sampler 从 TP1 改为 TP2,同时保持 Learner 在 SP1(Different TP)
- 如图 7 左图所示,随着并行性差异的增加,具有高 Max Mismatch(> 0.5)的响应数量增加
- 相同并行性情况仅产生一个这样的响应,而不同 TP 将其增加到两个
- 图 7:相同一组提示在不同并行性下的 Max Mismatch
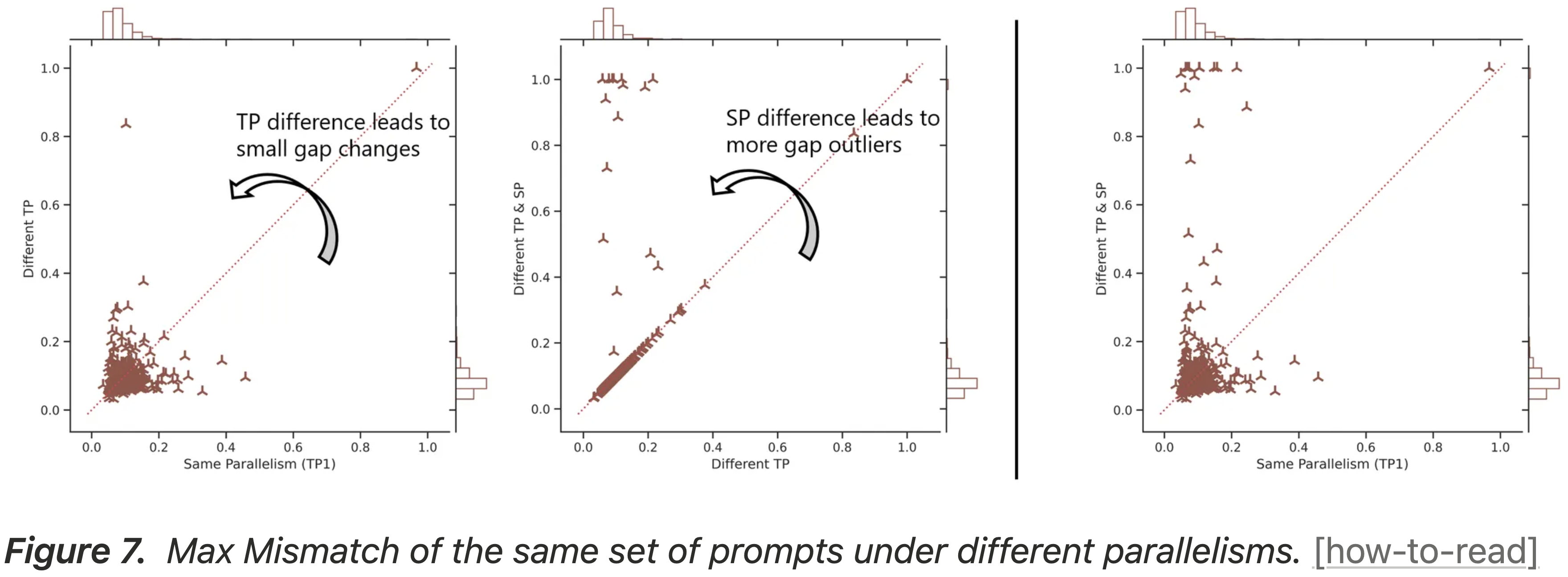
- 问题:为什么图 7 的第 1 和第 2 两张图中的 Different TP 显示的分布结果不一致?
Adding Sequence Parallelism
- 为了研究 Ulysses 序列并行差异的影响,博客将 Learner 从 SP1 改为 SP8(不同 TP 和 SP)
- 如图 7 中图所示,额外的 SP 差异将高 Max Mismatch 的数量从两个增加到两位数
Disentangling Parallelism and Sharding(解耦)
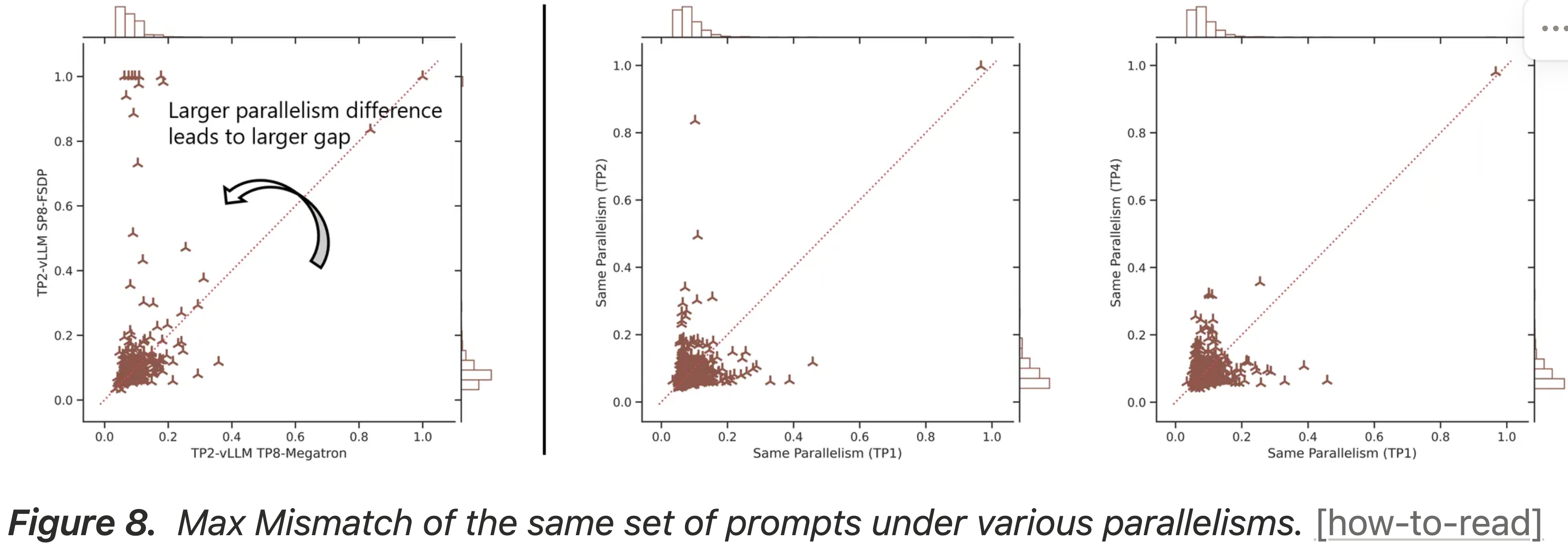
- 如图 8 左下图所示,对于相似的分布式世界大小(例如 8 个设备),在 Learner 中使用张量并行(TP8)与 TP2 Sampler 产生的 Mismatch ,比在使用序列并行(SP8)的 Learner 与 TP2 Sampler 产生的 Mismatch 要小
- 博客假设这是因为 TP8 Learner 与 TP2 Sampler 之间的实现差异,比 SP8 Learner 与 TP2 Sampler 之间的实现差异要小
- 这强化了博客的发现:最小化 Sampler 和 Learner 之间的并行性差异能持续减小差距
- 然后,博客测量了在 Learner 和 Sampler 中使用相同张量并行时的 Max Mismatch ,记为相同并行性(TP2)和相同并行性(TP4)
- 与最简单设置不同,这两种配置在多个设备上共享模型计算,因此更具可扩展性
- 如图 8 中图和右图所示,相同并行性(TP2)和相同并行性(TP4)只有少量响应具有高 Max Mismatch (> 0.5)
- 这表明在 Sampler 和 Learner 中使用相同的方式分片模型有助于减少 Mismatch ,应该是更可取的
- 图 8:相同一组提示在各种并行性下的 Max Mismatch
Mean Mismatch and KL
- 尽管博客在 Max Mismatch 上观察到一致的模式,但值得一提的是,博客没有在这些配置的平均 Mismatch/KL 散度上观察到任何显著差异
Longer Response, Larger Max Gap(响应越长,Max Gap 越大)
- 博客的实验一致表明,生成长度越长的序列会导致越大的 Max Mismatch ,而平均 Mismatch 受影响较小
- 注意:这里的 平均 Mismatch 并不是按照 Token 做归一化的!
- 博客使用 DAPO-32B 和 Polaris-7B 模型消融了序列长度的影响
- 图 9:
- 左图:不同响应长度的 Max Mismatch
- 右图:不同响应长度的平均 Mismatch
- 注:棕色表示 DAPO-32B;紫色表示 Polaris-7B 的结果
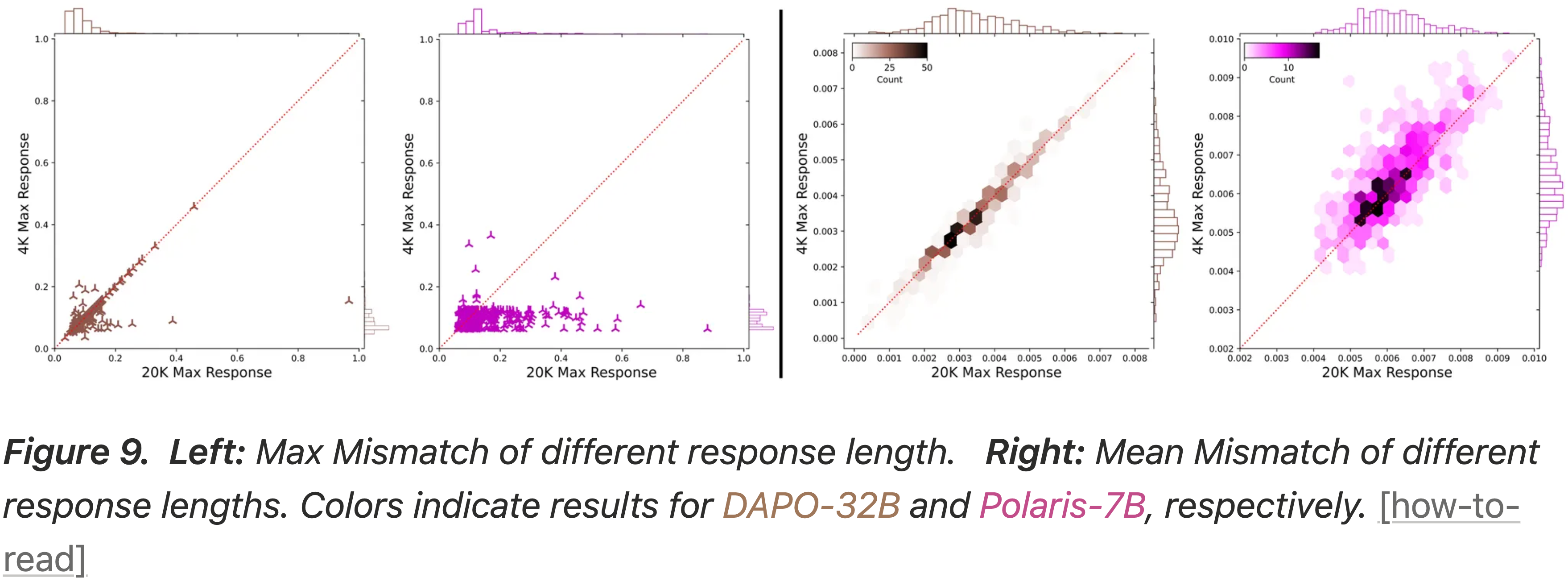
- 如图 9 所示
- 限制为 20K Token 的响应比限制为 4K Token 的响应表现出更高的 Max Mismatch
- 相比之下,平均 Mismatch 在两种设置下保持相似
- 这表明较长的序列为单个大的概率差异提供了更多机会,即使每个 Token 的平均差异保持稳定
- 为了验证这种效应是由序列长度驱动的,而不是生成的 Token 总数,博客进行了一个对照实验,比较单批 20K-Token 响应与多批(5 个)独立的 4K-Token 响应(针对同一组提示)
- 图 10:
- 左图:在相似 Token 数量下,不同响应长度的 Max Mismatch
- 右图:不同长度响应的 Max Mismatch
- 注:棕色表示 DAPO-32B;紫色表示 Polaris-7B 的结果
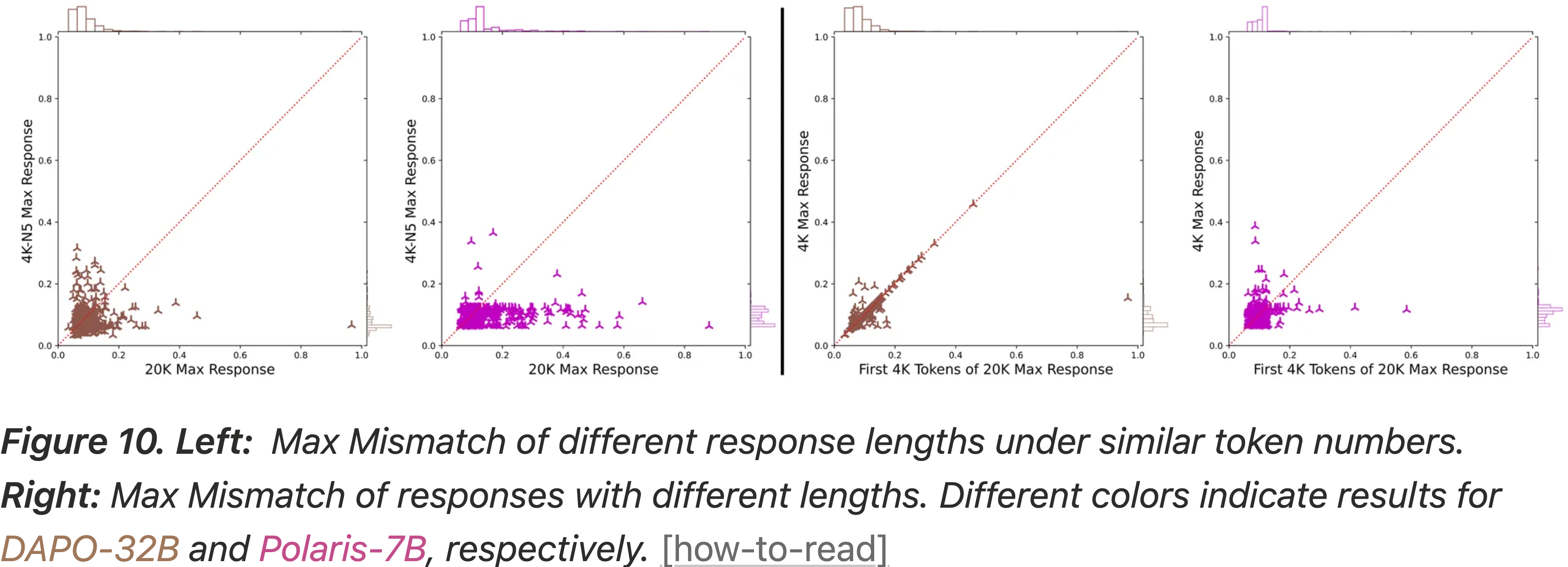
- 如图 10 左图所示
- 生成多个较短响应(5×4K)与单个 4K-Token 响应相比,仅导致 Max Mismatch 适度增加
- 但一个连续的 20K-Token 响应产生的 Mismatch 比两者都要大得多
- 这证实了差异由于序列的连续长度而加剧
- 有趣的是,博客观察到 Mismatch 随着生成的进行而累积:
- 一个 20K-Token 响应中仅前 4K Token 内的 Max Mismatch ,常常超过一个独立的 4K-Token 响应的 Max Mismatch
- 这表明 Sampler 和 Learner 的内部状态在长生成上下文中越来越发散
Altering Sampler Alone, Gap Still There(仅改变 Sampler 时,差距仍然存在)
- 最后,博客研究了 Sampler 后端本身的选择是否是导致 Mismatch 的主要因素
- 博客比较了 Sampler 的三种配置:
- 1)vLLM
- 2)SGLang
- 3)启用确定性内核的 SGLang
- 结果表明,仅 Sampler 后端本身没有决定性影响
- 对于 DAPO-32B 模型,SGLang 产生较小的平均 Mismatch ,而对于 Polaris-7B 模型,vLLM 表现更好(即 vLLM 的平均 Mismatch 更小)
- 因此,没有单一的 Sampler 后端在所有不同设置中 consistently 占主导地位
- 图 11:
- 左图:不同 Sampler 后端的 Max Mismatch
- 右图:不同 Sampler 后端的平均 Mismatch
- 注:棕色表示 DAPO-32B;紫色表示 Polaris-7B 的结果
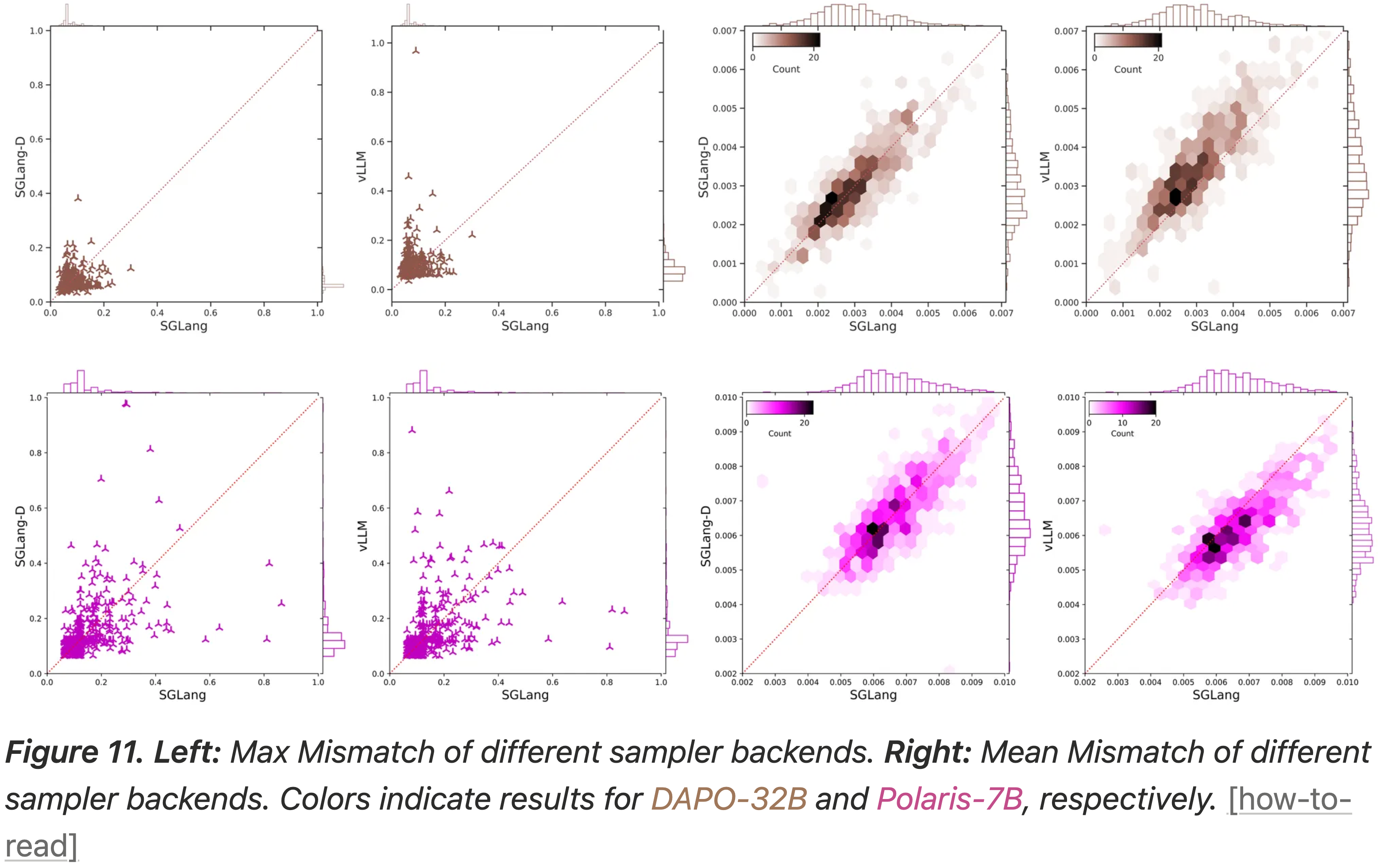
- 值得注意的是,在没有对齐训练配置的情况下,在 SGLang 中启用确定性采样并没有明显减小差距
- 这表明 Mismatch 主要源于更深层次的实现差异(例如并行性或数值精度),而不是仅仅来自随机采样
What’s More
- 还有其他维度可能影响 rollout-training 不匹配,包括 模型类型(例如,Dense vs. MoE,Based vs. Post-trained),提示 数据特征(例如,难度,领域),GPU 硬件 ,以及训练 后端(backend) 的选择
- 例如,博客相对一致地发现,规模相当(32B 和 30B)的 Dense 模型和 MoE 模型表现出不同程度的 Mismatch ,并且基础模型的 rollout-training Mismatch 比它们的后训练对应物要小
- 博客正在持续努力,以更深入地理解并更好地利用 rollout-training 不匹配,用于实际的大语言模型后训练。敬请期待!
Discussion
- 博客特别讨论了博客的修复方法(截断重要性采样,TIS)对 MoE 架构强化学习的潜在影响
- 博客还强调了 TIS 与最近旨在改进策略更新中重要性采样权重比的工作(例如 GSPO, GMPO)的联系
The gap can be amplified in MoE RL(Gap 在 MoE 强化学习中可能被放大)
- 虽然博客当前的实验和分析主要集中在 Dense 模型上,但博客相信这种分布差距也存在于 MoE 强化学习中,并且可能更加严重
- 主要有两个原因:
- 动态路由:
- 与 Dense 模型不同,MoE 利用路由器动态激活特定专家
- 这种路由机制本质上是精度敏感的;即使轻微的数值差异也可能导致显著不同的专家激活
- 专门优化的内核:
- MoE 模型通常规模很大,现代推理引擎(例如 vLLM)对 MoE 模型有相比于 Dense 模型独特的优化,这使得后端的数值不一致性更大
- 动态路由:
- 总之,这些特性可以显著放大分布不匹配,使得像 TIS 这样的解决方案在 MoE 强化学习中特别有价值
TIS is orthogonal and compatible with existing GxPOs(TIS 与现有的 GxPOs 正交且兼容)
- 最近的工作通过革新重要性采样权重比的计算来提高策略更新的稳定性
- 例如,GSPO 在 Sequence-level 别而不是 Token-level 别计算权重比,而 GMPO 计算几何平均值而不是算术平均值
- 与这些工作正交的是,博客的 TIS 修复解决了根源于系统级别的分布不匹配问题,这是由在 rollout 生成和模型训练中使用的不同计算内核带来的。这种问题广泛存在于采用混合计算设计的强化学习训练框架中
- 因此,博客的修复可以应用,而不论所使用的具体强化学习算法如何
附录:为什么 TIS 截断是单向的?
- 详情参见 Intuitions of TIS’s Working Mechanism 小节的讨论