NLP——LLM对齐微调-SimPO

注：本文包含 AI 辅助创作

参考链接：
- 原始论文：SimPO: Simple Preference Optimization with a Reference-Free Reward, arXiv 20240523 & 20240608 & 20241201, NeurIPS 2024
- 开源地址：github.com/princeton-nlp/SimPO

Paper Summary

TLDR：
- SimPO 是 DPO 方法的一个改进，通过将奖励函数与生成似然对齐并引入目标奖励间隔（margin），SimPO 无需参考模型即可实现高性能，同时避免了长度偏差的利用
- SimPO 优化点1（核心设计）：使用序列的平均对数概率作为隐式奖励
  - 这种奖励设计能更好地与模型生成过程对齐，并且无需参考模型，从而显著提升了计算和内存效率
- SimPO 优化点2：在 Bradley-Terry 目标中引入了目标奖励间隔（target reward margin），以鼓励获胜响应和失败响应之间的奖励差距更大，从而进一步提升算法性能
论文实验设置：
- 论文在多种先进训练配置（包括基础模型和指令调优模型，如 Mistral、Llama 3 和 Gemma 2）中将 SimPO 与 DPO 及其最新变体进行了对比
- 论文实验基于广泛的聊天式评估基准（包括 AlpacaEval 2、MT-Bench 和 Arena-Hard）
实验结果：SimPO 在不显著增加生成长度的情况下，始终显著优于现有方法
- SimPO 在 AlpacaEval 2 上比 DPO 高出 6.4 分，在 Arena-Hard 上高出 7.5 分
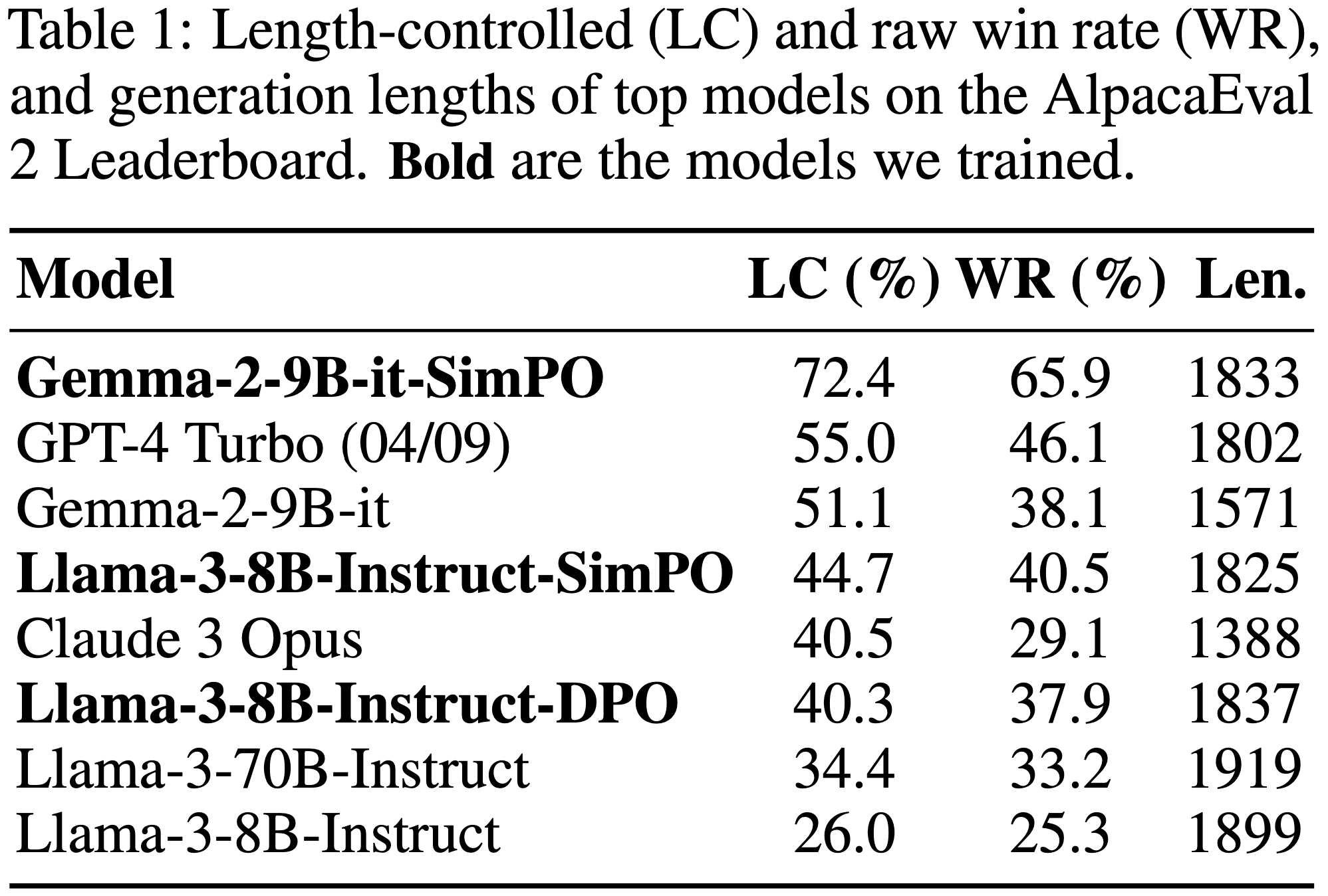
- 论文基于 Gemma-2-9B-it 训练的最佳模型在 AlpacaEval 2 上实现了 72.4% 的长度控制胜率，在 Arena-Hard 上实现了 59.1% 的胜率，并在 Chatbot Arena 的 <10B 模型中排名第一（基于真实用户投票）

Introduction and Discussion

从人类反馈中学习对于将 LLM 与人类价值观和意图对齐至关重要 (2021)，确保模型具备帮助性、诚实性和无害性 (2021)
基于人类反馈的强化学习（Reinforcement Learning from Human Feedback, RLHF）(2017, 2023, 2020) 是一种流行的微调方法，用于实现有效的对齐
尽管经典 RLHF 方法 (2023, 2020) 已展现出很好的结果，但其多阶段流程（包括训练奖励模型和优化策略模型以最大化奖励）带来了优化挑战 (2023)
近年来，研究者开始探索更简单的离线算法
- 直接偏好优化（Direct Preference Optimization, DPO）(2023) 是其中一种代表性方法
- DPO 通过重新参数化 RLHF 中的奖励函数，直接从偏好数据中学习策略模型，从而避免了显式奖励模型的需求。由于其简洁性和稳定性，DPO 在实际应用中得到了广泛采用
- 在 DPO 中，隐式奖励通过当前策略模型和监督微调（Supervised Fine-Tuned, SFT）模型对响应的似然比的对数来定义
- 但这种奖励设计与生成过程中使用的指标（即策略模型生成响应的平均对数似然）并未直接对齐
- 论文假设这种训练与推理之间的不一致可能导致性能不佳
论文提出 SimPO，一种简单但高效的离线偏好优化算法（如图 1 所示）
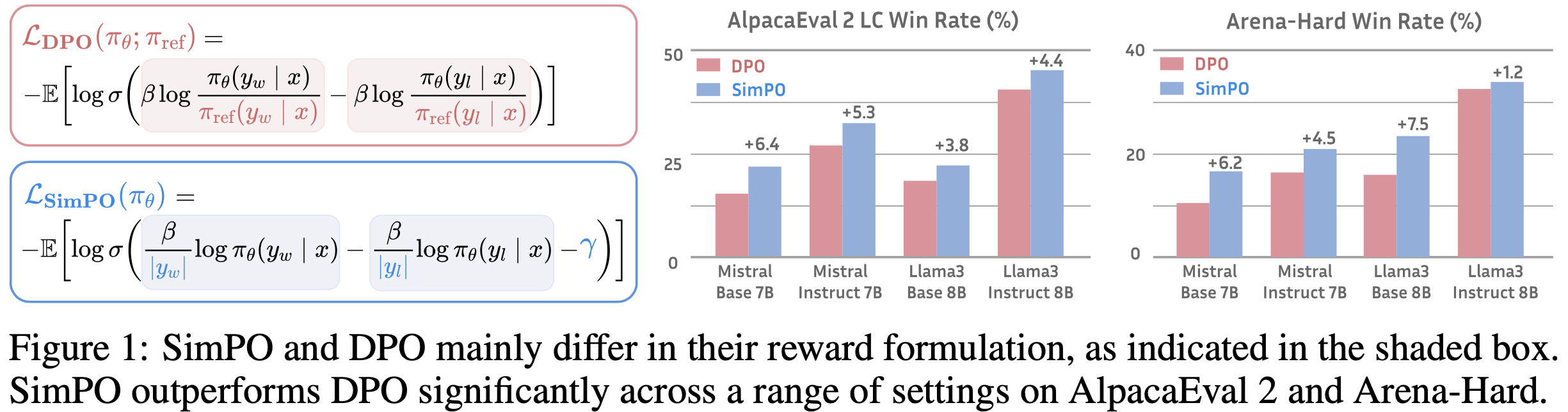
SimPO算法的核心是将偏好优化目标中的奖励函数与生成指标对齐。SimPO 包含两个主要组件：
- 1）长度归一化的奖励（a length-normalized reward） ，计算公式为策略模型对响应中所有 token 的平均对数概率：
  $$
  p_{\theta}(y \mid x) = \frac{1}{|y|} \log \pi_{\theta}(y \mid x) = \frac{1}{|y|} \sum_{i=1}^{|y|} \log \pi_{\theta}(y_i \mid x, y_{ < i}).
  $$
- 2）目标奖励间隔（target reward margin） ，用于确保获胜响应的奖励比失败响应至少高出该间隔值
SimPO 具有以下特性：
- 简洁性（Simplicity） ：SimPO 无需参考模型，与 DPO 和其他基于参考的方法相比更轻量且易于实现
- 显著性能优势（Significant performance advantage） ：尽管设计简单，SimPO 显著优于 DPO 及其最新变体（例如最近的无参考目标 ORPO (2024)）
  - 这种优势在多种训练配置和广泛的聊天式评估（包括 AlpacaEval 2 (2023, 2024) 和具有挑战性的 Arena-Hard (2024) 基准）中保持一致
  - 与 DPO 相比，SimPO 在 AlpacaEval 2 上提升高达 6.4 分，在 Arena-Hard 上提升高达 7.5 分（如图 1 所示）
- 最小长度利用（Minimal length exploitation） ：与 SFT 或 DPO 模型相比，SimPO 未显著增加响应长度（如表 1 所示），表明其对长度利用的抑制效果显著 (2024, 2023, 2023)

SimPO：简单偏好优化（SimPO: Simple Preference Optimization）

本节首先介绍 DPO 的背景（2.1 节），然后指出 DPO 奖励与生成似然指标之间的不一致性，并提出一种无参考的替代奖励设计以解决该问题（2.2 节）
最后，论文通过在 Bradley-Terry 模型中引入目标奖励间隔项来推导 SimPO 的目标函数（2.3 节）

Background: Direct Preference Optimization（DPO）

DPO (2023) 是最流行的偏好优化方法之一
与学习显式奖励模型 (2023) 不同，DPO 通过最优策略的闭式表达式重新参数化奖励函数 $ r $：
$$
r(x, y) = \beta \log \frac{\pi_{\theta}(y \mid x)}{\pi_{\text{ref} }(y \mid x)} + \beta \log Z(x), \tag{1}
$$
- 其中 $\pi_{\theta}$ 是策略模型，$\pi_{\text{ref} }$ 是参考策略（通常是监督微调模型），$Z(x)$ 是配分函数
- 通过将这一奖励设计融入 Bradley-Terry (BT) 排序目标 (1952)，即 $ p(y_w \succ y_l \mid x) = \sigma(r(x, y_w) - r(x, y_l)) $，DPO 用策略模型而非奖励模型表达偏好数据的概率，从而得到以下目标函数：
  $$
  \mathcal{L}_{\text{DPO} }(\pi_{\theta}; \pi_{\text{ref} }) = -\mathbb{E}_{(x,y_w,y_l) \sim \mathcal{D} } \left[ \log \sigma \left( \beta \log \frac{\pi_{\theta}(y_w \mid x)}{\pi_{\text{ref} }(y_w \mid x)} - \beta \log \frac{\pi_{\theta}(y_l \mid x)}{\pi_{\text{ref} }(y_l \mid x)} \right) \right], \tag{2}
  $$
  - 其中 $(x, y_w, y_l)$ 是来自偏好数据集 $\mathcal{D}$ 的偏好对，包含提示（prompt）、获胜响应和失败响应

A Simple Reference-Free Reward Aligned with Generation

DPO 奖励与生成的不一致性（Discrepancy between reward and generation for DPO）。使用公式 (1) 作为隐式奖励存在以下缺点：
- 1）训练时需要参考模型 $\pi_{\text{ref} }$，这会增加内存和计算成本；
- 2）训练优化的奖励与推理时优化的对数似然之间存在不匹配，而推理过程不涉及参考模型
  - 这意味着在 DPO 中，对于任意三元组 $(x, y_w, y_l)$，满足奖励排序 $ r(x, y_w) > r(x, y_l) $ 并不一定意味着满足似然排序 $ p_{\theta}(y_w \mid x) > p_{\theta}(y_l \mid x) $（此处 $ p_{\theta} $ 是公式 (3) 中的平均对数似然）
    - 理解：因为奖励排序中包含了 $\pi_\text{ref}(y|x)$ 在分母上，导致如果 $\pi_\text{ref}(y_w|x) < \pi_\text{ref}(y_l|x)$ 的话，即使奖励 $r(x, y_w) > r(x, y_l) $，也可能出现 $ p_{\theta}(y_w \mid x) < p_{\theta}(y_l \mid x) $ 的
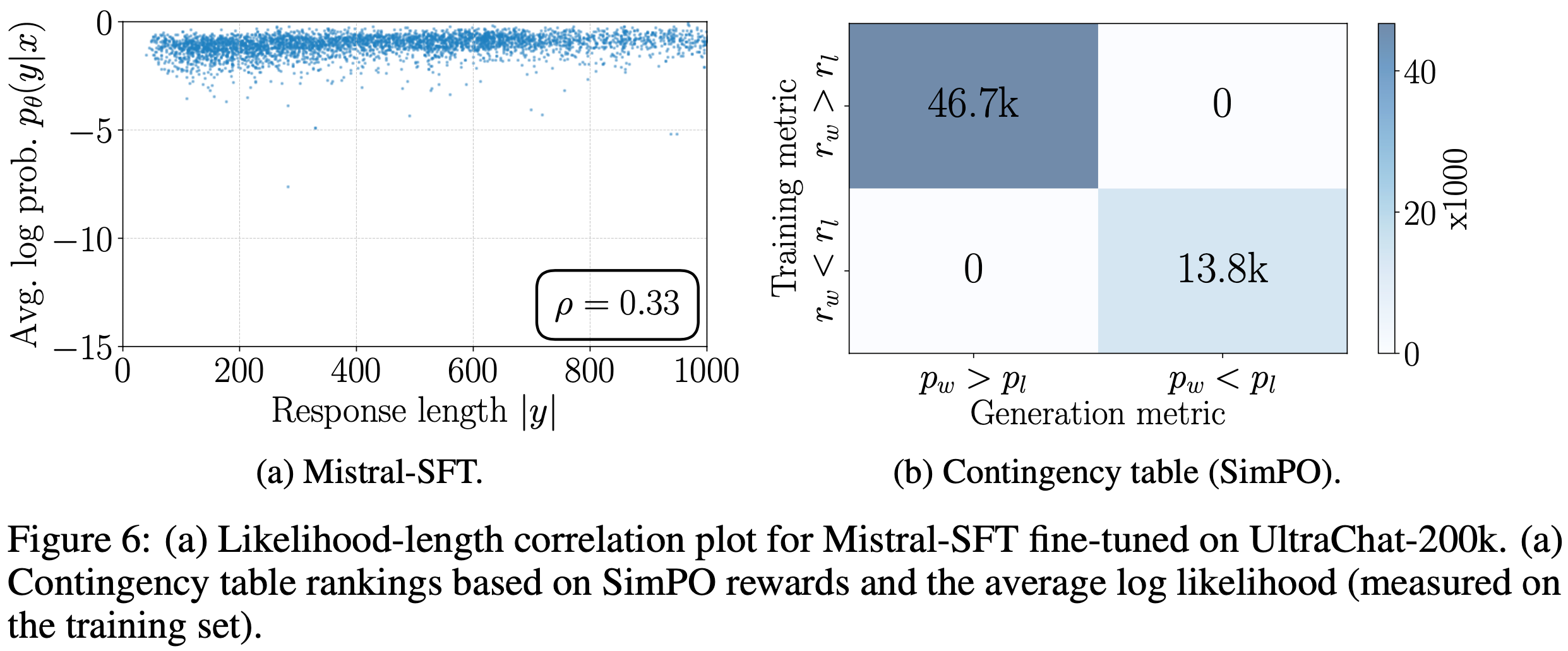
  - 实验中，论文观察到仅约 50% 的训练集三元组在 DPO 训练后满足这一条件（如图 4b 所示）
  - 这一发现与近期研究 (2024) 一致，后者发现现有 DPO 训练模型在平均对数似然排序上表现出随机性，即使经过大量偏好优化
长度归一化的奖励设计（Length-normalized reward formulation）
- 一种解决方案是使用 token 对数概率之和作为奖励，但这会受长度偏差影响（较长序列倾向于具有更低的对数概率）
  - 因此，当 $ y_w $ 比 $ y_l $ 长时，优化对数概率之和作为奖励会迫使模型人为提高较长序列的概率 ，以确保 $ y_w $ 的奖励高于 $ y_l $
- 这种过度补偿会增加模型退化的风险。为解决这一问题，论文考虑使用平均对数似然作为隐式奖励 ：
  $$
  p_{\theta}(y \mid x) = \frac{1}{|y|} \log \pi_{\theta}(y \mid x) = \frac{1}{|y|} \sum_{i=1}^{|y|} \log \pi_{\theta}(y_i \mid x, y_{ < i}). \tag{3}
  $$
  - 注：这里的 $|y|$ 表示队列长度
  - 这一指标常用于 Beam Search (2012, 2016) 和大语言模型中的多项选择任务 (2020, 2021, 2023)
  - 自然地，论文考虑用公式 (3) 中的 $ p_{\theta} $ 替换 DPO 的奖励设计，使其与指导生成的似然指标对齐。这产生了长度归一化的奖励：
    $$
    r_{\text{SimPO} }(x, y) = \frac{\beta}{|y|} \log \pi_{\theta}(y \mid x) = \frac{\beta}{|y|} \sum_{i=1}^{|y|} \log \pi_{\theta}(y_i \mid x, y_{ < i}), \tag{4}
    $$
    - 其中 $\beta$ 是控制奖励差异缩放的常数
    - 问题： $\beta$ 相当于是类似温度系数？
  - 论文发现奖励的长度归一化至关重要；
    - 从奖励设计中移除长度归一化项会导致生成长度更长但质量更低的序列（详见 4.4 节）
这种奖励设计消除了对参考模型的需求 ，与依赖参考的算法相比提升了内存和计算效率

The SimPO Objective

目标奖励间隔 (Target reward margin). ：
- 论文在 Bradley-Terry 目标函数中引入了一个目标奖励间隔项 $\gamma > 0$，用于确保获胜响应 $r(x,y_w)$ 的奖励至少比失败响应 $r(x,y_l)$ 的奖励高出 $\gamma$：
  $$
  p(y_w \succ y_l \mid x) = \sigma \left( r(x,y_w) - r(x,y_l) - \gamma \right). \tag{4}
  $$
- 类别之间的间隔已知会影响分类器的泛化能力 (2012; 1995)
  - 在标准训练设置中，随着目标间隔的增加，泛化能力通常会提升
- 在偏好优化中，两个类别分别是同一输入的获胜和失败响应
- 实践中，论文观察到生成质量最初会随着目标间隔的增加而提升，但当间隔过大时，质量会下降（见第 4.3 节）
- DPO 的一个变体 IPO (2023) 也提出了类似 SimPO 的目标奖励间隔，但其完整目标函数的效果不如 SimPO（见第 4.1 节）
目标函数 (Objective).
- 最后，论文将公式 (4) 代入公式 (5)，得到 SimPO 的目标函数：
  $$
  \mathcal{L}_{\text{SimPO} }(\pi_\theta) = -\mathbb{E}_{(x,y_w,y_l)\sim\mathcal{D} } \left[ \log \sigma \left( \frac{\beta}{|y_w|} \log \pi_\theta(y_w|x) - \frac{\beta}{|y_l|} \log \pi_\theta(y_l|x) - \gamma \right) \right]. \tag{5}
  $$
- 总结来说，SimPO 采用了一种与生成指标直接对齐的隐式奖励公式，无需参考模型
- 此外，它还引入了目标奖励间隔 $\gamma$ 来帮助区分获胜和失败响应
- 在附录 F 中，论文提供了 SimPO 和 DPO 的梯度分析，以进一步理解两种方法的差异
无需 KL 正则化即可防止灾难性遗忘 (Preventing catastrophic forgetting without KL regularization).
- 尽管 SimPO 没有施加 KL 正则化，但论文发现以下实际因素的组合可以确保从偏好数据中有效学习，同时保持泛化能力，从而使得与参考模型的 KL 散度在实验中保持较低水平。这些因素包括：
  - (1) 较小的学习率
  - (2) 覆盖多样领域和任务的偏好数据集
  - (3) LLM 从新数据中学习而不遗忘先验知识的内在鲁棒性
- 论文在第 4.4 节中展示了 KL 散度的实验结果

Experimental Setup

Models and training settings

论文使用两个模型家族进行偏好优化：Llama-3-8B 和 Mistral-7B，分别在基础（Base）和指令微调（Instruct）两种设置下进行实验
- 本节的目标是理解 SimPO 与其他偏好优化方法在不同实验设置下的性能表现
- 论文的最强模型基于 Gemma-2-9B（Instruct setup），并使用更强的奖励模型 RLHFlow/ArmoRM-Llama3-8B-v0.1（见表 1）
- 论文将在附录 J 中展示并讨论这些结果
对于基础设置（Base setup） ：论文遵循 Zephyr（2023）的训练流程
- 首先，论文在 UltraChat-200k 数据集上训练基础模型（如 mistralai/Mistral-7B-v0.1 或 meta-llama/Meta-Llama-3-8B），得到 SFT 模型
- 然后，论文使用 UltraFeedback 数据集对 SFT 模型进行偏好优化
  - 这一设置提供了高度透明性 ，因为 SFT 模型是基于开源数据训练的
对于指令微调设置（Instruct setup） ：论文使用现成的指令微调模型（如 meta-llama/Meta-Llama-3-8B-Instruct 或 mistralai/Mistral-7B-Instruct-v0.2）作为 SFT 模型
- 这些模型经过广泛的指令微调过程，比基础设置中的 SFT 模型更强大且更鲁棒
- 但它们的 RLHF 过程未公开，因此透明度较低
- 为了缓解 SFT 模型与偏好优化过程之间的分布偏移，论文按照（2023）的方法生成偏好数据集，使指令微调设置更接近在线策略（on-policy）设置
- 具体来说，论文使用 UltraFeedback 数据集中的提示，并用 SFT 模型重新生成偏好对 $(y_w, y_l)$
- 对于每个提示 $x$，论文以采样温度 0.8 生成 5 个响应，并使用 llm-blender/PairRM（2023）对响应评分，选择得分最高的作为 $y_w$，最低的作为 $y_l$
- 论文仅进行单轮数据生成，而非迭代生成（2023）
  - 注解：论文还尝试使用更强的奖励模型 RLHFlow/ArmoRM-Llama3-8B-v0.1（2024）对生成的数据排序，这显著提升了性能（见附录 H 和附录 J）（这是论文 Gemma 2 实验中使用的奖励模型）
总结来说，论文共有四种设置：Llama-3-Base、Llama-3-Instruct、Mistral-Base 和 Mistral-Instruct
- 这些配置代表了当前的最先进水平，使论文的模型在多个排行榜上名列前茅
- 论文鼓励未来研究采用这些设置，以便更公平地比较不同算法
- 此外，论文发现超参数调优对所有离线偏好优化算法（包括 DPO 和 SimPO）的性能至关重要
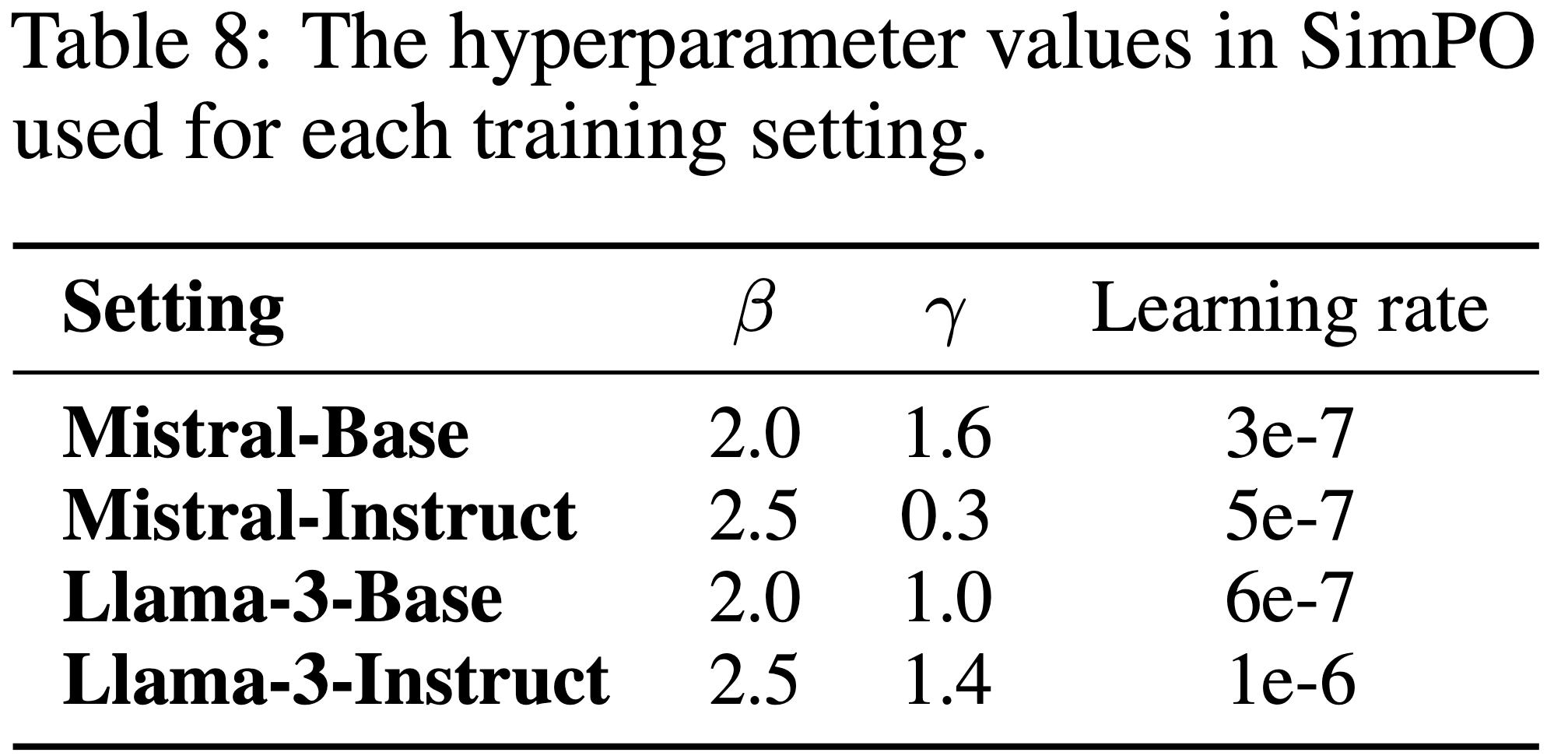
- 通常，对于 SimPO，将 $\beta$ 设为 2.0 到 2.5，$\gamma$ 设为 0.5 到 1.5 ，可以在所有设置中取得良好性能
- 更多细节请参考附录 B

Evaluation Benchmarks

论文主要使用三个流行的开放式指令遵循基准评估模型：MT-Bench（2023）、AlpacaEval 2（2023）和 Arena-Hard v0.1（2024）
这些基准测试模型在多样化查询中的对话能力，已被社区广泛采用（详见表 2）
- AlpacaEval 2 包含来自 5 个数据集的 805 个问题
- MT-Bench 涵盖 8 个类别的 80 个问题
- Arena-Hard（最新发布的）是 MT-Bench 的增强版，包含 500 个定义明确的技术问题求解查询
论文按照每个基准的评估协议报告分数
- 对于 AlpacaEval 2，论文报告原始胜率（raw win rate，WR）和长度控制胜率（length-controlled win rate，LC）（28）
  - LC 指标专门设计用于抵抗模型的冗余性
- 对于 Arena-Hard，论文报告相对于基线模型的胜率（WR）
- 对于 MT-Bench，论文使用 GPT-4 和 GPT-4-Preview-1106 作为评判模型，报告平均 MT-Bench 分数
  - 相对 GPT-4，GPT-4-Preview-1106 生成的参考答案和评判的精确率更高
- 解码细节请参考附录 B
论文还评估了 Huggingface Open Leaderboard 基准（2023）的下游任务，更多细节见附录 C

Baselines

论文将 SimPO 与其他离线偏好优化方法进行比较（见表 3）
- RRHF（2023）和 SLiC-HF（2023）是排序损失
  - RRHF 使用长度归一化的对数似然，类似于 SimPO 的奖励函数
  - SLiC-HF 直接使用对数似然并包含 SFT 目标
- IPO（2023）是一种理论 grounded 的方法，避免了 DPO 的假设（即点奖励可以替代成对偏好）
- CPO（2024）使用序列似然作为奖励，并与 SFT 目标联合训练
- KTO（2024）从非配对偏好数据中学习
- ORPO（2024）引入了一种无需参考模型的奇数比项，直接对比获胜和失败响应，并与 SFT 目标联合训练
  - ORPO 可以直接在偏好数据上训练而无需 SFT 阶段
  - 为公平比较，论文从与其他基线相同的 SFT 检查点开始训练 ORPO，这比从基础检查点开始效果更好
- R-DPO（2024）是 DPO 的改进版，增加了防止长度利用的正则项
- 论文为每个基线方法全面调优超参数并报告最佳性能
论文发现许多 DPO 变体在实证上并未优于标准 DPO （更多细节见附录 B）

Experimental Results

本节展示实验的主要结果，突出 SimPO 在各种基准测试中的优越性能（4.1节），并对以下组件进行深入分析：
- (1) 长度归一化（4.2节）
- (2) 边际项 $\gamma$（4.3节）
- (3) SimPO 优于 DPO 的原因（4.4节）
- 除非另有说明，消融研究均在 Mistral-Base 设置下进行

Main Results and Ablations

SimPO 一致且显著地优于现有偏好优化方法（SimPO consistently and significantly outperforms existing preference optimization methods） ：
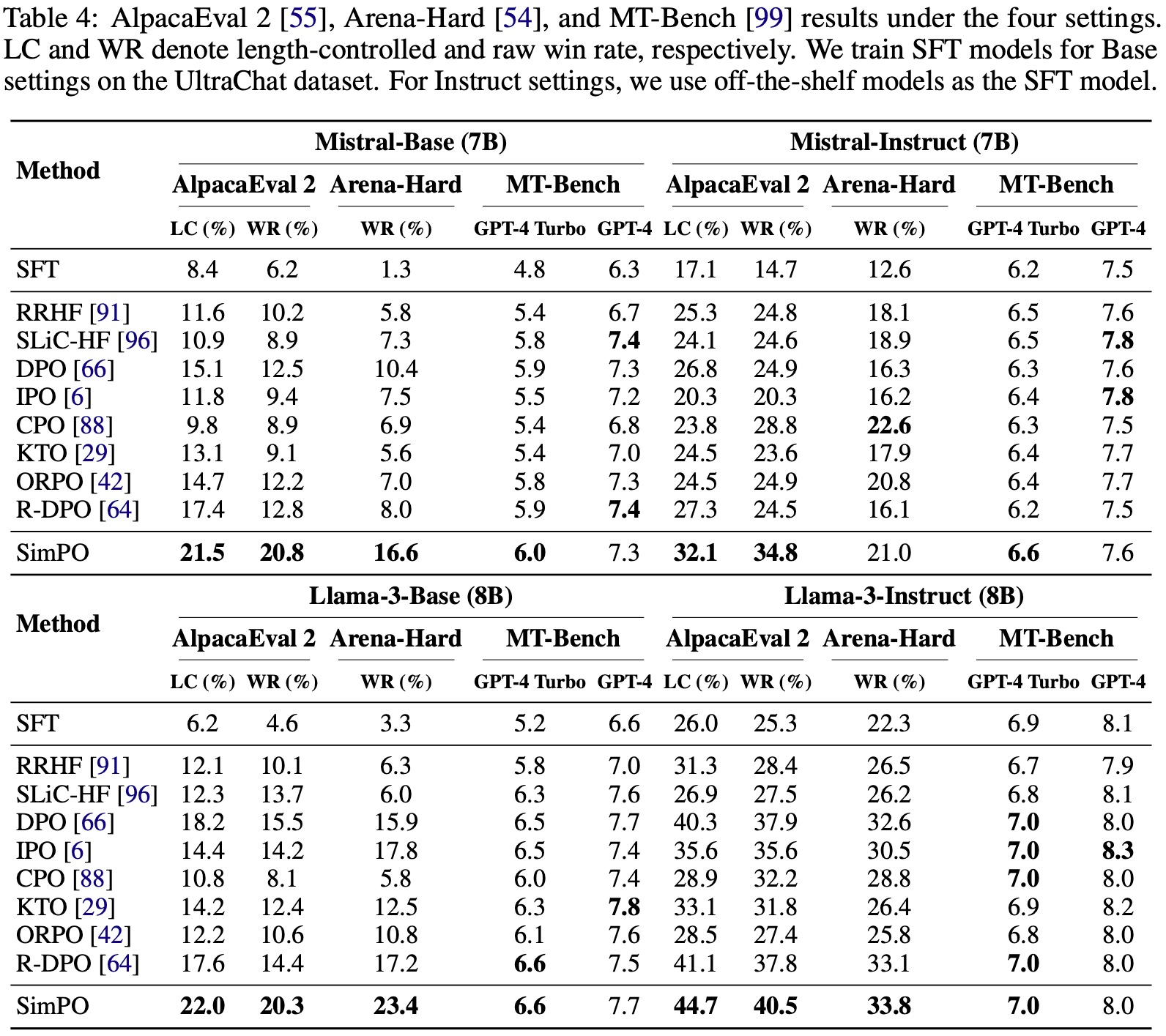
- 如表 4 所示，尽管所有偏好优化算法都能提升 SFT 模型的性能，但 SimPO 凭借其简洁性，在所有基准和设置中均取得了最佳整体表现
- 这些一致且显著的改进凸显了 SimPO 的鲁棒性和有效性
- 值得注意的是，SimPO 在 AlpacaEval 2 的 LC 胜率上比最佳基线高出 3.6 到 4.8 分
- 在 Arena-Hard 上，SimPO 同样表现优异，尽管偶尔被 CPO（2024）超越
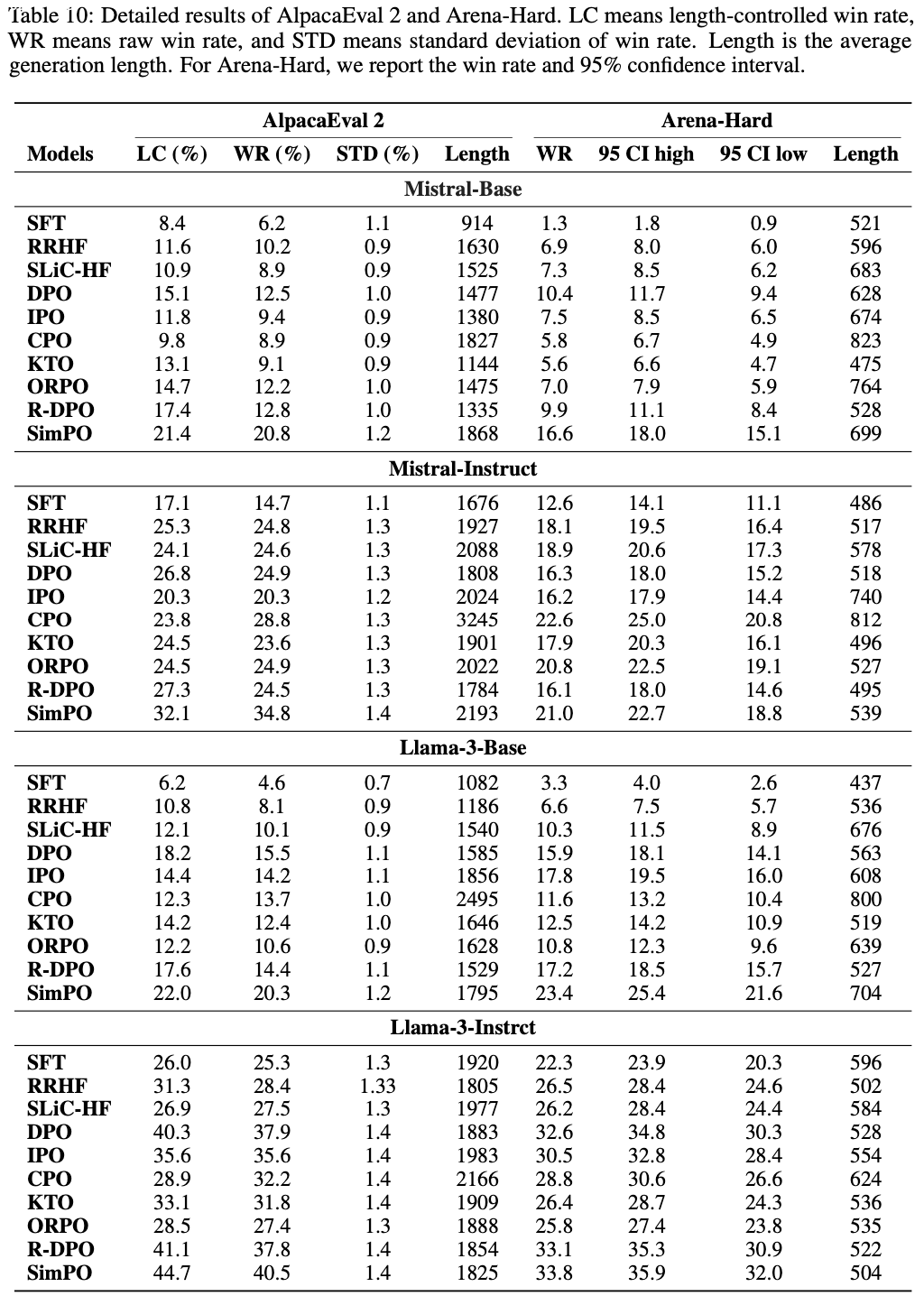
- 论文发现 CPO 生成的响应平均比 SimPO 长 50%（见表 10）
- Arena-Hard 可能因评估中未对长度设限而倾向于更长的生成结果
基准测试质量参差不齐（Benchmark quality varies）
- 尽管三个基准测试被广泛采用，但论文发现 MT-Bench 在不同方法间的区分度较差
- 方法间的微小差异可能源于随机性，这可能是由于其评估数据规模有限和单实例评分协议所致
  - 这一发现与（2024）的观察一致
- 相比之下，AlpacaEval 2 和 Arena-Hard 能更有意义地区分不同方法
- 论文注意到 Arena-Hard 的胜率显著低于 AlpacaEval 2，表明 Arena-Hard 是一个更具挑战性的基准
  - 尽管论文的模型在基准测试中表现优异，但这些评估存在局限性，包括查询空间受限和基于模型评估的潜在偏差
指令微调设置带来显著性能提升（The Instruct setting introduces significant performance gains）
- 在所有基准测试中，指令微调设置始终优于基础设置
- 这一改进可能源于初始化使用的 SFT 模型质量更高，以及这些模型生成的偏好数据质量更高
SimPO 的两个关键设计均至关重要（Both key designs in SimPO are crucial）
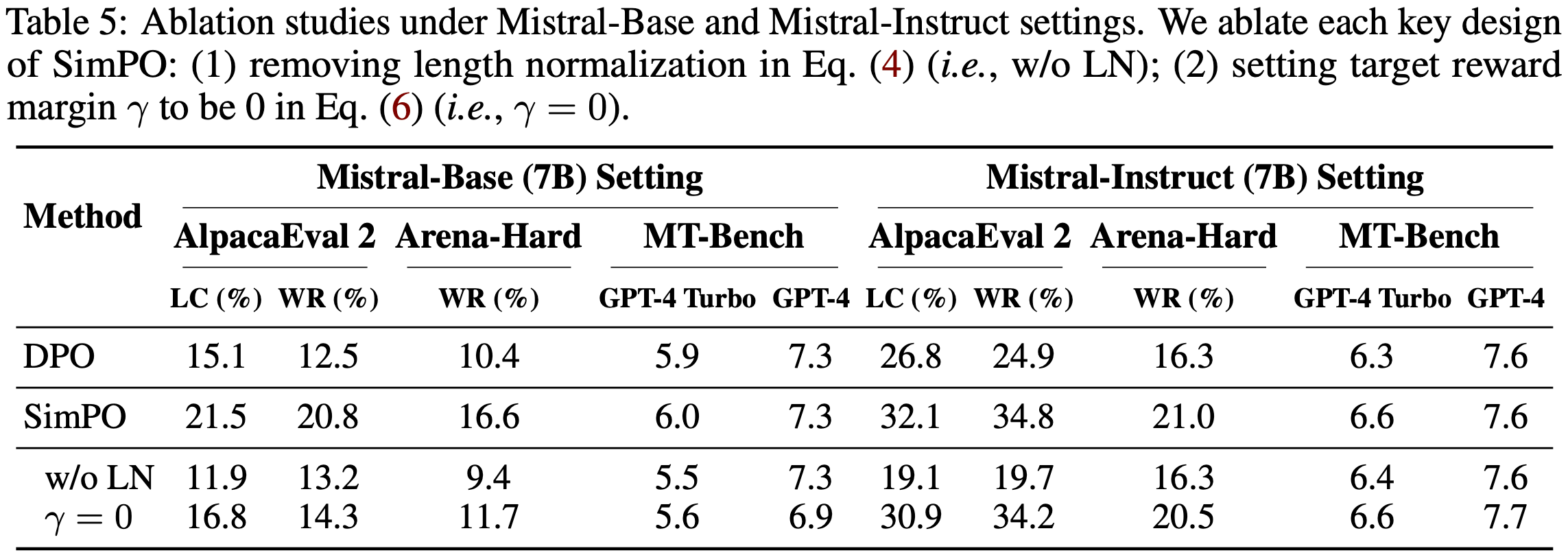
- 表 5 展示了 SimPO 每个关键设计的消融结果：
  - (1) 移除公式（4）中的长度归一化（即 w/o LN）；
  - (2) 将公式（6）中的目标奖励边际设为 0（即 $\gamma=0$）
- 移除长度归一化对结果负面影响最大
  - 作者的检查发现，这会导致生成冗长且重复的模式，显著降低输出质量（见附录 E）
- 将 $\gamma$ 设为 0 也会导致性能下降，表明 0 并非最优目标奖励边际
- 在以下小节中，论文将深入分析这两个设计选择

长度归一化（LN）防止长度利用（Length Normalization (LN) Prevents Length Exploitation）

LN 增加所有偏好对的奖励差异，无论其长度如何
- 公式（5）中的 Bradley-Terry 目标本质上是优化奖励差异 $\Delta r = r(x,y_w) - r(x,y_l)$，使其超过目标边际 $\gamma$
- 论文研究了从 UltraFeedback 训练集中获胜和失败响应的长度差异 $\Delta l = |y_w| - |y_l|$ 与学习到的奖励差异之间的关系
- 论文使用 SFT 模型、SimPO 模型以及未使用长度归一化的 SimPO 模型测量奖励差异（$r_{\text{SimPO} }$：公式（4））
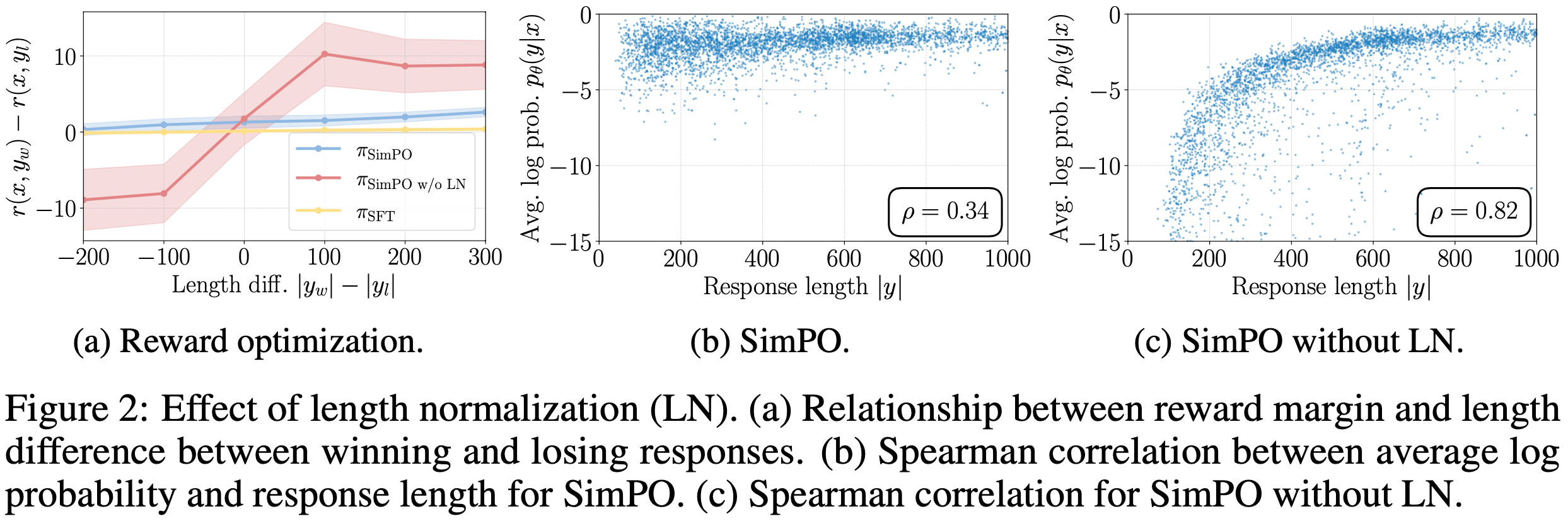
- 结果如图 2(a) 所示，论文发现带 LN 的 SimPO 对所有响应对均实现了正的奖励边际，无论其长度差异如何，并且始终比 SFT 模型提高了边际
  - 相比之下，不带 LN 的 SimPO 在获胜响应比失败响应短时会导致负的奖励差异，表明模型对这些实例的学习效果较差
移除 LN 会导致奖励与响应长度强正相关，引发长度利用
- 图 2(b) 和 2(c) 展示了在保留集上，使用 SimPO 和未使用 LN 的 SimPO 训练的模型的平均对数似然（公式（3）中的 $p_\theta$）与响应长度的关系
- 未使用 LN 训练的模型在似然与响应长度之间表现出更强的 Spearman 正相关性，表明其倾向于利用长度偏差生成更长序列（见附录 E）。相比之下，SimPO 的 Spearman 相关系数与 SFT 模型相似（见图 5(a)）

The Impact of Target Reward Margin in SimPO

$\gamma$ 对奖励准确性和胜率的影响（Influence of γ on reward accuracy and win rate）
- 论文研究了 SimPO 中目标奖励边际 $\gamma$ 对保留集上奖励准确性和 AlpacaEval 2 胜率的影响，结果如图 3(a) 所示。奖励准确性通过偏好对中获胜响应的奖励高于失败响应的比例（即 $r(x,y_w) > r(x,y_l)$）来衡量。论文观察到，奖励准确性随 $\gamma$ 的增加而提升，表明强制更大的目标奖励边际能有效提高奖励准确性。然而，AlpacaEval 2 的胜率随 $\gamma$ 的增加先升后降，说明生成质量并非仅由奖励边际决定
$\gamma$ 对奖励分布的影响（Impact of $\gamma$ on the reward distribution.）
- 论文在图 2(b) 和图 2(c) 中可视化不同 $\gamma$ 值下学习到的奖励边际 $r(x,y_w) - r(x,y_l)$ 和获胜响应奖励 $r(x,y_w)$ 的分布
- 增加 $\gamma$ 会使分布趋于平坦，并降低获胜序列的平均对数似然
  - 这最初会提升性能，但最终可能导致模型退化
- 论文假设在设置 $\gamma$ 值时，需要在准确逼近真实奖励分布和保持良好校准的似然之间进行权衡
  - 这一平衡的进一步探索留待未来工作

In-Depth Analysis of DPO vs. SimPO

本节论文从以下方面比较 SimPO 和 DPO：
- (1) 似然-长度相关性
- (2) 奖励公式
- (3) 奖励准确性
- (4) 算法效率
- 论文证明 SimPO 在奖励准确性和效率上优于 DPO
DPO 奖励隐含地促进长度归一化（DPO reward implicitly facilitates length normalization）
- 尽管 DPO 的奖励表达式：
  $$ r(x,y) = \beta \log \frac{\pi_\theta(y|x)}{\pi_{\text{ref} }(y|x)}$$
  - 该表达式（排除配分函数）没有显式的长度归一化项，但策略模型与参考模型之间的对数比可以隐式抵消长度偏差
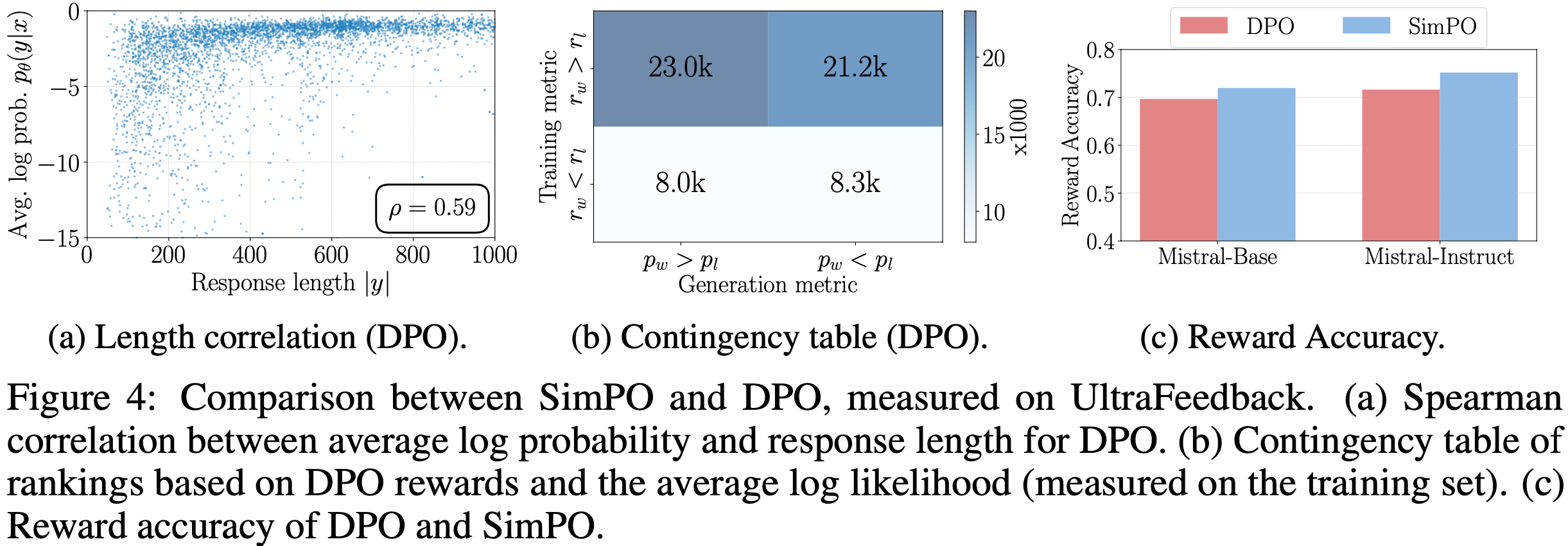
- 如表 6 和图 4(a) 所示，使用 DPO 降低了平均对数似然与响应长度之间的 Spearman 相关系数 ，但与 SimPO 相比仍表现出更强的正相关性
  - 注意这一相关性并未完全反映生成长度。尽管 DPO 显示出更强的相关性，但其生成响应的长度与 SimPO 模型相当甚至略短。更多细节见附录 E
DPO 奖励与生成似然不匹配（DPO reward mismatches generation likelihood）
- DPO 的奖励公式为：
  $$ r_\theta(x,y) = \beta \log \frac{\pi_\theta(y|x)}{\pi_{\text{ref} }(y|x)}$$
- 该奖励公式与直接影响生成的平均对数似然度量存在差异：
  $$ p_\theta(y|x) = \frac{1}{|y|} \log \pi_\theta(y|x)$$
- 如图 4(b) 所示，在 UltraFeedback 训练集中满足 $r_\theta(x,y_w) > r_\theta(x,y_l)$ 的实例中，近一半的偏好对满足 $p_\theta(y_w|x) < p_\theta(y_l|x)$
- 相比之下，SimPO 直接使用平均对数似然（按 $\beta$ 缩放）作为奖励表达式，完全消除了这种差异（见图 4(b)）
DPO 在奖励准确性上落后于 SimPO（DPO lags behind SimPO in terms of reward accuracy）
- 在图 4(c) 中，论文比较了 SimPO 和 DPO 的奖励准确性，评估它们最终学习到的奖励与保留集上偏好标签的匹配程度
- SimPO 始终比 DPO 取得更高的奖励准确性，表明论文的奖励设计有助于更好地泛化，从而生成更高质量的响应
SimPO 和 DPO 的 KL 散度（KL divergence of SimPO and DPO）
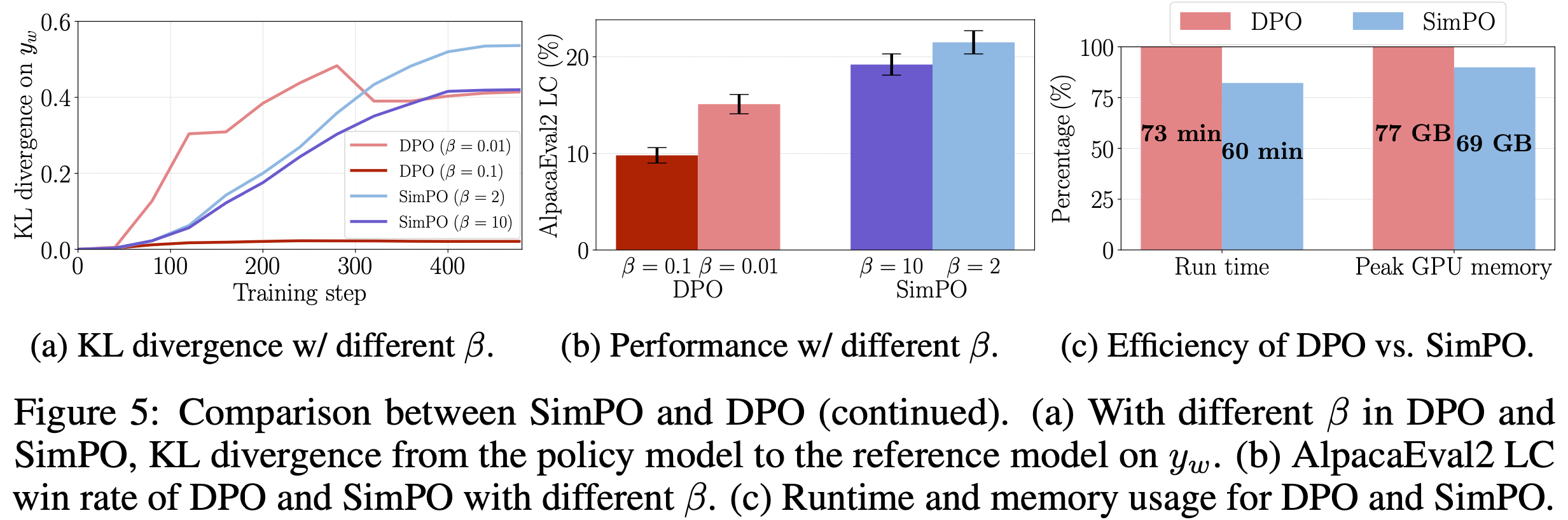
- 在图 5(a) 中，论文展示了在不同 $\beta$ 下，使用 DPO 和 SimPO 训练的策略模型与参考模型在保留集获胜响应上的 KL 散度
- 图 5(b) 展示了相应的 AlpacaEval 2 LC 胜率
- 尽管 SimPO 未对参考模型应用任何形式的正则化，但其 KL 散度保持在合理较低水平
- 增加 $\beta$ 会降低 DPO 和 SimPO 的 KL 散度，其中 DPO 在较高 $\beta$ 值时下降更明显
- 在此特定设置（Mistral-base）中，图 5(b) 显示较小的 $\beta$ 可以提升 AlpacaEval 2 性能，尽管 KL 散度更高
  - 论文观察到在某些设置（如 Llama-3-Instruct）中，较大的 $\beta$（如 $\beta=10$）会带来更好的性能
  - 论文假设当参考模型较弱时，严格约束策略模型可能无益
- 需要注意的是，尽管在适当调参下论文未观察到训练崩溃或退化，但 SimPO 理论上可能在没有显式正则化的情况下导致奖励破解（reward hacking） ，此时模型可能损失很低但生成结果退化
SimPO 比 DPO 更节省内存和计算资源（SimPO is more memory and compute-efficient than DPO）
- SimPO 的另一优势是其高效性，因为它不使用参考模型
- 图 5(c) 展示了在 Llama-3-Base 设置下，使用 8xH100 GPU 时 SimPO 和 DPO 的总体运行时间和单 GPU 峰值内存使用情况
- 与普通 DPO 实现相比，SimPO 通过消除参考模型的前向传递，减少了约 20% 的运行时间和 10% 的 GPU 内存使用
  - 如果将参考模型的前向传递与实际偏好优化分离，DPO 也能实现与 SimPO 相当的内存效率，但这一实现并非标准做法

RLHF

RLHF 是一种将 LLM 与人类偏好和价值观对齐的技术（2017; 2019; 2022）
经典的 RLHF 流程通常包含三个阶段：
- 监督微调（2021; 2023）
- 奖励模型训练（2023; 2024）
- 策略优化（2017）
近端策略优化（Proximal Policy Optimization, PPO）（2017）是 RLHF 第三阶段广泛使用的算法
RLHF 框架还被应用于多种任务，例如减少毒性（2023）、确保安全性（2023）、提升帮助性（2024）以及增强模型推理能力（2024）
近期研究（2023）指出，RLHF 从数据收集到模型训练的整个流程存在挑战
此外，RLHF 可能导致模型生成冗长输出（2023; 2024），这一问题也引发了广泛关注

Offline vs. Iterative Preference Optimization

由于在线偏好优化算法复杂且难以优化（2023），研究者开始探索更高效的离线算法
直接偏好优化（Direct Preference Optimization, DPO）（2023）是一个典型代表
但 DPO 缺乏显式的奖励模型，限制了其从最优策略中采样偏好数据的能力
为解决这一问题，研究者尝试通过训练监督微调策略（2023）或结合拒绝采样的改进策略（2024）生成偏好数据，使策略能够从最优策略生成的数据中学习
进一步研究将这种方法扩展到迭代训练框架（2024; 2024）
论文专注于离线设置 ，避免任何迭代训练过程

Preference Optimization Objectives

除 DPO 外，研究者还提出了多种偏好优化目标
- 排序目标支持对多个实例进行比较（2023; 2024）
另一类研究探索了不依赖参考模型的简化目标（2024），与 SimPO 类似
- （2024）提出了一种联合优化指令和响应的方法，发现其能有效改进 DPO
- （2024）专注于在监督微调和对齐模型之间进行后训练外推，以进一步提升模型性能
论文对比了 SimPO 与一系列离线算法，包括 RRHF（2023）、SLiC-HF（2023）、DPO（2023）、IPO（2023）、CPO（2024）、KTO（2024）、ORPO（2024）和 R-DPO（2024），发现 SimPO 在效率和性能上均优于它们
近期 GPO（Generalized Preference Optimization，2024）提出了一个统一不同离线算法的广义偏好优化框架，而 SimPO 可视为其特例

附录 A Limitations

更深入的理论分析（More in-depth theoretical analysis） ：
- 尽管 SimPO 在实验上取得了成功，但仍需更严格的理论分析以全面理解其有效性
- 此外，SimPO 引入了目标奖励间隔这一超参数，需手动调整
- 未来工作可探索如何自动确定最优间隔，并提供更理论化的解释
安全性与诚实性（Safety and honesty） ：
- SimPO 旨在通过优化生成质量来提升模型性能，但未显式考虑安全性和诚实性，而这在实际应用中至关重要
- 未来研究可将安全性和诚实性约束整合到 SimPO 中，确保生成内容既高质量又安全可靠
- 论文使用的数据集 UltraFeedback 主要关注有帮助性，未来的研究可以做更全面的研究（如考虑利用大规模偏好数据和更强调安全性的评估基准）
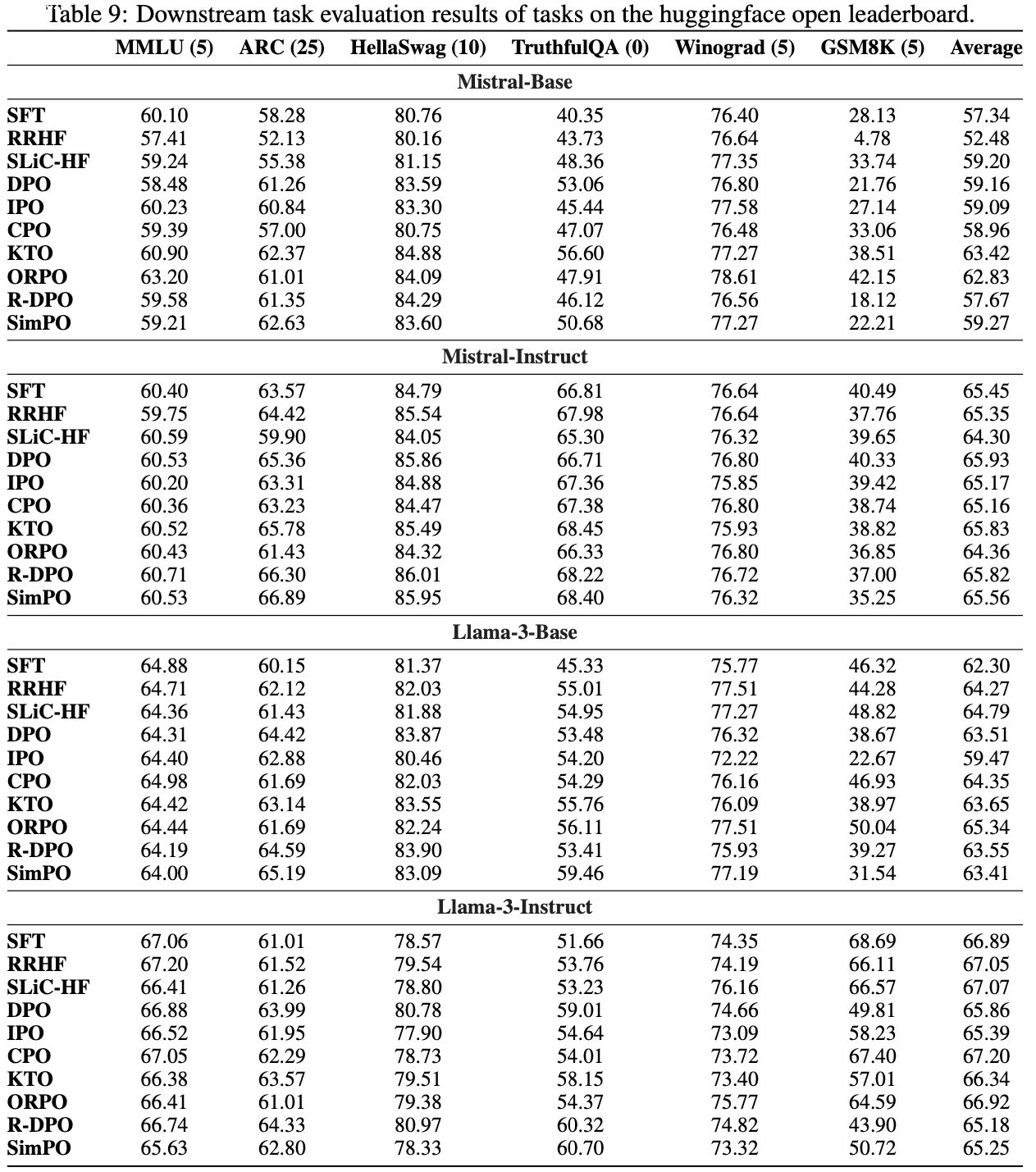
- 尽管如此，作者观察到在数据集 TruthfulQA 上，SimPO 方法一致优于表9中的其他方法，这显示了 SimPO 在安全性对齐方面的潜力
数学任务性能下降（Performance drop on math） ：
- 论文发现偏好优化算法通常会降低下游任务性能 ，尤其是在数学推理密集型（reasoning-heavy）任务（如 GSM8K）上（正如表9所展示的那样）
- SimPO 的表现有时与 DPO 相当或更差
  - 这可能与训练数据集的选择、超参数设置或评估模板不匹配有关
  - 一种解释是偏好优化目标可能在提升偏好序列的似然上没有效果（尽管提升了奖励间隔（Reward margin））
- （2024）首次观察到这一现象，并指出这可能妨碍从修改一个 Token 就发生翻转（flip）的数学偏好对中学习（比如将 2 + 2 = 4 修改为 2 + 2 = 5）
  - 该工作提出通过添加参考模型校准的监督微调损失来缓解问题
  - 未来工作可将此策略整合到 SimPO 中，以提升数学推理任务的性能

附录 B Implementation Details

论文发现超参数调优对偏好优化方法的性能至关重要，但其重要性在先前研究中可能被低估，导致基线结果未达最优
- 为确保公平对比，论文为所有方法进行了全面的超参数调优
通用训练超参数（General training hyperparameters） ：
- 在基础训练设置中，论文使用 UltraChat-200k 数据集（2023）训练监督微调模型
  - 学习率为 2e-5
  - 批量大小为 128
  - 最大序列长度为 2048
  - 采用余弦学习率调度
  - 预热步数为 10%
  - 训练 1 个 epoch
  - 所有模型均使用 Adam 优化器（2014）
- 在偏好优化阶段，论文通过初步实验搜索批量大小（32、64、128）和训练周期（1、2、3）
  - 作者发现批量大小为 128 和单周期（epoch=1）训练通常能带来最佳结果
  - 因此，论文将这些值固定用于所有偏好优化实验
  - 此外，设置最大序列长度为 2048，并在偏好优化数据集上应用 10% 预热步数的余弦学习率调度
方法特定超参数（Method-specific training hyperparameters） ：
- 论文注意到不同偏好优化方法的最佳学习率差异较大 ，且显著影响基准性能
- 因此，论文为每种方法单独搜索学习率（3e-7、5e-7、6e-7、1e-6）
- 表 7 展示了基线方法的超参数搜索范围
- 表 8 列出了 SimPO 在各设置下的超参数值
解码超参数（Decoding hyperparameters） ：
- 在 AlpacaEval 2 中，论文采用采样解码策略
  - 温度设置为 0.7（Mistral-Base）
  - 0.5（Mistral-Instruct）
  - 0.9（Llama 3）
- 在 Arena-Hard 中，所有设置和方法均使用贪婪解码
- 在 MT-Bench 中，遵循官方解码配置，为不同类别定义不同的采样温度
计算环境（Computation environment） ：
- 论文所有训练实验均在 8 块 H100 GPU 上完成，基于 alignment-handbook 代码库实现

附录 C：Downstream Task Evaluation

为了研究偏好优化方法如何影响下游任务性能，论文在 Huggingface Open Leaderboard (2023) 列出的多个任务上评估了不同方法训练的模型
这些任务包括 MMLU (2020)、ARC (2018)、HellaSwag (2019)、TruthfulQA (2022)、Winograd (2012) 和 GSM8K (2021)
论文遵循既定的评估协议，所有模型的结果如表 9 所示
- 总体而言，论文发现偏好优化对不同任务的影响各不相同
知识保留度高，损失小（Knowledge is largely retained with a small loss） ：
- 与监督微调（Supervised Fine-Tuned, SFT）检查点相比，所有偏好优化方法通常能保持 MMLU 性能，仅有小幅下降
- 在这方面，SimPO 与 DPO 基本相当
阅读理解和常识推理能力提升（Reading comprehension and commonsense reasoning improves） ：
- 对于 ARC 和 HellaSwag，偏好优化方法通常比 SFT 检查点表现更好
- 一种假设是偏好优化数据集中包含与这些任务类似的提示，这有助于模型更好地理解上下文，提升阅读理解和常识推理能力
真实性提高（Truthfulness improves） ：
- 令人惊讶的是，论文发现偏好优化方法能持续提升 TruthfulQA 性能，某些情况下提升幅度超过 10%
- 同样，论文假设偏好数据集中包含强调真实性的实例，这有助于模型更好地理解上下文并生成更真实的回答
数学性能下降（Math performance drops） ：
- GSM8K 是不同方法间表现波动最大的基准
- 值得注意的是，除了 ORPO，几乎所有方法在一个或多个设置中都会导致性能下降
  - 论文假设 ORPO 能保持性能主要是因为其监督微调损失起到了调节作用
- (2024) 的研究表明，在偏好优化目标中加入基于参考模型的监督微调损失可以有效解决这一问题，并保持数学任务上的性能
总体而言，下游性能的模式难以确定
- 由于使用了不同的预训练模型、偏好优化数据集和目标，进行全面分析较为困难
- 近期研究表明，基于梯度的方法可能有助于找到与下游任务相关的数据 (2024)，未来或可扩展用于理解偏好优化的影响
- 作者认为，未来需要对偏好优化如何影响下游性能进行更严谨和全面的研究

附录 D：AlpacaEval 2 和 Arena-Hard 的标准差 (Standard Deviation of AlpacaEval 2 and Arena-Hard)

论文在表 10 中展示了 AlpacaEval 2 的标准差和 Arena-Hard 的 95% 置信区间
- 所有指标均合理，未出现显著异常或不稳定情况

附录 E：Generation Length Analysis

长度归一化减少生成长度并提升生成质量（Length normalization decreases generation length and improves generation quality）
- 从 SimPO 目标中移除长度归一化（Length Normalization, LN）会得到类似于对比偏好优化（Contrastive Preference Optimization, CPO）(2024) 的方法
  - CPO 在机器翻译中表现优异
- 然而，如果没有监督微调损失 ，未使用长度归一化的奖励最大化目标在偏好优化中效果较差
- 论文分析了在 AlpacaEval 2 和 Arena-Hard 上使用或不使用长度归一化训练的模型的生成长度
- 如图 6 所示：
  - 长度归一化显著减少了生成长度，降幅高达 25%
  - 尽管生成长度更短，但使用长度归一化的模型在两个基准上的胜率显著更高
  - 这表明长度归一化能有效控制生成响应的冗余性，同时提升生成质量
长度并非生成质量的可靠指标（Length is not a reliable indicator of generation quality）
- 论文进一步分析了不同方法训练的模型在 AlpacaEval 2 和 Arena-Hard 上的生成长度，如表 10 所示
- 总体而言，论文发现没有一种方法能在所有设置中一致生成更长或更短的响应
- 此外，某些方法可能生成更长的响应，但未必在基准上取得更高的胜率
- 这表明生成响应的长度并不能可靠反映生成质量
SimPO 对响应长度的利用最小化（SimPO demonstrates minimal exploitation of response length.）
- 论文观察到，在 Llama-3-Instruct 案例中 ，SimPO 的生成长度比 DPO 更短 ，但在其他设置中生成长度更长
  - 在 AlpacaEval 2 上最多长出 26%
  - 在 Arena-Hard 上仅长约 5%
- 可以说，生成长度很大程度上取决于评估基准
- 更强的指标是 SimPO 在 AlpacaEval 2 上的长度控制胜率始终高于原始胜率 ，表明其对响应长度的利用最小化

附录 F：Gradient Analysis

作者检查了 SimPO 和 DPO 的梯度，以理解它们对训练过程的不同影响：
$$
\nabla_{\theta}\mathcal{L}_{\text{SimPO} }(\pi_{\theta})=-\beta\mathbb{E}_{(x,y_{w},y_{l})\sim\mathcal{D} }\left[s_{\theta}\cdot\left(\underbrace{\frac{1}{|y_{w}|}\nabla_{\theta}\log\pi_{\theta}(y_{w}|x)}_{\text{increase likelihood on } y_w }-\underbrace{\frac{1}{|y_{l}|}\nabla_{\theta}\log\pi_{\theta}(y_{l}|x)}_{\text{decrease likelihood on } y_l}\right)\right], \\
\nabla_{\theta}\mathcal{L}_{\text{DPO} }(\pi_{\theta})=-\beta\mathbb{E}_{(x,y_{w},y_{l})\sim\mathcal{D} }\left[d_{\theta}\cdot\left(\underbrace{\nabla_{\theta}\log\pi_{\theta}(y_{w}|x)}_{\text{increase likelihood on } y_w }-\underbrace{\nabla_{\theta}\log\pi_{\theta}(y_{l}|x)}_{\text{decrease likelihood on } y_l }\right)\right],
$$
其中：
$$
s_{\theta}=\sigma\left(\frac{\beta}{|y_{l}|}\log\pi_{\theta}(y_{l}|x)-\frac{\beta}{|y_{w}|}\log\pi_{\theta}(y_{w}|x)+\gamma\right), \quad d_{\theta}=\sigma\left(\beta\log\frac{\pi_{\theta}(y_{l}|x)}{\pi_{\text{ref} }(y_{l}|x)}-\beta\log\frac{\pi_{\theta}(y_{w}|x)}{\pi_{\text{ref} }(y_{w}|x)}\right)
$$
- 分别表示 SimPO 和 DPO 中的梯度权重
可以看出差异有两方面：
- (1) 比较梯度权重 $s_{\theta}$ 和 $d_{\theta}$
  - SimPO 的梯度权重 $s_{\theta}$ 不涉及参考模型，且具有直观解释：对于策略模型错误地为 $y_l$ 分配比 $y_w$ 更高似然的样本，权重会更高；
- (2) 比较梯度更新
  - SimPO 对 $y_l$ 和 $y_w$ 的梯度进行了长度归一化，而 DPO 没有
  - 这与实证发现 (2024) 一致：DPO 可能利用数据中的长度偏差 ，更长的序列会因包含更多 token 而在 DPO 中获得更大的梯度更新 ，从而主导训练过程

附录 G：Qualitative Analysis

论文在图 7 和图 8 中分别展示了 Mistral-Base 和 Mistral-Instruct 在 AlpacaEval 2 和 Arena-Hard 上的胜率热图
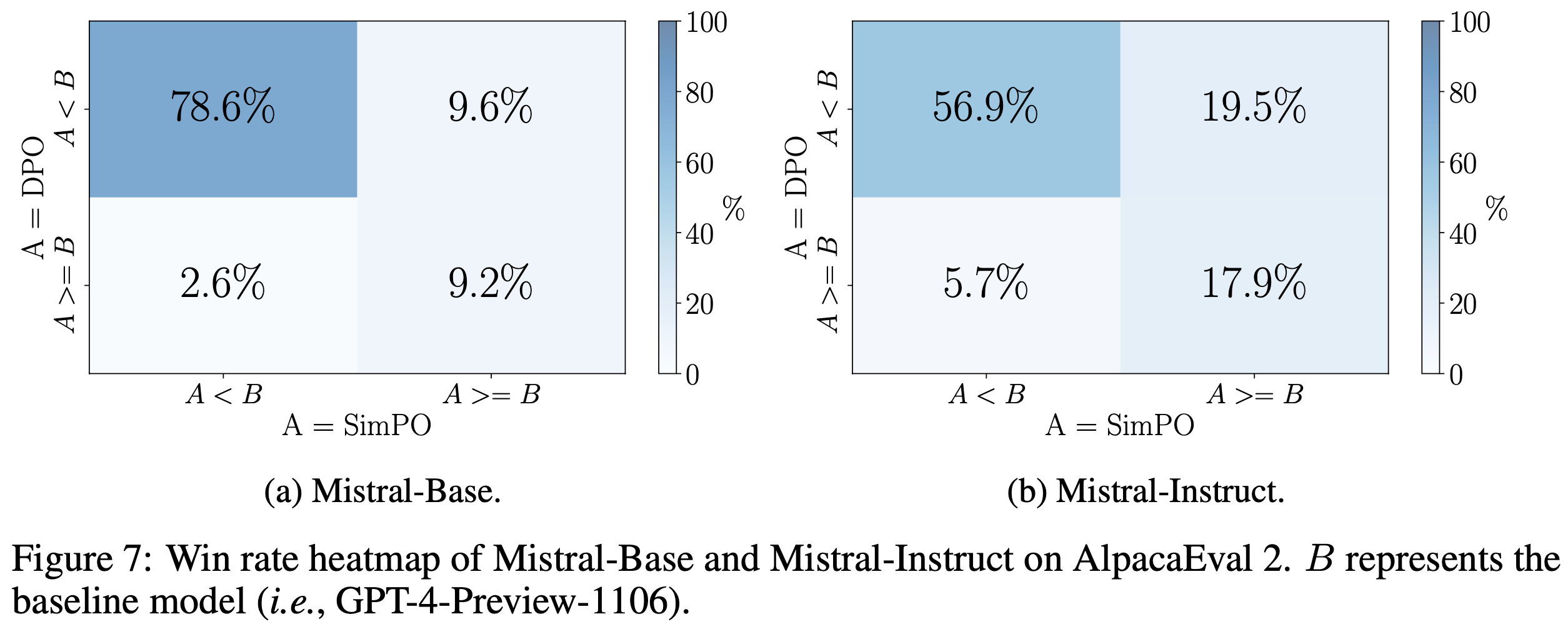
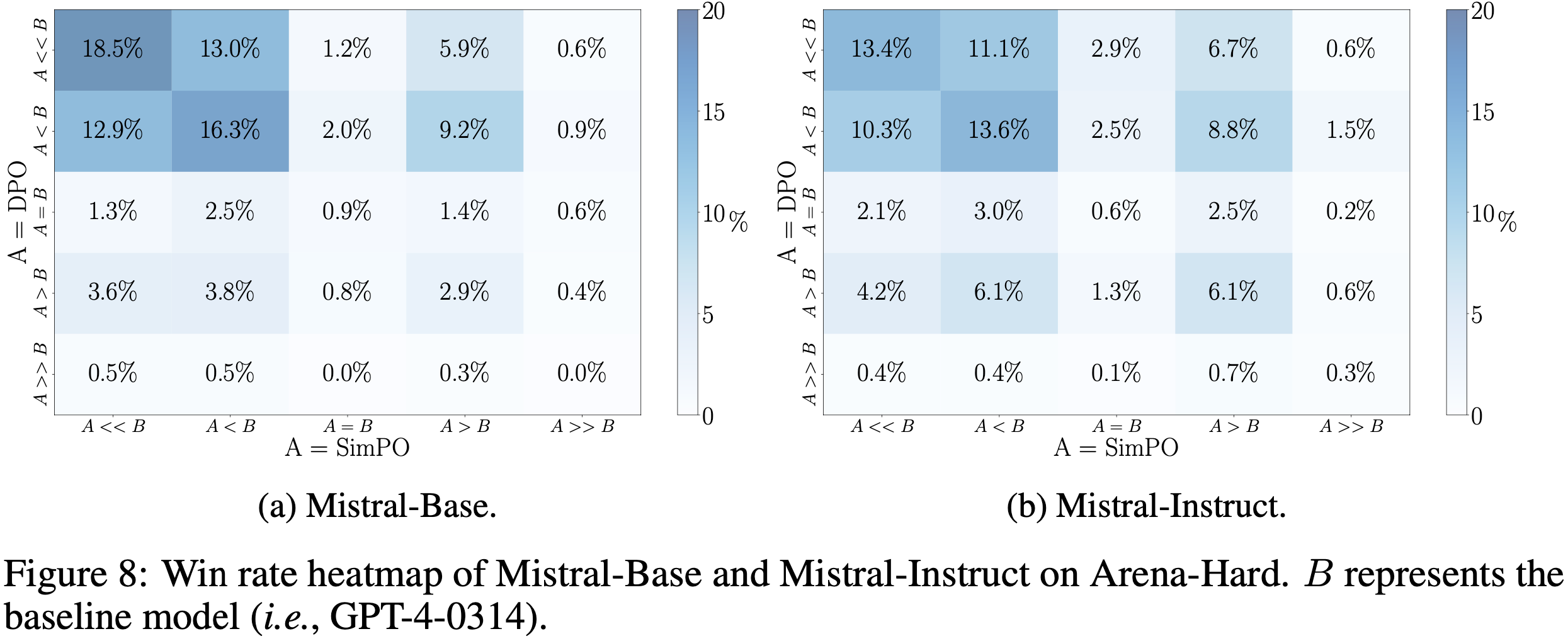
基于此分析，论文在 AlpacaEval 2 上展示了 SimPO 模型、DPO 模型和基线模型 GPT-4-Preview-1106 生成的响应示例
比较 SimPO 与 DPO
- 在图 9 和图 10 中，论文展示了一个案例，其中 Mistral-Base-SimPO 生成的答案比 Mistral-Base-DPO 结构更好
  - 给定问题“如何判断一个人对对话是真正感兴趣还是仅仅出于礼貌？”，DPO 模型生成了一长串要点，使得不同点之间的关系难以理解
  - 相比之下，SimPO 模型生成了一个结构良好的答案，首先对不同行为进行了高层分类，随后为每个类别提供了详细建议，使得答案更易读和理解
比较使用 SimPO 训练的 Instruct 模型与 Base 模型 ：
- 在图 11 中，论文展示了一个案例，其中 Llama-3-Instruct 生成的答案比基线模型以及 Llama-3-Base-SimPO 模型更详细且格式更好
- 对于问题“阿根廷人说什么语言？”，Llama-3-Base-SimPO 仅给出了非常简短的答案
- GPT-4-Preview-1106 的答案更详细，解释了阿根廷西班牙语与标准西班牙语的区别，但格式不够清晰，解析稍难
- Llama-3-Instruct-SimPO 提供了详细且格式良好的答案，更易阅读和理解，同时提供了足够的细节

附录 H：Llama-3-Instruct v0.2 (Jul 7, 2024)）

本节论文更新了 Llama-3-Instruct 的实验设置，主要改进是使用更强的奖励模型（reward model）来标注生成的偏好数据
更强的奖励模型显著提升效果（Enhanced reward model yields significantly better results）
- 在之前的版本中，论文使用 PairRM（2023）作为奖励模型对生成的候选回答进行排序
- 表 12 的结果显示，将排序数据的奖励模型从 PairRM 替换为 ArmoRM（2024）后，模型性能显著提升
- 这凸显了高质量偏好优化数据对性能的重要性
- SimPO 在 AlpacaEval 2 上的长度控制胜率（LC win rate）达到 53.7%，在 Arena-Hard 上达到 36.5%，分别比前一版本提升了 9.0 和 2.7 个百分点
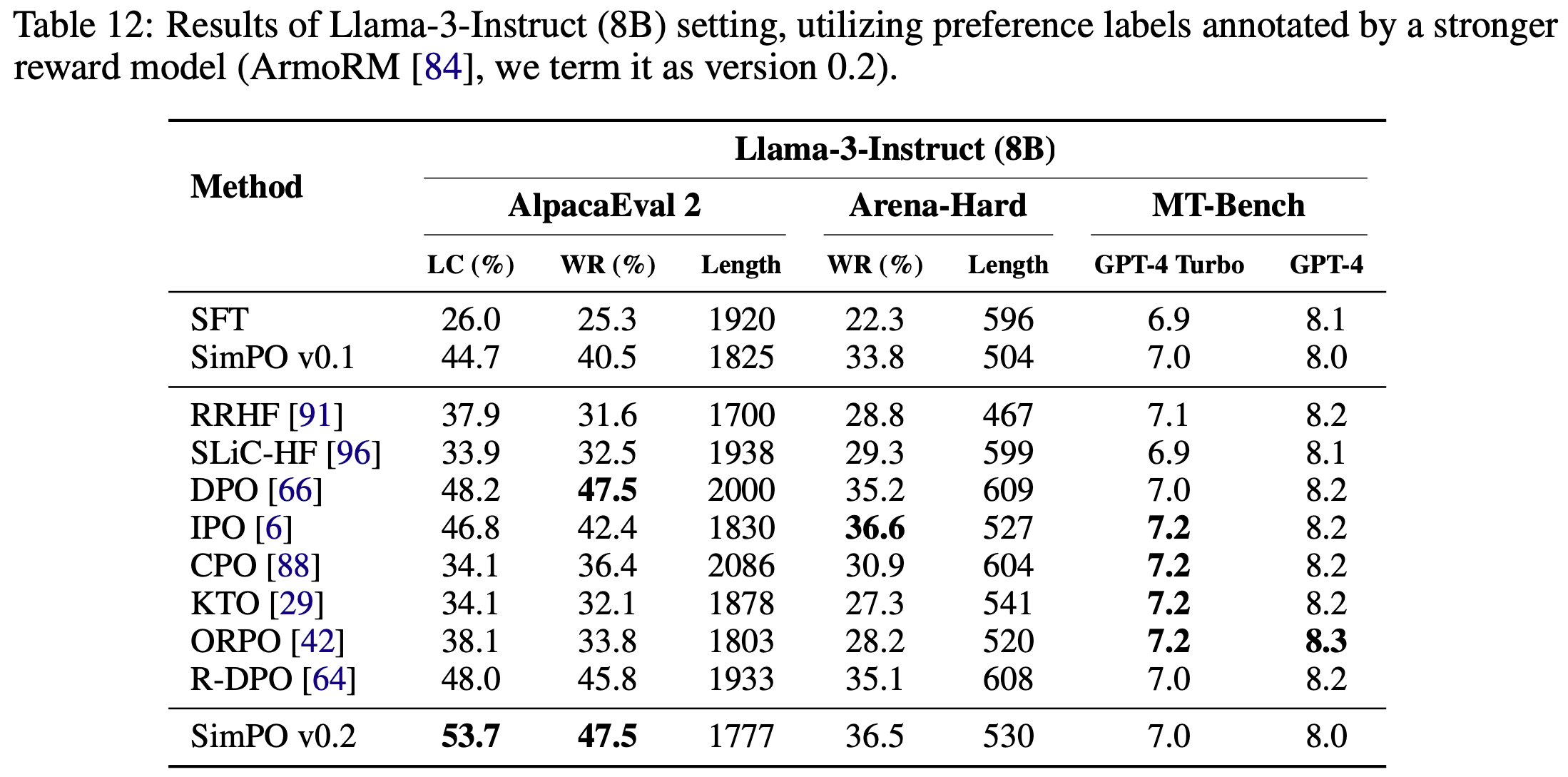
论文在 Llama-3-Instruct v0.2 设置下为 SimPO 使用了以下超参数：
- $\beta=10$ 和 $\gamma=3$
- 其他超参数（如学习率、批量大小、最大序列长度）与原始 Llama-3-8B-Instruct 设置保持一致
强大的 SFT 模型和高质量策略数据缩小了算法差异（Strong SFT model and high-quality policy data diminish algorithm differences）
- 当使用像 Llama-3-8B-Instruct 这样强大的 SFT 模型，并且偏好优化数据质量提高时，不同算法之间的差异变得不那么明显
- 例如，DPO 在原始胜率（raw win rate）上与 SimPO 表现接近，而 DPO、IPO 和 R-DPO 在 Arena-Hard 上的原始胜率也相当
- 然而，SimPO 仍保持优势，生成的序列更短，因此在 AlpacaEval 2 上的长度控制胜率显著更高
下游任务表现更强（Stronger downstream task performance）
- v0.2 版本在各种目标下的下游任务中也表现出更好的性能
- 不过，DPO、IPO、R-DPO 和 SimPO 在数学推理密集型任务（如 GSM8K）上仍然存在性能下降
- 相比之下，包含 SFT 组件的目标在数学任务上保持了更好的表现
在 SimPO 中加入 SFT 正则化（Incorporating SFT regularization in SimPO）
- 一些无需参考模型（reference-free）的算法（如 RRHF（2023）、SLiC-HF（2023）、CPO（2024）和 ORPO（2024））在其目标中使用了 SFT 正则化
- SFT 正则化是防止奖励破解（reward hacking）的有效方法，可以确保模型在保持低损失的同时不会生成质量下降的结果
- 论文也在 SimPO 中尝试加入 SFT 损失，得到以下目标函数：
  $$
  \mathcal{L}_{\text{SimPO w/ SFT} }(\pi_{\theta})=-\mathbb{E}_{(x,y_{w},y_{l})\sim\mathcal{D} }\left[\log\sigma\left(\frac{\beta}{|y_{w}|}\log\pi_{\theta}(y_{w}|x)-\frac{\beta}{|y_{l}|}\log\pi_{\theta}(y_{l}|x)-\gamma\right)\color{red}{+\lambda\log\pi_{\theta}(y_{w}|x)}\right].
  $$
- 如表 14 所示，加入 SFT 正则化后，模型在 AlpacaEval 2 上的性能有所下降
- 但论文发现 SFT 正则化对某些任务（如 GSM8K）有显著帮助（见表 12）
- 这些结果表明，SFT 在偏好优化中的作用可能因训练设置和任务性质而异
- 更全面的研究留待未来进行

附录 I：Applying Length Normalization and Target Reward Margin to DPO (Jul 7, 2024)）

论文发布后，有研究者提出疑问：SimPO 的两个关键设计（长度归一化（length normalization）和目标奖励间隔（target reward margin））是否也能提升 DPO 的效果？为此，论文推导了以下两个目标函数：
$$
\mathcal{L}_{\text{DPO w/ LN} }(\pi_{\theta};\pi_{\text{ref} })=-\mathbb{E}_{(x,y_{w},y_{l})\sim\mathcal{D} }\left[\log\sigma\left(\frac{\beta}{|y_{w}|}\log\frac{\pi_{\theta}(y_{w}\mid x)}{\pi_{\text{ref} }(y_{w}\mid x)}-\frac{\beta}{|y_{l}|}\log\frac{\pi_{\theta}(y_{l}\mid x)}{\pi_{\text{ref} }(y_{l}\mid x)}\right)\right]. \\
\mathcal{L}_{\text{DPO w/ }\gamma}(\pi_{\theta};\pi_{\text{ref} })=-\mathbb{E}_{(x,y_{w},y_{l})\sim\mathcal{D} }\left[\log\sigma\left(\beta\log\frac{\pi_{\theta}(y_{w}\mid x)}{\pi_{\text{ref} }(y_{w}\mid x)}-\beta\log\frac{\pi_{\theta}(y_{l}\mid x)}{\pi_{\text{ref} }(y_{l}\mid x)}-\gamma\right)\right].
$$
- 直观上，长度归一化可能对 DPO 有帮助，因为尽管 DPO 的奖励设计通过参考模型隐式归一化，但策略模型仍可能从数据中利用长度偏差，导致对较长序列赋予过高的概率
  - 长度归一化可以缓解这一问题
论文使用上述目标训练模型，并与 DPO 和 SimPO 的性能进行比较（见表 15）
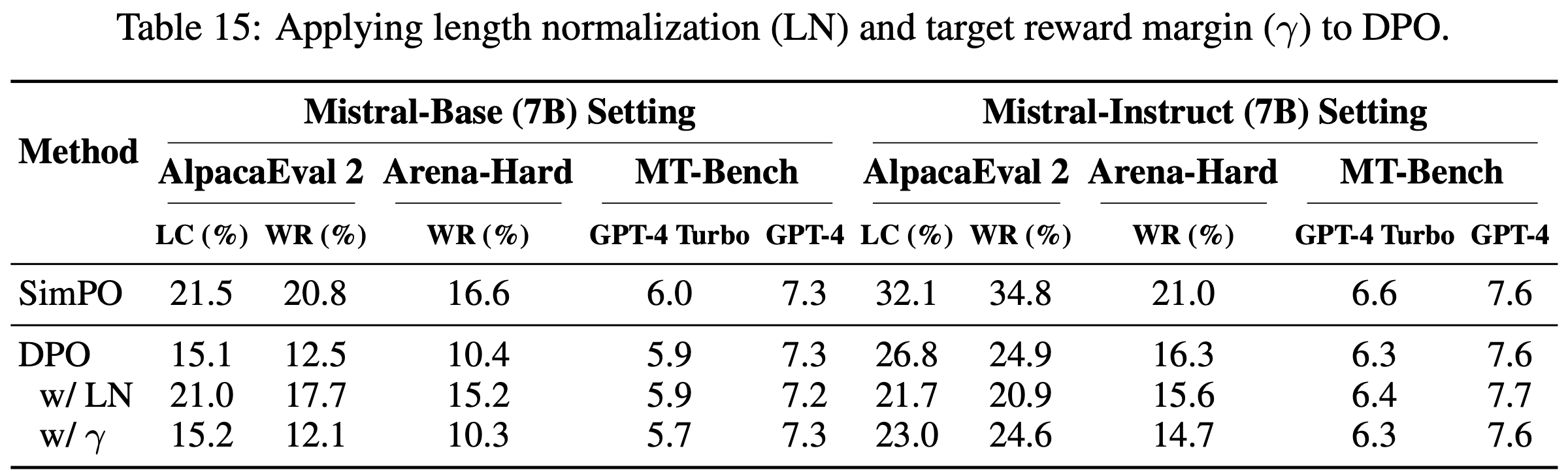
结果表明，与 SimPO 不同，长度归一化和目标奖励间隔并不能一致地提升 DPO
具体来说，长度归一化仅在 Mistral-Base 设置中显著提升 DPO 性能（该设置的偏好优化数据存在明显的长度偏差），但在 Mistral-Instruct 设置中无益（因为胜负响应的长度相近）
- 这可能是因为 DPO 已通过参考模型隐式实现了实例级的目标奖励间隔，如下式所示：
  $$
  \begin{align}
  \mathcal{L}_{\text{DPO} }&= \log\sigma\left(\beta\log\frac{\pi_{\theta}(y_{w}\mid x)}{\pi_{\text{ref} }(y_{w}\mid x)}-\beta\log\frac{\pi_{\theta}(y_{l}\mid x)}{\pi_{\text{ref} }(y_{l}\mid x)}\right) \\
  &= \log\sigma\bigg(\beta\log\pi_{\theta}(y_{w}\mid x)-\beta\log\pi_{\theta}(y_{l}\mid x)-\underbrace{\left(\beta\log\pi_{\text{ref} }(y_{w}\mid x)-\beta\log\pi_{\text{ref} }(y_{l}\mid x)\right)}_{=\gamma_{\text{ref} } }\bigg).
  \end{align}
  $$

附录 J：Applying SimPO to Gemma 2 Models (Sept 16, 2024)

Llama-3-SimPO 模型在其他基准测试上的性能下降（Performance degradation on other benchmarks for Llama-3-SimPO checkpoints）
- 在发布 Llama-3-SimPO 模型后，论文收到大量反馈，指出其在特定能力测试（如 MMLU 和 GSM8K）上的性能下降
- 为了研究这一问题，论文继续用不同学习率训练 Llama-3-8B-Instruct 模型（见表 16）
- 论文发现，使用较高的学习率会增强模型在聊天类基准上的表现，但会牺牲 GSM8K 和 MMLU 的性能
  - We evaluate the zero-shot performance of the models on GSM8K and MMLU using the ZeroEval repository which adopts a unified setup
- 而较低的学习率能略微降低聊天基准的性能，但更好地保留了 GSM8K 和 MMLU 的表现
- 这表明，在基于强大的指令微调模型继续训练时，需要在聊天基准和其他基准之间权衡
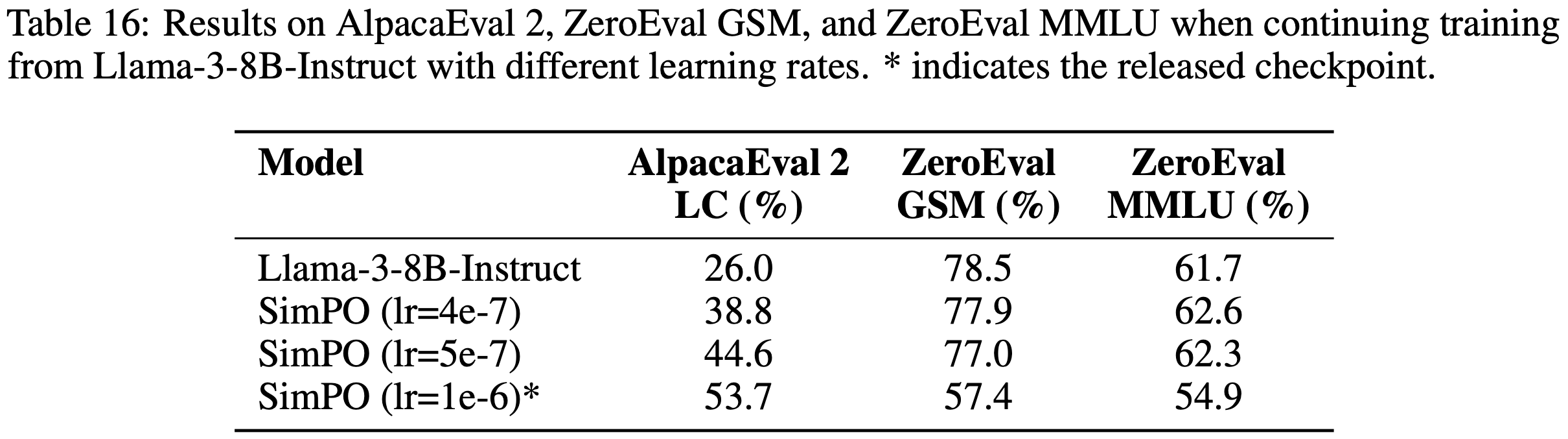
将 SimPO 应用于 Gemma 2 模型呈现不同趋势（Applying SimPO to Gemma 2 models persents a different trend）
- 论文使用谷歌最新发布的 Gemma-2-9B-it 模型（2024）评估 SimPO
- 对于训练数据，论文从 UltraFeedback 数据集（2024）中为每个提示生成最多 5 个回答，并使用 ArmoRM 模型（2024）标注偏好
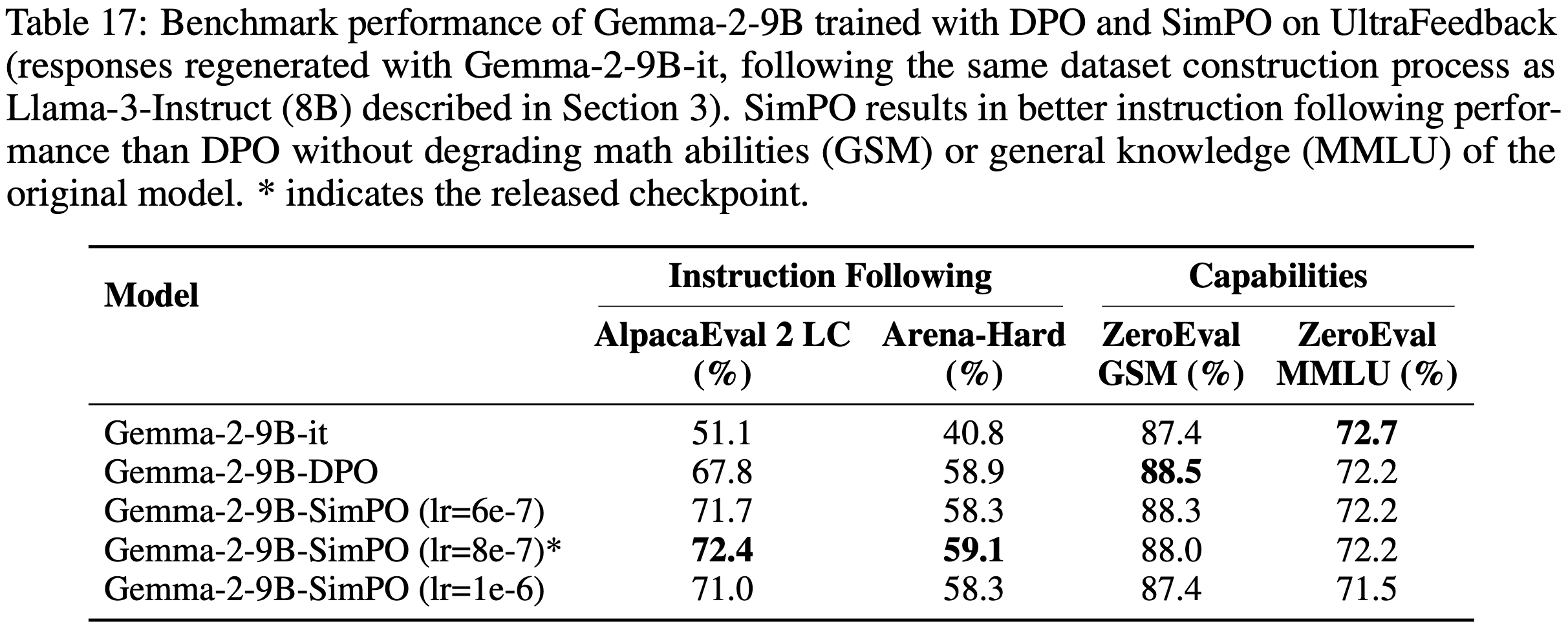
- 论文将 SimPO 与基于 Gemma-2-9B-it 微调的 DPO 变体进行比较
- 如表 17 所示，SimPO 在 AlpacaEval 2 和 Arena-Hard 等聊天基准上表现更优，同时保持了模型在 GSM8K 和 MMLU 等任务上的零样本能力
- 值得注意的是，论文发现微调时调整学习率对模型性能影响很小
- 这些结果表明，Llama-3 和 Gemma 2 的模型存在内在差异，值得进一步研究
Gemma-2-9B-it-SimPO 显著提升了原模型在 Chatbot Arena 的排名（Gemma-2-9B-it-SimPO significantly improved the ranking of the Gemma-2-9B-it model on Chatbot Arena）
- 在开发阶段，论文仅依赖自动化指标评估模型性能
- 为了验证这些指标是否与真实用户偏好一致，论文将表现最佳的 Gemma-2-9B-it-SimPO 模型提交至 LMSYS 的 Chatbot Arena 排行榜（2024）
- 结果显示，论文的模型将原 Gemma-2-9B-it 的排名从第 36 位提升至第 25 位，使其成为截至 2024 年 9 月 16 日用户投票排名最高的 10B 以下模型

Introduction and Discussion

SimPO：简单偏好优化（SimPO: Simple Preference Optimization）

Background: Direct Preference Optimization（DPO）

A Simple Reference-Free Reward Aligned with Generation

The SimPO Objective

Experimental Setup

Models and training settings

Evaluation Benchmarks

Baselines

Experimental Results

Main Results and Ablations

长度归一化（LN）防止长度利用（Length Normalization (LN) Prevents Length Exploitation）

The Impact of Target Reward Margin in SimPO

In-Depth Analysis of DPO vs. SimPO

Related Work

RLHF

Offline vs. Iterative Preference Optimization

Preference Optimization Objectives

附录 A Limitations

附录 B Implementation Details

附录 C：Downstream Task Evaluation

附录 D：AlpacaEval 2 和 Arena-Hard 的标准差 (Standard Deviation of AlpacaEval 2 and Arena-Hard)

附录 E：Generation Length Analysis

附录 F：Gradient Analysis

附录 G：Qualitative Analysis

附录 H：Llama-3-Instruct v0.2 (Jul 7, 2024)）

附录 I：Applying Length Normalization and Target Reward Margin to DPO (Jul 7, 2024)）

附录 J：Applying SimPO to Gemma 2 Models (Sept 16, 2024)