NLP——LLM对齐微调-SAPO

注：本文包含 AI 辅助创作

• 参考链接：
  • 原始论文：(SAPO)Soft Adaptive Policy Optimization, 20251125 & 20251201, Qwen Team, Alibaba

Paper Summary

• 整体说明：
  • 论文提出了一种平滑且 Token 自适应的强化学习算法 软自适应策略优化 (Soft Adaptive Policy Optimization, SAPO)
  • SAPO 旨在解决 LLM 中与硬裁剪策略优化相关的不稳定性和低效问题
  • 通过用温度控制的软门控取代不连续的裁剪，并采用非对称温度来更好地调节负 Token 梯度，SAPO 提供了更稳定且信息更丰富的优化信号
  • 在几个数学推理基准测试上的经验结果表明：
    • SAPO 延长了稳定训练的持续时间，并在可比的预算下实现了更高的 Pass@1 性能
  • 评价：平滑自适应的门控机制为提高大语言模型 RL 训练的鲁棒性和有效性提供了一个不错的选项（这个思路在 OneRec 中也看到过）
• 背景 & 问题：
  • RL 在增强 LLM 的推理能力方面发挥着越来越重要的作用，但稳定且高性能的策略优化仍然具有挑战性
  • Token-level 的重要性比值通常表现出高方差（这种现象在 MoE 模型中更为严重）导致更新不稳定
  • 现有的 Group-based 策略优化方法，如 GSPO 和 GRPO，通过硬裁剪缓解了这个问题，但这使得难以同时保持稳定性和有效的学习
• 作者提出的解法：
  • SAPO 用平滑的、温度控制的门控替代硬裁剪，该门控能够自适应地衰减 Off-policy 更新，同时保留有用的学习信号
  • 注：这里的温度不是采样的温度 和 Attention Softmax 的温度，是新定义的门控的一个温度参数
• SAPO vs GSPO and GRPO：
  • 与 GSPO 和 GRPO 相比，SAPO 既具有序列一致性又具有 Token 自适应性
  • 与 GSPO 相比：
    • 相同点：SAPO 和 GSPO 都 保持了 Sequence-level 的连贯性
    • 不同点：SAPO 软门控形成了一个连续的信任区域，避免了 GSPO 中使用的脆性硬裁剪带
      • 当一个序列包含少量高度 Off-policy 的 Token 时
        • GSPO 会抑制该序列的所有梯度
        • SAPO 则有选择地仅降低违规 Token 的权重，并保留近策略 Token 的学习信号，从而提高了样本效率
  • 与 GRPO 相比：
    • SAPO 用平滑的温度控制缩放取代了硬 Token-level 裁剪，实现了信息更丰富且更稳定的更新
• 数学推理基准测试结果：
  • 在 comparable 训练预算下，SAPO 表现出改进的训练稳定性和更高的 Pass@1 性能
• 作者使用 SAPO 来训练 Qwen3-VL 模型系列，证明了 SAPO 在不同任务和不同模型大小上都能带来一致的性能提升

---

Introduction and Discussion

• RL 已成为推动 LLM 近期进展的关键驱动力，使其能够在数学、编程和多模态理解等具有挑战性的任务中进行更深入和更长的推理 (OpenAI, 2024; DeepSeek-AI, 2025; Qwen, 2025)
• 在 RL 方法中， Group-based 策略优化已成为一种实用的方案：
  • 为每个查询采样多个 Response ，在组内对 Sequence-level 奖励进行归一化，并根据当前策略与行为策略之间的重要性比值对策略更新进行加权 (2024; 2025)
• 在这种设置中的一个核心挑战是 Token-level 重要性比值的高方差
  • 尤其是在 MoE 模型中，路由异构性和长 Response 会加剧不同 Token 间的偏差
  • 这种方差增加了更新不稳定的可能性
• GRPO (2024) 中使用的硬裁剪通过将固定范围外的梯度置零来约束大的偏差
• 虽然硬裁剪在遏制过大步长方面有效，但很难达成有利的权衡：
  • 过紧的裁剪限制了用于梯度计算的有效样本数量，而较宽松的裁剪则会引入来自 Off-policy 样本的噪声梯度
• 为了解决 Group-based 策略优化中硬裁剪的脆弱性，论文提出了SAPO
  • SAPO 是一种平滑自适应的策略梯度方法，它用温度控制的软门控取代了硬裁剪，如图 1 所示
• SAPO 通过一个有界的、以 On-policy 点为中心的 sigmoid 形状函数对重要性比值进行加权 ，从而对 Token-level 更新进行加权
  • SAPO 实现了一个连续的信任区域：
    • 在近策略处，梯度被保留以鼓励有用的更新和探索；
    • 随着比值偏离，梯度被平滑地衰减而非截断，为适度偏差保留学习信号，同时减少优化噪声
• 为了进一步增强大词汇量下的鲁棒性，SAPO 对正 Token 和负 Token 采用非对称温度，使得负 Token 的梯度衰减更快，这反映了它们不同的稳定性特性：
  • 负更新倾向于增加许多不恰当 Token 的 logits，因此比正更新更容易引入不稳定性
• 从概念上讲，SAPO 被设计为 Sequence-coherent 且 Token 自适应的
  • 在温和且经验上常见的条件下（小的策略步长和序列内 Token 对数比值的低离散度(low dispersion)），平均 Token 门控会集中到一个平滑的 Sequence-level 门控，从而以基于序列的方法（如 GSPO (2025)）的 spirit，使优化与 Sequence-level 奖励对齐
  • 当这些条件由于异构或离群 Token 而被违反时，SAPO 有选择地仅降低违规 Token 的权重，同时保留同一序列内近策略 Token 的信息梯度
  • 这种选择性衰减减轻了与硬裁剪相关的信号损失，在保持稳定更新的同时提高了采样效率
• Empirically，与 GSPO 和 GRPO 相比，SAPO 提供了改进的稳定性和任务性能
  • 虽然所有方法最终都可能表现出不稳定的迹象，但 SAPO 能在更长时间内维持连贯的学习，并在发散前达到更高的 Pass@1 准确率
    • 这源于 SAPO 能够保留超出硬裁剪阈值的信息梯度，同时有选择地抑制高方差的 Token 更新
  • Furthermore，论文的温度消融研究进一步揭示了非对称设计（对负 Token 更新使用更大的温度）至关重要：
    • 它抑制了高方差的负梯度，并显著降低了早期崩溃的可能性
  • 除了受控设置外（controlled settings），SAPO 在 Qwen3-VL 模型的实际训练中也证明是有效的，涵盖了广泛的文本和多模态任务，以及不同的模型规模和架构
• Together，这些结果表明，SAPO 的平滑门控和非对称温度控制使得大语言模型的 RL 训练更可靠、更有效

---

Preliminaries

Notation

• 论文将参数为 \(\theta\) 的自回归语言模型建模为 Token 序列上的随机策略 \(\pi_{\theta}\)
• 令 \(q\) 表示查询，\(\mathcal{D}\) 表示查询集
• 对于查询 \(q\) 的 Response \(y\)，其在 \(\pi_{\theta}\) 下的似然分解为
  $$ \pi_{\theta}(y \mid q)\ =\ \prod_{i=1}^{|y|}\pi_{\theta}(y_{i} \mid q,y_{ < i}) $$
  • 其中 \(|y|\) 是 \(y\) 中的 Token 数量

Group Relative Policy Optimization(GRPO)

• 对于每个查询 \(q\sim\mathcal{D}\)，GRPO (2024) 从行为策略 \(\pi_{\theta_{\text{old} } }\) 中采样一组 \(G\) 个 Response \(\{y_{1},\ldots,y_{G}\}\)，计算它们的奖励 \(\{\text{R}_{1},\ldots,\text{R}_{G}\}\)，并最大化以下 Token-level 目标：
  $$
  \mathcal{J}_{\text{GRPO} }(\theta)=\mathbb{E}_{q\sim\mathcal{D},\{y_{i}\}_{i=1}^{G}\sim\pi_{\theta_{\text{old} } }(\cdot|q)}\left[\frac{1}{G}\sum_{i=1}^{G}\frac{1 }{|y_{i}|}\sum_{i=1}^{|y_{i}|}\min \left(r_{i,t}(\theta)\widehat{A}_{i,t},\operatorname{clip}\left(r_{i,t}(\theta),1-\varepsilon,1+\varepsilon\right)\widehat{A}_{i ,t}\right)\right], \tag{1}
  $$
• 其中
  $$
  r_{i,t}(\theta)=\frac{\pi_{\theta}(y_{i,t}|q,y_{i,<t})}{\pi_{\theta_{\text{old} } }(y_{i,t}|q,y_{i,<t})},\quad \quad \widehat{A}_{i,t}=\widehat{A}_{i}=\frac{\text{R}_{i}-\operatorname{mean}(\{\text{R}_{j}\}_{j=1}^{G})}{\operatorname{std}\left(\{\text{R}_{j}\}_{j=1}^{G}\right)}, \tag{2}
  $$
  • \(\varepsilon>0\) 是裁剪范围
  • \(G\) 是组中 Response 的数量
  • \(\widehat{A}_{i,t}\) 是组归一化的优势度（在同一个 Response 内的 Token 间共享）

Group Sequence Policy Optimization(GSPO)

• GSPO (2025) 采用以下 Sequence-level 优化目标：
  $$
  \mathcal{J}_{\text{GSPO} }(\theta)=\mathbb{E}_{q\sim\mathcal{D},\{y_{i}\}_{i=1}^{G}\sim\pi_{\theta_{\text{old} } }(\cdot|q)}\left[\frac{1}{G}\sum_{i=1}^{G}\min\left(s_{i}(\theta)\widehat{A}_{i},\operatorname{clip}\left(s_{i}(\theta),1-\varepsilon,1+\varepsilon\right)\widehat{A}_{i}\right)\right], \tag{3}
  $$
• 其中
  $$
  s_{i}(\theta)=\left(\frac{\pi_{\theta}(y_{i}|q)}{\pi_{\theta_{\text{old} } }(y_{i}|q)}\right)^{\frac{1}{|y_{i}|} }=\exp\left(\frac{1}{|y_{i}|}\sum_{i=1}^{|y_{i}|}\log\frac{\pi_{\theta}(y_{i,t}|q,y_{i,<t})}{\pi_{\theta_{\text{old} } }(y_{i,t}|q,y_{i,<t})}\right),\quad\widehat{A}_{i}=\frac{\text{R}_{i}-\operatorname{mean}(\{\text{R}_{j}\}_{j=1}^{G})}{\operatorname{std}\left(\{\text{R}_{j}\}_{j=1}^{G}\right)} \tag{4}
  $$
  • GSPO 在 Sequence-level 而非每个 Token 上应用裁剪
  • \(s_{i}(\theta)\) 中的长度归一化减少了方差，并将其置于跨 Response 一致的数值尺度上
  • 注：GSPO 还使用了 同一个 Response 共享的重要性比例（Token 粒度重要性比例的几何平均）

---

Soft Adaptive Policy Optimization(SAPO)

• SAPO 是一种用于 RL 微调的平滑自适应策略梯度方法（adaptive policy-gradient method）
  • SAPO 用温度控制的软门控（temperature-controlled soft gate）取代硬裁剪（hard clipping）
  • 注：这里的温度不是采样的温度 和 Attention Softmax 的温度，是新定义的门控的一个温度参数，超参数 \(\tau\) 控制衰减率（较大的值产生更快的衰减）
• 平滑门控函数（Smooth gating functions）在传统 RL 设置中已有探索 (2023)
• 在 SAPO 中，论文将这个思想纳入 LLM 的 Group-Based RL 范式，并通过两个对 LLM 训练很重要的 additional components 进行扩展：
  • (1) 一个 Token-level 的 Soft Trust Region ，它自然地产生 Sequence-level 连贯性；
  • (2) 一个由正负 Token 更新的不同行为所启发的非对称温度设计
• Specifically，SAPO 最大化以下目标：
  $$
  \mathcal{J}(\theta)=\mathbb{E}_{q\sim\mathcal{D}_{t}\left[y_{i}\right]_{i=1}^{G}\sim\pi_{\theta_{\text{old} } }(\cdot|q)}\left[\frac{1}{G}\sum_{i=1}^{G}\frac{1}{\left|y_{i}\right|}\sum_{i=1}^{\left|y_{i}\right|}\color{red}{f_{i,t}(r_{i,t}(\theta))}\widehat{A}_{i,t}\right], \tag{5}
  $$
  • 其中
    • \(f_{i,t}(x)\) 定义为：
      $$
      f_{i,t}(x)=\sigma\left(\tau_{i,t}\left(x-1\right)\right)\cdot\frac{4}{\tau_{i,t} },\quad\tau_{i,t}=\begin{cases}\tau_{\text{pos} },&\text{if \(\widehat{A}_{i,t}>0\)}\\ \tau_{\text{neg} },&\text{otherwise}\end{cases}, \tag{6}
      $$
    • \(\widehat{A}_{i,t}\) 和 \(r_{i,t}(\theta)\) 如公式 (2) 计算（与 GRPO 一致）
    • \(\tau_{\text{pos} }\) 和 \(\tau_{\text{neg} }\) 分别是正负 Token 中 \(f_{i,t}(x)\) 的温度
    • \(\sigma(x)=\frac{1}{1+e^{-x}}\) 是 sigmoid 函数
    • 理解：这里的 \(f_{i,t}(x)\) 设置的如何奇怪是有原因的，是为了保证梯度权重 \(r_{i,t}(\theta)=1\) 时，无论 \(\tau_{i,t}\) 如何，梯度更新公式都与原始 PPO/GRPO 公式等价
• 对 公式 (5) 求导得到加权的对数策略梯度：
  $$
  \nabla_{\theta}\mathcal{J}(\theta)=\mathbb{E}_{q\sim\mathcal{D}_{t}\left[y_{i}\right]_{i=1}^{G}\sim\pi_{\theta_{\text{old} } }(\cdot|q)}\left[\frac{1}{G}\sum_{i=1}^{G}\frac{1}{\left|y_{i}\right|}\sum_{i=1}^{\left|y_{i}\right|}\color{red}{w_{i,t}(\theta)}r_{i,t}(\theta)\nabla_{\theta}\log\pi_{\theta}(y_{i,t}\mid q,y_{i,<t})\widehat{A}_{i,t}\right] \tag{7}
  $$
  • 其中
    $$
    w_{i,t}(\theta)=4p_{i,t}(\theta)\left(1-p_{i,t}(\theta)\right),\quad p_{i,t}(\theta)=\sigma\left(\tau_{i,t}\left(r_{i,t}(\theta)-1\right)\right), \tag{8}
    $$
  • 理解：这里的 \(\color{red}{w_{i,t}(\theta)}\) 是一种软性的截断，替代了原始 GRPO/PPO 中的硬截断
• 该权重在 \(r_{i,t}(\theta)=1\) 处达到峰值（峰值为 \(1\)），并随着 \(r_{i,t}(\theta)\) 偏离 \(1\) 而平滑且近似指数地衰减，从而实现一个 Soft Trust Region，防止梯度消失和过大的更新，如图 1 所示
  • 图 1 是优势度为正时策略更新目标的比较
  • 左侧 Panel：显示了代理目标值（Surrogate Objective Value）
  • 右侧 Panel：显示了作为策略比值 \(r_{i,t}(\theta)\) 函数的相应梯度权重 \(w_{i,t}(\theta)\)（注：可以看到在 \(r_{i,t}(\theta)=1\) 处达到峰值 \(1\)）
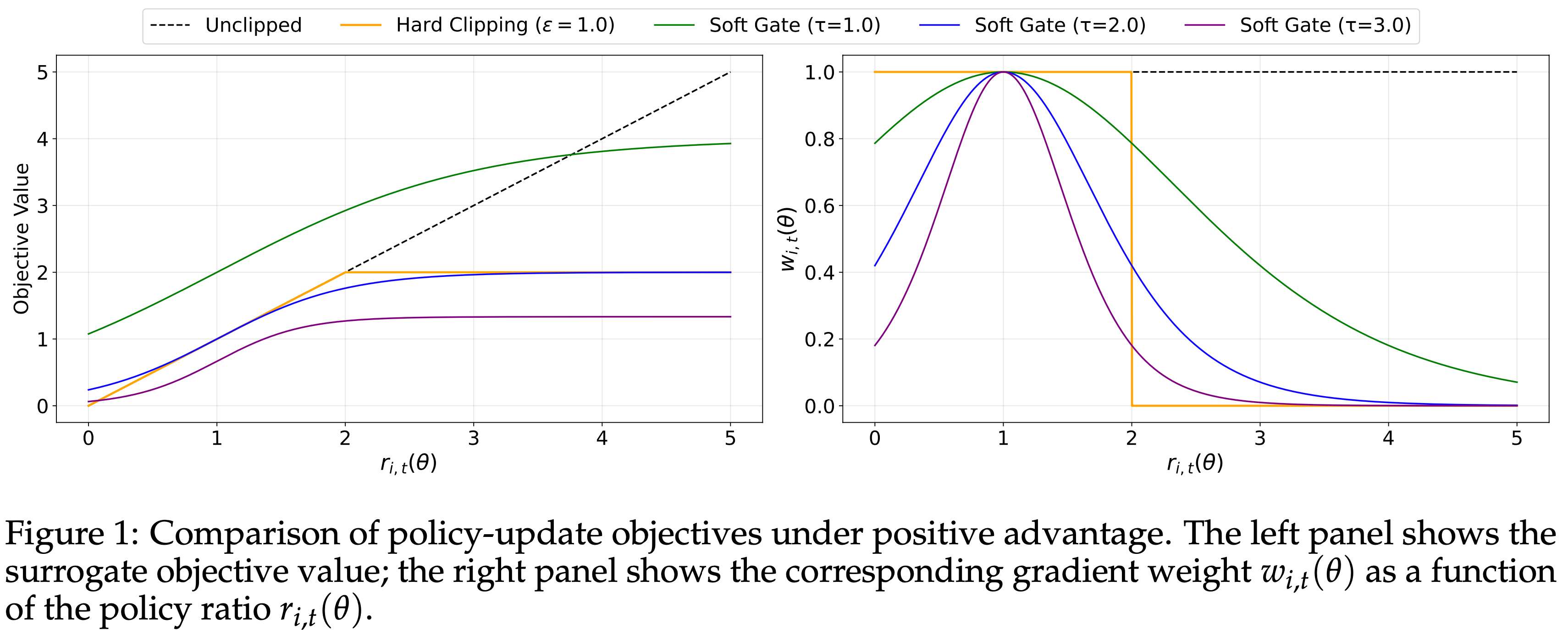
• Notably，在 \(r_{i,t}(\theta)=1\) 时，无论 \(\tau_{i,t}\) 如何，Soft-gated 梯度等于未裁剪目标 \(r_{i,t}(\theta)\widehat{A}_{i,t}\) 的梯度，从而保留了 On-policy 行为
  • 这也解释了 \(f_{i,t}\) 中存在 \(4/\tau_{i,t}\) 因子的原因
  • 理解：只有这样才能保证在 \(r_{i,t}(\theta)=1\) 时，无论 \(\tau_{i,t}\) 如何，梯度更新公式都与原始 PPO/GRPO 公式等价
• 与 GSPO (2025) 和 GRPO (2024) 相比，SAPO 同时提供了 Sequence-level 连贯性和 Token-level 自适应性：
  • (1) 在温和的假设（mild assumptions）下，即小的策略步长和序列内 Token 对数比值的低离散度(low dispersion)，平均 Token 门控 可以浓缩（concentrate）到一个平滑的 Sequence-level 门控
    $$ g(\log s_{i}(\theta))=\text{sech}^{2}(\frac{\tau_i}{2}\log s_{i}(\theta))$$
    • 理解：上面的 Sequence-level 平均 Token 门控是参照 Token-level 的 SAPO 专为对齐 GSPO 转化得到的近似公式，不严格与 Token-level 的 SAPO 公式等价
      • 推导详情见后文
    • Thus，SAPO 简化为类似 GSPO 的序列公式，但具有连续的信任区域
    • Crucially，当少数 Off-policy Token 将 \(s_{i}\) 推至 GSPO 的硬带之外时，GSPO 会抑制该序列中许多近策略 Token 的梯度，从而损害样本效率
    • SAPO, in contrast, 通过仅降低违规 Token 的权重，同时保持近策略 Token 的影响力，保留了信息梯度
  • (2) 相对于 GRPO，SAPO 避免了在固定范围外将梯度置零的硬 Token-level 裁剪
    • Instead，SAPO 平滑地缩放更新，提供了一种更平衡的方式来保留有用的学习信号，同时防止不稳定的策略转移
    • 更多细节见第 4 节

Why Different Temperatures for Positive and Negative Advantages(why 正负优势度使用不同温度)

• 超参数 \(\tau\) 的用途：用于控制衰减率（rate of attenuation），较大的值产生更快的衰减
• claim：负 Token 对于探索和防止过拟合至关重要，但它们通常比正 Token 引入更大的不稳定性
  • 作者通过分析 Token-level 梯度如何通过 logits 传播来证明这一说法（claim）
• 令 \(z=[z_{1},z_{2},…,z_{|\mathcal{V}|}]\) 表示 logits（词汇表大小为 \(|{\cal V}|\)），令 \(v\) 表示一个 Token ，并通过 softmax 操作计算输出概率，即
  $$ \pi_{\theta}(v \mid q,y_{i,<t})=\frac{\exp(z_{v})}{\sum_{v^{\prime} \in \mathcal{V}}\exp(z_{v^{\prime} })}$$
• 于是有
  $$
  \begin{align}
  \frac{\partial\log\pi_{\theta}(y_{i,t}\mid q,y_{i,<t})\widehat{A}_{i,t} }{\partial z_{v} } &=\frac{\partial\pi_{\theta}(y_{i,t}\mid q,y_{i,<t})}{\partial z_{v} }\cdot\frac{\widehat{A}_{i,t} }{\pi_{\theta}(y_{i,t}\mid q,y_{i,<t})} \\
  &=\frac{\mathbb{I}(v=y_{i,t})\exp(z_{y_{i,t} })\sum_{v^{\prime}\in{\cal V} }\exp(z_{v^{\prime} })-\exp(z_{y_{i,t} })\exp(z_{v})}{(\sum_{v^{\prime}\in{\cal V} }\exp(z_{v^{\prime} }))^{2} }\cdot\frac{\widehat{A}_{i,t} }{\pi_{\theta}(y_{i,t}\mid q,y_{i,<t})} \\
  &=\begin{cases}(1-\pi_{\theta}(y_{i,t}\mid q,y_{i,<t}))\cdot\widehat{A}_{i,t}&\text{if $v=y_{i,t}$}\quad\text{(Sampled Token )}\\ -\pi_{\theta}(v\mid q,y_{i,<t})\cdot\widehat{A}_{i,t}&\text{otherwise}\quad\text{(Unsampled Token )}\end{cases} \tag{9}
  \end{align}
  $$
  • 正优势度会增加被采样 Token 的 logit 并降低所有未被采样 Token 的 logit；
  • 负优势度则相反，会提高许多未被采样 Token 的 logits
  • 注：上面公式的相关推导和更详细的理解详情见附录
• 在 LLM 的 RL 微调中，动作空间是很大的词汇表（通常有数十万个 Token ），whereas 给定状态下理想动作的数量很少
  • Consequently，负梯度会扩散到大量不相关的 Token 上，提供了一些正则化，但也引入了不稳定性，尤其是在 Off-policy 场景中
  • Accordingly，论文对正负 Token 使用不同的温度，并设置 \(\tau_{\text{neg} }>\tau_{\text{pos} }\)，使得负 Token 上的梯度衰减更快，从而提高训练稳定性和性能

---

A Gating-Function Perspective on SAPO’s Connections to GRPO and GSPO（从门控函数视角看三者的联系）

• 统一代理目标 (Unified surrogate)
  • 论文考虑以下形式的统一代理目标：
    $$
    {\cal J}(\theta)=\mathbb{E}_{q\sim\mathcal{D}_{\epsilon}[y_{i}]\subseteq_{1}^{C}\sim\pi_{\theta_{\text{old} } }(\cdot|q)}\left[\frac{1}{G}\sum_{i=1}^{C}\frac{1}{|y_{i}|}\sum_{t=1}^{|y_{i}|}f_{i,t}(r_{i,t}(\theta))\widehat{A}_{i,t}\right], \tag{10}
    $$
    • 其中 \(f_{i,t}(\cdot)\) 是算法特定的门控函数
  • 进一步将长度归一化的 Sequence-level 比值定义为 Token 比值的几何平均（（Geometric Mean，GM））值：
    $$
    s_{i}(\theta)=\left(\frac{\pi_{\theta}(y_{i}\mid q)}{\pi_{\theta_{\text{old} } }(y_{i}\mid q)}\right)^{\frac{1}{|y_{i}|} }=\exp\left(\frac{1}{|y_{i}|}\sum_{t=1}^{|y_{i}|}\log r_{i,t}(\theta)\right),\quad s_{i,t}(\theta)=\operatorname{sg}\left[s_{i}(\theta)\right]\cdot\frac{\pi_{\theta}(y_{i,t}|q,y_{i,<t})}{\operatorname{sg}\left[\pi_{\theta}(y_{i,t}|q,y_{i,<t})\right]}, \tag{11}
    $$
    • 其中 \(\operatorname{sg}[\cdot]\) 表示停止梯度操作
• 不同算法对应的 \(f_{i,t}\) (Algorithm-specific \(f_{i,t}\))
  • 算法的区别在于 \(f_{i,t}\) 的选择：
    $$
    \begin{align}
    \text{SAPO:}\quad &f_{i,t}^{\text{SAPO} }(r_{i,t}(\theta))=\frac{4}{\tau_{i} }\sigma(\tau_{i}(r_{i,t}(\theta)-1)),\qquad\tau_{i}=\begin{cases}\tau_{\text{pos} },\quad\widehat{A}_{i}>0,\\ \tau_{\text{neg} },\quad\widehat{A}_{i}\leq 0,\end{cases} \\
    \text{GRPO:}\quad &f_{i,t}^{\text{GRPO} }(r_{i,t}(\theta);\widehat{A}_{i})=\begin{cases}\min(r_{i,t}(\theta),1+\varepsilon),\quad\widehat{A}_{i}>0,\\ \max(r_{i,t}(\theta),1-\varepsilon),\quad\widehat{A}_{i}\leq 0,\end{cases} \\
    \text{GSPO:}\quad &f_{i,t}^{\text{GSPO} }(r_{i,t}(\theta);\widehat{A}_{i})\equiv f_{i,t}^{\text{seq} }(s_{i,t}(\theta);\widehat{A}_{i})=\begin{cases}\min(s_{i,t}(\theta),1+\varepsilon),\quad\widehat{A}_{i}>0,\\ \max(s_{i,t}(\theta),1-\varepsilon),\quad\widehat{A}_{i}\leq 0.\end{cases}
    \end{align} \tag{12-14}
    $$
    • 注意，GSPO 的 \(f_{i,t}\) 在序列内是 Token 不变的，而 SAPO 和 GRPO 则是 Token 相关的
• SAPO/GRPO 的梯度形式 (Gradient form for SAPO/GRPO)
• 对 (10) 求导，并利用 \(\nabla_{\theta}r_{i,t}(\theta)=r_{i,t}(\theta)\nabla_{\theta}\log\pi_{\theta}(y_{i,t}\mid q,y_{i,< t})\)，可以得到
  $$
  \nabla_{\theta}{\cal J}(\theta)=\mathbb{E}\left[\frac{1}{G}\sum_{i=1}^{C}\frac{1}{|y_{i}|}\sum_{t=1}^{|y_{i}|}f_{i,t}^{\prime}(r_{i,t}(\theta))r_{i,t}(\theta)\nabla_{\theta}\log\pi_{\theta}(y_{i,t}\mid q,y_{i,<t})\widehat{A}_{i}\right]. \tag{15}
  $$

SAPO-GSPO Connection: Reduction to a Sequence-Level Soft Gate（简化为 Sequence-level 软门控 ）

• 可以证明，在温和条件下，SAPO 可以简化为类似 GSPO 的 Sequence-level 公式，同时在异构序列中保留 Token-level 自适应性
• SAPO 的 Token-level 软门控 (SAPO’s token-level soft gate)
  • 利用 \(\sigma(x)(1-\sigma(x))=\frac{1}{(e^{x/2}+e^{-x/2})^{2} }=\frac{1}{4}\text{sech}^{2}(x/2)\)，论文有
    $$
    f^{\text{SAPO}^{\prime} }_{i,t}(r_{i,t}(\theta))=4\sigma(\tau_{i}\left(r_{i,t}(\theta)-1\right))\Big(1-\sigma(\tau_{i}\left(r_{i,t}(\theta)-1\right))\Big)=\text{sech}^{2}\Big(\frac{\tau_{i} }{2}\left(r_{i,t}(\theta)-1\right)\Big). \tag{16}
    $$
• 假设 (Assumptions) （论文引入两个常见假设）
  • 假设 (A1) ：Small-step/On-policy，即 \(r_{i,t}(\theta)\approx 1\)
    • Thus，\(\log r_{i,t}(\theta)\approx r_{i,t}(\theta)-1\)
  • 假设 (A2) ：序列内离散度低（Low intra-sequence dispersion）：
    • Letting \(z_{i,t}(\theta):=\log r_{i,t}(\theta)\) 和 \(\mu_{i}(\theta):=\frac{1}{\left|y_{i}\right|}\sum_{t}z_{i,t}(\theta)=\log s_{i}(\theta)\)
      • 问题：这里 \(\log s_{i}(\theta) = \frac{1}{\left|y_{i}\right|}\sum_{t}\log r_{i,t}(\theta) = \frac{1}{\left|y_{i}\right|}\sum_{t}z_{i,t}(\theta)\)
    • 方差 \(\text{Var}_{i}(\theta):=\frac{1}{\left|y_{i}\right|}\sum_{t}(z_{i,t}(\theta)-\mu_{i}(\theta))^{2}\) 对大多数序列来说很小
  • 在 (A1) 下，有
    $$
    f^{\text{SAPO}^{\prime} }_{i,t}(r_{i,t}(\theta))=\text{sech}^{2}\Big(\frac{\tau_{i} }{2}\left(r_{i,t}(\theta)-1\right)\Big)\approx\text{sech}^{2}\Big(\frac{\tau_{i} }{2}\log r_{i,t}(\theta)\Big)=:\hskip-5.0ptg_{\tau_{i} }(z_{i,t}(\theta)). \tag{17}
    $$
• 平均 Token 门控 \(\Rightarrow\) 序列门控 (Average token gates \(\Rightarrow\) sequence gate)
  • 通过对平滑函数 \(g_{\tau}(z)=\text{sech}^{2}(\frac{\tau}{2}z)\) 在 \(\mu_{i}(\theta)=\log s_{i}(\theta)\) 附近进行二阶泰勒展开，
    $$
    g_{\tau_{i} }(z_{i,t}(\theta))=g_{\tau_{i} }(\mu_{i}(\theta))+g^{\prime}_{\tau_{i} }(\mu_{i}(\theta))(z_{i,t}(\theta)-\mu_{i}(\theta))+\frac{1}{2}g^{\prime\prime}_{\tau_{i} }(\xi_{i,t}(\theta))(z_{i,t}(\theta)-\mu_{i}(\theta))^{2}, \tag{18}
    $$
  • 对于某个介于 \(z_{i,t}(\theta)\) 和 \(\mu_{i}(\theta)\) 之间的 \(\xi_{i,t}(\theta)\)，对 Token 取平均消除了线性项：
    $$
    \frac{1}{\left|y_{i}\right|}\sum_{t=1}^{\left|y_{i}\right|}g_{\tau_{i} }(z_{i,t}(\theta))=g_{\tau_{i} }(\mu_{i}(\theta))+\frac{1}{2}\left(\frac{1}{\left|y_{i}\right|}\sum_{t=1}^{\left|y_{i}\right|}g^{\prime\prime}_{\tau_{i} }(\xi_{i,t}(\theta))(z_{i,t}(\theta)-\mu_{i}(\theta))^{2}\right). \tag{19}
    $$
  • 对于 \(g_{\tau}(z)=\text{sech}^{2}(\alpha z)\)，其中 \(\alpha=\frac{\tau}{2}\)，直接计算可得
    $$
    g^{\prime\prime}_{\tau}(z)=\alpha^{2}\Big(4\text{sech}^{2}(\alpha z)-6\text{sech}^{4}(\alpha z)\Big),\quad \sup_{z}|g^{\prime\prime}_{\tau}(z)|=2\alpha^{2}=\frac{\tau^{2} }{2}. \tag{20}
    $$
  • Hence，平均 Token 门控可以通过序列门控很好地近似，并有统一界：
    $$
    D_{i}(\theta)=\left|\frac{1}{\left|y_{i}\right|}\sum_{t}g_{\tau_{i} }(z_{i,t}(\theta))-g_{\tau_{i} }(\mu_{i}(\theta))\right|\leq\frac{1}{2}\sup_{z}|g^{\prime\prime}_{\tau_{i} }(z)|\text{Var}_{i}(\theta)=\frac{\tau^{2}_{i} }{4}\text{Var}_{i}(\theta). \tag{21}
    $$
  • 从 (15) 开始并应用 \(r_{i,t}(\theta)\approx 1\) (A1)，论文有
    $$
    \nabla_{\theta}\mathcal{J}_{\text{SAPO} }\approx\mathbb{E}\left[\frac{1}{G}\sum_{i=1}^{G}\frac{1}{\left|y_{i}\right|}\sum_{t=1}^{\left|y_{i}\right|}g_{\tau_{i} }(z_{i,t}(\theta))\nabla_{\theta}\log\pi_{\theta}(y_{i,t}\mid q,y_{i,<t})\widehat{A}_{i}\right]. \tag{22}
    $$
  • 利用 (21)，论文有
    $$
    \begin{align}
    \nabla_{\theta}\mathcal{J}_{\text{SAPO} } &\approx\mathbb{E}\left[\frac{1}{G}\sum_{i=1}^{G}g_{\tau_{i} }(\log s_{i}(\theta))\left(\frac{1}{\left|y_{i}\right|}\sum_{t=1}^{\left|y_{i}\right|}\nabla_{\theta}\log\pi_{\theta}(y_{i,t}\mid q,y_{i,<t})\right)\widehat{A}_{i}\right]\\
    &=\mathbb{E}\left[\frac{1}{G}\sum_{i=1}^{G}g_{\tau_{i} }(\log s_{i}(\theta))\nabla_{\theta}\log s_{i}(\theta)\widehat{A}_{i}\right].
    \end{align}
    $$
  • Thus，在 (A1) 和 (A2) 下，SAPO 简化为结构上类似于 GSPO 的 Sequence-level 更新，但带有平滑门控 \(g_{\tau_{i} }(\log s_{i}(\theta))=\text{sech}^{2}(\frac{\tau_{i} }{2}\log s_{i}(\theta))\)
• Do the two assumptions (A1) and (A2) hold?
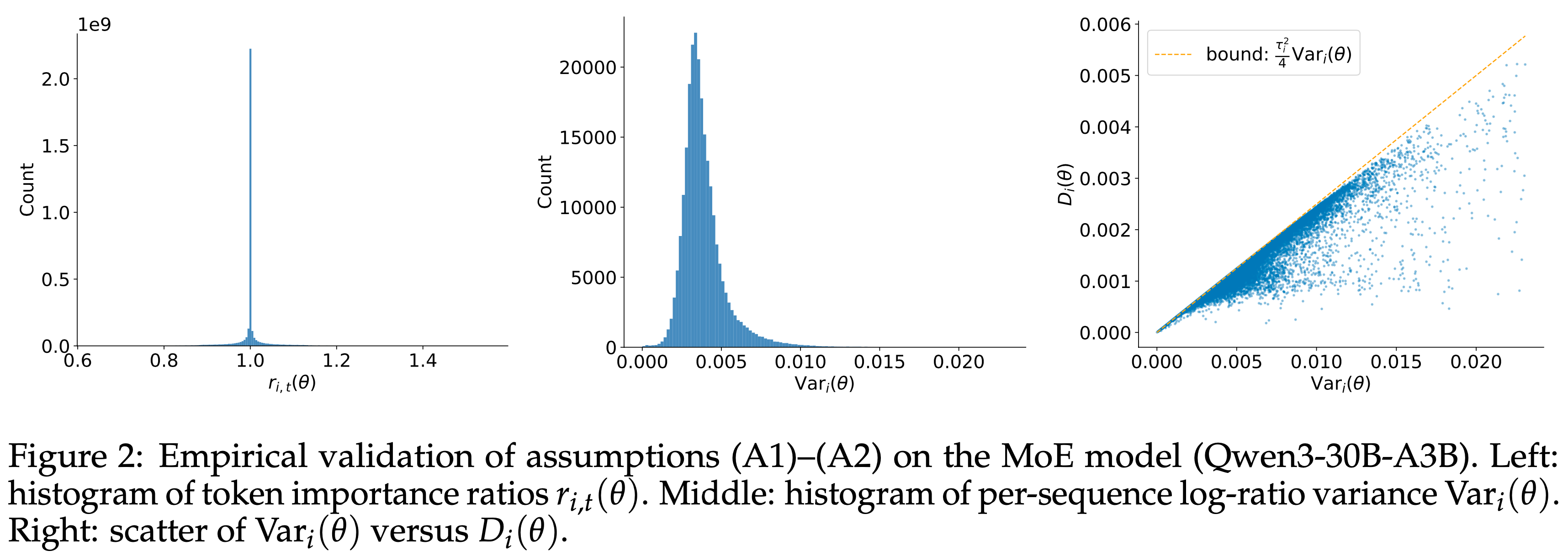
  • 论文通过绘制 MoE 和稠密模型的 Token 比值 \(r_{i,t}(\theta)\) 以及每序列对数比值方差 \(\text{Var}_{i}(\theta)\) 的直方图，在图 2 和图 3 中经验性地评估了小步长假设 (A1) 和序列内低离散度假设 (A2)
  • MoE 模型是 Qwen3-30B-A3B 的冷启动检查点，稠密模型是 Qwen3-4B 的冷启动检查点
  • 统计数据是在超过 \(10^{5}\) 个序列和 \(10^{9}\) 个来自 Off-policy 小批量的 Token 上计算的
  • 论文观察到 \(r_{i,t}(\theta)\) 尖锐地集中在 \(1\) 附近，\(\text{Var}_{i}(\theta)\) 通常保持在 \(0.02\) 以下，MoE 模型的分布相对更广（可能反映了专家路由引入的异构性），而稠密模型的分布更集中
  • 这些分布表明 (A1) 和 (A2) 在大多数情况下成立，特别是对于稠密架构
  • Moreover，小的 \(D_{i}(\theta)\) 直接意味着平均 Token 门控可以被 Sequence-level 门控很好地近似，这支持了论文的简化
• 图 2：MoE 模型 (Qwen3-30B-A3B) 上假设 (A1)–(A2) 的经验验证
  • 左： Token 重要性比值 \(r_{i,t}(\theta)\) 的直方图
  • 中：每序列对数比值方差 \(\text{Var}_{i}(\theta)\) 的直方图
  • 右：\(\text{Var}_{i}(\theta)\) 与 \(D_{i}(\theta)\) 的散点图
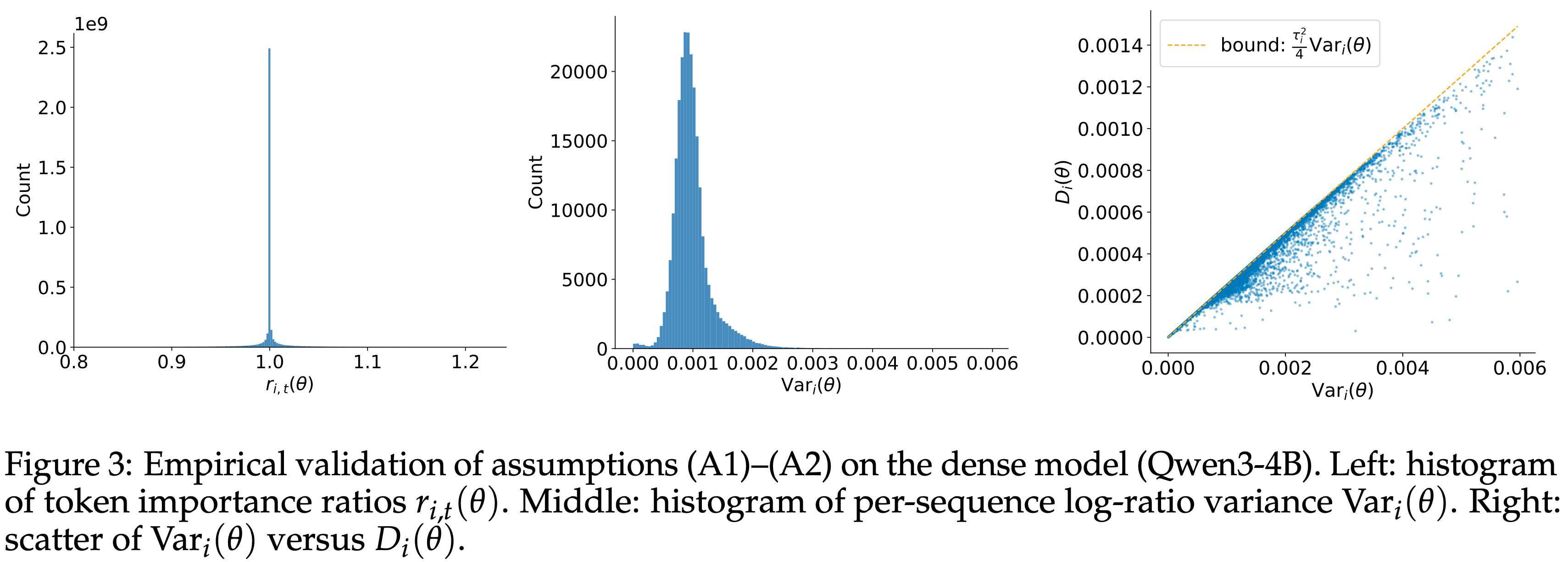
• 图 3：稠密模型 (Qwen3-4B) 上假设 (A1)–(A2) 的经验验证
  • 左： Token 重要性比值 \(r_{i,t}(\theta)\) 的直方图
  • 中：每序列对数比值方差 \(\text{Var}_{i}(\theta)\) 的直方图
  • 右：\(\text{Var}_{i}(\theta)\) 与 \(D_{i}(\hat{\theta})\) 的散点图
• 相对于 GSPO 的优势 (Advantages over GSPO) （与 GSPO 相比，SAPO 具有的优势）
  • (1) 平滑性和稳定性（Smoothness and stability）
    • 软门控随序列偏差连续变化，避免了硬裁剪的不连续性，并减少了优化噪声
  • (2) with Sequence-level 连贯性的 Token-level 自适应性（Token-level adaptivity with sequence-level coherence）
    • 在 (A1) 和 (A2) 下，SAPO 表现得像一个 Sequence-level 方法；
    • 当这些条件被违反时（异构 Token 或离群值），SAPO 会默认其 Token-level 门控，有选择地降低离群值的权重，同时保留信息丰富的 Token ——这是 GSPO 所缺乏的能力

SAPO-GRPO Connection: Smooth Token Gates vs. Hard Token Clipping

• GRPO 的分段硬 Token 门控 (GRPO’s piecewise-hard token gate)
  • 对于 GRPO，\(f_{i,t}^{\text{GRPO} }(r_{i,t}(\theta);\widehat{A}_{i})\) 关于裁剪带（respect to the clipping band）是分段常数
  • 求导可以得到
    $$
    f_{i,t}^{\text{GRPO}^{\prime} }(r_{i,t}(\theta);\widehat{A}_{i})=\begin{cases}1,&\widehat{A}_{i}>0\text{ and }r_{i,t}(\theta)\leq 1+\varepsilon,\\0,&\widehat{A}_{i}>0\text{ and }r_{i,t}(\theta)>1+\varepsilon,\\1,&\widehat{A}_{i}\leq 0\text{ and }r_{i,t}(\theta)\geq 1-\varepsilon,\\0,&\widehat{A}_{i}\leq 0\text{ and }r_{i,t}(\theta)<1-\varepsilon.\end{cases} \tag{24}
    $$
  • Hence，GRPO 采用了一个二值信任区域：
    • 内部的 Token 获得与未裁剪目标相同的梯度；
    • 外部的 Token 获得零梯度
• 相对于 GRPO 的优势 (Advantages over GRPO)
  • 与 GRPO 相比，SAPO 将 (24) 中的硬指示函数替换为平滑核
    $$ f_{i,t}^{\text{SAPO}^{\prime} }(r_{i,t}(\theta))=\text{sech}^{2}(\frac{\pi}{2}(r_{i,t}(\theta)-1))$$
    • 这避免了梯度消失并实现了更稳定的更新动态
  • 当策略变化较小时，梯度保持 Response 性并允许更大的参数更新；
  • 随着偏差增大，梯度平滑地收缩，导致更保守的调整
  • 相比之下，GRPO 的硬 Token 裁剪产生了一个全有或全无的门控，常常导致脆弱且不稳定的优化行为

Summary

• 这些 RL 算法的主要区别在于它们如何处理 \(r_{i,t}(\theta)\) 偏离 \(1\) 的 Off-policy Token
  • 从 Token-level 的角度来看，SAPO 提供了一种平滑的降权机制；
  • 从 Sequence-level 的角度来看，SAPO 抑制了序列中极端 Off-policy Token 的梯度，从而为训练构建了更有效的序列
• 相比之下，GRPO 和 GSPO 依赖于硬裁剪，这对于优化来说不如 SAPO 具有自适应性

---

Experiments

Controlled Experiments

• 论文使用从 Qwen3-30B-A3B-Base 冷启动模型在数学推理查询上微调进行实验
• 论文报告了在 AIME25 (2025)、HMMT25 (2025) 和 BeyondAIME (2025) 基准测试上的训练奖励和验证性能（超过 16 个样本的平均 Pass@1）
• 在 RL 训练期间，每批 rollout 数据被分成四个小批量用于梯度更新
• 对于 SAPO，论文在公式 (6) 中设置 \(\tau_{\text{pos} }=1.0\) 和 \(\tau_{\text{neg} }=1.05\)
• 论文将 SAPO 与 GSPO 和 GRPO-R2（即配备了路由回放的 GRPO）进行比较，使用与 Zheng 等 (2025) 中相同的超参数配置
• 图 4 显示，与 GSPO 和 GRPO-R2 相比，SAPO 在所有基准测试上持续提高模型性能，实现了更高的稳定性和更强的最终性能
  • GSPO 和 GRPO-R2 表现出早期训练崩溃，但 SAPO 保持了稳定的训练动态并最终获得了优异的性能
  • Notably，SAPO 不依赖路由回放来稳定或获得强大性能，这改善了探索并减少了 RL 系统的工程开销
  • 图 4：在不同 RL 算法下，从 Qwen3-30B-A3B-Base 微调的冷启动模型的训练奖励和验证性能
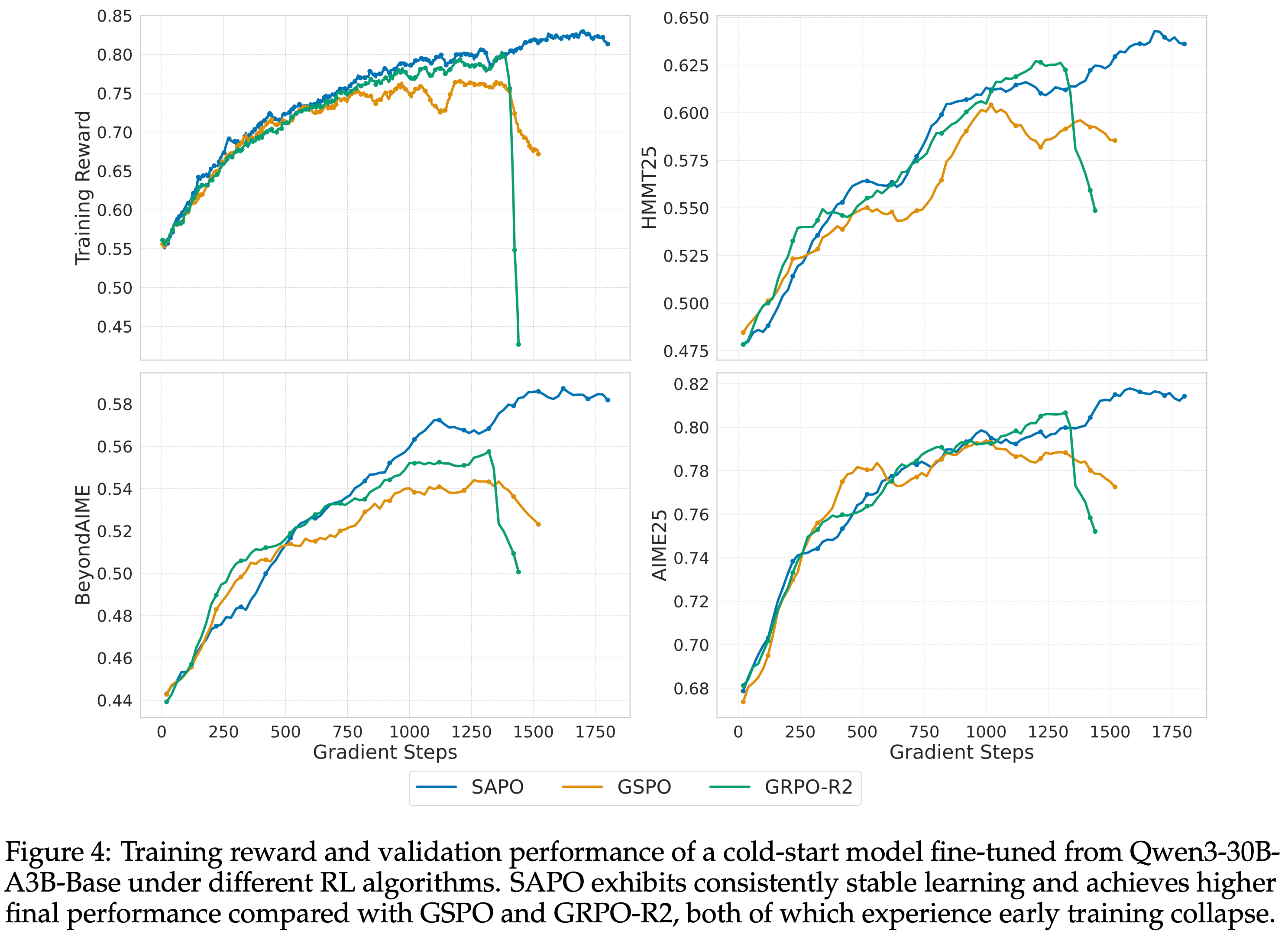
    • 与 GSPO 和 GRPO-R2 相比，SAPO 表现出持续稳定的学习，并实现了更高的最终性能，而 GSPO 和 GRPO-R2 都经历了早期训练崩溃
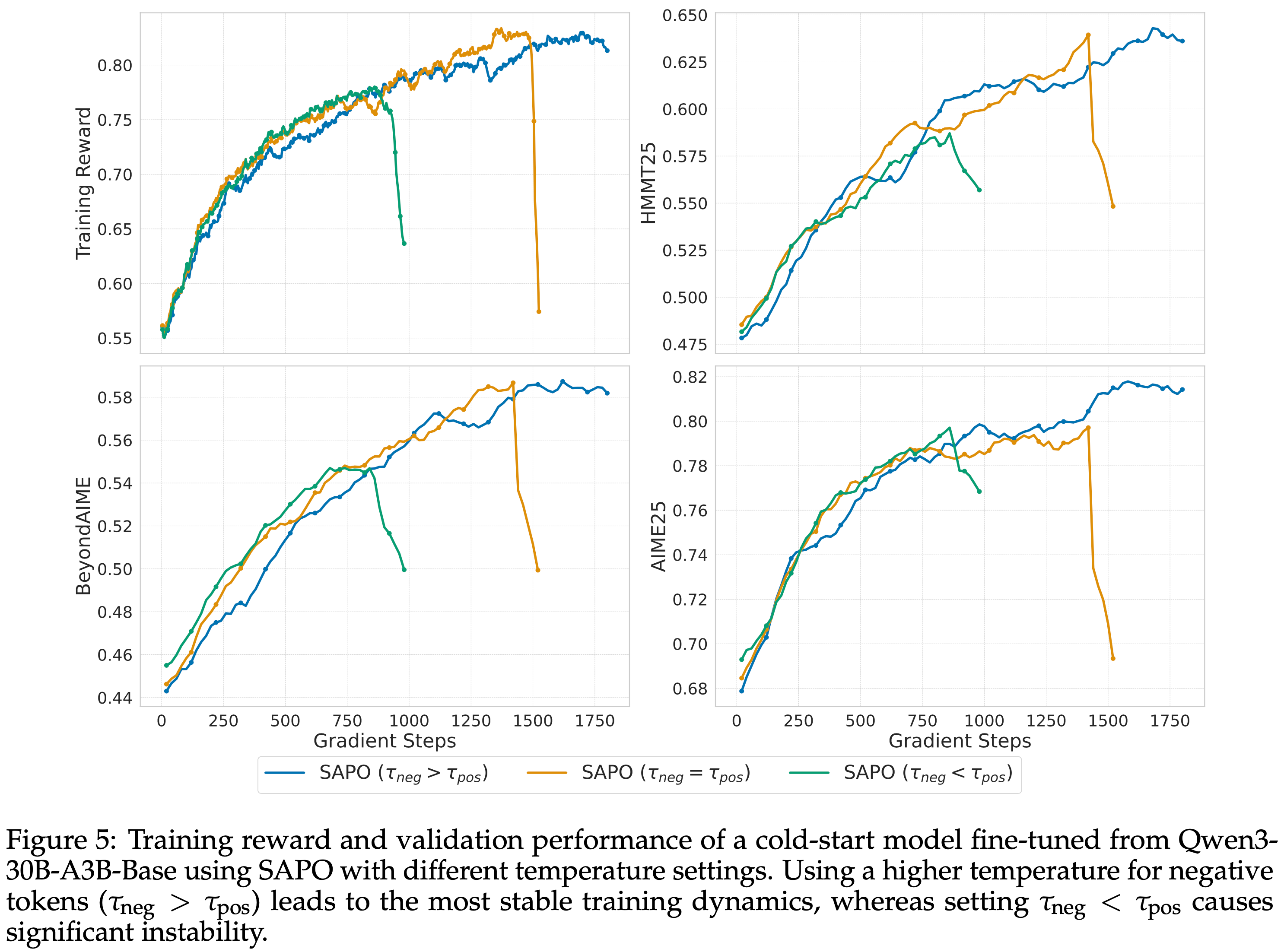
• 为了检验选择 \(\tau_{\text{neg} }>\tau_{\text{pos} }\) 的效果，论文评估了三种配置：
  • \(\tau_{\text{neg} }=1.05>\tau_{\text{pos} }=1.0\)
  • \(\tau_{\text{neg} }=\tau_{\text{pos} }=1.0\)
  • \(\tau_{\text{neg} }=0.95<\tau_{\text{pos} }=1.0\)
• 如图 5 所示
  • 当负 Token 被分配更高的温度（\(\tau_{\text{neg} }=1.05\)）时训练最稳定
  • 当它们被分配更低的温度（\(\tau_{\text{neg} }=0.95\)）时最不稳定
  • 这些结果表明，与负 Token 相关的梯度对训练不稳定性的贡献更大，而 SAPO 的非对称温度设计有效地缓解了这个问题
  • 图 5：使用 SAPO 不同温度设置下，从 Qwen3-30B-A3B-Base 微调的冷启动模型的训练奖励和验证性能
    • 对负 Token 使用更高的温度（\(\tau_{\text{neg} }>\tau_{\text{pos} }\)）导致最稳定的训练动态，而设置 \(\tau_{\text{neg} }<\tau_{\text{pos} }\) 会导致显著的不稳定性

Qwen3-VL Training

• 作者将 SAPO 应用于训练 Qwen3-VL 系列模型，以评估其在实际大规模设置中的有效性
• 实验表明：SAPO 在不同规模的模型以及 MoE 和稠密架构上都能持续提高性能
• 作者在广泛的文本和多模态任务集合上进行训练，包括数学、编码和逻辑推理
• 为了支持多任务学习，论文在每个批次内为每个任务保持固定的采样比例
• 论文还使用了大批量大小，将每批 rollout 数据分成两个小批量进行梯度更新，确保每个小批量为所有任务提供足够的学习信号
• 为了突出 SAPO 相对于 GSPO 和 GRPO-R2 的优势，论文从 Qwen3-VL-30B-A3B 的初步冷启动检查点开始，评估三种强化学习算法
• 论文报告了四个基准测试上的训练奖励和平均验证性能：AIME25 (AIME, 2025)（Pass@1，32 个样本）、LiveCodeBench v6 (2024)（Pass@1，8 个样本）、ZebraLogic (2025) 和 MathVision (2024)
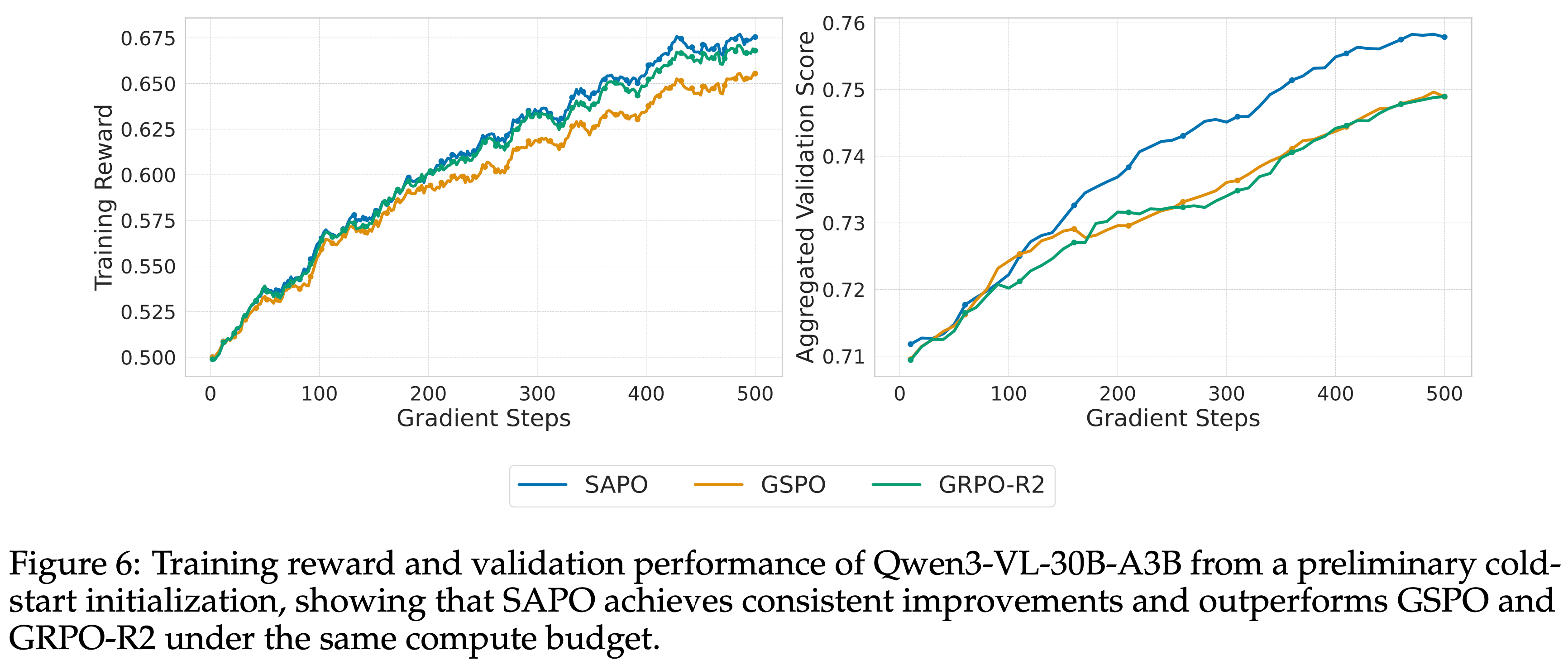
• 如图 6 所示，SAPO 在整个训练过程中实现了稳定的性能提升，并在相同的计算预算下优于两个基线
  • 图 6：从初步冷启动初始化的 Owen3-VL-30B-A3B 的训练奖励和验证性能，表明在相同的计算预算下，SAPO 实现了一致的改进并优于 GSPO 和 GRPO-R2

---

附录：正负梯度的推导和理解（公式 9）

• 该公式描述了在强化学习中，对于 Token-level 策略梯度的推导，尤其是关于 logits \( z_v \) 的梯度如何计算
  $$
  \begin{align}
  \frac{\partial\log\pi_{\theta}(y_{i,t}\mid q,y_{i,<t})\widehat{A}_{i,t} }{\partial z_{v} } &=\frac{\partial\pi_{\theta}(y_{i,t}\mid q,y_{i,<t})}{\partial z_{v} }\cdot\frac{\widehat{A}_{i,t} }{\pi_{\theta}(y_{i,t}\mid q,y_{i,<t})} \\
  &=\frac{\mathbb{I}(v=y_{i,t})\exp(z_{y_{i,t} })\sum_{v^{\prime}\in{\cal V} }\exp(z_{v^{\prime} })-\exp(z_{y_{i,t} })\exp(z_{v})}{(\sum_{v^{\prime}\in{\cal V} }\exp(z_{v^{\prime} }))^{2} }\cdot\frac{\widehat{A}_{i,t} }{\pi_{\theta}(y_{i,t}\mid q,y_{i,<t})} \\
  &=\begin{cases}(1-\pi_{\theta}(y_{i,t}\mid q,y_{i,<t}))\cdot\widehat{A}_{i,t}&\text{if $v=y_{i,t}$}\quad\text{(Sampled Token )}\\ -\pi_{\theta}(v\mid q,y_{i,<t})\cdot\widehat{A}_{i,t}&\text{otherwise}\quad\text{(Unsampled Token )}\end{cases} \tag{9}
  \end{align}
  $$

已知条件

• 设 \( z = [z_1, z_2, \dots, z_{|V|}] \) 为 logits 向量
• 输出概率通过 softmax 函数给出：
  $$
  \pi_{\theta}(v \mid q, y_{i,<t}) = \frac{\exp(z_v)}{\sum_{v’ \in \mathcal{V} } \exp(z_{v’})}
  $$

第一步：写出对数概率对 logits 的梯度

• 根据求导公式，容易得：
  $$
  \frac{\partial\log\pi_{\theta}(y_{i,t}\mid q,y_{i,<t})\widehat{A}_{i,t} }{\partial z_{v} } = \frac{\partial \log \pi_{\theta}(y_{i,t} \mid q, y_{i,<t})}{\partial z_v} \cdot \widehat{A}_{i,t}
  $$
• 其中，进一步可以将上式中的梯度部分化简：
  $$
  \frac{\partial \log \pi_{\theta}(y_{i,t} \mid q, y_{i,<t})}{\partial z_v} = \frac{1}{\pi_{\theta}(y_{i,t} \mid q, y_{i,<t})} \cdot \frac{\partial \pi_{\theta}(y_{i,t} \mid q, y_{i,<t})}{\partial z_v}
  $$

第二步：计算 softmax 输出对 logits 的偏导数

• 设：
  $$
  S = \sum_{v’ \in \mathcal{V} } \exp(z_{v’}), \quad M = \exp(z_{y_{i,t} })
  $$
• 则，根据 概率与 logits 的计算公式，有对于指定的 \(\exp(z_{y_{i,t} })\)，其概率分布为：
  $$
  \pi_{\theta}(y_{i,t} \mid q, y_{i,<t}) = \frac{\exp(z_{i,t})}{S} = \frac{M}{S}
  $$
• 原始公式中的后一项，表示让上述公式对任意 Token \(v\) 的 logits \(z_v\) 进行求导，即：
  $$
  \begin{align}
  \frac{\partial \pi_{\theta}(y_{i,t} \mid q, y_{i,<t})}{\partial z_v} = \frac{\partial}{\partial z_v} \left( \frac{M}{S} \right) = \frac{\frac{\partial M}{\partial z_v} \cdot S - M \cdot \frac{\partial S}{\partial z_v}}{S^2} \\
  \end{align}
  $$
  • 这里使用了分数求导公式：
    $$ \left(\frac{u}{v}\right)’ = \frac{u’v - v’u}{v^2} $$

情况 1：对当前采样的 Token

• 此时 \( v = y_{i,t} \)，所以 \(z_v = z_{y_{i,t}}\)，于是有：
  $$ \frac{\partial\exp(z_{y_{i,t} })}{\partial z_v} = \frac{\partial\exp(z_{y_{i,t} })}{\partial z_{y_{i,t} }} = \exp(z_{y_{i,t} })$$
• 于是有
  $$
  \begin{align}
  \frac{\partial \pi_{\theta}(y_{i,t} \mid q, y_{i,<t})}{\partial z_v}
  &= \frac{\frac{\partial M}{\partial z_v} \cdot S - M \cdot \frac{\partial S}{\partial z_v}}{S^2} \\
  &= \frac{\exp(z_{y_{i,t} }) \cdot S - \exp(z_{y_{i,t} }) \cdot \exp(z_v)}{S^2} \\
  &= \frac{\exp(z_{y_{i,t} }) \cdot S - \exp(z_{y_{i,t} })^2}{S^2} \\
  &= \frac{\exp(z_{y_{i,t} })}{S} \cdot \left(1 - \frac{\exp(z_{y_{i,t} })}{S}\right) \\
  &= \pi_{\theta}(y_{i,t} \mid q, y_{i,<t}) \cdot \big(1 - \pi_{\theta}(y_{i,t} \mid q, y_{i,<t})\big)
  \end{align}
  $$
• 结论：当 \( v = y_{i,t} \)（对应当前采样的 Token ）
  $$
  \frac{\partial \pi_{\theta}(y_{i,t} \mid q, y_{i,<t})}{\partial z_{v} } = \pi_{\theta}(y_{i,t} \mid q, y_{i,<t}) \cdot \big(1 - \pi_{\theta}(y_{i,t} \mid q, y_{i,<t})\big)
  $$

情况 2：对其他未采样的 Token

• 当 \( v \neq y_{i,t} \)，于是有
  $$
  \begin{align}
  \frac{\partial \pi_{\theta}(y_{i,t} \mid q, y_{i,<t})}{\partial z_v}
  &= \frac{\frac{\partial M}{\partial z_v} \cdot S - M \cdot \frac{\partial S}{\partial z_v}}{S^2} \\
  &= \frac{0 \cdot S - \exp(z_{y_{i,t} }) \cdot \exp(z_v)}{S^2} \\
  &= \frac{- \exp(z_{y_{i,t} })^2}{S^2} \\
  &= \frac{\exp(z_{y_{i,t} })}{S} \cdot \left(- \frac{\exp(z_{y_{i,t} })}{S}\right) \\
  &= \pi_{\theta}(y_{i,t} \mid q, y_{i,<t}) \cdot \big(- \pi_{\theta}(y_{i,t} \mid q, y_{i,<t})\big) \\
  &= - \pi_{\theta}(y_{i,t} \mid q, y_{i,<t}) \cdot \pi_{\theta}(y_{i,t} \mid q, y_{i,<t})
  \end{align}
  $$
• 结论：当 \( v \neq y_{i,t} \)（对应其他未采样的 Token ）
  $$
  \frac{\partial \pi_{\theta}(y_{i,t} \mid q, y_{i,<t})}{\partial z_{v} } = -\pi_{\theta}(y_{i,t} \mid q, y_{i,<t}) \cdot \pi_{\theta}(v \mid q, y_{i,<t})
  $$

第三步：代入梯度公式

• 将上述两种情况的偏导数代入第一步的梯度公式中：
• 当 \( v = y_{i,t} \)：
  $$
  \begin{align}
  \frac{\partial\log\pi_{\theta}(y_{i,t}\mid q,y_{i,<t})\widehat{A}_{i,t} }{\partial z_{v} } &= \frac{1}{\pi_{\theta}(y_{i,t} \mid q, y_{i,<t})} \cdot \big[ \pi_{\theta}(y_{i,t} \mid q, y_{i,<t}) \cdot \big(1 - \pi_{\theta}(y_{i,t} \mid q, y_{i,<t})\big) \big] \cdot \widehat{A}_{i,t} \\
  &= \big(1 - \pi_{\theta}(y_{i,t} \mid q, y_{i,<t})\big) \cdot \widehat{A}_{i,t}
  \end{align}
  $$
• 当 \( v \neq y_{i,t} \)：
  $$
  \begin{align}
  \frac{\partial\log\pi_{\theta}(y_{i,t}\mid q,y_{i,<t})\widehat{A}_{i,t} }{\partial z_{v} } &= \frac{1}{\pi_{\theta}(y_{i,t} \mid q, y_{i,<t})} \cdot \big[ -\pi_{\theta}(y_{i,t} \mid q, y_{i,<t}) \cdot \pi_{\theta}(v \mid q, y_{i,<t}) \big] \cdot \widehat{A}_{i,t} \\
  &= -\pi_{\theta}(v \mid q, y_{i,<t}) \cdot \widehat{A}_{i,t}
  \end{align}
  $$

第四步：合并为分段函数形式

• 综上，公式 (9) 的完整推导结果为：
  $$
  \frac{\partial \log \pi_{\theta}(y_{i,t} \mid q, y_{i,<t}) \cdot \widehat{A}_{i,t} }{\partial z_v} =
  \begin{cases}
  \big(1 - \pi_{\theta}(y_{i,t} \mid q, y_{i,<t})\big) \cdot \widehat{A}_{i,t} & \text{if } v = y_{i,t} \quad \text{(sampled token)} \\
  -\pi_{\theta}(v \mid q, y_{i,<t}) \cdot \widehat{A}_{i,t} & \text{otherwise} \quad \text{(unsampled token)}
  \end{cases}
  $$

对公式 (9) 的细致理解

• 不同 Token 对未采样 Token 带来的影响是不同的：
  • 当 \( \widehat{A}_{i,t} > 0 \) 时
    • 当前 Token 的 logits 会增加，其他 Token 的 logits 会减少
  • 当 \( \widehat{A}_{i,t} < 0 \) 时
    • 当前 Token 的 logits 减少，其他 Token 的 logits 增加，从而可能引入更多不稳定性
• 这也是 SAPO 中为什么对正负 Token 使用不同温度 \( \tau_{\text{pos} } \) 和 \( \tau_{\text{neg} } \) 的理论依据之一：负面更新更容易扩散到大量不相关 Token ，因此需要更快的衰减以保持稳定性