注:本文包含 AI 辅助创作
Paper Summary
- 总体评价:
- DFT 仅仅修改了一行代码,在 SFT 的损失函数上加入一个权重,得到了大幅的泛化能力提升
- DFT 本质是从梯度出发,将 SFT 的梯度对齐了 RL 的梯度,企图因此让 SFT 拥有 RL 的泛化性
- 问题:直接修改了 SFT 的损失函数,真的可行吗?靠近 RL 梯度而不进行探索,是否真的有利于泛化性?
- 背景:
- LLM 中,SFT 的泛化能力不如 RL
- 前置分析:
- 论文作者通过数学分析发现标准 SFT 的梯度隐式编码了一种有问题的奖励结构,可能会严重限制模型的泛化能力
- 为了纠正这一问题,论文提出了动态微调(Dynamic Fine-Tuning, DFT) ,通过用该 Token 的概率动态重新调整目标函数,从而稳定每个 Token 的梯度更新
- 实验结论:
- 在多个具有挑战性的基准测试和基础模型上显著优于标准 SFT,展示了大幅提升的泛化能力
- 在 Offline RL 场景中也表现出具有竞争力的结果,提供了一种更简单但有效的替代方案
- 这项工作结合了理论和实践解决方案,显著提升了 SFT 的性能
- 代码开源地址:github.com/yongliang-wu/DFT
DFT Method
Preliminaries
Supervised Fine-Tuning
- 设 \(\mathcal{D}=\{(x,y^{*})\}\) 表示专家示范的语料库,其中 \(y^{*}\) 是查询 \(x\) 的完整参考响应。SFT 最小化句子级的交叉熵:
$$
\mathcal{L}_{\textrm{SPT} }(\theta)\ =\ \mathbb{E}_{(x,y^{*})\sim\mathcal{D} }\big{[}-\log \pi_{\theta}\big{(}y^{*} \mid x\big{)}\big{]}. \tag{1}
$$ - 其梯度为:
$$
\nabla_{\theta}\mathcal{L}_{\textrm{SPT} }(\theta)\ =\ \mathbb{E}_{(x,y^{*})\sim\mathcal{D} }\big{[}-\nabla_{\theta}\log \pi_{\theta}\big{(}y^{*} \mid x\big{)}\big{]}.\tag{2}
$$
Reinforcement Learning
- 设 \(y\) 表示从策略 \(\pi_{\theta}(\cdot \mid x)\) 中采样的响应。给定奖励函数 \(r(x,y)\in\mathbb{R}\),策略目标为:
$$
J(\theta)\ =\ \mathbb{E}_{x\sim\mathcal{D}_{x},\ y\sim\pi_{\theta}(\cdot \mid x)}\big{[}r(x,y)\big{]}. \tag{3}
$$ - 其句子级策略梯度为:
$$
\nabla_{\theta}J(\theta)\ =\ \mathbb{E}_{x\sim\mathcal{D}_{x},\ y\sim\pi_{\theta}(\cdot \mid x)}\big{[}\nabla_{\theta}\log \pi_{\theta}(y \mid x)\ r(x,y)\big{]}. \tag{4}
$$
Unity SFT-RL Gradient Expression
- 通过重要性采样将 SFT 梯度重写为策略梯度(Rewriting SFT Gradient as Policy Gradient via Importance Sampling)
- 方程 2 中的 SFT 梯度是在固定的示范分布下计算的
- 论文通过插入一个重要性权重,将专家(狄拉克δ)分布与模型分布进行比较,将其转换为 On-policy 期望:
$$
\mathbb{E}_{(x,y^{*})\sim\mathcal{D} }\left[-\nabla_{\theta}\log \pi_{\theta}\big{(}y^{*} \mid x)\right]=\underbrace{\mathbb{E}_{x\sim\mathcal{D}_{x} }\ \mathbb{E}_{y\sim\pi_{\theta}(\cdot|x)}\frac{\mathbf{1}[y=y^{*}]}{\pi_{\theta}(y \mid x)}\left[-\nabla_{\theta}\log \pi_{\theta}\big{(}y \mid x)\right]}_{\text{resample + reweight} } \tag{5}
$$ - 定义辅助变量:
$$
w(y \mid x)=\frac{\mathbf{1} }{\pi_{\theta}(y \mid x)},\quad r(x,y)=\mathbf{1}[y=y^{*}],
$$ - 重组方程 5 并使用上述辅助变量重写,论文得到以下形式:
$$
\nabla_{\theta}\mathcal{L}_{\text{SFT} }(\theta)=-\mathbb{E}_{x\sim\mathcal{D}_{x},\ y\sim\pi_{\theta}(\cdot|x)}\big{[}\color{red}{w(y \mid x)}\ \nabla_{\theta}\log \pi_{\theta}(y \mid x),\color{red}{r(x,y)}\big{]}. \tag{6}
$$- 这种形式的 SFT 梯度现在与策略梯度方程 4 高度一致(除了梯度权重 \(\color{red}{w(y \mid x)}\))外
- 传统的 SFT 本质上是一种 On-policy 梯度,其奖励是匹配专家轨迹的指示函数,但受到重要性权重 \(1/\pi_{\theta}\) 的偏置
- 问题:这里改成任意策略都可以吧?岂不是也可以 Off-policy?
- 补充:从这个视角看,似乎改成任意策略都行,但是为了使用策略梯度法(On-policy),使用当前策略(即 On-policy)会更好
Proposed Method
- 通过动态重加权进行奖励修正(Rewriting SFT Gradient as Policy Gradient via Importance Sampling)
- 为了纠正从 RL 目标视角下发现的奖励偏差问题,论文通过乘以策略概率 \(1/w\) 给出的校正逆比率来动态重新加权奖励,得到的“动态微调”梯度为:
$$
\nabla_{\theta}\mathcal{L}_{\text{DFT} }(\theta)=\nabla_{\theta}\mathcal{L}_{\text{SFT} }(\theta)\ \cdot\ \operatorname{sg}(\frac{1}{w})=\nabla_{\theta}\mathcal{L}_{\text{SFT} }(\theta)\ \cdot\ \operatorname{sg}(\pi_{\theta}(y^{*} \mid x)).
$$- \(\operatorname{sg}(\cdot)\) 表示停止梯度操作符,确保梯度不通过奖励缩放项 \(w\) 流动
- 为了便于过渡到后续方程,论文直接将 \(1/w\) 写为 \(\pi_{\theta}(y^{*} \mid x)\) 而非 \(\pi_{\theta}(y \mid x)\),因为方程 5 或方程 6 中的指示函数会将所有 \(y \neq y^{*}\) 的情况置为 0
- 由于梯度不流动(Stop Gradient),修正后的 SFT 损失也变为一个简单的重加权损失,称为动态微调(DFT):
$$
\mathcal{L}_{\text{DFT} }(\theta)=\mathbb{E}_{(x,y^{*})\sim\mathcal{D} }\Big{[}\operatorname{sg}\big{(}\pi_{\theta}(y^{*}_{t} \mid x)\big{)}\log \pi_{\theta}(y^{*}_{t} \mid x)\Big{]}.
$$ - 在实践中,计算整个轨迹的重要性权重可能会引发数值不稳定性。解决此问题的常见方法是简单地应用 Token-level 的重要性采样(如 PPO (2017) 中所采用的那样),DFT 的最终损失函数为:
$$
\mathcal{L}_{\text{DFT} }(\theta)=\mathbb{E}_{(x,y^{*})\sim\mathcal{D} }\Big{[}-\sum_{t=1}^{|y^{*}|}\operatorname{sg}\big{(}\pi_{\theta}(y^{*}_{t} \mid y^{*}_{ < t},x)\big{)}\log \pi_{\theta}(y^{*}_{t} \mid y^{*}_{ < t},x)\Big{]}.
$$- 修正后的 SFT(以 RL 形式表示)的奖励,即 DFT,现在对所有专家轨迹统一为 1
- 这与当代基于验证的奖励方法 RLVR (2025) 类似,后者对所有正确样本分配统一的奖励
- 因此,它避免了对特定低概率参考 Token 的过度关注,从而在不引入额外采样或奖励模型的情况下实现更稳定的更新和更好的泛化能力
Related Work
- SFT 和 RL 之间的权衡是现代语言模型对齐的核心主题
- SFT 因其简单且能高效模仿专家行为而被广泛采用,这一过程类似于机器人学中的行为克隆(Behavioral Cloning)(2011; 2020)
- 但文献中经常指出,与 RL 相比,这种方法可能导致过拟合和较差的泛化能力,因为 RL 利用奖励信号来探索和发现更鲁棒的策略(2024; 2017; 2022)
- (2024) 对文本和视觉任务上的 SFT 和 RL 进行了系统比较,证实了“SFT 记忆,而 RL 泛化(SFT memorizes while RL generalizes)” 的结论
- 目前,SFT 仍然是必要的初始化步骤,用于在 RL 训练生效前稳定输出格式
- 但 RL 仍面临重大实际障碍,包括高计算成本、超参数敏感性以及对显式奖励函数的需求,这些因素常常限制其适用性(2017; 2019; 2025)
- 为了利用两种范式的优势,主流研究方向集中在混合方法上
- 最成熟的策略包括 SFT 预训练阶段和基于 RL 的细化阶段,通常使用学习的奖励模型(如 InstructGPT(2022))
- 最近的方法探索了替代组合,例如交替进行 SFT 和 RL 步骤以提高稳定性和性能(2025; 2025; 2025)
- 其他比较优秀的方法,如直接偏好优化(Direct Preference Optimization, DPO)(2023),通过直接在偏好数据上优化策略来绕过显式奖励建模,有效地将模仿和强化信号集成到单个损失函数中
- (2025) 提出的负感知微调(Negative-aware Fine-Tuning, NFT)通过隐式负策略使 LLM 能够通过建模自身错误生成来自我改进
- 尽管这些方法功能强大,但它们是为奖励信号、偏好对或负样本可用的场景设计的
- 它们扩展了训练流程,但并未从根本上改进 SFT 在其原生上下文中的过程(即仅存在正例专家行为的情况下)
- 论文的工作通过专注于增强 SFT 本身而无需任何外部反馈,从而与之分道扬镳
- 当前的理论探究试图统一 SFT 和 RL
- (2025) 将 RLHF 重新定义为奖励加权的 SFT 形式,简化了流程但仍依赖于显式奖励
- (2025) 证明 SFT 可以被视为具有隐式奖励的 RL 方法,并提出诸如较小学习率等解决方案来管理否则会消失的 KL 约束
- (2025) 分析了从正负反馈中学习的过程,展示了它们的平衡如何影响策略收敛
- (2025) 将 SFT 重新定义为 RL 的下界,并通过基于数据生成策略的重要性加权来改进它
- 尽管这些工作通过加权的视角指出了 SFT 和 RL 之间的一般联系,但它们未能提供 SFT 梯度和离线策略梯度之间的精确数学等价性
- 论文的工作首次严格建立了这种等价性,明确指出关键差异在于 SFT 中存在的逆概率加权项
- 特别说明:论文的方法产生了一种与著名的 Focal Loss(2017)截然相反的交叉熵(Cross-Entropy, CE)损失设计
- 论文修改后的 CE 是 \(-p \log(p)\),而 Focal Loss 是 \(-(1-p)^{\gamma} \log(p)\)
- Focal Loss 有意降低分类良好的样本的权重以提高对少数类的性能,而论文有意降低分类不佳的样本的权重以改善泛化能力
- 这种对比可能反映了 LLM 时代的一个根本性转变,即欠拟合变得不如过拟合问题严重
Experiments
- 实验效果比 SFT 好很多
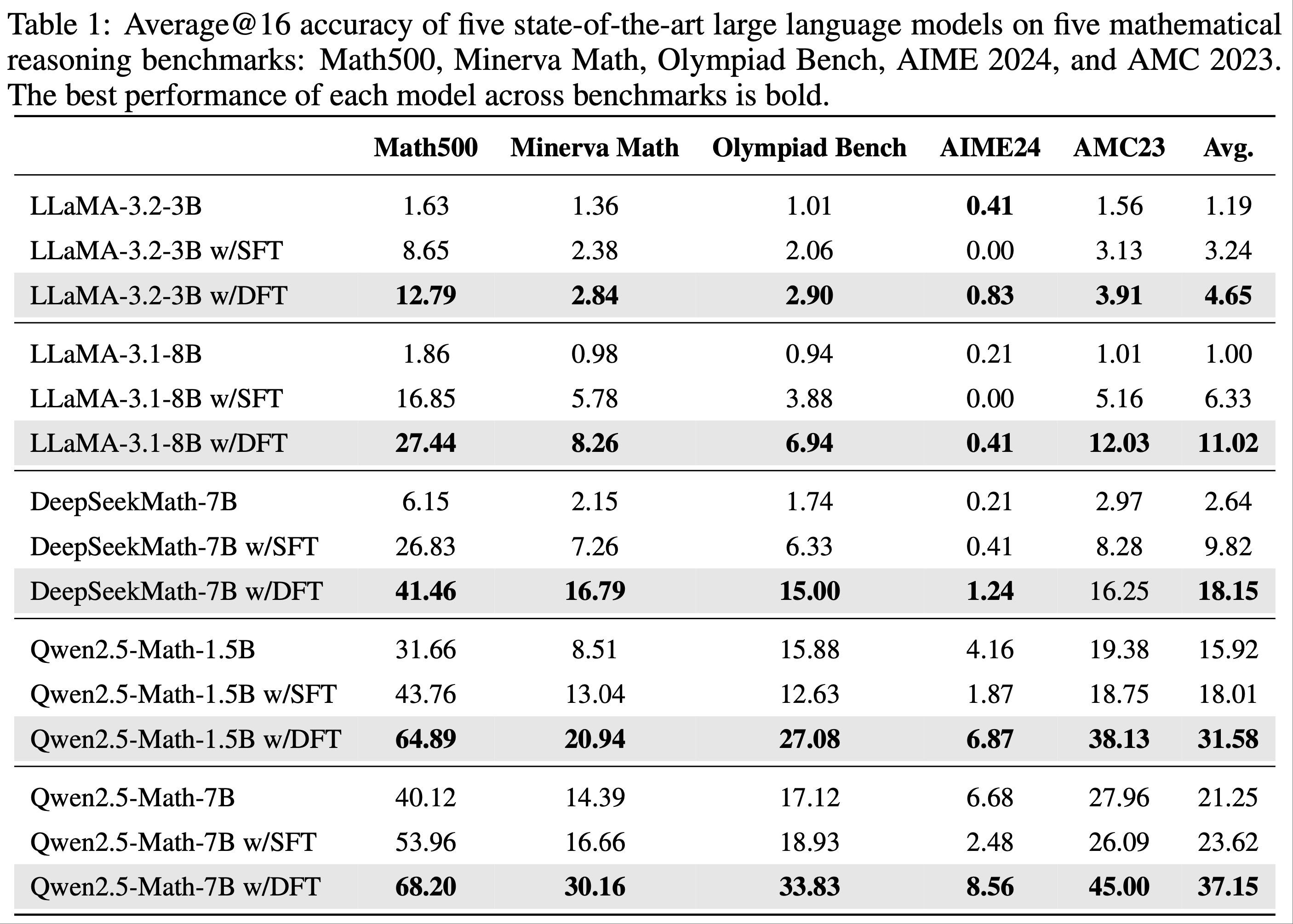
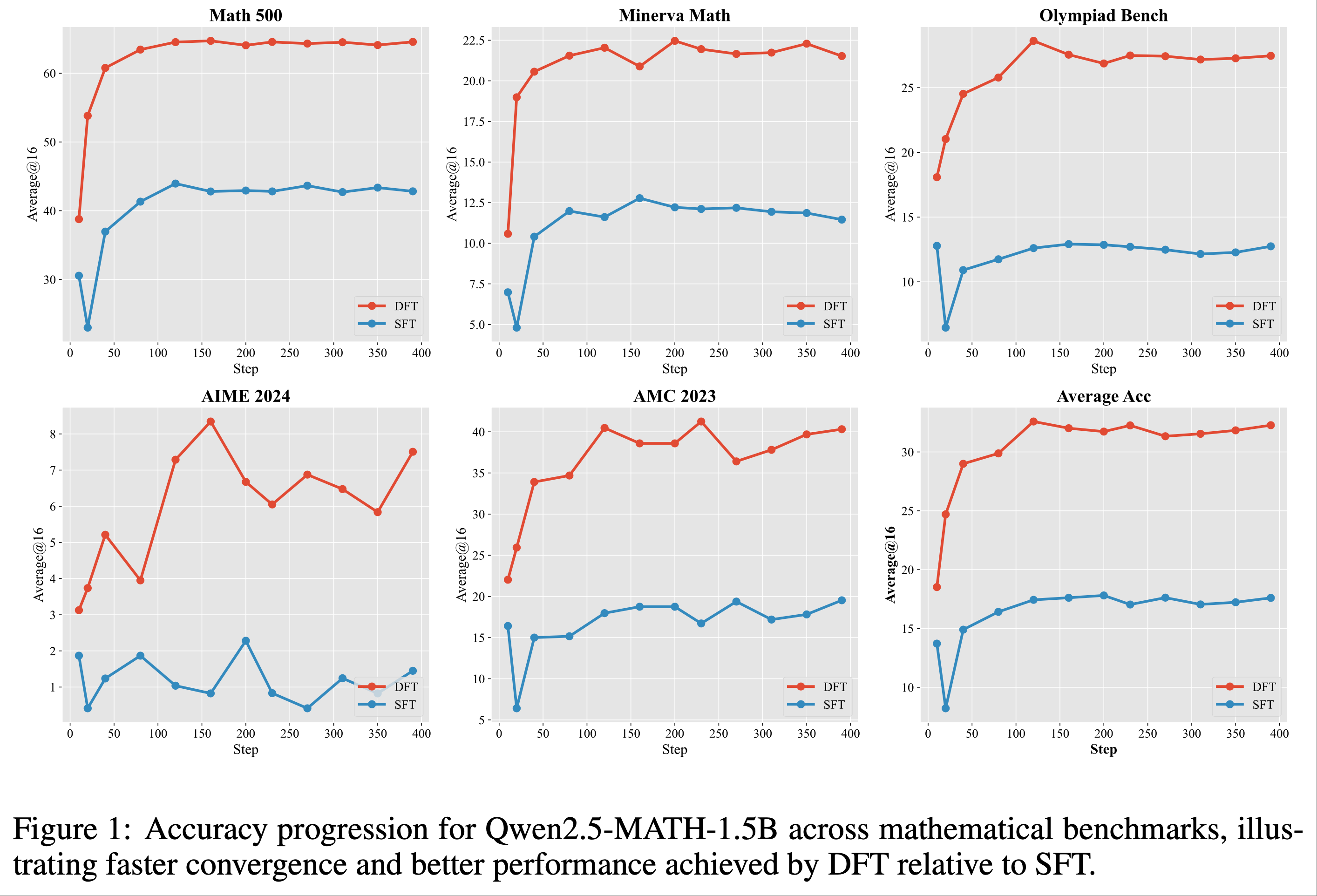
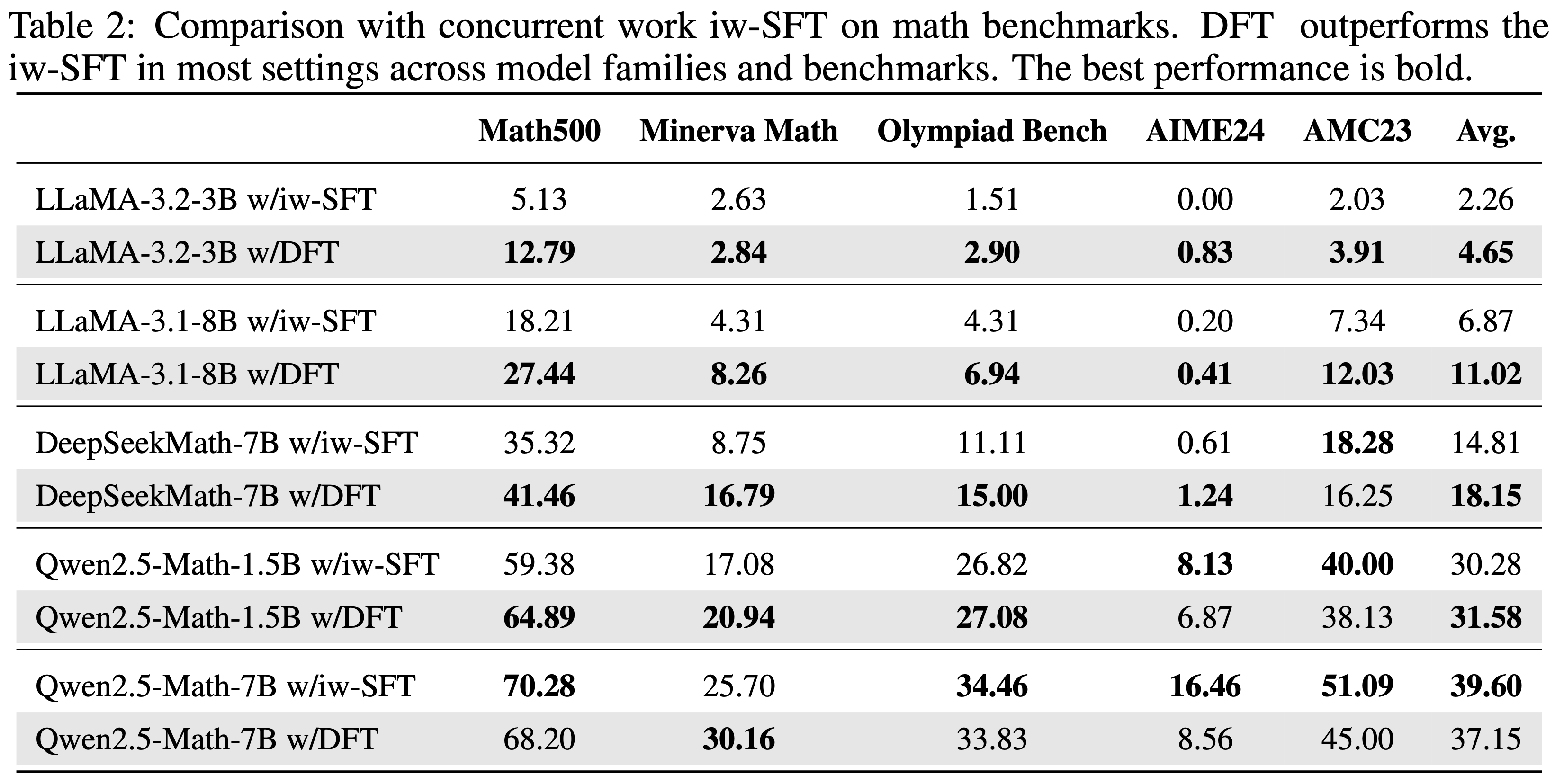
- 其中 iw-SFT 是 Importance weighted supervised fine-tuning,详情见论文:Supervised Fine Tuning on Curated Data is Reinforcement Learning (and can be improved), 20250717