注:本文包含 AI 辅助创作
- 参考链接:
Paper Summary
- 核心内容总结:
- 论文提出了是一个专为高效大规模 RL 训练设计的完全异步(fully asynchronous )系统 AReaL
- 论文还提出了多项算法创新,包括陈旧感知训练和解耦 PPO 目标(Decoupled PPO Objective) ,使异步环境中的 PPO 训练既高效又稳定
- 注:Decoupled PPO Objective 已经成为异步训练的标配 Feature
- 背景:RL 已成为训练 LLM 的一种流行范式,尤其在推理任务中,有效的 LLM 强化学习需要大规模并行化,因此亟需高效的训练系统
- 现有的大规模 RL 系统多为同步(synchronous)设计,即在批量设置中交替进行生成和训练,每个训练批次的样本由同一(或最新)模型生成 ,这种设计的优缺点如下:
- 优点:稳定
- 缺点:存在严重的系统效率问题,即生成阶段必须等待批次中最长的输出完成后才能更新模型,导致 GPU 利用率低下
- 论文提出 AReaL ,一种完全异步的 RL 系统 ,彻底解耦生成与训练
- AReaL 的 Rollout Worker无需等待即可持续生成新输出
- 训练 Worker (training worker)在收集到足够数据后立即更新模型
- AReaL 还引入了一系列系统级优化,显著提高了 GPU 利用率
- 为稳定 RL 训练,AReaL 通过平衡生成与训练 Worker 的负载控制数据陈旧性(staleness),并采用一种改进的 PPO(Proximal Policy Optimization)变体以更好地处理过时样本
- 实验结论:在数学和代码推理基准测试中,AReaL 相比同步系统实现了高达 2.77 倍的训练加速,同时保持甚至提升了最终性能
Introduction and Discussion
- RL 作为一种新的扩展范式,通过赋予 LLM 思考能力(thinking abilities)来增强其性能 (2022)
- 给定一个提示(prompt),RL 允许 LLM 在输出最终答案前生成思考 Token(thinking tokens),从而实现测试时扩展(test-time scaling)(2024; 2025)
- 这类具备思考能力的 LLM 被称为大型推理模型(Large Reasoning Model, LRM) ,在 challenging reasoning problems 上表现出色
- 即数学 (2021; 2021; 2023)、编程 (2021; 2023; 2023)、逻辑谜题(logic puzzles) (2025) 和智能体任务(agentic tasks) (2024) 等
- 有效的 RL 训练通常需要大规模并行化,以获取足够探索的大批量生成样本(rollouts),这是实现最优模型性能的关键
- 例如,PPO (2017) 和 GRPO (2024) 等流行 RL 算法通常需要数千个输出的有效训练批次 (2025; 2025; 2025)
- 此外,LRM 可能为每个输入提示生成数万个思考 Token (2025),这进一步凸显了对高效训练系统的迫切需求
- 开发高效的大规模 RL 系统具有挑战性,表现在:
- RL 系统需要频繁切换 LLM 生成与训练,若缺乏精心优化,会引入显著的系统开销
- 对于 LRM,训练模型的输出长度因提示不同而变化巨大,导致生成和训练的工作负载不断变化,常引发高性能硬件的空闲时间,造成计算浪费
- 经典的大规模 RL 算法(如 PPO 或 GRPO)通常需要 on-policy 训练数据(即由最新模型生成的样本)以确保最佳性能,这带来了额外的系统挑战
- 理解:on-policy 限制了最新模型生成的样本,导致效率进一步降低
- 基于以上原因,现有的大多数大规模 RL 系统采用完全同步设计 (2024; 2024; 2025; 2025),严格交替执行 LLM 生成与训练,确保模型始终基于最新输出进行训练以获得最佳性能
- 在这种同步设计中,生成阶段必须等待批次中最长的输出完成后才能开始训练
- 由于 LRM 的输出长度变化较大,同步 RL 系统会遭受严重的训练效率损失
- 最近,也有研究尝试并行生成与训练 (2025; 2024; 2025),这些工作使用先前模型版本生成的输出来更新当前模型
- 为保障性能,生成所用的模型版本仅允许比当前模型早一到两步
- 然而,这些系统仍 Following 批量生成设置,即一个训练批次内的所有样本来自同一模型版本,因此生成阶段的系统效率问题仍未解决
- 为从根本上解决系统设计问题,论文开发了 AReaL,一种完全异步的 LRM RL 训练系统 ,彻底解耦生成与训练且不影响最终性能
- AReaL 以流式方式(streaming manner)运行 LLM 生成,每个 Rollout Worker 无需等待即可持续生成新输出,从而实现高 GPU 利用率
- AReaL 的训练 Worker 在从 Rollout Worker 收集到训练批次后立即并行更新模型
- 模型更新后,系统会同步各 Rollout Worker 的模型权重
- 在这种异步设计中,AReaL 的每个训练批次可能包含来自不同模型版本的样本
- 因此,AReaL 结合了改进的 PPO 目标函数,能够利用更旧模型版本生成的样本且不会降低性能
- AReaL 还通过数据过滤过程(data filtering process)确保每个训练样本的陈旧性(staleness)得到控制
- AReaL 还引入了多项系统级优化,进一步提升了整体训练吞吐量,包括:
- 可中断的 Rollout Worker(interruptible rollout workers)
- 可变长度输出的动态批处理(dynamic batching for variable-length outputs)
- 并行奖励服务(parallel reward service)
- 论文在 32B 参数的模型上对 AReaL 进行了数学推理和代码生成任务的评估
- 相比 SOTA 同步系统(synchronous systems),AReaL 实现了高达 2.57 倍的训练吞吐量提升,并在 512 个 GPU 上展现出线性扩展效率
- 特别说明:不止加速 ,还带来了任务求解准确率的提升 ,表明 AReaL 在显著提高效率的同时并未牺牲模型性能(甚至增强了模型性能)
Background
Preliminaries about RL Training
RL Formulation and PPO
- 论文将问题形式化为马尔可夫决策过程(Markov Decision Process, MDP)(1994)
- 定义为元组 \( \langle \mathcal{S}, \mathcal{A}, r, P, \gamma, H \rangle \)
- 其中,\( \mathcal{S} \) 表示状态空间,\( \mathcal{A} \) 表示动作空间,\( P \) 是转移模型,\( r: \mathcal{S} \times \mathcal{A} \rightarrow \mathbb{R} \) 是奖励函数,\( \gamma \) 是折扣因子,\( H \) 是时间范围
- LRM(Large Reasoning Model)实现了一个参数化策略 \( \pi_{\theta}: \mathcal{S} \rightarrow \mathcal{A} \),每个动作 \( a_t \in \mathcal{A} \) 对应词汇表中的一个文本标记
- 状态 \( s_t \in \mathcal{S} \) 由问题 \( s_1 = q \) 和之前生成的响应标记 \( (a_1, \ldots, a_{t-1}) \) 组成
- 转移是确定性的:\( s_{t+1} = \text{concat}(s_t, a_t) \)
- 给定问题分布 \( \mathcal{D} \),论文优化以下目标:
$$
J(\theta) = \mathbb{E}_{q \sim \mathcal{D}, a_t \sim \pi_{\theta}(\cdot|q, a_{ < t})} \left[ \sum_{t=1}^{H} \gamma^{t-1} r(s_t, a_t) \right]. \tag{1}
$$
- 定义为元组 \( \langle \mathcal{S}, \mathcal{A}, r, P, \gamma, H \rangle \)
- Following 常见实践 (2025),论文使用基于规则的奖励函数 ,仅在最终动作提供非零反馈(表示答案正确性),并设 \( \gamma = 1 \)。论文使用近端策略优化(Proximal Policy Optimization, PPO)(2017) 来优化这一目标:
$$
J_{\text{PPO} }(\theta) = \mathbb{E}_{q \sim \mathcal{D}, a_t \sim \pi_{\text{old} }(\cdot|q, a_{ < t})} \left[ \sum_{t=1}^{H} \min \left( u_t(\theta) \hat{A}(s_t, a_t), \text{clip} \left( u_t(\theta), 1-\epsilon, 1+\epsilon \right) \hat{A}(s_t, a_t) \right) \right], \tag{2}
$$- \( u_t(\theta) = \frac{\pi_{\theta}(a_t|s_t)}{\pi_{\text{old} }(a_t|s_t)} \) 表示重要性比率(importance ratio)
- \( \hat{A}(s_t, a_t) \) 是估计的优势函数 (2016)
- Following RL 的标准实践 (2017, 2022),论文将全局批次划分为小批次以进行顺序参数更新(sequential parameter updates)
Distributed Systems for LRM Training
- 论文的工作专注于在 SFT 后增强 LRM 的推理能力,不同于激励(incentivize)预训练基模型推理的方法 (2025)
- 经过 SFT 的 LRM 生成长推理序列(例如 32K 标记),通常需要较大的全局批大小(例如每个问题 128 个响应)以实现稳定的 RL 训练 (2025, 2024)
- 在同步 RL 系统中,两个阶段交替执行:生成( rollout)和训练
- 生成阶段使用最新的模型参数为训练批次中的每个查询生成多个推理轨迹
- 训练阶段则基于生成的轨迹更新模型参数
- 这些阶段在同一 GPU 上迭代执行
Motivation for Asynchronous RL System
- 论文总结了同步 RL 系统的两个主要局限性:
- 1) 推理设备利用率低(Inference devices are underutilized) :
- 如图 1(左)所示,生成必须等待批次中最长序列完成后才能开始训练
- 这导致 GPU 解码长度不均匀,从而浪费计算资源
- 2) 同步 RL 系统的可扩展性差(Scalability is poor in synchronous RL systems) :
- 同步系统在所有设备上分配生成任务,降低了每 GPU 的解码批大小,使解码过程进入 memory-IO-bound 状态 (2024),此时增加设备无法提高吞吐量
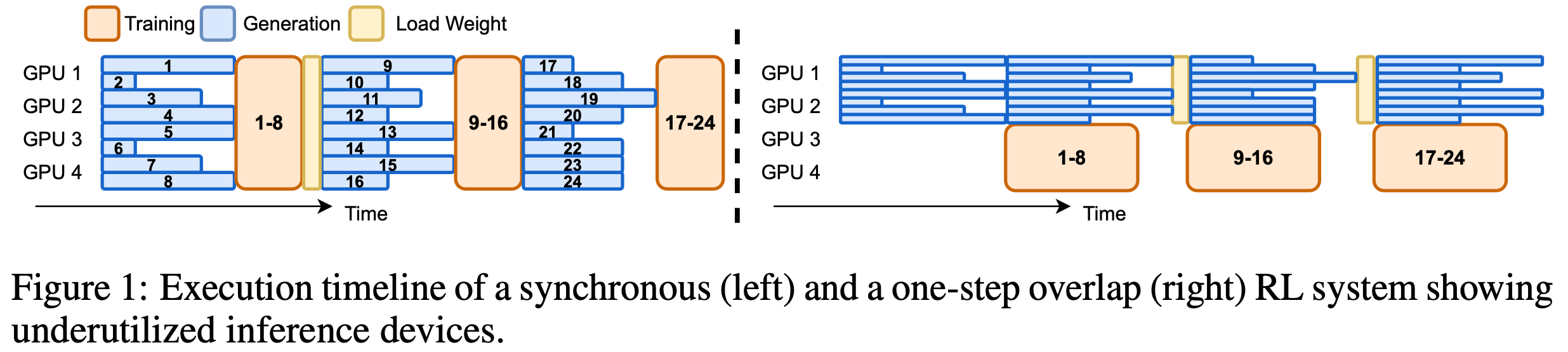
- 同步系统在所有设备上分配生成任务,降低了每 GPU 的解码批大小,使解码过程进入 memory-IO-bound 状态 (2024),此时增加设备无法提高吞吐量
- 1) 推理设备利用率低(Inference devices are underutilized) :
System Architecture
- 3.2节 中提到的局限性促使论文设计一个将生成和训练(training)完全解耦的系统 ,使其具备硬件高效性、可扩展性 ,并支持定制化的 RL 工作流
- 论文在 AReaL 中实现了这些原则,这是一个专为高效大规模 LRM 训练设计的异步 RL 系统
System Overview
- 图2 展示了 AReaL 的架构和数据流
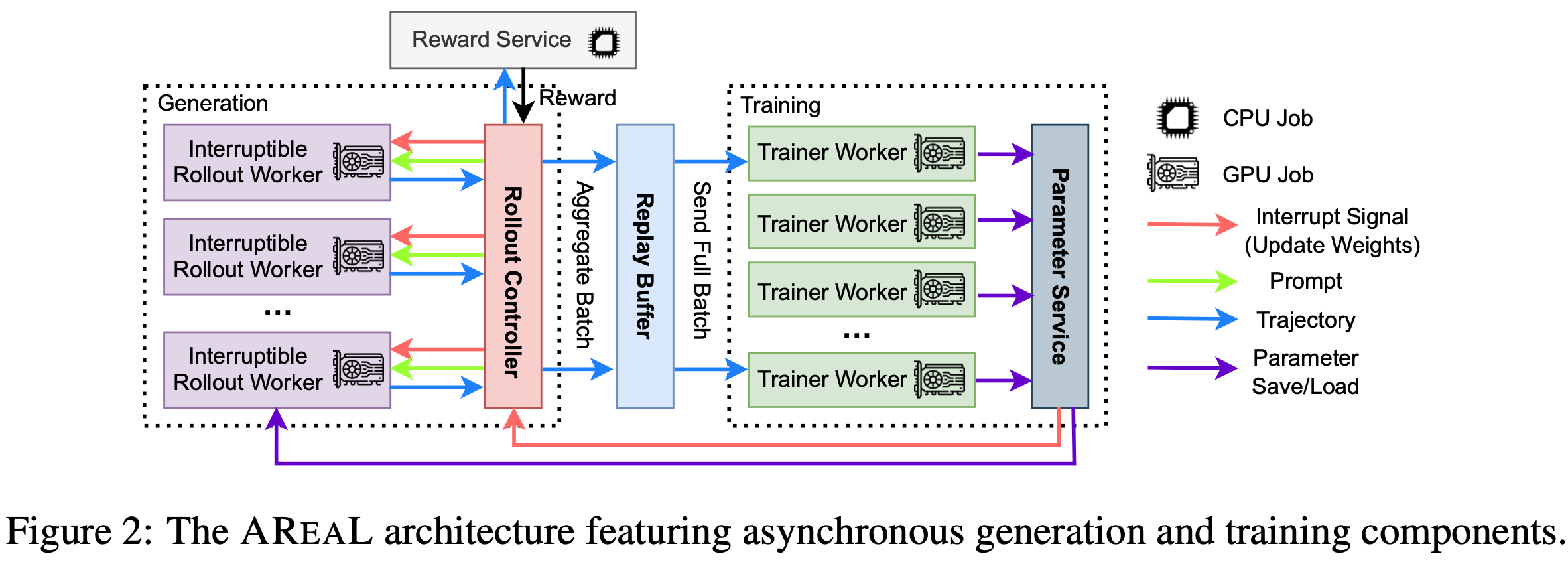
- 如图2 所示,AReaL系统包含4个核心组件:
- 可中断的 Rollout Worker(Interruptible Rollout Worker) 处理两种请求:
- 1) generate request :根据提示生成响应
- 2) 权重更新请求(update_weights request) :中断所有正在进行的生成任务,并加载新版本的参数
- 中断后, Rollout Worker 会丢弃由旧权重计算的 KV 缓存,并使用新权重重新计算
- 理解:注意这里没有抛弃之前已经生成的片段(已经生成的 token 会保留,只是从中断点开始使用新的权重(包括 KV 缓存也抛弃))
- 之后, Rollout Worker 继续解码未完成的序列,直到下一次中断或终止
- 需要注意的是,这种中断和权重更新会导致轨迹由不同模型版本生成的片段组成 ,这将带来新的算法挑战(详见第5节)
- 中断后, Rollout Worker 会丢弃由旧权重计算的 KV 缓存,并使用新权重重新计算
- Reward Service 评估模型生成响应的准确性
- 例如,在编码任务中,该服务会提取代码并执行单元测试以验证其正确性
- Trainer Workers
- 持续从回放缓冲区(replay buffer)中采样数据 ,直到达到配置的训练批次大小
- 执行 PPO 更新 ,并将结果参数存储在分布式存储中
- 为确保数据新鲜度,回放缓冲区中的数据仅使用一次
- Rollout Controller 承担以上三者( Rollout Worker、奖励服务和训练 Worker)之间的桥梁的角色,在训练过程如下:
- Step1(生成响应 by Rollout Worker):控制器从数据集中读取数据并调用 Rollout Worker 的生成请求,获取生成
- Step2(生成奖励 by 奖励服务器):控制器将生成的响应发送给奖励服务,奖励服务返回奖励给控制器
- Step3(储存缓冲区 for 训练 Worker):轨迹和奖励一起存入回放缓冲区,等待训练 Worker 处理
- Step4(训练 Worker 参数更新):当训练 Worker 更新参数后,控制器会调用 Rollout Worker 的权重更新请求
- 图3 展示了生成和训练的管理流程。这种异步流水线设计确保了生成和训练资源的持续高效利用
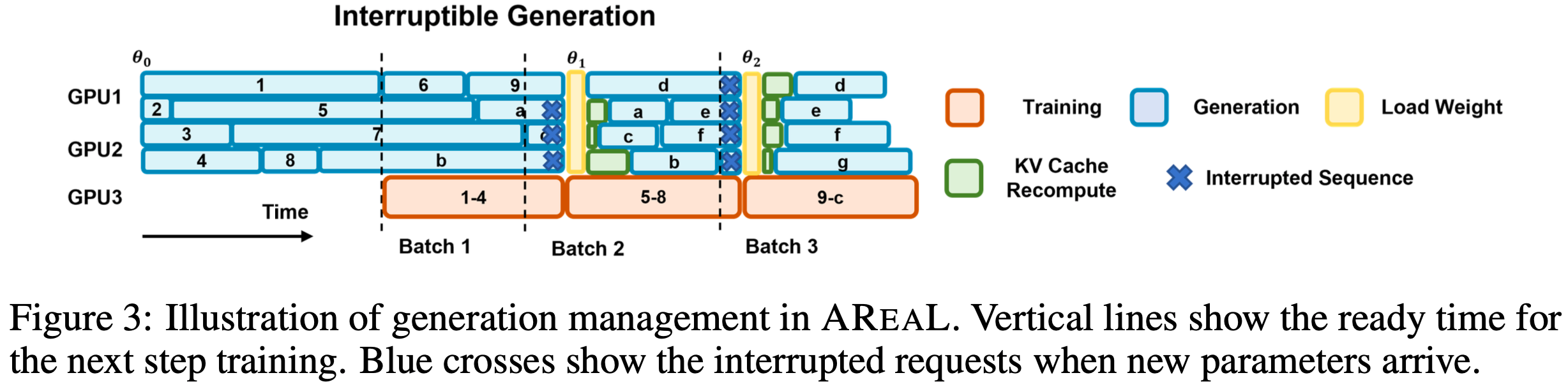
Algorithmic Challenges
- 异步系统设计虽然通过提高设备利用率显著加速了训练,但也引入了需要算法解决的技术挑战
- 挑战1:数据陈旧性(Data Staleness)
- 由于AReaL的异步特性,每个训练批次包含来自多个先前策略版本的数据
- 已有研究表明,这种陈旧性会降低 RLHF 和游戏环境中的学习性能 (2024; 2019)
- 在 LRM 的异步强化学习训练中,由于解码时间较长,这一问题可能更加严重
- 挑战2:策略版本不一致(Inconsistent Policy Versions)
- 如第4.1节所述,生成的轨迹可能包含由不同策略版本生成的片段
- 这种不一致性从根本上违背了标准 PPO 的假设(公式2),即所有动作均由单一策略 \(\pi_{\text{old} }\) 生成
- 理解:注意这里是同一个轨迹中的不同片段可能是不同策略采样得到的
- 在下一节中,论文将详细介绍克服这些挑战的技术创新,同时保留异步系统的效率优势
Addressing the Algorithmic Challenges in AReaL
Staleness-Aware Training
- 为避免因训练数据过于陈旧而导致性能下降,论文引入了一个超参数 \(\eta\),表示 每个训练批次中允许的最大陈旧性
- 具体来说,当 \(\eta=0\) 时,系统退化为同步强化学习,所有训练样本均由当前策略生成
- 论文在系统中通过动态控制生成请求的吞吐量来实现陈旧性控制
- 给定当前策略版本 \(i\)、生成的轨迹总数 \(N_r\) 和每个训练步骤的训练批次大小 \(B\),论文在提交新生成请求时强制执行以下公式:
$$
\lfloor(N_r - 1)/B \rfloor \leq i + \eta. \tag{3}
$$ - 理解:这也不能完全解决问题吧,只能是缓解问题?而且需要考虑数据的采样策略,从而计算重要性权重
- 论文还优先从数据缓冲区中选择较旧的轨迹组成训练批次
- 在系统实现中,生成控制器跟踪参数服务器中的生成样本数 \(N_r\) 和策略版本 \(i\),并拒绝可能违反陈旧性约束的新生成请求
- 问题:为什么是优先选择旧的,因为每个数据仅使用一次;
- 思考:优先使用旧的会导致模型总是使用不到最新的策略生成的样本吧
- 需要注意的是,这种速率限制协议在实践中是一种简单而有效的设计选择
- 但是,当 \(\eta\) 过小时,生成吞吐量可能会因某些极长轨迹的生成而降低
- 因此,论文建议在实践中采用较大的 \(\eta\) 值以获得最佳系统吞吐量
- 这一系统级实践也促使论文采用一种增强算法,能够有效利用更陈旧的数据进行强化学习训练
Decoupled PPO Objective
- 论文采用了一种解耦的 PPO 目标 (2022),将 行为策略(behavior policy) \(\pi_{\text{behav} }\) 和 近端策略(proximal policy) \(\pi_{\text{prox} }\) 分离
- 行为策略 用于采样轨迹
- 近端策略 作为最近的目标(用于正则化策略 \(\pi_\theta\) 的更新)
- 通过对采样轨迹应用重要性采样,论文推导出适用于异步强化学习训练的解耦 PPO 目标:
$$
\begin{align}
J(\theta) &= \mathbb{E}_{q \sim \mathcal{D}, a_t \sim \pi_{\text{behav} } } \left[ \sum_{t=1}^H \min \left( \underbrace{\color{red}{\frac{\pi_\theta}{\pi_{\text{behav} } }}}_{\text{Importance Ratio} } \hat{A}_t, \overbrace{\color{red}{\frac{\pi_{\text{prox} } }{\pi_{\text{behav} } }} \text{clip} \left( \underbrace{\color{red}{\frac{\pi_\theta}{\pi_{\text{prox} } }}}_{T_{\text{Trust Region Center} } } , 1-\epsilon, 1+\epsilon \right)}^{\text{Importance Ratio} } \hat{A}_t \right) \right] \tag{4} \\
&= \mathbb{E}_{q \sim \mathcal{D}, a_t \sim \pi_\text{behav} } \left[ \sum_{t=1}^H \color{red}{\frac{\pi_{\text{prox} } }{\pi_{\text{behav} } }} \min \left( \color{red}{u^{\text{prox} }_t(\theta)} \hat{A}_t, \text{clip}(\color{red}{u^{\text{prox} }_t(\theta)}, 1-\epsilon, 1+\epsilon) \hat{A}_t \right) \right], \tag{5}
\end{align}
$$- 其中 \(\color{red}{u^{\text{prox} }_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\text{prox} }(a_t|s_t)}}\) 是相对于近端策略的重要性比率
- 为简洁起见,论文省略了状态-动作项(state-action terms)
- 理解:重要性采样还是针对了行为策略的,这本身没有问题,\(\min\) 操作的第二项中,本质是通过增加一个中间概率 \(\pi_\text{prox}\) 实现了重要性采样比值
$$ \color{red}{\frac{\pi_\theta}{\pi_{\text{behav} } } = \frac{\pi_{\text{prox} } }{\pi_{\text{behav} } } \cdot \frac{\pi_\theta}{\pi_{\text{prox} } }}$$
- 异步 PPO 目标(公式5)与标准 PPO 目标(公式2)的主要区别在于用于正则化模型更新的近端策略 \(\pi_{\text{prox} }\)
- 在异步 PPO 训练中,使用行为策略作为近端策略会将最新策略 \(\pi_\theta\) 拉向旧版本和低质量策略,从而减缓模型改进
- 通过采用最近的策略作为近端策略 ,模型更新发生在高质量近端策略 \(\pi_{\text{prox} }\) 的信任区域内,从而稳定训练
- 理解:这里的 \(\pi_{\text{prox} }\) 是一个比 行为策略更新的策略,这意味着允许模型在新的策略(近端策略)的信任区域内更新而不是在旧的策略(行为策略)的信任区域内更新
- 一个问题:
- 在部分 实现中,将上一个 Global Step 更新后得到的策略作为近端策略,这是不对的,因为这样的话,每次更新前,当前策略 Actor 和 近端策略永远相等,他们的比值永远为 1
- 若每次 Rollout 只迭代一步(一个 RBS 对应一个 GBS),则行为策略、近端策略、待更新策略在更新前都相同
- 若每次 Rollout 迭代多步(一个 RBS 对应多个 GBS),则近端策略理论上是每一步更新后的 Actor
- 当每一步的 近端策略都和当前 Actor相同,也就是说近端策略的信任区域失效了(PPO Clip 的信任区域限制失效了!这是不符合预期的)
- 在异步训练的场景中,最好的近端策略应该是行为策略中的最新的那个策略(或者说 Old 策略),若一个 RBS 对应多个 GBS 更新,则在更新过程中,近端策略应该不变
- 在部分 实现中,将上一个 Global Step 更新后得到的策略作为近端策略,这是不对的,因为这样的话,每次更新前,当前策略 Actor 和 近端策略永远相等,他们的比值永远为 1
- 公式5 中的解耦 PPO 目标具有一个天然优势:它放宽了训练批次中所有数据必须由单一策略生成的要求
- 这一特性在将可中断生成与策略更新结合时,对保持算法正确性至关重要
- 论文提出以下命题:命题1(Proposition 1) :
- 对于由策略序列 \((\pi_\theta, \ldots, \pi_{\theta+k})\) 生成的任何序列 \((q, a_1, \ldots, a_H)\),其中 \(\pi_{\theta+i}\) 生成 Token \((a_{t_i}, \ldots, a_{t_{i+1} })\),且 \(1 = t_0 < \cdots < t_{k+1} = H\),存在一个行为策略 \(\pi_{\text{behav} }\),使得中断生成等效于完全从 \(\pi_{\text{behav} }\) 采样
- 这个命题在论文:Eligibility Traces for Off-Policy Policy Evaluation, 2000, Sutton Richard 中也有相关提及(未明确提及,但 Per-Decision 重要性采样隐式暗含了同一个轨迹可以经过不同策略采样,即来源于不同行为策略)
- 问题:实际代码中,得到行为策略 \(\pi_{\text{behav} }\) 时需要存储每次采样时的策略或推理 logits/概率
- 实践经验 :
- 虽然 Hilton 等人 (2022) 采用参数的指数移动平均作为 \(\pi_{\text{prox} }\),但这种方法对 LRM 来说计算成本过高
- 因此,论文简单地使用每次模型更新前的参数作为 \(\pi_{\text{prox} }\)
- 公式5 通过在每次训练步骤中重新计算 Token 概率来实现
Implementation
- 论文基于 Real_HF 框架 (2024),使用 Python 和 PyTorch (2019) 实现了 AReaL
- 论文的系统设计到以下框架:
- SGLang (2024) v0.4.6(用于生成服务)
- Megatron-Core (2019) v0.11.0(作为训练后端)
- 通过 SLURM (2003) 进行资源调度
- 为了最大化生成和训练阶段的吞吐量,论文实现了多项关键的系统级优化,解决了流水线中的瓶颈问题
- AReaL 将 GPU 计算与 CPU 操作(如基于规则的奖励计算和基于 TCP 的数据传输)解耦
- 通过在单独线程中执行这些操作并将工作流流水线化,论文将奖励计算和数据传输与后续生成请求重叠
- 论文使用 asyncio 协程在 Rollout Worker 中并发运行多个请求,以避免相互阻塞等待
- 为了处理可变长度序列的训练,论文采用了一种无填充的序列打包策略,并结合动态分配算法(见算法1)
- 该算法在固定内存约束下平衡微批次间的 Token 分布,最大化 GPU 内存利用率,同时最小化所需的前向-反向传播次数
Experiments
- 论文的评估包含三个部分:
- (1) 在不同模型规模下与 SOTA 开源框架进行全面对比;
- (2) 在不同计算资源下的强扩展性分析;
- (3) 通过消融实验验证论文的设计选择
Experiment Setup
- 论文在具有挑战性的数学和代码任务上评估 AReaL
- 论文使用来自 DeepSeek-R1 (2025) 的蒸馏 Qwen2 模型系列(即 R1-Distilled-Qwen)作为基础模型,参数规模从 1.5B 到 32B
- 对于每个任务-模型组合,论文固定 PPO 更新次数进行训练,并评估最终检查点
- 数学任务的评估 Following Qwen 评估协议 (2024; 2024),而代码模型则在 LiveCodeBench (2025) 上使用官方协议进行评估
- 除非另有说明,否则代码任务的最大陈旧度 \(\eta\) 设为 4,数学任务设为 8,并采用 7.2 节中的训练配置,其他超参数详见附录 A
- 实验在配备 64 个节点(每个节点 8 块 H800 GPU)的集群上进行
- 集群通过 NVLink 实现节点内连接,通过 RoCE(带宽 3.2Tbps)实现节点间通信
- 为确保快速收敛,论文为完整实验分配至少 16 个节点作为基准配置
- 模型规模增大时,论文按比例扩展节点数量,最终使用 48 个节点训练最大的 32B 参数模型
- 这种扩展策略使论文能够在保持高效资源利用的同时并行运行不同规模的实验
- 对于 AReaL,论文保持推理设备与训练设备的固定比例,将四分之三的设备分配给推理
- 这一配置是基于早期实验中 75-25 分配方案显示出更高训练吞吐量而选择的
- 尽管论文采用这一启发式配置,但最佳分配比例可能因不同设置而异,甚至可能受益于训练期间的动态调整,如第 8 节所述
End-to-End Comparison
- 论文使用同步 RL 系统建立了两个 SOTA 基线 :
- 针对 1.5B 模型数学推理任务的 DeepScaleR (2025)
- 针对 14B 模型代码生成任务的 DeepCoder (2024)
- 两者均使用 verl (2025) 进行训练
- 对于更大的 7B 和 32B 模型,由于缺乏可比基线,论文使用 AReaL 的同步变体从头开始训练
- 训练完成后,数学模型在 AIME24 基准上评估,代码模型在 LiveCodeBench (2025) 基准上评估
- 其他基准的评估结果见附录 B
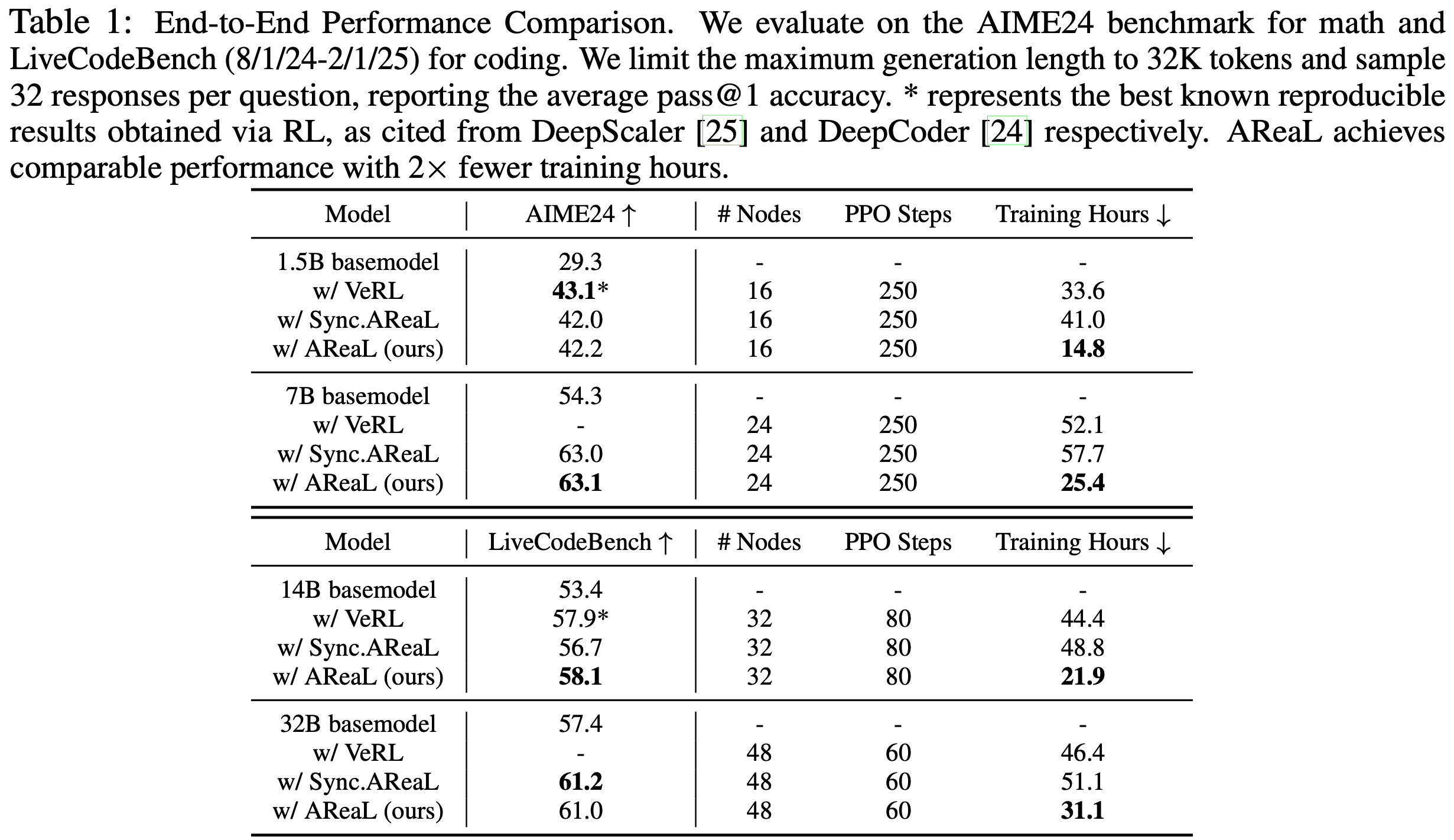
- 表 1 展示了主要结果
- 由于之前 SOTA 模型的代码可能过时,论文使用最新 verl 代码测量吞吐量并估算训练时长以确保公平对比
- AReaL 在性能不降的前提下,显著加速训练,端到端训练时间相比同步系统最多减少 \(2.77 \times\)
Scalability
- 论文比较了 AReaL 与 SOTA 同步 RL 系统 verl (2025) 在不同模型规模和上下文长度下的扩展性
- 对于 7B 模型和 32k 上下文长度,论文选择 verl 不出现 OOM 问题时的最小 GPU 数量,然后根据模型规模按比例调整 GPU 数量
- 论文测量训练的有效吞吐量,定义为 PPO 更新期间消耗生成 token 的速率(经过适当预热步骤后)
- 图 4 展示了 16k 和 32k 上下文长度的结果。此处上下文长度指提示长度与生成长度之和,最大提示长度限制为 1k
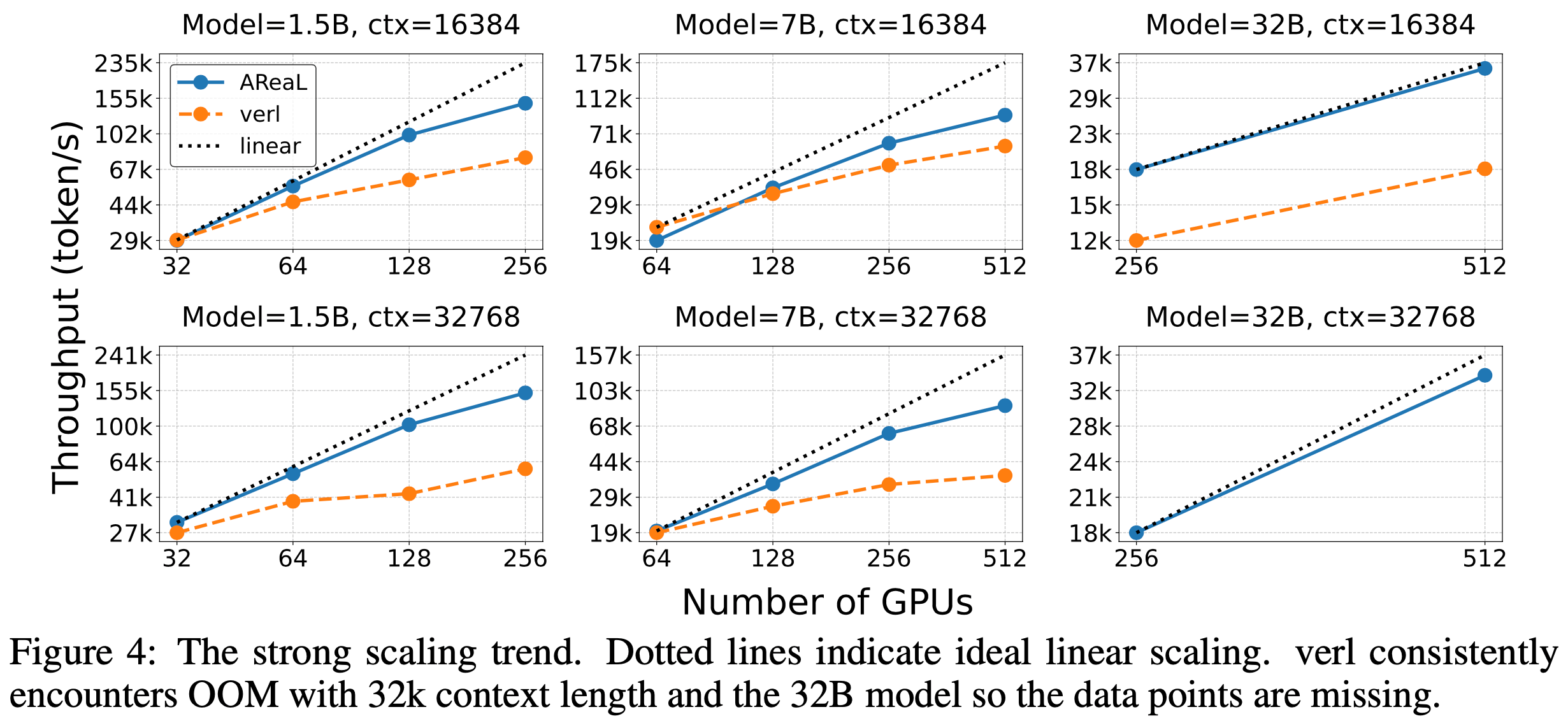
- 在所有设置中,AReaL 展现出近似线性的扩展趋势,而同步系统通常无法有效扩展
- AReaL 的吞吐量在大多数设置中超过基线,最高可实现 \(2.5 \times\) 加速
- 对于较短的上下文长度,AReaL 的优势可能较小,因为生成吞吐量无法匹配训练吞吐量
- 尽管生成了许多序列,但它们未被训练过程有效消耗
- AReaL 对生成长度的鲁棒性更强,因为异步和可中断的生成可以将长响应的生成完全隐藏在关键路径中,因此延长生成长度不会显著影响 AReaL 的有效训练吞吐量
Algorithm Ablations
- 论文通过消融实验验证第 5 节的算法创新,使用 1.5B LRM 在数学任务上进行训练
- Following DeepScaleR 的基本实验设置,并逐步增加 \(\eta\) 值进行消融
- 具体来说,论文改变最大允许陈旧度 \(\eta\),并比较是否使用解耦 PPO 目标的配置
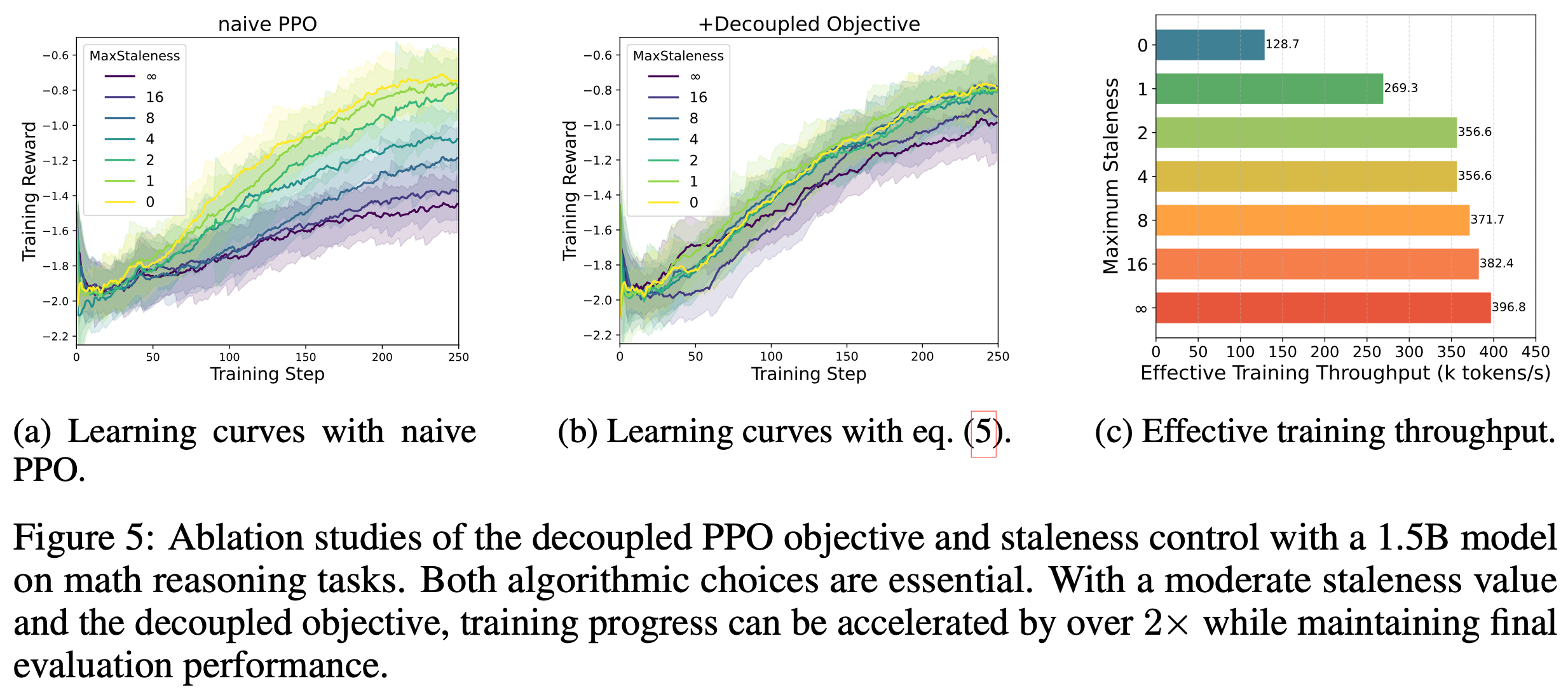
- 图 5a 和图 5b 展示了 250 训练步后的学习曲线
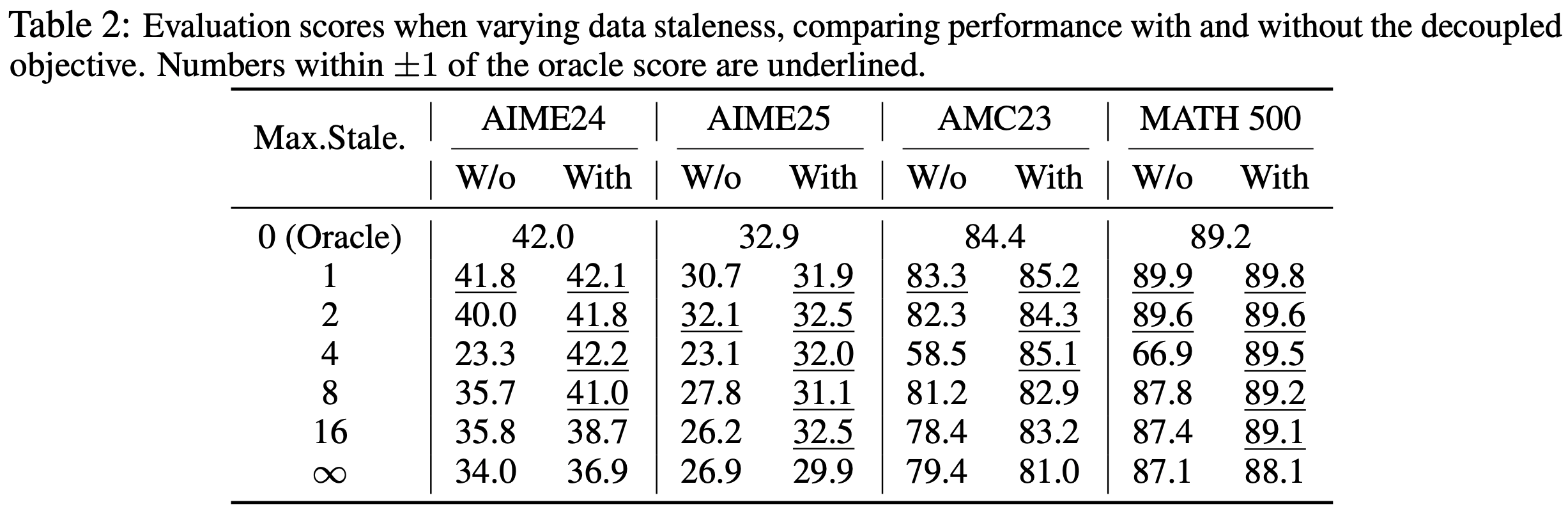
- 表 2 展示了多个数学推理基准上的最终评估性能
- 论文 Following PPO 的常见实践,在每个训练步内执行多次小批量更新
- 需要强调的是,\(\eta\) 限制了训练步级别的训练批次陈旧度
- 图 5a 显示,朴素 PPO 无法匹配同步 RL 的性能(即 \(\eta=0\) 时的性能)
- 即使轻微的陈旧度也会因不恰当的裁剪中心和可中断生成期间策略变化而显著降低最终性能
- 此外,增加数据陈旧度会持续降低学习性能,这与之前在其他领域的研究观察一致 (2022; 2024)
- 如图 5b 与图 5a 的对比所示,解耦 PPO 目标在处理陈旧数据时显著提高了训练稳定性,这与游戏领域的研究发现一致 (2022)
- 即使使用解耦目标,无界陈旧度(最大陈旧度 \(\rightarrow \infty\))的性能仍低于零陈旧度的基准
- 在适当约束下,中等陈旧度(如 \(\eta \leq 8\))对最终性能影响极小,同时通过异步流水线显著加速训练(如图 5c 和表 2 所示)
- 这些结果验证了论文将受控陈旧度与解耦 PPO 目标结合用于高效异步 RL 训练的方法
System Ablations
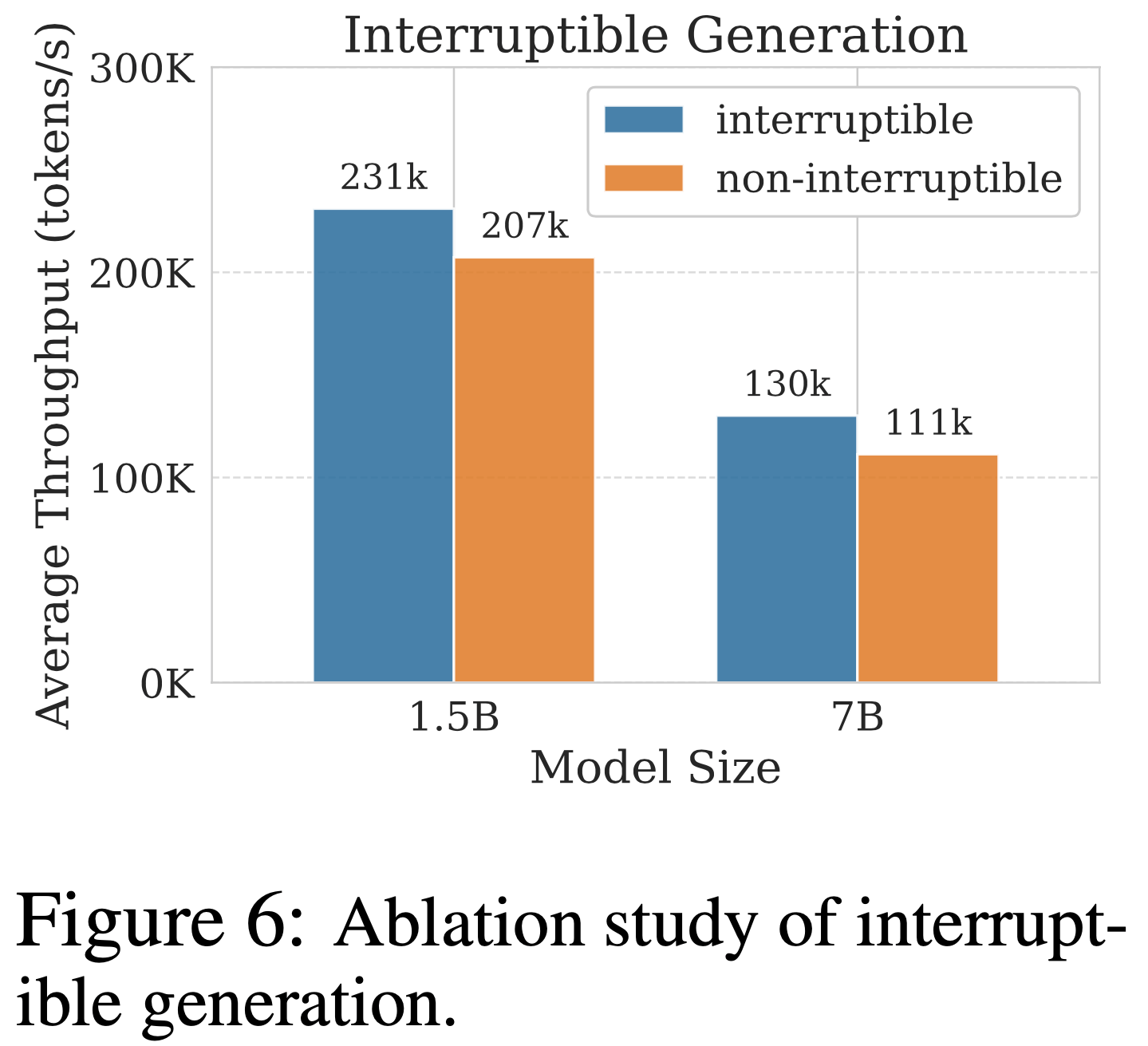
- 可中断生成(Interruptible Generation)
- 论文消融可中断生成功能,生成吞吐量结果如图 6 所示
- 若不可中断生成,控制器必须等待最长响应完成
- 具体而言,在 4 节点上,可中断生成使 1.5B 和 7B 模型的吞吐量分别提升 12% 和 17%,验证了论文的架构设计选择
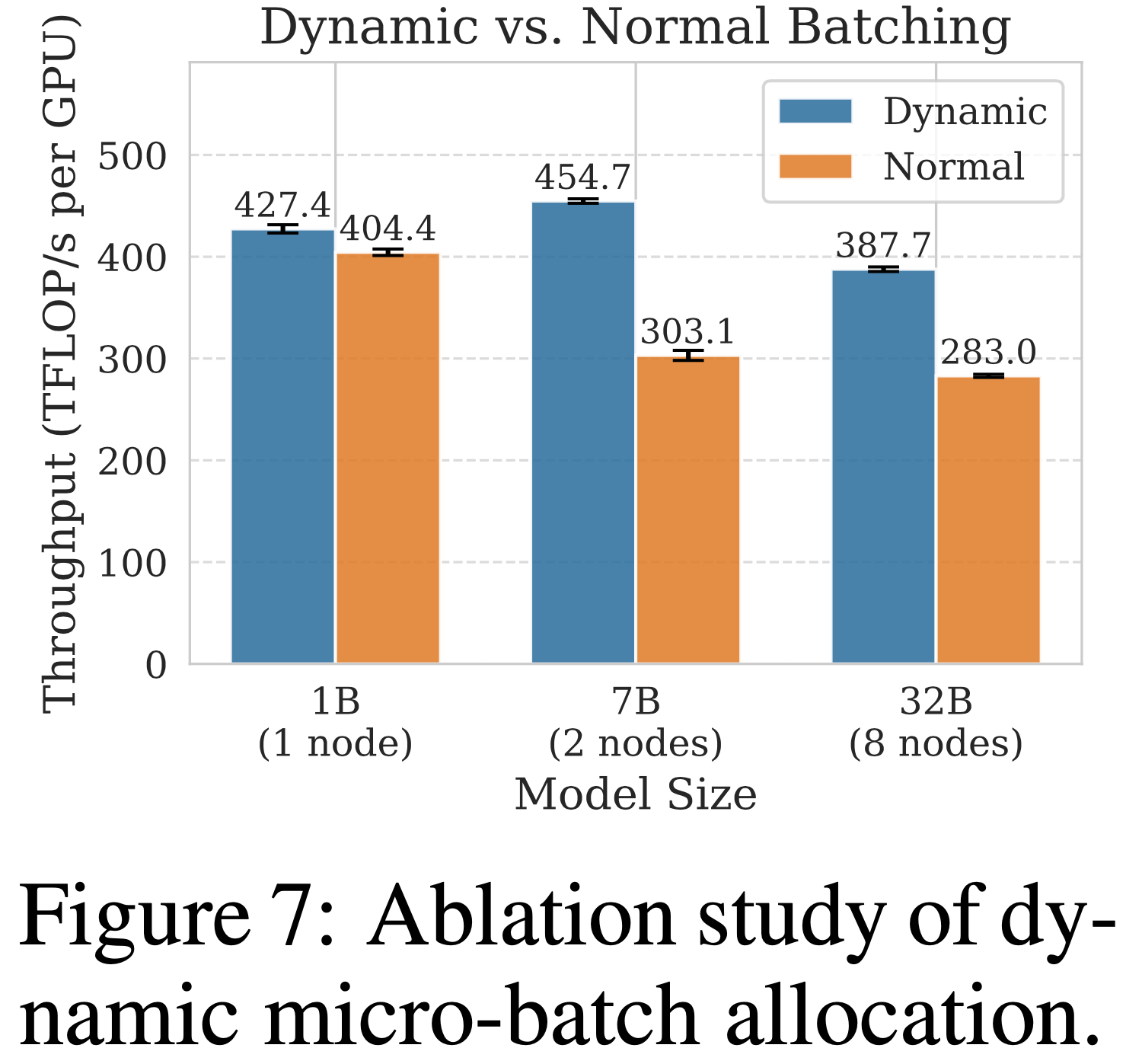
- 动态微批次分配(Dynamic Microbatch Allocation)
- 论文通过对比动态批处理与标准微批处理策略的 PPO 训练吞吐量,验证动态批处理的有效性
- 标准微批处理策略可能导致多个长序列分配到同一微批次,通常需要足够多的微批次以防止内存不足
- 实验中,论文为标准设置配置 32 个微批次,为动态批处理方法设置每微批次 32,768 token 的预算
- 如图 7 所示,动态批处理在不同模型规模下平均提升 30% 吞吐量
补充:Related Work
RL for LLMs
- RL 已成为增强 LLM 推理能力的主要范式 (2022)
- 现有的 RL 方法通常聚焦于具有明确定义奖励函数(well-defined reward functions)的任务,包括数学推理 (2021)、代码生成 (2021)、科学问题求解 (2023) 以及工具使用 (2024)
- 在训练过程中,模型通过逐步扩展 CoT 轨迹来学习推理 (2022)
- 最近的开源项目通过小型蒸馏模型展示了显著的成功 (2024, 2025)
- 论文的工作基于这一研究方向,与 preference-based RLHF (2022) 和零样本(zero-shot)推理方法 (2025) 不同
- zero-shot 推理方法试图从预训练模型中直接获取推理能力,而无需任务特定的微调
Asynchronous RL
- 解耦的异步 RL (decoupled asynchronous RL)架构 (2018, 2020) 结合相应的算法创新 (2018, 2019),在游戏应用中取得了显著成功 (2019, 2021)
- 尽管类似的异步方法已用于 LLM 训练,但它们通常关注短上下文场景(如 RLHF)(2024) 或仅支持一到两步的生成-训练重叠 (2024, 2025)
- 论文的研究扩展了这些工作,并在第 5 节展示了更灵活的陈旧性与训练速度之间的权衡
- 与并发工作 (2025) 追求系统级效率最大化(maximizes system-level efficiency)不同,论文采用算法-系统协同设计方法,同时提供了表达性强的系统和实用的算法实现
- 论文的可中断生成技术(interruptible generation technique)与同步 RL 系统中的部分轨迹生成 (2025) 概念相似
- 不同于固定长度预算,AReaL 动态中断生成,同时通过缓冲保持训练批大小的稳定性,从而确保 PPO 的稳定性
- 与先前方法 (2024, 2025) 相比,论文在异步设置中的算法创新能够容忍更高的数据陈旧性,并与可中断生成兼容
LLM Training and Inference
- 论文的研究聚焦于 Dense Transformer 模型 (2017)
- RL 训练主要包括生成(推理)和训练两个阶段
- 生成阶段涉及自回归解码,需要高效的 KV 缓存管理 (2023) 和优化的解码内核 (2024)
- 训练阶段则需要精心设计数据、张量和流水线并行策略 (2020, 2023)
- 传统的同步系统在同一硬件资源上顺序执行生成和训练,但二者需要不同的最优并行化策略
- 最近的研究提出了上下文切换 (context switching,2024) 或权重重分配技术 (weight resharding techniques,2024, 2025) 来解决这种不匹配问题
- AReaL 通过解耦生成和训练 ,完全消除了关键训练路径(critical training path)中的重分配开销(resharding overhead) ,从而超越了同步 RL 系统
附录 A 实现细节
A.1 PPO Details
- 论文禁用了 PPO 中的 Critic Model 和 Reference Model
- GAE 中的优势估计参数 \(\lambda\) 和强化学习的折扣因子 \(\gamma\) 固定为 1
- 问题:没有 Critic Model 如何评估 GAE?使用 GRPO 的评估方式吗?
- 如果答案正确,则在最后一个 token 处奖励为 5,否则为 -5
- 论文在全局批次中采用优势归一化(Advantage Normalization)以稳定训练
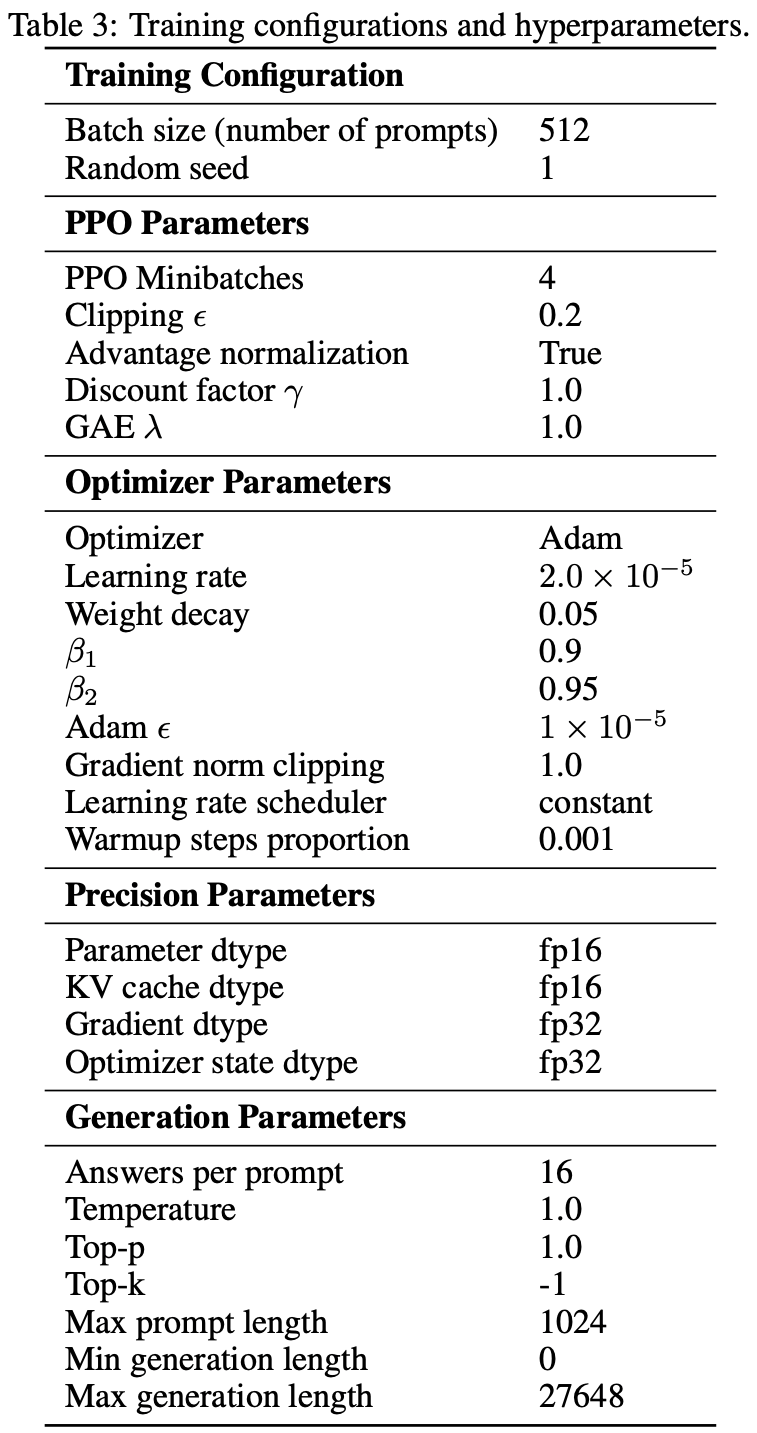
- 其他与学习相关的超参数和配置见表 3
A.2 Dataset Details
- 对于数学任务,论文使用了 DeepScaleR (2025) 的开源数据
- 对于代码训练,论文使用了 DeepCoder (2025) 发布的数据集
- 所有对比方法均使用相同的数据集
A.3 Dynamic Batching
- 动态批处理算法如算法 A.1 所示:

A.4 Baselines
- 在论文的实验中,论文使用 verl (2025) 的最新版本(20250507日的主分支)来评估图 4 中的训练吞吐量和表 1 中的训练时长
- 对于大多数结果,论文使用 SGLang (2024) v0.4.6 作为生成后端,并使用 PyTorch FSDP (2023) 作为训练后端
- 在少数情况下(例如 32B 模型或 64 节点的实验),如果 SGLang 报错,论文使用 vLLM (2023) v0.8.4 作为替代
附录 B Additional Results
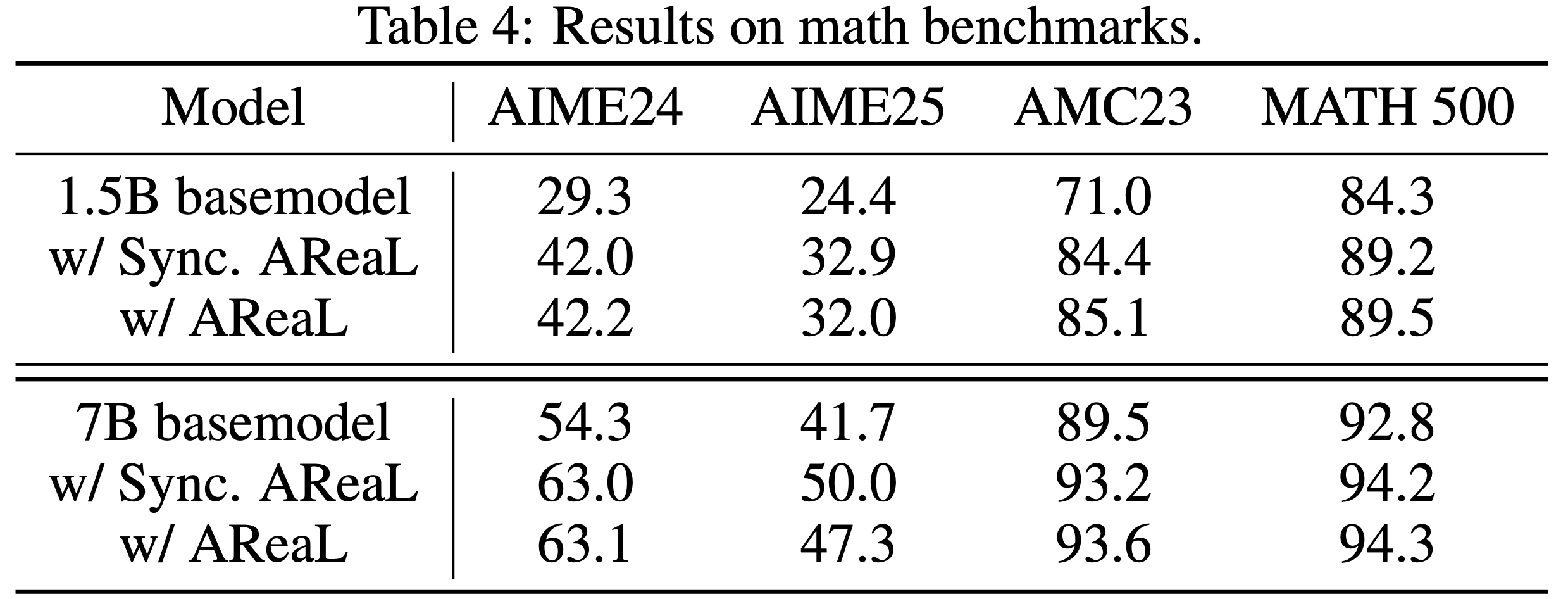
- 文在更多数学基准上评估了使用 AReaL 训练的模型,结果列于表 4
附录 C Proof of Proposition 1
- 命题 1 :对于任何由策略序列 \((\pi_\theta, \ldots, \pi_{\theta+k})\) 生成的序列 \((q, a_1, \ldots, a_H)\),其中 \(\pi_{\theta+i}\) 生成 tokens \((a_{t_i}, \ldots, a_{t_{i+1} })\),且 \(1 = t_0 < \cdots < t_{k+1} = H\),存在一个行为策略 \(\pi_{\text{behav} }\),使得中断生成等价于完全从 \(\pi_{\text{behav} }\) 采样
- 证明 :对于问题 \(q\),设 \(\mathcal{S}_i(q)\) 表示策略序列在步骤 \(t\) 遇到的状态。由于对于 \(i \neq j\) 有 \(\mathcal{S}_{t_i}(q) \cap \mathcal{S}_{t_j}(q) = \emptyset\)(理解:因为在 LLM 中,响应序列长度和时间步 \(t\) 唯一确定),我们可以构造:
$$
\pi_{\text{behav} }(\cdot|s) =
\begin{cases}
\pi_{\theta+j}(\cdot|s) & \text{if } \quad t_j \leq t \leq t_{j+1} \text{ and } s \in \mathcal{S}_t(q) \\
\text{arbitrary} & \text{otherwise}
\end{cases}
$$
附录 D Limitations and Future Work
- 论文的工作存在一些局限性,为未来研究提供了方向
- 首先,推理设备与训练设备的比例可以针对特定训练设置进一步优化
- 此外,这一比例可能受益于训练期间的动态调整,尤其是在微调预训练基础模型时,上下文长度通常会增加
- 虽然论文的评估集中在单步数学和编码任务上 ,但 AReaL 架构并不局限于这些领域
- 理解:这也算缺点?
- 论文将多轮交互和智能体场景的探索留给未来工作