本文介绍随机变量样本均值方差和整体均值方差的关系,同时还介绍样本和均值的方差和总体方差的关系
样本均值的方差与总体方差的关系
- 其他证明方式:

- 上式中,如果总体方差未知,想要用样本方差来作为总体方差的无偏估计,则样本方差的定义是应该是 \(S^2 = \frac{1}{n-1}\sum_i^n(X_i-\bar{X})^2\),(此时样本方差是总体方差的无偏估计)
样本方差为什么要除以n-1?
- 样本方差的定义:
$$
\sigma^2 \approx S^2 = \frac{1}{n-1}\sum_i^n(X_i-\bar{X})^2
$$ - 为什么样本方差是乘以 \(\frac{1}{n-1}\) 而不是 \(\frac{1}{n}\) ?
- 因为这样使用 \(\frac{1}{n}\) 会低估总体方差,此时样本方差不是总体方差的无偏估计
- 样本方差低估了总体方差的原因是因为从总体里面抽出来的数据会更倾向于集中,极端情况下,一个样本对应的方差为0
- 换个视角想,是因为我们不知道总体的均值,所以计算方差时使用的均值也是从样本中求平均得到的,这使得我们基于该均值得到的方差不够离散(因为使用了样本均值,所以自由度需要减一),也就是低估了总体方差
- 怎么理解自由度?
- 采样一个样本以后无法计算方差,此时方差为0,因为此时均值就等于样本本身,此时自由度为0
- 采样两个样本以后得到的方差只根第二个样本到第一个样本的距离有关(样本均值与这两个样本强相关),此时自由度为1
- 当采样的样本数非常多(假设为n)时,实际上单个样本与均值的关系很小了,此时自由度为n-1
- 怎么理解自由度?
- 当已知总体均值 \(\mu\) 时(个人理解:这里的 \(\mu\) 可以是其他采样方式下获得的近似均值,只要不跟当前用于计算方差的样本相关即可),样本方差可以使用:
$$
\sigma^2 \approx S^2 = \frac{1}{n-1}\sum_i^n(X_i-\mu)^2
$$ - 样本方差经过 \(\frac{1}{n-1}\) 修正以后可以用来估计总体方差(修正以后是总体方差的无偏估计)
- 这个修正叫做贝塞尔修正
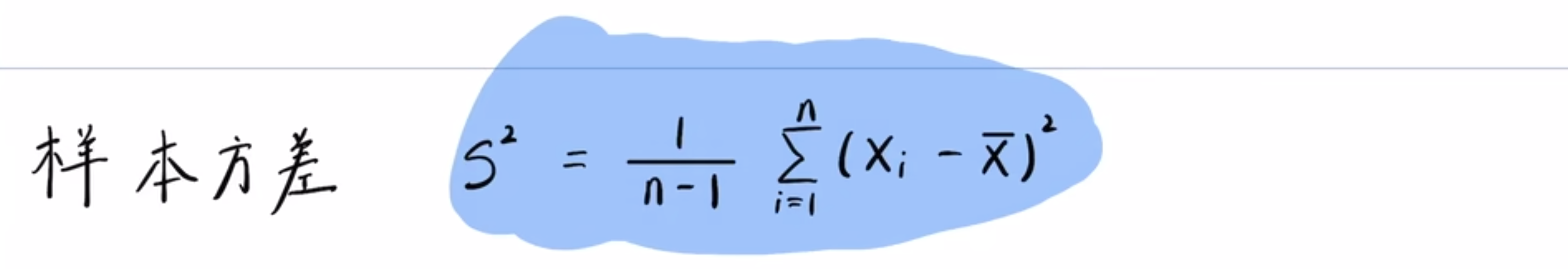
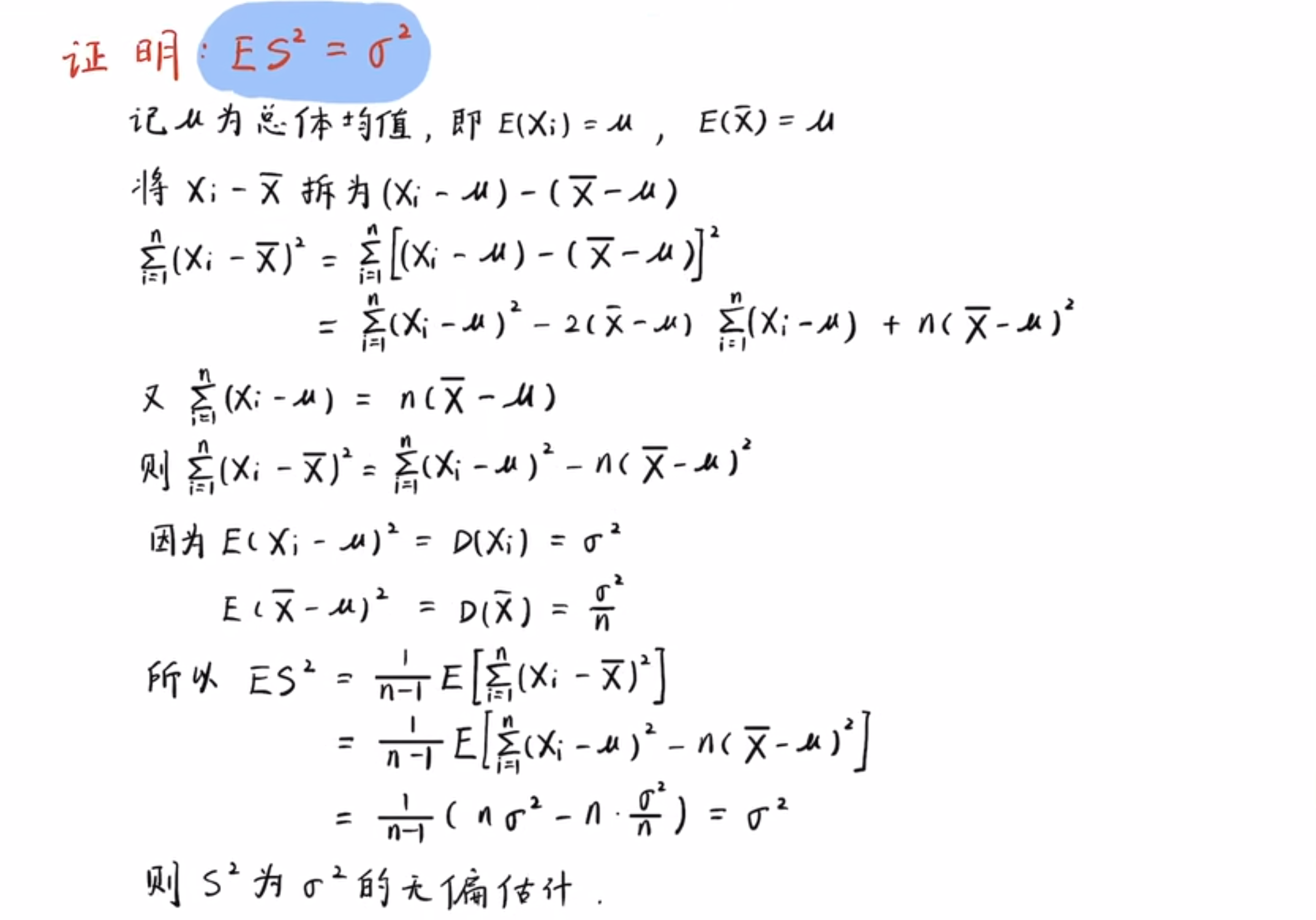
单样本均值和多样本均值的关系
问题定义
- 考虑以下采样方式
- 集合X :每次采样 B个样本 得到的样本集合
- 集合Y :每次采样 1个样本 得到的样本集合
- 问:多次采样时,集合X和B的均值和方差关系是什么?
- 即:如果我们重复多次进行这样的采样(每次采B个或1个),那么:这两种采样方式得到的样本均值的期望(即平均值的平均值)和样本均值的方差(即平均值的波动程度)之间有什么关系?
假设与符号定义
- 假设我们从一个总体中采样,总体的均值为 \(\mu\),方差为 \(\sigma^2\)
- 集合X :
- 每次采样 B个样本 :\(X_1, X_2, \dots, X_B\)
- 计算这B个样本的均值:\(\bar{X}_A = \frac{1}{B}\sum_{i=1}^B X_i\)
- 集合Y :
- 每次采样 1个样本 :\(Y_1\)
- 其“均值”就是它自己:\(\bar{X}_B = Y_1\)
- 我们重复多次这样的采样过程,得到一系列的 \(\bar{X}_A\) 和 \(\bar{X}_B\)
均值关系
- 集合X 的样本均值的期望:
$$
E[\bar{X}_A] = E\left[\frac{1}{B}\sum_{i=1}^B X_i\right] = \frac{1}{B} \sum_{i=1}^B E[X_i] = \frac{1}{B} \cdot B \mu = \mu
$$ - 集合Y 的样本均值的期望:
$$
E[\bar{X}_B] = E[Y_1] = \mu
$$ - 结论:两种采样方式得到的样本均值的期望是相同的 ,都等于总体均值 \(\mu\)
方差关系
- 集合X 的样本均值的方差:
$$
\text{Var}(\bar{X}_A) = \text{Var}\left(\frac{1}{B}\sum_{i=1}^B X_i\right) = \frac{1}{B^2} \sum_{i=1}^B \text{Var}(X_i) = \frac{1}{B^2} \cdot B \sigma^2 = \frac{\sigma^2}{B}
$$ - 集合Y 的样本均值的方差:
$$
\text{Var}(\bar{X}_B) = \text{Var}(Y_1) = \sigma^2
$$ - 结论:集合X 的样本均值的方差是 \(\frac{\sigma^2}{B}\),集合Y 的样本均值的方差是 \(\sigma^2\)
- 也就是说,集合X 的样本均值的方差更小,是集合Y 的 \(\frac{1}{B}\)
- 直观理解
- 均值方面:无论你是采1个还是采B个,平均来看,它们的中心位置(期望)都是一样的,都是总体的均值
- 方差方面:采B个样本求平均,相当于把单个样本的“噪声”给“平均掉”了,因此波动更小,方差更小;而采1个样本,没有“平均”的过程,波动就更大,方差也就更大