ML——EM算法

期望最大化(Exception Maximization Algorithm)EM算法

不同教材的不同形式

李航统计学习方法

算法步骤

  • 输入: 观测变量数据Y

  • 输出: 模型(参数\(\theta\))

  • E步: 计算\(Q(\theta, \theta^{i})\)
    $$
    \begin{align}
    Q(\theta, \theta^{i}) &= E_{Z}[logP(Y,Z|\theta)|Y,\theta^{i}] \\
    &= E_{Z\sim P(Z|Y,\theta^{i})}[logP(Y,Z|\theta)] \\
    &= \sum_{Z} P(Z|Y,\theta^{i})logP(Y,Z|\theta) \\
    &= \sum_{Z} logP(Y,Z|\theta)P(Z|Y,\theta^{i})
    \end{align}
    $$

  • M步: 求使得\(Q(\theta, \theta^{i})\)极大化的参数\(\theta=\theta^{i+1}\)
    $$\theta^{i+1} = \arg\max_{\theta}Q(\theta, \theta^{i})$$

  • 重复E步和M步,直到收敛

  • 理解: \(Q(\theta, \theta^{i})\)可以理解为\(Q(\theta|\theta^{i})\),表示在参数\(\theta^{i}\)已知的情况下,对数似然函数关于隐变量后验分布的期望函数,函数的参数为\(\theta\)

隐变量的期望还是分布?

参考博客:https://www.jianshu.com/p/c3ff1ae5cb66

仅考虑隐变量的期望
  • 应用场景为k-means聚类,但是k-means聚类E步求的是最可能的\(Z\)值(概率最大的\(Z\)值),而不是\(Z\)的期望
步骤 具体细节
E步 基于\(\theta^{i}\)推断隐变量\(Z\)的期望,记为\(Z^{i}\)
M步 基于已观测变量\(Y\)和\(Z^{i}\)对参数\(\theta\)做极大似然估计,得到\(\theta^{i+1}\) $$\theta^{i+1}=\arg\max_{\theta}P(Y,Z^{i}\mid\theta)$$
考虑隐变量的分布
  • 应用场景为GMM模型聚类
步骤 具体细节
E步 基于\(\theta^{i}\)推断隐变量\(Z\)的后验分布\(P(Z\mid Y,\theta^{i})\)
E步M步均可 基于隐变量的后验分布\(P(Z\mid Y,\theta^{i})\)
计算对数似然函数\(logP(Y,Z\mid\theta)\)关于隐变量\(Z\)的后验分布\(P(Z\mid Y,\theta^{i})\)的期望\(Q(\theta,\theta^{i})\)
$$Q(\theta,\theta^{i}) = E_{P(Z\mid Y,\theta^{i})}logP(Y,Z\mid \theta)$$
M步 基于期望函数\(Q(\theta, \theta^{i})\),对参数\(\theta\)求极值(极大似然估计),得到$$\theta^{i+1}=\arg\max_{\theta}Q(\theta, \theta^{i})=\arg\max_{\theta}E_{P(Z\mid Y,\theta^{i})}logP(Y,Z\mid \theta)$$
推导

  • 已知数据是观测数据Y,像极大似然法一样,使得似然函数最大化即可,这里为了方便计算使用对数似然

  • 我们的终极目标与极大似然法一样,求一个使得似然函数最大(可能是极大)的参数$$\theta^{\star}=\arg\max_{\theta}L(\theta)$$
    其中
    $$
    \begin{align}
    L(\theta)&=logP(Y|\theta)\\
    &=log\sum_{Z}P(Y,Z|\theta)\\
    &=log\left(\sum_{Z}P(Y|Z,\theta)P(Z|\theta)\right)
    \end{align}
    $$

  • 显然,上述似然函数比较难以求解,非凸,且涉及和(积分或加法)的对数等操作,难以展开(可能还有其他的原因)

  • 所以我们使用EM算法迭代不断逼近原始似然函数的最优解\(\theta^{\star}\)(注意:我们只能得到局部最优,但是一般来说局部最优也够用了)

  • 可用Jensen不等式得到\(L(\theta)\)的下界来作为优化目标不断迭代
    $$
    \begin{align}
    L(\theta)&=log\left(\sum_{Z}P(Y|Z,\theta)P(Z|\theta)\right)\\
    &=log\left(\sum_{Z}P(Z|Y,\theta^{i})\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{i})}\right)\\
    &\geq \sum_{Z}P(Z|Y,\theta^{i})log\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{i})}\\
    &=B(\theta,\theta^{i})
    \end{align}
    $$

  • 由于此时\(B(\theta, \theta^{i})\)是\(L(\theta)\)的下界(\(B(\theta, \theta^{i})\)是固定\(\theta^{i}\)时关于\(\theta\)的凸函数且容易求导,可以求极大值),所以使得前者增大的参数\(\theta\)也能使得后者增大,为了使得后者尽可能的增大,我们对前者取极大值

    • 下面的推导基于事实: 消去与\(\theta\)无关的项,极大值点(\(\theta^{i+1}\))不变

$$
\begin{align}
\theta^{i+1} &= \arg\max_{\theta}B(\theta,\theta^{i})\\
&=\arg\max_{\theta}\left( \sum_{Z}P(Z|Y,\theta^{i})log\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{i})}\right)\\
&=\arg\max_{\theta}\left( \sum_{Z}P(Z|Y,\theta^{i})logP(Y|Z,\theta)P(Z|\theta)-\sum_{Z}P(Z|Y,\theta^{i})logP(Z|Y,\theta^{i})\right)\\
&= \arg\max_{\theta}\left( \sum_{Z}P(Z|Y,\theta^{i})logP(Y|Z,\theta)P(Z|\theta)\right)\\
&=\arg\max_{\theta}Q(\theta,\theta^{i})
\end{align}
$$

  • 由上式可知,我们的EM算法步骤中E步和M步是正确的
  • 问题:推导第二步中为什么选择\(P(Z|Y,\theta^{i})\)而不是其他分布呢?
    • 解答: \(B(\theta, \theta^{i})\)和\(L(\theta)\)什么时候相等呢?(前面推导中Jensen不等式什么时候能取等号呢?)
    • Jensen不等式取等号当且仅当Jensen不等式中函数的值为常数,此处函数的值为\(log\frac{P(Y,Z|\theta)}{Q(Z)}\)
      $$
      \begin{align}
      L(\theta)&=log\left(\sum_{Z}P(Y,Z|\theta)\right)\\
      &=log\left(\sum_{Z}Q(Z)\frac{P(Y,Z|\theta)}{Q(Z)}\right)\\
      &\geq \sum_{Z}Q(Z)log\frac{P(Y,Z|\theta)}{Q(Z)}\\
      \end{align}
      $$
    • 不等式中当且仅当\(log\frac{P(Y,Z|\theta)}{Q(Z)}\)为常数,也就是\(\frac{P(Y,Z|\theta)}{Q(Z)}=c\), c为常数,时等号成立
    • 此时由于\(Q(Z)\)是一个分布(注意:正因为\(Q(Z)\)是一个分布才能用Jensen不等式),所以有
      $$
      \begin{align}
      Q(Z)=\frac{P(Y,Z|\theta)}{\sum_{Z}P(Y,Z|\theta)}=\frac{P(Y,Z|\theta)}{P(Y|\theta)}=P(Z|Y,\theta)
      \end{align}
      $$

吴恩达CS229

  • E步: 计算\(Q_{i}(Z)=P(Z|Y,\theta^{i})\)
  • M步: 求使得原始似然函数下界极大化的参数\(\theta=\theta^{i+1}\)
    $$
    \begin{align}
    \theta^{i+1} &= \arg\max_{\theta}\sum_{Z}P(Z|Y,\theta^{i})log\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{i})} \\
    &= \arg\max_{\theta}\sum_{Z}Q_{i}(Z)log\frac{P(Y|Z,\theta)P(Z|\theta)}{Q_{i}(Z)}
    \end{align}
    $$
    • 进一步消除与\(\theta\)无关的项可以得到
      $$
      \begin{align}
      \theta^{i+1} &= \arg\max_{\theta}\sum_{Z}Q_{i}(Z)logP(Y|Z,\theta)P(Z|\theta)
      \end{align}
      $$
  • 推导步骤和李航统计学习方法一样,核心是运用Jensen不等式

总结

  • 以上两个不同课程的E步不同,但完全等价,吴恩达CS229课程中E步计算\(Q_{i}(Z)=P(Z|Y,\theta^{i})\)就等价于计算出了李航统计学习方法中的\(Q(\theta, \theta^{i})\),二者关系如下:
    $$
    \begin{align}
    Q(\theta, \theta^{i})&=\sum_{Z}P(Z|Y,\theta^{i})logP(Y|Z,\theta)P(Z|\theta) \\
    &= \sum_{Z}Q_{i}(Z)logP(Y|Z,\theta)P(Z|\theta)
    \end{align}
    $$
  • M步中,二者本质上完全相同,但是吴恩达CS229中没消去与\(\theta\)无关的项,所以看起来不太简洁

实例

实例一
  • 三个硬币的抛硬币问题
    • 第一次:抛硬币A,决定第二次抛C还是B,选中B的概率为\(\pi\)
    • 第二次:抛硬币B或C,正面为1,反面为0
  • (第一个硬币A抛中B的概率为隐变量)
实例二
  • 200个人不知道男女的身高拟合问题(性别为隐变量)
  • 这里是高斯混合模型的代表
实例三
  • K-Means聚类
  • 参考<<百面机器学习>>P100-P101

进一步理解

我的理解

  • 初始化参数\(\theta^{0}\)

  • 1.根据参数\(\theta^{i}\)计算当前隐变量的分布函数\(Q_{i}(Z)=P(Z|Y,\theta^{i})\)

    • 这一步的本质是使得在参数 \(\theta = \theta^i\) 时, 求得一个隐变量 \(Z\) 的分布,使得原始式子中的不等式取等号

  • 2.根据\(Q_{i}(Z)=P(Z|Y,\theta^{i})\)得到对数似然函数下界函数\(B(\theta, \theta^{i})\)(求原始似然函数的下界B函数是因为直接对原始似然函数求极大值很难)或者\(Q(\theta,\theta^{i})\)
    $$\arg\max_{\theta}B(\theta, \theta^{i})=\arg\max_{\theta}Q(\theta,\theta^{i})$$
    (\(Q(\theta,\theta^{i})\)可以看作是\(B(\theta, \theta^{i})\)的简化版,\(B(\theta, \theta^{i})\)才是原始似然函数的下界,\(Q(\theta,\theta^{i})\)不是原始似然函数的下界)

    • 这里 \(B(\theta, \theta^{i})\) 就是原始似然函数的下界(也就是不等式取到等号)

  • 3.求使得函数\(B(\theta, \theta^{i})\)极大化的参数\(\theta=\theta^{i+1}\)

    • 这一步是在固定隐变量 \(Z\) 的分布时, 用极大似然求一个使得下界 \(B(\theta, \theta^{i})\) 最大的参数 \(\theta = \theta^{i+1}\) 使得 \(B(\theta^{i+1}, \theta^{i}) = \text{max} B(\theta, \theta^{i})\)

  • 4.循环1,2,3直到收敛(相邻两次参数的变化或者是似然函数的变化足够小即可判断为收敛)

    • \(||\theta^{i+1}-\theta^{i}||<\epsilon_{1}\)或者\(||Q(\theta^{i+1},\theta^{i})-Q(\theta^{i},\theta^{i})||<\epsilon_{2}\)

  • 总结:

    • 在吴恩达CS229课程中: E步包含1, M步包含2,3,其中第2步中求的是\(B(\theta, \theta^{i})\)
    • 在李航<<统计学习方法>>中: E步包含1,2, M步包含3,其中第2步中求的是\(Q(\theta,\theta^{i})\)
    • 两种表达等价
图示理解
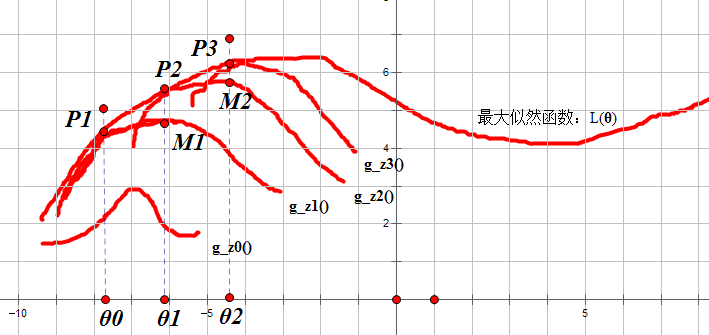
  • 也可参考李航<<统计学习方法>>第160页的图和解释

收敛性

  • 参考李航<<统计学习方法>>第160页-第162页推导过程
  • 参考<<百面机器学习>>第P099页-第P100页
    • 核心思想原始函数单调有界
    • 原始函数为\(L(\theta)\),函数下界为\(B(\theta,\theta^{i})\)
    • E步:
      • 找到使得在当前\(\theta^{i}\)确定时,原始函数的下界\(B(\theta, \theta^{i})\),在\(\theta^{i}\)处有
        \(\)
        $$
        \begin{align}
        L(\theta^{i}) = B(\theta,\theta^{i})
        \end{align}
        $$
    • M步:
      • 找到使得函数\(B(\theta,\theta^{i})\)取得极大值的\(\theta^{i+1}\)
    • i = i + 1,然后重新开始E和M步
      $$
      \begin{align}
      L(\theta^{i+1}) >= L(\theta^{i+1})
      \end{align}
      $$
    • 所以函数是单调的
    • 由于\(L(\theta)\)有界(这里原始函数有界可以从似然函数的定义得到)
    • 函数单调有界=>函数收敛(数学分析中的定理)

优劣性

优势
  • 简单性
  • 普适性
劣势
  • 不能保证收敛到最大值,只能保证收敛到极大值
  • 对初始值敏感,不同初始值可能收敛到不同极值点
  • 实际使用时通常采用多次选择不同的初始值来进行迭代,最终对估计值选最好的

EM算法的推广

  • 引入F函数
GEM1

F函数极大-极大法

  • 初始化参数\(\theta^{0}\)
  • E步: 求使得\(F(\tilde{P},\theta^{i})\)极大化的\(\tilde{P}^{i+1}\)
  • M步: 求使得\(F(\tilde{P}^{i+1},\theta)\)极大化的\(\theta^{i+1}\)
  • 重复E,M,直到收敛
GEM2
  • 初始化参数\(\theta^{0}\)
  • E步: 计算\(Q(\theta,\theta^{i})\)
  • M步: 求\(\theta^{i+1}\)使得\(Q(\theta^{i+1},\theta^{i}) > Q(\theta^{i},\theta^{i})\)
  • 重复E,M,直到收敛
  • 总结: \(Q(\theta,\theta^{i})\)的极大化难求时,这种方法可以简化计算
GEM3
  • 初始化参数\(\theta^{0}\)
  • E步: 计算\(Q(\theta,\theta^{i})\)
  • M步: 对参数\(\theta^{i}\)的每一个维度k,固定参数的其他维度,求使得\(Q(\theta,\theta^{i})\)极大化的\(\theta_{k}^{i+1}\),最终得到\(\theta^{i+1}\)
    • 使得\(Q(\theta^{i+1},\theta^{i}) > Q(\theta^{i},\theta^{i})\)
  • 重复E,M,直到收敛
  • 总结: 一种特殊的GEM算法,将M步分解为参数\(\theta\)的维度次来条件极大化