各种损失函数(Loss Function)总结,持续更新
名词概念
在机器学习和统计学中,成本函数(Cost Function)、经验风险(Empirical Risk)和损失函数(Loss Function)是三个密切相关但又有所区别的概念
- 损失函数(Loss Function): 损失函数衡量的是单个训练样本的预测值与实际值之间的差异。它是模型预测误差的量化表示。常见的损失函数包括均方误差(Mean Squared Error, MSE)、交叉熵损失(Cross-Entropy Loss)等
- 成本函数(Cost Function): 又名代价函数,等价于损失函数
- 期望风险(Expected Risk):所有样本(训练样本+验证样本+测试样本+未知样本)的损失函数的期望,用于评估模型的泛化能力
- 经验风险(Empirical Risk): 经验风险是在给定数据集上(一般是训练集),模型的平均损失。它是所有训练样本损失函数值的平均,用于评估模型在特定数据集上的表现。经验风险可以视为模型在有限数据集上的泛化能力的估计,本质是对期望风险的一种估计
- 结构风险(Structural Risk):用于平衡模型对样本的拟合能力和复杂度
$$
结构风险 = 经验风险 + \alpha 正则化项
$$ - 注意:在一般的书籍或者博客论文中,尝尝也用 损失函数 或 成本函数 笼统的表达了 成本函数、经验风险、损失函数、成本函数、甚至结构风险 等所有相关概念 ,所以本文下面也会比较笼统称为损失函数
损失函数总体说明
- 损失函数(Loss Function)又称为代价函数(Cost Function)
- 损失函数用于评估预测值与真实值之间的不一致程度
- 损失函数/成本函数是模型的优化目标函数,(神经网络训练的过程就是最小化损失函数的过程)
- 损失函数/成本函数越小,说明预测值越接近于真实值,模型表现越好
各种损失函数介绍
平方损失函数
最常用的回归损失函数
- 基本形式
$$loss = (y - f(x))^{2}$$ - 对应模型
- 线性回归
- 使用的均方误差来自于平方损失函数
$$loss_{MSE} = \frac{1}{m}\sum_{i=1}^{m}(y_{i} - f(x_{i}))^2$$
- 使用的均方误差来自于平方损失函数
- 其他扩展,RMSE(Root Mean Squared Error,常用作指标而不是损失函数)
$$loss_{RMSE} = \sqrt{\frac{1}{m}\sum_{i=1}^{m}(y_{i} - f(x_{i}))^2}$$
- 线性回归
MSLE/RMSLE损失函数
- MSLE,Mean Squared Logarithmic Error
$$loss_{MSLE} = \frac{1}{m}\sum_{i=1}^{m} \left(\log(1+y_{i}) - \log(1+f(x_{i})) \right)^2$$ - RMSLE,Root Mean Squared Logarithmic Error
- 损失函数形式
$$loss_{RMSLE} = \sqrt{\frac{1}{m}\sum_{i=1}^{m} \left(\log(1+y_{i}) - \log(1+f(x_{i})) \right)^2}$$ - MSLE和RMSLE可缓解长尾变量导致的异常值问题
MAPE/MSPE/RMAPE/RMSPE损失函数
- MAPE,Mean Absolute Percentage Error
$$loss_{MAPE} = \frac{1}{m}\sum_{i=1}^{m} \left|\frac{y_i-f(x_i)}{y_i}\right|$$ - MSPE,Mean Squared Percentage Error
$$loss_{MSPE} = \frac{1}{m}\sum_{i=1}^{m} \left(\frac{y_i-f(x_i)}{y_i}\right)^2$$ - RMAPE/RMSPE在MAPE/MSPE的基础上开根号即可
- MAPE/MSPE/RMAPE/RMSPE都可缓解长尾变量导致的异常值问题
绝对值损失函数
最常用的回归损失函数
- 基本形式
$$loss = |y - f(x)|$$ - 对应的经验风险:
$$loss_{MAE} = \frac{1}{m}\sum_{i=1}^{m}|y_{i} - f(x_{i})|$$
交叉熵损失函数(对数似然损失函数)
最常见的损失函数交叉熵损失函数 ,又名对数似然损失函数
- 基本形式(目标:在已知X时,样本标签Y出现的概率最大化,损失函数在概率前加个负号即可)
$$loss=L(P_{\theta}(Y|X))=-logP_{\theta}(Y|X)$$ - 二分类中的交叉熵损失函数:
$$loss_{CE} = \frac{1}{N} \sum_{i}^{N}-y_ilogy_i’ - (1-y_i)log(1-y_i’)$$- 二分类中对于单个样本的损失一般写为:
$$loss(x_i) = -y_ilogy_i’ - (1-y_i)log(1-y_i’)$$ - 写成最容易看清楚的形式为:
$$
\begin{align}
loss(x_i) &= -logy_i’, &\quad y_i = 1 \\
loss(x_i) &= -log(1-y_i’), &\quad y_i = 0
\end{align}
$$- \(y_i\) 为样本 \(x_i\) 的真实类别
- \(y_i’\) 为样本 \(x_i\) 在模型中的预测值(这个值在二分类中为Sigmoid函数归一化后的取值,代表样本分类为 \(y_i=1\) 的概率)
- \(y_i’\) 也可表达为 \(p_{i,1}\),即样本 \(i\) 分类为1的概率
- 二分类中对于单个样本的损失一般写为:
- 多分类中的交叉熵损失函数:
$$loss_{CE} = -\frac{1}{N} \sum_{i}^{N}\sum_{c=1}^{C} y_{i,c}\log p_{i,c}^{\theta}$$- \(y_{i,c} \in \{0, 1\}\):当样本 \(i\) 的真实分类是 \(c\) 时, \(y_{i,c}=1\),否则 \(y_{i,c}=0\)
- \(p_{i,c}^{\theta}\):表示样本 \(i\) 为分类 \(c\) 的预估概率,由 \(y_{i,c} \in \{0, 1\}\) 可知损失函数不需要关注样本预测为其他错误类别的概率,仅关注真实样本对应类别的概率即可
- 二分类的场景实际上是多分类的特定形式, \(1-y_i’\) 可以用来表示分类为0时的概率
- 凡是极大似然估计作为学习策略的模型,损失函数都为交叉熵损失函数(对数似然损失函数)
- 因为极大化似然函数等价于极小化对数似然损失函数,推导:
$$
\begin{align}
\theta^{*} &= \mathop{\arg\max}_{\theta} \prod_i P_{\theta}(y_i|x_i) \\
&= \mathop{\arg\max}_{\theta} \sum_i \log P_{\theta}(y_i|x_i) \\
&= \mathop{\arg\min}_{\theta} - \sum_i \log P_{\theta}(y_i|x_i) \\
&= \mathop{\arg\min}_{\theta} - \frac{1}{N} \sum_{i}^{N}\sum_{c=1}^{C} y_{i,c}\log p_{i,c}^{\theta}
\end{align}
$$ - <<统计学习方法>>第十二章中LR使用的是极大似然估计但是对应的损失函数是逻辑斯蒂损失函数,这里可以证明LR中对数似然损失函数和逻辑斯蒂损失函数完全等价,证明见统计学习方法212页笔记
- 因为极大化似然函数等价于极小化对数似然损失函数,推导:
- 对应模型
- 所有使用极大似然估计的模型
- 可以证明,极大似然估计法最大化样本出现概率的目标是最小化真实分布和预估分布的KL散度
- 为了方便证明,下面把 \(P_{\theta}(y_i|x_i)\) 写作 \(P_{\theta}(x_i)\),这里 \(x_i\) 包含了样本的label( \(y_i\) )信息
$$
\begin{align}
\theta^{*} &= \mathop{\arg\min}_{\theta} - \frac{1}{N} \sum_{i}^{N}\sum_{c=1}^{C} y_{i,c}\log p_{i,c}^{\theta} &\quad — 交叉熵损失函数\\
&= \mathop{\arg\min}_{\theta} - \sum_i \log P_{\theta}(x_i) &\quad — 交叉熵损失函数\\
&= \mathop{\arg\max}_{\theta} \sum_i \log P_{\theta}(x_i) \\
&= \mathop{\arg\max}_{\theta} \prod_i P_{\theta}(x_i) &\quad — 极大似然法\\
&= \mathop{\arg\max}_{\theta} \sum_i \log P_{\theta}(x_i) \\
&\approx \mathop{\arg\max}_{\theta} \mathbb{E}_{x \sim P_{data}}\log P_{\theta}(x) \\
&= \mathop{\arg\max}_{\theta} \int_{x} P_{data}(x) \log P_{\theta}(x) dx \\
&= \mathop{\arg\max}_{\theta} \int_{x} P_{data}(x) \log P_{\theta}(x) dx - \int_{x} P_{data}(x) \log P_{data}(x) dx &\quad — 减去一项与\theta无关的项\\
&= \mathop{\arg\max}_{\theta} \int_{x} P_{data}(x) \log \frac{P_{\theta}(x)}{P_{data}(x)} dx \\
&= \mathop{\arg\max}_{\theta} -\int_{x} P_{data}(x) \log \frac{P_{data}(x)}{P_{\theta}(x)} dx \\
&= \mathop{\arg\min}_{\theta} \int_{x} P_{data}(x) \log \frac{P_{data}(x)}{P_{\theta}(x)} dx \\
&= \mathop{\arg\min}_{\theta} KL(P_{data}|| P_{\theta}) &\quad — KL散度\\
\end{align}
$$ - 上式表明:似然函数最大化(极大似然法,对应交叉熵损失最小化),等价于最小化真实分布与预估分布的KL散度
- 注:式中 \(x_i\) 样本表示<特征,标签>对, \(P_{\theta}(x_i)\) 表示在模型 \(\theta\) 下,真实<特征,标签>出现的概率
- 为了方便证明,下面把 \(P_{\theta}(y_i|x_i)\) 写作 \(P_{\theta}(x_i)\),这里 \(x_i\) 包含了样本的label( \(y_i\) )信息
- 同理,可以证明,最小化交叉熵损失函数的目标也是最小化真实分布和预估分布的KL散度
- 可以证明,极大似然估计法最大化样本出现概率的目标是最小化真实分布和预估分布的KL散度
- 最大化后验概率等价于最小化对数似然损失函数
$$\theta^{\star} = \mathop{\arg\max}_{\theta} LL(\theta) = \mathop{\arg\min}_{\theta} -LL(\theta) = \mathop{\arg\min}_{\theta} -\log P(Y|X) = \mathop{\arg\min}_{\theta} -\sum_{i=1}^{N}\log p_{\theta}(y_{i}|x_{i})$$
- 所有使用极大似然估计的模型
指数损失函数
提升方法的损失函数
- 基本形式
$$loss=L(y,f(x))=e^{-yf(x)}$$ - 对应模型
- 提升方法
0-1损失函数
最理想的损失函数,但是不光滑,不可导
- 基本形式
$$loss=L(y,f(x))=0, \text{if} \ yf(x)>0 \\
loss=L(y,f(x))=1, \text{if} \ yf(x)<0$$ - 在由 \(f(x)\) 符号判断样本的类别的二分类问题中
- 分类正确时总有 \(yf(x)>0\),损失为0
- 分类错误时总有 \(yf(x)<0\),损失为1
- 在特定的模型中,比如要求 \(f(x)=y\) 才算正确分类的模型中
- 0-1损失函数可定义为如下
$$loss=L(y,f(x))=0, \text{if} \ y=f(x) \\
loss=L(y,f(x))=1, \text{if} \ y\neq f(x)$$
- 0-1损失函数可定义为如下
合页损失函数(Hinge 损失函数)
支持向量机的损失函数
- 一般基本形式为
$$loss = L(y,f(x))=[1-yf(x)]_{+}$$- \([z]_{+}\) 表示
- \(z>0\) 时取 \(z\)
- \(z\leq 0\) 时取0
- \([z]_{+}\) 表示
- 也可以写作(按单样本写并展开取正符号):
$$L(y_i, f(x_i)) = \max(0, 1 - y_i \cdot f(x_i))$$ - 损失函数分析:
- 当 \( y_i \cdot f(x_i) \geq 1 \) 时,损失为 0,说明样本被正确分类且与边界的距离足够大(满足间隔要求),无需惩罚了
- 当 \( y_i \cdot f(x_i) < 1 \) 时,损失为 \( 1 - y_i \cdot f(x_i) \),说明样本分类错误或距离边界太近,需要惩罚
- 对应模型
- 支持向量机
感知机的损失函数
感知机特有的损失函数<<统计学习方法>>
- 基本形式
$$loss=L(y,f(x))=[-yf(x)]_{+}$$ - 与合页损失函数对比
- 相当于函数图像整体左移一个单位长度
- 合页损失函数比感知机的损失函数对学习的要求更高
- 这使得感知机对分类正确的样本就无法进一步优化(分类正确的样本损失函数为0),学到的分类面只要能对样本正确分类即可(不是最优的,而且随机梯度下降时从不同点出发会有不同结果)
- 而SVM则需要学到最优的才行,因为即使分类正确的样本,依然会有一个较小的损失,此时为了最小化损失函数,需要不断寻找,直到分类面为最优的分类面位置
- 对应模型
- 感知机
感知损失函数
与感知机没有任何关系
- 基本形式
$$L(y,f(x))=1, \text{if} \ \left | y-f(x)\right |>t \\
L(y,f(x))=0, \text{if} \ \left | y-f(x)\right |< t$$ - 这里”感知”的意思是在一定范围内认为 \(y\approx f(x)\),满足小范围差距时,损失函数为0
Focal Loss
本文原文为: ICCV 2017: Focal Loss for Dense Object Detection
- 主要是为了解决正负样本严重失衡的问题
- 是交叉熵损失函数的一种改进
- 回归交叉熵损失函数的表达式为:
$$
\begin{align}
loss(x_i) &= -logy_i’, &\quad y_i = 1 \\
loss(x_i) &= -log(1-y_i’), &\quad y_i = 0
\end{align}
$$ - Focal Loss的损失函数如下
$$
\begin{align}
loss(x_i) &= -(1-y_i’)^\gamma logy_i’, &\quad y_i = 1 \\
loss(x_i) &= -y_i^\gamma\log(1-y_i’), &\quad y_i = 0
\end{align}
$$- \(\gamma\) 的取值在原始论文中使用了 0, 0.5, 1, 2, 5 等
- 当 \(\gamma > 0\) 时显然有
- 预测值 \(y_i’\) 与真实标签 \(y_i\) 差异越大的样本,他们的损失权重越大( \(y_i=1\) 时,预测值和真实值的差异为 \(1-y_i’\), \(y_i=0\) 时,差异为 \(y_i’\) )
- 预测值 \(y_i’\) 与真实标签 \(y_i\) 差异越小的样本,他们的损失权重越小
- 以上两点给了模型重视分类错误样本的提示,模型会重视分类出错的样本
- \(\gamma = 0\) 时Focal Loss退化为交叉熵损失函数
- \(\gamma\) 越大,说明, 分类错误的样本占的损失比重越大
- 实际使用中, 常加上 \(\alpha\) 平衡变量
$$
\begin{align}
loss(x_i) &= -\alpha(1-y_i’)^\gamma logy_i’, &\quad y_i = 1 \\
loss(x_i) &= -(1-\alpha)y_i^\gamma\log(1-y_i’), &\quad y_i = 0
\end{align}
$$- \(\alpha\) 用于平衡正负样本的重要性
- \(\gamma\) 用于加强对难分类样本的重视程度
- 假设正样本数量太少, 负样本数量太多, 那么该损失函数将降低负样本在训练中所占的权重, 可以理解为一种困难样本挖掘
- 困难样本挖掘的思想就是找到分类错误的样本(难以分类的样本), 然后重点关注这些错误样本
- 原论文中的实验结果:
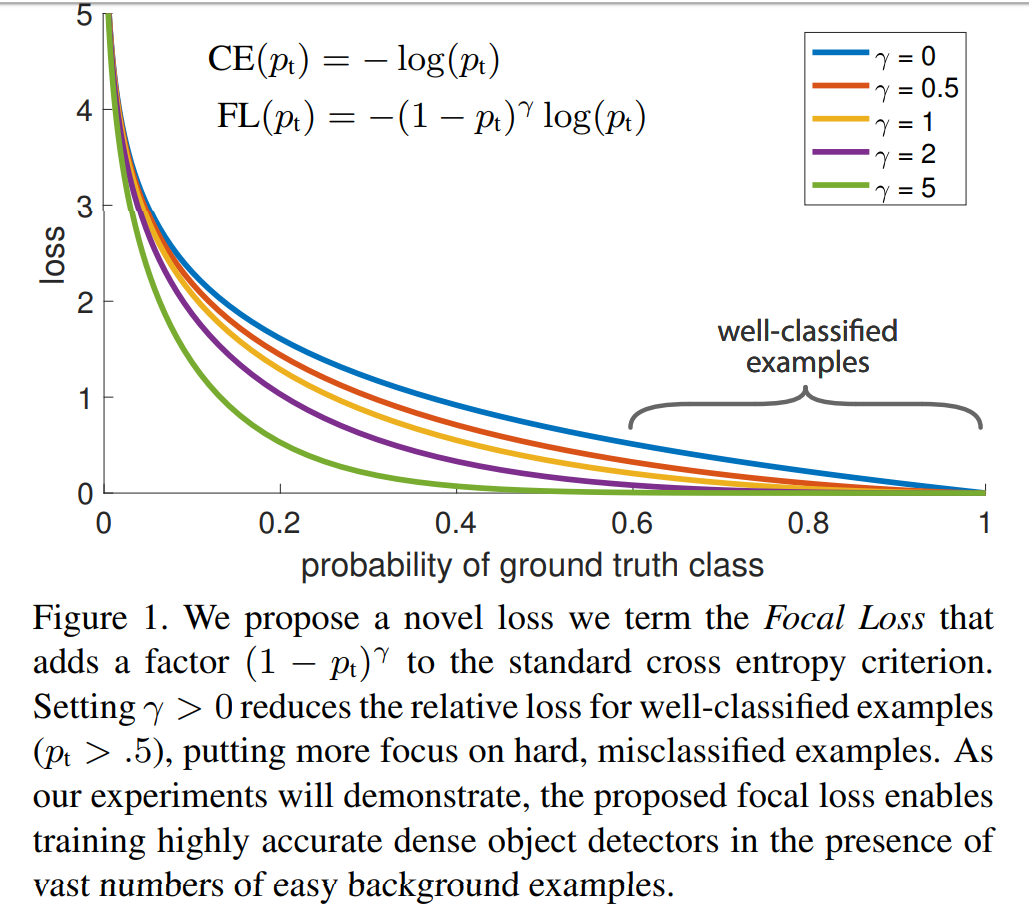
Huber Loss
总体来说:Huber损失函数是一种结合了均方误差(MSE)和平均绝对误差(MAE)优点的损失函数。它对小的残差表现得像MSE,对大的残差表现得更像MAE。这样可以减少异常值对模型的影响,同时保持梯度下降的有效性
Huber损失函数定义如下:
$$ L_\delta(y, f(x)) = \begin{cases}
\frac{1}{2}(y - f(x))^2 & \text{for } |y - f(x)| \leq \delta, \\
\delta (|y - f(x)| - \frac{1}{2}\delta) & \text{otherwise}.
\end{cases} $$- 其中 \(y\) 是目标变量, \(f(x)\) 是预测值,而 \(\delta\) 是一个超参数,用来控制从二次损失到线性损失转换的点
在Python中实现Huber损失函数,可以使用如下的代码:
1
2
3
4
5
6
7import numpy as np
def huber_loss(y_true, y_pred, delta=1.0):
residual = np.abs(y_true - y_pred)
condition = residual <= delta
small_res_loss = 0.5 * np.square(residual)
large_res_loss = delta * (residual - 0.5 * delta)
return np.where(condition, small_res_loss, large_res_loss)如果你使用的是深度学习框架比如TensorFlow或PyTorch,它们通常也内置了Huber损失函数,可以直接调用,例如在TensorFlow中:
1
2
3import tensorflow as tf
huber_loss_tf = tf.keras.losses.Huber(delta=1.0)
loss_tf = huber_loss_tf(y_true_tf, y_pred_tf)Huber Loss 也称为 Smooth_l1_loss
Smooth_l1_loss:它是一个“平滑”版本的L1损失,在误差较小时使用L2损失来提供平滑的梯度;相比于纯L1损失,smooth_l1_loss 在误差接近零时提供了更平滑的梯度变化,L1损失在误差为零时的梯度会发生突变(从-1变为1),而 smooth_l1_loss 使用平方误差部分避免了这种突变
岭回归
- 基本思路是在最小二乘的基础上加上L2正则
$$loss(\theta) = \frac{1}{m}\sum_{i=1}^{m}(y_{i} - f(x_{i}))^2 + \lambda \theta^2$$ - 其中 \(\lambda \theta^2\) 项是L2正则项,也称为收缩惩罚项(shrinkage penalty)
- 它试图缩小模型的参数,引入偏差来缓解参数估计中的方法问题,原始的最小二乘是无偏估计,但是引入了L2正则以后会变成有偏的,但是方差更小的参数估计
- 实际上,shrinkage参数,也称为收缩参数 ,是统计学里面的一个概念,是用于缓解参数估计时离群点带来的问题
几个回归损失函数的对比
不同模型的损失函数
决策树的损失函数
- 决策树有两个解释
- if-then规则
- 条件概率分布
- <<统计学习方法>>: 决策树的损失函数是对数似然
- 决策树可以看作是对不同概率空间的划分
Loss Function vs Cost Function
- 损失函数(Loss Function)应用于一个特定的样本计算误差
- 成本函数(Cost Function)是对所有样本而言的误差
损失函数相关思考
分类问题为什么不能用MSE?
- 参考链接:
- 原因:
- 在sigmoid函数拟合概率的情况下,使用MSE会导致预估值接近0或者为1时的梯度都接近0,不利于模型学习收敛
- 在sigmoid函数拟合概率的情况下,MSE是非凸优化问题,容易陷入局部最优;交叉熵损失则是凸优化问题,不会陷入局部最优
- 最小化交叉熵损失函数等价于不做任何假设的极大似然估计 ,其本质是在最小化真实样本分布和预估分布的KL散度(这里的分布可以是已知X时,label的条件分布)
- 最小化MSE损失函数等价于假设噪声服从高斯分布时的极大似然估计
- 推导可参考:MSE的推导、MSE,MLE和高斯分布的关系、为什么回归问题用MSE?
- 假设在回归问题中 \(y = z + \epsilon\),样本噪声 \(\epsilon\) 服从均值为0,方差为 \(\sigma\) 的高斯分布,即 \(\epsilon \sim N(0,\sigma)\),这里的 \(\sigma>0\)
- 则有原始样本 \(y\) 服从均值为 \(z\) 方差为 \(\sigma\) 的高斯分布 \(y \sim N(z,\sigma)\),我们的目标是用模型拟合非噪声部分 \(y_{pred} = \theta^T x = z\),此时有 \(y = y_{pred} + \epsilon\),即 \(y\) 服从高斯分布 \(y \sim N(y_{pred},\sigma)\)
- 正太分布的概率密度函数为 \(p(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-u)^2}{2\sigma^2}}\),则此时单个样本出现的概率为 \(\frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(y-\theta^T x)^2}{2\sigma^2}}\)
- 用极大似然法估计参数 \(\theta\),即最大化多个样本的联合概率为:
$$
\begin{align}
\theta^* &= \mathop{\arg\max}_\theta \prod_i \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(y^i-\theta^T x^i)^2}{2\sigma^2}} \\
&= \mathop{\arg\max}_\theta \prod_i e^{-\frac{(y^i-\theta^T x^i)^2}{2\sigma^2}} &\quad —去掉与\theta无关的常数项 \\
&= \mathop{\arg\max}_\theta \sum_i -\frac{(y^i-\theta^T x^i)^2}{2\sigma^2} &\quad —取对数 \\
&= \mathop{\arg\max}_\theta \sum_i -(y^i-\theta^T x^i)^2 &\quad —继续去除常数项 \\
&= \mathop{\arg\min}_\theta \sum_i (y^i-\theta^T x^i)^2 \\
\end{align}
$$ - 即当假设噪声服从高斯分布时,用极大似然法估计参数与MSE损失函数得到的参数相同
MSE和RMSE对反向传播过程一样吗?
- 答案是不一样
- MSE的梯度是:
$$ \nabla_{w} loss_{MSE} = \frac{1}{M}\sum_{i=1}^M 2(f_w(x_i)-y_i) \cdot \nabla_{w}f_w(x_i) $$ - RMSE的梯度是:
$$ \nabla_{w} loss_{RMSE} = \frac{1}{2} \left(\frac{1}{M}\sum_{i=1}^M (f_w(x_i)-y_i)^2\right)^{-\frac{1}{2}} \cdot \frac{1}{M}\sum_{i=1}^M 2(f_w(x_i)-y_i) \cdot \nabla_{w}f_w(x_i) $$
- MSE的梯度是:
- 由于两者的梯度不同,所以两者对参数的影响也不同,由于 \(\frac{1}{2} \left(\frac{1}{M}\sum_{i=1}^M (f_w(x_i)-y_i)^2\right)^{-\frac{1}{2}}\) 不是固定值,所以MSE和RMSE对梯度的影响也不是简单的固定倍数关系
- 可以简单理解为:
- RMSE的梯度相当于在MSE的基础上乘以 \(\frac{1}{2} \left(\frac{1}{M}\sum_{i=1}^M (f_w(x_i)-y_i)^2\right)^{-\frac{1}{2}}\),在不同的Batch中,该值不同,Loss越大,该值越大,Loss越小,该值越小
- 可以简单理解为:
- MSE是在假设误差服从均值为0的正太分布(即 \(\epsilon \sim N(0,\sigma)\) )的基础上基于极大似然法求得的目标函数
- 在同一个Batch内来看,RMSE与MSE的目标实际上是完全一致的,即MSE最小时,RMSE也最小;但是从不同Batch之间来看,RMSE的梯度系数不同无法实现在所有训练集上MSE最小
- 当所有数据只有一个Batch时,RMSE和MSE对梯度的影响是常数倍数关系(基于所有样本计算Loss得到的常数)
- 为了实现多次采样Batch后实现MSE(满足极大似然法推导结果),一般常用MSE作为损失函数,而不是RMSE,RMSE更多是一个指标