整体说明
- 预热(Warm-up)是一种训练技巧:
- 在模型训练初期采用一些策略,逐步调整超参数(如学习率、 Batch Size 大小等)或模型状态 ,使得训练过程更加稳定、高效的初始化阶段
- 通过合理预热,可以显著提升训练稳定性、收敛速度和最终性能
- 预热的核心目的是避免训练初期因参数随机初始化或学习率过高导致的梯度不稳定、收敛困难等问题
- 常见的预热技术主要包含两类:
- 学习率预热(Learning Rate Warm-up) :训练初期从极小的学习率(如0)逐步线性或非线性增加到预设值
- 优化器预热 :
- Adam 预热阶段可用小学习率,比如正常值的 \(1/10\)(Adam 优化器的自适应动量在初期可能不准确);
- Adam 在预热阶段启用偏差修正 ,避免初期估计偏差过大
- 其他预热技术还包括:Batch Size 预热(Batch Size 从小到大),模型参数预热(逐步解冻模型层) 和 混合精度预热等(初期禁用混合精度)
- 最常见的预热技术是学习率预热,其中 Transformer 常使用 学习率线性预热(比如 BERT 训练中常用 10,000 步线性预热)
- 术语:warm-up ratio
- 如 warm-up ratio 等于 0.03,表示 warm-up 阶段(学习率上升阶段)步数占总训练阶段步数的 3%
学习率预热的相关策略
- 学习率预热(Learning Rate Warm-up)是训练初期逐步增加学习率的策略,旨在稳定训练并提升最终性能。以下是常见的具体方法及其细节:
线性预热(Linear Warm-up)
- 在预热步数 \(N\) 内,学习率从 \(0\)(或极小值 \(\epsilon\))线性增长到初始学习率 \(lr_{\text{base} }\)
$$
lr_t = \epsilon + \left(\frac{t}{N}\right) \cdot (lr_{\text{base} } - \epsilon)
$$- 其中 \(t\) 是当前步数,\(t \leq N\)
- 最常用的方式之一
余弦预热(Cosine Warm-up)
- 结合余弦函数曲线调整学习率,初期缓慢增长,后期平滑过渡到目标值
$$
lr_t = \frac{1}{2} \left(1 + \cos\left(\pi \cdot \left(1 - \frac{t}{N}\right)\right)\right) \cdot lr_{\text{base} }
$$ - 注:也可与余弦退火结合,预热后直接进入衰减阶段
- 更平滑的过渡,减少初期学习率突变
- 一些大模型中会使用到
指数预热(Exponential Warm-up)
- 学习率从 \(\epsilon\) 开始指数增长到 \(lr_{\text{base} }\)
$$
lr_t = \epsilon \cdot \left(\frac{lr_{\text{base} } }{\epsilon}\right)^{\frac{t}{N} }
$$ - 较少使用,因可能过早进入高学习率阶段
阶梯预热(Step Warm-up)
- 将预热阶段分为多个离散区间,逐步跳跃式增加学习率
附录:torch 自带预热和学习率调度代码示例
一个完整的PyTorch示例:先进行学习率预热,再正常训练模型
以简单的图像分类任务(CIFAR-10)为基础,结合线性预热和余弦退火调度器
代码示例:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79import torch
import torch.nn as nn
import torch.optim as optim
from torch.optim.lr_scheduler import LambdaLR, CosineAnnealingLR
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
class SimpleCNN(nn.Module):
def__init__(self):
super().__init__()
self.conv1 = nn.Conv2d(3, 16, 3, padding=1)
self.conv2 = nn.Conv2d(16, 32, 3, padding=1)
self.fc = nn.Linear(32 * 8 * 8, 10) # CIFAR-10输入为32x32,经过两次池化后为8x8
self.pool = nn.MaxPool2d(2, 2)
self.relu = nn.ReLU()
def forward(self, x):
x = self.pool(self.relu(self.conv1(x)))
x = self.pool(self.relu(self.conv2(x)))
x = x.view(-1, 32 * 8 * 8)
x = self.fc(x)
return x
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])
train_set = datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)
train_loader = DataLoader(train_set, batch_size=128, shuffle=True)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = SimpleCNN().to(device)
## 注:学习率包含在优化器 optimizer 中,使用不同的学习率调度器来执行 step,就可以实现不同的学习率调度
optimizer = optim.AdamW(model.parameters(), lr=0.001) # 初始学习率设为0.001(预热目标值)
warmup_steps = 500 # 预热步数
total_steps = 5000 # 总训练步数
# 线性预热函数
def warmup_lambda(current_step):
if current_step < warmup_steps:
return float(current_step) / float(max(1, warmup_steps))
else:
return 1.0 # 预热结束后保持学习率
# 预热阶段调度器
warmup_scheduler = LambdaLR(optimizer, lr_lambda=warmup_lambda) # 基于优化器初始化调度器
# 预热后的余弦退火调度器(从预热结束开始)
cosine_scheduler = CosineAnnealingLR(
optimizer, # 与预热阶段调度器初始化相同的优化器
T_max=total_steps - warmup_steps, # 余弦周期长度
eta_min=1e-6 # 最小学习率
)
criterion = nn.CrossEntropyLoss()
lr_history = []
for step in range(total_steps):
inputs = torch.randn(128, 3, 32, 32).to(device)
labels = torch.randint(0, 10, (128,)).to(device)
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# 更新学习率
if step < warmup_steps:
warmup_scheduler.step() # 预热阶段,step 函数会按照 warmup_scheduler 的定义来修改学习率
else:
cosine_scheduler.step() # 预热后余弦退火,step 函数会按照 cosine_scheduler 的定义来修改学习率
# 记录学习率,可打印出来观测
lr_history.append(optimizer.param_groups[0]['lr'])
if step % 200 == 0:
print(f"Step {step}: LR = {optimizer.param_groups[0]['lr']:.6f}, Loss = {loss.item():.4f}")预热阶段(前500步):学习率从
0线性增长到初始值0.001
$$ lr = \text{base_lr} \times \frac{\text{current_step} }{\text{warmup_steps} } $$正常训练阶段(500步后):切换为余弦退火调度器(
CosineAnnealingLR),学习率从0.001逐渐衰减到1e-6- 注: 余弦退火的周期长度 \( T_{\text{max} } \) 设为总步数减去预热步数
总体来说,学习率曲线是先线性上升,后余弦式下降(平滑振荡衰减)的过程
附录:transformers 库的模型训练预热调度示例
transformers 库中使用模型训练预热代码(按照初始学习率 1e-4, epochs= )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52import matplotlib.pyplot as plt
import transformers
import torch
initial_lr = 1.0e-4 # 初始学习率
warmup_ratio = 0.1 # 预热比例
num_training_steps = 1000 # 总训练 step 数
num_warmup_steps = int(num_training_steps * warmup_ratio) # 计算 warmup 的 step 数
optimizer = torch.optim.AdamW([torch.tensor(0.0)], lr=initial_lr) # [torch.tensor(0.0)] 是虚拟的模型参数,可随意设置
# 使用 transformers 库创建余弦退火学习率调度器
lr_scheduler = transformers.get_cosine_schedule_with_warmup(
optimizer=optimizer,
num_warmup_steps=num_warmup_steps, # warmup step 数
num_training_steps=num_training_steps, # 训练总 step 数
# num_cycles=0.5, # 对应 cosine 曲线的周期,默认值是0.5,也就是半周期(递减)
# last_epoch=-1, # 用于从 checkpoint 启动时恢复训练,设置为 ckpt 对应 step-1 即可
# 比如从第 500 步的 ckpt启动,设置为499,从第0步启动,设置为-1(默认值)
)
learning_rates = []
for _ in range(num_training_steps):
learning_rates.append(optimizer.param_groups[0]["lr"])
lr_scheduler.step() # 更新 optimizer.param_groups[0]["lr"]
# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
# 以下为可视化代码
plt.figure(figsize=(10, 6))
plt.plot(learning_rates)
plt.title('学习率变化曲线')
plt.xlabel('训练步骤')
plt.ylabel('学习率')
plt.grid(True)
plt.axvline(x=num_warmup_steps, color='r', linestyle='--', label='预热结束')
plt.legend()
plt.annotate(f'初始学习率: {initial_lr}', xy=(num_warmup_steps, initial_lr),
xytext=(num_warmup_steps + 50, initial_lr * 1.5),
arrowprops=dict(facecolor='black', shrink=0.05))
plt.annotate(f'预热起点: 0', xy=(0, 0),
xytext=(50, initial_lr * 0.2),
arrowprops=dict(facecolor='black', shrink=0.05))
plt.annotate(f'最终学习率: {learning_rates[-1]:.8f}', xy=(num_training_steps-1, learning_rates[-1]),
xytext=(num_training_steps-200, learning_rates[-1] * 10),
arrowprops=dict(facecolor='black', shrink=0.05))
plt.tight_layout()
plt.savefig('warmup_learning_rate_curve_cycles_0.5.png', dpi=300)
# plt.show()可视化结果(半周期余弦
num_cycles=0.5的结果):- warmup 阶段,学习率从 0 开始逐步提升到最大值
- 正式训练阶段,学习率按照余弦调度器波动
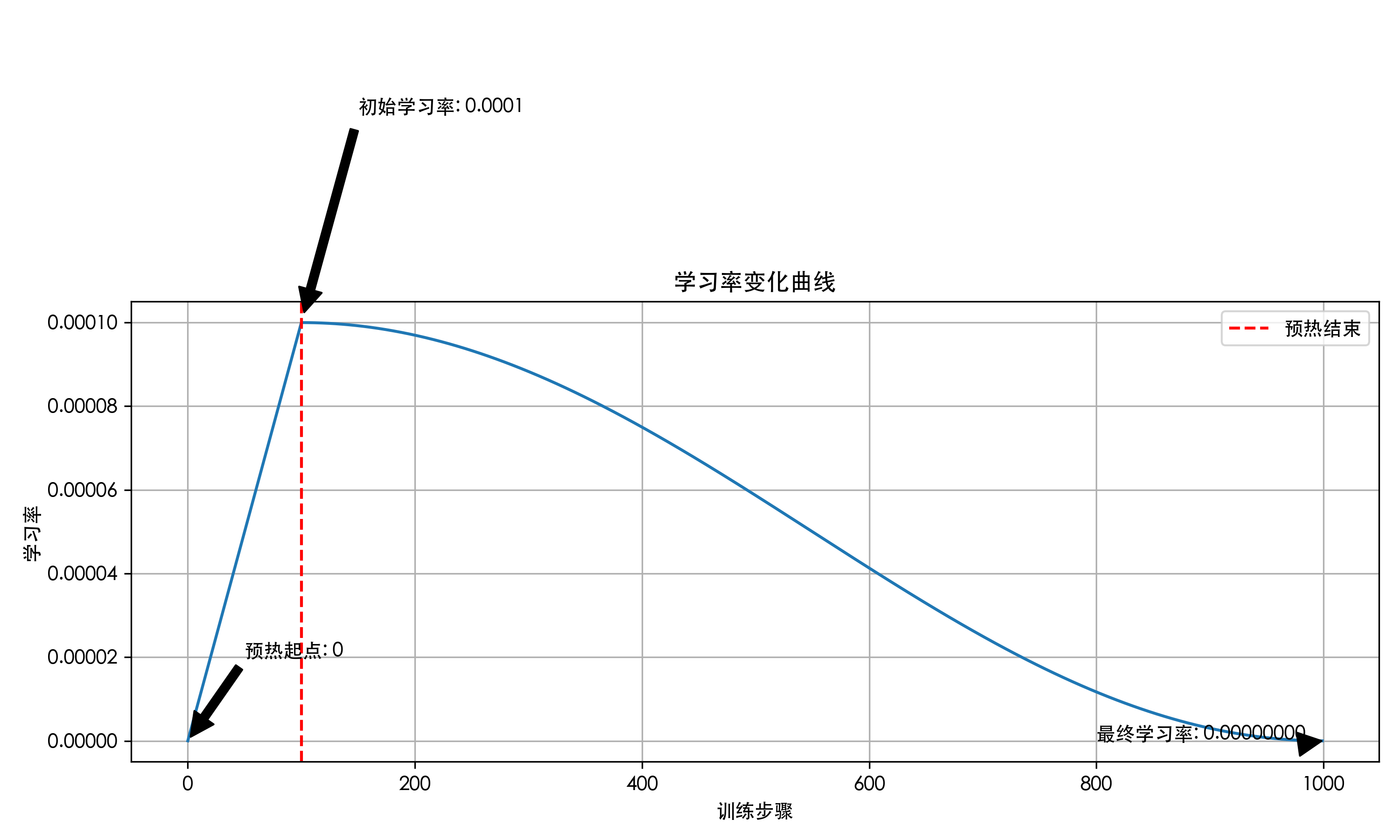
如果设置为
num_cycles=1,则会在指定训练步数内完成两个周期的学习率变化: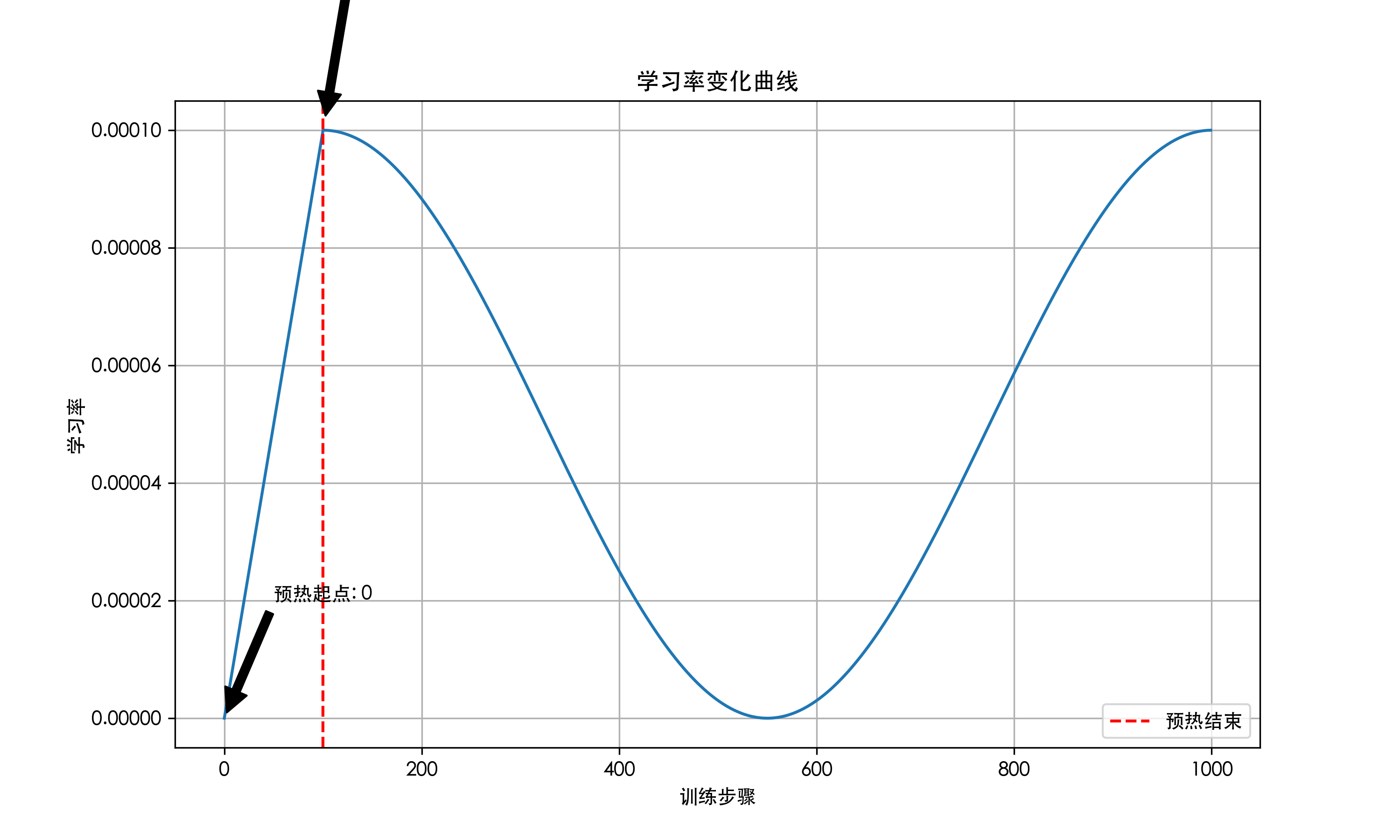
如果设置为
num_cycles=1.5,则会在指定训练步数内完成两个周期的学习率变化: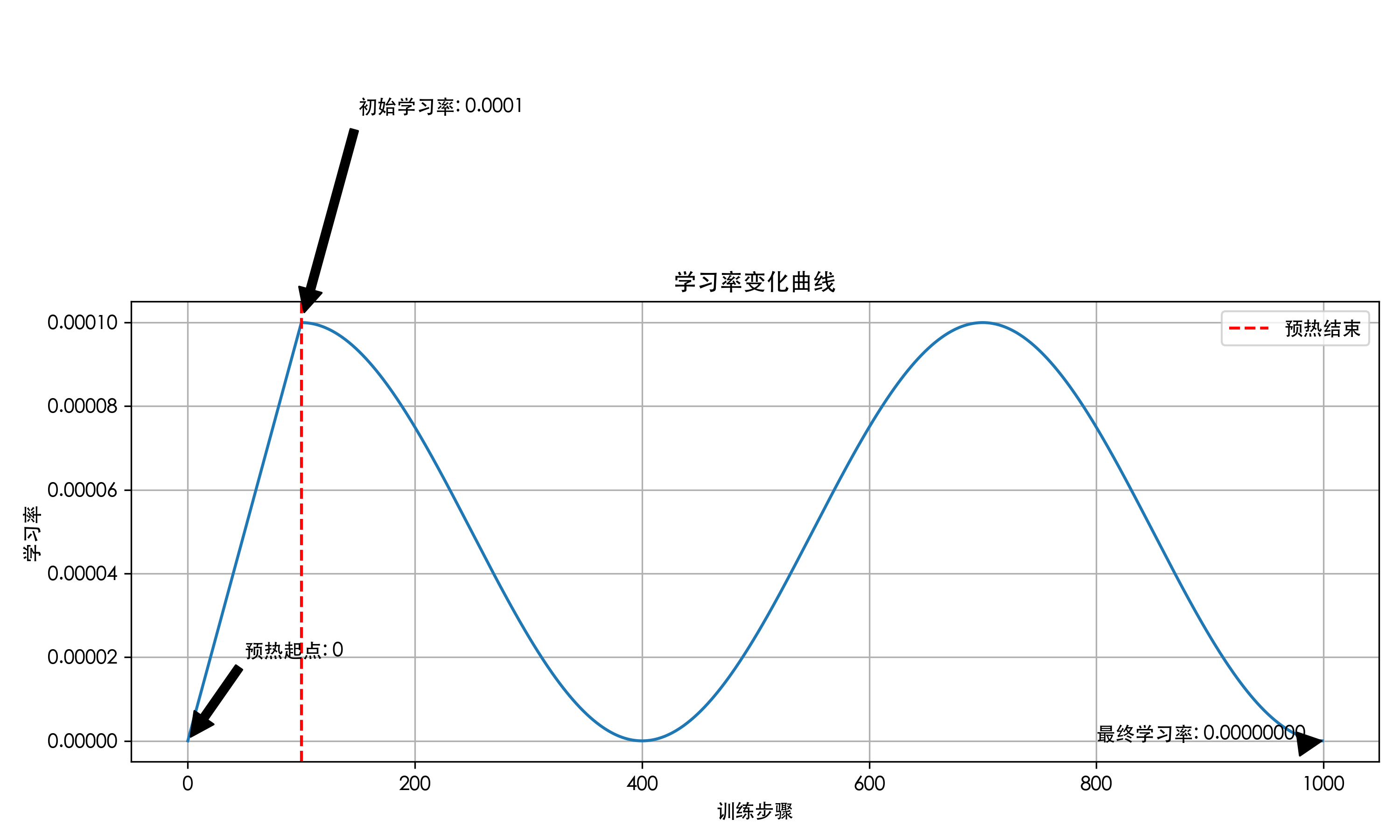
如果设置为
num_cycles=2,则会在指定训练步数内完成两个周期的学习率变化: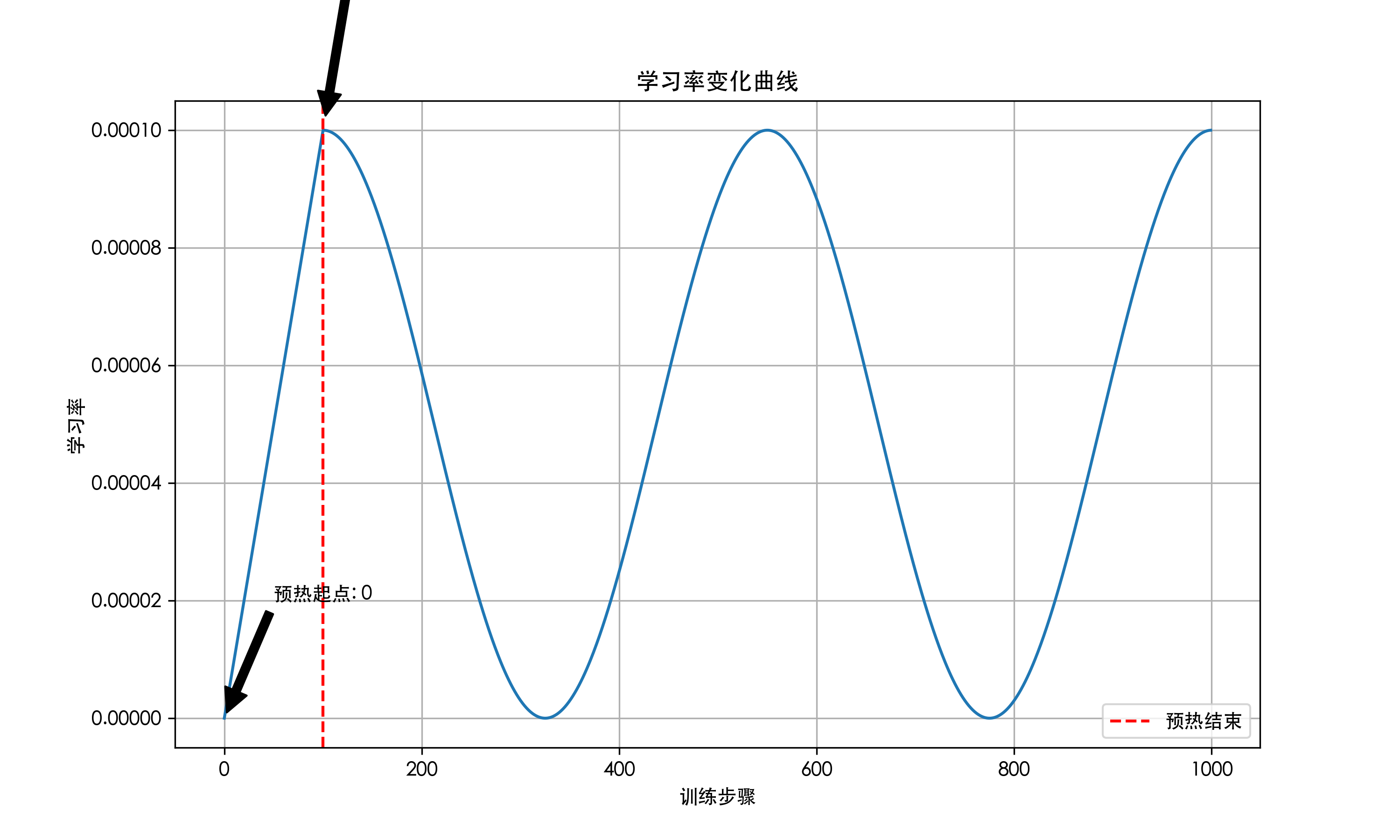
附录:预热有什么用?
- 解决梯度不稳定问题 :模型初始阶段参数随机初始化,直接使用高学习率可能导致梯度爆炸或震荡
- 解决学习率敏感性问题 :过大的初始学习率可能使模型跳过最优解附近区域;过小则导致收敛缓慢
- 保证优化器适应性 :如 Adam 等自适应优化器在初期需要积累梯度统计量(如动量、方差),预热阶段可为优化器提供更稳定的初始估计
附录:一般预热多少步更合适?
- 预热步数通常取决于模型规模和数据集大小:
- 小规模数据:数百到几千步
- 大规模训练(如LLM):数万步甚至更长(例如 GPT-3 的数千批次预热)
- 另一种设置方式是:通常为总训练步数的 5-10%(例如 BERT 的 10k 步预热,总步数 100k)