DL——Transformer

本文主要介绍Transformer和Attention相关内容

由于LaTex中矩阵的黑体表示过于复杂，在不会引起混淆的情况下，本文中有些地方会被简写为非黑体

Transformer讲解

最直观的动态图理解
本文讲解主要按照Google Brain, NIPS 2017: Attention Is All You Need的思路走，该论文的亮点在于:
- 不同于以往主流机器翻译使用基于 RNN 的 Seq2Seq 模型框架，该论文用 Attention 机制代替了 RNN 搭建了整个模型框架, 这是一个从换自行车零件到把自行车换成汽车的突破
- 提出了多头注意力(Multi-Head Attention)机制方法，在编码器和解码器中大量的使用了多头自注意力机制(Multi-Head self-attention)
- 在WMT2014语料库的英德和英法语言翻译任务上取得了先进结果

Transformer是什么?

Transformer 是个序列转换器 ：
进一步讲，是个 Encoder-Decoder 模型的序列转换器 ：
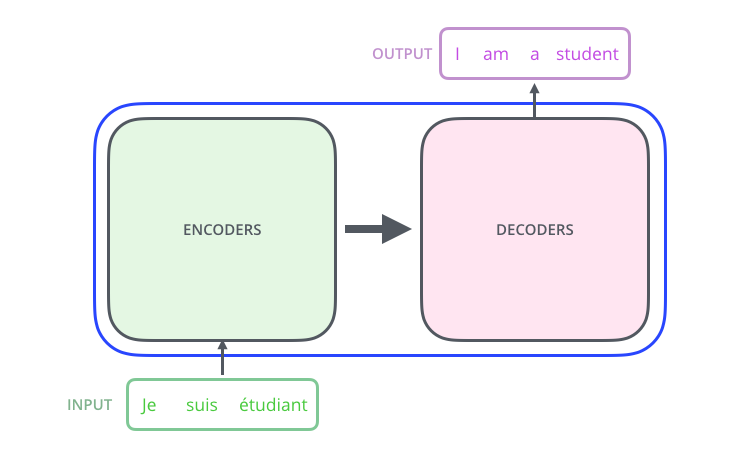
更进一步的讲,是个 6层Encoder + 6层Decoder 结构的序列转换器：
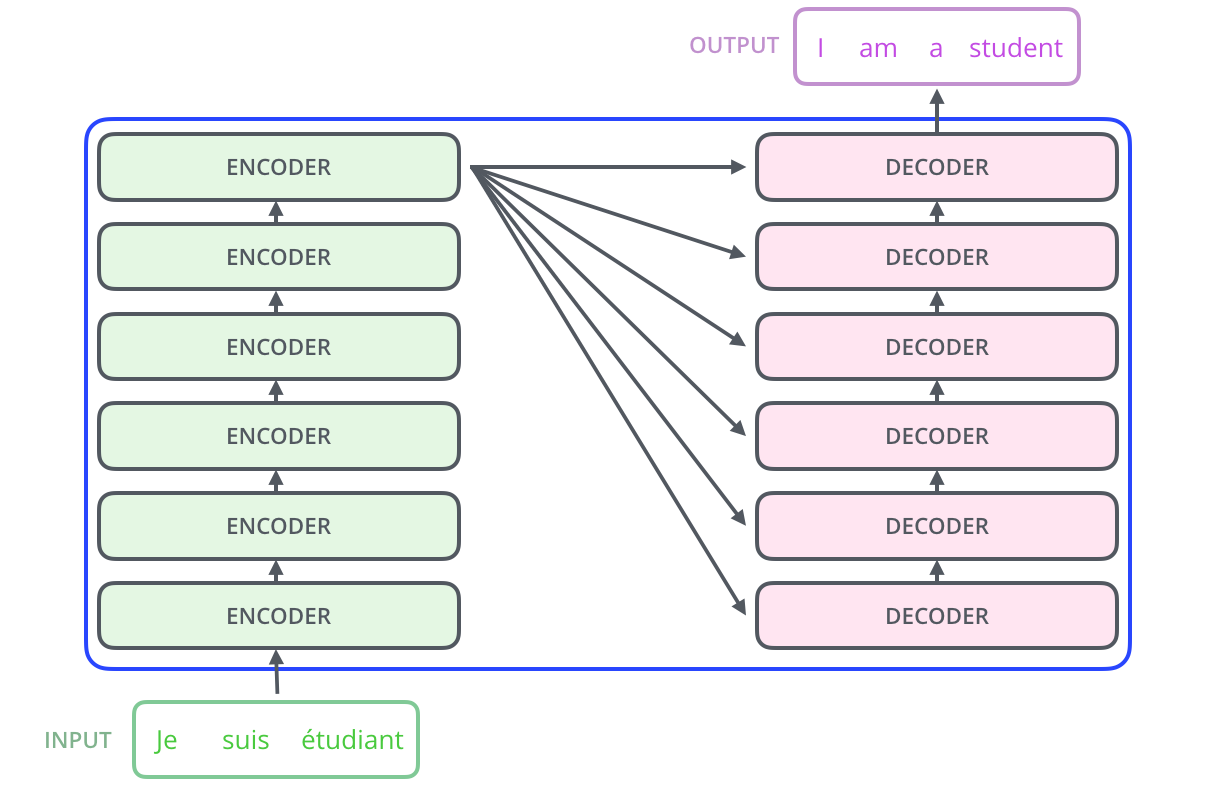
上面的图中,每个 Encoder 是：
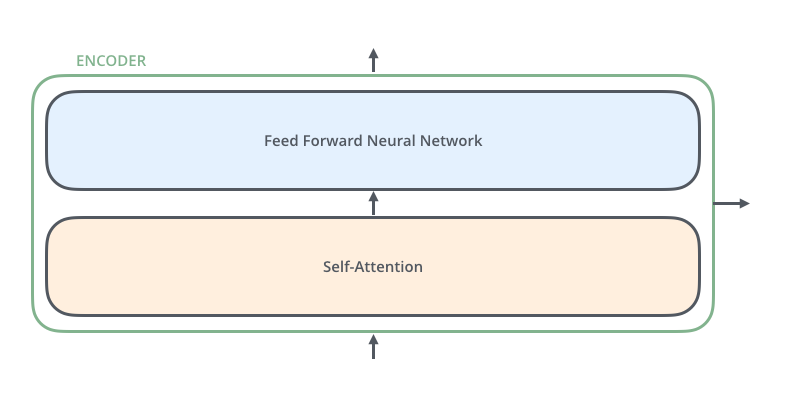
详细的讲, 每个Encoder是
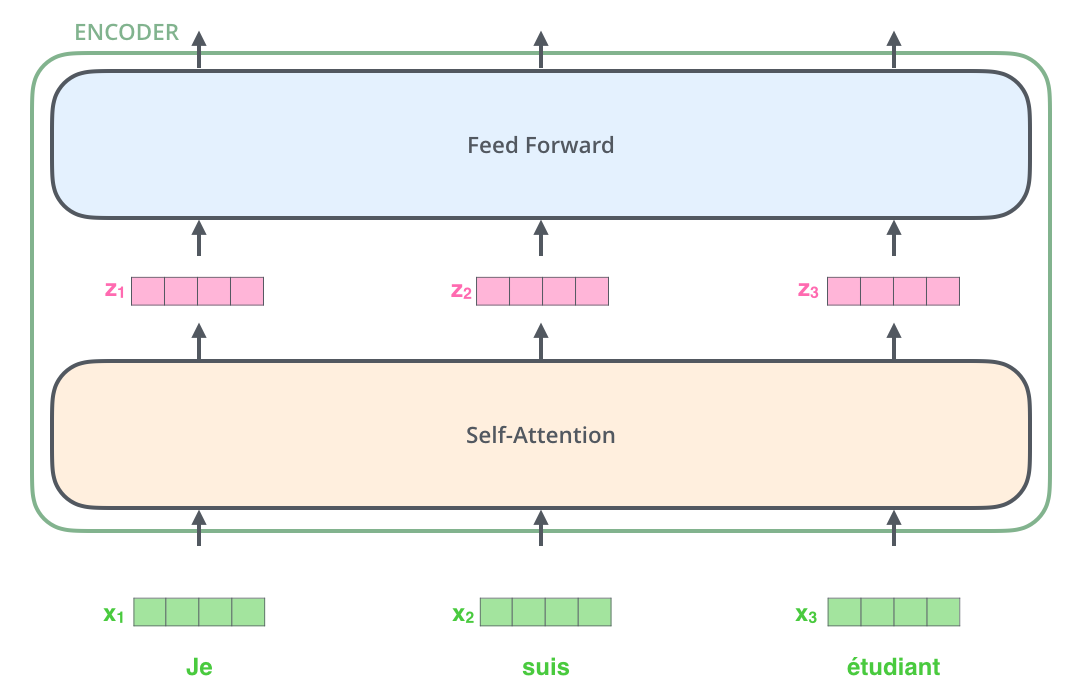
展开看里面 Encoder 中的数据流向
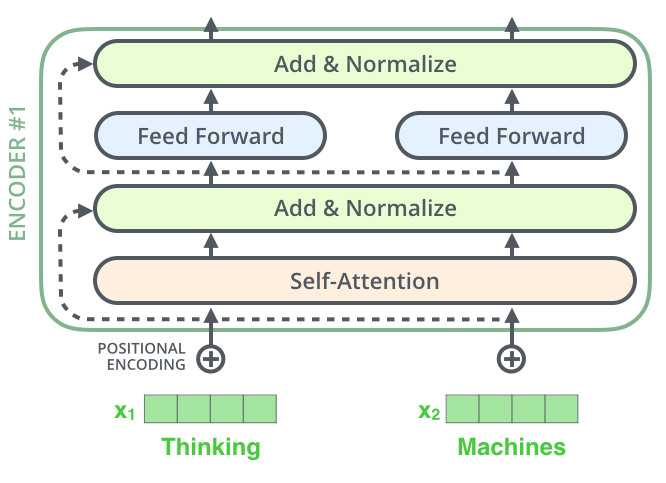
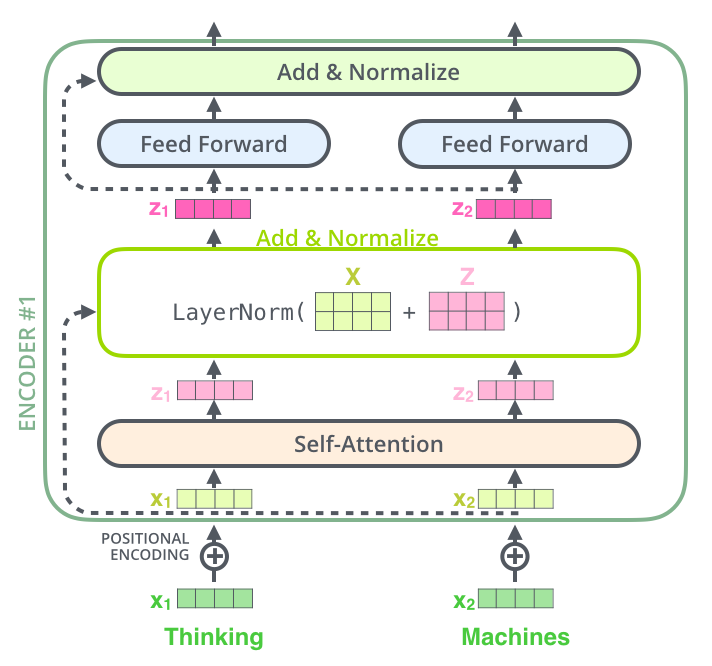
更进一步的展开看 Encoder 中的数据流向
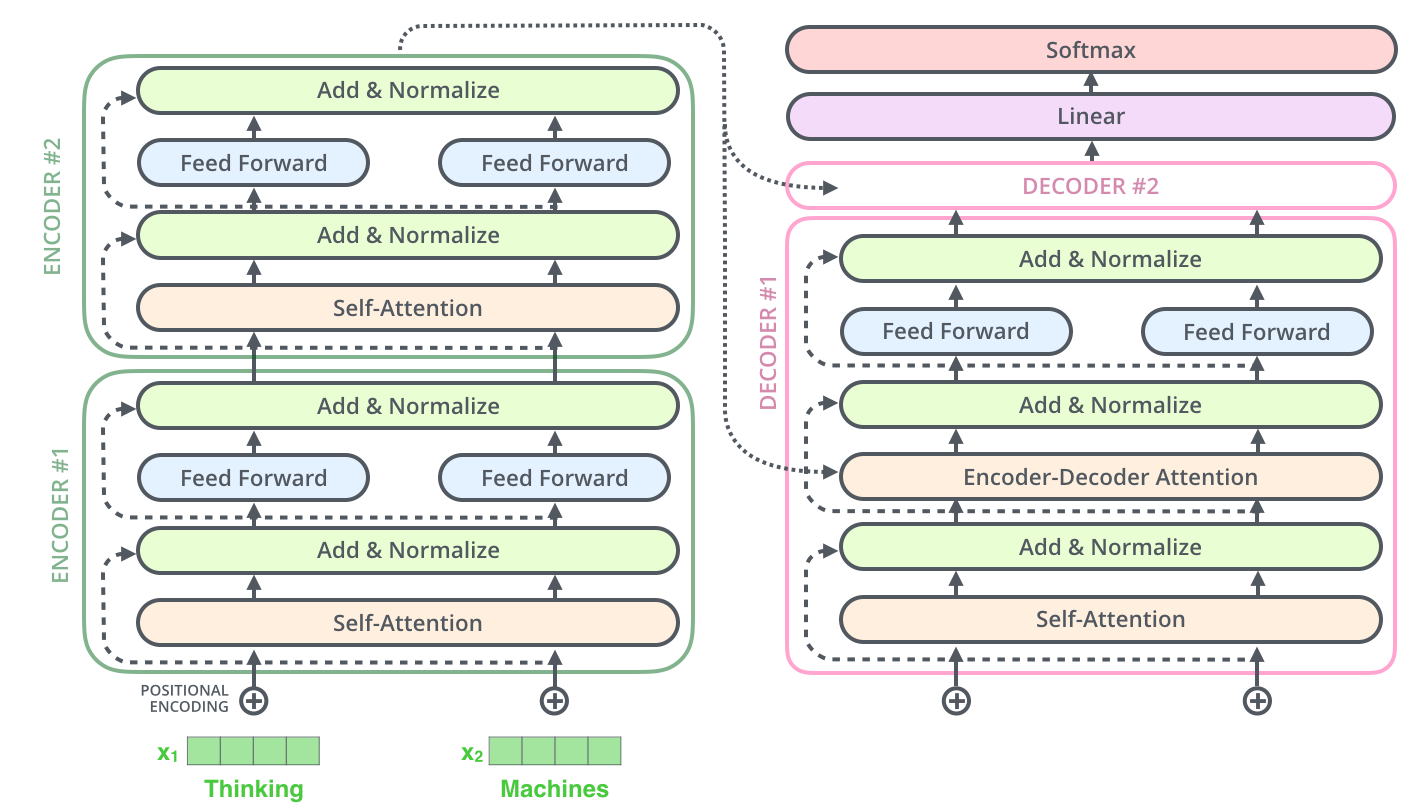
两层 Encoder + 两层Decoder (其中一个Decoder没有完全画出来) 的数据流向
带细节动图查看数据流向
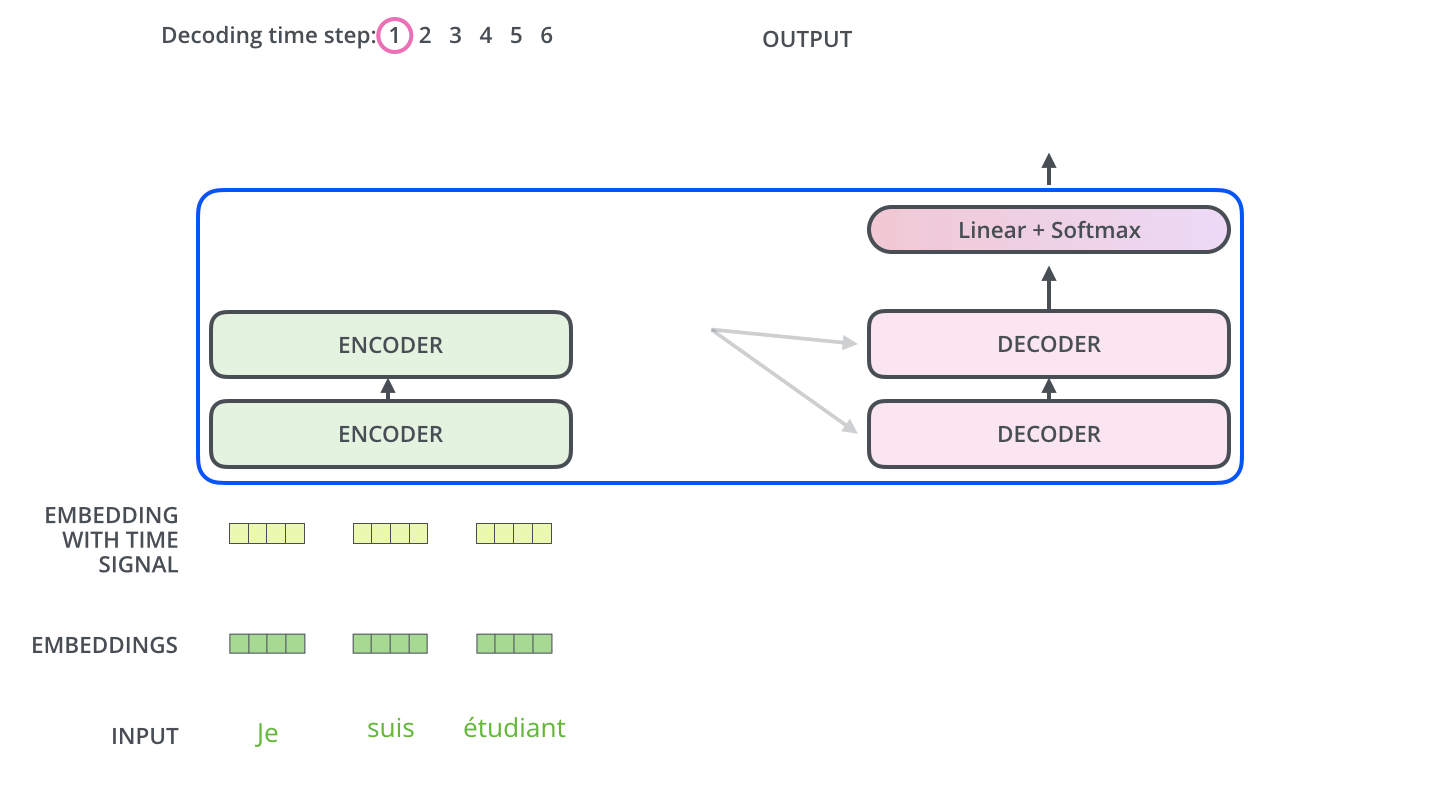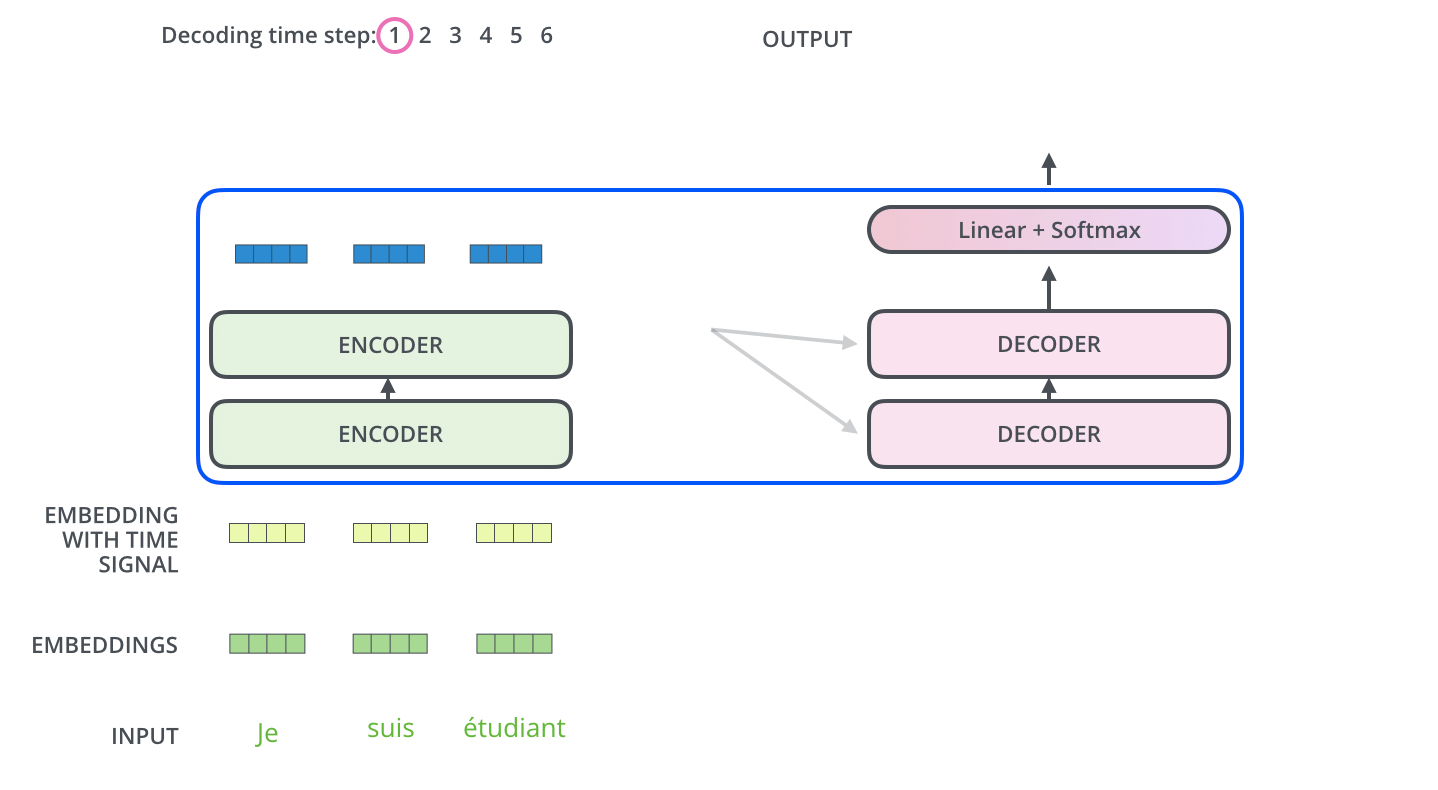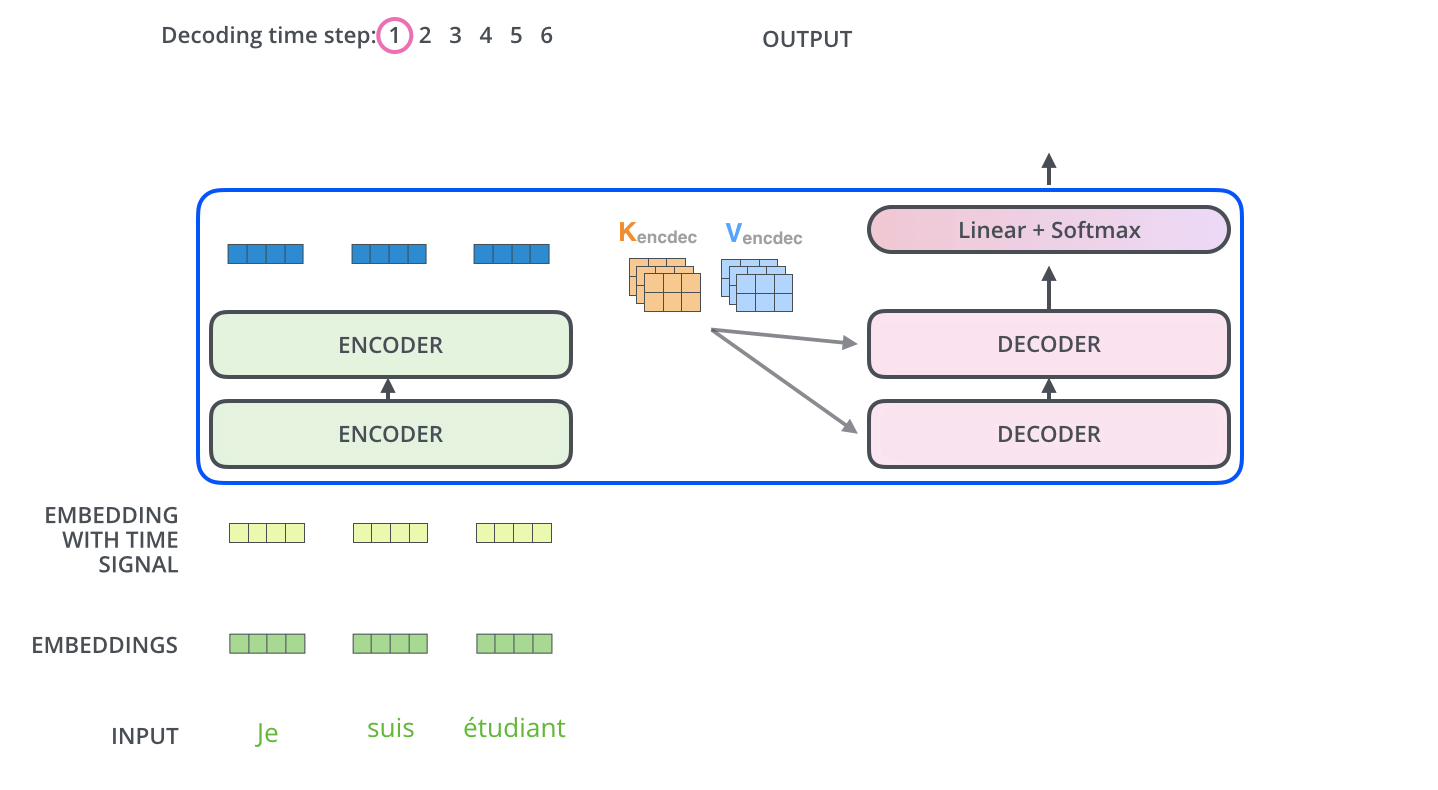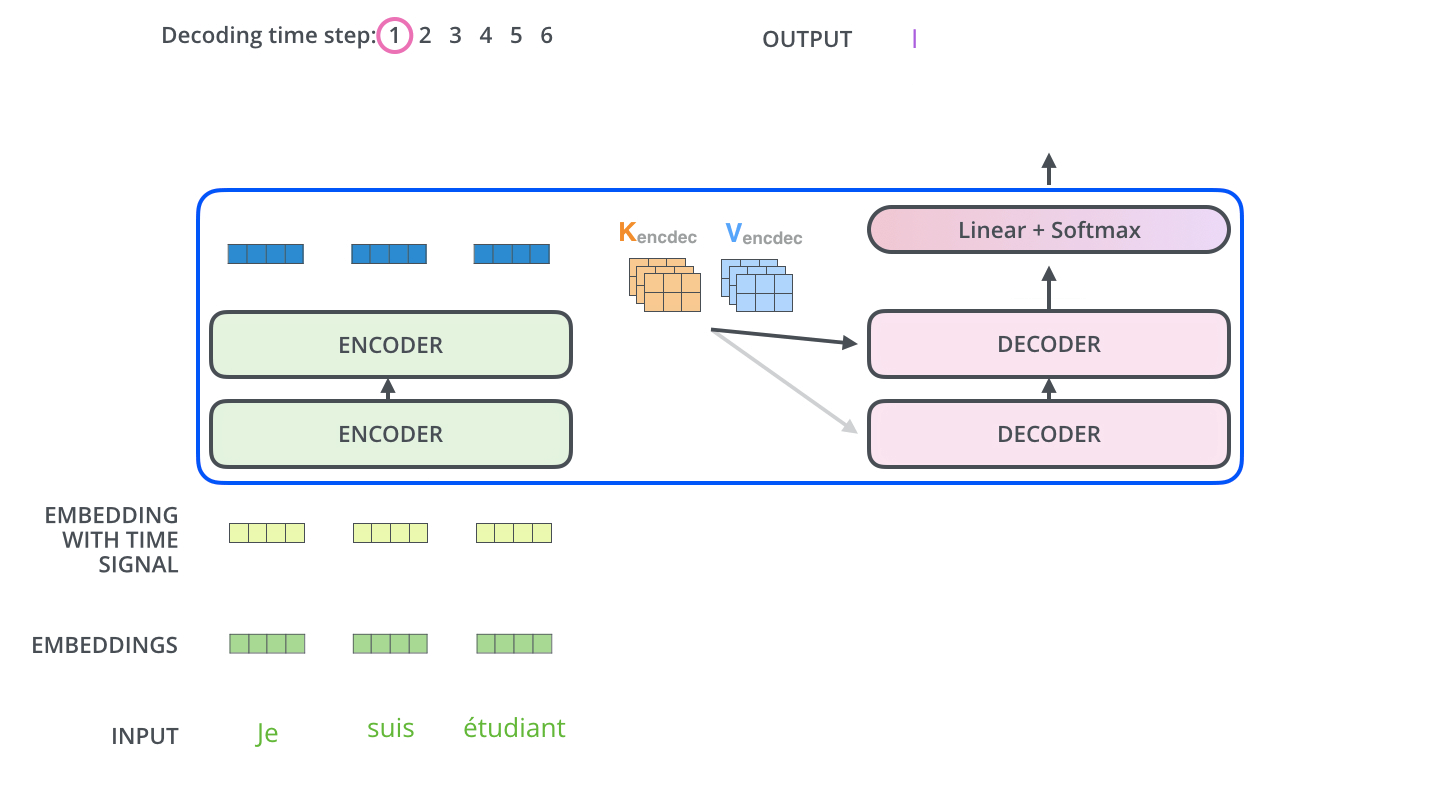
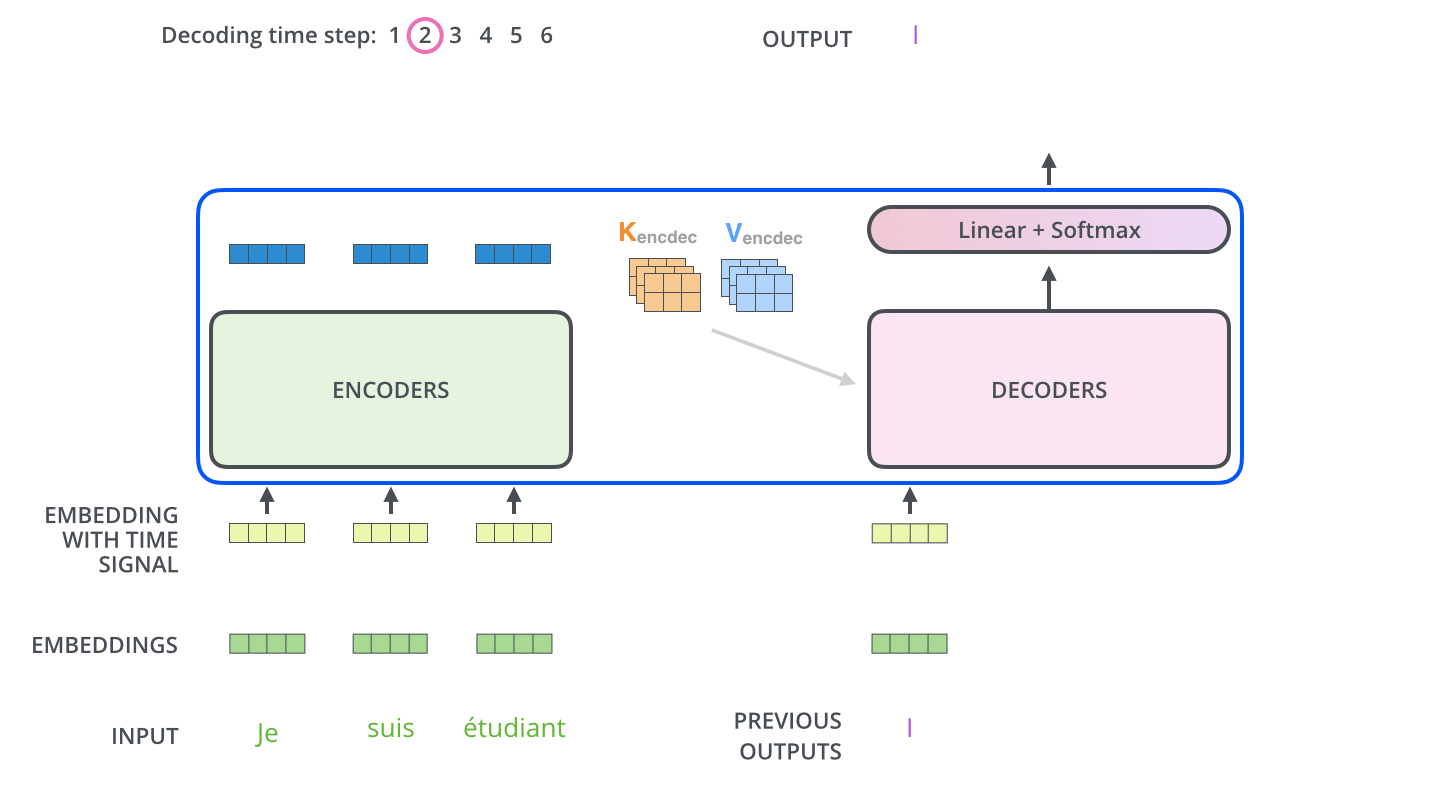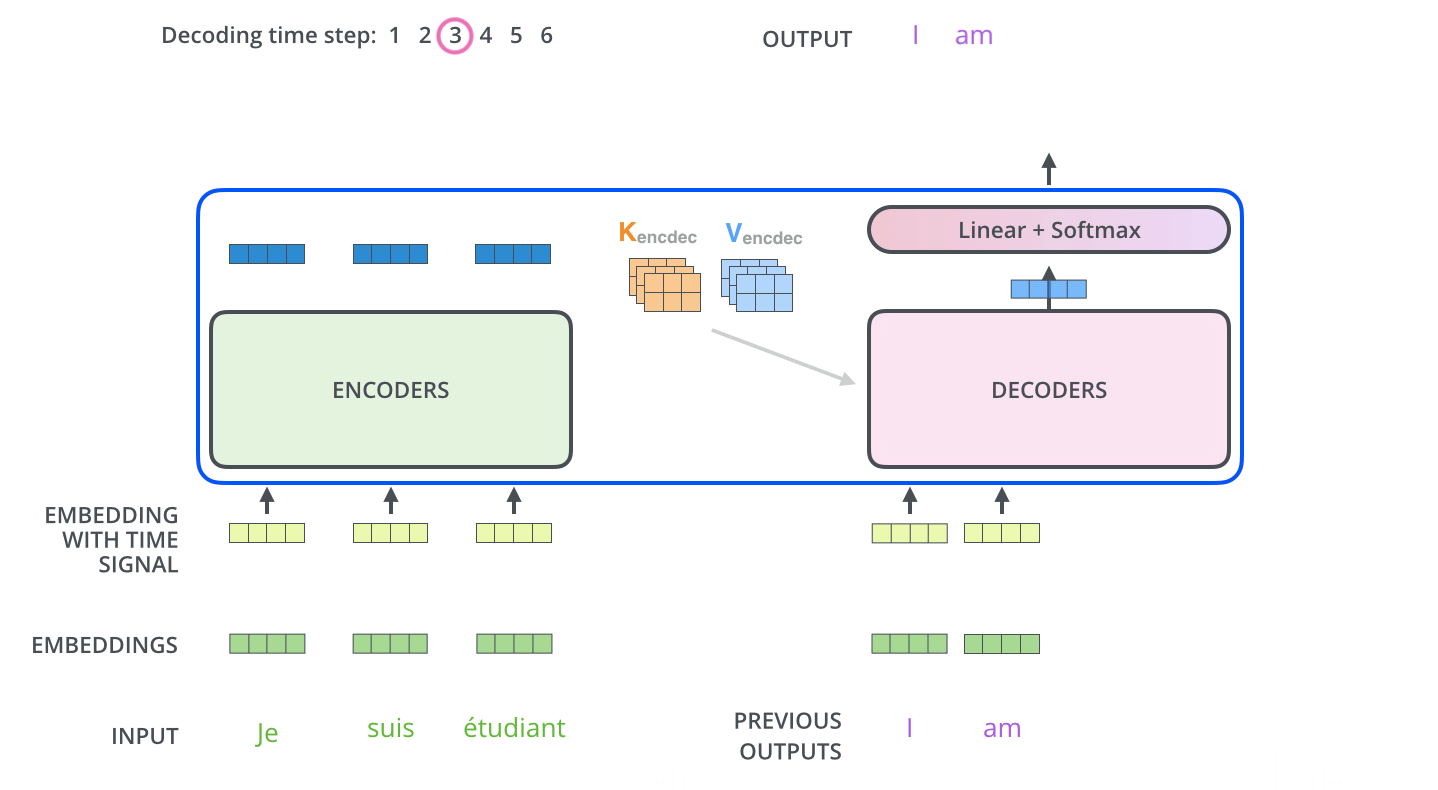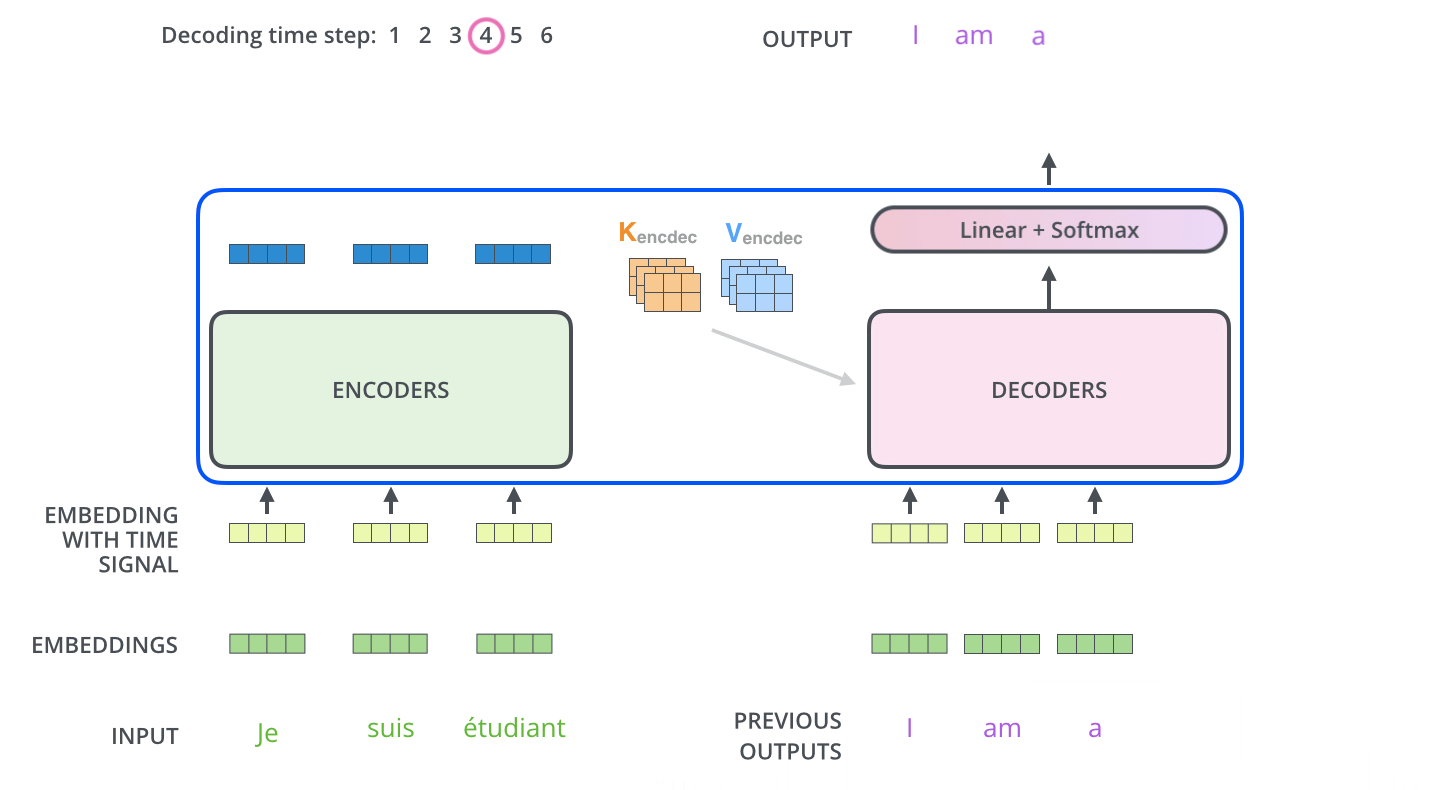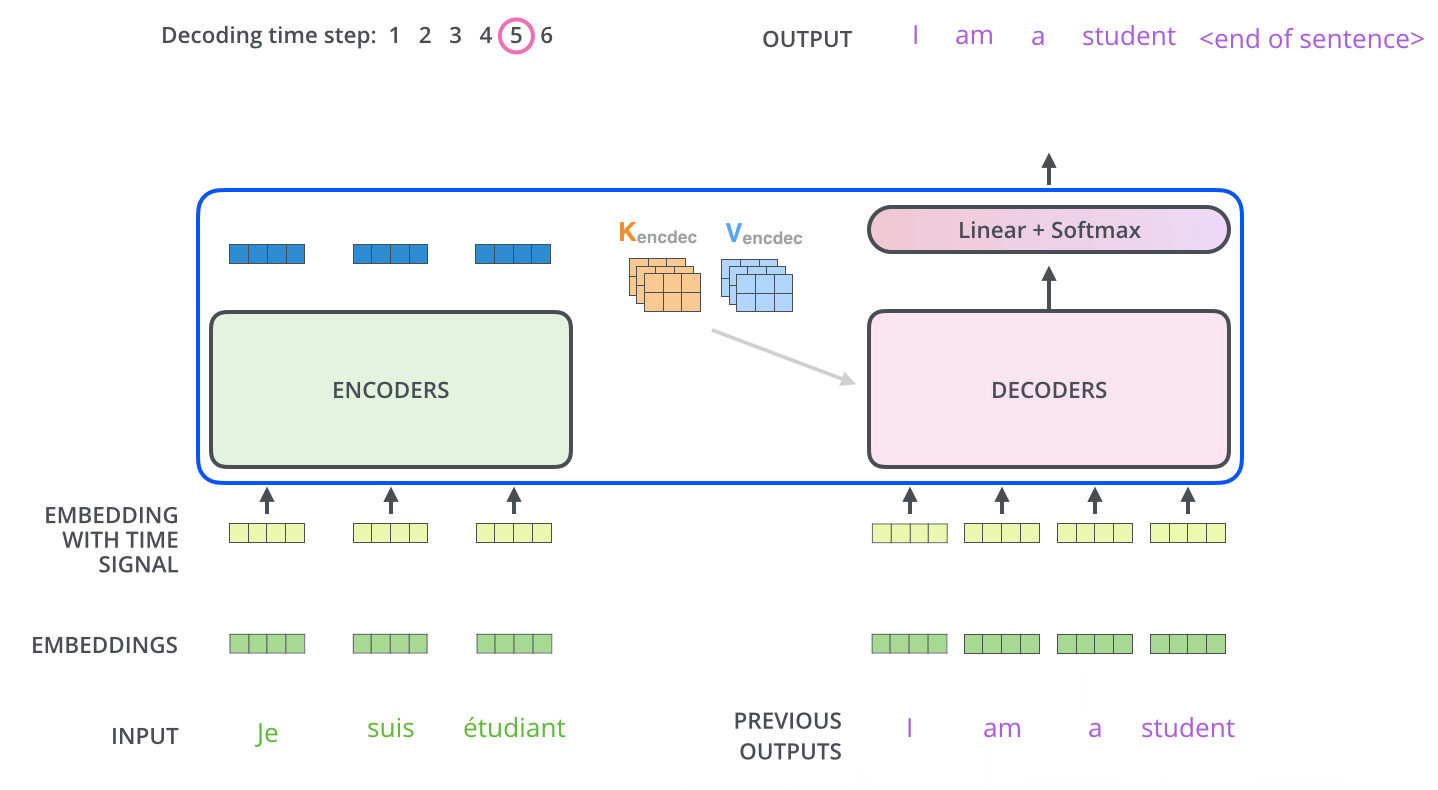
最后,我们给出Transformer的结构图(来自原文中)

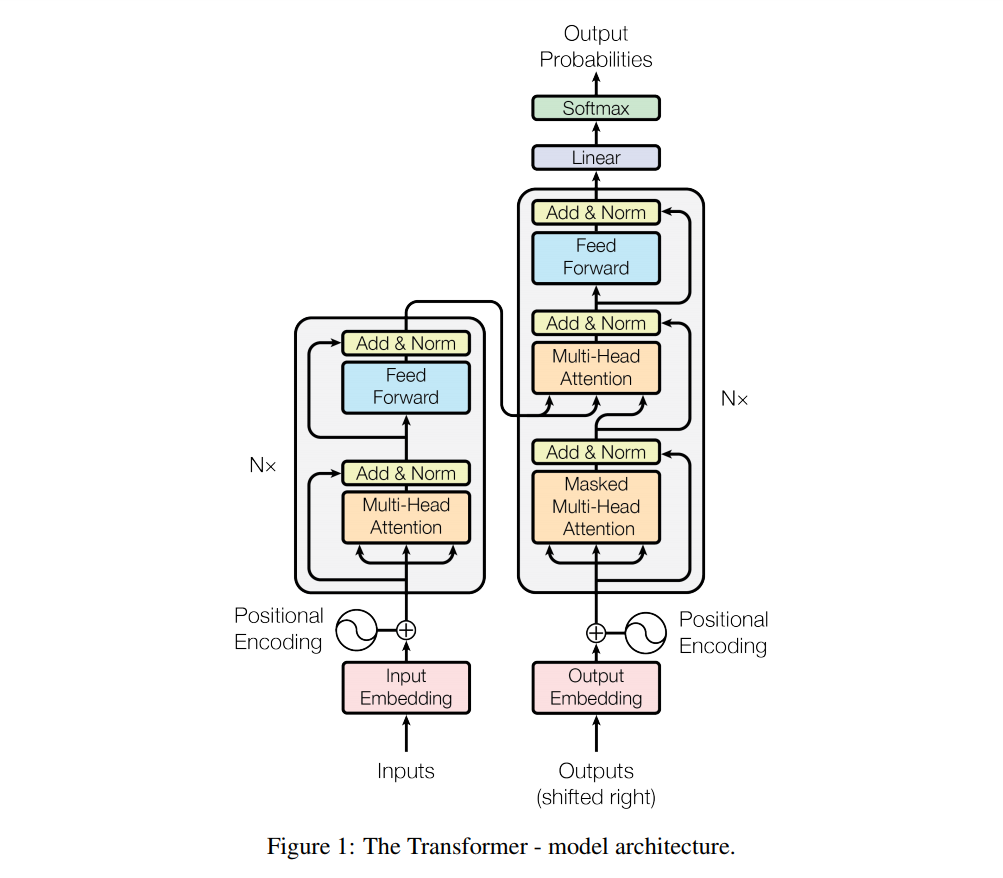
Transformer中的Attention

Transformer中使用了 Multi-Head Attention, 同时也是一种 Self Attention

由于Transformer的Multi_Head Attention中 Query == Key == Query ，所以也是一种 Self Attention
- 即
  $$\boldsymbol{Y_{AttentionOutput}} = Self Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = Attention(\boldsymbol{X},\boldsymbol{X},\boldsymbol{X})$$
更多关于广义Attention的理解请参考: DL——Attention

Multi-Head Attention

Muti-Head Attention，也称为多头Attention，由 $h$ 个 Scaled Dot-Product Attention和其他线性层和Concat操作等组成
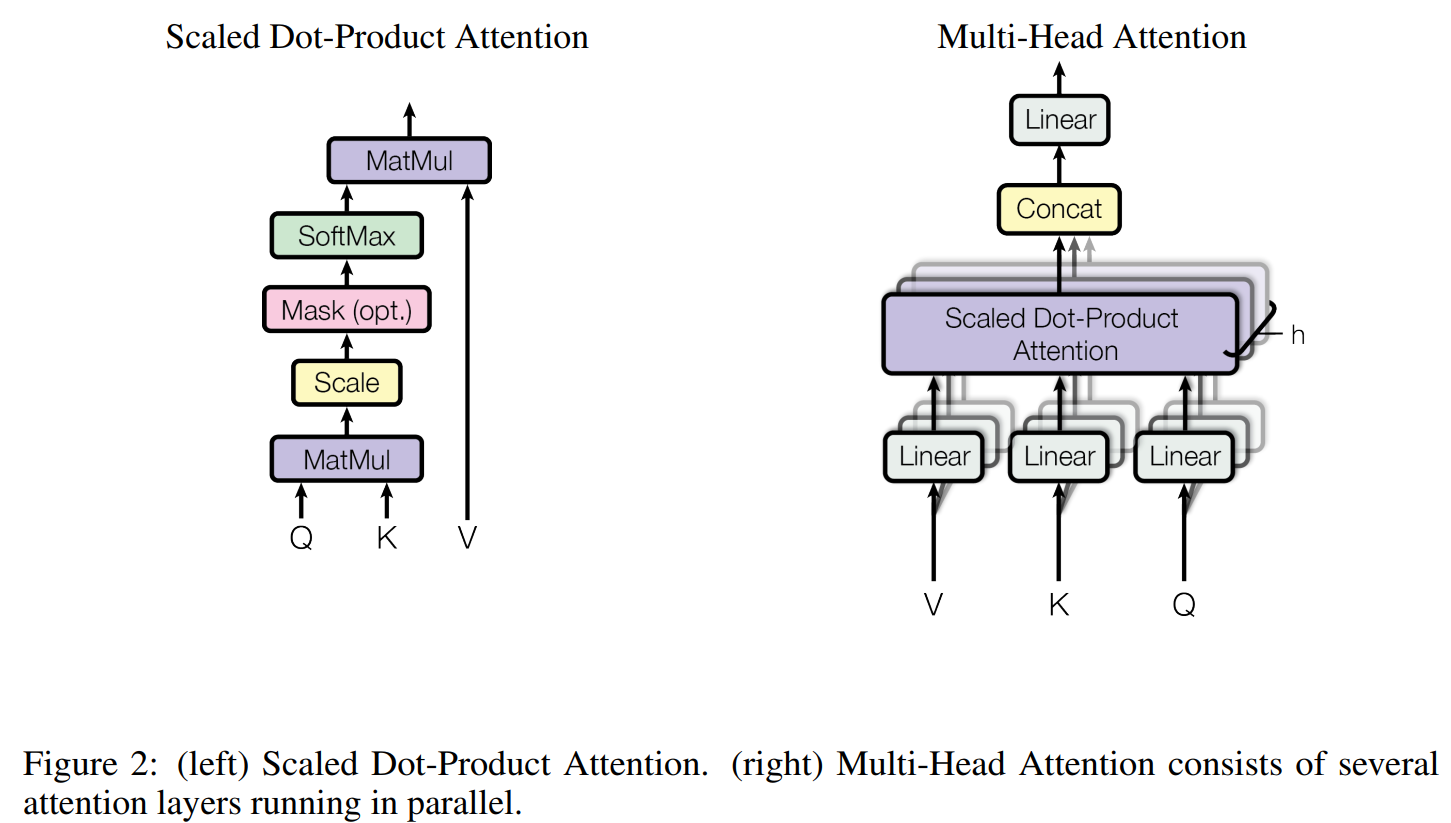
Scaled Dot Product Attention中Mask操作是可选的
Scaled Dot Product Attention数学定义为(没有Mask操作)
$$
\begin{align}
Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = softmax\left(\frac{\boldsymbol{Q}\boldsymbol{K}^{\top}}{\sqrt{d_k}}\right)\boldsymbol{V}
\end{align}
$$
- Softmax前除以 $\sqrt{d_k}$ 的原因是防止梯度消失问题，基本思想是（原始论文脚注中有提到）：假设 $\boldsymbol{Q},\boldsymbol{K}$ 中每个元素是服从均值为0，方差为1的正太分布（ $\sim N(0,1)$ ），那么他们任意取两个列向量 $\boldsymbol{q}_i,\boldsymbol{k}_i$ 的内积服从均值为0，方差为 $d_k$ 的正太分布（ $\sim N(0,d_k)$ ），具体证明可参考没有比这更详细的推导 attention为什么除以根号dk——深入理解Bert系列文章，过大的方差会导致softmax后梯度消失
Multi-Head Attention的某个输出的数学定义为
$$
\begin{align}
MultiHead(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V}) &= Concat(head_1,\dots,head_h)\boldsymbol{W}^{O} \\
where \quad head_i &= Attention(\boldsymbol{Q}\boldsymbol{W}_i^Q,\boldsymbol{K}\boldsymbol{W}_i^K,\boldsymbol{V}\boldsymbol{W}_i^V)
\end{align}
$$
- 注意，在一般的Attention中，没有 $\boldsymbol{W}^{O}$ 这个参数，这个是用于多头Attention中，将多头的输出Concat后映射一下再输出
  - 理解：若不是多头，其实加不加这个参数，本质都是一样的，因为连续的两个权重矩阵线性相乘，本质就是一个权重矩阵而已
  - 补充：在实现时，这里的 $\boldsymbol{W}^{O}$ 实际上是一个线性层 nn.Linear 的含义，就是一个简单的矩阵，不包含非线性信息的
- 一般来说， $head_i$ 的维度是 $\frac{d_{model}}{N_{head}}=\frac{d_{model}}{h}=d_v = d_k$，所以Multi-Head Attention的参数数量与head的数量无关，且无论多少个头，其的输出结果还是 $d_{model} = d_v * h$ 维
- 原始论文中常用 $d_{model} = h * d_k = h * d_v$，且base模型的参数设置为 $512 = 8 * 64$

有关Multi-Head Attention的理解

原论文的描述:

Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions,
理解:
- 所谓多头,就是多做几次($h$ 次)同样的事情(参数 $(W_i^Q, W_i^K, W_i^V)$ 不共享, 即当 $i \neq j $ 时, $(W_i^Q, W_i^K, W_i^V) \neq (W_j^Q, W_j^K, W_j^V)$),然后把结果拼接
- Multi-Head Attention中, 每个头(Scaled Dot-Product Attention)负责不同的子空间(subspaces at differect positions)
- 每个头权重不同, 所以他们的关注点也会不同,注意, 初始化时他们的参数不能相同, 否则会造成他们的参数永远相同, 因为他们是同构的
- 个人理解: 多头的作用可以类比于CNN中的卷积层, 负责从不同的角度提取原始数据的特征

Self Attention

Self Attention是只 Key和Query相同的 Attention, 这里因为 Key 和 Value 也相同,所以有 Query == Key == Query
即$$ \boldsymbol{Y_{AttentionOutput}} = Self Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = Attention(\boldsymbol{X},\boldsymbol{X},\boldsymbol{X})$$

Transformer中的Attention

既是Multi-Head Attention, 也是 Self Attention
所以有$$\boldsymbol{Y_{AttentionOutput}} = MultiHead(\boldsymbol{X},\boldsymbol{X},\boldsymbol{X})$$

Masked Multi-Head Attetion

MaskedMHA，掩码多头Attention，用于Decoder中防止前面的token看到后面的token，Encoder中不需要MaskedMHA
一般性的，Masked Self-Attention是更一般的实现，不一定非要和Multi-Head绑定
代码实现时，主要是在计算Softmax前，按照掩码将看不到的token对应的q,k内积替换为一个大负数，比如 $-1e9$

Cross Multi-Head Attention

CrossMHA不是Self-Attention，CrossMHA的Q,K是Encoder的输出，V来自Decoder

Transformer 输入层

Transformer的输入层使用了 Word Embedding + Position Embedding
由于Transformer去除RNN的Attention机制完全不考虑词的顺序, 也就是说, 随机打乱句子中词的顺序 (也就是将键值对 $(\boldsymbol{K}, \boldsymbol{V})$ 对随机打乱), Transformer中Attention的结果不变
实际上, 目前为止, Transformer中的Attention模型顶多是个非常精妙的”词袋模型” (这句话来自博客:https://kexue.fm/archives/4765)

Word Embedding

和之前的词嵌入一样, 将One-Hot值映射成词向量嵌入模型中
Tie Embedding ：嵌入层（Embedding Layer）和输出投影层（Unembedding Layer / Output Projection Layer）绑定（即共享权重）
- 基本思路：一个是 token 到 Embedding 映射，另一个是 Embedding 到 token 映射，绑定方式是W_out = W_embed^T
- 这种绑定的优势是节约存储、训练稳定；缺点是表达能力受限、梯度冲突可能严重（比如输入和输入的词分布差异大）
原始论文中关于参数绑定（Weight-Tying）的说明在3.4节：

In our model, we share the same weight matrix between the two embedding layers and the pre-softmax linear transformation, similar to [24]. In the embedding layers, we multiply those weights by $\sqrt{d_{\text{model}}}$

Position Embedding

FaceBook的《Convolutional Sequence to Sequence Learning》中曾经用过Position Embedding

在不使用RNN的情况下建模词的顺序, 弥补”词袋模型”的不足
用 Position Embedding来为每个位置一个向量化表示
- 将每个位置编号，然后每个编号对应一个向量
- 通过结合位置向量和词向量，就给每个词都引入了一定的位置信息，这样Attention就可以分辨出不同位置的词了
原始论文中, 作者提出了一种周期性位置编码的表示, 数学公式如下:
$$
\begin{align}
PE(pos,2i) &= sin(pos/10000^{2i/d_{\text{model}}}) \\
PE(pos, 2i+1) &= cos(pos/10000^{2i/d_{\text{model}}})
\end{align}
$$
我觉得上述公式太丑了,转换一下写法可能更容易理解
$$
\begin{align}
PE(pos,2i) &= sin\left (\frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}}\right) \\
PE(pos, 2i+1) &= cos\left (\frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}}\right)
\end{align}
$$
- $pos$ 是位置编号
- $i$ 表示位置向量的第 $i$ 维
- 从公式来看，为什么选择 $10000^{\frac{2i}{d_{\text{model}}}}$ ?
  - $i$ 表示频率随模型embedding维度变动（模型embedding不同维度频率不同，低维度高频，高维度低频）
  - $pos$ 表示周期，随着位置变化，每个维度的值呈现周期变化，但是不同维度的变化周期（频率）不同
  - 10000是一个放缩因子，理论上可以换，在transformer原始论文实现中用了这个，且效果不错
- 选择正弦函数的原因是假设这将允许模型学到相对位置信息
  - 因为对于固定的 $k$， $PE_{pos+k} = LinearFuction(PE_{pos})$，所以这给模型提供了表达相对位置的可能性

与之前的Position Embedding的区别

Position Embedding对模型的意义不同:
- 以前在RNN、CNN模型中Position Embedding是锦上添花的辅助手段，也就是“有它会更好、没它也就差一点点”的情况，因为RNN、CNN本身就能捕捉到位置信息
- 在Transformer这个纯Attention模型中，Position Embedding是位置信息的唯一来源，因此它是模型的核心成分之一，并非仅仅是简单的辅助手段
Position Embedding的向量构造方式不同
- 在以往的Position Embedding中，基本都是根据任务训练出来的向量
- 而Google直接给出了一个构造Position Embedding的公式:
  $$
  \begin{align}
  PE(pos,2i) &= sin\left (\frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}}\right) \\
  PE(pos, 2i+1) &= cos\left (\frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}}\right)
  \end{align}
  $$
- Google经过实验, 学到的位置嵌入和这种计算得到的位置嵌入结果很相近
- Google选用这种嵌入方式的原因是这种方式允许模型以后可以扩展到比训练时遇到的序列长度更长的句子

输入层的输出(Attention的输入)

综合词嵌入和位置嵌入信息,我们可以得到下面的公式
$$
\begin{align}
\boldsymbol{x} = \boldsymbol{x}_{WE} + \boldsymbol{x}_{PE}
\end{align}
$$
- $\boldsymbol{x}$ 为输入层经过词嵌入和位置嵌入后的输出, 也就是Attention的输入
- $\boldsymbol{x}_{WE}$ 指词嵌入的结果
- $\boldsymbol{x}_{PE}$ 指位置嵌入的结果

FFN

FFN，Feed Forward Network，前馈网络层
$$
FFN(\mathbf{X}) = ReLU(\mathbf{X}\mathbf{W}^U + \mathbf{b}_1)\mathbf{W}^D + \mathbf{b}_2
$$
原始 Transformer 使用的是 ReLU 作为激活函数，现在很多时候也会选用 sigmoid
可以看到前馈神经网络包含了两层
注：原始 Transformer 论文中，使用的 $H = d_\text{model} = 512$，$d_{ff} = 2048$，FFN 中间隐藏维度是 $d_\text{model} = 512$ 的 4 倍
- 即 FFN 的参数量为：$2 \times 4H \times H = 8H^2$

Layer Normalization

层归一化，是Transformer特有的一种归一化方法
Batch Normalization(BN)不适用与Transformer中，至少有以下原因：
- Transformer训练样本通常（特别是模型很大时）可能会比较小，在Batch较小时BN不再适用
- BN是按照token维度（特征维度）来归一化的，不利于处理变长输入序列
  $$
  LayerNorm(\mathbf{x}) = \frac{\mathbf{x}-\mathbf{\mu}}{\mathbf{\sigma}}\cdot \mathbf{\gamma} + \mathbf{\beta} \\
  \mathbf{\mu} = \frac{1}{H}\sum_{i=1}^H x_i, \quad \mathbf{\sigma} = \sqrt{\frac{1}{H}\sum_{i=1}^H(x_i-\mathbf{\mu})^2} \\
  $$
代码实现是会在分母的更号内增加一个极小量 $\epsilon$，防止出现除0的情况
显然，LayerNorm是基于token来归一化的，当前token的归一化结果与其他token无关，不受其他token影响
可能出现不同的token向量LayerNorm归一化以后输出相同的值，比如[1,2,3,4]、[2,3,4,5]和[2,4,6,8]的输出结果都相同
- 可以看到是因为这些向量维度之间的分布很相似，或者呈现倍数关系，才导致输出值为0，实际模型中，维度一般是64维或者128维等，而且是小数，几乎不会出现两个不同的token经过LayerNorm后输出相同的值

LN是token维度的

按照Transformer源码实现来看，LayerNorm是Token维度的，不是Seq维度，也就是说，token向量LayerNorm的结果只与token向量自身相关，与所在序列的其他token无关
- 这一点是Decoder可以增量解码的关键，这一点保证了Decoder的前序词不会受到后续词的影响
- 增量解码是指：Decoder中输出下一个词时，可以使用前序词的缓存结果，由于前面的词看不到后面的词，所以增加词前后Transformer-Decoder中前序每个词的输出在每一层都不会受到影响

一个LayerNorm的示例如下，Transformer源码中实现与这个类似

import torch.nn as nn
import torch

# 假设d_model=4，d_model在有些实现中为hidden_size
layer_norm = nn.LayerNorm(4) # 这里使用LayerNorm，也可以使用RMSNorm，两者作用维度相同，只是公式不同
# test case 1:
input_tensor = torch.Tensor([[[1, 2, 3, 4],
                              [2, 3, 4, 5]]])
output_tensor = layer_norm(input_tensor)
print(output_tensor)
# output:
# tensor([[[-1.3416, -0.4472,  0.4472,  1.3416],
#          [-1.3416, -0.4472,  0.4472,  1.3416]]],
#        grad_fn=<NativeLayerNormBackward0>)

# test case 2:
input_tensor = torch.Tensor([[[1, 2, 3, 4],
                              [200, 3, 4, 5]]])
output_tensor = layer_norm(input_tensor)
print(output_tensor)

# tensor([[[-1.3416, -0.4472,  0.4472,  1.3416],
#          [ 1.7320, -0.5891, -0.5773, -0.5655]]],
#        grad_fn=<NativeLayerNormBackward0>)

从示例中可以看出：
- 修改第二个token的某个元素值，只影响第二个token的LN输出，不影响第一个token

Transformer改进-LN

原始LN参见论文之前的内容

LN的改进——RMSNorm

RMSNorm 的公式如下：
$$
\begin{align}
RMSNorm(\mathbf{x}) &= \frac{\mathbf{x}-\mathbf{\mu}}{RMS(\mathbf{x})}\cdot \mathbf{\gamma} \\
RMS(\mathbf{x}) &= \sqrt{\frac{1}{H}\sum_{i=1}^H x_i^2} \\
\end{align}
$$
- 代码实现是会在分母的更号内增加一个极小量 $\epsilon$，防止出现除 0 的情况
- 其中 $\mu$ 和 $\gamma$ 是可学习参数，但一般的实现中没有 $\mu$，只有一个参数 $\gamma$

截止到24年，PyTorch 官方还没有提供标准的 RMSNorm 实现，下面是 HuggingFace Transformers 中的实现：

@use_kernel_forward_from_hub("RMSNorm")
class LlamaRMSNorm(nn.Module):
	def __init__(self, hidden_size, eps=1e-6):
		"""
		LlamaRMSNorm is equivalent to T5LayerNorm
		"""
		super().__init__()
		self.weight = nn.Parameter(torch.ones(hidden_size))
		self.variance_epsilon = eps

	def forward(self, hidden_states):
		input_dtype = hidden_states.dtype
		hidden_states = hidden_states.to(torch.float32)
		variance = hidden_states.pow(2).mean(-1, keepdim=True)
		hidden_states = hidden_states * torch.rsqrt(variance + self.variance_epsilon)
		return self.weight * hidden_states.to(input_dtype)

	def extra_repr(self):
		return f"{tuple(self.weight.shape)}, eps={self.variance_epsilon}"

LN的改进——DeepNorm

$$
DeepNorm(\mathbf{x}) = LayerNorm(\alpha\cdot \mathbf{x} + \text{Sublayer}(\mathbf{x})) \\
$$

这里的 $\text{Sublayer}(\mathbf{x})$ 是指Transformer中的前馈神经网络层或自注意力模块（两者都会作为LN的输入）
实际上，原始的Transformer中，每次LN的内容都是加上残差的，这里根据归一化位置的不同还有会有不同的实现
原始的Transformer中，相当于 $\alpha=1$ 的DeepNorm
这里叫做DeepNorm的原因是因为缩放残差 $\mathbf{x}$ 可以扩展Transformer的深度，有论文提到利用该方法可将深度提升到1000层（DeepNet: Scaling Transformers to 1,000 Layers）

归一化的位置

归一化的位置包括Post-Norm、Pre-Norm和Sandwich-Norm等
Post-Norm
- 原始Transformer使用的方法
- 将归一化模块使用到加法（需要把残差加到FFN/MHA的输出上）之后，详细公式是：
  $$
  \text{Post-Norm}(\mathbf{x}) = Norm(\mathbf{x} + \text{Sublayer}(\mathbf{x}))
  $$
- $\text{Sublayer}$
Pre-Norm
- 归一化模块放到FFN/MHA之前，详细公式是：
  $$
  \text{Pre-Norm}(\mathbf{x}) = \mathbf{x} + \text{Sublayer}(Norm(\mathbf{x}))
  $$
Sandwich_Norm
- 三明治归一化，从字面意思可以知道，是两个Norm将某个层夹起来，实际上，该层是前馈神经网络层或自注意力模块
  $$
  \text{Sandwish-Norm}(\mathbf{x}) = \mathbf{x} + Norm(\text{Sublayer}(Norm(\mathbf{x})))
  $$

归一化位置的比较

DeepNet: Scaling Transformers to 1,000 Layers中也有有关Pre-Norm和Post-Norm的探讨

一般来说，使用Post-Norm比较多，效果也更好
Pre-Norm在深层Transformer中容易训练（容易训练不代表效果好，Pre-Norm的拟合能力一般不如Post-Norm）
- 所以有些模型还是会使用Pre-Norm，因为它更稳定
浅层中建议使用Post-Norm
详情参考苏神的回答为什么Pre Norm的效果不如Post Norm？，其中引用到了如何评价微软亚研院提出的把 Transformer 提升到了 1000 层的 DeepNet？ - 唐翔昊的回答 - 知乎

Pre Norm的深度有“水分”！也就是说，一个 L 层的Pre Norm模型，其实际等效层数不如 L 层的Post Norm模型，而层数少了导致效果变差了
Pre Norm结构无形地增加了模型的宽度而降低了模型的深度，而我们知道深度通常比宽度更重要，所以是无形之中的降低深度导致最终效果变差了
直观上来说就是：
- Pre-Norm 是（不严谨的变换）近似将深度转换成了宽度
  $$
  \begin{align}
  \mathbf{x}_{t+1} &= \mathbf{x}_t + f(Norm(\mathbf{x}_t)) \\
  &= \mathbf{x}_{t-1} + f(Norm(\mathbf{x}_{t-1})) + f(Norm(\mathbf{x}_t)) \\
  &\approx \mathbf{x}_{t-1} + 2f(Norm(\mathbf{x}_{t}))
  \end{align}
  $$
  - 注：这里大家认为可假定在 $t$ 较大时， $\mathbf{x}_t$ 和 $\mathbf{x}_{t-1}$ 是基本相似的
  - 我们称 $x_1,x_2,\cdots,x_t$ 为主干，在 Pre-Norm 中，主干一直在加入新的东西，所以方差越来越大，且单层网络对主干的影响越来越小
  - 此外，如何评价微软亚研院提出的把 Transformer 提升到了 1000 层的 DeepNet？ - 唐翔昊的回答 - 知乎中还认为不同层的 $f$ （MHA 或 FFN）在统计上是相似的
    - TODO：这一点有待考证和理解
- Post-Norm 则是保持深度
  $$
  \begin{align}
  \mathbf{x}_{t+1} &= Norm(\mathbf{x}_t + f(\mathbf{x}_t)) \\
  &= Norm(Norm(\mathbf{x}_{t-1} + f(\mathbf{x}_{t-1})) + f(\mathbf{x}_t))
  \end{align}
  $$
  - Post-Norm 中，保证了主干方差是恒定的

Transformer改进-激活函数

原始激活函数是ReLU(Rectified Linear Unit)

Swish（SiLU）

参考文章：Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning
Swish 的全称为 “Scaled Exponential Linear Unit with Squishing Hyperbolic Tangent”,直译为“带有压缩的缩放指数线性单元”
$$
\text{Swish}_\beta(x) = x \cdot sigmoid(\beta x)
$$
- 许多实现中常常设置 $\beta=1$
注：Swish, 简称为 Sigmoid-weighted Linear Unit，所以一些文章中也称为 SiLU，

GELU

GELU, Gaussion Error Linear Unit，有时候也写作GeLU
$$
\text{GELU}(x) = 0.5x \cdot [1+\text{erf}(\frac{x}{\sqrt{2}})], \quad \text{erf}(x) = \frac{2}{\sqrt{\pi}}\int_1^x e^{-t^2} dt
$$
- erf 是 Gauss Error function 的缩写，在很 Torch 和 TensorFlow 中都是定义好的
从公式可以看出GELU的本质是对一个正太分布的概率密度函数进行积分，实际上就是累积分布函数
GELU和ReLU的比较如下（图片来自简单理解GELU 激活函数）：

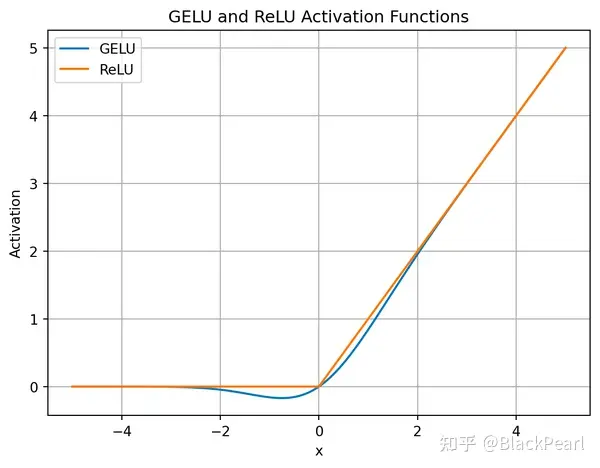
FastGELU

FastGELU, Fast Gaussion Error Linear Unit，出自论文 CodeGeeX: A Pre-Trained Model for Code Generation with Multilingual Benchmarking on HumanEval-X, KDD 2024, THU & Huawei，该方案作为 GELU 的近似，在升腾 910 芯片上能加速
$$ \text{FastGELU}(X_i) = \frac{X_i}{1+\exp(-1.702*|X_i|) \cdot \exp(0.851\cdot (X_i - |X_i|))} $$
FastGELU vs GELU图像对比如下：
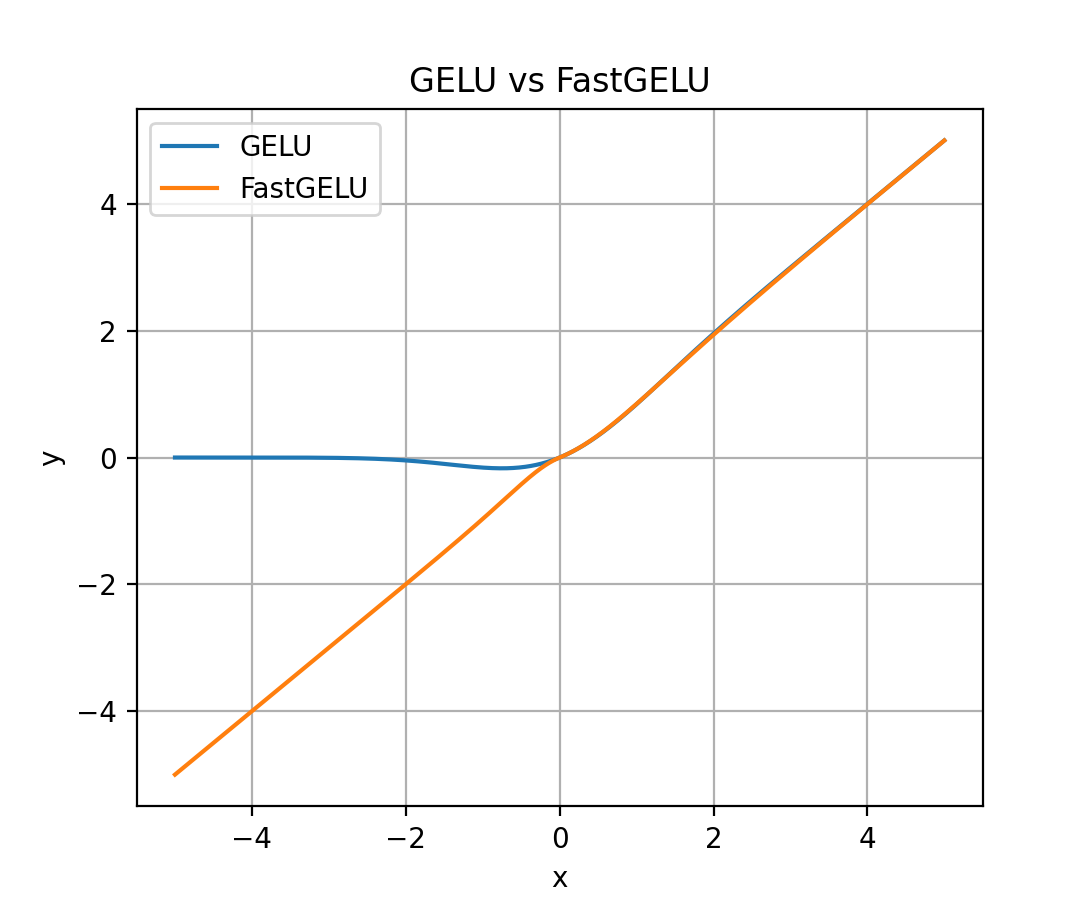
从图中可以看出：$x$ 在 0 附近，以及 $x \geq 0$ 时，FastGELU 和 GELU 的曲线几乎一致（未完全重合）

补充：GLU及其变换

GLU，Gated Linear Units，是一种利用门的思想实现的激活函数，该激活函数可以理解为对输入进行门控选择，一些维度的值可以通过门，一些则不可以，门一般是一个基础的非线性激活函数
原始GLU形式如下：
$$
GLU = \sigma(\mathbf{W}_1\mathbf{x} + \mathbf{b}_1) \odot (\mathbf{W}_2\mathbf{x} + \mathbf{b}_2)
$$
$\sigma$ 可以替换成其他非线性激活函数
- 注意整个公式中始终只有一个非线性激活函数，其他部分都是线性映射（线性激活函数）
$\odot$ 表示矩阵按照元素相乘， $W_1,W_2,b_1,b_2$ 是可学习的参数
该激活函数非常特殊，首先使用两个权重矩阵对输入数据进行线性变换，然后通过sigmoid激活函数进行非线性变换。这种设计使得GLU在前馈传播过程中能够更好地捕捉输入数据的非线性特征，从而提高模型的表达能力和泛化能力
原始论文GLU Variants Improve Transformer中也写作下面的形式(其中 $W,V,b,c$ 是可学习的参数)：
$$
GLU(\mathbf{x,W,V,b,c}) = \sigma(\mathbf{W}\mathbf{x} + \mathbf{b}) \odot (\mathbf{V}\mathbf{x} + \mathbf{c})
$$
去掉激活函数的版本也叫作Bilinear，写作
$$
Bilinear(\mathbf{x,W,V,b,c}) = (\mathbf{W}\mathbf{x} + \mathbf{b}) \odot (\mathbf{V}\mathbf{x} + \mathbf{c})
$$
其他相关形式
$$
ReGLU(x, W, V, b, c) = max(0, xW + b) \odot (xV + c) \\
GEGLU(x, W, V, b, c) = GELU(xW + b) \odot (xV + c) \\
SwiGLU(x, W, V, b, c, \beta) = Swish_\beta(xW + b) \odot (xV + c) \\
$$

补充：FFN激活函数形式

FFN的ReLU激活函数形式
$$
\text{FFN}(x, W_1, W_2, b_1, b_2) = max(0, xW_1 + b_1)W_2 + b_2
$$
为了表示方便，也因为在一些文章中使用了简化，后续该形式会被简化成没有偏置项(bias)的形式：
$$
\text{FFN}_{ReLU}(x, W_1, W_2) = max(xW_1, 0)W_2
$$

FFN各种激活函数形式

常用FFN的激活函数改进有，GLU,Bilinear,ReGLU,GEGLU(GeGLU),SwiGLU等
$$
\begin{align}
\text{FFN}_{GLU}(x, W, V, W_2) &= (\sigma(xW) \odot xV )W_2 \\
\text{FFN}_{Bilinear}(x, W, V, W_2) &= (xW \odot xV )W_2 \\
\text{FFN}_{ReGLU}(x, W, V, W_2) &= (max(0, xW) \odot xV )W_2 \\
\text{FFN}_{GEGLU}(x, W, V, W_2) &= (GELU(xW) \odot xV )W_2 \\
\text{FFN}_{SwiGLU}(x, W, V, W_2) &= (Swish_1(xW) \odot xV )W_2 \\
\end{align}
$$
可以理解为 $\mathbf{W}^G,\mathbf{W}^U$ 中包含了偏置项 $\mathbf{b}$，有些文章/模型中则会将偏置项 $\mathbf{b}$ 去掉
最常用的是SwiGLU
从形式上看，可以知道相对原始FFN激活函数形式，SwiGLU等改进增加了一个参数矩阵，为了保证原始参数数量不变，原始论文GLU Variants Improve Transformer中提出了一种方法，通过将矩阵设置为如下的大小来保证参数数量相等
- 原始FFN层参数为(下面 $d = d_{model}$ 是模型的隐藏层大小，注意，同一层的不同token是共享FFN的):
  $$
  W_1^{d\times d} + W_2^{d\times d}
  $$
- 使用SwiGLU且对齐参数数量后
  $$
  W^{r\times d} + V^{d\times r} + W_{2}^{r\times d}
  $$
- 显然，当 $r=\frac{2}{3}d$ 时，使用 SwiGLU 前后FFN层参数数量相同，都等于 $2d^2$
一个疑问：原始的SwiGLU函数会引入两个参数矩阵 $W,V$，原始的FFN包含两个参数矩阵 $W_1, W_2$，为什么两者结合以后只剩下 $\text{FFN}_{SwiGLU}$ 只剩三个参数 $W,V,W_2$ 呢？
- 回答：因为两个线性矩阵相乘，可以合并为 $W = WV$，虽然还叫做 $W$，但实际上是多了一个矩阵乘进去的，线上训练时也只需要训练这一个矩阵即可

Transformer总结

Transformer是一个特征提取能力非常强(超越LSTM)的特征提取器
一些讨论
- Transformer与CNN没关系,但是Transformer中使用多个 Scaled Dot-Product Attention 来最后拼接的方法(Multi-Head Attention), 就是CNN的多个卷积核的思想
- Transformer论文原文中提到的残差结构也来源于CNN
- 无法对位置信息进行很好地建模，这是硬伤。尽管可以引入Position Embedding，但我认为这只是一个缓解方案，并没有根本解决问题。举个例子，用这种纯Attention机制训练一个文本分类模型或者是机器翻译模型，效果应该都还不错，但是用来训练一个序列标注模型（分词、实体识别等），效果就不怎么好了。那为什么在机器翻译任务上好？我觉得原因是机器翻译这个任务并不特别强调语序，因此Position Embedding 所带来的位置信息已经足够了，此外翻译任务的评测指标BLEU也并不特别强调语序
- Attention如果作为一个和CNN,RNN平级的组件来使用,可能会集成到各自的优点, 而不是”口气”很大的 “Attention is All You Need”

附录：关于 Dropout

在 Transformer 原始论文中，在每个 sub-layer 的输出上使用了 Dropout，即输出被加到 sub-layer 的输入和归一化前进行 Dropout，称为 Residual Dropout
同时，原始论文还在 Embedding 和位置编码的和上使用了 Dropout（包括 Encoder 和 Decoder）
$P_\text{drop} = 0.1$

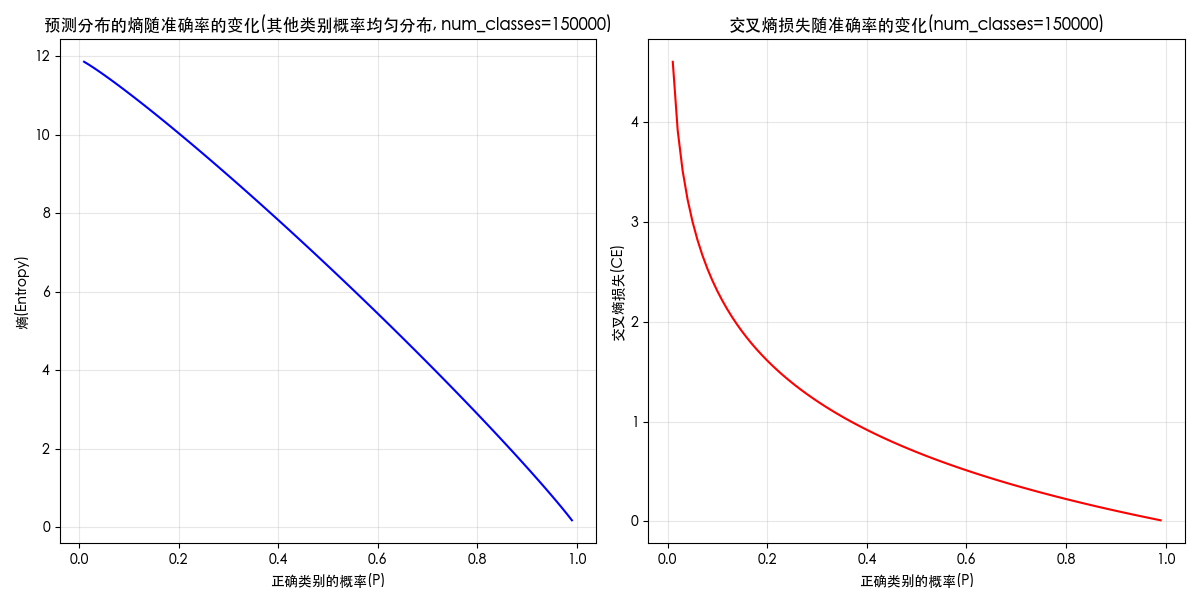
附录：熵、损失和概率的关系图

关键词：entropy curve；loss curve；熵和概率；概率和熵；熵和损失；损失和熵；损失和概率；概率和损失；曲线图；

展示三者关系的代码如下（正确类别分配指定概率（横轴），其余均匀分配剩余概率）：

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]

def entropy(prob_dist):
	"""计算概率分布的熵"""
	# 避免log(0)的情况
	prob_dist = np.clip(prob_dist, 1e-10, 1.0)
	return -np.sum(prob_dist * np.log(prob_dist))

def cross_entropy(true_dist, pred_dist):
	"""计算两个概率分布之间的交叉熵"""
	# 避免log(0)的情况
	pred_dist = np.clip(pred_dist, 1e-10, 1.0)
	return -np.sum(true_dist * np.log(pred_dist))

num_classes = 100000 # 分类问题数

# 创建一个真实分布（one-hot编码，表示第500类为正确类别）
true_dist = np.zeros(num_classes)
true_dist[499] = 1.0  # 索引从0开始，第500类

# 计算真实分布的熵（应该为0，因为是确定的）
true_entropy = entropy(true_dist)
print(f"真实分布的熵: {true_entropy:.6f}")

# 生成一系列预测分布，从非常不准确到非常准确
num_steps = 100
accuracies = np.linspace(0.01, 0.99, num_steps)
entropies = []
cross_entropies = []

for acc in accuracies:
	# 创建预测分布：正确类别分配acc的概率，其余均匀分配剩余概率
	pred_dist = np.ones(num_classes) * ((1.0 - acc) / (num_classes - 1))
	pred_dist[499] = acc

	# 计算熵和交叉熵
	entropies.append(entropy(pred_dist))
	cross_entropies.append(cross_entropy(true_dist, pred_dist))

# 绘制结果
plt.figure(figsize=(12, 6))

plt.subplot(1, 2, 1)
plt.plot(accuracies, entropies, 'b-')
plt.title('预测分布的熵随准确率的变化')
plt.xlabel('正确类别的概率')
plt.ylabel('熵')
plt.grid(True, alpha=0.3)

plt.subplot(1, 2, 2)
plt.plot(accuracies, cross_entropies, 'r-')
plt.title('交叉熵损失随准确率的变化')
plt.xlabel('正确类别的概率')
plt.ylabel('交叉熵损失')
plt.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

print("\nExample:")
example_acc = 0.8
pred_dist = np.ones(num_classes) * ((1.0 - example_acc) / (num_classes - 1))
pred_dist[499] = example_acc

print(f"当正确类别的概率为 {example_acc} 时:")
print(f"预测分布的熵: {entropy(pred_dist):.6f}")
print(f"交叉熵损失: {cross_entropy(true_dist, pred_dist):.6f}")

当类别为 1000 时，图像如下
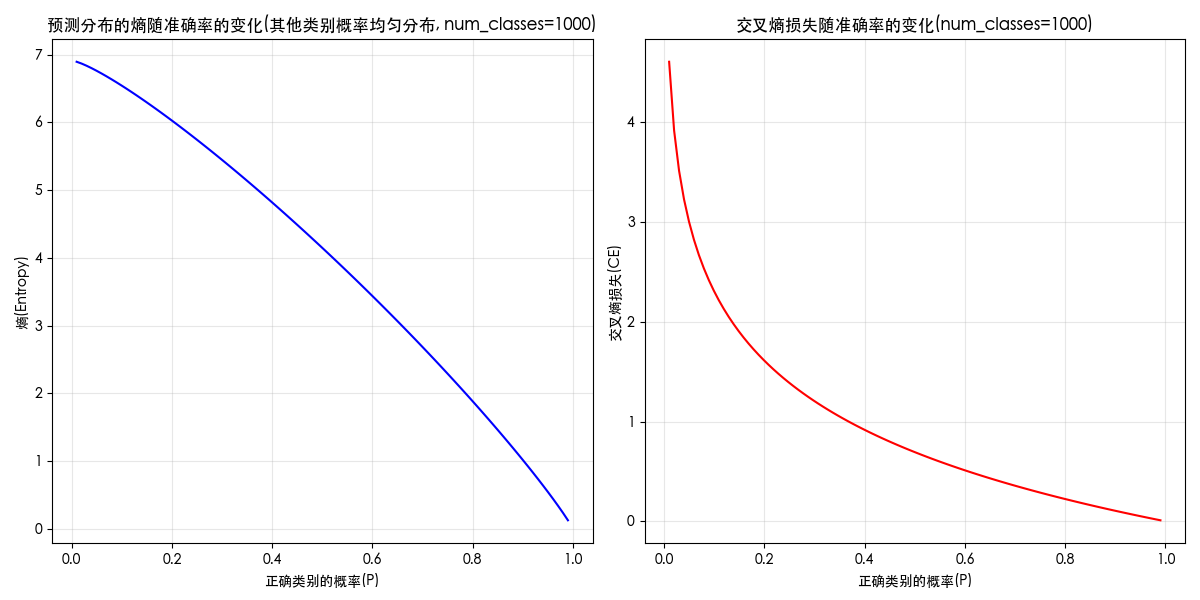
当类别为 10000 时，图像如下
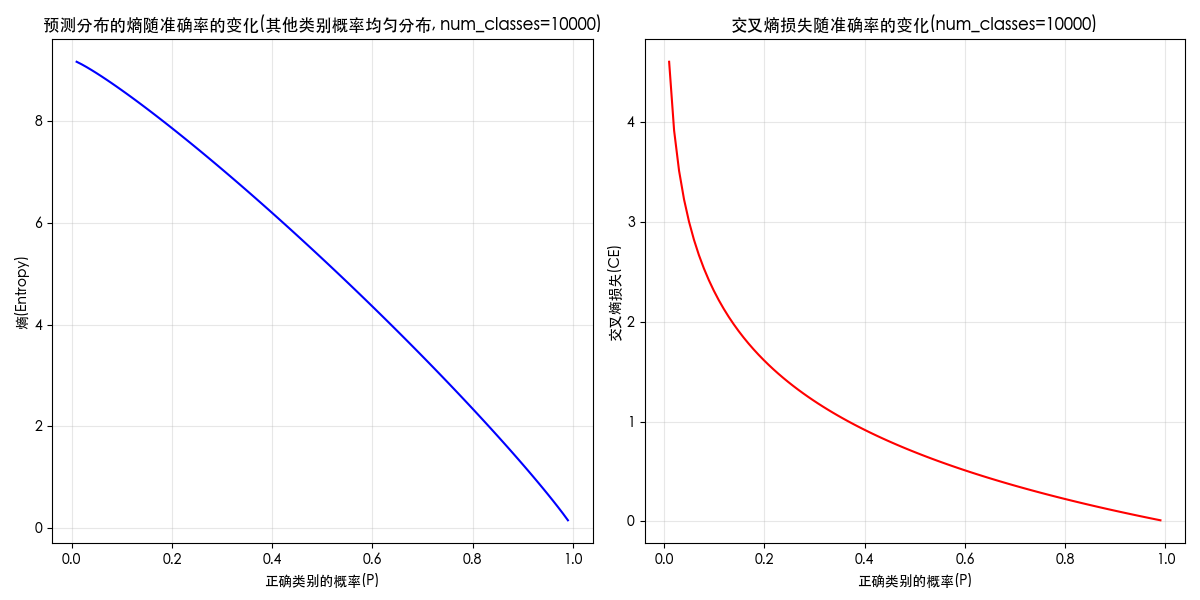
当类别为 100000 时，图像如下
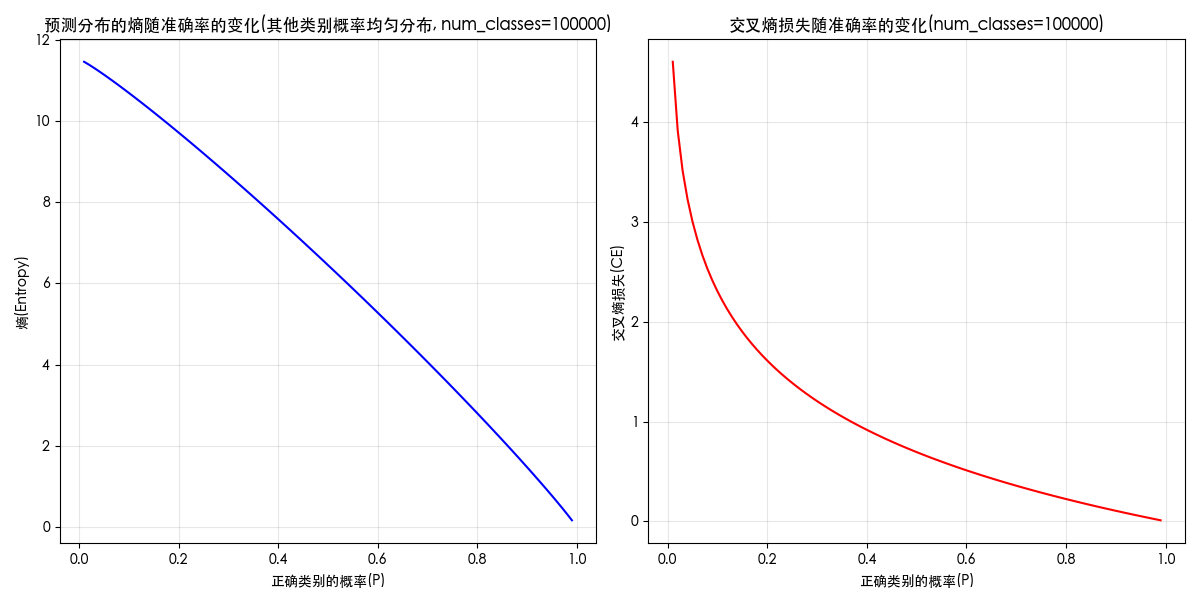
当类别为 150000 时，图像如下

DL——Transformer

相关论文介绍

相关博客介绍

Transformer讲解

Transformer是什么?

Transformer中的Attention

Multi-Head Attention

有关Multi-Head Attention的理解

Self Attention

Transformer中的Attention

Masked Multi-Head Attetion

Cross Multi-Head Attention

Transformer 输入层

Word Embedding

Position Embedding

与之前的Position Embedding的区别

输入层的输出(Attention的输入)

FFN

Layer Normalization

LN是token维度的

Transformer改进-LN

LN的改进——RMSNorm

LN的改进——DeepNorm

归一化的位置

归一化位置的比较

Transformer改进-激活函数

Swish（SiLU）

GELU

FastGELU

补充：GLU及其变换

补充：FFN激活函数形式

FFN各种激活函数形式

Transformer总结

附录：关于 Dropout

附录：熵、损失和概率的关系图