- 参考链接:
- 原始博客(Muon 最早出自该博客):kellerjordan.github.io/posts/muon, Muon: An optimizer for hidden layers in neural networks, 20241208
- 苏神的解读:Muon优化器赏析:从向量到矩阵的本质跨越,注:苏神博客中写的方案与原始博客方案不完全相同,增加了一些技巧
- Muon 的改进论文:Muon is Scalable for LLM Training, 20250224, Moonshot AI
- 本文以解读这篇论文为主
整体讨论
- 在 AdamW 已经大行其道的今天(24年底),已经很少有人在优化器上下功夫了,Muon (MomentUm Orthogonalized by Newton-Schulz) 就是其中一个不可多得的优秀方法
- Muon 最早由 Keller Jordan 2024年12月8日 在其博客 Muon: An optimizer for hidden layers in neural networks 中发表,后在业内引起了广泛讨论
《Muon is Scalable for LLM Training》 Paper Summary
- 基于矩阵正交化(Matrix Orthogonalization)的 Muon 优化器(2024)在小规模语言模型训练中表现出色,但其在大规模模型上的可扩展性尚未得到验证
- 论文发现了两种关键技术可以扩展 Muon:
- (1)加入权重衰减(weight decay)
- (2)精心调整每个参数的更新尺度
- 这些技术改进让 Muon 能够直接用于大规模训练,而无需调整超参数
- 扩展定律实验表明,在计算最优训练条件下,Muon 的计算效率比 AdamW 高约 2 倍
- 基于这些改进,论文推出了 Moonlight,这是一个使用 Muon 训练、包含 3B/16B 参数的 MoE 模型,训练数据量为 5.7T tokens
- 论文的模型改进了当前的帕累托前沿(Pareto frontier) ,在更少的训练浮点运算(FLOPs)下实现了更好的性能
- 论文开源了分布式 Muon 实现,该实现内存最优且通信高效(特别地:还发布了预训练、指令微调及中间检查点)
Introduction and Discussion
- LLM (2024;DeepSeek-2024;2024;2024)的快速发展显著推动了通用人工智能的进步
- 由于扩展定律(2020;2022)的存在,训练强大的 LLM 仍然是一个计算密集且资源需求高的过程
- 优化器在高效训练 LLM 中扮演着关键角色,其中 Adam(2015)及其变体 AdamW(2019)是大多数大规模训练的标准选择
- 近期优化算法的发展显示出超越 AdamW 的潜力(2024;2024;2024;2025;2018a;2018b;2024;2022;2024;2025)
- 其中,K. Jordan 等人(2024)提出了 Muon ,它通过牛顿-舒尔茨迭代(Newton-Schulz iteration)使用正交化梯度动量(orthogonalized gradient momentum)更新矩阵参数
- Muon 在小规模语言模型训练中的初步实验表现出色,但正如这篇博客(Muon: An optimizer for hidden layers in neural networks, 20241208)所讨论的,仍存在几个关键挑战未解决:
- (1)如何将基于矩阵正交化的优化器有效扩展到具有数十亿参数、训练数据量达数万亿 tokens 的大模型;
- (2)如何在分布式环境中计算近似正交化;
- (3)此类优化器是否能泛化到不同训练阶段,包括预训练和监督微调(Supervised Finetuning, SFT)
- 在本技术报告中,论文通过系统性研究解决了这些挑战
- 论文的工作基于 Muon,同时通过分析解决了其在大规模训练场景中的局限性。论文的技术贡献包括:
- Muon 有效扩展的分析(Analysis for Effective Scaling of Muon) :
- 通过广泛分析,论文发现权重衰减对 Muon 的可扩展性至关重要
- 论文提出了对 Muon 参数级更新规则的尺度调整
- 这些调整使得 Muon 无需超参数调优即可直接使用,并显著提高了训练稳定性
- 高效的分布式实现(Efficient Distributed Implementation) :
- 论文开发了基于 ZeRO-1(2020)风格的分布式 Muon 版本,实现了最优内存效率和降低的通信开销,同时保留了算法的数学特性
- 扩展定律验证(Scaling Law Validation) :
- 论文进行了扩展定律研究,比较 Muon 与强基线 AdamW,结果显示 Muon 性能更优(图 1a)
- 根据扩展定律结果,Muon 在仅需约 52% 的训练 FLOPs 时,即可达到与 AdamW 训练模型相当的性能
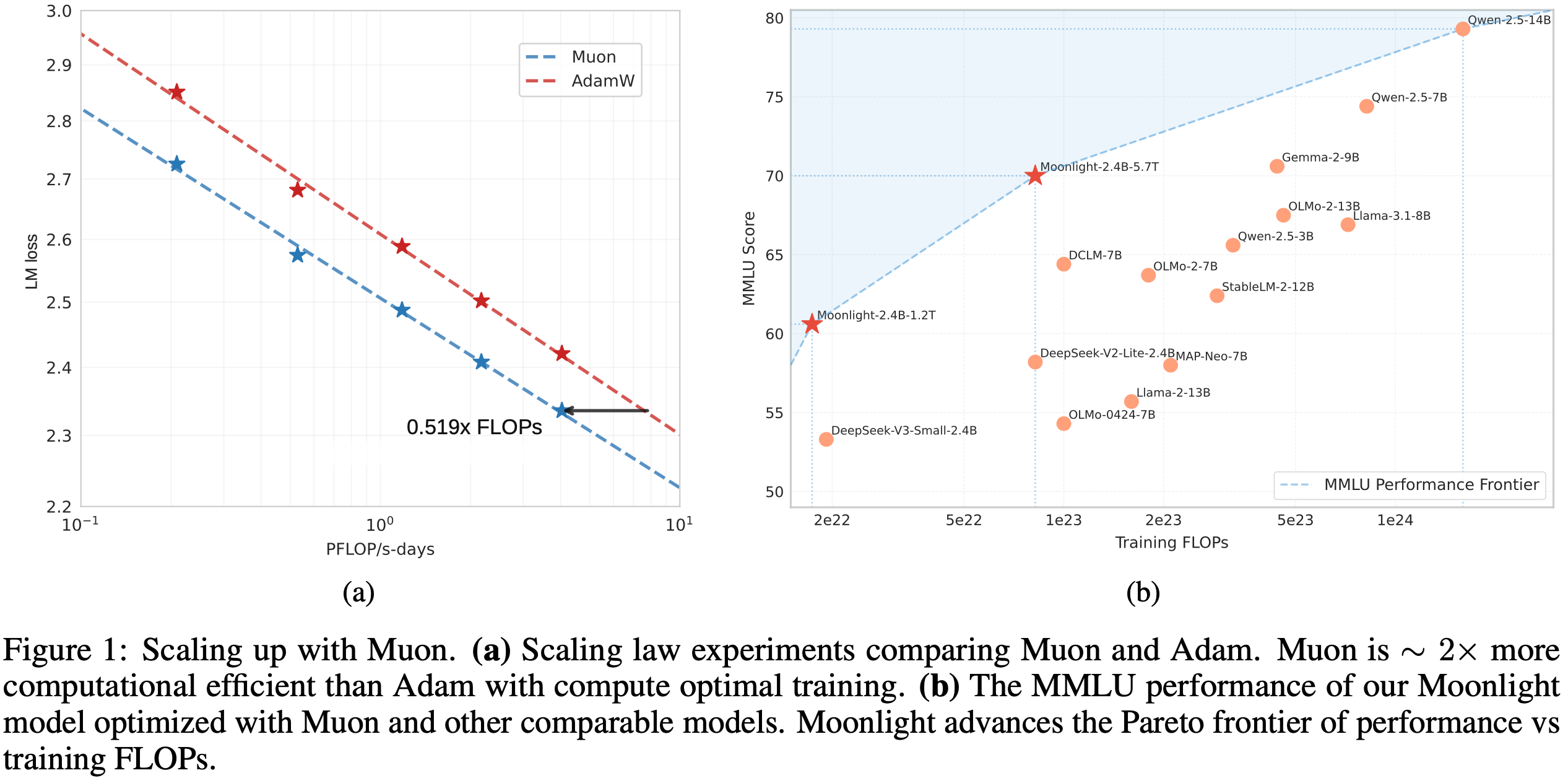
- Muon 有效扩展的分析(Analysis for Effective Scaling of Muon) :
- 论文的全面实验表明,Muon 可以有效地替代 AdamW 作为大规模 LLM 训练的实际优化器,在训练效率和模型性能上均带来显著提升
- 基于这项工作,论文发布了 Moonlight,这是一个使用 Muon 训练的 16B 参数 MoE 模型,同时开源了实现代码和中间训练检查点,以促进 LLM 可扩展优化技术的进一步研究
Methods
Background
Muon 优化器 Muon(2024)是一种针对矩阵参数优化的神经网络优化器
在迭代步 \( t \) 时,给定当前权重 \(\mathbf{W}_{t-1}\)、动量 \(\mu\)、学习率 \(\eta_t\) 和目标函数 \(\mathcal{L}_t\),Muon 的更新规则如下:
$$
\begin{split}
\mathbf{M}_t &= \mu\mathbf{M}_{t-1} + \nabla\mathcal{L}_t(\mathbf{W}_{t-1}) \\
\mathbf{O}_t &= \text{Newton-Schulz}(\mathbf{M}_t)^{\mathrm{i} } \\
\mathbf{W}_t &= \mathbf{W}_{t-1} - \eta_t\mathbf{O}_t
\end{split} \tag{1}
$$- 其中,\(\mathbf{M}_t\) 是第 \( t \) 步的梯度动量(初始时 \(\mathbf{M}_0\) 为零矩阵)
- 在公式1中,Newton-Schulz 迭代过程(2024)用于近似计算 \((\mathbf{M}_t\mathbf{M}_t^{\mathrm{T} })^{-1/2}\mathbf{M}_t\)
- 设 \(\mathbf{M}_t\) 的奇异值分解(SVD)为 \(\mathbf{U}\boldsymbol{\Sigma}\mathbf{V}^{\mathrm{T} }\),则 \((\mathbf{M}_t\mathbf{M}_t^{\mathrm{T} })^{-1/2}\mathbf{M}_t = \mathbf{U}\mathbf{V}^{\mathrm{T} }\),即将 \(\mathbf{M}_t\) 正交化
- 直观上,正交化能确保更新矩阵是同构的,避免权重沿少数主导方向学习(2024)
Newton-Schulz 迭代的矩阵正交化(Newton-Schulz Iterations for Matrix Orthogonalization) :公式1通过迭代过程计算
- 初始时,设:
$$\mathbf{X}_0 = \mathbf{M}_t / |\mathbf{M}_t|_{\mathrm{F} }$$- 注:\(|\mathbf{M}_t|_{\mathrm{F}}\) 是 F 范数,在 PyTorch 中的实现为
M.norm(),定义如下:
$$ |A|_F = \sqrt{\sum_{i=1}^{m} \sum_{j=1}^{n} |a_{ij}|^2} $$
- 注:\(|\mathbf{M}_t|_{\mathrm{F}}\) 是 F 范数,在 PyTorch 中的实现为
- 在每步迭代 \( k \) 中,按以下方式更新 \(\mathbf{X}_k\):
$$
\mathbf{X}_k = a\mathbf{X}_{k-1} + b(\mathbf{X}_{k-1}\mathbf{X}_{k-1}^{\mathrm{T} }) \mathbf{X}_{k-1} + c(\mathbf{X}_{k-1}\mathbf{X}_{k-1}^{\mathrm{T} })^{2} \mathbf{X}_{k-1} \tag{2}
$$- 其中,\(\mathbf{X}_N\) 是经过 \( N \) 次迭代后的结果,\( a \)、\( b \)、\( c \) 为系数
- 为确保公式2正确收敛,需调整系数使多项式 \( f(x) = ax + bx^{3} + cx^{5} \) 在 1 附近有固定点
- 在Jordan等人(2024)的原始设计中,系数设为 \( a=3.4445 \)、\( b=-4.7750 \)、\( c=2.0315 \),以加速小初始奇异值的收敛(论文沿用这一设置)
- 原始博客 Muon: An optimizer for hidden layers in neural networks, 20241208 中 Newton-Schulz 算法的实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15# Pytorch code
def newtonschulz5(G, steps=5, eps=1e-7):
assert G.ndim == 2
a, b, c = (3.4445, -4.7750, 2.0315)
X = G.bfloat16()
X /= (X.norm() + eps)
if G.size(0) > G.size(1):
X = X.T
for _ in range(steps):
A = X @ X.T
B = b * A + c * A @ A
X = a * X + B @ X
if G.size(0) > G.size(1):
X = X.T
return X
- 初始时,设:
范数约束下的最速下降法(Steepest Descent Under Norm Constraints)
- Bernstein等人(2024)提出将深度学习优化过程视为范数约束下的最速下降
- 注:最速下降法(Steepest Descent Method)和共轭梯度法(Conjugate Gradient Method, CG)类似,都是求解无约束最优化问题的优化方法
- 从这一视角看,Muon 与 Adam(2015;2019)的区别在于范数约束的不同:
- Adam 是动态调整的 Max-of-Max 范数约束下的最速下降,而 Muon 提供的是静态 Schatten-\( p \) 范数约束(Franz,2024)
- 当公式1精确计算时,Muon 的范数约束为谱范数
- 神经网络权重作为输入空间或隐藏空间的算子,通常(局部)是欧几里得的(Cesista,2024),因此权重的范数约束应为诱导算子范数(或矩阵的谱范数)
- 为什么神经网络可以看成算子?
- 从这个意义上说,Muon 的范数约束比 Adam 更合理
- Bernstein等人(2024)提出将深度学习优化过程视为范数约束下的最速下降
Scaling Up Muon
Weight Decay
- 虽然 Muon 在小规模模型上表现优于 AdamW(2024),但作者发现当扩展到更大模型和更多数据时,性能提升会减弱
- 作者观察到权重和层输出的 RMS 值持续增长 ,甚至超出 bf16 的高精度范围,可能损害模型性能
- 为解决这一问题,论文将 AdamW(2019)的标准权重衰减机制引入 Muon:
$$
\mathbf{W}_t = \mathbf{W}_{t-1} - \eta_t(\mathbf{O}_t \color{red}{+ \lambda\mathbf{W}_{t-1}}) \tag{3}
$$ - 通过实验对比带和不带权重衰减的 Muon,论文训练了一个 800M 参数、100B token 的模型(约为最优训练 token 量的 5 倍)
- 图2展示了使用 AdamW、原始 Muon(无权重衰减)和带权重衰减的 Muon 的验证损失曲线
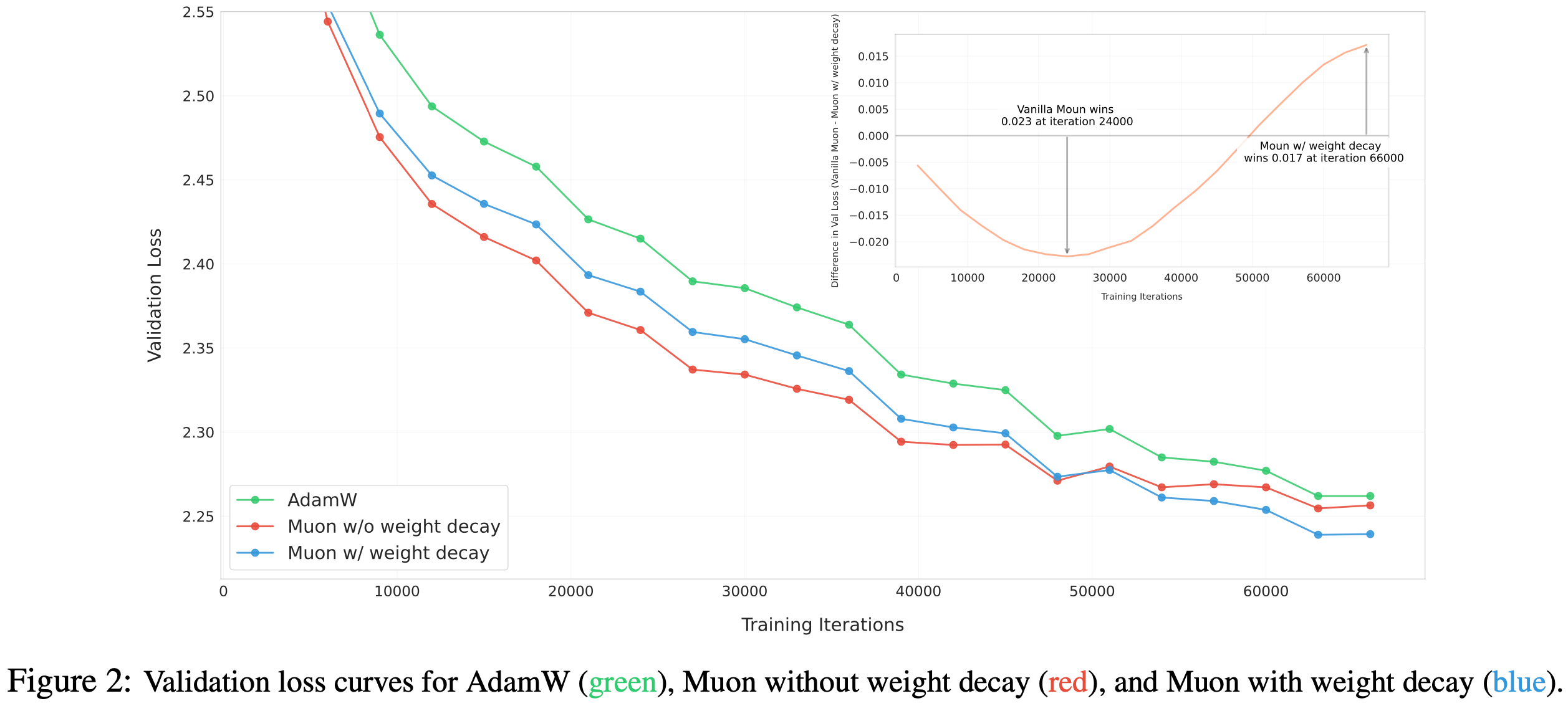
- 原始 Muon 初始收敛更快 ,但部分权重随时间增长过大 ,可能限制模型长期性能
- 加入权重衰减后,Muon 的表现优于原始 Muon 和 AdamW,在 “over-train regime”(过训练区域)中实现了更低的验证损失
- 因此,论文将更新规则调整为公式3 ,其中 \(\lambda\) 为权重衰减比率
Consistent Update RMS
- Adam 和 AdamW(2015;2019)的一个重要特性是其理论更新 RMS 保持在 1 附近
- 但 Muon 的更新 RMS 随参数形状变化,如下引理所示:
- 引理1 :对于形状为 \([A,B]\) 的满秩矩阵参数,其理论 Muon 更新 RMS 为 \(\sqrt{1/\max(A,B)}\)
- 注:\(A\) 和 \(B\) 矩阵的维度,比如 \(A = 4\) 表示 \(4 \times 4\) 大小的矩阵; 而 \(\max(A,B)\) 是一个数字,即 \(A\) 和 \(B\) 中的较大值
- 引理1 的证明和变量含义可见 附录A
- 论文监测了训练中 Muon 的更新 RMS,发现其通常接近上述理论值
- 这种不一致性在扩展模型规模时可能引发问题:
- 当 \(\max(A,B)\) 过大(如稠密 MLP 矩阵)时,更新过小,限制模型表征能力;
- 当 \(\max(A,B)\) 过小(如将 GQA(2019)或 MLA(DeepSeek-2024)中的每个 KV 头视为独立参数)时,更新过大,导致训练不稳定
- 为保持不同形状矩阵间更新 RMS 的一致性,论文提出对每个矩阵的 Muon 更新乘以 \(\sqrt{\max(A,B)}\) 以抵消引理1 的影响
- 第3.1节的实验证明这一策略对优化有益
Matching Update RMS of AdamW
- Muon 专为矩阵参数设计 ,实际训练中 AdamW 用于处理非矩阵参数(如 RMSNorm、LM Head 和 Embedding 参数)
- 作者希望优化器超参数(学习率 \(\eta\)、权重衰减 \(\lambda\))能在矩阵和非矩阵参数间共享
- 自回归模型中,LM Head 通常也只包含一个矩阵权重参数(
d_model x vocab_size维度大小)吧?
- 论文提出将 Muon 的更新 RMS 调整至与 AdamW 相近的范围
- 根据经验观察,AdamW 的更新 RMS 通常在 0.2 至 0.4 之间
- 问题:为什么要将 RMS 调整到 AdamW 相近范围,其他范围不行吗?
- 回答:是从实验验出来的,附录 A 中有实验说明
- 论文基于观察,通过以下公式调整将 Muon 的更新 RMS 缩放至该范围:
$$
\mathbf{W}_t = \mathbf{W}_{t-1} - \eta_t(\color{blue}{0.2 \cdot} \mathbf{O}_t \color{blue}{\cdot \sqrt{\max(A,B)}} + \color{red}{\lambda\mathbf{W}_{t-1}})
$$ - 这一选择的实证验证见附录A
- 此外,调整后 Muon 可直接复用为AdamW调优的学习率和权重衰减
Other Hyper-parameters
- Muon还有两个可调超参数:
- Newton-Schulz 迭代步数 \( N \) :
- 实验发现,当 \( N=10 \) 时,迭代结果比 \( N=5 \) 更精确,但性能未提升
- 因此,论文为效率考虑选择 \( N=5 \)
- 动量 \(\mu\) :
- 动量调优未带来一致性能提升,故沿用 Jordan等人(2024)的 0.95
- Newton-Schulz 迭代步数 \( N \) :
Distributed Muon
ZeRO-1 与 Megatron-LM
- ZeRO-1(2020)技术将昂贵优化器状态(如主权重、动量)分区存储于集群中
- Megatron-LM(2020)将 ZeRO-1 集成到其并行设计中
- 基于 Megatron-LM 的并行策略(如张量并行 TP、流水线并行 PP、专家并行 EP 和数据并行 DP),ZeRO-1 的通信负载从全局收集简化为仅需在数据并行组内收集
Based on Megatron-LM’s sophisticated parallel strategies, e.g. Tensor-Parallel (TP), Pipeline Parallel (PP), Expert Parallel (EP) and Data Parallel (DP), the communication workload of ZeRO-1 can be reduced from gathering all over the distributed world to only gathering over the data parallel group.
Method
- ZeRO-1 对 AdamW 高效,因其按元素计算更新
- 但 Muon 需完整梯度矩阵计算更新,故原始 ZeRO-1 不直接适用于 Muon
- 论文提出基于 ZeRO-1 的分布式 Muon 方案,称为 Distributed Muon,它在DP上分区优化器状态,并引入两项额外操作:
- 1) DP Gather :将本地 DP 分区的主权重(大小为模型权重的 1/DP)对应的分区梯度收集为完整梯度矩阵
- 2) 计算完整更新(Calculate Full Update) :对完整梯度矩阵执行 Newton-Schulz 迭代(如2.1节所述),随后丢弃部分更新矩阵,仅保留与本地参数对应的分区
- Distributed Muon 的实现如算法1所示,新增操作以蓝色标注

Analysis
- 论文从多角度对比 Distributed Muon 与经典 ZeRO-1 分布式 AdamW(简称 Distributed AdamW):
- 内存占用(Memory Usage) :Muon 仅需一个动量缓冲区,AdamW 需两个,故 Muon 的额外内存占用为 AdamW 的一半
- 通信开销(Communication Overhead) :每设备仅需为本地 DP 分区参数 \(\mathbf{p}\) 执行额外 DP 收集,通信成本低于 \(\mathbf{G}\) 的 reduce-scatter 或 \(\mathbf{P}\) 的 all-gather
- 此外,Muon 的 Newton-Schulz 迭代以 bf16 执行,通信开销比 fp32 降低 50%
- 总体而言,Distributed Muon 的通信量为 Distributed AdamW 的 1 至 1.25 倍
- 延迟(Latency) :Distributed Muon 因额外通信和 Newton-Schulz 迭代,端到端延迟高于 Distributed AdamW。但这并非主要问题,因为:
- (a)Newton-Schulz 仅需约 5 次迭代即可获得良好结果(见2.2节);
- (b)优化器导致的延迟仅占模型前向-反向传播时间的 1% 至 3%
- 此外,技术可进一步降低延迟,比如:
- overlapping gather and computation
- overlapping optimizer reduce-scatter with parameter gather
- 在大规模分布式集群中,Distributed Muon 的延迟开销与 AdamW 相当
- 论文将很快向开源 Megatron-LM 提交实现 Distributed Muon 的 PR
Experiments
Consistent Update RMS
- 如第 2.2 节所述,论文的目标是让所有矩阵参数的更新 RMS 保持一致,并与 AdamW 的更新 RMS 匹配
- 论文通过两种方法控制 Muon 的更新 RMS,并与仅保持与 AdamW 一致 RMS 的基线进行比较:
- Baseline :论文将更新矩阵乘以 \(0.2 \cdot \sqrt{H}\)(\(H\) 为模型隐藏层大小),以保持与 AdamW 一致的更新 RMS。注意,对于大多数矩阵,\(\max(A,B)\) 等于 \(H\)
$$
\mathbf{W}_{t} = \mathbf{W}_{t-1} - \eta_{t}(0.2 \cdot \mathbf{O}_{t} \cdot \sqrt{H} + \lambda \mathbf{W}_{t-1})
$$ - 更新归一化(Update Norm) :论文直接对通过牛顿-舒尔茨迭代计算的更新进行归一化,使其 RMS 严格等于 0.2:
$$
\mathbf{W}_{t} = \mathbf{W}_{t-1} - \eta_{t}(0.2 \cdot \mathbf{O}_{t} / \text{RMS}(\mathbf{O}_{t}) + \lambda \mathbf{W}_{t-1})
$$ - 调整学习率(Adjusted LR) :对于每个更新矩阵,论文根据其形状将学习率缩放 \(0.2 \cdot \sqrt{\max(A,B)}\) 倍:
$$
\mathbf{W}_{t} = \mathbf{W}_{t-1} - \eta_{t}(0.2 \cdot \mathbf{O}_{t} \cdot \sqrt{\max(A,B)} + \lambda \mathbf{W}_{t-1})
$$ - 分析 :论文设计了实验来说明 Muon 更新 RMS 在训练早期的影响,因为在更大规模的模型训练中,异常行为会很快出现
- 论文使用第 3.2 节描述的 800M 参数小模型进行实验
- 当矩阵维度差异较大时,更新 RMS 不一致的问题会更加明显,为了突出这一问题,论文略微修改了模型架构
- 将 Swiglu MLP 替换为标准的两层 MLP,将其矩阵参数的形状从 \([H, 2.6H]\) 改为 \([H, 4H]\)
- 论文评估了模型的损失,并监测了一些参数的 RMS,特别是注意力查询和 MLP:
- 注意力查询(形状 \([H, H]\))
- MLP(形状 \([H, 4H]\))
- 论文在 20B token 的训练计划中训练了 4B token 后评估模型
- 从表 1 中,论文观察到以下几点:
- 1)更新归一化和调整学习率方法均优于基线;
- 2)对于形状为 \([H, 4H]\) 的 MLP 权重矩阵,更新归一化和调整学习率得到的权重 RMS 大约是基线的两倍
- 这是因为 \(\sqrt{\max(H, 4H)} / \sqrt{H} = 2\),因此更新归一化和调整学习率的更新 RMS 大约是基线的两倍;
- 3)对于形状为 \([H, H]\) 的注意力查询权重矩阵,更新归一化仍然对更新进行归一化,而调整学习率则不会,因为 \(\sqrt{\max(H, H)} / \sqrt{H} = 1\)
- 因此,调整学习率得到的权重 RMS 与基线相似,而更新归一化的权重 RMS 则与其 MLP 类似;

- 因此,调整学习率得到的权重 RMS 与基线相似,而更新归一化的权重 RMS 则与其 MLP 类似;
- 基于这些发现,论文选择调整学习率方法用于后续实验,因为它的计算成本更低
Scaling Law of Muon
- 为了与 AdamW 进行公平比较,论文在 Llama 架构的一系列密集模型上进行了缩放定律实验
- 构建一个强大的基线对于优化器研究至关重要,因此论文按照计算最优训练设置(2022)对 AdamW 的超参数进行了网格搜索(网格搜索实验详见附录 B)
- 模型架构和超参数的细节见表 2
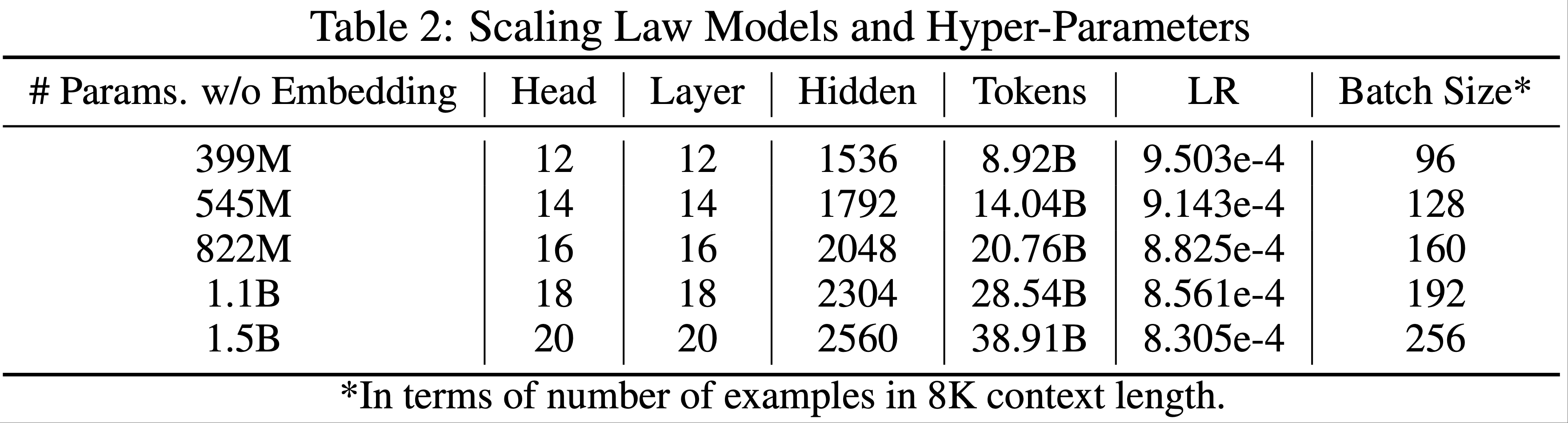
- 对于 Muon,如第 2.2 节所述,由于论文已将 Muon 的更新 RMS 与 AdamW 匹配,因此直接复用了 AdamW 基线的最优超参数
- 拟合的缩放定律曲线见图 3,拟合方程详见表 3

- 如图 1a 所示,在计算最优设置下,Muon 仅需约 52% 的训练 FLOPs 即可达到与 AdamW 相当的性能
Pretraining with Muon
- 模型架构 :为了评估 Muon 在现代模型架构中的表现,论文从头开始预训练了一个基于 deepseek-v3-small 架构(2024)的模型 ,因为该模型性能强大且原始结果可作为参考
- 论文的预训练模型激活参数为 2.24B,总参数为 15.29B(包含嵌入层时为 3B 激活参数和 16B 总参数)
- 对架构的微小修改详见附录 C
- 预训练数据 :预训练数据的细节可参考 Kimi k1.5: Scaling Reinforcement Learning with LLMs, 20250603
- 预训练的最大上下文长度为 8K
- 预训练过程 :模型训练分为多个阶段
- 在阶段 1 和 2 中,论文使用 1e-3 的 Auxfree Bias Update Rate,阶段 3 中为 0.0
- 问题:这里的 Auxfree Bias Update 是什么?
- 回答:是在 DeepSeek MoE 训练中使用到的无辅助损失负载均衡技巧(在此之前,常规的负载均衡技巧会使用 辅助负载均衡损失 auxiliary load-balancing loss,Auxfree 表示不需要这个辅助负载均衡项)
- 注:论文训练的模型架构和 Deepseek-v3-Small 模型一致,这一个 2.4B/16B 参数的 MoE 模型,训练了 1.33T token;
- 所有权重衰减均设为 0.1
- 更多训练细节和讨论见附录 D
- 具体训练流程为:
- 1)0 到 33B token :在此阶段,学习率在 2k 步内线性增加到 4.2e-4,批量大小保持在 2048 个样本;
- 2)33B 到 5.2T token :在此阶段,学习率从 4.2e-4 以余弦方式衰减到 4.2e-5
- 批量大小在 200B token 前保持为 2048,之后增加到 4096;
- 3)5.2T 到 5.7T token(冷却阶段):在此阶段,学习率在 100 步内增加到 1e-4,随后在 500B token 内线性衰减到 0,批量大小保持为 4096。此阶段使用最高质量的数据,重点关注数学、代码和推理任务
- 在阶段 1 和 2 中,论文使用 1e-3 的 Auxfree Bias Update Rate,阶段 3 中为 0.0
- 评估基准 :论文的评估涵盖四类主要基准,每类设计用于评估模型的不同能力:
- 英语语言理解和推理 :MMLU(5-shot)(2021)、MMLU-pro(5-shot)(2024)、BBH(3-shot)(2022)、TriviaQA(5-shot)(2017);
- 代码生成 :HumanEval(pass@1)(2021)、MBPP(pass@1)(2021);
- 数学推理 :GSM8K(4-shot)(2021)、MATH(2021)、CMATH(2023);
- 中文语言理解和推理 :C-Eval(5-shot)(2023)、CMMLU(5-shot)(2024)
- 性能 :论文将使用 Muon 训练的模型命名为“Moonlight”。论文在 1.2T token 处评估 Moonlight,并与以下同规模公开模型进行比较:
- Deepseek-v3-Small(2024):一个 2.4B/16B 参数的 MoE 模型,训练了 1.33T token;
- Moonlight-A :与 Moonlight 训练设置相同,但使用 AdamW 优化器
- 对于 Moonlight 和 Moonlight-A,论文使用了总预训练 5.7T token 中的 1.2T token 中间检查点,此时学习率尚未衰减到最小值,模型也未进入冷却阶段
- 如表 4 所示:
- Moonlight-A(论文的 AdamW 训练基线模型)与同类公开模型相比表现强劲
- Moonlight 的性能显著优于 Moonlight-A,证明了 Muon 的可扩展性
- 论文观察到 Muon 在数学和代码相关任务上表现尤为突出,鼓励研究社区进一步研究这一现象
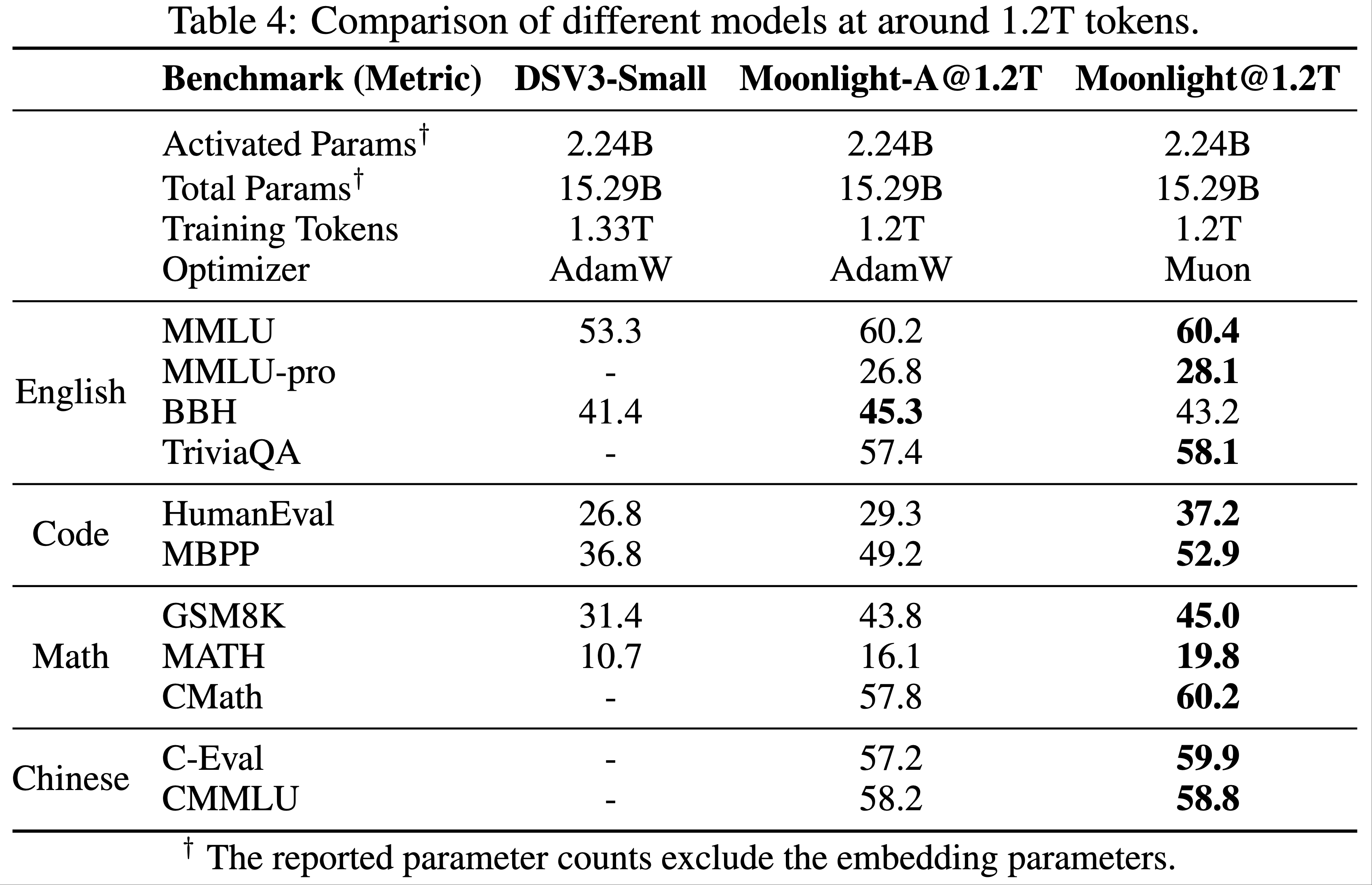
- 当 Moonlight 完全训练到 5.7T token 后,论文将其与同规模的公开模型进行比较,结果如表 5 所示:
- LLAMa3-3B(2024):一个 3B 参数的密集模型,训练了 9T token;
- Qwen2.5-3B(2024):一个 3B 参数的密集模型,训练了 18T token;
- Deepseek-v2-Lite(2024):一个 2.4B/16B 参数的 MoE 模型,训练了 5.7T token
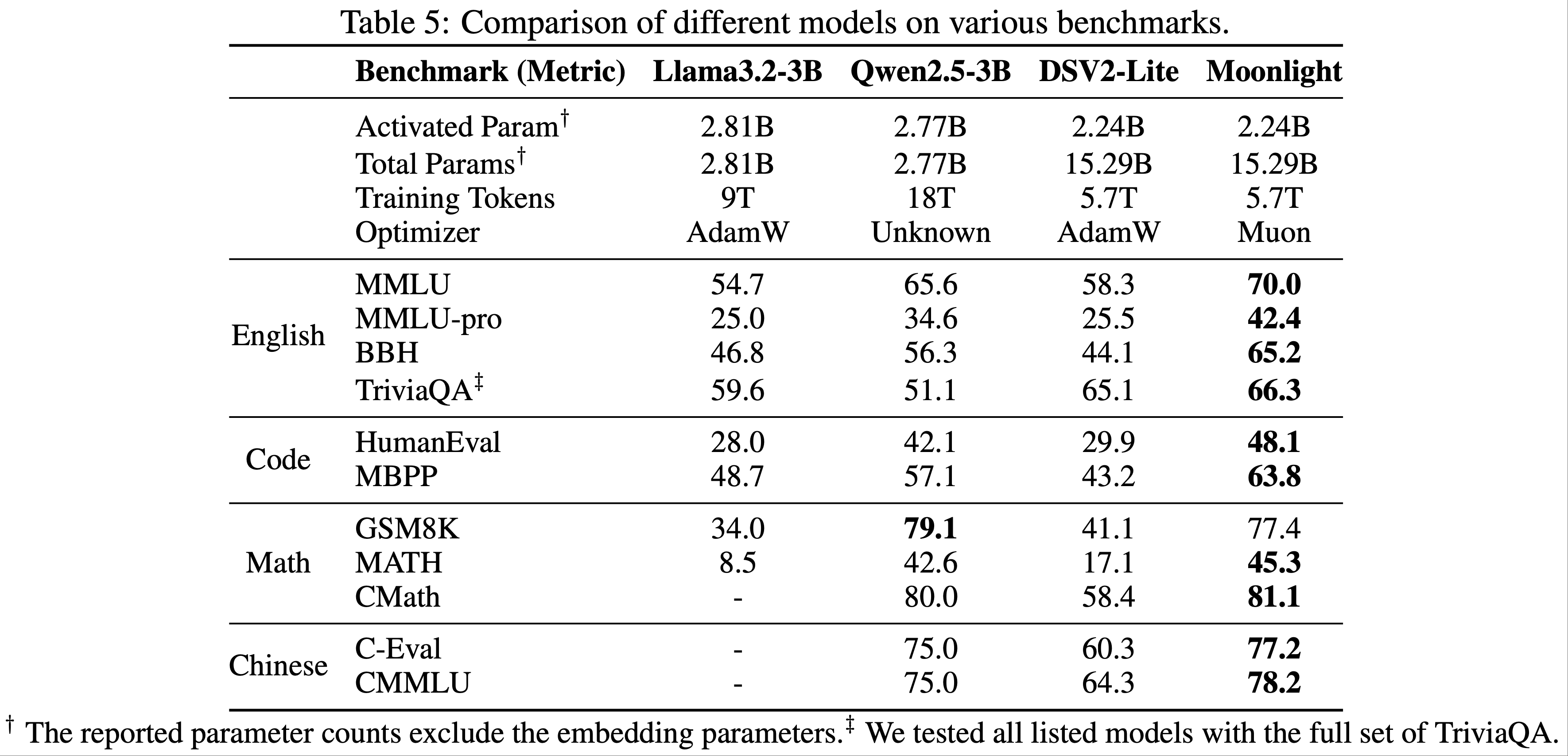
- 如表 5 所示,Moonlight 在相同 token 数量下优于同类模型
- 即使与训练数据量更大的密集模型相比,Moonlight 仍具有竞争力
- 详细比较见附录 E
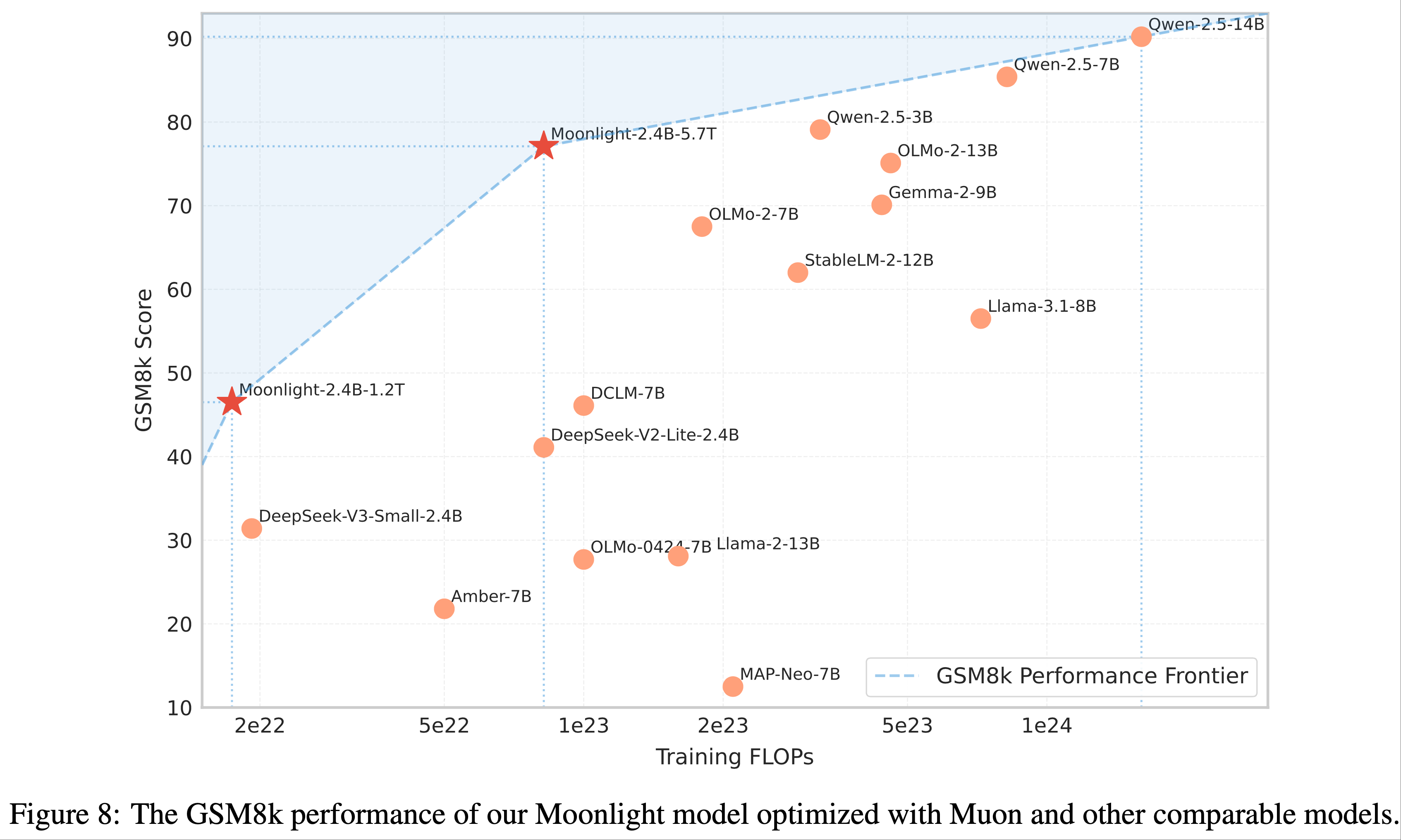
- Moonlight 的性能在 MMLU 和 GSM8k 上与其他知名语言模型进一步对比,如图 1b 和附录 E 图 8 所示
- 值得注意的是,Moonlight 位于模型性能与训练预算的帕累托前沿,优于许多其他规模的模型
Dynamics of Singular Spectrum(奇异谱)
- 为了验证 Muon 可以在更多样化的方向上优化权重矩阵的直觉,论文对使用 Muon 和 AdamW 训练的权重矩阵进行了谱分析
- 对于一个具有奇异值(singular values) \(\sigma = (\sigma_{1}, \sigma_{2}, \cdots, \sigma_{n})\) 的权重矩阵,论文计算其 SVD 熵(2000;2007)如下:
$$
H(\sigma) = -\frac{1}{\log n} \sum_{i=1}^{n} \frac{\sigma_{i}^{2} }{\sum_{j=1}^{n} \sigma_{j}^{2} } \log \frac{\sigma_{i}^{2} }{\sum_{j=1}^{n} \sigma_{j}^{2} }
$$- 直观上看,singular values 越平均,SVD 熵越大
- 如图 4 所示,论文可视化了预训练 1.2T token 过程中不同检查点的权重矩阵的平均 SVD 熵
- 可以看到,在所有训练检查点和所有权重矩阵组中,Muon 的 SVD 熵均高于 AdamW,这验证了 Muon 可以为权重矩阵提供更多样化的更新谱的直觉
- 这种差异在专家选择的路由权重中更为显著,表明混合专家模型可以从 Muon 中获益更多
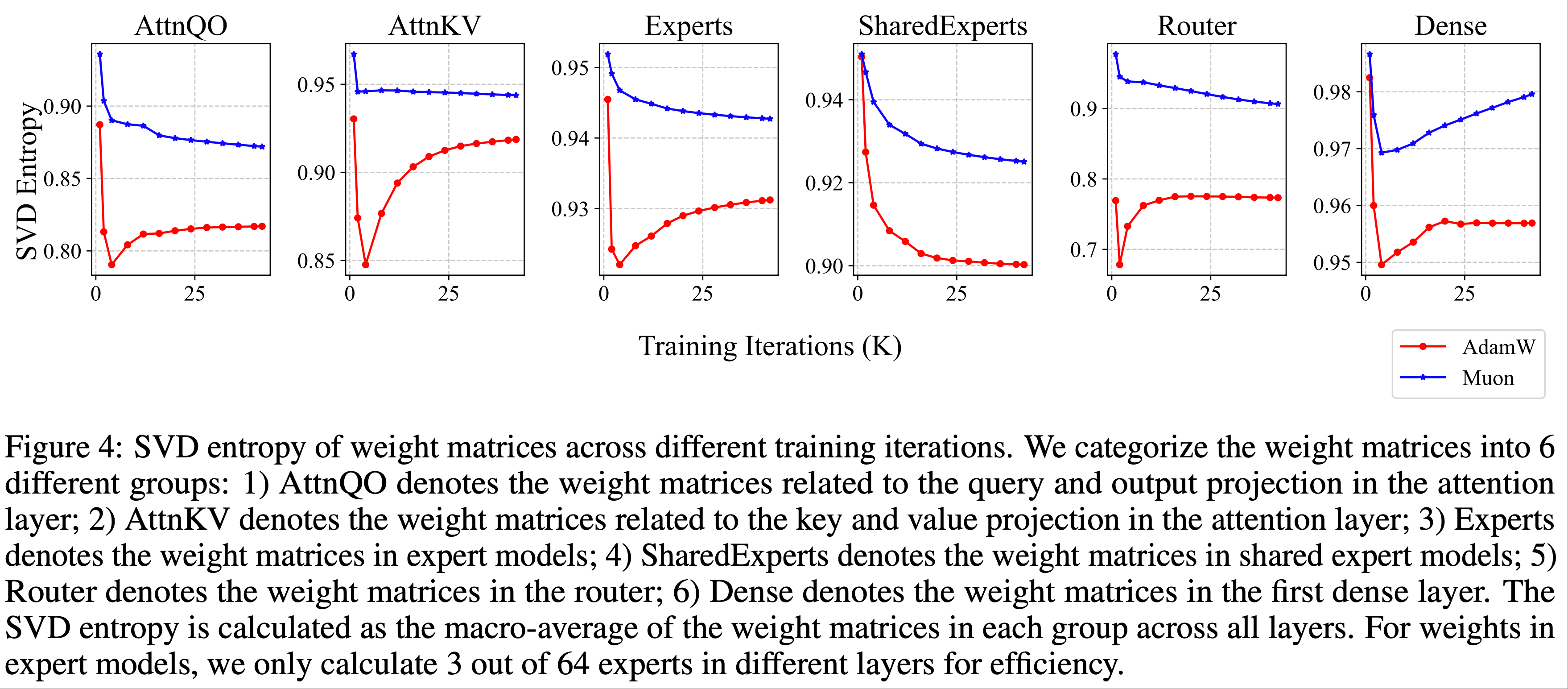
- 此外,论文在附录 F 中展示了 1.2T token 检查点处各权重矩阵的奇异值分布。论文发现,对于超过 90% 的权重矩阵,Muon 优化时的 SVD 熵高于 AdamW,这为 Muon 在探索多样化优化方向上的卓越能力提供了强有力的实证证据
SFT with Muon
- 本节论文展示了 Muon 优化器在标准 LLM 训练 SFT 阶段的消融研究
- 论文的结果表明,Muon 带来的优势在 SFT 阶段仍然存在
- 具体而言,同时使用 Muon 预训练和 Muon 微调的模型在消融研究中表现最佳
- 然而,论文也观察到,当 SFT 优化器与预训练优化器不同时,Muon 在 SFT 中并未显示出显著优于 AdamW 的优势
- 理解:SFT 阶段优化器的选择还与预训练阶段优化器的选择有关?
- 这表明仍有很大的探索空间,论文将其留待未来研究
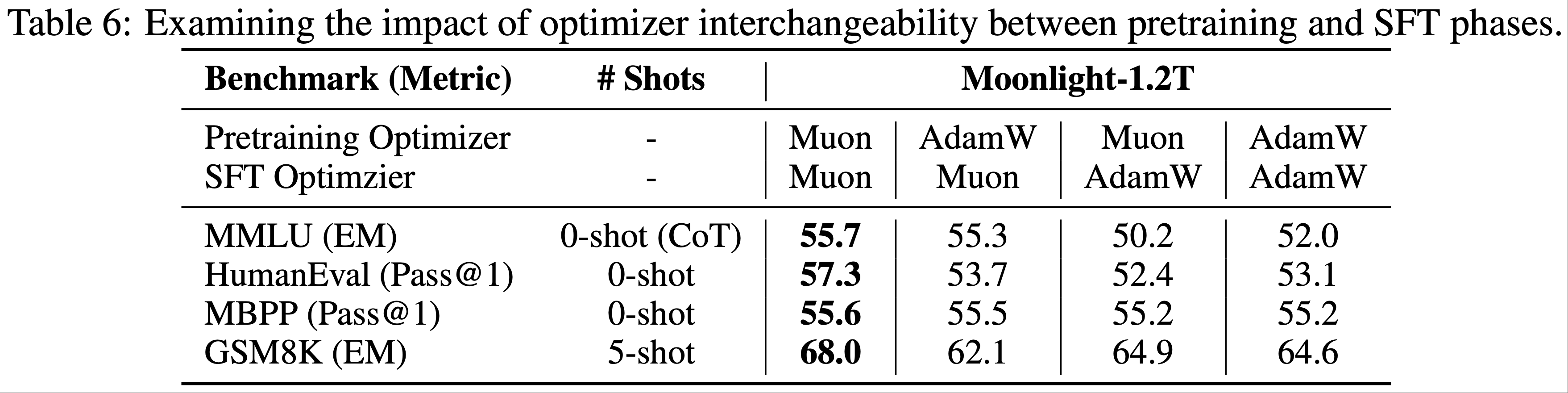
Ablation Studies on the Interchangeability of Pretrain and SFT Optimizers(预训练和 SFT 优化器互换性的消融研究)
- 为了进一步研究 Muon 的潜力,论文使用 Muon 和 AdamW 优化器分别对 Moonlight@1.2T 和 Moonlight-A@1.2T 进行了微调
- 这些模型在开源的 tulu-3-sft-mixture 数据集(2024)上微调了两个 epoch,数据序列长度为 4k
- 学习率采用线性衰减计划,从 \(5 \times 10^{-5}\) 逐渐降至 0
- 结果如表 6 所示,Moonlight@1.2T 的表现优于 Moonlight-A@1.2T
SFT with Muon on public pretrained models
- 论文进一步将 Muon 应用于公开预训练模型 Qwen2.5-7B 基础模型(2024)的 SFT ,使用了开源的 tulu-3-sft-mixture 数据集(2024)
- 数据集以 8k 序列长度打包,论文采用了余弦衰减学习率计划,从 \(2 \times 10^{-5}\) 逐渐降至 \(2 \times 10^{-6}\)
- 结果如表 7 所示: Muon 微调模型的性能与 Adam 微调模型相当
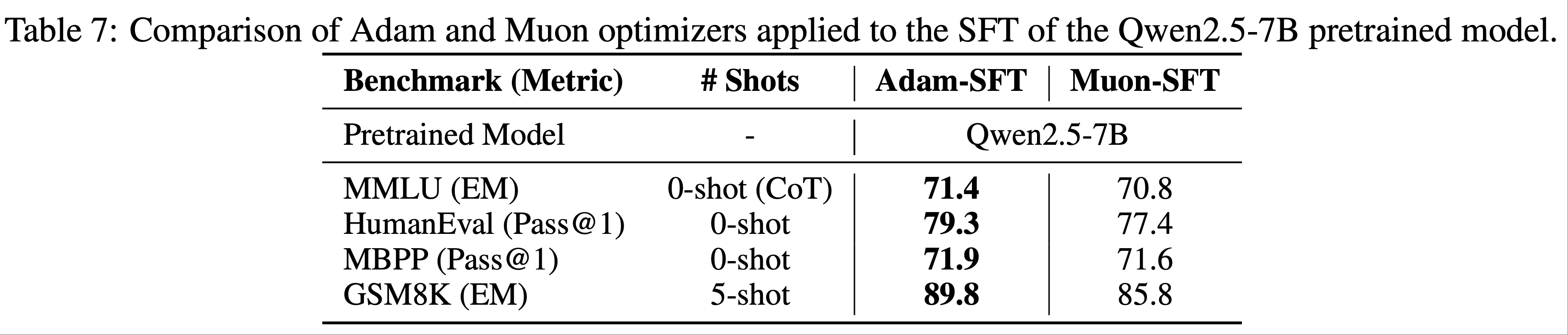
- 这些结果表明,为了获得最佳性能,在预训练阶段应用 Muon 比在监督微调阶段更有效
Discussions
- 未来研究有几个可能的方向可以进一步探索和扩展当前的发现
- 将所有参数纳入 Muon 框架(Incorporating All Parameters into the Muon Framework) :
- 目前,Muon 优化器与 Adam 优化器结合使用,某些参数仍由 Adam 优化
- 这种混合方法虽然可行,但仍有改进空间
- 将所有参数优化完全集成到 Muon 框架中是一个重要的研究方向
- 将 Muon 扩展到 Schatten 范数(Extending Muon to Schatten Norms) :
- Muon 优化器可以解释为谱范数下的最陡下降法
- 鉴于 Schatten 范数的广泛适用性和多功能性,将 Muon 扩展到一般 Schatten 范数是一个有前景的方向
- 这一扩展可能解锁额外的优化能力,并可能产生优于当前基于谱范数实现的结果
- 理解和解决预训练与微调的不匹配(Understanding and Solving the Pretraining-Finetuning Mismatch) :
- 在实践中观察到一个显著现象,使用 AdamW 预训练的模型在使用 Muon 微调时表现不佳,反之亦然
- 这种优化器不匹配对有效利用大量 AdamW 预训练检查点(训练 Muon)构成了重大障碍 ,因此需要进行严格的理论研究
- 精确理解其底层机制对于设计稳健有效的解决方案至关重要
Conclusions
- 在本技术报告中,论文全面研究了 Muon 在 LLM 训练中的可扩展性
- 通过系统分析和改进,论文成功将 Muon 应用于一个 3B/16B 参数的 MoE 模型,训练了 5.7T token
- 论文的结果表明,Muon 可以有效地替代 AdamW 作为大规模 LLM 训练的标准优化器,在训练效率和模型性能上均具有显著优势
- 通过开源论文的实现、Moonlight 模型和中间训练检查点,作者希望促进可扩展优化技术的进一步研究,并加速 LLM 训练方法的开发
附录 A Update RMS
引理 1 的证明
- 不失一般性,考虑正交矩阵 \( U \in \mathbb{R}^{n \times n} \) 和 \( V \in \mathbb{R}^{m \times m} \),其中 \( n \geq m \geq r \)
- 论文将证明对于 \( X = U_{[:,:r]} V_{[:r,:]} \)(Muon 的更新具有相同形式),其均方根值为 \( \sqrt{r/mn} \)
- 注:\( X^{n\times m} = {U_{[:,:r]}}^{n \times r} \cdot {V_{[:r,:]}}^{r \times m} \)
- 根据矩阵乘法的定义:
$$ X_{i,j} = \sum_{k=1}^{r} U_{i,k} V_{k,j} $$- 仅考虑 \(r\) 之前的值
- 均方根可以表示为:
$$
\begin{align}
\text{RMS}(X^{n\times m})^2 &= \frac{1}{mn} \sum_{i=1}^{n} \sum_{j=1}^{m} X_{i,j}^2 \\
&= \frac{1}{mn} \sum_{i=1}^{n} \sum_{j=1}^{m} \sum_{k=1}^{r} U_{i,k}^2 V_{k,j}^2 \\
&= \frac{1}{mn} \sum_{k=1}^{r} \left( \sum_{i=1}^{n} U_{i,k}^2 \right) \left( \sum_{j=1}^{m} V_{k,j}^2 \right) \\
&= \frac{1}{mn} \sum_{k=1}^{r} 1 \\
&= \frac{r}{mn}
\end{align}
$$- 注:\( U \in \mathbb{R}^{n \times n} \) 是正交矩阵,有 \(\sum_{i=1}^{n} U_{i,k}^2 = 1\)
- 证明:\(U^\top U = I\),从而 \(\sum_{i=1}^{n} U_{i,k}^2 = 1\) 是一个对角线元素
- 注:\( U \in \mathbb{R}^{n \times n} \) 是正交矩阵,有 \(\sum_{i=1}^{n} U_{i,k}^2 = 1\)
- 因此,\( \text{RMS}(X) = \sqrt{r/mn} \)
- 对于常见的满秩矩阵情况,\( r = m \),此时 \( \text{RMS}(X) = \sqrt{1/n} \)
Muon 与 AdamW 的更新均方根一致性
- 如 2.2 节所述,作者希望匹配 Muon 和 AdamW 优化器的更新均方根
- 这一假设通过小规模模型实验得到验证(问题:为什么刚好匹配 AdamW 优化器的均方根更好?)
- 论文将 Muon 的更新均方根设置为 \([0.05, 0.1, 0.2, 0.4, 0.8]\),并以 AdamW 为基线
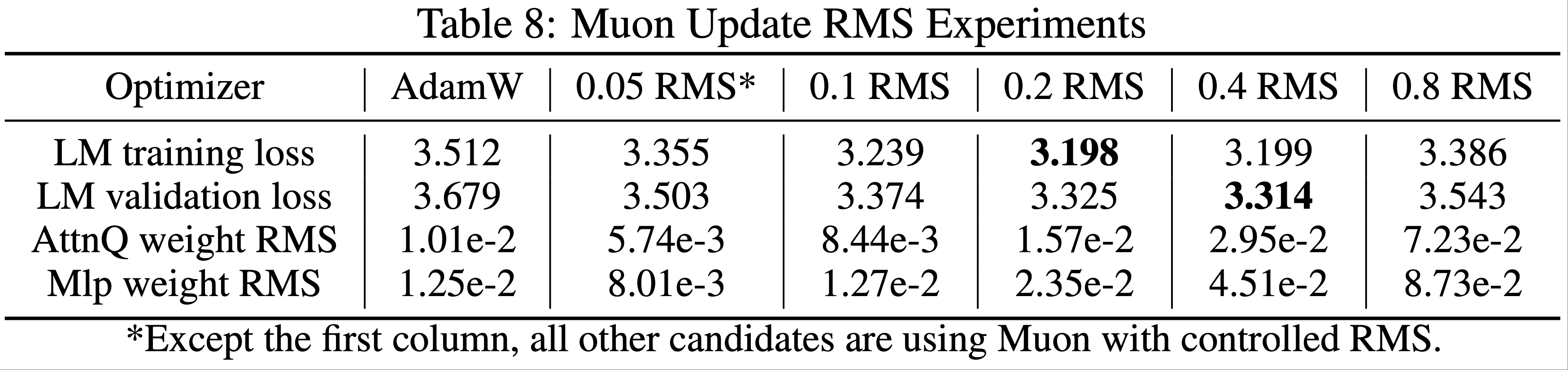
- 表 8 展示了在 2k 步(约 20 亿 token)时的损失和代表性权重矩阵的均方根结果
- 实验表明,0.2 和 0.4 的均方根设置表现相似且显著优于其他设置
- 这与论文观察到的 AdamW 更新均方根范围(0.2 至 0.4)一致,因此论文选择将 Muon 的更新均方根控制在 0.2
附录 B AdamW Baseline Scaling Law
- 为确保实验的公平性和准确性,论文在专有数据集上进行了一系列实验,以确定 AdamW 的最优缩放定律参数
- 这包括在计算预算(FLOPs,\( C \))约束下,确定最优模型大小(\( N \))、训练 token 数量(\( D \))、学习率(\( \eta \))和批大小(\( B \))(2022;2020)
- 表 9 展示了论文系统参数搜索的结果

- 超参数搜索 :为系统性地确定 AdamW 基线的最优缩放定律超参数,论文采用了多阶段搜索协议
- 首先,根据先前研究的经验准则,选择多个计算预算(FLOPs 级别),并初始化模型大小、学习率和批大小
- 对于每个固定的 FLOPs 约束 ,论文调整模型大小 \( N \) ,同时反向调整训练 token 数量 \( D \) ,以保持 \( C = 6ND \) ,从而探索模型容量与数据效率之间的权衡
- 每种配置训练至收敛,并记录验证损失以确定 \( N \) 和 \( D \) 的帕累托最优组合
- 随后,固定最优的 \( N-D \) 对 ,通过网格搜索优化学习率和批大小 ,确保配置的稳定性和收敛性
- 为减少局部最优并增强鲁棒性,此迭代过程重复 2-3 次,逐步缩小超参数空间
- 问题:重复 2-3 次的目的是什么?具体重复了哪些步骤?
- 首先,根据先前研究的经验准则,选择多个计算预算(FLOPs 级别),并初始化模型大小、学习率和批大小
- 图 5 进一步展示了优化过程,描绘了不同 FLOPs 预算下损失随训练 token、学习率和批大小的变化情况
- 每个碗形曲线代表特定 FLOPs 级别的损失曲面,其全局最小值对应最优超参数配置
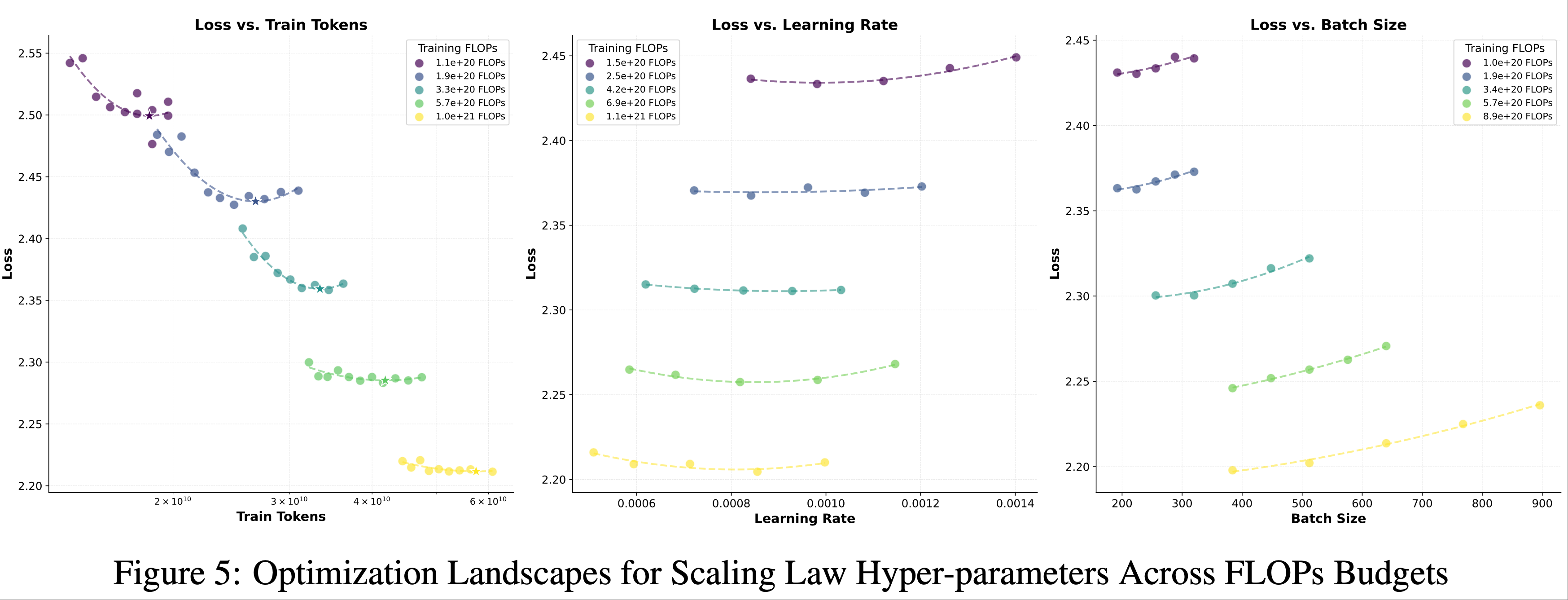
- 每个碗形曲线代表特定 FLOPs 级别的损失曲面,其全局最小值对应最优超参数配置
附录 C Model Architecture
- Muon 对模型架构无特定要求,论文采用了与 Deepseek-V3-Small(DeepSeek-2024)相似的模型,因为其作为基线模型具有开放的权重
- 论文在 Moonlight 模型中进行了几处小修改,具体如下:
- 多 token 预测(Multi-token Prediction, MTP)
- MTP 在论文的实验中未显示出对预训练的显著益处
- 为简化,Moonlight 模型未引入 MTP 层
- 无偏置更新(Auxfree Bias Update)
- 在 DeepSeek-V3-Small 中,无偏置更新通过以下公式实现:
$$ b_i = b_i + u \times \text{sign}(e_i) $$- \( u \) 为更新比例
- \( b_i \) 为第 \( i \) 个专家的偏置
- \( e_i \) 为专家的违反比例
- 论文略微修改了更新规则:
$$ b_i = b_i + u \times (\text{sign}(e_i) - \text{sign}(e).\text{mean}()) $$- \( \text{sign}(e).\text{mean}() \) 为所有专家违反比例符号的平均值,以控制偏置的幅度,同时不改变 topk 选择逻辑
- 在 DeepSeek-V3-Small 中,无偏置更新通过以下公式实现:
- 门控缩放因子(Gate Scaling Factor)
- Deepseek-V2-Lite 未使用门控缩放因子,而 Deepseek-V3 使用了 2.5 的缩放因子
- 论文采用 2.44 的缩放因子以控制与密集模型相似的输出均方根
- 计算门控缩放因子的代码如图 6 所示

附录 D Training Stability
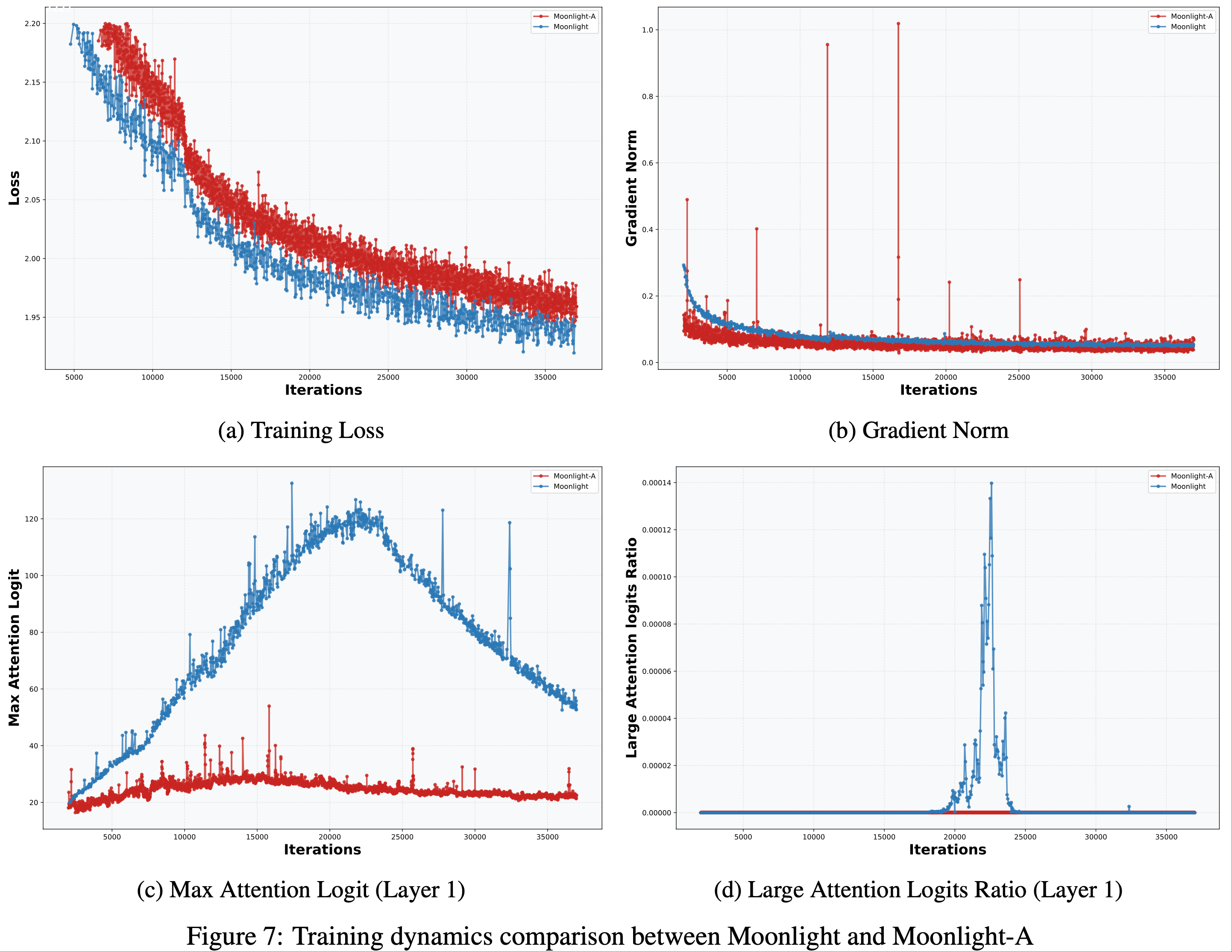
- 无损失或梯度范数尖峰 :Moonlight 的训练过程非常平稳,未出现损失或梯度范数尖峰
- 损失和梯度范数曲线如图 7 所示(Moonlight 为蓝色,AdamW 训练的 Moonlight-A 为红色)
- 损失和梯度范数曲线如图 7 所示(Moonlight 为蓝色,AdamW 训练的 Moonlight-A 为红色)
- 最大注意力对数(Max Attention Logit) :在训练过程中,论文观察到尽管训练损失和梯度范数始终保持稳定,但在某些层的初始训练阶段,最大注意力对数(全局批次中最大的对数值)明显上升,超过阈值 100
- 值得注意的是,AdamW 在控制这一指标上表现更优
- 为进一步研究这一现象的影响,论文引入了大注意力对数比例指标,定义为批次中超过 100 的注意力对数比例
- 如图 7 所示,该比例始终保持在较低水平(约 \( 10^{-4} \)),表明极端大的对数值是稀疏的
- 此外,随着训练的进行,最大对数值逐渐下降,表明优化动态趋于健康
- RMSNorm 伽马权重衰减(RMSNorm Gamma Weight Decay) :值得注意的是,对 RMSNorm 伽马参数应用权重衰减对确保训练稳定性至关重要,因为它能有效防止每层输出均方根过高
附录 E Comparison with More Expensive Models
- 表 10 对比了论文的 Moonlight 模型(使用 Muon 优化)与公开可用的更高计算资源训练的模型,包括 LLama3.1-8B(2024)、Gemma-9B(Gemma 2024)和 Qwen2.5-7B(2024)
- 图 8 展示了 Moonlight 与同类模型在 GSM8k 性能基准上的对比
附录 F Singular Value Distributions of Weight Matrices
- 论文通过绘制每个矩阵奇异值的降序排列线图来可视化权重矩阵的奇异值分布,并将其归一化为最大值
- 如图 9 和图 10 所示,论文发现对于大多数权重矩阵,Muon 优化的奇异值分布比 AdamW 更平坦,进一步验证了 Muon 能提供更多样化的更新谱的假设

