DL——各种梯度下降相关的优化算法

本文从梯度下降(Gradient Descent， GD)开始，讲述深度学习中的各种优化算法（优化器，Optimizer）

参考文章:【干货】深度学习必备：随机梯度下降（SGD）优化算法及可视化

---

三种梯度下降框架

随机梯度下降（Stochastic Gradient Descent， SGD）

核心思想

• 每次从随机从训练集中选择一个训练样本来计算误差，进而更新模型参数
• 单次迭代时参数移动方向可能不太精确甚至相反，但是最终会收敛
• 单次迭代的波动也带来了一个好处，可以到达一个更好的局部最优点，甚至到达全局最优点

参数更新公式

• 公式： \(\theta=\theta-\lambda\frac{\partial L(\theta;x_{i};y_{i})}{\partial \theta}\)
• 其中： \(L(\theta;x_{i};y_{i})=L(f(\theta;x_{i}),y_{i})\)

批量梯度下降（Batch Gradient Descent， BGD）

核心思想

• 每次使用全量的训练集样本（假设共 m 个）来计算误差，进而更新模型参数
• 每次参数能够朝着正确的方向移动
• 每次遍历所有数据，耗费时间较长

参数更新公式

• 公式：\(\theta=\theta-\lambda\frac{\partial L(\theta;x_{1:m};y_{1:m})}{\partial \theta}\)
• 一般来说：\(L(\theta;x_{1:m};y_{1:m}) = \frac{1}{m}\sum_{i=1}^{m} L(\theta;x_{i};y_{i})\)

小批量梯度下降（Mini-Batch Gradient Descent， MBGD）

核心思想

• 每次从随机从训练集中选择k(k < m)个训练样本来计算误差，进而更新模型参数
• 介于SGD和BGD之间
  • 波动小
  • 内存占用也相对较小

参数更新公式

• 公式： \(\theta=\theta-\lambda\frac{\partial L(\theta;x_{i:i+k};y_{i:i+k})}{\partial \theta}\)
• 一般来说： \(L(\theta;x_{1:k};y_{1:k}) = \frac{1}{k}\sum_{i=1}^{k} L(\theta;x_{i};y_{i})\)

总结

优点

• 梯度下降算法应用广泛，算法效果很好

缺点

学习速率

• 大小很难确定，太大容易震荡，太小则收敛太慢
• 学习速率一般为定值，有时候会实现为逐步衰减
• 但是无论如何，都需要事前固定一个值，因此无法自适应不同的数据集特点

局部最优

• 对于非凸的目标函数，容易陷入局部极值点中
• 比局部极值点更严重的问题:有时候会嵌入鞍点?

---

SGD 算法的优化

Momentum法(动量法)

核心思想

• 考虑一种情况，在峡谷地区(某些方向比另一些方向陡峭很多)
  • SGD (或者 MBGD，实际上，SGD 是特殊的 MBGD，平时可以认为这两者是相同的东西)会在这些放附近振荡，从而导致收敛速度变慢
  • 这里最好的例子是鞍点，鞍点出的形状像一个马鞍，一个方向两头上翘，一个方向两头下垂，当上翘的方向比下垂的方向陡峭很多时，SDG和MDG等方法容易在上翘方向上震荡
• 此时动量可以使得
  • 当前梯度方向与上一次梯度方向相同的地方进行加强，从而加快收敛速度
  • 当前梯度方向与上一次梯度方向不同的地方进行削减，从而减少振荡
• 动量可以理解为一个从山顶滚下的小球，遇到新的力(当前梯度)时，会结合之前的梯度方向决定接下来的运动方向

参数更新公式

• 公式：\(\theta=\theta-m_{t}\)
  • \(m_{t}\) 表示当前下降方向， \(m_{t-1}\) 表示上一次的下降方向
  • \(m_{t}=\gamma m_{t-1}+\lambda\frac{\partial L(\theta;x_{i};y_{i})}{\partial \theta}\)
  • \(\gamma<1\)，值一般取0.9
  • \(\gamma m_{t-1}\) 是动量项
  • \(\gamma\) 是衰减量
  • \(\lambda\) 是学习率

图示

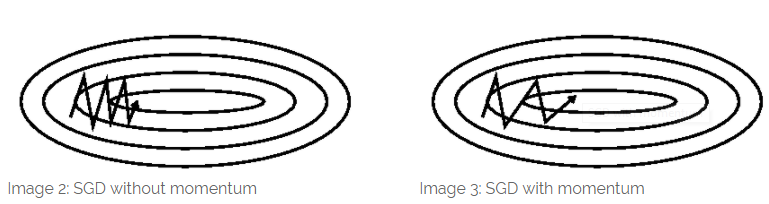
• 动量相关图示：

小结

• 学习过程
  • 从训练集中的随机抽取一批容量为m的样本 \({x_{1},…,x_{m}}\)，以及相关的输出 \({y_{1},…,y_{m}}\)
  • 计算梯度和误差，更新v和参数 \(\theta\)

NAG，涅斯捷罗夫梯度加速法（Nesterov Accelerated Gradient）

核心思想

• 继续考虑普通的 SDG 算法，添加了 Momentum，此时从山顶滚下的球会盲目的选择斜坡
• 更好的方式是在遇到向上的斜坡时减慢速度
• NAG在计算梯度时首先获取(近似获得)未来的参数而不是当前参数，然后计算未来参数对应的损失函数的梯度
• NAG在预测了未来的梯度后，根据未来(\(\theta - \gamma m_{t-1}\))梯度方向和之前梯度的方向决定当前的方向， 这样可以保证在遇到下一点为上升斜坡时适当减慢当前点的速度(否则可能由于惯性走上斜坡， 提前知道 \(\theta - \gamma m_{t-1}\) 处的梯度， 从而保证不要走上去)， 从而找到了比Momentum超前的更新方向
• 对比: Momentum是根据当前梯度方向和之前梯度方向决定当前的方向

参数更新公式

• 公式：\(\theta=\theta-m_{t}\)
  • \(m_{t}=\gamma m_{t-1}+\lambda\frac{\partial L(\theta - \gamma v_{t-1};x_{i};y_{i})}{\partial \theta}\)
  • NAG使用的是未来的梯度方向(Momentum使用的是当前梯度方向)和之前的梯度方向

图示

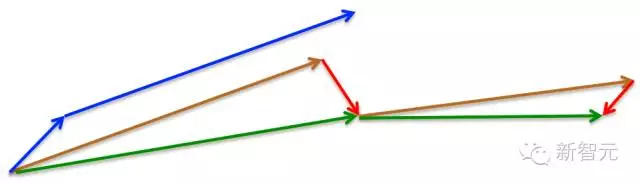
• Momentum(动量)法首先计算当前的梯度值(小蓝色向量)，然后在更新的积累向量（大蓝色向量）方向前进一大步
• NAG 法则首先(试探性地)在之前积累的梯度方向(棕色向量)前进一大步，再根据当前地情况修正，以得到最终的前进方向(绿色向量)
• 这种基于预测的更新方法，使我们避免过快地前进，并提高了算法地响应能力(responsiveness)，大大改进了 RNN 在一些任务上的表现
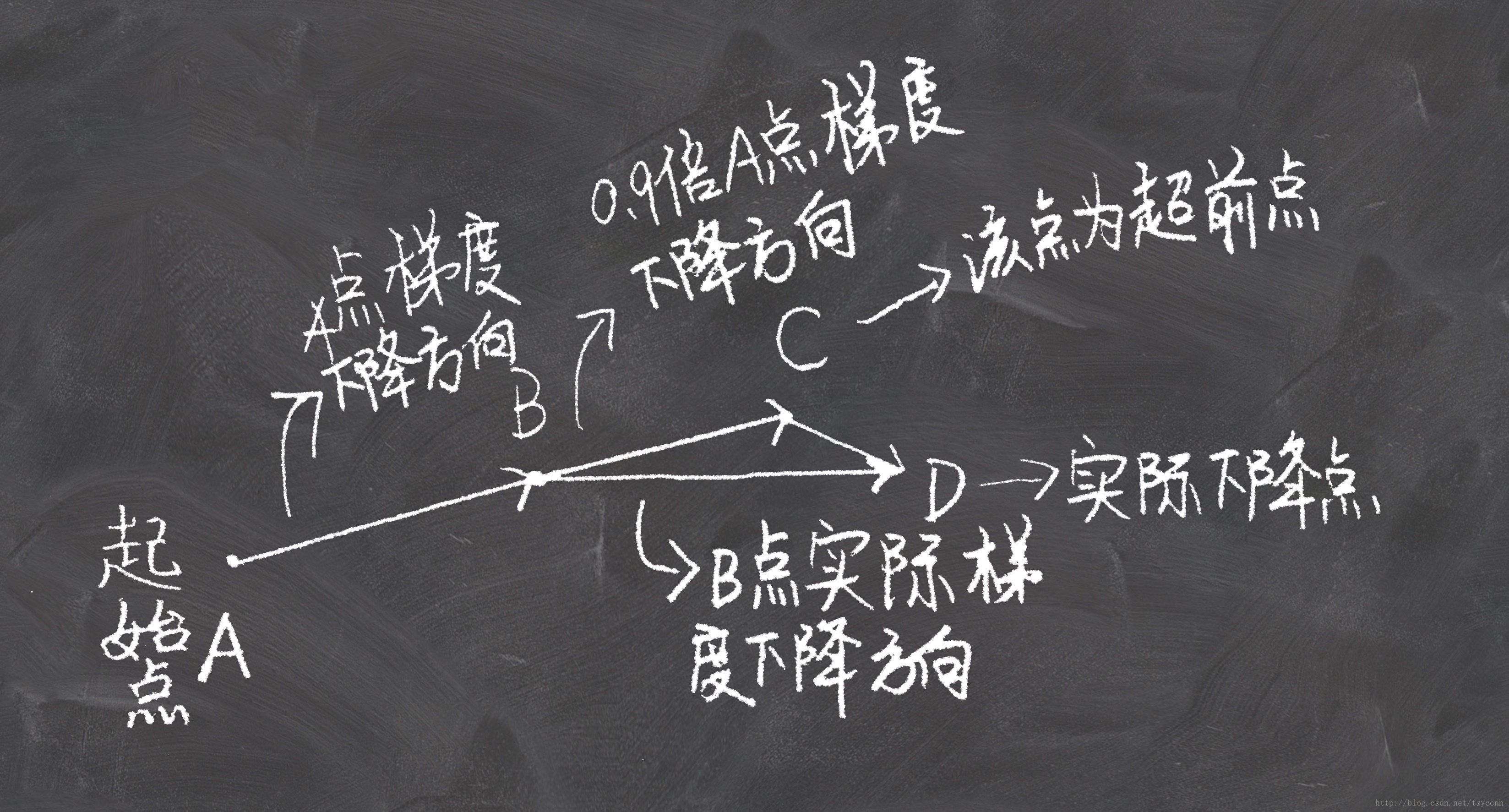
  • 公式中 \(-\gamma m_{t-1}\) 对应BC向量
  • \(\theta-\gamma m_{t-1}\) 就对应C点(参数)

小结

• Momentum和NAG法可以使得参数更新过程中根据随时函数的斜率自适应的学习，从而加速SGD的收敛
• 实际应用中，NAG将比Momentum收敛快很多
• 学习过程
  • 从训练集中的随机抽取一批容量为m的样本 \({x_{1},…,x_{m}}\)，以及相关的输出 \({y_{1},…,y_{m}}\)
  • 计算梯度和误差，更新 v 和参数 \(\theta\)

Adagrad

核心思想

• 对于较少出现的特征，使用较大的学习率更新，即对低频的参数给予更大的更新
• 对于较多出现的特征，使用较小的学习率更新，即对高频的参数给予更小的更新
• 很适合处理稀疏数据

参数更新公式

• 计算梯度
  • 分量形式: \(g_{t,k} = \frac{\partial L(\theta;x_{i};y_{i})}{\theta}|_{\theta = \theta_{t-1,k}}\)
    • \(g_{t,k}\) 是指第t次迭代时第k个参数 \(\theta_{t-1, k}\) 的梯度
    • 有些地方会这样表达: \(g_{t,k} = \frac{\partial L(\theta_{t-1,k};x_{i};y_{i})}{\theta_{t-1,k}}\)
      • 式子中使用 \(\theta_{t-1, k}\) 在梯度中，事实上不够严谨， 容易让人误解分子分母都不是函数，而是一个确定的值， 事实上我们是先求了导数然后再带入 \(\theta = \theta_{t-1}\) 的
  • 向量形式: \(g_{t} = \frac{\partial L(\theta;x_{i};y_{i})}{\partial \theta}|_{\theta=\theta_{t-1}}\)
• 此时普通的SGD如下更新参数
  • 分量形式: \(\theta_{t,k} = \theta_{t-1,k} - \lambda g_{t,k}\)
  • 向量形式: \(\theta_{t} = \theta_{t-1} - \lambda g_{t}\)
• 而Adagrad对学习率 \(\lambda\) 根据不同参数进行了修正
  • 分量形式: \(\theta_{t,k} = \theta_{t-1,k} - \frac{\lambda}{\sqrt{G_{t,kk}+\epsilon}} g_{t,k}\)
    • \(G_{t,kk}=\sum_{r=1}^{t}(g_{r,k})^{2}\)
  • 向量形式: \(\theta_{t} = \theta_{t-1} - \frac{\lambda}{\sqrt{G_{t}+\epsilon}}\bigodot g_{t}\)
    • \(G_{t}=\sum_{r=1}^{t}g_{r}\bigodot g_{r}\)
    • \(\bigodot\) 表示按照对角线上的值与对应梯度相乘
    • 进一步可以简化写为: \(G_t = G_{t-1} + g_t^2\)
      • 注意: 这里 \(g_t^2\) 是指向量按照维度分别相乘， 计算后还是原始向量维度
  • G是一个对角矩阵，对角线上的元素(\(G_{k,k}\))是从一开始到k次迭代目标函数对于参数(\(\theta_{k}\))的梯度的平方和
    • G的累计效果保证了出现次数多的参数(\(\theta_{k}\))对应的对角线上的元素(\(G_{k,k}\))大，从而得到更小的更新
  • \(\epsilon\) 是一个平滑项，用于防止分母为0
• 总结参数更新公式:
  • \(\theta_{t} = \theta_{t-1} - \frac{\lambda}{\sqrt{G_{t}+\epsilon}} g_{t}\)
  • \(g_{t} = \frac{\partial L(\theta;x_{i};y_{i})}{\partial \theta }|_{\theta = \theta_{t-1}}\)
  • \(G_t = G_{t-1} + g_t^2\)

小结

• 在分母上累计了平方梯度和 ，造成训练过程中G的对角线元素越来越大 ，最终导致学习率非常小 ，甚至是无限小的值，从而学不到东西
• 学习过程
  • 从训练集中的随机抽取一批容量为m的样本 \({x_{1},…,x_{m}}\)，以及相关的输出 \({y_{1},…,y_{m}}\)
  • 计算梯度和误差，更新G的每个元素，再根据G以及梯度计算参数更新量

Adadelta

核心思想

• 是Adagrad的一个扩展，目标是解决Adagrad学习率单调下降的问题
• 解决方案:只累计一段时间内的平方梯度值?
• 实际上实现是累加时给前面的平方梯度和一个衰减值
• 方法名delta的来源是选取部分

参数更新公式

• 将矩阵G的每一项变成当前梯度平方加上过去梯度平方的衰减值(指数衰减)即可
  • 指数衰减:前n-1项的系数是衰减率的n-1次方
  • 实现指数衰减
  • 在Adagrad的基础上修改为: \(G_t = \gamma G_{t-1} + (1-\gamma)g_t^2\)
    • 注意: 这里 \(g_t^2\) 是指向量按照维度分别相乘， 计算后还是原始向量维度
  • 我们通常也把 \(G_t\) 表达为 \(E[g^2]_t\)
    • 因为修改后的 \(G_t\) 可以视为于对 \(g_t^2\) 求期望(不同的 \(t\) 概率权重不一样的分布的期望)
    • 进一步表达为: \(E[g^2]_t = \gamma E[g^2]_{t-1} + (1-\gamma)g_t^2\)

小结

• 经过衰减后，G 的每一项(忽略掉平滑项 \(\epsilon\))相当于有权重的梯度均方差(Root Mean Square， RMS)，后面RMSprop算法就用了这个RMS来命名
  • 均方根的定义是:对所有数求平方和，取平均值(每一项的权重根据概率分布可以不同)，再开方
• 学习过程
  • 从训练集中的随机抽取一批容量为m的样本 \({x_{1},…,x_{m}}\)，以及相关的输出 \({y_{1},…,y_{m}}\)
  • 计算梯度和误差，更新G的每个元素，再根据G以及梯度计算参数更新量

RMSprop（Root Mean Square prop）

核心思想

• 一种适应性学习率方法，至今未公开发表
• 是 Adagrad 的一个扩展，目标也是解决 Adagrad 学习率单调下降的问题
• RMS 的来源是由于分母相当于(忽略掉平滑项 \(\epsilon\))是梯度的均方根(Root Mean Squared， RMS)

参数更新公式

• 参见 Adadelta
• RMSprop 的本质是对 Adadelta 简单的取之前值和当前值的权重为 0.9 和 0.1 实现指数加权平均， 即 \(\gamma = 0.9\)
• 有些地方也说 RMSprop 权重取的是 0.5 和 0.5 实现指数加权平均即 \(\gamma = 0.5\)
• 学习率 \(\lambda\) 一般取值为 0.001

小结

• RMSprop是Adadelta的一种特殊形式
• Adagrad的分母不能算是均方差(即使忽略平滑项 \(\epsilon\))，因为这里没有取平均值的操作
• 学习过程
  • 从训练集中的随机抽取一批容量为m的样本 \({x_{1},…,x_{m}}\)，以及相关的输出 \({y_{1},…,y_{m}}\)
  • 计算梯度和误差，更新 G 的每个元素，再根据G以及梯度计算参数更新量

Adam（Adaptive Moment Estimation）

核心思想

• 一种适应性学习率方法，相当于 RMSprop + Momentum + Bias Correction
• 像 Adadelta 和 RMSprop 一样存储了梯度的平方的指数衰减平均值
• 像 Momentum 一样保持了过去梯度的指数衰减平均值
• Bias Correction 是为了得到期望的无偏估计

参数更新公式

• \(\theta_{t} = \theta_{t-1} - \frac{\lambda}{\sqrt{\tilde{v}_t+\epsilon}} \tilde{m}_t\)
  • \(\tilde{m}_t=\frac{m_{t}}{1-\beta_{1}^{t}}\)
  • \(\tilde{v}_t=\frac{v_{t}}{1-\beta_{2}^{t}}\)
• \(\lambda\) 是外层学习率，实际使用中，常常可以通过指数衰减、固定步长衰减、余弦退火衰减等学习率衰减策略更新
• 梯度的指数衰减:
  $$ m_{t} = \beta_{1}m_{t-1}+(1-\beta_{1})g_{t} $$
• 梯度平方的指数衰减:
  $$ v_{t} = \beta_{2}v_{t-1}+(1-\beta_{2})g_{t}^{2} $$
  • \(m_t\) 和 \(v_t\) 也叫作一阶动量和二阶动量，是对梯度一阶矩估计和二阶矩估计
    • 数学定义：随机变量的一阶矩是随机变量的期望 \(E[X]\)，二阶矩是随机变量的方差 \(E[X-E[X]]\)
    • 其实梯度平方的期望不是梯度的方差，这只是一种近似，数学上，随机变量 \(X\) 二阶矩等价于方差，是 \(E[(X-E[X])^2] = E[X^2]-E[X]^2\)，当 \(E[X]=0\) 时， \(E[X^2]\) 就是方差
    • 这种滑动平均之所以能代表期望，是因为滑动平均的思想是一种折扣平均，确实可以用来作为期望和方差的估计
  • \(m_t\) 和 \(v_t\) 可以看做是对 \(E[g]_t\) 和 \(E[g^2]_t\) 的估计
  • \(\tilde{m}_t\) 和 \(\tilde{v}_t\) 是对 \(m_t\) 和 \(v_t\) 的 Bias Correction ， 这样可以近似为对对期望 \(E[g]_t\) 和 \(E[g^2]_t\) 的无偏估计
    • 注意：修正项 \(\tilde{v}_t=\frac{v_{t}}{1-\beta_{2}^{t}}\) 中的 \(\beta_{2}^{t}\) 是 \(\beta_{2}\) 的 \(t\) 次方的意思，基本思路可以理解为在每一步都尽量将梯度修正到 \(t=0\) 大小
    • 进行修正的原因是当 \(t\) 较小时， \(v_t\) 也较小，而 \(\beta\) 一般较大（0.9或者0.999），此时加权平均的结果也会很小，当 \(t\) 很大时，实际上可以不用修正了，个人理解：应该可以不用修正，只是前期训练时更新速度比较慢而已

小结

• 超参数设定推荐
  • 梯度平方衰减率: \(\beta_{2}=0.999\)
  • 梯度动量衰减率: \(\beta_{1}=0.9\)
  • 平滑项: \(\epsilon=10e^-8=10^{-8}\)
    • 传统深度学习中可能讲这个值设置为 1e-5 而不是 1e-8，防止因为分母过小而发生自适应学习率过于激进
  • 一阶动量 \(v\)，初始化为0
  • 二阶动量 \(m\)，初始化为0
• 学习过程
  • 从训练集中的随机抽取一批容量为 m 的样本 \({x_{1},…,x_{m}}\)，以及相关的输出 \({y_{1},…,y_{m}}\)
  • 计算梯度和误差，更新 \(v\) 和 \(m\)，再根据 \(v\) 和 \(m\) 以及梯度计算参数更新量
• 特别注意：
  • 不管是传统深度学习还是 LLM 中，虽然在使用 Adam 或者 AdamW 的情况下会有自适应的学习率，但是调整学习率还是很有必要的
    • Adam 中所谓的自适应学习率是将梯度量级对齐到一定稳定量级，符号不变（具体方式为当前步的梯度 除以 一个滑动平均的归一化因子（历史梯度平方加权平均开更号））
  • 而且对于学习率的使用，通常在预训练和 SFT 中都会大量使用 学习率 warmup 策略（从 0 逐步涨到最大值），最终余弦退火到一个极小值（约最大学习率的 1/10）

AdamW

Adam with Weight decay是Adam的一种优化

Adam 中的 L2 正则

• 一般的L2正则
  $$
  Loss(w) = f(w) + \frac{1}{2}\eta||w||^2
  $$
• 权重衰减后的参数更新如下
  $$
  \begin{align}
  w &= w - \alpha\nabla Loss(w) \\
  &= w - \alpha (\nabla f(w) + \eta w) \\
  &= w - \alpha \nabla f(w) - \alpha \eta w \\
  \end{align}
  $$
• 由于 L2 正则化项的存在，每次权重更新时都会减去一定比例的权重，即 \(\alpha \eta w \)，这种现象叫做权重衰减（L2 正则的目标就是让权重往小的方向更新，所以 L2 正则也叫作权重衰减）
• L2 正则也称为权重衰减，所以 Adam 优化的损失函数中添加L2正则的目标本应该也是为了权重衰减
• Adam 中的 L2 正则
  • 在每次求损失函数梯度前都计算 \(\nabla Loss(w) = \nabla f(w) + \eta w\)
  • 由于 L2 正则项的梯度 \(\eta w\) 也会被累加到一阶动量和二阶动量中，带有 L2 的 Adam 不再是简单的权重衰减，L2 正则项还会影响到其他值的更新
  • Adam 中的 L2 正则会产生我们不期望的结果，因为此时 L2 正则项影响了 Adam 参数的正常更新（我们想要 L2 做的仅仅是权重衰减，但在 Adam中，L2 产生了别的影响，这个不是我们想要的）

AdamW=Adam+权重衰减

• AdamW 则不直接将 L2 添加到损失函数中，而是显示的把权重衰减提出来，主要修改是下面两步
  • 在计算梯度时，将 L2 正则从损失函数中去除
  • 在更新参数时，显示增加权重衰减项
• 相当于在更新参数时增加了 L2 正则，但是计算梯度时没有 L2 正则
• 原始论文：Decoupled Weight Decay Regularization
  • 图中紫色是原始Adam+L2实现部分，在 AdamW 中会被去除；
  • 绿色是 AdamW 中新增的权重衰减部分（相当于更新参数时增加了L2正则项）
• 参考链接：Adam和AdamW，从梯度下降到AdamW一文读懂机器学习优化算法
• 目前大模型常用的就是 AdamW
• 在 Megatron 中，假设在类型为 optimizer=adam 的情况下
  • 配置参数为 decoupled_weight_decay=True 时表示 AdamW（LLM 中一般默认都是 True）
  • 配置参数为 decoupled_weight_decay=False 时表示 AdamW

LLM 中的参数设置说明

• 在 LLM 中，Adam \(\beta_2\) 是梯度平方 \(g_t^2\) 的指数移动平均（EMA）衰减率，控制着 Adam 对历史梯度方差的记忆长度
• 其有效窗口长度近似为：
  $$
  N \approx \frac{1}{1 - \beta_2}
  $$
• 不同 Adam \(\beta_2\) 取值的具体含义如下：
  • 0.999 ，有效窗口约 1000 步
    • 相当于 长期记忆（默认值）
    • 极其保守，对近期梯度变化反应迟钝，一旦发生尖峰会影响后续很多 Step
    • 传统 RL 、深度学习、LLM 预训练和 SFT 常用（因为传统的 RL 每次更新也不大，且一般训练都是几千到几十万步起）
  • 0.99 ，有效窗口约 100 步
    • 反应速度适中，平衡了稳定性和适应性
  • 0.95 ，有效窗口约 20 步
    • 相当于 短期记忆
    • 反应非常迅速，能快速适应当前梯度的剧烈变化，训练 LLM RL 时常用这个值
• 补充：针对 LLM RL 训练（如 RLHF/PPO/DPO），强烈推荐使用 \(\beta_2 = 0.95\) 的原因如下：
  • 业内公认好用 ：LLaMA 2 等前沿模型在训练时明确采用了 \((\beta_1, \beta_2) = (0.9, 0.95)\) 的配置
    • Hugging Face TRL 框架也已将默认值从 0.999 修改为 0.95
  • 部分研究会控诉 \(\beta_2 = 0.999\) 会导致二阶矩估计会对当前梯度变得不敏感，从而引发训练不稳定
    • 虽然 \(\beta_2 = 0.999\) 的二阶矩估计很平滑，但是很难快速适应当前的梯度（特别是在 RL 训练等数据分布/模型分布变化较大的场景中），从而导致“损失尖峰”和策略崩溃问题
    • \(\beta_2 = 0.95\) 则可以快速适应当前环境，有效避免了 RL 训练中常见的“损失尖峰”和策略崩溃问题
  • 其他好处：
    • 一旦发生尖峰， \(\beta_2 = 0.999\) 迟迟忘不掉这个尖峰，影响后续很多 Step，但 \(\beta_2 = 0.95\) 则可以快速适应新的梯度，几乎忘记尖峰

---

优化器与内存/显存

• 训练的过程中，需要的内存/显存大小与优化器（Optimizer）有关
  • 需要存储到内存的变量包括以下几个方面
    • 梯度
    • 参数
    • 优化器状态（Optimizer States），普通 SGD 没有这一项，而Adam和AdamW则需要存储一阶动量和二阶动量
• 优化器、参数量、内存/显存消耗、混合精度训练相关概念可参考ZeRO: Memory Optimizations Toward Training Trillion Parameter Models
  • 有些论文中也会直接将二阶动量叫做方差(Variance)或者二阶矩，因为二阶动量可以近似方差（当期望为0时）
• ZeRO论文中指出，在混合精度训练 + Adam/AdamW 时，需要存储的变量包括
  • FP16 的参数
  • FP16 的梯度
  • FP32 的参数
  • FP32 的一阶动量
  • FP32 的二阶动量
  • 注意：动量不能使用 FP16 吗？是的，不能，因为为了精度考虑使用时还是要被转换到 FP32

---

各种优化方法的比较

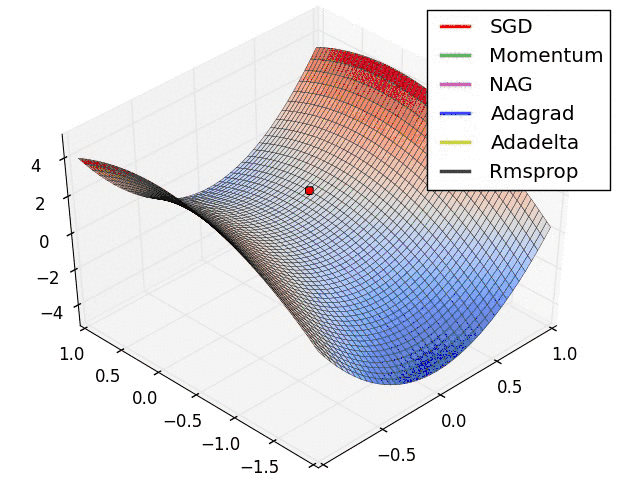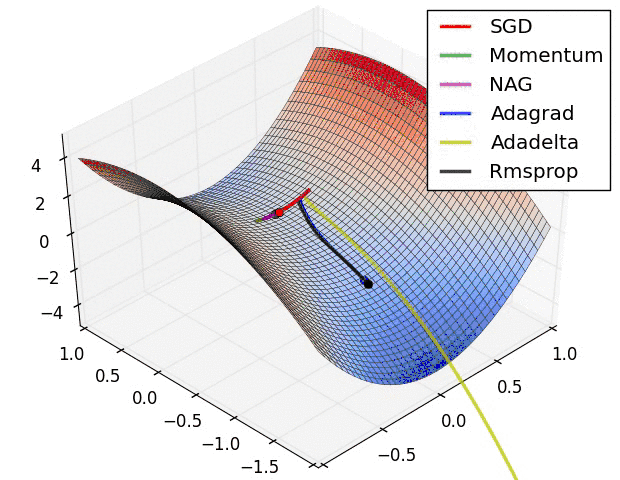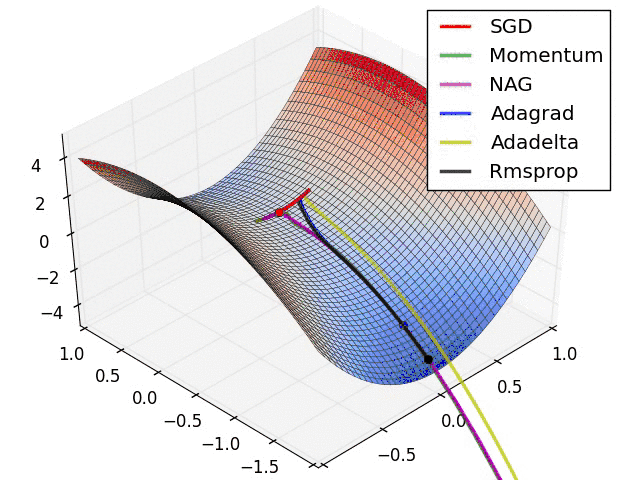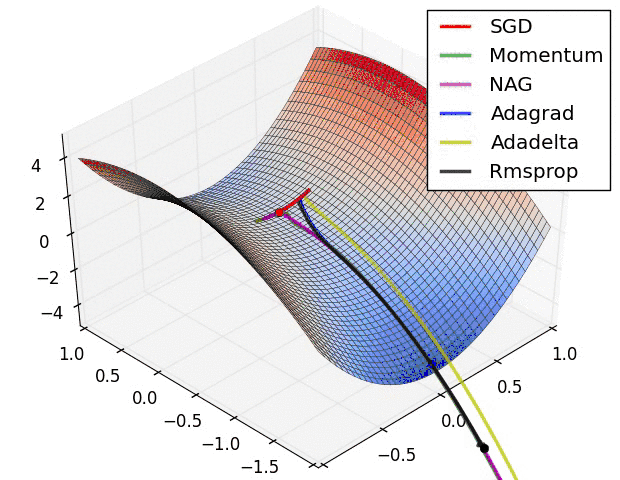
鞍点

• SGD optimization on saddle point

等高线表面

• SGD optimization on loss surface contours
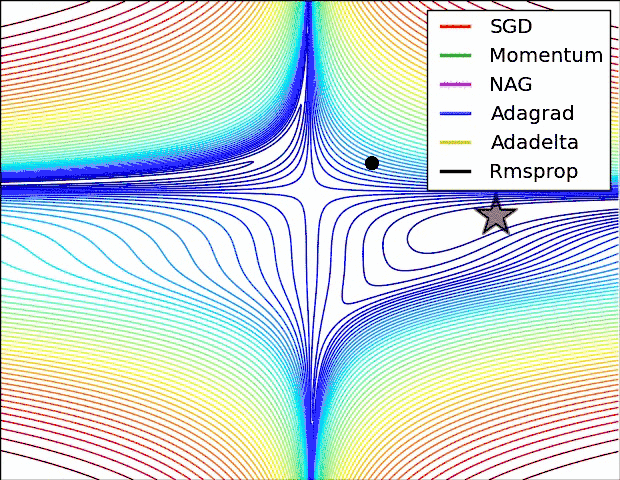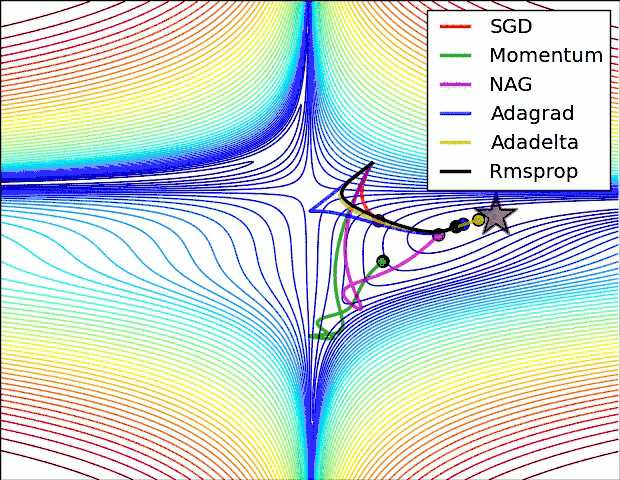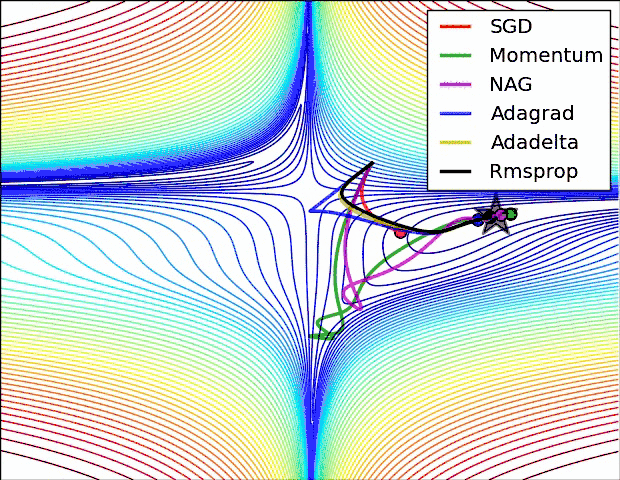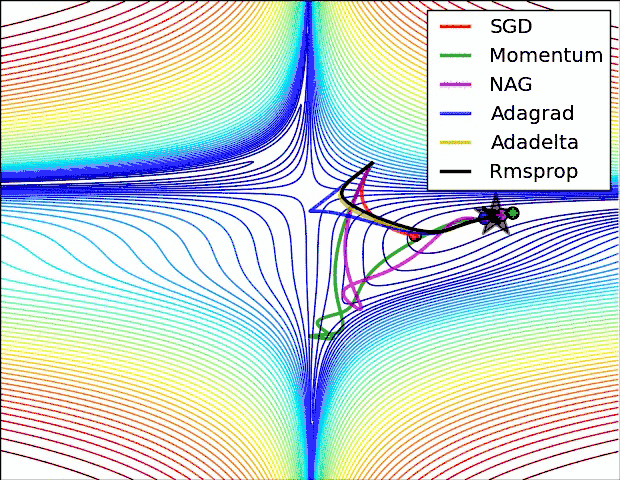
• 上面两种情况都可以看出，Adagrad， Adadelta， RMSprop 几乎很快就找到了正确的方向并前进，收敛速度也相当快，而其它方法要么很慢，要么走了很多弯路才找到
• 由图可知自适应学习率方法即 Adagrad， Adadelta， RMSprop， Adam 在这种情景下会更合适而且收敛性更好

如何选择

• 如果数据是稀疏的，就用自适用方法，即 Adagrad， Adadelta， RMSprop， Adam
  • 因为他们能够为出现更新次数少(确切的说是梯度累计结果小)的特征分配更高的权重
• RMSprop， Adadelta， Adam 在很多情况下的效果是相似的
• Adam 可解释为 RMSprop + Momentum + Bias Correction
• 随着梯度变的稀疏，Adam 比 RMSprop 效果会好
• 整体来讲，Adam 是最好的选择
• 很多论文里都会用 SGD，没有 momentum 等， SGD 虽然能达到极小值，但是比其它算法用的时间长，而且可能会被困在鞍点， 在不正确的方向上来回震荡
• 如果需要更快的收敛，或者是训练更深更复杂的神经网络，需要用一种自适应的算法

---

epoch 粒度的学习率调整

• 本文中提到的常规的梯度下降方法中学习率均是在以 batch 为单位变化，即同一个 batch 学习率相同，而不同 batch 学习率可能不同
• 深度学习中还有一类学习率调整方法，是以 epoch 为单位变化的，即同一个 epoch 学习率相同，而不同 epoch 学习率可能不同
• 常见的 epoch 为单位变化的学习率有：
  • StepLR：间隔调整学习率
  • MultiStepLR：按设定的间隔调整学习率
  • ExponentialLR︰按指数衰减调整学习率
  • CosineAnnealingLR：以余弦函数为周期，在每个周期最大值时重置学习率
  • CosineAnnealingWarmRestarts：CosineAnnealingLR 加上 warmup
  • ReduceLROnPlateau:当某指标不再变化（下降或升高），调整学习率
• 如果以 epoch 为单位的学习率(如 StepLR)和以 batch 为单位的学习率(如 Adam)调整同时被设置，则：
  • 两者会同时生效
  • StepLR 负责在每个 epoch开始时调整学习率
  • Adam 负责在每个 batch 开始时调整学习率

---

附录：关于 Adam 的更多讨论

• 参考链接：
  • 如何理解Adam算法(Adaptive Moment Estimation)？ - Summer Clover的回答 - 知乎
  • 梯度下降法的神经网络容易收敛到局部最优，为什么应用广泛？ - Summer Clover的回答 - 知乎

    （1）正因为梯度下降法 容易收敛到局部最优，所以大家几乎从来不用梯度下降做非凸优化，包括 训练神经网络
    （2）正因为随机梯度下降法 容易逃离鞍点 和泛化不好的 minima（主要是 sharp minima），所以 随机梯度下降（SGD）和它的变种（比如 Momentun、Adam）才是训练神经网络最流行的方法

  • Who is Adam? 重新审视大模型 RLVR 阶段的优化器选择

Adam vs SGD 的优缺点简单总结

• Adam 更容易逃离鞍点
• Adam 对学习率超参数不敏感，一般在一个范围内的学习率即可实现最优，无需精确对学习率调参；但 SGD 对超参数非常敏感，不同场景下的最优超参数变化剧烈
• Adam 收敛更快
• Adam 需要额外存储两倍参数量的优化器状态，这对超大规模模型来说成本非常高

大模型中的 Adam 和 SGD 对比

• 参考链接：Who is Adam? 重新审视大模型 RLVR 阶段的优化器选择
• 注意：这里的讨论仅限于 RLVR 这种不需要更新太多参数的场景
• TLDR：大模型中，在做 RLVR 时，由于 RLVR 任务需要修改变化的参数较少（以 1e-5 变化量为阈值，大概 0.01% 量级参数发生变化），所以使用不带 Momentum 的 SGD 优化基本就够了，能省下来 Adam 下的很多优化器状态显存占用
• 在 RLVR 下 SGD vs Adam：
  • SGD 审下来很多优化器状态，且效果和 Adam 差不多
  • 使用 SGD 时，需要使用较大的学习率（Adam 1e-6 ~ 1e-5 是，SGD 需要 0.1 左右），且 SDG 对学习率超参敏感

Adam 尺度不变性的四个漏洞

• Adam 只对“全部梯度、全部历史、统一缩放”不变，以下情形会漏进来
• 多项 loss 的相对尺度
  • 在多个 loss 组合时，只针对某个 loss 乘以倍数会导致 loss 之间出现偏差，Adam 归一化以后则造成部分 loss 的梯度被弱化
• 梯度裁剪，尺度相关且逐步变化
  • 梯度范数大时，clip 把 grad_norm 序列上端压平到 1，进入 \(v\) 的是尺度不一致的序列
  • 真正尖锐 spike 被压成 1，其对 \(m\) 的贡献相对 \(\sqrt v\) 缩小
    • 因此 Adam 下 clip 的实际作用是抑制离群 step 对 \(m,v\) 的污染，而非缩小平均步长
• 时间上的尺度突变表现
  • \(Z\) 每步随 batch 波动；\(v\) 以约 20 步时间常数追踪
  • 一次突增 10 倍，用 \(0.9/0.95\) 算，瞬时比值约 \(0.78\)，步长反而略缩
  • 突减 10 倍，瞬时比值约 \(0.93\)
  • 影响是暂态、有界的，不会放大到 10 倍
• \(\epsilon\) 的影响
  • 当下面的情况时，Adam 对该参数退化成 SGD，尺度不变性失效
    $$
    \sqrt{\hat v_i}\lesssim\epsilon=10^{-8}
    $$
• weight decay 与 bias correction
  • 解耦权重衰减与梯度尺度无关：
    $$
    \text{衰减项}=\eta\lambda\theta,
    $$
    • 改 \(\eta\) 会等比例改衰减强度，是降 lr 的隐含副作用
  • bias correction：
    $$
    \hat m=\frac{m}{1-\beta_1^t},\qquad
    \hat v=\frac{v}{1-\beta_2^t}
    $$
    • \(\beta_2=0.95\) 时约 60 步后 \(\approx1\)
    • 逐参数统一、与尺度无关，bias correction 以上各种结论

---

附录：Adam 和 grad-norm 相关讨论

• Adam 中的自适应学习率本质就是想将梯度更新的 grad-norm 量纲消除，只留下梯度方向，然后每一步走多远靠学习率来控制
  • 注意：上报 grad-norm 一般是 clip-grad 生效前的，但 Adam 自适应学习率使用的是 clip-grad 后的

补充：针对 grad-norm 的理解

• grad-norm 的数学定义：
  $$
  \begin{align}
  |g|_2&=\sqrt{\sum_{i=1}^{N}g_i^2}\\
  g_i&=\frac{\partial L}{\partial \theta_i}
  \end{align}
  $$
  • 基本含义：把整个模型所有参数的梯度拼成一个 \(N\) 维向量，并取 L2 范数
• grad-norm 受三类因素影响：
  • 1）loss 的绝对尺度：若 loss 乘 \(c\)，则 grad_norm 乘 \(c\)
  • 2）样本间梯度的抵消程度：比如 RL 训练时 GRPO 组内正负 advantage 的梯度抵消越充分，范数越小
  • 3）梯度噪声，详情见下文

梯度噪声和梯度范数的理解

• 回顾带噪声的梯度表达式：
  $$
  \mathbb E|g_B|^2=|g_\infty|^2+\frac{\operatorname{tr}\Sigma}{B_{\text{eff} } }
  $$
  • \(B\)：实际小批量大小
  • \(g_B\)：用这个小批量算出来的随机梯度
    • \(|g_B|^2\) 是这个梯度向量的 L2 范数平方
  • \(g_\infty\)：真实梯度，也叫总体梯度、全量梯度
    $$
    g_\infty=\mathbb E[g^{(i)}]=\nabla L(\theta)
    $$
    • 也就是如果能看到全部数据、或者无穷多样本，得到的那个“真正想走的梯度方向”，\(g_\infty\) 是公式中的信号项，不含噪声
  • \(\Sigma\)：单个样本梯度的协方差矩阵
    • 设单个样本梯度 \(g^{(i)}\) 的期望是 \(g_\infty\)（期望即真实梯度），定义其协方差矩阵为
      $$
      \Sigma=\mathbb E\left[(g^{(i)}-g_\infty)(g^{(i)}-g_\infty)^\top\right]
      $$
    • 这是一个 \(N\times N\) 矩阵
    • 对角线元素是每个参数维度上单样本梯度的方差，非对角线元素是不同参数维度之间的协方差
    • 另一个视角理解这个协方差矩阵：
      $$
      g^{(t)}=g_\infty+\varepsilon^{(t)},\qquad
      \mathbb E[\varepsilon^{(t)}]=0,\qquad
      \operatorname{Cov}(\varepsilon^{(t)})=\Sigma
      $$
  • \(\operatorname{tr}\Sigma\)：该协方差矩阵的迹
    $$
    \operatorname{tr}\Sigma=\sum_{j=1}^N \operatorname{Var}(g_j^{(i)})
    $$
    • 等于所有参数维度上单样本梯度方差之和
    • 可以把 \(\operatorname{tr}\Sigma\) 理解为总噪声功率 ：即等价于单个样本的梯度围绕真实梯度 \(g_\infty\) 波动得有多厉害
  • \(B_{\text{eff} }\)：有效样本数
    • 如果小批量是等权平均，且样本独立同分布，那么
      $$
      B_{\text{eff} }=B
      $$
    • 但如果样本权重不均匀，比如
      $$
      g_B=\sum_{i=1}^B w_i g^{(i)},\qquad \sum_i w_i=1,
      $$
      • 则有效样本数定义为
        $$
        B_{\text{eff} }=\frac{1}{\sum_{i=1}^B w_i^2}
        $$
    • 理解：
      • 当所有 \(w_i=1/B\) 时，
        $$
        \sum_i w_i^2=\frac1B,\qquad B_{\text{eff} }=B
        $$
      • 当权重高度集中，例如某个 \(w_1\approx1\)，其余接近 0，则
        $$
        \sum_i w_i^2\approx1,\qquad B_{\text{eff} }\approx 1
        $$
        • 也就是说，虽然抽了 \(B\) 个样本，但真正起作用的样本数只有 1 个
  • \(\frac{\operatorname{tr}\Sigma}{B_{\text{eff} } }\)：梯度噪声项
    • 噪声项 ：表示由于只用了有限个有效样本，小批量梯度中混入了多少额外方差
      • 当 \(B_{\text{eff} }\) 很大时，噪声项很小
      • 当 \(B_{\text{eff} }\) 很小时，噪声项很大
      • 当 \(B_{\text{eff} }\to\infty\) 时，噪声项趋于 0，小批量梯度趋近真实梯度
• 在单样本真实梯度 \(g_\infty\) 固定，且单样本方差固定为 \(\Sigma\) 时，有效样本数 \(B_{\text{eff} }\) 越少，平方范数的期望越大
  • 更多的有效样本数下梯度估计更稳定，更接近真实梯度，样本够多时只剩下真实信号
• 上述公式描述的是：小批量梯度 \(g_B\) 的平方范数，在随机抽样下的期望，可以分解为“真实信号”与“噪声方差”两部分

grad-norm 不是参数更新幅度的度量

• grad-norm 不是参数更新幅度的度量的原因有：

  • 第一：grad-norm 可能会被裁剪

    • 梯度裁剪的细节见：NLP——LLM相关问题记录

  • 第二：在 Adam 中，grad-norm 上报不变，但 Adam 的自适应学习率会将 grad-norm 的量纲对齐

    • 详情见下文

  • 补充：裁剪与 Adam 的关系：在一般的框架实现中（比如 Megatron）中，顺序可能是：

    prepare_grads()                      # 计算梯度
    grad_norm = get_grad_norm()          # 上报的 actor/grad_norm，裁剪前
    clip_grad_by_total_norm_fp32(...)    # 原地缩放梯度，也称为梯度裁剪（本质是等比例放缩）
    step_with_ready_grads()              # Adam 使用裁剪后的梯度更新 m, v, θ

    • 裁剪与 Adam 的关系
      • 裁剪发生在 Adam 之前
      • Adam 累积的是裁剪后的梯度
      • 日志中的 actor/grad_norm 是裁剪前的值
      • grad-norm 反映 loss 本身的梯度尺度，不直接反映 Adam 实际吃到的梯度

学习率、grad-norm 和 更新幅度的控制

• SGD 中的直觉
  $$
  \Delta\theta=-\eta g \qquad |\Delta\theta|=\eta|g|
  $$
  • 所以 grad_norm 大 10 倍，更新也大 10 倍
  • 要维持更新幅度 ，需要把 \(\eta\) 降为 \(1/10\)
    • 注意：这里是维持更新幅度，其他论文（比如 Decoupled PPO）中，常常使用固定噪声量级来确定
• Adam 中的情况：
  $$
  \begin{align}
  m_i&\leftarrow\beta_1m_i+(1-\beta_1)g_i \\
  v_i&\leftarrow\beta_2v_i+(1-\beta_2)g_i^2 \\
  \Delta\theta_i&=-\eta\frac{\hat m_i}{\sqrt{\hat v_i}+\epsilon} \\
  \end{align}
  $$
  • \(m_i\) 是最近梯度的加权均值（动量），\(\sqrt{v_i}\) 是最近梯度的均方根（二者单位相同，比值无量纲）
    • \(\sqrt{v_i}\) 本质是对近期梯度二阶矩的低方差估计，其实只用当前这步也行（就是方差比较大，属于是高方差估计）
    • Adam 的本质是用 动量 \(m_i\) 除以该参数的典型梯度幅度 \(\sqrt{v_i} \approx \mathcal{E}[g_i^2]\)
  • 若全部历史梯度乘常数 \(c\)：
    $$
    \frac{c \cdot m_i}{|c|\sqrt{v_i} }=\frac{m_i}{\sqrt{v_i} }
    $$
    • 尺度被完全约掉
  • 因此 Adam 下，梯度和学习率倍数差异是：
    • 梯度整体乘 10，更新幅度基本不变
    • 学习率乘 \(1/10\)，更新幅度精确乘 \(1/10\)

Adam 更新幅度

• 原始 Adam 逐元素更新幅度是：
  $$
  |\Delta\theta_t|=\alpha \frac{|\hat m_t|}{\sqrt{\hat v_t}+\epsilon}
  $$
• 关键量是：
  $$
  \frac{\hat m_t}{\sqrt{\hat v_t} }
  $$
  • 大致表示：最近梯度的方向一致性
• 特别说明：它不保证在 \([-1,1]\) 内，因为：
  • \(\hat m_t\) 是梯度的一阶指数滑动平均
  • \(\hat v_t\) 是梯度平方的二阶指数滑动平均
  • 而且原始 Adam 中一般设置下两者系数不同：
    $$
    \beta_1=0.9,\qquad \beta_2=0.999
    $$
    • 所以不能把 \(\hat m_t\) 和 \(\hat v_t\) 写成同一组权重下的加权平均，也就不能直接推出：
      $$
      \left|\frac{\hat m_t}{\sqrt{\hat v_t} }\right|\le 1
      $$
• 直观理解
  • 梯度持续同号且稳定 （比如梯度一直是固定值）：
    • \(\hat m_t\) 和 \(\sqrt{\hat v_t}\) 接近同一个尺度，比值接近 \(\pm 1\)，更新幅度约等于 \(\alpha\)
  • 梯度正负乱跳 ：
    • \(\hat m_t\) 相互抵消变小，而 \(\hat v_t\) 仍然较大，比值趋于 0，几乎不动
  • 历史梯度很小，当前突然很大 ：
    • 由于 \(\beta_1<\beta_2\)，\(\hat m_t\) 记得快，\(\hat v_t\) 记得慢
    • \(\hat m_t\) 快速上升，\(\hat v_t\) 上升较慢，比值可能大于 1，更新幅度可以超过 \(\alpha\)
    • 极端例子
      • 历史梯度全是 0，当前梯度突然为 1：
        $$
        g_1=\cdots=g_{t-1}=0,\qquad g_t=1
        $$
      • 长期后近似：
        $$
        \hat m_t\approx 1-\beta_1=0.1 \\
        \hat v_t\approx 1-\beta_2=0.001
        $$
      • 于是：
        $$
        \frac{\hat m_t}{\sqrt{\hat v_t} }\approx\frac{0.1}{\sqrt{0.001} }\approx 3.16
        $$
• 总结：
  • Adam 中 \( \frac{\hat m_t}{\sqrt{\hat v_t} }\) 大致表示方向一致性，但不是严格的 [-1,1]
  • 原始 Adam 不保证逐元素更新幅度 \(|\Delta\theta_t|\le\alpha\)
  • 极端情况下，默认参数(\(\beta_1=0.9,\beta_2=0.999\))下更新幅度可达约 \(3.16\alpha\)
• 准确表达：
  • Adam 的更新幅度通常受学习率 \(\alpha\) 控制，但不是严格不超过 \(\alpha\)
  • \(\frac{\hat m_t}{\sqrt{\hat v_t} }\) 只表示方向一致性：方向一致时接近 \(\pm1\)，方向混乱时接近 0

Adam 下的第一步是特例，最开始的步骤可能不稳定（因为估计值不准确）

• 虽然有校准保证无偏，但是仍然是不准确的（方差大，波动大）

• \(t=1\) 时 bias correction 后：
  $$
  \hat m=g, \qquad \hat v=g^2
  $$

  • 理解：第一步时的 bias correction 公式如下：
    $$
    \begin{align}
    \hat m = \frac{(1-\beta_1)g_1 + \beta_1 0}{1-\beta_1} = g_1 \\
    \hat v = \frac{(1-\beta_2)g_1^2 + \beta_2 0}{1-\beta_2} = g_1^2 \\
    \end{align}
    $$

• 所以：
  $$
  \frac{\hat m_i}{\sqrt{\hat v_i} }=\operatorname{sign}(g_i)
  $$

• 每个参数都以满速 \(\eta\) 走，与噪声、尺度无关

  • 这是 Adam 冷启动头几步最莽、需要 warmup 的原因，尤其在大学习率下（比如 1e-5 级别就算大了，1e-6 就还好）

• 收敛需要的时间窗口：\(\beta_1=0.9\) 约 10 步窗口，\(\beta_2=0.95\) 约 20 步窗口

• Adam 代码输出前几步效果示例：

  import math
  
  # GRADS = [0.000001] * 2 + [-0.00001]*2
  GRADS = [0.1, -0.1] * 10
  
  
  def adam_steps(grads, alpha=1.0, beta1=0.9, beta2=0.999, eps=1e-8):
      m, v = 0.0, 0.0
      rows = []
      for t, g in enumerate(grads, start=1):
          m = beta1 * m + (1 - beta1) * g
          v = beta2 * v + (1 - beta2) * g * g
          m_hat = m / (1 - beta1 ** t)
          v_hat = v / (1 - beta2 ** t)
          step = alpha * m_hat / (math.sqrt(v_hat) + eps)
          rows.append(
              {
                  "t": t,
                  "g": g,
                  "m": m,
                  "v": v,
                  "m_hat": m_hat,
                  "v_hat": v_hat,
                  "sqrt_v_hat": math.sqrt(v_hat),
                  "step": step,
              }
          )
      return rows
  
  
  def print_table(rows, alpha):
      header = f"{'t':>3} {'g_t':>12} {'m_t':>14} {'v_t':>16} {'m̂_t':>14} {'v̂_t':>16} {'√v̂_t':>12} {'Δθ_t (α=' + str(alpha) + ')':>16}"
      print(header)
      print("-" * len(header))
      for r in rows:
          print(
              f"{r['t']:>3} {r['g']:>12.6g} {r['m']:>14.8g} {r['v']:>16.10g} "
              f"{r['m_hat']:>14.8g} {r['v_hat']:>16.10g} {r['sqrt_v_hat']:>12.8g} {r['step']:>16.6f}"
          )
  
  
  if __name__ == "__main__":
      print(f"grads={GRADS}\n")
      rows = adam_steps(GRADS)
      print_table(rows, alpha=1.0)
      print("\n每步更新幅度:", [round(r["step"], 6) for r in rows])
      print("累计位移:", round(-sum(r["step"] for r in rows), 6))
  
  # 每步更新幅度: [1.0, -0.052632, 0.335793, -0.052632, 0.204415, -0.052632, 0.149137, -0.052632, 0.119204, -0.052632, 0.100771, -0.052632, 0.088507, -0.052632, 0.079923, -0.052632, 0.0737, -0.052632, 0.069072, -0.052632]
  # 累计位移: -1.694207

  • 说明：
    • 在一个梯度期望为 0，交叉更新的情况下，第 1 步会更新会比较大，后续会逐步衰减，但是参数依然会有少量更新
    • 如果加上冷启，则明显可以跳过/减少前几步的参数更新，从而让梯度更新到指定的期望（0，即参数不应该被更新）