本文研究智能出价下的Truthful拍卖
- 参考链接:
目标及思路
- 研究自动出价下的 Truthful 拍卖机制(即:也称为激励兼容(incentive-compatible)或说真话(truth-telling)的拍卖机制)
- Truthful拍卖机制需要同时满足:激励兼容性 和 个体理性
- 激励兼容性(Incentive Compatibility, IC) :竞拍者通过报告其真实估价获得的效用不低于任何其他策略下所能获得的效用。这意味着对于竞拍者来说,诚实是最好的策略
- 个体理性(Individual Rationality, IR) :如果竞拍者赢得拍卖,他支付的价格不会超过他对该物品的真实估价。因此,他的净收益(即他的估价减去支付的价格)将是非负的。即使竞拍者没有赢得拍卖,由于他没有支付任何费用,他的净收益也是零或正数
- Truthful拍卖机制需要同时满足:激励兼容性 和 个体理性
- 设定场景:商家设定ROI + 预算约束 (传统的拍卖模型不再适合这种新的广告范式)
- 分配:采用排名分数作为确定 item 分配的标准,这与广义第二价格(GSP)拍卖的思想相似
- 计费:在保证私人约束的真实性方面,设计了一个关键ROI ,即在不超出预算约束的情况下能够赢得最多 item 的最大ROI,这等价于将预算转换为与ROI相同的维度,从而允许论文找到一个紧约束,限制竞拍者获得额外效用,并利用该紧约束防止虚假报告
场景定义及讨论
- 自动出价(auto-bidding):广告主向平台提交其高层优化目标和约束条件,然后由机器学习算法驱动的出价代理代表广告主在每次广告拍卖中做出详细的出价决策。借助自动出价工具,广告主可以在高层面上根据其财务约束优化其整体广告目标
- 传统的拍卖模型 :在传统模型中,广告主对 item (即广告展示)具有私人价值,并在每次拍卖中进行相应的策略性出价
- 自动出价场景的拍卖模型 :自动出价中,广告主的私人信息实际上是其整个广告活动的约束条件 ,公开信息是用户的潜在行为(如点击和转化 ,这些行为可以被视为广告主对 item 的公开价值,因为此时通过预估模型可以将CTR和CVR预估出来);机制设计的目标是找设计一种新的广告拍卖模型,以激励广告主在** item 价值公开的情况下如实揭示其高层私人约束**
- 论文自动出价场景定义 :广告主提交预算和投资回报率(ROI)要求作为其 (私人)约束 ,并旨在最大化在一定时期内从多次拍卖中获得的累积价值
- 论文主要内容:
- 提出了一种自动出价(即价值最大化的竞拍者具有私人约束作为私人信息,而 item 的价值是公开的(即CTR,CVR等公开))下的拍卖模型
- 研究了在公开价值设置下,预算和ROI这两个私人约束的真实性条件,为Truthful拍卖的分配和支付的可行空间提供了完整的特征描述
- 基于推导出的真实性条件,论文设计了一类用于自动出价的真实广告拍卖机制
- 实验评估拍卖机制在社会福利和收入方面的有效性
整体分析
在线广告系统
在线广告拍卖系统的工作过程如图1所示
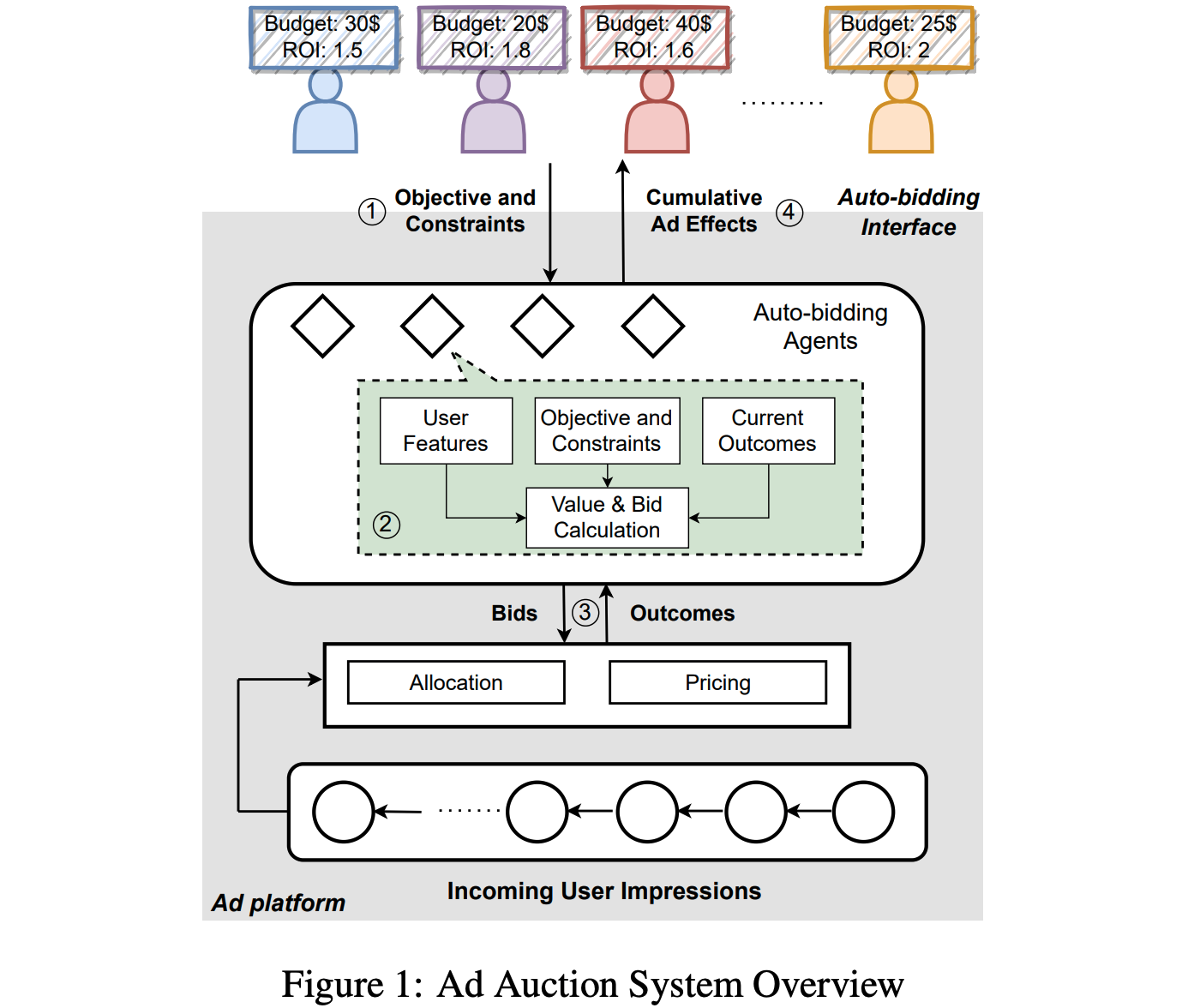
从广告主的角度来看,它可以描述如下:
- 广告主在选择优化目标(例如,最大化点击或转化)并设置成本约束(例如,每日预算、目标投资回报率(ROI)和每次点击的最大成本)。广告主要求其实现的ROI(定义为获得的价值与支付的比率)高于其目标ROI
- 根据广告主的配置,自动出价代理代表广告主在多次拍卖中做出出价决策。当每次用户展示出现时,自动出价代理参加广告拍卖以竞争广告展示机会
- 自动出价代理会预测每个请求下,用户展示为广告主带来的价值(点击率或转化率),并在考虑成本约束的情况下为每次展示/点击出价
- 在多次拍卖中,广告主可以查看累积的拍卖结果,包括花费的预算、获得的展示、点击、转化和平均成本。广告主可以进一步调整其自动出价设置以实现其广告目标
自动出价服务的在线广告与传统在线广告的不同:
- 广告主仅在出价配置中报告优化目标和约束 ,而不是每次拍卖的细粒度出价
- 广告主仅评估多次拍卖的累积长期表现和成本 ,而不是每次单独拍卖的结果
- 由于在线平台可以访问广告中产生的所有数据,因此可以合理地声称特定广告主对请求位置展示/点击的货币价值可以精确计算(公开信息)
由于广告主和在线平台的行为模式在自动出价中发生了显著变化,论文需要研究自动出价下的新机制
注:接下来论文主要研究展示计费的场景
拍卖模型
拍卖场景定义:
- 有 \(n\) 个广告主在 \(m\) 个时间段内竞争 \(m\) 个 item(用户展示),每个时间段只出现一个 item
- 广告主是价值最大化(value-maximizing)的竞拍者,他们在支付不超出其财务约束的情况下关心其分配到的展示的累积价值
- 每个广告主 \(i\) 具有预算( \(B_{i}\geq 0\) )和ROI( \(R_{i}>0\) )约束,这些是私人信息(在机制设计文献中也称为类型 \(t_{i}=(B_{i},R_{i})\) )
- 所有广告主的类型概况为 \(\mathbf{t}=(t_{i})_{i=1}^{n}\) ,类型概况的空间为 \(\mathcal{T}=\prod_{i=1}^{n}\mathcal{T}_{i}\) ,其中 \(\mathbf{t}\in\mathcal{T}\) 且 \(\mathcal{T}_{i}={\cal B}_{i}\times{\cal R}_{i}\) ;除竞拍者 \(i\) 之外的其他竞拍者的报告类型为 \(\mathbf{t}_{-i}=(t_{1},\ldots,t_{i-1},t_{i+1},\ldots,t_{n})\) ,且 \(\mathcal{T}_{-i}=\prod_{k\neq i}^{n}\mathcal{T}_{k}\)
- 假设广告主对 item 的估值是平台的公开信息 ,使用 \(v_{i,j}>0\) 表示广告主 \(i\) 对 item \(j\) 的估值
机制设计:在收集所有竞拍者的预算和ROI后,在线平台采用某种拍卖机制( \(\mathcal{A},\mathcal{P}\) )来决定广告分配和支付
- 其中 \(\mathcal{A}\) 表示(随机化的)分配规则 \(\mathcal{A}:\mathcal{T}\rightarrow[0,1]^{n\times m}\)
- \(\mathcal{P}\) 表示(随机化的)支付规则 \(\mathcal{P}:\mathcal{T}\rightarrow\mathbb{R}^{n}\)
- 具体来说,对于报告的类型概况 \(\mathbf{t}^{\prime}\in\mathcal{T}\) ,竞拍者 \(i\) 被分配到 item \(j\) 的概率表示为 \(a_{i,j}(\mathbf{t}^{\prime})\) ,竞拍者 \(i\) 的预期支付表示为 \(p_{i}(\mathbf{t}^{\prime})\) 。对于任何 item \(j\in[m]\) ,分配约束为 \(\sum_{i=1}^{n}a_{i,j}(\mathbf{t}^{\prime})\leq 1\)
- 一些变量和符号说明:
- 竞拍者 \(i\) 在这些拍卖中的累积价值为:
$$v_{i}(\mathbf{t}^{\prime})=\sum_{j=1}^{m}v_{i,j}a_{i,j}(\mathbf{t}^{\prime}),$$ - 其实现的ROI为(注:如果 \(p_{i}(\mathbf{t}^{\prime})=0\) ,则视为 \(+\infty\) ):
$$ \text{ROI}_{i}(\mathbf{t}^{\prime}):=\frac{v_{i}(\mathbf{t}^{\prime}) }{p_{i}(\mathbf{t}^{\prime})} $$
- 竞拍者 \(i\) 在这些拍卖中的累积价值为:
具有预算和ROI约束且真实类型为 \(t_{i}=(B_{i},R_{i})\) 的竞拍者在报告 \(t^{\prime}_{i}\) 时的效用定义为
$$u_{i}\left(t_{i},\mathbf{t}^{\prime}\right)=\begin{cases}v_{i}(\mathbf{t}^{\prime}),\text{if }p_{i}(\mathbf{t}^{\prime})\leq B_{i}\text{ And }\text{ROI}_{i}(\mathbf{t}^{\prime})\geq R_{i},\\ \ -\infty,\text{otherwise},\end{cases}$$- 其中类型概况 \(\mathbf{t}^{\prime}=(t^{\prime}_{i},\mathbf{t}^{\prime}_{-i})\)
论文的目标是设计满足激励相容(IC)和个体理性(IR)条件的真实拍卖机制
论文设定下的一些定义
- 定义 2.1 一个拍卖机制是占优策略激励相容(DSIC)的,如果 \(\forall i\in[n]\) , \(t_{i},t^{\prime}_{i}\in\mathcal{T}_{i},\mathbf{t}_{-i}\in\mathcal{T}_{-i}\) : \(u_{i}(t_{i},(t_{i},\mathbf{t}_{-i}))\geq u_{i}(t_{i},(t^{\prime}_{i},\mathbf{t}_{-i}))\)
- 定义 2.2 一个拍卖机制是个体理性(IR)的,如果 \(\forall\mathbf{t}\in\mathcal{T}\) , \(i\in[n]\) : \(p_{i}(\mathbf{t})\leq B_{i}\) 且 \(\text{ROI}_{i}(\mathbf{t})\geq R_{i}\) 。(注:这个定义与传统定义完全相同)
- 在线平台通常有一些需要最大化的目标。两个常见的设计目标是收入和社会福利。收入定义为竞拍者支付的总和,即 \(\sum_{i}p_{i}(\mathbf{t})\) 。对于社会福利,论文需要一个同义的指标,即流动性福利(Liquid welfare),定义为在不违反IR约束的情况下可以从竞拍者中提取的最大收入 ,以纳入财务约束的存在。在论文的背景下,流动性福利可以定义为:
$$\text{LW}=\sum_{i\in[n],u_{i}(t_{i},\mathbf{t}^{\prime})\geq 0}\min\left(\frac{v_{i }(\mathbf{t}^{\prime})}{R_{i}},B_{i}\right).$$
真实性条件的特征
预算的真实性的条件
- 特殊说明:为了满足预算上的激励相容性(IC)属性,论文需要确保竞拍者不会通过报告较小或较大的预算来获得更高的效用 ,以防止虚假报告:
- 由于报告较小的预算不会导致竞拍者超出其原始预算约束,因此减少预算所获得的效用应该减少;
- 对于报告较大预算并获得更高价值的竞拍者 ,论文需要通过收取费用使其超出原始预算约束(注:这里的原始预算约束是其真实预算约束),从而导致负无穷的效用
- 定理 3.1 一个拍卖机制在预算 \(B\) 上是占优策略激励相容(DSIC)的,仅当 \(\forall i\in[n]\) , \(R\in\mathcal{R}_{i}\) , \(\mathbf{t}_{-i}\in\mathcal{T}_{-i}\) 时:
- (1) \(v_{i}\left((B,R),\mathbf{t}_{-i}\right)\) 在 \(B\) 上是非递减的;
- (2)如果对于 \(B^{\prime}>B\) , \(v_{i}\left((B^{\prime},R),\mathbf{t}_{-i}\right)>v_{i}\left((B,R),\mathbf{t}_{-i}\right)\) ,则
$$p_{i}\left((B^{\prime},R),\mathbf{t}_{-i}\right)>B.$$- 理解:ROI不变的情况下,更多的收益意味着需要付出更多的钱。如果预算大与B导致获得的收益大比预算B时的大,则一定要付出比B更多的钱;当然,如果没有因为预算变大而获得比预算B下更多的收益,则计费是可以不用大于预算B的
- 注意:不是当且仅当,是必要条件
ROI的真实性条件
- ROI也可以同预算相关我们可以通过类似的陈述来说明ROI,表明竞拍者没有动机虚假报告其ROI
- 定理 3.2 一个拍卖机制在ROI \(R\) 上是占优策略激励相容(DSIC)的,仅当 \(\forall i\in[n]\) , \(B\in\mathcal{B}_{i}\) , \(\mathbf{t}_{-i}\in\mathcal{T}_{-i}\) 时:
- (1) \(v_{i}\left((B,R),\mathbf{t}_{-i}\right)\) 在 \(R\) 上是非递增的;
- (2)如果对于 \(R^{\prime}<R\) , \(v_{i}\left((B,R^{\prime}),\mathbf{t}_{-i}\right)>v_{i}\left((B,R),\mathbf{t}_{-i}\right)\) ,则
$$\text{ROI}_{i}\left((B,R^{\prime}),\mathbf{t}_{-i}\right)<R.$$- 理解:预算不变的情况下,更多的收益意味着更小的ROI
- 注意:不是当且仅当,是必要条件
ROI和预算下的真实性条件
- 说明:定理3.1和3.2中条件(1)所需的单调性属性与具有私人估值的准线性竞拍者的真实性条件(例如Myerson引理)相似,但条件(2)揭示了它们的基本差异:为了防止虚假报告,必须通过收取费用来打破至少一个约束(导致负无穷的效用)
- 这里第二个条件是与Myerson引理最大的不同
- 定理3.1和3.2自然地为二维类型 \((B,R)\) 的DSIC提供了必要条件。以下结果表明,这些条件也提供了充分条件。也就是说,如果竞拍者无法通过虚假报告其一个约束来获得更高的效用,那么虚假报告两个约束也无法获得更高的效用
- 注:仅包括 \((B,R)\) 两个维度,所以称为二维类型
- 定理 3.3 一个拍卖机制在预算和ROI上都是占优策略激励相容(DSIC)的,当且仅当它满足定理3.1和3.2
From 自动出价下机制设计系列 (二) : 面向私有约束的激励兼容机制设计:
上述引理中的单调递增/递减是非严格的。引理3与引理4自然地构成了 \((B,R)\) 双参数DSIC的必要条件。论文进一步证明了,它们实际上也构成了充要条件,也就是说,当竞拍者无法通过在单参数上的虚报获得更高效益时,也同样无法通过双参数上的同时虚报来获得更高的效益- 详细证明还需要再思考
可行分配规则的结构(Structures of Feasible Allocation Rule)
本节描述了可行的分配规则应该长什么样
- 可行的分配规则定义:如果分配规则 \(\mathcal{A}\) 是可行的,则存在一个支付规则 \(\mathcal{P}\) 使得机制 \(\mathcal{A},\mathcal{P}\) 满足 Truthful(这里 Truthful 指的是拍卖机制能够激励参与者诚实地报告他们的估值或偏好)
- 可行分配规则的集合是我们可以搜索真实拍卖的空间,尽管可能存在多个构成可行分配规则 \(\mathcal{A}\) 的真实拍卖的支付规则(问题:一个分配规则应该对应唯一的DSIC的拍卖规则吧?),但下面的定理允许论文专注于最大支付规则
- 在激励相容的或者说是 truthful(真实的)的机制下,参与者的最佳策略是根据他们对物品的真实价值进行出价,而不是试图通过策略性出价来获得优势。而 最大支付规则 则指的是一种特定的支付规则,它确保了机制的激励兼容性,并且在这种规则下,支付额度是在保证机制真实性的前提下的最大值
- 定义这种规则有助于简化拍卖机制的设计与分析
定理3.4 :对于一个可行的分配规则 \(\mathcal{A}\),下面的计费机制 \(\mathcal{P}\) 对于所有的 \(i\in[n],(B_{i},R_{i})\in\mathcal{T}_{i}\),\(\boldsymbol{t}_{-i}\in\mathcal{T}_{-i}\),构成一个真实的拍卖机制(注意:这里不是唯一的 Truthful 拍卖机制):
$$
p_{i}\left((B_{i},R_{i}),\boldsymbol{t}_{-i}\right)=\min\left(\frac{v_{i}\left((B_{i},R_{i}),\boldsymbol{t}_{-i}\right)}{R_{i}},B_{i}\right),
$$- 定理3.4的证明(注:论文的证明都在附录里):由于 \(\mathcal{A}\) 是可行的,存在对应的 \(\mathcal{P}^{\prime}\),使得 \((\mathcal{A},\mathcal{P}^{\prime})\) 是一个满足DSIC和IR条件的机制。注意到 \(p_{i}(B_{i},R_{i})=\min\left(\frac{v_{i}(B_{i},R_{i})}{R_{i}},B_{i}\right)\) 是从竞拍者 \(i\) 的类型 \((B_{i},R_{i})\) 中提取的最大可能支付,以满足竞拍者的ROI和预算要求。也就是说,\(p^{\prime}_{i}(B_{i},R_{i})\leq p_{i}(B_{i},R_{i})\)。另一方面,增加某个类型的支付不会破坏原本满足的定理3.1和3.2中的条件。因此,将支付从 \(p^{\prime}_{i}\) 修改为 \(p_{i}(B_{i},R_{i})=\min\left(\frac{v_{i}(B_{i},R_{i})}{R_{i}},B_{i}\right)\) 满足竞拍者的 预算和ROI 要求,并保持DSIC条件,因此 \((\mathcal{A},\mathcal{P})\) 是一个真实的机制
定理3.5 :一个分配规则 \(\mathcal{A}\) 可以导出一个真实的拍卖机制,当且仅当对于所有的 \(\boldsymbol{t}\in\mathcal{T}\),\(i\in[n]\):
- (1)累积价值 \(v_{i}\left((B,R),\boldsymbol{t}_{-i}\right)\) 在 \(R=R_{i}\) 时关于 \(B\) 是非递减的,并且在 \(B=B_{i}\) 时关于 \(R\) 是非递增的;
- (2)如果 \(v_{i}\left((B_{i},R_{i}),\boldsymbol{t}_{-i}\right)>\lim_{B\to B_{i}^{-}}v_{i}\left((B,R_{i}),\boldsymbol{t}_{-i}\right)\),则
$$
v_{i}\left((B_{i},R_{i}),\boldsymbol{t}_{-i}\right)\geq B_{i}\times R_{i};
$$- 理解:实际上应该是等于号吧?
- (3)如果 \(v_{i}\left((B_{i},R_{i}),\boldsymbol{t}_{-i}\right)>\lim_{R\to R_{i}^{+}}v_{i}\left((B_{i},R),\boldsymbol{t}_{-i}\right)\),则
$$
v_{i}\left((B_{i},R_{i}),\boldsymbol{t}_{-i}\right)\leq B_{i}\times R_{i}.
$$ - 定理3.5的证明 :
- 充分条件方向:可以通过应用定理3.3和3.4来验证
- 必要条件方向:条件(1)直接来自定理3.3。为了证明条件(2),如果 \(v(B_{i},R_{i}) \lt B_{i}\times R_{i}\),则 \(p(B_{i},R_{i})\leq \frac{v(B_{i},R_{i})}{R_{i}} \lt B_{i}\),这与定理3.3在 \(B^{\prime}_{i}\to B^{-}_{i}\)(表示某个 \(B^{\prime}_{i} \lt B_{i}\) 无限接近 \(B_{i}\))时矛盾。条件(3)的分析类似
- 问题:如何理解条件(2)的证明?若 \(v_{i}\left((B_{i},R_{i}),\boldsymbol{t}_{-i}\right) > v_{i}\left((B^-_i,R_{i}),\boldsymbol{t}_{-i}\right)\),则\(p(B_{i},R_{i}) \gt B^-_i = B_i\),进一步有:\( v_{i}\left((B_{i},R_{i}),\boldsymbol{t}_{-i}\right) \geq p(B_{i},R_{i}) \times R_i \geq B_i \times R_i \)
定理3.5完全描述了可行分配规则的条件。在本小节中,论文将进一步利用定理3.5所指示的可行分配规则的结构,为真实拍卖设计提供更多指导
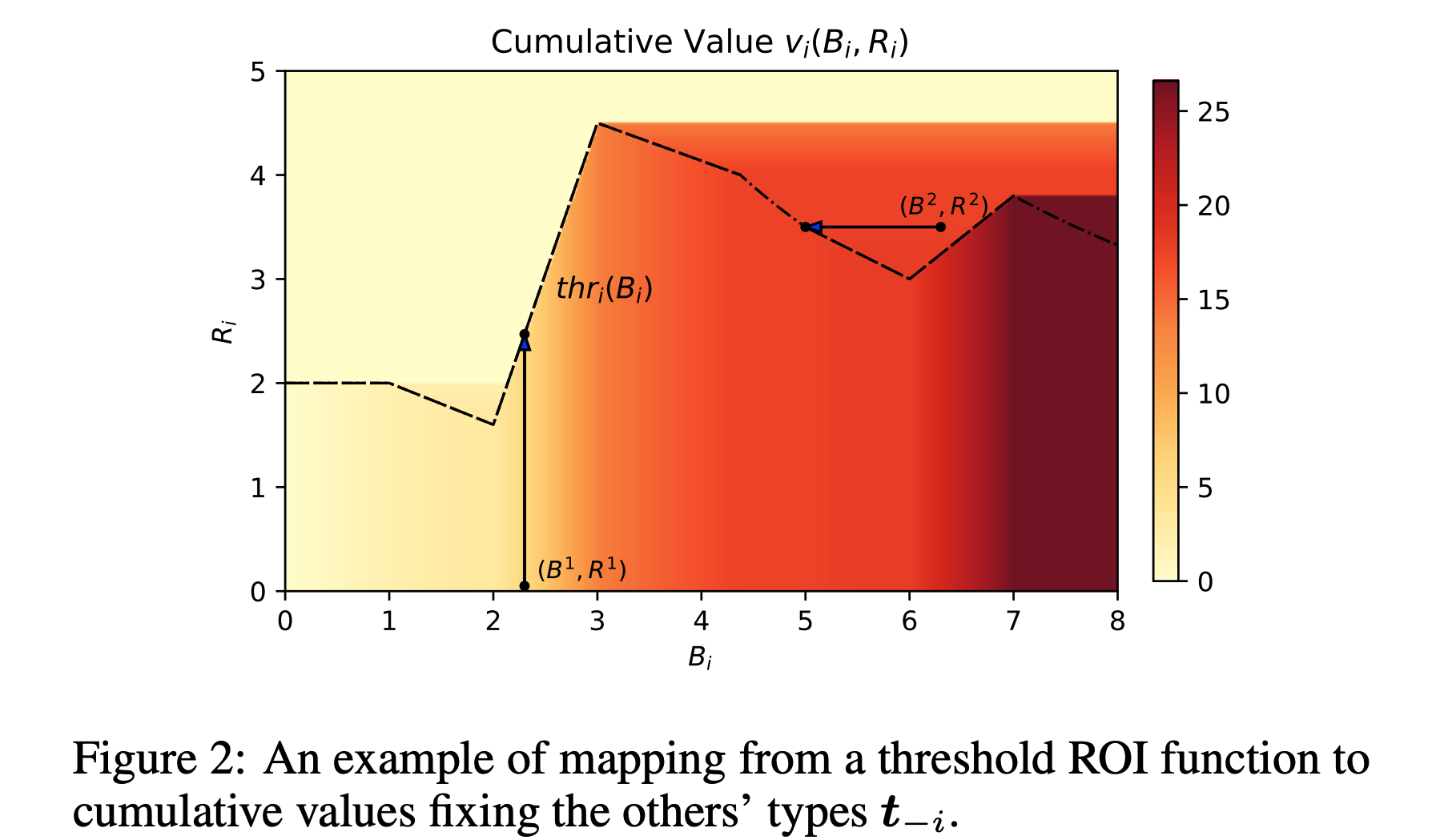
根据定理3.5,累积价值 \(v\) 与项 \(B\times R\) 之间的关系严格描述了该类型是否与其邻近类型共享相同的累积价值,这使论文能够更清晰地表示 \(v\) 的结构。固定预算,随着ROI的减少,分配给该类型的累积价值应增加,注意项 \(B\times R\) 随着 \(R\) 的减少而减少;然而,定理3.5中的条件(3)要求,如果在此过程中累积价值严格增加,则其值不应超过 \(B\times R\) 。因此,必须存在某个阈值ROI,使得增加的累积价值与减少的 \(B\times R\) 相交,并且累积价值不能再增加。基于上述观察,论文定义
$$\operatorname{thr}_{i}(B,\mathbf{t}_{-i})=\sup_{R\in\mathcal{R}_{i}}\left(v_{i} \left((B,R),\mathbf{t}_{-i}\right)\geq B\times R\right)$$- 说明:这里 \(\sup_{R\in\mathcal{R}_{i}}\) 表示 \(\operatorname{thr}_{i}(B,\mathbf{t}_{-i})\) 是一个ROI值
- 如果所考虑的集合非空且有界,否则为 \(0\) 。结果表明,分配给该阈值ROI的累积价值正好是 \(B\times R\)
定理 3.6 \(\forall i\in[n]\) , \(\mathbf{t}_{-i}\in\mathcal{T}_{-i}\) , \(B_{i}\in\mathcal{B}_{i}\) , \(R_{i}\leq\operatorname{thr}_{i}(B_{i},\mathbf{t}_{-i})\) :
$$v_{i}\left((B_{i},R_{i}),\mathbf{t}_{-i}\right)=\operatorname{thr}_{i}(B_{i},\mathbf{t }_{-i})B_{i}.$$然后,我们可以将不同的预算组合在一起,以获得二维类型空间中可行分配的完整特征。由于所有高于阈值ROI的类型的累积价值 \(v \lt B\times R\) ,根据thr函数的定义,它们无法满足定理3.5中的条件(2),因此被迫与具有较小预算的邻近类型共享相同的累积价值
定理 3.7 \(\forall i\in[n]\) , \(\mathbf{t}_{-i}\in\mathcal{T}_{-i}\) , \(B_{i}\in\mathcal{B}_{i}\backslash{0}\) , \(R_{i}>\operatorname{thr}_{i}(B_{i},\mathbf{t}_{-i})\) :
$$v_{i}((B_{i},R_{i}),\mathbf{t}_{-i})=\lim_{B\to B_{i}^{-}}v_{i}\left((B,R_{i}),\mathbf{t }_{-i}\right).$$由于低于(定理3.6)和高于(定理3.7)ROI阈值的类型都已被完全描述,如果给定 \(\operatorname{thr}_{i}(B_{i},\mathbf{t}_{-i})\) 并且 \(\mathbf{t}_{-i}\) 固定,则整个类型空间上的累积价值可以完全定义。论文在图2中提供了一个示例来说明这些特征。对于低于阈值ROI曲线且具有相同预算 \(B\) 的类型(即位于同一垂直线上的类型),它们共享相同的累积价值 \(\operatorname{thr}_{i}(B)\times B\) 。对于曲线上的每个类型,其累积价值等于其具有较小预算的邻近类型的累积价值,直到达到其对应的ROI阈值上的某个类型。这相当于水平向左搜索以找到其对应的ROI阈值上最接近的类型,其中沿此水平搜索的所有类型共享相同的累积价值
论文已经证明,当其他竞拍者的概况固定时,每个可行的二维累积价值函数(其输入为 \((B,R)\) )可以由一维阈值ROI函数(其输入为 \(B\) )表示,但尚不清楚哪些一维阈值ROI函数可以表示可行的累积价值函数。根据定理3.5中的条件(1),当 \(R\) 无限接近于 \(0\) 时,不同 \(B\) 的累积价值应增加,这表明 \(\operatorname{thr}_{i}(B,\mathbf{t}_{-i})\times B\) 需要在 \(B\) 上是非递减的。由于每个从非递减的 \(\operatorname{thr}_{i}(B,\mathbf{t}_{-i})\times B\) 映射的累积价值函数都满足定理3.5,这成为可行 \(\operatorname{thr}_{i}\) 函数的唯一要求
推论 3.8 存在一个双射映射 \(m:\mathcal{G}\rightarrow\mathcal{V}\) ,其中
$$
\begin{align}
(m\circ g)(B,R)=
\begin{cases}g(B) &\text{if }R\leq\frac{g(B)}{B},\\
g\left(\sup\limits_{B^{\prime}\leq B}\left\{R\leq\frac{g(B^{\prime})}{B^{ \prime}}\right\}\right) &\text{otherwise,}\end{cases}
\end{align}
$$- 为了方便表示,论文记 \(g_{i}(B_{i},\mathbf{t}_{-i})=\operatorname{thr}_{i}(B_{i},\mathbf{t}_{-i})\times B_{i}\) 。论文记 \(\mathcal{V}\) 为当 \(i\) 和 \(\mathbf{t}_{-i}\) 固定时的可行累积价值函数空间,即 \(v_{i}:T_{i}\rightarrow\mathbb{R}^{+}\) ,并记 \(\mathcal{G}\) 为非递减函数 \(g:\mathbb{R}^{+}\rightarrow\mathbb{R}^{+}\) 且 \(g(0)=0\) 的空间
- 其中论文定义 \(\sup\varnothing=0\)
- 换句话说,给定任何一维非递减函数且 \(g(0)=0\) ,我们可以通过上述映射过程将其转换为可行的累积价值函数
Truthful 拍卖设计
推导出的可行分配规则的结构引发了一种价值分组现象。从上述给定阈值ROI曲线找到某个类型的累积价值的过程来看,阈值ROI曲线上的每个类型与两组类型共享相同的累积价值:垂直位于其下方的类型,以及水平位于其右侧且高于其对应阈值ROI的类型,如图2所示。这种复杂的价值分组现象是由真实性条件而非优化要求强制执行的。正如论文在图2中所观察到的,由于水平搜索在遇到阈值ROI曲线上的类型时终止,分组形状由不同 \(B_{i}\) 的 \(thr_{i}(B_{i},\mathbf{t}_{-i})\) 的相对排名决定。然而,尽管 \(thr_{i}(B_{i},\mathbf{t}_{-i})\) 需要保持 \(g(B)\) 非递减,但它本身不需要单调,这导致水平搜索的终止和分组形状的不规则。这也使得难以推导出共享相同分配的类型的闭式条件。此外,尽管分组类型的累积价值被迫相同,但它们的支付是根据定理3.4计算的,导致分组类型之间的支付不同,并且收入相对于阈值ROI是非线性的
上述价值分组现象的特征,即分组形状的不规则性和支付的非线性,使得任何分析或数学规划方法都难以采用。为了实现可行且可实施的拍卖设计,论文提出了一类基于新设计的排名分数函数的简单真实拍卖
Truthful 拍卖算法:

- 对于每个 item ,竞拍者根据其虚拟出价 \(b_{i,j}\) 进行排名,虚拟出价定义为 \(v_{i,j}\) 乘以某个预定义的非递增函数 \(f_{i,j}(R_{i})\) 的排名分数(第2行)
- 然后,item 暂时分配给每个具有最高虚拟出价的竞拍者(第3-6行)
- 在确定每个竞拍者 \(i\) 的候选分配集 \(A_{i}\) 后,论文计算竞拍者 \(i\) 在 item \(j\in A_{i}\) 中排名第一的相应ROI要求 \(r_{i,j}\) ,即竞拍者 \(i\) 需要报告 \(R_{i}\leq r_{i,j}\) 以保持在 item \(j\) 中排名第一(第8行)
- 注意,这里使用逆运算和第二高价 \(c_j\) 是为了按照二价计费的思想,计算刚好保证拿到第一位竞胜位置需要的ROI
- 第9行中的关键ROI是论文保证真实性的关键设计,它计算竞拍者可以报告的最大ROI以赢得 \(A_{i}\) 中的足够 item 并花费其预算。直观地说,关键ROI模拟了竞拍者在其预算约束下的最佳响应ROI,这不涉及并因此独立于其真实的ROI约束。论文自然地利用这个关键ROI,它将预算转换为与ROI相同的维度,作为阈值ROI函数,并根据第3节中的真实性条件设计其余部分
- 关键ROI的理解:关键ROI是一个针对预算的虚拟的ROI,即赢得足够多的物品以消耗完预算的最大ROI ,每个用户 \(i\) 都有一个关键ROI \(R_i^c\) ,如果用户按照关键ROI去作为阈值,则对于竞胜所需 \(r_{i,j} \geq R_i^c\) 的 item \(j\) 都会被分配给用户 \(i\)。对于用户 \(i\),要求所有被分配的 item 都按照其价值和关键ROI来售卖 \(p_{i,j} = \frac{v_{i,j}}{R_i^c}\)。最终挑选的关键ROI \(R_i^c\) 是且使得用户总支出收入刚好大于用户设置的预算 \(B_i\) 的最大关键ROI(注意:相同预算下,关键ROI越大,能分配到的 item 就越少 ,所以其他条件不变情况下,预算越小,分配到的 item 越多,关键ROI就越大)
- 第10-11行旨在保证 \(A_{i}\) 中剩余 item 的价值正好等于竞拍者的预算乘以计算的关键ROI(定理3.6)
- 问题:\(d\) 是左边减去右边的差值吗? 【是的】
- 问题:如何理解移除竞胜ROI与关键ROI相等的 item ?【是因为这样可以精准的使得左右两边相等,即剩余 item 的价值正好等于竞拍者的预算乘以计算的关键ROI】
- 问题:清除的 item 卖给谁呢?
- 第12-13行旨在保证ROI大于相应关键ROI的类型将根据其报告的ROI进行分配(定理3.7)并获得所有 \(r_{i,j}\geq R_{i}\) 的 item
- 如果商家设置的ROI小于关键ROI,则说明预算对应的虚拟ROI大于商家ROI,也就是预算时紧约束,需要将小于关键ROI的部分 item 清除出去
- 问题:清除的 item 卖给谁呢?
- 第14行根据定理3.4确定每个竞拍者的支付。由于其低时间复杂度,算法1具有良好的实现可扩展性
定理 4.1 如果预定义的函数 \(f_{i,j}(R)\) 在 \(R\) 上是非递增的,则算法1对应的拍卖机制是真实的
- 论文的证明通过找出并验证算法1的相应 \(g(B)\) 和阈值ROI函数来进行。我们可以根据拍卖目标和广告活动前的先验知识(如竞拍者的类型分布和即将到来的 item 的信息)为竞拍者和 item 设计个性化的 \(f_{i,j}(R)\)
Experiments
- 在本节中,论文使用合成数据进行了实验,以验证论文提出的拍卖机制的性能。(注意:没有真实上线验证)
Experiment Setup
论文进行了两组实验,分别针对独立同分布(i.i.d.)和非独立同分布(non-i.i.d.)的竞拍者。论文通过改变竞拍者和 item 的数量来模拟需求和供应的变化。所呈现的结果是50次运行的平均值。论文根据广告市场中的常见波动选择分布参数,并对 \(v_{i,j}\) 的下界进行归一化
- 对称竞拍者 竞拍者是对称的, \(v_{i,j}\sim U[1,4]\) , \(B_{i}\sim U[40,80]\) , \(R_{i}\sim U[1,3]\) ,其中 \(U[a,b]\) 表示范围 \([a,b]\) 内的均匀分布
- 混合竞拍者 对于 \(v_{i,j}\) 、 \(B_{i}\) 和 \(R_{i}\) ,存在低分布和高分布作为竞拍者的可能类型。具体来说, \(v_{i,j}\sim U[1,2]\) 或 \(v_{i,j}\sim U[2,3]\) , \(B_{i}\sim U[20,40]\) 或 \(B_{i}\sim U[80,100]\) , \(R_{i}\sim U[1,2]\) 或 \(R_{i}\sim U[2,3]\) 。这些类别的组合形成了8组竞拍者
基线拍卖 由于现有的机制无法保证预算和ROI的激励相容性(IC)属性,论文考虑了常见的重复拍卖形式:第一价格拍卖和第二价格拍卖。由于它们的非真实性(见论文的完整版本),论文在这些拍卖中引入了虚假报告
- 重复第一价格和第二价格拍卖 :拍卖者为每个 item 举行第一价格(第二价格)拍卖,竞拍者 \(i\) 对 item \(j\) 出价 \(\frac{v_{i,j}}{R_{i}}\) 。拍卖者将 item 分配给排名最高且有剩余预算支付的竞拍者,并收取第一价格(第二价格)支付。论文通过经典的最佳响应动态模拟竞拍者的虚假报告行为,以真实概况为起点。在重复第一价格(第二价格)拍卖中,竞拍者没有动机虚假报告其预算。论文计算最佳响应ROI为在历史拍卖中实现最高效用的最小ROI
- 非真实最优基线 :通过线性规划可以计算出最优离线收入,其中论文将每个竞拍者 \(i\) 对 item \(j\) 的支付设置为 \(\frac{v_{i,j}\times a_{i,j}}{R_{i}}\) ,并且其总支付不超过 \(B_{i}\)
评估指标 论文考虑收入和社会福利作为优化目标。由于定理3.4中的支付公式(Eq.2)与方程(Eq.1)中社会福利的定义一致,当没有竞拍者获得负无穷效用时,收入和社会福利的指标将相同,因此论文将在结果中仅报告收入。此外,由于广告主在不同时间段内的拍卖表现可能波动,公平性也应被考虑,以保持竞拍者参与拍卖的意愿。使用社会福利替代传统的估值函数,公平性定义为
$$\text{fairness}=\min_{i\in[n]}\min\left(\frac{v_{i}(\boldsymbol{t}^{\prime})}{R_{i}},B_{i}\right).$$排名分数函数 论文采用形式为 \(f_{i,j}(R)=\alpha_{i,j}\times e^{-\beta R}\) 的排名分数,其中 \(\alpha_{i,j}\) 从修正的正态分布 \(N(\mu_{i},\sigma_{i}^{2})\) 中抽取, \(\beta,\mu_{i},\sigma_{i}\) 是预设参数。在 \(f(R)\) 中, \(\beta\) 用于调整ROI对等效出价的影响, \(\alpha\) 保持不同竞拍者的排名分数在可比范围内。由于当某些竞拍者赢得过多 item 时, item 可能会被丢弃(算法1中的第13行),为了避免社会福利和收入的损失,论文应在供应充足时为其他竞拍者提供非平凡的获胜机会,这是通过 \(\alpha\sim N(\mu_{i},\sigma_{i}^{2})\) 中的随机性提供的。对于每个自动出价环境,论文为遵循相同分布的竞拍者设置相同的排名分数函数参数,并选择在该环境中收入较好的参数
实验结果
- 实验结果如下:
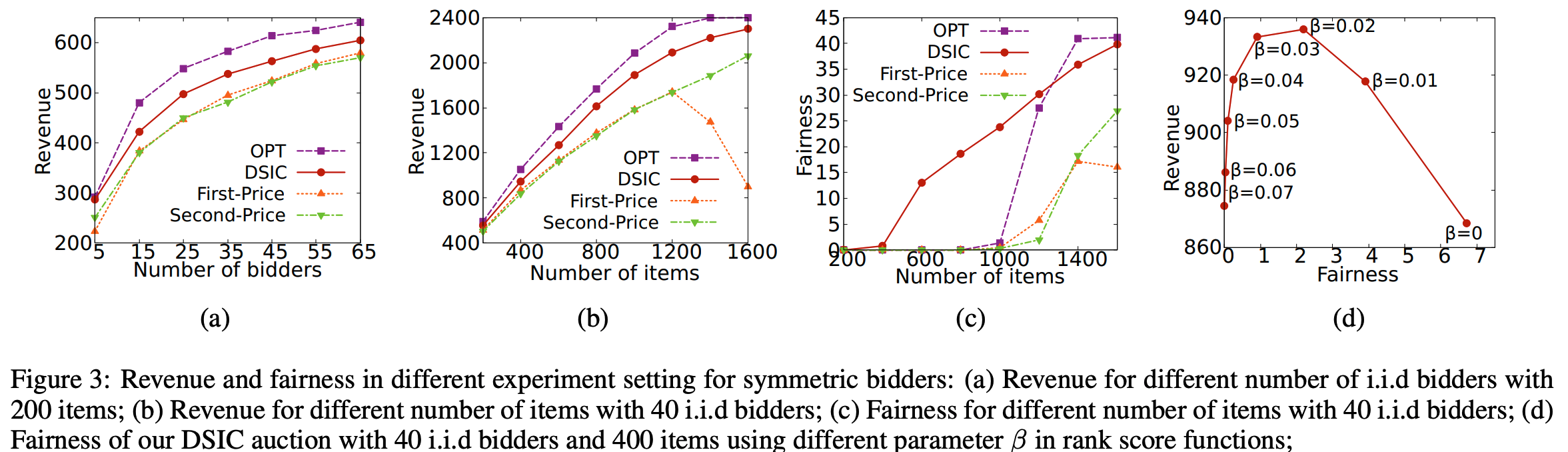
- 对称竞拍者 :Figure 3(a)报告了论文的真实拍卖(称为DSIC)和基线拍卖在不同竞拍者数量下的收入,Figure 3(b)报告了 item 数量变化时的收入。论文的真实拍卖比第一价格和第二价格拍卖实现了更好的收入,并且通常实现了接近最优基线90%以上的收入。值得注意的是,当 item 过多时,第一价格拍卖的收入明显下降,这也导致了公平性的下降(Figure 3(c))。这是因为竞拍者在面对一些低价未售出的 item 时过度增加了其报告的ROI,导致所有支付按比例减少。在Figure 3(c)中,论文报告了在固定40个竞拍者的情况下,不同 item 数量下的公平性结果,如Figure 3(b)所示。正如排名分数函数中所设计的,论文的拍卖不会将过多的 item 分配给某个竞拍者,以避免 item 浪费,因此在 item 数量在600到1200之间时,比最优基线实现了更好的公平性。当 item 短缺时(Figure 3(c)中的200/400个 item ),论文的真实拍卖由于追求收入而在一定程度上损害了公平性。我们可以通过不同的排名分数函数参数 \(\beta\) 来控制公平性和收入之间的权衡。Figure 3(d)报告了在400个 item 的情况下,不同 \(\beta\) 的一组收入和社会福利表现。为了实现更高的收入,不可避免地会在不同竞拍者之间进行歧视性分配,并在 item 不充足时损害公平性
- 混合竞拍者 :论文展示了在非独立同分布设置中选择适当排名分数函数的重要性。论文选择了三组排名分数函数,分别在三种典型设置中表现良好:40个混合竞拍者,200/1000/1600个 item ,并在其他两种设置中测试它们的表现。结果如图4所示,其中DSIC- \(n\) 表示在设置 \(n\) 中表现良好的真实拍卖。DSIC-n机制仅在设置 \(n\) 中表现良好,原因应来自于实现高收入所需的不同分配方法。例如,为了在 item 短缺时实现高收入(设置1),DSIC-1拍卖将大多数 item 分配给具有高价值和低ROI的竞拍者,导致在设置2和3中将这些竞拍者分配过多的 item 而忽略其他竞拍者
附录:思考
- 智能出价中保成本技术是否还需要?
- 答案是不需要。当前这种拍卖方式下,并不需要使用控制算法去保成本,假定预估值足够准确的情况下,按照 \(v_{i,j} \times f_{i,j}(R_i)\) 反算对应位置上的出价即可,这里常见是使用 \(v_{i,j} \times \frac{1}{R_i}\) 作为出价公式
- 是否有部分 item 无法卖出去?
- 目前看是的,特别是当广告主的 ROI和关键ROI(即预算) 之间差异较大时